In vitro cell cycle oscillations exhibit a robust and hysteretic response to changes in cytoplasmic density

Significance

The cytoplasm, where most cellular reactions occur, has a variable density. We currently lack an understanding of how density variations affect cellular functions because of the challenge of controlling it experimentally. Here, we systematically modulate the density of an in vitro cytoplasm using microfluidics and analyze how the cell cycle behaves in turn. We found that mitotic cycles maintain their function across 0.2× to 1.2× of the natural density. Higher densities arrest cell cycles, and dilution recovers oscillations. However, the density at which cycles reappear is lower than the natural density. This behavior suggests a history-dependent mechanism called hysteresis, common in physics, chemistry, and engineering. Our approach paves the way for studying the responses of other processes to density changes.

Abstract

Cells control the properties of the cytoplasm to ensure proper functioning of biochemical processes. Recent studies showed that cytoplasmic density varies in both physiological and pathological states of cells undergoing growth, division, differentiation, apoptosis, senescence, and metabolic starvation. Little is known about how cellular processes cope with these cytoplasmic variations. Here, we study how a cell cycle oscillator comprising cyclin-dependent kinase (Cdk1) responds to changes in cytoplasmic density by systematically diluting or concentrating cycling Xenopus egg extracts in cell-like microfluidic droplets. We found that the cell cycle maintains robust oscillations over a wide range of deviations from the endogenous density: as low as 0.2× to more than 1.22× relative cytoplasmic density (RCD). A further dilution or concentration from these values arrested the system in a low or high steady state of Cdk1 activity, respectively. Interestingly, diluting an arrested cytoplasm of 1.22× RCD recovers oscillations at lower than 1× RCD. Thus, the cell cycle switches reversibly between oscillatory and stable steady states at distinct thresholds depending on the direction of tuning, forming a hysteresis loop. We propose a mathematical model which recapitulates these observations and predicts that the Cdk1/Wee1/Cdc25 positive feedback loops do not contribute to the observed robustness, supported by experiments. Our system can be applied to study how cytoplasmic density affects other cellular processes.

Robustness, the ability to maintain function despite environmental perturbations, appears ubiquitous across many areas of biology. Processes as diverse as bacterial chemotaxis, osmoregulation, circadian rhythms, and development have been found insensitive to certain conditional changes over a wide range of magnitudes (1–4). Rather than requiring the precise tuning of parameters, studies have attributed the stability of their functioning to a robust property of their underlying biochemical networks.

At the cellular level, biochemical reactions take place in the cytoplasm, a highly complex and dynamic environment. Activities including synthesis, degradation, nucleocytoplasmic translocation, osmosis, endocytosis, and exocytosis may all impose perturbations to the state of a eukaryotic cytoplasm. It is crucial to understand how the cytoplasmic properties vary and how the internal processes respond to these fluctuations and remain functioning correctly.

Recent advances in precise cell density measurement, particularly by the suspended microchannel resonator, fluorescence exclusion method, and quantitative phase microscopy, have revealed significant changes in the overall cytoplasmic density throughout the cell cycle (5–8). Different mammalian cell types display a common phenomenon of mitotic swelling with a significant volume increase (10 to 30%) and a constant dry mass, resulting in a drop of cell density during mitosis (7, 8).

Additionally, it has been shown that large deviations from the physiological range of cytoplasmic density can induce detrimental cell states such as senescence and apoptosis (9–13). Interestingly, some processes remain unaffected despite considerable variations in the density. For example, after a 25% loss of intracellular water, glucose metabolism in rat liver cells shows no noticeable change in its reaction rates (14). In contrast, changes in macromolecular concentrations are known to modify biochemical reaction kinetics through the effects of crowding (15–17). For instance, osmotic compression of yeast cells, which concentrates cytoplasmic components, triggered a slowdown of signaling cascades, protein mobility, endocytosis, and vesicular trafficking (18). Increased crowding in the cytoplasm to a high level was also reported to reduce the mobility of macromolecules and induce a liquid-to-glass transition in bacterial and yeast cytoplasm and Xenopus extracts (19–22). Thus, cells must tolerate some degree of cytoplasmic density changes but can respond to severe deviations from the physiological state. Although the cytoplasmic density has gained increasing recognition as an essential parameter in controlling proper cellular function, it remains unclear how fundamental cellular processes such as the cell cycle behave under variations in cytoplasmic density thereof.

Computational studies have demonstrated the capability of cell-cycle networks to perform robust functions. The yeast cell-cycle network shows persistent dynamical properties against small perturbations to the network topology (23). Another study associated the positive-plus-negative feedback architecture at the core of the embryonic cell-cycle network with increased robustness to changes in the system’s parameters (24). However, no computational or experimental work exists to date that shows how the cell-cycle network would react to dilution or concentration of its components as the cytoplasm fluctuates. It is also experimentally challenging to flexibly manipulate the cytoplasmic density in live cells without impairing other essential functions.

Here, we address this question by analyzing how in vitro cell cycle dynamics change with the density of Xenopus cell-free cytoplasmic extracts in a microfluidic droplet system. We used programmed pressure-driven control of inlet flow in a microfluidic device to generate droplets encapsulating extracts with different dilution factors. We then measured the period and persistence of oscillations in these droplets using a cyclin-dependent kinase (Cdk1) activity fluorescence resonance energy transfer (FRET) sensor. We found that cell cycle oscillations withstand both dilution and concentration for an extensive range of cytoplasmic densities. We further developed a mathematical model to investigate the role of cytoplasmic density in the oscillatory behavior of the cell-cycle network. Finally, we explored whether Wee1 and Cdc25, the key components underlying the positive-plus-negative feedback architecture, are necessary for the robustness of the cell cycle to cytoplasmic density changes. We noticed that modulating these feedback strengths changes the total number of cycles, revealing a role of Wee1 and Cdc25 in controlling the cycle number of early embryonic extracts.

Results

In Vitro Cell Cycle Oscillations Are Robust to Cytoplasmic Dilutions.

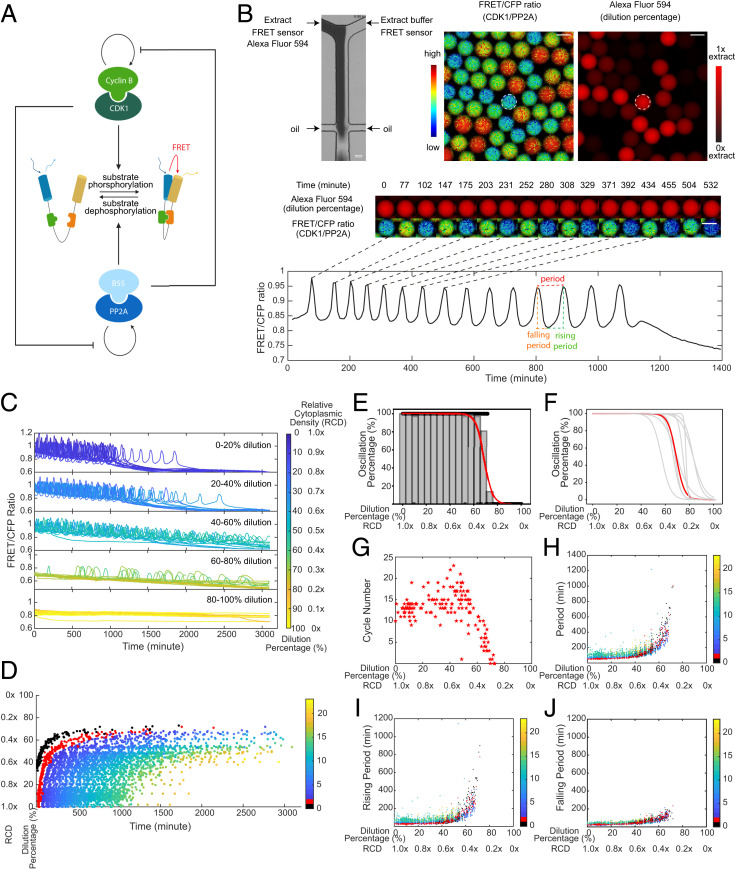
We first reconstituted mitotic oscillations in vitro using cycling Xenopus cytoplasmic extracts. The system periodically alternates between interphase and mitotic phases via a self-sustained cell-cycle oscillator centered on the Cdk1. The phosphorylation–dephosphorylation cycle of mitotic substrates is coregulated by the protein kinase Cdk1–cyclin B and its antagonistic phosphatase PP2A-B55δ, which mutually regulate each other's autoactivation loops (Fig. 1A). To measure the activity ratio between Cdk1–cyclin B and PP2A-B55δ in extracts, we applied a recently developed Cdk1 FRET sensor (25), which contains a mitotic substrate Cdc25C-ligand domain and a proline-directed tryptophan–tryptophan (WW) phospho-binding domain. When extracts are in a high Cdk1–cyclin B activity state, phosphorylated groups on the Cdc25C-ligand domain are detected by sensing the WW domain, bringing the donor, cyan fluorescent protein (CFP), and the acceptor, yellow fluorescent protein, in proximity for energy transfer.

Fig. 1.

In vitro cell-cycle oscillators are robust to cytoplasmic dilutions. (A) Schematic diagram of the phosphorylation and dephosphorylation cycles of mitotic substrates driven by kinase, Cdk1–cyclin B, and its counteracting phosphatase, PP2A-B55δ, which mutually modulate each other’s auto-activation loops. The full diagram for the cell-cycle oscillator is in Fig. 3A. A Cdk1 FRET sensor is used to measure the ratio of Cdk1–cyclin B to PP2A:B55δ activity throughout oscillations. (B) FRET-based quantification of cell-cycle dynamics in microemulsion droplets containing 0 to 100% diluted Xenopus extracts. (Top Left) A microfluidic device generates droplets containing extracts and extract buffer mixed at different ratios. The extracts supplied with Alexa Fluor 594 Dextran dye flow through one inlet and the extract buffer through the other, both containing the same concentration of the Cdk1-FRET sensor. The diluted extracts are then encapsulated by surfactant oil into uniform-sized microemulsion droplets. (Top Right) Snapshots of FRET/CFP ratio and Alexa Fluor 594 Dextran channels for a field of droplets indicating the ratio of Cdk1/PP2A activity and the dilution percentage. (Middle) Time-lapse series of a selected droplet showing the first 550-min imaging in both channels. Selected time points correspond to either a peak or trough in FRET/CFP signals. The droplet has a constant red fluorescence intensity over time, indicating no leakage of the dye. (Scale bar, 100 μm.) (Bottom) Time course of FRET/CFP ratio of the selected droplet showing 15 undamped oscillations in 1,400 min. The oscillation period is quantified as the time interval between two consecutive peaks. The rising period (interphase duration) is defined as the time interval between a trough to the subsequent peak and the falling period (duration of mitosis) as the time interval between a peak to the subsequent trough. (C) Time courses of FRET/CFP ratio for droplets with 0 to 100% diluted extracts show the cell-cycle robustness to cytoplasmic dilutions. Each line represents a droplet, and the color of the line indicates the dilution percentage (RCD) of the droplet. The cytoplasmic density of undiluted droplets (dilution 0%) is defined as 1.0×. A total of 20 droplets are randomly selected from each dilution range and presented in the plot. In both C and D, t = 0 represents the start of imaging which was typically 1 h after extract preparation. (D) Raster plot showing peak times of FRET/CFP ratio as a function of dilution. The entry of the first cycle is significantly delayed as dilution percentage increases, and the overall oscillation time (from the start of the first peak to the last peak) is extended as well. Each dot represents a cycle peak in a droplet. The color bar indicates the order of peaks in time. The first peak observed in undiluted extracts is labeled in red and noted as cycle 1. Because of delays caused by dilution, a previous peak can be observed for some droplets with high levels of dilution which we note as cycle 0 (labeled in black). Cycle 0 is not observed in undiluted extracts because of the 1-h gap between extract preparation and the start of imaging. (E) Oscillation percentage of droplets over different dilution ranges. Oscillation percentage is calculated as the percentage of droplets that exhibit oscillations in all tracked droplets within each bin range. The bin width in the histogram is five. The red curve is the logistic regression fitting result for oscillation percentage data. This dataset includes 655 detected droplets in which 351 droplets yield oscillations. (F) Logistic regression fits for oscillation percentage versus dilution for nine replicates, showing the cell cycle robustness to dilutions is highly conserved across all different day experiments. The red highlighted curve corresponds to the experiment in E. (G) The cycle number versus dilution of individual droplets presents an initial plateau within low-moderate dilution ranges and subsequently decreases as a function of dilution. Cycle number for each droplet was quantified by a total number of peak-to-peak FRET/CFP oscillations. (H) Oscillation periods remain relatively constant up to 50% dilution and afterward increase dramatically with dilution until the dilution is close to 80%. Similar trends are observed in (I) rising periods and (J) falling periods. Each dot indicates one cycle in a droplet. The color bar represents the order of cycles.

To study the effect of cytoplasmic dilution on cell cycles, we encapsulated cytoplasmic extracts into water-in-oil microemulsions (26, 27) and employed a microfluidic device with two inlets to perform dilutions. Programmed pressure-driven control of the flow through the inlets continuously adjusts ratios of cytoplasmic extract and extract buffer in individual droplets, resulting in a full spectrum of cytoplasmic dilution from 0 to 100% (1.0 to 0× relative cytoplasmic density [RCD]) (Fig. 1 B, Top). Each droplet was supplied with 1 μM Cdk1 FRET sensor to track the oscillation progression and a fluorescent dye (Alexa Fluor 594) that coinjects with the extracts into one inlet to quantify the dilution percentage. These droplets were loaded into Teflon-coated glass tubes, recorded for up to 3 d using time-lapse fluorescence microscopy, and analyzed for their FRET/CFP ratio time courses to extract oscillation parameters (Fig. 1 B, Middle and Bottom and Movie S1).

Surprisingly, droplets retained oscillations for dilutions as large as 80% (0.2× RCD) (Fig. 1C). The overall waveform was invariant up to 40% dilutions (0.6× RCD), with the remaining range from 40 to 80% showing longer rising and falling phases. Nevertheless, the system settled into a stable steady state of Cdk1 in the range of 80 to 100% dilution. We recapitulated these trends in a raster time series of oscillation peaks of all individual droplets sorted by their dilution percentage (Fig. 1D). This further revealed that the start and end of oscillations in each droplet were also dilution dependent. As the dilution percentage increases, both the entry of the first peak and the peak time of the last cycle were delayed, resulting in an overall longer time window of oscillation. The phenomenon was more pronounced when extracts were greatly diluted (dilution by more than 40% or RCD below 0.6×).

To quantify the impact of cytoplasmic dilution on mitotic oscillations, we calculated the percentage of oscillatory droplets within each dilution range (Fig. 1E). Between 0 and 60%, all tracked droplets showed oscillations. Close to 80%, the oscillation percentage dropped abruptly to zero. This observation was well conserved across nine independent experiments (each performed on a different day), except for slightly different absolute half-maximal thresholds (defined by the dilution percentage at which 50% of the droplets oscillate), which are likely due to batch variations in Xenopus egg extracts (Fig. 1F). These results demonstrate oscillation robustness to cytoplasmic dilution.

Additionally, we observed that the total number of cycles in each droplet displayed an initial plateau followed by an abrupt decrease near 50% dilution (0.5× RCD) (Fig. 1G). We also analyzed three other properties of the oscillations, namely the total period (Fig. 1H), rising period (duration of interphase) (Fig. 1I), and falling period (duration of M phase) (Fig. 1J). The total period of oscillations remained relatively unchanged until 50% dilution when it increased abruptly. The rising and falling periods followed a similar trend as the total period, although the rising periods showed a greater fold change at a given dilution than the falling ones (SI Appendix, Fig. S1). This differential sensitivity of rising and falling phases to variations has been previously reported in other studies in which mitosis seems temporally insulated from variability in other cell-cycle events (28, 29). In addition, we observed batch variations in the period and cycle number responses to dilution across different day experiments (SI Appendix, Fig. S2), emphasizing the influence of the initial egg conditions on the robustness of mitotic oscillators. Nevertheless, the overall trend in the period was conserved for all replicates. Together, these results indicate that the system not only is robust in its ability to oscillate but maintains invariant oscillation profiles for a broad range of dilutions.

To test whether the behavior near the transition threshold could be solely explained by partitioning variability during encapsulation, we generated droplets with two different diameters of 83.18 ± 2.21 and 55.29 ± 1.83 μm (SI Appendix, Fig. S3A). If the halt of oscillations was caused by the uneven distribution of cytoplasmic material, smaller droplets would be more impacted by partition errors and display a lower oscillation threshold and a larger variation in the high dilution regions. However, we did not observe a significant difference between the two cases when we compared their oscillation percentage curves (SI Appendix, Fig. S3B), distribution of period lengths (SI Appendix, Fig. S3C), and total cycle numbers (SI Appendix, Fig. S3D). Thus, the behavior of the system near the transition threshold was likely inherent to the response of the mitotic circuit to changes in cytoplasmic density rather than caused by an uneven distribution of cytoplasmic material. In all dilution experiments, we used the extract buffer as opposed to water for dilutions to maintain the ionic strengths and osmolality, as these are essential for the system to function properly (SI Appendix, Fig. S4).

Cytoplasmic Concentration Leads to a Reversible Loss of Oscillation and Displays Hysteresis.

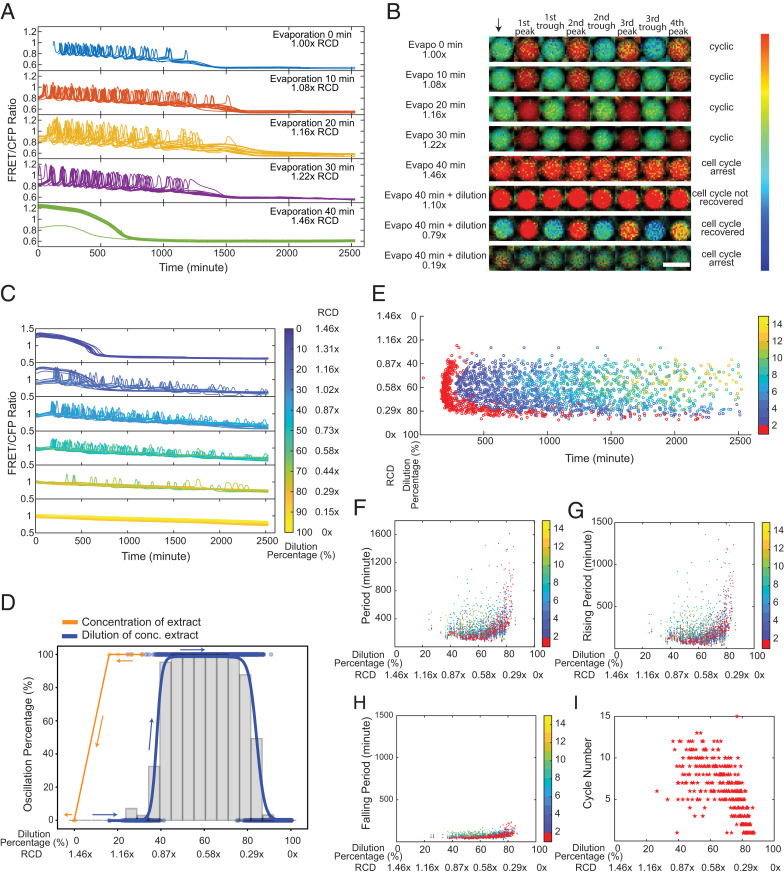
Next, we investigated the effect of concentrating the cytoplasm by vacuum evaporation of the bulk cycling Xenopus extract before encapsulation. We used the fluorescent intensity changes of Alexa Fluor 594 to quantify the resultant relative cytoplasmic density after concentration, confirmed by other measurements using Nanodrop or by estimating the loss of volume (SI Appendix, Table S1). We found the system sustained oscillations with no noticeable change for evaporation time up to 30 min (1.22× RCD) (Fig. 2 A and B, rows 1 to 4 and Movie S2). When further concentrating the extract for 40 min (1.46× RCD), the system settled to a steady state (Fig. 2 A and B, row 5). The results suggested a threshold of RCD between 1.22 and 1.46×, beyond which the cell cycle arrests, and in this case, at a high stable state of Cdk1 compared to the stably low Cdk1 activity for a highly diluted system (Fig. 1C, row 5). These two distinct Cdk1 steady states imply that the two cytoplasmic density extremes may differentially affect the mitotic entry or exit to cause the system to arrest either at interphase or the mitotic phase.

Fig. 2.

Cytoplasmic concentration leads to a reversible loss of oscillation but displays hysteresis. (A) Time courses of FRET/CFP ratio for individual droplets with concentrated extracts, showing cell cycles are robust to cytoplasmic concentrations. Extracts are concentrated via vacuum evaporation with the resultant relative cytoplasmic densities quantified by the intensity changes in Alexa Fluor 594 dextran dye before and after the concentration process. We define the cytoplasmic density of undiluted extracts as 1×, and the RCD for extracts with 10-, 20-, 30-, and 40-min evaporation are measured to be 1.08, 1.16, 1.22, and 1.46×, respectively. For ease of visualization, oscillation profiles of 20 droplets are randomly selected from each condition and presented in the plot. The sample size for different conditions (from Top to Bottom) is 46, 471, 140, 98, and 506, respectively. (B) FRET/CFP ratio images of representative droplets with varying cytoplasmic densities by initial concentration (from the first row to the fifth row) then dilution (from sixth row to eighth row), which demonstrates dilution of nonoscillatory concentrated extracts restores oscillations. The arrow indicates the start of imaging. Each following image is associated with either a trough or a peak of the selected droplets. (Scale bar, 100 μm.) The color bar indicates the FRET/CFP ratio as bright red corresponds to a high FRET/CFP ratio and dark blue corresponds to a low FRET/CFP ratio. The data for dilutions of concentrated extracts contains two replicates, resulting in a sample size of 1,198 detected droplets and in which 538 droplets have at least one cycle. (C) Time courses of FRET/CFP fluorescence intensity ratio in droplets containing 1.46× concentrated extracts with different dilutions, showing clear transitions from a high Cdk1 activity arrested state to oscillations to a low Cdk1 state. Each line is for one droplet, and the color of the line indicates the dilution percentage of the droplet. A total of 20 droplets are shown for each dilution range. Here, zero dilution has 1.46× RCD. (D) Cell cycle shows a hysteretic response to the change of cytoplasmic density. The change in oscillation percentage follows the orange curve when we concentrate the cytoplasmic density from 1.00 to 1.46×. When we start to dilute the concentrated extracts at 1.46× RCD, the oscillation percentage changes along the blue curve. These two distinct paths show a “history-dependent” nature. Histogram bars are measured oscillation percentage within each 5% dilution range as we dilute the 1.46× RCD extracts. (E) Raster plot for the dilution of concentrated extract experiment. The first peak onset has larger variations for droplets lying at the highly diluted threshold end (∼80%). The color bar indicates the order of cycle peaks, and the peak of the first cycle is highlighted in red. (F) Periods remain relatively constant at moderate dilutions after restoring oscillations (following the blue curve in D) with the RCD ∼0.80 to 0.44×. The variations are significant near two ends, especially the diluted end (0.29× RCD). Similar trends are observed in (G) rising periods and (H) falling periods. Each dot represents a cycle in a droplet. The color bar indicates the order of cycles, and the first cycle is highlighted in red. (I) Droplets with moderate dilutions have more cycles than those with either too low or too high dilution percentages at two ends.

Interestingly, as we diluted the cell-cycle–arrested extract (1.46× RCD) with extract buffer by using the same two-inlet microfluidics, oscillations reappeared, and we observed a clear transition from a stable high Cdk1 steady state (1.10× RCD, Fig. 2B, row 6) to limit cycle oscillations (0.79× RCD, Fig. 2B, row 7) to an arrested state again with stable low Cdk1 activity (0.19× RCD, Fig. 2B, row 8) as the dilution increases (Fig. 2C and Movie S3). Thus, the oscillatory behavior can be modulated in a reversible manner by cytoplasmic density. Additionally, by diluting the 1.46× concentrated extract, the oscillation percentage of droplets recovered from 0 to 100% around 40% dilution (0.87× RCD) and then back to 0% at a higher dilution (0.29× RCD) (Fig. 2D, blue curve), defining the two boundaries of the distribution throughout the entire dilution range. Compared to the threshold to stop oscillations (between 1.22 and 1.46× RCD) when concentrating the extracts (Fig. 2D, orange curve), the same system could not restore oscillations by dilution until a significantly lower threshold of about 0.87× RCD. Therefore, the transitions between the two states (i.e., an oscillatory state and a high Cdk1 stable steady state) did not follow the same path the system follows in the opposite direction, suggesting the system may have a persistent memory of the past, a characteristic of hysteresis. This hysteretic response is likely an intrinsic property of the system, as opposed to an artifact from the nonisotonic initial and final states caused by the evaporation of water followed by dilution with the extract buffer, since we observed a similar behavior when diluting the evaporated extracts by water (SI Appendix, Fig. S5).

We also observed high variations in the time of the first peaks near the two boundaries, 0.87 and 0.29× RCD (Fig. 2E, red). The variation was the largest among droplets of low density (near 0.29× RCD) as also observed for highly diluted extracts in Fig. 1D. By contrast, the droplets with intermediate RCD (0.80 to 0.44×) showed oscillation peaks at relatively similar times. We observed a similar trend for the total period (Fig. 2F), rising period (Fig. 2G), and falling period (Fig. 2H), which varied the most at the boundaries. The total number of cycles reached a maximum when the RCD was ∼0.80 to 0.44× and decreased at both ends of cytoplasmic densities (Fig. 2I). These results suggest a lower tendency of the system to oscillate near two boundaries as evidenced by the oscillation percentage (Fig. 2D, blue curve).

Mathematical Modeling Recapitulates the Robustness to Changes in Cytoplasm Density and its Hysteretic Response.

To explore the mechanisms behind the observed robustness, we developed a mathematical description of the density effects on cell-cycle dynamics. We started from a previously published model of Xenopus early embryonic cycles that describes the dynamics of the network’s two master regulators (Cdk1-cyclin B1 and PP2A-B55δ) (30). Fig. 3 A, Top shows a diagram of the principal biochemical reactions and the influence between proteins. Briefly, cell cycles are driven by the synthesis and regulated degradation of cyclin B1. Additional layers of control provide bistability to the activity of the master regulators: kinase Cdk1–cyclin B1 complexes switch between a high and low state because of the positive feedback regulation of Cdc25C and Wee1A; similarly, the phosphatase PP2A-B55δ alternates between high and low activity because of the positive feedback regulation created by Greatwall kinase and the stoichiometric inhibitor alpha-endosulfine. The pathways of both master regulators are interconnected through mutual inhibition of each other's positive feedback. When Cdk1–cyclin B1 reaches its high activity state, proteolytic degradation of cyclin B1 is activated in an ultrasensitive way through the activated anaphase-promoting complex/cyclosome by Cdk1. Cyclin B1 degradation restarts the system for a new cycle.

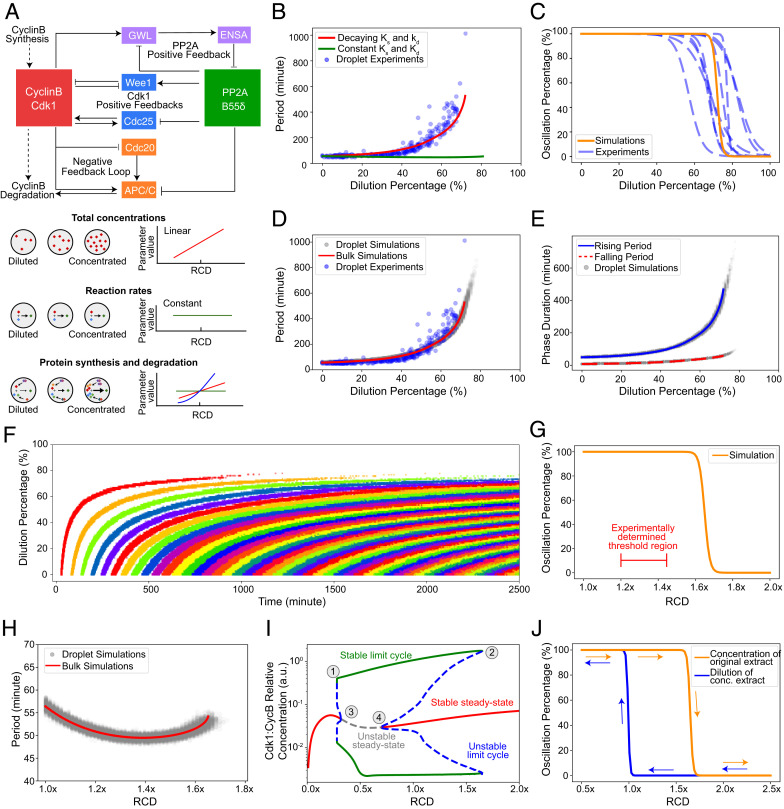
Fig. 3.

Dynamic model of the cell cycle reproduces the observed robustness of oscillations and the hysteretic response to cytoplasmic density. (A) Schematic view of the network controlling cell-cycle progression and dependency of parameters with cytoplasmic density. (Top) Each solid arrow corresponds to an influence present in the model. Pointed-headed arrows indicate activation and blunt-headed arrows inhibitions. Activation/inhibitions arise from phosphorylation/dephosphorylation reactions or binding/unbinding events. Dashed arrows represent synthesis and degradation processes. (Bottom) Different dependencies with cytoplasmic density are assumed for the parameters of the model. Total concentrations of proteins are considered to scale linearly with cytoplasmic density. In contrast, phosphorylation/dephosphorylation and binding/unbinding rates are considered to be constant because they are considered elementary reactions. Dependency of synthesis and degradation rate on cytoplasmic density are more complex, as many reactions underlie their effective reaction rate and are thus determined by comparing model predictions with experimental observations. (B) Period of oscillations as a function of dilution percentage. Comparison between models with decaying or constant synthesis/degradation rates. The decaying model has k_s ∼ d³ and k_d ∼d² with d the RCD. Both models include a linear scaling of total concentrations with dilution. The model without decaying rates does not feature an increase in periods consistent with experimental observations. (C) A sigmoidal fit to the simulated oscillation percentage of droplets versus dilution is shown as a solid orange curve. Experimental curves (dashed blue line) are repeated from Fig. 1F for comparison. At a threshold of close to 80%, most droplets settle into a steady state consistent with experimental observations. (D) Simulated period as a function of dilution for droplet (gray dots) and bulk (red line) models. Bulk simulations are performed with a single set of ODE parameters representing the droplet's average parameters. Experimental data (blue dots) is presented for comparison. Both simulated and experimentally determined periods follow a similar trend with a slow increase at first and a sudden increase close to the threshold. (E) Duration of the rising and falling phases of the oscillation. Solid blue and dashed red lines represent bulk simulations for rising and falling periods, respectively. Dots represent droplet simulations. For both types of simulations, the rising period is more affected than the falling period. (F) Raster plot of the oscillation peaks over time for different dilution values. Each cycle is colored differently for visual clarity. Simulations show a similar trend for the start of oscillations observed in experiments. (G) Oscillation percentage from droplet simulations when the RCD is increased. The experimentally determined threshold is smaller than the one obtained through simulations. (H) Period as a function of RCD for concentration of extracts. Bulk and droplet simulations are shown. For the concentration of the extract, the period remains comparatively constant with respect to dilution. (I) Bifurcation diagram with RCD as a control parameter. Vertical axis shows the maximum and minimum of Active Cdk1:CyclinB1 concentration. Stable dynamical states are represented by solid lines and unstable ones by dashed lines. Each color represents a different dynamical behavior. The stable limit cycle solution disappears through a saddle-node bifurcation by meeting with an unstable limit cycle solution (1, 2). Two supercritical Hopf bifurcations (3, 4) are observed for both concentration and dilution of the extract. This bifurcation structure leads to a hysteretic behavior in the appearance/disappearance of oscillations. (J) Hysteresis in the onset of limit cycle oscillations. Two different initial conditions are used for the simulations of each curve: one that is closer to the limit cycle and another one closer to the steady state in the concentrated extract.

Modifying cytoplasmic density alters the kinetics of a system at the molecular level (5). We considered possible changes to the underlying parameters that govern the biochemical reactions of the system (Fig. 3 A, Bottom). Here, we introduced a single scaling factor in our model to characterize changes in cytoplasmic density and scale all parameters appropriately. We first assumed the macromolecular concentrations scale linearly with the cytoplasmic density. Second, we assumed that the rates of fundamental reactions such as phosphorylation/dephosphorylation and binding/unbinding events are not directly affected by changes in the cytoplasmic density. Nevertheless, it is important to note that phosphorylation/dephosphorylation and binding/unbinding reactions will be indirectly affected by changes in the total concentration of the reactants. This indirect effect was taken care of via the scaling of total concentrations but not directly through modifications of the reaction rates. Lastly, two major processes (i.e., synthesis and degradation of cyclin B1) involve multiple proteins and complex interactions and are likely to be affected by changes in cytoplasmic density. However, the detailed reactions such as ribosome–messenger RNA (mRNA) interactions and ubiquitin–proteasome pathways are not explicitly modeled in our present level of description. To obtain an appropriate scaling function for both the synthesis and degradation rates, we simulated the change in the period as a function of cytoplasmic dilution with different polynomial scaling of both rates (SI Appendix, Fig. S6 and Text S2). For our model to describe the data appropriately, we found that the parameters associated with the synthesis and degradation of cyclin B1 need to decay with dilution. When this decay is considered, oscillations remain up to 80%, and the period increases abruptly after 60% as observed experimentally (Fig. 3B and SI Appendix, Fig. S7 and Text S2). A model in which only total concentrations decay with dilution does not explain the experimental trend (Fig. 3B, green curve). Note that all models in Fig. 3 assumed the rates of phosphorylation/dephosphorylation, and binding/unbinding reactions do not explicitly change with the cytoplasmic density, which is generally reasonable for a system without crowding. As we detailed in Discussion, macromolecular crowding may require us to release the constraint and allow these rates to decay with dilution (SI Appendix, Fig. S8 and Text S2).

Biochemical reactions encapsulated in cell-sized volumes can show different behaviors than their bulk counterparts (31). Not only the absolute number of molecules is different in each case but the process of droplet encapsulation usually implies a compositional variability between compartments. To explain the experimentally observed variability in the period and likelihood of oscillation among droplets with the same cytoplasmic density, we considered partitioning effects in our model and simulated a population of in silico droplets. Each droplet draws its parameters from a gamma distribution which represents the partition errors that occur when the cytoplasm is encapsulated (SI Appendix, Text S3 and Fig. S9). This broader-than-Poisson distribution has been previously shown to accurately capture the multiple factors affecting a compartment’s composition in the process of encapsulation (31). Additionally, we used the average of each parameter in a deterministic model to describe the bulk reaction (SI Appendix, Fig. S9, red curves).

After simulating a population of droplets for each dilution, we observed that the ensemble probability of oscillation follows the same trend as experiments with a threshold within the range of the experimentally measured values (Fig. 3C). We also observed an agreement of the period-to-dilution dependency among in silico droplets, bulk simulation, and experiments (Fig. 3D). Interestingly, droplet simulations extended beyond the threshold set by the bulk system, highlighting the importance of considering single-cell variability in sensitive zones of parameter space. The rising and falling phases of the oscillation also showed the same trend as in experiments with rising periods more sensitive to large dilutions than the falling ones (Fig. 3E). Notably, droplet simulations also showed the same trends in the dispersion of the period as experiments. Namely, the period is less dispersed for low dilutions (less than 5 min) than near the threshold, when the period varies within a range of 45 min. Finally, when we simulated our system with the same initial condition of low Cdk1–cyclin B1 activity for all dilutions, we obtained a delay in the onset of oscillations similar to the trend observed in experiments (Fig. 3F). In conclusion, the observed robustness to dilution is maintained when droplet-to-droplet variability is included in our modeling framework.

Next, we explored how concentrating the components of a system affects its properties. For consistency, we assumed that the same scaling functions that ruled the effect of dilution also explain the behavior during density increase. We observed that a population of simulated droplets stops oscillating as the cytoplasmic density passes a threshold value (Fig. 3G). The predicted threshold is overestimated compared to the experimentally measured values, which may be because both the synthesis and degradation rates become saturated after certain concentrations rather than continue to increase polynomially as in our proposed scaling. Nevertheless, the periods of these oscillations do not present large deviations, consistent with experiments, underscoring the robustness of the oscillator (Fig. 3H). We summarized the complete dynamical behavior of the system in a bifurcation diagram (Fig. 3I). As the cytoplasmic density decreases or increases, stable oscillatory solutions (green curve) eventually disappear (points 1 and 2), and the system settles into a steady state (red curve). Intriguingly, the bifurcation diagram also presents a rich dynamical phenomenon: the coexistence of multiple stable solutions for a specific cytoplasmic density. For example, when cytoplasmic density is 1.25×, the system can either be oscillating or in a stable steady state, depending on the initial condition. This is evidenced by the subcritical Hopf bifurcations present in the diagram (points 3 and 4). In addition, the existence of this multistability provides a hysteretic transition between oscillatory and steady-state behaviors. If the system starts from an initial condition that promotes oscillations, as the cytoplasmic density increases, oscillations stop close to 1.7×. However, if the system starts from an initial condition that promotes a stable steady state, the threshold is closer to 1.0×. This is shown in simulations in which the hysteresis can be explicitly observed (Fig. 3J). These results suggest a theoretical explanation for the different thresholds observed experimentally (Fig. 2D) when concentrating and subsequently diluting the system.

Cdk1 Positive Feedback Loops Are Not Essential for Robustness to Cytoplasmic Dilution.

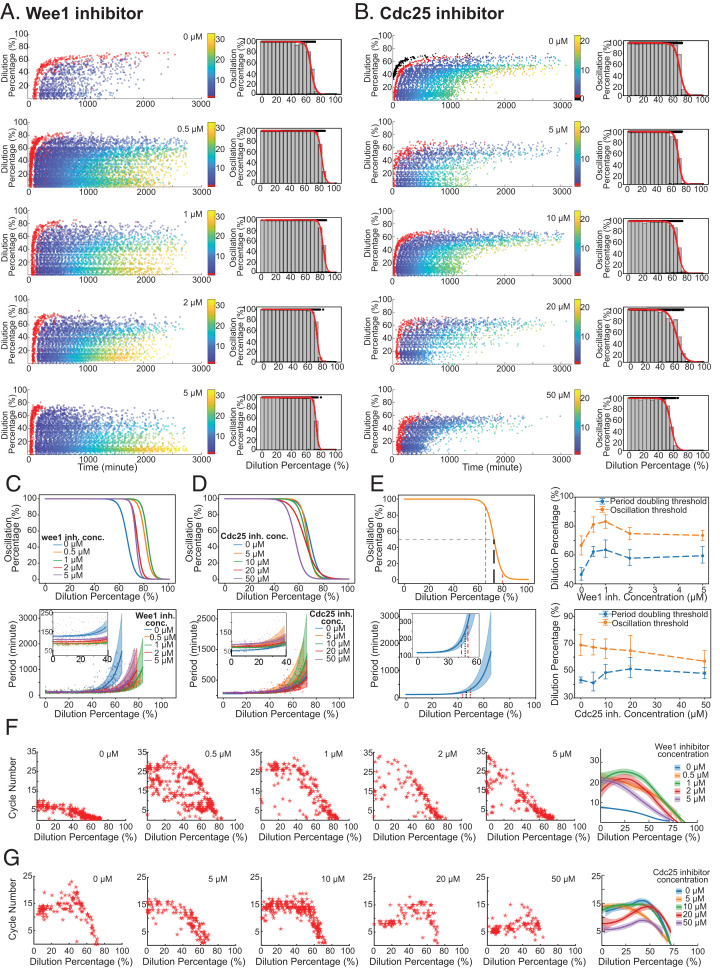
Previous computational studies have suggested that the two positive feedback loops formed by Cdk1 with its activating phosphatase Cdc25 and inhibitory kinase Wee1 underlie the robustness of mitotic oscillations against molecular noise and parameter perturbations (24, 32). To explore whether these Cdk1 positive feedbacks contribute to cell-cycle robustness to cytoplasmic density changes, we performed dilution experiments as before but in the presence of Wee1 inhibitors (0 to 5 μM, PD166285) or Cdc25 inhibitors (0 to 50 μM, NSC95397). Both inhibitors have been characterized and shown to be effective in previous in vivo and in vitro studies (33, 34). We found that diminishing Wee1 or Cdc25 activity had no noticeable effect on the ability of the system to oscillate (Fig. 4 A and B). As summarized in Fig. 4C (Wee1 inhibition) and Fig. 4D (Cdc25 inhibition), the system maintained a 100% oscillation percentage (Top) and stable period (Bottom) for low to moderate dilutions regardless of the concentrations of inhibitors, suggesting the compromised positive feedbacks do not substantially affect the cell-cycle robustness to cytoplasmic density dilution. Nevertheless, the Wee1 and Cdc25 inhibitions could modify the period itself independent of dilution, consistent with established knowledge of their role as part of the cell cycle network. The Wee1 inhibition causes the threshold for mitotic entry to be lower (less cyclin B production is needed) and thus shortens the period (Fig. 4 C, Bottom Inset and SI Appendix, Fig. S10); on the contrary, inhibiting Cdc25 increases the amount of cyclin B needed for mitotic entry, which causes the period to elongate (Fig. 4 D, Bottom Inset and SI Appendix, Fig. S11). These trends agree with our model simulated results (SI Appendix, Fig. S9 and Text S4). These investigations suggest that the fine-tuning of the feedback motifs does not appear essential to sustain cell-cycle robustness to changes in cytoplasmic density.

Fig. 4.

Cdk1 positive feedbacks are not essential for robustness to cytoplasmic dilution. (A and B) Extracts were supplemented with 0, 0.5, 1, 2, and 5 μM Wee1 activity’s inhibitor PD166285 (A) or with 0, 5, 10, 20, and 50 μM NSC95397 for inhibiting Cdc25 phosphatase activity (B) and then tested for their robustness to dilution. For each inhibitor concentration, the raster plot of the experimental result is shown as well as the oscillation percentage obtained. The system retains its function for most of the dilution range (0 to 60%) for all inhibitor concentrations with a slight difference in the absolute threshold values and the onset time and end time of oscillations. (C and D, Top) All oscillation percentage curves together to highlight the differences observed near the thresholds at different inhibitor concentrations of PD166285 (C) and NSC95397 (D). (Bottom) The obtained period profiles as a function of dilutions. (Insets) Zoomed-in views for the changes in period for low dilutions in which the curve is mostly flat. Period curves were fitted to exponential functions, and bootstrap was performed on the data to obtain CIs for the parameters. Shaded region represents one SD from the average parameters. (E) Quantification of robustness to dilution. (Left) Two different ways of measuring robustness based on oscillation percentage (Top) and period curves (Bottom). For oscillation percentage, we extract the dilution required for 90, 50, and 10% oscillation percentage and define the oscillation threshold as the dilution percentage at 50% oscillation percentage. For period curves, we calculate the dilution percentage at which period doubles to be defined as the period-doubling threshold. The estimated error on the parameters is used to infer a CI for the period-doubling dilution. (Right) The oscillation and period-doubling threshold change as a function of inhibitor concentration. Top corresponds to Wee1 inhibitor experiments and Bottom to Cdc25. (F and G) Total number of cycles as a function of dilution percentage for different concentrations of Wee1 inhibitor (F) and Cdc25 inhibitor (G). Rightmost plots show all the curves together smoothed by locally weighted scatterplot smoothing for ease of comparison. It can be appreciated that the inhibition of Wee1 increases the cycle number for low dilutions. The addition of the Cdc25 inhibitor tends to decrease the number of cycles in the system for most dilutions.

On the other hand, the system's responses at high dilution (>60%) showed a dependency on positive feedback inhibitions. The half-maximal threshold for the oscillation percentage increased and then decreased as the Wee1 inhibitor concentration increased, yielding a nonmonotonic function of Wee1 inhibition (Fig. 4 C, Top). On the contrary, adding the Cdc25 inhibitor seemed to monotonously decrease the oscillation threshold (Fig. 4 D, Top). To quantify the qualitative changes observed in both oscillation percentage and the period of the system, we fit the data curves with logistic regression and an exponential function, respectively. These fits allowed us to extract the half-maximal threshold (Fig. 4 E, Top Left) as well as the dilution percentage value at which the period doubles from its value at 0% dilution (defined as the period-doubling threshold, Fig. 4 E, Bottom Left). We observed that both half-maximal and period-doubling thresholds followed a nonmonotonic trend when the Wee1 inhibitor was added (Fig. 4 E, Top Right). On the other hand, adding Cdc25 inhibitor decreased the half-maximal threshold monotonously while the period-doubling value increased slightly. For both cases, we observed similar trends in simulations (SI Appendix, Fig. S12 and Text S4).

Interestingly, the total number of cycles showed notable changes with the Cdk1 positive feedback inhibitions. The Wee1 inhibition increased the total number of cycles from a maximum of 10 (Wee1 inhibitor of 0 μM) up to 33 cycles in maximum (Wee1 inhibitor of 5 μM) (Fig. 4F). The system with the Wee1 inhibition also presented a longer overall oscillation time than the system without (Fig. 4A). In contrast, the Cdc25 inhibition reduced the system's ability to sustain oscillations for many cycles and a long time. As the concentration of the Cdc25 inhibitor rose, the total number of cycles decreased (Fig. 4G), and the overall oscillation time was shortened (Fig. 4B). In summary, we find that both dilution and feedback strength modify the total number of cycles in the system, suggesting a previously unexplored role of Wee1 and Cdc25 in modulating the cycle number in oscillating extracts.

Discussion

We have investigated how variations in cytoplasmic density affect cell-cycle functioning. Our experiments in vitro imply that the cell-cycle network can carry out oscillations over a large span of changes above or below the density of an endogenous cytoplasm of Xenopus eggs. On the other hand, near the boundaries of the functioning range (0.2 to 1.22× RCD), the system becomes sensitive to cytoplasmic density variation and switches from oscillation to an arrested state in a sharp, sigmoidal manner, revealing a role for the cytoplasm in controlling the states of a cell when too diluted or concentrated.

Studies have also suggested that the density of the cytoplasm is involved in cell homeostasis. In fission yeast, cells with higher cytoplasmic density (higher total protein concentration) tend to undergo super growth at a higher rate to achieve proteome homeostasis (35). In human cells, cytoplasmic dilution of the cell cycle inhibitor Rb through cell growth in the G1 phase has been shown to trigger cell division, providing a mechanism to promote cell-size homeostasis (36). Interestingly, while the cell-cycle period is highly tunable to cyclin B mRNA concentration (varied by adding recombinant mRNAs or morpholinos of cyclin B) (37), we found that the period is very robust to density changes of the whole cytoplasm even though this causes variations in the cytoplasmic cyclin B mRNA concentration. We hypothesized that instead of the absolute concentrations of each component, the ratios between components are what influence the robustness of the mitotic oscillator. This divergent response of cell cycles to changes in the overall concentration (where cell cycle is resilient) versus specific signaling activity (in which the cell cycle is sensitive and tunable) may help decouple possible cell homeostasis control mechanisms from cell-cycle tuning capability.

Under certain conditions, Xenopus cell-free extracts undergo irreversible physiological changes because of the activation of apoptotic pathways (38, 39). In particular, the cell cycle arrests. However, we demonstrated that the concentration-induced arrest can be reversed by dilution. Despite apoptosis’ association with cell shrinkage and a condensed cytoplasm (40), the observed reversibility rules it out as an explanation for this phenomenon. Furthermore, we find that recapitulating oscillations in an arrested extract via dilution requires a significantly lower density (0.87× RCD) than that for arresting the extract through concentration (between 1.22 and 1.46× RCD). This threshold difference may come from the dynamic properties of the cell-cycle interaction network as suggested by mathematical modeling. A hysteresis produced by a subcritical Hopf bifurcation causes different thresholds to switch between the oscillation/nonoscillation states depending on which state the system originates from. The existence of this type of bifurcation has also been reported theoretically in the cell cycle (41) and other biological systems such as Bacillus subtilis biofilms (42). The present work provides an experimental observation of a dynamic hysteresis in mitotic oscillations. Moreover, multiple studies have previously analyzed the hysteresis in switches between two stable steady states of Cdk1 in response to the total concentration of its regulatory protein cyclin B. Here, in contrast, we show that oscillatory behavior presents hysteresis as a function of cytoplasmic density. This opens the possibility to the presence of hysteresis with respect to other parameters of the system, for example, cyclin B synthesis rate rather than the total protein concentration of cyclin B in the case of the bistable switch of Cdk1. Future experiments could test whether oscillations appear and disappear for the same threshold value when increasing and decreasing the synthesis rate of cyclin B.

Hysteresis is widely present in physics, chemistry, and biology. Our discovery of the hysteretic response of the cell cycle to cytoplasmic density adds an example of this important universal phenomenon. It is not yet clear if it is advantageous for the cell cycle to possess this property, but hysteresis could function as a memory switch for cells entering an altered state whose cytoplasm has been extremely concentrated, so they do not easily return to normal cell-cycle progression by small fluctuations. Curiously, the model does not predict the same level of hysteresis to happen at the other extreme (i.e., to arrest the system via dilution and recover its oscillations by concentration). Further experimentation could investigate this effect by concentrating highly diluted extracts and comparing the observed thresholds.

To explain most experimental observations, our model assumed the reactions driving the increase and decrease of Cdk1–cyclin B1 complexes scale with cytoplasmic density. Interestingly, Neurohr et al. found that, in oversized cells (cell density reduction from ∼1.10 to ∼1.07) (9), transcription and translation machinery become limiting and do not scale with cell size, suggesting that our assumption of decreased synthesis rate with cytoplasmic density might be appropriate. However, our level of description does not let us discern which particular biochemical reactions are being scaled. We hypothesize that several factors could modulate the dependence of biochemical reaction rates on cytoplasmic density. In particular, cytoplasmic density could regulate physical properties of the cytoplasm such as crowding and viscosity. Crowding affects enzymatic rates (43), macromolecular association (44), and protein diffusion (21, 45–47). Additionally, cytoplasmic viscosity is known to suddenly increase when it is concentrated regardless of the cytoplasmic composition both in vivo and in vitro (48, 49). These effects were not taken into account in our model in which we assumed that reactants are well mixed and homogeneously distributed. To expand the scope of our model to include the potential crowding effects on reaction rates, we explored the possibility of binding/unbinding and phosphorylation/dephosphorylation decaying with dilution and found that, for some experimental days, the best match between experiments and simulations was achieved when these processes were affected by cytoplasmic density (SI Appendix, Fig. S8 and Text S2). The observed cell-cycle arrest after the concentration of the cytoplasm could be caused by an increased macromolecular crowding. However, in compressed yeast cells, where crowding triggered a biochemical slowdown, researchers observed an immediate recovery of signaling after decompression (18). This is in stark contrast to the hysteresis of our experimental system. The arrest could also be caused by an increased viscosity (49). It remains unknown if cytoplasmic viscosity displays a hysteretic response that could explain the observed difference in the thresholds for the arrest and recovery of oscillations. Finally, in synthetic cellular nanosystems, macromolecular crowding regulated gene expression and increased the output’s robustness (50), suggesting another possible cause for the observed robustness in this article. Future experimentation could explore the relationship between viscosity, crowding, and cell-cycle signaling to assess their influence on the cell-cycle responses.

The proposed coarse-grained model does not capture every experimental observation. For example, when concentrated, extracts settle into a high Cdk1 activity level while our model settles to a relatively low activity level. The high Cdk1 activity in extracts could be explained by accumulated cyclin B caused by an increased protein synthesis rate. However, our model does not explicitly include the dynamics of cyclin B binding and unbinding with Cdk1. Therefore, it prevents such accumulation and eventual saturation of Cdk1 molecules. In future studies, quantitative cell-free experimentation can be used to analyze the role of cytoplasmic density on protein synthesis and degradation. Additionally, our model could be expanded to explicitly include the dynamic binding between cyclin B and Cdk1 as well as crowding effects (51, 52). Both approaches could help underpin the mechanisms by which this network achieves robustness when cytoplasmic density is modified.

Robustness to changes in environmental variables has been observed in other biological oscillators. Studies have shown neuronal oscillations are robust to changes in temperature and pH while at the same time displaying a rich dynamic structure (53). Similarly, the KaiABC circadian oscillator remains unchanged when the concentration of all components is scaled at constant adenosine triphosphate (ATP) initial input (from 5.0 to 0.1×) but settles into a steady state when further diluted (54).

We demonstrate that modifying the strength of Cdk1’s positive feedback does not compromise the robustness to changes in cytoplasmic density. This implies that the fine-tuning of these interactions is not essential for robustness to dilution. Which interactions of the network are responsible for the robustness to changes in cytoplasmic density are still unclear. A sensitivity analysis of our model suggests various candidates for future experimentation (SI Appendix, Fig. S13 and Text S5). Both PP2A and Greatwall-associated reactions appear promising candidates. Conversely, Wee1 and Cdc25 inhibition modified the total amount of cycles observed in extracts. The Wee1 inhibition increased the total number of cycles, while the Cdc25 inhibition decreased them. This observation suggests that the termination of the cell cycle in cell-free cytoplasm is tightly regulated and might not be entirely due to the total consumption of resources such as energy as previously speculated (26). This opens the possibility to consider several hypotheses as to why oscillations stop. First, extracts could recapitulate certain events associated with the midblastula transition (MBT) in normal development. Namely, maternal mRNA is cleared, and checkpoints arise in the cell cycle (55). Since no DNA is present in our extract preparations, mRNA clearance could mean the depletion of cyclin B mRNA from the system and thus the elongation of the cell cycle and eventually termination. In fact, RNA sequencing studies show that cyclin B mRNA is depleted after stage 12 of Xenopus laevis development (56). Real-time PCR could aid in the investigation of this hypothesis. Also, it could be possible that checkpoints arise within the extract in a timed fashion. The main checkpoint arising after MBT is mediated by the protein Chk1, which shares a signaling pathway with Wee1 and Cdc25 via the protein 14-3-3 (57, 58). Tracking Chk1 concentration and activity throughout the lifespan of an extract could shed light on this hypothesis. In either case, our results present an avenue of research for understanding what regulates the total number of cycles in Xenopus egg extracts.

Finally, our results could be expanded by including nuclei in our extract preparations, which could be achieved by supplying demembranated sperm chromatin into Xenopus extracts. Theoretical work suggested that the extra dynamic bistable switch induced by nuclear translocation promotes the robustness of cell-cycle oscillations to noise (59). How changes in cytoplasmic density affect a system in which nuclei are present is currently unknown and can be a promising avenue for research. It has been reported that the relative density of the nucleus and cytoplasm is robust during cell growth in human cells (60), which opens the question of whether a balance between the density of the nucleus and the cytoplasm is necessary for the correct progression of the cell cycle. Importantly, the spatial self-organization in Xenopus egg extracts has also been shown to be robust to dilution (61), expanding our results from the time domain to the spatial domain. How both spatial and temporal dynamics together are affected by dilution appears as an exciting new direction of research. The experimental platform developed in the current study can be easily generalizable to quantitatively studying various other cellular processes under different cytoplasmic densities.

Materials and Methods

Cycling Xenopus laevis Extract Preparation, Dilution, and Concentration.

Cycling Xenopus extracts were prepared following previous protocols with a few modifications (26). Sexually mature female frogs were purchased from Xenopus1 and Nasco Education. We primed the frogs for ovulation with an injection of 100 IU human chorionic gonadotropin (HCG) (02198591, MP Biomedicals) 1 wk before and induced them with 600 IU HCG 12 to 16 h before acquiring the eggs. The eggs were activated by 0.5 μg/mL calcium ionophore A23187 (C7522, MilliporeSigma). A 10-min followed by a 5-min centrifugation at 20,000 × g was conducted in a Beckman Avanti J-E Centrifuge with a JS-13.1 swinging bucket rotor to crush eggs and extract cytosolic materials. The ATP mix was not added. In all dilution experiments of the main text, the extracts were diluted with freshly prepared Extract Buffer (100 mM KCl, 1 mM MgCl2, 0.1 mM CaCl2, 50 mM sucrose, and 10 mM Hepes, pH 7.8) to minimize the perturbations of ionic strengths and pH. In the dilution experiments of SI Appendix, Figs. S4 and S5, the extracts were diluted with autoclaved water, 1× Extract Buffer, or 2× Extract Buffer. In the concentrating experiments, the bulk extracts were loaded into a 96-well microplate with 40 μL per well, and the whole plate was placed in a vacuum for 10-min intervals up to 40 min. After each time interval, the concentrated extracts in two or three wells were taken out and combined to ensure a minimum sample volume of 50 μL for each condition. The concentrating efficiency was estimated by the changes in Nanodrop measurement, volume loss, and Alexa Fluor 594 dextran intensity before and after evaporation (details shown in SI Appendix, Table S1). Notably, the average intensity of droplets after evaporation was calculated by fitting a normal distribution to the histogram of droplet intensity.

Fluorescence-Labeled Reporters and Inhibitors.

The Cdk1-FRET sensors were prepared following a method described earlier (25). A final concentration of 1 μM Cdk1-FRET sensors was added to monitor the dynamics of Cdk1/PP2A activities. Dextran–Alexa Fluor 594 (D22913, Invitrogen) at a final concentration of 200 nM was added to the extracts for measuring the dilution percentage of extracts encapsulated within each droplet. For the experiments shown in Fig. 4, 0 to 5 μM PD166285 (PZ0116, MilliporeSigma) or 0 to 50 μM NSC95397 (N1786, MilliporeSigma) was added into bulk extracts to manipulate the positive feedback strengths.

Device Fabrication, Tuning, and Droplet Generation.

Two-channel microfluidic device fabrication, droplet generation, and droplet loading were performed as previously reported (29). Dow Sylgard 184 silicone encapsulant (4019862, Ellsworth) was poured on SU-8 modes on silica wafers to produce polydimethylsiloxane slabs with microfluidic channels. In a two-channel microfluidic device, extracts supplied with dextran–Alexa Fluor 594 and the Cdk1-FRET sensor were flown in from one inlet via a transfer tubing (EW-0641711, Cole-Parmer), while the extract buffer for dilution with the same concentration of Cdk1-FRET sensor was flown in from another inlet. A multichannel pressure controller (OB1 MK3+, Elveflow) controlled the flow rate in each inlet precisely. By changing the temporal pressure profiles of individual inlets periodically while keeping the total aqueous pressure constant, we mixed extracts with the extract buffer at different ratios, covering the whole 0 to 100% dilution spectrum continuously. The boundaries of 0 and 100% dilution were confirmed by the observation of one aqueous flow pushing the other back to its inlet completely. These diluted extracts were then encapsulated by two weight % 008-FluoroSurfactant oil (008-FluoroSurfactant-2wtH-50g, Ran Biotechnologies) into uniform-sized droplets. The size of droplets examined in most experiments has a diameter between 70 and 90 μm, except the smaller droplets (55.29 ± 1.83 μm in diameter) investigated in SI Appendix, Fig. S3. The generated droplets were collected in the reservoir of the microfluidic device, and via a simple dipping step, these droplets were loaded into hollow glass tubes (inner height: 100 μm; width: 2 mm, 5012, VitroCom) to form a single layer of droplets. These glass tubes were precut into 3- to 5-mm pieces and precoated with Trichloro (1H,1H,2H,2H-perfluorooctyl)silane (448931, MilliporeSigma). Loaded glass tubes were then placed in a glass-bottom sterile Petri dish (70674, Electron Microscopy Sciences) and immersed with mineral oil (8012951, Macron Fine Chemicals) to prevent surfactant oil and sample evaporation.

Time-Lapse Fluorescence Microscopy and Image Processing.

All imaging was carried out at room temperature on an inverted Olympus IX83 fluorescence microscope with a 4× air objective, a light emitting diode fluorescence light source, a motorized x-y stage, and a digital complementary metal–oxide–semiconductor camera (C13440-20CU, Hamamatsu). The open-source software μManager v1.4.23 was used to control the automated imaging acquisition. Bright-field and multiple fluorescence images of CFP, FRET, and red fluorescent protein (RFP) were recorded at a frequency of one cycle every 4 to 8 min for 1 to 3 d for each sample. Custom scripts in MATLAB 2019a were written to perform image processing. Bright-field images were used for individual droplet segmentation and tracking. Only individual droplets tracked from the beginning (first 50 frames) were selected for analysis. Intensity peaks and troughs were first auto-selected by MATLAB and then manually corrected for reliability. Other oscillation characteristics such as rising periods and falling periods were also calculated for further analysis.

Statistical Analysis.

In the dilution experiments, Alexa Fluor 594 intensities were used as references to quantify dilution percentage. The RFP intensity of individual droplets was first sorted and normalized, with the 99th percentile defined as 0% dilution and the first percentile defined as 100% dilution. For Figs. 1 E and F and 4 A, B, C, Top, and D, Top, logistic regression was employed to infer the percentage of oscillation as a function of dilution. For each experiment, individual droplets were recorded as either oscillatory or nonoscillatory, and these discrete data were used for the regression. Fitting was performed in Python 3.7.10 using the logistic regression function from the package scikit-learn 0.22.2. Each bar in Figs. 1E, 2D, and 4 A and B represents a percentage of oscillatory droplets over total droplets detected within the bin range. Fig. 2D applied nonlinear least-square fitting from the function curve_fit to the data of concentrating extracts and the dilution of concentrated extracts. The fitting results were shown in orange and blue, respectively. In Fig. 3 C, G, and J, simulation results were directly transformed to oscillation percentage by taking the ratio of oscillatory droplets and total simulated systems. For comparison with experimental curves, a logistic function was obtained from the simulation results via fitting using the function curve_fit from the package scipy 1.4.1. The same functionality was used to fit an exponential function to the period versus dilution curves presented in Fig. 4 C, Bottom and Fig. 4 D, Bottom. CIs are obtained by bootstrapping the data. Specifically, the data were resampled (the new sample size was the same as the original sample size) with replacement 104 times. For each resampling, the new set of points was fitted and the coefficients recorded. The 25th and 75th percentiles of the parameter distributions were taken as estimates on the uncertainty of the parameters. The shaded areas in Fig. 4 C, Bottom and Fig. 4 D, Bottom represent the obtained curves with the limit uncertainty values of each parameter. In Fig. 4 E and F, locally weighted scatterplot smoothing with a span of 0.75 was applied to smooth the total cycle number curves for different inhibitor concentrations. Package ggplot2 in Rstudio 1.2.5019 was installed and utilized. The shaded areas represent the moving first and third quantiles.

Mathematical Modeling.

All time series were obtained by numerical integration of the ordinary differential equations (ODE). The simulations were performed using custom scripts in Python 3.7.10. Oscillatory or steady-state behavior was differentiated by the norm of the system's velocity/vector in conjunction with an analysis of the signal's peak detection features. Droplet simulations are ODE simulations in which the corresponding total concentrations, synthesis rate, and degradation rate were sampled from a Gamma distribution representing the encapsulation error. In all cases, 500 droplets were simulated per RCD value. The bifurcation diagram in Fig. 3I was performed in XPPAUT 8.0. The diagram was started from a high dilution converged steady state. Stable and unstable steady states were first tracked while the Hopf bifurcations were continued in a second iteration of the algorithm. Model equations and setup details were provided in the accompanying supporting information texts.

Data Availability

The data reported in this paper have been deposited in the Dryad Digital Repository (https://doi.org/10.5061/dryad.sf7m0cg78) (62). Computational models and analysis codes will be available in GitHub at https://github.com/ftavella/cell-cycle-modeling/tree/cytoplasmic-density-changes.