Abstract
Nitrogen, the most dominant constituent of Earth’s atmosphere, is critical for the habitability and existence of life on our planet. However, its distribution between Earth’s major reservoirs, which must be largely influenced by the accretion and differentiation processes during its formative years, is poorly known. Sequestration into the metallic core, along with volatility related loss pre- and post-accretion, could be a critical process that can explain the depletion of nitrogen in the Bulk Silicate Earth (BSE) relative to the primitive chondrites. However, the relative effect of different thermodynamic parameters on the alloy-silicate partitioning behavior of nitrogen is still poorly known. Here we present equilibrium partitioning data of N between alloy and silicate melt () from 67 new high pressure (P = 1–6 GPa)-temperature (T = 1500–2200 °C) experiments under graphite saturated conditions at a wide range of oxygen fugacity (logfO2 ~ΔIW - 4.2 to - 0.8), mafic to ultramafic silicate melt compositions (NBO/T = 0.4 to 2.2), and varying chemical composition of the alloy melts (S and Si contents of 0–32.1 wt.% and 0–3.1 wt.%, respectively). Under relatively oxidizing conditions (~ΔIW - 2.2 to - 0.8) nitrogen acts as a siderophile element ( between 1.1 and 52), where decreases with decrease in fO2 and increase in T, and increases with increase in P and NBO/T. Under these conditions remains largely unaffected between S-free conditions and up to ~17 wt.% S content in the alloy melt, and then drops off at > ~20 wt.% S content in the alloy melt. Under increasingly reduced conditions (< ~ ΔIW - 2.2), N becomes increasingly lithophile ( between 0.003 and 0.5) with decreasing with decrease in fO2 and increase in T. At these conditions fO2, along with Si content of the alloy under the most reduced conditions (< ~ΔIW - 3.0), is the controlling parameter with T playing a secondary role, while, P, NBO/T, and S content of the alloy have minimal effects. A multiple linear least-squares regression parametrization for based on the results of this study and previous studies suggests, in agreement with the experimental data, that fO2 (represented by Si content of the alloy melt and FeO content of the silicate melt), followed by T, has the strongest control on . Based on our modeling, to match the present-day BSE N content, impactors that brought N must have been moderately to highly oxidized. If N bearing impactors were reduced, and/or there was significant disequilibrium core formation, then the BSE would be too N-rich and another mechanism for N loss, such as atmospheric loss, would be required.
1. Introduction
Nitrogen (N) is the sixth most abundant element in the Solar System and is ubiquitously present in all of its known reservoirs, i.e., the solar photosphere, the inner and outer Solar System planets and moons, as well as in the undifferentiated and differentiated meteorites, asteroids and comets - albeit with variations in abundances, isotopic signatures and speciation (e.g., Andersen et al., 1964; Sugiura, 1998; Grady and Wright, 2003; Meibom et al., 2007; Bergin et al., 2015; Füri and Marty, 2015). Because of its volatile character, it is an important constituent of the atmospheres of the rocky planets and the moons - both in the inner as well as the outer Solar System (e.g., Sagan and Mullen, 1972; Owen et al., 2001; Mikhail and Sverjensky, 2014; Wordsworth, 2015). Despite its widespread prevalence, nitrogen, analogous to primitive chondrite normalized abundances of other major volatiles such as carbon (C) and water (H2O), is depleted in the bulk silicate Earth (BSE = atmosphere + hydrosphere + crust + mantle) (Marty, 2012; Halliday, 2013; Dauphas and Morbidelli, 2014) (Fig. 1A). N depletion in the BSE has been directly linked to its highly volatile and/or moderately siderophile character, i.e., either Earth was predominantly accreted from N-depleted material, or, if Earth was composed of a significant contribution from relatively N-rich bodies, then large amounts of N were lost either to the space during-/post-accretion or to an inaccessible reservoir such as the core (Marty, 2012; Roskosz et al., 2013; Dauphas and Morbidelli, 2014; Tucker and Mukhopadhyay, 2014; Bergin et al., 2015; Hirschmann, 2016; Dalou et al., 2017; Grewal et al., 2019). However, the relative importance of these early Solar System processes related to the terrestrial N accretion and differentiation, especially the effect of core-mantle separation for a wide range of alloy-silicate equilibration scenarios, in setting up the N budget of the BSE is poorly known.
Fig. 1:
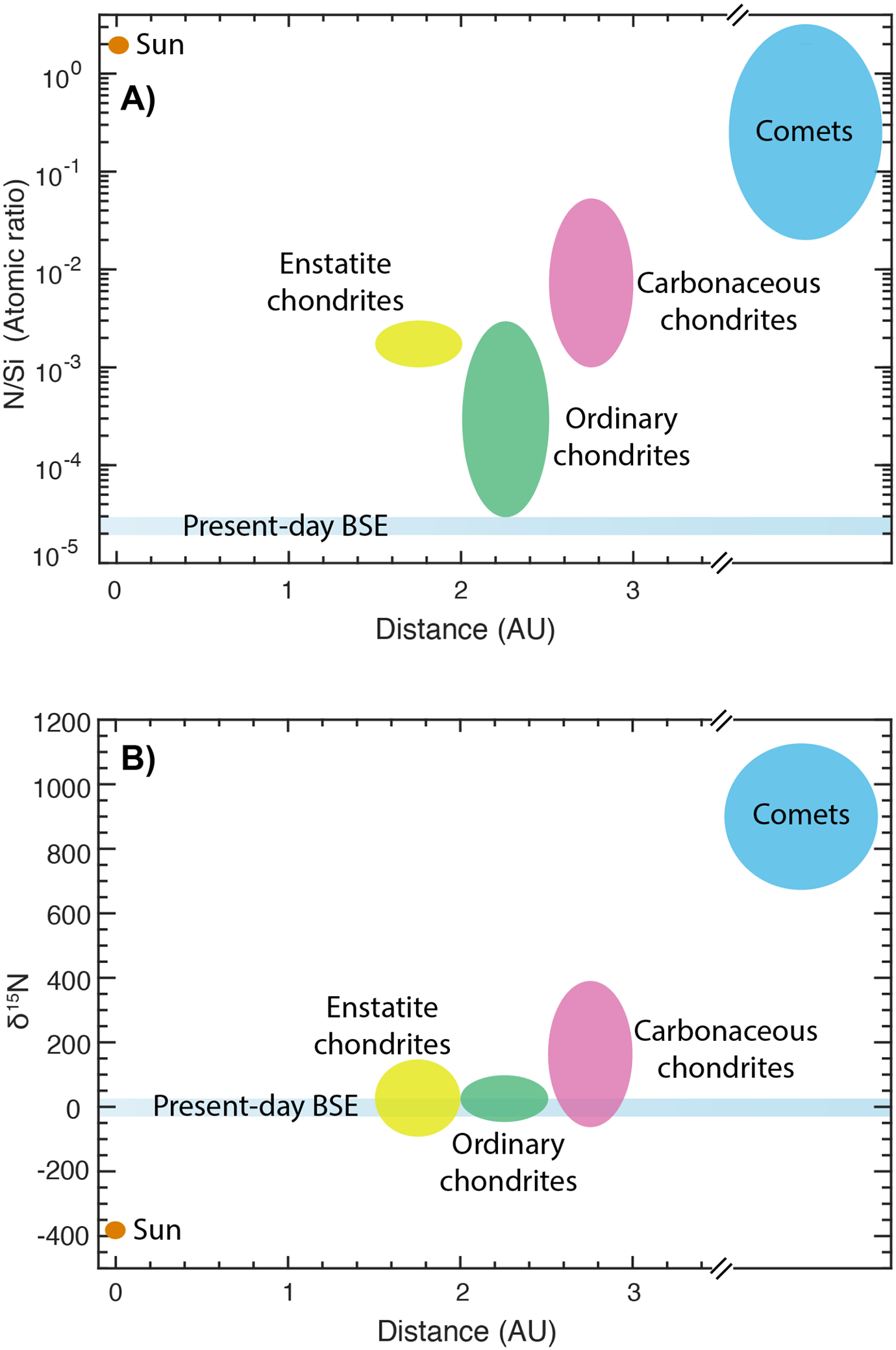
Comparison of the N abundance and N isotopic composition of the BSE with relevant cosmochemical reservoirs. (A) N/Si atomic ratio of the present-day BSE is extremely low relative to all relevant cosmochemical reservoirs (Data from Bergin et al., 2015). (B) The estimated variation in δ15N of the BSE lies in the range of various classes of chondritic meteorites, while it is distinctly different to solar and cometary reservoirs (Grady et al., 1985; Grady et al., 1986; Alexander et al., 1994; Pearson et al., 2006; Alexander et al., 2012; Cartigny and Marty, 2013; Dauphas and Morbidelli, 2014; Alexander et al., 2018).
15N/14N and D/H isotopic signatures of the BSE, the Martian mantle and the silicate fractions of the Moon, Vesta and the angrite parent body are distinctly different from those of the proto-solar nebula (PSN) and comets, but are similar to those of the primitive carbonaceous chondrites, especially volatile-rich CI- and CM-chondrites; therefore, it has been postulated that the primitive carbonaceous chondrites were the primary source of volatiles such as N and H2O for rocky bodies in the inner Solar System (Marty, 2012; Alexander et al., 2012; Sarafian et al., 2014; Füri and Marty, 2015; Sarafian et al., 2017b; Sarafian et al., 2017a; Alexander et al., 2018) (Fig. 1B). On a closer look, the 15N/14N ratio of Earth’s upper mantle, sampled by peridotitic diamonds and Mid-Oceanic Ridge Basalts (MORBs), is similar to the 15N/14N isotopic signature of the enstatite chondrites (Javoy et al., 1984; Javoy et al., 1986; Cartigny and Marty, 2013) (Fig. 1B); therefore, if Earth is primarily accreted from enstatite-chondrite like material (Javoy, 1995; Javoy et al., 2010; Dauphas, 2017), then the contribution of volatile-depleted enstatite chondrites to the N inventory in the BSE may be non-negligible, especially considering the extremely N-poor nature of the BSE (~1.1–3.4 ppm) (Marty and Zimmermann, 1999; Marty, 2012; Halliday, 2013; Dauphas and Morbidelli, 2014).
Hf/W systematics and several mass independent isotopic anomalies suggest that a larger terrestrial planet like Earth had a protracted growth history spread over ~50–100 Ma with several episodes of core formation (Kleine et al., 2009; Dauphas, 2017). Additionally, to satisfy the near-chondritic Platinum-group element (PGE) abundances in the BSE, the addition of ~0.5–2% ME (ME = mass of the present-day Earth) relatively oxidized CI-chondrite like late veneer material has been proposed (Holzheid et al., 2000; Drake and Righter, 2002). Until recently, the delivery of a volatile-rich late veneer has been presumed to also be the primary source of volatiles in the BSE provided the proto-Earth primarily accreted from volatile-depleted material and whatever volatiles were accreted pre-late veneer were either lost during accretionary impacts or to the core (Albarède, 2009). However, several recent observations - (1) Delivery of volatile-rich material within ~5–20 Ma in the inner Solar System (Sarafian et al., 2014; Sarafian et al., 2017b), (2) Volatile-depleted enstatite chondrite like character of the late veneer (Dauphas, 2017; Fischer-Gödde and Kleine, 2017), (3) Super-chondritic C/N and sub-chondritic C/H ratio of present-day BSE (Marty, 1995; Hirschmann and Dasgupta, 2009; Marty, 2012; Halliday, 2013) - necessitate the delivery of volatiles during the main stage of Earth’s accretion. Therefore, if N and other major volatiles were delivered during the main stage of Earth’s accretion, then core formation can have a significant effect on the N budget of the residual bulk silicate reservoirs.
Recently, there has been a growing experimental campaign to constrain the effect of core-mantle separation on the N budget in the BSE. High P-T experiments by Roskosz et al. (2013) at 1.8–17.7 GPa and 2350–2850 °C in a limited fO2 range between ΔIW - 2.7 to - 1.46 (where, ΔIW represents oxygen fugacity relative to the oxygen fugacity of iron-iron wüstite buffer, IW) demonstrated moderately siderophile character of N ( of 8–19), while Li et al. (2016b) demonstrated a comparatively higher siderophile character ( of 8–150) at 1.5–7 GPa and 1600–1800 °C in a relatively high fO2 range (ΔIW from - 0.24 to - 0.07). Meanwhile, experiments at 1–3 GPa and 1400–1600 °C over a wide fO2 range (ΔIW between - 3.51 to - 0.75) show that N becomes less siderophile at increasingly reduced conditions and it even shows lithophile character at less than logfO2 < ΔIW - 2.6 (Kadik et al., 2011; Kadik et al., 2013; Kadik et al., 2015; Dalou et al., 2017; Kadik et al., 2017). Assuming a single stage core formation, Roskosz et al. (2013) suggested that for a bulk N content of ~30 ppm, alloy-silicate equilibration in P range of 30 GPa can put sufficient amounts of N in the core to explain the N budget in the BSE, while Dalou et al. (2017) advocated loss of N-rich atmosphere and a C-rich late veneer in addition to N-segregation into the core to explain depletion of N relative to C in the BSE. Recently, Grewal et al. (2019) studied the effect of varying amounts of S in the alloy on at 1–7 GPa and 1600–1800 °C in a relatively oxidizing fO2 range (ΔIW from - 1.71 to - 0.83). Aligning with the theoretical models of early Solar System evolution, Grewal et al. (2019) postulated that the delivery of N, in addition to other volatiles like C, S and H2O, by a volatile-bearing, Mars-sized differentiated planetary embryo with an S-rich core (22–35 wt.% S) to a volatile-free proto-Earth can not only explain the N budget of the BSE, but also the depletion of N relative to C and S in the BSE. Each of these recent studies, however, explored a limited range of parameter space in constraining For example, Roskosz et al. (2013) and Grewal et al. (2019) did not explore the effects of fO2, whereas Dalou et al. (2017) constrained over a very limited P-T range in S- and Si-free alloys. The experiments of Li et al. (2016) also yielded unrealistic abundance of Pt in the equilibrating alloy melt, the effects of which on remain unclear. In other words, none of the experimental studies till date provide a complete account on the relative influence of individual parameters such as P, T, fO2, and silicate and alloy melt compositions, in affecting the alloy-silicate partitioning behavior of N. Given a lack of consensus in the scientific community on the accretion and initial differentiation history of our planet, it is important to expand the intensive and extensive variable space of experiments to better constrain the possible role played by different core-mantle equilibration scenarios in setting up the N budget of the present-day BSE. This is particularly necessary to resolve possible contributions of various chondrite classes, such as relatively oxidized carbonaceous chondrites or reduced enstatite chondrites, in the N budget of the present-day BSE and their respective volatility related losses prior to delivery to Earth.
In this study we present results of several sets of high P-T experiments to constrain the fate of N during alloy-silicate equilibration over a wide range of conditions. Multiple linear least-squares regression parametrization is presented to compare the effects of P, T, fO2 and silicate and alloy melt compositions on . The parameterization is used to discuss the effect of different accretion and differentiation scenarios via traditional single stage core formation or multi-stage core formation models that take into account the evolving chemical composition of the accreting materials in influencing the partitioning behavior of N during alloy-silicate equilibration. In addition, we also discuss the relative contributions of N loss due to parent body processing of chondritic material, degree of alloy-silicate equilibration, as well as volatility-related loss of N, via atmospheric escape, in setting up the N budget of the present-day BSE.
2. Methods
2.1. Starting materials
The experiments were performed using alloy-silicate mixtures containing ~30–35 wt.% alloy and 65–70% wt.% silicate in graphite capsules. To study the effect of fO2 and varying S and Si contents in the alloy, seven different alloy mixtures were prepared as listed in Table 1. Reagent grade Fe and Ni powders were used to make the alloy mixtures. The N content in the alloy mixtures was fixed at 5 wt.% by introducing fine powders of Fe4N or Fe7N3. Few experiments (G545–1 to 4 and G549–1 to 4) were conducted by using solely Fe4N powder to produce Ni-S-Si-free alloys. Alloy mixtures containing variable amounts of S were prepared using either reagent grade FeS or natural pyrite (FeS2). To simulate the increasingly reduced conditions and/or to study the effect of Si-bearing alloy, variable amounts of Si and/or Si3N4 were added in the alloy mixtures as reagent grade powders. The metal mixes were prepared under ethanol using an agate mortar and pestle and after drying they were stored in a desiccator for >72 hours.
Table 1.
Chemical compositions of starting materials (in wt.%)
| Silicate Mix | SiO2 | TiO2 | Al2O3 | Cr2O3 | FeO | MnO | MgO | CaO | Na2O | K2O | P2O5 | Sum | NBO/T |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ThB1 | 51.19 | 16.12 | 0.03 | 9.18 | 0.23 | 8.75 | 11.35 | 3.05 | 0.10 | 100.00 | 0.76 | ||
| ThB | 50.50 | 0.93 | 15.90 | 0.03 | 9.06 | 0.23 | 8.63 | 11.20 | 3.01 | 0.10 | 99.59 | 0.75 | |
| KOM | 46.00 | 0.35 | 7.61 | 0.34 | 10.40 | 0.17 | 25.80 | 7.45 | 0.51 | 0.11 | 98.74 | 1.85 | |
| BCR | 54.10 | 2.26 | 13.50 | 12.42 | 0.20 | 3.59 | 7.12 | 3.16 | 1.79 | 0.35 | 98.49 | 0.55 | |
| MO#1 | 49.21 | 1.57 | 15.71 | 0.10 | 9.95 | 0.22 | 9.42 | 10.99 | 2.62 | 0.21 | 100.00 | 0.80 | |
| MO#2 | 49.05 | 1.31 | 13.56 | 0.18 | 9.91 | 0.22 | 13.56 | 9.91 | 2.09 | 0.21 | 100.00 | 1.01 | |
| MO#3 | 48.14 | 1.03 | 11.26 | 0.28 | 9.73 | 0.17 | 18.44 | 9.22 | 1.53 | 0.21 | 100.01 | 1.30 | |
| MO#4 | 47.49 | 0.76 | 9.10 | 0.36 | 9.60 | 0.16 | 23.24 | 8.09 | 1.01 | 0.20 | 100.01 | 1.59 | |
| Alloy mix | Fe | Ni | N | S | Si | Sum | |||||||
| Fe-5N | 95 | 5 | 100 | ||||||||||
| Fe-5Ni-5N | 90 | 5 | 5 | 100 | |||||||||
| Fe-5Ni-5N-7.5Si | 82.5 | 5 | 5 | 0 | 7.5 | 100 | |||||||
| Fe-5Ni-5N-12.5Si | 77.5 | 5 | 5 | 0 | 12.5 | 100 | |||||||
| Fe-5Ni-5N-17.5Si | 72.5 | 5 | 5 | 0 | 17.5 | 100 | |||||||
| Fe-5Ni-5N-10S | 80 | 5 | 5 | 10 | 100 | ||||||||
| Fe-5Ni-5N-20S | 70 | 5 | 5 | 20 | 100 | ||||||||
| Fe-5Ni-5N-10S-7.5Si | 72.5 | 5 | 5 | 10 | 7.5 | 100 | |||||||
| Fe-5Ni-5N-10S-12.5Si | 67.5 | 5 | 5 | 10 | 12.5 | 100 | |||||||
| Fe-5Ni-5N-10S-17.5Si | 62.5 | 5 | 5 | 10 | 17.5 | 100 | |||||||
| Fe-5Ni-5N-20S-7.5Si | 62.5 | 5 | 5 | 20 | 7.5 | 100 |
The silicate mixes used in this study were taken from the studies of Grewal et al. (2019) - ThB1; Dasgupta et al. (2013) - ThB, KOM (MT-7C); Tsuno et al. (2018) - BCR; Duncan et al. (2017) - MO#1, MO#2, MO#3, and MO#4
To study the effect of silicate melt compositions, eight different silicate mixtures were prepared as listed in Table 1. Close to half of all experiments were performed with a TiO2-free synthetic tholeiite basalt (ThB1) mixture used in Grewal et al. (2019). ThB1 was prepared TiO2-free to avoid interference of N Kα line and fluorescence line produced by Ti Lα in microprobe analyses (Lengauer et al., 1992). Additional silicate mixtures were composed of: a synthetic tholeiite basalt (ThB) similar to the composition of a natural tholeiite basalt (Dasgupta et al., 2013; Chi et al., 2014; Li et al., 2015; Li et al., 2016a), a natural komatiite (KOM) from Munro Township in Abitibi belt of Canada (Dasgupta et al., 2013), four synthetic compositions (MO#1, MO#2, MO#3, and MO#4) spanning the compositional range between natural basalts and peridotite (Duncan et al., 2017), and a natural Columbia River basalt (BCR) (Tsuno et al., 2018). All silicate mixes (except KOM and BCR) were constructed with reagent grade oxides and carbonates. Prior to mixing, the oxides and carbonates were dehydrated by firing them overnight and then mixed under ethanol in an agate mortar for 2–3 hours. All silicate mixtures were individually loaded in a gold crucible and fired at 1000 °C using a Deltech gas mixing furnace for 24 hours at logfO2 ~FMQ - 2 established by CO-CO2 gas streams in order to reduce Fe2O3 to FeO and decarbonate the carbonate phases.
2.2. High P-T experiments
All high P-T experiments were performed at Rice University. An end-loaded piston cylinder (PC) apparatus with a with a half inch BaCO3/MgO assembly was used to perform the experiments at 1–3 GPa and 1500–1800 °C. P-T calibrations and procedural details for this PC assembly are listed in several previous studies (e.g., Tsuno and Dasgupta, 2011; Dasgupta et al., 2013; Chi et al., 2014). The experiments at 3 GPa and 2200 °C were performed using an 1100ton Walker-type multi-anvil (MA) device. WC anvils with 12 mm truncations and cast MgO-Al2O3-SiO2 octahedral assembly with 18 mm edge length and integrated gasket fins and straight-walled graphite heaters with Mo rings were used for these experiments. All experiments at P >3 GPa were performed with the MA device using WC anvils with 8 mm truncations and COMPRES octahedral assembly with 14 mm edge length using rhenium heater and pyrophyllite gaskets. P-T calibrations and procedural details of 18–12 assembly are detailed in Ding et al. (2014), while those of 14–8 assembly are detailed in Tsuno et al. (2018).
For each experiment, homogeneous alloy-silicate mixes were loaded in graphite capsules, which allowed achieving high T approaching planetary magma ocean conditions. To examine the effect of either fO2, NBO/T, and/or S content in the alloy melt at a fixed P-T, some experiments were conducted with 3 to 4 starting compositions being loaded in a single graphite stock by drilling separate sample chambers (Fig. 2A), similar to the design in previous studies (e.g., Walker et al., 2013; Dalou et al., 2017; Tsuno et al., 2018). Other experiments were conducted by loading a single composition into a graphite capsule (Fig. 2B). A few experiments were performed in double Pt-graphite capsules (inner graphite and outer Pt) to determine whether there is a significant difference of N loss in comparison to experimental charges encapsulated in single graphite capsules. After the initial pressurization to the target pressure at room temperature, all experiments were heated to 850–900 °C at a heating rate of 100 °C/min and sintered overnight to reduce the porosity in graphite capsule, which is known to prevent percolation of alloy melt through graphite capsule. After the sintering step, the experiments were heated to the target temperature at 100 °C/min, held for the desired duration and then were rapidly cooled by cutting off power to the heater. Given the fast diffusivity of N in Fe-alloy melt at high T (Villegas, 1976) experimental duration of 5–300 minutes was deemed sufficient and the compositional homogeneity of the silicate and alloy melt phases, including N contents, confirmed that the experiments approached equilibrium. Our experimental duration at similar temperatures also are comparable to or longer than those that have been employed in previous alloy-silicate experimental studies (varied from minutes to few hours; e.g., Roskosz et al., 2013; Dalou et al., 2017). The temperature during the experiments was monitored and controlled using a type C thermocouple. Post de-pressurization, multi chambered samples were cut transversely into two halves using a tungsten wire saw to observe 3 or 4 chambers simultaneously, while single chambered samples were cut longitudinally. Both halves were mounted in Crystalbond™, ground using 1200-grit sand paper and polished using 0.3-micron alumina slurry on a velvet cloth. Polished samples were soaked in acetone overnight to remove Crystalbond™ followed by either carbon (silicate phase analysis) or aluminum coating (alloy phase analysis) to determine N as well as major and minor elemental composition using electron microprobe.
Fig. 2:
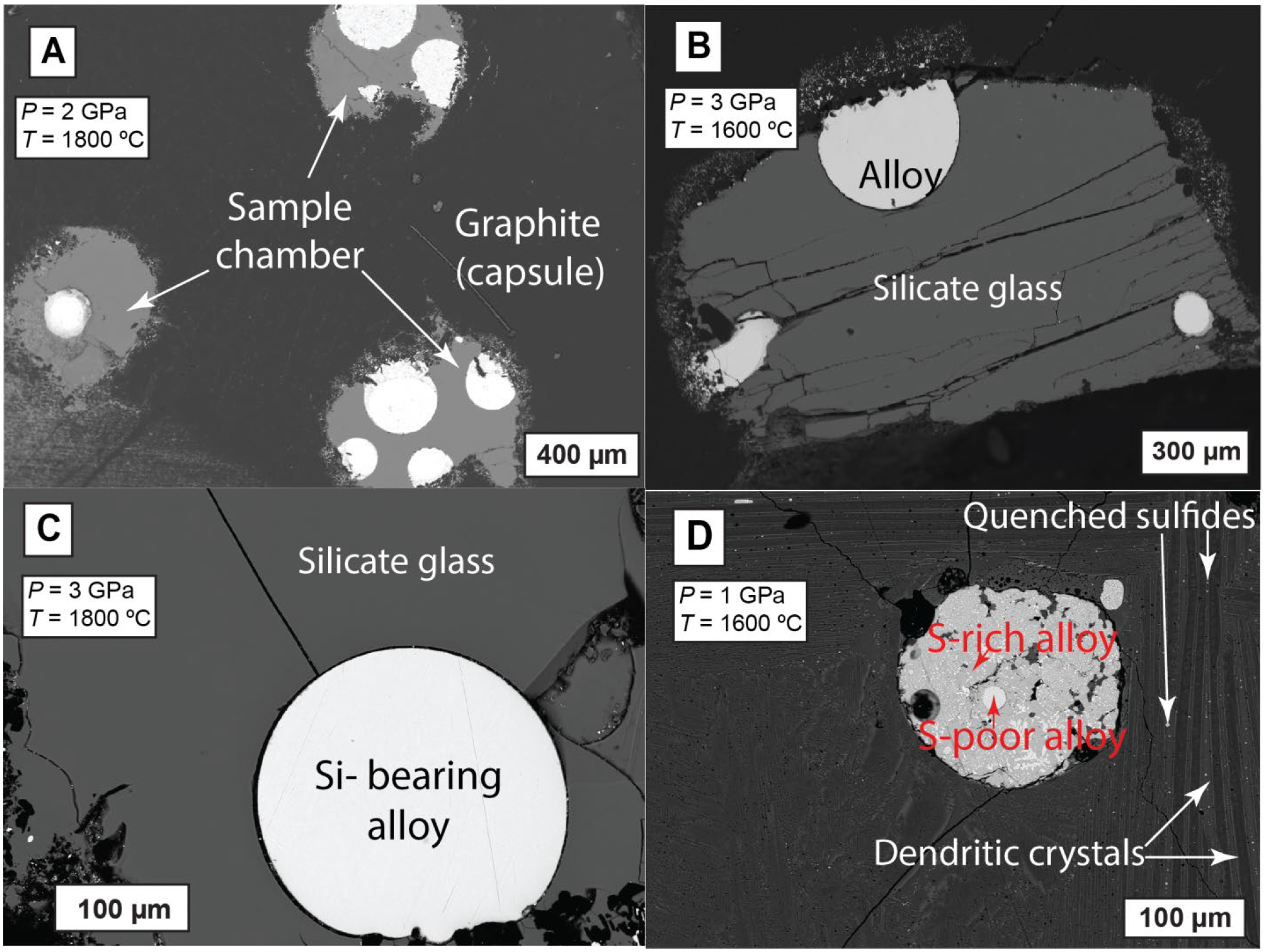
Back-scattered electron images of typical experimental products: (A) Three chambered graphite capsule with each chamber having a different starting mix. The panel shows co-existing metallic alloy blobs and quenched silicate phase in each sample chamber (G523). (B) Co-existing metallic alloy blobs and quenched silicate glass for a single chambered graphite capsule experiment (G511). (C) Detailed textures of quenched Si-bearing alloy and silicate glass (G554–0S-17.5Si). (D) Immiscible S-bearing alloy melt with S-rich (dark) and S-poor (bright) phases surrounded by the silicate melt that quenched to a matte with dendritic crystals and interstitial patches along with quenched sulfide microblobs (G505).
2..3. Analyses of Experimental Samples
Abundances of major and minor elements as well as nitrogen content of the experimental alloy and silicate melts, following previous studies (Roskosz et al., 2013; Dalou et al., 2017; Speelmanns et al., 2018; Grewal et al., 2019), were measured using a JEOL JXA8530F Hyperprobe EPMA at the Department of Earth, Environmental and Planetary Sciences, Rice University. For all samples, the silicate phase was analyzed using carbon coated samples, while the alloy phase was analyzed using aluminum coating, with the standards and experimental samples being coated together in the same session (e.g., Dasgupta and Walker, 2008). Natural glasses and mineral standards from Smithsonian Institute and SPI Supply, respectively, were used to measure all elements except N in the silicate phase. The following principal standards were used for measuring the characteristic Kα X-ray lines of the analyzed elements: Si, Al, Ca, Mg, Fe, Na, K, and P - various Smithsonian glasses, Ti - rutile, Cr - chromite, Mn - rhodonite, and Ni - pentlandite. The alloy phase analyses were carried out using - laboratory synthesized stoichiometric Fe3C (e.g., Walker et al., 2013) for C, natural troilite for S, natural magnetite for O, synthetic Fe and Si metals for Fe and Si, respectively. In order to establish optimal conditions to analyze N along with other elements in both quenched silicate and alloy melts, several test acquisitions were performed on synthetic boron nitride (BN) and laboratory synthesized iron nitride (Fe3N) standards for measuring N in the silicates and alloys, respectively.
Taking into account the heterogeneity of the quenched products, a beam size of 20 microns was used. Varying the accelerating voltage from 10 kV to 25 kV at 50 nA and the beam current from 10 nA to 550 nA at 10 kV, nitrogen X-ray counts per second (cps) were found to decrease with increasing accelerating voltage at a constant beam current, and to increase with increasing beam current at a constant accelerating voltage. Therefore, an optimum beam current and accelerating voltage had to be established to simultaneously measure N with other elements. Therefore, similar to Grewal et al. (2019), an accelerating voltage of 15 kV and beam current of 50 nA for silicate analysis, and 12 kV and 80 nA for alloy melt analyses were chosen as beam conditions. Multiple tests were performed to compare the N Kα cps using LDE2 and LDE1. It was found that the peak intensity of NKα was stronger while measured using LDE2. Therefore, nitrogen in our study was measured on an LDE2 analyzing crystal.
All elements in the silicate phase, except N, were analyzed with a counting time of 10 s on peak and 5 s on each upper and lower background, while for N the counting time was 80 s on peak and 60 s on each upper and lower background. The above-mentioned analytical conditions gave an N detection limit of ~300–340 ppm. If the measured N was close to or below the detection limit for a given experimental phase, then those phases were re-analyzed with longer counting times for N in order to decrease its detection limit. Nitrogen measurement with counting times of 150 s on peak and 300 s on each background resulted in an average detection limit of ~70–100 ppm.
Additionally, we used two different standards to measure Si in the silicate phase. Initially, a Smithsonian Institute basaltic glass standard was used to measure Si in the silicate phase for all the samples. However, reduced samples with >55 wt.% SiO2 always gave sum totals (sum of wt.% of all oxides and elemental N and S) greater than 100 wt.%. A similar observation can be made in the study by Dalou et al. (2017) where anomalously higher sum totals (as much as ~104 wt.%) were reported for all the reduced experimental glasses that had greater than 55 wt.% SiO2. To tackle this issue, Si in all the silicate melt phases with anomalously high sum totals were analyzed using an andesitic glass standard with a SiO2 matrix that is similar to the experimental silicate glasses, which resulted in acceptable analytical totals in the reduced glasses as well as more accurate SiO2 contents.
Similar to the measurements in the silicates, all elements in the alloy, except N, were analyzed using a counting time of 10 s on peak and 5 s on each lower and upper background. N was analyzed using a counting time of 80 s per peak and 60 s per each background. If the measured N was close to the detection limit (~300 ppm), then similar to N measurement in the silicates, those samples were re-analyzed with 150 s counting time on peak and 300 s on each upper and lower background. To account for the effect of C deposition on samples and standards during analysis, the standards were re-analyzed again after every 40–60 points on samples. C values in the alloy products were corrected by taking into account C blank in Fe-metal and troilite standards as well as any C deposition effect during an analytical run following the previous studies (e.g., Dasgupta and Walker, 2008; Tsuno et al., 2018; Grewal et al., 2019).
3. Results
Summary of the experimental conditions, phase assemblage, and partitioning data are given in Table 2. Major element compositions of the alloy and silicate phases along with nitrogen concentrations are reported in Supplementary Table 1 and 2, respectively.
Table 2.
Summary of experimental conditions, quench products, oxygen fugacity, and alloy-silicate partitioning coefficient of nitrogen (N)
| Exp No. | P (GPa) | T (°C) | cDuration (mins.) | bStarting composition | Quench Products | clog fO2 (ΔIW) Ideal | dlog fO2 (ΔIW) Non-ideal | e1-σ | |
|---|---|---|---|---|---|---|---|---|---|
| MA216 | 3 | 2200 | 5 | 70%ThB1+30%Fe-5Ni-5N | Glass+Alloy | −1.51 | −0.94 | 2.75 | 0.34 |
| MA178–0S | 4.5 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N | Glass+Alloy | −1.51 | −0.94 | 8.33 | 1.35 |
| G522–0S | 1 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −3.00 | −2.43 | 1.59 | 0.54 |
| G520–0S | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.62 | −2.02 | 2.17 | 0.31 |
| G511 | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.61 | −2.01 | 4.86 | 0.69 |
| G554–0S-7.5Si | 3 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.35 | −1.78 | 2.32 | 0.33 |
| MA-218 | 3 | 2200 | 5 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.02 | −1.45 | 1.01 | 0.19 |
| MA213–0S-7.5Si | 4.5 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.44 | −1.74 | 1.37 | 0.09 |
| MA214–0S-7.5Si | 6 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.13 | −1.48 | 1.96 | 0.34 |
| G526–0S-12.5Si | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-12.5Si | Glass+Alloy | −3.84 | −3.20 | 0.26 | 0.06 |
| G525–0S-12.5Si | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-12.5Si | Glass+Alloy | −4.02 | −3.37 | 0.33 | 0.08 |
| G554–0S-12.5Si | 3 | 1800 | 30 | 70%ThB1+30%Fe-5Ni-5N-12.5Si | Glass+Alloy | −3.43 | −2.74 | 0.17 | 0.03 |
| MA217 | 3 | 2200 | 5 | 70%ThB1+30%Fe-5Ni-5N-12.5Si | Glass+Alloy | −2.81 | −2.17 | 0.05 | 0.01 |
| MA213–0S-12.5Si | 4.5 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-12.5Si | Glass+Alloy | −2.92 | −2.28 | 0.41 | 0.05 |
| MA214–0S-12.5Si | 6 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-12.5Si | Glass+Alloy | −2.77 | −2.13 | 0.60 | 0.14 |
| G526–0S-17.5Si | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-17.5Si | Glass+Alloy | −3.89 | −3.20 | 0.012 | 0.004 |
| G525–0S-17.5Si | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-17.5Si | Glass+Alloy | −4.72 | −3.97 | 0.025 | 0.005 |
| G554–0S-17.5Si | 3 | 1800 | 30 | 70%ThB1+30%Fe-5Ni-5N-17.5Si | Glass+Alloy | −4.17 | −3.43 | 0.004 | 0.001 |
| MA215 | 3 | 2200 | 5 | 70%ThB1+30%Fe-5Ni-5N-17.5Si | Glass+Alloy | −3.05 | −2.40 | 0.013 | 0.006 |
| MA213–0S-17.5Si | 4.5 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-17.5Si | Glass+Alloy | −3.81 | −3.21 | 0.020 | 0.011 |
| MA214–0S-17.5Si | 6 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-17.5Si | Glass+Alloy | −3.85 | −3.11 | 0.018 | 0.009 |
| G420-N-01 | 2 | 1500 | 300 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −3.24 | −2.64 | 1.85 | 0.47 |
| G425-N-02 | 2 | 1600 | 120 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −3.32 | −2.71 | 1.57 | 0.42 |
| G427-N-03 | 2 | 1700 | 120 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.20 | −1.66 | 10.36 | 6.25 |
| G432-N-04 | 2 | 1750 | 60 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.93 | −2.36 | 2.96 | 0.91 |
| G437-N-05 | 2 | 1800 | 30 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.96 | −2.38 | 1.41 | 0.27 |
| G457-N-06 | 2 | 1800 | 30 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.82 | −2.22 | 1.17 | 0.31 |
| MA147-N-07 | 4 | 1800 | 15 | 70%ThB+30%Fe-5Ni-5N-7.5Si | Glass+Alloy | −2.33 | −1.65 | 1.03 | 0.03 |
| G524–0S | 1 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N | Matte+Alloy | −1.79 | −1.20 | 17.05 | 15.44 |
| G523–0S | 2 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N | Matte+Alloy | −1.62 | −1.01 | 25.64 | 10.93 |
| G507 | 3 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N | Matte+Alloy | −1.81 | −1.29 | 25.60 | 12.51 |
| MA219–0S | 4.5 | 1800 | 15 | 70%KOM+30%Fe-5Ni-5N | Matte+Alloy | −1.30 | −0.74 | 22.95 | 6.05 |
| MA186–0S | 6 | 1800 | 15 | 70%KOM+30%Fe-5Ni-5N | Matte+Alloy | −1.67 | −1.06 | 52.00 | 9.63 |
| G545_1d | 1 | 1600 | 120 | 70%MO#1+30%Fe-5N | Glass+Alloy | −1.60 | −1.02 | 8.75 | 4.74 |
| G545_3c | 1 | 1600 | 120 | 70%MO#2+30%Fe-5N | Glass+Alloy | −1.67 | −1.09 | 8.73 | 3.98 |
| G545_4a | 1 | 1600 | 120 | 70%MO#3+30%Fe-5N | Glass+Alloy | −1.69 | −1.13 | 19.34 | 11.61 |
| G545_2b | 1 | 1600 | 120 | 70%MO#4+30%Fe-5N | Glass+Matte+Alloy | −1.72 | −1.15 | 17.05 | 10.84 |
| G549_2 | 1 | 1700 | 120 | 70%MO#1+30%Fe-5N | Glass+Alloy | −1.67 | −1.13 | 6.50 | 2.87 |
| G549_4 | 1 | 1700 | 120 | 70%MO#2+30%Fe-5N | Glass+Alloy | −1.56 | −1.02 | 7.43 | 4.45 |
| G549_3 | 1 | 1700 | 120 | 70%MO#3+30%Fe-5N | Glass+Alloy | −1.66 | −1.10 | 11.60 | 4.33 |
| G549_1 | 1 | 1700 | 120 | 70%MO#4+30%Fe-5N | Glass+Matte+Alloy | −1.68 | −1.10 | 9.32 | 5.34 |
| G483 | 3 | 1600 | 120 | 70%BCR+30%Fe-5Ni-5N | Glass+Alloy | −1.55 | −0.96 | 7.83 | 1.28 |
| MA178–10S | 4.5 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-10S | Glass+Alloy | −1.25 | −0.85 | 9.90 | 1.58 |
| G522–10S | 1 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-7.5Si | Glass+S-poor alloy+S-rich alloy | −2.47 | −1.92 | 6.39, 0.82 | 3.31, 0.44 |
| G520–10S | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-7.5Si | Glass+Alloy | −2.53 | −2.03 | 2.90 | 0.29 |
| G509 | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-7.5Si | Glass+Alloy | −2.53 | −2.02 | 5.21 | 0.56 |
| G526–10S-12.5Si | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-12.5Si | Glass+S-poor alloy+S-rich alloy | −3.68 | −3.11 | 0.90, 0.61 | 0.19, 0.21 |
| G525–10S-12.5Si | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-12.5Si | Glass+Alloy | −3.48 | −2.99 | 0.59, 0.011 | 0.09, 0.003 |
| G526–10S-17.5Si | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-17.5Si | Glass+S-poor alloy+S-rich alloy | −4.74 | −4.12 | 0.011, b.d.l. | 0.003, n.a. |
| G525–10S-17.5Si | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-10S-17.5Si | Glass+S-poor alloy+S-rich alloy | −4.91 | −4.30 | 0.005, b.d.l. | 0.002, n.a. |
| G505 | 1 | 1600 | 120 | 70%KOM+30%Fe-5Ni-5N-10S | Matte+S-poor alloy+S-rich alloy | −1.05 | −1.47 | n.a., b.d.l. | n.a., n.a. |
| G524–10S | 1 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N-10S | Matte+S-poor alloy+S-rich alloy | −1.70 | −1.16 | 21.86, 1.53 | 18.31, 1.36 |
| G523–10S | 2 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N-10S | Matte+Alloy | −1.51 | −0.96 | 25.80 | 11.69 |
| G506 | 3 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N-10S | Matte+Alloy | −1.58 | −1.21 | 27.62 | 13.13 |
| MA219–10S | 4.5 | 1800 | 15 | 70%KOM+30%Fe-5Ni-5N-10S | Matte+Alloy | −1.22 | −1.00 | 20.62 | 5.23 |
| MA186–10S | 6 | 1800 | 15 | 70%KOM+30%Fe-5Ni-5N-10S | Matte+Alloy | −1.50 | −1.12 | 65.74 | 16.13 |
| MA178–20S | 4.5 | 1800 | 15 | 70%ThB1+30%Fe-5Ni-5N-20S | Glass+Alloy | −1.21 | −1.31 | 6.50 | 1.60 |
| G522–20S | 1 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-20S-7.5Si | Glass+S-poor alloy+S-rich alloy | −3.26 | −2.71 | 1.50, b.d.l. | 0.46, n.a. |
| G520–20S | 2 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-20S-7.5Si | Glass+Alloy | −2.44 | −2.35 | 1.97 | 0.33 |
| G510 | 3 | 1600 | 120 | 70%ThB1+30%Fe-5Ni-5N-20S-7.5Si | Glass+Alloy | −2.22 | −2.24 | 2.83 | 0.49 |
| G524–20S | 1 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N-20S | Matte+S-poor alloy+S-rich alloy | −1.56 | −0.95 | 11.47, b.d.l. | 8.12, n.a. |
| G523–20S | 2 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N-20S | Matte+Alloy | −1.34 | −1.39 | 16.07 | 9.11 |
| G508 | 3 | 1800 | 30 | 70%KOM+30%Fe-5Ni-5N-20S | Matte+Alloy | −1.37 | −1.42 | 14.21 | 6.08 |
| MA219–20S | 4.5 | 1800 | 15 | 70%KOM+30%Fe-5Ni-5N-20S | Matte+Alloy | −1.26 | −1.27 | 14.04 | 3.57 |
| MA186–20S | 6 | 1800 | 15 | 70%KOM+30%Fe-5Ni-5N-20S | Matte+Alloy | −1.29 | −1.34 | 29.95 | 12.96 |
| G484 | 3 | 1600 | 120 | 67%BCR+33%Fe-5Ni-5N-20S | Glass+Alloy | −1.07 | −1.43 | 2.29 | 0.97 |
| G488 | 3 | 1600 | 120 | 67%BCR+33%Fe-5Ni-5N-20S | Glass+Alloy | −1.13 | −1.21 | 3.25 | 1.25 |
The experiments were held at 850–900 °C for 2–12 h before raising to the target temperature in order to reduce the porosity of graphite capsules and prevent the leakage of slicate melt and alloy melt
For details see Table 1
fO2 with respect to iron-wüstite buffer (ΔIW) calculated using ideal solution model for both alloy and silicate melts
fO2 with respect to iron-wüstite buffer (ΔIW) calculated using non-ideal solution model for both alloy and silicate melts (see text for details)
fO2 calculations are made using the average FeO* and Fe contents of silicate melts and alloys, respectively
1-σ error for is obtained by propagating 1-σ deviation error on N content in the alloy and silicate melt
n.a. - not applicable
b.d.l. - below detection limit
Matte = Silicate melt domain that quenched to an aggregate of dendritic crystals
values for S-poor and S-rich alloys and their respective errors are reported in the same cell separated by a comma
3.1. Texture of experimental products
All experiments produced quenched metal blobs in silicate glass pools (Table 2; Fig. 2B, C), except for experiments with KOM silicate starting material which exclusively produced quenched dendritic crystals in silicate melt (Fig. 2D). Additionally, other silicate melts with high MgO content (~22 wt.%), i.e., G545–4 and G549–4, produced glassy melt pools surrounded by quenched crystal aggregates. At relatively oxidized conditions (>5 wt.% FeO in silicate), S-bearing alloys at P > 1 GPa showed quenched textures of S-rich and S-poor micro-phases, while experiments at 1 GPa produced two immiscible alloys phases (sulfide melt and S-poor alloy melt). However, at increasingly reduced conditions (< 5 wt.% FeO in silicate), similar to N-free systems (Li et al., 2015), S-bearing alloy melts exsolved into immiscible S-rich, Si-poor and Spoor, Si-rich quenched phases also at 2 and 3 GPa.
3.2. Estimation of oxygen fugacity
Oxygen fugacity (fO2) was determined based on the co-existence of Fe-rich alloy melt and silicate melt (Table 2), by using the following equilibrium reaction:
| (Eqn. 1) |
where fO2 relative to fO2 of the iron-wüstite buffer (ΔIW), at P-T condition of an experiment, is defined by:
| (Eqn. 2) |
where, is the activity of FeO in the silicate melt phase and is the activity of Fe in the alloy melt phase. and are the mole fractions of FeO and Fe in the silicate and alloy melt, respectively, and and are the activity coefficients of FeO and Fe in the silicate and alloy melt, respectively. Oxygen fugacity, fO2 relative to the IW buffer was calculated using both ideal ( and ) and non-ideal solution models () (Holzheid et al., 1997). ε approach in Wagner equations, which takes into account non-ideal interactions between the components in the alloy melt (Ma, 2001) was used to calculate via the ‘Online Metal Activity Calculator’ (http://norris.org.au/expet/metalact/).
3..3. N content in the alloy and silicate melt
We show that the N contents in the alloy and silicate melts are dependent on a range of thermodynamic variables, i.e., P, T, fO2, NBO/T and S and Si contents in the alloy, albeit in varying proportions. Based on different targeted set of experiments, in subsections 3.3.1 and 3.3.2, we constrain the effect of every single thermodynamic parameter on the N content in the alloy and silicate melt, respectively. For comparison we have plotted data only from Grewal et al. (2019) because all other previous studies on N partitioning between alloy and silicate melt have widely different bulk N content in their starting mixes. Because this and other previous studies in alloy-silicate systems did not target N solubility in the alloy and silicate phases (discussed in detail in Section 4.1), comparisons of the N contents in the alloy and silicate melt phases with different bulk N content is not appropriate.
3.3.1. Variation of N content in the alloy melt with various intensive and extensive variables
Variation as a function of S content in the alloy melt
The effect of S on the N content in the alloy melt as a function of P is shown in Fig 3A. To constrain the effect of varying amount of S in the alloy melt, experiments in a relatively oxidized range (ΔIW - 1.2 to - 0.7), within a narrow T interval (1600–1800 °C) for ThB1 and KOM silicate melt composition are plotted. In agreement with the data from Grewal et al. (2019), we find that for a given amount of S in the alloy melt, the N content increases with increase in P till 6 GPa followed by a small drop at 7 GPa. Similar to C-S bearing alloys at 1 GPa (e.g., Corgne et al., 2008; Dasgupta et al., 2009), C-N-S bearing alloys exsolved into two immiscible alloy melts - a S-poor alloy and a sulfide-like alloy. At 1 GPa, for S-poor alloys (< 2 wt.% S) the N content lies between ~0.3–0.5 wt.%, while for S-rich alloys (~28–32 wt.% S), it is < ~200 ppm. For S-free experiments in the P range of 2–7 GPa, the N content in the alloy lies between ~1.6 and 3.4 wt.%. For any given P-T, with an increase to ~17 wt.% S in the alloy, the N content in the alloy lies in a similar range (~1.6–4.0 wt.%) to S-free conditions, except for experiments at 6–7 GPa which show an increase of ~0.4–0.7 wt.% in the N content relative to S-free alloys. At > 20 wt.% S in the alloy, the N content drops by ~50%, lying between ~0.6 and 2 wt.%. Therefore, only at very high concentrations the presence of S can affect the incorporation of N in the alloy melt.
Fig. 3:
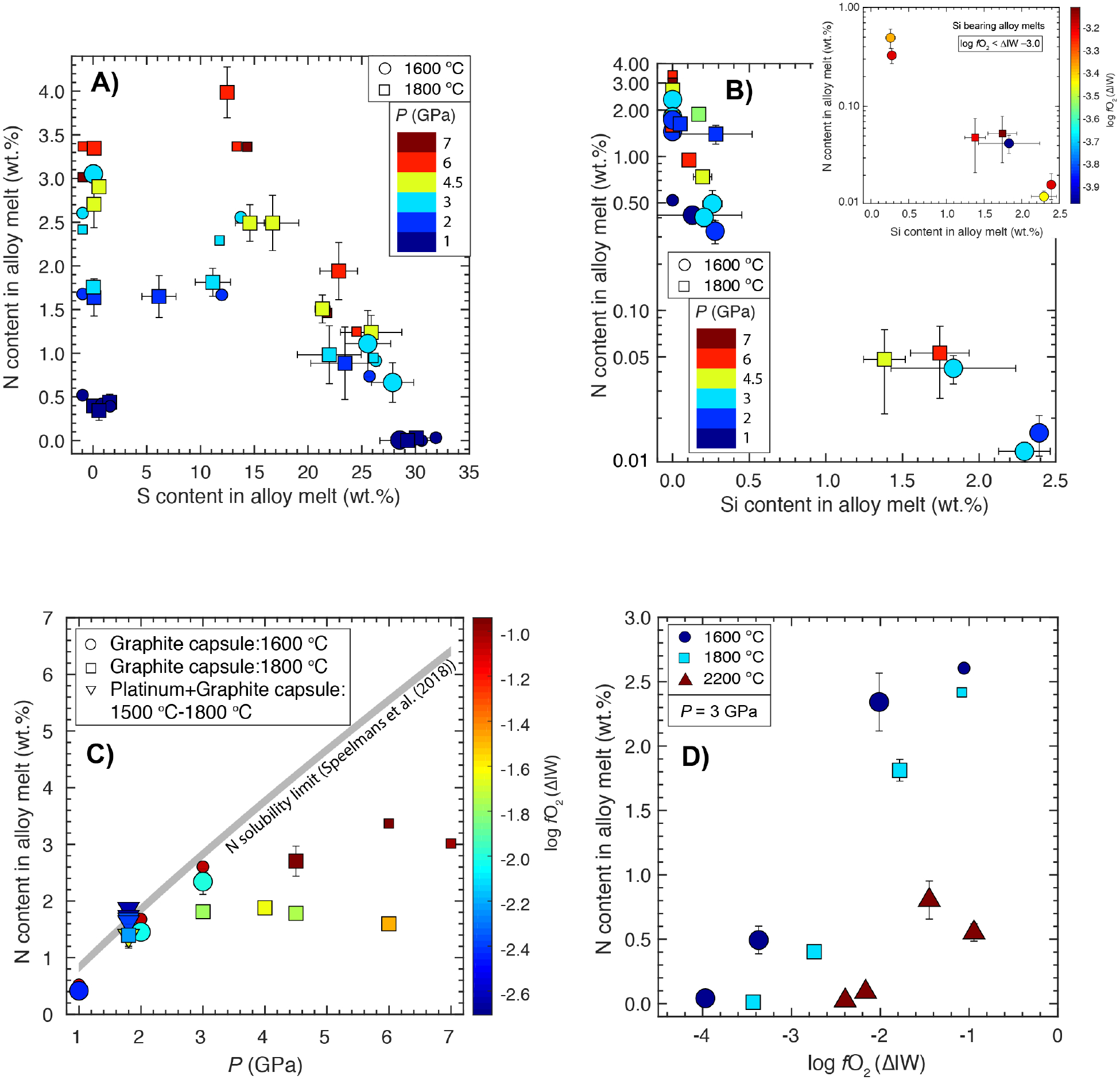
Nitrogen content in the graphite-saturated Fe-Ni-C-N±S±Si alloy melts equilibrating with the silicate melts as a function of A) S content in the alloy and pressure, B) Si content in the alloy and pressure, C) pressure and log fO2 D) log fO2 and temperature. In panel (B), the inset shows the effect of Si on the N content in the alloy melt under extremely reduced conditions. In panel (C), the modelled N saturation limit in the relevant P-T, calculated using eqn. (7) from Speelmanns et al. (2018) is plotted for comparison. Larger symbols (circles, squares, and uppointing triangles) show data from this study, while smaller symbols represent data from Grewal et al. (2019). Some data points are moved slightly on the X-axis to increase their visibility for comparison (e.g., in A) and B) data at 0 wt.% S and Si are moved to the left of 0). Error bars represent ±1-σ deviation based on the replicate electron microprobe analyses; where absent, the error bars are smaller than the symbol size.
Variation as a function of Si content in the alloy melt
To constrain the effect of Si on the N content in the alloy melt, we have plotted S-free experiments over the entire P and fO2 range within a narrow T interval (1600–1800 °C) in Fig. 3B. In contrast to the S content in the alloy, incorporation of even small amounts of Si leads to an exponential decrease in the N content in the alloy melt regardless of P-T. In Si-free alloys, the N content varies between ~0.5 and 3.4 wt.%, with a higher N content in the alloy corresponding to higher P. An increase in Si content in the alloy, with values as low as ~0.2 wt.%, leads to a considerable drop in the N content and with > 1 wt.% Si in the alloy, the N content drops to < 0.1 wt.% with near P independence.
Although a decrease in fO2 is generally followed by an increase in the Si content of the alloy under extremely reduced conditions, we observe that the incorporation of Si in the alloy plays a major role in controlling the N content of the alloy at similar log fO2. In the inset of Fig. 3B we have plotted a subset of the experimental data for Si bearing alloys for the most reduced experiments (< ΔIW - 3.0) from Fig. 3B. It can be clearly seen that for extremely reduced condition, the N content in the alloy melt is largely set by Si content in the alloy, i.e., alloy melts having similar fO2 have lower N content with higher amount of Si content in the alloy.
Variation with Pressure
Fig. 3C shows that for Si- and S-free alloys, at a given fO2, P has a positive effect on N incorporation in the alloy melt, while at a given P, the N content in the alloy melt decreases with decrease in fO2.(in agreement with Dalou et al. (2017)). Additionally, it can be observed from Fig. 3A and Fig. 3B that P also has a positive effect on incorporation of N in the S-bearing alloy melt under relatively oxidized conditions (> ~ΔIW - 1.1) while it has a minimal effect on Si-bearing alloys (> ~0.5 wt.% Si) at extremely reduced conditions. In contrast to the Si-free alloys, where N incorporation follows Sievert’s Law (e.g., Abdulrahman and Hendry, 2001; Kowanda and Speidel, 2003), the N content in the alloy at increasingly reduced conditions shows a limited dependence on P because under those conditions it is controlled by the strong negative chemical interactions between Si and N.
Additionally, we observed a drop in the N content in the alloy melt with increase in P from 6 to 7 GPa in Fig. 3A, C under relatively oxidized conditions for S-free as well as S-bearing alloys. A similar effect has been observed in the dissolution behavior for Ni, Co and W in the alloy melt and has been explained by the possible change in the structure of the Fe-alloy melt around 5.2 GPa (Kegler et al., 2008; Sanloup et al., 2011). However, no such kink for N dissolution in the alloy melt at ~6 GPa was observed by Roskosz et al. (2013) where they showed a monotonic increase in the N content in the alloy melt with increasing P. Therefore, more experiments at higher P are needed to corroborate the change in N dissolution in the alloy melts at P > ~6 GPa because it can have a strong influence on partitioning behavior of N between the alloy and silicate melts, especially for alloy-silicate equilibration in deep MOs.
Variation with Temperature
To constrain the effect of T, we plotted in Fig. 3D, experiments at a fixed P (3 GPa) within 1600–2200 °C and over a wide fO2 range (~ΔIW - 4.0 to - 1.0). At ~ΔIW of - 1.0, N content in the alloy drops from ~2.6 wt. % at 1600 °C to ~0.6 wt.% at 2200 °C. Similarly, for ΔIW of - 2.0 to - 1.0, N content in the alloy melt shows a similar negative T dependence. For fO2 < ~ΔIW - 2.0, higher T alloys also have a lower N content, but the overall T effect begins to diminish due to greater effect of incorporation of Si in the alloy, which becomes the controlling variable under these extremely reduced conditions.
3.3.2. Variation of N content in the silicate melt with various intensive and extensive variables
Variation with Pressure
To show the effect of P on the N content in the silicate melt, we plotted S-free experiments for ThB1 and KOM silicate melts at 1600–1800 °C in a relatively oxidized fO2 (ΔIW - 1.2 to - 0.7) range in Fig. 4A. The N content in ThB1 melt increases from ~0.03 to ~0.32 wt.% with increase in P from 1 to 4.5 GPa, while in KOM melt, it increases from ~0.02 to ~0.13 wt.%. However, with increase in P from 4.5 to 6 GPa, the N content in ThB1 melt drops by a factor of three to ~0.11 wt.% followed by another increase at 7 GPa to ~0.16 wt.%, while for KOM melt the N content drops by a factor of two to ~0.6 wt.% from 4.5 to 6 GPa. This behavior is in contrast to the observations of Roskosz et al. (2013) who found out that N content in the silicate melt levels-off >3 GPa.
Fig. 4:
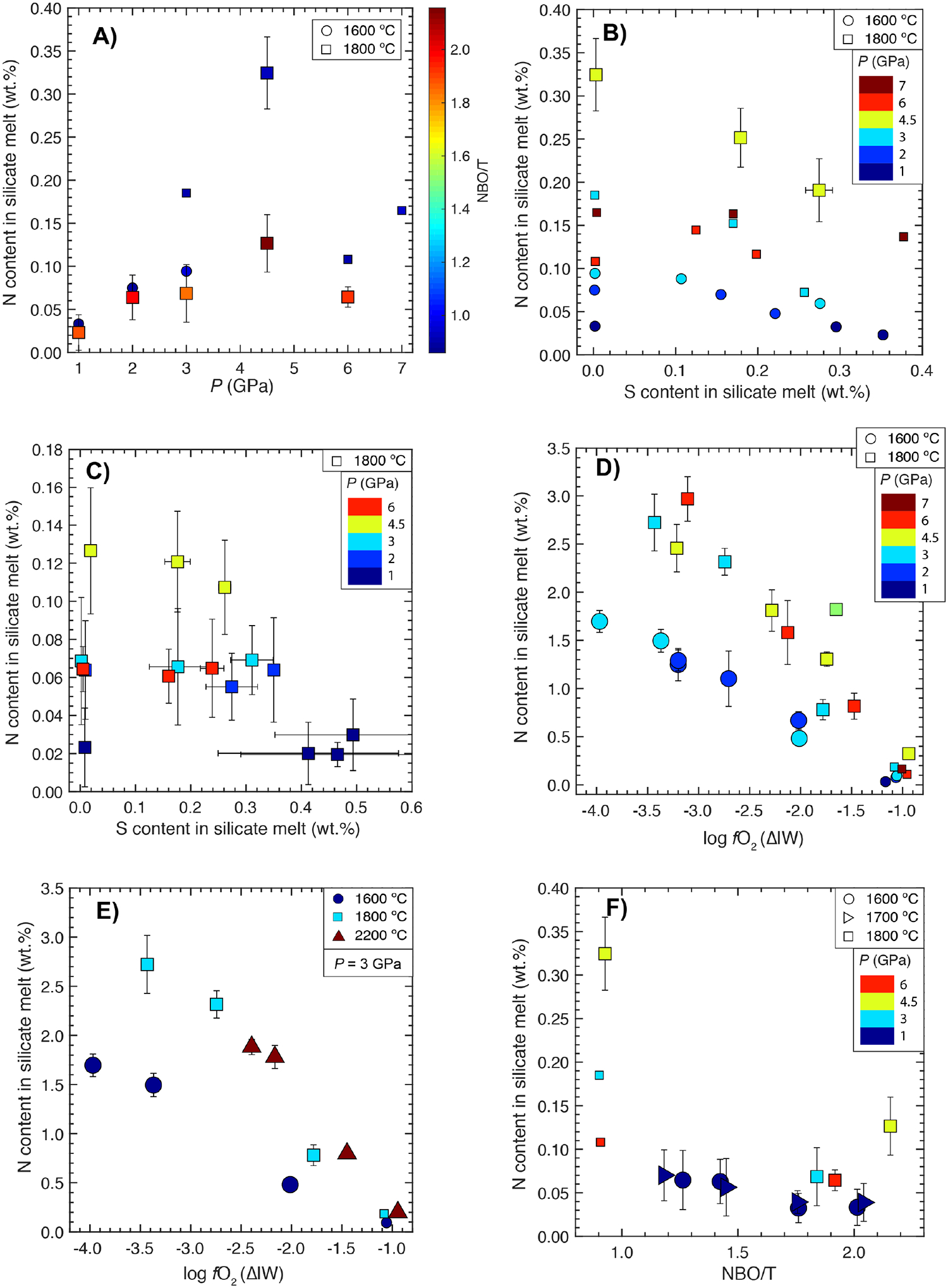
Nitrogen content in the graphite saturated silicate melts equilibrating with Fe-Ni-CN±S±Si alloy melts as a function of: A) pressure and NBO/T for starting ThB1 and KOM silicate melt compositions, B) and C) S content in the silicate melt and pressure for starting ThB1 and KOM silicate melt compositions, respectively, D) log fO2 and pressure for starting ThB1 silicate melt composition, E) log fO2 and temperature for the starting ThB1 silicate melt composition, and F) NBO/T and pressure for the starting ThB1, KOM and MO#1, #2, #3 and #4 silicate melt composition. Larger symbols (circles, squares, and up-and side-pointing triangles) show data from this study, while smaller symbols represent data from Grewal et al. (2019). Error bars represent ±1-σ deviation based on the replicate electron microprobe analyses; where absent, the error bars are smaller than the symbol size.
Variation as a function of S content in the silicate melt
To show the effect of S on the N content in the silicate melt, we plotted experiments in a relatively oxidized fO2 range (ΔIW - 1.2 to - 0.7) at 1600–1800 °C for ThB1 and KOM melts in Fig. 4B and Fig. 4C, respectively. As discussed earlier, the N content in the silicate melt for S-free conditions is highest at 4.5 GPa, and this trend continues for S bearing melts as well. At 4.5 GPa in ThB1 melt (Fig. 4B), the N content drops from 0.33 wt.% to 0.19 wt.% with an increase in S from 0 to ~0.27 wt.%. For other P-T conditions, although there is a no clear drop in the N content in ThB1 melt with an increase in S from 0 to ~0.2 wt.%, but with a further increase in the S content > 0.2 wt.%, the N content drops slightly relative to S-free conditions. Although for KOM melts (Fig. 4C) there is a small drop in the N content with increase in S at 4.5 GPa, for all other P, the N content remains almost unchanged with increase in S.
Variation with Oxygen fugacity (fO2)
To constrain the effect of fO2 on the N content in the silicate melt, we plotted S-free experiments at 1–7 GPa and 1600–1800 °C over a wide range of fO2 (~ΔIW - 4.0 to - 0.7) for starting ThB1 melt composition. Similar to the observations in previous alloy-silicate partitioning studies (e.g., Li et al., 2016a; Dalou et al., 2017), melt SiO2 increases and melt FeO decreases with decrease in fO2 according to the following reaction:
| (Eqn. 3) |
Similarly, our silicate melt composition changes from basaltic (~45 wt.% SiO2) to dacitic (~68 wt.% SiO2) with decrease in log fO2 from ~ΔIW - 0.7 to - 4.0.
In agreement with results from several previous experimental studies (Libourel et al., 2003; Mysen et al., 2008; Kadik et al., 2011; Kadik et al., 2013; Kadik et al., 2015; Dalou et al., 2017; Kadik et al., 2017), the N content in the silicate melt increases with decrease in fO2 (Fig. 4D). The N content increases from ~0.05–0.4 wt.% to ~1.7–3.0 wt.% with decrease in log fO2 from ΔIW - 0.7 to - 4.0. Compared to the relatively oxidized conditions (~ΔIW of −1.0) (Fig. 4A), the N content in the silicate melt loses its P dependence with increasingly reduced conditions, while T has a strong positive effect over the entire fO2 range.
Variation with Temperature
To isolate the effect of T on the N content in the silicate melt, in Fig. 4E we plotted S-free experiments at 3 GPa and 1600–2200 °C over a wide fO2 range (~ΔIW - 4.0 to - 1.0) for starting ThB1 melt composition. For a given fO2, as T increases from 1600 to 1800 °C, the N content in the silicate melt increases by a factor of ~1.5–2, but the strength of T effect diminishes with a further increase in T to 2200 °C. Even though all three sets of experiments at 1600 °C, 1800 °C and 2200 °C were performed with similar starting alloy-silicate mixes depending upon the desired fO2, increasingly higher T experimental products are more oxidized, therefore, highest T (2200 °C) experiments capture a smaller fO2 range. A similar increase in the experimental fO2 at similarly high T (>2000 °C) has been observed by Li et al. (2016a). Despite this experimental caveat, in agreement with Roskosz et al. (2006), we observe that at a given fO2, T has a strong positive effect on N dissolution in the silicate melt.
Variation with Silicate Melt Composition
To isolate the effect of silicate melt composition on N dissolution in silicate melts, we compare data between two sets of experiments within a narrow fO2 range (~ΔIW - 1.1 to - 0.9) at similar T (Fig. 4F). We did not include reduced experiments (~ < ΔIW - 1.1) in the comparison, because even though more reduced experiments have lower NBO/T (where NBO/T is a measure of degree of silicate melt polymerization and is expressed as total non-bridging oxygens per tetrahedral cations; NBO/T = (2 × Total O)/T - 4, where T = Si + Ti + Al + Cr + P (e.g., Mysen et al., 1982)), under those conditions fO2 has a primary control on N dissolution in the silicate melt and the silicate melt composition changes only in response to the imposed fO2 (Eqn. 3).
Fig. 4F shows that for a given P (3, 4.5 and 6 GPa) and at a fixed T (1800 °C), the N content in the silicate melt drops by a factor of ~2 as we move from ThB1 (less mafic, lower NBO/T) to KOM (more mafic, higher NBO/T) melts in a narrow fO2 range. Even though there is a possibility that the N content in KOM quench products may not represent the equilibrium concentration of N in the silicate melt (as quenched KOM melts are composed of interstitial glassy patches between blades of dendritic olivine crystals, there is a possibility of N loss during quenching of the experiment), but a similar drop observed for 6 GPa experiments between ThB1 melt (composed of quenched micro-crystals) and KOM shows that the effect of NBO/T is real and substantial. This observation is further substantiated by another set of experiments at 1 Gpa-1600 ° and 1 GPa-1700 °C with NBO/T of silicate melt compositions varying from that of a basalt towards ultramafic compositions (MO#1, #2, #3 and #4 in Table 1) (Fig. 4F). MgO content of the silicate melt compositions in this set varies from ~10 to 23 wt.%, therefore, as we traverse from MO#1 to MO#4, NBO/T of the silicate melts increases. MO#1 to MO#3 silicate melts quenched as glasses. Although MO#4 partially quenched to a glass, but yielded large enough glassy pools that could be analyzed for N. Therefore, we could clearly map out the effect of NBO/T on N dissolution in the silicate melts without the potential problem of N loss due to quenching. For a given silicate melt composition, the N content in the silicate melt is higher at a higher T, except for MO#2. The N content is almost similar for MO#1 and MO#2, lying in a range of ~0.06–0.07 wt.%, but from MO#2 to MO#3 it drops to ~0.03–0.04 wt.% and finally converging to a similar value for MO#4. This shows that N dissolution in the silicate melts drops by a factor of ~2 from basaltic to ultramafic melts under relatively oxidized conditions. A similar drop of N content in the silicate melt with an increase in NBO/T has also been observed in Roskosz et al. (2006).
4. Discussion
Because experimentally determined depends both on the N content in the alloy and silicate melt, it is directly dependent on P, T, fO2, and alloy and silicate melt compositions. In Section 4.3, we discuss the effect of each thermodynamic variable on and in Section 4.4, we compare the relative effect of these variables on , which directly dictates the N budget in the alloy and silicate reservoirs of Earth for a range of relevant core formation scenarios. However, first we discuss (1) whether along with providing N partitioning data, the experimental phases are nitrogen-vapor saturated and therefore yield N-vapor solubility data (Section 4.1). In the same section we also assess whether our experimental capsules remained a closed system with respect to N, and (2) the potential effect of speciation change of N in the silicate melt, primarily as a function of fO2, and its effect in controlling (Section 4.2).
4.1. Are the experiments N-rich fluid saturated?
The textural analyses of our experiments do not show any obvious signs of vapor bubbles, however, the presence of submicroscopic bubbles especially in the graphite capsule pores is difficult to rule out. In Fig. 3C we compared the N contents in Si- and S-free alloy melts from our experiments with the nitrogen solubility model of Speelmanns et al. (2018). This comparison shows that at 2 GPa the alloy melts might have reached their N-vapor saturation limits irrespective of their corresponding fO2, while alloy melts at P = 3 GPa might have been N saturated only at the most oxidized conditions while increasingly reduced conditions led to the formation of N undersaturated alloy melts. However, all alloy melts at P > 3 GPa fall distinctly below N-vapor saturation limit irrespective of fO2. Therefore, at P < 3 GPa, our experiments could be yielding solubility of N-rich vapor in both alloy and silicate melts in addition to yielding , while all other experiments provide constraints on only. To test this further, we estimate below the total N inventory that may be stored in the alloy + silicate melt phases in each experiment and how such total N abundance compare with the added bulk N contents.
All experiments presented in this study were conducted with ~5 wt.% N in the starting alloy mixture (except G545–1 to 4 and G549–1 to 4) - with Fe4N, Fe7N3 or Si3N4 as the N source depending upon the desired fO2. This translates to ~1.4–1.8 wt.% bulk N in the starting alloy-silicate mixture with an alloy: silicate mass ratio of ~1:2. Thermal decomposition reaction of N-bearing phases, which proceeds via the release of molecular nitrogen (Batha and Whitney, 1973; Ertl et al., 1979; Widenmeyer et al., 2014), can be written as:
| (Eqn. 4) |
| (Eqn. 5) |
| (Eqn. 6) |
We did not find any unreacted Fe4N, Fe7N3 or Si3N4 domains in any of our resulting experimental products; therefore, N-bearing reactants must have decomposed entirely in the course of heating or during the experiments. Fe4N, Fe7N3 or Si3N4 thermally decompose above 800 °C at ambient pressure (Goodeve and Jack, 1948; Batha and Whitney, 1973; Ertl et al., 1979); therefore, at higher pressures, following Le Chatelier’s principle, endothermic thermal decomposition of N-bearing phases must have taken place after the sintering phase of the experiment - either during the heating phase or at the target T of the experiment.
If the experiments were N-vapor undersaturated, then the entire amount of bulk N would be dissolved in the molten alloy and silicate melt phases and the net weight of N in the quenched alloy and silicate products would add up approximately to the initial weight of N in the starting mixture; on the other hand, if the experiments were N-vapor saturated, there should be a deficit between the bulk N and the total N inventory contained in the alloy plus silicate melt phases. Assuming a mass ratio of ~1:2 for the equilibrating alloy and silicate melts, we calculated the net amount (wt.%) of N in the quenched alloy + silicate phases (Fig. 5A). Although the exact mass ratio of the equilibrating alloy and silicate melts cannot be accurately estimated, a first order approximation can be used to assume their mass ratio to be 1:2, i.e., approximately equal to the mass ratio of alloy and silicate in the starting mixtures. It is important to note that extremely reduced experiments over predict net the N content in quenched alloy+silicate melts because reduction of FeO in the silicate melt by metallic Si leads to the production of extra metallic Fe in the reaction products, thereby leading to an increase in the alloy/silicate mass ratio above 1:2 for such cases. To compare amongst only a few controlling variables, we have plotted experiments with starting ThB1 and ThB silicate melt composition and S-free alloys in a narrow T range (≤ 1800 °C; Fig 5A). Additionally, we have also plotted contributions of N concentrations (wt.%) in the alloy (Fig. 5B) and silicate melt (Fig. 5C) to the total N content in alloy+silicate mix.
Fig. 5:
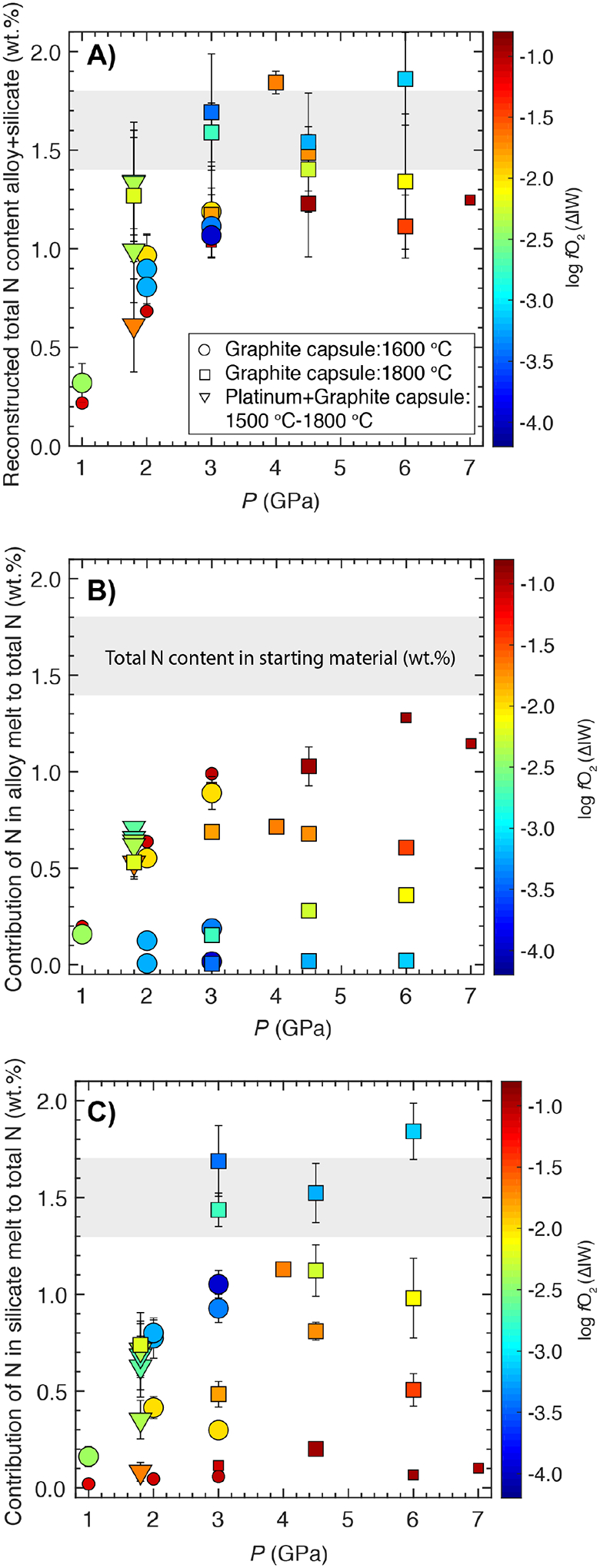
Nitrogen content in A) the alloy+silicate melt, and the contributions of: B) N in the alloy melt and C) N in the silicate melt (C) to the total N (assuming an alloy/silicate mass ratio in the quenched products to be ~1:2) as function of pressure and log fO2 for either the starting ThB1 or ThB silicate melt composition equilibrating with Fe-Ni-C-N±S±Si alloy melts under graphite saturated conditions. Grey band represents estimated the N content (wt.%) in the starting alloy+silicate mixture. Larger symbols show data from this study (circles, squares, and downpointing triangles), while smaller symbols represent data from Grewal et al. (2019). Some data points are moved slightly on the X-axis to increase their visibility for comparison (e.g., in A), B) and C) data at 2 GPa for starting ThB melt composition are moved to the left of 2). The error bars are same as in Fig. 4.
Fig. 5A shows that the total amount of N in the final experimental products is less or approximately equal to the initially added N with the differences being higher at lower P. Fig. 5A also shows that in addition to P, the net amount of N in the experimental products (alloy+silicate) depends on fO2 for Si free alloys and fO2 as well as the Si content of the alloy for Si bearing alloys. Fig. 5B shows that the contribution from the N content in the alloy phase decreases with decrease in log fO2. For the oxidized experiments (> ~ΔIW - 1.1), the N content in the alloy melt increases with increase in P, which means under those conditions it supports Sievert’s Law behavior, i.e., XN,alloy melt ∝ (pN2)0.5 (where, X represents concentration (wt.%) and p represents partial pressure). At increasingly reduced conditions (< ~ΔIW - 1.1), the N content in the alloy melt slowly loses its P dependence and it is controlled by Si content in the alloy, i.e., the chemical composition of the alloy melt, for the most reduced experiments. Similarly, Fig. 5C shows that contribution from the N content in the silicate melt is also dependent on P and fO2 where under relatively oxidized conditions the N content in the silicate melt increases with increase in P according to Henry’s Law, while under increasingly reduced conditions the N content in the silicate melt loses its P dependence, which means that it is controlled by the chemical interactions of N with the silicate melt structure.
We conclude that even though there might be a loss of varying amount of N-bearing vapor for low P (< 3 GPa) experiments, our experiments yield meaningful information on because at any given P, is strongly dependent on fO2, i.e., the composition of the alloy and silicate melts. Additionally, in contrast to Speelmanns et al. (2018), we find that there is no significant difference of N content in the resulting experimental products irrespective of whether a single graphite or double Platinum-graphite capsule is used (Fig. 5). This would mean that the enclosing graphite capsule remained closed and any possible deficit of N during the experimental run would be stored in the pores of graphite capsules (Kadik et al., 2017).
4.2. Mechanism of nitrogen dissolution in the silicate melt
Because is inversely proportional to the N content in the silicate melt, the mechanism of N incorporation in silicate melt is critical for understanding any variation of it. Previous studies on N solubility in the silicate melts have reported that at relatively oxidized conditions (~ > ΔIW - 1.1), N dissolves predominantly as molecular N2 while at increasingly reduced conditions (~ < ΔIW - 1.1), N begins to chemically interact with the silicate melt structure through formation of reduced species linking via anhydrous Si-N bonds and/or hydrated Si-N-H bonds (Miyazaki et al., 1995; Libourel et al., 2003; Miyazaki et al., 2004; Roskosz et al., 2006; Mysen et al., 2008; Armstrong et al., 2015; Mosenfelder et al., 2019). At 1 atm and relatively oxidized conditions, N dissolution, similar to noble gases, is shown to follow Henry’s law behavior with its Henry’s constant being approximate equal to that of Ar owing to the similarity of size between N2 and Ar (Miyazaki et al., 1995; Libourel et al., 2003). If the N dissolution in the silicate melts follows predicted Henry’s Law behavior in relatively oxidized conditions throughout the entire P range (Miyazaki et al., 1995; Libourel et al., 2003; Roskosz et al., 2006), then the N content in silicate melt should monotonically increase with increase in P from 1 to 7 GPa at a fixed T. However, the N content in both ThB1 and KOM silicate melt composition increases with increase in P till 4.5 GPa, followed by a drop (Fig. 4A). This drop in the N content in the silicate melts at P > 4.5 GPa can be explained either by N loss during quenching, or a change in the silicate melt structure at ~4.5 GPa. In contrast to ThB1 melts between 1 and 4.5 GPa, which quenched as a homogenous glass, optical examination of the quenched ThB1 melts at 6 and 7 GPa shows the uniform presence of micro-crystals. However, if the loss of N in ThB1 melts at 6 and 7 GPa was chiefly due to the crystallization of the melt during quenching, then KOM melt, which had a uniform quench texture of blades of olivine crystals with interstitial glassy patches across the entire P range of 1–6 GPa, would not have showed the observed drop of the N content with increase in P from 4.5 to 6 GPa.
Previous studies (except Schmidt and Keppler (2002)) observed a similar drop in Ar solubility from 5 to 6 GPa followed by a slight increase at 7 GPa in SiO2 melts (Chamorro-perez et al., 1996), San Carlos Olivine melts (Chamorro-Perez et al., 1998) and CI-chondritic melts (Bouhifd and Jephcoat, 2006). These studies confirmed the Ar solubility trend irrespective of the presence of re-crystallization textures in the silicate melts. Chamorro-Perez et al. (1996) postulated that the drop in Ar solubility at P > 5 GPa was due to important structural changes in the silicate melts, with a possible decrease in the size of silicate tetrahedral clusters and voids, around 5 GPa. Because Ar and N2, owing to similarity of their sizes, show similar solubility behavior in silicate melts at relatively oxidized conditions (e.g., Miyazaki et al., 1995), a change of the silicate melt structure can be the controlling variable in affecting N incorporation in the silicate melts at P > 5 GPa.
Under increasingly reducing conditions (~ < ΔIW - 1.1), N dissolution in the silicate melt gradually loses its P dependence (Fig. 4D) and has been explained by the chemical interaction of N with the silicate melt structure. Several previous experimental studies have postulated that under such conditions, N present in −3 oxidation state, i.e., as N3− or NH2− or , dissolves in the silicate melt structure by replacing either bridging oxygen or non-bridging oxygen in the silicate melt structure (Libourel et al., 2003; Roskosz et al., 2006; Mysen et al., 2008; Kadik et al., 2011; Kadik et al., 2013; Armstrong et al., 2015; Kadik et al., 2015; Kadik et al., 2017; Mosenfelder et al., 2019). However, whether N dissolves primarily as hydrous Si-N-H or anhydrous Si-N linkage depends upon whether the N content in the silicate melt under these reduced conditions correlates with the bulk hydrogen content of the melt. Decrease in fO2 along with the presence of water leads to an increase in fH2, which can account for an increase in N-H speciation in the silicate melt structure. Although the presence of N-H speciation in the reduced silicate melts has been corroborated by spectrographic analysis (Kadik et al., 2011; Kadik et al., 2013; Armstrong et al., 2015; Kadik et al., 2015; Kadik et al., 2017; Mosenfelder et al., 2019), the lack of any correlation between N content in the silicate melt and bulk hydrogen content at increasingly reduced conditions from the data of Dalou et al. (2017) shows that Si-N-H linkage cannot solely explain high N dissolution in silicate melts under reduced conditions. This observation has also been confirmed by Mosenfelder et al. (2019). Additionally, Libourel et al. (2003) observed an increase in N solubility in the silicate melt under increasingly reduced conditions for a nominally hydrogen-free vapor system; therefore, they postulated N dissolution primarily as N3− either as Si-N or Ti-N linkage as the primary contributors of N dissolution in reduced silicate melts. Hence, we argue that although a fraction of the increase in N content of silicate melts with decreasing fO2 is owing to N-H species formation, the main increase and resultant decrease in is likely caused by the increased stabilization of dissolved anhydrous Si-N and/or Ti-N species in the silicate melt.
4.3. Partition coefficient of N between alloy and silicate melt ()
4.3.1. Effect of Pressure
The effect of P on is shown in Fig. 6A () and Fig. 6B (). The plotted experiments are for ThB1 silicate melt-bearing compositions from this study in a narrow T range (1600–1800 °C) and S-free conditions and over the entire P range (1–7 GPa). Relevant data in a similar T range from previous studies (Dalou et al., 2017; Grewal et al., 2019) are also plotted. Fig. 6A shows that at any given P, decreases with decrease in fO2. For the most oxidized experiments, increases from ~16 to 28 with an increase in P from 1 to 3 GPa at 1600 °C. At 3 GPa, drops from ~28 to 13 with increase in T from 1600 to 1800 °C and it drops to ~8 with further increase in P from 3 to 4.5 GPa. From 4.5 to 6 GPa, increases to ~32 followed by a drop to ~18 at 7 GPa. increases with increase in P from 1 to 3 GPa at 1600 °C because increase in the N content in the alloy melt outpaces the N content in the silicate melt in that range. The N content in the alloy melt increases monotonically from 1 to 6 GPa with a small drop at 7 GPa (Fig. 3A), while the N content in the silicate melt shows a similar trend as with increase in P (Fig. 4A); therefore, the overall pattern of variation with increase in P for the most oxidized experiments replicates N content in the silicate melt variation with P. It is important to note that the overall trend of variation with increase in P is also shown by relatively reduced set of experiments, albeit in a smaller range due to decrease in the siderophile character of N with decreasing fO2 (Fig. 6A).
Fig. 6:
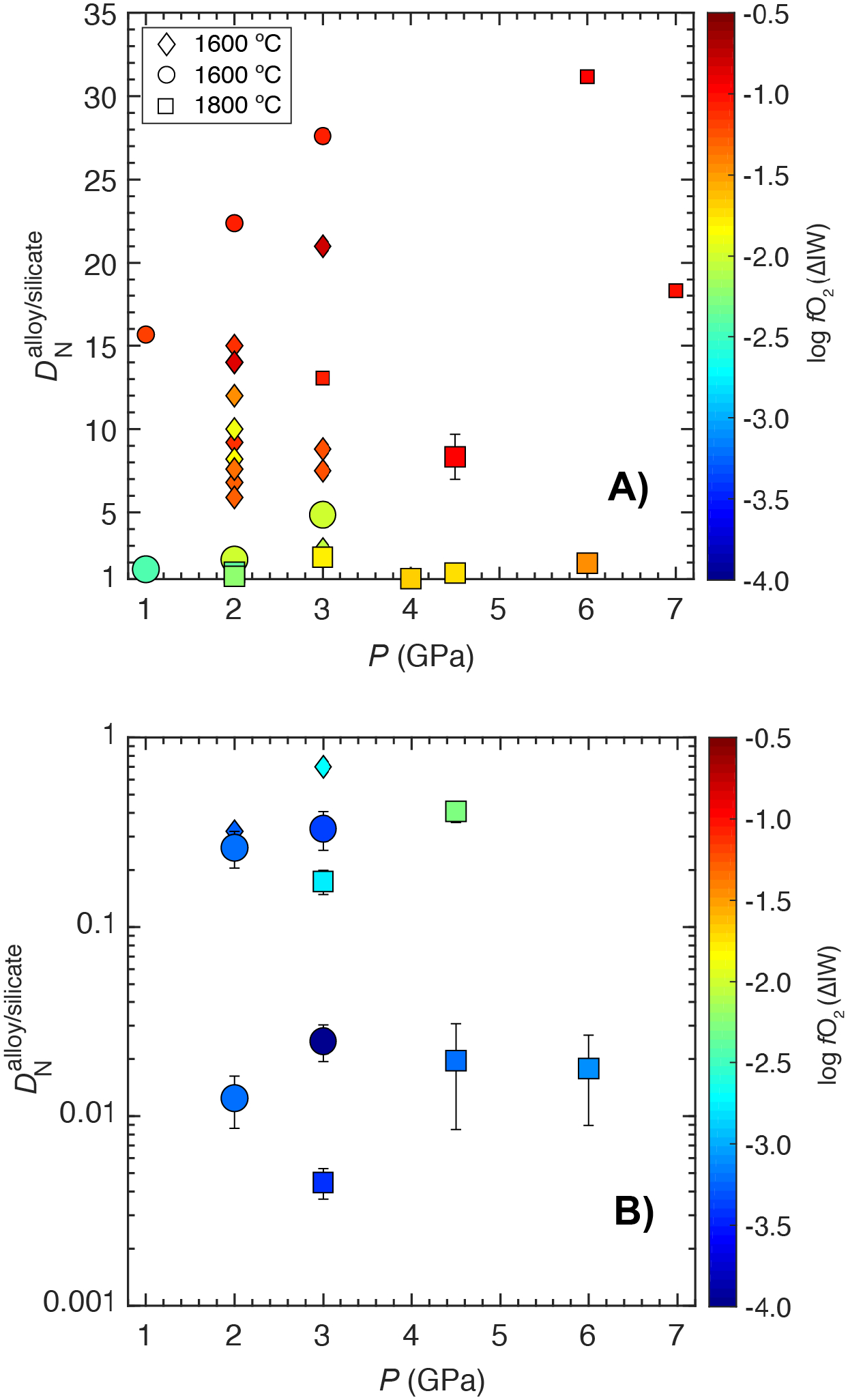
for the starting ThB1 silicate melt-Fe-Ni-C-N±S±Si alloy melt in equilibrium under graphite saturated conditions as function of pressure and log fO2 when nitrogen shows A) siderophile, and B) lithophile character. Effect of P on decreases with decrease in log fO2 when N acts as a siderophile element, whereas P has negligible effect on when N acts a lithophile element. Larger symbols show data from this study (circles and squares), while smaller symbols (circles and squares) represent data from Grewal et al. (2019), and diamonds from Dalou et al. (2017). Error bars represent ±1-σ deviation based on the replicate electron microprobe analyses; where absent, the error bars are smaller than the symbol size.
Under increasingly reduced conditions where N shows lithophile behavior (Fig. 6B), does not show any clear correlation with P, because as discussed earlier, under extremely reduced conditions the N content in both the alloy and silicate melts are controlled by their respective chemical compositions, i.e., Si content of the alloy and chemical bonding of N in the silicate melt, respectively.
4.3.2. Effect of S content in the alloy melt
In agreement with Grewal et al. (2019), we found out that at 4.5 GPa and 1800 °C (Fig. 7A), similar to any other given P-T, increases slightly from S-free alloy melt-bearing system to a system with ~16 wt.% S in the alloy melt, and it drops by a factor of two for a system with > ~20 wt.% S in the alloy melt for ThB1 silicate melt composition in a relatively oxidized range (ΔIW - 1.2 to - 0.7). Similar effect of S content in the alloy melt on for experiments with KOM silicate melt compositions (Fig. 7B) demonstrates that this effect holds irrespective of the silicate melt composition. For KOM silicate melt composition at 6 GPa, increases sharply with increase in the S content in the alloy melt from 0 to ~12 wt.% followed by a drop in the S-rich alloys. Because there is a significant drop in the N content of the alloy melt in S-rich systems (Fig. 3A) without any significant effect on N content in the silicate melt (except for 4.5 GPa experiments; Fig. 4B,C), negative interaction between N and S in the alloy melt under such conditions is the controlling factor for the trend in .
Fig. 7:
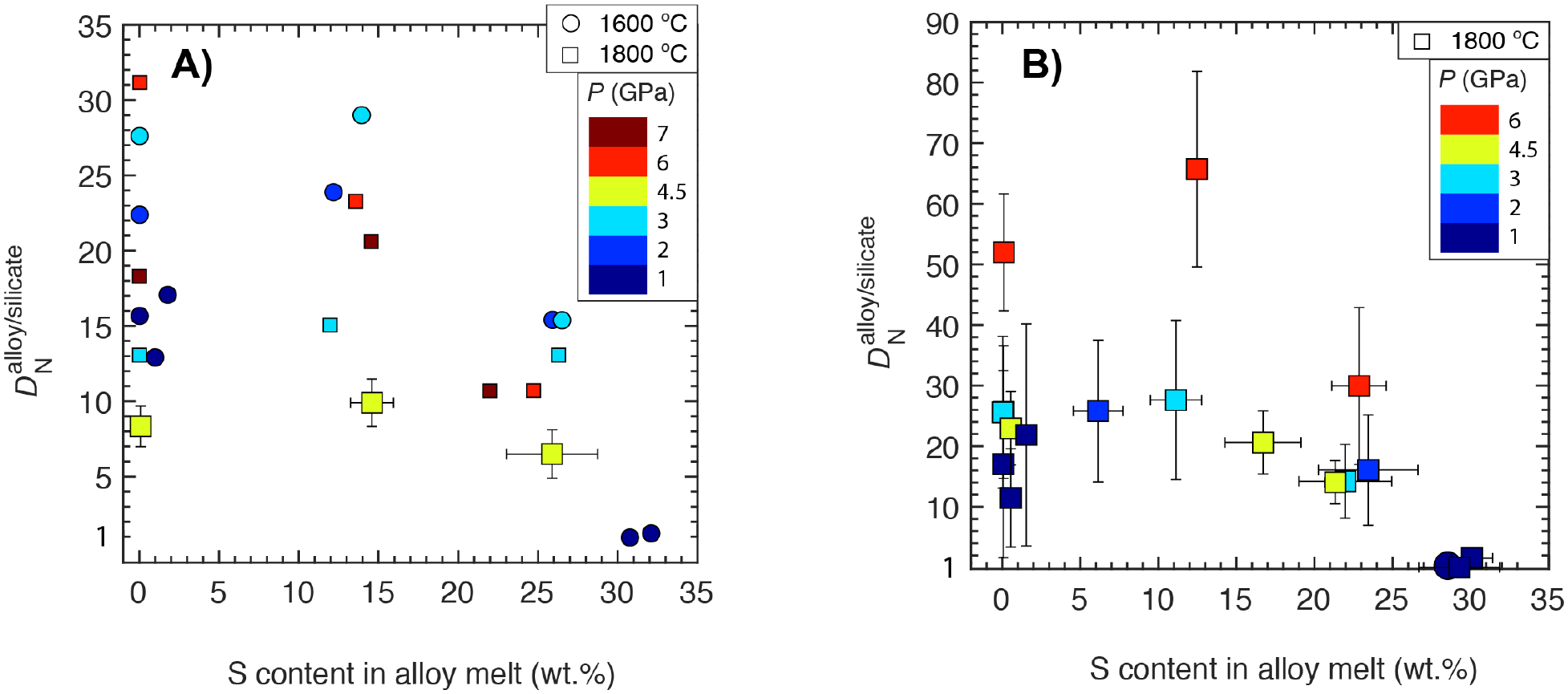
for the starting A) ThB1 and B) KOM silicate melt equilibrating with FeNi-C-N±S alloy melt under graphite saturated conditions content as a function of S content in the alloy melt and pressure in a relatively oxidized log fO2 range (< ~ΔIW - 1.2). For a similar P-T, for KOM bearing silicate melt-bearing systems is generally higher than ThB1 silicate melt-bearing systems as N content in KOM melts is lower than ThB1 silicate melts. The symbols and the error bars are same as in Fig. 6.
It is important to note that the experiments with extremely S-rich immiscible alloy melts (>30 wt.% S) from 1 GPa experiments have extremely low values in comparison to experiments at P > 1 GPa. To determine whether the extremely low for > 30 wt.% S in the alloy estimated at 1 GPa is due to the strong negative chemical interaction of S and N in extremely S-rich systems and holds true even for experiments at P > 1 GPa or is primarily a consequence of low P, more experimental work at higher pressures for extremely S-rich systems would be required.
4.3.3. Effect of oxygen fugacity (fO2) and Si content in the alloy melt
To constrain the effect of fO2, we have plotted experiments with starting ThB1 composition from this study and other previous studies (Dalou et al., 2017; Grewal et al., 2019) in a wide P (1–7 GPa) and limited T range (1600–1800 °C) for S-free systems (Fig. 8A). Fig. 8A shows, in accordance with results of Dalou et al. (2017), that drops exponentially with decrease in log fO2. As the N content in the alloy melts decreases, while the N content in the silicate melts increases with decrease in log fO2 (Fig. 3D, Fig. 4D); therefore, due to their cumulative effect, drops exponentially with decreasing log fO2.
Fig. 8:
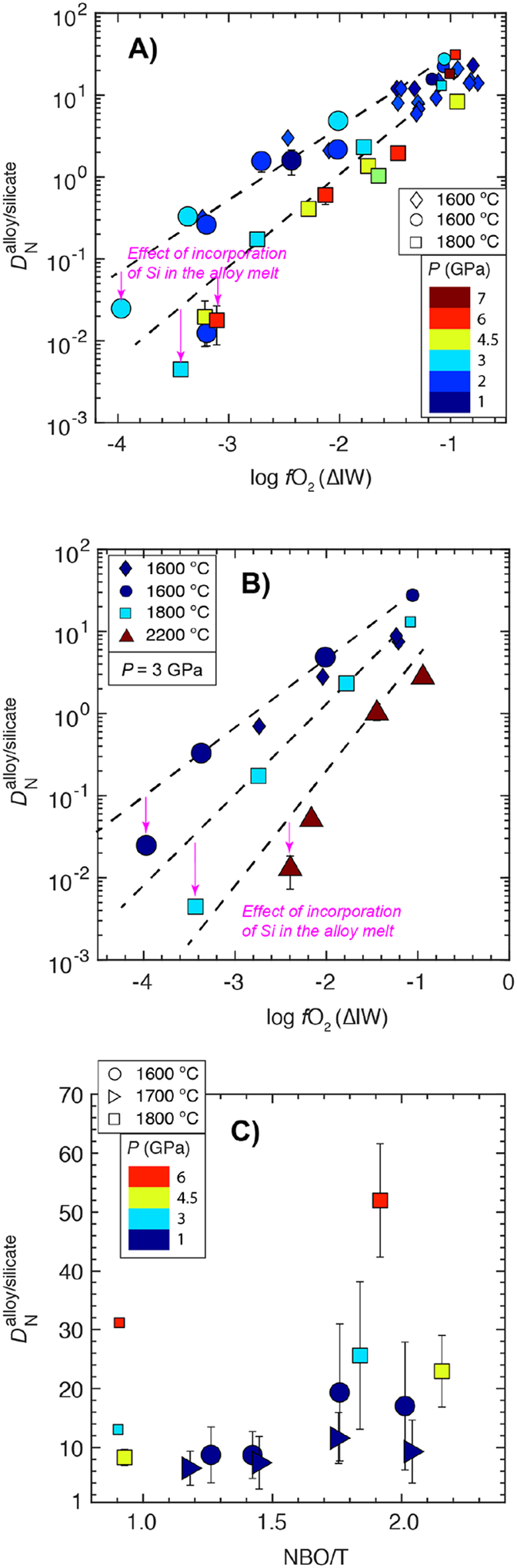
for silicate melt-Fe-Ni-C-N±S±Si alloy melt equilibria in graphite saturated conditions as functions of A) oxygen fugacity and pressure, B) oxygen fugacity and temperature, and C) NBO/T and pressure. The dashed lines represent the trend of decrease in with decrease in log fO2 while downwards pointing pink arrows demarcate the additional effect of incorporation of Si in the alloy melt under extremely reducing conditions. See texts for the description of data trends. The symbols and the error bars are same as in Fig. 6.
However, under extremely reduced conditions there is an extra drop in , in addition to the log fO2 trend, at a given T which can only be explained by the incorporation of Si in the alloy melt (Fig. 8A,B). The experimental dataset from this study has small variations in the amounts of Si in the alloy (0 to 2.5 wt.%), hence, the log fO2 term is more sensitive to the variations in the FeO content of the silicate melt (wt.%) as the incorporation of small amounts of Si in the alloy melt has a minimal effect on the calculated log fO2 term. Therefore, the variation in log fO2 term only is not able to capture the variation of under extremely reducing conditions (< ΔIW - 3.0) which makes the Si content of the alloy, in addition to the log fO2 term, important.
4.3.4. Effect of Temperature
To constrain the effect of T with change in fO2 on , we have plotted experiments with a starting ThB1 composition at 3 GPa at 1600–2200 °C over the entire fO2 range (Fig. 8B). For comparison we have also plotted values from Dalou et al. (2017) and Grewal et al. (2019) at 3 GPa. At a given fO2, decreases with increase in T because the N content in the alloy melt decreases (Fig. 3D), while the N content in the silicate melt increases (Fig. 4E) with increase in T at a fixed fO2. Furthermore, the negative effect of T on increases at increasingly reduced conditions. For example, at ~ΔIW of - 0.7, drops from ~20 to 2 with an increase in T from 1600 °C to 2200 °C, while at ~ΔIW of - 2.2, drops by two orders of magnitude with an increase in T in a similar range.
4.3.5. Effect of Silicate Melt Composition (NBO/T)
We compare the effect of silicate melt composition on by plotting two different sets of experiments in a limited fO2 range (~ΔIW - 1.1 to - 0.9) and S-free conditions. First, we compare for the experiments at 4, 4.5, and 6 GPa and at a fixed T (1800 °C) with two distinct silicate melt compositions, ThB1 (NBO/T ~0.9) and KOM (NBO/T ~1.8–2.2) (Fig. 8C). At any given P, increases by a factor of ~2 as the system changes from ThB1 to KOM silicate melt compositions due to a drop in the N content in the silicate melt by a factor of ~2 in more mafic melts, while the N content in the alloy remains unchanged at a fixed P. For the second set of experiments, is compared for systems with the silicate melt compositions MO#1, MO#2, MO#3, and MO#4 (NBO/T ~1.2–2.1) at 1 GPa-1600°C and 1 GPa-1700 °C (Fig. 8C). Between MO#1 and #2, is almost unchanged (~6–9) without any significant effect of T, while from MO#2 to MO#3 and #4, increases by a factor of ~2 at 1600 °C (~17–19), while at 1700 °C, increase in (~9–12) is not significant because the N content in the alloy melt drops by ~0.15 wt.% as T increases from 1600 °C to 1700 °C, while the N content in the silicate melt for MO#3 and MO#4 is almost unchanged for the T variation. The results from these two sets of experiments suggest that at a fixed P-T, increases by a factor of ~2 as NBO/T increases from 1 to 2. As terrestrial MOs are thought to have peridotite-like melt composition, which have an even higher NBO/T (~2.6–2.8), therefore, the effect of silicate melt composition on can be significant when experimental data is extrapolated to MO conditions. Given almost all of the previous studies till date (Kadik et al., 2011; Kadik et al., 2013; Kadik et al., 2015; Li et al., 2016b; Dalou et al., 2017; Kadik et al., 2017; Grewal et al., 2019) have constrained using basaltic or even more polymerized melts, their reported , especially for relatively oxidized conditions, would represent a minimum bound.
4.4. Parametrization of
The MO conditions during Earth’s differentiation may cover a wide compositional range, especially in terms of the depth, temperature, redox state, and composition of the equilibrating alloy (e.g., Wade and Wood, 2005; Wood et al., 2008; Rubie et al., 2011; Badro et al., 2015). Even though the deep MO conditions for Earth may be more extreme than those tested in our experiments, especially in terms of P and T, parametrized relationships between different variables explored in this study and several previous studies (Kadik et al., 2011; Kadik et al., 2013; Roskosz et al., 2013; Kadik et al., 2015; Li et al., 2016b; Dalou et al., 2017; Kadik et al., 2017; Grewal et al., 2019) based on equilibrium thermodynamic quantification can be used to predict the fate of nitrogen during alloy-silicate equilibration for a wide range of accretion and differentiation scenarios on Earth.
for all sets of experiments in this study and all previous studies (Kadik et al., 2011; Kadik et al., 2013; Roskosz et al., 2013; Kadik et al., 2015; Li et al., 2016b; Dalou et al., 2017; Kadik et al., 2017; Grewal et al., 2019) as a function of log fO2 and T shows that fO2 followed by T has the strongest control on the alloy-silicate partitioning behavior of N (Fig. 9). However, it should be noted that from Roskosz et al. (2013) lying in a T range of 2277–2577 °C do not show a negative T dependence of . As the experiments at higher T in Roskosz et al. (2013) were also conducted at higher P; therefore, the effects of P and T maybe coupled for those experiments, which could be one of the primary reasons on the lack of T effect on in that study.
Fig. 9:
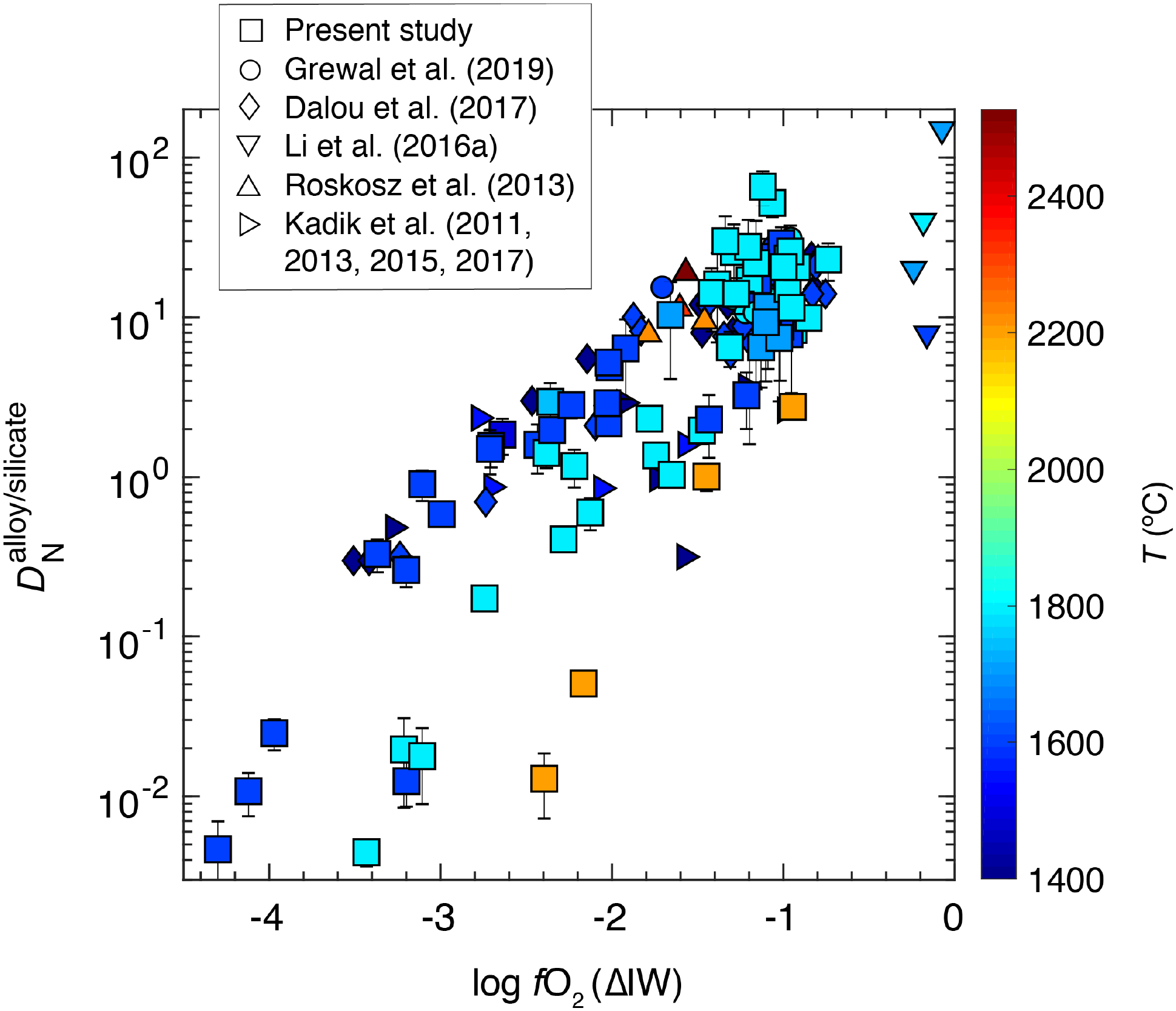
for Fe-Ni±C-N±S±Si alloy melt-silicate melt equilibria as a function of oxygen fugacity and temperature. Broadly, decreases with decrease in log fO2 with the negative effect of T becoming stronger under increasingly reduced conditions. Symbols represent all data from this study (except for experiments with immiscible alloy melts) and several previous studies (Kadik et al., 2011; Kadik et al., 2013; Roskosz et al., 2013; Kadik et al., 2015; Li et al., 2016b; Dalou et al., 2017; Kadik et al., 2017; Grewal et al., 2019). The error bars are same as in Fig. 6.
Because fO2 is the controlling parameter for , alloy-silicate equilibration can be studied by assuming an exchange reaction between reduced N dissolved in −3 oxidation state in the silicate melt (does not necessarily mean that N3− is the speciation of N in the silicate melt) and neutral N atoms dissolved in interstitial voids in Fe-alloy (Li et al., 2016b):
| (Eqn. 7) |
Accordingly, it can be seen from Fig. 9, log increases by a factor of ~0.75 with increase in log fO2, therefore, it can be assumed that N in - 3 oxidation state is the dominant N species in the silicate melt under increasingly reduced conditions. However, we cannot use log fO2 term to parametrize because log fO2 calculation itself can have inherent uncertainties due to , especially due to strong non-ideal interactions between C, N, and S in S-rich metallic liquid (Wang et al., 1991; Corgne et al., 2008; Dasgupta et al., 2009; Grewal et al., 2019). Moreover, may also not remain constant, especially for extremely reduced conditions. Therefore, to avoid the incorporation of such uncertainties in parameterization, we use (wt.% of FeO in the silicate melt) instead of log fO2 to account for the change in fO2 via the exchange reaction:
| (Eqn. 8) |
| (Eqn. 9) |
where, Keq denotes the equilibrium constant of the reaction (Eqn. 8) at a given P-T, represents the activity of Fe3/2N0 in the alloy melt, and represent the activities of N3− and Fe2+ in the silicate melt, respectively.
| (Eqn. 10) |
where, and represent the concentration (wt.%) and the activity coefficient of Fe3/2N0 in the alloy melt, respectively, and represent the concentration (wt.%) and the activity coefficient of N3− in the silicate melt, respectively, and and represent the mole fraction and the activity coefficient of Fe2+ in the silicate melt, respectively. Assuming , and remain constant over the entire P-T range, an additional constant ‘a’ is added.
Eqn. 10 can now be written as:
| (Eqn. 11) |
Expanding the Gibbs free energy term, Eqn. 11 can be written as:
where, P is pressure in GPa, T is temperature in K and is the FeO content of the silicate melt in wt.%. It has been shown in several previous studies that the chemical composition of the alloy and silicate melts strongly affect the alloy-silicate partition coefficients of other light elements such as C and S. To account for the presence of other elements in the alloy melt we include additional terms , , , , and , where , , , and denote wt.% of S, Si, C, O and Ni in alloy melt, respectively. An additional term in is incorporated to capture the parabolic increase in from S-free alloy melts to ~15 wt.% S in the alloy melt and its parabolic decrease with > ~15 wt.% S in the alloy melt (Fig. 7A,B). Whereas to delineate the effect of silicate melt composition, we include an additional NBO/T term.
| (Eqn. 12) |
Eqn. 12 was calibrated against the experimental data from this study and previous studies with a total of 133 experimental (Kadik et al., 2011; Kadik et al., 2013; Roskosz et al., 2013; Kadik et al., 2015; Li et al., 2016b; Dalou et al., 2017; Kadik et al., 2017; Grewal et al., 2019) with P in the range of 1–17.7 GPa, T from 1400 to 2577 °C, oxygen fugacity varying between ΔIW - 4.2 to - 0.2 and NBO/T from 0.4 to 2.5. Our regression does not show, unlike Roskosz et al. (2013), any significant effect of on because this study, and the other experimental datasets that the parametrization is calibrated on, did not systematically study the effect of variation of Ni content in the alloy. The effect of is only observed to be significant at high (Roskosz et al., 2013), however for our Solar System planetary bodies where the alloy cores are thought to have < 5–6 wt.% Ni, is not expected to have much dependence on . Additionally, and also do not show any significant effect on the regression fit. Therefore, dropping these terms we present a simplified empirical equation for multiple linear least-squares regression parametrization of represented as:
| (Eqn. 13) |
The regression was performed by using the built-in ‘regress’ function in Matlab® which is an unweighted least squares minimization scheme. The resulting coefficients based on our results are shown in Table 3. The values of the coefficients largely agree with experimentally determined dependence of thermodynamic parameters on (Fig. 10). A large positive value for b shows that the temperature has a strong negative dependence on while c is an order of magnitude smaller than b which means that in comparison to temperature, pressure has a smaller effect on . Coefficient d is positive while e is negative and is an order of magnitude smaller than d which means that , in accordance with Grewal et al. (2019), provided all other variables are constant, shows a slight parabolic increase from 0 to ~15 wt.% S in the alloy but it begins to decrease at > ~15 wt.% S in the alloy due to a large positive value of d. A positive value for confirms that incorporation of Si in the alloy has a negative effect on , while a positive value of g means that increases with increasing melt depolymerization. Coefficient h is positive, which shows that increases with increasing . Additionally, we assumed in Eqn. 8 that speciation of N in the alloy to be Fe3/2N0 with the coefficient of Fe2+ in the silicate melt to be 1.5. The predicted value of ℎ, coefficient of Fe2+ in the silicate melt, is 1.1 which confirms that the assumed average formula of N bearing alloy could indeed be Fe3/2N0 if uncertainty in the value of is taken into account. Lastly, an increase in with decrease in Si content of the alloy and increase in FeO content of the silicate melt re-affirms the positive correlation between and log fO2 as shown in this and by previous studies (Kadik et al., 2015; Dalou et al., 2017; Kadik et al., 2017).
Table 3.
Coefficients of regression for parameterization
| Parameters | Coefficents | 1-σ |
|---|---|---|
| a | −1415.40 | 323.97 |
| b | 5816.24 | 3183.14 |
| c | 166.14 | 151.01 |
| d | 343.44 | 135.88 |
| e | −38.36 | 15.24 |
| f | 139.52 | 28.13 |
| g | 0.82 | 0.29 |
| h | 1.13 | 0.17 |
Coefficients of regression for parameterization using Eq. (13) given in the text.
Fig. 10:
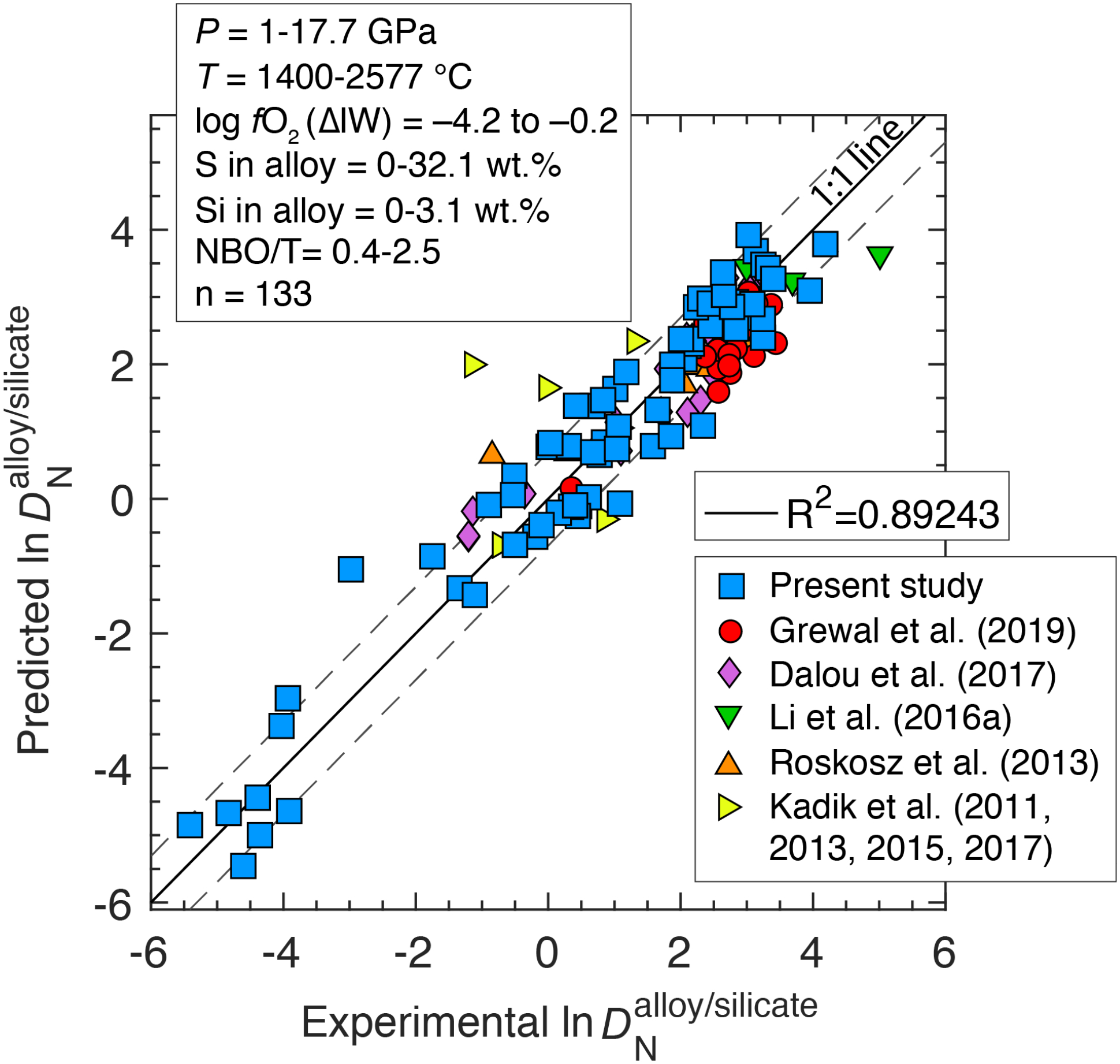
Theoretically predicted ln (using Eqn. 14) plotted against experimentally determined ln for Fe-Ni±C-N±S±Si alloy melt-silicate melt equilibria. ‘n’ in the figure represents the total number of experiments that were used to calibrate the parameterized equation. Solid line represents 1:1 fit while the dashed lines represent error within a factor of 2. log fO2 for all the previous studies was re-calculated using the methodology stated in the text. Symbols represent all data from this study and several previous studies (Kadik et al., 2011; Kadik et al., 2013; Roskosz et al., 2013; Kadik et al., 2015; Li et al., 2016b; Dalou et al., 2017; Kadik et al., 2017; Grewal et al., 2019).
4.5. The origin of nitrogen on Earth
Earth’s protracted growth period means that its core formation was a multi-step process with varying P-T of alloy-silicate equilibration along with variations in the identity and mass of the accreting material at different pulses of accretion (e.g., Wade and Wood, 2005; Kleine et al., 2009; Rudge et al., 2010; Rubie et al., 2011; Badro et al., 2015). The nitrogen budget in the BSE is dependent on the budget of the accreted N, physio-chemical conditions of alloy-silicate equilibration, and the amount of volatility-induced N loss to space. Quantifying the relative importance of these processes, is a non-trivial task as the budget of the accreted N, which depends on volatility-related losses due to parent body processing of the accreting material, as well as the role of volatility-related N loss post-accretion, either due to impact related atmospheric loss or hydrodynamic escape, is a poorly known quantity. Therefore, our experimental data and resulting parameterization on alloy-silicate fractionation of N are essential in constraining the role of various scenarios of core-mantle equilibration in setting the N budget in the BSE and the core which indirectly can place first order bounds on the bulk budget of the accreted N as well as the importance of N loss to space post accretion.
4.5.1. Bulk N that underwent alloy-silicate fractionation - input from geochemistry of building blocks
Earth is presumed to be a heterogeneously accreted planet made up both of volatile-poor material like enstatite chondrites and volatile-rich material like CI-chondrites in hitherto unknown proportions (Marty, 2012; Dauphas and Morbidelli, 2014). This heterogeneity is also reflected in the N isotopic signature of the different BSE reservoirs as well: the MORB source of N in the mantle (δ15N - 40 to - 5‰) has an isotopic similarity with enstatite chondrites (δ15N ~ - 40‰), while the plume source (δ15N ~ + 3‰), atmosphere (δ15N = 0‰), oceans (δ15N ~ + 6‰), vegetation (δ15N ~ 0‰), and sediments (δ15N ~ + 6‰) are isotopically similar to either a carbonaceous-chondrite like source (δ15N > 0‰) or some degree of mixing between these two end members (Marty and Dauphas, 2003; Cartigny and Marty, 2013; Dauphas and Morbidelli, 2014). Therefore, the 15N/14N isotopic variation in the BSE may also reflect a mixed contribution by both enstatite and carbonaceous chondrites (Marty, 2012).
Marty (2012) and Roskosz et al. (2013) had postulated that N delivery exclusively via a 2±1% contribution from volatile-rich carbonaceous chondritic-like material, i.e., bulk Earth N content of 30±15 ppm, to an otherwise N-free proto-Earth followed by segregation of N into the core can satisfy the present-day N budget of the BSE. However, even though carbonaceous chondrites are N-rich (500–5500 ppm) (e.g., Grady and Wright, 2003; Pearson et al., 2006; Alexander et al., 2012), they host N primarily in a thermally unstable phase such as organic matrix which makes it particularly susceptible to volatile loss pre-accretion to Earth (Alexander et al., 2018). On the other hand, even though enstatite chondrites are N-poor (10–800 ppm) (Moore et al., 1969; Grady et al., 1986; Grady and Wright, 2003) relative to carbonaceous chondrites, they host N in refractory phases like Si3N4 and Si2N2O (Ryall and Muan, 1969; Grady and Wright, 2003), which would make their contribution to the overall N budget of Earth non-negligible, especially if most of the proto-Earth was accreted from enstatite chondrite-like material (Dauphas, 2017).
Previous studies have treated a nominally dry proto-Earth as a body that is essentially free of volatiles such as N or at least having a silicate fraction that is volatile-poor (Roskosz et al., 2013; Dauphas and Morbidelli, 2014; Li et al., 2016a; Tsuno et al., 2018). As enstatite chondrites are thought to be depleted in water relative to the BSE (Hutson and Ruzicka, 2000), while carbonaceous chondrites have ~1–2 orders of magnitude more water relative to the BSE (Kerridge, 1985; Alexander et al., 2018), water delivery to the BSE by some contribution of carbonaceous chondrite-like material is considered a necessity. On the other hand, N abundance in the BSE is lower relative to both enstatite as well as carbonaceous chondrites (Fig. 1A; Marty, 2012; Bergin et al., 2015; Hirschmann, 2016). Even though the bulk N budget of volatile-rich and volatile-depleted chondrites vary within an order of magnitude, the respective thermal stability of their host N-bearing phases would narrow down the difference of the N budget delivered by these end-member chondrites. Therefore, depending on the N abundance in the hidden reservoirs such as the core as well as the N loss during accretion and differentiation owing to its volatile character, N accretion to the bulk Earth solely via volatile-rich carbonaceous chondrite-like material may not be a necessity. This is especially important if the N isotopic heterogeneity of the BSE reservoirs is taken into account (Fig. 1B). Moreover, allowing for contributions from enstatite chondrite-like material towards the bulk N budget also has implications for the conditions of alloy-silicate equilibration because their reduced character could enforce a lithophile behavior of N, thereby making their contribution to the N budget in the BSE a non-negligible quantity.
Accounting for its mixed origin and volatility related loss during accretion, the overall budget of accreted N in the bulk Earth can be much higher than the hitherto assumed ~30 ppm (Mcdonough, 2003; Roskosz et al., 2013); therefore, in all our calculations, we assume an average value of 100 ppm as bulk budget of accreted N to Earth. It is important to note that the assumed bulk budget of accreted N (100 ppm) in this study is different from the previously assumed bulk N budget of the present-day Earth and this number is primarily chosen: (1) To account for the contribution to the N budget in the BSE via enstatite chondrite-like material, and (2) To place first order constraints on the importance of volatility related loss of N post accretion to Earth.
4.5.2. Effect of equilibrium core-mantle differentiation on the N budget of the BSE
Two end-member equilibrium core formation models are generally used to constrain the effect of core formation on the elemental abundances in BSE −1) A single stage core formation model which averages the entire core formation processes throughout Earth’s accretion history in a single step, i.e., using an average set of intensive and extensive variables. 2) Multi stage core formation models, which account for the inherent heterogeneity of the accreting material to Earth as well as an increasing P-T of alloy-silicate equilibration by incrementally adding mass during the entire growth stage of Earth (e.g., Wade and Wood, 2005). In the following sections, we discuss the implications of these core formation models on the origin of N in the BSE.
Single stage core formation
For a single stage core formation event, we used the most recent estimates with P = 45–65 GPa and T = 3500–4000 K (Ricolleau et al., 2011; Siebert et al., 2012), and NBO/T fixed at 8 wt.% (present-day value of primitive upper mantle) and 2.76 (peridotitic melt composition), respectively, while S content in the equilibrating alloy was varied between 0 and 4 wt.%. Owing to the increasingly siderophile character of Si at extremely high P-T relevant for a deep MO, Si content in the alloy may decouple from FeO content in the silicate melt under such conditions (Ricolleau et al., 2011; Siebert et al., 2012), i.e., significant amounts of Si may be incorporated in the equilibrating alloy at relatively oxidized conditions relevant for a single stage core formation in a deep MO. Therefore, Si content in the equilibrating alloy was also varied from 0 to 7.5 wt.%.
Because Earth’s core is supposed to have undergone inefficient equilibration with Earth’s mantle (Rudge et al., 2010), the residual N content in post core formation MO was studied as a function of alloy:silicate ratio for a bulk N of 100 ppm as shown in Fig. 11A. To assess the full range of solutions, we performed 4 sets of ~107 Monte-Carlo simulations at fixed Si content in the alloy (0, 2.5, 5 and 7.5 wt.%), while for each set of calculations, P, T and S content in the alloy were varied in their above-mentioned entire ranges. As discussed earlier, for the given range of Si content of the equilibrating alloy in our simulations, Si has a strong negative effect on the presence of N in the alloy. However, the S content of the alloy in the given range has a weak effect on N in the alloy because S only begins to considerably affect the presence of N in the alloy if the alloy S content is very high (> ~15 wt.%); such a high S in the alloy is not applicable if the average composition of the Earth’s core is considered (e.g., Dreibus and Palme, 1996).
Fig. 11:
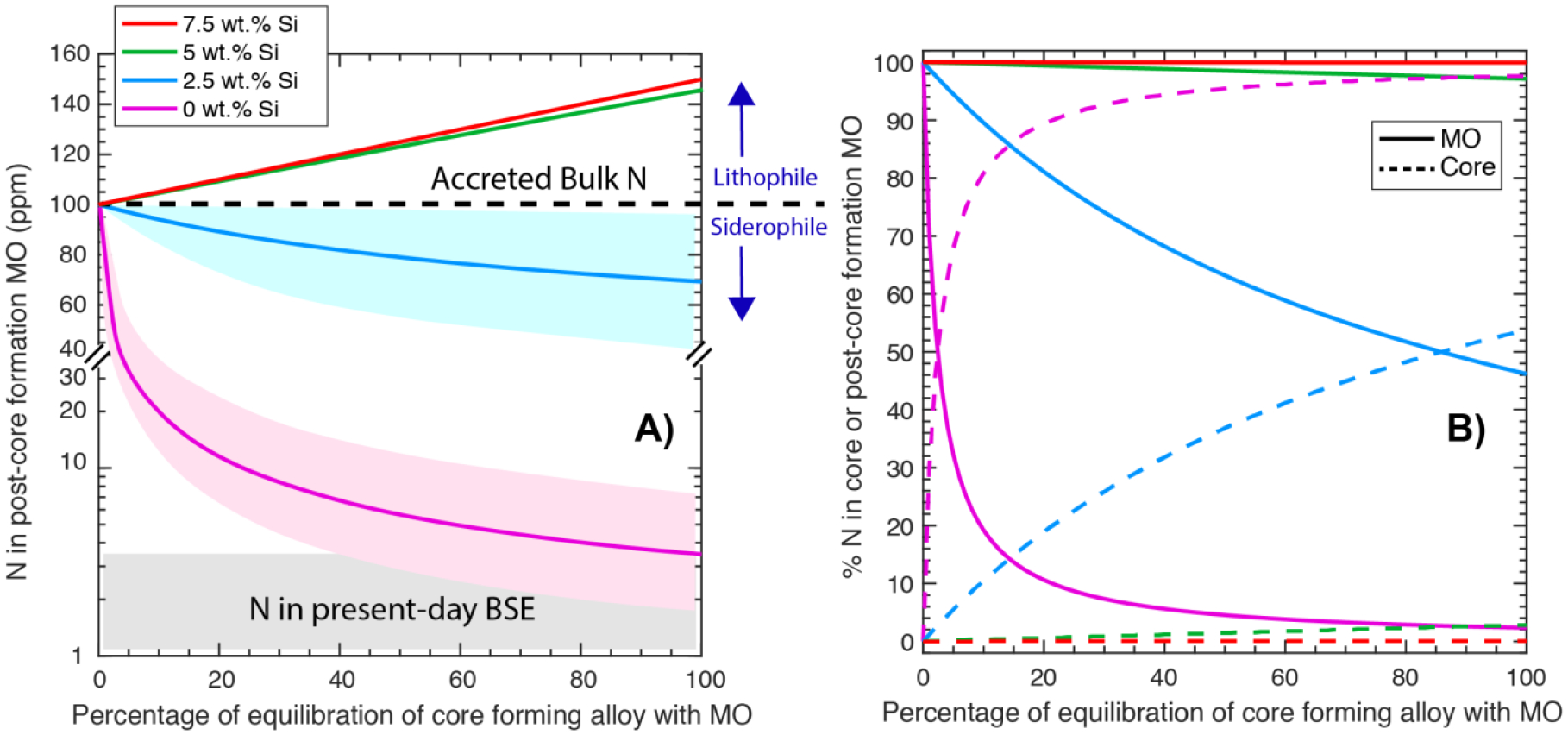
The effect of different degrees of alloy-silicate equilibration and varying Si and S content in the alloy on the equilibrium alloy-silicate partitioning behavior of nitrogen for a single stage core formation event in a deep magma ocean. A) Modelled N concentration in post-core formation MO (using parametrization from this study) as a function of degree of alloy-silicate equilibration with different Si contents in the alloy, while S content in the alloy is varied between 0 to 4 wt.% in each case. Alloy-silicate equilibration takes place at P = 45–65 GPa, T = 3500–4000 K, (present-day value of primitive upper mantle) and NBO/T = 2.76 (peridotitic silicate melt composition). For each scenario, colored lines show the most probable solution, while the shaded regions, where present, represent probable solutions over the entire P-T for that scenario via forward Monte-Carlo simulations. B) Percentage of N either in the core (solid lines) or the MO (dashed lines) as a function of degree of alloy-silicate equilibration for each scenario.
At the high P-T relevant for a deep MO, N acts as a lithophile element with > ~2.5 wt.% Si in the equilibrating alloy, while for an alloy having < ~2.5 wt.% Si, it acts as a siderophile element. For > ~3 wt.% Si in the alloy, P-T of alloy-silicate equilibration has a minor effect on the N abundance in the MO and N remains a lithophile element with its N abundance in the MO increasing linearly with increase in degree of alloy-silicate equilibration. With decrease in the Si content of the alloy (< ~2.5 wt.%), N becomes increasingly siderophile and at a given Si content of the alloy under these conditions, T of alloy-silicate equilibration becomes an important parameter with higher T corresponding to higher N values in the MO and vice-versa. If the equilibrating alloy contains > ~2.5 wt.% Si, then greater than 50% of the bulk Earth N budget would reside in the residual MO after core formation, assuming complete alloy-silicate equilibration, while only extremely Si-poor alloys would leave an N-poor MO, i.e., less than 10% of the bulk Earth N budget in the MO with as less as 20% alloy-silicate equilibration.
A single stage core formation event has important implications on the accretion and differentiation history of N on Earth. (1) At a fixed fO2 ( = present day mantle value of 8 wt.%), if the core forming alloy was extremely Si-poor or Si-free, then residual MO post core formation would be N-poor, and Earth’s core would be the primary reservoir for N (> 90% of bulk N) (Fig. 11B). For such a scenario, the bulk N budget could be approximately 100 ppm provided there is minimal loss of N to space from the bulk-Earth system; however, if there was a substantial amount of N loss to space then the bulk Earth budget of accreted N could be several hundreds of ppm. This observation would be in accordance with relatively N-rich character of all class of chondrites in comparison to the BSE. (2) If the equilibrating core of Earth had Si content > ~2.5 wt.%, then the residual MO would have considerable amount of N (> 60% of the bulk N budget) (Fig. 11B), which would imply that if the estimate of the present-day N budget of the BSE is accurate, then a large amount of N had to be lost to space either during accretion or post-accretion as impact related N-bearing atmospheric loss (Schlichting et al., 2015), or the bulk N budget of Earth should have been extremely N-poor (even <10 ppm). This would mean that either the BSE lost most of its accreted nitrogen owing to volatile character of N and Earth’s extremely violent accretion history, and/or, all primary building blocks of Earth suffered extreme N-loss before accreting to Earth (e.g., due to large scale melting, core formation loss and/or thermal metamorphism) which would make the bulk N budget of Earth extremely N-poor.
Our predictions for a deep MO equilibrating with Si-free alloys or Si-poor alloys are in broad agreement with those of Roskosz et al. (2013), where the core of Earth acts as a major reservoir for the accreted N. However, our predictions differ if there is a possible incorporation of Si in the alloy even under relatively oxidized conditions relevant for a single stage core formation as it may enforce a lithophile character of N, thereby making the core a reservoir of secondary importance for storing an important fraction of the bulk terrestrial N. Future experiments at high P-T relevant for deep MO are needed to test whether incorporation of significant amounts of Si in the equilibrating alloy at relatively oxidized conditions can induce a lithophile character in N.
Multi stage core formation
A multi-stage core formation model provides a more realistic growth mechanism for a relatively large planet like Earth which had a protracted growth over ~50–100 Ma with several intermittent episodes of alloy-silicate equilibration (Kleine et al., 2009; Rudge et al., 2010). For continuous core formation, we follow the framework of Wade and Wood (2005), where 1 wt.% of the present-day Earth’s mass is accreted at each step of accretion till Earth’s present-day mass is attained. Although this framework does not account for episodic accretion of large differentiated planetary embryos with specific compositions, i.e., having extremely S- rich or Si-rich cores, especially at later stages of Earth’s accretion (Wohlers and Wood, 2015; Li et al., 2016a; Wohlers and Wood, 2017; Tsuno et al., 2018; Grewal et al., 2019), it accounts for more degrees of freedom in comparison to the single stage core formation model. This model chiefly tracks varying fO2 of the accreting material and P-T of alloy-silicate equilibration.
Similar to the models by Ricolleau et al. (2011) and Boujibar et al. (2014), we assume that at each step of accretion, the accreting alloy undergoes 100% equilibration with the MO at approximately half of core-mantle boundary depth for that step followed by diapiring of the alloy through the solid mantle without any additional equilibration. The mass of the accreting alloy and silicate is fixed at 0.3 and 0.7, respectively, at each step of accretion, while T of alloy-silicate equilibration is either fixed at the liquidus of pyrolytic mantle or 500 K above the liquidus. Following the methodology of Ricolleau et al. (2011) and Boujibar et al. (2014), we have assumed four distinct end-member accretion paths which account for variation of fO2 in the accreting material or of the equilibrating mantle, with culmination at the present-day FeO content for the primitive upper mantle () (Fig. 12A): In the accretion path 1 (very reduced), initiates at 0.35 wt.% and initially increases slowly through time followed by a sharp increase when MO depth intersects perovskite stability field (Wade and Wood, 2005). In accretion path 2 (reduced), initiates at 1 wt.% and increases linearly through time (Javoy et al., 2010). In accretion path 3 (intermediate), remains fixed throughout Earth’s growth at 8 wt.% and in accretion path 4 (oxidized), drops linearly from 20 wt.% (Rubie et al., 2004; Siebert et al., 2013; Badro et al., 2015). With gradual increase in Earth’s mass, Si content of the alloy decreases from 7.5 to 0 wt.% in path 1 and 6 to 0 wt.% in path 2, while paths 3 and 4 have Si free alloys. The S content in the alloy is fixed at 2 wt.% for all four models. For the sake of simplicity, we have coupled Si content in the alloy to FeO content of the silicate MO in these models, i.e., unlike single stage core formation model we have not considered incorporation of Si in the equilibrating alloy for a deep MO in relatively oxidized conditions.
Fig. 12:
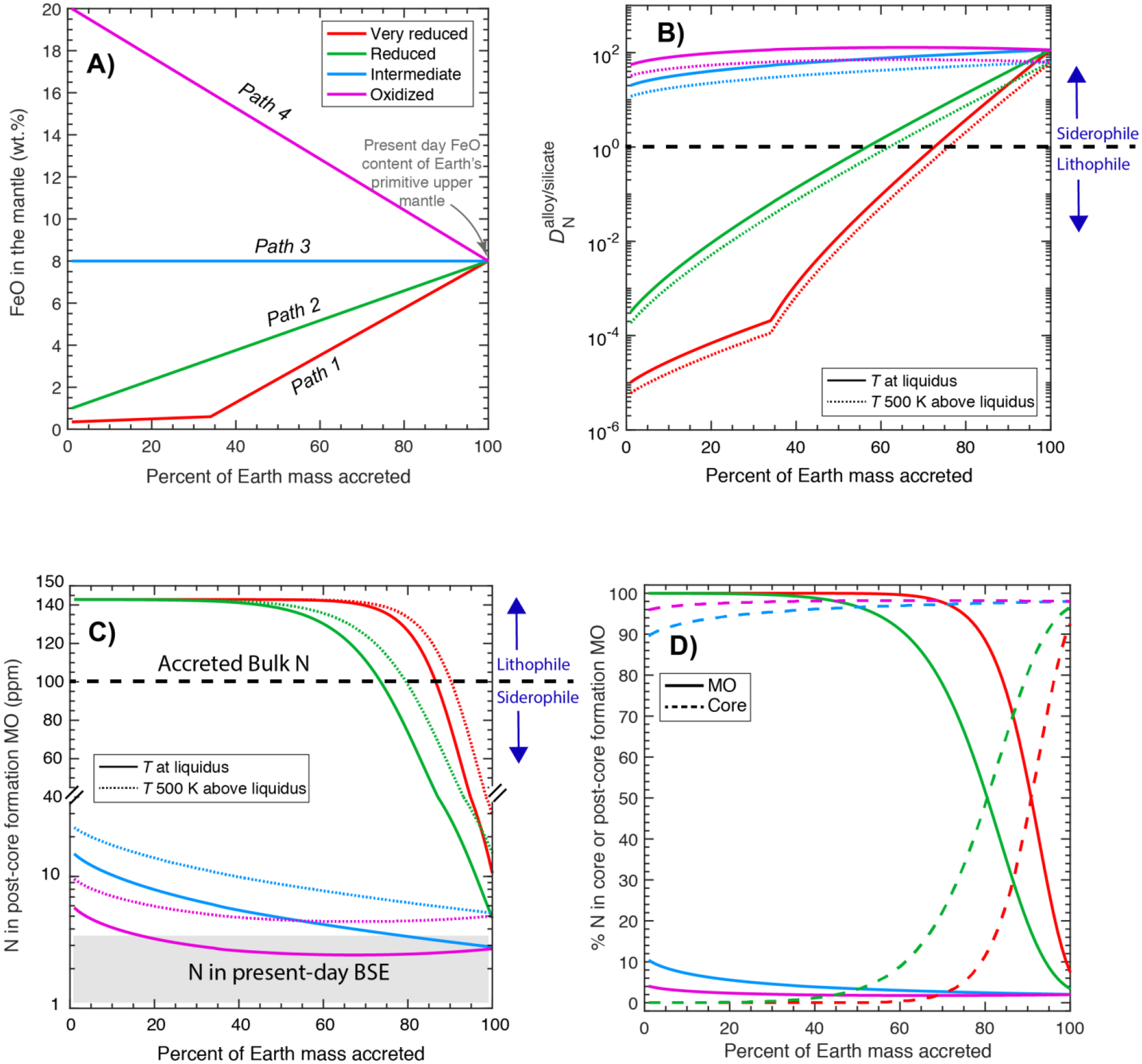
The comparison of four widely different accretion scenarios and their corresponding effects on the equilibrium alloy-silicate partitioning behavior of nitrogen and the residual nitrogen budget in the post-core formation magma ocean along with the proportional distribution of initially accreted nitrogen between the core and magma ocean. A) Four possible accretion scenarios where fO2 of accreting material evolves from either reduced to oxidized (‘Path 1-Very Reduced’ or ‘Path 2-Reduced’) or oxidized to reduced (‘Path 4-Oxidized’) or over time till the target (equivalent to FeO content of Earth’s primitive upper mantle) is attained or the accreting material has a fixed throughout Earth accretion history (‘Path 3-Intermediate’). 1% of present-day Earth mass is accreted at each step of accretion while the depth of alloy-silicate equilibration is fixed at half of the depth of the core-mantle boundary. At each step of differentiation, 100% alloy-silicate equilibration is assumed. The S content of the alloy is fixed at 2 wt.% and the Si content of the alloy decreases over time for ‘Very Reduced’ and ‘Reduced scenarios’, while alloys for ‘Intermediate’ and ‘Oxidized’ scenarios are assumed to be Si-free. B) Modelled curves for the evolution of (using parametrization from this study) as a function of percentage of mass accreted for different accretion scenarios. For solid curves T of alloy-silicate equilibration is kept at the liquidus of peridotite, while dashed curves represent T of alloy-silicate equilibration 500 K above the peridotite liquidus. C) Modelled N concentration in the post-core formation MO as a function of the percentage of mass accreted for different accretion scenarios for a bulk N content of 100 ppm assuming complete alloy-silicate equilibration. D) Percentage of N in the core or MO for different accretion scenarios.
Using our parameterized relationship for , we observe that can vary ~7–8 orders of magnitude for different accretion scenarios as shown in Fig. 12B. For paths 1 and 2, at the beginning of Earth’s accretion when the accreting material is reduced, N acts as a strongly lithophile element with its lying in the range of ~10−5-10−4 primarily due to the presence of significant amount of Si in the alloy at extremely low fO2, while it transforms to a siderophile element after ~55–70% of Earth’s accretion when either gradual increase in accretion of relatively oxidized material or self-oxidation of the mantle via perovskite precipitation or both, along with minimal incorporation of Si in the core become important factors. For paths 3 and 4, N shows siderophile character across the entire accretion range with its lying in the range of ~20 to 120. It is important to note that at relatively oxidized conditions, P has a smaller effect on relative to T because even though, P increases by factor of 40 along the mantle liquidus, T increases only by a factor less than 2, but does not change significantly with increase in P-T of alloy-silicate equilibration throughout Earth’s growth period. However, if T of alloy-silicate equilibration is higher than T at liquidus, then is lower at any given P irrespective of the accretion path. For example, if alloy-silicate equilibration T is 500 K greater than liquidus T of that depth, then drops by a factor of ~2–3 at every step (Fig. 12B).
Nitrogen in the silicate portion of the Earth after separation of the equilibrated alloy at every single step for the different accretion scenarios is shown in Fig. 12C. Paths 1 and 2 show that due to highly lithophile character of N under extremely reduced conditions, N is enriched in the residual MO mantle and its abundance is greater than the building blocks by a factor of ~1.4 and it only begins to drop at > ~40% of Earth’s accretion. At the final stages of Earth’s accretion when the building blocks are oxidized, if all of the accreting metal equilibrates with the MO then the siderophile character of N would allow the equilibrating alloy to remove huge quantities of N from a relatively larger MO. This would result in the N abundance in the mantle post core-formation to be ~5–10% of the budget of the building blocks, while final Earth’s core would contain ~90–95% of the accreted N. On the other hand, paths 3 and 4 predict that if the building blocks of Earth were more oxidized, then growing mantle of Earth would be depleted in N relative to the building blocks during its entire growth history. Post core-formation residual mantle would retain ~2–3% of the delivered N inventory while the core would contain ~97–98% of the delivered N budget.
Recent studies have postulated that during the protosolar nebula stage in the early Solar System, proto-Earth grew via the accretion of undifferentiated planetisimals while after the dissipation of the nebular gas, the growth was primarily fueled by the accretion of differentiated planetary embryos (e.g., Rubie et al., 2011; Morbidelli et al., 2012; Rubie et al., 2015). However, the size, composition, and the number of planetary embryos that might have accreted at the Earth’s late stage growth are still poorly known. To satisfy the present-day abundances of a variety of non-volatile and volatile elements like Ni, Co, W, Sm, Nd, C, S and N, as well as dynamical constrains on the Moon formation event, accretion of either extremely reduced or relatively oxidized planetary embryos with either Si-rich or S-rich cores, respectively, with their total mass varying from 1 to 50% of present-day Earth’s mass has been postulated (Canup and Asphaug, 2001; Rubie et al., 2011; Canup, 2012; Cuk and Stewart, 2012; Wohlers and Wood, 2015; Li et al., 2016a; Rubie et al., 2016; Wohlers and Wood, 2017; Tsuno et al., 2018; Grewal et al., 2019). The late stage accretion of differentiated planetary embryos to a growing proto-Earth also introduces another uncertainty - percentage of equilibration of a differentiated planetary embryo’s core with the proto-Earth’s mantle (Deguen et al., 2011; Deguen et al., 2014; Piet et al., 2017; Grewal et al., 2019). Recent dynamical and geochemical studies estimate that if the accreted planetary embryos are reasonably large in size, then the percentage of the equilibration of the impactor’s core would be minimal to none (Deguen et al., 2011; Deguen et al., 2014; Rubie et al., 2015). Using Hf-W and U-Pb data, Rudge et al. (2010) estimated that only 36% of the entire Earth’s core mass would have equilibrated with the Earth’s mantle. This could mean that the mass of the core of late accreted planetary embryos equilibrating with proto-Earth’s mantle would have been minimal. In all of our models, we have assumed that all of the accreting alloy equilibrates with the entire mantle down to the base of the MO at each step of accretion. However, if accreted core forming alloy at late stage had minimal interaction with proto-Earth’s mantle, it would have significant implications on our accretion scenarios, especially paths 1 and 2. For growth under extremely reduced conditions, Earth’s mantle is highly enriched in N, even higher abundance than the building blocks, therefore, inefficient equilibration of core-forming alloy at the late stage of accretion when the MO is oxidized and the equilibrating alloy is Si-free would leave the post core-formation mantle to be extremely N-rich relative to the present-day BSE. Additionally, if there is incorporation of significant amounts of Si in the equilibrating alloy for a deep MO at relatively oxidized conditions during late stage of accretion, then even an efficient equilibration of the core forming alloy in a deep MO would not be sufficient to strip off significant amount of N, thereby leaving an N-rich residual MO.
Most of the geodynamical constraints, aligning with paths 1 and 2, argue for the evolution of Earth’s building blocks from reduced to oxidized material (e.g., Walsh et al., 2011; Morbidelli et al., 2012; O’Brien et al., 2014). Therefore, inefficient alloy-silicate equilibration at the late stage of Earth’s accretion would mean that either the building blocks would have to be extremely N-poor or almost N-free, and/or proto-Earth suffered large degrees of N loss to space. Nitrogen loss to space could occur primarily due to atmospheric escape owing either to weak gravitational field of a smaller proto-Earth or impact related losses, throughout its accretion history thereby making bulk silicate portion of the proto-Earth N-poor prior to the late stage accretion of differentiated planetary embryo(s). Accretion of N and other volatiles by oxidized, differentiated planetary embryo(s) to an almost N-free bulk silicate portion of the proto-Earth could also satisfy the present-day abundance of N relative to other major volatiles like C and S in the BSE (Grewal et al., 2019).
4.5.3. Effect of equilibrium core-mantle differentiation on the N budget of Earth’s core
The density deficit of Earth’s core is postulated to be explained by the presence of ~10 wt.% light elements like Si, S, O, H and C in the Fe-Ni alloy (e.g., Poirier, 1994; Allègre et al., 1995). Using the experimental estimates of the solubility of N in the core forming alloy (wt.%), Speelmanns et al. (2018) called for a non-insignificant contribution of N to the density deficit of Earth’s core. However, the N-poor nature of all classes of building blocks (< ~0.5 wt.%) necessitates that rather than N solubility in the alloy phase would control the N content of the Earth’s core. Our calculations for single- and multi-stage core formation models show that for alloy-silicate equilibration for Si-free or Si-poor alloys can put ~98% of Earth’s accreted bulk N budget into the core, while Si-rich alloys would be extremely N-poor, i.e., < ~2% of Earth’s accreted bulk N budget into the core. Therefore, if the BSE budget of N was set solely via core-mantle equilibration with Si-free or Si-poor alloys, then the Earth’s core can contain up to 100 ppm N. However, if volatility related loss post-accretion such as atmospheric loss (es) also played an important role in shaping the N abundance in the present-day BSE, then the bulk accreted N budget of Earth could be much higher which would result in as high as ~0.1–0.5 wt.% N in Earth’s core. These estimates are well within the range of N content in the iron meteorites (Sugiura, 1998). While if the core forming alloy was had significant amounts of Si (> 3 wt.%), then the core would not be a major reservoir of Earth (few tens of ppm), regardless of whether the accreting material of Earth was N-rich or N-poor. Irrespective of the exact scenario, these constraints on the N content in Earth’s core are well within the upper limit (≪2 wt.%) constrained by the effect of dissolved N on density and seismic velocity of liquid Fe at Earth’s outer core conditions (Bajgain et al., 2018).
5. Concluding Remarks
Our experimental data shows that increases with increase in pressure, oxygen fugacity and silicate melt depolymerization, while it decreases with increase in temperature as well as increase in S (> ~15 wt.% S) and Si contents in the alloy, with oxygen fugacity followed by temperature being the controlling parameters. It is important to note that all of the experiments conducted in this study and relevant previous studies (except for a few experiments of Roskosz et al., 2013) to constrain alloy-silicate partitioning behavior of N were conducted in graphite saturated conditions. Significant solubility of C in alloy melts under such conditions can result in diminishing incorporation of N in the alloy (Speelmanns et al., 2018) which as a result can significantly affect especially under extremely reduced conditions, with Si bearing alloys, when N shows strongly lithophile character. Future high P-T experiments conducted in C-free conditions are required to validate extreme variation of with change in oxygen fugacity.
Our multivariable parameterization for shows that oxygen fugacity of the accreting material, along with Si content of the equilibrating alloy under extremely reducing conditions, followed by the temperature of alloy-silicate equilibration are the thermodynamic variables that primarily control nitrogen content in the residual MO for core formation scenarios applicable for Earth. Application of parametrized for an averaged single stage core formation for a deep MO (P = 45–65 GPa and T = 3500–4000 K) shows that the amount of N retained in the post-core formation MO would depend on whether significant amount of Si can be incorporated in the equilibrating alloy at conditions relevant for a deep MO. If the equilibrating alloy was either extremely Si-poor or Si-free and alloy-silicate equilibration was highly efficient, then an accreted bulk N budget of ~100 ppm would be sufficient to satisfy the present-day N abundance of BSE without any significant loss of N to space post accretion. But, if N loss to space post-accretion via impact related atmospheric losses was considerable, then the overall N budget of accreting material can be much higher. However, if the equilibrating alloy had appreciable amount of Si or if alloy-silicate equilibration was inefficient (even for Si-poor alloys), then either loss of large amounts of N to space is necessary for a bulk N budget of 100 ppm, or the accreted N budget of the bulk Earth should have been extremely N-poor (i.e., even less than 10 ppm). Similarly, multi stage core formation models predict that if Earth’s accreting material had an FeO content similar to that of the present-day Earth’s upper mantle (~8 wt.% FeO) or evolved from relatively oxidized to present-day values with minimal incorporation of Si into the equilibrating alloy (especially for a deep MO), then ~100 ppm bulk accreted N can satisfy the present-day BSE budget of N with minimal loss of N to space. However, if the proto-Earth initially accreted material that was much more reduced before evolving to the present-day FeO contents in the upper mantle, then during the initial stages of alloy-silicate equilibration, when significant amount of Si enters into the equilibrating alloy as well as due to extremely reduced state of the silicate MO, almost all of the accreted N is retained in the MO. For such scenarios, final stages of very efficient alloy-silicate equilibration with effectively Si free alloys is necessary to scavenge large amounts of N from the MO provided Earth’s accreted bulk N budget was 100 ppm. If alloy-silicate equilibration was inefficient during the final stages of accretion and/or late stage core forming alloys had significant amounts of Si, then such scenarios demand that Earth’s accreting material should either be extremely N-poor or large amounts of N have to be lost to space if Earth accreted material that was relatively N-rich. Therefore, if the late stage accretion of relatively large planetary embryo(s) (>0.01 ME) proceeded with inefficient equilibration of planetary embryo’s core with proto-Earth’s mantle and the bulk silicate portion of planetary embryo(s) was N-bearing, then the proto-Earth’s mantle has to be N-poor or N-free owing to high degree of N loss to space prior to the accretion of planetary embryo(s). However, to gain further insight on the timing and delivery mechanism of N relative to the BSE, future studies need to explore coupled N accretion with other volatiles, especially C, for a wide range of accretion and differentiation scenarios applicable for Earth.
Supplementary Material
Acknowledgments
The authors thank Ben Crejan for his help during aluminum coating of the samples and Chenguang Sun for insightful discussions. Celia Dalou, Mathieu Roskosz, and Jonathan Tucker are thanked for their thorough reviews, which helped to improve our communication. This work received support from NASA grants 80NSSC18K0828 and 80NSSC18K1314, and a Packard fellowship for Science and Engineering to R.D.
References:
- Abdulrahman RF and Hendry A (2001) Solubility of nitrogen in liquid nickel-based alloys. Metall. Mater. Trans. B 32, 1103–1112. [Google Scholar]
- Albarède F (2009) Volatile accretion history of the terrestrial planets and dynamic implications. Nature 461, 1227–1233. [DOI] [PubMed] [Google Scholar]
- Alexander CMO, Bowden R, Fogel ML, Howard KT, Herd CDK and Nittler LR (2012) The Provenances of Asteroids, and Their Contributions to the Volatile Inventories of the Terrestrial Planets. Science (80-.). 337, 721–723. [DOI] [PubMed] [Google Scholar]
- Alexander CMO, McKeegan KD and Altwegg K (2018) Water Reservoirs in Small Planetary Bodies: Meteorites, Asteroids, and Comets. Space Sci. Rev 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander CMO, Swan P and Prombo CA (1994) Occurrence and implications of silicon nitride in enstatite chondrites. Meteoritics 29, 79–85. [Google Scholar]
- Allègre CJ, Poirier JP, Humler E and Hofmann AW (1995) The chemical composition of the Earth. Earth Planet. Sci. Lett 134, 515–526. [Google Scholar]
- Andersen CA, Keil K and Mason B (1964) Silicon Oxynitride: A Meteoritic Mineral. Science (80-.). 146, 256–257. [DOI] [PubMed] [Google Scholar]
- Armstrong LS, Hirschmann MM, Stanley BD, Falksen EG and Jacobsen SD (2015) Speciation and solubility of reduced C-O-H-N volatiles in mafic melt: Implications for volcanism, atmospheric evolution, and deep volatile cycles in the terrestrial planets. Geochim. Cosmochim. Acta 171, 283–302. [Google Scholar]
- Badro J, Brodholt JP, Piet H, Siebert J and Ryerson FJ (2015) Core formation and core composition from coupled geochemical and geophysical constraints. Proc. Natl. Acad. Sci 112, 12310–12314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajgain SK, Mookherjee M, Dasgupta R, Ghosh D and Karki BB (2018) Nitrogen Content in the Earth’s Outer Core. Geophys. Res. Lett [Google Scholar]
- Batha HD and Whitney ED (1973) Kinetics and Mechanism of the Thermal Decomposition of Si3N4. J. Am. Ceram. Soc 56, 365–369. [Google Scholar]
- Bergin EA, Blake GA, Ciesla F, Hirschmann MM and Li J (2015) Tracing the ingredients for a habitable earth from interstellar space through planet formation. Proc. Natl. Acad. Sci 112, 8965–8970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouhifd MA and Jephcoat AP (2006) Aluminium control of argon solubility in silicate melts under pressure. Nature 439, 961–964. [DOI] [PubMed] [Google Scholar]
- Boujibar A, Andrault D, Bouhifd MA, Bolfan-Casanova N, Devidal JL and Trcera N (2014) Metal-silicate partitioning of sulphur, new experimental and thermodynamic constraints on planetary accretion. Earth Planet. Sci. Lett 391, 42–54. [Google Scholar]
- Canup RM (2012) Forming a moon with an Earth-like composition via a giant impact. Science (80-.). 338, 1052–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canup RM and Asphaug E (2001) Origin of the Moon in a giant impact near the end of the Earth’s formation. Nature 412, 708–712. [DOI] [PubMed] [Google Scholar]
- Cartigny P and Marty B (2013) Nitrogen isotopes and mantle geodynamics: The emergence of life and the atmosphere-crust-mantle connection. Elements 9, 359–366. [Google Scholar]
- Chamorro-perez E, Gillet P and Jambon A (1996) Argon solubility in silicate melts at high pressures. Experimental set-up and preliminary results for silica and anorthite merlts. Earth Planet. Sci. Lett 145, 97–107. [Google Scholar]
- Chamorro-Perez E, Gillet P, Jambon A, Badro J and McMillan P (1998) Low argon solubility in silicate melts at high pressure. Nature 393, 352–355. [Google Scholar]
- Chi H, Dasgupta R, Duncan MS and Shimizu N (2014) Partitioning of carbon between Fe-rich alloy melt and silicate melt in a magma ocean - Implications for the abundance and origin of volatiles in Earth, Mars, and the Moon. Geochim. Cosmochim. Acta 139, 447–471. [Google Scholar]
- Corgne A, Wood BJ and Fei Y (2008) C- and S-rich molten alloy immiscibility and core formation of planetesimals. Geochim. Cosmochim. Acta 72, 2409–2416. [Google Scholar]
- Cuk M and Stewart ST (2012) Making the Moon from a Fast-Spinning Earth: A Giant Impact Followed by Resonant Despinning. Science (80-.). 338, 1047–1052. [DOI] [PubMed] [Google Scholar]
- Dalou C, Hirschmann MM, von der Handt A, Mosenfelder J and Armstrong LS (2017) Nitrogen and carbon fractionation during core-mantle differentiation at shallow depth. Earth Planet. Sci. Lett 458, 141–151. [Google Scholar]
- Dasgupta R, Buono A, Whelan G and Walker D (2009) High-pressure melting relations in FeC-S systems: Implications for formation, evolution, and structure of metallic cores in planetary bodies. Geochim. Cosmochim. Acta 73, 6678–6691. [Google Scholar]
- Dasgupta R, Chi H, Shimizu N, Buono AS and Walker D (2013) Carbon solution and partitioning between metallic and silicate melts in a shallow magma ocean: Implications for the origin and distribution of terrestrial carbon. Geochim. Cosmochim. Acta 102, 191–212. [Google Scholar]
- Dasgupta R and Walker D (2008) Carbon solubility in core melts in a shallow magma ocean environment and distribution of carbon between the Earth’s core and the mantle. Geochim. Cosmochim. Acta 72, 4627–4641. [Google Scholar]
- Dauphas N (2017) The isotopic nature of the Earth’s accreting material through time. Nature 541, 521–524. [DOI] [PubMed] [Google Scholar]
- Dauphas N and Morbidelli A (2014) Geochemical and Planetary Dynamical Views on the Origin of Earth’s Atmosphere and Oceans. In Treatise on Geochemistry Elsevier. pp. 1–35. [Google Scholar]
- Deguen R, Landeau M and Olson P (2014) Turbulent metal-silicate mixing, fragmentation, and equilibration in magma oceans. Earth Planet. Sci. Lett 391, 274–287. [Google Scholar]
- Deguen R, Olson P and Cardin P (2011) Experiments on turbulent metal-silicate mixing in a magma ocean. Earth Planet. Sci. Lett 310, 303–313. [Google Scholar]
- Ding S, Dasgupta R and Tsuno K (2014) Sulfur concentration of martian basalts at sulfide saturation at high pressures and temperatures - Implications for deep sulfur cycle on Mars. Geochim. Cosmochim. Acta 131, 227–246. [Google Scholar]
- Drake MJ and Righter K (2002) Determining the composition of the Earth. Nature 416, 39–44. [DOI] [PubMed] [Google Scholar]
- Dreibus G and Palme H (1996) Cosmochemical constraints on the sulfur content in the Earth’s core. Geochim. Cosmochim. Acta 60, 1125–1130. [Google Scholar]
- Duncan MS, Dasgupta R and Tsuno K (2017) Experimental determination of CO2 content at graphite saturation along a natural basalt-peridotite melt join: Implications for the fate of carbon in terrestrial magma oceans. Earth Planet. Sci. Lett 466, 115–128. [Google Scholar]
- Ertl G, Huber M and Thiele N (1979) Formation and Decomposition of Nitrides on Iron Surfaces. Zeitschrift fur Naturforsch. - Sect. A J. Phys. Sci 34, 30–39. [Google Scholar]
- Fischer-Gödde M and Kleine T (2017) Ruthenium isotopic evidence for an inner Solar System origin of the late veneer. Nature 541, 525–527. [DOI] [PubMed] [Google Scholar]
- Füri E and Marty B (2015) Nitrogen isotope variations in the Solar System. Nat. Geosci 8, 515–522. [Google Scholar]
- Goodeve C and Jack KH (1948) Kinetics of nitrogen evolution from an iron-nitrogen interstitial alloy. Discuss. Faraday Soc 4, 82. [Google Scholar]
- Grady MM and Wright IP (2003) Elemental and isotopic abundances of carbon and nitrogen in meteorites. Space Sci. Rev 106, 231–248. [Google Scholar]
- Grady MM, Wright IP, Carr LP and Pillinger CT (1986) Compositional differences in enstatite chondrites based on carbon and nitrogen stable isotope measurements. Geochim. Cosmochim. Acta 50, 2799–2813. [Google Scholar]
- Grady MM, Wright IP, Swart PK and Pillinger CT (1985) The carbon and nitrogen isotopic composition of ureilites: Implications for their genesis. Geochim. Cosmochim. Acta 49, 903–915. [Google Scholar]
- Grewal DS, Dasgupta R, Sun C, Tsuno K and Costin G (2019) Delivery of carbon, nitrogen and sulfur to the silicate Earth by a giant impact. Sci. Adv 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halliday AN (2013) The origins of volatiles in the terrestrial planets. Geochim. Cosmochim. Acta 105, 146–171. [Google Scholar]
- Hirschmann MM (2016) Constraints on the early delivery and fractionation of Earth’s major volatiles from C/H, C/N, and C/S ratios. Am. Mineral 101, 540–553. [Google Scholar]
- Hirschmann MM and Dasgupta R (2009) The H/C ratios of Earth’s near-surface and deep reservoirs, and consequences for deep Earth volatile cycles. Chem. Geol 262, 4–16. [Google Scholar]
- Holzheid A, Palme H and Chakraborty S (1997) The activities of NiO, CoO and FeO in silicate melts. Chem. Geol 139, 21–38. [Google Scholar]
- Holzheid A, Sylvester P, O’Neill H, Rubie DC and Palme H (2000) Evidence for a late chondritic veneer in the Earth’s mantle from high pressure partitioning of palladium and platinum. Nature 406, 396–399. [DOI] [PubMed] [Google Scholar]
- Hutson M and Ruzicka A (2000) A multi-step model for the origin of E3 (enstatite) chondrites. Meteorit. Planet. Sci 35, 601–608. [Google Scholar]
- Javoy M (1995) The integral enstatite chondrite model of the Earth. Geophys. Res. Lett 22, 2219–2222. [Google Scholar]
- Javoy M, Kaminski E, Guyot F, Andrault D, Sanloup C, Moreira M, Labrosse S, Jambon A, Agrinier P, Davaille A and Jaupart C (2010) The chemical composition of the Earth: Enstatite chondrite models. Earth Planet. Sci. Lett 293, 259–268. [Google Scholar]
- Javoy M, Pineau F and Delorme H (1986) Carbon and nitrogen isotopes in the mantle. Chem. Geol 57, 41–62. [Google Scholar]
- Javoy M, Pineau F and Demaiffe D (1984) Nitrogen and carbon isotopic composition in the diamonds of Mbuji Mayi (Zaïre). Earth Planet. Sci. Lett 68, 399–412. [Google Scholar]
- Kadik AA, Koltashev VV, Kryukova EB, Plotnichenko VG, Tsekhonya TI and Kononkova NN (2015) Solubility of nitrogen, carbon, and hydrogen in FeO-Na2O-Al2O3-SiO2 melt and liquid iron alloy: Influence of oxygen fugacity. Geochemistry Int. 53, 849–868. [Google Scholar]
- Kadik AA, Kurovskaya NA, Ignat’ev YA, Kononkova NN, Koltashev VV and Plotnichenko VG (2011) Influence of oxygen fugacity on the solubility of nitrogen, carbon, and hydrogen in FeO-Na2O-SiO2-Al2O3 melts in equilibrium with metallic iron at 1.5 GPa and 1400°C. Geochemistry Int. 49, 429–438. [Google Scholar]
- Kadik AA, Kurovskaya NA, Lukanin OA, Ignat’ev YA, Koltashev VV, Kryukova EB, Plotnichenko VG and Kononkova NN (2017) Formation of N-С-О-Н molecules and complexes in the basalt-basaltic andesite melts at 1.5 Gpa and 1400°C in the presence of liquid iron alloys. Geochemistry Int. 55, 151–162. [Google Scholar]
- Kadik AA, Litvin YA, Koltashev VV, Kryukova EB, Plotnichenko VG, Tsekhonya TI and Kononkova NN (2013) Solution behavior of reduced N-H-O volatiles in FeO-Na2O-SiO2-Al2O3 melt equilibrated with molten Fe alloy at high pressure and temperature. Phys. Earth Planet. Inter 214, 14–24. [Google Scholar]
- Kegler P, Holzheid A, Frost DJ, Rubie DC, Dohmen R and Palme H (2008) New Ni and Co metal-silicate partitioning data and their relevance for an early terrestrial magma ocean. Earth Planet. Sci. Lett 268, 28–40. [Google Scholar]
- Kerridge JF (1985) Carbon, hydrogen and nitrogen in carbonaceous chondrites: Abundances and isotopic compositions in bulk samples. Geochim. Cosmochim. Acta 49, 1707–1714. [DOI] [PubMed] [Google Scholar]
- Kleine T, Touboul M, Bourdon B, Nimmo F, Mezger K, Palme H, Jacobsen SB, Yin QZ and Halliday AN (2009) Hf-W chronology of the accretion and early evolution of asteroids and terrestrial planets. Geochim. Cosmochim. Acta 73, 5150–5188. [Google Scholar]
- Kowanda C and Speidel MO (2003) Solubility of nitrogen in liquid nickel and binary Ni-Xialloys (Xi= Cr, Mo, W, Mn, Fe, Co) under elevated pressure. Scr. Mater 48, 1073–1078. [Google Scholar]
- Lengauer W, Bauer J, Guillou A, Ansel D, Bars JP, Bohn M, Etchessahar E, Debuigne J and Ettmayer P (1992) WDS-EPMA nitrogen profile determination in TiN/Ti diffusion couples using homotypic standard materials. Mikrochim. Acta 107, 303–310. [Google Scholar]
- Li Y, Dasgupta R and Tsuno K (2015) The effects of sulfur, silicon, water, and oxygen fugacity on carbon solubility and partitioning in Fe-rich alloy and silicate melt systems at 3 GPa and 1600 °C: Implications for core-mantle differentiation and degassing of magma oceans and reduced planet. Earth Planet. Sci. Lett 415, 54–66. [Google Scholar]
- Li Y, Dasgupta R, Tsuno K, Monteleone B and Shimizu N (2016a) Carbon and sulfur budget of the silicate Earth explained by accretion of differentiated planetary embryos. Nat. Geosci 9, 781–785. [Google Scholar]
- Li Y, Marty B, Shcheka S, Zimmermann L and Keppler H (2016b) Nitrogen isotope fractionation during terrestrial core-mantle separation. Geochemical Perspect. Lett, 138–147. [Google Scholar]
- Libourel G, Marty B and Humbert F (2003) Nitrogen solubility in basaltic melt. Part I. Effect of oxygen fugacity. Geochim. Cosmochim. Acta 67, 4123–4135. [Google Scholar]
- Ma Z (2001) Thermodynamic description for concentrated metallic solutions using interaction parameters. Metall. Mater. Trans. B 32, 87–103. [Google Scholar]
- Marty B (1995) Nitrogen content of the mantle inferred from N2—Ar correlation in oceanic basalts. Nature 377, 326–329. [Google Scholar]
- Marty B (2012) The origins and concentrations of water, carbon, nitrogen and noble gases on Earth. Earth Planet. Sci. Lett 313–314, 56–66. [Google Scholar]
- Marty B and Dauphas N (2003) The nitrogen record for crust-mantle interaction and mantle convection from Archean to Present. Earth Planet. Sci. Lett 206, 397–410. [Google Scholar]
- Marty B and Zimmermann L (1999) Volatiles (He, C, N, Ar) in mid-ocean ridge basalts: assesment of shallow-level fractionation and characterization of source composition. Geochim. Cosmochim. Acta 63, 3619–3633. [Google Scholar]
- Mcdonough WF (2003) Compositional Model for the Earth’s Core. Treatise On Geochemistry, 547–568. [Google Scholar]
- Meibom A, Krot AN, Robert F, Mostefaoui S, Russell SS, Petaev MI and Gounelle M (2007) Nitrogen and carbon isotopic composition of the Sun inferred from a hightemperature solar nebular condensate. Astrophys. J 656, 33–36. [Google Scholar]
- Mikhail S and Sverjensky DA (2014) Nitrogen speciation in upper mantle fluids and the origin of Earth’s nitrogen-rich atmosphere. Nat. Geosci 7, 816–819. [Google Scholar]
- Miyazaki A, Hiyagon H and Sugiura N (1995) Solubilities of nitrogen and argon in basalt melt under oxidizing conditions. AIP Conf. Proc 341, 276–283. [Google Scholar]
- Miyazaki A, Hiyagon H, Sugiura N, Hirose K and Takahashi E (2004) Solubilities of nitrogen and noble gases in silicate melts under various oxygen fugacities: Implications for the origin and degassing history of nitrogen and noble gases in the earth. Geochim. Cosmochim. Acta 68, 387–401. [Google Scholar]
- Moore CB, Gibson EK and Keil K (1969) Nitrogen abundances in enstatite chondrites. Earth Planet. Sci. Lett 6, 457–460. [Google Scholar]
- Morbidelli A, Lunine JI, O’Brien DP, Raymond SN and Walsh KJ (2012) Building Terrestrial Planets. Annu. Rev. Earth Planet. Sci 40, 251–275. [Google Scholar]
- Mosenfelder JL, von der Handt A, Füri E, Dalou C, Hervig RL, Rossman GR and Hirschmann MM (2019) Nitrogen incorporation in silicates and metals: results from SIMS, EPMA, FTIR, and laser-extraction mass spectrometry. Am. Mineral 104, 31–46. [Google Scholar]
- Mysen BO, Virgo D and Seifert FA (1982) The structure of silicate melts: Implications for chemical and physical properties of natural magma. Rev. Geophys 20, 353. [Google Scholar]
- Mysen BO, Yamashita S and Chertkova N (2008) Amorphous materials: Properties, structure, and durability: Solubility and solution mechanisms of NOH volatiles in silicate melts at high pressure and temperature-amine groups and hydrogen fugacity. Am. Mineral 93, 1760–1770. [Google Scholar]
- O’Brien DP, Walsh KJ, Morbidelli A, Raymond SN and Mandell AM (2014) Water delivery and giant impacts in the “Grand Tack” scenario. Icarus 239, 74–84. [Google Scholar]
- Owen T, Mahaffy PR, Niemann HB, Atreya S and Wong M (2001) Protosolar Nitrogen. Astrophys. J 553, 77–79. [Google Scholar]
- Pearson VK, Sephton MA, Franchi IA, Gibson JM and Gilmour I (2006) Carbon and nitrogen in carbonaceous chondrites: Elemental abundances and stable isotopic compisitions. Meteorit. Planet. Sci 41, 1899–1918. [Google Scholar]
- Piet H, Badro J and Gillet P (2017) Geochemical Constraints on the Size of the Moon-Forming Giant Impact. Geophys. Res. Lett 44, 11,770–11,777. [Google Scholar]
- Poirier JP (1994) Light elements in the Earth’s outer core: A critical review. Phys. Earth Planet. Inter 85, 319–337. [Google Scholar]
- Ricolleau A, Fei Y, Corgne A, Siebert J and Badro J (2011) Oxygen and silicon contents of Earth ‘ s core from high pressure metal - silicate partitioning experiments. Earth Planet. Sci. Lett 310, 409–421. [Google Scholar]
- Roskosz M, Bouhifd MA, Jephcoat AP, Marty B and Mysen BO (2013) Nitrogen solubility in molten metal and silicate at high pressure and temperature. Geochim. Cosmochim. Acta 121, 15–28. [Google Scholar]
- Roskosz M, Mysen BO and Cody GD (2006) Dual speciation of nitrogen in silicate melts at high pressure and temperature: An experimental study. Geochim. Cosmochim. Acta 70, 2902–2918. [Google Scholar]
- Rubie DC, Frost DJ, Mann U, Asahara Y, Nimmo F, Tsuno K, Kegler P, Holzheid A and Palme H (2011) Heterogeneous accretion, composition and core-mantle differentiation of the Earth. Earth Planet. Sci. Lett 301, 31–42. [Google Scholar]
- Rubie DC, Gessmann CK and Frost DJ (2004) Partitioning of oxygen during core formation on the Earth and Mars. Nature 429, 58–61. [DOI] [PubMed] [Google Scholar]
- Rubie DC, Jacobson SA, Morbidelli A, O’Brien DP, Young ED, de Vries J, Nimmo F, Palme H and Frost DJ (2015) Accretion and differentiation of the terrestrial planets with implications for the compositions of early-formed Solar System bodies and accretion of water. Icarus 248, 89–108. [Google Scholar]
- Rubie DC, Laurenz V, Jacobson SA, Morbidelli A, Palme H, Vogel AK and Frost DJ (2016) Highly siderophile elements were stripped from Earths mantle by iron sulfide segregation. Science (80-.). 353, 1141–1144. [DOI] [PubMed] [Google Scholar]
- Rudge JF, Kleine T and Bourdon B (2010) Broad bounds on Earths accretion and core formation constrained by geochemical models. Nat. Geosci 3, 439–443. [Google Scholar]
- Ryall WR and Muan A (1969) Silicon Oxynitride Stability. Science (80-.). 165, 1363–1364. [DOI] [PubMed] [Google Scholar]
- Sagan C and Mullen G (1972) Earth and Mars: Evolution of Atmospheres and Surface Temperatures. Science (80-.). 177, 52–56. [DOI] [PubMed] [Google Scholar]
- Sanloup C, van Westrenen W, Dasgupta R, Maynard-Casely H and Perrillat JP (2011) Compressibility change in iron-rich melt and implications for core formation models. Earth Planet. Sci. Lett 306, 118–122. [Google Scholar]
- Sarafian AR, Hauri EH, McCubbin FM, Lapen TJ, Berger EL, Nielsen SG, Marschall HR, Gaetani GA, Righter K and Sarafian E (2017a) Early accretion of water and volatile elements to the inner Solar System: Evidence from angrites. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci 375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarafian AR, Nielsen SG, Marschall HR, Gaetani GA, Hauri EH, Righter K and Sarafian E (2017b) Angrite meteorites record the onset and flux of water to the inner solar system. Geochim. Cosmochim. Acta 212, 156–166. [Google Scholar]
- Sarafian AR, Nielsen SG, Marschall HR, McCubbin FM and Monteleone BD (2014) Early accretion of water in the inner solar system from a carbonaceous chondrite-like source. Science (80-.). 346, 623–626. [DOI] [PubMed] [Google Scholar]
- Schlichting HE, Sari R and Yalinewich A (2015) Atmospheric mass loss during planet formation: The importance of planetesimal impacts. Icarus 247, 81–94. [Google Scholar]
- Schmidt BC and Keppler H (2002) Experimental evidence for high noble gas solubilities in silicate melts under mantle pressures. Earth Planet. Sci. Lett 195, 277–290. [Google Scholar]
- Siebert J, Badro J, Antonangeli D and Ryerson FJ (2012) Metal-silicate partitioning of Ni and Co in a deep magma ocean. Earth Planet. Sci. Lett 321–322, 189–197. [Google Scholar]
- Siebert J, Badro J, Antonangeli D and Ryerson FJ (2013) Terrestrial accretion under oxidizing conditions. Science (80-.). 339, 1194–1197. [DOI] [PubMed] [Google Scholar]
- Speelmanns IM, Schmidt MW and Liebske C (2018) Nitrogen solubility in core materials. Geophys. Res. Lett, 1–10. [Google Scholar]
- Sugiura N (1998) Ion probe measurements of carbon and nitrogen in iron meteorites. Meteorit. Planet. Sci 33, 393–409. [Google Scholar]
- Tsuno K and Dasgupta R (2011) Melting phase relation of nominally anhydrous, carbonated pelitic-eclogite at 2.5–3.0 GPa and deep cycling of sedimentary carbon. Contrib. to Mineral. Petrol 161, 743–763. [Google Scholar]
- Tsuno K, Grewal DS and Dasgupta R (2018) Core-mantle fractionation of carbon in Earth and Mars: The effects of sulfur. Geochim. Cosmochim. Acta 238, 477–495. [Google Scholar]
- Tucker JM and Mukhopadhyay S (2014) Evidence for multiple magma ocean outgassing and atmospheric loss episodes from mantle noble gases. Earth Planet. Sci. Lett 393, 254–265. [Google Scholar]
- Villegas EA (1976) The diffusion of nitrogen in liquid iron alloys at 1600 C. Dep. Appl. Geosci. Stanford Univ PhD Thesis, 247. [Google Scholar]
- Wade J and Wood BJ (2005) Core formation and the oxidation state of the Earth. Earth Planet. Sci. Lett 236, 78–95. [Google Scholar]
- Walker D, Dasgupta R, Li J and Buono A (2013) Nonstoichiometry and growth of some Fe carbides. Contrib. to Mineral. Petrol 166, 935–957. [Google Scholar]
- Walsh KJ, Morbidelli A, Raymond SN, O’Brien DP and Mandell AM (2011) A low mass for Mars from Jupiter’s early gas-driven migration. Nature 475, 206–209. [DOI] [PubMed] [Google Scholar]
- Wang C, Hirama J, Nagasaka T and Ban-Ya S (1991) Phase Equilibria of Liquid Fe-S-C Ternary System. ISIJ Int. 31, 1292–1299. [Google Scholar]
- Widenmeyer M, Hansen TC, Meissner E and Niewa R (2014) Formation and decomposition of iron nitrides observed by in situ powder neutron diffraction and thermal analysis. Zeitschrift fur Anorg. und Allg. Chemie 640, 1265–1274. [Google Scholar]
- Wohlers A and Wood BJ (2015) A Mercury-like component of early Earth yields uranium in the core and high mantle 142Nd. Nature 520, 337–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wohlers A and Wood BJ (2017) Uranium, thorium and REE partitioning into sulfide liquids: Implications for reduced S-rich bodies. Geochim. Cosmochim. Acta 205, 226–244. [Google Scholar]
- Wood BJ, Wade J and Kilburn MR (2008) Core formation and the oxidation state of the Earth: Additional constraints from Nb, V and Cr partitioning. Geochim. Cosmochim. Acta 72, 1415–1426. [Google Scholar]
- Wordsworth RD (2015) Atmospheric nitrogen evolution on Earth and Venus. Earth Planet. Sci. Lett 447, 103–111. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


