Skip to main content
PMC home page
Wolters Kluwer - PMC COVID-19 Collection logoLink to Wolters Kluwer - PMC COVID-19 Collection
. 2022 Jan 31;15(2):e008368. doi: 10.1161/CIRCOUTCOMES.121.008368

Estimation of the Absolute Risk of Cardiovascular Disease and Other Events: Issues With the Use of Multiple Fine-Gray Subdistribution Hazard Models

Peter C Austin 1,2,4,✉, Hein Putter 5, Douglas S Lee 1,2,3,6, Ewout W Steyerberg 5,7
PMCID: PMC8833235  PMID: 35098725

Supplemental Digital Content is available in the text.

Keywords: heart failure, implantable defibrillators, incidence, proportional hazards model, survival analysis

Abstract

Background:

The Fine-Gray subdistribution hazard model is frequently used in the cardiovascular literature to estimate subject-specific probabilities of the occurrence of an event of interest over time in the presence of competing risks. A little-known limitation of this approach is that, for some subjects and for some time points, the sum of the subject-specific probabilities for the different event types (eg, cardiovascular and noncardiovascular death) can exceed one.

Methods:

We used data on 8238 patients hospitalized with congestive heart failure in Ontario, Canada. We fit 2 Fine-Gray subdistribution hazards models, one for cardiovascular death and one for noncardiovascular death and estimated the probability of death due to each cause within 5 years of hospital admission. We also fit 2 cause-specific hazard models for the 2 event types and combined the estimated cause-specific hazard functions to obtain subject-specific estimates of the probabilities of each of the 2 event types occurring within 5 years.

Results:

When adding the probabilities of 5-year cardiovascular death and 5-year noncardiovascular death obtained from the Fine-Gray subdistribution hazard models, 8.6% of subjects had an estimated probability of 5-year all-cause mortality that exceeded 1 (100%). This problem was avoided by fitting 2 cause-specific hazard models, one for each outcome type, and combining the estimated cause-specific hazard functions to obtain subject-specific estimates of the risk of cardiovascular and noncardiovascular death.

Conclusions:

The Fine-Gray subdistribution hazard model may be problematic to use for a comprehensive assessment of absolute risks of multiple outcomes, while the combination of 2 cause-specific hazard models shows better statistical behaviour. Cause-specific modeling should not be discarded in competing risk situations.

What Is Known

  • The Fine-Gray subdistribution hazard model is frequently used to estimate subject-specific probabilities of the occurrence of an event of interest over time in the presence of competing risks.

  • A limitation of this approach is that, for some subjects and for some time points, the sum of the subject-specific probabilities for the different event types (eg, cardiovascular and noncardiovascular death) can exceed one.

  • This problem can be avoided by combining the cause-specific hazard functions for all the different types of events.

What the Study Adds

  • We illustrated the existence of this problem using data on patients hospitalized with congestive heart failure.

Survival analysis is concerned with the analysis of outcomes that occur over time. A common example in medical research is time to all-cause mortality. A competing risk is an event whose occurrence precludes the occurrence of the primary event of interest. If the primary event of interest is death due to cardiovascular causes, then death due to noncardiovascular causes is a competing risk, since subjects who die of noncardiovascular causes are no longer at risk of death due cardiovascular causes.

There have been a substantial number of tutorial and expository articles on the analysis of competing risk data, both in the general literature and the cardiovascular literature.1–7 Cardiovascular researchers are increasingly aware of the need to use appropriate statistical methods when analyzing data in which competing risks are present. For example, a model for incident acute myocardial infarction may consider mortality from other causes as a competing event. It is increasingly acknowledged that in the presence of competing risks, the use of the Kaplan-Meier survival function (by censoring on the competing risks) results in biased estimation of the absolute risk of events over time. Similarly, the use of a single Cox proportional hazards model (ie, a single cause-specific hazards model) can result in biased estimation of the absolute risk of the event of interest over time in the presence of competing risks.

There are 2 primary options when using regression models to obtain subject-specific estimates of the absolute risk of an event over time in the presence of competing risks. The first is the Fine-Gray subdistribution hazard model, which allows for modeling the effect of covariates on the cumulative incidence function (CIF).8 Second, one can fit cause-specific hazard models for each of the different event types and then combine the resultant cause-specific hazard models to estimate the absolute risk of each of the different event types over time.1,9 Note that this latter approach is different from fitting a single cause-specific hazard function for the primary cause of interest. While the former approach is increasingly frequently used, our impression is that the latter approach is rarely used in applied applications. A little-known limitation of the Fine-Gray subdistribution hazard model is that, for specific covariate patterns and for certain values of time, the sum of the estimated absolute risk for the different event types can exceed one. Thus, one can obtain estimates of the probability of all-cause events that are not constrained to lie between 0 and 1, which is clearly impossible.

Increasingly, cardiovascular research has expanded beyond all-cause mortality for challenging healthcare issues, especially when considerations extend beyond this one outcome. For example, heart failure is a challenge because of the multiplicity of potentially important outcomes including heart failure hospitalization, ischemia-related hospitalization, emergency department visits, sudden death, cardiovascular death, and worsening heart failure.10,11 These outcomes may have different degrees of importance to subspecialist physicians (eg, heart failure specialists, cardiac electrophysiologists, interventional cardiologists, cardiac surgeons), generalists, and hospitalists. Based on our prior work engaging patients,12,13 the outcomes that are important to patients extend beyond all-cause mortality. This reinforces the importance of being able to provide accurate estimates of the absolute risk of multiple outcomes, as these are easier for patients to understand and enable appropriate patient decision making.

The objective of this article is to illustrate some limitations with estimation of subject-specific estimates of absolute risk when using the Fine-Gray subdistribution hazard model in patients with congestive heart failure. Using cause-specific hazard models for all event types will be shown to circumvent the problems of the Fine-Gray model.

Methods

The data sets used in these analyses were linked using unique encoded identifiers and analyzed at ICES. While data sharing agreements prohibit ICES from making the data set publicly available, access may be granted to those who meet prespecified criteria for confidential access, available at www.ices.on.ca/DAS. The use of data in this project was authorized under section 45 of Ontario’s Personal Health Information Protection Act, which does not require review by a Research Ethics Board.

Data Sources

We used data from first phase of EFFECT (The Enhanced Feedback for Effective Cardiac Treatment) Study,14 which collected data on patients hospitalized with congestive heart failure between April 1, 1999, and March 31, 2001 at 86 hospital corporations in Ontario, Canada. For the current study, individual patient data were available on 8238 patients hospitalized with a diagnosis of congestive heart failure.

The outcome was time to death, with subjects censored 5 years after the date of hospital admission. Death was categorized as either death due to cardiovascular causes or death due to noncardiovascular causes. Outcome ascertainment was through linkage with the provincial death registry. Of the 8238 patients, 3416 (41.5%) died of cardiovascular causes within 5 years of admission, while 2228 (27.0%) died of noncardiovascular causes within 5 years of admission. All subjects were followed to either the date of death or 5 years postadmission, whichever came first.

We considered 28 predictor variables consisting of demographic characteristics (age, sex); vital signs on presentation (systolic blood pressure, heart rate, respiratory rate); presenting signs and symptoms (neck vein distension, S3, S4, rales >50% of lung field, pulmonary edema, cardiomegaly); cardiovascular history and comorbid conditions (diabetes, cerebrovascular disease/transient ischemic attack, previous acute myocardial infarction, atrial fibrillation, peripheral vascular disease, chronic obstructive pulmonary disease, dementia, cirrhosis, cancer); results of ECG (left bundle branch block); initial laboratory test results (hemoglobin, white blood count, sodium, potassium, glucose, urea, and creatinine).

Statistical Analysis

We regressed the subdistribution hazard of cardiovascular death on the 28 covariates described above. Using the fitted model, we estimated the absolute risk of cardiovascular death within 5 years for each subject in the sample. We then repeated this analysis for noncardiovascular death. For each subject, we added the probabilities of cardiovascular and noncardiovascular death within 5 years to obtain the probability of all-cause mortality within 5 years.

We fit 2 cause-specific hazard models using the 28 covariates described above. The cause-specific hazard models for cardiovascular and noncardiovascular death were estimated separately. Using the 2 fitted cause-specific hazard models, we obtained the estimated absolute risk of cardiovascular and noncardiovascular death within 5 years for each subject in the sample using methods described elsewhere.1,9 For each subject, we added the probabilities of cardiovascular and noncardiovascular death within 5 years.

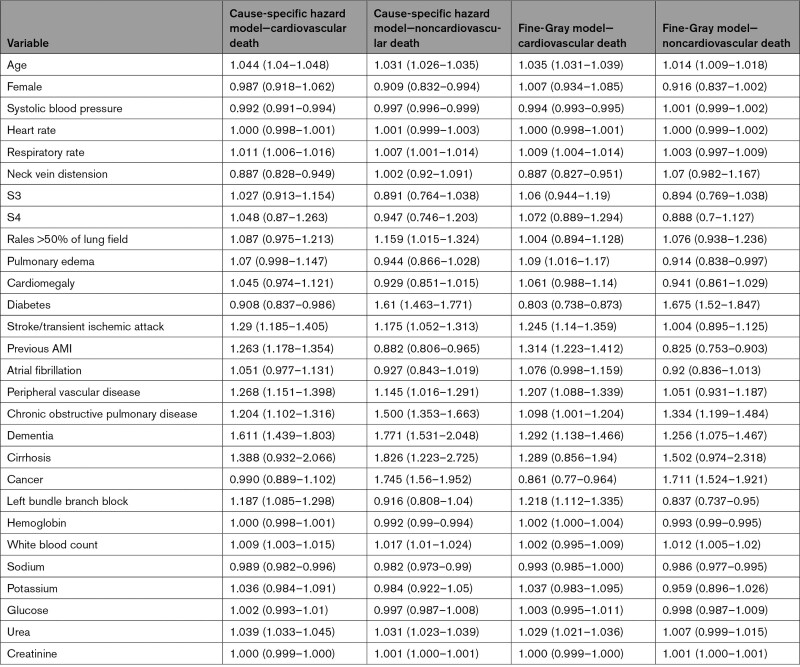
We also fit a Cox proportional hazards model for all-cause mortality using the 28 covariates described above (note that all-cause death is comprised of death due to cardiovascular causes and death due to noncardiovascular causes). Using the fitted model, we estimated for each subject the probability of all-cause mortality within 5 years. Note that the 5 regression models (2 Fine-Gray subdistribution hazard models, 2 cause-specific hazard models; 1 Cox proportional hazard model) all incorporated the same 28 covariates described above, with similar coding. The cause-specific and subdistribution hazard ratios along with associated 95% CIs for the 2 type of events are reported in Table.

Table 1.

Hazard Ratios and 95% CIs From the Cause-Specific Hazard Models and the Fine-Gray Subdistribution Hazard Models

graphic file with name hcq-15-e008368-g001.jpg

Open in a new tab

We assessed the calibration of the models for estimating the absolute risk of cardiovascular death within 5 years using a method described before.5 For a given modeling approach (combining the 2 cause-specific hazard models or the Fine-Gray subdistribution hazard model), we divided subjects into ten risk strata using the deciles of the estimated risk of 5-year cardiovascular mortality. Within each stratum, we computed the mean estimated probability of 5-year cardiovascular mortality. Then, within each stratum we estimated the observed risk of 5-year cardiovascular mortality using a CIF. We plotted the observed risk against the mean estimated risk across the 10 risk strata. This process was then repeated for noncardiovascular mortality.

The Fine-Gray subdistribution hazard models and the cause-specific hazard models were fit using the GFR and CSC functions, respectively, in the riskRegression package (version 2019.11.03) for R (version 3.5.1). R code for fitting the 2 Fine-Gray subdistribution hazard models, the 2 cause-specific hazard models, and the Cox proportional hazards model, along with estimating subject-specific probabilities of 5-year cardiovascular death, 5-year noncardiovascular death, and 5-year all-cause death is provided in appendix A in the Supplemental Material, while corresponding SAS code is provided in appendix B in the Supplemental Material.

Results

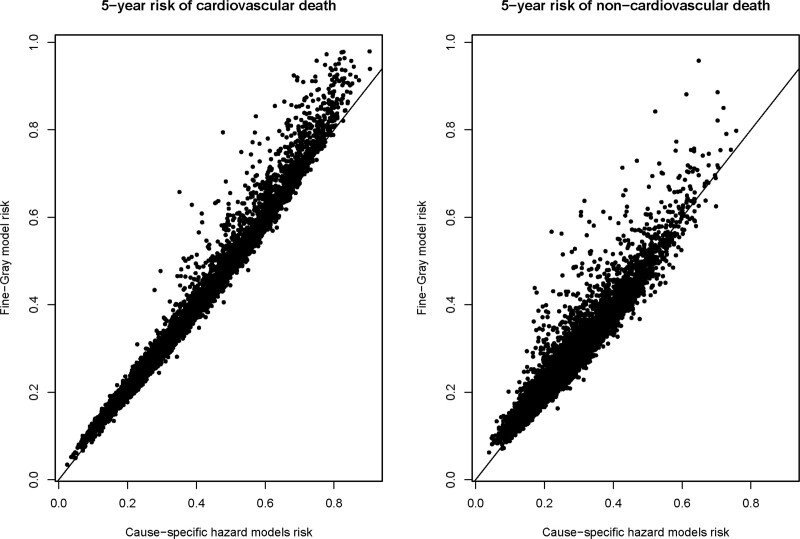
Overall, the estimates from the 2 approaches (Fine-Gray versus cause-specific hazard modeling) tended to be comparable for each outcome (Figure 1). The median difference in the estimated probability of 5-year cardiovascular death between the 2 approaches was 0.5% (25th and 75th percentiles: −0.8% and 1.4%), while the minimum and maximum differences were

Figure 1.

Figure 1.

Open in a new tab

Five-year risk of cause-specific death for each subject from 2 modeling approaches Comparison of Fine-Gray with cause-specific hazard modeling.

−31.6% and 7.4%, respectively (these differences are cause-specific hazard minus Fine-Gray). The median difference in the estimated probability of 5-year noncardiovascular death between the 2 approaches was 0.5% (25th and 75th percentiles: −1.1% and 1.6%), while the minimum and maximum differences were −34.6% and 11.0%, respectively.

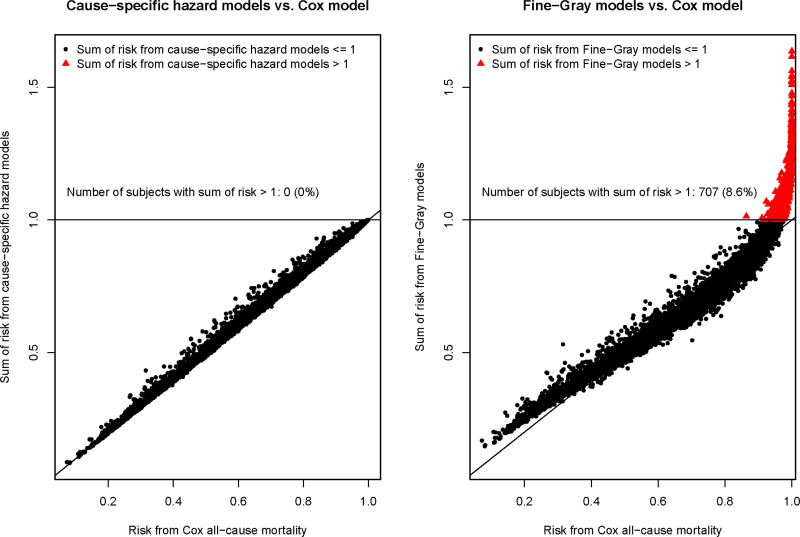
The estimated risk of death due to any cause within 5 years obtained from a single Cox model was compared with that obtained from adding the 2 estimates of the absolute risk of cause-specific mortality derived from the 2 cause-specific hazard models (left pane of Figure 2). There was good agreement between the 2 approaches. Importantly, the estimated risk of all-cause mortality was ≤1 for all subjects using both the Cox proportional hazards model for all-cause mortality and the method based on combining the 2 cause-specific hazard models. The median difference in the estimated probability of 5-year all-cause mortality between the 2 approaches was 0.3% (25th and 75th percentiles: −0.3% and 0.7%), while the minimum and maximum differences were −11.6% and 3.0%, respectively (these differences are Cox minus cause-specific hazard).

Figure 2.

Figure 2.

Open in a new tab

Cox all-cause mortality vs sum of absolute risk estimates for cause-specific mortality for each subject.

Finally, the estimated risk of death due to any cause within 5 years obtained from a single Cox model was compared with that obtained from adding the 2 estimates of absolute risk derived from the 2 Fine-Gray subdistribution hazard models (right panel of Figure 2). The median difference in the estimated probability of 5-year all-cause mortality between the 2 approaches was 0.9% (25th and 75th percentiles: −2.2% and 3.2%), while the minimum and maximum differences were −63.6% and 15.7%, respectively (these differences are Cox minus Fine-Gray). The agreement was hence inferior for the combination of 2 Fine-Gray models than the combination of 2 cause-specific hazard models. Importantly, the sum of risk estimates from the Fine-Gray models exceeded 1 (or 100%) in 707 (8.6%) out of 8238 of subjects, in contrast to in none of the subjects when using the 2 cause-specific hazard modeling approach.

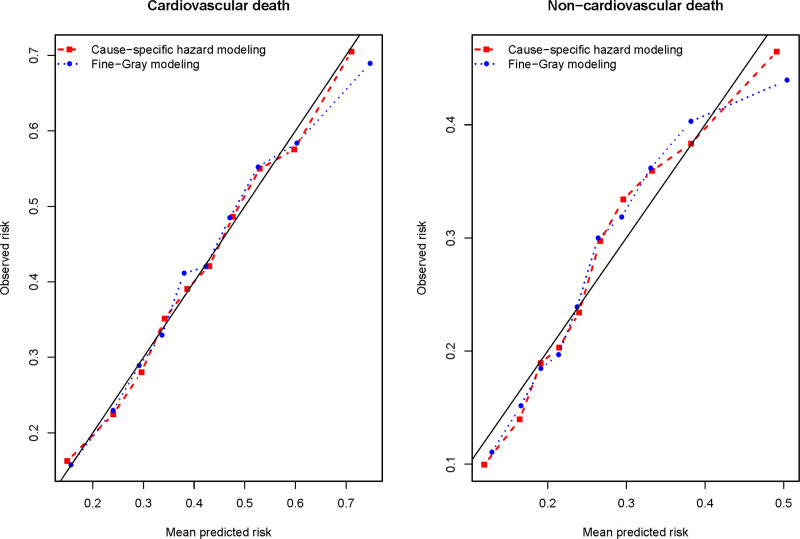
Both methods displayed very good calibration for cardiovascular death (Figure 3). For noncardiovascular death, calibration was slightly worse for both approaches, with the cause-specific modeling approach having slightly better calibration than the subdistribution hazard modeling approach.

Figure 3.

Figure 3.

Open in a new tab

Calibration of 2 methods for estimating absolute risk of cause-specific death.

Discussion

We demonstrated that using the Fine-Gray subdistribution hazard model can result in estimated probabilities of events occurring within specified durations of time such that the sum of these probabilities across all event types exceeds one for a non-negligible proportion of patients. This is clearly undesirable, as the probability of all-cause events is necessarily constrained to be at most one. This problem can be avoided by fitting all the cause-specific hazard models and combining the estimated cause-specific hazard functions. Moreover, the sum of absolute risks for cardiovascular and noncardiovascular events was slightly off from what would be predicted by a simple Cox model for the combination of events in the lower risk range.

Despite these problems with the Fine-Gray subdistribution hazard model, there are attractive features. First, the Fine-Gray subdistribution hazard model is interpretation-friendly.15 This is because the direction of the regression coefficients (ie, positive versus negative) indicate the direction (but not the magnitude) of the effect of the associated covariate on the cumulative incidence (or risk) of the occurrence of the outcome.16 Thus, increasing values of covariates that have a positive regression coefficient in a subdistribution hazard model are associated with increases in the cumulative incidence of the event, while increasing values of covariates that have a negative regression coefficient are associated with decreases in the cumulative incidence of the event. Second, if a researcher publishes the baseline cumulative incidence function (eg, at 5 years) and the regression coefficients, then one can easily compute the absolute risk of the event of interest for any covariate pattern at that time point (eg, 5 years). In contrast to the interpretation-friendly nature of the subdistribution hazard model, it is difficult to determine the direction of the effect of individual covariates on the absolute risk of the outcome when combining cause-specific hazard functions. Furthermore, one cannot derive a direct expression for the absolute risk of the occurrence of the outcome as a function of the baseline risk, the regression model coefficients and subject characteristics, since both risk functions need to be combined.5

Our assessment of calibration indicates that the limitation of the Fine-Gray model that we have illustrated is masked when examining predictions in aggregate. Both modeling approaches displayed very good calibration and the mean estimated risk of cause-specific death within 5 years within each of the 10 risk strata was comparable between the 2 approaches. A limitation of the Fine-Gray model is evident when the focus is on subject-specific probabilities of all event types. Indeed, it is these very probabilities that are of key importance for informing clinical decision making. In some contexts, only the probabilities of the primary event may be of interest, while in other contexts, all the event types may be of interest. In the context of heart failure, there is increasing interest in determining the risk of cardiovascular and noncardiovascular hospitalizations, with death treated as a competing risk.17 The Fine-Gray model is increasingly used to enable these types of analyses.11 Furthermore, the Fine-Gray model is being used to estimate the risk of not just the primary event of interest, but also of competing events. For example, in the context of prophylactic primary prevention implantable cardioverter defibrillators for left ventricular systolic dysfunction, clinicians, and patients may benefit from risk prediction methods to decide whether to implant a device or forego the procedure. While implantation of a defibrillator may treat life-threatening ventricular arrhythmias, recipients of the device may be subject to complications, device infections, device recalls, and inappropriate shocks.18,19 Since implantable cardioverter defibrillators reduce the risk of arrhythmic death but do not impact nonarrhythmic death, it is important to enable prediction of these competing events with better estimates of the risk of arrhythmic death and nonarrhythmic death, since the former is preventable by a defibrillator while the latter is not.20

An explanation for the phenomenon that we observed is that in the context of there being 2 types of events and when fitting 2 separate subdistribution hazard models, at least one of the fitted models will be incorrect.21 This occurs because, when fitting 2 subdistribution hazard models, the regression coefficients of the second model are completely determined by the regression coefficients of the first model and the 2 CIFs for a reference subject (a subject whose covariates are all equal to 0). However, when each model is fit separately, this constraint is no longer observed and thus the regression coefficients for the second model will be incorrect. This will lead to incorrect estimates of the CIF for at least one of the models, leading to the possibility that the sum of the CIFs may exceed one for some values of time, as we have illustrated.

There are certain limitations to the current study. The study was not intended to be a comprehensive evaluation of the Fine-Gray subdistribution hazard model, nor was it intended to comprehensively compare all available methods for estimating incidence in the presence of competing risks. Rather, our intent was to advertise a little-known issue with the use of the Fine-Gray model. While the phenomenon of total event probability exceeding one is not unknown, it has received little coverage, even in the statistical literature. We refer the interested reader to a article in the statistical literature in which this issue is explored in substantially greater depth, including a mathematical proofs of its existence.22 We are only aware of a few other instances where this phenomenon has been discussed: once in a vignette associated with the survival package for R and 3 times in passing elsewhere.23–26 In our case study, we observed that 8.6% of subjects had a total event probability at 5 years (as derived from the 2 fitted Fine-Gray models) that exceeded 1. It is likely that the magnitude of this issue varies across samples and across times at which cumulative incidence is estimated.

In the current study, we have illustrated that using all cause-specific hazard functions allows one to circumvent this limitation of the Fine-Gray model. Another advantage to the use of the cause-specific hazard approach compared with the subdistribution hazard approach is that the cause-specific risk set is more easily interpretable than the subdistribution risk set, as the latter retains subjects who have experienced a competing event.1,2 Alternative modeling approaches are also available.24–29

We are not arguing against the use of the Fine-Gray subdistribution hazard model. As noted above, the Fine-Gray model is both an interpretation-friendly model and allows for simple communication of risk estimates by reporting only the estimated regression coefficients and the baseline CIF. However, we encourage researchers to be cautious in the use of the Fine-Gray model when the focus is on the absolute risk of >1 of the different event types, where a combination of cause-specific models may be more sensible.

In conclusion, a little-known limitation of the Fine-Gray subdistribution hazard model is that the sum of the cause-specific estimates of absolute risk can exceed one (or 100%) for some subjects and for some time points. Using all the cause-specific hazard models allows one to avoid this limitation. Investigators are encouraged to consider this latter approach, particularly when the focus is on providing the absolute risk of each of the different types of events.

Article Information

Acknowledgments

ICES is an independent, nonprofit research institute funded by an annual grant from the Ontario Ministry of Health (MOH) and the Ministry of Long-Term Care (MLTC). As a prescribed entity under Ontario’s privacy legislation, ICES is authorized to collect and use health care data for the purposes of health system analysis, evaluation, and decision support. Secure access to these data is governed by policies and procedures that are approved by the Information and Privacy Commissioner of Ontario. The opinions, results, and conclusions reported in this article are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOH or MLTC is intended or should be inferred. Parts of this report are based on Ontario Registrar General (ORG) information on deaths, the original source of which is ServiceOntario. The views expressed therein are those of the author and do not necessarily reflect those of ORG or the Ministry of Government and Consumer Services. The data set from this study is held securely in coded form at ICES. While legal data sharing agreements between ICES and data providers (eg, health care organizations and government) prohibit ICES from making the dataset publicly available, access may be granted to those who meet prespecified criteria for confidential access, available at www.ices.on.ca/DAS (email: das@ices.on.ca). The use of data in this project was authorized under section 45 of Ontario’s Personal Health Information Protection Act, which does not require review by a research ethics board.

Sources of Funding

This research was supported by operating grant from the Canadian Institutes of Health Research (CIHR; PJT 166161). Dr Austin is supported in part by a Mid-Career Investigator award from the Heart and Stroke Foundation of Ontario.

Disclosures

None.

Supplemental Material

Supplemental software code: R code (Appendix A) and SAS code (Appendix B).

Supplementary Material

hcq-15-e008368-s001.pdf (150.2KB, pdf)

Nonstandard Abbreviations and Acronyms

CIF
cumulative incidence function
EFFECT
The Enhanced Feedback for Effective Cardiac Treatment

For Sources of Funding and Disclosures, see page 167.

Contributor Information

Hein Putter, Email: h.putter@lumc.nl.

Douglas S. Lee, Email: douglas.lee@ices.on.ca.

Ewout W. Steyerberg, Email: e.steyerberg@erasmusmc.nl.

References

  • 1.Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: competing risks and multi-state models. Stat Med. 2007;26:2389–2430. doi: 10.1002/sim.2712 [DOI] [PubMed] [Google Scholar]
  • 2.Lau B, Cole SR, Gange SJ. Competing risk regression models for epidemiologic data. Am J Epidemiol. 2009;170:244–256. doi: 10.1093/aje/kwp107 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Koller MT, Raatz H, Steyerberg EW, Wolbers M. Competing risks and the clinical community: irrelevance or ignorance? Stat Med. 2012;31:1089–1097. doi: 10.1002/sim.4384 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Wolbers M, Koller MT, Stel VS, Schaer B, Jager KJ, Leffondré K, Heinze G. Competing risks analyses: objectives and approaches. Eur Heart J. 2014;35:2936–2941. doi: 10.1093/eurheartj/ehu131 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Wolbers M, Koller MT, Witteman JC, Steyerberg EW. Prognostic models with competing risks: methods and application to coronary risk prediction. Epidemiology. 2009;20:555–561. doi: 10.1097/EDE.0b013e3181a39056 [DOI] [PubMed] [Google Scholar]
  • 6.Austin PC, Lee DS, Fine JP. Introduction to the analysis of survival data in the presence of competing risks. Circulation. 2016;133:601–609. doi: 10.1161/CIRCULATIONAHA.115.017719 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Varadhan R, Weiss CO, Segal JB, Wu AW, Scharfstein D, Boyd C. Evaluating health outcomes in the presence of competing risks: a review of statistical methods and clinical applications. Med Care. 2010;48(6 suppl):S96–S105. doi: 10.1097/MLR.0b013e3181d99107 [DOI] [PubMed] [Google Scholar]
  • 8.Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc. 1999;94:496–509. [Google Scholar]
  • 9.Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. 2002. New York, NY: John Wiley and Sons [Google Scholar]
  • 10.Kosyakovsky LB, Austin PC, Ross HJ, Wang X, Abdel-Qadir H, Goodman SG, Farkouh ME, Croxford R, Lawler PR, Spertus JA, et al. Early invasive coronary angiography and acute ischaemic heart failure outcomes. Eur Heart J. 2021;42:3756–3766. doi: 10.1093/eurheartj/ehab423 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Dewan P, Rørth R, Raparelli V, Campbell RT, Shen L, Jhund PS, Petrie MC, Anand IS, Carson PE, Desai AS, et al. Sex-related differences in heart failure with preserved ejection fraction. Circ Heart Fail. 2019;12:e006539. doi: 10.1161/CIRCHEARTFAILURE.119.006539 [DOI] [PubMed] [Google Scholar]
  • 12.Lee DS, Armstrong R, Mohamed S; Investigators of the COACH trial. Patient engagement in a trial testing a new strategy of care for acute heart failure. CMAJ. 2018;190(suppl)S34–S36. doi: 10.1503/cmaj.180462 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Lee DS, Straus SE, Austin PC, Mohamed S, Taljaard M, Chong A, Fang J, Prasad T, Farkouh ME, Schull MJ, et al. Rationale and design of the comparison of outcomes and access to care for heart failure (COACH) trial: A stepped wedge cluster randomized trial. Am Heart J. 2021;240:1–10. doi: 10.1016/j.ahj.2021.05.003 [DOI] [PubMed] [Google Scholar]
  • 14.Tu JV, Donovan LR, Lee DS, Wang JT, Austin PC, Alter DA, Ko DT. Effectiveness of public report cards for improving the quality of cardiac care: the EFFECT study: a randomized trial. JAMA. 2009;302:2330–2337. doi: 10.1001/jama.2009.1731 [DOI] [PubMed] [Google Scholar]
  • 15.Beyersmann J, Dettenkofer M, Bertz H, Schumacher M. A competing risks analysis of bloodstream infection after stem-cell transplantation using subdistribution hazards and cause-specific hazards. Stat Med. 2007;26:5360–5369. doi: 10.1002/sim.3006 [DOI] [PubMed] [Google Scholar]
  • 16.Austin PC, Fine JP. Practical recommendations for reporting Fine-Gray model analyses for competing risk data. Stat Med. 2017;36:4391–4400. doi: 10.1002/sim.7501 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Sud M, Yu B, Wijeysundera HC, Austin PC, Ko DT, Braga J, Cram P, Spertus JA, Domanski M, Lee DS. Associations between short or long length of stay and 30-day readmission and mortality in hospitalized patients with heart failure. JACC Heart Fail. 2017;5:578–588. doi: 10.1016/j.jchf.2017.03.012 [DOI] [PubMed] [Google Scholar]
  • 18.Lee DS, Krahn AD, Healey JS, Birnie D, Crystal E, Dorian P, Simpson CS, Khaykin Y, Cameron D, Janmohamed A, et al. ; Investigators of the Ontario ICD Database. Evaluation of early complications related to De Novo cardioverter defibrillator implantation insights from the Ontario ICD database. J Am Coll Cardiol. 2010;55:774–782. doi: 10.1016/j.jacc.2009.11.029 [DOI] [PubMed] [Google Scholar]
  • 19.MacFadden DR, Crystal E, Krahn AD, Mangat I, Healey JS, Dorian P, Birnie D, Simpson CS, Khaykin Y, Pinter A, et al. Sex differences in implantable cardioverter defibrillator outcomes: findings from a prospective defibrillator database. Ann Intern Med. 2012;156:195–203. doi: 10.7326/0003-4819-156-3-201202070-00007 [DOI] [PubMed] [Google Scholar]
  • 20.Lee DS, Hardy J, Yee R, Healey JS, Birnie D, Simpson CS, Crystal E, Mangat I, Nanthakumar K, Wang X, et al. ; Investigators of the Ontario ICD Database. Clinical risk stratification for primary prevention implantable cardioverter defibrillators. Circ Heart Fail. 2015;8:927–937. doi: 10.1161/CIRCHEARTFAILURE.115.002414 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Beyersmann J, Allignol A, Schumacher M. Competing Risks and Multistate Models with R. 2012. New York, NY: Springer [Google Scholar]
  • 22.Austin PC, Steyerberg EW, Putter H. Fine-Gray subdistribution hazard models to simultaneously estimate the absolute risk of different event types: cumulative total failure probability may exceed 1. Stat Med. 2021;40:4200–4212. doi: 10.1002/sim.9023 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Therneau T, Crowson C, Atkinson E. Multi-State Models and Competing Risks. 2020. https://cran.r-project.org/web/packages/survival/vignettes/compete.pdf Accessed September 24, 2021.
  • 24.Gerds TA, Scheike TH, Andersen PK. Absolute risk regression for competing risks: interpretation, link functions, and prediction. Stat Med. 2012;31:3921–3930. doi: 10.1002/sim.5459 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Choi S, Huang X. Maximum likelihood estimation of semiparametric mixture component models for competing risks data. Biometrics. 2014;70:588–598. doi: 10.1111/biom.12167 [DOI] [PubMed] [Google Scholar]
  • 26.Bakoyannis G, Yu M, Yiannoutsos CT. Semiparametric regression on cumulative incidence function with interval-censored competing risks data. Stat Med. 2017;36:3683–3707. doi: 10.1002/sim.7350 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Jeong JH, Fine J. Direct parametric inference for the cumulative incidence function. J R Stat Soc Ser C Appl Stat. 2006;55:187–200. [Google Scholar]
  • 28.Shi H, Cheng Y, Jeong JH. Constrained parametric model for simultaneous inference of two cumulative incidence functions. Biom J. 2013;55:82–96. doi: 10.1002/bimj.201200011 [DOI] [PubMed] [Google Scholar]
  • 29.Klein JP, Andersen PK. Regression modeling of competing risks data based on pseudovalues of the cumulative incidence function. Biometrics. 2005;61:223–229. doi: 10.1111/j.0006-341X.2005.031209.x [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

hcq-15-e008368-s001.pdf (150.2KB, pdf)

Articles from Circulation. Cardiovascular Quality and Outcomes are provided here courtesy of Wolters Kluwer Health

RESOURCES