GluD2- and Cbln1-mediated Competitive Interactions Shape the Dendritic Arbors of Cerebellar Purkinje Cells

SUMMARY

The synaptotrophic hypothesis posits that synapse formation stabilizes dendritic branches, yet this hypothesis has not been causally tested in vivo in the mammalian brain. Presynaptic ligand cerebellin-1 (Cbln1) and postsynaptic receptor GluD2 mediate synaptogenesis between granule cells and Purkinje cells in the molecular layer of the cerebellar cortex. Here we show that sparse but not global knockout of GluD2 causes under-elaboration of Purkinje cell dendrites in the deep molecular layer and overelaboration in the superficial molecular layer. Developmental, overexpression, structure-function, and genetic epistasis analyses indicate that these dendrite morphogenesis defects result from a deficit in Cbln1/GluD2-dependent competitive interactions. A generative model of dendrite growth based on competitive synaptogenesis largely recapitulates GluD2 sparse and global knockout phenotypes. Our results support the synaptotrophic hypothesis at initial stages of dendrite development, suggest a second mode in which cumulative synapse formation inhibits further dendrite growth, and highlight the importance of competition in dendrite morphogenesis.

INTRODUCTION

Nervous system function requires proper dendrite morphogenesis and synapse formation. Disruptions of these processes are associated with many neurodevelopmental and psychiatric disorders such as autism and schizophrenia (Kulkarni and Firestein, 2012). Research in the past decades has elucidated mechanisms underlying dendrite morphogenesis (Jan and Jan, 2010) and synapse formation (Südhof, 2018; Yogev and Shen, 2014). However, the relationship between these two developmental events is less explored. Dendrite growth is usually considered to occur prior to synapse formation during neuronal differentiation, as a neuron must extend dendritic branches before it can form synapses with incoming axons. However, these two processes occur largely concurrently in many cases. Thus, synapse formation and maturation could in principle influence dendritic branching and elongation.

Observation of fixed central nervous system tissue led to the synaptotrophic hypothesis of dendrite growth, which postulates that synapse formation and maturation promote dendrite growth (Cline and Haas, 2008; Vaughn, 1989). Live imaging in amphibians and fish have provided evidence for this hypothesis: synapse formation and signaling stabilizes nascent dendritic branches, allowing them to extend further (Chen et al., 2010; Haas et al., 2006; Niell et al., 2004). Disrupting synaptic activity revealed that it regulates dendrite growth and branching in mammalian spinal motor neurons (Kalb, 1994), but a direct test of the synaptotrophic hypothesis requires in vivo manipulation of synapse formation and visualization of dendritic arbors with single-cell resolution. To our knowledge, no such experiments have been performed in the mammalian brain. Here, we investigate this relationship by examining the role of glutamate receptor delta 2 (GluD2)—one of the best-characterized synaptogenic proteins—in dendrite morphogenesis.

GluD2 belongs to the ionotropic glutamate receptor family but is atypical in that it neither binds glutamate nor exhibits direct channel activity upon binding of known ligands. However, GluD2 has a well-established role in synapse formation and maintenance, as GluD2 knockout mice lose nearly half of all synapses between the axons of cerebellar granule cells (parallel fibers) and the dendrites of Purkinje cells at the ultrastructural level (Ichikawa et al., 2016; Kashiwabuchi et al., 1995), concomitant with a reduction in physiological responses of Purkinje cells to parallel fiber activation (Kurihara et al., 1997). GluD2 present on Purkinje cell dendrites acts as a receptor for cerebellin-1 (Cbln1) secreted by granule cells. Cbln1 also binds neurexin, a presynaptic plasma membrane protein on parallel fibers (Yuzaki, 2017). Thus, neurexin, Cbln1, and GluD2 form a tripartite synaptic adhesion complex that promotes parallel fiber→Purkinje cell synapse formation and maintenance (Matsuda et al., 2010; Uemura et al., 2010; Yuzaki, 2017) (Figure 1A). In support of the synaptogenic role of this tripartite complex, Cbln1 knockout also substantially depletes parallel fiber→Purkinje cell synapses, and addition of recombinant Cbln1 in adults rescues this phenotype (Hirai et al., 2005; Matsuda et al., 2010). Indeed, knockout of GluD2 or Cbln1 causes among the strongest synapse loss defects in mouse knockouts of single genes reported. Thus, GluD2^−/− Purkinje cells provide an opportunity to examine the effects of disrupting synapse formation and maintenance on dendrite growth.

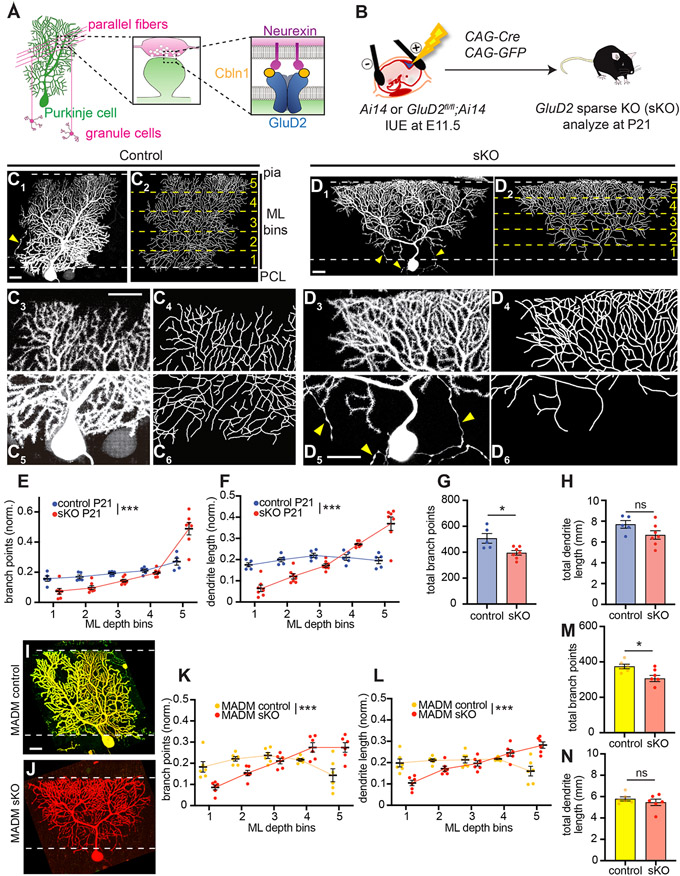
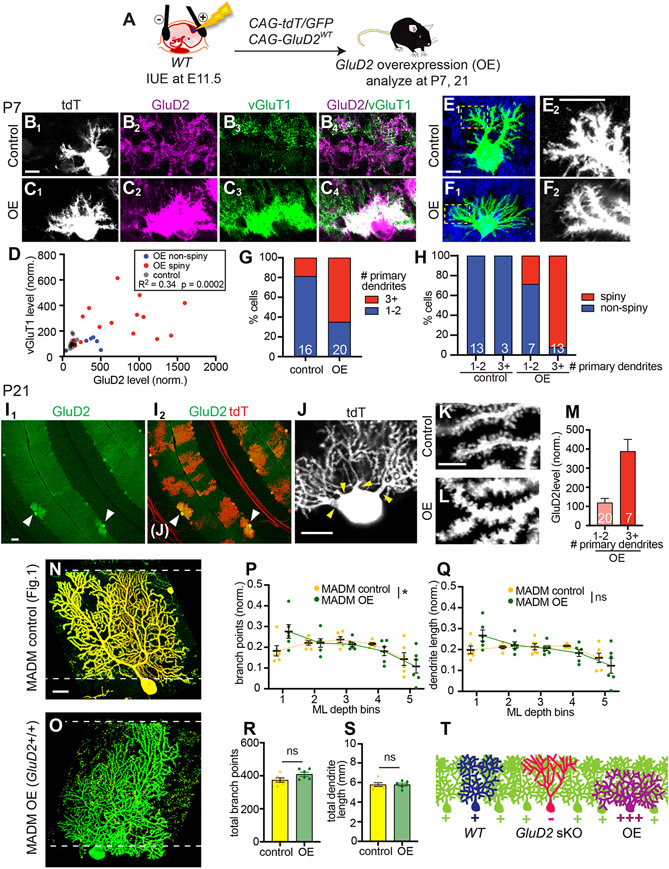
Figure 1. GluD2 Sparse Knockout Phenotypes in Purkinje Cells.

(A) Schematic summary. Left, anatomy, morphology, and connectivity of cerebellar granule cells (magenta) and Purkinje cells (green). Center, schematic of parallel fiber→Purkinje cell synapses. Right, the tripartite synaptic adhesion complex.

(B) Schematic of in utero electroporation (IUE) for genetically accessing Purkinje cells in GluD2^fl/fl; Ai14 or Ai14 (control) embryos. Plasmids encoding Cre recombinase and GFP were co-injected into the fourth ventricle at embryonic day 11.5 (E11.5). Cerebellar samples were collected at postnatal day 21 (P21).

(C) Control Purkinje cells labeled via IUE exhibit similar levels of dendritic elaboration in the deep and superficial molecular layer at P21. Representative confocal image of a control Purkinje cell (C₁) and its tracing (C₂) are magnified for the superficial (C₃, C₄) and deep (C₅, C₆) molecular layer. The top and bottom dashed lines in C₁ and C₂ represent boundaries between the molecular layer (ML) and the pial surface (pia) and Purkinje cell layer (PCL), respectively. The yellow dashed lines in C₂ represent divisions between the five numbered ML bins. Yellow arrowheads, Purkinje cell axons.

(D) Same as (C) except that GluD2 is knocked out (sKO) of this isolated Purkinje cell, which exhibits an inverted triangular shape, with overelaboration in the superficial (D₃–D₄) and under-elaboration in the deep (D₅–D₆) molecular layer.

(E, F) Quantification of the number of branch points (E) and dendrite length (F) in each molecular layer (ML) depth bin in control (blue) and GluD2 sKO (red) Purkinje cells. Data was normalized to the total number of dendritic branch points or dendrite length across the tree.

(G, H) Quantification of the total number of branch points (G) and length (H) of control and GluD2 sKO Purkinje cells. Data are mean ± SEM; n = 5 control, 7 sKO cells from 2 (control), 3 (sKO) mice for E–H.

(I, J) Representative confocal images of a GluD2^+/− (I) and GluD2^−/− (J) cells produced by MADM.

(K, L) Quantification of the normalized number of branch points (K) and dendrite length (L) in each molecular layer (ML) depth bin in MADM control (yellow) and GluD2 sKO (red) Purkinje cells.

(M, N) Quantification of total number of branch points (M) and dendrite length (N) of MADM control and GluD2 sKO Purkinje cells. Data are mean ± SEM; n = 6 GluD2^+/− control, 6 GluD2^−/− sKO cells from 2 mice for K–N.

Note that the baseline parameters for controls in IUE and MADM experiments (panels G, H, M, N) are different (see STAR Methods for details), likely caused by different genetic background.

Statistics: For binned plots in this (panels E, F, K, L) and all subsequent figures, p-values were calculated using two-way ANOVA between control and experimental values in each bin. For bar plots in this (panels G, H, M, N) and all subsequent figures, p-values were calculated using unpaired, two-tailed t tests unless otherwise noted. *p < 0.05, **p < 0.01, ***p < 0.001.

Scale bars, 20 μm.

See also Figures S1 and S2.

RESULTS

Sparse Knockout of GluD2 in Purkinje Cells Reduces Dendritic Branching in the Deep Molecular Layer but Enhances Dendritic Branching in the Superficial Molecular Layer

To gain genetic access to developing mouse Purkinje cells, we performed in utero electroporation (IUE) at embryonic day 11.5 (Nishiyama et al., 2012; Takeo et al., 2015). To delete GluD2 in Purkinje cells and examine the morphology of mutant dendrites, we electroporated plasmids expressing Cre recombinase and a fluorescent marker into wild-type (control) or GluD2^fl/fl embryos (homozygous for a floxed allele of GluD2; Takeuchi et al., 2005) (Figure 1B). Typically, only a small fraction of isolated Purkinje cells expressed the plasmids (Nishiyama et al., 2012); thus, the morphology of the entire dendritic arbor could be readily imaged (Figure 1C₁) and branching patterns completely traced (Figure 1C₂). Likewise, IUE into GluD2^fl/fl embryos resulted in GluD2 knockout in a sparse population of Purkinje cells in an otherwise wild-type environment; we refer to such cells as sparse knockout (sKO) cells hereafter. Antibody staining validated that Cre/GFP-expressing cells, but not neighboring cells, lacked GluD2 protein (Figure S1A, B).

We first examined the morphology of Purkinje cells at postnatal day 21 (P21), when their dendritic arbors have reached the pial surface. Control dendritic arbors, when viewed face-on, typically assumed a nearly rectangular shape in the plane orthogonal to parallel fibers, with similar widths in the deep (close to the Purkinje cell layer) and superficial (close to the pial surface) portions of the molecular layer (Figure 1C, Figure S1C). By contrast, GluD2 sKO Purkinje cells exhibited an inverted triangular shape (Figure 1D, Figure S1D). In the superficial molecular layer, GluD2 sKO exhibited much enhanced branching (Figure 1D₃, D₄) compared to controls (Figure 1C₃, C₄). Conversely, in the deep molecular layer, GluD2 sKO Purkinje cells exhibited much reduced arbors (Figure 1D₅, D₆) compared to controls (Figure 1C₅, C₆). To quantify these effects, we divided the entire molecular layer into five bins of equal depth and quantified the distribution of total dendritic branch points and length within each bin following dendrite tracing (Figure 1C, D; STAR Methods). Compared to controls, GluD2 sKO Purkinje cells had fewer branch points and reduced dendritic length in the deepest layer but more branch points and increased dendritic length in the most superficial layer (Figure 1E, F; Figure S1E, F). When the entire dendritic tree was measured, GluD2 sKO Purkinje cells exhibited fewer total dendritic branch points than controls but similar total dendritic length (Figure 1G, H).

To validate the GluD2 sKO dendrite morphogenesis phenotypes via an independent method, we used mosaic analysis with double markers (MADM; Contreras et al., 2020; Zong et al., 2005) to knock out GluD2 in a sparse population of neurons uniquely marked in an otherwise GluD2^+/− background (Figure S2A). MADM-mediated sKO was also confirmed by a loss of GluD2 protein (Figure S2B, S2C). Compared to MADM GluD2^+/− controls (Figure 1I, Figure S2D), which resembled wild-type cells, P21 MADM GluD2^−/− Purkinje cells exhibited dendrite morphogenesis defects similar to those generated via IUE-based sKO, with reduced branching in the deep molecular layer and enhanced branching in the superficial molecular layer (Figure 1J, Figure S2E). Quantifying the distribution of dendritic branches and lengths in five depth bins across the molecular layer revealed phenotypes in MADM GluD2 sKO cells (Figure 1K, L; Figure S1G, H) similar to IUE-mediated GluD2 sKO cells (Figure 1E, F; Figure S1E, F). MADM GluD2 sKO cells also exhibited fewer total dendritic branch points than controls but similar total dendritic length (Figure 1M, N). Together, these findings demonstrate that GluD2, a receptor essential for parallel fiber→Purkinje cell synapse formation, regulates Purkinje cell dendritic branching.

Evidence that GluD2 Sparse Knockout Phenotypes Are Related to Synaptogenesis Defects

Several lines of evidence suggest that GluD2 sKO disrupted synaptogenesis, consistent with the established role of GluD2 in synapse formation and maintenance (Kurihara et al., 1997). First, fine morphological analysis of P21 Purkinje cells revealed that sKO dendrites had fewer mature dendritic spines and more filopodia-like extensions than control dendrites (Figure 2A₁, A₂). This effect was statistically significant when comparing the head widths of all dendritic protrusions (Figure 2B₁, B₂) or the density of mature spines (Figure 2C₁, C₂; see STAR Methods for classification criteria). These data suggest that sKO dendrites persist in an immature, exploratory state compared to controls.

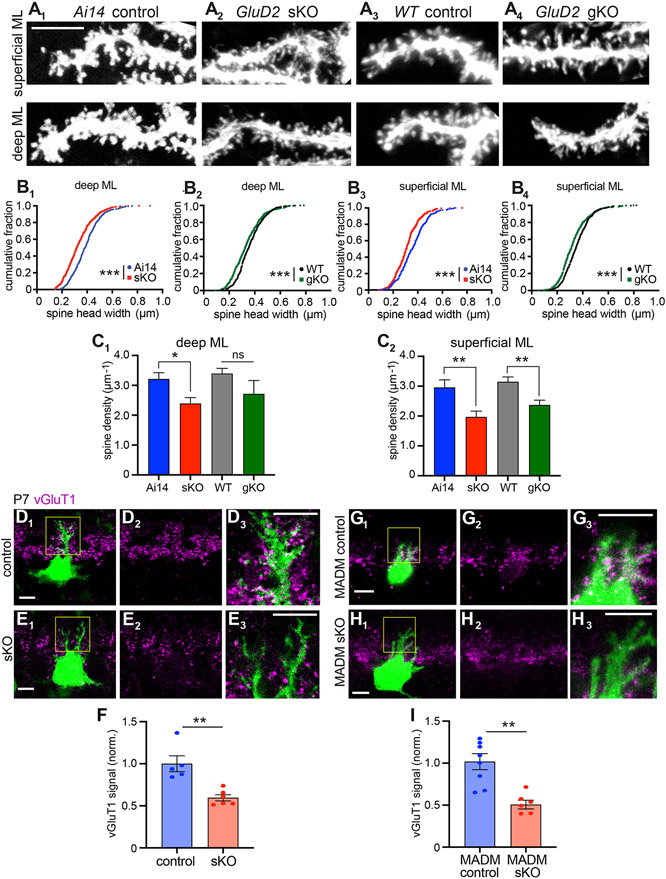
Figure 2. Evidence that GluD2 sKO Disrupts Synaptogenesis.

(A) Representative dendritic segments in the deep (bin 1) and superficial (bin 5) molecular layer showing the morphology of dendritic protrusions in P21 Ai14 control (A₁), GluD2 sKO (A₂), wild-type (WT) control (A₃), and GluD2 gKO (A₄) Purkinje cells at P21. Scale bar, 5 μm.

(B) Cumulative distribution of the head widths of dendritic protrusions. n = 444 (Ai14 control), 442 (GluD2 sKO), 405 (WT control), 414 (GluD2 gKO) deep molecular layer protrusions and n = 417 (Ai14 control), 414 (GluD2 sKO), 383 (WT control), 453 (GluD2 gKO) superficial molecular layer protrusions; ***p < 0.001; Kolmogorov-Smirnov test.

(C) Dendritic spine density. Data are mean ± SEM; n = 10 cells for each condition; *p < 0.05, **p < 0.01; ns, not significant (p > 0.05); t test.

For panels B–C, data were collected from from 2 (Ai14 control), 3 (GluD2 sKO), 2 (WT control), 2 (GluD2 gKO) mice.

(D, E, G, H) Representative single-section confocal images of IUE-based (D, E) or MADM-based (G, H) GluD2 sKO Purkinje cells labeled with GFP (D, E, G) or tdTomato (H) (green). Magenta indicates vGluT1 staining to label presynaptic terminals of parallel fibers. D_2–3, E_2–3, G_2–3, and H_2–3 are high magnification images (vGluT1 only or vGluT1 with GFP or tdTomato) of D₁, E₁, G₁ and H₁ (boxed regions). Scale bars, 10 μm.

(F, I) Quantification of normalized vGluT1 intensities on dendrites from IUE (F) and MADM (I) experiments. Data are mean ± SEM; n = 5 (control), 6 (sKO) cells from 1 control and 1 sKO mice for IUE; n = 8 (control; GluD2^+/− ), 6 (MADM sKO; GluD2^−/−) cells from 3 mice; **p < 0.01; t test.

See also Figure S3.

Second, previous studies found that climbing fibers (axons from inferior olive neurons), which normally synapse onto Purkinje cell dendrites within the deepest 80% of the molecular layer, invade the superficial-most 20% of the molecular layer when parallel fiber→Purkinje cell synapses are disrupted (Bosman and Konnerth, 2009; Hashimoto et al., 2001; Hirai et al., 2005; Ichikawa et al., 2002). Thus, evidence of climbing fiber superficial over-innervation via vGluT2 staining provides indirect evidence of disrupted parallel fiber→Purkinje cell synapses. GluD2 sKO cells exhibited this phenotype when examined in adults (Figure S3).

Third, we immunostained for vesicular glutamate transporter 1 (vGluT1), a presynaptic marker of parallel fiber→Purkinje cell synapses (Miyazaki et al., 2003), at P7; at this stage, Purkinje cell dendritic branches are not too dense, such that most vGluT1 signal could be assigned to individual Purkinje cell dendrites in a given plane. In both IUE-based (Figure 2D-F) and MADM (Figure 2G-I) experiments, we found a significant reduction in vGluT1 intensity abutting GluD2 sKO dendrites compared to controls. This trans-cellular effect on a presynaptic marker suggests that GluD2 sKO caused a cell-autonomous synaptogenesis defect.

Global Knockout of GluD2 Does Not Grossly Affect Purkinje Cell Dendrite Morphogenesis

The effects of GluD2 sKO on the shape of Purkinje cell dendritic tree were unexpected, as previous studies of Purkinje cells in germline GluD2 knockout animals did not report such phenotypes (Kaneko et al., 2011; Kashiwabuchi et al., 1995). To determine if the phenotypes are specific to sparse knockout, we sparsely labeled wild-type control and GluD2 germline (global) knockout (gKO) Purkinje cells using IUE (Figure 3A). Consistent with previous reports, we did not find gross changes in the morphology of GluD2 gKO Purkinje cell dendritic arbors compared to controls (Figure 3B, C; Figure S2F, G; quantified in Figure 3D, E). The total number of branch points and dendritic length in GluD2 gKO cells were not significantly different from controls (Figure 3F, G). Like sKO cells, gKO cells also had fewer mature spines compared to control cells (Figure 2A-C), consistent with GluD2’s essential role in synaptogenesis.

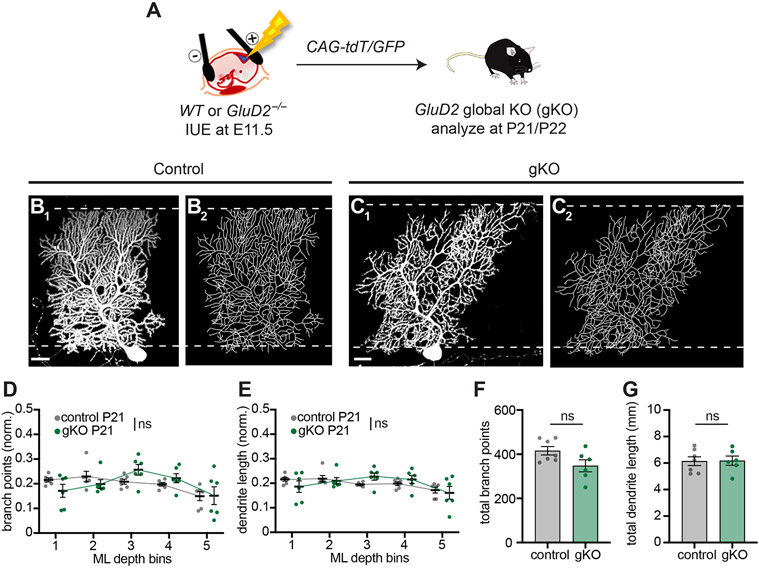
Figure 3. GluD2 Global Knockout Does Not Disrupt Dendrite Morphology.

(A) Schematic depicting labeling of Purkinje cells in wild-type (WT) and GluD2^−/− (gKO) embryos.

(B, C) WT control and global GluD2^−/− gKO Purkinje cells exhibit similar levels of dendritic elaboration in the deep and superficial molecular layer around P21, as seen in representative confocal images (B₁, C₁) and tracings (B₂, C₂) of Purkinje cell dendrites. Scale bars, 20 μm.

(D, E) Quantification of the normalized number of branch points (D) and dendrite length (E) in each ML bin.

(F, G) Quantification of total number of branch points (F) and dendrite length (G) of control (grey) and GluD2 gKO (green) Purkinje cells.

Data from D–G are mean ± SEM; n = 6 control, 6 gKO cells from 2 control, 2 gKO mice; ns, not significant (p > 0.05); by two-way ANOVA (D, E) or t test (F, G).

See also Figure S2 and S3.

Taken together with the sKO phenotypes, these data reveal that Purkinje cell dendrite morphology is affected more by relative differences in GluD2 signaling between neighboring Purkinje cells than by the absolute level of GluD2 signaling within individual cells. Given the established function of GluD2 in parallel fiber→Purkinje cell synaptogenesis (see also Figures 2 and S3), these data suggest that the GluD2 sKO dendritic branching phenotypes may result from Purkinje cell dendrites competing with their neighbors for synaptogenesis with parallel fibers.

GluD2 Sparse Knockout Phenotypes Arise Early and Persist into Adulthood

When does the GluD2 sKO phenotype arise during development? Cerebellar morphogenesis occurs primarily during the first three postnatal weeks. At birth, granule cell progenitors occupy the most superficial external granular layer (EGL), where they undergo rapid proliferation. As granule cells exit mitosis, they extend their axons as parallel fibers into the developing molecular layer between the EGL and Purkinje cells, while their cell bodies descend past the Purkinje cell layer into the internal granular layer, giving rise to the granule cell layer in adults (Altman, 1972a) (Figure 4A). Later-born granule cells stack their parallel fibers superficially to those from earlier-born granule cells (Espinosa and Luo, 2008). Developing parallel fibers are the substrate onto which Purkinje cell dendrites grow, branch, and form synapses, expanding the molecular layer in the process. As granule cell neurogenesis proceeds, the EGL is gradually replaced by the molecular layer until P21, when granule cell neurogenesis is complete and Purkinje cell dendrites reach the pial surface (Figure 4A).

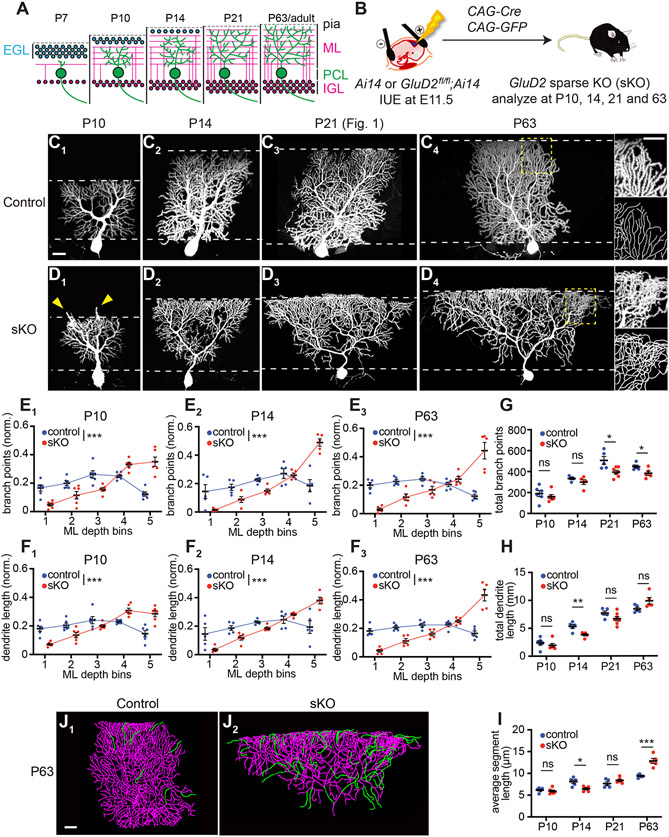
Figure 4. GluD2 Sparse Knockout Phenotypes Arise Early and Persist into Adulthood.

(A) Schematic time course of cerebellar development. Pia, pial surface; EGL, external granular layer; ML, molecular layer; PCL, Purkinje cell layer; IGL, internal granular layer.

(B) Schematic for genetically accessing Purkinje cells in Ai14 and GluD2^fl/fl; Ai14 embryos.

(C, D) Control Purkinje cells (C) exhibit similar levels of dendritic elaboration in the deep and superficial molecular layer between P10 and P63. GluD2 sKO Purkinje cells (D) exhibit an inverted triangular shape, beginning around P10 and persisting at P63. Arrowheads in D₁ indicate overextension of dendritic branches beyond the superficial border of the molecular layer. Higher magnification of superficial portions of dendritic trees and traced images are shown in insets in C₄ and D₄, highlighting frequent dendritic branch crossing-over in sKO but not control cells.

(E, F) Quantification of the normalized number of branch points (E) and dendrite length (F) in each ML bin in control (blue) and GluD2 sKO (red) Purkinje cells at P10, P14, and P63 (see Figure 1E, F for P21).

(G–I) Quantification of the total number of branch points (G), dendrite lengths (H) and average segment lengths (I) of control (blue) and GluD2 sKO (red) Purkinje cells.

For panel E–I, data are mean ± SEM; n = 6, 6, 5, 5, 5, 5 cells from 2, 2, 2, 2, 2, 4 mice for P10 control, P10 sKO, P14 control, P14 sKO, P63 control, P63 sKO mice, respectively; P21 data are from Figure 1. *p < 0.05, **p < 0.01, ***p < 0.001; ns, not significant (p > 0.05); two-way ANOVA (for E, F) or t-test (for G–I).

(J) Representative tracings (from C₄ and D₄) of P63 control and GluD2 sKO Purkinje cell dendritic arbors with dendritic segments longer than 30 μm highlighted in green.

Scale bars, 20 μm.

See also Figure S4.

To determine how GluD2 regulates dendrite morphogenesis across development, we analyzed the GluD2 sKO phenotype at postnatal days 7, 10, 14, 21, and ~63 using IUE (Figure 4B). We found reduced branching in the deep molecular layer and over-branching in the superficial molecular layer of GluD2 sKO cells as early as P10 (Figure 4C₁, D₁; see P7 analysis in Figure S4A-I), after parallel fibers have started to form synapses onto Purkinje cells (Altman, 1972b; West and del Cerro, 1976). These phenotypes persisted across all later stages, with the superficial molecular layer over-branching phenotype becoming more pronounced with age (Figure 4C₂-C₄, D₂-D₄; Figure S4J, K; quantified in Figure 4E, F). Notably, at P10, GluD2 sKO cells had more dendritic branches extending beyond the superficial border of the molecular layer (arrowheads in Figure 4D₁ and Figure S4J₁, quantified in Figure S4J₂). Quantification of total dendritic branch points, lengths, and average segment lengths (Figure 4G-I) indicated a general trend of fewer total dendritic branch points in sKO cells, reaching statistical significance at P21 and P63 (Figure 4G). A trend of decreased total dendritic length in sKO cells appeared in early stages but was reversed at P63 (Figure 4H). The combination of the above resulted in a highly significant increase in the average dendritic segment length of sKO dendrites compared to controls at P63 (Figure 4I), mostly due to long terminal branches (Figure 4J). In addition, P21 and particularly P63 sKO Purkinje dendritic trees exhibited crossing-over of dendritic branches caused by branches that extended out of the 2D plane that normal dendritic trees are restricted to (compare Figure 1D₃, D₄ with Figure 1C₃, C4; insets of Figure 4D₄ with 4C₄). In summary, the GluD2 sKO phenotypes appear early and persist into adulthood.

GluD2 Overexpression Causes Dendritic Over-branching in the Deep Molecular Layer

To complement the sparse knockout studies, we next examined the effects of sparsely overexpressing GluD2 (GluD2 OE) in Purkinje cells of wild-type mice via IUE (Figure 5A). At P7, regions adjacent to GluD2 OE Purkinje cell dendrites exhibited increased vGluT1 staining intensity (Figure 5B, C), with vGluT1 staining levels positively correlated with GluD2 OE levels (Figure 5D). These data support a synaptogenic role of GluD2. Compared to controls (Figure 5E), GluD2 OE Purkinje cells also exhibited supernumerary primary dendrites (Figure 5F₁, G) and numerous spine-like protrusions from dendritic segments (Figure 5F₂); these were largely absent on control Purkinje cells at this stage (Figure 5E₂). To quantify these effects, we categorized imaged Purkinje cells as having 1–2 primary dendrites or 3+ primary dendrites and, independently, as “spiny” or “non-spiny”, blind to genotype and GluD2 level. 81% of controls at P7 had 1–2 primary dendrites, whereas only 35% of GluD2 OE cells had 1–2 primary dendrites (Figure 5G). Furthermore, whereas all control cells were non-spiny, 92% of GluD2 OE cells with 3+ primary dendrites were spiny (Figure 5H). The minority of non-spiny GluD2 OE cells tended to have lower GluD2 levels than the more typical spiny cells (Figure 5D). These results suggest that GluD2 overexpression promotes Purkinje cell synaptogenesis, with accompanying exuberant dendritic branching.

Figure 5. GluD2 Overexpression Causes Dendrite Overelaboration in the Deep Molecular Layer.

(A) Schematic of IUE for overexpressing GluD2 in wild-type mice.

(B, C) tdTomato (tdT) expression (B₁, C₁), immunostaining for GluD2 (B₂, C₂) and vGluT1 (B₃, C₃) and merge (B₄, C₄) in control (B) and GluD2 OE (C) Purkinje cells at P7. Scale bar, 10 μm.

(D) Relationship between vGluT1 and GluD2 levels of each P7 control and GluD2 OE cell (dot).

(E, F) Representative images of control (E₁) and GluD2 OE (F₁) P7 Purkinje cells, showing supernumerary primary dendrites on the GluD2 OE cell. Blue, DAPI. E₂ and F₂ are high magnification images of distal dendrites of E₁ and F₁ (boxed regions), showing many spine-like processes in the GluD2 OE but not control cell. Scale bars, 10 μm.

(G) Percentage of control and GluD2 OE cells with 1–2 or 3+ primary dendrites. The numbers of cells within each category are indicated.

(H) Percentage of spiny and non-spiny cells according to genotype and number of primary dendrites. The numbers of cells within each category are indicated.

For panels D, G, H, n = 16 cells from 2 mice (control) and 20 cells from 2 mice (OE).

(I) Low magnification images of P21 cerebellar cortex showing GluD2 expression levels (I₁) of cells transfected by IUE that are also labeled by tdT (I₂). Arrowheads indicate two Purkinje cells with high levels of GluD2 overexpression and shorter dendritic trees. Scale bar, 50 μm.

(J) Representative images of a GluD2 OE cell with multiple primary dendrites (arrowheads in I₂). Scale bar, 20 μm.

(K, L) High magnification confocal images showing dendritic spines in control (K) and GluD2 OE (L) dendritic segments. Scale bar, 5 μm.

(M) GluD2 overexpression level according to the number of primary dendrites of P21 GluD2 OE cells (n = 27 cells from 2 mice) with 1–2 or 3+ primary dendrites. Data are mean ± SEM; the numbers of cells within each category are indicated.

(N, O) Representative confocal images of P21 MADM control (GluD2^+/−) and MADM OE (GluD2^+/+) cells. Scale bar, 20 μm.

(P, Q) Quantification of the normalized number of branch points (P) and dendrite length (Q) in each ML bin for control (yellow) and MADM OE (green) Purkinje cells. *p < 0.05; ns, not significant (p > 0.05); two-way ANOVA.

(R, S) Quantification of the total number of branch points (R) and dendrite lengths (S) of control and MADM OE Purkinje cells. Data are mean ± SEM; ns, not significant (p > 0.05); t test. n = 6 (GluD2^+/− control), 6 (GluD2^+/+ OE) cells from 2 mice for panels P–S.

(T) Schematic comparing WT, GluD2 sKO, and GluD2 OE dendritic trees.

See also Figure S5.

To test whether these early phenotypes persist in more mature Purkinje cells, we examined GluD2 OE Purkinje cells at P21. Strikingly, some GluD2 OE Purkinje cells had exuberant dendritic branches in the deep molecular layers but failed to extend branches to the pial surface (Figure 5I). These cells also had supernumerary primary dendrites (Figure 5J). While control Purkinje cells had developed wellspaced dendritic spines by this stage (Figure 5K), in GluD2 OE Purkinje cells, individual dendritic protrusions were no longer easily resolved and dendritic trunks appeared thicker, suggesting supernumerary dendritic spines (Figure 5L). We took an unbiased approach to quantifying these effects by imaging randomly selected transfected cells and then categorizing them based on their number of primary dendrites and, independently, their spine morphology (normal vs. “hyper-spiny”), blind to genotype and GluD2 level. Of the 35 cells we quantified, all 7 cells with 3+ primary dendrites came from the GluD2 OE group (with 11 ± 2.4 primary dendrites; mean ± SEM). Furthermore, whereas all control cells and 95% of GluD2 OE cells with 1–2 primary dendrites had normal dendritic spines, 88% of GluD2 OE cells with 3+ primary dendrites exhibited the hyper-spiny phenotype (Figure S5A). Finally, cells with the supernumerary primary dendrite phenotype had higher levels of GluD2 overexpression (Figure 5M; see Figure S5B for representative images of Purkinje cells and their GluD2 intensities). Examination of GluD2 OE cells from unselected samples and additional samples selected based on their failure to reach the pial surface revealed that Purkinje cells with shorter dendritic trees also had very high levels of GluD2 overexpression, supernumerary primary dendrites, and increased thickness in the plane orthogonal to the plane of Purkinje cell dendrite elaboration (Figure S5C-E).

In MADM cerebella, sparse GluD2^+/+ cells in an otherwise GluD2^+/− background (Figure S2A) can also be considered cells with GluD2 overexpression relative to its neighbors. Interestingly, these GluD2^+/+ MADM OE cells also exhibited dendritic over-branching in the deep molecular layer (Figure 5N-O, Figure S5F, quantified in Figure 5P). The distribution of dendrite length within each bin, total number of branching points, and total dendrite length were not affected (Figure 5Q-S).

Taken together, these data indicate that GluD2 overexpression causes morphological phenotypes opposite to GluD2 sparse knockout (Figure 5T): over-branching in the deep molecular layer and, in extreme cases, failure to extend dendritic branches to the superficial molecular layer altogether.

GluD2 That Does Not Bind Cbln1 Cannot Rescue the GluD2 sKO Phenotypes

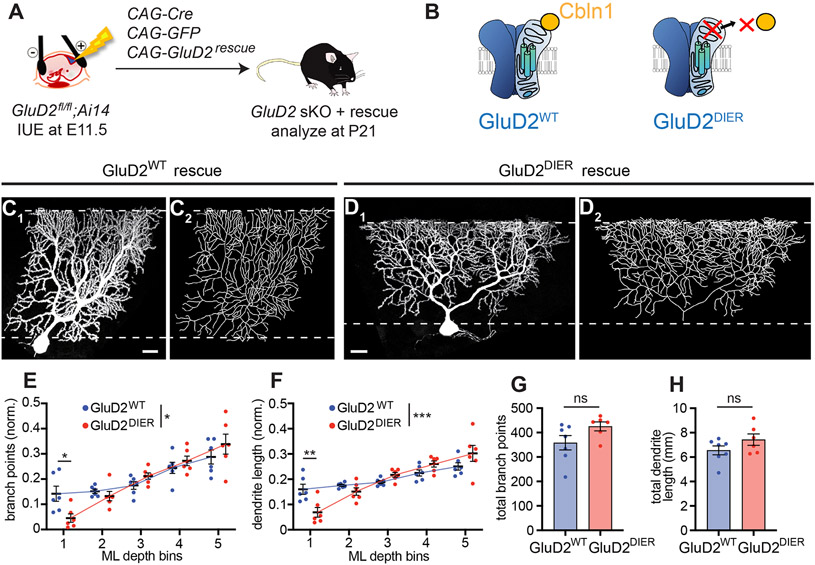
To test if GluD2’s interactions with its ligand Cbln1 are required for proper dendrite morphogenesis, we established an in vivo structure–function assay. The overexpression studies indicated that the gain-of-function phenotypes of GluD2 are expression level-dependent (Figure 5D), as low levels of IUE-based GluD2 overexpression did not cause overt dendrite morphogenesis phenotypes. Thus, we used mild expression of wild-type GluD2 to rescue GluD2 sKO phenotypes by co-electroporating a plasmid encoding wild-type GluD2 (Figure 6A). We then compared this to the effect of expressing, at similar levels, a mutant GluD2 containing four point mutations (D24A, I26A, E61A, R345A; GluD2^DIER in short; Figure 6B) that abolish binding to Cbln1 (Elegheert et al., 2016) (Figure S6A-C).

Figure 6. GluD2 that Does Not Bind Cbln1 Cannot Rescue the GluD2 sKO Phenotypes.

(A) Schematic of GluD2 rescue assay.

(B) Schematic showing that GluD2^DIER (with four point mutations) does not bind the GluD2 ligand Cbln1.

(C, D) Confocal image (C₁, D₁) and tracing (C₂, D₂) of a representative GluD2 sKO Purkinje cell expressing a GluD2^WT (C) or GluD2^DIER (D) rescue construct. Scale bars, 20 μm.

(E, F) Quantification of the normalized number of branch points (E) and dendrite length (F) in each ML bin.

(G, H) Quantification of total number of branch points (G) and dendrite length (H) of GluD2^WT (blue) and GluD2^DIER (red) rescue Purkinje cells.

Data from E–H are mean ± SEM; n = 6 cells from 2 mice for each condition; *p < 0.05, **p < 0.01, ***p < 0.001; ns, not significant (p > 0.05); two-way ANOVA (between genotype) followed by Sidak’s multiple comparisons tests between GluD2^WT rescue and GluD2^DIER rescue values in each bin (C, D); or t test (G, H).

See also Figure S6.

Expression of the GluD2^WT construct successfully rescued the GluD2 sKO branching and length distribution phenotypes (Figure S6D, E). Compared to GluD2^WT rescue Purkinje cells (Figure 6C, Figure S6F), GluD2^DIER rescue Purkinje cells (Figure 6D, Figure S6G) exhibited significantly fewer dendritic branches and reduced dendrite length in the deep molecular layer (quantified in Figure 6E, F). Total branch points and length did not differ significantly between these two conditions (Figure 6G, H). These results support the notion that dendritic branching defects caused by GluD2 sKO result from a disruption of signaling mediated by Cbln1-GluD2 interactions.

Dendritic Morphology Phenotypes of GluD2 Sparse Knockout Are Suppressed by Loss of Cbln1

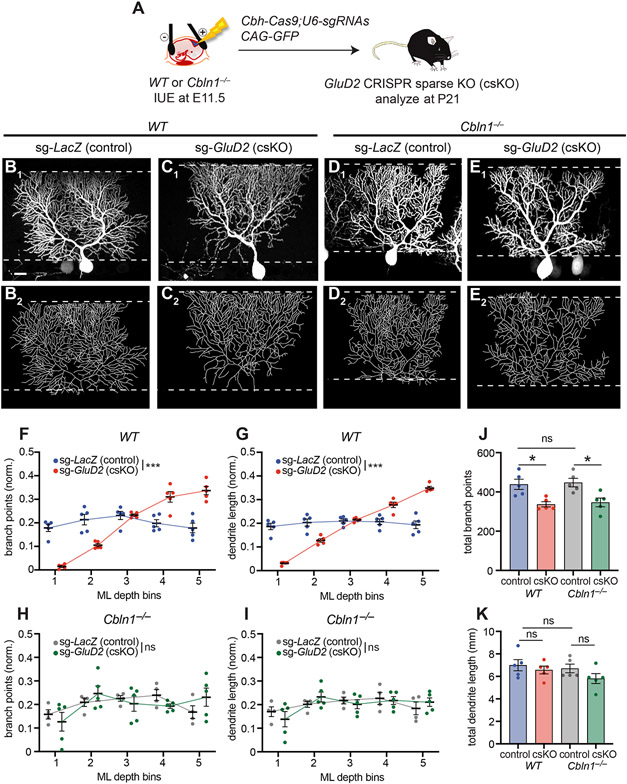
Our data thus far suggest that Cbln1-GluD2 signaling-mediated competition between neighboring Purkinje cells regulates dendritic branching. If so, a complete loss of Cbln1 should remove such competition, and thereby suppress the GluD2 sKO phenotypes.

To test this prediction, we combined Cbln1 knockout with GluD2 sKO. To simplify genetic crosses, we developed a CRISPR/Cas9-based GluD2 sKO approach using plasmids expressing Cas9 and short guide RNAs (sgRNAs) against GluD2, along with GFP as a marker for IUE (Figure 7A; STAR Methods). GluD2 staining validated loss of GluD2 expression in GluD2 CRISPR-based sparse knockout (GluD2 csKO) cells, but not in control cells with sgRNAs against lacZ (Figure S7A-D). When introduced into Purkinje cells in wild-type mice, GluD2 csKO caused phenotypes (Figure 7B, C, S7E, S7F) similar to those produced by IUE of Cre into GluD2^fl/fl mice (Figure 1C, D) or MADM (Figure 1I, J). Quantification revealed both fewer dendritic branch points and reduced dendrite length in the deep molecular layer, and more dendritic branch points and increased length in the superficial layer compared to controls (Figure 7F, G). However, GluD2 csKO in Purkinje cells of Cbln1^−/− mice no longer exhibited the typical sKO dendrite branching phenotypes (Figure 7D, E, S7G, S7H, quantified in Figure 7H, I).

Figure 7. Sparse GluD2 Knockout Phenotypes Are Blocked by Loss of Cbln1.

(A) Schematic of CRISPR-mediated sparse control (LacZ) or GluD2 sKO in Purkinje cells of wild-type or Cbln1^−/− mice.

(B, C) Confocal image (B₁, C₁) and tracing (B₂, C₂) of a representative wild-type (WT) Purkinje cell expressing Cas9 and sgRNAs against LacZ [sg-LacZ (control), B], or GluD2 [sg-GluD2 (csKO), C].

(D, E) Same as B, C except in Cbln1^−/− mice. Scale bar, 20 μm for B–E.

(F–I) Quantification of the normalized number of branch points (F, H) and dendrite length (G, I) of Purkinje cell dendrites in each ML bin in control (sg-LacZ: WT, blue; Cbln1^−/−, grey) and GluD2 csKO (sg-GluD2: WT, red; Cbln1^−/−, green) in wild-type (F, G) or Cbln1^−/− (H, I) animals.

(J, K) Quantification of total number of branch points (J) and dendrite length (K) of sg-LacZ/WT, sg-GluD2/WT, sg-LacZ/ Cbln1^−/− and sg-GluD2/ Cbln1^−/− cells.

Data from F–K are mean ± SEM; n = 5 cells from 2 mice for each condition; ***p < 0.001; *p < 0.05; ns, not significant; two-way ANOVA (F–I); or one-way ANOVA followed by Sidak’s multiple comparisons test (J, K).

See also Figure S7.

Quantification across the entire dendritic tree revealed that loss of Cbln1 did not affect total dendritic branch points and length (Figure 7J, K). GluD2 csKO reduced dendritic branch points in wild-type mice (Figure 7J), consistent with IUE and MADM-mediated sKO data (Figure 1G, 1M). Curiously, this phenotype persisted in Cbln1^−/− mice (Figure 7J), suggesting that GluD2 may have a Cbln1-independent effect of promoting dendritic branching.

Taken together, these experiments demonstrate that the altered dendritic branch distribution of GluD2 sKO Purkinje cells requires the presence of Cbln1 and support the notion that Cbln1/GluD2-mediated competitive synaptogenesis between neighboring Purkinje cells underlies the dendrite morphological defects exhibited in GluD2 sKO cells.

A Generative Model Recapitulates Key Aspects of Purkinje Cell Dendrite Morphogenesis

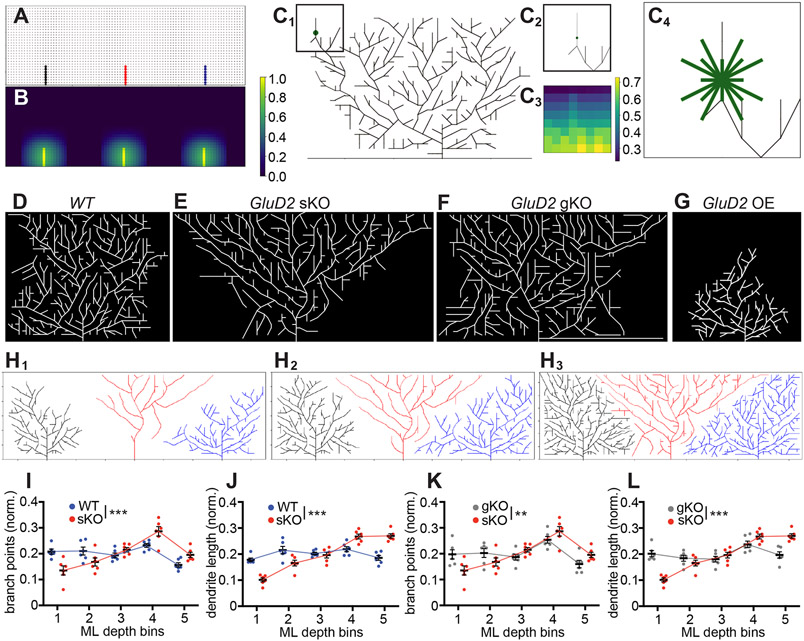
To better understand the dynamics of dendrite growth and the consequences of GluD2 manipulations, we developed a generative model of Purkinje cell dendrite morphogenesis. Due to the competitive nature of GluD2’s influence on dendrite growth, we first modeled the growth of three adjacent wild-type Purkinje cells. This model uses nodes on a 2D lattice to represent synapses with parallel fibers, where occupied nodes indicate an existing synapse and unoccupied nodes indicate the potential for a synapse at that location (Figure 8A). Elongation extends an existing branch, while branching generates a new dendritic process that forks off of an existing branch. At every point in time and at each location in the dendritic arbor, the probabilities of elongation and branching are determined by three factors: (1) cell-autonomous drives to elongate and branch that lessen as the total number of synapses on the tree increases; (2) repulsion from other dendritic processes in the vicinity of the node (Figure 8B); and (3) a force that attracts new dendrite growth upward toward the pial surface. The model iterates through each eligible node in the tree and makes the decision to elongate, branch, or neither based on these probabilities (Figure 8C). New parallel fibers progressively enter the simulation over time to model the developmental trajectory of the molecular layer (see STAR Methods for details). Wild-type cells grown as described tile the 2D grid and display a distinctly square-like morphology (Figure 8D, S8A; Movie S1).

Figure 8. A Generative Model Recapitulates Key Aspects of Experimental Data.

(A) Skeleton of trees that the model begins with. Each node, denoted by a circle and representing a parallel fiber, is marked occupied when the tree extends a branch through that point on the 2D lattice. This branch (edge) is indicated by a solid line, and the color of the line indicates which tree the edge belongs to (black, red, and blue for the left, middle, and right tree, respectively). Other potential nodes for synapses are marked gray. Occupied nodes contribute to repulsion felt in that part of the grid (STAR Methods).

(B) Heat map of repulsion throughout the 2D grid shown in (A) with brighter colors indicating stronger repulsion, which discourages growth. For a given cell, the repulsion from nodes occupied by neighboring cells are stronger than repulsion from nodes occupied by itself. Color bar indicates amount of repulsion normalized to the largest value of repulsion in this heat map.

(C) Example of a decision a cell might make about whether to branch from a certain point, with eligible directions of branching indicated. (C₁) A Purkinje cell with a decision point for branching denoted by the green circle. Color bar indicates amount of repulsion normalized to largest value of repulsion in this heat map. (C₂) The vicinity of the green node shown in (C₁). (C₃) A heat map of the repulsion around the green node, which determines the probability of branching in each direction. (C₄) Eligible directions for branching from the central node marked by green edges. Note that some of these directions will have 0 probability of branching if they result in crossings with current branches, but all are pictured. The endpoint for each direction is determined by the closest lattice point in that direction; because this introduces different lengths, the probabilities of branching in longer directions are adjusted accordingly.

(D) Representative example of a simulation with three wild-type Purkinje cells, showing the middle cell only.

(E) Representative example of a simulation with one GluD2 knockout Purkinje cell and two neighboring wild-type cells on either side, showing the middle cell only. This mimics the sKO condition.

(F) Representative example of a simulation with three GluD2 knockout Purkinje cells, showing the middle cell only. This mimics the gKO condition.

(G) Representative example of a simulation with one GluD2 overexpressing Purkinje cell and two neighboring wild-type cells on either side, showing the middle cell only. This mimics the OE condition.

(H₁–H₃) In-progress simulation at iteration 600 (H₁), 800 (H₂), and 1400 (H₃) with one GluD2 knockout Purkinje cell (red) and two neighboring wild-type cells on either side (black and blue). Note that there is an expansion step between iteration 800 (H₂) and 1400 (H₃).

(I, J) Mean (± SEM) normalized dendritic branch points (I) and length (J) of bins in the molecular layer for wild-type (blue) and GluD2 sKO (red) conditions.

(K, L) Mean (± SEM) normalized dendritic branch points (I) and length (J) of bins in the molecular layer for sKO (red) and gKO (gray) conditions.

For panels I–L, data are mean ± SEM; n = 6 for all three conditions; ** p<0.01; ***p < 0.001; two-way ANOVA.

See also Figure S8 and Movies S1-S3.

To simulate GluD2 knockout conditions, we reduced the ratio of a cell’s drive to branch relative to its drive to elongate. This simulates decreased efficacy in stabilizing new synaptic partners and is based on our findings of reduced branching in the deep molecular layer (Figure 1F, 4E) and over-extension of dendritic branches beyond the upper border of the molecular layer in the initial stages of growth (Figure 4D, S4J). We also modified the growth parameters to mimic a reduction in synaptogenesis of GluD2 knockout cells compared with wild-type cells (Ichikawa et al., 2016).

We simulated sparse knockout by only “mutating” the middle cell and observed an inverted triangular morphology like that of sKO cells (Figures 8E, S8B; Movie S2). Analysis of time-lapse sequences (Movie S2, Figure 8H) indicated that mutant cells extended fewer branches in the deep molecular layer than neighboring wild-type cells but reached the superficial molecular layer first and extended laterally before wild-type dendrites. Quantification of the final dendritic trees showed fewer dendritic branch points and reduced length in the deep molecular layers (Figure 8I, J). The total dendritic length in the superficial molecular layer was also increased in simulated sKO cells compared to controls (Figure 8J), but the over-branching phenotype in the superficial molecular layer was less pronounced (Figure 8I). These differences with experimental data may be due to our simulated dendritic trees growing exclusively in a single plane, whereas GluD2-deficient cells exhibited increased branching in and out of the dendritic plane, likely accounting for the dendritic branch crossings in the superficial layers of sKO cells (Figure 1F; Figure 4F3, inset). Simulating GluD2 OE by “mutating” the middle cell in the opposite direction as sKO recapitulated the failure-to-reach-the-pial-surface phenotype, but not the dendritic over-branching phenotypes (Figure 8G, S8D), also likely due to the 2D constraint of our model.

When we mutated all three cells in the 2D grid to simulate gKO conditions, all cells maintained a square-like morphology like that of wild-type cells (Figure 8F, S8C; Movie S3; quantified in Figure 8K, L). Thus, these simulations recapitulated key features of sparse and global GluD2 knockout cells, supporting the competitive nature of GluD2’s effects on dendritic morphogenesis.

DISCUSSION

Here, we explore the relationship between synaptogenesis and dendrite morphogenesis by examining the effects of disrupting GluD2, a postsynaptic receptor required for synapse formation and maintenance, on dendrite morphology of cerebellar Purkinje cells. Several lines of evidence support the notion that the dendrite morphogenesis defects of GluD2 sKO cells were due to disruption of its established function in synapse formation and maintenance. (1) We observed in GluD2 sKO cells prevalence of thin filopodia-like protrusions in place of mature dendritic spines at P21 (Figure 2A-C) and invasion of climbing fibers onto distal dendritic branches (Figure S3), consistent with disrupted synaptogenesis. (2) GluD2 sKO cells were apposed to less vGluT1 signal than control cells (Figure 2D-I), indicating a relative inability to attract presynaptic partners. (3) GluD2 OE in Purkinje cells recruited more vGluT1 signal and produced more filopodial protrusions at P7 (Figure 5), consistent with GluD2’s role in promoting synapse formation with parallel fibers. (4) GluD2 rescue required the ability to bind its ligand Cbln1 (Figure 6). (5) Dendrite morphogenesis phenotypes of GluD2 sKO cells were suppressed by concurrent loss of Cbln1 (Figure 7), suggesting that they were caused by neighboring Purkinje cells competing to form synapses with parallel fibers. (6) By simulating a synaptogenesis defect in a competitive dendrite growth model, we largely recapitulated GluD2 sparse and global knockout morphological phenotypes (Figure 8), suggesting that reducing synaptogenesis in a competitive environment is sufficient to cause the dendrite morphogenesis defects we observed. Nevertheless, we cannot formally rule out the possibility that Cbln1-GluD2 interactions have a hitherto unidentified function unrelated to synaptogenesis that also contributes to the observed phenotypes.

Sparse GluD2 knockout Purkinje cells feature two prominent and countervailing characteristics: under-elaboration of the dendritic tree in the deep molecular layer and overelaboration in the superficial molecular layer (Figure 1). Morphological analyses across Purkinje cell postnatal development (Figure 4) reveal that the under-elaboration in the deep molecular layer coincides with reduced branching in the same locale, suggesting that the under-elaboration may be caused in part by a marked local reduction in dendritic branching. Without time-lapse imaging data, we cannot determine whether this is caused by a deficit in forming new branches or stabilizing newly formed branches. However, GluD2 overexpression caused supernumerary primary dendrites at P7, some of which persisted to P21 (Figure 5), suggesting that parallel fiber→Purkinje cell synaptogenesis may help stabilize dendritic branches. These phenotypes resemble those caused by perturbation of the neurexin/neuroligin synaptic organizers in Xenopus tectal neurons, where dendritic filopodia are destabilized by neuroligin disruption and stabilized by neuroligin overexpression (Chen et al., 2010). Indeed, the tripartite neurexin-Cbln1-GluD2 synaptic adhesion complex is believed to function in synaptogenesis in the cerebellum analogously to the neurexin-neuroligin complex elsewhere (Südhof, 2018; Yuzaki, 2017). Thus, just as in the Xenopus study (Chen et al., 2010), a reduction in dendritic branching of GluD2 sKO dendrites in the deep molecular layer supports the synaptotrophic hypothesis (Cline and Haas, 2008; Vaughn, 1989). We note, however, that whereas both global and sparse perturbations of neuroligin affect dendritic filopodia stability in Xenopus tectal neurons (Chen et al., 2010), the reduction of Purkinje cell dendritic branching in the deep molecular layer only occurs in sparse GluD2 knockout cells, highlighting the importance of competition (English et al., 2012; Joo et al., 2014) in the regulation of Purkinje cell dendrite morphogenesis.

The overelaboration of Purkinje cell dendrites in the superficial molecular layer in sparse GluD2 knockout cells appears to oppose the prediction of the synaptotrophic hypothesis and reveals a bimodal relationship between synaptogenesis and dendrite growth, echoing previous studies in Xenopus tectal neurons when manipulating effectors of synaptic transmission (Haas et al., 2006; Liu et al., 2009). We propose two explanations for this overelaboration phenotype. (1) Each Purkinje cell’s dendrite growth may be homeostatically regulated by the total number of synapses formed with parallel fibers, which account for the vast majority of input synapses onto Purkinje cells. Under-elaboration of GluD2 sKO dendrites in the deep molecular layer may be compensated for by overelaboration in the superficial molecular layer in order to reach a set point of total synapses formed. (2) The formation of a stable synapse may signal to a dendritic growth cone to stop further exploration. By reducing the ability of Purkinje cell dendrites to form stable synapses with parallel fibers, GluD2 sKO may thus also prevent growth cessation, causing exuberant branching and dendritic over-extension. This is supported by our observation of preferential enrichment of long terminal segments in P63 mice (Figure 4I-J). We note that these two explanations are not mutually exclusive: synapse formation as a signal to stop further dendritic exploration could be a mechanism underlying homeostatic regulation. Our generative model contains both elements, featuring the assumption that an increase in the number of synapses in a dendritic tree results in a homeostatic decrease in the drive for a tree to branch, like a signal to reduce further exploration, and such modelling yielded results similar to our experimental observations (Figure 8). To our knowledge, this is the first generative model of dendrite growth across development, which likely applies only to dendrites that tile and grow in a 2D plane.

Interestingly, both the under-elaboration and overelaboration phenotypes were observed only via sparse but not global knockout of GluD2. We expect that neighboring wild-type Purkinje cells would alter their dendrite morphology to tile the space as seen in our simulation (Figure 8H, Movie S2), though due to technical limitations, we could not experimentally validate this. These findings resemble those of our previous study of neurotrophin-3 (NT3)/TrkC signaling, in which sparse but not global knockout of the neurotrophin receptor TrkC caused a marked reduction in Purkinje cell dendrite length and branching (Joo et al., 2014). TrkC has been implicated as a synaptogenic receptor in hippocampal and cortical neurons (Takahashi et al., 2011); however, evidence suggest that the effect of TrkC sKO in dendrite morphogenesis is distinct from its function as a synaptogenic receptor. The synaptogenic role of TrkC is independent of its NT3-binding and kinase activities (Takahashi et al., 2011), whereas TrkC’s role in regulating Purkinje cell dendrite morphogenesis requires its kinase activity and interaction with NT3 (Joo et al., 2014). Furthermore, unlike GluD2 sKO, TrkC sKO causes a global decrease in dendritic branching and length. If the homeostasis hypothesis described above were true, loss of NT3/TrkC may disrupt homeostasis, whereas loss of Cbln1/GluD2 may selectively impact morphological mechanisms downstream of competitive synaptogenesis without perturbing homeostatic regulation. While further exploration of the relationship between NT3/TrkC signaling and Cbln1/GluD2 signaling will enrich our understanding of the mechanisms of dendrite morphogenesis, both studies highlight the competitive nature of dendrite morphogenesis in mammalian central nervous system neurons and reinforce the importance of studying dendrite development using mosaic methods such as in utero electroporation and MADM.

STAR*METHODS

RESOURCE AVAILABILITY

Lead Conact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Liqun Luo (lluo@stanford.edu)

Material Availability

New plasmids will be deposited at Addgene. Other materials will be made available upon requests.

Data Availability

All data have been presented in Figures and Supplemental Figures. Original images and modeling codes will be made available upon requests.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mice

All procedures followed animal care and biosafety guidelines approved by Stanford University’s Administrative Panel on Laboratory Animal Care and Administrative Panel of Biosafety in accordance with NIH guidelines. Mice were housed in plastic cages with disposable bedding on a 12 hours light/dark cycle with food and water available ad libitum. Pregnant CD1 dams were ordered from Charles River. GluD2^fl frozen embryos were a kind gift from M. Mishina. Cbln1^fl mice were a kind gift from T.C. Südhof and were generated by J. Morgan. GluD2^fl mice and Cbln1^fl mice were crossed to Hprt^Cre mice obtained from The Jackson Laboratory to generate GluD2^−/− (gKO) and Cbln1^−/− mice, respectively. Ai14 mice were obtained from The Jackson Laboratory. Nestin-Cre8.5 mice were a kind gift from W. Zhong. MADM-mediated GluD2 sparse knockout mice were generated using MADM6^GT and MADM6^TG alleles (Contreras et al., 2020) assembled into MADM6-GluD2^fl mice as previously described (Joo et al., 2014), with the Nestin-Cre8.5 transgene driving Cre expression in neural progenitor cells.

METHOD DETAILS

In utero electroporation

In utero electroporation into mouse cerebellar Purkinje cells was performed as described (Nishiyama et al., 2012) with some modifications. Embryonic day 11.5 (E11.5) pregnant dams were anesthetized by isoflurane (starting at 2.5% and maintained at 1.5% 1 L O₂/min). After cleaning the abdomen with betadine, a laparotomy was performed, uterine horns were exposed, and DNA was injected within the following 20–30 minutes. To relax the myometrium, ritodrine hydrochloride (0.4–0.8 μg/g; Sigma-Aldrich, St Louis, MO, USA) was injected into the abdominal cavity or directly onto the exposed uterine horns. Warm sterile PBS was continually applied to the embryos to hydrate them. Under the illumination of a fiber optic light source (Dolan Jenner) with a flexible light guide (Allied Electronics), a plasmid DNA solution in a glass capillary needle was injected into the fourth ventricle using a microinjector (Eppendorf FemtoJet 4I; Eppendorf) until the rostral region of the fourth ventricle was filled with DNA, as visualized with Fast Green dye (Sigma). The volume injected into each embryo was approximately 2–3 μL. After injection, the embryo was held through the uterus with tweezer-style electrodes (CUY650P3; NEPAGENE) so that the positive metal electrode was placed on the rostral rhombic lip of the fourth ventricle, and 1–2 sets of electrical pulses (33–38 V, each with a duration of 30 ms, five pulses at intervals of 970 ms per pulse) were delivered using an electroporater (ECM 399, BTX). After electroporation, the uterus was repositioned in the abdominal cavity, 0.05–0.10 mg/kg buprenorphine-SR was injected directly into the intraperitoneal space. The abdominal wall and skin were then sutured closed. The dams were kept on a heating pad until recovery from anesthesia, then returned to their home cages. The embryos were allowed to continue developing and were typically born on E19. After birth, pups were screened for successful electroporation by examining their cerebella through the skin and skull under a fluorescence stereomicroscope, then returned to their home cage with the dam.

For deleting GluD2 by introducing Cre into GluD2^fl/fl mice, we used the Ai14 mouse line as the background. Because tdTomato (tdT) is also expressed sparsely in some cell types other than Purkinje cells (see below), in order to label single Purkinje cell morphology, we co-electroporated GFP with Cre. For Figures 1 and 4, we detected possible knockout cells by Cre-dependent expression of tdT from the Ai14 allele, and validated deletion of GluD2 by antibody staining. We found that all the imaged tdT/GFP-double positive Purkinje cells lacked GluD2 staining. Therefore, based on the assumption that most of tdT-positive Purkinje cells are GluD2 knockout, we analyzed tdT/GFP-double possitive Purkinje cells without staining GluD2 for sKO experiments in Figure 2D-F and Figure S3B. The expression of plasmid genes by IUE is highly specific to the Purkinje cells (Nishiyama et al., 2012), because at the timing of IUE (E11.5), Purkinje cells are the majority of cells that have finished terminal differentiation by the rostral 4th ventricular zone. There is a chance that plasmids can be introduced in other cell types near the ventricular zone, but most of them are still progenitors and actively dividing, diluting the plasmids to the point the transgenes are no longer detectable. However, when Cre plasmids are electroporated, expression of Cre, even briefly, can activate recombination in such progenitor cells. For our experiments using Cre plasmids for IUE into Ai14 mice, some granule cells, molecular layer interneurons and radial glial cells are occasionally sparsely labeled by tdT but not by GFP. It is unlikely that sparse deletion of GluD2 (if it occurs) in such Cre-expressing non-Purkinje cells affects Purkinje cell dendrite morphology because (1) GluD2 is not expressed in granule cells and radial glial cells, and (2) while molecular layer interneurons express GluD2, they also express GluD1, which plays a more central role and can compensate for loss of GluD2 (Konno et al., 2014).

Cloning and Plasmids

Standard cloning procedures were used to generate new DNA constructs. GluD2 overexpression constructs had two hemagglutinin (HA) tags inserted immediately following the GluD2 signal sequence and followed by GSG linkers. GluD2 expression constructs were subcloned into a pCAG vector derived from pCAG-Cre (Addgene). The DIER mutant had four point mutations (D24→A, I24→A, E61→A, R345→; Elegheert et al., 2016) that abolish binding to cerebellin-1 (Cbln1). Two independent sgRNAs were subcloned into the pX333 plasmid vector (Addgene) for CRISPR-mediated experiments (sgLacZ primer sequences: tgcgaatacgcccacgcgat, cggcgcgtaaaaatgcgctc; sgGluD2 primer sequences: tgatagaatcagcggtcgcc, ccttctgttggtctcgaacc).

Plasmid DNA for IUE was purified using the Qiagen plasmid maxiprep kit (Qiagen) and, following ethanol precipitation, dissolved in HEPES-buffered saline. The plasmid solutions were colored with 0.01% Fast Green so that they were visible when injected into the fourth ventricle. The plasmid DNA used for IUE and their final concentrations were as follows: 1 and 2 μg/μL for pCAG-eGFP (or pCAG-GFP) and pCAG-Cre, respectively (Figures 1, 2 and 4); 3 μg/μL for pCAG-eGFP or pCAG-tdTomato (pCAG-tdT) alone (Figures 3 and 5); 1 and 2 μg/μL for pCAG-tdT and pCAG-HA-GluD2^WT, respectively (Figure 4); and 1, 2 and 1 μg/μL for pCAG-eGFP, pCAG-Cre and pCAG-HA-GluD2^WT/pCAG-HA-GluD2^DIER, respectively (Figure 6); and 1 and 2 μg/μL for pCAG-eGFP and pX333-CBh-Cas9-U6-sgRNA-LacZ/GluD2, respectively (Figure 7).

Typically, the rate of co-expression of multiple plasmids in Purkinje cells by IUE is usually very high (>95%, see (Nishiyama et al., 2012). For example, for the cells shown in Figure 5I, 95.2% (20 out of 21 cells) of the tdTomato-positive cells were HA-positive (HA staining not shown), suggesting that most of the transfected Purkinje cells co-expressed both of the two plasmids electroporated.

Histology and image acquisition

Mice were deeply anesthetized using 2.5% Avertin and perfused transcardially using 4% paraformaldehyde (PFA) in PBS. The fixed brains were dissected out and postfixed for 1–4 hours at room temperature or overnight at 4°C in 4% PFA in PBS. After washing in PBS, 100-μm thick sagittal cerebellar sections were collected from the cerebellar vermis using a vibratome (Leica), blocked in 10% normal donkey serum in 0.1% Triton X-100 in PBS, and incubated with primary antibodies overnight at room temperature or over two nights at 4°C. Sections were then washed in PBS three times, incubated with Alexa Fluor secondary antibodies (Jackson ImmunoResearch Laboratories) for at least 1 hour at room temperature, washed three times in PBS and mounted and coverslipped on glass slides using Fluoromount-G (Thermo Fisher Scientific). Sections were imaged using a Zeiss LSM 780 laser-scanning confocal microscope (Carl Zeiss).

The z-stacked images for dendrite tracing were acquired using a 40×/1.4 Plan-Apochromat oil immersion objective (Carl Zeiss), at 2048 x 2048 pixels per frame with 0.4 μm z-steps. For IUE-based experiments, Purkinje cells in the bank region of the cerebellar primary fissure were imaged. For experiments using MADM mice, Purkinje cells in the bank regions of the cerebellar primary fissure and lobules III and IV were imaged.

To measure GluD2, vGluT1, and vGluT2 expression and image dendritic spines used in the unbiased analyses in Figure 5, an 20×/0.8 Plan-Apochromat air immersion objective (Carl Zeiss) and an 40X/1.4 Plan-Apochromat oil immersion objective (Carl Zeiss) were used. Images in Figure 5I were collected using a 10X/0.3 Plan-Neofluar air immersion objective (Carl Zeiss). For certain experiments, P7 Purkinje cells from lobules III and IV/V and P21 Purkinje cells from lobules III–VIII were imaged.

For Figure S3A, z-stack images of dendritic spines were acquired using an 63×/1.4 Plan-Apochromat oil immersion objective (Carl Zeiss) at 2048 × 2048 pixels per frame, with a zoom factor of 3 and 0.4 μm z-steps. For each Purkinje cell, two z-stack images of isolated distal dendrites were obtained, one from the deepest molecular layer depth bin and another from the most superficial bin. Each image included 1 or 2 distal dendrite segments.

Antibodies

We used the following primary antibodies: goat anti-GluD2 (Santa Cruz Biotechnology or Frontier Institute; 1:200), rabbit anti-HA (Cell Signaling Technology; 1:500), guinea pig anti-vGluT1 (Millipore Sigma or Frontier Institute, 1:200), guinea pig anti-vGluT2 (Millipore Sigma, or Frontier Institute, 1:200). In some MADM experiments, chicken anti-GFP (Aves; 1:500), rabbit anti-DsRed (Clontech; 1:500) were used.

Image analysis and processing

Imaris 9.3 FilamentTracer (Oxford Instruments) was used to trace the dendrites of cerebellar Purkinje cells from z-stack confocal images (see above). Dendrites were traced using semi-automatic AutoPath and Manual modes with a fixed dendrite diameter of 5 pixels. The dendrite beginning point was defined as the location where the primary dendrite thickness is 8 μm in diameter for P14 and older Purkinje cells. For Purkinje cells at P7 and P10, because the primary dendrites tend to be thicker than that of older ages (see Figure 4C₁ and C₄), the thickness at the dendrite beginning point was defined as 10 μm in diameter. All dendritic protrusions longer than 2.5 μm were traced as dendrites. Only three dendritic segments were allowed to form a single dendrite branch point. After tracing all the dendrites, total dendritic length, total number of branch points and total number of dendritic segments were automatically computed by the software and obtained via the Statistics function. Images in Figure 3J were obtained by the Snapshot function of Imaris9.3. For all the other reconstructed dendritic tracing images shown in the figures, the traced dendrites (“filament” objects) were converted to a z-stack image of a dendritic skeleton using the Create Channel function of Imaris9.3 XTension, and the z projection images were created by maximum intensity projection using ImageJ.

Quantification of dendrite branch points and dendrite length in the molecular layer depth bins were performed as follows. To determine the heights of molecular layer depth bins for each Purkinje cell, two points were marked in an orthogonal view to the x-y plane at the superficial surface of the molecular layer on each side of the Purkinje cell where no labeled dendrites existed (the molecular layer surface was visible by background fluorescent signal). A straight line connecting the two points was drawn and defined to be the superficial surface of the molecular layer. Another straight line passing through the dendrite beginning point was drawn parallel to the superficial surface of the molecular layer. When the Purkinje cell had multiple primary dendrites, the dendrite beginning point of the longest dendrite was used. The region between those two lines was defined as the molecular layer, and the distance between the lines was divided equally into five sublayers, which constitute the molecular layer depth bins. The branch points or dendrites above the 5^th (most superficial) bin and those below the 1^st (deepest) bin were included into the 5^th and 1^st bins, respectively. To quantify the dendrite branch points in each bin, x-y coordinates of all branching points were obtained via the FilamentTracer Statistics function. The x-y coordinates were rotated and translated so that the molecular layer was parallel to the x-axis. The dendrite branch points in each bin were sorted according to their y coordinates. To quantify dendrite lengths, the traced dendrites were converted to three-dimensional dendritic skeletons using the Create Channel function of Imaris9.3 XTension. The dendritic skeleton had a uniform dendritic thickness (5 pixel). The images were opened using ImageJ (or Fiji, NIH), rectangular selections of each bin were made using the ROI Manager, and signal intensities of each ROI were measured from all of the z-sections and summed. The resulting signal intensities were divided by the total signal intensities to determine the relative dendrite lengths in each bin. Normalized number of dendritic branch points or normalized dendrite length in each bin was calculated as a ratio to the total number of dendritic branch points or the total dendrite length across the dendritic tree, respectively.

Quantification of head widths of dendritic protrusions (Figure 2B) and spine densities (Figure 2C) were performed using ImageJ (NIH), blind to the genotypes and molecular layer depth bins. For each protrusion oriented into the x-y plane, the largest diameter of the protrusion head was drawn with a straight line perpendicular to the protrusion shaft and quantified as the head width. For quantification of spine density (Figure S3C), we first classified dendritic protrusions as spines and filopodia. We defined “spine” as a mushroom-shaped dendritic protrusion with a spine neck thinner than the spine head, while “filopodia” as a dendritic protrusion whose head is as thin as the stem. We randomly chose and measured the spine head width of 30 such typical “filopodia” and “mushroom spines” from the Purkinje cell images used for the quantification in Figure 2A. The distributions of head width of mushroom spine and filopodia were sufficiently bimodal (mushroom spine, mean head width = 0.385 μm, SD = 0.0594; filopodia, mean head width = 0.184 μm, SD = 0.050), justifying classification of these processes based on their head width. We used the cut-off of 0.2665 μm (= mean − 2SD of mushroom spine head width) to classify dendritic processes as “spine” (head width ≥ 0.2665 μm). We then randomly selected one or two dendritic segments from each of the z-stacked confocal images, quantified the number of all dendritic protrusions oriented into the x-y plane across all the z sections, their head widtsh, and the lengths of the dendritic segment. The dendritic spine density was calculated by dividing the number of spines (head width ≥ 0.2665 μm) by the length of dendritic segment.

For quantification of GluD2 levels in Figure S6C, GluD2 levels in cytosolic regions of the somata of labeled and neighboring non-transfected control Purkinje cells were quantified. Background GluD2 levels were defined as the GluD2 levels in the internal granular layer and were subtracted from the somata measurements. The percentages of resulting GluD2 intensities in the labeled cells to those of non-transfected control Purkinje cell were defined to be the relative GluD2 levels. To quantify normalized vGluT1 or GluD2 levels in dendrites at P7 (Figure 2 and 5), dendritic regions of a labeled cell were selected using Otsu’s thresholding of GFP or tdT (Figure 2), or GluD2 (Figure 5) and the mean intensities of vGluT1 or GluD2 were measured. The mean intensities of neighboring vGluT1-positive molecular layer regions (for Figure 2) or non-transfected dendrites (for Figure 5) were also measured. Background intensities were defined as the darkest regions in the external granule layer and subtracted from the selected regions. The resulting values of sKO dendrites were divided by those of non-transfected dendrites and normalized to average vGluT1 or GluD2 values determined in the same manner from the dendrites of control cells. To quantify normalized GluD2 levels in dendrites at P21 (Figures 5, S5), tdT⁺ dendrite regions were selected using Otsu’s thresholding and GluD2 levels in the tdT⁺ regions were recorded. Control GluD2 levels were defined as neighboring unlabeled molecular layer regions selected using the Rectangular tool. Background intensities were defined as the signal in neighboring interneurons’ nuclei and subtracted from the selected regions. The percentage of GluD2 levels of labeled dendrites to that of non-transfected regions was normalized to that of control Purkinje cell dendrites expressing only tdT.

GluD2 overexpressing Purkinje cells in Figure S5 often had other labeled cells in their vicinity, due to their increased dendrite thickness. Therefore, to highlight their morphologies, masked images were created for Figure S5C, D₂ and E. To do so, dendrites belonging to other cells were removed from each z-section using ImageJ (NIH). The modified images were then opened in Imaris9.3 and Surface objects were created based on the modified images. The original raw images were then masked using the Surface objects.

Evaluating baseline parameters for controls

In this study, we used different methods to disrupt GluD2: IUE (GFP and Cre) into control (Ai14) or GluD2^fl/fl embryos (sKO), MADM, IUE (GFP or tdT) into WT or GluD2^−/− embryos (gKO), and CRISPR-Cas9-based IUE into wild-type or Cbln1^−/− embryos (csKO). While each experiment has a control, each control was on a different genetic background and may thus have shown different baseline parameters for Purkinje cell dendrites. For example, in Figure 1, the Ai14 controls (for IUE) have more branch points and a longer total dendritic length than MADM control cells (GluD2^+/− cells in the same sample). We statistically compared all four control conditions used in this study (Ai14 controls, MADM controls, WT controls for gKO, and sg-LacZ/WT controls for csKO) and found that only Ai14 controls have a significantly greater number of total branch points and total dendrite length than gKO controls or csKO controls (one-way ANOVA followed by Tukey’s multiple comparison test; total branch points, *p < 0.05 for Ai14 control vs. csKO control; total dendrite length, *p < 0.05 for Ai14 control vs. gKO control, and **p < 0.01 for Ai14 control vs. csKO control; p values were calculated by Tukey’s multiple comparison of all 4 groups; n = 5, 6, 7, 5 cells from two mice each for Ai14, MADM, gKO and csKO controls, respectively). There were no significant differences between any other pairs among MADM, gKO and csKO controls. These results indicate that the Purkinje cells of our Ai14 mice expressing GFP and Cre have a larger dendritic tree. Such discrepancies in control base values may be due to differences in mouse genetic background and underscore the importance of control samples of similar conditions (including mouse strain and plasmids introduced by IUE). Likewise, our observations were controlled for in each of our experiments (MADM allows comparison to within-sample control cells).

QUANTIFICATION AND STATISTICAL ANALYSIS

Prism 8.4 (GraphPad) and Excel (Microsoft) were used for data analysis and plotting. All statistical tests were performed using Prism 8.4 (GraphPad).

MODELLING AND SIMULATION METHODS

Overview of Basic Algorithm

We simulated Purkinje cell (PC) dendritic tree growth on a single 2D plane pierced by orthogonal intersecting parallel fibers. Specifically, we started with 3 adjacent PCs at an early developmental stage (Figure 8A). Growth occurs either through extension of dendritic segments from their terminals (elongation) or interstitial branching from an existing non-terminal segment (which we hereafter refer to as branching). Both elongation and branching result in the growth of a new segment. Every dendritic segment consists of a straight line that starts and ends at nearby discretized lattice points on the 2D parallel fiber (PF) grid. Each such lattice point corresponds to a potential PF→PC synapse, which is then realized when a dendritic segment occupies that lattice point. Note that in our simplified 2D planar growth model, we do not consider influences from PC’s at other 2D planes. We model only PF→PC synapses and omit the impact of climbing fiber inputs.

The dendritic segments of a modeled PC can be oriented along one of 16 directions, corresponding to 16 possible nearby lattice displacements between the start and end of every dendritic segment: (Δx, Δy) ∈ {(0, ±1), (±1,0), (±1, ±1), (±1, ±2), (±2, ±1)} (Figure 8C₄). These 16 choices of lattice displacements correspond to an approximate angular separation of 22.5 degrees between adjacent directions. Our final lattice grid of PFs extends across 3 × 38 = 114 lattice points horizontally and 38 lattice points vertically. We model 3 adjacent PC’s under 4 different conditions: (1) WT, (2) GluD2 sparse knockout (sKO) (i.e., modifying growth parameters of the central PC only), (3) global knockout (gKO) (changing the growth parameters of all three PCs), or (4) GluD2 sparse overexpression (OE). The probability of successful elongation or branching at any given point to one of the 16 directions follows the general rules below for all PCs, albeit with different growth parameters for WT and GluD2 knockout cells:

1. To restrict excessive dendrite turning, elongation from a terminal point is limited to 3 directions (0 degrees or approximately ± 22.5 degrees) relative to the orientation of the terminal segment from which elongation is initiated.

2. Branching can occur in any one of the 16 directions.

3. The probability of elongation and branching upwards is higher (mimicking a presumptive attractant from the pial surface).

4. To enforce lack of collisions, neither elongation nor branching can result in the creation of a new dendritic segment that terminates at a lattice point already occupied by a previously grown dendritic segment, and no new segment can intersect any such previous segment.

5. In addition, both the probabilities of elongation and branching to regions with a high density of nearby dendritic segments are diminished through specific modelling of longer range dendro-dendritic repulsion from the same tree, as well as competition from the dendritic tree of neighboring cells.

To execute these rules, at each iteration we randomly picked an occupied lattice point of one of the three existing dendritic trees. Any such chosen lattice point can belong to one of three classes: (1) it is a terminal point on the tree, in which case, in our model, elongation is the only possibility for growth from this point; (2) it is a non-terminal point from which the dendrite extends in two directions, in which case branching is the only possibility for growth from this point; (3) it is a branch point in which the tree already extends in three directions, in which case we do not allow further growth from this point. For the randomly chosen point, our model makes a probabilistic decision as to whether or not to elongate or branch when feasible.

More specifically, let E and B be the events that successful elongation or branching, respectively, actually occurs from a candidate growth point on the tree. The probability P(E) (or P(B)) of successful elongation (or branching) from that growth point is not necessarily 1 and could actually fail due to hard constraints involving collision avoidance or soft factors due to longer range repulsion in all possible directions. However, when a successful elongation or branching event actually occurs, the direction θ along which growth occurs is also chosen probabilistically from the conditional distributions P(θ∣E) for elongation and P(θ∣B) for branching. In general, directions θ in which appreciable dendrodendritic repulsion is far away or directions that are closer to the upwards direction are favored in the distributions P(θ∣E) and P(θ∣B). This process of randomly choosing a growth point, randomly deciding whether or not to grow, and then randomly deciding which direction to grow, is repeated for 2000-4000 iterations to grow all three trees.

Below, we describe in sequence how we modeled dendrodentritic repulsion, how this repulsion determines the conditional probability distributions P(θ∣E) and P(θ∣B) for which direction θ to elongate or branch respectively, and how the total level of repulsion, along with intrinsic drives for growth, determine the probabilities P(E) and P(B) of successful growth or elongation in the first place. We then describe which growth parameters are different in WT and GluD2 knockout cells. Finally, we end with a high-level intuitive description of the key principles enabling our model to account for the experimental data.

Modeling dendrodentritic repulsion

We define r_i(x, y) to be the repulsion field of neuron i = 1,2,3, which always equals the convolution of the current dendritic tree with a spatially decaying kernel. The kernel occupies 17 × 17 lattice points with a central value of 1.875 and all other elements of the kernel fall of as $\frac{1}{16}$. Euclidean distance from the center. This kernel, when convolved with the dendritic tree of neuron i, yields a spatially decaying repulsion field r_i(x, y) around each tree. Examples of the three repulsion fields are shown at an early growth state in Figure 8B. The growth of a given tree involves a total repulsion field r(x, y) that combines its own self-repulsion field with that of its neighbors. For example, for the middle cell, r(x, y) = 5 * r₁(x, y) + r₂(x, y) + 5 * r₃(x, y); this ensures that neighbor repulsion is five times stronger than selfrepulsion.

Repulsion as a function of angle determines which direction to grow

To determine the conditional probabilities P(θ∣E) and P(θ∣B) conditioned on a successful elongation (E) or branching (B) event, we first define a growth score s(θ) that describes how favorable it would be to grow in a direction θ, where θ is one of the 16 possible directions for growth shown in Figure 7C4. For growth directions θ in which a collision would occur, s(θ) = 0, which effectively forbids growth. Otherwise, $s(\theta )=\frac{d(\theta )}{r(\theta )}+b(\theta ,y)$. In the first term, d(θ) is the distance along the growth direction θ to the nearest lattice point (x, y) with nonzero repulsion r(x, y) and r(θ) is the value of this repulsion. Thus directions θ in which appreciable repulsion is far away yield a larger value of the ratio $\frac{d(\theta )}{r(\theta )}$, thereby increasing the growth score s(θ).

The second term b(θ, y) promotes vertical growth, with increasing strength the closer the growth point is in y to the pial surface and the closer the growth angle θ is to the upward direction. More specifically, we define $f_y=\frac{y}{h_{ML}}$ to be the fraction of the vertical distance y the growth point is to the height of the molecular layer h_ML. For angles θ in which Δy ≤ 0, b(θ, y) = max(0.75,1 − f_y). For angles θ in which (Δx, Δy) = (±2,1), b(θ, y) = 0.5 · f_y. For angles θ in which (Δx, Δy) = (±1,1), b(θ, y) = f_y. For angles θ in which (Δx, Δy) = (±1,2), b(θ, y) = 1.5 · f_y. For the vertical θ = 90 degrees in which (Δx, Δy) = (0,1), b(θ, y) = 2 · f_y. Basically, the vertical bias score simply increases linearly with both the height of the growth point and with the rank ordering of the possible slopes. Thus, in summary, the growth score s(θ) is larger when appreciable repulsion is further away in direction θ, and also larger when this direction is closer to upwards. However, it is 0 if growth in direction θ would lead to a collision. Finally, this growth score determines the angular conditional probability distributions of growth through

$$P(\theta \mid E)=\frac{s(\theta )}{{\sum }_{{\theta }_E}s({\theta }_E)},P(\theta \mid B)=\frac{s(\theta )}{{\sum }_{{\theta }_B}s({\theta }_B)}.$$

Here, for elongation, the sum over θ_E extends over only 3 angles: 0 degrees or approximately ± 22.5 degrees, relative to the orientation of the terminal segment from which elongation is initiated and P(θ∣E) can be nonzero only for these 3 angles, yielding a normalized probability distribution. Conversely, the sum over θ_B extends over all 16 possible directions. In summary, these probabilities determine the randomly chosen angle of growth, by forbidding collisions, avoiding the repulsion field, favoring upwards growth, and restricting dendritic turning for elongation but not branching.

A balance between total repulsion and intrinsic drive determines the decision to grow

We next describe how our model computes the probabilities P(E) and P(B) of successful elongation or branching events in the first place. Both these probabilities are inversely related to the total repulsion R_TOT summed across all directions and directly related to overall growth drives E(n_syn) and B(n_syn). These latter drives depend on the number of synapses n_syn already formed and stabilized by the tree and are decreasing functions of n_syn, reflecting that the total growth drive decays as the number of synapses increases. Thus, in our model, synapse formation acts as a soft slow-down inhibitor of dendritic growth. Specifically, the probabilities of successful growth are obtained by balancing the growth drives against the total repulsion through

$$P(E)=\text{min}(\frac{E(n_{syn})}{\sqrt{R_{TOT}}},1),P(B)=\text{min}(\frac{B(n_{syn})}{R_{TOT}^{0.8}},1).$$

Thus, high total repulsion R_TOT in the local vicinity of a candidate growth point and larger numbers of stable synapses n_syn across the entire tree both decrease the probabilities of successful elongation or branching from that growth point. We next describe how we compute the total repulsion R_TOT and the growth drives E(n_syn) and B(n_syn).

The total repulsion R_TOT is defined as follows. Let R(θ) be a measure of the repulsion in direction θ. We define $R(\theta )=\text{min}(\frac{1}{s(\theta )-b(\theta ,y)},200)$ where s(θ) is the growth score defined above. Basically, in a direction θ in which growth would lead to a collision, R(θ) would take a maximal penalizing value of 200. Conversely, in a direction θ in which growth would lead to no such collision, $R(\theta )=\frac{r(\theta )}{d(\theta )}$, where, again, d(θ) is the distance along the growth direction θ to the nearest lattice point (x, y) with nonzero repulsion r(x, y), and r(θ) is the value of this repulsion. Then we have R_TOT = Σ_θmax(1, R_θ)). In simulations, R_TOT is typically on the order of 10⁰ to 10¹.

Now the growth drives are given by

$$E(n_{\text{syn}})=0.2+\frac{{\lambda }_E}{e^{\frac{n_{\text{syn}}-{\theta }_E}{N_E^{\ast }}}+1},B(n_{\text{syn}})=0.05+\frac{{\lambda }_B}{e^{\frac{n_{\text{syn}}-{\theta }_B}{N_B^{\ast }}}+1}.$$

Both are sigmoidal decreasing functions of the number of synapses n_syn already formed. θ_E and θ_B are threshold parameters; when n_syn is significantly above either threshold, the corresponding growth drives starts to diminish. Correspondingly, $N_E^{\ast }$ and $N_B^{\ast }$ set the scale, in terms of number of synapses above threshold, at which diminished growth starts to set in. Finally, λ_E and λ_B are overall constants that contribute to the corresponding growth drive when n_syn is at the corresponding threshold θ_E or θ_B. For wild-type PCs, $N_E^{\ast }=1000$, θ_E = 500, and λ_E = 0.5. This yields a modulation of E(0) ≈ 0.5 at the beginning of growth and an E(1000) ≈ 0.4 at a late stage of growth. Also, for wild-type PCs, $N_B^{\ast }=500$, θ_B = 250, and λ_B = 10 for wild-type PCs. This yields a modulation of B(0) ≈ 6.3 at the beginning of growth and a B(1000) ≈ 1.9 at a late stage of growth. Then when combined with the total repulsion, for wild-type PCs the elongation probability P(E) is in the range 0.01 to 0.02 in early growth and is close to 0.009 in later growth stages. In contrast, the branching probability P(B) is typically in the range 0.01 to 0.025 in early growth stages, and close to 0.007 in later stages.

Parallel Fiber Expansion

Once the dendritic trees for each condition have elaborated enough such that branches stop growing (due to excessive repulsion in every direction), we expand the grid of parallel fibers available as synaptic partners. We do so by adding a set of rows and 3 times that number of columns (due to having 3 cells). After the expansion, each cell has an equal amount of excess space to grow both upwards and to either side. The parallel fiber lattice starts as a 90×30 lattice, and then expands to 102×34 and finally to 114×38.

Modeling the loss and overexpression of the GluD2 receptor

To simulate the effect of losing the GluD2 receptor, we make two changes:

• 6.We change λ_E and λ_B from (λ_E, λ_B)_WT = (0.5,10) to (λ_E, λ_B)_KO = (4,0.5). Thus, the intrinsic growth drive for elongation is increased, while the growth drive for branching is decreased. We justify this change based on experimental evidence that there are fewer branching points in the 2D plane for knockout cells than for WT cells. Also, a decrease in branching likelihood simulates a tree being less effective at growing outward (which involves growing at more angles than just upwards or at a 22.5-degree offset from upward). Because this model is probabilistic and each branch is final, having a decrease in likelihood of branching simulates the process of two growth cones, one from a knockout cell and one from a wild-type cell, competing for a synapse with a PF and the knockout growth cone losing and thus retracting. Then the likelihood of elongation is also increased so as to compensate for the consequent reduction in number of synapses formed—the PC dendrites extend throughout the molecular layer even without the GluD2 receptor; indeed, GluD2 sKO cells overextended dendrites beyond the upper border of the molecular layer at P10 (Figure S4J).
• 7.The knockout cell is less effective at forming synapses because the deletion of GluD2 will diminish its ability to stabilize synapses. Experimental evidence also suggests that only 60% of synapses are retained in a GluD2 knockout condition. Thus, we stochastically count 60% of the number of synapses total in a given knockout cell (used to parametrize the E(n_syn) and B(n_syn) curves), which is on average equivalent to replacing n_syn with 0.6 · n_syn for the knockout cell. This means that the knockout cell will experience a diminished reduction in growth drives E(n_syn) and B(n_syn).

Overall, this simple change of only two parameters λ_E and λ_B in going from WT to knockout is sufficient to account for two striking experimentally observed morphological phenotypes: square dendritic trees in the WT condition (where all three cells are WT), and an inverted triangular dendritic tree for the middle knockout cell in the sKO condition (with a WT neighbor on either side). While we made various choices about model parameters, we do not claim that these are the only sets of parameters that will result in these phenotypes. This is certainly one such set that mimics the experimental data, but there is likely a diversity of parameter choices that can explain the data.

To simulate the effect of overexpressing the GluD2 receptor, we simply change λ_E and λ_B from (λ_E, λ_B)_WT = (0.5,10) to (λ_E, λ_B)_OE = (0.005,50). Thus, the effect is the opposite of what happens in the KO case. Note that many branches that would grow three-dimensionally are lost by our 2D model.

Key principles underlying model behavior

Regardless of detailed parameter choices, a few key principles explain the behavior of the model. First, in going from WT to knockout, elongation becomes favored while branching is suppressed. In the sKO condition, the suppressed branching forces the knockout cell to lose the competition with its WT neighbors to grow its tree by forming synapses in the deep layers where two WT and one sKO tree are all initially present. Thus, the WT neighbor dendritic trees invade the territory of the sKO tree and prevents its outward branching in the deep layers. However, the enhanced elongation of the sKO cell relative to WT cells enables it to reach the superficial layers before the WT does. Moreover, even if the WT tree catches up to the sKO tree in the superficial layers, it has a more diminished drive for branching (reduced E(n_syn) and therefore reduced P(B)) because it has already formed more synapses than the sKO tree due to its already winning the competition in the deep layers (i.e. it has a larger n_syn).

Thus, a combination of three effects enables the sKO cell to win the competition for territory with its WT neighbors in the superficial layers despite the fact that it lost the competition in the deep layers: (1) the sKO tree reaches the superficial layer earlier, (2) the WT cell has diminished drive for branching in the superficial layers due to a larger number of already formed synapses in the deep layers, and (3) the sKO has a less diminished drive for branching in the superficial layers due to formation of fewer synapses in the deep layers. Combined, these effects explain the emergence of the inverted triangular phenotype of the sKO cell through the loss of a competition with its WT neighbors in the deep (superficial) layers.

Supplementary Material

Movie S1

Movie S1. Simulations of Dendritic Growth of Three Wild-type (WT) Cells, Related to Figure 8.

Movie S2

Movie S2. Simulations of Dendritic Growth of One Glud2^−/− (KO) Cell Flanked by Two Wild-type (WT) Cells, Related to Figure 8.

Movie S3

Movie S3. Simulations of Dendritic Growth of Three Glud2^−/− (KO) Cells, Related to Figure 8.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
goat anti-GluD2	Santa Cruz Biotechnology	Cat# sc-26118; RRID:AB_2114046
goat anti-GluD2	Frontier Institute	RRID: AB_2571602
rabbit anti-HA	Cell Signaling Technology	Cat# 3724;RRID:AB_1549585
guinea pig anti-vGluT1	Millipore EMD	Cat# AB5905; RRID:AB_2301751
guinea pig anti-vGluT1	Frontier Institute	RRID: AB_2571602
guinea pig anti-vGluT2	Millipore EMD	Cat# AB2251-I; RRID:AB_2665454
guinea pig anti-vGluT2	Frontier Institute	RRID: AB_2571621
chicken anti-GFP	Aves Labs	Cat# GFP-1020; RRID:AB_2307313
rabbit anti-DsRed/tdTomato	Clontech/Takara Bio	Cat# 632496; RRID: AB_10013483
Alexa Fluor 488 Donkey Anti-Chicken IgY (IgG) antibody	Jackson ImmunoResearch Labs	Cat# 703-545-155; RRID:AB_2340375
Cy3 Donkey Anti-Rabbit IgG antibody	Jackson ImmunoResearch Labs	Cat# 711-165-152; RRID:AB_2307443
Alexa Fluor 647 Donkey Anti-Goat IgG antibody	Jackson ImmunoResearch Labs	Cat# 705-605-003; RRID:AB_2340436
DyLight 405 Donkey Anti-Rabbit IgG antibody	Jackson ImmunoResearch Labs	Cat# 711-475-152; RRID:AB_2340616
Alexa Fluor 647 Donkey Anti-Rabbit IgG antibody	Jackson ImmunoResearch Labs	Cat# 711-605-152; RRID:AB_2492288
Alexa Fluor 647 Donkey Anti-Guinea Pig IgG antibody	Jackson ImmunoResearch Labs	Cat# 706-605-148; RRID:AB_2340476
Alexa Fluor 488 Donkey Anti-Guinea Pig IgG antibody	Jackson ImmunoResearch Labs	Cat# 706-545-148; RRID:AB_2340472
Cy3 Donkey Anti-Guinea Pig IgG antibody	Jackson ImmunoResearch Labs	Cat# 706-165-148; RRID:AB_2340460
Bacterial and Virus Strains
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
Isoflurane	Henry Schein Animal Health	CAS# 26675-46-7; CHEBI:6015
Avertin (2,2,2-Tribromoethanol)	Sigma	SKU# T48402
DAPI	ThermoFisher Scientific	Cat# D1306
Fast Green dye	Millipore Sigma	Cat# F7258
Buprenorphine-SR	ZooPharm	lot # BSRLAB0.5-191112
Ritodrine hydrochloride	Sigma	R0758
Triton X-100	Millipore Sigma	T8787
Fluoromount-G	ThermoFisher Scientific	Cat# 00-4958-02
normal donkey serum	Jackson ImmunoResearch Labs	Cat# 017-000-121; RRID:AB_2337258
Critical Commercial Assays
Deposited Data
Experimental Models: Cell Lines
Experimental Models: Organisms/Strains
Mouse: Crl:CD1(ICR)	Charles River	RRID:IMSR_CRL:022
Mouse: Ai14	JAX	JAX stock #007908; RRID:IMSR_JAX:00 7908
Mouse: GluD2-fl	Takeuchi et al., 2005	N/A
Mouse: Cbln1-fl	T.C. Sudhof/J.I. Morgan	N/A
Mouse: Hprt-Cre	JAX	JAX stock #004302; RRID:IMSR_JAX:00 4302
Mouse: Nestin-Cre8.5	Petersen et al., 2002	N/A
Mouse: MADM6-GT	Contreras et al., 2020	N/A
Mouse: MADM6-TG	Contreras et al., 2020	N/A
Oligonucleotides
LacZ-sg1 target sequence: TGCGAATACGCCCACGCGAT	This paper	N/A
LacZ-sg2 target sequence: CGGCGCGTAAAAATGCGCTC	This paper	N/A
Grid2-sg1 target sequence: TGATAGAATCAGCGGTCGCC	This paper	N/A
Grid2-sg2 target sequence: CCTTCTGTTGGTCTCGAACC	This paper	N/A
Recombinant DNA
pCAG-Cre	Matsuda and Cepko, 2007	RRID:Addgene_13775
pCAG-GFP	Matsuda and Cepko, 2004	RRID:Addgene_11150
pAAV-CAG-eGFP	E. Boyden, unpublished	RRID:Addgene_37825
pCAG-tdTomato	W. Joo	N/A
pCAG-2xHA-GluD2WT	This paper	N/A
pCAG-2xHA-GluD2-DIER	This paper	N/A
pX333	Maddalo et al., 2014	RRID:Addgene_64073
pX333-CBh-Cas9-U6-sgRNA-LacZ	This paper	N/A
pX333-CBh-Cas9-U6-sgRNA-GluD2	This paper	N/A
Software and Algorithms
ZEN	Carl Zeiss	RRID: SCR_013672
Imaris 9.3	Oxford Instruments	RRID:SCR_007370; https://imaris.oxinst.com/
ImageJ (Fiji)	NIH	https://imagej.net/Fiji/Downloads
Prism 8.4	GraphPad	RRID:SCR_002798; https://www.graphpad.com/
Excel	Microsoft	RRID:SCR_016137
Python	Python Software Foundation	https://www.python.org
Other