Abstract
This paper is a discussion of the results of tests intended to (i) estimate the effects of component mix ratios and heat curing of an adhesive joint on the tensile strength, and (ii) to determine the adhesive component mix ratio for which heat curing is insignificant to the strength of adhesive butt joints. Experimental tests were carried out at ambient temperature and elevated temperature during which adhesive butt joints were loaded with a tensile force until failure. The variables were the mix ratio of epoxy adhesive components and the application of heat holding at the adhesive curing stage. An LSTM (long short-time memory) forecast was used to determine the point corresponding to the mix ratio of adhesive components at which heat holding of the adhesive joint no longer has a positive and significant importance to the final tensile strength of the joint.
Keywords: artificial neural networks, LSTM, modelling, adhesive joints, epoxy, resin, hardener, mix ratio, temperature degradation
1. Introduction
Joining with adhesives which are sometimes underestimated is a major complement to the traditional techniques of joining materials. Adhesive joining or bonding is applied not only where the operating conditions of a joint do not require it to have high strength but also for the joining of structural materials, such as metals, and beyond simple applications, which means the aerospace industry, for example, to produce structures which require superior strength to mass ratios [1,2].
There is a number of requirements to be met for the final adhesive joint to be produced properly, meaning strong and durable. The requirements include proper pretreatment of the surfaces to be joined, preparation of the adhesive, and suitable conditions for adhesive curing. The final quality of an adhesive joint also depends on its operating conditions, both in terms of the behaviour of the joint, the joint’s operating temperature and its range of variation, the operating humidity, and more. These issues belong to different scientific disciplines, thus adhesive bonding can be called an interdisciplinary process, which combines chemistry, physics, and mechanics [3,4,5,6,7,8,9].
The sheer diversity of adhesive compositions in use requires engineers to understand the methods and parameters of adhesive curing. Some adhesives become cured by chemical reactions while other adhesives develop their properties by evaporation of solvents and for some adhesives, curing is achieved by solidification of their melts. In this selection of the basic groups of adhesives, subgroups of adhesives can be refined by the detailed mechanism of curing. Chemical reaction-cured adhesives include two-component adhesives, single-component adhesives activated with catalysts or hardeners, moisture-cured adhesives, UV-cured adhesives, and substrate-catalysed anaerobic adhesives. Between the adhesive groups, the adhesive joints produced with them vary in performance, but first they vary in the recommendations and processes for proper fabrication of adhesive joints [7,10,11].
A study of chemically cured two-component adhesives, namely epoxy materials, revealed that the quantitative mix ratio of the epoxy resin to its hardener is significant to the final performance characteristics of the adhesive. If there is too little of a hardener per unit of resin, incomplete polymerisation may occur, whereas too much of the hardener may result in brittleness and fragility of the cured compound, leading to corrosion of the metallic interfaces [12,13,14]. Other characteristics of adhesives, such as resistance to heat or rigidity, may also change with deviations from the specified resin-to-hardener ratios or when admixtures are used [15,16,17,18,19,20]. This is due to the different degree of crosslinking, i.e., the case of an incomplete or different mode of curing the polymeric adhesive material when there is a shortage of hardener; on the other hand, when there is an excess, a certain amount of unreacted hardener remains in the adhesive.
One of the ways for optimising the results of adhesive joining is curing of the adhesive while holding the joint at heat [4]. The heat holding is intended to change the physical properties of the adhesive joint by altering the crosslinking performance. The technical data sheets of adhesives are usually rather vague in specifying that as the curing temperature increases, so does the joint strength, while the curing time is reduced [21,22,23].
An analysis of mechanical performance durability is critical to the estimation of adhesive joint life and the design engineering of modern materials. This is especially important because these materials are often required to withstand elevated temperature conditions and the adhesive strength of epoxy is decreases with increased temperature [24]. However, a large number of experimental tests is often infeasible, for example, because of the constraints of time and costs. One of the solutions can be the application of computer methods, such as the finite element method (FEM) [25,26,27,28,29,30], the boundary element method (BEM) [31,32,33,34], predictive modelling [35,36,37,38,39], and data analytics [40,41,42,43,44,45]. Mathematical modelling with a modest dataset acquired may help to determine the relationships between the individual parameters and mechanical properties, to identify the most promising direction of research, to reduce the number of physical tests, and to markedly reduce the time and costs of research.
Another way of approaching the problem of eliminating quality level deviations in manufacturing processes from the desired values may be the Taguchi method, a technique of optimising process parameters by reducing the variation in the process and examining how different parameters can affect both the mean and variance of the outcome characteristics of the process, as well as which variables have a significant effect. The method defines product quality as the difference between the characteristics of the process result and the value to be achieved (target), which is defined as a function. The Taguchi method uses a procedure that applies orthogonal arrays to statistical design experiments to obtain good results with a minimum number of experiments. This can reduce the cost and time required for the experiment. The objective function of this experimental matrix is the signal-to-noise (S/N ratio. It is used to measure the yield characteristics of the process and the percentage contribution of the process parameters through an analysis of variance. If these characteristics are continuous, then the S/N ratio can be classified into three categories: nominal-the-best, smaller-the-better, and larger-the-better characteristics. The optimal level of process parameters for this optimisation is the level that produces the largest S/N ratio transformation [46]. There are known studies in the field of polymer engineering in which this method was applied [47,48], however, the subject of this paper has not been studied with this method so far.
Response Surface Methodology (RSM) is a set of mathematical and statistical methods for experimental model building and the optimisation of any process in which the response of interest is influenced by several independent factors and their interactions. Central composite design (CCD) is the most suitable experimental design used in RSM, which helps to optimise effective parameters with a minimum number of experiments, as well as to study the interaction between parameters. As it allows for evaluation of the influence of multiple factors and their interactions on one or more response variables, it is a very useful method [49,50,51].
This paper was an attempt at analysing the accuracy of the results produced with the tools for modelling the effects of deviation from the specified adhesive mix ratios on the potential reduction of the performance of an adhesive in operation at temperatures higher than ambient. The modelling tool considered was artificial neural networks (ANNs) capable of memorising and processing information of random input data sequences. The tasks of classification and forecasting was based on a full dataset used as the input data for teaching the ANN. ANNs are designed to process data by classifying it into specific sequences. When solving problems with artificial neural networks, the type and operating principle of an ANN must always be considered or the ANN can be ‘overtrained’ [52,53]. Overtraining is symptomatic by overt matching of the ANN to the teaching data. Specific sequences and structures present in one-off runs can also be memorised by ANNs. Although the capacity of ANNs for information acquisition is very useful, certain problems benefit just as well from the capacity of an ANN to ‘forget’ past states. An example of this application is an information stream which contains a sequence within which subsequences exist with a variable structure. Given these types of processing tasks, a need emerged to build ANNs capable of resetting the memorised states by setting their values to zero without any need for a system operator to intervene and manually delete the states. This is what led to artificial recurrent neural networks (RNN) with the architecture termed LSTM (long short-time memory) [54].
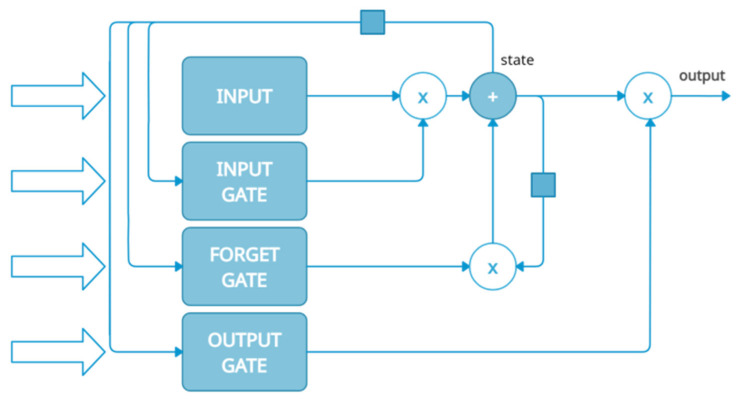
The essence of LSTM is feedback loops existing between the basic network units, which are the memory cells. Another distinguishing feature of LSTM is that it has specific logic gates: an input gate, a forget gate, and an output gate. The input data is calculated by regular artificial neuron units. The accumulation of their values to a state is governed by an input gate, which learns to protect the error flow present in the memory cells against interference from irrelevant input data [55]. The steady, non-decaying, and non-increasing error flow is managed by a feedback loop and the forget gate, which controls the maintenance of the stability of the weight. The output gate opens and closes access to the steady error flow, learning to protect other memory cells against interference from their currently irrelevant contents. A diagram of information processing in LSTM [56] is shown in Figure 1.
Figure 1.
LSTM information processing diagram.
An LSTM RNN was applied in this work to complete the reliable forecast of the full-strength characteristics and maximum breaking forces of specimens. An information sequence containing several sets of full-strength characteristics was a dataset for which the capability to control the changes in the data structures of a narrower range was relevant.
In summary, the study analysed the results of tensile strength tests of adhesive joints made using an adhesive with a deviation from the manufacturer’s recommended A/B ratio (resin/hardener). Two methods of joint curing were tested: at ambient temperature and with additional heating. Samples were tested at ambient and elevated temperatures. LSTM RNN analyses were performed to determine the limiting proportion of adhesive components for which the reheating process at the stage of the adhesive crosslinking of polymeric material would not influence the improvement of the mechanical parameters of the adhesive bond.
2. Materials and Methods
2.1. Materials and Sample Preparation
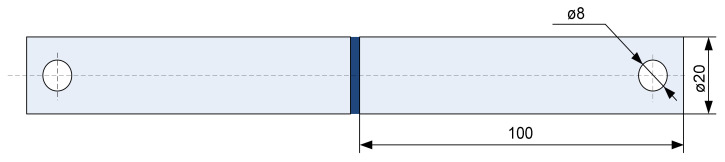
Experimental tests were performed on adhesive butt joints made with ø20 × 100 mm cylindrical specimens made of grade 1.0037 steel (EN 10025:2019–S235JR; Figure 2). The butt surfaces were pretreated per EN 13887:2005 (Structural adhesives—Guidelines for surface preparation of metals and plastics prior to adhesive bonding) with steady processing parameters to ensure the geometric repeatability of the surface pretreatment for all specimens.
Figure 2.
Cylindrical specimen comprising two bars butt-joined by adhesive bonding.
The specimens were bonded with Loctite Hysol 9492 (Henkel, Düsseldorf, Germany), a commercially available, two-component adhesive composition. The adhesive was supplied in a manually emptied cartridge which provides a constant resin-to-hardener mix ratio of 2:1 [21]. To precisely estimate the weight ratio, the components were mixed manually after precise dispensing of the correct amounts by weight. The adhesive was mixed by hand and degassed in a vacuum chamber. The surfaces of the steel specimens to be adhesively bonded specimens were degreased with Loctite 7036 [57]. The specimens were fabricated by adhesive joining under an identical pressure (approx. 8 Pa) to obtain identical joints of a constant adhesive thickness of 0.08 mm in all specimens. The adhesive joints were cured according to the test plan (Table 1) with one of the two methods: a long cure at ambient temperature (3 days/25 °C) and a fast cure with heat holding (1 h/100 °C). To ensure the axial alignment of the upper and bottom specimen halves, a self-alignment fixture was used (a stand with vee blocks—Figure 3). Nine specimens were fabricated for each tested combination of the mix ratio, curing method, and planned strength testing temperature. The flashes of the adhesive were not removed, as permitted by EN 15870:2009 [58]. In the presented study, the degree of curing of the adhesive was not analysed for the conditions considered, assuming that the resulting inaccuracy of the proportions of the components of the adhesive is an accidental, unintentional error occurring at the stage of preparation of the adhesive and resulting in an unintentional change in the final strength properties of the joint made with such an adhesive. Crosslinking degree is of course an important factor in a detailed explanation of the mechanism of changes in joint strength.
Table 1.
Experimental test plan.
| Adhesive Component A/B Mix Ratio (Resin/Hardener) | Curing Conditions |
Test Temperature |
||
|---|---|---|---|---|
| 1.4:1/1:0.71 | x | 3 days/25 °C | x | 25 °C |
| 1.8:1/1:0.55 | ||||
| 2.0:1/1:0.50(manufacturer-specified “m”) | ||||
| 2.2:1/1:0.45 | 1 h/100 °C | 70 °C | ||
| 2.6:1/1:0.40 | ||||
| 3.0:1/1:0.33 |
Figure 3.
Self-alignment fixture in heating chamber.
2.2. Mechanical Testing
The produced specimen joints were tensile-tested. This was done in fixtures with clamps on both ends of the specimen to ensure that no bending moment was introduced during the tensioning (Figure 4). The test plan provided for different operating conditions of the adhesive joints, thus the specimens were tested in ambient temperature and elevated temperature (70 °C). The specimens tested at the elevated temperature were heated in an oven so that their entire volume was heated to the planned temperature level. Each specimen was tensioned at a steady rate of 4 mm/min and the failure force of the adhesive joint was recorded and converted to the joint strength by dividing the failure force by the cross-sectional area of the adhesive joint. For each of the tested adhesive joints, its failure mode was recorded with a total of three failure mode types: cohesive failure (within the adhesive joint), adhesive failure (between the adhesive layer and the bonded material), and mixed failure according to ISO 10365 Standard—Designation of main failure patterns [59] (Table 2).
Figure 4.
Fixtures with clamps (double-Cardan universal joint).
Table 2.
Failure patterns: (a) CF—cohesion failure, (b) AF + CF—mixed, (c) ACFP—adhesion and cohesion failure with peel, and (d) AF—adhesion failure.
| CF | AF + CF | ACFP | AF |
|---|---|---|---|

|

|

|

|
2.3. Statistical Analysis
To verify if there were significant differences in the strength values between the heat-held and the non-heat-held adhesive joints, the experimental test results were analysed statistically [4,60] in the Statistica 13 suite from TIBCO Software Inc. (2017; Palo Alto, CA, USA). The significance level assumed was α = 0.05. A selection of strength test results (in pairs) was analysed using:
The Shapiro–Wilk W-test (for the normality of distribution in the produced series of resultant joint strength test values);
The tests by Fisher, Levene, and Brown–Forsythe (for the equality of group variances); and
Student’s t-test (for the results characterised by normality of distribution and equality of variances to analyse the equality of the average resultant joint strength values at the adopted significance level).
2.4. Long Short-Term Memory Artificial Recurrent Neural Network
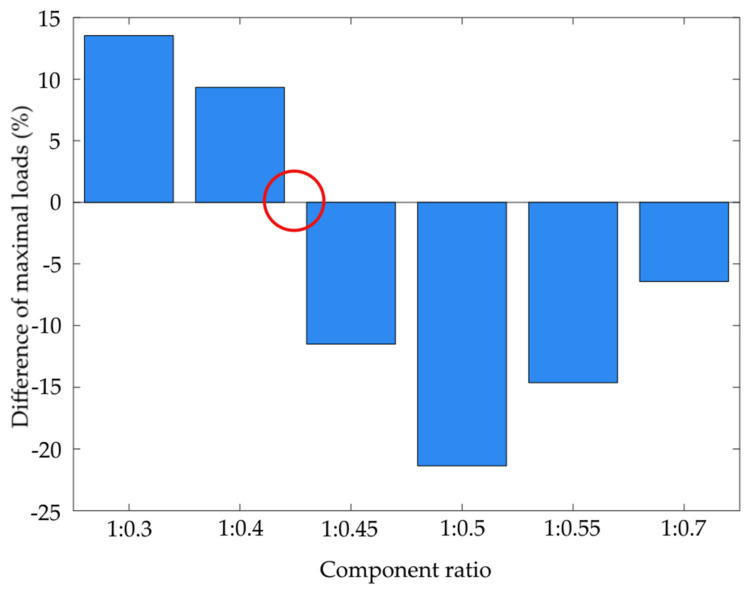
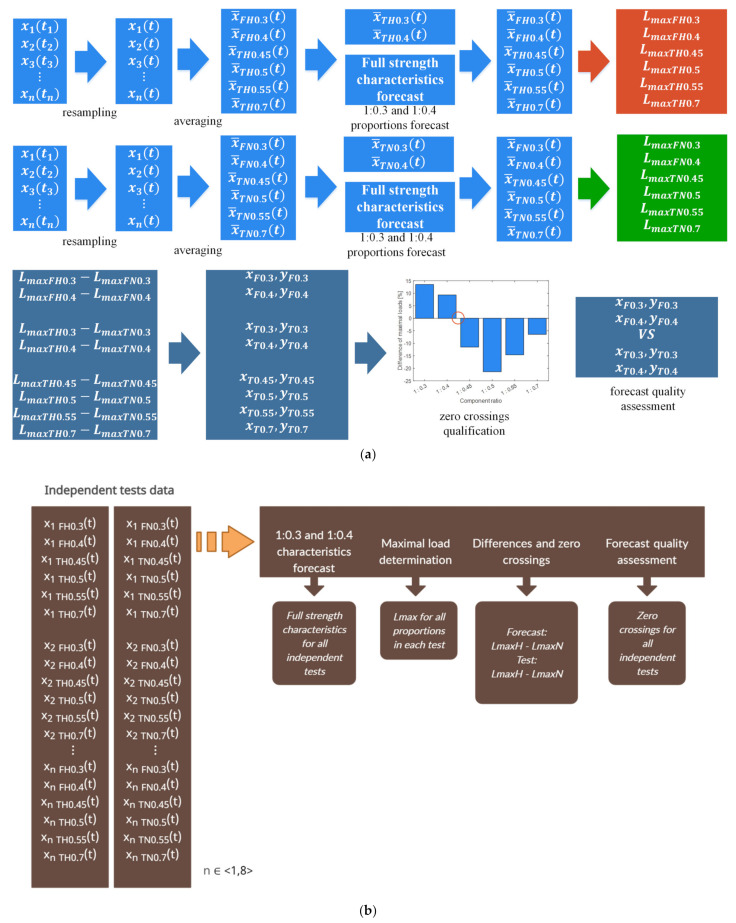
The recorded experimental test data was analysed with two approaches: first, a set of averaged data was tested, and second, the processing was run on the samples at random within the assumed range of adhesive composition mix ratios. The common core of both approaches is the generic diagram of signal processing, consisting of the determination of the zero crossings for the differential maximum breaking force vs. the selection of component mix ratios (Figure 5). The columns show the values of the differences of the maximum destructive loads between the heated and non-heated joints, expressed as a percentage increase/decrease in relation to the non-heated joint load. The red circle marks the assumed area of the sought component ratio. Generally speaking, the test data, which included a specific mix ratio of the applied adhesive components, was analysed by forecasting the full-strength characteristics. The input data was the strength characteristics for the mix ratios at which the static strength was found to be reduced after heat-held curing. The sequence of input data was set from the highest to the lowest hardener ratio: 1:0.7; 1:0.55; 1:0.5; 1:0.45; 1:0.4; and 1:0.3.
Figure 5.
Relative change of the average static strength between the heat-held cured joints and the ambient temperature-cured joints.
The signal processing diagram for the first approach involved preprocessing by resampling and averaging the data. The trends within the specified mix ratios were forecast. The declared teaching data was the averaged trends with the hardener ratio order from the highest to the lowest. Here, the ratios were 1:0.7; 1:0.55; 1:0.5; and 1:0.45, equal to 67% of the entire signal length (Figure 6). The remainder of the signal which included two full-strength characteristics (for mix ratios 1:0.4 and 1:03) were forecast with a DLN LSTM algorithm (Deep Learning Networks—Long Short-Term Memory). For the downstream data processing, the experimental test data was also included for mix ratios 1:0.4 and 1:0.3 (independent of the forecast). Based on the produced test results, the maximum breaking forces, namely Lmax, were determined for the heat-held cured joints (LmaxH) and the ambient temperature-cured joints (LmaxN). Based on the breaking force determined for the values obtained by experimental testing (LmaxT) and the values from the forecast characteristics (LmaxF), the following differences were determined:
| (1) |
| (2) |
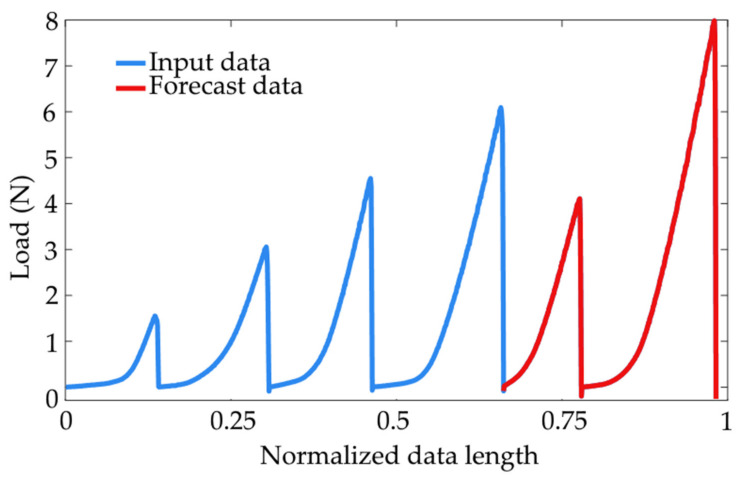
Figure 6.
Range of forecast-processed data.
The values of the differences present within the assumed mix ratios were used to determine the node points. The zero crossings of the static strength change vs. tested adhesive mix ratio were determined by node interpolation. The diagram of this procedure is shown in Figure 7a.
Figure 7.
LSTM processing diagram: (a) averaged tests and (b) independent tests.
However, assuming it is feasible to reduce the number of experimental/laboratory tests, complementing the data with forecast values might lead to certain inaccuracies in the specification of adhesive component mix ratios. To more accurately verify the produced results due to the natural measurement discrepancies, it was decided to run a second analysis by testing random samples within the range of the tested mix ratios.
This second analysis included separate forecasting of the strength characteristics for a set of adhesive joints within the tested mix ratios. Like in the previous analysis of the experimental test results, the specimens were sequenced from the highest to the lowest hardener ratio. This time, the share of teaching data in the signal length was between 54% and 76%. The difference was a result of the different lengths of the strength characteristics. No resampling algorithm was implemented in order to avoid distortion in the individual signals. Like in the first analysis, two strength characteristics were forecast for the adhesive joints with the lowest hardener ratios. As in the first analysis, the DLN LSTM integrated in Matlab 2021a was used for the forecasting process.
The first dataset analysed was the specimens with and without the heat-held curing at the test temperature of 70 °C. This dataset was resampled, followed by averaging over the limits of the test temperature, mix ratios, and curing specifications. The next step was to forecast the locations of nodes for the function of strength change following heat holding of the adhesive joints. The zero crossings were determined by interpolation with a cubic spline and a function obtained by the least-squares method.
The second dataset was random samples in the following range: test temperature, mix ratios, and curing specifications. Similar to the first analysis, the input (teaching) data for the forecast was the trends with the decreasing mix ratios: 1:0.7; 1:0.55; 1:0.5; and 1:0.45. The output was the forecasts of subsequent trends for mix ratios 1:0.4 and 1:0.3. Each resulting trend had the maximum breaking force of the specimen determined separately for the forecasts and the experimental tests. The produced breaking force values for all tested mix ratios were adopted as the nodes for the subsequently interpolated functions. In line with the objective of this paper, each set of specimens had zero crossings determined, denoting the proportions of the components at which holding at heat was no longer relevant to the adhesive joint strength. The processing diagram of the algorithm for independent tests is shown in Figure 7b.
3. Results and Discussion
3.1. Mechanical Testing
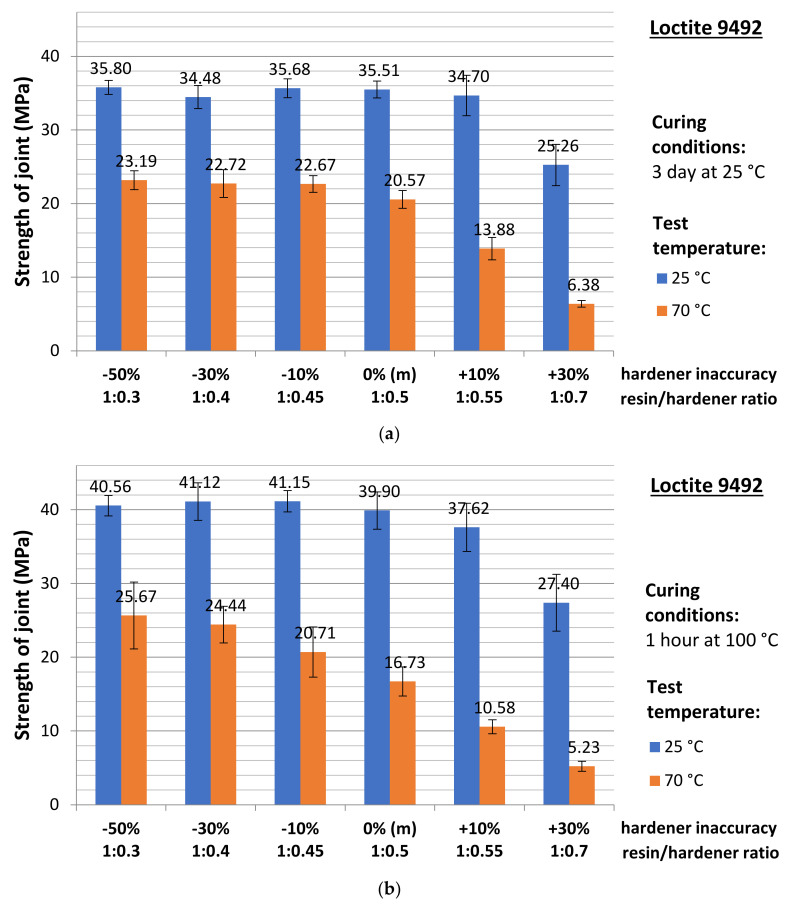
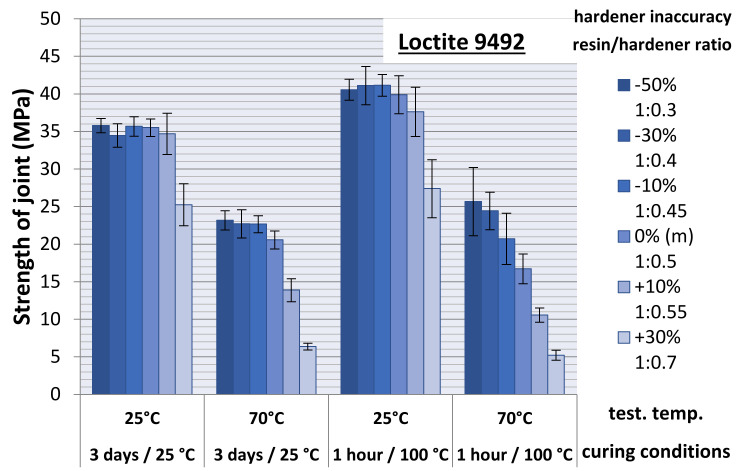
The obtained values of the adhesive joint breaking (failure) force were converted to the adhesive joint strength by dividing the force value by the joint (specimen) cross-sectional area. The strength results for the adhesive joints cured at ambient temperature are illustrated in Figure 8a. For the adhesive joints cured by heat holding (for 1 h at 100 °C), the strength results are shown in Figure 8b. Both charts include a slight scatter of the results, being a standard deviation. A summary of all obtained experimental results, allowing for a general comparison of the series between each other, is shown in Figure 9.
Figure 8.
Change in the adhesive joint strength from the test temperature for the joints (a) cured without heat holding and (b) cured with heat holding.
Figure 9.
Summary of the strength test results.
For each of the tested adhesive joints, its failure mode was recorded according to ISO 10365 Standard—Designation of main failure patterns [59], with a total of four failure mode types: cohesion failure (within the adhesive joint), adhesion failure (between the adhesive layer and the bonded material), mixed adhesion/cohesion failure, and adhesion/cohesion failure with peel (Table 2).
A summary combining the individual joint series with the resulting tensile strength and failure mode of the joint is shown for the series tested at room temperature in Table 3. Samples tested at elevated temperature are summarised in Table 4.
Table 3.
Failure mode change after heat curing samples tested at 25 °C.
| A/B Mix Ratio (Resin/Hardener) |
Cured 3 Days at 25 °C | Cured 1 h at 100 °C | ||
|---|---|---|---|---|
| Mean Tensile Strength (MPa) |
Failure Mode | Mean Tensile Strength (MPa) |
Failure Mode | |
| −50% 1:0.3 | 35.80 | CF | 40.56 | CF |
| −30% 1:0.4 | 34.48 | CF | 41.12 | CF |
| −10% 1:0.45 | 35.68 | CF | 41.15 | CF |
| m: 1:0.5 | 35.51 | CF | 39.90 | CF |
| +10% 1:0.55 | 34.70 | CF | 37.62 | 78% AF + CF, 22% CF |
| +30% 1:0.7 | 25.26 | 89% AF + CF, 11% CF | 27.40 | AF + CF |
Table 4.
Failure mode change after heat curing samples tested at 70 °C.
| A/B Mix Ratio (Resin/Hardener) |
Cured 3 Days at 25 °C | Cured 1 h at 100 °C | ||
|---|---|---|---|---|
| Mean Tensile Strength (MPa) |
Failure Mode | Mean Tensile Strength (MPa) |
Failure Mode | |
| −50% 1:0.3 | 23.19 | CF | 25.67 | CF |
| −30% 1:0.4 | 22.72 | AF + CF | 24.44 | AF + CF |
| −10% 1:0.45 | 22.67 | 78% CF, 22% AF + CF | 20.71 | AF + CF |
| m: 1:0.5 | 20.57 | 56% AF + CF, 44% CF | 16.73 | 78% AF + CF, 22% AF |
| +10% 1:0.55 | 13.88 | AF + CF | 10.58 | 56% AF + CF, 44% AF |
| +30% 1:0.7 | 6.38 | ACFP | 5.23 | AF |
Preliminary analyses indicate a clearly positive character of the adhesive heat curing process for samples tested at ambient temperature. In each case of the resin/hardener ratio tested, the average compressive strength values obtained are ~8–20% higher for the heat-cured samples. The same is true for samples tested at elevated temperature but only for samples with significant non-hardener addition (−50% and −30%). From a deficiency of about −10% hardener, through the manufacturer’s recommended proportion, to adhesives with excess of hardener, the average strength of the heated joints is lower than that of the unheated ones.
It can also be seen that the nature of the joint failure changes with the amount of hardener in the adhesive formulation. At ambient temperature, an excess of hardener will result in a change in the type of failure from cohesive to cohesive–adhesive. Depending on how the adhesive is cured, this happens differently: for an unheated adhesive, this is at about 30% excess hardener and a heat-cured adhesive shows this change with as little as 10% excess hardener. Interestingly, the correct amount of hardener and its deficiency always resulted in cohesive failure of the joint. The same adhesive compositions tested at elevated temperatures showed a similar trend, with purely cohesive failure being recorded only at very high hardener deficiency (−50%), regardless of whether the bond was heated or not. Smaller values of hardener deficiency, the manufacturers ratio, and a ratio up to 10% hardener excess resulted in joints with mixed failure characteristics. The most significant change in the mode of joint failure between the non-heated and heated adhesive was observed for samples tested at elevated temperature. This can be seen from a hardener deficiency of −10%, where the failure mode changes from 3/4 purely cohesive to mixed (adhesive–cohesive) as a result of samples’ heating. Furthermore, at the manufacturer’s recommended ratio, the mode changes from cohesive-mixed (~50–50%) to approximately ¾ mixed, and at 10% hardener excess from purely mixed to mixed-adhesive (~50–50%).
A large hardener excess (+30%) resulted in adhesive failure, from adhesive–cohesive with peel for samples that were not heated to purely adhesive failure for samples that were heated while curing. Improved adhesive parameters after heat curing can be explained by the higher mobility of the heated particles of resin, which further supports polymerisation. The adhesive subjected to thermal curing achieves a significantly higher degree of crosslinking, becomes stiffer, and, at the same time, its strength increases. However, for an adhesive tested at elevated temperatures, these changes lead to a deterioration of the adhesive properties and, consequently, to a change in the mode of destruction towards the adhesive one.
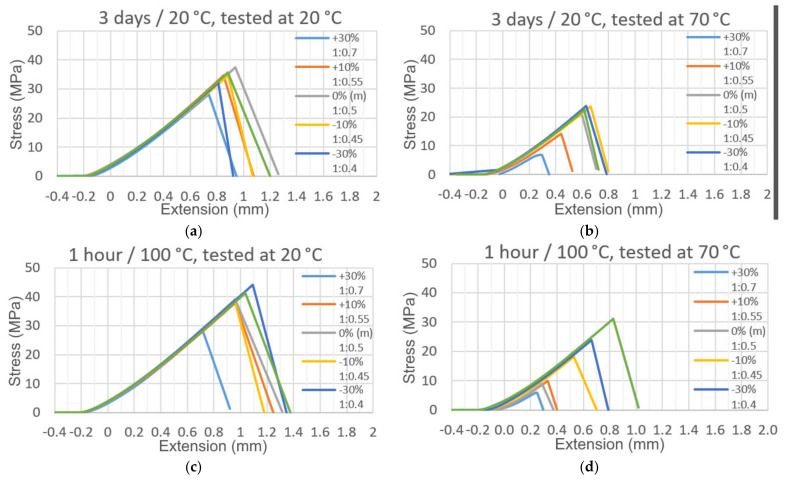
Figure 10 shows examples of strain-to-stress diagrams obtained during tests at ambient and elevated temperatures of samples made with adhesives of the tested composition and curing conditions.
Figure 10.
Stress–extension graphs of tested adhesive joints prepared under inaccurate addition of hardener component in adhesive (random samples): (a) cured 3 days at 20 °C, tested at 20 °C; (b) cured 1 h at 100 °C, tested at 20 °C; (c) cured 3 days at 20 °C, tested at 70 °C; and (d) cured 1 h at 100 °C, tested at 70 °C.
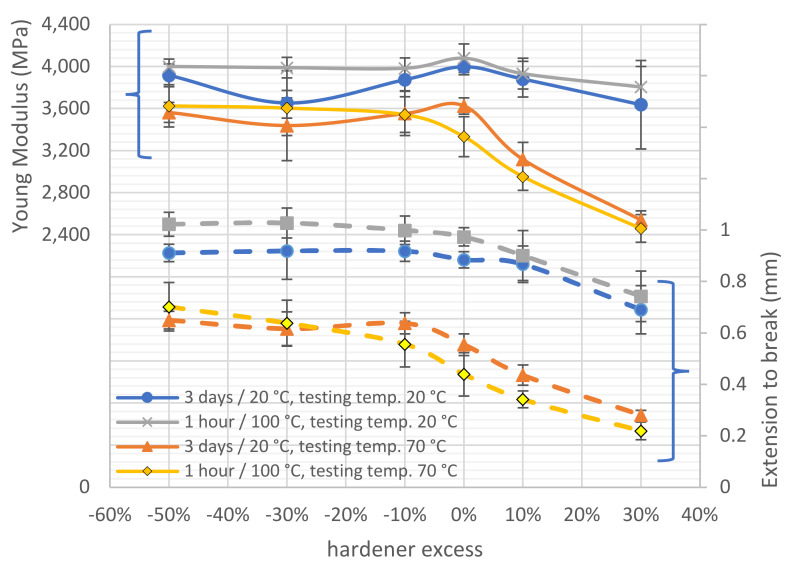
A summary of other important test results, i.e., the value of the maximum strain at which the joint failed or the value of Young’s modulus for joints made with adhesives of different compositions, curing conditions, and test temperatures is shown in Figure 11.
Figure 11.
Mean Young’s modulus and mean extension-to-break of tested adhesive joints prepared under inaccurate addition of hardener component in adhesive.
There is a clear decrease in the mean Young’s modulus with an excess of hardener in the adhesive formulation, especially for samples tested at elevated temperatures, with a simultaneous reduction in mean strain to joint failure. A noticeable effect of thermal curing was also observed, which was almost always associated with an increase in the Young’s modulus of the adhesive regardless of its test temperature and the ratio in which the adhesive was made. This can be explained by the higher mobility of the heated particles during curing, aiding polymerisation. An adhesive subjected to thermal curing achieves a significantly higher degree of crosslinking, becomes stiffer, and, at the same time, its cohesive strength increases [61].
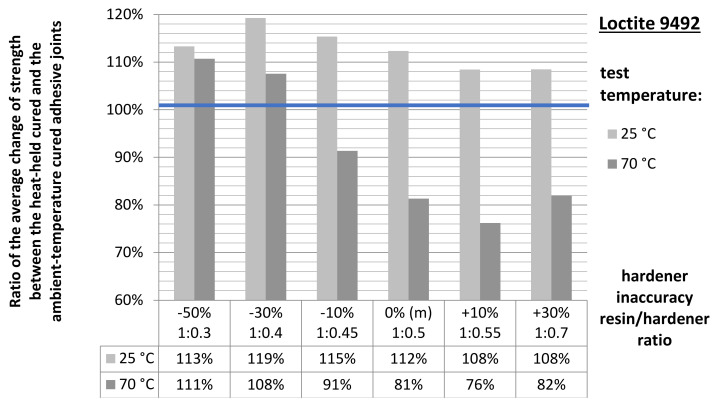
The quotient of the produced heat-held cured adhesive joint strength and the ambient temperature-held adhesive joint strength was the average coefficient of change in the adhesive joint strength following heat holding for the adhesive compositions varying in the mix ratio and the test temperature of the joint (Figure 12).
Figure 12.
Average strength ratio of the heat cured to the ambient temperature-cured adhesive joints.
The foregoing summary is only a comparison of the average joint strength values. To understand the relationships between the applied heat holding of cured adhesive joints and their final strength at both various degrees of distortion of the relevant adhesive composition mix ratio and different adhesive joint test temperatures, the produced results underwent mathematical and statistical analysis.
To verify that significant differences were present between them, checks were done with Student’s t-tests, preceded by the Leven and Brown–Forsythe tests of the equality of variances and a normality test. A graphical comparison from which the comparisons were removed for the series that had no statistically significant difference demonstrated is shown in Figure 13.
Figure 13.
Statistically significant change in the ratio of the average strength between the heat-cured and the ambient temperature-cured adhesive joints.
In the constant cure cycle for all tests, the rate of polymerisation or cure is dependent on the stoichiometric ratio, r, between the two reacting co-monomers. For adhesives based on diglycidyl ether of bisphenol A (DGEBA) resins cured with 4,4′-diaminodiphenyl sulfone (DDS) hardener, the epoxy-rich ratio resulted in the lowest glass transition temperature (Tg). On the other end, the excess of amine hardener led to lower Tg due to the formation of rings consisting of partially reacted diamine molecules and epoxy chains which increase the free volume of the system [62,63]. Other research [64] attributed the differences in Tg with stoichiometry to be as a direct result of differences in molecular weight between crosslinks, whereby higher Tg resins have a smaller distance between crosslinks. For higher-functionality epoxy resins (tetraglycidyl-4,4’-diaminodiphenylmethane—TGDDM and an anhydride curing agent), the distance between crosslinks was measured and it was lower for resins cured within this stoichiometric range. Additionally, better mechanical properties were obtained for mixtures slightly in excess of epoxy, assuming the improvements were due to an increase in etherification reactions between epoxy groups and hydroxyls, which resulted in an increase in crosslink density [65].
3.2. LSTM Forecast Adhesive Joint Strength Values at Elevated Temperature
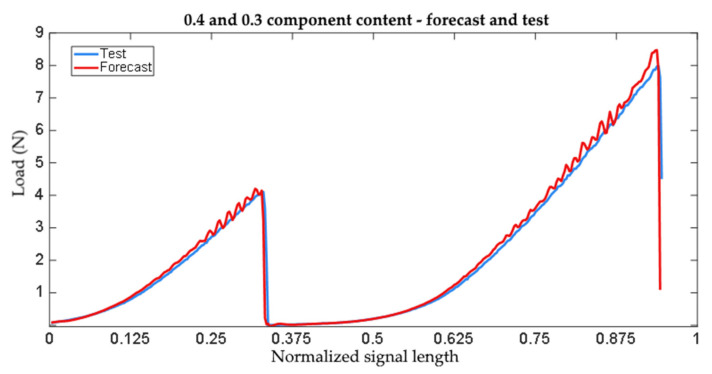
The analyses produced forecasts of the full-strength characteristics of the adhesive joints within the limits of the tested mix ratios. An example summary of the tested and forecast trends is shown in Figure 14.
Figure 14.
Comparison of the forecast quality to the experimental test values.
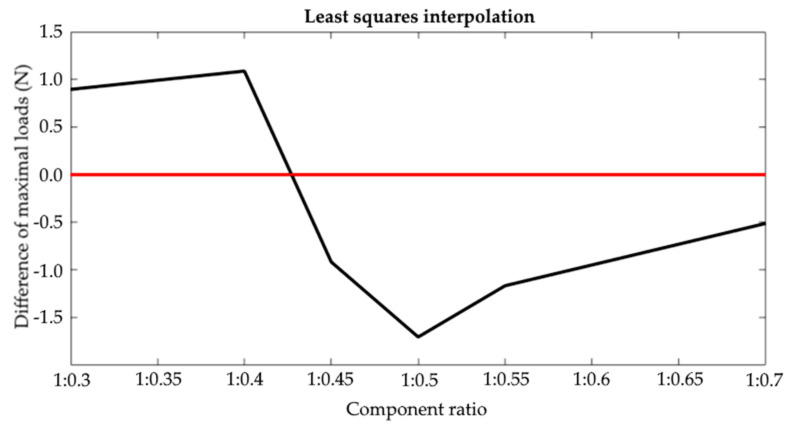
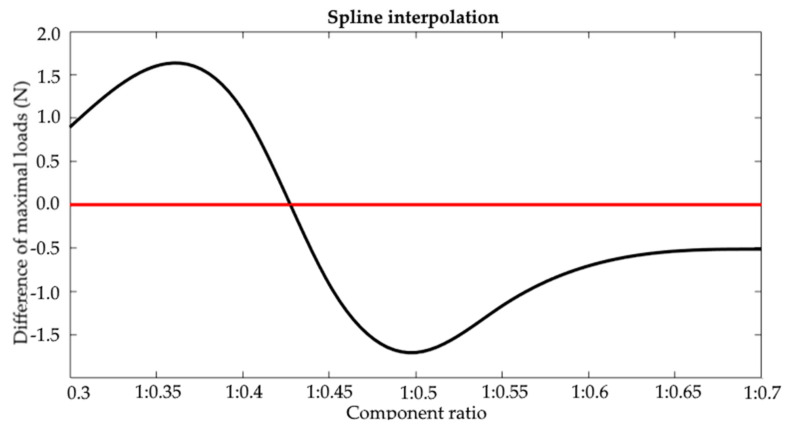
Based on the characteristics produced, differences in the maximum breaking forces were determined between the heat-held cured joints and the ambient temperature-cured joints. The result was the node points with the coordinates which denoted the values of the differences between the maximum breaking forces. The zero crossings were determined by interpolation. This process was applied separately for the values from the experimental tests and the forecasts. Examples of the interpolation results are shown in Figure 15 (least-squares method) and Figure 16 (cubic spline). The full summary of the produced values is shown in Table 5.
Figure 15.
Least-squares interpolation.
Figure 16.
Cubic spline interpolation.
Table 5.
Independent test and forecast results.
| # | Test | Cubic Spline Forecast | Error (%) | Least-Squares Forecast |
Error (%) |
|---|---|---|---|---|---|
| 1 | 0.424 | 0.352 | 16.98 | 0.353 | 16.75 |
| 2 | 0.392 | 0.400 | 2.04 | 0.398 | 1.53 |
| 3 | 0.465 | 0.465 | 0.00 | 0.465 | 0.00 |
| 4 | 0.438 | 0.437 | 0.23 | 0.437 | 0.23 |
| 5 | 0.431 | 0.432 | 0.23 | 0.432 | 0.23 |
| 6 | 0.417 | 0.416 | 0.23 | 0.417 | 0.00 |
| 7 | 0.475 | 0.476 | 0.23 | 0.476 | 0.23 |
| 8 | 0.418 | 0.417 | 0.23 | 0.418 | 0.00 |
The test results in the second analysis (comprising the averaging of all tests) provided a result consistent with the experimental test (0% error). The tests and simulations proved that 1:0.427 was the mix ratio at which heat curing becomes irrelevant to increasing the tensile strength of adhesive joints.
4. Conclusions
This paper demonstrates the feasibility of a numerical method for determining accurate adhesive component mix ratios above which heat holding to cure an adhesive joint will no longer be a significant and positive contributor to the strength of the adhesive joint tested at an elevated temperature. The applied numerical methods, i.e., the LSTM (long short-term memory) artificial recurrent neural network complemented the experimental test methods, allowing for the production of precise results from partial input data without any need for additional and detailed experimental testing. Otherwise, the tests would require more tensile loading of adhesive joint specimens up to their failure. The application of the presented LSTM RNN test methodology will lead to research which is less time and cost intensive.
On the basis of the conducted error analysis in the context of the averaged data and independent tests, and in the context of the minimum number of necessary experiments, it can be concluded that the application of the above method allows for reducing the samples subjected to testing. Taking into account the possibility of the future use of higher sampling rates of signals and thus obtaining longer waveforms (reduction of the amount of necessary learning data with minimal losses in the registration of dynamic link breakage), it is achievable to reduce the amount of input data to 50% of the conducted tests while maintaining the error level within 10%.
The fact that satisfactory analytical results were repeatedly produced leads to the conclusion that the forecasting capabilities are broad and can substitute for other tests which require a considerably higher expense of resources (time and money).
The use of additional methods of mathematical and statistical analysis of data obtained from experimental studies (Taguchi and Response Surface Method RSM) may provide additional information and is planned in further studies.
In the presented results, due to the assumed random nature of the component inaccuracies, it was not analysed whether the adhesive under conditions of inaccuracy of resin and hardener proportions achieves full crosslinking and no quantitative and qualitative relations between this parameter and the resulting strength of the bond were considered. Therefore, as an extension study, differential thermal analysis (DTA), i.e., DSC analysis (differential scanning calorimetry; based on ISO 11357 [66,67]) is planned to determine the level of cure achieved and the time needed to achieve both full cure and thermal parameters, such as the glass transition temperature. The results will allow for extending the knowledge on the thermal processes occurring during the curing process, such as making recommendations on the optimum curing conditions for a joint with an inaccurate (known) resin/hardener component ratio.
Author Contributions
Conceptualisation, J.S. and R.K.; methodology, J.S. and R.K.; software, A.M.; validation, J.S. and R.K.; formal analysis, J.S. and R.K.; investigation, J.S. and A.M.; resources, J.S. and R.K.; data curation, A.M.; writing—original draft preparation, J.S., R.K. and A.M.; writing—review and editing, J.S. and R.K.; visualisation, J.S.; supervision, J.S. and R.K.; project administration, J.S. and R.K.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
The research study was financed in the framework of the project Lublin University of Technology-Regional Excellence Initiative, funded by the Polish Ministry of Science and Higher Education (contract no. 030/RID/2018/19).
Data Availability Statement
Data presented in this study is available from corresponding authors upon request.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Doluk E., Rudawska A., Stančeková D., Mrázik J. Influence of surface treatment on the strength of adhesive joints. Manuf. Technol. 2021;21:585–591. doi: 10.21062/mft.2021.068. [DOI] [Google Scholar]
- 2.Rudawska A., Miturska-Barańska I., Doluk E. Influence of Surface Treatment on Steel Adhesive Joints Strength—Varnish Coats. Materials. 2021;14:6938. doi: 10.3390/ma14226938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Miturska I., Rudawska A., Niedziałkowski P., Szabelski J., Grzesiczak D. Selected Strength Aspects of Adhesive Lap Joints and Butt Welded Joints of Various Structural Materials. Adv. Sci. Technol. Res. J. 2018;12:135–141. doi: 10.12913/22998624/86258. [DOI] [Google Scholar]
- 4.Szabelski J. Effect of incorrect mix ratio on strength of two component adhesive Butt-Joints tested at elevated temperature. MATEC Web Conf. 2018;244:01019. doi: 10.1051/matecconf/201824401019. [DOI] [Google Scholar]
- 5.Rudawska A., editor. Adhesives and Adhesive Joints in Industry Applications. IntechOpen; London, UK: 2019. [Google Scholar]
- 6.Da Silva L.F.M., Adams R.D., Sato C., Dilger K., editors. Industrial Applications of Adhesives: 1st International Conference on Industrial Applications of Adhesives. Springer; Singapore: 2021. Lecture Notes in Mechanical Engineering. [Google Scholar]
- 7.Petrie E.M. Handbook of Adhesives and Sealants. 3rd ed. McGraw-Hill; New York, NY, USA: 2021. [Google Scholar]
- 8.Rudawska A., Sikora J., Müller M., Valášek P. The effect of environmental ageing at lower and sub-zero temperatures on the adhesive joint strength. Int. J. Adhes. Adhes. 2020;97:102487. doi: 10.1016/j.ijadhadh.2019.102487. [DOI] [Google Scholar]
- 9.Müller M., Valášek P. Influence of Environment Temperature on Strength of Quick-Setting Adhesives Based on Cyanoacrylates. Adv. Mater. Res. 2014;1030-1032:272–275. doi: 10.4028/www.scientific.net/AMR.1030-1032.272. [DOI] [Google Scholar]
- 10.Özer H., editor. Applied Adhesive Bonding in Science and Technology. InTech; Rijeka, Croatia: 2018. [Google Scholar]
- 11.Pizzi A., Mittal K.L. Handbook of Adhesive Technology. CRC Press; Boca Raton, FL, USA: 2020. [Google Scholar]
- 12.Kuczmaszewski J. Fundamentals of Metal-Metal Adhesive Joint Design. Polish Academy of Sciences; Lublin, Poland: 2006. [Google Scholar]
- 13.Shields J. Adhesives Handbook. Elsevier; Amsterdam, The Netherlands: 2013. [Google Scholar]
- 14.Minty R.F., Yang L., Thomason J. The influence of hardener-to-epoxy ratio on the interfacial strength in glass fibre reinforced epoxy composites. Compos. Part A Appl. Sci. Manuf. 2018;112:64–70. doi: 10.1016/j.compositesa.2018.05.033. [DOI] [Google Scholar]
- 15.Rudawska A. Mechanical Properties of Epoxy Compounds Based on Bisphenol a Aged in Aqueous Environments. Polymers. 2021;13:952. doi: 10.3390/polym13060952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rudawska A., Frigione M. Cold-Cured Bisphenolic Epoxy Adhesive Filled with Low Amounts of CaCO3: Effect of the Filler on the Durability to Aqueous Environments. Materials. 2021;14:1324. doi: 10.3390/ma14061324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Packham D.E., editor. Handbook of Adhesion. 2nd ed. John Wiley; Hoboken, NJ, USA: 2005. [Google Scholar]
- 18.Rudawska A., Czarnota M. Selected aspects of epoxy adhesive compositions curing process. J. Adhes. Sci. Technol. 2013;27:1933–1950. doi: 10.1080/01694243.2013.766558. [DOI] [Google Scholar]
- 19.Doyle G., Pethrick R.A. Environmental effects on the ageing of epoxy adhesive joints. Int. J. Adhes. Adhes. 2009;29:77–90. doi: 10.1016/j.ijadhadh.2008.02.001. [DOI] [Google Scholar]
- 20.Shin P.-S., Wang Z.-J., Kwon D.-J., Choi J.-Y., Sung I., Jin D.-S., Kang S.-W., Kim J.-C., DeVries K.L., Park J.-M. Optimum mixing ratio of epoxy for glass fiber reinforced composites with high thermal stability. Compos. Part B Eng. 2015;79:132–137. doi: 10.1016/j.compositesb.2015.04.032. [DOI] [Google Scholar]
- 21.Loctite Research, Development & Engineering, Technical Data Sheet: EA 9492 (Hysol) 2007. [(accessed on 17 November 2021)]. Available online: https://docs.rs-online.com/0399/0900766b812689d9.pdf.
- 22.3M Scotch-WeldTM Epoxy Adhesive 2216 B/A Technical Data 2018. [(accessed on 17 November 2021)]. Available online: https://multimedia.3m.com/mws/media/153955O/3mtm-scotch-weldtm-epoxy-adhesive-2216-b-a.pdf.
- 23.Huntsman Araldite® 420 A/B Structural Adhesives Data Sheet 2012. [(accessed on 17 November 2021)]. Available online: https://samaro.fr/pdf/FT/Araldite_FT_420_AB_EN.pdf.
- 24.Tsai H.-Y., Nakamura Y., Fujita T., Naito M. Strengthening epoxy adhesives at elevated temperatures based on dynamic disulfide bonds. Mater. Adv. 2020;1:3182–3188. doi: 10.1039/D0MA00714E. [DOI] [Google Scholar]
- 25.Rozylo P. Failure analysis of thin-walled composite structures using independent advanced damage models. Compos. Struct. 2021;262:113598. doi: 10.1016/j.compstruct.2021.113598. [DOI] [Google Scholar]
- 26.Jonak J., Karpiński R., Wójcik A. Influence of the Undercut Anchor Head Angle on the Propagation of the Failure Zone of the Rock Medium. Materials. 2021;14:2371. doi: 10.3390/ma14092371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jonak J., Karpiński R., Wójcik A. Influence of the Undercut Anchor Head Angle on the Propagation of the Failure Zone of the Rock Medium—Part II. Materials. 2021;14:3880. doi: 10.3390/ma14143880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rozylo P. Stability and failure of compressed thin-walled composite columns using experimental tests and advanced numerical damage models. Int. J. Numer. Methods Eng. 2021;122:5076–5099. doi: 10.1002/nme.6757. [DOI] [Google Scholar]
- 29.Falkowicz K., Debski H. The post-critical behaviour of compressed plate with non-standard play orientation. Compos. Struct. 2020;252:112701. doi: 10.1016/j.compstruct.2020.112701. [DOI] [Google Scholar]
- 30.Falkowicz K., Debski H., Wysmulski P. Effect of extension-twisting and extension-bending coupling on a compressed plate with a cut-out. Compos. Struct. 2020;238:111941. doi: 10.1016/j.compstruct.2020.111941. [DOI] [Google Scholar]
- 31.Cheng A.H.-D., Cheng D.T. Heritage and early history of the boundary element method. Eng. Anal. Bound. Elements. 2005;29:268–302. doi: 10.1016/j.enganabound.2004.12.001. [DOI] [Google Scholar]
- 32.Aliabadi M.H. The Boundary Element Method, Volume 2: Applications in Solids and Structures. Volume 2. John Wiley & Sons; Hoboken, NJ, USA: 2002. [Google Scholar]
- 33.Liu Y.J., Mukherjee S., Nishimura N., Schanz M., Ye W., Sutradhar A., Pan E., Dumont N.A., Frangi A., Saez A. Recent Advances and Emerging Applications of the Boundary Element Method. Appl. Mech. Rev. 2011;64:030802. doi: 10.1115/1.4005491. [DOI] [Google Scholar]
- 34.Liu Y. Fast Multipole Boundary Element Method: Theory and Applications in Engineering. Cambridge University Press; Cambridge, UK: 2009. [Google Scholar]
- 35.Machrowska A., Karpiński R., Jonak J., Szabelski J., Krakowski p. Numerical prediction of the component-ratio-dependent compressive strength of bone cement. Appl. Comput. Science. 2020;16:88–101. [Google Scholar]
- 36.Machrowska A., Szabelski J., Karpiński R., Krakowski P., Jonak J., Jonak K. Use of Deep Learning Networks and Statistical Modeling to Predict Changes in Mechanical Parameters of Contaminated Bone Cements. Materials. 2020;13:5419. doi: 10.3390/ma13235419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rogala M.K. Neural Networks in Crashworthiness Analysis of Thin-Walled Profile with Foam Filling. Adv. Sci. Technol. Res. J. 2020;14:93–99. doi: 10.12913/22998624/120989. [DOI] [Google Scholar]
- 38.Rogala M., Gajewski J., Górecki M. Study on the Effect of Geometrical Parameters of a Hexagonal Trigger on Energy Absorber Performance Using ANN. Materials. 2021;14:5981. doi: 10.3390/ma14205981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rogala M., Gajewski J. Numerical analysis of porous materials subjected to oblique crushing force. J. Physics Conf. Ser. 2021;1736:012025. doi: 10.1088/1742-6596/1736/1/012025. [DOI] [Google Scholar]
- 40.Tucki K., Mruk R., Orynycz O., Botwińska K., Gola A., Bączyk A. Toxicity of Exhaust Fumes (CO, NOx) of the Compression-Ignition (Diesel) Engine with the Use of Simulation. Sustainability. 2019;11:2188. doi: 10.3390/su11082188. [DOI] [Google Scholar]
- 41.Świć A., Wołos D., Gola A., Kłosowski G. The Use of Neural Networks and Genetic Algorithms to Control Low Rigidity Shafts Machining. Sensors. 2020;20:4683. doi: 10.3390/s20174683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sobaszek Ł., Gola A., Kozłowski E. Prediction of variable technological operation times in production jobs scheduling. IFAC-PapersOnLine. 2019;52:1301–1306. doi: 10.1016/j.ifacol.2019.11.378. [DOI] [Google Scholar]
- 43.Ciesla B. Practical Application Of Fuzzy Logic In Production Control Systems Of Engineer To Order Smes. ACS. 2021;17:17–25. [Google Scholar]
- 44.Jonak J., Karpiński R., Siegmund M., Machrowska A., Prostański D. Experimental Verification of Standard Recommendations for Estimating the Load-Carrying Capacity of Undercut Anchors in Rock Material. Adv. Sci. Technol. Res. J. 2021;15:230–244. doi: 10.12913/22998624/132279. [DOI] [Google Scholar]
- 45.Świć A., Gola A., Sobaszek Ł., Orynycz O. Control of Machining of Axisymmetric Low-Rigidity Parts. Materials. 2020;13:5053. doi: 10.3390/ma13215053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Anggoro P., Purharyono Y., Anthony A.A., Tauviqirrahman M., Bayuseno A. Jamari Optimisation of cutting parameters of new material orthotic insole using a Taguchi and response surface methodology approach. Alex. Eng. J. 2021;61:3613–3632. doi: 10.1016/j.aej.2021.08.083. [DOI] [Google Scholar]
- 47.Babu K.A., Jeyapaul R. An Investigation into the Wear Behaviour of a Hybrid Metal Matrix Composite Under Dry Sliding Conditions Using Taguchi and ANOVA Methods. J. Bio-Tribo-Corros. 2021;8:1–12. doi: 10.1007/s40735-021-00608-2. [DOI] [Google Scholar]
- 48.Esmaeili J., Andalibi K., Gencel O. Mechanical characteristics of experimental multi-scale steel fiber reinforced polymer concrete and optimization by Taguchi methods. Constr. Build. Mater. 2021;313:125500. doi: 10.1016/j.conbuildmat.2021.125500. [DOI] [Google Scholar]
- 49.Aydar A.Y. Statistical Approaches With Emphasis on Design of Experiments Applied to Chemical Processes. IntechOpen; London, UK: 2018. Utilization of Response Surface Methodology in Optimization of Extraction of Plant Materials. [DOI] [Google Scholar]
- 50.Ashrafi M., Hamadanian M., Ghasemi A.R. Epoxy/Polyethylene Glycol/TiO2: Design, Fabrication and Investigation of Mechanical Properties, Thermal Cycling Fatigue and Antibacterial Activity. J. Polym. Environ. 2021;29:3867–3877. doi: 10.1007/s10924-021-02115-4. [DOI] [Google Scholar]
- 51.Dean A., Voss D., Draguljić D. Design and Analysis of Experiments. Springer International Publishing; New York, NY, USA, : Cham, Switzerland: 2017. Response Surface Methodology; pp. 565–614. Springer Texts in Statistics. [Google Scholar]
- 52.Alman D.H., Ningfang L. Overtraining in back-propagation neural networks: A CRT color calibration example. Color Res. Appl. 2002;27:122–125. doi: 10.1002/col.10027. [DOI] [Google Scholar]
- 53.Sjöberg J., Ljung L. Overtraining, regularization and searching for a minimum, with application to neural networks. Int. J. Control. 1995;62:1391–1407. doi: 10.1080/00207179508921605. [DOI] [Google Scholar]
- 54.DiPietro R., Hager G.D. Handbook of Medical Image Computing and Computer Assisted Intervention. Elsevier BV; Amsterdam, The Netherlands: 2020. Deep learning: RNNs and LSTM; pp. 503–519. [Google Scholar]
- 55.Hochreiter S., Schmidhuber J. LSTM Can Solve Hard Long Time Lag Problems. Adv. Neural Inf. Process. Syst. 1997:473–479. [Google Scholar]
- 56.Goodfellow I., Bengio Y., Courville A. Deep Learning. MIT Press; Cambridge, MA, USA: 2016. [Google Scholar]
- 57.Loctite Research, Development & Engineering, Technical Data Sheet: LOCTITE® SF 7063TM. 2013. [(accessed on 17 November 2021)]. Available online: https://www.techsil.co.uk/media/pdf/TDS/HECL50002-tds.pdf.
- 58.Adhesives. Determination of Tensile Strength of Butt Joints. Polish Committee for Standardization; Warszawa, Poland: 2009. [Google Scholar]
- 59.Adhesives—Designation of Main Failure Patterns. Polish Committee for Standardization; Warszawa, Poland: 1998. [Google Scholar]
- 60.Karpiński R., Szabelski J., Maksymiuk J. Seasoning Polymethyl Methacrylate (PMMA) Bone Cements with Incorrect Mix Ratio. Materials. 2019;12:3073. doi: 10.3390/ma12193073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Szabelski J.F., Domińczuk J., Kuczmaszewski J., Lubelska P. Ciepla Na Właściwości Połączeń Klejowych Wpływ, Wydawnictwo. Wydawnictwo Politechniki Lubelskiej; Lublin, Poland: 2019. [Google Scholar]
- 62.Meyer F., Sanz G., Eceiza A., Mondragon I., Mijović J. The effect of stoichiometry and thermal history during cure on structure and properties of epoxy networks. Polymer. 1995;36:1407–1414. doi: 10.1016/0032-3861(95)95918-Q. [DOI] [Google Scholar]
- 63.Poynton G. Multi-Component Epoxy Resin Formulation for High Temperature Applications. The University of Manchester; Manchester, UK: 2014. [Google Scholar]
- 64.Boye J., Martinez J., Demont P., Lacabanne C. Molecular mobility associated with the Tg in DGEBAn-DDM networks. Thermochim. Acta. 1991;192:147–154. doi: 10.1016/0040-6031(91)87156-Q. [DOI] [Google Scholar]
- 65.Guerrero P., De la Caba K., Valea A., Corcuera M., Mondragon I. Influence of cure schedule and stoichiometry on the dynamic mechanical behaviour of tetrafunctional epoxy resins cured with anhydrides. Polymer. 1996;37:2195–2200. doi: 10.1016/0032-3861(96)85865-4. [DOI] [Google Scholar]
- 66.Plastics—Differential Scanning Calorimetry (DSC)—Part 1: General Principles. Beuth Verlag; Berlin,Germany: 2016. [Google Scholar]
- 67.Plastics—Differential Scanning Calorimetry (DSC)—Part 2: Determination of Glass Transition Temperature and Step Height. ISO Copyright Office; Geneva, Switzerland: 2020. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data presented in this study is available from corresponding authors upon request.