Relative precision of top-down attentional modulations is lower in early visual cortex compared to mid- and high-level visual areas

Abstract

Top-down spatial attention enhances cortical representations of behaviorally relevant visual information and increases the precision of perceptual reports. However, little is known about the relative precision of top-down attentional modulations in different visual areas, especially compared with the highly precise stimulus-driven responses that are observed in early visual cortex. For example, the precision of attentional modulations in early visual areas may be limited by the relatively coarse spatial selectivity and the anatomical connectivity of the areas in prefrontal cortex that generate and relay the top-down signals. Here, we used functional MRI (fMRI) and human participants to assess the precision of bottom-up spatial representations evoked by high-contrast stimuli across the visual hierarchy. Then, we examined the relative precision of top-down attentional modulations in the absence of spatially specific bottom-up drive. Whereas V1 showed the largest relative difference between the precision of top-down attentional modulations and the precision of bottom-up modulations, midlevel areas such as V4 showed relatively smaller differences between the precision of top-down and bottom-up modulations. Overall, this interaction between visual areas (e.g., V1 vs. V4) and the relative precision of top-down and bottom-up modulations suggests that the precision of top-down attentional modulations is limited by the representational fidelity of areas that generate and relay top-down feedback signals.

NEW & NOTEWORTHY When the relative precision of purely top-down and bottom-up signals were compared across visual areas, early visual areas like V1 showed higher bottom-up precision compared with top-down precision. In contrast, midlevel areas showed similar levels of top-down and bottom-up precision. This result suggests that the precision of top-down attentional modulations may be limited by the relatively coarse spatial selectivity and the anatomical connectivity of the areas generating and relaying the signals.

INTRODUCTION

The ability to voluntarily attend to a part of the visual field to process relevant sensory information is key to navigating visually cluttered environments. Attentional control signals are thought to originate in subregions of prefrontal cortex (PFC) and parietal cortex and target neurons in early visual cortex to improve information processing. However, relatively large receptive field (RF) sizes and the anatomical organization of feedback pathways in PFC may impose structural constraints on the precision of these top-down attentional modulations in earlier visual areas.

Previously, behavioral studies have shown that voluntary, or top-down, selective attention leads to spatially precise improvements in sensory processing (1–3). For example, the selective deployment of top-down attention to a relevant spatial position promotes more efficient perception in a variety of visual tasks (4, 5) by improving discriminability of basic visual features such as contrast (6, 7), spatial frequency (8), and textures (9). Moreover, top-down spatial attention can accelerate the speed of processing (2), enhance spatial resolution (10), and suppress nearby distractors (11, 12).

In addition to the changes in behavior, neurophysiological recording studies in monkeys and functional MRI (fMRI) studies in humans have found signal enhancement, noise reduction, and shifts in spatial tuning in visual areas when top-down attention is directed inside single-unit or population-level receptive fields (Refs. 13–22; reviewed in Refs. 23, 24). Indeed, top-down modulations in early and later visual areas have been reported even in the absence of any kind of external stimulation (25–34), and activation patterns in visual cortex can be used to decode attended spatial locations and nonspatial features (35–44). However, these studies primarily focused on establishing the presence of different kinds of attention effects, so little is known about the precision of top-down attentional modulations across different areas of the visual hierarchy.

The high precision of bottom-up sensory representations in early visual areas like V1 makes these areas potentially ideal targets for supporting equally precise top-down attentional modulations. For example, receptive fields of early visual area neurons are quite small (smaller than 1° at fovea and ∼1° at 10° periphery in V1; Ref. 45) and are highly tuned to specific features such as orientation, motion trajectory, spatial frequency, or color (46–48). Thus, neurons in early visual areas can precisely code low-level visual features compared with neurons in mid- and high-level visual areas that have larger and more complex receptive fields, such as V4 (49–55).

Contrarily, regions in parietal and frontal cortex that are thought to be sources of top-down attentional control signals, such as the lateral intraparietal area (LIP) or the frontal eye fields (FEFs), have much larger spatial receptive fields and thus relatively coarse codes for spatial position (e.g., receptive fields are ∼10–20° with a large variance at 10° periphery in FEF; Refs. 56–59). In addition, anatomical studies suggest that areas such as FEF primarily send feedback projections to midlevel visual areas such as V4, with only sparse connections to earlier areas such as V1 (60–63). Consistent with these anatomical observations, microstimulations to FEF neurons lead to a spatially selective increase in the firing rates in V4 neurons (64), and V4 shows larger and earlier attentional enhancements in firing rates compared with V1 and V2, suggesting that attentional feedback signals target midlevel visual areas first and then are backpropagated to earlier visual areas (65). Thus, the precision of top-down attention signals in early visual areas might be limited by the coarser selectivity of the higher-level “control” areas and the midlevel areas that appear to serve as the primary relay stations for top-down feedback to the highly selective neurons in early visual cortex.

In this study, we tested whether the precision of top-down attentional modulations was relatively coarser than bottom-up modulations in early visual areas compared with later visual areas. First, to measure the precision of bottom-up spatial representations in each visual area, participants were shown a series of small checkerboard stimuli at different locations in the visual field (termed the bottom-up spatial mapping task). Then, we used a separate task in which participants were cued to attend to a small or a large part of the visual field to measure the precision of top-down modulations in each visual area (termed the top-down spatial attention task). Note that, by necessity, the bottom-up mapping task and the top-down attention task are different (e.g., one has a small and highly salient peripheral stimulus, whereas the other requires covert attention to a cued location). However, despite using different paradigms, we can still compare the relative precision of both bottom-up and top-down modulations in early versus later areas (and, critically, the same tasks were used to assess the respective precision in all visual areas). As such, the key comparison in our analysis was evaluating the interaction between task type (bottom-up vs. top-down) and visual area, which indicates that there is a change in the relative precision of bottom-up and top-down modulations that cannot be explained by differences between the two tasks.

We applied multivariate pattern analysis (MVPA) to single-trial voxel activation patterns to generate several measures of the precision of spatial representations. Bottom-up representational precision was measured as decoding accuracy for a single stimulus location in the bottom-up mapping task. Top-down attentional precision was measured as decoding accuracy for attended locations in the attention task. In addition to the decoding accuracy, we also analyzed confusion matrices from the raw classifier outputs to provide a more nuanced assessment of the spatial precision in visual areas during each task. We found that earlier visual areas, such as V1, showed higher relative precision for bottom-up representations compared with top-down representations. However, midlevel and parietal areas such as V3, V4, and intraparietal sulcus (IPS) showed comparable bottom-up and top-down precision, leading to an interaction between region of interest (ROI) and the relative precision of different modulations. Overall, these findings are consistent with the hypothesis that the precision of top-down modulations in early visual cortex is limited by the precision of areas that generate and relay top-down feedback signals.

METHODS

Participants

Five participants (3 females), who had normal or corrected-to-normal vision and were right-handed, were recruited from the University of California, San Diego (UCSD) community (mean age 26.0 ± 2.7 yr). All participants performed a 1-h behavioral training session followed by two fMRI scan sessions of the two main experimental tasks, each session lasting 2 h. Participants were also scanned to obtain data for retinotopic mapping of occipital and parietal cortex in one or two separate fMRI sessions. In addition, extra runs of the bottom-up spatial mapping task were obtained for some participants who also participated in a separate study that used the same mapping task. Participants were compensated for their participation at a rate of $10/h for the behavioral training and $20/h for the scanning sessions. The local Institutional Review Board at UCSD approved the experiment, and all participants provided written informed consent.

Stimulus Generation and Presentation

All stimuli were projected on a 24 × 18-cm screen placed inside the bore of the scanner and viewed through a head coil-mounted mirror from 47 cm in a darkened room. Stimuli were generated and presented with MATLAB and the Psychophysics Toolbox (66, 67). The luminance output from the projector was linearized in the stimulus presentation software, and all stimuli were presented against a uniform gray background (286 cd/m²).

Bottom-Up Spatial Mapping Task

To estimate the precision of bottom-up spatial representations, we presented 1 of 24 wedge-shaped flickering checkerboards at full contrast on each trial (see Fig. 1B). The wedges tiled an imaginary donut-shaped annulus that was 5 degrees of visual angle from the inner to the outer edge and spanned 4.5–9.5 degrees of visual angle from the center fixation point. Thus, each wedge covered 15° of arc (360°/24). The annulus covered the target locations in the top-down attention task. The checkerboard stimulus on each trial was presented on a uniform gray background, and a 0.2° central fixation point was present throughout the task. Participants were instructed to indicate, using a button press with their right index finger, changes in the contrast of the fixation dot that occurred on 20 out of 96 (20.8%) trials in each run, evenly split between increment and decrement of the contrast.

Figure 1.

A: task procedure of top-down spatial attention task. Each trial started with a brief flicker of the white fixation dot at the center of the screen. After 300 ms, 1 of the 2 central cues indicating the quadrant (Diffuse) or the exact location (Focused) of the upcoming target was shown for 500 ms. The cues validly predicted the target location in all trials. A cue-to-target delay period followed, and the duration of the delay period varied between 2 and 8 s (2 s in catch trials and 6–8 s in noncatch trials; for details, see Top-Down Spatial Attention Task). A uniform flickering noise stimulus that was at the same contrast level as the target for the trial was present during the delay period. After the delay, the target grating was presented for 150 ms in 1 of the 12 possible locations, and the participants responded by button press whether the orientation of the target was closer to a horizontal or a vertical orientation. Placeholders (black circular lines) were present throughout the task, marking the possible target locations arranged on an imaginary circle. After the target offset, the subsequent trial started after an intertrial interval (ITI) of 5–7 s. Prescan training sessions used a slightly modified version of this task (see Prescan Training Session for details). B: task procedure for bottom-up spatial mapping task. In each of the 3-s trials, a wedge-shaped flickering checkerboard was presented in 1 of 24 locations, arranged on an imaginary circle. The 24 wedges altogether tiled the target location areas in the attention task, and in the decoding analyses data from adjacent wedges were combined to match the 12 target locations for the cross-generalization analysis (see Multivariate Pattern Decoding). In this task, participants responded by button press whenever the contrast of the fixation changed. C and D: behavioral performance for the top-down spatial attention task, data combined from the scanning sessions and an independent eye-tracking session (see Supplemental Methods). C: mean behavioral accuracy. Accuracy was higher in the diffuse compared with the focused condition by 2%. D: mean tilt offset. Tilt offsets were higher in the diffuse than in the focused condition. Colored dots represent data from individual participants. Error bars represent ±1 SE.

Each trial consisted of a 3-s stimulus presentation period without any intertrial intervals (ITIs). The location of the wedge was randomly selected on each trial with the constraint that wedges did not appear in the same quadrant consecutively. The contrast of the fixation dot changed at least 7 s after the previous change. To ensure that participants performed below ceiling, we manually adjusted the task difficulty after every run by changing the percent contrast change of the contrast increment/decrement of the fixation. Each run consisted of 96 trials, a 12.8-s blank period at the beginning of the run, and a 12-s blank period at the end of the run, adding up to 312.8 s. Participants completed a total of 9–15 runs of the spatial mapping task across two to four separate sessions.

Top-Down Spatial Attention Task

Throughout the top-down spatial attention task, a white central fixation dot (0.2° diameter) on a dark gray central dot (105 cd/m², 2° diameter) was used as a central fixation point. There were also placeholders for target locations present throughout the task, which consisted of 12 black circular lines equidistant from the center of the screen, marking the 12 possible target locations. The placeholders tiled a donut-shaped annulus with a thickness of 5° visual angle, spanning 4.5–9.5° from the center of the screen, with three placeholders positioned in each of the four quadrants. Placeholders were used to facilitate attentional selection of the cued location(s). Each trial started with the white fixation dot flickering to indicate the trial onset and 300 ms later, followed by a cue presented for 500 ms (see Fig. 1A). One of two attention cues was presented on the dark gray central dot. The cue was either a diffuse cue or a focused cue; the diffuse cue was a filled white arc covering a quadrant of the dark gray dot, indicating the quadrant that contained the upcoming target, and the focused cue was a 0.08°-thick white line extending from the center to the outer edge of the dark gray dot, indicating the exact target location out of the 12 possible locations. The cues always validly predicted the target location, and the participants were explicitly instructed to covertly attend to the cued location while maintaining fixation at the white fixation dot.

There was a delay period between the cue and the target, which, in 24 trials (noncatch) out of 27 trials in a single run, varied between 6 and 8 s in steps of 400 ms and, in the remaining 3 trials (catch), was fixed at 2 s. These different lengths of delay period were used to ensure that we had enough time points during the delay period to estimate neural response patterns before the onset of the target and at the same time to force participants to direct attention right after the presentation of the cue in anticipation of the rare 2-s delays. The 2-s delay catch trials were excluded from all analyses, behavioral or fMRI. During the delay period, a donut-shaped Fourier-filtered noise stimulus, which spanned 4.5–9.5° from the center of the screen, covering all possible target locations, counterphase flickered at 4 Hz. The noise stimulus consisted of white noise filtered to include only spatial frequencies between 1 and 4 c/°. During the first second of the delay period, the contrast of the noise ramped up linearly from 0% to the contrast of the target grating for that trial and continued flickering until target offset. The noise stimulus served as a dynamic continuous bottom-up input and also reduced transient signals caused by abrupt onset or offset of the target (68).

After the delay, one of the placeholders switched to the target grating for 150 ms. Participants were instructed to report whether the orientation of the target was closer to a vertical or a horizontal orientation, with a button press with their right index or middle finger, within 2 s after the target onset. The target stimulus was a circular sinusoidal grating (2.7° radius) with a smoothed edge (filtered through a 2.7° radius, 0.9° SD Gaussian kernel), presented at the eccentricity of 7° from the center fixation. The grating was presented in a phase that was chosen at random on each trial and at one of five possible contrast levels (0%, 5%, 10%, 20%, 50% Michelson contrast). The grating had a spatial frequency of 0.91 c/° and an orientation that was tilted clockwise or counterclockwise from 45° or 135° by variable offsets. The tilt offsets for each of the cue and the contrast conditions (10 conditions in total) started at the orientation threshold values measured from the prescan behavioral training session (see Prescan Training Session) and were adjusted manually by the experimenter between every run to match the cumulative accuracies across all conditions around 75%. For example, if the cumulative accuracy for a given condition (i.e., 5% contrast, focused cue condition) was lower than 75%, the tilt offset for that condition was adjusted to a higher value, making it easier to detect the tilted direction. The response mapping was counterbalanced between participants.

The ITI between the offset of the target and the onset of the next trial varied between 5 and 7 s in steps of 400 ms. Each run consisted of 27 trials and 12.8-s and 8-s blank periods at the beginning and the end of the run, respectively, adding up to 383.2 s. Two cue conditions (diffuse or focused), five levels of contrast, and 12 target locations were fully counterbalanced across five runs. The reference orientation (45° or 135°) and the direction of tilt from the reference (clockwise or counterclockwise) were balanced for each of the cue, contrast, and target location combinations across the total of 20 runs carried out across two separate sessions. Because of technical difficulties, for one of the participants, behavioral and fMRI data for the 20% contrast level in one session and behavioral responses for two runs were not collected.

Prescan Training Session

Before the scanning sessions, participants were trained on the top-down attention task in a separate prescanning session in the laboratory using the same task with the following exceptions. The cue-to-target delay period was shortened to 1 s, and there was no ITI between trials so that the next trial started as soon as the response for the current trial was made. Responses were made by pressing one of the two keys on a keyboard. The target grating was shown at lower contrast levels (2%, 3%, 5%), and tilt offsets were fixed at five levels (0°, 5°, 10°, 15°, 20°). There were 24 trials for each of the cue, contrast, and tilt offset combinations, and a total of 720 trials were split up into 12 blocks with short breaks in between.

Analysis of Behavioral Data

To assess the effect of the attention cue and the contrast of the target on behavior, we performed a two-way ANOVA on the behavioral accuracy and the tilt offset. Cue was considered as a categorical factor, and contrast was considered as a continuous factor. First, we tested the main effect of the two factors on accuracy. P values were computed using randomization testing to avoid assumptions that usually accompany parametric tests. Thus, to test the effect of cue, cue labels were shuffled across trials, restricted within each contrast level and participant, and then accuracy was averaged across trials to obtain the mean accuracy for each condition. Then, we performed the ANOVA on these data with the two factors, only testing for the main effects without the interaction term, to obtain the F value for the main effect of cue. This procedure was repeated 1,000 times, yielding a distribution of 1,000 F values under the null hypothesis that cue type did not affect the behavioral accuracy. A P value was obtained by taking the proportion of F values from this null distribution that exceeded the F value obtained by using the data with the unshuffled labels. The same procedure was repeated to test the main effect of contrast but shuffling the contrast labels instead of the cue labels.

Next, we tested the interaction effect between cue and contrast. We first performed an ANOVA on the accuracy data with only the main effects and obtained the residuals from this test. This was done to exclude the variance explained by the main effects. To test the interaction between cue and contrast, we shuffled the labels of the residual data, restricted within each participant. Then, we performed the two-way ANOVA on the residuals, testing for the two main effects and the two-way interaction effect, to obtain the F value for the interaction effect between cue and contrast. This procedure was repeated across 1,000 iterations, yielding a distribution of 1,000 F values, and a P value was obtained by taking the proportion of F values from this null distribution that exceeded the F value obtained using the data with unshuffled labels. The same series of the randomization tests was repeated on the tilt offset.

Localizer Task

To localize voxels that maximally respond to the target locations in the bottom-up spatial mapping task and the top-down attention task, we presented a flickering checkerboard stimulus at full contrast shaped as a circular annulus, spanning 4.5–9.5° radius from the center fixation point (corresponding to the spatial locations of the bottom-up mapping stimuli and the attention target stimuli). The flickering localizer stimulus was presented on a uniform gray background with the same background luminance as in the top-down attention task, and a 0.2° central fixation point was present throughout the task. Each trial consisted of a 13-s stimulus presentation followed by a 13-s blank ITI. The task for the participants was the same as the bottom-up mapping task in which participants reported occasional changes in the contrast of the fixation point. Each run consisted of 12 trials and a 12.8-s blank period at the beginning of the run, adding up to 324.8 s.

Magnetic Resonance Imaging

All MRI scanning was performed on a General Electric (GE) Discovery MR750 3.0 T research-dedicated scanner at the UC San Diego Keck Center for Functional Magnetic Resonance Imaging. Functional echo-planar imaging (EPI) data were acquired with a Nova Medical 32-channel head coil (NMSC075-32-3GE-MR750) and the Stanford Simultaneous Multi-Slice (SMS) EPI sequence (MUX EPI), with a multiband factor of 8 and 9 axial slices per band [72 total slices; voxel size = 2-mm³ isotropic; 0-mm gap; matrix = 104 × 104; field of view = 20.8 cm; repetition time (TR)/echo time (TE) = 800/35 ms; flip angle = 52°; in-plane acceleration = 1]. Image reconstruction procedures and unaliasing procedures were performed on local servers with reconstruction code from CNI (Center for Neural Imaging at Stanford). The initial 16 TRs collected at the onset of each run served as reference images required for the transformation from k-space to image space. Two short (17 s) “topup” data sets were collected during each session, using forward and reverse phase-encoding directions. These images were used to estimate susceptibility-induced off-resonance fields (69) and to correct signal distortion in EPI sequences using FSL (FMRIB Software Library; http://www.fmrib.ox.ac.uk/fsl) topup (70).

During each functional session, we also acquired an accelerated anatomical scan using parallel imaging (GE ASSET on a FSPGR T1-weighted sequence; 172 slices; 1 × 1 × 1-mm³ voxel size; TR = 8,136 ms; TE = 3,172 ms; flip angle = 8°; 1-mm slice gap; 256 × 192-cm matrix size) using the same 32-channel head coil. We also acquired one additional high-resolution anatomical scan (172 slices; 1 × 1 × 1-mm voxel size; TR = 8,136 ms; TE = 3,172 ms; flip angle = 8°; 1-mm slice gap; 256 × 192-cm matrix size) during a separate retinotopic mapping session using an Invivo eight-channel head coil. This scan produced higher-quality contrast between gray and white matter and was used for segmentation, flattening, and visualizing retinotopic mapping data.

Preprocessing

All imaging data were preprocessed with software tools developed and distributed by FreeSurfer (https://surfer.nmr.mgh.harvard.edu) and FSL. Cortical surface gray-white matter volumetric segmentation of the high-resolution anatomical image was performed with the “recon-all” utility in the FreeSurfer analysis suite (71). Segmented T1 data were used to define regions of interest (ROIs) for use in subsequent analyses. The first volume of every functional run was then coregistered to this common anatomical image. Transformation matrices were generated with FreeSurfer’s manual and boundary-based registration tools (72). These matrices were then used to transform each four-dimensional 4-D functional volume with FSL FLIRT (73, 74), such that all cross-session data from a single participant were in the same space. Next, motion correction was performed with the FSL tool MCFLIRT (73) without spatial smoothing, a final sinc interpolation stage, and 12 degrees of freedom. Slow drifts in the data were removed last, with a high-pass filter (1/40 Hz cutoff). No additional spatial smoothing was applied to the data apart from the smoothing inherent to resampling and motion correction. Signal amplitude time series were normalized via z-scoring on a voxel-by-voxel and run-by-run basis. z-Scored data were used for all further analyses unless otherwise mentioned. Because trial events were jittered with respect to TR onsets, they were rounded to the nearest TR. The analyses performed after preprocessing were all carried out in MATLAB 9.1 with custom in-house functions. All preprocessed fMRI and behavioral data, the experiment code used during data collection, and the analysis code used to generate the figures in the main manuscript and Supplemental Materials are available on the Open Science Framework (OSF) at https://osf.io/nbdj5.

Identifying Regions of Interest

To identify voxels that were visually responsive to the target locations, a general linear model (GLM) was performed on data from the localizer task with FSL FEAT (FMRI Expert Analysis Tool, version 6.00). Individual localizer runs were analyzed with BET brain extraction (75) and data prewhitening with FILM (76). Predicted blood oxygen level-dependent (BOLD) responses were generated for blocks of annulus stimulus by convolving the stimulus sequence with a canonical gamma hemodynamic response function (phase = 0 s, SD = 3 s, lag = 6 s). The temporal derivative was also included as an additional regressor to accommodate slight temporal shifts in the waveform to yield better model fits and to increase explained variance. Individual runs were combined using a standard weighted fixed-effects model, and spatial smoothing was applied [2-mm full-width half-maximum (FWHM)]. Voxels that were significantly activated by the localizer stimulus [P < 0.05; false discovery rate (FDR) corrected] were defined as visually responsive and used in all subsequent analyses (see Supplemental Table S2 for the number of selected voxels for each ROI; all Supplemental Materials are available at https://doi.org/10.17605/OSF.IO/NBDJ5). Note that the voxels in each ROI were identified on the basis of their responsiveness to bottom-up stimulus drive. However, this should not lead to the identification of voxels that are less sensitive to top-down modulations, given that top-down and bottom-up factors are known to target the same regions of retinotopically organized visual areas (29, 77–79). Supplementary control analyses were conducted by selecting voxels based on activations during the top-down attention task, and the results are shown in Supplemental Figs. S8 and S9.

Retinotopic Mapping Stimulus Protocol

Retinotopic mapping data were acquired during an independent scanning session, following previously published retinotopic mapping protocols to define the visual areas V1, V2, V3, V3AB, V4, IPS0, IPS1, IPS2, and IPS3 (80–85). The participants viewed a contrast-reversing checkerboard stimulus (4 Hz) configured as a rotating wedge (10 cycles, 36 s/cycle), an expanding ring (10 cycles, 36 s/cycle), or a bowtie (8 cycles, 40 s/cycle). To increase the quality of data from parietal regions, participants performed a covert attention task on the rotating wedge stimulus, which required them to detect contrast-dimming events that occurred occasionally (on average, 1 event occurred every 7.5 s) in a row of the checkerboard. This stimulus was limited to a 22° × 22° field of view.

Anatomical and functional retinotopy analyses were performed with a set of custom wrappers around existing FreeSurfer and FSL functionality. ROIs were combined across left and right hemispheres and across dorsal and ventral areas (for V2–V3) by concatenating voxels.

Only visually responsive voxels, selected with the localizer procedure described in Localizer Task, were included in each of the retinotopically defined ROIs. For MVPA, IPS0, IPS1, IPS2, and IPS3 were combined into a single “IPS” ROI for each participant, because some IPS ROIs of some participants did not have a high enough number of visually responsive voxels to train and test classifiers (<50 voxels).

Multivariate Pattern Decoding

The purpose of MVPA was to compare the precision of bottom-up stimulus-driven representations of spatial location and the precision of top-down attentional modulations based on the amount of information in voxel activation patterns in each ROI.

Before performing MVPA, we first shifted all time points by 4 s to account for the hemodynamic lag. Then, we averaged voxel activation patterns for each trial across the time points of the whole trial from the bottom-up mapping task (3-s duration) and the cue-to-target delay period from the attention task (6- to 8-s duration). To make sure that we were measuring information related to the relative pattern of activation across voxels in each ROI rather than information solely related to mean signal changes across conditions, we mean-centered each single-trial voxel activation pattern: For each trial and within each ROI, we calculated the mean amplitude across voxels and subtracted that value from the amplitude of each voxel, which resulted in trial-wise voxel activation patterns that have the across-voxel mean value at 0.

We performed all decoding analyses with a linear support-vector machine (SVM). First, to measure the precision of bottom-up representations, the classifier was trained and tested on the bottom-up spatial mapping task data in a leave-one-run-out manner. Critically, data points for two adjacent wedges were grouped together under the same location label to match the 12 target locations in the attention task. Decoding accuracy was calculated as the proportion of trials where the location predicted by the classifier matched the location where the wedges were presented. Next, to measure the precision of top-down attentional modulations, we used cross-generalization in which the classifier was trained using all data from the bottom-up mapping task and then tested on the top-down attention task data. Decoding accuracy was calculated as the proportion of trials where the location predicted by the classifier matched the location where the target was presented, separately for cue conditions. Finally, as a control analysis, the classifier was trained and tested on the top-down attention task data in four folds, as task conditions were counterbalanced across five runs. That is, the first 15 of 20 runs were used to train the classifier, using the target location as the labels, and then the classifier predicted the target location for each trial in the 5 runs that were left out. This procedure was repeated four times, leaving out a different fold (5 counterbalanced runs) each time. Decoding accuracy was calculated as the proportion of trials where the location predicted by the classifier matched the location where the target was presented, separately for cue conditions. As it was not the focus of the present study, contrast levels in the top-down attention task were not considered as a factor, and data were collapsed across contrast levels (see Supplemental Figs. S3 and S4 for analysis results with contrast as an additional factor; also see Supplemental Fig. S2 for univariate BOLD response changes across contrast).

Assessing Spatial Precision of Top-Down and Bottom-Up Representations with Decoding Errors

To make further inferences on the qualitative aspects of the spatial representation based on the decoding errors in the above analyses, we acquired classifier predictions in each trial for each ROI, sorted them by the stimulated (in the bottom-up mapping task) or the cued (in the top-down attention task) locations, and organized the output into 12 × 12 matrices (see Fig. 4). For analysis and visualization purposes, we labeled spatial positions arbitrarily from 1 to 12, 1 being the leftmost position in the first quadrant and the number increasing in clockwise direction. To make quantitative comparisons between these confusion matrices, we performed a linear regression on each matrix with a diagonal and an off-diagonal regressor (see Fig. 5A). Both regressors were 12 × 12 matrices, and the diagonal regressor was created by assigning 1’s in the cells on the diagonal and 0’s in the rest. The off-diagonal regressor was created by first assigning 1’s in the 3 × 3 groups of cells reflecting the quadrants of the spatial locations and 0’s in the rest and then subtracting the diagonal regressor from it so that there was no overlap between the two regressors. These regressors and a constant term were used as predictors in the linear regression model, which was fit to individual confusion matrices to obtain beta weights for each participant and regressor. Then, to compare these beta weights across ROIs and tasks/conditions, we computed ratios by dividing the diagonal beta weight by the off-diagonal beta weight and then log transforming the result (see Fig. 5B).

Figure 4.

Confusion matrices of classifier predictions for the presented stimulus location in the bottom-up mapping task and the cued location in the top-down attention task. For analysis and visualization purposes, spatial locations were arbitrarily labeled from 1 to 12, 1 being the leftmost position in the first quadrant with numbers increasing in the clockwise direction. Each cell within the matrices was colored based on values within the range of 0–80% for the bottom-up mapping task and 0–50% for the top-down attention task conditions, as indicated in the color bars on right (this was done to make patterns easier to discern). The vertical dashed white lines in the diffuse condition matrices (middle) divide the 12 spatial locations into the 4 cued quadrants. In the bottom-up mapping task (top), classifier predictions were clustered on the diagonal, where the predicted location closely tracked the actual stimulus location. In the focused condition of the top-down attention task (bottom), the diagonal pattern was visible but to a lesser degree than that in the bottom-up mapping task. In the diffuse condition of the top-down attention task (middle), classifier predictions were clustered within the cued quadrant, indicating that the attentional modulation was spread across the whole quadrant, consistent with subjects using the diffuse cue as intended.

Figure 5.

A: diagonal and off-diagonal regressors used to fit the confusion matrices shown in Fig. 4. Cells colored black were assigned 1’s, and cells colored white were assigned 0’s. B: ratio of beta weights in the bottom-up mapping task and the diffuse and focused conditions from the top-down attention task. The beta weights for the diagonal regressor were divided by the beta weights for the off-diagonal regressor and then plotted on a logarithmic scale. Beta ratios above 0 indicate that the diagonal beta weight was larger than the off-diagonal beta weight, and beta ratios below 0 indicate that the off-diagonal beta weight was larger than the diagonal beta weight. Beta weight ratios in the bottom-up mapping task were all above 0, with the highest value in V1 and gradually decreasing in later areas. Beta weight ratios in the diffuse condition from the top-down attention task were close to 0 across all regions of interest (ROIs). Beta weight ratios in the focused condition from the attention task were above 0 for all ROIs, but compared with the ratios from the bottom-up task the ratios for earlier areas were much smaller whereas ratios for later areas were at a similar level. Colored dots represent data from individual participants. Error bars are ±1 SE. IPS, intraparietal sulcus.

Statistical Procedures for MVPA

To be conservative, all statistics reported regarding the MVPA results were based on nonparametric randomization tests over 1,000 iterations (note that all results reported as significant are also significant by standard parametric approaches). To assess the significance of decoding accuracy in the bottom-up mapping task (see Fig. 2A), within each iteration of the leave-one-run-out procedure, the location labels for the test data were shuffled when computing the decoding accuracy for each ROI. Then, average decoding accuracy for each ROI was obtained by taking the mean across all runs. We repeated this procedure 1,000 times to compute a distribution of decoding accuracies for each participant and each ROI under the null hypothesis that the location of the stimulus had no impact on voxel activation patterns. To assess the significance of decoding accuracy at the group level, we then performed t tests between the shuffled decoding accuracies across all participants and chance accuracy (1/12) to obtain a single distribution of 1,000 t values. We obtained P values for each ROI by calculating the proportion of iterations on which the shuffled t values exceeded the real t value that was obtained with the unshuffled data. To assess whether decoding accuracies were significantly different across ROIs, we shuffled the ROI labels within each participant and performed one-way repeated-measures ANOVA on the decoding accuracies with ROI as a factor to obtain 1,000 F values under the null hypothesis that ROI had no impact on decoding performance. The P value was calculated as the proportion of shuffled F values that exceeded the real F value.

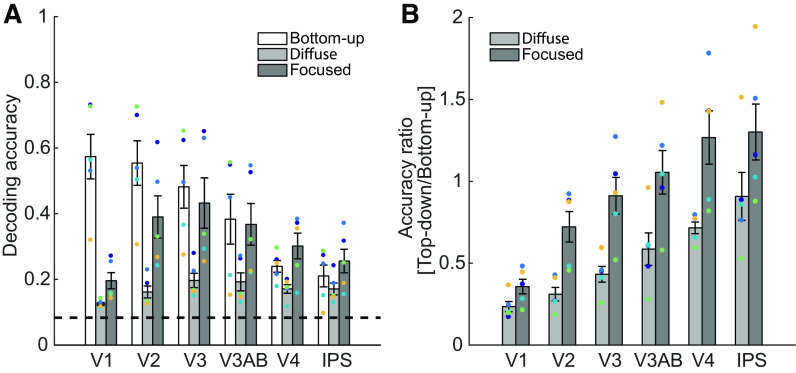
Figure 2.

A: decoding accuracy based on functional MRI (fMRI) activation patterns in the bottom-up spatial mapping task (white bars) and the top-down spatial attention task (Diffuse and Focused conditions, light and dark gray bars, respectively). In the bottom-up mapping task, decoding accuracy was highest in V1 and decreased in later visual areas. In the top-down attention task, decoding accuracy was generally higher in the focused than in the diffuse condition. Whereas top-down decoding accuracy was much lower than bottom-up decoding accuracy in V1, accuracy in the bottom-up mapping task and the focused condition was comparable in later areas [e.g., V3AB, V4, intraparietal sulcus (IPS)], leading to an interaction between task type (bottom-up vs. top-down) and visual areas. Filled colored dots represent data from individual participants, and error bars represent ±1 SE. The dashed line indicates chance performance (1/12 or ∼0.083). B: to better visualize the interaction between task type and visual areas, we computed the ratio between bottom-up and top-down decoding accuracies for each region of interest (ROI). To obtain this ratio, the top-down decoding accuracy was divided by the bottom-up decoding accuracy within each ROI, separately for the diffuse and focused conditions. A low ratio score indicates that an ROI had higher decoding accuracy in the bottom-up mapping task, consistent with higher precision of bottom-up representations. A high ratio score indicates that an ROI had higher decoding accuracy in the top-down task, consistent with higher precision of top-down representations. Although V1 showed higher bottom-up precision, later areas showed comparable levels of bottom-up and top-down precision. Colored dots represent data from individual participants. Error bars are ±1 SE.

To assess the precision of top-down modulations in the attention task (see Fig. 2A), we first assessed the significance of classifier decoding performance in each ROI by collapsing data across cue conditions and comparing it to chance (1/12). We performed a randomization test by shuffling the location labels in the test (attention task) data 1,000 times, and then we computed paired t tests on the decoding accuracy against chance. The P value for each ROI was obtained by computing the proportion of shuffled t values that exceed the real t value.

To evaluate the impact of the attention cue on the top-down precision, we performed a randomization test for two-way ANOVA on the decoding accuracy with cue and ROI as factors. First, we tested the main effect of the two factors. To test the effect of cue type, cue labels were shuffled across trials, restricted within each ROI and participant, and then the classifier correctness for each trial was averaged to obtain decoding accuracy for each condition. Then, we performed an ANOVA on this data, only testing for the two main effects without the interaction terms, to obtain the F value for the main effect of cue. This procedure was repeated across 1,000 iterations, which yields a distribution of 1,000 F values under the null hypothesis that cue conditions did not affect the decoding accuracy. A P value was obtained by taking the proportion of F values from this null distribution that exceeded the F value obtained using the data with unshuffled labels. The same procedure was repeated to test the main effects of ROI.

Next, we tested the interaction effects between the two factors. We first performed an ANOVA on the decoding accuracy with only the main effects and obtained the residuals. This was done to exclude the variance explained by the main effects. To test the interaction between cue type and ROI, we shuffled the labels of the residual data, restricted within each participant. Then, we performed an ANOVA on the residuals, testing for the two main effects and the interaction effect, to obtain the F value for the interaction effect between cue type and ROI. This procedure was repeated 1,000 times, yielding a distribution of 1,000 F values, and a P value was obtained by taking the proportion of F values from this null distribution that exceeded the F value obtained using the data with unshuffled labels.

To further examine the significant interaction effects between cue type and ROI from the above analysis, we tested the effect of cue type within each ROI. We first shuffled the cue labels across trials within each ROI and participant and averaged classifier accuracy across trials to obtain decoding accuracy for each cue condition. Next, we performed a paired t test between the decoding accuracies from each cue condition to obtain the t value for each ROI. This procedure was repeated across 1,000 iterations, yielding a distribution of 1,000 t values for each ROI, under the null hypothesis that cue conditions did not affect decoding accuracy. Then, a P value for each ROI was calculated by taking the proportion of iterations where shuffled t values exceed the real t value, the proportion of iterations where the real t value exceeded the shuffled t values, and then taking the minimum value and multiplying it by 2 for a two-tailed test.

To compare the difference between the precision of bottom-up and top-down modulations across ROIs (Fig. 2B), we divided the decoding accuracy for each cue condition in the top-down attention task by the decoding accuracy in the bottom-up spatial mapping task, for each ROI. To assess the effect of cue and ROI on these ratio scores, we performed a randomization test using a two-way ANOVA on the ratio scores with cue type and ROI as factors. First, we tested the main effect of the two factors on the ratio score. To test the effect of cue type, cue labels were shuffled across trials in the attention task data, restricted within each participant and ROI, and then the accuracy on each trial was averaged to obtain average accuracy for each condition. Then, decoding accuracies for each condition in the top-down attention task were divided by the decoding accuracy from the bottom-up mapping task. We performed the two-way ANOVA on this ratio score, only testing for the main effects of cue and ROI, to obtain the F value for the main effect of cue. This procedure was repeated 1,000 times, yielding a distribution of 1,000 F values under the null hypothesis that cue conditions did not affect the ratio scores. A P value was obtained by taking the proportion of F values from this null distribution that exceeded the F value obtained using the data with unshuffled labels. The same procedure was repeated to test the main effect of ROI, in which ROI labels for each trial were shuffled within each cue condition and participant instead of cue labels. Next, we tested the interaction effect between cue and ROI. We first performed a two-way ANOVA on the ratio scores with only the main effects and obtained the residuals. This was done to exclude the variance explained by the main effects. To test the interaction between cue and ROI, we shuffled the labels of the residual data, restricted within each participant. Then, we performed the two-way ANOVA on the residuals, testing for the two main effects and the two-way interaction effect, to obtain the F value for the interaction effect between cue type and ROI. This procedure was repeated 1,000 times, yielding a distribution of 1,000 F values, and a P value was obtained by taking the proportion of F values from this null distribution that exceeded the F value obtained using the data with unshuffled labels.

To assess the significance of difference between task conditions and ROIs on the beta weight ratios from the confusion matrices obtained in Assessing Spatial Precision of Top-Down and Bottom-Up Representations with Decoding Errors, the same procedure of the two-way ANOVA as described in the above paragraph was applied to the beta weight ratios, but using task labels (Bottom-up, Diffuse, and Focused) instead of cue types.

Additional Control and Single-Subject Analyses

In all analyses reported, we performed MVPA using all visually responsive voxels from each ROI as defined with the functional localizer (the circular annulus stimulus, see Localizer Task). In the interest of making classification performance more comparable across ROIs, we also repeated all analyses after restricting the voxels to the top 300 voxels that were most responsive to the functional localizer in each ROI (ranked by F values). Overall, reducing the number of voxels did not lead to significant changes in the pattern of decoding performance across ROIs (see Supplemental Fig. S5).

In addition, to assess how many individual subjects also showed the same effects that we report in the group data, we also performed the randomization tests described above within each participant. This was done by shuffling the condition labels corresponding to the effect we wanted to test 1,000 times, performing statistical tests (t test or ANOVA) on the single-trial data, and then calculating the proportion of shuffled t or F values that exceeded the statistical values from real data. We counted how many participants showed a significant result for each test and reported them in addition to the group-level statistics (Supplemental Table S1).

RESULTS

We first report the behavioral results of the top-down attention task. Then, we present fMRI results from the bottom-up mapping task, estimating the precision of stimulus-driven responses in each visual area. Finally, we present fMRI results from the top-down attention task and compare them with the precision of the stimulus-driven responses to estimate the relative precision of both types of modulation.

To be conservative with our statistical tests, we evaluated significance by using nonparametric randomization tests over 1,000 iterations (see Analysis of Behavioral Data and Statistical Procedures for MVPA). In addition, we performed statistical analyses on single-subject data and reported the number of participants who showed significant results in the same direction as in the group-level analyses (see Additional Control and Single-Subject Analyses and Supplemental Table S1).

Behavior

Participants (n = 5), analyzed at the single-subject and group levels, performed a top-down spatial attention task in which they were cued to the quadrant (Diffuse condition) or the exact location (Focused condition) of the target. When the target grating appeared, participants indicated whether its orientation was closer to a horizontal or a vertical orientation (Fig. 1A). During a 6- to 8-s cue-to-target delay period (2 s on catch trials), a spatially uniform noise stimulus was presented. The contrast of the noise stimulus matched the contrast of the target, which varied across five different levels (0%, 5%, 10%, 20%, 50% Michelson contrast). To equate task difficulty across all cue and contrast conditions, we adjusted the task difficulty (tilt offset of the target relative to 45° or 135°; see Top-Down Spatial Attention Task for details). Task difficulty adjustments were performed separately for each condition between every run to maintain accuracy at ∼75% across all conditions.

Since there was no interaction between contrast and other factors (see Supplemental Figs. S3 and S4), behavioral data were collapsed across contrast (see Analysis of Behavioral Data). In addition to the scanning sessions, participants completed an additional eye-tracking session in which they performed the same attention task, and data from the eye-tracking session and the scanning sessions were combined (see Supplemental Fig. S1 for behavioral results of individual sessions and Supplemental Fig. S7 for eye-tracking results). A paired t test between cue types (Diffuse vs. Focused) was performed separately on the accuracy and the tilt offset. The effect of cue on the tilt offset was significant, as the tilt offset was larger in the diffuse compared to the focused condition (P < 0.05; Fig. 1D). Accuracy in the diffuse condition was also slightly higher compared with the focused condition (by 2% difference, P < 0.01; Fig. 1C). These results indicate that participants were able to detect smaller perceptual changes in the focused condition compared with the diffuse condition. That said, there was a small change in accuracy that may contribute to the observed effect of attention on the size of the tilt offset. However, this trade-off was not a major concern, as the focus of the fMRI analyses was on the comparison of the relative precision between top-down and bottom-up representations as opposed to focused versus diffuse attention.

Bottom-Up Spatial Mapping Task: Estimating the Precision of Bottom-Up Stimulus-Driven Representations

To measure the spatial precision of stimulus-driven representations in retinotopically defined regions of interest (ROIs) in occipital and parietal cortex, we performed a separate bottom-up spatial mapping task in which participants viewed a series of small stimuli presented in 1 of 24 locations around an imaginary circle centered on fixation (Fig. 1B). To equate the number of spatial positions across the bottom-up and the top-down attention tasks, the bottom-up task data from adjacent wedges were collapsed to match the 12 target locations in the top-down attention task (analysis results without collapsing reported in Supplemental Fig. S6). To control for any differences in the mean signal level across tasks, we calculated and subtracted the mean amplitude across all voxels on a trial-by-trial basis separately for each ROI, which centered the average amplitude across voxels on zero for both tasks. We then trained and tested a linear classifier on the activation patterns extracted from each visual area to decode the spatial location of the stimulus on each trial using leave-one-run-out cross-validation (see Multivariate Pattern Decoding).

Decoding accuracy was above chance in all ROIs (Fig. 2A, white bars; 1-tailed t test, all P’s < 0.02, P value computed via randomization test, see Statistical Procedures for MVPA). However, decoding accuracy was significantly different across ROIs and was numerically highest in V1 and numerically lower across subsequent areas of the visual hierarchy (1-way ANOVA on decoding accuracy across ROIs, P < 0.001). This pattern is consistent with prior reports indicating that the spatial precision of bottom-up sensory representations is most precise in V1, less precise in midlevel occipital regions, and lowest in IPS (see Refs. 22, 86).

Top-Down Attention Task: Estimating the Spatial Precision of Top-Down Attentional Modulations

Next, to estimate the spatial precision of top-down attentional modulations, we trained a classifier on the bottom-up mapping task and cross-generalized that classifier to decode attended spatial locations during the cue-to-target delay period in the top-down attention task. We performed this cross-generalization analysis with the assumption that training the classifier with precise and focal mapping stimuli would allow us to estimate the spatial precision of top-down attentional modulations relative to the precision of bottom-up representations. Thus, a high degree of cross-generalization would suggest that top-down attentional modulations are as precise as bottom-up stimulus-driven representations. In contrast, a lower degree of cross-generalization would suggest that top-down modulations are less precise than the bottom-up representations observed in the bottom-up mapping task. Note that this logic holds only if the neural codes for spatial position share a common format across the bottom-up and top-down tasks. To account for a case in which this is not true, in Complementary Approach to Comparing Bottom-Up and Top-Down Spatial Precision we report a complementary decoding analysis performed within the top-down attention task.

As with behavioral results reported above, all statistical analyses were performed after collapsing across contrast levels (analysis results without collapsing reported in Supplemental Figs. S3 and S4). First, all ROIs showed cross-generalized decoding performance that was above chance when collapsed across cue conditions (Fig. 2A, light and dark gray bars; 1-tailed t test against chance, P’s < 0.01; see Supplemental Table S1 for the number of participants who showed significant effect when tested within individual participants). A two-way ANOVA on decoding accuracies with cue type (Diffuse vs. Focused) and ROI as factors revealed significant main effects of both factors (both P < 0.001). There was also a significant interaction between cue type and ROI (P < 0.001). To further explore the cause of this interaction, we tested the effect of cue type within each ROI. Decoding accuracy was significantly higher in the focused than the diffuse condition in all ROIs except V1 (2-tailed t test, V1: P = 0.07, other ROIs: P’s < 0.05).

To directly assess the interaction between ROI and the precision of top-down and bottom-up modulations, we next computed the ratio between the bottom-up and top-down decoding accuracies. For this analysis, top-down decoding accuracies were divided by the bottom-up accuracies for each ROI (Fig. 2B). A low ratio score means higher bottom-up decoding accuracy compared to top-down decoding accuracy, consistent with higher precision of bottom-up representations. A high ratio score means higher top-down decoding accuracy compared to bottom-up decoding accuracy, consistent with higher precision of top-down representations. As shown in Fig. 2B, V1 had the lowest ratio score, indicating that the bottom-up decoding accuracy was much higher than top-down decoding accuracy in V1. Critically, there was a gradual decrease in the magnitude of ratio scores across the visual hierarchy, with later regions showing a similar level of top-down and bottom-up decoding accuracy. For instance, the ratio scores in V3AB, V4, and IPS were close to or above 1, demonstrating that top-down decoding accuracy is comparable to or even slightly higher than the bottom-up decoding accuracy in these areas. We also found that there was a relatively higher top-down decoding accuracy across areas in the focused cue condition. A two-way ANOVA on the ratio scores with cue type and ROI as factors revealed significant main effects of both factors (both P < 0.001; see Supplemental Table S1 for the number of participants who showed significant effect when tested within individual participants) and a significant interaction between these factors (P < 0.001). Thus, even though the absolute value of decoding accuracies cannot be compared within a single ROI given differences in task parameters, the relative precision of bottom-up and top-down modulations changes systematically across visual areas.

Finally, to control for the possibility that top-down and bottom-up information about spatial position might be represented in different formats, we performed an additional analysis in which the classifier was trained and tested using only data from the top-down attention task. V1 still yielded the lowest top-down decoding accuracy (Fig. 3), and other ROIs followed the similar pattern observed in the cross-generalization results presented in Fig. 2.

Figure 3.

Similar to Fig. 2 but only using data from the top-down attention task to train and test the classifier for the top-down decoding accuracy. A: decoding accuracy based on functional MRI (fMRI) activation patterns in the bottom-up spatial mapping task (white bars) and the top-down spatial attention task (Diffuse and Focused conditions, light and dark gray bars, respectively). For comparison, bottom-up decoding accuracies from Fig. 2A are plotted together. The general pattern of results followed Fig. 2A: decoding accuracy in the top-down attention task was generally higher in the focused than the diffuse condition, albeit to a lesser degree. Comparing across regions of interest (ROIs), although V1 showed much lower top-down decoding accuracy relative to bottom-up decoding accuracy, later areas [e.g., V3AB, V4, intraparietal sulcus (IPS)] showed comparable decoding accuracies across tasks, leading to an interaction between task type and visual areas. Filled colored dots represent data from individual participants, and error bars represent ±1 SE. The dashed line indicates chance performance (1/12 or ∼0.083). B: ratio of decoding accuracies between top-down attention and bottom-up mapping tasks. To obtain this ratio score, the top-down decoding accuracy for each ROI was divided by the bottom-up decoding accuracy in that ROI, separately for the diffuse and focused conditions. A low ratio score indicates that an ROI had higher decoding accuracy in the bottom-up mapping task, consistent with higher bottom-up precision. A high ratio score indicates that an ROI had higher decoding accuracy in the top-down task, consistent with higher top-down precision. Although V1 showed relatively higher bottom-up precision, later areas showed comparable levels of bottom-up and top-down precision, showing a pattern of results similar to Fig. 2B. Colored dots represent data from individual participants. Error bars are ±1 SE.

Complementary Approach to Comparing Bottom-Up and Top-Down Spatial Precision

As an additional assessment of bottom-up and top-down precision, we next quantified the confusability of decoded spatial positions in the bottom-up mapping and top-down attention tasks, because classifier errors should track the similarity between the activation patterns associated with nearby spatial positions. Thus, the pattern of decoding errors provides a more nuanced description of the relationship between voxel activation patterns associated with different spatial positions and the precision of those representations.

Figure 4 shows the group-averaged confusion matrices for the actual target locations plotted against the classifier-predicted locations in the bottom-up mapping and top-down attention tasks. For the attention task, confusion matrices from the cross-generalization analysis (reported in Fig. 2A) are plotted, and data were collapsed across contrast levels as well. Each cell within a matrix is color-coded to indicate the proportion of trials for which the classifier predicted the spatial position labeled by the row, out of all trials in which the target was presented at the spatial position labeled by the column. For example, for the bottom-up mapping task, in the most upper left cell of the V1 confusion matrix the high value marked with light green color (50.17%) indicates that out of all trials in which the target was presented at position 1 the classifier correctly predicted approximately half of those trials as position 1.

In the bottom-up mapping task and the focused condition in the top-down attention task, predictions were centered on and around the main diagonal, consistent with the classifier inferring the correct spatial position. In contrast, predictions in the diffuse condition showed a clustering pattern within the quadrant of the presented target. This clustering indicates that the classifier was distributing guesses more uniformly across the three locations within each quadrant, corresponding to the cued locations in the diffuse condition.

To quantify differences in representational precision reflected in the confusion matrices between tasks and task conditions, we used a general linear model with diagonal and off-diagonal predictors (Fig. 5A). The diagonal predictor captures a narrow, precise spatial representation, and the off-diagonal predictor captures a broad, quadrant-wide spatial representation. These two predictors were used as regressors on each of the confusion matrices in Fig. 4 to calculate beta weights in each task/condition, separately for each participant. We then computed a ratio between the two beta weights by dividing the diagonal beta weight by the off-diagonal beta weight and log-transforming the resulting value. Thus, the ratio value should be near 0 if both beta weights are similar, larger than 0 if the diagonal weight is higher than the off-diagonal weight, and below 0 if the diagonal weight is lower than the off-diagonal weight (Fig. 5B).

The results were consistent with our earlier comparison of bottom-up and top-down decoding accuracies. Representations in the bottom-up mapping task were highly precise, with the beta weight ratios highest in V1 and gradually decreasing in later areas. Compared with the bottom-up representation, top-down spatial representations in the focused condition were less precise in earlier areas, especially in V1, but reached a comparable level of precision in later areas. Finally, top-down representations in the diffuse condition were not precise and spread across a quadrant, showing beta weight ratios close to 0 across all ROIs. A two-way ANOVA on the beta weight ratios with task condition (Bottom-Up vs. Diffuse vs. Focused) and ROI as factors supports this trend, with significant main effects of task condition and ROI as well as a significant interaction between these factors (all P’s < 0.001).

DISCUSSION

Although top-down attention is critical for selecting and enhancing the processing of relevant sensory stimuli, the role of anatomical constraints in frontal and parietal areas (e.g., larger receptive fields) in determining the precision of top-down attentional modulations is not well understood. Here, we used a bottom-up mapping task and a top-down attention task to assess decoding accuracy based on voxel activation patterns in human visual areas. Because the tasks were—by necessity—different, we cannot directly compare decoding accuracies within a single visual area. However, the pattern of relative decoding accuracy across areas is revealing: Bottom-up decoding accuracy was significantly higher than top-down decoding accuracy in V1, but decoding accuracy was comparable in midlevel occipital areas and in IPS. These observations are consistent with the idea that the representational precision of the areas generating top-down control signals, coupled with the precision of midlevel areas that are the primary targets of these signals (61, 87), limits the precision of modulations in early parts of the visual system that have the highest bottom-up fidelity.

As a measure of precision, we used decoding accuracy to quantify the information content of spatial representations and the associated confusion matrices to provide a more descriptive assessment of the representational precision. Note that our measure of precision, decoding accuracy, and the pattern of decoding errors might be impacted by several different single-neuron modulations like a change of gain and/or tuning bandwidth in individual neurons. However, these underlying single-unit modulations jointly contribute to the overall amount of spatial information in the voxel activation patterns, and thus the decoding accuracy provides an overall assessment of aggregate changes in the representational precision in a visual area. In addition, the low degree of cross-generalization from the bottom-up mapping task to the top-down attention task in V1 might be due to differences in stimulus attributes, such as spatial frequency, between the two tasks. However, Fig. 3 reveals that the same pattern is observed even when evaluating top-down decoding accuracy using only data from the top-down attention task, in which all low-level stimulus attributes are equated. Furthermore, our decoding methods do not rule out the possibility that differences in the signal-to-noise ratio across brain areas or tasks contributed to the observed pattern of results. That said, we consider noise as one key factor that is partially responsible for the differences in spatial precision across ROIs. On this account, it should be noted that lower signal and/or higher noise could both contribute to lower overall spatial precision in this study.

Our initial hypothesis was that the spatial resolution of attentional modulations in early visual cortex would be limited because of the large receptive field (RF) sizes in attentional control areas where the top-down signals presumably originate. However, the precision of a spatial representation in a population of neurons is not just limited by the size of RFs. Instead, the spatial precision of a given area can be substantially higher than that of individual neurons via pooling information across many neurons (88–93). However, even if precision gets higher with pooling, the precision of neural codes in areas with smaller RFs (and more neurons, such as V1) is still likely to reach a higher theoretical asymptote than areas with larger RFs (and fewer neurons). That said, this logic relies on assumptions about how the information is pooled and utilized by subsequent stages of processing (e.g., pooling may be suboptimal, thus undercutting the theoretical upper limit of precision).

At first glance, our results may seem contradictory to previous studies that have reported evidence for highly detailed representations in V1 that rely on top-down feedback. For example, studies of visual working memory have shown that mnemonic representations held over a long period of time can be highly precise in V1 and less so in later cortical regions, which is opposite to the pattern we observed here (e.g., Refs. 94–97). However, in these working memory studies, the initial presentation of the to-be-remembered sample stimulus likely evoked a highly precise bottom-up response that could be maintained with high fidelity during the delay period via top-down modulatory signals. In contrast, the present task provides a more direct assessment of the precision of purely top-down modulations, as there was no initial stimulus that evoked a spatially specific bottom-up response. Instead, participants were only given a symbolic central cue to guide the deployment of spatial attention, which enabled us to measure top-down attention that is not contaminated by bottom-up stimulus drive.

Our results likewise provide more information about the precision of top-down modulations by requiring attention to 1 of 12 contiguous locations, which is a more fine-grained manipulation of top-down attention than commonly used. For example, previous studies that focused on pure top-down processes have reported univariate BOLD modulations in early visual cortex, even before any physical stimulus is presented (26, 29). However, in these studies, univariate BOLD responses were averaged over a relatively broad region of visual cortex and participants attended to one of only a few possible locations (e.g., left visual field vs. right visual field, or 1 of the 4 quadrants). Thus, these prior studies do not directly reveal information about the precision of top-down modulations in situations where highly focused attention is required. Similarly, other studies of mental imagery have reported that multivariate activation patterns in early areas like V1 carry item-specific information even in the absence of a bottom-up stimulus (35, 38, 41–43). However, these mental imagery studies typically used a small set of categorical images, which means that the activation patterns only need to be sufficiently precise to successfully discriminate coarsely related exemplars. More recently, Breedlove et al. (98) used an encoding model and found that identification accuracy for 64 visual images was higher for presented versus imagined images in early visual areas and comparable in later areas of the visual hierarchy such as IPS. Furthermore, Favila et al. (99) modeled population receptive fields (pRFs) to map evoked responses during cued memory recall of spatial locations and found that recalled representations had lower spatial precision compared with representations during stimulus presentation in earlier areas of the visual hierarchy, whereas their precision was comparable in areas such as hV4 and later. These recent reports from studies on mental imagery and memory, which also involve top-down feedback signals, appear to converge with the present results that focus on spatial attention to specific locations in the visual field.

Finally, for the decoding analysis of spatial position on the diffuse cue trials, we used the presented target locations as the “correct” labels to compute the decoding accuracy. This would naturally lead to lower decoding performance for the diffuse cue condition, given that the attention manipulation results in a broad modulation across the whole quadrant and the participant, unlike the classifier, does not know the target location until the target is presented. Thus, it is not surprising, because of the setup of the classifier, that the decoding accuracy for the exact target position is lower in the diffuse compared with the focused condition. However, we do not view this as problematic for several reasons. First, the results indicate that the classifier confused locations within a quadrant with about equal probability, consistent with participants spreading spatial attention appropriately across a quadrant in response to the diffuse cues (see Fig. 4, middle). Therefore, lower decoding accuracy in the diffuse condition accurately reflects lower spatial precision of the top-down representation. Second, our primary focus was on the comparison between bottom-up and top-down precision across visual areas, so the key findings rely primarily on the bottom-up mapping task and the focused cue trials.

In conclusion, our findings reveal an interaction between visual areas and the relative precision of bottom-up and top-down modulations, suggesting that top-down modulations are not as precise as bottom-up modulations in early visual areas compared with later areas. This is important because these early areas, particularly V1, have small receptive fields and are thus ideal candidates for high-fidelity top-down modulations. This comparative lack of top-down precision may be the result of relatively coarse spatial coding in frontal and parietal cortex and the anatomical pattern of feedback projections that primarily target midlevel visual areas as opposed to earlier areas with the highest potential for spatially focal representations.

DATA AND CODE AVAILABILITY

All preprocessed fMRI and behavioral data, the experiment code used during data collection, and the analysis code used to generate the figures in the main manuscript and Supplemental Materials are available on the Open Science Framework (OSF) at https://osf.io/nbdj5.

SUPPLEMENTAL DATA

Supplemental Materials: https://doi.org/10.17605/OSF.IO/NBDJ5.

GRANTS

Research was supported by National Eye Institute Grant R01 EY025872 (J.T.S.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.P. and J.T.S. conceived and designed research; S.P. performed experiments; S.P. analyzed data; S.P. and J.T.S. interpreted results of experiments; S.P. prepared figures; S.P. drafted manuscript; S.P. and J.T.S. edited and revised manuscript; S.P. and J.T.S. approved final version of manuscript.