Reproducibility of graph measures derived from resting‐state MEG functional connectivity metrics in sensor and source spaces

Abstract

Prior studies have used graph analysis of resting‐state magnetoencephalography (MEG) to characterize abnormal brain networks in neurological disorders. However, a present challenge for researchers is the lack of guidance on which network construction strategies to employ. The reproducibility of graph measures is important for their use as clinical biomarkers. Furthermore, global graph measures should ideally not depend on whether the analysis was performed in the sensor or source space. Therefore, MEG data of the 89 healthy subjects of the Human Connectome Project were used to investigate test–retest reliability and sensor versus source association of global graph measures. Atlas‐based beamforming was used for source reconstruction, and functional connectivity (FC) was estimated for both sensor and source signals in six frequency bands using the debiased weighted phase lag index (dwPLI), amplitude envelope correlation (AEC), and leakage‐corrected AEC. Reliability was examined over multiple network density levels achieved with proportional weight and orthogonal minimum spanning tree thresholding. At a 100% density, graph measures for most FC metrics and frequency bands had fair to excellent reliability and significant sensor versus source association. The greatest reliability and sensor versus source association was obtained when using amplitude metrics. Reliability was similar between sensor and source spaces when using amplitude metrics but greater for the source than the sensor space in higher frequency bands when using the dwPLI. These results suggest that graph measures are useful biomarkers, particularly for investigating functional networks based on amplitude synchrony.

Test–retest reliability of resting‐state magnetoencephalography global graph measures was quantified and compared for three connectivity metrics in sensor and source space. Reliability and sensor versus source association was greater for amplitude than phase metrics. Reliability for the phase metric was greater in source than sensor space at higher frequencies.

Abbreviations

AEC

amplitude envelope correlation

ANOVA

analysis of variance

CC

clustering coefficient

CPL

characteristic path length

CSD

cross‐spectral density

DTI

diffusion tensor imaging

dwPLI

debiased weighted phase lag index

EEG

electroencephalography

FC

functional connectivity

FDR

false discovery rate

FIR

finite impulse response

fMRI

functional magnetic resonance imaging

GCE

global cost efficiency

GE

global efficiency

HCP

Human Connectome Project

ICA

independent component analysis

ICC

intraclass correlation coefficient

iEEG

intracranial electroencephalography

IQR

interquartile range

lcAEC

leakage‐corrected amplitude envelope correlation

LCMV

linearly constrained minimum variance

MEG

magnetoencephalography

MNI

Montreal Neurological Institute

MRI

magnetic resonance imaging

MST

minimum spanning tree

OMST

orthogonal minimum spanning tree

PLI

phase lag index

PLV

phase locking value

ROI

region of interest

rs‐EEG

resting‐state electroencephalography

rs‐MEG

resting‐state magnetoencephalography

S

synchronizability

T

transitivity

wMNE

weighted minimum norm estimate

wPLI

weighted phase lag index

1. INTRODUCTION

Over the past two decades, graph theoretical analysis of resting‐state brain networks has increasingly been applied to the investigation of a wide variety of neurological, neuropsychiatric, and neurodevelopmental conditions (Hallquist & Hillary, 2019; Liu et al., 2017). Brain networks are often derived from structural connectivity analysis of diffusion tensor imaging (DTI) and functional connectivity (FC) analysis of functional magnetic resonance imaging (fMRI), magnetoencephalography (MEG), electroencephalography (EEG), or intracranial EEG (iEEG). Global graph measures characterize the overall network topology and include measures of functional integration, functional segregation, and network synchronization capability (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006; Rubinov & Sporns, 2010). Nodal graph measures characterize individual node properties and the influence of the nodes on the network (Rubinov & Sporns, 2010). Many of these measures have been shown to reflect disease‐related abnormalities in the brain networks of patients with epilepsy (Garcia‐Ramos, Song, Hermann, & Prabhakaran, 2016; Pourmotabbed, Wheless, & Babajani‐Feremi, 2020; Quraan, McCormick, Cohn, Valiante, & McAndrews, 2013), Alzheimer's disease (Hojjati, Ebrahimzadeh, & Babajani‐Feremi, 2019; Khazaee, Ebrahimzadeh, & Babajani‐Feremi, 2015; Stam et al., 2009), schizophrenia (Hadley et al., 2016; Jalili & Knyazeva, 2011), autism (Tsiaras et al., 2011; Zeng et al., 2017), or other disorders. This suggests that graph measures have the potential to be useful as clinical biomarkers.

A present challenge for researchers is that there are many available graph measures, FC metrics, and network construction strategies to choose from. Model‐based metrics of FC quantify the linear phase, amplitude, or power interactions between oscillating signals whereas model‐free metrics based on information theory can quantify both non‐linear and linear interactions (Bastos & Schoffelen, 2015). For MEG and EEG, the FC can be estimated based on the sensor signals or after projection of the sensor signals to the source space. In the sensor space, volume conduction or field spread of common source activity can introduce spurious inflations in the connectivity estimate (Nolte et al., 2004). Source reconstruction does not completely mitigate this effect because of the imperfect unmixing of the sources, which results in spatial leakage of source activity (Schoffelen & Gross, 2009). Therefore, several FC estimation techniques have been proposed that are robust against the effects of volume conduction, field spread, and source leakage (Brookes, Woolrich, & Barnes, 2012; Colclough, Brookes, Smith, & Woolrich, 2015; Nolte et al., 2004; Vinck, Oostenveld, van Wingerden, Battaglia, & Pennartz, 2011).

After construction of the brain networks, weak and insignificant connections are often removed via topological filtering (Rubinov & Sporns, 2010). A standard topological filtering approach applies a proportional weight threshold, where a certain percentage (i.e., density) of the strongest connections is retained and the rest of the connections are discarded (Rubinov & Sporns, 2010). Another popular approach is the formation of a minimum spanning tree (MST) that, unlike proportional thresholding, does not require specification of a particular density and ensures all the nodes remain connected to the network (Stam et al., 2014). However, MST thresholding typically results in very sparse networks and is problematic for the computation of several graph measures (such as those based on triangular connections) (Tewarie, van Dellen, Hillebrand, & Stam, 2015). A thresholding method has been introduced as an improvement to the MST and is based on the aggregation of multiple orthogonal MSTs (OMSTs) to achieve a target density level (Dimitriadis, Antonakakis, Simos, Fletcher, & Papanicolaou, 2017; Dimitriadis, Salis, Tarnanas, & Linden, 2017). An open problem for researchers is choosing which thresholding method to apply as well as finding the optimal density level.

The reproducibility of the graph measures across multiple scanning sessions is an important criterion for their use as biomarkers, particularly for the investigation of disease or treatment progression (Deuker et al., 2009; Welton, Kent, Auer, & Dineen, 2015). Therefore, the test–retest reliability can provide guidance to researchers on which network construction strategies to employ. Previous resting‐state studies have examined the test–retest reliability of FC metrics, nodal graph measures, and global graph measures derived from fMRI (Ball, Goldstein‐Piekarski, Gatt, & Williams, 2017; Dimitriadis, Salis, et al., 2017; Liao et al., 2013; Shehzad et al., 2009), EEG (Hardmeier et al., 2014; Kuntzelman & Miskovic, 2017; van der Velde, Haartsen, & Kemner, 2019), and MEG (Babajani‐Feremi, Noorizadeh, Mudigoudar, & Wheless, 2018; Colclough et al., 2016; Deuker et al., 2009; Dimitriadis, Routley, Linden, & Singh, 2018; Garces, Martin‐Buro, & Maestu, 2016; Jin, Seol, Kim, & Chung, 2011). However, to the best of our knowledge, test–retest reliability analysis has not been performed on global graph measures derived from resting‐state MEG (rs‐MEG) in the source space. One of the goals of our study was to address this gap in the literature.

Our study compared the test–retest reliability of rs‐MEG global graph measures for three FC metrics, in the sensor and source spaces, and across a wide range of network density levels. The FC metrics included a metric of phase synchrony (i.e., the debiased weighted phase lag index [dwPLI]) and metrics of amplitude synchrony (i.e., the amplitude envelope correlation [AEC] and the leakage‐corrected AEC [lcAEC]). The AEC is sensitive to common source effects while the dwPLI and lcAEC are insensitive. Both the proportional and OMST methods were used for thresholding in order to determine which method resulted in a greater reliability at each density level. In addition to the reliability analysis, the association between the graph measures of the sensor and source spaces was also examined. Ideally, measures that characterize the global network topology should not depend on whether the analysis was performed in the sensor or source space. The data used in this study were provided by the Human Connectome Project (HCP) and consist of 89 healthy young adults with three sessions of resting‐state recordings for each subject.

2. METHODS

2.1. MEG database and preprocessing

This current study included the preprocessed rs‐MEG data of the 89 healthy subjects (22–35 years of age, 41 females) provided with the HCP S1200 data release (Larson‐Prior et al., 2013; Van Essen et al., 2012). The HCP young adult study, led by Washington University and the University of Minnesota, sought to investigate healthy human brain function and connectivity in a large cohort of twins and their non‐twin siblings (Van Essen et al., 2012). The subjects comprise 19 monozygotic twin pairs, 13 dizygotic twin pairs, and 25 non‐twin individuals who are not diagnosed with any significant neurodevelopmental, neuropsychiatric, or neurologic disorders.

A 248‐magnetometer Magnes 3600 MEG system (4D Neuroimaging, San Diego, CA) was used to collect three 6‐min sessions of resting‐state data for each subject in an eyes‐open condition. The MEG data were obtained from the online ConnectomeDB database (https://db.humanconnectome.org/app/template/Login.vm) after prior preprocessing was performed using the open‐source HCP MEG pipeline (Larson‐Prior et al., 2013). Briefly, the pipeline included the following steps for each MEG session: artifact‐contaminated time segments (e.g., corresponding to head or eye movements) and noisy MEG sensors (i.e., exhibiting a high variance ratio or low correlation to neighboring sensors) were rejected, the data were 60 and 120 Hz band‐stop filtered to remove power line noise, and independent component analysis (ICA) was used to identify and regress out noise components from the entire scan based on correspondence to certain artifactual signatures (e.g., eye‐blinks, cardiac interference, or environmental noise). A total of three to six (interquartile range [IQR]) noise components were regressed out from the MEG data. After preprocessing, the data consisted of 135–147 (IQR) 2‐s trials and 243–246 (IQR) sensors. The exact details of the preprocessing can be found in the overview publication (Larson‐Prior et al., 2013) and in the open‐source software available online (https://www.humanconnectome.org/software/hcp-meg-pipelines).

The MEG analysis pipeline described in the following sections was adapted from our previous work (Pourmotabbed et al., 2020). An overview of the analysis pipeline is shown in Figure 1. In addition to the prior preprocessing performed using the HCP MEG pipeline, the MEG data (in the sensor space) were 0.1 Hz high‐pass (fourth order, zero‐phase/two‐pass Butterworth) and 150 Hz low‐pass (sixth order, zero‐phase/two‐pass Butterworth) filtered. To avoid edge artifacts, filtering was performed on the data after concatenation of the 2‐s trials into one time segment (Gross et al., 2013). Spherical spline interpolation was used to reconstruct the removed noisy sensors (Perrin, Pernier, Bertrand, & Echallier, 1989).

FIGURE 1.

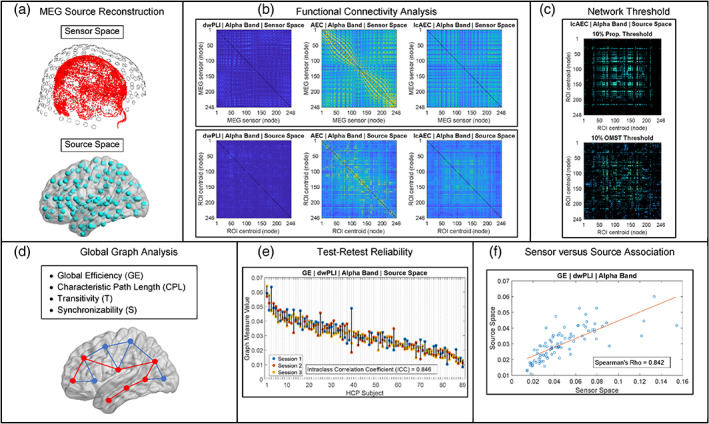
Overview of the magnetoencephalography (MEG) analysis pipeline. See Section 2 for details

2.2. Source reconstruction of MEG data

Source reconstruction of the preprocessed MEG data was performed using an atlas‐based beamforming approach adapted from previous MEG studies (Hillebrand et al., 2016; Hillebrand, Barnes, Bosboom, Berendse, & Stam, 2012; Nissen et al., 2017). Brain source time‐series were reconstructed for the centroids of the 246 (210 cortical and 36 subcortical) regions of interest (ROIs) of the Brainnetome atlas (Fan et al., 2016). Scalar beamformer weights were computed for each centroid using a regularized estimate of the broadband (0.1–150 Hz) data covariance matrix and using lead‐fields calculated from precomputed single‐shell volume conductor models (Nolte, 2003) provided with the HCP data release. The lead‐field was projected in the optimal direction given by the eigenvector of the maximum eigenvalue of the output source power matrix (Sekihara, Nagarajan, Poeppel, & Marantz, 2004). The beamformer weights are derived such that the output source power at the location of interest is minimized subject to the constraint that the signal in the MEG data due to the source at that location is passed with unit gain (van Veen, van Drongelen, Yuchtman, & Suzuki, 1997). This forms a linearly constrained minimum variance (LCMV) spatial filter that attenuates signal leakage from other sources that are correlated across the sensors (van Veen et al., 1997).

The coordinates of the centroids for each subject were determined from subject‐specific 4‐mm resolution volumetric grids provided with the HCP data release. To obtain the volumetric grids, a template MRI grid in the Montreal Neurological Institute (MNI) space was nonlinearly warped to the co‐registered MRI of each subject. The template MRI grid was included with the HCP MEG pipeline. The Brainnetome atlas was used to label each voxel in the template grid, and, for each ROI, the k‐medoids (k = 1) algorithm was performed in order to locate the voxel (i.e., the centroid) with the least squared Euclidean distance to all other voxels of the ROI. The centroids were transformed from the MNI to the individual subject space by indexing the voxel locations in the template grid to those in the subject‐specific volumetric grid. For construction of the beamformer weights, all the 2‐s trials that remained after preprocessing were used to estimate the broadband data covariance matrix, as per the suggestion made in Brookes et al. (2008). The covariance matrix was noise‐regularized with a diagonal loading factor equal to 5% of the mean sensor variance. Noise‐regularization increases the signal‐to‐noise ratio of the source time‐series (Brookes et al., 2008) and accounts for the rank deficiency due to the ICA preprocessing step and sensor interpolation.

2.3. FC analysis in sensor and source space

The phase lag index (PLI) is an FC metric of phase synchrony that measures the asymmetry in the distribution of the observed phase differences between two oscillating signals (Stam, Nolte, & Daffertshofer, 2007). Because the PLI is insensitive to interactions with a zero (modulus π) phase difference, the metric is robust against common source activity from volume conduction, field spread, and source leakage (Stam et al., 2007). The weighted PLI (wPLI) is a variant of the PLI that is more robust against the influence of common sources (Vinck et al., 2011). Both the PLI and wPLI are dependent on the number of trials used to compute them (Vinck et al., 2011). The debiased wPLI‐square estimator (i.e., the dwPLI) is an improvement on the wPLI that reduces the effects of this sample size bias and is computed at a particular frequency f using the following equation (Vinck et al., 2011):

$$\text{dwPLI}\left(f\right)=\frac{{\sum }_{k=1}^K{\sum }_{j\ne k}\mathrm{Im}\left[s_k\left(f\right)\right]\mathrm{Im}\left[s_j\left(f\right)\right]}{{\sum }_{k=1}^K{\sum }_{j\ne k}\left|\mathrm{Im}\left[s_k\left(f\right)\right]\mathrm{Im}\left[s_j\left(f\right)\right]\right|}$$ (1)

where s _k (f) is the cross‐spectral density (CSD) between the two signals for trial k, Im[.] denotes the imaginary part operator, and K is the total number of trials.

The AEC is an FC metric of amplitude synchrony that measures the linear correlation between the oscillating amplitude envelopes of two bandlimited signals (O'Neill, Barratt, Hunt, Tewarie, & Brookes, 2015):

$$\begin{array}{c}r\left(A_x,,A_y\right)=\frac{\mathrm{cov}\left(A_x,A_y\right)}{\sqrt{\mathrm{var}\left(A_x\right)\mathrm{var}\left(A_y\right)}}\end{array}$$ (2)

where A _x and A _y are the amplitude envelopes of signals x and y, respectively. The instantaneous amplitude envelope of a band‐pass‐filtered signal x at time t can be determined as follows (Kiebel, Tallon‐Baudry, & Friston, 2005; O'Neill et al., 2015):

$$\begin{array}{c}{A}_x\left(t\right)=\sqrt{{\left(x\left(t\right)\right)}^2+{\left(H\left[x\left(t\right)\right]\right)}^2}\end{array}$$ (3)

where H[.] denotes the Hilbert transform operator. The AEC is susceptible to the effects of volume conduction, field spread, and source leakage (Brookes et al., 2012). A pairwise orthogonalization procedure has been proposed to correct for this susceptibility by removing zero (modulus π) phase lag interactions between the two signals (Brookes et al., 2012; Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012).

In this current study, three metrics (i.e., the dwPLI, AEC, and lcAEC) were used to estimate the FC for both the sensor and the source signals in the delta (1–4 Hz), theta (4–7 Hz), alpha (8–13 Hz), low beta (13–20 Hz), high beta (20–30 Hz), and low gamma (30–50 Hz) frequency bands. This resulted in 248‐by‐248 adjacency matrices in the sensor space and 246‐by‐246 adjacency matrices in the source space, corresponding to 248 MEG sensors and 246 Brainnetome ROIs, respectively. A description of the three FC metrics examined in this study and the methods used to compute them is shown in Table 1. To compute the dwPLI for frequencies from 4 to 50 Hz, the Fourier spectrum of each 2‐s trial was obtained via the Fast Fourier Transform algorithm with a Hann window and used to calculate the individual trial CSDs. For frequencies in the delta (1–4 Hz) band, consecutive 2‐s trials were concatenated to form 4‐s trials (66–73 [IQR] 4‐s trials for all the subjects) before the frequency transformation, ensuring that each trial contained a sufficient number of cycles (10 cycles on average for the delta band) for adequate FC estimation. The dwPLI was computed from the individual trial CSDs (Equation (1)) and averaged over all the frequencies in each of the six bands.

TABLE 1.

Description of the three functional connectivity metrics examined in this study and the methods used to compute them

Abbreviation	Connectivity metric	Type	Leakage‐corrected	Frequency transform	Toolbox	Reference
dwPLI	Debiased weighted phase lag index	Phase synchrony	Yes	Fourier	FieldTrip	Stam et al. (2007) and Vinck et al. (2011)
AEC	Amplitude envelope correlation	Amplitude synchrony	No	Hilbert	MEG‐ROI‐nets	O'Neill et al. (2015)
lcAEC	Leakage‐corrected amplitude envelope correlation	Amplitude synchrony	Yes, pairwise orthogonalization	Hilbert	MEG‐ROI‐nets	Brookes et al. (2012), Hipp et al. (2012), and O'Neill et al. (2015)

To compute the AEC and lcAEC, all the trials were concatenated into a single time segment and band‐pass filtered (zero‐phase/two‐pass finite impulse response, order = 3 cycles of the low frequency cutoff) into the six frequency bands. For the lcAEC, the band‐pass filtered data were leakage corrected using the pairwise orthogonalization procedure. The instantaneous amplitude envelopes were obtained from the entire time segment using the Hilbert transform (Equation (3)) and then downsampled after low‐pass filtering (eighth order, zero‐phase/two‐pass Chebyshev Type I) at 0.25 Hz for the delta band (output sampling rate = 0.625 Hz) and at 0.5 Hz for the other frequency bands (output sampling rate = 1.25 Hz). Downsampling and low‐pass filtering optimizes the temporal scale of the data for amplitude synchrony metrics and was performed according to the recommendation made in Luckhoo et al. (2012). The AEC and lcAEC were computed from the linear correlation of the logarithm of the downsampled amplitude envelopes (Equation (2)). Because pairwise leakage correction results in an asymmetric adjacency matrix (Hipp et al., 2012), corresponding elements in the upper and lower triangular matrices were averaged to ensure symmetry for the lcAEC.

2.4. Graph theoretical analysis

Four global graph measures (i.e., the global efficiency [GE], characteristic path length [CPL], transitivity [T], and synchronizability [S]) were computed for the adjacency matrices of the three FC metrics and six frequency bands in the sensor and source spaces. This was performed for network density levels ranging from 2.5 to 100% in 2.5% steps using the standard proportional weight thresholding method and using the OMST thresholding method. For proportional thresholding, each density level indicates the percentage of the strongest connections of the adjacency matrix to retain (Rubinov & Sporns, 2010). The rest of connections are discarded by setting their weights equal to 0 (Rubinov & Sporns, 2010). The procedure for the OMST thresholding method involves aggregation of multiple OMSTs to achieve the target density level and is described in detail elsewhere (Dimitriadis, Antonakakis, et al., 2017; Dimitriadis, Salis, et al., 2017). Unlike proportional thresholding, the OMST thresholding method ensures that all the nodes remain connected to the network (Dimitriadis, Antonakakis, et al., 2017).

The GE and CPL are measures of functional integration, which indicates the ability of the brain to combine information from distributed brain regions (Rubinov & Sporns, 2010). Short paths imply a greater potential for functional integration between brain regions (Rubinov & Sporns, 2010). The GE is mainly influenced by short paths (Rubinov & Sporns, 2010) and is defined as the mean inverse shortest path length between all node pairs (Latora & Marchiori, 2001):

$$\begin{array}{c}\mathrm{GE}=\frac{1}{N\left(N-1\right)}{\sum }_{i=1}^N{\sum }_{j\ne i}\frac{1}{d_{\mathit{ij}}}\end{array}$$ (4)

where N is the total number of nodes and d _ij is the shortest path length between nodes i and j. The connection weights were transformed to lengths by computing their inverse (Boccaletti et al., 2006), and the shortest path length (aka distance) between each node pair was derived from the length matrix using Dijkstra's algorithm. The CPL is mainly influenced by long paths (Rubinov & Sporns, 2010) and is defined as the mean shortest path length between all node pairs (Watts & Strogatz, 1998):

$$\begin{array}{c}\mathrm{CPL}=\frac{1}{N\left(N-1\right)}{\sum }_{i=1}^N{\sum }_{j\ne i}{d}_{\mathit{ij}}\end{array}$$ (5)

The shortest path length between nodes that became disconnected from the network because of the proportional threshold was set to infinity and excluded from computation of the CPL.

The T is a measure of functional segregation, which indicates the ability for distributed processing to occur in the brain (Rubinov & Sporns, 2010), and is defined as follows (Newman, 2003; Onnela, Saramaki, Kertesz, & Kaski, 2005):

$$\begin{array}{c}T=\frac{{\sum }_{i=1}^{N}2t_i}{{\sum }_{i=1}^N{k}_i\left(k_i-1\right)}\end{array}$$ (6)

where t _i is the sum of the geometric mean of the connection weights of all the triangles around node i and k _i is the degree (i.e., number of nonzero connections) of node i. The T is an improvement on the mean clustering coefficient (CC) that is not disproportionately influenced by nodes with a small number of neighbors (Newman, 2003).

The S is a spectral graph measure that quantifies the synchronization capability of a network and is defined as the ratio of the second smallest eigenvalue λ ₂ of the Laplacian matrix to the largest eigenvalue λ _N (Arenas, Díaz‐Guilera, Kurths, Moreno, & Zhou, 2008; Khambhati, Davis, Lucas, Litt, & Bassett, 2016):

$$\begin{array}{c}S=\frac{{\lambda }_2}{{\lambda }_N}\end{array}$$ (7)

The Laplacian matrix is computed as L = D − W, where W is the adjacency matrix, D is the diagonal matrix of nodal strengths, and the strength of a node is the sum of all of that node's connection weights (Arenas et al., 2008).

2.5. Statistical analysis of graph measures

The test–retest reliability of the graph measures across the three MEG sessions for each FC metric, frequency band, and network density level in the sensor and source spaces was evaluated with the intraclass correlation coefficient (ICC) (McGraw & Wong, 1996; Shrout & Fleiss, 1979). The ICC(3,1) corresponds to a two‐way mixed effects model and was used as a measure of the test–retest reliability as per the suggestion made in Chen et al. (2018). For each graph measure, a two‐way analysis of variance (ANOVA) model was fit to an 89‐by‐3 design matrix with rows representing individual subjects and columns representing individual MEG sessions. The ICC(3,1) was computed from the ANOVA model using the following equation (McGraw & Wong, 1996; Shrout & Fleiss, 1979):

$$\begin{array}{c}\mathrm{ICC}=\frac{\mathrm{M}{\mathrm{S}}_R-\mathrm{M}{\mathrm{S}}_E}{\mathrm{M}{\mathrm{S}}_R+\left(k-1\right)\mathrm{M}{\mathrm{S}}_E}\end{array}$$ (8)

where MS _R is the mean square for rows, MS _E is the residual mean square, and k is the number of MEG sessions. Although the ICC is theoretically bounded by 0 and 1, negative values can still occur in practice and are reported in this study for clarity (Chen et al., 2018). Following the common practice in previous studies on the test–retest reliability of graph measures (Hardmeier et al., 2014; Jin et al., 2011; Kuntzelman & Miskovic, 2017), the reliability was scored as poor (ICC < 0.4), fair (0.4 ≤ ICC < 0.6), good (0.6 ≤ ICC < 0.75), or excellent (ICC ≥0.75). 95% confidence intervals were estimated for the ICC values using the cluster bootstrap procedure with 10,000 repetitions (Field & Welsh, 2007; Ukoumunne, Davison, Gulliford, & Chinn, 2003).

A permutation procedure was used to test whether the reliability of the graph measures at each network density level was significantly different (p < .05) between the proportional and OMST thresholding methods. An empirical null distribution for the difference between the ICC of the two thresholding methods was generated by randomly permuting the elements of the design matrix across the two methods, computing the ICC for each method, and taking the difference between the two ICC values. This was repeated 10,000 times. The p‐values of the permutation test were false discovery rate (FDR)‐adjusted for 40 density levels (Benjamini & Hochberg, 1995). An overall optimal density level of 100% was chosen based on the reliability scores of the graph measures at the different density levels.

Rather than applying a threshold with the same density to the adjacency matrices of all the MEG sessions, other studies have proposed using a data‐driven thresholding approach based on maximizing the global cost efficiency (GCE) to determine an optimal density for each session independently (Achard & Bullmore, 2007; Bassett et al., 2009; Dimitriadis, Salis, et al., 2017). The ICC(3,1) and the permutation procedure described previously were used to compare the graph measure reliability obtained at a 100% density level to the reliability obtained using the GCE approach for both the proportional and OMST thresholding methods. Before computation of the graph measures, an optimal density was chosen for each MEG session and thresholding method by maximizing the GCE over density levels ranging from 2.5 to 100% in 2.5% steps. The p‐values of the permutation test were FDR‐adjusted for three pairwise comparisons (Benjamini & Hochberg, 1995).

At a density level of 100%, the Spearman rank correlation was used to test for a significant association (p < .05) between the graph measures of the sensor and source spaces for each FC metric and frequency band. Before computing the rank correlation, the graph measures were averaged across all the MEG sessions for each subject. The p‐values of the correlation were FDR‐adjusted for four graph measures, three FC metrics, and six frequency bands (Benjamini & Hochberg, 1995).

2.6. Software implementation

The data analysis was implemented using in‐house software developed in the MATLAB R2018b environment (MathWorks Inc., Natick, MA) and adapted from the following open‐source toolboxes. The FieldTrip toolbox v20180905 (Oostenveld, Fries, Maris, & Schoffelen, 2011) was used to preprocess the MEG data, perform beamformer source reconstruction, and compute the dwPLI. The MEG‐ROI‐nets toolbox v2.0 (Colclough et al., 2015) was used to compute the AEC and lcAEC. The Brain Connectivity Toolbox v20170115 (Rubinov & Sporns, 2010) was used to apply the proportional weight thresholding method and compute the GE, CPL, and T. A custom MATLAB function, adapted from the topological filtering networks toolbox (Dimitriadis, Salis, et al., 2017), was written to apply the OMST thresholding method. The Statistics and Machine Learning Toolbox of MATLAB R2018b was used to perform the statistical analysis of the graph measures. Custom MATLAB functions were written to implement the S, ICC, and GCE.

3. RESULTS

3.1. Graph measure reliability for OMST versus proportional thresholding

The ICC versus density response of the graph measures in the source space for the theta and alpha bands is shown in Figures 2 and 3, respectively. The response in the source space for the other frequency bands and in the sensor space for all the frequency bands follows similar trends and is provided as supplementary material (Figures S1–S10).

FIGURE 2.

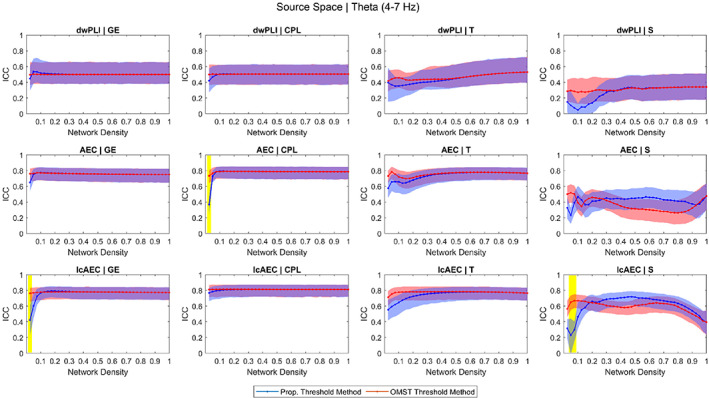
Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the source space for the theta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, false discovery rate [FDR]‐adjusted) between the proportional and OMST thresholding methods. Similar plots are provided as supplementary material (Figures S1 – S10) for all the frequency bands in the sensor and source spaces

FIGURE 3.

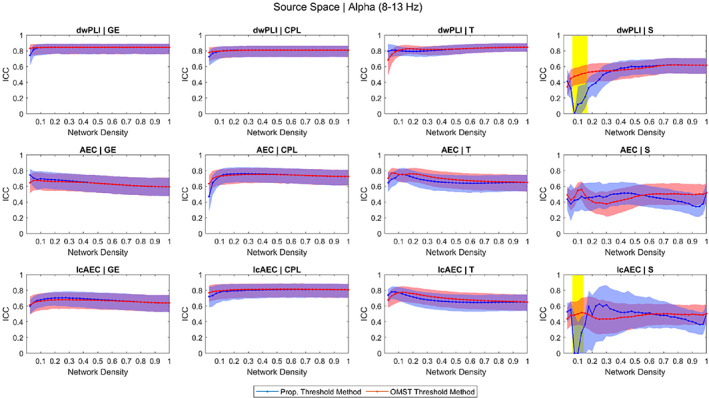
Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the source space for the alpha band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, false discovery rate [FDR]‐adjusted) between the proportional and OMST thresholding methods

In the 20–100% density range, there was not a large variation in the ICC of the GE, CPL, and T across the different density levels for any of the 36 parameters (three FC metrics and six frequency bands in the sensor and source spaces). Likewise, the reliability of the GE, CPL, and T was not significantly different between the proportional and OMST thresholding methods at any of the levels in the 20–100% density range. However, at low density levels (<10%), the reliability of the GE and CPL for a small number of the parameters (six for the GE, four for the CPL) was significantly greater for the OMST than for the proportional thresholding method. Examples of this include, in the source space, the reliability of the GE for the lcAEC in the theta band and the reliability of the CPL for the AEC in the theta band.

In the 20–100% density range, the ICC versus density response of the S varied considerably for the different parameters. For some of the parameters, the reliability was not significantly different between the OMST and proportional thresholding methods while, for other parameters, the reliability was significantly lower or greater for the OMST than for the proportional thresholding method. However, at levels in the lower (<20%) density range, the reliability of the S for 26 out of the 36 parameters was significantly greater for the OMST than for the proportional thresholding method. Examples of this include, in the source space, the reliability of the S for the lcAEC in the theta band and the reliability of the S for the dwPLI and lcAEC in the alpha band.

For most of the parameters (24 for the GE, 33 for the CPL, 19 for the T, 23 for the S), the reliability score at a 100% density level was better than or the same as the score at lower density levels. Therefore, an overall optimal density level of 100% was chosen and used for the results presented in the following sections (Sections 3.2 and 3.3). The ICC values (along with their 95% bootstrap confidence intervals) for all the density levels and for the GCE‐proportional and GCE‐OMST approaches are provided as supplementary material in a CSV file.

A comparison of the ICC of the graph measures computed using the no threshold (i.e., 100% density), GCE‐proportional, and GCE‐OMST thresholding approaches in the source space for the lcAEC is shown in Figure 4. Figures showing the comparison for the other FC metrics in the source space and for all the FC metrics in the sensor space are provided as supplementary material (Figures S11–S15). The optimal density (median [IQR] across all the MEG sessions) determined from the GCE‐proportional and GCE‐OMST approaches is provided as supplementary material (Table S1). For all the parameters, the reliability of the GE and CPL and, for 27 out of the 36 parameters, the reliability of the T were not significantly different between any of the three thresholding approaches. For most of the parameters, the reliability of the S was significantly lower for the GCE‐proportional approach than for both the no threshold (11 for the dwPLI, 1 for the AEC, and 10 for the lcAEC) and GCE‐OMST (10 for the dwPLI, 3 for the AEC, and 7 for the lcAEC) approaches. For some of the parameters (3 for the dwPLI and 7 for the lcAEC), the reliability of the S was significantly greater for the no threshold than for the GCE‐OMST approach. However, for only 2 of the AEC parameters, the reliability of the S was significantly lower for the no threshold than for the GCE‐OMST approach, and there was no significant difference between the no threshold and GCE‐OMST approaches for the rest of the 10 AEC parameters.

FIGURE 4.

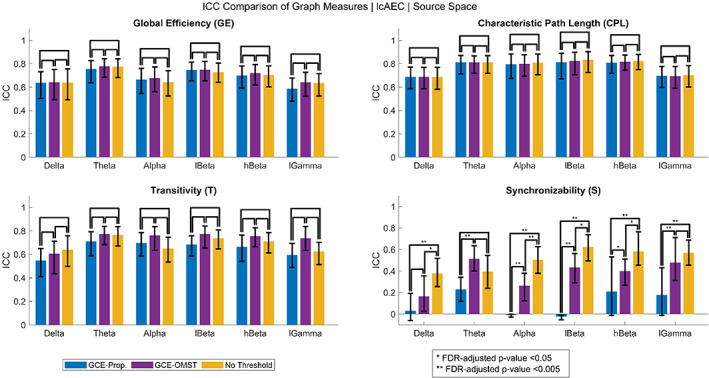
Intraclass correlation coefficient (ICC) of the four graph measures for the leakage‐corrected amplitude envelope correlation (lcAEC) in the source space obtained using no threshold (i.e., 100% density) and obtained using the global cost efficiency (GCE) approach for both the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The error bars represent 95% bootstrap confidence intervals for the ICC values. Similar bar graphs are provided as supplementary material (Figures S11–S15) for all the functional connectivity metrics in the sensor and source spaces

3.2. Comparison of the graph measure reliability for the FC metrics

The ICC of the graph measures in the sensor and source spaces for the different FC metrics and frequency bands at a 100% density level is shown in Table 2. In the source space, the ICC ranged from 0.17 to 0.85, with a mean ± SD of 0.62 ± 0.16. For each FC metric except for the dwPLI in the delta band, the reliability of the GE, CPL, and T ranged from fair to excellent. For all the FC metrics, the reliability of the S ranged from poor to good. The ICC of the S was lower than that of the GE, CPL, and T for all the FC metrics except for the dwPLI in the delta and low gamma bands.

TABLE 2.

ICC of the four graph measures (calculated at a 100% density level) for the three functional connectivity metrics and six frequency bands in the sensor and source spaces

Source space							Sensor space
	Delta	Theta	Alpha	lBeta	hBeta	lGamma		Delta	Theta	Alpha	lBeta	hBeta	lGamma
dwPLI							dwPLI
GE	.174	.500	.846*	.634*	.699*	.610*	GE	.466	.526	.825*	.303	.426	.357
CPL	.177	.505	.809*	.654*	.642*	.530	CPL	.390	.490	.768*	.549	.574	.340
T	.192	.530	.848*	.626*	.659*	.528	T	.408	.584	.828*	.373	.463	.336
S	.219	.341	.618*	.427	.486	.579	S	.492	.518	.549	.480	.431	.519
AEC							AEC
GE	.614*	.750*	.595	.704*	.680*	.631*	GE	.589	.748*	.708*	.732*	.673*	.713*
CPL	.652*	.786*	.725*	.792*	.761*	.683*	CPL	.618*	.792*	.811*	.799*	.773*	.744*
T	.639*	.767*	.648*	.736*	.716*	.632*	T	.603*	.762*	.731*	.751*	.691*	.694*
S	.447	.477	.520	.621*	.574	.365	S	.326	.459	.663*	.651*	.527	.518
lcAEC							lcAEC
GE	.638*	.773*	.640*	.728*	.704*	.635*	GE	.594	.747*	.681*	.724*	.660*	.679*
CPL	.688*	.812*	.809*	.835*	.823*	.702*	CPL	.627*	.816*	.833*	.798*	.789*	.715*
T	.641*	.765*	.650*	.737*	.712*	.626*	T	.596	.749*	.693*	.738*	.668*	.667*
S	.379	.395	.505	.623*	.583	.569	S	.325	.503	.654*	.667*	.533	.588

Note: Bold entries denote fair to excellent test–retest reliability (ICC ≥0.4). An asterisk denotes good to excellent test–retest reliability (ICC ≥0.6).

Abbreviations: AEC, amplitude envelope correlation; CPL, characteristic path length; dwPLI, debiased weighted phase lag index; GE, global efficiency; ICC, intraclass correlation coefficient; lcAEC, leakage‐corrected amplitude envelope correlation; S, synchronizability; T, transitivity.

In the sensor space, the ICC ranged from 0.30 to 0.83, with a mean ± SD of 0.61 ± 0.15. For the dwPLI, the reliability of the GE, CPL, and T ranged from fair to excellent in the theta, alpha, and high beta bands and from poor to fair in the delta, low beta, and low gamma bands. For the AEC and lcAEC, the reliability of the GE, CPL, and T ranged from fair to excellent in all the frequency bands. The reliability of the S was fair for the dwPLI and ranged from poor to good for the AEC and lcAEC. The ICC of the S was lower than that of the GE, CPL, and T for all the FC metrics except for the dwPLI in the delta, theta, low beta, high beta, and low gamma bands.

In the sensor and source spaces, the ICC of all the graph measures was mostly greater for the AEC and lcAEC than for the dwPLI except for in the alpha band. For the dwPLI, the ICC was mostly greater for the source than for the sensor space in the low beta, high beta, and low gamma bands. However, the ICC for the dwPLI was greater for the sensor than for the source space in the delta band. The ICC was largely similar for the AEC and lcAEC both within and across the sensor and source spaces. A graphical comparison of the mean ICC, averaged across the graph measures, for the three FC metrics in the sensor and source spaces is shown in Figure 5.

FIGURE 5.

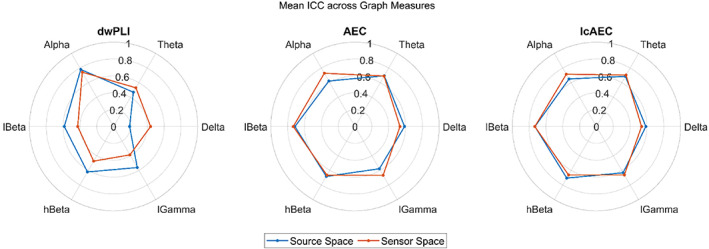
Graphical comparison of the mean intraclass correlation coefficient (ICC), averaged across the four graph measures calculated at a 100% density level, for the three functional connectivity metrics in the sensor and source spaces

3.3. Sensor versus source association of the graph measures

The Spearman rank correlation of the graph measures between the sensor and source spaces for the different FC metrics and frequency bands at a 100% density level is shown in Figure 6. The correlation was significant (p < .05) for all the graph measures except for the S of the dwPLI in the theta band and the S of the AEC in the low gamma band. For the dwPLI, the GE, CPL, and T in the alpha, low beta, high beta, and low gamma bands, the T in the theta band, and the S in the alpha and low beta bands exhibited a moderate to high correlation (rho ≥0.5). For the AEC, the GE, CPL, and T in all the frequency bands and the S in the alpha and low beta bands exhibited a moderate to high correlation. For the lcAEC, the GE, CPL, and T in all the frequency bands and the S in the theta, alpha, low beta, high beta, and low gamma bands exhibited a moderate to high correlation. The correlation was typically lower for the dwPLI than for the AEC and lcAEC, particularly in the delta and theta bands, while the correlation was largely similar for the AEC and lcAEC. For all the FC metrics and frequency bands, the correlation was lower for the S than for the GE, CPL, and T.

FIGURE 6.

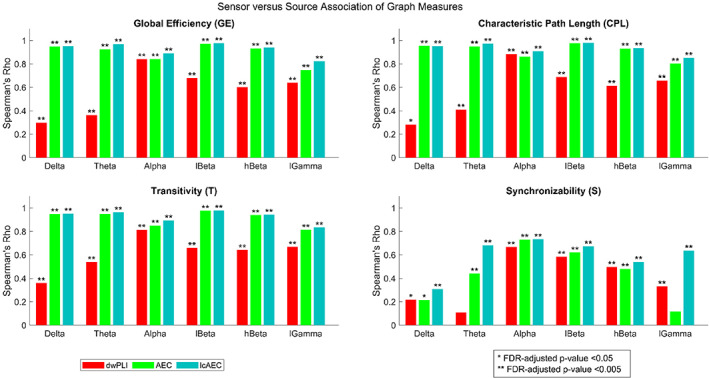
The Spearman rank correlation of the four graph measures (calculated at a 100% density level) between the sensor and source spaces for the three functional connectivity metrics and six frequency bands

4. DISCUSSION

The purpose of our study was to assess the utility of rs‐MEG global graph measures as clinical biomarkers and to provide guidance to researchers on which network construction strategies to employ. This was accomplished by quantifying the test–retest reliability and sensor versus source association of the graph measures. For computation of the graph measures, an atlas‐based beamforming approach was used to reconstruct the brain sources from the MEG data, and brain networks were constructed in both the sensor and source spaces using three different FC metrics (i.e., the dwPLI, AEC, and lcAEC). Therefore, our study examined whether more reliable graph measures were achieved when using amplitude or phase synchrony metrics and when performing sensor or source space analysis. Another open problem in graph theoretical analysis is choosing which thresholding method and network density level to apply before computing the graph measures. To address this problem, our study also examined the reliability of the graph measures over a wide range of network density levels and compared the reliability for two different thresholding methods (i.e., the proportional weight and OMST methods). An overall optimal density level was chosen based on the reliability scores of the graph measures.

At the optimal density level of 100%, the reliability of the graph measures was, in general, different between the sensor and source spaces when using the dwPLI but similar when using the AEC and lcAEC. Likewise, the sensor versus source association of the graph measures was typically greater for the AEC and lcAEC than for the dwPLI. Other rs‐MEG and EEG studies have not compared the reliability of graph measures between the sensor and source spaces for the dwPLI, AEC, and lcAEC. A rs‐EEG study found that the sensor versus source association of MST‐based global graph measures in the alpha band was low (rho <0.35) and that the association was greater for leakage‐insensitive FC metrics (i.e., the PLI and lcAEC) than for corresponding leakage‐sensitive metrics (i.e., the phase locking value [PLV] and AEC, respectively) (Lai, Demuru, Hillebrand, & Fraschini, 2018). A comparison of the sensor versus source association for the FC metrics in the other frequency bands was not reported (Lai et al., 2018). The results of Lai et al. were not consistent with our study, which found that all the graph measures had a moderate to high (rho ≥0.5) sensor versus source association in the alpha band and that this association was mostly similar for the dwPLI, AEC, and lcAEC. The inconsistency in the results may be related to the use of MST‐based graph measures, a different imaging modality (EEG vs. MEG), and/or a different source reconstruction technique (weighted minimum norm estimate [wMNE] vs. LCMV beamformer).

The reliability of the graph measures in both the sensor and source spaces was similar between the AEC and lcAEC while the reliability was mostly greater for the AEC and lcAEC than for the dwPLI. Sensor space rs‐EEG studies have examined the reliability of global graph measures for the dwPLI but not for the AEC and lcAEC (Hardmeier et al., 2014; Kuntzelman & Miskovic, 2017). Kuntzelman and Miskovic found that the reliability of the CPL, GE, and T for the dwPLI was greater (i.e., fair to excellent) in the alpha and beta bands and lower (i.e., poor to fair) in the delta, theta, and low gamma bands (Kuntzelman & Miskovic, 2017). This is comparable with our reliability results for the dwPLI except for the low and high beta bands in the sensor space (i.e., poor to fair) and the low gamma band in the source space (i.e., fair to good). On the other hand, Hardmeier et al. found that the reliability of the normalized CPL and the normalized mean CC for the dwPLI was poor to fair in the theta, low alpha, high alpha, and beta bands (Hardmeier et al., 2014). Both of these rs‐EEG studies compared the reliability of graph measures computed using the dwPLI with that of graph measures computed using other FC metrics (Hardmeier et al., 2014; Kuntzelman & Miskovic, 2017). Kuntzelman and Miskovic found that the graph measures had a greater reliability (i.e., fair to excellent) for the coherence in the delta and theta bands but a greater reliability for the dwPLI in the alpha and beta bands (Kuntzelman & Miskovic, 2017). Hardmeier et al. found that most of the graph measures had a greater reliability (i.e., fair to good) for the PLI than for the dwPLI in the theta, alpha, and beta bands (Hardmeier et al., 2014).

Sensor space rs‐MEG studies have examined the reliability of global graph measures for FC metrics other than the dwPLI, AEC, and lcAEC (Babajani‐Feremi et al., 2018; Deuker et al., 2009). Deuker et al. found that the reliability of the GE, CPL, mean CC, and S for the mutual information was poor in the low delta, high delta, theta, beta, and gamma bands and good to excellent in the alpha band (Deuker et al., 2009). However, Deuker et al. computed the graph measures based on binary, not weighted, networks and used a model‐free, information theoretic FC metric rather than a model‐based, amplitude or phase synchrony metric (Deuker et al., 2009). Babajani‐Feremi et al. found that the reliability of the CPL and T for the PLV was fair to excellent in the theta, alpha, and beta bands for both healthy subjects and patients with epilepsy (Babajani‐Feremi et al., 2018).

Although other source space rs‐MEG studies have not examined the test–retest reliability of global graph measures, they have examined the reliability of a large number of FC metrics (Colclough et al., 2016; Garces, Martin‐Buro, & Maestu, 2016). Garces et al. found that the reliability of leakage‐sensitive metrics (i.e., the PLV and AEC) was greater than that of leakage‐insensitive metrics (i.e., the PLI and lcAEC) (Garces, Martin‐Buro, & Maestu, 2016). The greater reliability of the PLV and AEC may be explained by their sensitivity to source leakage, which Garces et al. reported to have a significant effect on the reliability (Garces, Martin‐Buro, & Maestu, 2016). This agrees with Colclough et al., which also found that the reliability of leakage‐sensitive metrics (e.g., the AEC, PLV, coherence, and mutual information) was greater than that of leakage‐insensitive metrics (e.g., the PLI, wPLI, imaginary part of coherency, and lcAEC) (Colclough et al., 2016). However, in our study, the reliability of the graph measures was largely similar for the AEC and lcAEC, indicating that source leakage did not have a large effect on the reliability. This suggests that while source leakage may influence the reproducibility of the functional connections, it does not influence the reproducibility of the global network topology. Both Garces et al. and Colclough et al. reported that, for leakage‐insensitive FC metrics, the reliability of amplitude synchrony metrics was greater than that of phase synchrony metrics (Colclough et al., 2016; Garces, Martin‐Buro, & Maestu, 2016), which is comparable to our results for the reliability of the graph measures.

The reliability of the S in both the sensor and source spaces was lower than that of the GE, CPL, and T except for the dwPLI in some of the frequency bands. Additionally, the sensor versus source association of the S was lower than that of the GE, CPL, and T for all the FC metrics and frequency bands. Although this may indicate that the S is an inherently more noisy and less reliable graph measure, other studies have shown the potential of the S as a clinical biomarker. For instance, iEEG studies have employed the S as a dynamic network measure to describe different seizure states (Khambhati et al., 2016) and to predict the seizure outcome after resection surgery (Kini et al., 2019). The S has also been used as a static measure in rs‐MEG studies to characterize the abnormal network properties of patients with epilepsy (Niso et al., 2015; van Dellen et al., 2012) and patients with Alzheimer's disease (de Haan et al., 2012).

A potential factor influencing the reproducibility of the graph measures is the relationship between the functional and structural connectivity. Functional network characteristics may be more stable over time if the functional network is physically constrained by the underlying structural connections (Shen, Hutchison, Bezgin, Everling, & McIntosh, 2015). During the resting‐state, it is generally considered that structural connectivity has a greater influence on amplitude than on phase synchrony (Engel, Gerloff, Hilgetag, & Nolte, 2013). Studies have reported significant associations between structural connectivity and amplitude synchrony in multiple frequency bands for rs‐MEG (Cabral et al., 2014; Garces, Pereda, et al., 2016). However, other studies have also reported significant associations between structural connectivity and phase synchrony, particularly in the alpha band, for rs‐MEG (Meier et al., 2016; Tewarie et al., 2014) and rs‐EEG (Finger et al., 2016). Likewise, our results showed that the reliability of the graph measures was mostly greater for the AEC and lcAEC than for the dwPLI except for in the alpha band. For the dwPLI, the reliability was noticeably greater in the alpha band than in other frequency bands. The greater reliability in the alpha band may also be related to the high signal‐to‐noise ratio of the alpha band in resting‐state measurements (Martin‐Buro, Garces, & Maestu, 2016).

An optimal density level of 100% was determined from the reliability scores of the graph measures. The reliability obtained using no threshold (i.e., 100% density) was also compared to the reliability obtained using the data‐driven GCE‐proportional and GCE‐OMST thresholding approaches. The GCE approach may result in a different density for each MEG session and typically produces sparse networks with low density levels, as evidenced by the values obtained using the data in our study (i.e., 7.5–15% [IQR] across all the MEG sessions and parameters for the proportional method, 5–10% [IQR] for the OMST method). For most of the parameters, the reliability of the S was significantly greater for the no threshold and GCE‐OMST approaches than for the GCE‐proportional approach. This effect was less prominent when using the GCE approach with the AEC. Likewise, for most of the parameters, the reliability of the S at lower density levels (<20%) was significantly greater for the OMST than for the proportional method. Based on these results, the OMST method may be a more appropriate thresholding method to apply if a low density level or the GCE approach is used. A limitation of the proportional method is that the S attains values close to zero if a threshold, usually at a low density level, causes a node to become disconnected from the network (Arenas et al., 2008). This is not a limitation for the OMST method, which prevents disconnection of nodes (Dimitriadis, Antonakakis, et al., 2017). In contrast to the S, the reliability of the GE, CPL, and T did not depend heavily on which thresholding method was applied, particularly at density levels in the 20–100% range.

Studies examining the test–retest reliability of global graph measures differ on the thresholding approach used. Furthermore, a limited number of rs‐MEG and EEG studies have examined the reliability at different density levels and only for a small range of values. Deuker et al. binarized the networks by applying a proportional threshold and chose a different density level for each frequency band, with the criterion being the lowest density at which all the nodes remained connected to the network (Deuker et al., 2009). Deuker et al. also examined the reliability at density levels 5% lower and higher than the ones chosen and found that there was not a significant effect of density level on the reliability (Deuker et al., 2009). Babajani‐Feremi et al. applied a proportional threshold with an optimal density level of 10% determined from the GCE approach (Babajani‐Feremi et al., 2018) while Hardmeier et al. and Kuntzelman and Miskovic did not report applying a threshold (Hardmeier et al., 2014; Kuntzelman & Miskovic, 2017). In our study, the graph measure reproducibility was evaluated using a fixed density approach and using the GCE approach with both the proportional weight and OMST thresholding methods. Other topological filtering methods have also been employed in the literature and may be of interest for future reproducibility studies. Such methods include the use of surrogate data analysis to identify and remove statistically insignificant connections from the adjacency matrix (Dimitriadis et al., 2018).

Although our study used the graph measure reproducibility as an empirical criterion for evaluating different thresholding methods, other criteria may be just as important, if not more so, for selection of the optimal approach. For instance, studies have demonstrated that FC estimation may suffer from the presence of spurious interactions, even when using metrics insensitive to source leakage (Palva et al., 2018). Spurious interactions in the connectivity estimate may artificially inflate the reproducibility, as shown for the test–retest reliability of FC metrics susceptible to source leakage (Colclough et al., 2016; Garces, Martin‐Buro, & Maestu, 2016). Topological filtering may be beneficial for the removal of these interactions in order to reveal the true network topology. Interestingly, our study showed that the graph measure reliability at a 100% density was similar for the AEC and lcAEC. This indicates that the reproducibility of the global graph measures was not affected by the spurious correlations introduced by source leakage.

Our study focused on investigating the effect of different network construction strategies on the reliability of global graph measures. Another important consideration is the reliability of nodal graph measures. Other rs‐MEG studies have examined the reliability of nodal graph measures for the mutual information in the sensor space (Jin et al., 2011) and for the lcAEC and imaginary part of the PLV in the source space (Dimitriadis et al., 2018). Jin et al. found that nodal measures had a lower reliability in the gamma band and a greater reliability in the alpha and beta bands (Jin et al., 2011). Dimitriadis et al. found that the reliability of nodal measures was greater for the lcAEC than for the imaginary part of the PLV (Dimitriadis et al., 2018), which is similar to our results for the reliability of global graph measures and to Garces et al. and Colclough et al. for the reliability of FC metrics (Colclough et al., 2016; Garces, Martin‐Buro, & Maestu, 2016). In addition to analyzing their test–retest reliability, the use of global and nodal graph measures as biomarkers can be further supported by establishing them as heritable traits. Heritable network characteristics can be expected to have a certain degree of replicability across different scanning sessions. For rs‐MEG, studies have reported a significant effect of heritability on FC metrics in the source space (Colclough et al., 2017; Demuru et al., 2017) and on global graph measures in the sensor space (Babajani‐Feremi et al., 2018).

It is reasonable to expect that the reproducibility of FC metrics and graph measures is contingent on each step of the analysis pipeline. A rs‐EEG study examined the consistency of the imaginary part of coherency in the alpha band across several source reconstruction techniques and software packages (Mahjoory et al., 2017). Mahjoory et al. found a high consistency between the widely implemented FieldTrip and Brainstorm toolboxes when using the LCMV beamformer for source reconstruction but a lower consistency when using the wMNE (Mahjoory et al., 2017). Mahjoory et al. also found a high consistency between the LCMV beamformer and wMNE for the Brainstorm toolbox but a lower consistency for the FieldTrip toolbox (Mahjoory et al., 2017). Another methodological consideration is whether the Fourier, Hilbert, or wavelet transform is used to compute the FC metrics although there is some evidence to suggest that these approaches achieve similar results (Bruns, 2004). Studies on the reliability of global graph measures have employed the Fourier (Kuntzelman & Miskovic, 2017), Hilbert (Hardmeier et al., 2014), and wavelet transform (Deuker et al., 2009). Our study used the FieldTrip toolbox, which computes the dwPLI based on the Fourier transform, and the MEG‐ROI‐nets toolbox, which computes the AEC and lcAEC based on the Hilbert transform. Future work may be done that investigates the influence of the source reconstruction technique, spectral analysis approach, and software package on the reliability of the graph measures. Additionally, while our study demonstrated that the graph measures typically had a significant sensor versus source association, these measures only capture certain characteristics of the global network topology and may not be generalizable across different analysis pipelines. A recent study has proposed the use of an information theoretic distance measure, referred to as portrait divergence, for comparison of the global network topology irrespective of the particular pipeline used to construct the networks (Luppi & Stamatakis, 2021).

5. CONCLUSIONS

In this study, the test–retest reliability and sensor versus source association of rs‐MEG global graph measures was investigated. The reliability of the GE, CPL, and T was relatively stable across different network density levels and was similar between the proportional weight and OMST thresholding methods. The reliability of the S was dependent on the density level and, at lower density levels (<20%), was significantly greater for the OMST than for the proportional method. Based on the reliability scores, an optimal density level of 100% was chosen. At a density level of 100%, all the graph measures had acceptable reliability (i.e., fair to excellent) for most of the parameters. The GE, CPL, and T for all the parameters and the S for most of the parameters had a significant sensor versus source association. In general, the graph measure reliability and sensor versus source association was greater for the amplitude synchrony metrics (i.e., AEC and lcAEC) than for the phase synchrony metric (i.e., dwPLI). Additionally, the reliability and sensor versus source association of the GE, CPL, and T was mostly greater than that of the S. The reliability for the AEC and lcAEC was similar between the sensor and source spaces while the reliability for the dwPLI was greater for the source than the sensor space in the low beta, high beta, and low gamma bands. Overall, these results indicate that although most of the graph measures may be useful as clinical biomarkers, more reliable values are likely to be achieved when using FC metrics of amplitude rather than phase synchrony. If using phase synchrony metrics, it may be more prudent to perform the analysis in the source space.

CONFLICT OF INTEREST

The authors declare no potential conflicts of interest.

Supporting information

Figure S1 Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the source space for the delta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S2. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the source space for the low beta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S3. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the source space for the high beta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S4. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the source space for the low gamma band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S5. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the sensor space for the delta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S6. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the sensor space for the theta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S7. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the sensor space for the alpha band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S8. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the sensor space for the low beta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S9. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the sensor space for the high beta band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S10. Intraclass correlation coefficient (ICC) of the four graph measures computed using three functional connectivity metrics in the sensor space for the low gamma band across different network density levels achieved using the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The blue and red shaded areas represent 95% bootstrap confidence intervals for the ICC values. The yellow shaded area represents ICC values that were significantly different (p < .05, FDR‐adjusted) between the proportional and OMST thresholding methods.

Figure S11. Intraclass correlation coefficient (ICC) of the four graph measures for the debiased weighted phase lag index (dwPLI) in the source space obtained using no threshold (i.e., 100% density) and obtained using the global cost efficiency (GCE) approach for both the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The error bars represent 95% bootstrap confidence intervals for the ICC values.

Figure S12. Intraclass correlation coefficient (ICC) of the four graph measures for the amplitude envelope correlation (AEC) in the source space obtained using no threshold (i.e., 100% density) and obtained using the global cost efficiency (GCE) approach for both the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The error bars represent 95% bootstrap confidence intervals for the ICC values.

Figure S13. Intraclass correlation coefficient (ICC) of the four graph measures for the debiased weighted phase lag index (dwPLI) in the sensor space obtained using no threshold (i.e., 100% density) and obtained using the global cost efficiency (GCE) approach for both the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The error bars represent 95% bootstrap confidence intervals for the ICC values.

Figure S14. Intraclass correlation coefficient (ICC) of the four graph measures for the amplitude envelope correlation (AEC) in the sensor space obtained using no threshold (i.e., 100% density) and obtained using the global cost efficiency (GCE) approach for both the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The error bars represent 95% bootstrap confidence intervals for the ICC values.

Figure S15. Intraclass correlation coefficient (ICC) of the four graph measures for the leakage‐corrected amplitude envelope correlation (lcAEC) in the sensor space obtained using no threshold (i.e., 100% density) and obtained using the global cost efficiency (GCE) approach for both the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods. The error bars represent 95% bootstrap confidence intervals for the ICC values.

Table S1. The optimal density (median [IQR] across all the MEG sessions) determined using the global cost efficiency (GCE) approach with the proportional weight and orthogonal minimum spanning tree (OMST) thresholding methods for the three functional connectivity metrics and six frequency bands in the sensor and source spaces. The density levels are expressed as percentages.

Appendix S1: Supporting Information

Pourmotabbed, H. , de Jongh Curry, A. L. , Clarke, D. F. , Tyler‐Kabara, E. C. , & Babajani‐Feremi, A. (2022). Reproducibility of graph measures derived from resting‐state MEG functional connectivity metrics in sensor and source spaces. Human Brain Mapping, 43(4), 1342–1357. 10.1002/hbm.25726

DATA AVAILABILITY STATEMENT

The processing scripts and the de‐identified and processed data (i.e., adjacency matrices and graph measures) are available from the corresponding author upon reasonable request, consistent with the policy of and subject to confirmation by the Human Connectome Project data use agreement. The open‐access MEG data are available from ConnectomeDB (https://db.humanconnectome.org/app/template/Login.vm).