Intravoxel Incoherent Motion MRI in skeletal muscle: Review and future directions

Abstract

Throughout the body, muscle structure and function can be interrogated using a variety of non-invasive magnetic resonance imaging (MRI) methods. Recently, intravoxel incoherent motion (IVIM) MRI has gained momentum as a method to evaluate components of blood flow and tissue diffusion simultaneously. Much of the prior research has focused on highly vascularized organs, including the brain, kidney, and liver. Unique aspects of skeletal muscle, including the relatively low perfusion at rest and large dynamic range of perfusion between resting and maximal hyperemic states, may influence the acquisition, post-processing, and interpretation of IVIM data. Here, we introduce several of those unique features of skeletal muscle, review existing studies of IVIM in skeletal muscle at rest, in response to exercise, and in disease states, and consider possible confounds that should be addressed for muscle-specific evaluations. Most studies used segmented non-linear least squares fitting with a b-value threshold of 200 s/mm² to obtain IVIM parameters of perfusion fraction (f), pseudo-diffusion coefficient (D*) and diffusion coefficient (D). In healthy individuals, across all muscles the average ± standard deviation of D was 1.46 ± 0.30 ×10⁻³ mm²/s, D* was 29.7 ± 38.1 ×10⁻³ mm²/s, and f was 11.1 ± 6.7%. Comparisons of reported IVIM parameters in muscles of the back, thigh, and leg of healthy individuals showed no significant difference between anatomic locations. Throughout the body, exercise elicited a positive change of all IVIM parameters. Future directions including advanced post-processing models and potential sequence modifications are discussed.

INTRODUCTION

Quantification of blood flow to an organ provides insight into the underlying tissue health and can be used to understand the vascular and metabolic responses to stimuli. Blood flow to skeletal muscle is of particular interest as there is large variation between the resting and active states, there is a strong link between muscle activity and blood flow, and the resting and exercise response magnitude and temporal kinetics may be disturbed in pathologic conditions. Many non-invasive methods have been developed for the measurement of blood flow, including several magnetic resonance imaging (MRI) approaches. These MRI methods, including phase contrast, arterial spin labeling (ASL), dynamic contrast-enhanced (DCE) MRI, and intravoxel incoherent motion (IVIM) provide insight into somewhat different aspects of the blood flow and vascular responses. Each has strengths and weaknesses in both their characterization of the vascular space(s) as well as in the description (or lack thereof) of the surrounding muscle myofibers. For instance, phase contrast MRI can be used to quantify bulk arterial and venous blood flow velocity in units of cm/s (1). Evaluation of flow waveforms over the cardiac cycle can provide insight into the overall vascular resistance, where it has been shown that the normal triphasic waveform is augmented in pathologies like peripheral artery disease (PAD) (2,3). Like phase contrast, ASL can quantify blood flow in physiologically relevant units; however, rather than evaluating bulk blood flow, ASL provides a measure of tissue perfusion in mL blood/min/100g tissue (4). In ASL, a magnetic label is applied to arterial blood, allowing the blood to act as an endogenous tracer as it travels from the arteries/arterioles into the capillary bed. ASL can quantify tissue perfusion in response to various vasoactive stimuli such as induced ischemia (5,6), or exercise (7–9); however, the measurement of baseline perfusion remains difficult due to the very low perfusion of skeletal muscle at rest. DCE measures signal intensity changes after administration of a T1-shortening contrast agent and using tracer kinetic models. The change in signal intensity over time can be used to estimate perfusion, blood flow velocities, and provide insight into vascular permeability (10,11).

IVIM, on the other hand, uses diffusion-encoding gradients to sensitize the acquisition to incoherent motion of the water molecules (12). IVIM is sensitive to not only the intravascular motion of blood flowing in the capillaries, but also the molecular diffusion of water in the intracellular and extracellular (together called extravascular) spaces. The scale of motion in the intravascular and extravascular spaces differs by approximately an order of magnitude, allowing the two pools to be separated in post-processing. Therefore, IVIM provides simultaneous insight into both blood flow and molecular diffusion of the tissue (13).

IVIM has been broadly applied to investigate tissues that are highly vascular. However, muscle has unique anatomical features related to its vascular function and dynamic range of perfusion states that warrant consideration for both the acquisition and post-processing of IVIM data. Here, the body of work on IVIM studies in skeletal muscle is reviewed and their results are discussed in the context of the current understanding of the skeletal muscle microvasculature. We seek to highlight methodologic considerations for acquisition and analysis of IVIM data, and to discuss specific issues for future studies using IVIM to evaluate blood flow and activation in skeletal muscle.

Unique Features of Healthy Skeletal Muscle

Microvascular densities in skeletal muscle of healthy humans are roughly equivalent to other tissues such as kidney (14), cancers/tumors (15), and brain (16); however, it receives a much lower proportion of the circulating blood volume at rest (1–7ml/100g tissue/min) (17). Figure 1 shows the relationship between myofibers and capillaries from a preclinical microscopy study (18). The dynamic range of blood flow in response to a vasoactive stimulus is quite large, and blood flow can increase by 20 to 50-fold when approaching hyperemia (19–21). The blood flow response range is primarily driven by the physiological need to balance mean arterial pressure with muscle oxygen demand through modulation of perfusion pressure and vascular tone (22). In humans, this reaction is initiated with redistribution of blood flow from visceral organs to skeletal muscle and followed by vasodilation of the vascular bed with contraction, creating a “muscle pump” that permits rapid increases in perfusion pressure (23). The most functionally significant pressure differentials are observed at the level of the smallest arterioles which are mostly vasoconstricted at rest, allowing for substantial increases in blood flow during vasodilation (Figure 2a,b), in contrast to capillaries which are 100% perfused with plasma and >80% perfused with red blood cells at rest (24). Across species, this process is influenced by body size and branch order scaling of the vasculature (25).

Figure 1.

Preclinical fluorescence microscopy images of murine anterior tibialis muscle showing longitudinal (a) and transverse (b) views of skeletal muscle fibers (green) and interdigitated microvasculature (red). Figure taken from (18) with permission.

Figure 2:

Representative illustrations of vascular anatomy in healthy muscle (A), muscle after an exercise stimulus (B), and in pathological muscle (C). Healthy muscle is characterized by larger arterioles and venules interfacing with smaller, tortuous capillaries along the length of myofibers. In the presence of a stimulus, vasodilation occurs primarily at the interface between the arterioles and capillaries, and arteriole and capillary diameter increases along with increases in myofiber intracellular fluid. In pathological muscle, myofiber diameters and arteriole and capillary rarefaction is observed, and myofibers are interspersed with fatty (yellow) and fibrotic (grey) tissue.

Blood flow heterogeneity within and between muscles also contributes to the dynamic response range during vascular challenges (17). Intra- and inter-muscle blood flow heterogeneity is influenced by factors such as a) variability in location of microvascular units as compared to motor units within a muscle, b) heterogeneity in fiber type composition and associated vascular control mechanisms, and c) spatial heterogeneity of motor unit recruitment during muscle contraction (26). The spatial mismatch between domains of microvascular and motor units within a muscle is evidence that capillaries are not randomly dispersed throughout the muscle. The functional result of this spatial heterogeneity is that during a non-tetanic or partial muscle contraction, only certain muscle fibers are perfused, leading to non-uniform distribution of capillary blood (27). However, with sustained motor unit activation, a hierarchical recruitment strategy is used for increasing muscle contraction force, and perfusion reaches homeostasis after a period of time to meet oxidative demand (28,29). This perfusion response directly relates to the metabolic demands of muscle, which can be observed in the distribution of slow-twitch oxidative, fast-twitch glycolytic, and mixed (fast-twitch oxidative, glycolytic) fiber types (30). Because the hierarchical recruitment of motor units is initiated by the fiber types with the most oxidative capacity (31), this further introduces fiber-type specific differences in vascular control. Indeed, larger values of diffusion tensor imaging (DTI) metrics fractional anisotropy and mean diffusivity of muscles have been observed in muscles with a higher proportion of slow-twitch oxidative fibers (32), although the spatial heterogeneity of oxygen consumption seems to be more influenced by fiber diameter than fiber type (33).

Despite heterogeneity in blood flow capacity, the anatomical structures of capillaries within human skeletal muscle are relatively well established and constant. Although the trajectory of capillaries is tortuous, the organization of muscle fibers in parallel provides an ultrastructural boundary within which the capillaries can travel. As such, the relative anisotropy of capillaries increases and decreases along with muscle extension and contraction respectively. Median capillary densities have been shown to range from 300–500 capillaries/mm², with diameters ranging from 4–8 μm (34). The capacity for capillary dilation in response to an acute bout of exercise or other vascular challenge has not been well described, however general vasodilation in response to exercise is thought to be on the order of 20–30% of the resting diameter. A similar magnitude increase (20%) is observed in capillary density as a result of long-term adaptations to exercise training (35), reflecting increases in long-term oxidative capacity.

The Influence of Pathology

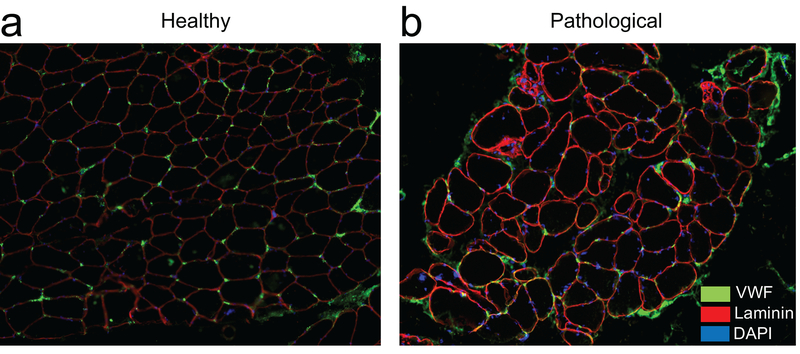
The microvasculature of skeletal muscle is further influenced by pathological conditions, making IVIM an attractive tool to distinguish between different patient populations and obtain mechanistic insight into disease processes. Whether resulting from a primary injury to the muscle itself or secondary to other local and systemic pathologies, inflammation, atrophy, and tissue compositional change (e.g. fatty infiltration, fibrosis) are the most commonly observed muscle adaptations (Figure 2c, Figure 3). Inflammation is a common feature of primary musculoskeletal conditions such as myositis, muscular dystrophy, and arthritis, resulting in increased intracellular and extracellular fluid content (cellular swelling), increased cellular and vascular permeability, and in some cases membrane disruption (36,37). Despite increases in vascular permeability and fluid content, capillary densities are lower in chronically inflamed muscle (38), and heterogeneity of capillary network spacing is greater (39). Figure 3 shows example histologic sections of healthy (Figure 3a) and pathologic (Figure 3b) human spine muscle with stains illustrating some of these features.

Figure 3.

Representative immunohistochemical cross-sections of human paraspinal muscle from normal (A) and pathological (B) human paraspinal muscle illustrating the distribution and location of capillaries (green) in-between myofibers (outlined in red). Myofiber nuclei are stained in blue. Reduced capillary density and clustering as well as heterogeneous myofiber size and distribution can be observed in the pathological sample.

Atrophy, the reduction of fiber area as a result of disuse, denervation, or pain, directly influences capillary density due to changes in capillary: fiber ratios. Reductions in arteriole and capillary density typically precede reductions in fiber area and are commonly observed with aging and sedentary lifestyle, with capillary densities in individuals over 60 years of age being 12–25% lower than their younger (20–30 years) counterparts (40). In addition, blood flow to skeletal muscle may be secondarily disturbed due to cardiovascular diseases such as heart failure or PAD. The functional result of both capillary rarefaction and reduced fiber areas in these contexts of atrophy is that muscle fiber activity-induced perfusion is reduced 7 to 14-fold (29).

A secondary consequence of chronic inflammation and atrophy is a change in tissue composition of the muscle compartment, with fatty infiltration being a common occurrence (41). Increases in fat deposition within and between muscle fibers changes the metabolic and oxidative demands of the tissue (42), and also influences microvascular organization (43). Additionally, since adipocyte morphology and deposition is less organized than parallel myofiber microstructure, there is a reduction in overall tissue anisotropy as well as in lower diffusion and pseudo-diffusion coefficients, with little impact on perfusion fraction (44).

IVIM THEORY

The theory behind IVIM has been thoroughly reviewed elsewhere (13,45,46). Here, we briefly summarize the underlying principles. Application of magnetic field gradients will lead to spatially dependent accrual of phase. A pair of bi-polar gradients, in the absence of motion, will impart and then exactly reverse the phase accumulated between the first and second gradient modules, leading to zero net phase. In the presence of motion, both at the macroscopic and microscopic scales, the spins will experience different magnetic field histories from the first to second gradient module, leading to net phase accumulation, phase dispersion, or both. With coherent motion, this effect can be used to quantify the velocity of the moving spins (e.g. phase contrast (1,47)). However, if the motion is incoherent within a voxel, such as the case for capillary blood flow and molecular diffusion, then the destructive coherence of phase leads to relative signal loss (12).

The strength and temporal separation of the gradient lobes will determine how sensitive the measurement is to motion, described by the b-value in s/mm²: b = γ² G² δ² (Δ-δ/3), where γ is the gyromagnetic ratio, G the gradient amplitude, δ the gradient duration, and Δ the temporal separation between gradients. With higher b-value, the measured signal becomes increasingly sensitive to smaller net motion. In IVIM, a voxel is considered to be composed of two signal sources: microstructural and intravascular hydrogen nuclei. The scale of translational motion from those two sources is quite different, as microstructural (extravascular) displacement is governed by Brownian motion, while the average displacement of blood water in the capillaries is much larger due to convective and pulsatile flow and the complexity of the vascular network. This leads to two distinctly different diffusion coefficients: D, the molecular diffusion coefficient, and D*, the pseudo-diffusion coefficient representing the mean squared displacement of water in the capillaries. Therefore, the normalized signal decay as a function of b-value takes the form of a weighted bi-exponential:

$$\mathrm{S}\left(\mathrm{b}\right)/{\mathrm{S}}_0=\mathrm{f}{\mathrm{e}}^{-\mathrm{b}\mathrm{D}*}+\left(1-\mathrm{f}\right){\mathrm{e}}^{-\mathrm{b}\mathrm{D}},$$

where S₀ is the equilibrium magnetization without diffusion sensitizing gradients, and f is the perfusion fraction, representing the relative contribution of intravascular versus extravascular signal sources (Figure 4).

Figure 4.

Example of signal decay as a function of b-value if considering only the extravascular (e.g. molecular diffusion, D) hydrogen molecules (top), only the intravascular (e.g. pseudo-diffusion, D*) hydrogen molecules (middle), and total imaging voxel where signal decay is a bi-exponential of the molecular diffusion and pseudo-diffusion processes, weighted by the perfusion fraction (f). Simulated parameters for D, D*, and f were 1.46 ×10⁻³ mm²/s; 29.7×10⁻³ mm²/s; and 11.1%, respectively, corresponding to the mean values observed in healthy individuals.

Fitting the bi-exponential equation to estimate IVIM parameters f, D*, and D requires acquisition of diffusion weighted data over a range of b-values. Various fitting strategies can be employed to obtain the parameters of interest, generally categorized as constrained non-linear least squares (NLLS), Bayesian, or most recently deep learning approaches (48). Within the constrained NLLS, all IVIM parameters can be obtained from a single step or a segmented approach can be used. Because D* is generally thought to be at least an order of magnitude greater than D, the intravascular contribution to the bi-exponential decay is negligible at high b-values. When employing a segmented NLLS fitting approach, the high b-value regime can be used to solve for D (and sometimes f), and with D fixed, all data can be used to solve for f and D*, generally reducing the complexity of the problem. In addition to the parameters obtained directly from the bi-exponential fitting, some studies also report the product of f and D* (fD*), thought to represent the total fluid flux, analogous to parameters of perfusion weighted imaging as demonstrated in the context of cerebral blood flow (49).

SYSTEMATIC REVIEW

Literature Search

A total of 51 studies were identified through PubMed and Embase searches conducted through May 20, 2021. We excluded articles that were not written in English, did not report IVIM parameters in humans, and case reports of only a single subject. These criteria excluded 16 studies, leaving a total of 37 reports of IVIM parameters in skeletal muscle throughout the body, detailed in Table 1. Examples of IVIM parameter maps in the calf (50) are illustrated in Figure 5.

Table 1.

List of all reports of IVIM in skeletal muscle at rest. Numerical results are reported as mean (SD) unless otherwise specified.

Study	Field (T)	Anatomy	Stimulus?	Participant characteristics	D (×10−3 mm2/s)	f (%)	D* (×10−3 mm2/s)
Morvan, et al. (51)	0.5	Forearm – flexor digitorum	Exercise	Healthy	1.74 (0.11)	3.6 (1.3)	46 (37)
Yamada, et al. (148)	1.5	Abdominal muscle – not specified		Hepatic lesions	0.69 (0.28)	23 (16)
Yao, et al. (59)	1.5	Leg – combined tibialis anterior, tibialis posterior, and medial gastrocnemius muscles	Exercise & cuff compression	Healthy		−0.2 (2.7)
Qi, et al. (44)	1.5	Thigh – RF, VL, VI, VM, BF, ST, SM, AD		Healthy (unaffected muscles)	1.44 (0.1)	10.6 (5.2)	19.4 (12.1)
				Patients with DM, PM, amyloid angiopathy (inflamed muscles)	1.78 (0.17)	8.1 (4.5)	35.0 (36.3)
Karampinos, et al. (98)*	3	Leg – MG		Healthy		~2.54
Sasaki, et al. (149)	1.5	Masticator – masseters	Exercise	Healthy	1.26 (0.23)	17 (10)	21.3 (18.5)
Hiepe, et al. (52)*	3	Paraspinal muscle – right erector spinae	Exercise	Healthy	1.69 (0.04)	5.2 (2.3)
Jerome, et al. 2014 (65)	1.5	Paraspinal – not specified		Healthy	1.25 (0.03)	11.8 (0.4)	48 (2)
Filli, et al. (60)*	3	Forearm – FDS/FDP	Exercise	Healthy	1.45 (0.09)	3 (1)	28.5 (11.4)
Filli, et al. (150)	3	Paraspinal – erector spinae		Healthy	1.58 (0.06)	10.22 (3.05)	16.32 (1.72)
Wurnig, et al. (63)	3	Paraspinal – erector spinae		Healthy	1.36 (0.04)	7.4 (3)	21.7 (19)
Nguyen, et al. (151)*	3	Shoulder - Subscapularis	Exercise	Healthy	1.52 (0.04)	10.17 (2.21)	13.63 (3.31)
Wurnig, et al. (64)+	3	Paraspinal – erector spinae		Healthy	~ 1.4	~ 20	~18
Xu, et al. (152)	3	Masticator – masseter		Supra-hyoid tumor	1.59 (0.13)	14 (7)	287.8 (218.7)
Becker, et al. (153)	3	Neck - sternocleidomastoid		Healthy & 1 patient with autonomous adenoma in the left thyroid lobe	0.5 (0.21)	26.5 (9.3)	58.3 (10.9)
Cameron, et al. (82)	3	Thigh – hamstring muscles		Healthy	1.87 (0.08)	3.3 (1.9)	30.4 (37.7)
Ciritsis, et al. (154)	3	Paraspinal – erector spinae		Healthy	1.35 (0.20)	18 (12)	9 (9)
De Luca, et al. (62)*$	3	Leg – medial gastrocnemius		Healthy		6 (2)	14.16 (2.88)
Hilbert, et al. (54)	1.5	Leg – upper calf muscle		Children with known or suspected juvenile idiopathic arthritis	1.64 (0.09)	9.6 (1.8)
Kang, et al. (55)	1.5	Masticator – not specified		Healthy	1.48	10.3	51.38
Ngamsom, et al. (61)+	3	Masticator – lateral pterygoid		Patients with temporo-mandibular joint disorder	~0.59	~33
Nguyen, et al. (155)*	3	Shoulder - supraspinatus	Exercise	Healthy	1.45 (0.04)	6.36 (1.18)	10.77 (3.08)
Mastropietro, et al. (50)*	3	Leg – gastrocnemius	Exercise	Healthy	1.54 (0.05)	6.8 (1.3)	21 (6.7)
Ohno, et al. (156)*	3	Leg – medial gastrocnemius		Healthy	1.48 (0.13)		17.9 (3.5)
Phi Van, et al. (56)	3	Paraspinal – erector spinae		Healthy	1.38 (0.20)	13 (3)	8.07 (3.06)
Sigmund, et al. (76)*	3	Thigh - quadriceps		Healthy	1.46 (0.15)	9.01 (3.36)	39.21 (18.66)
				Patients with DM	1.43 (0.18)	8.75 (2.93)	31.38 (14.90)
Suo, et al. (73)*%	3	Leg – gastrocnemius	Cuff compression	Healthy	1.61 (1.50–1.70)	4.7 (3.6–5.3)	19.8 (17.1–21.3)
				Patients with PAD	1.51 (1.33–1.88)	5.6 (3.7–7.7)	17.3 (12.5–21.9)
Yoon, et al. (78)*	3	Thigh – anterior compartment (RF, VL, VM, VI)		Healthy	1.56 (0.05)	8.7 (1.8)	26.26 (4.7)
Adelnia, et al. (53)*	3	Thigh – RF	Exercise	Healthy	2.19 (0.03)	4.63 (0.62)	214.2 (15.5)
Jungmann, et al. (157)*	1.5	Lower extremity – all muscles (gluteal to foot)	Exercise	Healthy	1.2 (0.18)	15.7 (6.4)	10.9 (4.8)
Thapa, et al. (158)	1.5	Gluteus – gluteus maximus		Patients with cervical lesions	1.24 (0.11)	0.23 (0.04)	16.44 (3.9)
Federau, et al. (75)	1.5	Paraspinal – not specified	Exercise	Healthy (right side)	1.4 (0.2)	10 (4)	32 (22)
				Patients with AIS (convexity)	1.4 (0)	16 (10)	40 (48)
Ogura, et al. (72)*+	1.5	Thigh – not specified	Exercise	Healthy		~17	~18
Ohno, et al. (74)	3	Leg – tibialis anterior	Exercise	Healthy	1.55 (0.19)	6.5 (3)	8.9 (4.8)
Ran, et al. (77)%	3	Thigh – individual muscles not reported		Patients with DM, PM	1.53 (1.41–1.64)	7 (4–10)	9.41 (5.16–15.90)
				Patients with MD	1.38 (1.15–1.49)	9 (5–12)	9.06 (4.72–14.22)
Riexinger, et al. (57)*	3	Leg - Gastrocnemius	Exercise	Healthy	1.8 (0.06)	5.4 (1.2)
Kemesiene, et al. (58)	3	Back – Psoas	Fluid deprivation & after water intake	Healthy	0.86 (0.22)	24 (17)	4.67 (4.74)

^*Manuscript includes results for multiple muscles, see referenced paper for additional details.

⁺Results are estimated from plots

^$Results from supplemental material of the original paper

^%Results are median (range)

Muscles: Thigh: Rectus femoris (RF), vastus lateralis (VL), vastus intermedius (VI), vastus medialis (VM), biceps femoris (BF), semitendinosus (ST), semimembranosus (SM), adductor (AD); Leg: medial gastroc (MG); Forearm: flexor digitorum superficialis (FDS), flexor digitorum profundus (FDP)

Pathologic conditions: Dermatomyositis (DM), peripheral artery disease (PAD), adolescent idiopathic scoliosis (AIS), polymyositis (PM), muscular dystrophy (MD)

Figure 5.

Example IVIM parameter maps in the calf of a healthy volunteer at rest and in response to a bout of intermittent plantar flexion contractions. Increases of f, D*, and D are observed during exercise. Figure from (50) with permission.

Summary of Pulse Sequence Parameters

Across these studies summarized in the table above, a variety of pulse sequences parameters have been employed to encode the IVIM signal into the measured data, generally acquired with a diffusion-weighted (DW) spin echo acquisition. Of the 37 studies, one was conducted at 0.5T (51), 11 at 1.5T, and 25 at 3T. The average TR/TE for data acquired at 1.5T was 3990/79ms and at 3T was 4278/65ms. It should be noted that these acquisitions are heavily T2-weighted given the short T2 of muscle. The number of signal averages was not always reported, but in the 22 studies where available, the mean was 3.7±2.1. In addition, several studies varied the number of averages depending on whether data were acquired at rest or following exercise (52,53), or as a function of b-value (54–58). Signal to noise ratio (SNR) was not often reported and may be important to place these in vivo results in context (53).

Fitting Method & b-values

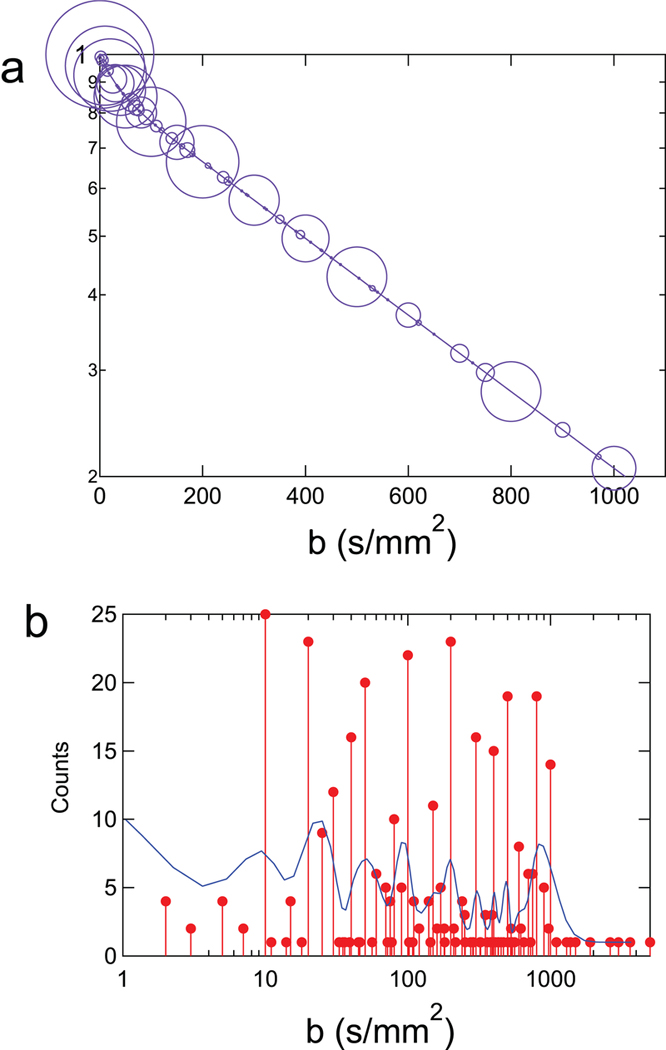
On average, data were acquired with 12±5 b-values. Almost all studies applied diffusion-encoding gradients along the three principal axes. A few notable exceptions: Yao, et al. applied diffusion encoding gradients on all three axes simultaneously, which rather than imparting trace weighting, will sensitize the data to motion along some single arbitrary direction (59), and Adelnia, et al. (53) and Riexinger, et al. (57) both applied diffusion encoding gradients along the slice-selection direction only. As seen in Table 1, both Adelnia, et al. and Riexinger et al.’s reported coefficients were higher than others, possibly due to the relative alignment of the capillaries, muscle fibers, and diffusion sensitizing direction. The minimum b-value ranged from 0.5 to 50 s/mm², with an average of 15±12 s/mm². Most studies used a maximum b-value of 800 s/mm², however the maximum b-value ranged from 500 (50,60,61) to 1300 (62) s/mm². Figure 6 illustrates the frequency of b-value sampling across studies.

Figure 6.

Summary depiction of distribution of b-values employed in skeletal muscle IVIM studies in the literature. (a) Biexponential signal decay curve is simulated based on global average reported IVIM parameters (see text) and size of circle indicates number of studies employing a given b-value. (b) Histogram presentation of the b-value distribution in the literature (original counts and smoothed distribution) showing similar amount of sampling in the microcirculation regime (10< b < 200 s/mm²) and the microstructure regime (200<b<1000 s/mm²).

Nearly all studies used a constrained NLLS fitting method to obtain the IVIM parameters from the diffusion-weighted data. Most employed a segmented approach, first solving for D from the high b-value data where the pseudo-diffusion effect has already dissipated. Subsequently, f and D* can be solved for simultaneously via NLLS, with D fixed from the prior step, or can be estimated individually by extrapolating back to b=0 s/mm² and using the offset between the obtained y-intercept and S(b=0)/S₀=1 to determine the perfusion fraction, f. Of the studies summarized herein, 28 used a segmented NLLS approach.

In the 16 studies where the b-value threshold was reported, the average was b=212±88 s/mm², and 200 s/mm² was the most common threshold (n=9). Two studies (63,64) specifically evaluated the optimal threshold value by iterating through solutions obtained first with all b-values, then incrementally only the data from the highest b-values until the lowest sum of squares residual was obtained. Using this approach, the optimal threshold was b=150 s/mm² (63) and b=245 s/mm² (64) for paraspinal muscles at rest. Importantly, we can assume that the pseudo-diffusion signal would decay faster during or following exercise, given that blood flow velocity increases during the post-exercise hyperemic state. Thus, these thresholds set by Wurnig, et al. (63,64) would represent a conservative value for post-exercise evaluations. Assuming a threshold of 200 s/mm², data were acquired with an average of 6±3 in the low and 5±2 in the high b-value regime.

In the studies reviewed here, only one reported IVIM parameters derived from a Bayesian fitting approach to obtain f and D* following NLLS fitting of high b-value data to fit for D (65). A prior study in the pancreas (66) directly compared results between constrained NLLS approaches and Bayesian where they observed improved reliability of results using a Bayesian approach, but noted that it did not significantly out-perform a NLLS approach that used a fixed value for D*. A recent study by Koopman, et al. (48) evaluated repeatability of IVIM parameters in the tonsils and pterygoid muscles using a variety of fitting methods including NLLS fitting, Bayesian, and a neural network approach. They found that both Bayesian and their neural network approach outperformed NLLS in terms of having lower within-subject coefficient of variations, however the average IVIM parameter values were not provided. Given the improved repeatability observed by Koopman, et al. in muscle (48), and reliability observed in other organs (66), Bayesian approaches may prove useful for estimation of IVIM parameters in future investigations.

Results in Healthy Individuals

A total of 30 studies reported IVIM parameters in skeletal muscle at rest in healthy volunteers. We excluded the study from Yao, et al (59) as the reported f at rest was negative. The rest of the studies are summarized as a function of anatomic location in Figure 7. Across all studies, the average ± standard deviation of D was 1.46±0.30 ×10⁻³ mm²/s, D* was 29.7±38.1 ×10⁻³ mm²/s, and f was 11.1±6.7%. Comparing the average parameter values between muscles with at least three reported values using ANOVA, no significant differences were observed between paraspinal, thigh, and calf muscles in terms of the average reported parameter values of D (p=0.15), f (p=0.38), or D* (p=0.25).

Figure 7.

IVIM parameters D (top), D* (middle) and f (bottom) in healthy individuals grouped by anatomic location.

In addition, we evaluated whether relationships existed between quantified IVIM parameters and field strength or pulse sequence parameters. Restricting this evaluation to only reports from healthy individuals, we sought to remove the potential confound of pathology. Of the 29 studies, 1 study was performed at 0.5T (51), 7 at 1.5T, and 21 at 3T. Results of unpaired student’s t-tests used to compare parameters obtained 1.5T and 3T found no statistical differences in D (p=0.34), f (p=0.23), or D* (p=0.85). Pearson’s correlation coefficients were determined among the measured IVIM parameters and between IVIM parameters and pulse sequence parameters of TR, TE, minimum and maximum b-value, total number of b-values, as well as number of b-values under 200 s/mm² and over 200 s/mm². Significant associations were observed between D and D* (r=0.43, p=0.03) and between D and f (r=−0.865, p<0.001). In addition, the number of b-values in the low b-value regime was significantly positively associated with D* (r=0.463, p=0.02), and echo time was significantly correlated with D (r=−0.416, p=0.03) and f (r=0.476, p=0.01). No other significant associations were observed.

Response to Stimuli

Sixteen prior studies evaluated the response of IVIM parameters to exercise, and two studies evaluated changes in response to cuff compression. Representative images from a thigh muscle study by Adelnia et.al. are shown in Figure 8 (53). Generally, there was a significant increase in all IVIM parameters in response to exercise (Table 2).

Figure 8:

Representative IVIM parameter maps of healthy volunteer thigh muscles calculated before and after knee extension exercise, showing increases in D and f in the quadriceps muscles. Figure adapted from (53) with permission.

Table 2.

Studies evaluating IVIM response to exercise in skeletal muscle.

Study	Muscle	Participant characteristics	Exercise stimulus and imaging timing	D	f	D*
Sasaki, et al. (149)	Masticator (masseter)	Healthy	During jaw clenching	-	↑	↑
Morvan, (51)	Forearm (flexor digitorum)	Healthy	Immediately following handgrip exercise (4 min)	↑	↑	↑
Filli, et al. (60)	Forearm (flexor digitorum superficialis and profundus)	Healthy	Immediately following handgrip exercise (performed until exhaustion)	↑	↑	↑
Nguyen, et al. (151)	Shoulder (subscapularis)	Healthy	15–30 s after resisted lift-off test of varying duration (30, 60, 120 s)	↑	↑ (after 30 and 120 s, not 60 s duration)	↑
Nguyen, et al. (155)	Shoulder (subscapularis)	Healthy	Immediately after lift-off (2 min exercise duration)	↑	↑	↑
			Immediately after Jobe test (2 min exercise duration)	↑+	↑	↑
Hiepe, et al. (52)	Paraspinal (erector spinae & multifidus)	Healthy	1.5 – 2 min after isometric back extension exercise (10 min duration, perceived as hard)	↑	↑	Not reported
Federau, et al. (75)	Paraspinal (erector spinae & multifidus)	Healthy	<20 s after dynamic series of resisted lumbar extension exercise (performed until exhaustion)	↑	↑	↑
		Patients with AIS (concavity/ convexity)		↑ / ↑	- / -	- / ↑
Adelnia, et al. (53)	Thigh (rectus femoris)	Healthy	Immediately after resisted dynamic knee extension exercise (2.5 min duration)	↑	↑	-
Jungmann, et al. (157)	Thigh (all muscles)	Healthy	Immediately after treadmill walking and running (15 min walking or running)	↑	-	-
Ogura, et al. (72)	Thigh (not specified)	Healthy	Immediately, 3h, 6h, and 24h after walking up and down 140 steps ten times	Not reported	↑	↑
Yao, et al. (59)	Leg (gastrocnemius, tibialis anterior)	Healthy	Immediately after single stair stepping exercise (15 min duration)	Not reported	-	Not reported
Mastropietro, et al. (50)	Leg (gastrocnemius & soleus)	Healthy	During/1 min after intermittent isometric plantar flexion exercise (approximately 10 min duration)	- / -	↑/ -	- / -
Jungmann, et al. (157)	Leg (all muscles)	Healthy	Immediately after treadmill walking and running (15 min walking or running)	↑	↑	↑
Ogura, et al. (72)	Leg (gastrocnemius)	Healthy	Immediately, 3h, 6h, and 24h after walking up and down 140 steps ten times	Not reported	↑	-
Ohno, et al. (74)	Leg (tibialis anterior)	Healthy	Immediately after series of maximal dorsiflexion contractions (1 contraction/s for 60 s)	↑	↑	↑
Riexinger, et al. (57)	Leg (gastrocnemius)	Healthy	Immediately, 30 min, 6h, and 48 h after exhausting plyometric and eccentric exercise (with unilateral compression)	↑	↑	Not reported

⁺Depends on stimulus order.

From the studies where pre- and post-exercise results were reported, the average change in D following exercise was 0.13±0.09 ×10⁻³ mm²/s, f was 4.0±3.5 %, and D* was 14.8±25.8 ×10⁻³ mm²/s. The mean changes observed in D and f were significantly different from zero, (p=0.0002 and p=0.0003, respectively), and trended toward significance for D* (p=0.06). However, one study reported a very high resting D* value of more than 10 times the average of the rest, likely due to the use of diffusion sensitization gradients only in the slice-selection direction (largely parallel to the muscle fibers) and the very low b-values employed therein (53). If we exclude that study, the average change in D* was significant with a mean of 19.2±21.1 ×10⁻³ mm²/s, p=0.009.

Figure 9 shows the relationship between resting and post-exercise IVIM parameters. Interestingly, it appears that there is a strong relationship between the pre- and post-exercise parameters, suggesting some degree of universality for relative changes in muscle IVIM parameters in the considered studies. Notably, the order of magnitude of relative changes is consistent with physiologic expectations described above: f increases by 37% (similar to the 20–30% expectation of capillary vasodilation), and D* increases by 100% (consistent with even larger increases in blood flow). However, we find the universality of exercise changes unexpected since it is known that degree of exercise intensity, duration, and work does modulate MR contrast post-exercise, when using methods such as BOLD, T2 or diffusion-weighted imaging (67–70). The universality here could originate from all IVIM studies prescribing sufficient exercise tasks (in intensity or duration) to approach a maximal hyperemia, with similar relative changes in microstructural (fiber size, extracellular fluid), microvascular (blood volume/flow), or other (temperature, pH) occurring in this regime. A direct comparison of the IVIM response to varying exercise intensities in the same subjects is needed to fully address this question. A study by Lyu, et al. evaluated the IVIM responses in Sprague-Dawley rats to varying exercise programs of varying duration and intensity (71). Data acquired 30 min after exercise showed similar increases of D and D* in the four exercise groups compared to controls. Significant differences of both D and D* were observed between groups at all time points, and the interactions of group and time were also significant (p<0.001 for D, p=0.005 for D*), however comparisons among only those groups who performed exercise were not reported.

Figure 9.

Summary of IVIM parameter values in healthy individuals before and after exercise across all anatomic locations. Generally, there was a consistent percentage increase of values from the pre- to post-exercise condition, regardless of exercise prescription or anatomic location.

From the studies that evaluated the response at several time points following cessation of exercise, we can obtain some insight into the temporal response of the IVIM signal. Ogura, et al. found that f and D* in both the thigh and leg muscles returned to their relative resting state 3 hours after a stair stepping exercise (72). Adelnia, et al. collected IVIM data for approximately 25 minutes following resisted knee extension exercise in young and old healthy subjects (53). Significant increases were observed in both cohorts for f that persisted for approximately 15 minutes, and D was significantly increased through the end of data collection. Mastropietro, et al. found that f increased during an intermittent plantar flexion contraction series, but all parameters returned to resting state 1–3 minutes after exercise cessation (50). Filli, et al. found that all IVIM parameters remained elevated at least 20 minutes after handgrip exercise performed until exhaustion (60). Riexinger, et al. reported significant elevations of f and D immediately following exhaustive plyometric and eccentric exercise in the gastrocnemius muscle (57). The perfusion fraction returned to the relative baseline at the 6-hour post-exercise imaging session, while D remained elevated from the pre-exercise baseline for at least 48 hours. D* was not independently reported. Lyu, et al’s study in rats showed that D and D* continued to increase for 24–48 hours after exercise, and generally returned to baseline after 96 hours for D* and 120 hours for D (71). Given the different muscle targets and exercise stimuli used between these studies, it is difficult to generalize aside from saying that a response, if elicited, may last upwards of 30 minutes for f and may persist much longer for D* and D.

Comparison to Other Metrics

Few studies have evaluated the relationship between IVIM parameters and other metrics of blood flow and metabolic activity. For example, Hiepe, et al. acquired IVIM, T2, and 31P MRS data in the paraspinal muscles at rest and in response to an isometric lumbar extension exercise (52). Results showed significant positive correlations between changes in measured T2 and changes in f, D, and phosphocreatine drop. Results from linear mixed models suggested that exercise-induced changes in T2 were primarily associated with altered tissue perfusion and changes in metabolite concentration.

Suo, et al. compared IVIM to ASL and BOLD in response to induced ischemia via cuff compression. In addition to the MRI measures, they also used transcutaneous oxygen pressure (TcPO₂) to evaluate tissue oxygenation (73). No significant associations were observed between IVIM, ASL and BOLD measures, however there were positive correlations between TcPO₂ and ASL and BOLD, and a negative correlation between TcPO₂ and f. This finding would suggest that increased extraction is occurring in regions of lower blood volume.

Ohno, et al. evaluated exercise-induced changes in both ASL and IVIM in response to a bout of dynamic dorsiflexion contractions (74). Identical exercise conditions were repeated on two separate days to remove any potential pre-conditioning effect. In addition, T2 was quantified after the IVIM acquisition on the second day. Correlation coefficients were calculated between IVIM, ASL, and T2 metrics at rest and following exercise. At rest, a significant positive correlation was observed between the product of f and D* (fD*) and mean blood flow (MBF) measured by ASL, but neither f nor D* on their own were correlated with ASL. Following exercise, fD* and D* were highly correlated with MBF. In addition, a positive correlation was observed between D and T2.

Evaluation of Aging and Pathology

As detailed in Table 1, most studies reported parameters in healthy individuals. Even in the studies that included patients with hepatic lesions, tumors, or cervical lesions, the muscle of those patients is not likely to have pathologic changes. To date, there have been six studies to evaluate conditions that involve pathologies that result in changes to skeletal muscle, including evaluation of children with juvenile idiopathic arthritis (54), and adolescent idiopathic scoliosis (AIS) (75), in addition patients with myopathies including dermatomyositis (76,77), polymyositis and muscular dystrophy (77), and finally patients with peripheral artery disease (73).

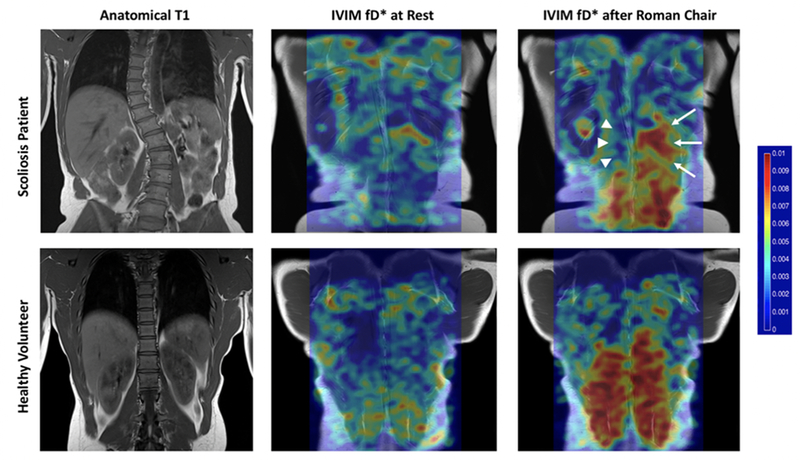
Federau, et al. investigated IVIM parameters at rest and in response to exercise in patients with AIS (75). They found differences of f and D* between the convexity and concavity of the scoliotic curve following lumbar extension exercise, where the convexity had significantly elevated responses compared to the concavity. These results highlight the differences in muscle activation between the convex and concave aspects of the scoliotic curve (Figure 10). Ran, et al. compared patients with autoimmune myositis (e.g. dermatomyositis and polymyositis) to patients with muscular dystrophies and found significant differences of D and f between these groups (77). Patients with autoimmune myositis tended to have higher D, likely due to the underlying edema, and a lower perfusion fraction. D* was reduced in the quadriceps of patients with dermatomyositis (76), and in the lateral compartment of the leg in patients with PAD, which could be related to stiffening of the arterioles and capillaries (73).

Figure 10.

This comparison between a patient with adolescent idiopathic scoliosis (AIS) and a healthy volunteer highlights the sensitivity of IVIM to detect changes associated with pathology. The patient with AIS has a markedly reduced response to exercise on the convex region of the scoliotic curve (arrowheads) relative to the concavity (arrows), while the healthy volunteer shows a symmetric response to exercise. Figure from (75) with permission.

In addition, three studies compared IVIM parameters in muscle across the lifespan (53,73,78). Suo, et al. reported significantly different f, D, and D* in the gastrocnemius muscle between young and old healthy individuals (73), however specific changes were not detailed. Yoon, et al. found only significant age-related differences in D in the anterior compartment of the thigh (78). No differences of f or D were reported between young and old individuals in Adelnia et al’s study of the thigh at rest. However, both f and D showed greater increases and faster returns to the relative baseline state in the young group following knee extension exercise (53). Generally, a consensus on the changes in IVIM in response to pathologic conditions or aging is not yet possible given the limited number of studies and variable results.

CAVEATS, CORRECTIONS, & ADVANCED ANALYSES

Fat Suppression

Diffusion MRI in skeletal muscle poses some specific challenges arising from co-localization of skeletal muscle and fat within a single voxel. This is particularly important in studies where comparisons are made between individuals or groups that span a wide range of muscle quality (i.e., neuromuscular disorders and aging). When unaccounted for in diffusion models, fatty replacement of contractile tissue can be a source of parameter estimation bias due to slow diffusion of lipids which is ~2 orders of magnitude slower than tissue water (79). The slow apparent diffusion coefficient (ADC) of fat can lead to lower estimates of D in voxels containing mixtures of muscle and fat. The propagation of unwanted fat signal into quantitation of diffusion measurements has been studied in detail (80,81). Several fat suppression approaches have been implemented in DWI of skeletal muscle to reduce the contribution of fat, but complete elimination is a difficult technical problem. As models like IVIM which exhibit sub-optimal numerical stability are utilized to study populations exhibiting changes in body composition, interpretation of model fit parameters should consider the efficiency of fat suppression and the influences of residual signal from fat on fitting procedures. The interdependence of parameters in the bi-exponential model used for IVIM makes all parameters potentially susceptible to the presence of fat in unpredictable ways (53,82). Monte Carlo simulations by Adelnia et al. demonstrate bias errors, particularly in D*, that covary with tissue parameters (i.e. fat fraction, perfusion fraction, and ADC) and SNR. In skeletal muscle at rest, muscle with increased fat fraction could appear as having lower D* due to this bias effect alone. This effect is more problematic in dynamic exercise studies where an increase in f and ADC in muscle with high fat fraction will exhibit an apparent greater increase in D* than muscle with low fat fraction.

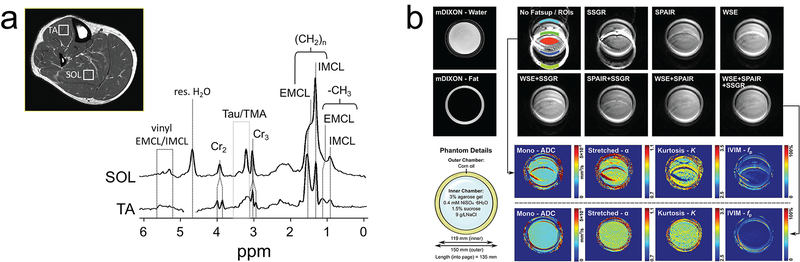
Unsuppressed fat also produces chemical shift artifacts that can bias in IVIM parameters. Skeletal muscle contains multiple lipid types that can exhibit a complex chemical shift spectrum with large amplitude signals up-field and down-field from water (83), making efficient fat suppression difficult. With many of the DWI acquisitions relying on single-shot and low-bandwidth readouts, unsuppressed or poorly suppressed fat from within a single voxel can be shifted to multiple locations several voxels away into neighboring voxels leading to IVIM parameter bias (Figure 11). Individuals exhibiting more advanced myopathy pose more substantial difficulties with efficient fat suppression and thus bias in IVIM parameters should be expected and addressed in the interpretation of imaging findings.

Figure 11.

Impact of fat suppression on skeletal muscle IVIM. (a) Fat suppressed proton spectrum in calf muscle shows several resonances from extramyocellular and intramyocellular lipids (EMCL/IMCL) appearing upfield and downfield from water. Taken from Ref. (83) with permission. (b) Phantom study of quantitative DWI (including IVIM) with various fat suppression approaches illustrating the impact of unsuppressed chemically shifted fat on IVIM quantitation. Taken from Ref. (82) with permission.

Of the studies reviewed herein, 13 used spectral attenuation inversion recover (SPAIR), 13 did not specify a fat suppression method, 3 used spectral-spatial fat suppression, 3 used frequency selective pre-saturation, and 5 used a combination of at least two methods. Significantly lower diffusion coefficients (1.35 vs. 1.81 ×10⁻³ mm²/s, p=0.012) were reported in studies using none or a single fat suppression method compared with studies using two or more suppression methods. This was accompanied by trending larger average resting f in studies using a single fat suppression method (11.4% vs 5.4%, p=0.13). The bias effect of unsuppressed fat signals on DWI and IVIM parameters has been explored in a limited number of studies reflecting similar trends (53,80–82,84).

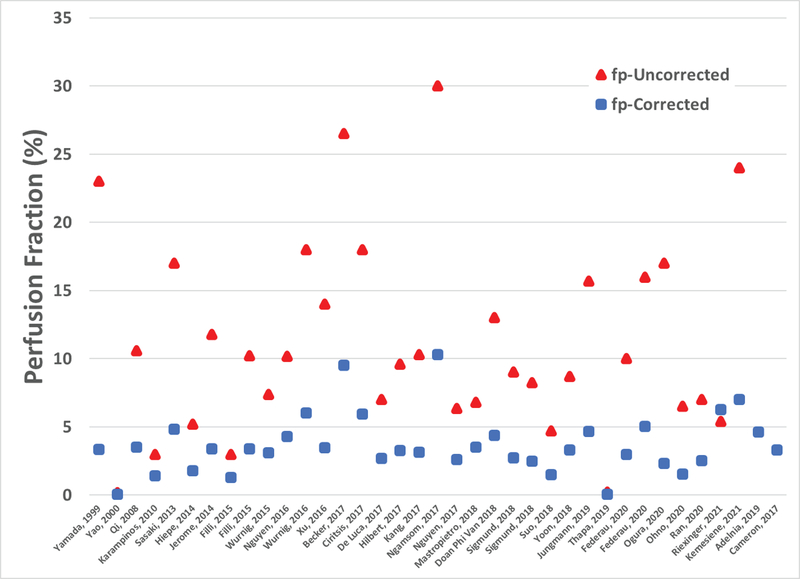
Despite wide-spread use of IVIM in muscle, consensus of normal and abnormal measures can be hampered by differences in imaging protocols which impart a varying degree of relaxation on the blood and muscle water compartments. Correction for relaxation effects have been applied to other body regions to account for differences in tissue and blood relaxation parameters, with notable variation in perfusion fraction measures between uncorrected and relaxation corrected values (85). Of the skeletal muscle literature in this review, correction for relaxation effects is neglected with the exception of two studies (53,82). As detailed above, IVIM studies in skeletal muscle report a wide range of acquisition parameters, with repetition times ranging from 300 to 8708 ms, echo times ranging from 46 to 123 ms, and magnetic fields ranging from 0.5T to 3T. The impact of relaxation effects is illustrated in Figure 12, showing reported raw perfusion fractions and those corrected based on reported acquisition parameters. Corrected values are computed assuming T1 and T2 relaxation properties of blood and muscle reported in the literature (86) and reported imaging parameters and field strengths for each study. This nominal comparison demonstrates that accounting for relaxation effects can alter relationships of reported perfusion fractions between studies and should be considered when comparing between protocols.

Figure 12.

Reported perfusion fractions (red) based on IVIM model fits and relaxation corrected perfusion fractions (blue) estimated based on reported imaging parameters and field strength. Relaxation properties assumed at 3T: T1blood = 1932ms, T2blood = 275ms, T1muscle = 1412ms, and T2muscle = 45ms. Relaxation properties assumed at 1.5T: T1blood = 1200ms, T2blood = 290ms, T1muscle = 1000ms, and T2muscle = 45ms. * Riexinger, et al. (57) corrected for T2 effects so fp-corrected only includes T1 correction.

Extended Models Based on IVIM

The IVIM model imposes several simplifying assumptions on the physical system to extract and estimate perfusion indices from a complex aggregate diffusion signal comprised of the superposition of water translational motions from several compartments. One primary assumption is that the incoherent motion of the microvascular blood pool exhibits Gaussian distributed motions. This assumption is not well-supported by experimental observations of the microvascular system. For example, intra-vital microscopy studies of red blood cell velocities within networks of skeletal muscle capillaries suggest distributions of motions that are not normally distributed (i.e., non-Gaussian) (87,88). Additionally, the microvascular architecture resembles a space-filling fractal network, with a power-law relationship between branch and feed vessel diameters (89). Quantitative analyses of the microvascular network using microCT exhibit a broad distribution of vessel diameters skewed towards larger vessel diameters (90). Consequently, efforts have been made to generalize IVIM analysis beyond one pseudo-diffusion component in the kidney (91), liver (92), and brain (93). However, these multiexponential efforts have not yet been performed in skeletal muscle, possibly due to the limited sensitivity/SNR of the effect even when one component is considered. Alternatively, more general models of displacement probabilities have been used that can capture greater particle spread than the single Gaussian or multi-Gaussian case, i.e. super-diffusion. Recently, a model based on an alpha-stable probability distribution has been proposed, which connects the stretched exponential signal model parameters to super-diffusion probability statistics (94). This stretched exponential signal model effectively captures the IVIM signal behavior in low b-value DWI from muscle (94) and has been used in other regions within the body as an empirical alternative to IVIM (95–97).

An additional assumption of the IVIM model that is most widely used in skeletal muscle is that microcirculation produces isotropic movement of water. Indeed, skeletal muscle studies reviewed here predominantly use trace diffusion weighted signals to obtain blood pool fractions and perfusion flow indices. For acquisitions with more highly sampled b-values and directions, studies have shown that including IVIM quantification can reduce bias in microstructural metrics from DTI and DKI analysis (62). Beyond correcting microstructural metrics of anisotropy, skeletal muscle microvasculature itself is known to course along muscle fibers and expected to exhibit similar anisotropy with a larger proportion of vessels oriented along the length of muscle fibers. An extension of the IVIM model termed “intravoxel partially coherent motion” (IVPCM) has been proposed to account for these known structural characteristics, showing sensitivity to perfusion anisotropy in muscle (98). This approach uses a combination of separately acquired DTI and IVIM data, where the high-directional single b-value DTI is used to estimate the directional dependence of the perfusion fraction as a measure of preferential orientation of the microvasculature. When coupled with multiple b-value IVIM images obtained with fewer directions, the model provides a statistical metric of the degree of dispersion of capillary orientation around a mean orientation, total vascular volume fraction, and the mean microvascular velocity. Additional efforts to extend the IVIM model into a tensor format have been made outside of skeletal muscle (99–103). Characterization of these microvascular properties could represent important markers of pathology in skeletal muscle beyond those provided by the more frequently used IVIM model.

FUTURE DIRECTIONS

Beyond the conventional IVIM model and the advancements described above, more detailed quantitative treatment is possible, delivering even more specific measures of microstructure/microcirculation in skeletal muscle. Microscopy indicates that the two components are intermingled in nontrivial ways (18), so improvements on the IVIM analysis workflow capturing this complexity may provide corresponding diagnostic improvements in skeletal muscle pathology. We provide several examples of these possible future directions below, illustrated in Figure 13. It should be noted that each of these methods involves collection of additional encodings and therefore increase in acquisition time over a single IVIM measurement. This limitation must be balanced with the potentially increased information content.

Figure 13.

(a) Diagram of microstructural /microcirculatory features in skeletal muscle. (b) Hypothetical IVIM contrast modulation with variation of diffusion time Td, flow encoding moment M1, cardiac cycle, and multiple pool modeling. Each technique offers the possibility of additional specificity to individual tissue aspects.

Diffusion Time Variation

Unrestricted water transport is time-invariant in the sense that the measured diffusion coefficient (mean-squared displacement per unit time) does not depend on the time allotted for the water molecules to diffuse (also referred to as the diffusion time). However, in complex porous media such as biological tissue, this is not the case, and both compartments of the IVIM model (microvascular and microstructural) will show apparent diffusivities that depend on diffusion time. Microstructurally, longer diffusion time presents more barriers to diffusing spins, lowering the overall ADC (104,105). If the diffusion length is on the order of the primary restriction scale (e.g. the myofiber diameter in skeletal muscle), this reduction is measurable. Indeed, a survey of published DTI metrics from skeletal muscle as a function of their reported diffusion time shows a clear correlation of lower diffusivities (in particular in the radial direction perpendicular to the myofiber axis) with longer diffusion time (106). With appropriate modeling (107), this dependence can also provide estimates of microstructural properties of fiber size and sarcolemma permeability (108), an approach that has been applied to a range of pathological scenarios in skeletal muscle (109). Other modeling approaches analogously vary diffusion time and other protocol parameters to extract microstructural features (110–114).

However, the time-dependence of the microvascular component in skeletal muscle has received far less attention to date. Since the advent of IVIM in MRI applications (12), the importance of diffusion time and the relevant dynamical regimes have been well recognized (115). In the vascular compartment, the key timescale is that required to traverse a microvessel segment before changing direction. Below this timescale, the motion can be treated as “ballistic” with each segment having a single velocity vector independent of the others, while at much longer timescales, the motion is “diffusive” as the multiple changes in direction as a spin traverses the network randomize its trajectory analogously to Brownian motion in the structural compartment. The observed pseudo-diffusivity D* thus shows an increasing time dependence in the ballistic regime and a time-independent value in the diffusive regime. With advanced modeling (116,117), parameters such as segment length and fluid velocity can be estimated, which may be important biomarkers in muscle pathologies that exhibit capillary spacing heterogeneity.

This trend has been observed in abdominal organs (117) and preclinical brain imaging (93,118), but not yet in skeletal muscle. We may hypothesize how the diffusion time variable may be revelatory in skeletal muscle. First, interpretation of microvascular hierarchy in the IVIM signal (arterioles vs. venules vs. capillaries) may be aided by diffusion time considerations. Arterioles and venules will tend to have a longer segment length and higher velocity than the capillary bed, which might be teased apart in analysis of time-dependent pseudo-diffusion. The more specific parameters of segment length and fluid velocity may also be diagnostically helpful in microvascular disease such as inflammatory myopathies, muscular dystrophies, or PAD (e.g. exercise-mediated angiogenesis (119)). Also, while some methods like BOLD are confounded by vessel orientation, the arbitrary sampling orientation of the diffusion gradient may remove this limitation. Finally, isolating microvascular and macrovascular response is also key to maximizing sensitivity to disease and treatment response, which might be conferred by a combination of these advanced methods.

Flow-compensation

Another control variable that goes hand-in-hand with diffusion time variation is the flow encoding of the diffusion gradient waveform. Basic MR physics dictates that constant velocity motion induces a phase shift proportional to the first moment of the gradient waveform (M₁). However, waveforms can be chosen to vary M₁ to modulate or eliminate (flow-compensated, M₁ = 0) this flow encoding and, in the case of IVIM, reduce signal attenuation. The combination of flow-compensated and non-flow-compensated data can also aid in IVIM signal analysis and biophysical modeling. Flow compensated IVIM measurements have been shown in phantom (120–122), brain (118,123,124), liver (92,115,117), placenta (125) and heart (126) studies; in one study of the liver, a continuous range of gradient moments M₁ was implemented for more complete contrast variation and tissue modeling (115).

The use of gradient waveform modulation may also pay dividends for skeletal muscle evaluation. With flow-compensated gradients some of the pseudo-diffusive decay coming from the longer segments may be eliminated, permitting study of the capillary bed. Since the vasodilation of arterioles and capillaries in response to exercise can be very different, this separation may be useful. More generally, the range of blood velocities in the microvascular network, as well as in feeding arterioles or draining venules, may be teased apart by a range of flow encodings.

Cardiac Gating

The cardiac cycle poses a natural additional control parameter for modulating perfusion IVIM contrast. Pseudo-diffusion effects are maximal in the systolic phase of a given organ, and minimal in the diastolic phase. This has been observed in IVIM studies of the kidney (127,128), brain (129), heart (126), ventricular CSF (130), and liver (131), but not yet explored in muscle. Cardiac gating in skeletal muscle IVIM may have several advantages. First, choosing maximum systole will increase sensitivity to the IVIM effect and thereby improve robustness of its derived parameters. Secondly, the comparison of systolic/diastolic IVIM contrast may provide insight on vascular compliance through the cardiac cycle, which may be modulated in some neuromuscular diseases. Finally, capturing a range of cardiac cycles may again allow separation of multiple blood pools (arteriole, capillary, venous) based on their prominence or absence throughout the pulse waveform.

ASL-prepared IVIM

Another approach to decomposing the vascular component of the IVIM signal, as demonstrated in preclinical (103) and clinical (132–134) brain imaging, is to preface the IVIM measurement with an arterial spin labeling (ASL) preparation. The resulting 2D signal pattern vs. b-value and post-labeling delay allows scrutiny of the IVIM characteristics of different generations of the vasculature in sequential filling order and/or estimation of vascular permeability through exchange with the extravascular space. While this approach would require calibration to skeletal microvascular/microstructural properties, it offers another encoding route to potentially higher specificity.

FUTURE APPLICATIONS

As described above, a host of approaches in other organs—both experimental and analytical—may provide a blueprint for future developments in IVIM of skeletal muscle. As the prevalence and quality of IVIM data acquisition has increased significantly, these avenues may hold potential for clinical advances. Some specific speculations about such paths forward are given below.

Regarding healthy skeletal muscle function and response to challenge, the existing IVIM literature has already shown correspondence with expectations regarding relative magnitude of blood volume and blood flow velocity changes, represented by f and D* respectively. Going further, the decomposition of the IVIM signal into arterial/capillary/venule contributions using multiple pool modeling, cardiac gating, and/or flow compensation may provide more insight, since the vasodilation of arterioles and capillaries in response to exercise can be very different. Furthermore, the heterogeneity of muscular blood flow in response to challenge has not been extensively mapped beyond monitoring the primary activated compartment. Given the interplay of microvascular and motor units (the latter of which have been recently probed by a variant of diffusion MRI (135,136)), as well as the redistribution of existing perfusion to activated muscles, more detailed spatial mapping of IVIM response may yield useful insight as well.

Regarding neuromuscular pathologies, reduced perfusion fraction or pseudo-diffusivities have been observed e.g. in myositis, along with either increased (signifying edema) or decreased (reflecting fat infiltration) tissue diffusivities. Beyond mean values, however, since capillary spacing heterogeneity can occur in some muscle pathologies and as part of normal aging, higher order analysis may prove useful. Here again, the tools of alternative modeling, cardiac gating, flow compensation, and anisotropy characterization may increase specificity by quantifying segment length and blood velocity. These metrics may also be useful in characterizing exercise challenge in neuromuscular disease, where multiple features may be anomalous (fiber atrophy, fatty replacement, perfusion changes) and disentangling them may be key to proper treatment.

As mentioned previously, advanced approaches suggested here all involve more data collection which adds to the already significant sampling requirements of multiple b-values for IVIM. Thus, another practical future direction would be acceleration of the IVIM protocol. This might involve a combination of parsimonious b-value selection (137,138) and/or denoising modules (139–141) when conventional pulse sequences are employed to maintain fidelity with fewer input data. Alternatively, multi-echo acquisitions that accelerate the diffusion encoding dimension (142–144) might be a powerful tool for skeletal muscle IVIM.

Finally, in parallel with the potential for more detailed explorations of IVIM contrast, this review has also revealed a need for efforts toward standardization of the most common variant. The literature summaries in Figures 5, 6, 8, and 11 and Tables 1 and 2 have highlighted the pervasiveness of IVIM contrast in skeletal muscle in medical research around the world, but also some quantitative variability that would obstruct pooling results from multiple sites to achieve a higher evidence level in pursuit of broader impact. In that spirit, a concerted effort within the skeletal muscle imaging community to include poolable research in their portfolio might pay considerable dividends in terms of useful clinical biomarkers. Though beyond the scope of this article, a consensus document from active researchers of optimal parameters, practices, and reporting standards would be a significant advance, as has occurred in other subspecialties (e.g. (46,145,146)).

In the near term, example best practices suggested by the current survey include:

1. full reporting of acquisition parameters including b-values, diffusion times, repetition/echo times, diffusion gradient waveform types, fat suppression options, and fit algorithms;

2. equal b-value sampling in the pseudo-diffusion (b<200 s/mm²) and tissue diffusion (b>200 s/mm²) regimes, with at least 3–4 b-values in each regime;

3. a maximal b-value of b=800 s/mm² unless a non-Gaussian analysis of the tissue compartment is performed;

4. using the average of 3 orthogonal diffusion directions unless anisotropy analysis is performed;

5. reporting some estimate of signal-to-noise ratio (SNR), for example using the difference method for repeated b=0 acquisitions (147);

6. reporting of IVIM parameters both with and without relaxation weighting corrections;

7. acquisition of test-retest reproducibility data where possible.

In conclusion, IVIM can provide insight into blood flow and tissue diffusion in skeletal muscle. Exercise generally leads to an increase in all parameters, but no clear patterns of changes in disease states can be identified based on the limited amount of literature to date. A tradeoff between continued advancement of the acquisition and analysis strategies needs to be weighed against standardization to facilitate comparison among muscle groups and between muscle pathologies.