Summary
Polygenic scores (PGS) are commonly evaluated in terms of their predictive accuracy at the population level by the proportion of phenotypic variance they explain. To be useful for precision medicine applications, they also need to be evaluated at the individual level when phenotypes are not necessarily already known. We investigated the stability of PGS in European American (EUR) and African American (AFR)-ancestry individuals from the Philadelphia Neurodevelopmental Cohort and the Adolescent Brain Cognitive Development study using different discovery genome-wide association study (GWAS) results for post-traumatic stress disorder (PTSD), type 2 diabetes (T2D), and height. We found that pairs of EUR-ancestry GWAS for the same trait had genetic correlations >0.92. However, PGS calculated from pairs of same-ancestry and different-ancestry GWAS had correlations that ranged from <0.01 to 0.74. PGS stability was greater for height than for PTSD or T2D. A series of height GWAS in the UK Biobank suggested that correlation between PGS is strongly dependent on the extent of sample overlap between the discovery GWAS. Focusing on the upper end of the PGS distribution, different discovery GWAS do not consistently identify the same individuals in the upper quantiles, with the best case being 60% of individuals above the 80th percentile of PGS overlapping from one height GWAS to another. The degree of overlap decreases sharply as higher quantiles, less heritable traits, and different-ancestry GWAS are considered. PGS computed from different discovery GWAS have only modest correlation at the individual level, underscoring the need to proceed cautiously with integrating PGS into precision medicine applications.
Keywords: PTSD, height, type 2 diabetes, Philadelphia Neurodevelopmental Cohort, Adolescent Brain Cognitive Development study, PRS-CS, UK Biobank, African American, ancestry, methods development
This study compares polygenic scores computed from sequential iterations of discovery GWAS from large consortia. We find that scores are weakly to moderately correlated from one GWAS to another and that different individuals are identified as high risk, despite the GWAS having substantially overlapping samples.
Introduction
Polygenic scores (PGS) are increasingly being used to draw inferences regarding genetic contributions to a variety of complex anthropometric and disease-related traits. Numerous methods1 have been developed for computing PGS for a target population using summary statistics from a discovery genome-wide association study (GWAS) run for an independent population, with newer Bayesian-based techniques such as LDpred,2 SBayesR,3 and PRS-CS4 generally yielding more predictive PGS than those produced using older methodologies that rely on a combination of linkage disequilibrium (LD) clumping and p-value thresholding.5
One goal is to utilize PGS in clinical settings to facilitate the diagnosis and treatment of a wide range of heritable diseases,6 such as inflammatory bowel disease,7 diabetes,8 cardiovascular disease,9,10 cancer,11 Alzheimer disease,12 attention-deficit/hyperactivity disorder,13 major depressive disorder,14 bipolar disorder,15 and schizophrenia.16 While progress has been made toward reaching this goal,17, 18, 19, 20 numerous challenges remain to be solved.6,21, 22, 23, 24 Given that the GWAS required for computing PGS have been disproportionately run for European-ancestry populations,25, 26, 27, 28, 29 a fundamental challenge will be ensuring that diverse populations have equitable access to medically beneficial PGS,30 as it has been demonstrated that that PGS are less predictive when the target and discovery populations have differing genetic ancestry or varying degrees of admixture.31, 32, 33, 34, 35
To leverage the power of larger sample sizes, consortia, such as the Psychiatric Genetics Consortium (PGC), the Diabetes Genetics Replication and Meta-Analysis (DIAGRAM) consortium, and the Genetic Investigation of Anthropometric Traits (GIANT) consortium, routinely produce updated meta-GWAS incorporating new cohorts and samples. Hence, there is a growing pool of discovery GWAS that could be used for computing PGS, and this year's largest, best-powered meta-GWAS may soon be eclipsed by next year's newer, larger meta-GWAS. In general, these larger, more powerful GWAS explain greater proportions of the trait variance and improve the predictive power of the PGS on an aggregate level. However, there has been little examination of the performance of successive generations of PGS at the individual level. Given the potential usefulness of PGS for stratifying individuals based on their genetic risk for developing a given disorder,20,36 the question arises as to whether the same individuals would be classified as having high genetic risk by PGS produced from subsequent generations of meta-GWAS. From a clinical perspective, identifying substantially different sets of individuals as “high risk” from one generation of meta-GWAS to the next would be problematic.
Previous studies have evaluated PGS performance in terms of how well they predict phenotypes at the population level. However, it is also necessary to examine how well PGS perform at predicting the risk for individuals.37 To this end, we examined the stability of PGS computed for individuals across discovery GWAS. Specifically, we evaluated the correlations between the PGS computed for European American (EUR) and African American (AFR) individuals from pairs of same- and different-ancestry discovery GWAS for post-traumatic stress disorder (PTSD),38,39 type 2 diabetes (T2D),40, 41, 42 and height.43,44 These specific traits were chosen because they had sufficiently powered, publicly available AFR-ancestry GWAS. We also addressed the question of whether the same individuals were consistently identified as belonging to the top PGS quantiles. For this work, we targeted EUR- and AFR-ancestry youth from the Philadelphia Neurodevelopmental Cohort (PNC) and the Adolescent Brain Cognitive Development (ABCD) study to compare PGS on an individual level across discovery GWAS.
Subjects and methods
This study, which uses publicly available de-identified data, was approved by the Institutional Review Board of Boston Children's Hospital.
PNC
Genotype data for the PNC, a population-based sample of youth who were aged 8–21 years at the time of study enrollment,45 were obtained from dbGaP (phs000607.v2.p2). Biological samples from PNC subjects were genotyped in 15 batches (Table S1) using 10 different types of Affymetrix and Illumina arrays by the Center for Applied Genomics at the Children's Hospital of Philadelphia.46 Analysis was limited to the 5,239 EUR- and 3,260 AFR-ancestry individuals for whom genotype data were available after the quality control (QC) process described below.
ABCD study
Results were replicated using post-QC genotype data for 5,815 EUR and 1,741 AFR individuals in the independent ABCD cohort (NDA no. 2573, fix release 2.0.1). This cohort is comprised of adolescents who were aged 9–10 years at the time that their saliva samples were collected for genotyping.47 The Rutgers University Cell and DNA Repository stored and genotyped all samples using the Affymetrix NIDA SmokeScreen array.
QC and imputation
The PNC dataset was processed by array batch and merged after imputation, whereas the ABCD dataset was processed as a single batch. For each batch, PLINK 1.948 was used to remove single-nucleotide polymorphisms (SNPs) with >5% missingness, samples with more than 10% missingness, and samples with a genotyped sex that did not match the reported sex phenotype. As a final step, each batch was checked with a pre-imputation perl script that compared SNP frequencies against the 1000 Genomes ALL reference panel.49 This script fixed strand reversals and improper Ref/Alt assignments and also removed palindromic A/T and C/G SNPs with minor allele frequency (MAF) > 0.4, SNPs with alleles that did not match the reference panel, SNPs with allele frequencies differing by more than 0.2 from the reference, and SNPs not present in the reference panel.
Genotypes were phased (Eagle v.2.4) and imputed by chromosome to the 1000 Genomes Other/Mixed GRCh37/hg19 reference panel (Phase 3 v.5) using Minimac 4 via the Michigan Imputation Server.50 All post-imputation QC was run using bcftools.51 The 15 imputation batches for the PNC dataset were merged by chromosome, and then post-imputation QC was run using the average imputation quality and average MAF for the merged chromosome files. Only polymorphic sites with (average) imputation quality R2 ≥ 0.7 and (average) MAF ≥ 0.01 were included in the final PLINK 1.9 hard-call PNC and ABCD post-imputation datasets.
Ancestry and kinship analysis
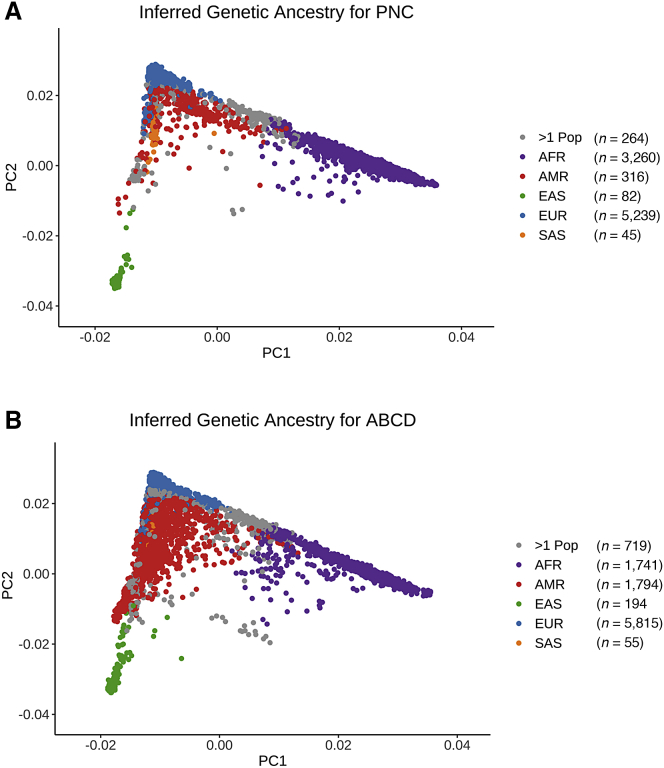
Multi-dimensional scaling (MDS) was conducted using KING (v.2.2.4)52 to identify the top 10 ancestry components for each sample. (Note that while these components are technically axes in MDS space, we refer to them as principal components [PCs] for the sake of simplicity.) The ancestry PCs were projected onto the 1000 Genomes PC space, and genetic ancestry was inferred using the e107153 support vector machines package in R54 (Figure 1). Based on these inferences, AFR- and EUR-ancestry cohorts were created for the PNC and ABCD datasets; all other ancestry groups were excluded from further analysis. A second round of unprojected MDS was then performed within the EUR- and AFR-ancestry groups to produce ten PCs that were regressed out of the standardized PGS to adjust for array batch effects and genetic ancestry (Figures S1–S5).
Figure 1.
First and second principal components of cohort genotypes
Principal components (PCs) were computed and projected to a 1000 Genomes reference using KING (Manichaikul et al.52). Colors indicate inferred genetic ancestry for the (A) 9,206 Philadelphia Neurodevelopmental Cohort (PNC) and (B) 10,318 Adolescent Brain Cognitive Development (ABCD) genotyped samples.
KING was also used to identify all pairwise relationships out to third-degree relatives based on estimated kinship coefficients and inferred IBD segments. Although the PNC was not recruited as a family study, it does include some related individuals (i.e., siblings and cousins). We ran a sensitivity analysis using a reduced PNC dataset that included only one individual from each family (chosen as the lowest individual ID number for a given family ID number), which reduced the size of the PNC EUR cohort from 5,239 to 4,928 and the AFR cohort from 3,260 to 2,954. After establishing that the PNC PTSD PGS correlation results obtained using only unrelated individuals did not differ meaningfully from those obtained using the full dataset (Tables S4 and S5), we performed all subsequent analyses using the complete EUR and AFR cohorts.
Polygenic score computation with PRS-CS
PRS-CS4 was used to infer posterior mean effects by chromosome for the SNPs in a given dataset that overlapped with both the discovery GWAS summary statistics and an external 1000 Genomes LD panel that was matched to the ancestry group used for the discovery GWAS. Posterior mean effects were only inferred for SNPs located on the 22 autosomal chromosomes. PGS for the EUR and AFR subsets of PNC and ABCD were computed using both EUR and AFR discovery GWAS for PTSD,38,39 T2D,40, 41, 42 and height43,44 (Table 1). To ensure convergence of the underlying Gibbs sampler algorithm, we ran 25,000 Markov chain Monte Carlo (MCMC) iterations and designated the first 10,000 MCMC iterations as burn-in. The PRS-CS global shrinkage parameter was set to 0.01 when the discovery GWAS had an SNP sample size that was less than 200,000; otherwise, it was learned from the data using a fully Bayesian approach. Default settings were used for all other PRS-CS parameters. Given the stochastic nature of the Bayesian algorithm used by PRS-CS, PGS replicability was confirmed by completing multiple PRS-CS runs using the same discovery GWAS. The PLINK 1.9 score function was used to produce raw PGS from the posterior means of the estimated SNP effects returned by PRS-CS for each chromosome, and then R54 was used to standardize the PGS for a given cohort to mean = 0 and SD = 1. Standardized PGS were then adjusted by regressing out the first ten within-ancestry PCs.
Table 1.
Discovery GWAS used to compute polygenic scores with PRS-CS
| Trait | Discovery GWAS | GWAS ancestry | GWAS sample sizea for PRS-CS | SNP countb for PNC PGS calculations | SNP count for ABCD PGS calculations |
|---|---|---|---|---|---|
| PTSD | Nievergelt et al.39 (Freeze 2 PGC) |
AFR | 11,321 | 1,162,502 | 1,064,574 |
| EUR | 70,237 | 1,087,435 | 1,016,161 | ||
| Duncan et al.38 (Freeze 1 PGC) |
AFR | 9,691 | 1,157,302 | 1,059,197 | |
| EUR | 9,954 | 1,086,644 | 1,015,369 | ||
| T2D | Chen et al.42 | AFR | 4,146 | 1,114,936 | 1,020,579 |
| Scott et al.40 (DIAGRAM) |
EUR | 152,599 | 1,087,724 | 1,016,440 | |
| Mahajan et al.41 (DIAGRAM) |
EUR | 231,420 | 1,089,613 | 1,018,372 | |
| Height | Marouli et al.44 (GIANT) |
AFR | 27,494 | 18,580 | 15,720 |
| EUR | 381,625 | 18,035 | 15,767 | ||
| Wood et al.43 (GIANT) |
EUR | 252,048 | 987,760 | 920,889 |
PTSD, post-traumatic stress disorder; T2D, type 2 diabetes; PNC, Philadelphia Neurodevelopmental Cohort; PGS, polygenic score; ABCD, Adolescent Brain Cognitive Development study; PGC, Psychiatric Genomics Consortium; DIAGRAM, Diabetes Genetics Replication and Meta-Analysis Consortium; GIANT, Genetic Investigation of Anthropometric Traits Consortium.
PRS-CS requires a single GWAS sample size; see supplemental methods for how we derived this measure when the sample size varied by SNP.
The "SNP count" is the number of SNPs in common between the discovery GWAS, the PRS-CS LD panel, and the genomic dataset.
LD score regression
LD score regression (LDSC) was used to calculate the mean for each EUR-ancestry GWAS as a proxy for GWAS power (Table S14).55,56 We also used LDSC to compute the genetic correlation for each pair of same-trait GWAS (Table S15). Standard error was estimated by jackknifing over blocks of adjacent SNPs. Our LDSC calculations only included SNPs with MAF > 0.01. Given that LDSC may yield biased estimates for admixed populations,57 we did not perform LD score regression for the AFR-ancestry discovery GWAS.
Quantile-based comparisons
We counted the number of samples in common at or above the 80th percentile, the 90th percentile, and the 95th percentile of the PC-adjusted standardized PGS distributions. Specifically, we counted how many individuals were jointly identified as being at or above a given percentile of the PGS computed from a pair of different discovery GWAS. As an example, consider the n = 3,260 individuals in the PNC AFR cohort. There are n = 652 individuals with PGS at or above the 80th percentile, n = 326 with PGS at or above the 90th percentile, and n = 163 with PGS at or above the 95th percentile of PGS. The proportional overlap for PGS at or above the 80th percentile was calculated by identifying which 652 samples were located within that region of each of the two PGS distributions being compared (e.g., those computed from an AFR GWAS for trait X and those computed from a EUR GWAS for trait X), counting how many of those samples were present at or above that quantile for both distributions, and then dividing that count by 652. A proportional overlap of 1 would indicate that the same 652 individuals had PGS that were among the top 20% of PGS for both distributions.
UK Biobank experiment
We obtained imputed genotypes and standing height phenotypes for 276,107 unrelated white British individuals in the UK Biobank.58 The supplemental methods describe an experiment we designed using these data to explore the degree to which our primary findings could be attributed to differing GWAS sample sizes. In brief, we used PRS-CS and PLINK 1.9 as described above to compute height PGS for an independent test group using seven discovery GWAS with controlled differences in their sample sizes and degree of sample overlap (Figure S7; Table S16). GWAS A and GWAS B were run using non-overlapping samples (each n = 134,000), whereas GWAS C and GWAS D were run using sub-samples (each n = 75,000) that were randomly drawn from the individuals included in GWAS A and GWAS B, respectively. GWAS E and GWAS F were run using sub-samples (each n = 10,000) that were randomly drawn from the individuals included in GWAS C and GWAS D, respectively. Finally, GWAS AB was run using a superset comprised of the individuals included in either GWAS A or GWAS B (n = 268,000). We performed LD score regression (Table S17) and genetic correlation (Table S19) analyses for these GWAS as described above. We also analyzed the correlation between the height PGS computed from the different GWAS and assessed how well the PGS predicted height for a test group of individuals who were not included in any of the GWAS (n = 8,107).
Statistical analysis
All statistics and graphical displays were generated using R.54 Pearson correlation coefficients were calculated to assess the strength of correlations between PC-adjusted standardized PGS that were calculated for a given trait using different discovery GWAS. We quantified the association between PGS computed from different discovery GWAS using Pearson's linear correlation coefficient (r), and we ran two-tailed t tests for linear association to determine whether the observed correlations were statistically significant.
To evaluate the predictive accuracy of the PGS produced from our height GWAS experiment, we used each set of standardized PGS to predict the height of the test subjects via an additive multiple linear regression model that also included sex, age at height measurement, and the first 20 ancestry PCs supplied by the UK Biobank as covariates. We calculated the coefficient of determination (R2) for each model as a measure of how well the PGS from a given GWAS predicted height in conjunction with these covariates, and we also ran a partial F test for each predictive model to assess the effect of adding the standardized PGS to a base model that included sex, age, and the first 20 ancestry PCs as predictors of height.
Results
Reproducibility across PRS-CS runs
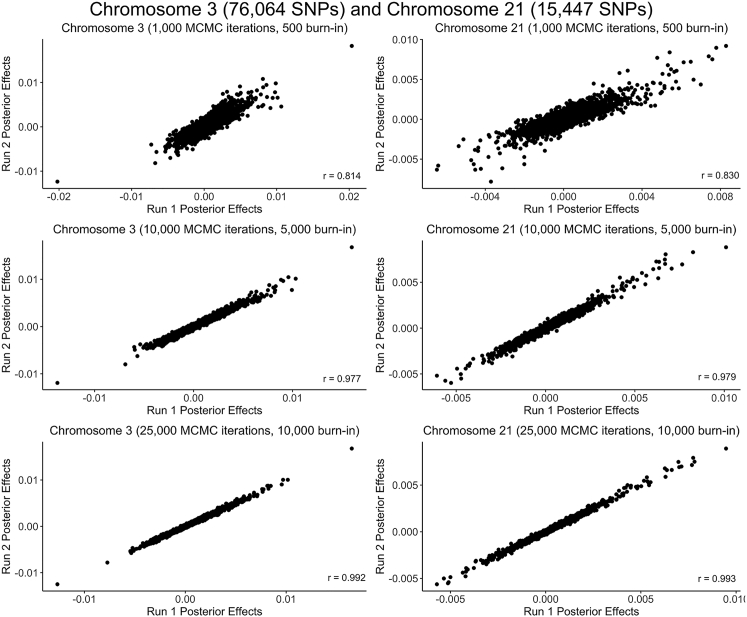
Given that PRS-CS relies on Bayesian methodology to infer posterior effects for the SNPs on each chromosome,4 it was necessary to confirm that we had used enough MCMC iterations and burn-in trials to ensure convergence of the underlying Gibbs sampler algorithm. We checked for convergence indirectly by assessing the correlation between the posterior effects calculated across multiple runs for a given chromosome (Figure 2). The PRS-CS default setting of 1,000 MCMC iterations with the first 500 iterations serving as burn-in produced relatively inconsistent posterior effects (r ≈ 0.8), suggesting incomplete convergence. The correlation between the posterior effects computed during multiple runs of PRS-CS improved to r ≈ 0.98 when we increased the number of MCMC iterations to 10,000 (5,000 burn-in) and further improved to r > 0.99 for both large and small chromosomes when we used 25,000 MCMC iterations (10,000 burn-in). Given that the computational time increases substantially as more MCMC iterations are run, we opted to use 25,000 MCMC iterations with the first 10,000 as burn-in rather than pursuing even stronger correlations.
Figure 2.
Reproducibility of Bayesian posterior effects computed by PRS-CS
As illustrated for chromosome 3 (76,064 SNPs) and chromosome 21 (15,447 SNPs) using the Nievergelt et al.39 EUR PTSD discovery GWAS with the PNC EUR dataset, posterior effects were more strongly correlated between PRS-CS runs as the number of MCMC iterations (and burn-in iterations) increased.
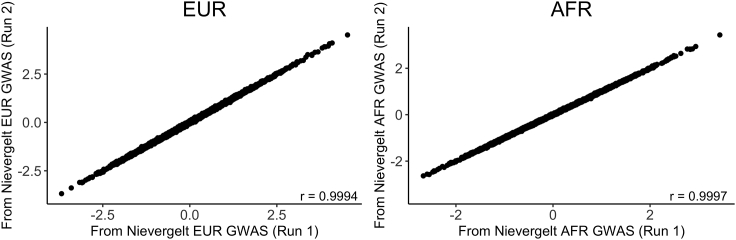
The next concern was whether the PGS calculated by PLINK 1.9 from the Bayesian posterior effects would also be reproducible across PRS-CS runs. To address this question, we ran PRS-CS twice using the PGC Freeze 2 PTSD discovery GWAS,39 and calculated PGS from both sets of posterior effects. For both the EUR and AFR PNC cohorts, the correlation between the adjusted PGS was greater than 0.999 (Figure 3). Hence, we are confident that PRS-CS yields reproducible PGS for a given discovery GWAS provided that enough MCMC iterations are used.
Figure 3.
Reproducibility of PGS across multiple runs of PRS-CS
PC-adjusted standardized PGS computed from posterior effects generated by two runs of PRS-CS using the same PTSD discovery GWAS from Nievergelt et al.39 had correlations greater than r = 0.999 for both the EUR (n = 5,239) and AFR (n = 3,260) cohorts of PNC.
Stability of PGS computed from different same-ancestry discovery GWAS
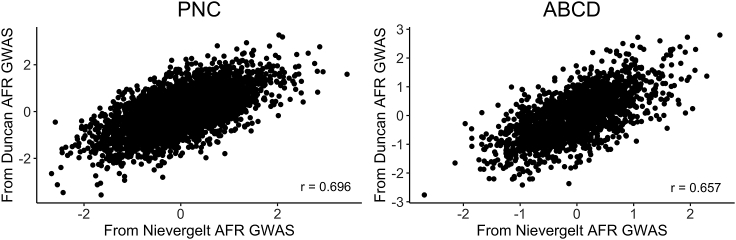
Of the three traits that we analyzed, only PTSD had two publicly available AFR-ancestry GWAS.38,39 We computed PGS using both GWAS for each AFR-ancestry individual and then assessed the correlation between the two sets of PGS (Figure 4). We found a moderately strong positive correlation between the PGS computed from the PGC Freeze 138 and Freeze 239 AFR-ancestry PTSD GWAS for the AFR-ancestry cohorts of both PNC (r = 0.696, t(3,258) = 55.26, p < 2 × 10−16) and ABCD (r = 0.657, t(1,739) = 36.34, p < 2 × 10−16).
Figure 4.
Correlation between PGS computed from two different AFR-ancestry PTSD discovery GWAS for AFR-ancestry individuals
Significant positive correlations were observed between the AFR PGS computed from the PGC Freeze 138 and Freeze 239 AFR PTSD GWAS for both the PNC (r = 0.696, t(3,258) = 55.26, p < 2 × 10−16) and ABCD (r = 0.657, t(1,739) = 36.34, p < 2 × 10−16) AFR cohorts.
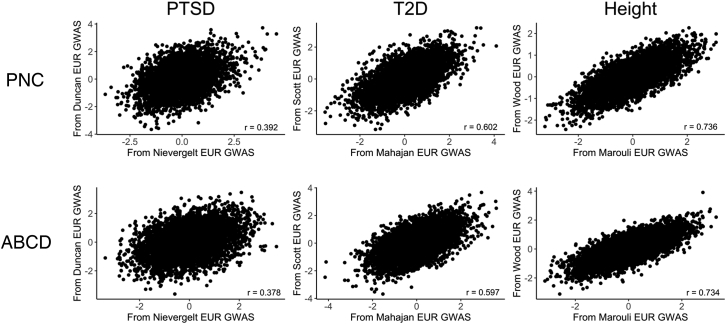
The wider availability of EUR-ancestry GWAS allowed us to compute PGS for EUR-ancestry individuals using pairs of EUR-ancestry discovery GWAS for PTSD,38,39 T2D,40,41 and height43,44 (Figure 5). Statistically significant positive correlations between the pairs of PGS were observed for all three traits for both the PNC (Table S8) and ABCD (Table S9) EUR-ancestry cohorts, with the strongest association observed between the height PGS (PNC: r = 0.736; ABCD: r = 0.734) and the weakest observed for the PTSD PGS (PNC: r = 0.392; ABCD: r = 0.378).
Figure 5.
Correlation between PGS computed from two different EUR-ancestry discovery GWAS for EUR-ancestry individuals
Pairs of PGS computed for the EUR samples of PNC (n = 5,239) and ABCD (n = 5,815) using two different EUR discovery GWAS for PTSD,38,39 T2D,40,41 and height43,44 all showed significant positive correlations.
Stability of PGS computed from different-ancestry discovery GWAS
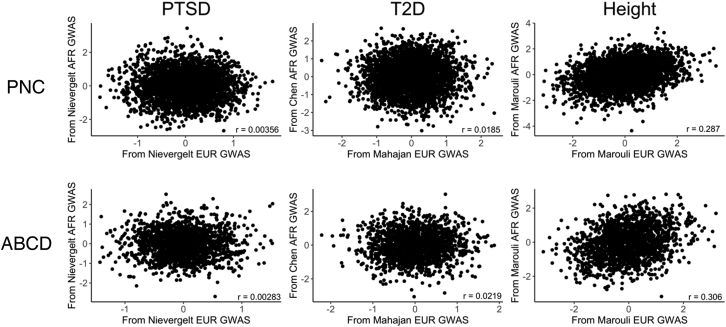
Given the scarcity of AFR-ancestry GWAS, it is often tempting to compute PGS for AFR-ancestry individuals using EUR-ancestry discovery GWAS. To assess the feasibility of this approach, we computed PGS for AFR-ancestry individuals in PNC and ABCD using both AFR-ancestry discovery GWAS and EUR-ancestry GWAS and then assessed the correlation between the two sets of PGS (Figure 6).
Figure 6.
Correlation between PGS computed from AFR-ancestry and EUR-ancestry discovery GWAS for AFR-ancestry individuals
Pairs of PGS computed for the AFR samples of PNC and ABCD from the newer EUR and AFR discovery GWAS were not significantly correlated for either PTSD39 or T2D,41,42 but there was a significant positive correlation for height.44
For PTSD, there was no significant correlation between the PGS computed from the newer Freeze 2 PGC AFR and EUR discovery GWAS39 for AFR-ancestry individuals in either PNC (r = 0.00356, t(3,258) = 0.203, p = 0.839) or ABCD (r = 0.00283, t(1,739) = 0.118, p = 0.906). The AFR PGS computed using the Freeze 1 PGC PTSD AFR and EUR discovery GWAS38 were uncorrelated for ABCD (r = −0.00320, t(1,739) = −0.133, p = 0.894), but we observed a weak positive correlation for PNC (r = 0.0417, t(3,258) = 2.379, p = 0.0174).
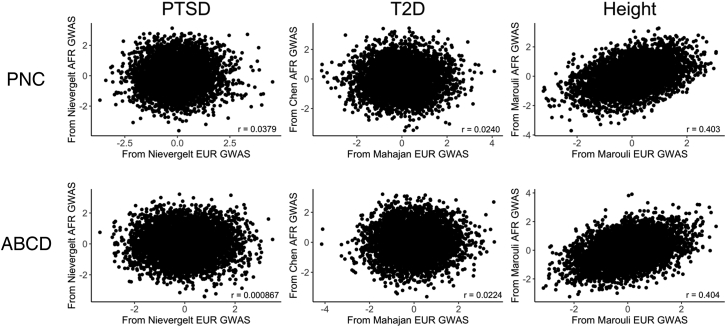
We made the same different-ancestry GWAS comparisons for the EUR-ancestry individuals in the PNC and ABCD study populations (Figure 7). As was the case for AFR-ancestry individuals, we found no significant correlation between PGS computed from the PGC Freeze 2 EUR- and AFR-ancestry PTSD discovery GWAS.39 While we observed no significant correlation between the PGS computed using the PGC Freeze 1 EUR- and AFR-ancestry PTSD discovery GWAS for EUR-ancestry individuals in ABCD (r = −0.00109, t(5,813) = −0.083, p = 0.934), we did observe a weak positive correlation for the EUR cohort of PNC (r = 0.0379, t(5,237) = 2.746, p = 0.0065).
Figure 7.
Correlation between PGS computed from EUR-ancestry and AFR-ancestry discovery GWAS for EUR-ancestry individuals
Pairs of PGS computed for the EUR samples of PNC and ABCD from the newer EUR and AFR discovery GWAS were not significantly correlated for either PTSD39 or T2D,41,42 but there was a significant positive correlation for height.44
We compared T2D PGS computed from an AFR-ancestry discovery GWAS42 to those computed using two EUR discovery GWAS40,41 published by the DIAGRAM consortium. The newer EUR-ancestry T2D discovery GWAS41 yielded PGS that were uncorrelated with those computed from the AFR-ancestry discovery GWAS42 for the AFR-ancestry individuals in both PNC (r = 0.0185, t(3,258) = 1.055, p = 0.292) and ABCD (r = 0.0219, t(1,739) = 0.912, p = 0.362). Similarly, there was no significant correlation between the different-ancestry T2D PGS that we computed for the EUR-ancestry individuals in PNC (r = 0.0240, t(5,237) = 1.739, p = 0.082) and ABCD (r = 0.0224, t(5,813) = 1.71, p = 0.0872). We observed a weak positive correlation between the PGS computed from the older EUR-ancestry T2D discovery GWAS40 and the PGS computed from the AFR-ancestry T2D discovery GWAS42 for the PNC AFR cohort (r = 0.0432, t(3,258) = 2.469, p = 0.0136), but there were no significant correlations between the two sets of PGS computed for the ABCD AFR cohort (r = −0.0458, t(1,739) = −1.911, p = 0.0562), the PNC EUR cohort (r = 0.00528, t(5,237) = 0.382, p = 0.703), or the ABCD EUR cohort (r = 0.0188, t(5,813) = 1.431, p = 0.152).
We also computed different-ancestry PGS using EUR- and AFR-ancestry height discovery GWAS that we obtained from the GIANT consortium.43,44 We observed significant positive correlations between the PGS computed from the newer EUR- and AFR-ancestry height discovery GWAS44 for the PNC AFR (r = 0.287, t(3,258) = 17.09, p < 2 × 10−16), ABCD AFR (r = 0.306, t(1,739) = 13.42, p < 2 × 10−16), PNC EUR (r = 0.403, t(5,237) = 31.82, p < 2 × 10−16), and ABCD EUR (r = 0.404, t(5,813) = 33.69, p < 2 × 10−16) cohorts. Likewise, we found significant positive correlations between the PGS computed from the older EUR-ancestry height discovery GWAS43 and the AFR-ancestry height discovery GWAS44 for the PNC AFR (r = 0.258, t(3,258) = 15.22, p < 2 × 10−16), ABCD AFR (r = 0.312, t(1,739) = 13.68, p < 2 × 10−16), PNC EUR (r = 0.335, t(5,239) = 25.25, p < 2 × 10−16), and ABCD EUR (r = 0.327, t(5,813) = 26.39, p < 2 × 10−16) cohorts. As was the case for T2D, there was only one AFR-ancestry height discovery GWAS44 available to use for computing PGS.
The supplemental methods includes complete statistical results for the comparisons between PGS computed from different discovery GWAS for the PNC AFR (Table S6), ABCD AFR (Table S7), PNC EUR (Table S8), and ABCD EUR (Table S9) cohorts.
GWAS power
We hypothesized that PGS would be more stable for traits with more powerful discovery GWAS. As such, we used LDSC to compute the mean χ2 as a proxy for power for each of the EUR-ancestry discovery GWAS that we used to compute PGS (Table S14). We found that the two height GWAS had higher mean χ2 than the two T2D GWAS, which had higher mean χ2 than the two PTSD GWAS. Also, the newer, larger GWAS had higher mean χ2 than the older GWAS for each trait. The genetic correlation calculated by LDSC for each pair of GWAS was essentially perfect (Table S15), with the lowest rg = 0.9225 ± 0.1807 for PTSD.
Sample-size effects
In an effort to disentangle the effect of GWAS sample size from other factors differing between the height, T2D, and PTSD GWAS, such as trait heritability and sample overlap, we computed height PGS from seven GWAS that we ran using unrelated white British samples from the UK Biobank. The heights, male-female ratios, and ages at height measurement were comparable across all seven GWAS groups and the test set (Table S16). The LDSC mean χ2 for our seven height GWAS, which ranged from 1.0982 for GWAS E to 3.7259 for GWAS AB (Table S17), spanned the range of the mean χ2 we found for the EUR-ancestry meta-GWAS we used for our primary analyses (Table S14), suggesting that our height GWAS had a similar range of power. The genetic correlations between the GWAS computed by LDSC were essentially perfect for all comparisons (Table S19). All seven of our height GWAS identified genome-wide significant SNPs (p < 5 × 10−8), with the larger GWAS identifying more such SNPs than the smaller GWAS (Table S18).
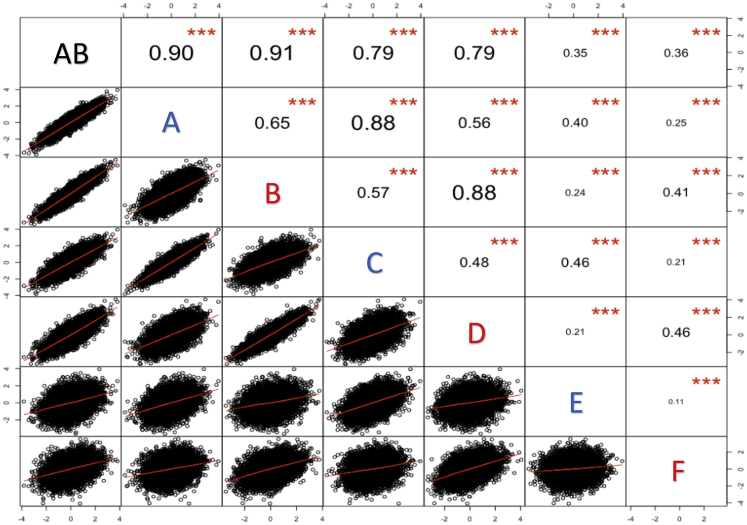
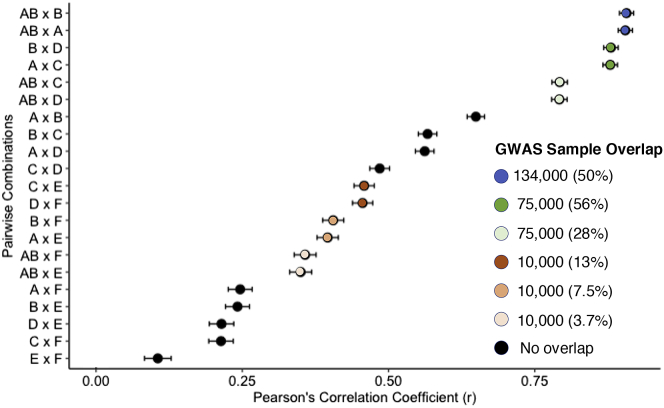
We used our seven discovery GWAS to generate height PGS for an independent test group of 8,107 unrelated white British individuals who had standing height measurements. We found that the correlation between PGS is driven by both the discovery GWAS sample size and the degree of sample overlap between the discovery GWAS (Figures 8 and 9; Table S20). The PGS that were computed from GWAS AB (n = 268,000), which overlaps with all of the other GWAS, showed similar degrees of correlation with the PGS from the GWAS A and B (each n = 134,000; both r ≈ 0.91), GWAS C and D (each n = 75,000; both r ≈ 0.79), and GWAS E and F (each n = 10,000; both r ≈ 0.35) (Figure 8). However, the PGS computed from GWAS A, which overlapped only with GWAS C and GWAS E, showed a stronger correlation with the PGS computed from the overlapping, smaller GWAS C (r = 0.88) than they did with the PGS computed from the non-overlapping, larger GWAS B (r = 0.65). In general, the percentage overlap between discovery GWAS was relatively more important than the number of subjects in common (Figure 9). When the discovery that GWAS had 10,000 subjects in common, the PGS correlation was stronger when the percentage overlap between the discovery GWAS was 13% (C × E; D × F) than it was when the percentage overlap was 7.5% (A × E; B × F) or 3.7% (AB × E; AB × F). Likewise, when two discovery GWAS had 75,000 subjects in common, the correlation was stronger when that number represented a 56% overlap between the GWAS (A × C; B × D) than when it represented a 28% overlap (AB × C; AB × D). Moreover, PGS computed from GWAS A were more strongly correlated with those from GWAS C (r = 0.88) than they were with those from GWAS D (r = 0.56), which was the same size as GWAS C (n = 75,000) but had no overlap with GWAS A. When considering only non-overlapping discovery GWAS, the correlation was stronger for PGS computed from larger GWAS; for example, the PGS computed from GWAS A were more strongly correlated with those from GWAS B (r = 0.65) than with those from either GWAS D (r = 0.56) or GWAS F (r = 0.25). The additive models including, sex, age, 20 ancestry PCs, and the PGS computed from our height GWAS explained between 54.82% (GWAS E) and 62.86% (GWAS AB) of the variability in the measured heights for the test group (Table S21). Moreover, the PGS computed from the height GWAS all explained a significant amount of variability in the height phenotypes beyond what was explained by sex, age at height measurement, and 20 ancestry PCs alone (Table S21). We obtained these experimental results using a highly heritable trait (height), and the discovery GWAS and test samples were drawn from the same ancestrally homogeneous population (white British). The fact that we observed variable degrees of correlation between PGS even under these controlled conditions implies that the differing degrees of correlation that we report for pairs of PTSD, T2D, and height PGS cannot be attributed solely to differing discovery GWAS sample sizes. The proportional overlap between the discovery GWAS is also important, as are the individual subjects who are included in a discovery GWAS.
Figure 8.
Correlation between PGS computed from seven white British height GWAS for an independent test set of 8,107 unrelated white British individuals from the UK Biobank
GWAS A and GWAS B were each run for n = 134,000 non-overlapping, unrelated white British individuals using sex, age at height measurement, and the first 20 ancestry PCs as covariates. The GWAS A and GWAS B samples were combined to run GWAS AB (n = 268,000). GWAS C was run using a random subsample (n = 75,000) of the individuals included in GWAS A, and GWAS E was run using a random subsample (n = 10,000) of the individuals included in GWAS C. The same relationship exists between GWAS B, GWAS D (n = 75,000), and GWAS F (n = 10,000). The strength of the correlation between PGS is driven by both GWAS sample size and the degree of sample overlap between the GWAS. ∗∗∗p < 0.001.
Figure 9.
Contributions of GWAS sample size and proportional sample overlap to the correlation between height PGS
Height GWAS A and GWAS B were each run for n = 134,000 non-overlapping, unrelated white British individuals using sex, age at height measurement, and the first 20 ancestry PCs as covariates. The GWAS A and GWAS B samples were combined to run GWAS AB (n = 268,000). GWAS C was run using a random subsample (n = 75,000) of the individuals included in GWAS A, and GWAS E was run using a random subsample (n = 10,000) of the individuals included in GWAS C. The same relationship exists between GWAS B, GWAS D (n = 75,000), and GWAS F (n = 10,000). Black dots correspond to the Pearson correlation coefficients for height PGS computed from pairs of discovery GWAS with no sample overlap. When the PGS were computed from overlapping discovery GWAS, the correlation coefficients are depicted using colored dots; the legend lists the number of samples in common as well as the proportion of samples in common for each color. Error bars denote 95% confidence intervals. PGS from pairs of discovery GWAS are more strongly correlated when there is a higher proportion of sample overlap between the GWAS.
Quantile-based comparisons
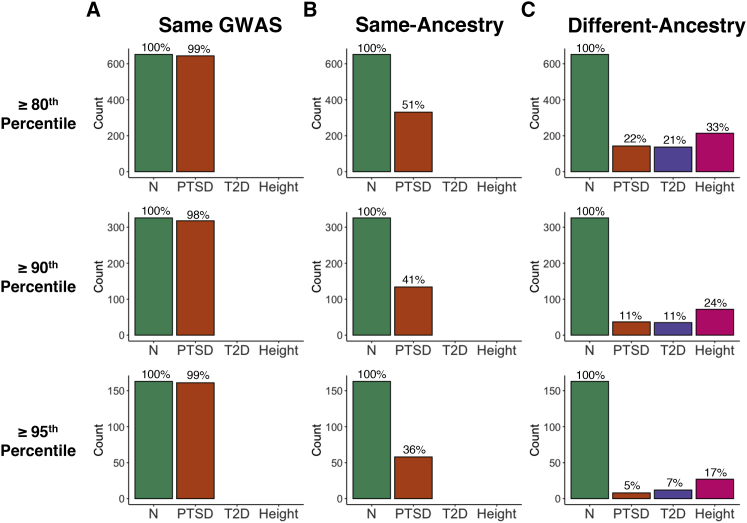
Given that much of the interest in PGS is in identifying individuals at high genetic risk for a disorder, we evaluated whether there would be more stability if we focused on the individuals who had PGS located in the upper tail of the distribution. As a baseline comparison, we determined the degree of overlap between the individuals in the top quantiles of PGS computed from two PRS-CS runs using the Freeze 2 AFR- and EUR-ancestry PTSD discovery GWAS39 for the AFR (Figure 10A) and EUR (Figure 11A) PNC cohorts, respectively. Of the n = 3,260 individuals in the PNC AFR cohort, there are n = 652 individuals with PGS at or above the 80th percentile, n = 326 with PGS at or above the 90th percentile, and n = 163 with PGS at or above the 95th percentile of PGS. We found an overlap of 644 of the 652 AFR-ancestry individuals who had PGS at or above the 80th percentile from the two runs using the same AFR-ancestry PTSD discovery GWAS, which is a 98.7% overlap. Comparable degrees of overlap were observed between the PNC AFR-ancestry individuals with PTSD PGS at or above the 90th (318/326 = 0.975) and 95th (161/163 = 0.988) percentiles. Similarly, the proportional overlap between the PTSD PGS computed from two PRS-CS runs using the Freeze 2 EUR-ancestry PTSD discovery GWAS39 for the EUR-ancestry cohort (n = 5,239) was 1,026/1,048 = 0.979 at or above the 80th percentile, 513/524 = 0.979 at or above the 90th percentile, and 255/262 = 0.973 at or above the 95th percentile.
Figure 10.
Comparison of the samples comprising the top PGS quantiles for the PNC AFR cohort
(A) The samples located at the top 20%, 10%, and 5% of the PTSD PGS distribution were virtually the same when PGS were computed twice using the same discovery GWAS. For example, 644 out of the 652 samples (98.7%) at or above the 80th percentile were the same between the two batches of PGS. (B) The overlap between samples at all three quantiles dropped substantially when the PGS computed from the AFR PGC Freeze 1 PTSD discovery GWAS38 were compared with those computed from the AFR Freeze 2 PTSD discovery GWAS (Nievergelt et al.39), with the degree of overlap being reduced at higher quantiles. (C) The degree of overlap was further reduced when comparing PGS computed from an AFR-ancestry discovery GWAS to those computed from a EUR-ancestry GWAS for PTSD (Nievergelt et al.39), T2D,41,42 and height (Marouli et al.44). For context, the green bars depict the number of samples included at or above the 80th percentile (n = 652), 90th percentile (n = 326), and 95th percentile (n = 163). Additional results can be found in Tables S10 and S11.
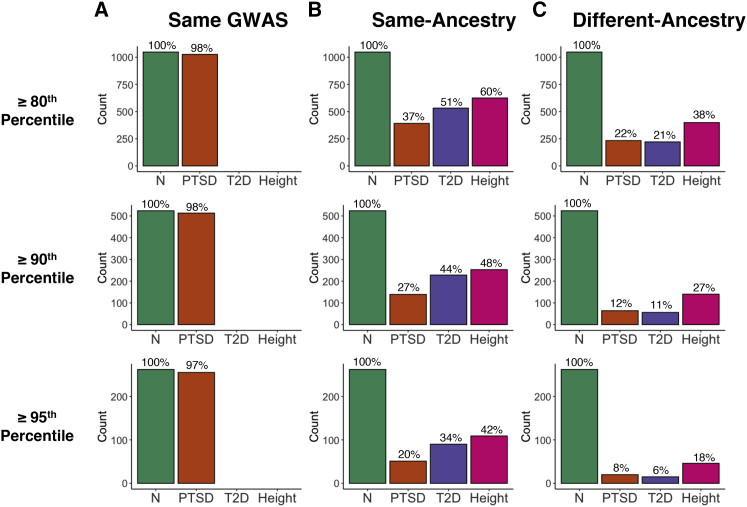
Figure 11.
Comparison of the samples comprising the top PGS quantiles for the PNC EUR cohort
(A) The EUR samples located within the top 20%, 10%, and 5% of the PTSD PGS distribution were nearly the same when PGS were computed twice using the same EUR discovery GWAS (Nievergelt et al.39). For example, 1,026 out of the 1,048 samples (97.9%) at or above the 80th percentile were the same between the two runs of PRS-CS. (B) The overlap between samples at all three quantiles dropped substantially when the PGS computed from two different EUR discovery GWAS were compared for PTSD,38,39 T2D,40,41 and height.43,44 (C) The degree of overlap was dramatically reduced when comparing PGS computed from an AFR-ancestry discovery GWAS with those computed from an EUR-ancestry GWAS for PTSD (Nievergelt et al.39), T2D,41,42 and height.43,44 Green bars depict the number of samples included at or above the 80th percentile (n = 1,048), 90th percentile (n = 524), and 95th percentile (n = 262). Additional results can be found in Tables S12 and S13.
The proportional overlap decreases if we consider PGS computed from two different same-ancestry discovery GWAS. For the PNC AFR-ancestry cohort (Figure 10B), PC-adjusted standardized PGS computed from the Freeze 138 and Freeze 239 PTSD AFR-ancestry discovery GWAS had 53.6% of individuals in common at or above the 80th percentile, 47.5% at or above the 90th percentile, and 36.3% at or above the 95th percentile. The decrease in proportional overlap was even more pronounced for PGS computed from two different EUR-ancestry GWAS for the PNC EUR-ancestry cohort (Figure 11B). The proportion of overlap became progressively smaller as we considered progressively higher percentiles for PTSD, T2D, and height. Moreover, the amount of overlap was greatest for height and smallest for PTSD at each of the percentiles that we considered.
Proportional overlap was even more dramatically decreased when we compared the top quantiles of the PGS that had been computed from an AFR-ancestry discovery GWAS with those that had been computed from a EUR-ancestry discovery GWAS (Figures 10C and 11C). For the AFR cohort of PNC, the proportional overlap ranged from a low of 4.91% for different-ancestry PTSD PGS at the 95th percentile to a high of 32.8% for different-ancestry height PGS at the 80th percentile, whereas the proportional overlap for the PNC EUR cohort ranged from 3.82% for different-ancestry T2D PGS at the 95th percentile to 38.1% for height PGS at the 80th percentile. For both the EUR and AFR cohorts, the general pattern is that proportional overlap is largest for different-ancestry PGS at the 80th percentile and smallest at the 95th percentile. Within a given percentile, the proportional overlap is largest for height and smallest for either PTSD or T2D.
Note that Figures 10 and 11 only include comparisons for PNC between the PGS computed using the newer discovery GWAS if there was more than one comparison possible. We observed similar results for the ABCD cohort and also for additional different-ancestry comparisons. See the supplemental methods for complete results of our quantile-based analyses for the PNC AFR (Table S10), ABCD AFR (Table S11), PNC EUR (Table S12), and ABCD EUR (Table S13) cohorts.
Discussion
Our work focused on comparing the PGS computed from different discovery GWAS at the individual level. The correlation in PGS across discovery GWAS was higher for a strongly heritable anthropometric trait (e.g., height) as compared with medical and psychiatric disorders, such as T2D and PTSD; higher between GWAS with overlapping samples than between non-overlapping GWAS; and higher for same-ancestry versus different-ancestry GWAS. These patterns of stability extended to comparisons between the upper quantiles of PGS, underscoring the need to proceed cautiously with integrating PGS into precision medicine applications.
This relatively modest correlation in PGS is especially noteworthy given that it was observed for PGS computed using successive generations of meta-GWAS that were produced by the PGC,38,39 DIAGRAM,40,41 and GIANT41,43 consortia. The fact that even same-ancestry meta-GWAS computed by the same consortia using overlapping samples and SNPs (Tables 1 and 2) could yield PGS with correlations <0.7 at the individual level raises serious concerns. If PGS are going to be used clinically, then they need to be reproducible. In many ways, our UK Biobank experiment provided the best-case scenario for PGS stability. We considered height, a highly heritable, easily measured quantitative trait, and the phenotyping, genotyping, statistical analyses, and study population were constant across all discovery GWAS and the test set. PGS were most correlated between the largest GWAS, but the degree of sample overlap appeared to be a stronger predictor of correlation strength than sample size.
Table 2.
Estimated sample overlap between same-ancestry GWAS
| Trait | Discovery GWAS ancestry | No. of overlapping samplesa | No. of new samplesb | Percentage increase in sample size (%)c | Correlation between PGS: |
|
|---|---|---|---|---|---|---|
| PNC | ABCD | |||||
| PTSD38,39 | AFR | 9,691 | 1,630 | 16.82 | 0.696 | 0.657 |
| EUR | 9,954 | 60,283 | 605.62 | 0.392 | 0.378 | |
| T2D40,41 | EUR | 152,599 | 78,821 | 51.65 | 0.602 | 0.597 |
| Height43,44 | EUR | 252,048 | 129,577 | 51.41 | 0.736 | 0.734 |
PTSD, post-traumatic stress disorder; T2D, type 2 diabetes; PNC, Philadelphia Neurodevelopmental Cohort; PGS, polygenic score; ABCD, Adolescent Brain Cognitive Development study.
Discovery GWAS references: Duncan et al.,38 Nievergelt et al.,39 Scott et al.,40 Mahajan et al.,41 Wood et al.,43 Marouli et al.44
PRS-CS sample size for the older GWAS in the pair; calculated as described in the supplemental methods.
Calculated as the difference between the PRS-CS sample size for the newer GWAS and that for the older GWAS run by the consortium. This is an estimate, as we do not know the exact degree of overlap between the two GWAS.
Calculated as the number of new samples divided by the number of overlapping samples.
Even if stand-alone PGS are not yet useful clinically, they could still be used to help identify those individuals at highest disease risk.59 For instance, PGS for psychiatric traits could be used in conjunction with environmental factors to identify adolescents most at risk for developing psychosis and other mental health disorders.17 We are actively pursuing such applications with the PNC and ABCD cohorts and have found that ancestry-specific PTSD PGS do indeed add predictive value to models that include other non-genetic factors.60 Nonetheless, we caution that it is dangerous to rely solely on PGS quantiles to identify at-risk individuals. Successive generations of discovery GWAS yielded PGS that did not identify the same individuals at the top quantiles of the distribution, and the amount of overlap decreased as higher quantiles were considered (Figures 10 and 11; Tables S10–S13). Hence, the instinctive decision to focus only on the upper tail of the PGS distribution will not mitigate the lack of PGS stability across different discovery GWAS.
We chose to use the Bayesian PRS-CS Python package to compute PGS for this study. It has been demonstrated5 that Bayesian methods generally yield more predictive PGS than those produced via traditional p-value thresholding approaches. The advantage of PRS-CS over other Bayesian methods is that it employs a very robust Strawderman-Berger continuous shrinkage prior rather than a discrete mixture prior, which allows for more accurate multivariate modeling of local LD in the polygenic prediction.4 When enough MCMC iterations are used to ensure convergence of the underlying Gibbs sampler algorithm, PRS-CS yields very consistent posterior means of the estimated SNP effects (Figure 2). PGS computed using the same discovery GWAS are highly correlated when computed using multiple PRS-CS runs (Figure 3), and others have previously shown that PGS computed from the same discovery GWAS are strongly correlated when computed using PRS-CS and other Bayesian and non-Bayesian approaches.5 Hence, the limited PGS stability across discovery GWAS that we report here cannot be attributed to the stochastic nature of Bayesian methods; there must be differences between the discovery GWAS.
By choosing to use multiple generations of GWAS produced by the same consortia, we hoped to minimize potential methodological differences between the same-trait meta-GWAS. As expected, the genetic correlation between each pair of same-trait GWAS was nearly perfect, no doubt due to the large overlap between SNPs and samples within each pair (Table 1). Initially, we had assumed that the newer GWAS in each pair would be the "better" GWAS since we thought that the larger sample size would yield more explanatory power. We cannot rule out this possibility, but the results of our UK Biobank experiment suggest that factors beyond sample size also contribute to PGS stability.
It is not surprising that the two height GWAS had higher mean χ2, a proxy for GWAS power, as compared with the PTSD and T2D GWAS (Table S14). Height is an easily measured quantitative trait that is less susceptible to ascertainment bias than qualitative disease traits. Furthermore, environmental factors make substantial contributions to the development of both PTSD61 and T2D.62 Even so, LDSC gave an unusually high estimate of mean χ2 (6.4544) for the newer height GWAS.44 While it is possible that the LDSC calculations could have been biased due to being based only on a small number of low-frequency SNPs, we believe that a plausible explanation could lie in the design of this GWAS. Specifically, the newer height GWAS included a small number of targeted rare and low-frequency SNPs (MAF between 0.1% and 4.8%) on a specially designed exome array rather than casting the same wide net as the earlier GWAS, although our LDSC and PRS-CS calculations only included the low-frequency SNPs (i.e., those with MAF > 1%). This modification coupled with a substantially increased sample size and an easily ascertained quantitative trait could have yielded this improvement in explanatory power.
Our results add to the growing body of evidence that PGS should be computed from an ancestrally matched discovery GWAS. It is well established that EUR-ancestry GWAS typically yield PGS that are less predictive for AFR and other non-EUR-ancestry groups.20,22,26,31,32,35,63, 64, 65, 66, 67 We have further demonstrated that PGS computed from same-ancestry GWAS for PTSD and T2D are uncorrelated with those computed from different-ancestry GWAS for both AFR- and EUR-ancestry study participants (Figures 6 and 7), and we also found that there is very little overlap between the individuals in the upper tails of the PGS distributions computed using EUR-ancestry GWAS as compared with those computed using AFR-ancestry GWAS (Figures 10C and 11C; Tables S10–S13). Given the dearth of AFR-ancestry and other non-EUR-ancestry discovery GWAS, our results underscore the urgent need for more high-powered GWAS analyses to be run for non-EUR-ancestry populations.
We chose to study PTSD, T2D, and height because all three traits had publicly available GWAS for both EUR- and AFR-ancestry populations. Of these three, PTSD was the only trait that had two AFR-ancestry GWAS available for comparison purposes. While we focused our current work on the EUR- and AFR-ancestry individuals in the PNC and ABCD cohorts, we hope that methodology and GWAS data will soon exist to make it possible expand our analyses to the admixed American and other ancestral groups that are also included in these cohorts (Figure 1). The recent release of PRS-CSx68 will make it possible to use discovery GWAS that include a combination of East Asian-, AFR-, and EUR-ancestry samples. Although it offers an improvement over the current requirement that the discovery GWAS be limited to only one of these three ancestry groups, PRS-CSx still does not enable analyses of admixed samples from other genetic backgrounds.
Ultimately, we envision a future where genetic ancestry will not be a necessary consideration before computing PGS. Given that genetic ancestry is continuous, it is rather artificial to assign samples to discrete ancestry groups.27 Within the AFR-ancestry group alone, there is an enormous degree of genetic diversity.32,69 We controlled for such diversity by calculating PGS separately for each ancestry group and then regressing out within-ancestry principal components from the standardized PGS. We are optimistic that new methods that incorporate local ancestry34,70 will eventually allow us to embrace this diversity and compute stable, accurate PGS for admixed populations. Increasingly economical whole-genome sequencing,71 coupled with expanded (i.e., less Eurocentric) genotyping arrays67 and improved imputation to diverse reference panels from TOPMed,72 should also facilitate the further development of inclusive approaches, such as BOLT-LMM,73,74 trans-ethnic GWAS,75 and multi-ethnic PGS.33 While it certainly would be easier to continue to focus PGS development on EUR-ancestry populations, we do so at the grave risk of further exacerbating the inequities in medical care between EUR-ancestry populations and the rest of the world.30,76
Data and code availability
The PNC and ABCD genomic datasets used in this study are available by application from dbGaP (phs00060) and NDAR (NDA no. 2573), respectively. UK Biobank data are also available by application. All discovery GWAS summary statistics and software used in this study are publicly available; see Web resources for access information.
Acknowledgments
This work was supported by the following National Institute of Mental Health grants: 5U01MH119690, 3U01MH119690, 5K23MH120437, and 5R01MH119219.
Data used in the preparation of this article were obtained from the Adolescent Brain Cognitive Development (ABCD) study (https://abcdstudy.org), held in the NIMH Data Archive (NDA). This is a multisite, longitudinal study designed to recruit more than 10,000 children aged 9–10 years and follow them over 10 years into early adulthood. The ABCD study is supported by the National Institutes of Health and additional federal partners under award numbers U01DA041048, U01DA050989, U01DA051016, U01DA041022, U01DA051018, U01DA051037, U01DA050987, U01DA041174, U01DA041106, U01DA041117, U01DA041028, U01DA041134, U01DA050988, U01DA051039, U01DA041156, U01DA041025, U01DA041120, U01DA051038, U01DA041148, U01DA041093, U01DA041089, U24DA041123, and U24DA041147. A full list of supporters is available at https://abcdstudy.org/federal-partners.html. A listing of participating sites and a complete listing of the study investigators can be found at https://abcdstudy.org/consortium_members/. ABCD consortium investigators designed and implemented the study and/or provided data but did not necessarily participate in the analysis or writing of this report. This manuscript reflects the views of the authors and may not reflect the opinions or views of the NIH or ABCD consortium investigators.
Support for the collection of the data for Philadelphia Neurodevelopment Cohort (PNC) was provided by grant RC2MH089983 awarded to Raquel Gur and RC2MH089924 awarded to Hakon Hakonarson. Subjects were recruited and genotyped through the Center for Applied Genomics (CAG) at The Children's Hospital in Philadelphia (CHOP). Phenotypic data collection occurred at the CAG/CHOP and at the Brain Behavior Laboratory, University of Pennsylvania.
This research has been conducted using data from UK Biobank, a major biomedical database, under data use agreement 40980.
Declaration of interests
R.B. reports serving on the scientific board and owning stock in Taliaz Health, with no conflict of interest relevant to this work. The other authors declare no competing interests.
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.xhgg.2022.100091.
Web resources
McCarthy Group imputation checking perl script, https://www.well.ox.ac.uk/∼wrayner/tools/index.html#Checking
McCarthy Group genotyping chip strand and build files, https://www.well.ox.ac.uk/∼wrayner/strand/
Plink 1.9, https://www.cog-genomics.org/plink/1.9/
Bcftools, https://github.com/samtools/bcftools
Michigan Imputation Server, https://imputationserver.sph.umich.edu/index.html
KING: Kinship-based Inference for GWAS, http://people.virginia.edu/∼wc9c/KING/index.html
The R Project for Statistical Computing, https://www.r-project.org
R package e1071, https://cran.r-project.org/web/packages/e1071/e1071.pdf
R package qqman, https://cran.r-project.org/web/packages/qqman/vignettes/qqman.html
PRS-CS, https://github.com/getian107/PRScs
LDSC, https://github.com/bulik/ldsc
DIAGRAM GWAS summary statistics, http://diagram-consortium.org/downloads.html
GIANT GWAS summary statistics, https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files
Psychiatric Genomics Consortium GWAS summary statistics, https://www.med.unc.edu/pgc/data-index/
UK Biobank, https://www.ukbiobank.ac.uk/
Supplemental information
References
- 1.Ma Y., Zhou X. Genetic prediction of complex traits with polygenic scores: a statistical review. Trends Genet. 2021;37:995–1011. doi: 10.1016/j.tig.2021.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vilhjálmsson B.J., Yang J., Finucane H.K., Gusev A., Lindström S., Ripke S., Genovese G., Loh P.-R., Bhatia G., Do R., et al. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am. J. Hum. Genet. 2015;97:576–592. doi: 10.1016/j.ajhg.2015.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lloyd-Jones L.R., Zeng J., Sidorenko J., Yengo L., Moser G., Kemper K.E., Wang H., Zheng Z., Magi R., Esko T., et al. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun. 2019;10:5086. doi: 10.1038/s41467-019-12653-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ge T., Chen C.-Y., Ni Y., Feng Y.-C.A., Smoller J.W. Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun. 2019;10:1776. doi: 10.1038/s41467-019-09718-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ni G., Zeng J., Revez J.A., Wang Y., Zheng Z., Ge T., et al. A comparison of ten polygenic score methods for psychiatric disorders applied across multiple cohorts. Biol. Psychiatry. 2021;90:611–620. doi: 10.1016/j.biopsych.2021.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Khera A.V., Chaffin M., Aragam K.G., Haas M.E., Roselli C., Choi S.H., Natarajan P., Lander E.S., Lubitz S.A., Ellinor P.T., et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018;50:1219–1224. doi: 10.1038/s41588-018-0183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gettler K., Levantovsky R., Moscati A., Giri M., Wu Y., Hsu N.-Y., Chuang L.-S., Sazonovs A., Venkateswaran S., Korie U., et al. Common and rare variant prediction and penetrance of IBD in a large, multi-ethnic, health system-based biobank cohort. Gastroenterology. 2021;160:1546–1557. doi: 10.1053/j.gastro.2020.12.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Padilla-Martínez F., Collin F., Kwasniewski M., Kretowski A. Systematic review of polygenic risk scores for type 1 and type 2 diabetes. Int. J. Mol. Sci. 2020;21:1703. doi: 10.3390/ijms21051703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rao A., Knowles J. Polygenic risk scores in coronary artery disease. Curr. Opin. Cardiol. 2019;34:435–440. doi: 10.1097/HCO.0000000000000629. [DOI] [PubMed] [Google Scholar]
- 10.Dikilitas O., Schaid D.J., Kosel M.L., Carroll R.J., Chute C.G., Denny J.A., Fedotov A., Feng Q., Hakonarson H., Jarvik G.P., et al. Predictive utility of polygenic risk scores for coronary heart disease in three major racial and ethnic groups. Am. J. Hum. Genet. 2020;106:707–716. doi: 10.1016/j.ajhg.2020.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Graff R.E., Cavazos T.B., Thai K.K., Kachuri L., Rashkin S.R., Hoffman J.D., Alexeeff S.E., Blatchins M., Meyers T.J., Leong L., et al. Cross-cancer evaluation of polygenic risk scores for 16 cancer types in two large cohorts. Nat. Commun. 2021;12:970. doi: 10.1038/s41467-021-21288-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhou X., Li Y.Y.T., Fu A.K.Y., Ip N.Y. Polygenic score models for Alzheimer's disease: from research to clinical applications. Front. Neurosci. 2021;15:650220. doi: 10.3389/fnins.2021.650220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ronald A., de Bode N., Polderman T.J.C. Systematic review: how the attention-deficit/hyperactivity disorder polygenic risk score adds to our understanding of ADHD and associated traits. J. Am. Acad. Child Adolesc. Psychiatry. 2021;60:1234–1277. doi: 10.1016/j.jaac.2021.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mistry S., Harrison J.R., Smith D.J., Escott-Price V., Zammit S. The use of polygenic risk scores to identify phenotypes associated with genetic risk of bipolar disorder and depression: a systematic review. J. Affective Disord. 2018;234:148–155. doi: 10.1016/j.jad.2018.02.005. [DOI] [PubMed] [Google Scholar]
- 15.Biederman J., Green A., DiSalvo M., Faraone S.V. Can polygenic risk scores help identify pediatric bipolar spectrum and related disorders?: a systematic review. Psychiatry Res. 2021;299:113843. doi: 10.1016/j.psychres.2021.113843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mistry S., Harrison J.R., Smith D.J., Escott-Price V., Zammit S. The use of polygenic risk scores to identify phenotypes associated with genetic risk of schizophrenia: systematic review. Schizophr. Res. 2018;197:2–8. doi: 10.1016/j.schres.2017.10.037. [DOI] [PubMed] [Google Scholar]
- 17.Murray G.K., Lin T., Austin J., McGrath J.J., Hickie I.B., Wray N.R. Could polygenic risk scores be useful in psychiatry?: a review. JAMA Psychiatry. 2021;78:210–219. doi: 10.1001/jamapsychiatry.2020.3042. [DOI] [PubMed] [Google Scholar]
- 18.Lambert S.A., Abraham G., Inouye M. Towards clinical utility of polygenic risk scores. Hum. Mol. Genet. 2019;28:R133–R142. doi: 10.1093/hmg/ddz187. [DOI] [PubMed] [Google Scholar]
- 19.Torkamani A., Wineinger N.E., Topol E.J. The personal and clinical utility of polygenic risk scores. Nat. Rev. Genet. 2018;19:581–590. doi: 10.1038/s41576-018-0018-x. [DOI] [PubMed] [Google Scholar]
- 20.Wray N.R., Lin T., Austin J., McGrath J.J., Hickie I.B., Murray G.K., Visscher P.M. From basic science to clinical application of polygenic risk scores: a primer. JAMA Psychiatry. 2021;78:101–109. doi: 10.1001/jamapsychiatry.2020.3049. [DOI] [PubMed] [Google Scholar]
- 21.Wand H., Lambert S.A., Tamburro C., Iacocca M.A., O’Sullivan J.W., Sillari C., Kullo I.J., Rowley R., Dron J.S., Brockman D., et al. Improving reporting standards for polygenic scores in risk prediction studies. Nature. 2021;591:211–219. doi: 10.1038/s41586-021-03243-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Peterson R.E., Kuchenbaecker K., Walters R.K., Chen C.-Y., Popejoy A.B., Periyasamy S., Lam M., Iyegbe C., Strawbridge R.J., Brick L., et al. Genome-wide association studies in ancestrally diverse populations: opportunities, methods, pitfalls, and recommendations. Cell. 2019;179:589–603. doi: 10.1016/j.cell.2019.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Choi S.W., Mak T.S.-H., O’Reilly P.F. Tutorial: a guide to performing polygenic risk score analyses. Nat. Protoc. 2020;15:2759–2772. doi: 10.1038/s41596-020-0353-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wray N.R., Yang J., Hayes B.J., Price A.L., Goddard M.E., Visscher P.M. Pitfalls of predicting complex traits from SNPs. Nat. Rev. Genet. 2013;14:507–515. doi: 10.1038/nrg3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sirugo G., Williams S.M., Tishkoff S.A. The missing diversity in human genetic studies. Cell. 2019;177:26–31. doi: 10.1016/j.cell.2019.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Duncan L., Shen H., Gelaye B., Meijsen J., Ressler K., Feldman M., Peterson R., Domingue B. Analysis of polygenic risk score usage and performance in diverse human populations. Nat. Commun. 2019;10:3328. doi: 10.1038/s41467-019-11112-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Manolio T.A. Using the data we have: improving diversity in genomic research. Am. J. Hum. Genet. 2019;105:233–236. doi: 10.1016/j.ajhg.2019.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mills M.C., Rahal C. A scientometric review of genome-wide association studies. Commun. Biol. 2019;2:9. doi: 10.1038/s42003-018-0261-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hindorff L.A., Bonham V.L., Brody L.C., Ginoza M.E.C., Hutter C.M., Manolio T.A., Green E.D. Prioritizing diversity in human genomics research. Nat. Rev. Genet. 2018;19:175–185. doi: 10.1038/nrg.2017.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Martin A.R., Kanai M., Kamatani Y., Okada Y., Neale B.M., Daly M.J. Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet. 2019;51:584–591. doi: 10.1038/s41588-019-0379-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Martin A.R., Gignoux C.R., Walters R.K., Wojcik G.L., Neale B.M., Gravel S., Daly M.J., Bustamante C.D., Kenny E.E. Human demographic history impacts genetic risk prediction across diverse populations. Am. J. Hum. Genet. 2017;100:635–649. doi: 10.1016/j.ajhg.2017.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Majara L., Kalungi A., Koen N., Zar H., Stein D.J., Kinyanda E., et al. Low generalizability of polygenic scores in African populations due to genetic and environmental diversity. bioRxiv. 2021 doi: 10.1101/2021.01.12.426453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Márquez-Luna C., Loh P.-R., South Asian Type 2 Diabetes (SAT2D) Consortium. SIGMA Type 2 Diabetes Consortium. Price A.L. Multiethnic polygenic risk scores improve risk prediction in diverse populations. Genet. Epidemiol. 2017;41:811–823. doi: 10.1002/gepi.22083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bitarello B.D., Mathieson I. Polygenic scores for height in admixed populations. G3 (Bethesda) 2020;10:4027–4036. doi: 10.1534/g3.120.401658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Grinde K.E., Qi Q., Thornton T.A., Liu S., Shadyab A.H., Chan K.H.K., Reiner A.P., Sofer T. Generalizing polygenic risk scores from Europeans to Hispanics/Latinos. Genet. Epidemiol. 2019;43:50–62. doi: 10.1002/gepi.22166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Slunecka J.L., van der Zee M.D., Beck J.J., Johnson B.N., Finnicum C.T., Pool R., Hottenga J.-J., de Geus E.J.C., Ehli E.A. Implementation and implications for polygenic risk scores in healthcare. Hum. Genomics. 2021;15:46. doi: 10.1186/s40246-021-00339-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wald N.J., Old R. The illusion of polygenic disease risk prediction. Genet. Med. 2019;21:1705–1707. doi: 10.1038/s41436-018-0418-5. [DOI] [PubMed] [Google Scholar]
- 38.Duncan L.E., Ratanatharathorn A., Aiello A.E., Almli L.M., Amstadter A.B., Ashley-Koch A.E., Baker D.G., Beckham J.C., Bierut L.J., Bisson J., et al. Largest GWAS of PTSD (N=20070) yields genetic overlap with schizophrenia and sex differences in heritability. Mol. Psychiatry. 2018;23:666–673. doi: 10.1038/mp.2017.77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Nievergelt C.M., Maihofer A.X., Klengel T., Atkinson E.G., Chen C.-Y., Choi K.W., Coleman J.R.I., Dalvie S., Duncan L.E., Gelernter J., et al. International meta-analysis of PTSD genome-wide association studies identifies sex- and ancestry-specific genetic risk loci. Nat. Commun. 2019;10:4558. doi: 10.1038/s41467-019-12576-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Scott R.A., Scott L.J., Mägi R., Marullo L., Gaulton K.J., Kaakinen M., Pervjakova N., Pers T.H., Johnson A.D., Eicher J.D., et al. An expanded genome-wide association study of type 2 diabetes in Europeans. Diabetes. 2017;66:2888. doi: 10.2337/db16-1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mahajan A., Wessel J., Willems S.M., Zhao W., Robertson N.R., Chu A.Y., Gan W., Kitajima H., Taliun D., Rayner N.W., et al. Refining the accuracy of validated target identification through coding variant fine-mapping in type 2 diabetes. Nat. Genet. 2018;50:559–571. doi: 10.1038/s41588-018-0084-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chen J., Sun M., Adeyemo A., Pirie F., Carstensen T., Pomilla C., Doumatey A.P., Chen G., Young E.H., Sandhu M., et al. Genome-wide association study of type 2 diabetes in Africa. Diabetologia. 2019;62:1204–1211. doi: 10.1007/s00125-019-4880-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wood A.R., Esko T., Yang J., Vedantam S., Pers T.H., Gustafsson S., Chu A.Y., Estrada K., Luan J.a., Kutalik Z., et al. Defining the role of common variation in the genomic and biological architecture of adult human height. Nat. Genet. 2014;46:1173–1186. doi: 10.1038/ng.3097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Marouli E., Graff M., Medina-Gomez C., Lo K.S., Wood A.R., Kjaer T.R., Fine R.S., Lu Y., Schurmann C., Highland H.M., et al. Rare and low-frequency coding variants alter human adult height. Nature. 2017;542:186–190. doi: 10.1038/nature21039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Calkins M.E., Merikangas K.R., Moore T.M., Burstein M., Behr M.A., Satterthwaite T.D., Ruparel K., Wolf D.H., Roalf D.R., Mentch F.D., et al. The Philadelphia Neurodevelopmental Cohort: constructing a deep phenotyping collaborative. J. Child Psychol. Psychiatry. 2015;56:1356–1369. doi: 10.1111/jcpp.12416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Glessner J.T., Reilly M.P., Kim C.E., Takahashi N., Albano A., Hou C., Bradfield J.P., Zhang H., Sleiman P.M.A., Flory J.H., et al. Strong synaptic transmission impact by copy number variations in schizophrenia. Proc. Natl. Acad. Sci. U S A. 2010;107:10584. doi: 10.1073/pnas.1000274107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Uban K.A., Horton M.K., Jacobus J., Heyser C., Thompson W.K., Tapert S.F., Madden P.A.F., Sowell E.R. Biospecimens and the ABCD study: rationale, methods of collection, measurement and early data. Dev. Cogn. Neurosci. 2018;32:97–106. doi: 10.1016/j.dcn.2018.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chang C.C., Chow C.C., Tellier L.C.A.M., Vattikuti S., Purcell S.M., Lee J.J. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience. 2015;4:7. doi: 10.1186/s13742-015-0047-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rayner N.W. HRC-1000G-check-bim-v4.2.9. 2018. https://www.well.ox.ac.uk/∼wrayner/tools/index.html#Checking
- 50.Das S., Forer L., Schönherr S., Sidore C., Locke A.E., Kwong A., Vrieze S.I., Chew E.Y., Levy S., McGue M., et al. Next-generation genotype imputation service and methods. Nat. Genet. 2016;48:1284–1287. doi: 10.1038/ng.3656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Danecek P., Bonfield J.K., Liddle J., Marshall J., Ohan V., Pollard M.O., et al. Twelve years of SAMtools and BCFtools. GigaScience. 2021;10 doi: 10.1093/gigascience/giab008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Manichaikul A., Mychaleckyj J.C., Rich S.S., Daly K., Sale M., Chen W.-M. Robust relationship inference in genome-wide association studies. Bioinformatics. 2010;26:2867–2873. doi: 10.1093/bioinformatics/btq559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Meyer D., Dimitriadou E., Hornik K., Weingessel A., Leisch F., Chang C.-C., Lin C.-C. Misc functions of the department of statistics, probability theory group (Formerly: E1071), TU Wien. 2020. https://CRAN.R-project.org/package=e1071
- 54.R Core Team . R Foundation for Statistical Computing; 2019. R: A Language and Environment for Statistical Computing. [Google Scholar]
- 55.Bulik-Sullivan B.K., Loh P.-R., Finucane H.K., Ripke S., Yang J., Patterson N., Daly M.J., Price A.L., Neale B.M., Schizophrenia Working Group of the Psychiatric Genomics Consortium LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 2015;47:291–295. doi: 10.1038/ng.3211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bulik-Sullivan B., Finucane H.K., Anttila V., Gusev A., Day F.R., Loh P.-R., Duncan L., Perry J.R.B., Patterson N., Robinson E.B., et al. An atlas of genetic correlations across human diseases and traits. Nat. Genet. 2015;47:1236–1241. doi: 10.1038/ng.3406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Luo Y., Li X., Wang X., Gazal S., Mercader J.M., Neale B.M., et al. Estimating heritability and its enrichment in tissue-specific gene sets in admixed populations. Hum. Mol. Genet. 2021;30:1521–1534. doi: 10.1093/hmg/ddab130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bycroft C., Freeman C., Petkova D., Band G., Elliott L.T., Sharp K., Motyer A., Vukcevic D., Delaneau O., O’Connell J., et al. The UK Biobank resource with deep phenotyping and genomic data. Nature. 2018;562:203–209. doi: 10.1038/s41586-018-0579-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gibson G. On the utilization of polygenic risk scores for therapeutic targeting. PLoS Genet. 2019;15:e1008060. doi: 10.1371/journal.pgen.1008060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Daskalakis N.P., Schultz L.M., Visoki E., Moore T.M., Argabright S.T., Harnett N.G., DiDomenico G.E., Warrier V., Almasy L., Barzilay R. Contributions of PTSD polygenic risk and environmental stress to suicidality in preadolescents. Neurobiol. Stress. 2021;15:100411. doi: 10.1016/j.ynstr.2021.100411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wolf E.J., Miller M.W., Sullivan D.R., Amstadter A.B., Mitchell K.S., Goldberg J., Magruder K.M. A classical twin study of PTSD symptoms and resilience: evidence for a single spectrum of vulnerability to traumatic stress. Depress. Anxiety. 2018;35:132–139. doi: 10.1002/da.22712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dendup T., Feng X., Clingan S., Astell-Burt T. Environmental risk factors for developing type 2 diabetes mellitus: a systematic review. Int. J. Environ. Res. Public Health. 2018;15:78. doi: 10.3390/ijerph15010078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Curtis D. Polygenic risk score for schizophrenia is more strongly associated with ancestry than with schizophrenia. Psychiatr. Genet. 2018;28:85–89. doi: 10.1097/YPG.0000000000000206. [DOI] [PubMed] [Google Scholar]
- 64.Reisberg S., Iljasenko T., Läll K., Fischer K., Vilo J. Comparing distributions of polygenic risk scores of type 2 diabetes and coronary heart disease within different populations. PLoS One. 2017;12:e0179238. doi: 10.1371/journal.pone.0179238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wang Y., Guo J., Ni G., Yang J., Visscher P.M., Yengo L. Theoretical and empirical quantification of the accuracy of polygenic scores in ancestry divergent populations. Nat. Commun. 2020;11:3865. doi: 10.1038/s41467-020-17719-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gurdasani D., Barroso I., Zeggini E., Sandhu M.S. Genomics of disease risk in globally diverse populations. Nat. Rev. Genet. 2019;20:520–535. doi: 10.1038/s41576-019-0144-0. [DOI] [PubMed] [Google Scholar]
- 67.Kim M.S., Patel K.P., Teng A.K., Berens A.J., Lachance J. Genetic disease risks can be misestimated across global populations. Genome Biol. 2018;19:179. doi: 10.1186/s13059-018-1561-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Ruan Y., Lin Y.-F., Feng Y.-C.A., Chen C.-Y., Lam M., Guo Z., et al. Improving polygenic prediction in ancestrally diverse populations. medRxiv. 2021 doi: 10.1101/2020.12.27.20248738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pereira L., Mutesa L., Tindana P., Ramsay M. African genetic diversity and adaptation inform a precision medicine agenda. Nat. Rev. Genet. 2021;22:284–306. doi: 10.1038/s41576-020-00306-8. [DOI] [PubMed] [Google Scholar]
- 70.Atkinson E.G., Maihofer A.X., Kanai M., Martin A.R., Karczewski K.J., Santoro M.L., Ulirsch J.C., Kamatani Y., Okada Y., Finucane H.K., et al. Tractor uses local ancestry to enable the inclusion of admixed individuals in GWAS and to boost power. Nat. Genet. 2021;53:195–204. doi: 10.1038/s41588-020-00766-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Homburger J.R., Neben C.L., Mishne G., Zhou A.Y., Kathiresan S., Khera A.V. Low coverage whole genome sequencing enables accurate assessment of common variants and calculation of genome-wide polygenic scores. Genome Med. 2019;11:74. doi: 10.1186/s13073-019-0682-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Taliun D., Harris D.N., Kessler M.D., Carlson J., Szpiech Z.A., Torres R., Taliun S.A.G., Corvelo A., Gogarten S.M., Kang H.M., et al. Sequencing of 53,831 diverse genomes from the NHLBI TOPMed Program. Nature. 2021;590:290–299. doi: 10.1038/s41586-021-03205-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Loh P.-R., Kichaev G., Gazal S., Schoech A.P., Price A.L. Mixed-model association for biobank-scale datasets. Nat. Genet. 2018;50:906–908. doi: 10.1038/s41588-018-0144-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Loh P.-R., Tucker G., Bulik-Sullivan B.K., Vilhjálmsson B.J., Finucane H.K., Salem R.M., Chasman D.I., Ridker P.M., Neale B.M., Berger B., et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 2015;47:284–290. doi: 10.1038/ng.3190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Li Y.R., Keating B.J. Trans-ethnic genome-wide association studies: advantages and challenges of mapping in diverse populations. Genome Med. 2014;6:91. doi: 10.1186/s13073-014-0091-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.De La Vega F.M., Bustamante C.D. Polygenic risk scores: a biased prediction? Genome Med. 2018;10:100. doi: 10.1186/s13073-018-0610-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The PNC and ABCD genomic datasets used in this study are available by application from dbGaP (phs00060) and NDAR (NDA no. 2573), respectively. UK Biobank data are also available by application. All discovery GWAS summary statistics and software used in this study are publicly available; see Web resources for access information.