Abstract
In this paper, we demonstrate the possibility to perform spectroscopy simulations of solvated biological species taking into consideration quantum effects and explicit solvation. We achieve this goal by interfacing our recently developed divide-and-conquer approach for semiclassical initial value representation molecular dynamics with the polarizable AMOEBABIO18 force field. The method is applied to the study of solvation of the thymidine nucleoside in two different polar solvents, water and N,N-dimethylformamide. Such systems are made of up to 2476 atoms. Experimental evidence concerning the different behavior of thymidine in the two solvents is well reproduced by our study, even though quantitative estimates are hampered by the limited accuracy of the classical force field employed. Overall, this study shows that semiclassically approximate quantum dynamical studies of explicitly solvated biological systems are both computationally affordable and insightful.
In contemporary science, there is great effort to address and fully understand the molecular properties of constituent fragments of DNA and RNA. The importance of such building blocks of life lies mainly in the fact that even a minor modification in their molecular structure can largely affect their biological functionality.1 Therefore, nucleobases and nucleosides, with the latter differing from the former owing to the presence of an additional five-membered furanose ring, have been largely studied both experimentally and theoretically. Specifically, the possibility to simulate such systems in their natural environment, i.e., water, is crucial to understand their behavior in vivo.
It is well-known that water solvation has a great influence in the majority of biological processes ranging from cellular function to biomolecular interactions, from biopolymer stability to solvation of simple solutes.2−5 In such systems, water is not a simple passive medium but has a leading role.6 When polar solutes are involved, for example, solvation takes place engaging the dipole moment of water that reorients itself in response to the solute charge distribution. Remarkably, it has been estimated that electronic solvation could account for up to half of the overall solvation free energy.6 Even in the presence of hydrophobic solutes, water behavior is active and plays an important role, for instance, in the hydrophobic effect. Several works, based on different experimental techniques such as nuclear magnetic resonance (NMR), high-performance liquid chromatography (HPLC), and neutron scattering, show that, in the presence of an apolar solute, water rearranges its hydrogen bond network creating a cavity.7−10 Interactions between the solute and the solvent, for nonpolar solvation, derive mainly from weak dispersion forces originating from the fluctuation of induced dipoles within solvent and solute molecules rather than from the electrostatics of charge distributions as in the polar solutes case.11−15 Furthermore, water can also interact with solutes in a site-specific and “nonbulk” manner. Nucleic acids offer a good example of how water can interact in a sequence-specific manner, such as the zigzag spine of hydration in the minor groove of B-DNA.3,16−20
For all these reasons, when these kinds of systems have to be computationally simulated, an explicit treatment of the solvent should be in principle preferred over an implicit one. However, simulating biological molecules using explicit water molecules requires high computational costs and resources. These requirements entirely exclude the possibility of using accurate ab initio molecular dynamics methods (AIMD), in which the potential energy is evaluated adopting an ab initio quantum method, such as MP2, Coupled Cluster, or the family of DFT functionals. Therefore, the most common type of potential employed in explicit solvation is obtained from classical molecular mechanics (MM) carried out by using popular and well-tested force fields, such as AMBER,21,22 CHARMM,23,24 or AMOEBABIO18.25,26 This approach permits even dynamical studies of large dimensional systems, because the quantum electronic structure is not calculated and polarization effects are quite approximated. To recover a more accurate chemical description, the hybrid quantum mechanical/molecular mechanics method (QM/MM) is a feasible option, often used to treat the electronic problem in case of chemical reactions or enzymatic processes in condensed phase.27−30 In such an approach, the total system is partitioned into subsystems treated with different theories according to the level of detail needed. QM/MM represents a good compromise between feasibility and chemical accuracy, but it presents some difficulties such as domain partitioning and dynamical continuity between the partitions.27
In this work, we employ the affordable molecular mechanics description of the potential, through the polarizable AMOEBABIO18 force field, with the aim to investigate the vibrational power spectrum of thymidine in explicit solvents. Specifically, the general importance of thymidine lies in the fact that some of its analogues were intensively employed as anti-HIV drugs. In the literature, several studies involving experimental work about thymidine in water and the theoretical analysis of thymidine interacting with one or more water molecules are found.31−35 To recover a high level of chemical description in detecting the vibrational spectrum, we use the divide-and-conquer semiclassical initial value representation (DC SCIVR) method, which relies on classical trajectories but is able to provide quantum effects by means of the semiclassical formalism.36−38 Indeed, one of the strengths of semiclassical dynamics (and the DC-SCIVR approach) lies in its capability to include all kinds of quantum effects like anharmonic overtones and combination bands, in addition to the anharmonic contributions of the potential energy surface.39−48 By choosing this method and by accounting for the water solvent explicitly, we aim at reproducing solvation in a remarkably accurate and complete way.
In this context, after investigating the spectroscopy of nucleobases,49 we recently presented a study that involves four nucleosides.50 In that paper we showed and discussed their vibrational power spectra in gas phase, obtained by means of the semiclassical DC-SCIVR method performed with AMOEBABIO18 calculations. In that analysis, we compared the AMOEBABIO18 performance against ab initio DFT calculations in reproducing experimental vibrational frequencies by means of DC SCIVR. This allowed us to point out the reasonable quality of the predictions obtained with that force field with respect to the perhaps more popular AMBER competitor. Furthermore, we presented the power spectrum of thymidine in the range of 1500–1800 wavenumbers, where some important nucleobase spectral signatures are located. In particular, we could analyze the C4O and C5C6 stretchings (see Figure 1 for the atom numbering employed) that are also detected by the gas phase experiment.51
Figure 1.
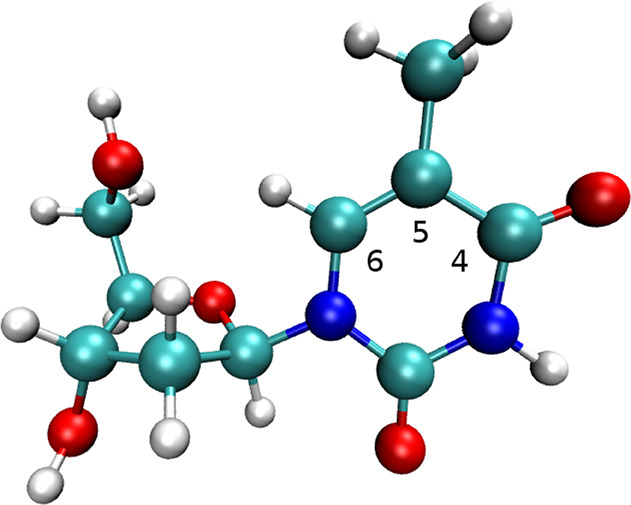
Relevant atomic numbering of isolated thymidine.
In the present work, the experimental frequencies we take as a reference for thymidine in condensed phase are instead offered by the research of Loppnow and co-workers.33 In their paper they showed a comparison between Raman spectra of thymine and thymidine recorded in the 750–1850 cm–1 frequency range employing different solvents, among which are water and N,N-dimethylformamide (N,N-DMF). They noticed that stretching signals associated with thymidine C4O and C5C6 bonds were basically degenerate at around 1710 cm–1 in the case of water and almost all other solvents, with the exception of N,N-DMF, in which case a double peak in the same frequency region was detected. This scenario offers us the possibility to demonstrate that the semiclassical DC-SCIVR method, together with AMOEBA force fields, can be efficiently employed for simulation of biological systems in condensed phase, reproducing at least qualitatively the correct effect of different solvents on the vibrational features of thymidine.
All the simulations have been performed using the AMOEBA force fields, as implemented in the Tinker 8.6.1 software. In particular, we present our studies of thymidine in water, as parametrized in the AMOEBABIO18 force field, while we used AMOEBA09 parameters to model the N,N-DMF solvent, since it is not present in AMOEBABIO18.35,52 For both solvents, we inserted the thymidine molecules in a cubic box whose sides measured 30 Å, as represented in Figure 2. In all calculations, the periodic boundary conditions are fully considered, using the particle mesh Ewald (PME) scheme for the long-range interactions.53,54
Figure 2.
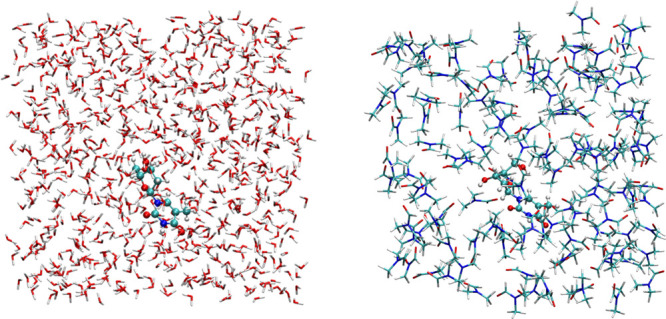
Thymidine in a box of water (left) and N,N-DMF (right) molecules.
The minimization and the subsequent Hessian matrix calculation led us to estimate the harmonic vibrational frequencies. After the optimization phase, NVE trajectories have been propagated using periodic boundary conditions and Beeman’s integration algorithm for a total time of 0.6 ps, employing a time step equal to 0.2 fs. To produce the spectra, we adopted the DC-SCIVR theoretical method. Such a methodology has its foundation in the earlier time averaged (TA-SCIVR) and multiple coherent (MC-SCIVR) semiclassical initial value representation approaches, and it can be fruitfully applied to large dimensional systems thanks to the projection of all quantities involved onto subsystems of reduced dimensionality.36,55−63 The DC-SCIVR working formula we employed is
| 1 |
where 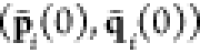 are the projected configurations
and momenta
of the system degrees of freedom at the beginning of the trajectory, T is the total simulation time,
are the projected configurations
and momenta
of the system degrees of freedom at the beginning of the trajectory, T is the total simulation time, 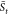 is the instantaneously
projected classical
action at time t,
is the instantaneously
projected classical
action at time t, 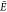 is the Fourier-transform projected
energy,
and
is the Fourier-transform projected
energy,
and 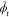 is the phase
of the projected prefactor,
whose definition is
is the phase
of the projected prefactor,
whose definition is
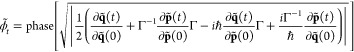 |
2 |
Such an approach
requires evaluation of the
Hessian matrix step by step along the trajectory and the potential
projected in the subspace, which contributes to the evaluation of  . Following a well-consolidated
protocol
of semiclassical spectroscopy,37,59 we employed a single
trajectory characterized by a harmonic estimate of the NVE trajectory
energy. Among all the existing procedures to partition the total degrees
of freedom in subspaces, we chose the average Hessian matrix criterion,61 which led to monodimensional subspaces for the
C5C6 and C4O stretchings under examination for both solvents. We adopted
the Hessian update approximation by evaluating only one Hessian matrix
every 100 dynamics steps and using the gradient to estimate it for
the other steps.64,65 The rationale behind this choice
is that the approximation has been demonstrated in several applications
to be accurate enough65 and the amount
of data that 3000 Hessian matrix calculations produce would be too
high to be stored, in spite of the limited computational cost required
for Hessian matrix calculations with AMOEBABIO18. For the simulation
using water as the solvent, we chose the zero point energy (ZPE) trajectory.
This is a trajectory in which every normal mode has a starting velocity
derived from the estimated harmonic ZPE energy. For the simulation
of thymidine in N,N-DMF solvent,
one trajectory was run for each mode under investigation and, to better
account for the coupling between modes, the trajectory was prepared
in a different way as successfully tested in previous applications
of semiclassical dynamics.66−69 Specifically, atomic velocities were determined such
that the total energy included a quantum of excitation in the vibrational
mode of thymidine under investigation in addition to the ZPE energy,
while the starting geometry was slightly displaced from the equilibrium
one. Details can be found in the Supporting Information.
. Following a well-consolidated
protocol
of semiclassical spectroscopy,37,59 we employed a single
trajectory characterized by a harmonic estimate of the NVE trajectory
energy. Among all the existing procedures to partition the total degrees
of freedom in subspaces, we chose the average Hessian matrix criterion,61 which led to monodimensional subspaces for the
C5C6 and C4O stretchings under examination for both solvents. We adopted
the Hessian update approximation by evaluating only one Hessian matrix
every 100 dynamics steps and using the gradient to estimate it for
the other steps.64,65 The rationale behind this choice
is that the approximation has been demonstrated in several applications
to be accurate enough65 and the amount
of data that 3000 Hessian matrix calculations produce would be too
high to be stored, in spite of the limited computational cost required
for Hessian matrix calculations with AMOEBABIO18. For the simulation
using water as the solvent, we chose the zero point energy (ZPE) trajectory.
This is a trajectory in which every normal mode has a starting velocity
derived from the estimated harmonic ZPE energy. For the simulation
of thymidine in N,N-DMF solvent,
one trajectory was run for each mode under investigation and, to better
account for the coupling between modes, the trajectory was prepared
in a different way as successfully tested in previous applications
of semiclassical dynamics.66−69 Specifically, atomic velocities were determined such
that the total energy included a quantum of excitation in the vibrational
mode of thymidine under investigation in addition to the ZPE energy,
while the starting geometry was slightly displaced from the equilibrium
one. Details can be found in the Supporting Information.
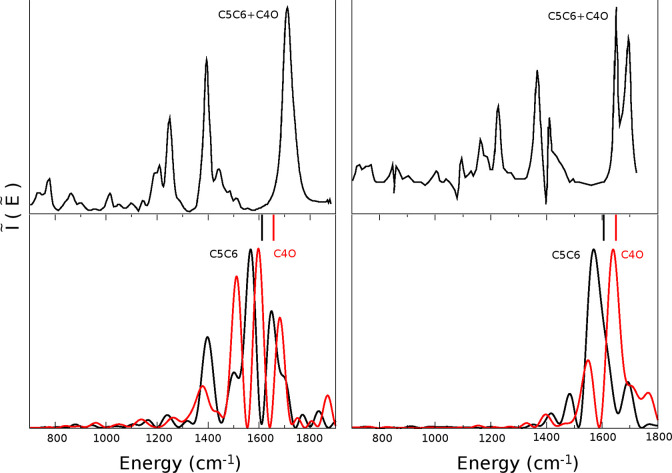
All the calculated frequencies are reported in Table 1, while Figure 3 shows the comparison between the experimental findings and the AMOEBABIO18 DC-SCIVR spectra. The harmonic frequencies are reported in the figure with vertical sticks positioned above the semiclassical peaks. As already discussed in our previous work,50 AMOEBABIO18 can be successfully employed to obtain qualitative results. For this reason, we started looking at gaps between spectral signals rather than single frequency values. In fact, the isolated thymidine C5C6 and C4O stretching frequencies reported in our previous paper highlight the correct gap between these stretchings, equal to 70 cm–1, to be compared with the gas-phase experiment which reports a gap equal to 52 cm–1. We obtained similarly reliable results upon moving to solvated systems. Figure 3 shows that when thymidine is solvated by water, the two semiclassical fundamental peaks for C5C6 and C4O are very close to each other, being only 30 cm–1 apart. When N,N-DMF is employed as a solvent, instead, we expect a different picture because the experiment displays a clear double peak. This feature is well reproduced in our DC-SCIVR calculations, which indicate a 70 cm–1 gap in this case. It is important to note that the simple harmonic calculation is not able to regain the same difference, giving for both solvents a gap approximately equal to 50 cm–1.33 Furthermore, in the case of N,N-DMF, the investigated thymidine peaks appear much less split than in water, since fewer interactions influencing them are present. To further prove that, we notice that the semiclassical spectra of thymidine in water present more than one pronounced peak around the fundamental one, in particular for the C4O signal. They are present because of all the interactions that affect the C4O stretch, which come from the solvent but also from other thymidine modes of vibrations like the C5C6 stretch. We recall that we are calculating the power spectrum, i.e., the vibrational density of states, and there are several vibrational states coupled to the C4O stretch within the investigated energy range. In fact, the DC-SCIVR methodology is able to recover overtones and combination bands, which certainly contribute to enrich the vibrational spectrum.
Table 1. Experimental, Harmonic, and Semiclassical Vibrational Frequencies for All the Systems Investigateda.
| expt | harm | DC-SCIVR | |
|---|---|---|---|
| isolated thymidine50 | |||
| C4O | 1714 | 1688 | 1670 |
| C5C6 | 1662 | 1578 | 1600 |
| Δ | 52 | 110 | 70 |
| thymidine in water | |||
| C4O | ∼1710 | 1657 | 1597 |
| C5C6 | ∼1710 | 1611 | 1567 |
| Δ | 0 | 46 | 30 |
| thymidine in N,N-DMF | |||
| C4O | ∼1700 | 1650 | 1640 |
| C5C6 | ∼1620 | 1606 | 1570 |
| Δ | 80 | 44 | 70 |
Δ is the difference between the C4O and C5C6 stretching frequencies.
Figure 3.
Comparison between semiclassical spectra of thymidine in a box of water (left) and N,N-DMF (right) and the results of Loppnow’s Raman experiment.
Moving to the analysis of the frequencies of vibration, we observe that the harmonic estimates obtained with AMOEBABIO18 are lower than the experimental frequencies for both simulated solvents, as it was in our previous work.50 Our anharmonic method returns even lower frequencies. Indeed, the DC-SCIVR prediction of the two frequencies in water is 1567 and 1597 cm–1 for the C5C6 and C4O normal modes, respectively, while the experiment highlights a single peak positioned at around 1710 cm–1. Due to the intrinsic accuracy of our method, this result for the closing gap is consistent with the experimental finding and much smaller than the gap for isolated thymidine (70 cm–1). Moving to the N,N-DMF solvent, we obtained 1570 and 1640 cm–1, once again for C5C6 and C4O, respectively. This should be compared to the experiment having the two signals roughly located at 1620 and 1700 cm–1 respectively. Therefore, the gap is correctly described, definitely larger than the one found in water, but the frequencies are somewhat shifted with respect to the experiment. However, we are not interested in reproducing exactly peak positions, a task which is not feasible due to the limited accuracy of the employed force fields and would require a higher level potential energy surface, but their behavior under different conditions. In particular, we want to demonstrate that our approach, combined with AMOEBA force fields, is able to reliably reproduce the effect that different solvents can have on a solvated molecule. Finally, there is one aspect in which our calculations somewhat differ from the experiment: while experimentally the closing gap in water is due to the blue shift of the C5C6 frequency, in our simulations it is the C4O frequency which strongly red shifts. The force field is overestimating the interaction between the C4O lone pair and water hydrogens generating the red shift. Indeed, this issue disappears in the simulation for N,N-DMF, which is not characterized by the same hydrogen bond network as water.
In this work, we applied our DC-SCIVR method for the first time to study a condensed phase system of biological interest. The limited computational cost required by AMOEBA force fields allowed us to study the thymidine nucleoside in two different solvents, water and N,N-DMF, in an explicit fashion, and even adopting periodic boundary conditions to mimic a complete molecular solvation. Our DC-SCIVR method, in conjunction with AMOEBABIO18, confirms its capability to reproduce qualitatively the experimental observations at the quantum mechanical level. Even if a quantitative prediction is not possible due to the limited accuracy of AMOEBABIO18, qualitative studies may open the route to vibrational studies of solvated biological molecules, bringing the community to a deeper understanding of structures and properties of biomolecules.
As a final remark, it should be noticed that in AMOEBABIO18 quantum effects are included in a meanfield way via the force field parametrization to directly reproduce a list of experimental condensed phase properties. Therefore, the force field is designed for classical simulations and performing quantum (semiclassical) calculations could lead to a “double counting” of quantum effects deteriorating the accuracy of the results. While this issue may affect the simulation of vibrational modes involving mainly hydrogen atoms (for instance, high frequency C–H, N–H, and O–H stretches) this is not the case for the simulations presented here.
Acknowledgments
The authors acknowledge financial support from the European Research Council [Grant Agreement No. (647107)—SEMICOMPLEX—ERC-2014-CoG] under the European Union’s Horizon 2020 research and innovation program, and from the Italian Ministry of Education, University, and Research (MIUR) (FARE Program No. R16KN7XBRB-project QURE).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c04087.
The authors declare no competing financial interest.
This paper was published on February 3, 2022, with equation 2 incorrectly written. The corrected version was reposted on February 3, 2022.
Supplementary Material
References
- Gabelica V.Nucleic Acids in The Gas Phase; Springer Nature: London, 2014. [Google Scholar]
- Parsegian V. A.; Rau D. C. Water near intracellular surfaces. J. Cell Biol. 1984, 99, 196s–200s. 10.1083/jcb.99.1.196s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auffinger P.; Hashem Y. Nucleic acid solvation: from outside to insight. Curr. Opin. Struct. Biol. 2007, 17, 325–333. 10.1016/j.sbi.2007.05.008. [DOI] [PubMed] [Google Scholar]
- Prabhu N.; Sharp K. Protein- solvent interactions. Chem. Rev. 2006, 106, 1616–1623. 10.1021/cr040437f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill K. A.; Truskett T. M.; Vlachy V.; Hribar-Lee B. Modeling water, the hydrophobic effect, and ion solvation. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 173–199. 10.1146/annurev.biophys.34.040204.144517. [DOI] [PubMed] [Google Scholar]
- Ren P.; Chun J.; Thomas D. G.; Schnieders M. J.; Marucho M.; Zhang J.; Baker N. A. Biomolecular electrostatics and solvation: a computational perspective. Q. Rev. Biophys. 2012, 45, 427. 10.1017/S003358351200011X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuno K.; Oda K.; Maeda S.; Shindo Y.; Okumura A. 1H-NMR study on water structure in halogenoalcohol-water mixtures. J. Phys. Chem. 1995, 99, 3056–3059. 10.1021/j100010a014. [DOI] [Google Scholar]
- Soper A.; Phillips M. A new determination of the structure of water at 25 C. Chem. Phys. 1986, 107, 47–60. 10.1016/0301-0104(86)85058-3. [DOI] [Google Scholar]
- Soper A. The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa. Chem. Phys. 2000, 258, 121–137. 10.1016/S0301-0104(00)00179-8. [DOI] [Google Scholar]
- Silveston R.; Kronberg B. Water structuring around nonpolar molecules as determined by HPLC. J. Phys. Chem. 1989, 93, 6241–6246. 10.1021/j100353a054. [DOI] [Google Scholar]
- Curutchet C.; Orozco M.; Luque F. J.; Mennucci B.; Tomasi J. Dispersion and repulsion contributions to the solvation free energy: comparison of quantum mechanical and classical approaches in the polarizable continuum model. J. Comput. Chem. 2006, 27, 1769–1780. 10.1002/jcc.20480. [DOI] [PubMed] [Google Scholar]
- Levy R. M.; Zhang L. Y.; Gallicchio E.; Felts A. K. On the nonpolar hydration free energy of proteins: surface area and continuum solvent models for the solute- solvent interaction energy. J. Am. Chem. Soc. 2003, 125, 9523–9530. 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- Gallicchio E.; Kubo M.; Levy R. M. Enthalpy- entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation. J. Phys. Chem. B 2000, 104, 6271–6285. 10.1021/jp0006274. [DOI] [Google Scholar]
- Floris F. M.; Tomasi J.; Ahuir J. P. Dispersion and repulsion contributions to the solvation energy: refinements to a simple computational model in the continuum approximation. J. Comput. Chem. 1991, 12, 784–791. 10.1002/jcc.540120703. [DOI] [Google Scholar]
- Cupellini L.; Amovilli C.; Mennucci B. Electronic Excitations in Nonpolar Solvents: Can the Polarizable Continuum Model Accurately Reproduce Solvent Effects?. J. Phys. Chem. B 2015, 119, 8984–8991. 10.1021/jp507962n. [DOI] [PubMed] [Google Scholar]
- Auffinger P.; Westhof E. RNA solvation: a molecular dynamics simulation perspective. Biopolymers: Original Research on Biomolecules 2000, 56, 266–274. . [DOI] [PubMed] [Google Scholar]
- Auffinger P.; Westhof E. Water and ion binding around RNA and DNA (C, G) oligomers. J. Mol. Cell Biol. 2000, 300, 1113–1131. 10.1006/jmbi.2000.3894. [DOI] [PubMed] [Google Scholar]
- Drew H. R.; Samson S.; Dickerson R. E. Structure of a B-DNA dodecamer at 16 K. Proc. Natl. Acad. Sci. U. S. A. 1982, 79, 4040–4044. 10.1073/pnas.79.13.4040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arai S.; Chatake T.; Ohhara T.; Kurihara K.; Tanaka I.; Suzuki N.; Fujimoto Z.; Mizuno H.; Niimura N. Complicated water orientations in the minor groove of the B-DNA decamer d (CCATTAATGG) 2 observed by neutron diffraction measurements. Nucleic Acids Res. 2005, 33, 3017–3024. 10.1093/nar/gki616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar N.; Marx D. How do ribozymes accommodate additional water molecules upon hydrostatic compression deep into the kilobar pressure regime?. Biophys. Chem. 2019, 252, 106192. 10.1016/j.bpc.2019.106192. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D. Jr; Feig M.; Brooks C. L. Improved treatment of the protein backbone in empirical force fields. J. Am. Chem. Soc. 2004, 126, 698–699. 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- Best R. B.; Zhu X.; Shim J.; Lopes P. E.; Mittal J.; Feig M.; MacKerell A. D. Jr Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone ϕ, ψ and side-chain χ1 and χ2 dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rackers J. A.; Wang Z.; Lu C.; Laury M. L.; Lagardere L.; Schnieders M. J.; Piquemal J.-P.; Ren P.; Ponder J. W. Tinker 8: software tools for molecular design. J. Chem. Theory Comput. 2018, 14, 5273–5289. 10.1021/acs.jctc.8b00529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C.; Lu C.; Jing Z.; Wu C.; Piquemal J.-P.; Ponder J. W.; Ren P. AMOEBA polarizable atomic multipole force field for nucleic acids. J. Chem. Theory Comput. 2018, 14, 2084–2108. 10.1021/acs.jctc.7b01169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.-N.; Liu W.; Li P.; Mo Y.; Hu W.; Zheng J.; Pan X.; Shao Y.; Mei Y. Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference-Potential. 4. Adaptive QM/MM. J. Chem. Theory Comput. 2021, 17, 1318–1325. 10.1021/acs.jctc.0c01149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunk E.; Rothlisberger U. Mixed quantum mechanical/molecular mechanical molecular dynamics simulations of biological systems in ground and electronically excited states. Chem. Rev. 2015, 115, 6217–6263. 10.1021/cr500628b. [DOI] [PubMed] [Google Scholar]
- Senn H. M.; Thiel W. QM/MM methods for biomolecular systems. Angew. Chem., Int. Ed. 2009, 48, 1198–1229. 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- Hu H.; Yang W. Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods. Annu. Rev. Phys. Chem. 2008, 59, 573. 10.1146/annurev.physchem.59.032607.093618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foloppe N.; Nilsson L. Toward a full characterization of nucleic acid components in aqueous solution: simulations of nucleosides. J. Phys. Chem. B 2005, 109, 9119–9131. 10.1021/jp044513u. [DOI] [PubMed] [Google Scholar]
- Zhu X.-M.; Wang H.-g.; Zheng X.; Phillips D. L. Role of ribose in the initial excited state structural dynamics of thymidine in water solution: A resonance raman and density functional theory investigation. J. Phys. Chem. B 2008, 112, 15828–15836. 10.1021/jp806248b. [DOI] [PubMed] [Google Scholar]
- Beyere L.; Arboleda P.; Monga V.; Loppnow G. The dependence of thymine and thymidine Raman spectra on solvent. Can. J. Chem. 2004, 82, 1092–1101. 10.1139/v04-052. [DOI] [Google Scholar]
- Erickson B. A.; Heim Z. N.; Pieri E.; Liu E.; Martinez T. J.; Neumark D. M. Relaxation Dynamics of Hydrated Thymine, Thymidine, and Thymidine Monophosphate Probed by Liquid Jet Time-Resolved Photoelectron Spectroscopy. J. Phys. Chem. A 2019, 123, 10676–10684. 10.1021/acs.jpca.9b08258. [DOI] [PubMed] [Google Scholar]
- Palafox M. A.; Iza N.; Fuente M. d. l.; Navarro R. Simulation of the first hydration shell of nucleosides D4T and Thymidine: structures obtained using MP2 and DFT methods. J. Phys. Chem. B 2009, 113, 2458–2476. 10.1021/jp806684v. [DOI] [PubMed] [Google Scholar]
- Ceotto M.; Di Liberto G.; Conte R. Semiclassical ”Divide-and-Conquer” Method for Spectroscopic Calculations of High Dimensional Molecular Systems. Phys. Rev. Lett. 2017, 119, 010401. 10.1103/PhysRevLett.119.010401. [DOI] [PubMed] [Google Scholar]
- Conte R.; Ceotto M.. Semiclassical Molecular Dynamics for Spectroscopic Calculations; Wiley, 2019; pp 595–628. [Google Scholar]
- Gandolfi M.; Rognoni A.; Aieta C.; Conte R.; Ceotto M. Machine learning for vibrational spectroscopy via divide-and-conquer semiclassical initial value representation molecular dynamics with application to N-methylacetamide. J. Chem. Phys. 2020, 153, 204104. 10.1063/5.0031892. [DOI] [PubMed] [Google Scholar]
- Heller E. J. The semiclassical way to molecular spectroscopy. Acc. Chem. Res. 1981, 14, 368–375. 10.1021/ar00072a002. [DOI] [Google Scholar]
- Miller W. H. The semiclassical initial value representation: A potentially practical way for adding quantum effects to classical molecular dynamics simulations. J. Phys. Chem. A 2001, 105, 2942–2955. 10.1021/jp003712k. [DOI] [Google Scholar]
- Miller W. H. Quantum dynamics of complex molecular systems. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6660–6664. 10.1073/pnas.0408043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossmann F. A semiclassical hybrid approach to many particle quantum dynamics. J. Chem. Phys. 2006, 125, 014111. 10.1063/1.2213255. [DOI] [PubMed] [Google Scholar]
- Buchholz M.; Grossmann F.; Ceotto M. Application of the mixed time-averaging semiclassical initial value representation method to complex molecular spectra. J. Chem. Phys. 2017, 147, 164110. 10.1063/1.4998510. [DOI] [PubMed] [Google Scholar]
- Buchholz M.; Grossmann F.; Ceotto M. Simplified approach to the mixed time-averaging semiclassical initial value representation for the calculation of dense vibrational spectra. J. Chem. Phys. 2018, 148, 114107. 10.1063/1.5020144. [DOI] [PubMed] [Google Scholar]
- Bertaina G.; Di Liberto G.; Ceotto M. Reduced rovibrational coupling Cartesian dynamics for semiclassical calculations: Application to the spectrum of the Zundel cation. J. Chem. Phys. 2019, 151, 114307. 10.1063/1.5114616. [DOI] [PubMed] [Google Scholar]
- Gabas F.; Di Liberto G.; Conte R.; Ceotto M. Protonated glycine supramolecular systems: the need for quantum dynamics. Chem. Sci. 2018, 9, 7894–7901. 10.1039/C8SC03041C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rognoni A.; Conte R.; Ceotto M. Caldeira–Leggett model vs ab initio potential: A vibrational spectroscopy test of water solvation. J. Chem. Phys. 2021, 154, 094106. 10.1063/5.0040494. [DOI] [PubMed] [Google Scholar]
- Rognoni A.; Conte R.; Ceotto M. How many water molecules are needed to solvate one?. Chem. Sci. 2021, 12, 2060–2064. 10.1039/D0SC05785A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabas F.; Di Liberto G.; Ceotto M. Vibrational investigation of nucleobases by means of divide and conquer semiclassical dynamics. J. Chem. Phys. 2019, 150, 224107. 10.1063/1.5100503. [DOI] [PubMed] [Google Scholar]
- Gabas F.; Conte R.; Ceotto M. Semiclassical Vibrational Spectroscopy of Biological Molecules using Force Fields. J. Chem. Theory and Comput. 2020, 16, 3476. 10.1021/acs.jctc.0c00127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov A. Y.; Stepanian S.; Karachevtsev V.; Adamowicz L. Nucleoside conformers in low-temperature argon matrices: Fourier transform IR spectroscopy of isolated thymidine and deuterothymidine molecules and quantum-mechanical calculations. Low Temp. Phys. 2019, 45, 1008–1017. 10.1063/1.5121271. [DOI] [Google Scholar]
- Alcolea Palafox M.; Kattan D.; Afseth N.K. FT-IR spectra of the anti-HIV nucleoside analogue d4T (Stavudine). Solid state simulation by DFT methods and scaling by different procedures. J. Mol. Struct. 2018, 1157, 587–601. 10.1016/j.molstruc.2017.12.079. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Kaledin A. L.; Miller W. H. Time averaging the semiclassical initial value representation for the calculation of vibrational energy levels. J. Chem. Phys. 2003, 118, 7174–7182. 10.1063/1.1562158. [DOI] [Google Scholar]
- Kaledin A. L.; Miller W. H. Time averaging the semiclassical initial value representation for the calculation of vibrational energy levels. II. Application to H2CO, NH3, CH4, CH2D2. J. Chem. Phys. 2003, 119, 3078–3084. 10.1063/1.1589477. [DOI] [Google Scholar]
- Ceotto M.; Tantardini G. F.; Aspuru-Guzik A. Fighting the curse of dimensionality in first-principles semiclassical calculations: Non-local reference states for large number of dimensions. J. Chem. Phys. 2011, 135, 214108. 10.1063/1.3664731. [DOI] [PubMed] [Google Scholar]
- Ceotto M.; Valleau S.; Tantardini G. F.; Aspuru-Guzik A. First principles semiclassical calculations of vibrational eigenfunctions. J. Chem. Phys. 2011, 134, 234103. 10.1063/1.3599469. [DOI] [PubMed] [Google Scholar]
- Ceotto M.; Atahan S.; Tantardini G. F.; Aspuru-Guzik A. Multiple coherent states for first-principles semiclassical initial value representation molecular dynamics. J. Chem. Phys. 2009, 130, 234113. 10.1063/1.3155062. [DOI] [PubMed] [Google Scholar]
- Ceotto M.; Atahan S.; Shim S.; Tantardini G. F.; Aspuru-Guzik A. First-principles semiclassical initial value representation molecular dynamics. Phys. Chem. Chem. Phys. 2009, 11, 3861–3867. 10.1039/b820785b. [DOI] [PubMed] [Google Scholar]
- Di Liberto G.; Conte R.; Ceotto M. ”Divide and conquer” semiclassical molecular dynamics: A practical method for spectroscopic calculations of high dimensional molecular systems. J. Chem. Phys. 2018, 148, 014307. 10.1063/1.5010388. [DOI] [PubMed] [Google Scholar]
- Cazzaniga M.; Micciarelli M.; Moriggi F.; Mahmoud A.; Gabas F.; Ceotto M. Anharmonic Calculations of Vibrational Spectra for Molecular Adsorbates: A Divide-and-Conquer Semiclassical Molecular Dynamics Approach. J. Chem. Phys. 2020, 152, 104104. 10.1063/1.5142682. [DOI] [PubMed] [Google Scholar]
- Di Liberto G.; Conte R.; Ceotto M. ”Divide-and-conquer” semiclassical molecular dynamics: An application to water clusters. J. Chem. Phys. 2018, 148, 104302. 10.1063/1.5023155. [DOI] [PubMed] [Google Scholar]
- Zhuang Y.; Siebert M. R.; Hase W. L.; Kay K. G.; Ceotto M. Evaluating the Accuracy of Hessian Approximations for Direct Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 54–64. 10.1021/ct300573h. [DOI] [PubMed] [Google Scholar]
- Ceotto M.; Zhuang Y.; Hase W. L. Accelerated direct semiclassical molecular dynamics using a compact finite difference Hessian scheme. J. Chem. Phys. 2013, 138, 054116. 10.1063/1.4789759. [DOI] [PubMed] [Google Scholar]
- Micciarelli M.; Conte R.; Suarez J.; Ceotto M. Anharmonic vibrational eigenfunctions and infrared spectra from semiclassical molecular dynamics. J. Chem. Phys. 2018, 149, 064115. 10.1063/1.5041911. [DOI] [PubMed] [Google Scholar]
- Conte R.; Parma L.; Aieta C.; Rognoni A.; Ceotto M. Improved semiclassical dynamics through adiabatic switching trajectory sampling. J. Chem. Phys. 2019, 151, 214107. 10.1063/1.5133144. [DOI] [PubMed] [Google Scholar]
- Micciarelli M.; Gabas F.; Conte R.; Ceotto M. An Effective Semiclassical Approach to IR Spectroscopy. J. Chem. Phys. 2019, 150, 184113. 10.1063/1.5096968. [DOI] [PubMed] [Google Scholar]
- Aieta C.; Micciarelli M.; Bertaina G.; Ceotto M. Anharmonic quantum nuclear densities from full dimensional vibrational eigenfunctions with application to protonated glycine. Nat. Commun. 2020, 11, 4338. 10.1038/s41467-020-18211-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.