Abstract
We propose a methodology for estimating the evolution of the epidemiological parameters of a SIRD model (acronym of Susceptible, Infected, Recovered and Deceased individuals) which allows to evaluate the sanitary measures taken by the government, for the COVID-19 in the Spanish outbreak. In our methodology the only information required for estimating these parameters is the time series of deceased people; due to the number of asymptomatic people produced by the COVID-19, it is not possible to know the actual number of infected people at any given time. Therefore, among the different time series that quantify the pandemic we consider just the number of deceased people to minimize the square sum of errors.
The time series of deaths considered runs from March to the end of September and is divided into four sub-periods reflecting the different isolation measures taken by the Spanish government. The parameters that we can estimate are the time from the beginning of the disease, the transmission rate, and the recovery rate; these last two ratios are estimated in each of the different sub-periods. In this way the model considered has 2x4+1=9 parameters that are estimated jointly over the whole period from the data of deceased. Given the complexity of the model, to estimate the parameters that minimize the square sum of errors, a Genetic Algorithm is used.
Our methodology confirms the effectiveness of the sanitary measures taken by the Spanish government showing a dramatic reduction in the basic reproductive number during confinement; also, a further increase in after the end of the alarm state decreed by the government on June 21 was detected. Our results also point out that the Patient Zero in the COVID-19 Spanish outbreak emerged between the end of December and early January, at least four weeks before January 31st, that was the moment when the Spanish authorities reported the first positive case.
Keywords: COVID-19, SIRD model estimation, Predictive modelling, Genetic Algorithm
1. Introduction
The raison d’être of Epidemiology as a science related to the distribution patterns, spread, and causes of diseases was last has been put to the test on January 30, 2020. On that day the World Health Organization (WHO) declared the COVID-19 outbreak to be a public health emergency of international concern due to its amazing spreading power and potential harm.
Since this epidemic was first reported in Wuhan, China, and after its fast spreading all over the world, the research on the domestic and international epidemics and the future development trend has become a hot topic of current research; thus, many teams have studied the transmission law and preventive measures of the COVID-19, trying to find relevant models and data analysis capable of providing some basis and guidance about epidemic prevention and control.
In this sense, predicting the extent of the epidemic in each country is critical to predict the future impact of the disease, and to take immediate actions to prevent the collapse of sanitary services.
Following the WHO, Coronavirus Disease Situation Report 73, the COVID-19 has the following characteristics: (1) A long incubation period; (2) Prevalence of asymptomatic transmission; (3) Detection of infection by PCR (Polymerase Chain Reaction) tests.
From this point of view, one of the main challenges in modelling the evolution of the disease is the existence of many asymptomatic patients who can infect others; thus, the only observable variables of the infectious process are the number of positive cases confirmed by a PCR test and the number of deaths.
Traditionally, the dynamics of infectious diseases such as influenza have been modelled by means of deterministic compartmental models described by differential equations such as the SIR family of models [5], [11], [22]; these compartmental models attempt to model the complex interactions between the different compartment (e.g., susceptible, the infected, and the recovered persons), which have different dynamics.
Alternatively, compartmental models can also be formulated by means of stochastic processes described by a renewal integral equation [16], Markov Chain models [25], time series prediction models such as ARIMA [29], and by integrating with the Gaussian mixture model and the composite logistic growth model [30]; finally, there have also been agent type models simulating individual activities for a population [12]. See Hethcote [19] for a broad perspective on SIR-type models.
It is not easy to give a summary of the several hundred papers in the Mathematical Epidemiology literature devoted to modelling and prediction of COVID-19 that have emerged after its outbreak. Firstly, one could cite the work of Pei and Zhan [28] on the prediction of Covid-19 in various countries using a classical SEIR-type compartmental model. This work is also interesting because of the numerous citations on this topic that appear within it.
In the field of predictive modelling of COVID-19 evolution, it is also of very interesting the Special issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, published in the journal Infectious Disease Modelling [9]. In this sense, we quote the following papers that we consider most relevant from the point of view of our contribution in the present article:
Odagaki [27] analyses the outbreak of COVID-19 in Japan considering that the number of the daily confirmed new cases is explicitly treated as an observable and using a SIQR model, where, in addition to the usual Susceptible, Infected and Recovered compartments, a quarantined patient (Q) compartment is added.
Zhao [33] develops a simple likelihood-based framework to estimate the instantaneous case fatality ratio (CFR), using the publicly available COVID-19 surveillance data in Canada as an example. The CFR, which quantifies the mortality risk of infectious disease when being infected, is commonly calculated as a constant. Nevertheless, changes in some external factors may vary the scale of CFR, e.g., pathogenic evolution, health status, changes in treatment strategies or medication, which could have important implications for the supply of healthcare and critical care resources.
Abusama et al. [3] study the adequacy of Logistic models for describing the dynamics of COVID-19 pandemic. They conclude that the parameters of these models cannot be identified with high certainty, and the models shown to have structural problems as they could not predict reasonably the validation data. Thus, they suggest the use of compartmental models to predict the long-term evolution of COVID-19.
Lia et al. [23], in their analysis of COVID-19 propagation and prediction, use Gaussian distribution theory to construct a new model of coronavirus transmission. They found that the curves of proposed model well simulate the official data curves of Hubei, Non-Hubei area of China, and also, South Korea, Italy, and Iran. The study points out the key factors that affect the spread of the virus are: the basic reproduction number, virus incubation period, and daily infection number.
Ding and Gao [14] propose to evaluate the effect of public health intervention and expect to search the faster way to prevent the COVID-19 in Italy, by means of a data-driven modelling analysis. They consider that the exponential model is not suitable to the Italian situation and tried the SEIR model and modified its parameters’ system according to this country lockdown state; they also considered asymptomatic cases since the similar SIR model was applied in the process of interpretation to prevent and control COVID-19 in China.
Anirudh [6] provides a relevant comparative study on different methodologies in Covid 19 prediction. The paper describes the outcome and the challenges of SIR, SEIR, SEIRU, SIRD, SLIAR, ARIMA, SIDARTHE, etc. models used in prediction of spread, peak, and reduction of COVID-19 cases.
In the continuing stream of new publications on the COVID-19 prediction, it is also worth citing Mellone et al. [26], which propose a new epidemic model that can predict the future number of active cases and deaths when lockdowns with different stringency levels or durations are enforced. They use an extension of the SEIR model of differential equations where new compartments such as infected Undetected, infected Detected, Extinct, undetected Recovered, and detected Recovered are added. The model can capture the abrupt social habit changes caused by lockdowns on the data of Israel and Germany. This work also contains an extensive survey of bibliographical references on mathematical modelling in epidemiology.
It is also interesting to mention the immense repository of preprints that, on COVID-19 SARS-CoV-2, offers the web page www.medRxiv.org. Although these are only preliminary reports of work that have not been certified by peer review, their existence can be very useful in promoting a rapid flow of new ideas.
For the purposes of this paper, it is of particular interest to quote some works on the estimation of parameters in the epidemiological models. In general, the parameter estimation is a crucial problem because the performance of the predictions obtained on the number of infected people and their evolution over time depends to a large extent on the precise knowledge of these parameters. This problem is particularly acute in the case of COVID-19 where, the existence of asymptomatic cases that can transmit the disease prevents a specific knowledge of the reality of the health situation. So, the lack of knowledge of the true parameters controlling the dynamic of the model in a country entails that it is difficult to assess the effectivity of the quarantine measures taken by the government and the actual state of the epidemic at a particular time.
There is not a universal methodology for estimating the key parameters of an epidemic, like , and it is usually calculated with complex mathematical models on disease spread patterns, developed using various sets of assumptions Dietz [13]. In this sense, we quote, among others, the following papers:
Zhao et al. [34] have estimated the by using the serial intervals (SI) of two other well-known coronavirus diseases, MERS and SARS, as approximations for the true unknown SI. They estimated that the ranges from 2.24 (95%CI: 1.96–2.55) to 3.58 (95%CI: 2.89–4.39) associated with 8-fold to 2-fold increase in the reporting rate.
In Wu et al. [31] serial interval calculations were based on previous studies of severe acute respiratory syndrome coronavirus (SARS-CoV). A susceptible–exposed–infectious–recovered metapopulation model was used to simulate the epidemics across all major cities in China. The was estimated using Markov Chain Monte Carlo methods and presented using the resulting posterior mean and 95% credible interval. So, the was estimated at 2.68 (95% CI: 2.47–2.86) with a doubling time of 30 every 6.4 days (95% CI: 5.8–7.1). Imai et al. [21], in order to estimate , they generate a set of simulated epidemic trajectories using a mathematical model of 2019-nCoV transmission and examine the extent to which each trajectory is consistent with their prior estimates of outbreak size (namely 4000 cases by 18th January).
Finally, Yarsky [32] proposes the use of a genetic algorithm to fit parameters of a COVID-19 SEIR model for US states, considering the implications of re-opening and hospital resource utilization. This paper has opened a new door to parameter estimation in the compartmental models of the SIR family.
Our work is in line with the recent work by Yarsky [32] also using a Genetic Algorithm to adjust the model parameters; however, we add several specific contributions to the new methodology. First of all, it only requires the deceased time series to estimate the model parameters; this avoids the complications caused by asymptomatic individuals when establishing the real number of susceptible individuals. Secondly, it is able to jointly estimate the temporal evolution of the epidemiological parameters of COVID-19 in different sub-periods, which makes it possible to evaluate the effectiveness of the successive measures taken by any authority to contain the pandemic. Finally, it allows us to obtain the time at which Patient Zero emerged.
Specifically, we provide a data driven methodology based on a SIRD model (a model from the SIR family that also incorporates the number of deceased people) that permits the estimation of the model parameters that best fit the deceased time series. The number of parameters of the model depends on the number of sub-periods we consider in the analysed sample. Each sub-period is specified by two parameters, the transmission rate or effective contact rate , and the recovery rate . In addition, the date of onset of the epidemic is considered another parameter to be estimated . Thus, in the empirical applications of this work there are 2 × 4 1 9 parameters because the sample has been divided into four sub-periods. These parameters are estimated jointly during the whole period from the date of deceased. Given the complexity of the model, to estimate the parameters that minimize the square sum of errors, a Genetic Algorithm (GA hereafter) is used.
From the beginning of the pandemic some countries have imposed strict measures of full lockdown and successful policies for testing and tracing promptly at the onset of the pandemic; on the other hand, other countries like Spain have imposed these measures after a certain threshold regarding the number of infected individuals. Our procedure allows to know the time evolution of the Basic Reproduction Number in Spain during the first seven months of the pandemic and so assess the effectivity of the successive quarantine measures taken by the Spanish government after the COVID-19 outbreak.
The rest of this paper is organized as follows. The methodology approach is discussed in Section 2. The empirical application is shown in Section 3. Finally, the main conclusions drawn are summarized in Section 4.
2. Methodology
To take into account, the number of deceased people during an epidemic process, we consider an alternative version of SIR model called the SIRD (see [12] as general reference for SIRD model). In this model a population of size is divided into four groups, for the number of susceptible individuals to the infection in the total population, for the number of infected individuals, for the number of recovered individuals and for the number of deceased individuals.
The transition between and takes place with a rate ; where stands for the transmission rate; as usual in the literature , where is the average rate of contacts between susceptible and infected individuals per day, and is the probability of infection given contact between a susceptible and infected individual.
In discrete terms, the four equations of the SIRD model are shown below
| (1) |
In the last three equations, the parameter represents the mean time to recovery of the disease that, as usual, is supposed to be the same as the time that an infected person dies. The parameter represents the recovery rate (e.g., the rate of infected that end up recovering), so, is the daily recovery rate; finally, represents the daily mortality rate.
The initial conditions of the SIRD model are supposed to be
where N represents the total population size. As usual, we work under the assumption that there is no entry into or departure from the population, except through death from the disease. The parameter , that signal the moment when COVID-19 outbroke, is also another crucial parameter for observing the dynamics and temporary location of the effects of the disease.
So, the crucial parameters that we are going to determine are the transmission rate , the recovery rate , and the moment when COVID-19 outbroke; the time to recovery of the disease , is considered to be 16.5 days.1 The knowledge of these parameters permits us to estimate the basic reproduction number (the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection). We also estimate the effective reproduction number which is the average number of secondary cases per infectious case in a population consisting of both susceptible and non-susceptible hosts. This last number is crucial for the control of the disease because indicates that the number of cases will increase, and that will decline.
As Brauer and Castillo-Chavez [8] remark, it is generally difficult to estimate the transmission rate , which depends on the disease being studied but may also depend on social and behavioural factors. The possibility of determining the initial and final number of susceptible by means of serological studies (measurements of immune responses in blood samples before and after an epidemic), permits estimate de basic reproduction number using the equation
(see [8], page 354). However, this estimate is retrospective and can be derived only after the epidemic has run its course.
Another possibility for estimating the parameters of a SIR-type model is by means of non-linear least squares based on the knowledge of the temporal evolution of the number of infected. However, in the case of COVID-19, the existence of a considerable number of asymptomatic individuals and the lack of knowledge from the beginning of the disease, make impossible to apply this procedure. In the model proposed in this paper, all the mentioned parameters are estimated only using the time series of daily deceased people. Despite the inaccuracies it may have as a result of errors and changes in methodologies that occur in the collection of information, we believe that among the time series that describe the process of the current epidemic, the series of deceased is the one that best reflects the reality of it.
A fundamental aspect of the methodology employed in this work to estimate the parameters of the SIRD model is the use of a GA. This problem cannot be solved by classical mathematical programming procedures because the system of difference (or differential) equations that constitute the SIRD model does not have an analytical solution for any of the variables of the model; thus, any time path of the variables of the SIRD model can only be obtained by a numerical method; In particular, this implies that the sum of the square of the errors, which is the objective function we want to minimize to obtain the parameters, has no explicit analytical expression with respect to time and the parameters of the model; thus, we must minimize a function of which we do not know its analytical form and for which only numerical values are available. Moreover, the parameter estimation problem becomes even more complicated because, in order to assess the effects of the measures taken by the government, the parameters we are looking for are not constant over the whole period and may change in the four different sub-periods considered. For these reasons, we employ a heuristic optimization procedure such as GAs to estimate the model parameters by minimizing the sum of squared prediction errors of the deceased.
GAs are a class of random optimization methodology initially introduce by Holland [20], based on the principles of Darwin’s theory of natural evolution and Mendelian inheritance. GAs are commonly used to generate high quality solutions to a very wide class of optimization problems where, neither gradient-based methods nor Mathematical Programming, can be used. That is the case of fitting the parameters of a SIRD model with several periods involved.
To carry out the GA in the present problem of fitting the parameters of a SIRD model, the following steps were followed:
(1) Start with large number of randomly generated potential solutions
| (2) |
to the optimization problem. All these parameters are randomly generated in specific intervals that must be selected in advance. These potential solutions are usually called chromosomes, being (in our case, K 4) is the number of sub-periods and the number of chromosomes. The chromosomes can be encoded in binary form or by real coding. Coding means the structure and content of the chromosome that is assigned to a solution in the search space. In this work we use the real coding (see [17], as general reference).
Each chromosome is able to generate a solution for the system of the difference equations (1), which gives rise a time series for the three four variables . Due to the existence of asymptomatic cases in COVID-19 that can transmit the disease and shortage of diagnostic tests to determine the number of individuals actually infected, we consider that the closest series to reality is that of the daily number of deceased .
(2) The objective function assigns each chromosome a fitness value, ranking chromosomes from best to worst. As we have mention above, the objective function for the GA is the sum of square prediction errors of daily number of dead. Finally, in this step we select an elite of 25% from betters fitted.
(3) These better fitted chromosomes will be the parents of the next generation. Then, a recombination process is taken out to produce descendants. So, an offspring is created combining information from two parent chromosomes to form a couple of children that have the potential to outperform their parents. The recombination process is accomplished as follows: giving rise two chromosome (parents) and like (2), two children and that share the genetic information of their parents are obtained doing and , where is a randomly selected number between 0 and 1.
(4) In order to avoid reaching local optima instead of global optima, all chromosomes, except those best fitted as for the objective function, are candidates to be transformed by a mutation operator, which is essentially a mechanism by which certain information encoded within the chromosome is randomly altered. For example, if the chromosome (in this case ) and the element are selected by random, is substituted by another real value also selected at random in the interval originally specified for the parameter. So, the new chromosome after mutation will be . To not destroy promising solutions, present in the current chromosomes, a small rate of mutation is selected; in our case 10%, but an elite of 25% of better fitted chromosomes are always preserved.
(5) After recombination and mutation, a next generation of chromosomes is obtained applying again the same steps as before; the process ends when a convergence criterion is reached: either when the best of chromosomes remains stable during a given number of successive generations or when we reach a predetermined number of generations, this number being fixed beforehand.
Intuitively, the role of the GA can be summarized as follows: starting from initial conditions for the model variables, a random set of parameter values in each of the sub-periods into which the sample has been divided and an initial time , also random, when patient zero of the disease appears, the GA simulates numerous numerical solutions of the corresponding SIRD system. These solutions, by means of the parameters associated with them, are recombined, mutated and improved until an optimal solution is obtained in the sense of producing the best fit to the deceased data.
3. Empirical applications
Data on deceased cases used in this paper were obtained from the reports published by Spanish Ministry of Health and the Carlos III Health Institute (ISCIII) [18].
The time series of deaths considered runs from March 11th, 2020 (when the Spanish government announced the first one hundred deaths), to the end of September. To assess the effectivity of quarantine measures taken by the government, we consider four sub-periods that correspond with the main restrictions on the movement of Spanish population. It is important to note that although the sample period is divided into four sub-periods, the estimation of the parameters is done jointly and not separately for each of the sub-periods:
Sub-period 1: From March 11th, 2020 (first day in which the accumulated figure of more than 100 deaths was reached), until March 30th (beginning of total confinement with suspension of non-essential activities until April 9th). On March 14th, the Spanish government decrees the state of alarm and quarantine begins throughout the country.
Sub-period 2: From March 31st to May 4th (beginning of the de-escalation of the quarantine measures in four phases). From March 31st to April 9th, quarantine measures are reinforced, with suspension of non-essential activities. After April 9th, the quarantine measures are similar to those of the first sub-period.
Sub-period 3: From May 5th to June 21st (end of the state of alarm). In this sub-period Spain tries to adapt to the “new normality”, which is characterized by a gradual and phased return to various social and economic activities.
Sub-period 4: From June 22nd to September 30th, 2020.
The parameters that we must estimate are the time from the beginning of the disease , the transmission rate , and the recovery rate ; these last two ratios are estimated in each of the different sub-periods. In this way the model considered has 2 × 4 1 9 parameters that are estimated jointly during the whole period from the data of deceased. Thus, the nine parameter values of the model can be represented in the form: where the subindex refers to the period where the parameters are estimated. Given the complex nature of the model, in order to fit the optimal solution of these parameters in the sense of ordinary least squares, the usual optimization procedures are not able to solve this minimization problem; for this reason, the use of a heuristic optimization method as a GA is necessary [4].
Using a GA, we have estimated the nine parameters of our model corresponding to the four sub-periods considered. The number of chromosomes of the algorithm was stablished in 5000, and the stopping criterium for convergence was stablished in 1000 generations. Of course, higher values of these hyper-parameters of the algorithm can be considered but the figures employed in this paper were selected to permit everybody reproduce the results in an ordinary PC, without a super-computation. In any case, it has been observed that the use of higher values than the previous ones, when they improve the results, does so only marginally.
Specifically, the selected initial intervals that the algorithm needs to randomly select the initial values of the parameters are: , for the time from the beginning of the disease ; , for the transmission rate ; and , for the recovery rate .
Table 1 shows that the lowest transmission rate is reached in sub-period 3. It is widely accepted that the pandemic was taken under control the second week of May after the quarantine period. More specifically, our results indicate that, in the first sub-period that cover the first two weeks of the quarantine, the value of was 3.44, the transmission rate 0.21 and a mortality rate of 9.3%. In the second sub-period, as a result of the measures taken since the beginning of the state of alarm, these figures were reduced to 0.30, 0.02 and 6.5%, respectively. In the third sub-period, which marks the end of the alarm state on June 21st, the lowest disease transmission and mortality rates are reached. Concretely, the value of was 0.16, the transmission rate 0.01 and a mortality rate of 4.4%. Finally, because of the relaxation of the alarm measures, the levels of disease transmission increased in the fourth sub-period, without reaching the high levels recorded in the first sub-period. The results also highlight the continuous decrease in the mortality rate throughout the four periods, something that could be associated both with an improvement in the effectiveness of the treatments used and better self-protection of the most vulnerable groups. It is also important to note that during the first sub-period, healthcare in several hospitals collapsed due to the lack of ICU beds. For this same sub-period, Ceylan [10] obtains a higher mortality ratio for Spain than the one we have obtained in this work.
Table 1.
Estimated parameters for the SIRD model in the four sub periods considered and the confidence intervals of these parameters. Sample: From March 11th, 2020 to September 30th, 2020. Breakpoints (3): March 30th, 2020; May 04th, 2020; Jun 21st, 2020. Initial parameter intervals: ; ; .
| Sub-periods | Symbol parameter |
|||||
|---|---|---|---|---|---|---|
| basic reproduction number | transmission rate | mortality rate | ||||
| March 11th, 2020–March 30th, 2020 | 3.43939 | (3.28772, 3.72766)a | 0.20845 | (0.19926, 0.22592)a | 0.09315 | (0.06470, 0.09360)a |
| (3.14354, 3.71452)b | (0.19052, 0.22512)b | (0.06894, 0.09607)b | ||||
| March 31st, 2020–May 04th, 2020 | 0.29758 | (0.20598, 0.32080)a | 0.01803 | (0.01248, 0.01944)a | 0.06458 | (0.04438, 0.67916)a |
| (0.17768, 0.31312)b | (0.01077, 0.01898)b | (0.04776, 0.07704)b | ||||
| May 05th, 2020–Jun 21st, 2020 | 0.15537 | (0.02958, 0.24094)a | 0.00942 | (0.00179, 0.01460)a | 0.04408 | (0.03184, 0.05788)a |
| (0.03705, 0.24976)b | (0.00224, 0.01514)b | (0.03373, 0.06672)b | ||||
| Jun 22nd, 2020–September 30th, 2020 | 1.69067 | (1.63060, 1.75482)a | 0.10246 | (0.09882, 0.10634)a | 0.01211 | (0.00636, 0.02012)a |
| (1.61552, 1.73134)b | (0.09791, 0.10493)b | (0.00760, 0.02524)b | ||||
In the upper panel, intervals where the AG randomly selects the initial values of the different parameters.
On the bottom panel, in bold, estimated parameters for the SIRD model in the four periods considered.
In brackets, two types of confidence intervals of the estimated parameters are presented: sensitivity and usual confidence intervals.
The sensitivity intervals that reveal the sensitivity of the parameters to possible GA repetitions. These intervals show the 5 and 95 percentiles of the parameters obtained in 100 different estimates of the parameters by means of the GA on real data.
The usual confidence intervals, which reveal the sensitivity of the parameters to possible random fluctuations in the data. These intervals show the 5 and 95 percentiles of the parameters obtained by means of estimations made by the GA on 100 bootstrap replications from the original series of deceased.
Our results also point out that the Patient Zero in the COVID-19 Spanish outbreak emerged between the end of December and early January (see [24]), at least four weeks before January 31st, that was the moment when the Spanish authorities reported the first positive case.
Table 1 shows two types of confidence intervals of the estimated parameters: sensitivity and usual confidence intervals. With (a), the sensitivity intervals that reveal the sensitivity of the parameters to possible GA repetitions. These intervals show the 5 and 95 percentiles of the parameters obtained in 100 different estimates of the parameters by means of the GA on real data. With (b), the usual confidence intervals, which reveal the sensitivity of the parameters to possible random fluctuations in the data. These intervals show the 5 and 95 percentiles of the parameters obtained by means of estimations made by the GA on 100 bootstrap replications from the original series of deceased. As it is possible to observe both the sensitivity intervals and the usual confidence intervals, are very narrow, which means the accuracy of the estimates made. We will explain later how the sensitivity intervals and usual confidence intervals were obtained for this methodology based on GAs.
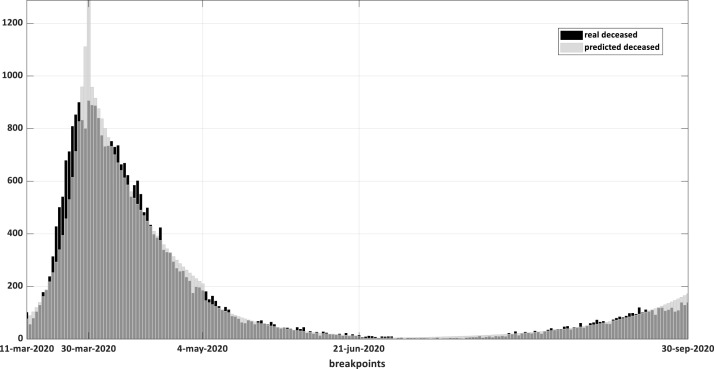
In the following figures of this section we will present graphically the results obtained in Table 1. In these figures we can see, in a concrete way, the effectiveness of the quarantine measures taken by the Spanish government and the subsequent emergence of the disease after the relaxation of the isolation measures. In Fig. 1 we present the real daily deceased people during the Spanish epidemic by September 30th, 2020; we also show its estimation obtained by our methodology of fitting the SIRD model with a GA.
Fig. 1.
Real and predicted daily deceased during the Spanish epidemic by September 30, 2020.
The three vertical lines delimit the four sub-periods considered. In the last two days of the first sub-period there is a significant error between the number of deaths and their predictions, basically due to the change in trend observed at that time. This change in trend is mainly due to the increase in mobility restrictions set by the government. However, once these two days have passed, the model adjusts the parameters, immediately corrects the error, and captures the decreasing trend in deceased.
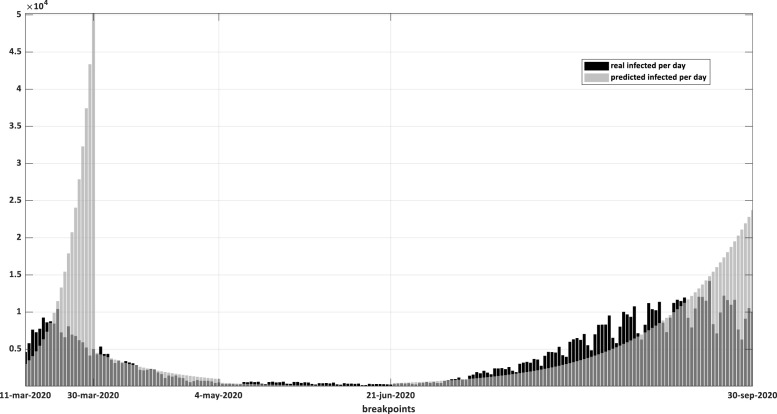
In Fig. 2 we present the actual and model-predicted number of infections, per day. As it is possible to observe, a sharp decline in the number of infected people was produced because of the quarantine measured taken by the Spanish government on March 14th.
Fig. 2.
Number of new infections, per day, actual and predicted by the model.
It is clear that the large difference between the actual and predicted infected in the first sub-period is due to the lack of PCR testing in the country at the beginning of the pandemic and the large number of asymptomatic individuals typical of this disease. It is interesting to note the trend of predicted infected at the end of the fourth sub-period, which apparently does not correspond to the actual number of infected per day. This increasing trend in predictions is heralding the arrival of the third wave of the pandemic.2
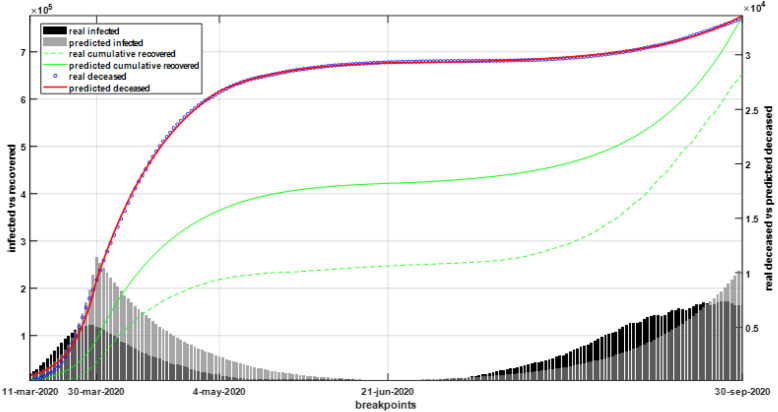
Fig. 3 shows, in right axis, the real and predicted deceased (overlapping upper curves), the real cumulative recovered (green dotted line) and predicted cumulative recovered (green continuous line); in left axis the real active infected3 (in black bands) and predicted active infected and recovered (in grey bands) are also presented.4
Fig. 3.
Right axis: Real and predicted deceased (overlapping upper curves); real cumulative recovered (green dotted line) and predicted cumulative recovered (green continuous line). Left axis: Real active infected (in black bands) and predicted active infected and recovered (in grey bands). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Firstly, it should be noted that, due to the good performance of the GA, whose objective was precisely to adjust the fatality series, the cumulative, actual and predicted fatality curves are almost superimposed each other at the top of Fig. 3.
The differences between actual and predicted cumulative recoveries shown in Fig. 3 are explained by the fact that the SIRD model does not take into account the existence of asymptomatic individuals and the actual recoveries series only includes those recoveries that have shown symptoms of the disease or have undergone a diagnostic test. Thus, the gap between the two sets of recoveries gives an idea of asymptomatic individuals not detected in diagnostic tests. Also, the differences between actual and predicted daily infections in the first sub-period can also be explained by the existence of asymptomatic individuals and the lack of PCR testing initially carried out in Spain.
On the other hand, the differences between actual and predicted active infections at the end of the fourth sub-period could be explained by the end of the quarantine period. With the arrival of summer, there were numerous super-infections in the country associated with agricultural activities (at this time many of the workers in the agricultural sector came from abroad) and the large increase in mobility due to holidays. This led to a significant increase in contacts through interpersonal networks producing much more intense and complex local interactions. Such local interactions are not captured in a SIRD model that presupposes mass-action mixing of individuals where susceptible and infectious individuals meet one another at random in a closed system with no entry of outsiders. However, the model perfectly captures the increasing trend of active infections at the end of the fourth period, a trend that predicts the arrival of the third wave of the epidemic.
3.1. Sensitivity analysis
GAs are stochastic optimization procedures. So, if we run several times the AG, the fitted solutions obtained may slightly differ in each case in the sense that the estimated parameters may change by the fourth or fifth decimal place. Thus, by performing 100 AG replications, we can calculate sensitivity intervals for each of the parameters by means of the 5 and 95 percentiles of their respective estimates. With one asterisk, these sensitivity intervals are shown in Table 1.
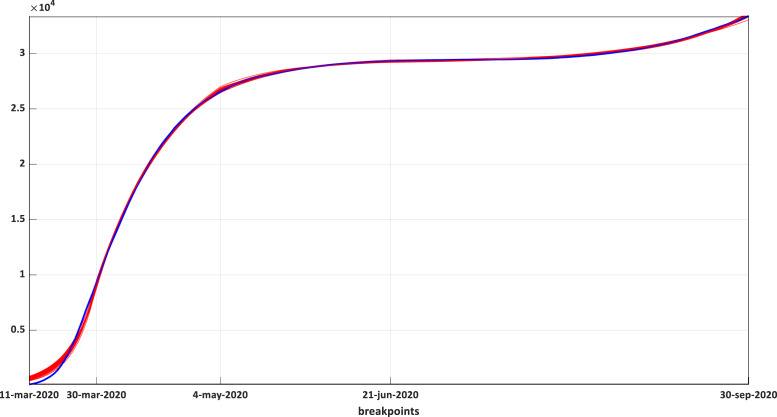
As further evidence of the low sensitivity of our results to GA replication, Fig. 4 shows that the solutions obtained by different realizations of the GA are similar in the sense that all of them provide very similar dynamics in the SIRD model which each one generates. The blue line corresponds to the real accumulated deceased; in red, we present one hundred predictions of accumulated deceased for the SIRD model, where its parameters have been obtained minimizing the square error of prediction with a GA. Due to the precision of the prediction all curves are superposed and result indistinguishable in the figure. This accuracy should not be surprising since the objective function that minimizes the GA is precisely the error in the number of deaths.
Fig. 4.
Real (blue line) and one hundred predictions of accumulated deceased for the SIRD model (in red), where its parameters have been obtained minimizing the square error of prediction with a GA. Due to the precision of the prediction all curves are superposed and result indistinguishable in the figure. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
What Fig. 4 shows is that, unless we use a very large number of chromosomes and generations in the GA, which can lead to very long run times, the prediction of the cumulative number of deaths may suffer small variations; however, these variations are tiny as reflected in the overlay of the blue curve, with real data, on the red curves corresponding to 100 different predictions.
As we observe, due to the precision of the prediction of our procedure, except for the beginning of the pandemic where the number of infected people is still small and the strong mixing hypothesis stablish for a SIRD-type model often has difficulty describing the reality, all curves are superposed and result indistinguishable in the figure. Fig. 4 also shows that we have a pronounced increase of the accumulated deceased people by the beginning of May; after that, the confinement measures decreed by the Spanish government have flatten the curve; nevertheless, after the summer the curve increased again, and the pandemic began to get out of control.
3.2. Usual confidence intervals
To take into account that the real series of deceased contains a stochastic part that is obtained as the difference between the real series of deceased and the one estimated by the SIRD model, confidence intervals have been estimated for the parameters of the SIRD model.
Note that these confidence intervals are associated with the possible randomness of the data; therefore, their nature is completely different from the sensitivity intervals shown in Table 1 which are associated with the random optimization aspects that are present in the GA.
A bootstrapping procedure has been used to calculate the confidence intervals, Efron and Tibshirani [15] being the main bibliographic reference. Specifically, the procedure used has had the following steps5 :
-
•
Let us consider an estimate of the number of deaths given by the AG during the total period of 204 days considered (from March 11st to September 30th); this estimate is given by the nine parameters that have been estimated in the four sub-periods (initial time of the outbreak, infection rates, and the recovery rates).
-
•
Then, subtracting the estimate from the real number of deaths we obtain the prediction errors .
-
•
These errors are modelled using an ARIMA stochastic process which in turn produces a time series of residues associated with each of the 204 days of the estimate. Also, because the variance of varies over time, it is modelled as a generalized autoregressive conditional heteroscedasticity (GARCH) stochastic process [7]: .
-
•
Obtain 100 bootstrapped replicas of the series of residues by means of 100 random shuffles of the residue series .
-
•
Introduce the 100 bootstrapped replicas of the series of residuals in the estimate ARIMA model to obtain 100 replicas of the series of errors: .
-
•
Adding each of the 100 replicas of the error series to the original dead series we get 100 bootstrap replicas of the dead series: .
-
•
Apply the AG to each of the 100 bootstrapped replicas of the dead series to estimate in each of them the nine parameters of the model.
-
•
With these 100 estimations for each of the parameters of the model, the confidence intervals will be obtained through the 5 and 95 percentiles.
4. Conclusions
In this work, the temporal evolution of the parameters of a SIRD model is studied through the adjustment of the time series of deaths produced in Spain during the first seven months of the COVID-19 pandemic.
The main contribution of this article is a new methodology for estimating the evolution of the epidemiological parameters of a SIRD model and value the sanitary measures implemented by the Spanish government, for the COVID-19, at the beginning of the outbreak. In this approach the only information required for estimating these parameters is the time series of the deceased. This methodology allows several sub-periods with structural changes in parameters and can be applied much more generally in other epidemiological models when the effect of measures taken by a government is to be evaluated. Given the complex nature of the model the sum of the square of the errors, which is the objective function we want to minimize to obtain the parameters, has no explicit analytical expression with respect to time and the parameters of the model; thus, we must minimize a function of which we do not know its analytical form and for which only numerical values are available. For this reason, we employ a heuristic optimization procedure such as GAs to estimate the model parameters by minimizing the sum of squared prediction errors of the deceased.
This methodology for estimating parameters could be extended to other models of the SIR family where there is precise knowledge of a time series corresponding to one of the variables of the model.
Another crucial aspect of our methodology is that it allows considering several sub-periods where the values of the parameters can change; this is essential when assessing the effectiveness of the measures taken by the government in the fight against COVID-19 by checking the evolution of the variables of the model in the sub-periods.
The results obtained in this empirical application reveal a drastic reduction in the parameter after the total containment measures carried out by the Spanish government between March 15th and June 21st, 2020. The relaxation of the confinement produced during the summer has brought with it a significant increase in and the subsequent outbreak of a new wave of contagion.
Generally, our model obtains an estimate of the number of infected people that is higher than the official figures provided by the authorities; these official figures were obtained, at the time, with a small number of PCR tests carried out on the population. The implementation of our model in those days would have given a much more realistic picture of the epidemiological situation.
The model also predicts the evolution of the number of recoveries, which also differs from the official figures, which are only able to record either symptomatic recoveries or the few asymptomatic patients who have undergone a diagnostic test. Thus, the difference between the number of predicted and actual recoveries provides an estimate of the number of asymptomatic individuals missed by diagnostic tests.
Another important feature of our methodology is that it also allows us to estimate the initial moment when the pandemic started. However, it should be noted that in our SIRD model we have associated the beginning of the pandemic with the existence of a patient zero, which may be unrealistic considering the high mobility of the world population at that time and the possible existence of several foci that could have affected Spain, such as China or Italy. In any case, it is striking that our results point to the fact that the Patient Zero in the COVID-19 Spanish outbreak emerged between the end of December and early January (see [24]), at least four weeks before January 31st, that was the moment when the Spanish authorities reported the first positive case.
In theory, assuming that the country’s authorities take no action against the pandemic, the implemented SIRD model could have predictive capacity in the long term. However, amid the successive restrictions that were taken, the predictive horizon of the SIRD model can at best be reduced to two to three weeks, which is the time it would take for any governmental measures to take effect (recall that the recovery time for this disease is in the order of two to three weeks). This justifies the fact that we have divided the sample into four sub-periods marked by changes in government measures and that our model has been able to predict the third wave of the pandemic occurring after the fourth period and starting in Spain at the end of September 2020.
The results obtained in this work are directly related to the quality of the time series of deaths elaborated by the Spanish authorities. In this sense, the number of people who have been infected in Spain, by the end of September 2020, according to the model proposed in this work is approximately one million, figures that are approximately in line with the official figures. However, as there is a possibility that not all the deaths from coronavirus have been counted in the official statistics [2], the actual number of people who have been infected could be higher.
Given that the methodology presented in this paper allows estimating the epidemiological parameters of a SIRD model from the time series of deaths, the final conclusion is that having an accurate estimate of the number of deaths in an epidemic of these characteristics is very important; this allows predicting the prevalence of the disease and thus the possible number of hospitalizations, thus allowing for optimal management of health resources.
Nomenclatures
| GAs | Genetic Algorithms |
| WHO | World Health Organization |
| Basic reproductive number | |
| Effective reproductive number | |
| SIR | Susceptible–Infected–Recovered |
| SIRD | Susceptible–Infected–Recovered–Deceased |
| Transmission rate | |
| Average rate of contacts between susceptible and infected individuals per day | |
| p | Probability of infection |
| d | Mean time to recovery of the disease |
| Recovery rate | |
| Date of onset of the epidemic | |
| S | Susceptible population size |
| I | Infected population size |
| R | Recovered population size |
| D | Deceased population size |
| N | Total population size |
| PCR | Polymerase chain reaction |
CRediT authorship contribution statement
Eduardo Acosta-González: Conceived and designed the analysis, Analysis tools, Performed the analysis, Wrote parts of the paper. Julián Andrada-Félix: Conceived and designed the analysis, Analysis tools, Performed the analysis, Wrote parts of the paper. Fernando Fernández-Rodríguez: Conceived and designed the analysis, Analysis tools, Performed the analysis, Wrote parts of the paper.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Footnotes
This value has been obtained taking into account that the average time from the onset of symptoms to recovery is 2 weeks, when the disease has been mild and 3–6 weeks when it has been severe or critical [1], and that the number of severe or critical cases are very few in relation to the total number of infected.
The evolution of the number of infected people up to the present time can be seen on the website www.worldometers.info/coronavirus/country/spain/.
Actively infected means the number of people who are infected at any given time.
It should be noted that neither the series of active infected nor the series of recovered cases are available on the website of the Carlos III Institute, which is the official data source of the Spanish government; for this reason, we have had to reconstruct them using unofficial data from the website www.worldometers.info/coronavirus/country/spain/.
In order not to make the presentation excessively long, we have summarized the most important aspects of the procedure in the following steps. More detailed information is available to readers on request.
References
- 1.Spanish Ministry of Health . Centro de Coordinación de Alertas y Emergencias Sanitarias; 2020. Coronavirus Disease, COVID-19. Last update: https://www.mscbs.gob.es/profesionales/saludPublica/ccayes/alertasActual/nCov/documentos/ITCoronavirus.pdf. [Google Scholar]
- 2.MoMo . Centro Nacional de Epidemiología (Instituto de Salud Carlos III); 2020. Sistema de Monitorización de la Mortalidad Diaria, Vigilancia de Los Excesos de Mortalidad por Todas las Causas. accessed November 4th, 2020. https://www.isciii.es/QueHacemos/Servicios/VigilanciaSaludPublicaRENAVE/EnfermedadesTransmisibles/MoMo/Documents/informesMoMo2020/MoMo_Situacion%20a%204%20de%20noviembre_CNE.pdf. [Google Scholar]
- 3.Abusama A., Abusamb R., Al-Anzi B. In: Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling, Vol. 5. Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. 2020. Adequacy of logistic models for describing the dynamics of COVID-19 pandemic; pp. 536–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Acosta-González E., Fernández-Rodríguez F. Model selection via genetic algorithms illustrated with cross- country growth data. Empir. Econ. 2007;33(2):313–337. doi: 10.1007/s00181-006-0104-3. [DOI] [Google Scholar]
- 5.Anderson R.M., May R.M. Directly transmitted infections diseases: control by vaccination. Science. 1982;215(4536):1053–1060. doi: 10.1126/science.7063839. [DOI] [PubMed] [Google Scholar]
- 6.Anirudh A. In: Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling, Vol. 5. Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. 2020. Mathematical modelling and the transmission dynamics in predicting the Covid-19 - What next in combating the pandemic; pp. 366–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J. Econometrics. 1986;31(3):307–327. doi: 10.1016/0304-4076(86)90063-1. [DOI] [Google Scholar]
- 8.Brauer F., Castillo-Chavez C. second ed. Springer; New York NY: 2012. Mathematical Models in Population Biology and Epidemiology. [Google Scholar]
- 9.Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling. 2020. https://www.sciencedirect.com/journal/infectious-disease-modelling/special-issue/10W6FJNSL0C. [Google Scholar]
- 10.Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci. Total Environ. 2020;729:1–7. doi: 10.1016/j.scitotenv.2020.138817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chowell G., Nishiura H., Bettencourt L.M.A. Comparative estimation of the reproduction number for pandemic influenza from daily case notification data. J. R. Soc. Interface. 2006;4(12):155–166. doi: 10.1098/rsif.2006.0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cuevas E. An agent-based model to evaluate the COVID-19 transmission risks in facilities. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dietz K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res. 1993;2(1):23–41. doi: 10.1177/096228029300200103. [DOI] [PubMed] [Google Scholar]
- 14.Ding Y., Gao L. In: Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling, Vol. 5. Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. 2020. An evaluation of COVID-19 in Italy: A data-driven modelling analysis; pp. 495–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Efron B., Tibshirani R.J. first ed. Chapman & Hall; New York: 1994. An Introduction to the Bootstrap. [Google Scholar]
- 16.Fraser C., Riley S., Anderson R.M., Ferguson N.M. Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. USA. 2004;101(16):6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goldberg D. first ed. Addison-Wesley Publishing Company, Inc.; New York NY: 1989. Genetic Algorithms in Search, Optimization, and Machine Learning. [Google Scholar]
- 18.[dataset] Spanish Ministry of Health and the Carlos III Health Institute (ISCIII), accessed November 6th, 2020. https://www.mscbs.gob.es/profesionales/saludPublica/ccayes/alertasActual/nCov-China/documentos/Fallecidos_COVID19.xlsx.
- 19.Hethcote H.W. The mathematics of infectious diseases. Soc. Ind. Appl. Math. 2000;42(4):599–653. doi: 10.1137/S0036144500371907. [DOI] [Google Scholar]
- 20.Holland J. first ed. MIT Press Ltd.; United States US: 1992. Adaptation in Natural and Artificial Systems. [Google Scholar]
- 21.Imai N., Dorigatti I., Cori A., et al. 2020. Preprint Published by the Imperial College London; China: 2020. Report 2 - Estimating the Potential Total Number of Novel Coronavirus (2019-nCoV) Cases in Wuhan City. https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-2-update-case-estimates-covid-19/ [Google Scholar]
- 22.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A. 1927;115:700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- 23.Lia L., Yang Z., Dang Z., Meng C., et al. In: Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling, Vol. 5. Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. 2020. Propagation analysis and prediction of the COVID-19; pp. 282–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lopreite M., Panzarasa P., Puliga M., Riccaboni M. Early warnings of COVID-19 outbreaks across Europe from social media. Nat. Sci. Rep. 2021;11:2147. doi: 10.1038/s41598-021-81333-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marfak A., Achak D., Azizi A., et al. The hidden Markov chain modelling of the COVID-19 spreading using Moroccan dataset. Data Brief. 2020;32 doi: 10.1016/j.dib.2020.106067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mellone A., Gong Z., Scarciotti G. Modelling, prediction and design of COVID-19 lockdowns by stringency and duration. Nat. Sci. Rep. 2021;11:15708. doi: 10.1038/s41598-021-95163-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Odagaki T. In: Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling, Vol. 5. Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. 2020. Analysis of the outbreak of COVID-19 in Japan by SIQR model; pp. 691–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pei L., Zhan M. Long-term predictions of COVID-19 in some countries by the SIRD model. Complexity. 2021;2021 doi: 10.1155/2021/6692678. [DOI] [Google Scholar]
- 29.Sahai A.K., Rath N., Sood V., Singh M.P. ARIMA modelling & forecasting of COVID-19 in top five affected countries. Diabetes Metab. Syndr.: Clin. Res. Rev. 2020;14(5):1419–1427. doi: 10.1016/j.dsx.2020.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Singh P., Singhal A., Fatimah B., Gupta A. ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2021. An improved data driven dynamic SIRD model for predictive monitoring of COVID-19; pp. 8158–8162. [DOI] [Google Scholar]
- 31.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yarsky P. Using a genetic algorithm to fit parameters of a COVID-19 SEIR model for US states. Math. Comput. Simulation. 2021;185:687–695. doi: 10.1016/j.matcom.2021.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhao S. In: Special Issue on Modelling and Forecasting the 2019 Novel Coronavirus (2019-nCoV) Transmission, Infectious Disease Modelling, Vol. 5. Castillo-Chavez C., Chowell-Puente G., Yan P., Wu W., editors. 2020. A simple approach to estimate the instantaneous case fatality ratio: Using the publicly available COVID-19 surveillance data in Canada as an example; pp. 575–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhao S., Lin Q., Ran J., et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]