Abstract
We studied the anisotropy of 1H NMR spin–lattice and spin–spin relaxations in a fresh celery stem experimentally and modeled the sample theoretically as the water-containing nano- and micro-cavities. The angular dependence of the spin–lattice and the spin–spin relaxation times was obtained, which clearly shows the presence of water-filled nano- and micro-cavities in the celery stem, which have elongated shapes and are related to non-spherical vascular cells in the stem. To explain the experimental data, we applied the relaxation theory developed by us and used previously to interpret similar effects in liquids in nanocavities located in biological tissues such as cartilages and tendons. Good agreement between the experimental data and theoretical results was obtained by adjusting the fitting parameters. The obtained values of standard deviations (0.33 for the mean polar angle and 0.1 for the mean azimuthal angle) indicate a noticeable ordering of the water-filled nano- and micro-cavities in the celery stem. Our approach allows the use of the NMR technique to experimentally determine the order parameters of the microscopic vascular structures in plants.
Keywords: Spin–lattice relaxation, Spin-spin relaxation, Anisotropy, Nano- and microcavity, Celery stem
1. Introduction
Nuclear Magnetic Resonance (NMR) and Magnetic Resonance Imaging (MRI) have proven to be excellent tools for the study of the physical, chemical, and biological properties of matter, for diagnosing pathological tissue changes at early degradation stages and understanding organ malfunctioning due to diseases [1–6]. A wide range of biological samples has been studied by NMR, ranging from single cells to organs and tissues, including the study of plant metabolism impacts, a broad range of domains such as plant cultural practices, plant breeding, human or animal nutrition, phytochemistry and green biotechnologies [3,4,7]. In particular, NMR has the capability to determine the chemical composition, micro- and nano-structures and ionic transport in biological samples non-invasively and non-destructively [4,8–12].
Among the various NMR methods, a special place is occupied by the NMR relaxation technique [3,4], which is very useful for studying microstructure, internal spin interactions and the motion of molecules in solids, liquids and soft matter [1–4]. In particular, the anisotropy (angular dependence) of relaxation times of a 1H NMR signal has been found in water-filled tissues that contains organized fibers; and whose anisotropy correlates with microscopic anatomy of the organs (their fibril structure), that can be characterized by water molecules filled between or inside fibrils of 280–300 nm in length and several tens nanometers in diameter [4]. Such anisotropy is not observed in non-fibrillar tissues. In several publications the anisotropy was explained by orientation of water molecules along the tissue fibrils [4,13–16]. Another explanation of the anisotropy is based on representation of a sample by a set of micro- and nano-cavities containing water molecules and averaging of the restricted molecular motion in such cavities [17,18]. It was shown that the relaxation times of the water contained inside the nano-cavity depend on the orientation of the cavity relative to the external magnetic field. The angular dependences of different relaxation times are different [17].
The most common relaxation mechanism is the magnetic dipole–dipole (DD) interaction between the magnetic moments of nuclei (spins). This interaction depends on the distance between nuclear spins (for example, a pair of protons in a water molecule) and on the orientation of the proton-proton vectors relative to the external magnetic field. The perturbed spin system relaxes to an equilibrium state and is characterized by two relaxation times: the spin–lattice (longitudinal relaxation) time T1 and the spin–spin (transverse) relaxation time T2 [1,2]. The study of the spin–spin and spin–lattice relaxations requires solving the Liouville - von Neumann equation for the spin system and considering all interactions of spins with each other and their environment. This is a very difficult task because the spin–spin and spin–lattice interactions can be time dependent. One of the effective methods for analytically describing the evolution of spin systems is to average the Hamiltonian over time; as a result of that, the systems are described by time-independent Hamiltonians [19–21]. The averaged method, based on the averaging of only a Hamiltonian spin part, has been successfully applied to explain the results of high-resolution NMR experiments with solids. One of the main results of the application of the averaged Hamiltonian theory was the explanation of the observed narrowing of the line in solid-state NMR experiments [19–21].
Another method, based on averaging a Hamiltonian space part over lattice variables [22,23] has been successfully used to explain the anisotropy of the transverse and longitudinal relaxation times in liquids entrapped in a nano-cavities [17,18,24–30]. Restriction of the Brownian motion of molecules in liquid or gas, enclosed in nano-cavities [17,18,24–30], results in the averaged Hamiltonian which describes the averaged DD interactions and can be characterized by a single averaged coupling constant. This simplification of a lattice part of the Hamiltonian by averaging over the Brownian chaotic motion has led to analytically solvable models with non-trivial spin dynamics, which allows one to obtain the analytical expressions for the transverse and longitudinal relaxation times and the relaxation time under spin-locking [31,32]. This approach was applied to explain anisotropy obtained in the experiments with biological tissues, such as collagen fibril tissues (tendons, cartilages, nerves) [17,18,24–30]. The transverse and longitudinal relaxation times in liquid entrapped in a nano-cavity depend on the structural and dynamic parameters of samples and demonstrate noticeable anisotropy [4,17,18,33]. However, in these works various relaxations were studied in different samples; for each sample good agreement between the experimental data and the theoretical results were achieved by adjustment of several fitting parameters, which cannot be theoretically predicted. The fitting parameters can be considered as characteristics of nanocavities and fibril structure of a sample.
In the present work, we investigate both experimentally and theoretically the spin–lattice and spin–spin relaxation of the spin system in the same sample containing a liquid-trapped in a micro-/nano-cavity - a celery stalk. We measure the spin–lattice relaxation times T1 and the spin–spin relaxation times T2 of protons of water molecules. These relaxation times are of particular importance since they have been shown to be sensitive to the tissue structure and responsible for the MRI visualization in samples [4].
2. Theory
2.1. Space averaged spin Hamiltonian
In a nano-cavity, in contrast to a bulk material, space where molecules of gas or liquid diffuse is restricted; but the molecules can still move randomly throughout the whole cavity with the characteristic time tdif. When the characteristic time tdif is much shorter than the NMR time scale tNMR, tdif ≪ tNMR, the spin evolution in a single nanocavity can be described by an averaged of the space part of the dipole–dipole interaction (DD) Hamiltonian [23,24]. The time-averaged of the secular part of the DD interaction Hamiltonian, can be presented in the following form for an axis-symmetrical nano-cavity [23,24]:
| (1) |
where is the square of the total nuclear spin-1/2 operator, are the operators of the projections of the total spin operator on the v- axes (v = x, y, z), N is the number of spins in a nano-cavity. D(0) is the space-averaged pair coupling constant
| (2) |
where γ is the nuclear gyromagnetic ratio, V is the cavity volume, , φ is the angle between the main axis ZC of the nano-cavity and the external magnetic field, (Fig. 1), and F is the form factor, which varies for an ellipsoidal nanocavity from to and a cylindrical nano-cavity from 0 to 2π.
Fig. 1.
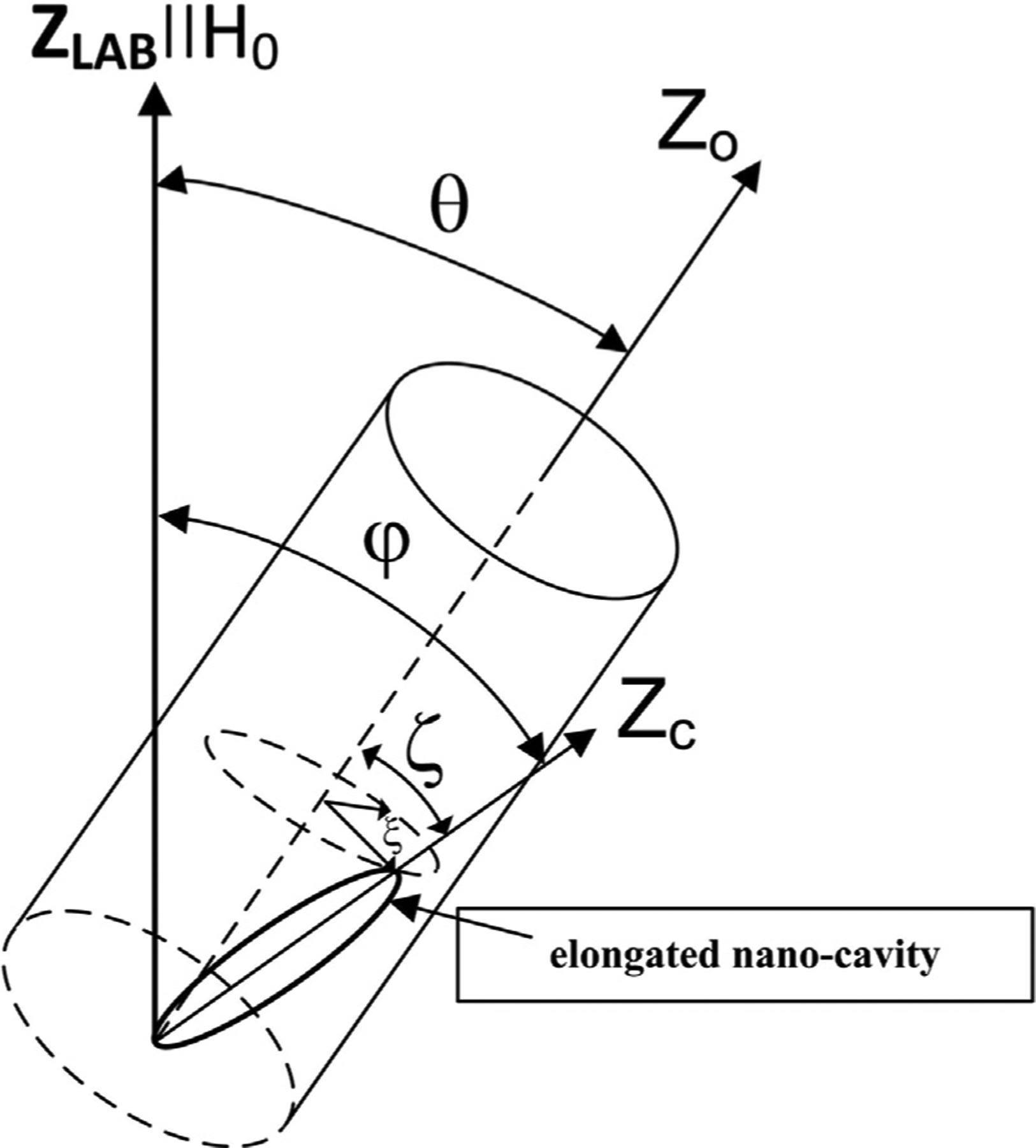
The coordinate systems and angles used to describe the model of plant tissue. ZLAB denotes the z-axis of the laboratory frame. θ is the angle between the external magnetic field and the Z0-axis chosen as an axis of the sample in the experiment. ζ and ξ are the polar and azimuthal angles characterizing the deviation of the main ZC -axis of an elongated nano-cavity from the Z0-axis of the sample.
The non-secular part of the DD interaction Hamiltonian, after time-averaged takes the form [34]
| (3) |
where D(q) are the averaged dipolar coupling constants:
| (4) |
S(q) are operators acting only on the spin variables:
| (5) |
are the total raising and lowering operators, ψ is the azimuthal angle of the main ZC-axis of the nano-cavity.
The averaged non-secular part of the Hamiltonian containes four effective constants for each pair of spins. Similary to the effective constant of the secular part these constants depend on the volume, form, and orientation of the nano-cavity.
2.2. Transverse relaxation time
The transverse relaxation time T2 can be calculated using its relationship with the local dipolar field [35]. Using the expression for the local dipole field calculated in the case of a liquid entrapped in a nano-cavity [19,20], the transverse relaxation rate can be obtained
| (6) |
where C is the spin density of the liquid. A remarkable result is that anisotropy of the transverse relaxation time is determined by only angle φ between the magnetic field direction and the main ZC-axis of the nanocavity. Fig. 2a shows the angle dependence of the normalized relaxation time calculated using Eq. (6) for a single nano-cavity or for a set of the perfectly ordered nano-cavities. One can see from Fig. 2a that the normalized transverse relaxation time has a period equaled to π and reaches the local minimum of about 2T2(0) at φ = π/2. At the magic angles, φ = 0.96 and 2.19 the relaxation time tends to infinity.
Fig. 2.
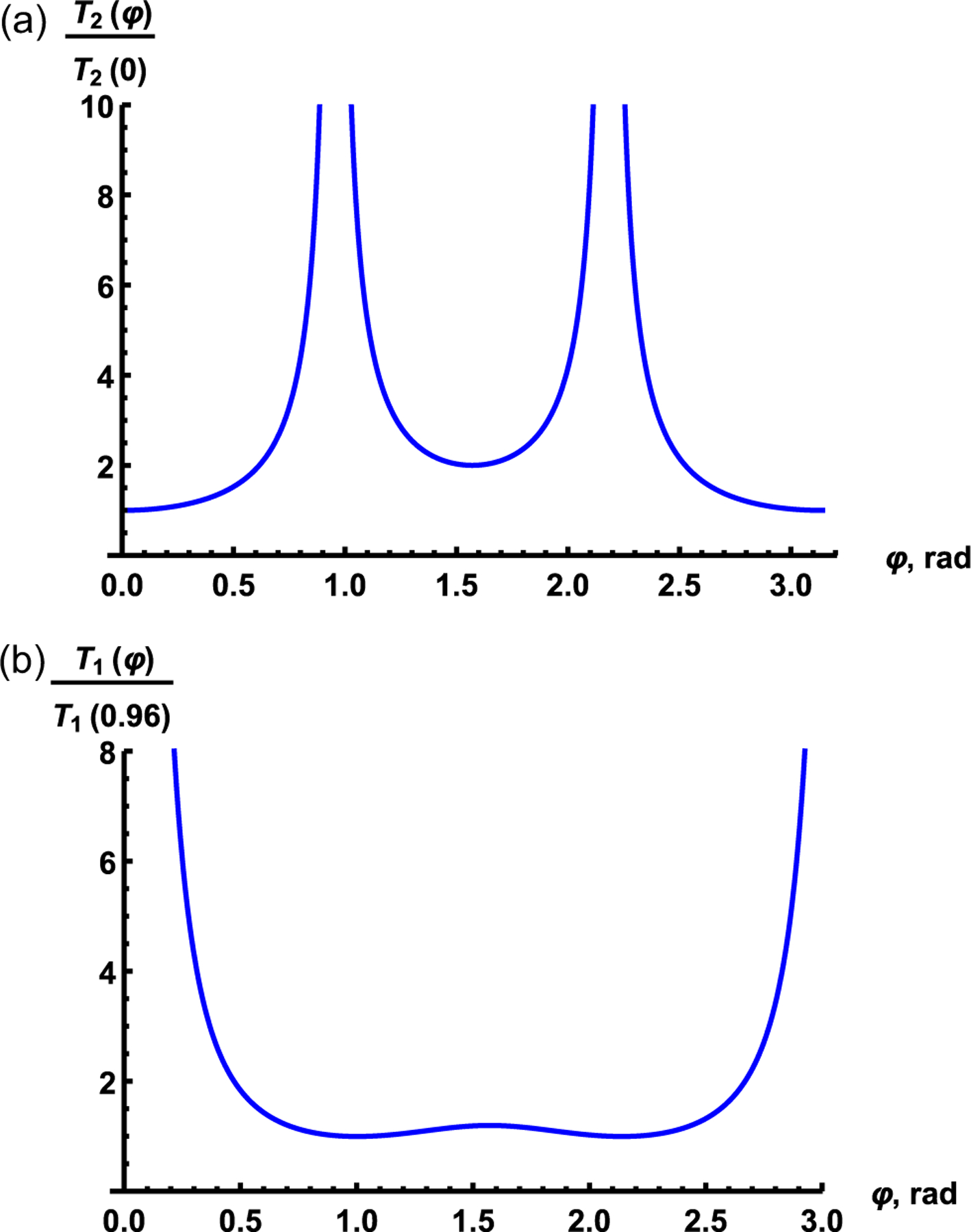
Angular dependence of the normalized transverse (a) and longitudinal (b) relaxation times in a single nano-cavity, calculated using Eq. (6) and Eq. (8), respectively.
Estimation for a nanocavity with characteristic volume V ≈ 106 nm3, the spin density for water , |(3cos2φ – 1)F| = 2.3, and for a proton gives the spin–spin relaxation time T2 ≈ 170 ms, which agrees with the experimental data (Fig. 3a).
Fig. 3.
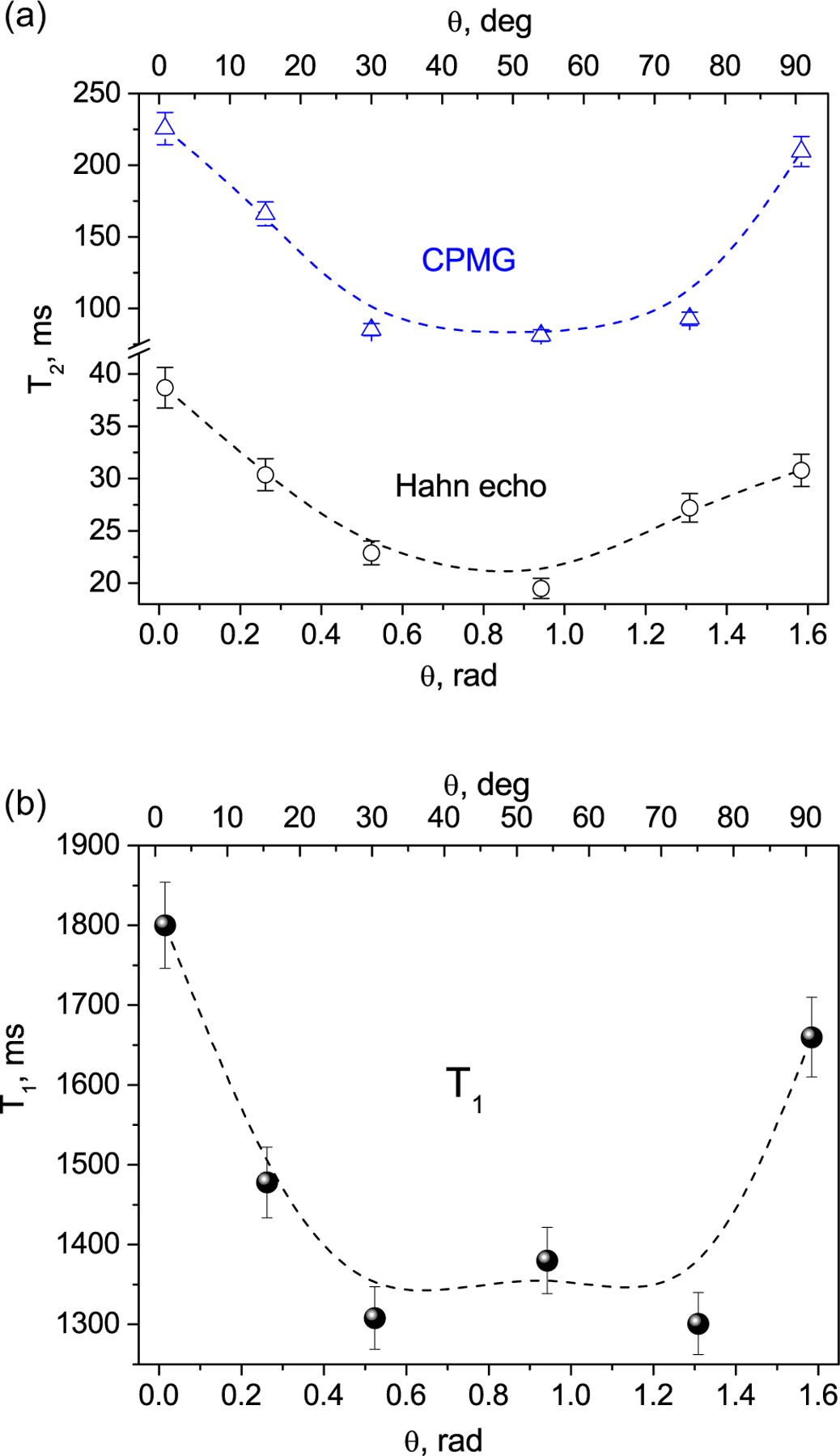
Experimental dependence of the transverse relaxation T2 (a) and longitudinal relaxation T1 (b) times of water molecules in the celery stem on the angle h between the sample axis and direction of the applied magnetic field. Dash lines are B-Spline fits. Error bars include both experimental and simulation errors.
2.3. Longitudinal relaxation time
Method for the classical description of a lattice is well adapted to study of relaxation in liquids, where the Brownian motion of molecules is responsible for random variation in the lattice parameters [1,2]. The lattice parameters included in the non-secular part of the DD interaction Hamiltonian are then given by functions of time.
However, in the case of a liquid enclosed in a nano-cavity, the Hamiltonian after averaging does not contain terms describing random Brownian motion and is independent of time. The averaged Hamiltonian contains parameters characterizing a nano-cavity (volume V, form factor F), its orientation relative to the magnetic field, and liquid in the nano-cavity. Random oscillations of these parameters cause spin–lattice relaxation in a liquid enclosed in a nano-cavity. Assume that the reduced correlation functions g(1)(τ) and g(2)(τ) are represented by [34]
| (7) |
where τc is the correlation time of random fluctuation of a nano-cavity wall and using the standard procedure (see e.g. [1]) we obtain the spin–lattice relaxation rate:
| (8) |
where
| (9) |
Eq. (8) gives the dependence of the spin–lattice relaxation time on the Larmor frequency ω0, volume V, density of nuclear spins C, shape (form factor F) and nano-cavity orientation relative to the magnetic field given by the angle φ. Estimation of the spin–lattice relaxation time T1 at the field strength of 8.0 T according to Eq. (8) with , B ≈ 10, characteristic size V ≈ 106 nm3 and τc ≈ 10−2 s gives T1 ≈ 1.7 s which agrees with the experimental data (Fig. 3b). Fig. 2b shows the angle dependence of normalized relaxation time calculated using Eq. (8) for a single cavity or for a set of the perfectly ordered nanocavities.
3. Experimental
3.1. Sample
The stem of celery consists of four main types of structural components: (i) the vascular bundles that contain water-transporting xylems and (ii) nutrient-transporting phloems, (iii) collenchyma which provides support for the plant and (iv) parenchyma (ground tissue). Xylem and phloem vessels are created by overlapping cells, which form hollow cavities interconnected into one long micrometer-diameter tube. Collenchyma is made up of elongated living cells filled with water and is located along the outer edges of the stem and the vascular bundle tissue, being in a longitudinal orientation. The cell walls possess a fibril structure and consist of nano-fibers with their diameters in the range of 6–25 nm [36]. Parenchyma is made up of non-oriented living cells filled by water and cellular liquid, which are bigger in diameter and often shorter when comparing with collenchyma [37]. Water is also a part of the fibril structure and is located between the microfibrils, presumably serving to stabilize them through hydrogen bonding.
Celery studied was purchased from a local supermarket. For the NMR measurements, we cut out from the outer (lateral) part of the celery stalk a small piece of ~ 1 cm long and ~ 2 mm wide, which mainly consists of collenchyma, xylem and phloem, avoiding the parenchyma as much as possible. Thus, we worked in the most part with oriented fibril tissues. The specimen did not contain the skin (epidermis). We note that celery is highly hydrated, having the water content up to 95% w.t., thus the NMR signal comes mainly from water molecules.
3.2. NMR measurements
We measured the spin–lattice (T1) and spin–spin (T2) relaxation times of water molecules in the celery stem at different angles between the sample’s long axis and the direction of the applied magnetic field. The 1H NMR measurements were carried out at ambient temperature (293 ± 0.5 K) using a Tecmag pulse solid state NMR spectrometer and an Oxford superconducting magnet with the magnetic field B0 = 8.0 T, corresponding to the 1H resonance frequency ω0 = 340.54 MHz, and a home-built NMR probe. The spin–spin relaxation times T2 were measured using the Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence [38]; in addition (for comparison), the Hahn echo measurements were also carried out. The duration of the π/2 RF pulse in the sequences was 1.6 μs. To determine the relaxation time T2 we processed the decays of echo amplitudes as M(t) ~ exp(−2t/T2) and M(2nτ) ~ exp (−2nτ/T2) for the Hahn echo and CPMG method, respectively (here t is the pulse spacing and τ is the echo spacing, respectively). The CPMG pulse train consisted of 2048 pulses separated by a time interval of 2 msec. Spin-lattice relaxation time T1 was measured using the inversion recovery pulse sequence [1]. Magnetization recovery in the T1 measurements of a sample was well described by a stretched exponential function , where M∞ is the equilibrium magnetization and α is the stretched exponential parameter. Such approach is usually used in the case of a distribution of the relaxation times in a system with a number of different relaxation environments, resulting in a multi-component relaxation behavior with the impossibility of separating into individual components. Repetition time was chosen as 5 T1. To get an intense signal, 16 acquisitions were usually required.
All measurements were carried out with non-spinning sample to preserve the contributions of the proton DD interactions to the spin–lattice and spin–spin relaxations, which are studied in the present article. To obtain the orientation dependences of the relaxation times, the sample was placed at different angles between the stem axis and the direction of the applied magnetic field with an accuracy of ~1.50.
4. Experimental results and discussion
The relaxation times of bulk distilled water are T1 = 3.8 s and T2 = 2.4 s [39] and are known to be independent on the sample orientation relative to the applied magnetic field. Herewith our measurements of the celery stem demonstrate noticeable dependences of both the transverse and longitudinal relaxations of the water protons on the angle θ between the stem axis and the direction of the external magnetic field (Fig. 3a and b). According to the above theory, such anisotropy of relaxation times should be observed in a liquid located in a restricted space/volume formed by nano- and micro-cavities in a material [17,18]. In our case, the observed anisotropy of relaxation times in celery should be associated with nano- and micro-sized water-filled cavities in the studied tissues. The stretched exponential parameter when fitting of the T1 data was found to be around 0.9.
We note that the CPMG measurements show longer spin–spin relaxation times compared with the Hahn echo measurements, since the latter are affected by diffusion of the water molecules [26] and will not be considered further. The CPMG curves are well fit by a single exponential, corresponding to the water-filled elongated nano/micro-cavities in the tissues relaxing with short T2 As it was mentioned above, our sample is almost free of the parenchyma tissue with non-oriented water-filled cavities. Even if such tissue is present in the sample, it represents only a small fraction of water and, therefore, corresponds to a minor component of the relaxation signal, relaxing with long T2 and located at the tail of the CPMG signal. Therefore, its contribution can be practically neglected. Thus, the observed angular dependence of the relaxation times (Fig. 3) is associated with the elongated micro- and nano-sized water-filled cavities.
Comparison of the experimental results shown in Fig. 3 with the calculations presented for a set of perfectly ordered cavities (Fig. 2) shows a significant difference. The reason is that the above-mentioned calculations were done for a single cavity or for a number of cavities perfectly oriented in the same direction. However, the celery stem contains a set of the cavities which are somewhat differently oriented and have different shapes and volumes. To explain the difference between the angular dependences of the relaxation times T2 and T1 given by Eqs. (6) and (8) and the experimentally observed dependences, we consider a plant tissue as a set of imperfectly orientated water-containing cavities. For further analysis, it is convenient to use expressions for the normalized relaxation rates
| (10) |
where Rk(θ) is the normalized relaxation rates for a single nanocavity, k = 1 for the spin–lattice relaxation time T1 and k = 2 for the spin–spin relaxation time T2, respectively. In Eq. (10) we assume that the spin–lattice relaxation is described by an exponential function of time with (α = 1). Calculations according to Eq. (8) with α = 1 and with α = 0.9 give almost the same result.
Volume and form factor are various for different nanocavities. Assuming that the angular distributions of all cavity types are the same, we obtain the normalized relaxation rate averaged over whole sample [34]
| (11) |
In the NMR experiments, the relaxation times were measured as functions of the angle θ between the sample Z0-axis and magnetic field. Herewith the main axes of the cavities are distributed about some “preferred direction”, an averaged orientation of the elongated cavities. Let us determine the deviation of the main axis of each cavity from the Z0- direction by the polar angle ζ and azimuthal angle ξ. Suggesting the Gaussian distribution of the elongated cavities directions over both the angles, the polar ζ and azimuthal ξ angles with the bivariate normal distribution function
| (12) |
where Ψk(ζ, ξ, ρ) is the probability density function
| (13) |
ρ is the correlation parameter of the polar ζ and azimuthal ξ angles, σkζ and σkξ are the standard deviations, ζ0k and ξ0k are the means of the distributions of the angels and give distinction of the “preferred direction” of the elongated cavities from the sample axis,
| (14) |
The angular dependences of the normalized relaxation rate 〈Rk(θ)〉 are given by Eq. (12) in which there are unknown parameters: the correlation parameter (ρ), standard deviations (σkζ and σkξ) and distribution means (ζ0k and ξ0k). These parameters can be considered as parameters which characterize the fine structure of celery.
Our numerical experiments showed that varying the correlation parameter ρ from 0 to 1 has practically no effect on the fitting parameters, which indicates that there is no correlation between the polar and azimuthal angles.
The best matching of the calculations for two data sets is achieved simultaneously for both relaxation rates at the standard deviations of σkζ = 0.33 and σkξ = 0.1 for the polar and azimuthal angles, respectively (here k = 1, 2). The averaged transverse relaxation 〈R2(θ)〉 and longitudinal relaxation 〈R1(θ)〉 rates calculated according to Eq. (12) together with the experimental data are presented in Fig. 4. Since the standard deviation describes the distribution of nano-cavities within the sample and measurements of the relaxation rates were carried out in the same sample, this result is expected.
Fig. 4.
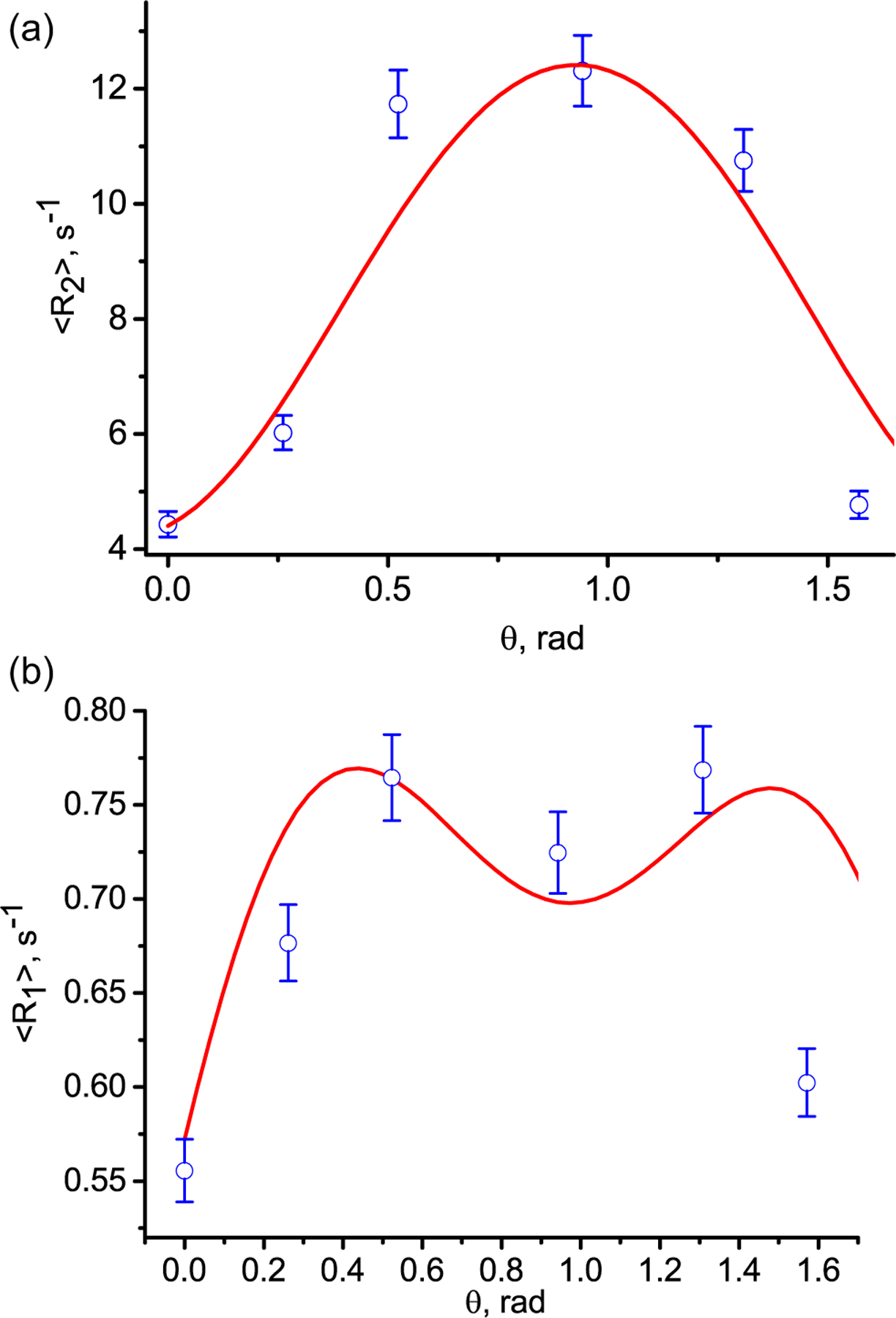
Angular dependence of the transverse 〈R2(θ)〉 (a) and tlongitudinal 〈R1(θ)〉 (b) relaxation rates in the celery stem. The blue circles are the experimental rate 〈R2(θ)〉 measured with the CPMG pulse sequence and 〈R1(θ)〉 measured with inversion recovery pulse sequence. The solid red curves are according to Eq. (12) for the standard deviations of 0.33 and 0.1 for the polar and azimuthal angles, respectively, for both relaxation rates.
We consider the agreement between the theoretical values and the experimental data to be quite satisfactory. Some discrepancies between the calculations and experimental data must come from the heterogeneities of the specimen containing several types of tissues (collenchyma, xylem, phloem). We found that for the mean values of the distributions, the best agreement of calculations with experimental data is achieved with the following values: ζ01 = 0.43 and ζ02 = 2.3 and ξ01 = ξ02 = 0.1. Note that the relaxation rates in a single nanocavity possess a period of π relatively to the angle φ (Fig. 3). For the sample we observed 3D space symmetry of the relaxation rates and change of the averaged angle by and that gives the same dependence of the relaxation rates on angle θ. For example, using the averaged values: ζ01 = 0.43 and and ξ01 = 0.1 and we obtained the relaxation rate angle dependences presented in Fig. 4. The standard deviations and averaged angles can be considered as parameters which characterize the fine structure of tissue components of celery.
5. Conclusion
We have studied both experimentally and theoretically the proton spin–spin and spin–lattice relaxations of water molecules entrapped in the celery stem. The angular dependence of both relaxation times was obtained. This behavior was attributed to the elongated water-filled nano-/micro-cavities. The obtained findings were interpreted in the frameworks of the theory, previously developed by us [17,18,26,32], which was successfully applied to explain similar effects in liquids located in nanocavities of biological tissues. We averaged the normalized relaxation rates over orientations of the cavities relative to the applied magnetic field. Good agreement between the calculations and experimental data was obtained by adjustment of a few fitting parameters - the standard deviations and averaged cavities direction. The approach allows using NMR data to non-invasively and non-destructively determine the order parameters of plant tissues.
An important feature of this study is that both transverse and longitudinal relaxation times were measured with the same sample and under the same conditions. The results obtained are well described by theoretical expressions with the same parameters characterizing the ordering of the micro-/nano-cavities in the sample. The obtained values of the standard deviations (σζ = 0.33 and σξ = 0.1) indicate a noticeable ordering of the cavities by both the transverse and the longitudinal relaxation times .
Our straightforward approach (measuring different relaxation times) showed that NMR methods can be used to study the microscopic vascular structure of plants. Variations in these vascular structures in plants can be associated with the economic characteristics of plants, for example, high/low yields of food crops or long/short growth times of vegetables [40,41]. Since NMR and MRI methods are totally non-invasive and non-destructive, we can conclude that the considered experimental NMR approach [29,32] can be used to study the fine vascular structures of living organisms, as well as to determine deviations of the fine anatomical structure of tissues from the norm in living organisms.
Acknowledgment
This research was supported by a grant from the United States - Israel Binational Science Foundation (BSF), Jerusalem, Israel (No. 2019033), and by a grant from the National Institutes of Health in the United States (AR 069047). The authors are grateful to Dr. Noam Ben-Eliezer for helpful discussions.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Ethical approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
References
- [1].Abragam A, The Principles of Nuclear Magnetism, Oxford Clarendon Press, 1961. [Google Scholar]
- [2].Abragam A, Goldman M, Nuclear Magnetism: Order and Disorder, Oxford University, New York, 1982. [Google Scholar]
- [3].Callaghan PT, Principles of Nuclear Magnetic Resonance Microscopy, Oxford Clarendon Press, 1991. [Google Scholar]
- [4].Xia Y, Momot K, Biophysics and Biochemistry of Cartilage by NMR and MRI, The Royal Society of Chemistry, Cambridge UK, 2016. [Google Scholar]
- [5].Enzinger C, Barkhof F, Ciccarelli O, Filippi M, Kappos L, Rocca MA, Ropele S, Rovira T, de Schneider N, Stefano H, Vrenken C, Wheeler-Kingshott JW, Fazekas F, Nonconventional MRI and microstructural cerebral changes in multiple sclerosis, Nat. Rev. Neurol 11 (2015) 676. [DOI] [PubMed] [Google Scholar]
- [6].Ratcliffe RG, Roscher A, Shachar-Hill Y, Plant NMR spectroscopy, Prog. Nucl. Magn. Reson. Spectrosc 39 (2001) 267–300. [Google Scholar]
- [7].Deborde C, Moing A, Roch L, Jacob D, Rolin D, Giraudeau P, Plant metabolism as studied by NMR spectroscopy, Prog. Nucl. Magn. Reson. Spectrosc 102–103 (2017) 61–97. [DOI] [PubMed] [Google Scholar]
- [8].Fenwick KM, Jarvis MC, Apperley DC, Estimation of Polymer Rigidity in Cell Walls of Growing and Nongrowing Celery Collenchyma by Solid-State Nuclear Magnetic Resonance in Vivo, Plant Physiol. 11 (5) (1997) 587–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Lau Hazel, Anna Karen Carrasco Laserna, Sam Fong Yau Lia, 1H NMR-based metabolomics for the discrimination of celery (Apium graveolens L. var. dulce) from different geographical origins. Food Chem. 332 (2020) 127424. [DOI] [PubMed] [Google Scholar]
- [10].Ovodova RG, Golovchenko VV, Popov SV, Popova G.Yu., Paderin NM, Shashkov AS, Ovodov YS, Chemical composition and anti-inflammatory activity of pectic polysaccharide isolated from celery stalks, Food Chem. 114 (2009) 610–615. [Google Scholar]
- [11].Phyo P, Wang T, Kiemle SN, O’Neill H, Pingali SV, Hong M, Cosgrove DJ, Gradients in Wall Mechanics and Polysaccharides along Growing Inflorescence Stems, Plant Physiol. 175 (4) (2017) 1593–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ratkovic S, Baĉiĉ G, 1H NMR Techniques in Studies of Transport of Paramagnetic Ions in Multicellular Systems Gen, Physiol. Biophys 6 (1987) 609–615. [PubMed] [Google Scholar]
- [13].Wang N, Xia Y, Anisotropic analysis of multi-component T2 and T1r relaxations in Achilles tendon by NMR spectroscopy and microscopic MRI, JMRI 38 (2013) 625–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Shao H, Pauli C, Li S, Ma Y, Tadros AS, Kavanough A, Chang EY, Tang G, Du J, Magic angle effect plays a major role in both T1rho and T2 relaxation in articular cartilage, Osteoarthritis and Cartilage 25 (2017) 2022–2030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Xia Y, Moody JB, Alhadlaq H, Orientational dependence of T2 relaxation in articular cartilage: a microscopic MRI (mMRI) study, Magn. Reson. Med 48460–469 (2002). [DOI] [PubMed] [Google Scholar]
- [16].Navon G, Eliav U, Demco DE, Blümich B, Study of Order and Dynamic Processes in Tendon by NMR and MRI, J Magn Reson Imaging 25 (2) (2007) 362–380. [DOI] [PubMed] [Google Scholar]
- [17].Furman GB, Goren SD, Meerovich VM, Sokolovsky VL, Anisotropy of spin–spin and spin–lattice relaxation times in liquids entrapped in nanocavities: Application to MRI study of biological systems, JMR 263 (2016) 71–78. [DOI] [PubMed] [Google Scholar]
- [18].Furman GB, Goren SD, Meerovich VM, Sokolovsky VL, Correlation of transverse relaxation time with structure of biological tissue, JMR 270 (2016) 7–11. [DOI] [PubMed] [Google Scholar]
- [19].Mehring M, High Resolution NMR Spectroscopy in Solids, Springer-Verlag, 1978. [Google Scholar]
- [20].Haeberlen U, High resolution NMR in solids, Academic Press, 1978. [Google Scholar]
- [21].Haeberlen U, Waugh JS, Coherent averaging effects in magnetic resonance, Phys. Rev 175 (1968) 453. [Google Scholar]
- [22].Baugh J, Kleinhammes A, Han D, Wang Q, Wu Y, Confinement effect on dipole-dipole interactions in nanofluids, Science 294 (2001) 1505. [DOI] [PubMed] [Google Scholar]
- [23].Fel’dman EB, Rudavets MG, Nonergodic nuclear depolarization in nano-cavities, J. Exp. Theor. Phys 98 (2004) 207. [Google Scholar]
- [24].Fel’dman EB, Furman GB, Goren SD, Spin locking and spin–lattice relaxation in a liquid entrapped in nanosized cavities, Soft Matter 8 (35) (2012) 9200, 10.1039/c2sm26326b. [DOI] [Google Scholar]
- [25].Furman G, Goren S, Dipolar order and spin-lattice relaxation in a liquid entrapped into nanosize cavities, Z. Naturforsch 66a (2011) 779. [Google Scholar]
- [26].Furman G, Goren S, Spin-lattice relaxation of dipolar energy in fluid confined to nanosized cavities, Mater. Sci. Forum 721 (2012) 47. [Google Scholar]
- [27].Furman GB, Goren SD, Meerovich VM, Sokolovsky VL, Multiple-pulse spin locking in nanofluids, RSC Adv. 5 (55) (2015) 44247–44257. [Google Scholar]
- [28].Furman GB, Goren SD, Meerovich VM, Sokolovsky VL, Nuclear spin–lattice relaxation in nanofluids with paramagnetic impurities, JMR 261 (2015) 175–180. [DOI] [PubMed] [Google Scholar]
- [29].Furman GB, Goren SD, Meerovich VM, Sokolovsky VL, Dipole-dipole interactions in liquids entrapped in confined space, J. Mol. Liq 272 (2018) 468–473. [Google Scholar]
- [30].Furman G, Meerovich V, Sokolovsky V, Xia Y, Spin locking in liquid entrapped in nanocavities: Application to study connective tissues, J. Magn. Reson 299 (2019) 66–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Kimmich R, NMR - Tomography, Relaxometry, Springer-Verlag, Berlin Heidelberg, Diffusometry, 1997. [Google Scholar]
- [32].Furman Gregory, Kozyrev Andrey, Meerovich Victor, Sokolovsky Vladimir, Xia Yang, Dynamics of Zeeman and dipolar states in the spin locking in a liquid entrapped in nano-cavities: Application to study of biological systems, JMR 325 (2021) 106933, 10.1016/j.jmr.2021.106933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].G D Fullerton I Cameron L, Ord VA, Orientation of tendons in the magnetic field and its effect on T2 relaxation times, Radiology 155 (2) (1985) 433–435. [DOI] [PubMed] [Google Scholar]
- [34].Furman G, Meerovich V, Sokolovsky V, Xia Y, Spin-lattice relaxation in liquid entrapped in a nanocavity, J. Magn. Reson 311 (2020) 106669, 10.1016/j.jmr.2019.106669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Goldman M, Spin Temperature and Nuclear Magnetic Resonance in Solids, Oxford Clarendon Press, 1970. [Google Scholar]
- [36].Thimm JC, Burritt DJ, Ducker WA, Melton LD, Thimm JC, Burritt DJ, Ducker WA, Melton LD, Celery (Apium graveolens L.) parenchyma cell walls examined by atomic force microscopy, Planta 212 (1) (2000) 25–32. [DOI] [PubMed] [Google Scholar]
- [37].Leroux O, Collenchyma: a versatile mechanical tissue with dynamic cell walls, Ann. Bot 110 (2012) 1083–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Meiboom S, Gill D, Modified Spin-Echo Method for Measuring Nuclear Relaxation Times, Rev. Sci. Instrum 29 (8) (1958) 688–691. [Google Scholar]
- [39].Panich AM, Salti M, Goren SD, Yudina EB, Alexenskii AE, A.Ya Vul’, Shames AI, Gd(III)-Grafted Detonation Nanodiamonds for MRI Contrast Enhancement, J. Phys. Chem. C 123 (2019) 2627–2631. [Google Scholar]
- [40].Jenner CF, Xia Y, Eccles CD, Callaghan PT, Circulation of water within wheat grain revealed by nuclear magnetic resonance micro-imaging, Nature 336 (6197) (1988) 399–402. [Google Scholar]
- [41].Xia Y, Sarafis V, Campbell EO, Callaghan PT, Non Invasive Imaging of Water Flow in Plants by NMR Microscopy, Protoplasma 173 (1993) 170–176. [Google Scholar]


