Abstract
Purpose
It is unclear how the iris deforms during changes in pupil size. Here, we report an application of a multi-feature iris tracking method, which we call irissometry, to investigate how the iris deforms and affects the eye position signal as a function of pupil size.
Methods
To evoke pupillary responses, we repeatedly presented visual and auditory stimuli to healthy participants while we additionally recorded their right eye with a macro lens–equipped camera. We tracked changes in iris surface structure between the pupil and sclera border (limbus) by calculating local densities (distance between feature points) across evenly spaced annular iris regions.
Results
The time analysis of densities showed that the inner regions of the iris stretched more strongly as compared with the outer regions of the iris during pupil constrictions. The pattern of iris densities across eccentricities and pupil size showed highly similar patterns across participants, highlighting the robustness of this elastic property. Importantly, iris-based eye position detection led to more stable signals than pupil-based detection.
Conclusions
The iris regions near the pupil appear to be more elastic than the outer regions near the sclera. This elastic property explains the instability of the pupil border and the related position errors induced by eye movement and pupil size in pupil-based eye-tracking. Tracking features in the iris produce more robust eye position signals. We expect that irissometry may pave the way to novel eye trackers and diagnostic tools in ophthalmology.
Keywords: irissometry, pupillometry, eye tracking, iris elasticity, pupil size, gaze estimation
The iris is an anatomically distinct and, one may say, rather magnificent piece of the eye. It is rich in texture, containing complex features that constitute numerous individual landmarks and variations in appearance across the eyes.1–3 Variations in the spatial layout and colors are mostly distributed across two regions: an inner, pupillary region that extends to the collaret and an outer, ciliary region that extends to the sclera border, also called the limbus. The more thickly layered collaret lies between the inner and outer regions where the underlying constrictor and radial muscles touch. The numerous ridges demark blood vessels that extend radially across both regions. Sometimes the iris contains circular contraction furrows in the outer region caused by wrinkling due to changes in pupil size.4 It also contains many variations in pigments caused by differences in melanin types, dark pigment spots,5 bright collagen spots (Wolfflin nodules6), thin-layered gaps (Fuchs crypts7), and sometimes brownish pigment spots surrounding the limbus (conjunctival melanosis8).
Although all of these beautiful iris features have been studied in great detail separately, it is currently unclear how the iris may deform and how the positions of these features change over time as the eye rotates or as the pupil changes in size. Current literature on this topic reports inconsistent results, describing radial movement trajectories of iris features as either nonlinear or linear.9–13 Here, we aimed to study iris deformations in more detail. To accomplish this, we used a novel iris-tracking algorithm, which we term irissometry. To put the usability of irissometry in context, we first provide a short overview of traditional eye-tracking algorithms and how iris deformations may decrease their accuracy.
The spatially distributed iris features make them ideal for video-based tracking, a method employed in eye-tracking devices to track a subject's gaze.14 However, so far video-oculography has limited these methods mostly to the detection of the pupil border or limbus to determine the angle of the eye.15 Most studies have accomplished gaze angle detection through the employment of filter-, intensity-, or appearance-based image template matching methods that take into account photometric properties of the eye region. Such methods typically detect the iris, pupil, and/or eye corners by looking for specific edge or blob patterns, which proves to be especially useful for low-resolution eye images or long-distance recordings “in the wild.”16 Specifically, the pupil-based methods come with several disadvantages, as well, mostly related to artifacts and measurement inaccuracies caused by pupil characteristics. Pupil-based gaze angle detection depends on detection of the center of the pupil.17 The center position depends, however, on the shape of the pupil, which varies (so far) unpredictably as a function of its size,18 causing errors in position estimation.19,20 Also, the pupil border is highly deformable12 and may flexibly wobble during fast rotational accelerations or decelerations of the eye,21,22 causing small but significant errors in eye position and saccade velocity detection. Finally, the border of the pupil provides only a limited number of unique tracking points. Detecting the limbus (i.e., sclera–iris border) rather than the pupil–iris border23–27 solves some of these problems but then incorporates another problem related to occlusion. Due to its peripheral location, the limbus is more likely to be occluded by the upper and lower eyelids, sometimes leaving only a small portion of the limbus visible, which may lead to inaccurate elliptical model fitting.
We propose that the detection of features within the surface of the iris rather than the border serves as a solution to the problems described above and as a method to study how the iris may deform. Its unique structure allows the detection and tracking of many features between the pupil border and limbus. As far as we know, no study has aimed to fully exploit the vast richness of features within the surface of the iris in high-resolution, close-up images while manipulating pupil size. Here, we report on (1) the implementation of a point tracking algorithm based on robust features detected across the iris surface, (2) the examination of how pupil size affects feature locations, and (3) which features produced the most robust and pupil-size-invariant eye position measurements.
Material and Methods
Participants
A total of 23 Dutch students of Leiden University with normal or lens-corrected vision participated in the experiment (mean ± SD age, 21.0 ± 2.5 years; range, 18–27 years; seven males, 16 females). They provided written informed consent and were debriefed about the purpose of the study after the experiment. The students received study credits for participation. The experiment was approved by the local ethics committee of Leiden University's Institute for Psychology Research.
Procedure, Stimuli, and Apparatus
Participants wore headphones (over-ear, stereo sound) and held their head in a chin and forehead rest at a fixed viewing distance of 50 cm in front of a liquid-crystal display screen (33° × 26° in width and height; 1280 × 1024 pixels; 60 frames per second). To evoke strong pupillary responses, a bright screen light was repeatedly turned on and off within a block. For the sake of result generalization, pupillary responses were also evoked in another block by presenting sudden sounds of screaming people that we collected from online sound libraries. The emotional content of the sounds was disclosed to the participants upfront. In the light stimuli block, the screen displayed a total of 10 periods of luminance alternations between 0 cd/m2 and 300 cd/m2 at a rate of 0.1 Hz (i.e., 10 bright and dark onsets, each lasting 5 seconds). In the sound stimuli block, the participants listened to 10 consecutive distinct sounds presented with a stereo headphone at 80 decibels at the same rate as the visual stimuli with 5-second soundless episodes in between while the screen presented a mid-level grayscale luminance (118 cd/m2). Participants fixated a small blue dot at the center of the screen during both blocks and tried to minimize blinking. An RGB Flea3 USB3 camera (Point Grey Research, Richmond, BC, Canada) with a Tokina AT-X 90-mm macro lens (Tokina, Tokyo, Japan) recorded close-up videos of the iris (grayscale; 640 pixels in width by 480 pixels in height; 40-Hz frame rate; no compression or encoding) using the MATLAB 2019b (The MathWorks, Natick, MA) Image Acquisition Toolbox.
Irissometry
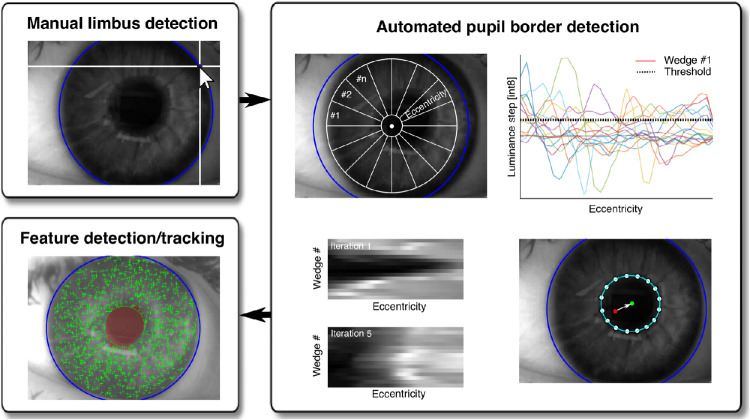
We set some parameters manually and implemented several automated image processing steps in MATLAB to detect the pupil border and features in the iris (for a flowchart, see Fig. 1; for code, see https://github.com/marnixnaber/Irissometry). First, author MN determined the radius of the iris by manually fitting a circle to the limbus in the first frame of each video. Second, a home-made, automated algorithm, similar to the well-known starburst method,28 detected 16 points on the pupil border at different radial angles per frame. A pupil border point was based on the detection of peaks in pixel value changes (moving window of 5 pixels) along a radial axis of image wedges, extending from the image center to the limbus in an initial iteration. However, the coordinates of the center of the pupil did not always match the coordinates of the image center, and accurate pupil border detection required the wedges to extend from the pupil center rather than the image center. As such, the algorithm iterated the pupil border detection process five times, improving the detection of the coordinates of the pupil center accordingly. This iteration process was performed for the 10th video frame following the video start or a blink episode to ensure that the eyes would be fully open at redetection of the pupil border. Otherwise, the pupil center coordinates were adjusted during the frame iterations as follows: After the pupil border was detected, the coordinates of the actual pupil center were calculated based on the properties of a circle fitted to the pupil border. These coordinates were then used as a starting point for the detection of pupil borders in the next frame.
Figure 1.
Image processing steps for irissometry. First, the limbus must be selected manually by using a computer mouse pointer (blue circle in top-left panel). Then, a startburst-like method calculates luminance changes per wedge (see #1 to #n in the top-left image of the right panel) across eccentricity, extending from the image center toward the limbus within a predefined suitable range. A pupil border per wedge (colored lines in top-right image) is detected based on the maximum luminance change above a predefined threshold (dotted line). In this study, the process was repeated (iterations) five times with an adjustment of the starting point for the wedge extensions per iteration, causing the pupil border to be detected at equal distance from the center of the pupil across wedges (bottom-left image depicts the luminance values of wedges across eccentricity for the first and last iterations). Within an iteration, detection of the pupil borders allowed calculation of the coordinates of the center of the pupil based on a circle fitted to the border points (cyan dot in bottom-right image), which served as a starting point instead of the image center (red dot) for the next frame. Finally, unique corner point features were detected between the pupil border and limbus, to be tracked from frame to frame (see bottom-left panel). Blinks or eye movements caused the pupil to deform, decreasing the fitted circular shape (see red surface) to a degree that could easily be detected using a predefined threshold.
A small residual (fit error) of a circle fitted to the pupil border coordinates (i.e., the mean absolute Euclidian distance between fitted and border coordinates; residual threshold > 0.16) indicated blink episodes. A polynomial binary mask, fitted to the pupil border points and subsequently filled with a convex hull method, served as the basis for the final pupil border. We computed the circularity and area of the final pupillary mask using the MATLAB regionprops function. The shape with the largest area within a range of 50 to 150 pixel radius (2.8- to 8.3-mm diameter) was recognized as the pupil. We calculated the pupil fit residual by taking the absolute of the circularity property minus 1. Finally, MATLAB implementations of corner point detection, Eigenvalue feature dissimilarity comparisons,29 and the maximum bidirectional error Kanade–Lucas–Tomasi algorithm30,31 detected and tracked unique features within the iris region frame to frame. These algorithms only track features (or corner points) with high qualities, meaning that the comparison of textures of two subsequent frames surrounding the feature coordinates produces two large eigenvalues. Large values indicate well-trackable corners, textures with contrast, and other patterns due to their invariance to orientation and intensity changes. A minimum of 600 features were tracked to ensure that enough features were detected across the range of iris eccentricities. Author MN determined this number after systematic adjustments and visual inspection of all output videos. A maximum of 2000 features was set to limit computational demands and time. The algorithm tracked features robustly across conditions and participants, and the manual inspection of feature presence indicated that occasionally just a few features (<5%) disappeared or reappeared between frames. A blink caused a full re-initialization of new features to be tracked. Only in rare cases did a blink cause a temporary (until a subsequent blink) lack of tracking features in the upper part of the iris due to too early re-initialization of the features.
Statistical Analyses
We performed three distinct analyses. The first analysis assessed whether the pupil changed significantly in size after a stimulus onset. We analyzed pupil responses in an event-related manner with a window size of 10 seconds (40 data points per second, resulting in 400 data points per response). Pupil responses were calculated per pair of stimulus on- and offset and per block of stimulus type (light and sound condition; 10 stimulus trials per stimulus type condition). The time traces of pupil responses, averaged across trials per participant, served as input (two-dimensional matrix of 23 participants by 400; time points in size) for paired, two-tailed Student's t-tests that compared pupil size at 10 intervals (time range, 0–10 seconds) to baseline pupil size at t = 0 seconds per stimulus type condition.
The second analysis assessed at which eccentricity the iris stretched most during pupil constrictions. The statistical assessment consisted of the creation of a linear mixed-effects model testing for fixed effects of iris annulus eccentricity (10 bins between 0% and 100%) and pupil state (constricted vs. dilated) on the feature distances (i.e., spacing) (see Fig. 3C). The model incorporated participant number as a random effect. The model received input data as a table with feature spacing averaged across time (pooling all stimulus trials) per stimulus type block (sounds and lights), for which the data were split between a dilated and constricted state by selecting all pupil size above and below the 50th percentile, respectively. The data table contained four different data types separated in columns: feature spacing as continuous data; a categorical annulus number treated as a continuous data (1–10, 1 = 0%–10% eccentricity; 10 = 90%–100% eccentricity); categorical constriction (1) versus dilation (2) state; and categorical participant number (1–23). The reported abbreviated indicators of statistical values consisted of F-statistic values, P values, β values (estimates), confidence intervals (CIs), and standard deviations (SDs) from the mean (M) estimates for random effects.
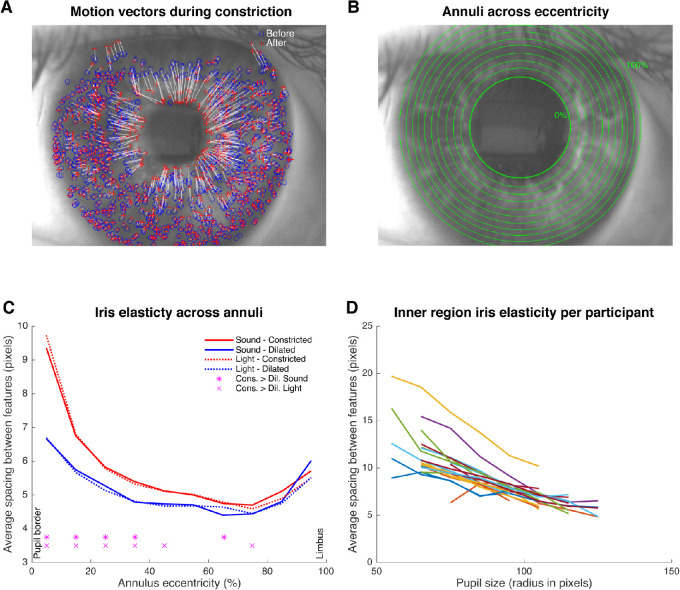
Figure 3.
Irissometry results. (A) Example snapshot from a video in which the pupil is in a state after constriction in response to the onset of a light stimulus. We detected unique features in the iris, here displaying their locations before (blue circles) and after (red plus signs) pupil constriction, with the white lines representing their motion vectors. Note that the pupil border before constriction laid somewhere near the innermost blue circles. (B) Each adjacent pair of circles represents a binned annulus region in which the spacing between features within that region is calculated. These regions correspond to the bins used for the plot in panel (C). The radius and width of the annuli move adaptively with changing pupil size to ensure an equal and consistent number of iris features across annuli and pupil sizes, respectively. The image displays the dilated pupil state preceding the constricted pupil state shown in panel (A). (C) Pattern of feature- and participant-averaged spacing between features falling within the annuli across eccentricities, per stimulus type and per constricted (red) versus dilated (blue) pupil state (split analysis). Asterisks and crosses at the bottom of the panel indicate at which iris eccentricities spacing significantly differed between pupil size states caused by sounds and lights, respectively (P < 0.001). (D) Lines show the average spacing within the innermost iris region (eccentricity = 5%) across binned pupil size per participant (one color per participant).
We performed a third analysis to test for differences in eye position signal robustness across feature locations (inner iris, outer iris, or pupil border features). A linear mixed-effects model tested for fixed effects of feature location on standard deviations of x and y eye positions across time during a pupil response. The standard deviation was calculated on the eye position time traces that were averaged stimulus trials per participant. The model incorporated participant number as a random effect. Note that we pooled the stimulus trials of both stimulus types (sound and light) because this factor did not affect the results. The data table contained four columns: standard deviation in eye position as continuous data; a categorical feature location (1–3, where 1 = inner iris; 2 = outer iris; 3 = pupil border); categorical eye position coordinate (1 = x; 2 = y); and categorical participant number (1–23).
Post hoc tests consisted of Student's t-tests for pairwise, two-tailed comparisons to assess differences between feature spacing per stimulus type (model 1) and deviation of eye position per horizontal and vertical coordinates (model 2).
Results
To restate the research goals, we aimed to examine (1) changes in iris texture as a function of pupil size, and (2) the robustness of eye position detection based on iris tracking as compared with pupil tracking. To examine the changes in iris textures, we first needed to confirm that the stimuli altered pupil size: Sudden on- and offsets of sounds and lights evoked changes in pupil sizes of participants, as can be seen in the exemplar Supplementary Videos S1 (sound) and S2 (light). In line with the literature,32,33 onsets of sounds and screen lights resulted in significant pupil dilations and constrictions, respectively (Fig. 2; for statistical results, see Supplementary Table S1).
Figure 2.
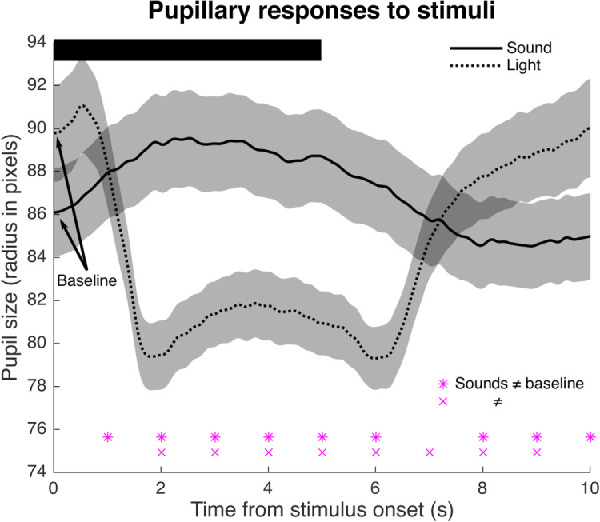
Iris recordings and results. Lines indicate stimulus- and participant-averaged pupillary responses to sounds (solid) and lights (dotted), and the transparent patches display the standard errors from the mean across participants. A pupil size of 90 image pixels in radius corresponds to approximately 5.0-mm diameter. Asterisks and crosses at the bottom of the panel indicate at which time points pupil size significantly differed from baseline pupil size at sound and light onset (t = 0 seconds), respectively (P < 0.001; arrows pinpoint baseline pupil size). The black bar at the top highlights the stimulus on-screen period.
Next, we examined how the iris structure deformed in parallel with the changes in pupil size. Figure 3A depicts an example of the detected iris features and their movement vectors. It shows the effect of a light-evoked pupil constriction on the locations of iris features between stimulus onset (t = 0 seconds) and stimulus offset (t = 5 seconds). Especially the features within the inner area of the iris, near the pupil border, showed strong constriction-induced displacements. To further quantify these effects, we computed the spacing between features per iris annulus as a function of eccentricity from the pupil border to the limbus (Fig. 3B).
As shown in Figure 3C, features located in the inner regions of the iris (i.e., low annulus eccentricity, near the pupil border) were spaced farther apart, especially during a constricted pupil state as compared with a dilated pupil state. We statistically tested this effect by creating a linear mixed-effects model with iris annulus eccentricity, F(396) = −9.06, P < 0.001, β = −0.56, CI = −0.68 to −0.44, random SD = 0.04, and pupil state, F(396) = −6.94, P < 0.001, β = −1.82, CI = −2.32 to −1.30, random SD = 0.35, as fixed within-subject factors and with participant number as a random between-subject factor (model input data were first averaged across all stimulus trials and then across the stimulus types sound and light). The nonlinear pattern of spacing suggests that the inner regions of the iris stretch more strongly than outer regions of the iris during a pupil constriction, as supported by a significant interaction between iris annulus eccentricity and pupil state in the linear model, F(396) = 4.71, P < 0.001, β = −0.20, CI = −2.42 to −0.70 (for post hoc tests, see Supplementary Table S2). Surprisingly, the spacing between features within the innermost iris region, where effects of pupil size were expressed most strongly, showed highly linear and similar patterns across participants (angle of fitted linear regression lines: M = 35, SD = 9, range = 19–53) (Fig. 3D). The latter finding indicates that the elastic stretch property of the inner iris is best described as linearly related to pupil size and robust across individuals.
As a last analysis, we examined the robustness of the detection of the position of the eye. Eye position based on the detected pupil border varied substantially during pupil responses (Supplementary Fig. S1). To investigate whether iris features produced more robust eye positions, we calculated the averaged standard deviations of eye position across time based on features located on the pupil border and in the inner and outer iris regions (Fig. 4). Horizontal eye position and vertical eye position showed the most stable traces across time (i.e., position deviated least across pupil size changes) when based on the inner and outer iris features, respectively. Following are the results of a linear mixed-effects model: feature locations, F(134) = 1.30, P = 0.195, β = −0.14, CI = −2.42 to −0.70, random SD = 1.97; x–y eye coordinates, F(134) = 3.58, P < 0.001, β = −1.56, CI = −0.34 to −0.07, random SD = 0.04; and interaction, F(134) = 2.06, P = 0.042, β = 0.13, CI = 0.01–0.26 (for post hoc tests, see Supplementary Table S3). As compared with the pupil border, the inner and outer iris features thus appear to offer more robust measures of x and y eye positions, respectively.
Figure 4.
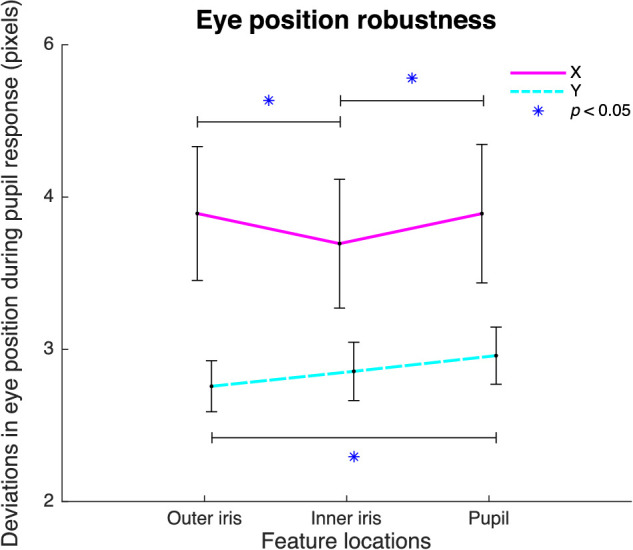
Eye position stability. Lines display the pattern of stimulus- and participant-averaged standard deviations of eye position (horizontal, x: solid; vertical, y: dashed) traces in pixels during pupillary responses per feature location type. Vertical lines indicate standard errors from the mean.
Discussion
This paper reports three findings: (1) the inner regions of the iris stretched more strongly than the outer regions during a pupil constriction, (2) this elastic property of the iris was comparably similar across individuals, and (3) the estimation of eye position showed less variable traces during pupil responses when based on the iris as compared with the pupil border.
Nonlinearity of Elastic Iris Property
The inspection of close-up videos of the iris during a pupil light response (e.g., see Supplementary Video S2) revealed that the changes in mostly the inner rim of the iris covary with changes in pupil size. Although the rigidity of the outer, ciliary portion of the iris and the elastic flexibility of the inner, pupillary portion of the iris are well observable, it is remarkable that this eye property has not been studied in detail before. In contrast, a previous iris deformation assessment by Pamplona and colleagues suggested a constant ratio between eye feature displacement across iris eccentricities during changes in pupil size.13 The latter disagrees with practices by pattern recognition scientists that aim to exploit the unique structure of the iris for person identification. They typically model nonlinear deformations across iris eccentricities caused by lux increments to deal with potential stretch differences.9–12 Also note that Pamplona and colleagues13 based their conclusions on a limited number of photographs and iris features, and they used an image set of pupils dilated by mydriatic drugs rather than light decrements, perhaps accounting for the inconsistency with the current results.
We provide two anatomical explanations for the nonlinear elastic property of the iris. First, the degree to which an elastic material stretches under stress depends on its thickness. As the pupillary iris region contains less substance in both depth and concentrically across its surface, it is expected to stretch more strongly. Second, the iris shape is determined by the antagonistic radial dilator and concentric sphincter muscles.34 As the sphincter muscle lies in the pupillary region, on top of the radial muscles that cover both pupillary and ciliary regions,35,36 it is not unlikely that the constrictor muscle causes the strongest anatomical changes in the pupillary region when activated.
Similarity of Elastic Iris Property Across Individuals
After quantification of the elastic stretching property of the inner pupillary iris region, we continued to explore the similarity of this property across individuals. Qualitative and quantitative inspection of the slopes of the linear relationship between the degree of inner iris stretching and pupil size revealed highly similar patterns across a homogeneously young group of individuals. We speculate that the robustness of this property makes it ideal for further investigation into its potential application as a biomarker of ocular diseases in a heterogeneous population. For example, the thickness of the iris varies across races,37,38 and a stronger thickness is associated with increased risk at a blockage of the flow of aqueous humor, raising ocular pressure and causing a condition referred to as primary angle-closure glaucoma.39,40 The raised levels of ocular pressure may cause damage to the optic nerve, resulting in irreversible impairment of central vision.41 We hypothesize that both iris thickness and ocular pressure may affect the iris stretching properties. Thus, an interesting line of research to pursue would be the exploration of irissometry as a non-contact diagnostic imaging method of iris thickness and primary angle-closure glaucoma.
Robustness of Iris-Based Eye Center Detection
The accurate detection of eye position is an important goal for eye-tracking technologies. As outlined in the introduction, pupil-based detection algorithms are the most commonly applied techniques but their accuracy depends on pupil size and shape variations.19,21,22 Here we demonstrate that an iris-based detection algorithm decreases the variability in eye position during pupil responses. More specifically, the horizontal and vertical position of a circle fitted on inner and outer iris features, respectively, resulted in less pupil-response–evoked variance than a circle fitted on the pupil border. For a yet unknown reason, the outer iris features improved the vertical but not horizontal eye position robustness. This latter finding is surprising, as the outer features should be least affected by pupil size changes. Outer iris features can, however, be occluded by eyelids but that should have led to instabilities in vertical rather than horizontal eye positions.
Limitations and Other Future Prospects for Irissometry
One limitation of the current irissometry solution is the manual selection of the center of the pupil and the limbus at the first frame, and the manual setting of parameters such as the minimal allowed fit error of the pupil border. Although such manual settings are even required in state-of-the-art eye trackers such as the EyeLink system (SR Research, Ottawa, ON, Canada), the implementation of more sophisticated computer vision and deep neural network techniques should be able to detect pupil–iris and iris–sclera borders automatically.42,43 This may also potentially solve pupil border detection problems in case of light reflections of bright objects such as the computer screen in the current study.
Despite the limitations described above, all iris features taken together still produced more stable eye position signals than the pupil border. Although out of scope of the current study, future research should explore the robustness of iris-based techniques when participants make eye movements. Participants maintained strict fixation during our experiment, but we expect to observe even stronger eye position deviations after saccades.21
Supplementary Material
Acknowledgments
Dominique Lippelt supported data collection. This work was partially inspired by Ignace Hooge's talk about the problems with pupil-based eye-tracking technologies. The video data that support the findings of this study can be requested from author MN (m.naber@uu.nl). The irissometry analysis code can be downloaded from https://github.com/marnixnaber/Irissometry.git.
Disclosure: C. Strauch, None; M. Naber, None
Supplementary Material
Supplementary Video S1. Recording of iris and pupil during on- and offset of sound stimulus.
Supplementary Video S2. Recording of iris and pupil during on- and offset of light stimulus.
References
- 1. Edwards M, Cha D, Krithika S, Johnson M, Parra EJ.. Analysis of iris surface features in populations of diverse ancestry. R Soc Open Sci. 2016; 3: 150424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ng RYF, Tay YH, Mok KM.. A review of iris recognition algorithms. Proc Int Symp Inform Technol. 2008; 2: 1–7. [Google Scholar]
- 3. Kaur N, Juneja M.. A review on iris recognition. In: Recent Advances in Engineering and Computational Sciences (RAECS). Piscataway, NJ: Institute of Electrical and Electronics Engineers; 2014: 1–5. [Google Scholar]
- 4. Eagle R Jr. Iris pigmentation and pigmented lesions: an ultrastructural study. Trans Am Ophthalmol Soc. 1988; 86: 581–687. [PMC free article] [PubMed] [Google Scholar]
- 5. Rennie I. Don't it make my blue eyes brown: heterochromia and other abnormalities of the iris. Eye (Lond). 2012; 26: 29–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Williams RB. Brushfield spots and Wolfflin nodules in the iris: an appraisal in handicapped children. Dev Med Child Neurol. 1981; 23: 646–650. [DOI] [PubMed] [Google Scholar]
- 7. Purtscher E. On the development and morphology of iris crypts. Acta Ophthalmol. 1965; 43: 109–119. [Google Scholar]
- 8. Damato B, Coupland SE.. Conjunctival melanoma and melanosis: a reappraisal of terminology, classification and staging. Clin Exp Ophthalmol. 2008; 36: 786–795. [DOI] [PubMed] [Google Scholar]
- 9. Clark AD, Kulp SA, Herron IH, Ross AA.. Exploring the nonlinear dynamics of iris deformation. In: Proceedings of the Biometric Consortium 2011 Conference. Gaithersburg, MD: National Institute of Standards and Technology; 2011. [Google Scholar]
- 10. Wei Z, Tan T, Sun Z.. Nonlinear iris deformation correction based on Gaussian model. In: Lee SW, Li SZ, eds. Advances in Biometrics. Berlin: Springer; 2007: 780–789. [Google Scholar]
- 11. Wyatt HJ. A ‘minimum-wear-and-tear'meshwork for the iris. Vision Res. 2000; 40: 2167–2176. [DOI] [PubMed] [Google Scholar]
- 12. Songjang T, Thainimit S.. Tracking and modeling human iris surface deformation. In: 2015 12th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON). Piscataway, NJ: Institute of Electrical and Electronics Engineers; 2015: 1–5. [Google Scholar]
- 13. Pamplona VF, Oliveira MM, Baranoski GV.. Photorealistic models for pupil light reflex and iridal pattern deformation. ACM Trans Graph. 2009; 28: 1–12. [Google Scholar]
- 14. Duchowski A. Eye tracking methodology: theory and practice. 2nd ed. London: Springer; 2007: 51–59. [Google Scholar]
- 15. Hansen DW, Ji Q. In the eye of the beholder: a survey of models for eyes and gaze. IEEE Trans Pattern Anal Mach Intell. 2009; 32: 478–500. [DOI] [PubMed] [Google Scholar]
- 16. Cristina S, Camilleri KP.. Unobtrusive and pervasive video-based eye-gaze tracking. Image Vis Comput. 2018; 74: 21–40. [Google Scholar]
- 17. Holmqvist K, Nyström M, Andersson R, Dewhurst R, Jarodzka H, Van de Weijer J.. Eye tracking: a comprehensive guide to methods and measures: Oxford: Oxford University Press; 2011. [Google Scholar]
- 18. Wyatt HJ. The form of the human pupil. Vision Res. 1995; 35: 2021–2036. [DOI] [PubMed] [Google Scholar]
- 19. Hooge I, Hessels R, Nyström M.. Do pupil-based binocular video eye trackers reliably measure vergence? Vision Res. 2019; 156: 1–9. [DOI] [PubMed] [Google Scholar]
- 20. Hooge I, Niehorster D, Hessels R, Cleveland D, Nyström M.. The pupil-size artefact (PSA) across time, viewing direction, and different eye trackers. Behav Res Methods. 2021; 53: 1986–2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Nyström M, Hooge I, Holmqvist K.. Post-saccadic oscillations in eye movement data recorded with pupil-based eye trackers reflect motion of the pupil inside the iris. Vision Res. 2013; 92: 59–66. [DOI] [PubMed] [Google Scholar]
- 22. Hooge I, Holmqvist K, Nyström M.. The pupil is faster than the corneal reflection (CR): are video based pupil-CR eye trackers suitable for studying detailed dynamics of eye movements? Vision Res. 2016; 128: 6–18. [DOI] [PubMed] [Google Scholar]
- 23. Feng G-C, Yuen PC.. Variance projection function and its application to eye detection for human face recognition. Pattern Recognit Lett. 1998; 19: 899–906. [Google Scholar]
- 24. Herpers R, Michaelis M, Lichtenauer K-H, Sommer G.. Edge and keypoint detection in facial regions. In: Proceedings of the Second International Conference on Automatic Face and Gesture Recognition. Piscataway, NJ: Institute of Electrical and Electronics Engineers; 1996: 212–217. [Google Scholar]
- 25. D'Orazio T, Leo M, Cicirelli G, Distante A. An algorithm for real time eye detection in face images. In: Proceedings of the 17th International Conference on Pattern Recognition, 2004 ICPR 2004. Piscataway, NJ: Institute of Electrical and Electronics Engineers; 2004: 278–281. [Google Scholar]
- 26. Sirohey S, Rosenfeld A, Duric Z.. A method of detecting and tracking irises and eyelids in video. Pattern Recognit. 2002; 35: 1389–1401. [Google Scholar]
- 27. Tian Y-l, Kanade T, Cohn JF.. Dual-state parametric eye tracking. In: Proceedings Fourth IEEE International Conference on Automatic Face and Gesture Recognition. Piscataway, NJ: Institute of Electrical and Electronics Engineers; 2000: 110–115. [Google Scholar]
- 28. Li D, Winfield D, Parkhurst DJ.. Starburst: a hybrid algorithm for video-based eye tracking combining feature-based and model-based approaches. In: 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05). Piscataway, NJ: Institute of Electrical and Electronics Engineers; 2005: 79. [Google Scholar]
- 29. Shi J, Tomasi C.. Good features to track. In: 1994 Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: Institute of Electrical and Electronics Engineers; 1994: 593–600. [Google Scholar]
- 30. Lucas BD, Kanade T.. An iterative image registration technique with an application to stereo vision. In: Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI ’81). IJCAI; 1981. [Google Scholar]
- 31. Tomasi C, Kanade T.. Detection and tracking of point features. Pittsburgh, PA: Carnegie Mellon University; 1991. [Google Scholar]
- 32. Naber M, Alvarez GA, Nakayama K.. Tracking the allocation of attention using human pupillary oscillations. Front Psychol. 2013; 4: 919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Zekveld AA, Koelewijn T, Kramer SE.. The pupil dilation response to auditory stimuli: current state of knowledge. Trends Hear. 2018; 22: 2331216518777174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Loewenfeld I, Lowenstein O.. The pupil: anatomy, physiology, and clinical applications. Detroit, MI: Wayne State University Press; 1993. [Google Scholar]
- 35. Freddo TF. Ultrastructure of the iris. Microsc Res Tech. 1996; 33: 369–389. [DOI] [PubMed] [Google Scholar]
- 36. Adler FH. Physiology of the eye. Acad Med. 1965; 40: 720. [Google Scholar]
- 37. Lee RY, Huang G, Porco TC, Chen Y-C, He M, Lin SC.. Differences in iris thickness among African Americans, Caucasian Americans, Hispanic Americans, Chinese Americans, and Filipino-Americans. J Glaucoma. 2013; 22: 673–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Sidhartha E, Gupta P, Liao J, et al.. Assessment of iris surface features and their relationship with iris thickness in Asian eyes. Ophthalmology. 2014; 121: 1007–1012. [DOI] [PubMed] [Google Scholar]
- 39. Wang B, Narayanaswamy A, Amerasinghe N, et al.. Increased iris thickness and association with primary angle closure glaucoma. Br J Ophthalmol. 2011; 95: 46–50. [DOI] [PubMed] [Google Scholar]
- 40. Lee RY, Kasuga T, Cui QN, et al.. Association between baseline iris thickness and prophylactic laser peripheral iridotomy outcomes in primary angle-closure suspects. Ophthalmology. 2014; 121: 1194–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Wright C, Tawfik MA, Waisbourd M, Katz LJ.. Primary angle-closure glaucoma: an update. Acta Ophthalmol. 2016; 94: 217–225. [DOI] [PubMed] [Google Scholar]
- 42. Fuhl W, Santini T, Kasneci G, Kasneci E.. Pupilnet: convolutional neural networks for robust pupil detection. arXiv. 2016, arXiv:1601.04902v1. [Google Scholar]
- 43. Vera-Olmos FJ, Pardo E, Melero H, Malpica N.. DeepEye: deep convolutional network for pupil detection in real environments. Integr Comput Aided Eng. 2019; 26: 85–95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.