Abstract
Global downwelling plane irradiance is a necessary variable to normalize the water-leaving radiance measurements, reducing the magnitude and spectral variabilities introduced by the incident light field. As a result, the normalized measurements, known as remote sensing reflectance, have higher correlation with the inherent optical properties of the water body and so to the composition of optically active water components. For in situ measurements, the global downwelling plane irradiance can be estimated from the exitant radiance of sintered polytetrafluoroethylene plaques or other diffuse reflectance standards. This allows use of a single spectrometer to measure all necessary variables to estimate the remote sensing reflectance, reducing cost in acquisition and maintenance of instrumentation. However, despite being in use for more than 30 years, the uncertainty associated with the method has been only partially evaluated. In this study, we use a suite of sky radiance distributions for twenty four atmospheres and nine solar zenith angles in combination with full bidirectional reflectance distribution function determinations of white and grey plaques to evaluate the uncertainties. The isolated and interactive effects of bidirectional reflectance distribution, shadowing and tilt error sources are evaluated. We found that under the best performing geometries of each plaque, and with appropriate estimation functions, average standard uncertainty ranges from 1% to 6.5%. The simulated errors are found to explain both previous empirical uncertainty estimates and new data collected during this study. Those errors are of the same magnitude as uncertainties of plane irradiance sensors (e.g., cosine collectors), and overlap with uncertainty requirements for different uses of in situ data, which supports the continued use of the plaque method in hydrologic optics research and monitoring. Recommendations are provided to improve the quality of measurements and assure that uncertainties will be in the range of those calculated here.
1. Introduction
In remote sensing studies of water color, a fundamental variable is the remote sensing reflectance, , defined as the water-leaving radiance, Lw, normalized by the global downwelling plane irradiance (Eg):
| (1) |
where θ and φ are the zenith and azimuth angles, respectively, λ denotes the wavelength, subscript v identifies the view direction, subscript s identifies the Sun’s direction and all variables are defined just above the water surface [1]. Rrs is retrieved by in situ or remote sensors primarily for the estimation of the optical properties and the concentration of optically active water components [2–6]. In situ measurements are also of interest for algorithm development, validation of atmospheric compensation methods for airborne or orbital sensors [7] and vicarious calibration of orbital sensors [8–10].
When in situ measurements are performed above the water surface, Lw can be measured directly if the tip of the foreoptics shield breaks the air-water interface [11–13]. This prevents the contamination of the Lw signal with the sky radiance reflected by the surface. If, however, the water radiance measurements are performed at a distance above the surface, the sky glint component must be removed from the total upwelling signal (Lu). This correction is performed by measuring a third variable, the sky radiance at the nominal specular angle, Lsky:
| (2) |
where ρf is a wind dependent effective Fresnel reflectance factor [14].
The two or three variables necessary for calculation of Rrs can be measured by an equal number of cross-calibrated spectrometers or by a single spectrometer if the radiance reflected from a level reference plaque of known reflectance is used to estimate Eg [15]. This method was first introduced in hydrologic optics by Carder and Steward [16] following terrestrial studies, where exitant radiance from reference plaques is used to estimate bi-directional reflectance factors [17,18]. Use of a single instrument and reflectance standard to measure all necessary variables to calculate Rrs has the advantage of removing the uncertainty associated with the absolute radiance and irradiance calibration (e.g., laboratory calibration uncertainty, uncertainty from differences between laboratory to environment light field) when reflectance is calculated at full instrument resolution. It also removes the interaction effects between uncertainties from multiple calibrated spectrometers, particularly when different instrument models are used (e.g., spectral noise from spectral resampling artifacts). Additionally, this configuration reduces costs associated with acquisition, maintenance and transport of multiple spectrometers systems. The main disadvantage is that targets are measured sequentially, requiring stable illumination conditions for the time interval necessary per measurement cycle [19].
Despite being in use for more than 30 years [2,20–26], research to characterize the plaque method uncertainties for water applications is scarce. Common to land applications, uncertainties arise from the absolute calibration of the plaque reflectance and from plaque deviations from a perfectly lambertian reflector [27–29]. But when deployed from floating platforms, typical for water applications, additional errors sources are present. To compensate for the continuously varying pitch and roll inclinations of the platform, the plaque is generally held by hand. This results in additional shadowing from (and reflection by) the operator to that possibly present due to platform superstructure. The manual stabilization of the plaque might also under or overcompensate for the platform inclination, adding to the total uncertainty.
Evaluations of the plaque method have been performed by consecutive measurements with multiple spectrometer systems [30–34]. Most studies however, report comparisons only in terms of Rrs [33,34], which include additional error sources that might dominate the uncertainty. Dekker [30] provided the first comparisons of Eg estimation between spectrometers adapted with cosine collectors and the plaque method. His experiments over Dutch lakes ranged from clear skies to overcast conditions, presumably under continental aerosol types. Measurements through most of the spectrum agree within ±20%, with an average ratio of 0.99 ± 0.08. If the ratio distribution is assumed to be normal and the plane irradiance sensor is treated as a reference measurement, the mean absolute percentage error (MAPE) of the plaque method in the visible range is estimated as 6.4%. Toole et al. [31] provided similar measurements in a marine environment taken over a year in Santa Barbara Channel, reporting a normalized root mean squared error (NRMSE) of 10%. If the same assumptions are made about the error distribution and reference of irradiance sensor, the MAPE is estimated as 8%. Doxaran et al. [32] reported measurements made in Plymouth Sound, with values agreeing within ±15% to ±20% under clear skies to broken clouds, depending on the measurement protocol, but with differences up to 60% under overcast conditions. Under clear skies to broken clouds, Doxaran et al. [32] measurements agree within the range of those measured by Dekker [30], while overcast conditions suggest a MAPE of about 12.5%.
Though valuable efforts, those studies remain tentative since inter-comparison studies can only provide relative agreement between instruments or methods. Dekker [30] proposed that it might not be adequate to take the plane irradiance sensor as a reference measurement (i.e., negligible error), while the study of Toole et al. [31] report even larger disagreement between different plane irradiance sensors (average NRMSE of 13%, with an estimated MAPE of 10%). A recent uncertainty study for multiple spectrometer systems as deployed in hydrologic optics research estimated the uncertainty of plane irradiance sensors to be between 4.4% to 5.8%, with relative agreement determinations of 4.1% to 6.4% for sensors on floating platforms [35]. Those uncertainties for plane irradiance sensors are in the same magnitude of the average errors reported by the plaque method evaluation studies, with the exception of the large errors under overcast conditions reported by Doxaran et al. [32]. As a consequence, it is not possible to attribute the differences observed in the method comparison studies solely to the plaque measurements. Another limitation of the experimental comparisons is the difficulty in isolating the different sources of errors, generally providing little insight about the uncertainty budget that could be used to improve measurement protocol.
The objective of this research is to budget the error sources associated with the plaque method for the estimation of Eg as a normalization factor for Rrs calculation. This error budget will provide guidance for improvements in accuracy and aid in the assessment of uncertainties from historical datasets. It will also allow us to evaluate if total uncertainties are comparable to other modern methods and so evaluate if the plaque method is appropriate for the multiple purposes of in situ measurements.
2. Theoretical background
The directional and spectral exitant radiance from the reference plaque, , is the integral product of the plaque bidirectional reflectance distribution function (BRDF), , and the radiance distribution incident on the plaque surface, :
| (3) |
| (4) |
In Eq. 3 and 4, Ω is the solid angle, subscript i identifies the incident direction, is the differential directional incident plane irradiance and the integral is taken over all directions in the incident hemisphere. The integral in Eq. 3 results in the loss of directional information and even with knowledge of the full BRDF, Lp from a single direction cannot be inverted for the incident (ir)radiance distribution. However, under specific conditions, Eq. 3 can be solved for the total incident plane irradiance, :
| (5) |
Solution of Eq. 3 for is only possible when the directional dependency of the incident (ir)radiance is simplified (e.g., collimated beam) and/or is absent in the reference plaque (e.g., perfect lambertian diffuser). When the incident irradiance is a collimated beam, all directions different from the collimated beam direction have a directional irradiance of zero, and do not contribute to the integral. And for a perfectly lambertian reflector, the BRDF is equal to for all illumination and viewing geometries, where is the hemispherical-directional reflectance (unitless) and π has units of steradians. Eq. 3 can then be simplified to:
| (6) |
| (7) |
Those conditions are only approximately valid under practical applications. As an example, the direct solar component of Eg, Es, is approximately collimated and will dominate Eg in the visible range under clear skies (e.g., visibility > 5 km for θs < 60°; [36]). In addition, approximately lambertian reflectors are commercially available, such as high reflectance (99 %) sintered polytetrafluoroethylene (PTFE), that show weak dependence on geometry [37]. Therefore Eq. 6 and 7 are useful approximations and are used for practical inversions [14,15].
Relevant for application to aquatic remote sensing, Ei will equal Eg when the plaque normal is oriented to the zenith and when there are no disturbances on the (ir)radiance distribution incident over the reference plaque compared to that incident over the area of the water body contributing to the measured Lw. In practical applications, differences will arise due to those factors. The tilt of the plaque normal away from the zenith will expose the plaque to radiance from the lower hemisphere and overall change the incident angle of the directional irradiance from the upper hemisphere. The presence of superstructures result in radiance reflected from the superstructure substituting for the radiance from equivalent directions that are incident over the water body. When the magnitude of those effects is small, Ei will be approximately equal to Eg.
The generic Eq. 3 can then be rewritten to incorporate the conditions of natural illumination from the upper hemisphere. It is useful to differentiate between the Es and the diffuse component of Eg, Ed, and to introduce the averaged BRDFs weighted by the directional irradiances:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
In Eq. 8 to 12, subscript d identifies variables related to the diffuse fraction of Eg. Inspection of equations 3 to 12 shows that the error caused by using Lp with Eq. 6 and 7 to estimate Eg decreases as the magnitude of Ei approaches the magnitude of Eg, i.e. . Additionally, for Eq. 6 errors will reduce as , which is expected to happen as and/or . For Eq. 7, error reduces as . An explicit dependency on θv was added to ρ, as necessary to account for departures of real materials from constant BRDF. Importantly, under the presence of light field disturbances and tilt of the plaque, the weightings in and are given by Ei and the diffuse fraction of Ei, respectively, and not by Eg and Ed. The unknown divergence from the conditions where Eq. 6 and 7 are valid solutions to Eq. 8 generates the uncertainty of Eg estimation and is a function of the material, the incident (ir)radiance distribution and the measurement geometry.
3. Simulations
3.1. Sky radiance model
The directional and spectral sky radiance distributions for clear sky conditions was based on Zibordi and Voss [38]. This model uses an approximate solution for a purely scattering atmosphere [39] with absorbers contained in a dimensionless bounding layer at the top. The atmosphere model was updated in the treatment of air mass [40], Rayleigh optical thickness [41], and ozone absorption coefficients [42]. The model was run for Sun zenith angles from 0° to 80° in steps of 10°, for wavelengths between 350 nm and 1000 nm in steps of 10 nm, and with 1° spacing in zenith (θ) and azimuth () angles covering the upper hemisphere. For all simulations, the molecular atmosphere composition was set to 1.39 kmol m−2 (2.5 cm m−2) of precipitable water, 133.86 mmol m−2 (300 Dobson Unit) of ozone, 19.81 mmol m−3 (450 mmol mol−1) of CO2 and a surface pressure of 101.25 kPa.
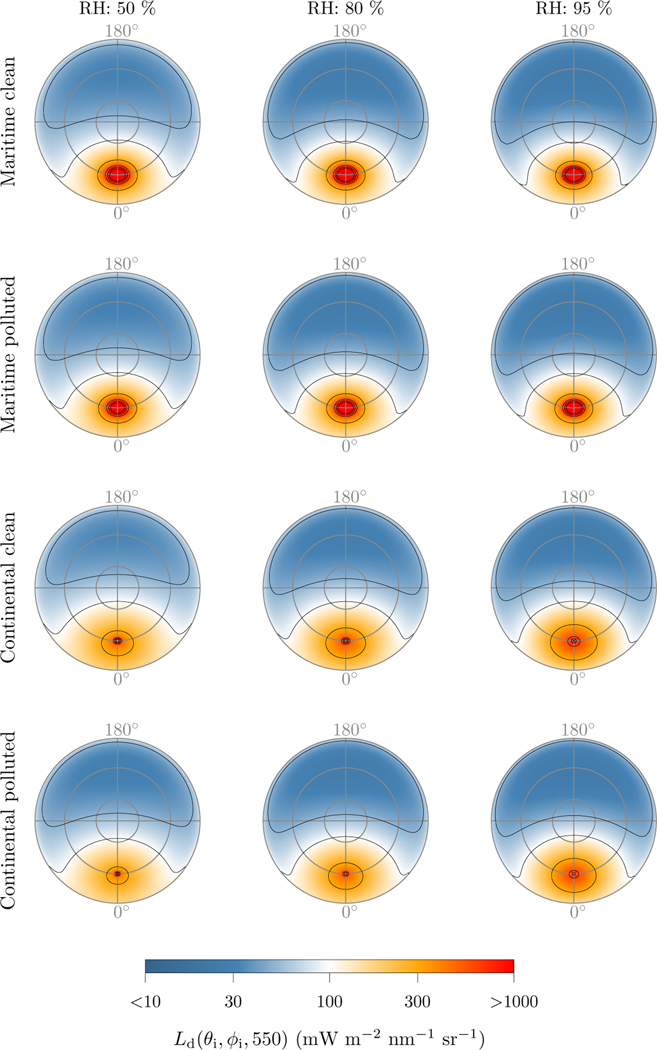
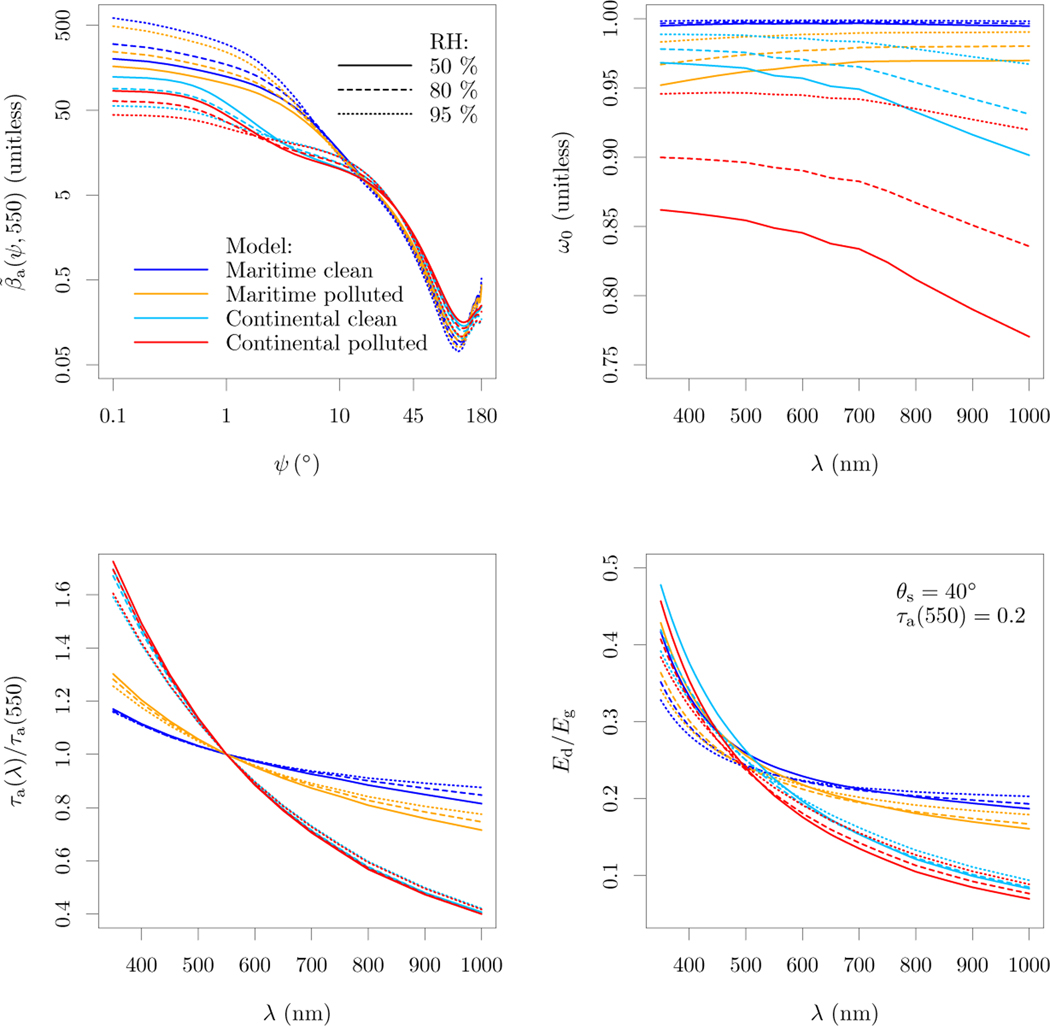
The Optical Properties of Aerosols and Clouds code (OPAC, version 4b; [43,44]) was used to generate the aerosol optical properties for the simulations. Four default OPAC aerosol models were used, representing maritime clean, maritime polluted, continental clean and continental polluted aerosols. The optical properties of these aerosol models were retrieved for three relative humidities (50%, 80% and 95%) and two aerosol loads representing an aerosol optical thickness at 550 nm (τa(550)) of 0.1 and 0.2. The sky radiance distribution at 550 nm for τa(550) = 0.2 and θs = 40° for each model and relative humidity combination is shown in Fig. 1. The optical properties of the aerosols are presented in Fig. 2 together with the diffuse fraction of Eg for the sky radiances of Fig. 1.
Fig. 1:
Sky radiance distribution at 550 nm with θs = 40° and τa(550) = 0.2, for each aerosol model and relative humidity combination. Inner to outer concentric circles represent zeniths of 15°, 40° and 90°. Data presented in orthographic projection (r = cos θ).
Fig. 2:
Optical properties of the aerosol models used in the simulations and resulting diffuse fraction at a subset of conditions. (, 550) is the aerosol phase function at 550 nm, is the scattering angle, ω0 is the aerosol single scattering albedo, τa is the aerosol optical thickness, and Ed/Eg is the diffuse fraction.
Broken clouds were not simulated, but a heavily overcast (OC) condition was included, modeled as a cardioidal distribution [45]. The relative directional distribution of radiance in this scenario is independent of wavelength and azimuth. Since the cardioidal distribution results in higher radiance in the zenith and under heavily overcast conditions the Sun in not apparent, the BRDF used with Eq. 6 was that for incidence from the zenith.
The surface reflectivity (ρs) used for the sky radiance distribution calculation was modeled as a combination of Fresnel reflectance for an isotropic incident radiance over a flat surface and an isotropic water-leaving reflectance (ρw) representing coastal waters. The real part of the refractive index of the pure water was calculated with the Water Optical Properties Processor code (WOPP, version 1.7; [46]) for a salinity of 34 g kg−1 and temperature of 15°C. For the computation of the radiance distribution of the lower hemisphere, Fresnel reflectance was used to convert the sky radiance distribution into specular reflection, to which an isotropic water-leaving radiance was added.
The reference Eg, , was calculated for each wavelength and sky model with Eq. 9. Plaque estimation bias for each error source was simulated by first calculating Lp from the BRDF and incident directional irradiance as in Eq. 3, to which the radiance contribution from the direct beam was added using the Es and the BRDF of the Sun-sensor geometry. Equations 6 and 7 were then applied to Lp to retrieve the plaque estimate of Eg, . Errors due to BRDF effects alone arise solely from the use of the approximations represented by Eq. 6 and 7.
Shadow was created by setting to zero the radiance from directions that intersect the user and instrument before Lp calculation. The shadows are dependent on measurement geometry, instrument size and distance from the plaque. Here we assumed a measurement holding the plaque at neck height, 40 cm from the body, with sensor at a distance of 30 cm to 40 cm from the plaque (depending on view geometry). The two shadow masks used in this study are discussed and presented in section 3.3. Tilts were simulated from 3° to 12° in steps of 3° and for all azimuths in steps of 45°. Tilt of the plaque is considered independent of sensor and result in changes in the view geometry. The tilt of the platform itself (e.g., pitch and roll of a ship), would not produce independent tilts of plaque and sensor if both are fixed. The situation modeled here focuses on the case where plaque is held and stabilized by hand or potentially a gimbal. Tilt was simulated by rotating the reference frame of the radiance distribution and by scaling Es by the original to tilted θs cosine ratio. Under tilt, Lp calculations used the BRDF for the realized θv. As the tilt is unintended and the operator is unaware of it, the BRDF at the nominal Sun-sensor geometry was used when converting Lp to Eg with Eq. 6, resulting in a further addition to the error. Similarly, when using Eq. 7, the nominal θv is used for . The values used in the scaling of the normalized BRDFs are calculated by the integral of the BRDF over all incident angles, i.e., .
All simulations were run in R version 3.3.3 [47] and analysis made with aid of packages abind [48], akima [49], sp [50] and raster [51]. Sky radiance simulations and error estimations are available in the Code File 1 (Ref. [52]), as well as the scripts and ancillary data necessary to reproduce the results. Synthesis of the results will be presented as the MAPE and the standard deviation of the absolute percentage errors in the visible range (400 nm to 700 nm) over subsets of the data representing overcast conditions and recommended sky conditions. The recommended sky conditions, as justified in section 6, are clear skies with 20° ≤ θs ≤ 60°.
3.2. Sintered PTFE BRDF
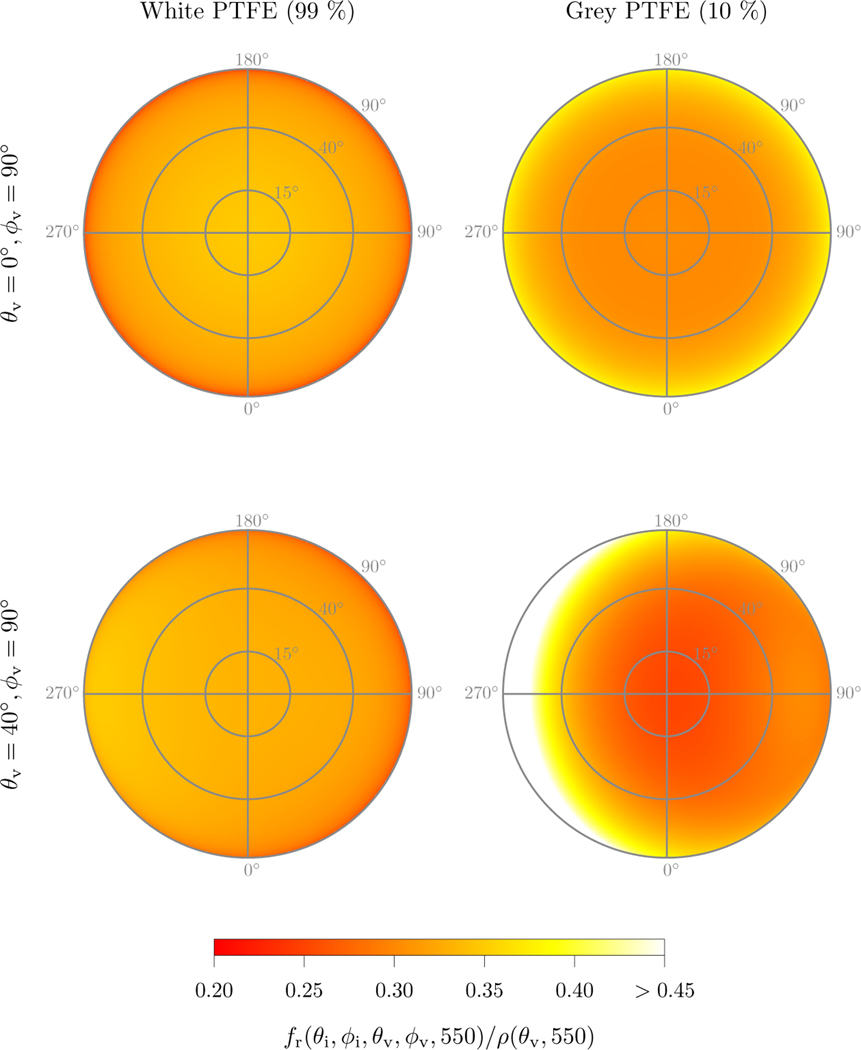
The four-dimensional and reciprocal Mueller matrix BRDF of highly reflective (99%) sintered PTFE was measured by Germer [37]. The multiwavelength Zernike Polynomial coefficients fitted to the data were used with functions from the SCATMECH C++ library [53] to calculate the unpolarized BRDF for the view geometries in the same wavelength grid as the atmospheric model. Similar coefficients for a grey (10%) sintered PTFE measured at 532 nm were determined with the same method as in Germer [37] and used to evaluate the uncertainty with a darker reference, that show stronger departure from an ideal lambertian reflector. In order to extend the analysis with the grey plaque to the full range of wavelengths used in this study, it is assumed that the normalized BRDF has negligible wavelength dependency and the normalized values at 532 nm are taken as a constant [54]. Grey references are used in hydrologic optics when the dynamic range of the sensors at a given integration time cannot accommodate the dim water-leaving radiance signal with the exitant radiance from a white (99%) plaque. The Zernike Polynomial coefficients of the grey plaque at 532 nm determined in this study are provided in the Code File 1. The normalized BRDFs of both plaques as a function of θi and for the nominal viewing geometries used in this study (section 3.3) are presented in Fig 3.
Fig. 3:
Normalized BRDFs for the 99% and 10% nominal reflectance plaques at 550 nm for the two viewing geometries considered in this study (section 3.3). For reference, the BRDF of a perfectly reflective lambertian surface is 0.318 sr−1. is the integral of over all incident solid angles. Inner to outer concentric circles represent zeniths of 15°, 40° and 90°. Data presented in orthographic projection (r = cos θ).
3.3. Observation geometry
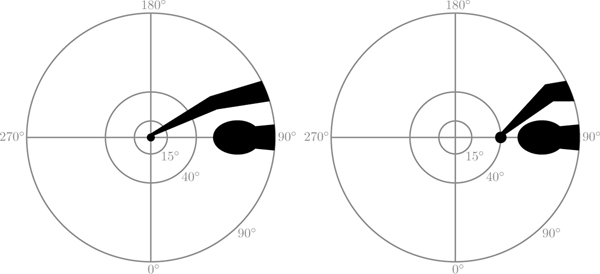
Two view geometries were considered, nadir () and at a relative azimuth () of 90° to the Sun. The nadir view is recommended for the plaque method [15] because determination of the BRDF is simpler, and measurements show that the reflectance properties of darker PTFE plaques are considerably more homogeneous at nadir view or illumination (this study; cf. Fig. 3). The view at 40° was considered for the case of fixed sensors, and due to recommendations to hold the view geometry stable between plaque and water measurements [14]. We justify the relative azimuth by the expectation that it will result in lowest interference with the sky radiance distribution. Smaller would result in shadowing of directions closer to the Sun that have higher radiance and higher would result in reflectance of the direct beam by the shadowing structure onto the plaque. The shadow solid angle that would be generated by the observation geometries are shown in Fig. 4.
Fig. 4:
Shadow solid angle created by the two viewing geometries used in this study, θv = 0° and θv = 40°, at a = 90°. Inner to outer concentric circles represent zeniths of 15°, 40° and 90°. Data presented in stereographic projection (r = tan θ).
4. Measurements
An inter-comparison experiment on the estimation of Eg between an irradiance sensor and the plaque method was carried out in Long Island Sound, USA, from 27th to 29th of June, 2017. Measurements were made onboard R/V Lowell Weicker, from the University of Connecticut, an eleven meter vessel with a two meter high cabin above the deck. A calibrated hyperspectral radiometer (FieldSpec 4, Analytical Spectral Devices) equipped with an 8° field of view foreoptics was used to measure the exitant radiance of an aged grey (12%) sintered PTFE reference plaque (Spectralon™, Labsphere). Before the start of the campaign the aged grey plaque was cross-calibrated against a reference white PFTE, under natural illumination conditions represented by clear skies and θs = 42° for the nadir view and θs = 24° for the side view of θv = 40°. Cross-calibrations per view geometry were performed on a level surface, side by side, with minimum surrounding structures, that nevertheless represented equal conditions for both plaques. During field measurements, the plaque was held by hand and measurements performed at = 90°, at nadir and θv = 40°. Measurements were compared to two calibrated irradiance sensors (HyperOCR, Satlantic, Inc.) positioned above the water. The first one was available through the cruise and was deployed on a buoy (Satlantic HyperPro Profiler) and allowed to float away from the ship before measurements. The second irradiance sensor was available only on the last day and was deployed at the top of the ship.
Measurements were filtered to remove irradiance sensors data with inclination larger than 5° from the zenith [15], and averaged for the time span of the plaque measurements. Since the BRDF of the aged grey plaque was not known, irradiance was estimated only with Eq. 7, using the values from the cross-calibration with the white PTFE. FieldSpec 4 data was convolved into the bandwidth of the HyperOCRs before comparison. Irradiance sensors were cross-calibrated at the end of the field campaign. In total, seven stations had concomitant data between the plaque measurements and the buoy mounted sensor and two with the ship mounted sensor. Sky conditions during measurements varied between clear skies to 60% cloud cover, with θs between 20° and 30°. Sea-state was mostly moderate, with three stations presenting low to moderate swell.
The commercial equipment, instruments, and materials are identified in this study in order to adequately specify the experimental procedure. It is not intended to imply recommendation or endorsement by the authors or the institutions they represent, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
5. Results
5.1. Simulated BRDF effects
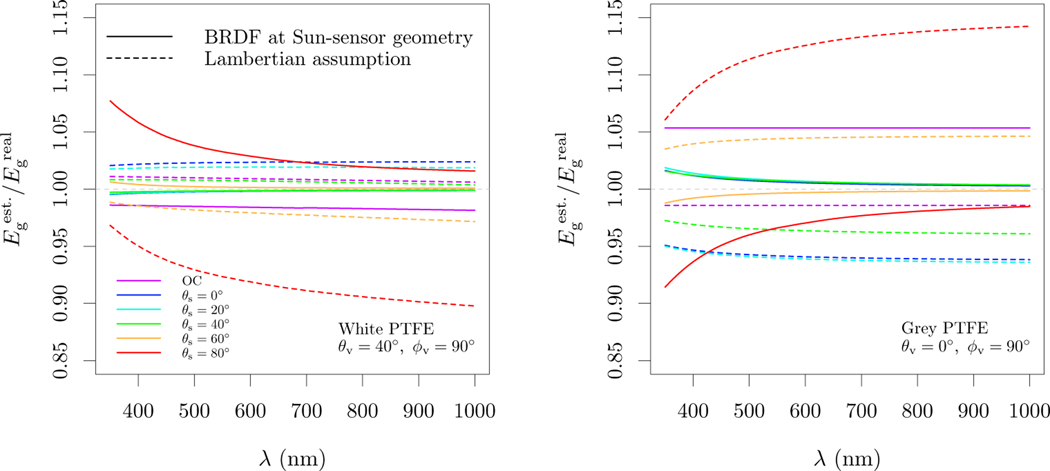
As expected from theory, BRDF effects have a spectral shape dependent on the diffuse fraction (cf. Fig. 2), showing approximately exponential spectral shapes under clear skies conditions (Fig. 5). For a white plaque, clear skies with θs < 50° result in underestimation of Eg, with overestimation for higher θs. This pattern is inverted for the grey plaque. The best performing geometries for each plaque also differ, being nadir for the grey plaque and θv = 40° for the white. Under recommended sky conditions and best performing geometries for each plaque, errors remain below 1.8% in the visible, and average 0.2% and 0.7% for the white and grey PTFE, respectively, when using Eq. 6 (Table 1). Under OC conditions for the same recommended geometries, errors are higher, reaching 1.6% for the white plaque and 5.4% for the grey. The use of the lambertian assumption (i.e., Eq. 7) will increase errors under clear skies and decrease them under OC conditions, changing the bias direction of the error for all conditions, geometries and plaques. Eq. 7 results in average errors of 1.0% and 1.4% in the visible for the white and grey PTFE, respectively, under OC conditions (Table 1).
Fig. 5:
Simulated BRDF effects on the estimation of Eg from Lp measured over sintered PTFE reference plaques without disturbances to the incident light field. Only the best performing geometry for each plaque is shown. is the ratio of the Eg estimated from Lp to the real Eg. Line colors represent the sky conditions from OC to clear skies with θs from 0° to 80°.
Table 1:
Mean absolute percentage errors (%) in the visible range due to BRDF effects for two conversion schemes from Lp to Eg represented by Eq. 6 and Eq. 7. Smallest errors for each sky condition and plaque are formatted in bold. Numbers in parenthesis are the standard deviations. Statistics calculated over all simulations included in each evaluation and over all visible wavelengths.
| Conversion | Measurement | White PTFE | Grey PTFE | |
|---|---|---|---|---|
| BRDF (Eq. 6) | θv = 0° | Clear* | 0.41(±0.26) | 0.66 (±0.35) |
| OC | 5.68(±0.14) | 5.35† | ||
| θv = 40° | Clear* | 0.16 (±0.09) | 1.74(±1.26) | |
| OC | 1.55(±0.07) | 24.40† | ||
| Lambertian (Eq. 7) | θv = 0° | Clear* | 2.69(±1.67) | 3.91(±2.08) |
| OC | 1.16(±0.03) | 1.43 † | ||
| θv = 40° | Clear* | 1.26(±0.66) | 9.74(±5.77) | |
| OC | 0.95 (±0.07) | 3.22† | ||
Clear skies for 20° ≤ θs ≤ 60°.
Standard deviation is zero since both relative sky radiance distribution for overcast conditions and the normalized BRDF of grey plaque are independent of wavelength.
5.2. Simulated shadow effects
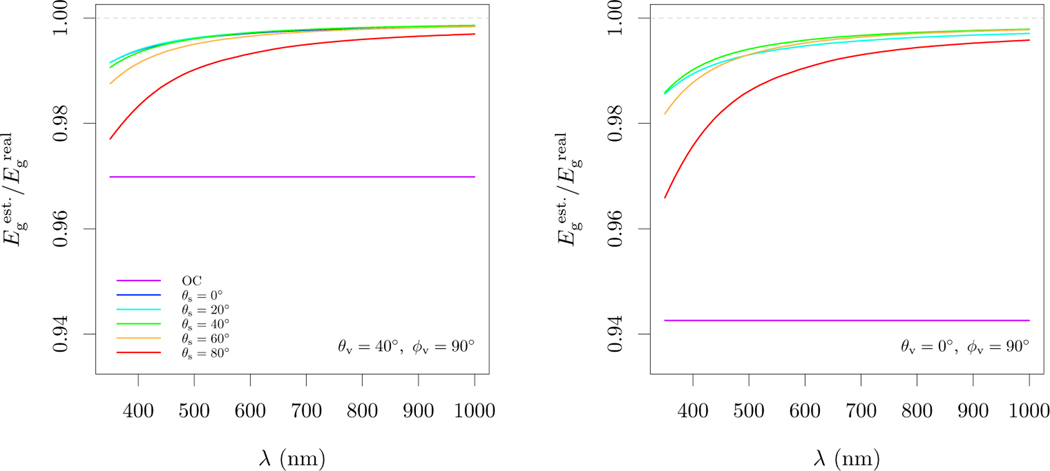
For a level perfectly lambertian reference plaque, errors will arise in the presence of an operator and superstructure causing an underestimation of Eg depending of the total fraction of the sky dome and the specific regions shadowed. The underestimation is contingent to the side view, where we ignore reflections from the operator and superstructure into the plaque and the only effect is the shadowing of sky radiance. For a θv of 40°, errors in the visible are 3.0% under overcast conditions and lower than 1.5% for clear skies, averaging 0.4% for the recommended θs range (Fig. 6 and Table 2). In nadir view, errors are 1.5 times higher in magnitude for clear skies and double for overcast, reaching 5.7%. Errors are approximately linear with diffuse fraction and the linear relation is independent of θs.
Fig. 6:
Simulated shadow effects of operator and instrument on the estimation of Eg from a level perfectly lambertian reflector. Differences in view geometry translate into different areas and fractions of the sky dome being shadowed. For the nadir view (θv = 0°), the blue line representing the Sun in the zenith is not shown, as shadowing of direct beam results in a ratio < 0.2 in the visible range. Line colors represent the sky conditions from OC to clear skies with θs from 0° to 80°.
Table 2:
Mean absolute percentage errors (%) in the visible range due to shadow effects and combined shadow and BRDF effects. Conversion from Lp to Eg are provided with Eq. 6 and Eq. 7. Smallest errors for each sky condition and plaque are formatted in bold. Numbers in parenthesis are the standard deviations. Statistics calculated over all simulations included in each evaluation and over all visible wavelengths.
| Conversion | Measurement | Shadow | Comb., White PTFE | Comb., Grey PTFE | |
|---|---|---|---|---|---|
| BRDF (Eq. 6) | θv = 0° | Clear* | 0.59(±0.26) | 0.95(±0.44) | 0.38 (±0.42) |
| OC | 5.74† | 11.06(±0.13) | 0.77 † | ||
| θv = 40° | Clear* | 0.38 (±0.17) | 0.44 (±0.21) | 1.49(±1.03) | |
| OC | 3.02 † | 4.34(±0.06) | 20.84† | ||
| Lambertian (Eq. 7) | θv = 0° | Clear* | 0.59(±0.26) | 2.51(±1.46) | 4.25(±2.11) |
| OC | 5.74† | 4.61(±0.02) | 7.16† | ||
| θv = 40° | Clear* | 0.38 (±0.17) | 1.22(±0.71) | 9.92(±5.92) | |
| OC | 3.02 † | 1.91 (±0.06) | 5.98† | ||
Clear skies for 20° ≤ θs ≤ 60°.
Standard deviation of shadow effects for OC is zero since the relative sky radiance distribution for OC is independent of wavelength. For the combined effects of BRDF and shadow for the grey plaque under OC, standard deviation is zero because the normalized BRDF of grey plaque is assumed to be independent of wavelength in this study.
The resulting interaction between BRDF and shadow depend on the direction of their bias. For the grey plaque, the negative bias of shadowing is partially offset by the positive bias of the BRDF effect when using Eq. 6 for both overcast and clear sky conditions with θs < 50°. Combined errors are then smaller than for shadow alone in nadir view (Table 2). For a white plaque, BRDF effects for overcast and clear sky condition with θs < 50° are already negative, albeit small. It results in approximately the same average error magnitudes for shadow alone in the visible range for clear skies under recommended θs, with a more pronounced increase in error for overcast conditions. If the lambertian assumption is used for overcast skies, errors for the white plaque will reduce to 1.9%, while for the grey it will increase to 7.2% due to the same additive effects (cf. Fig. 5 and Table 2).
5.3. Simulated tilt effects
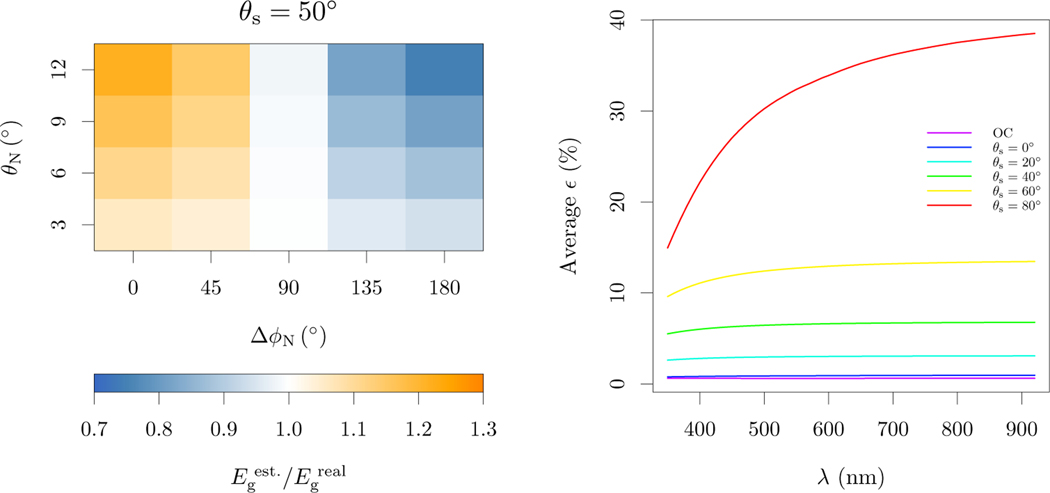
For a perfectly lambertian reference plaque, the unintentional tilt can represent the largest error source for Eg estimation under clear skies even for small departures from the zenith (Fig. 7), reaching an average of 5.7%(±6.8%) in the visible range under recommended sky conditions (Table 3). The error has a cosine pattern due to the change in the relative zenith angle of the Sun to the plaque normal (Fig. 7). The same cosine pattern, but with smaller magnitude, occurs for the diffuse fraction, since directions close to the Sun have higher radiance. This result in the tilt error reducing with the increase of the diffuse fraction (Fig. 7). Tilt effects are minimal if tilt occurs near the cross-plane to the Sun, since the angle of incidence of the direct beam and of radiance from directions close to the Sun are minimally affected. When the sky is heavily overcast, direct irradiance is zero and diffuse irradiance is constant with azimuth, resulting in reduced effects of tilt (maximum of 0.5% ± 0.5%).
Fig. 7:
Tilt effects on the estimation of Eg from a perfectly lambertian reflector and without shadow. Left panel show an example of tilt effect per tilt angle and azimuth for a θs = 50°. Right panel show the averages for all tilts zeniths and azimuths. θN and define the angular direction of the plaque’s normal relative to the local zenith and to the Sun, respectively. When tilt effects are considered alone, azimuthal dependency is simplified to relative azimuth ().
Table 3:
Mean absolute percentage errors (%) in the visible range due to tilt of the plaque and due to combined effects (BRDF, shadow and tilt) for clear skies and for overcast condition. Statistics calculated from level surface (0° tilt) to maximum zenith tilt angle as indicated on the table, including all azimuths. Smallest errors for each sky condition and plaque are formatted in bold. Numbers in parenthesis are the standard deviations. Statistics calculated over all simulations included in each evaluation and over all visible wavelengths.
| θv = 0° | |||||||
|---|---|---|---|---|---|---|---|
| Conversion | Max. Tilt | Tilt | Total, White PTFE | Total, Grey PTFE | |||
| Clear* | OC | Clear* | OC | Clear* | OC | ||
| BRDF (Eq. 6) | 3° | 1.4(±2.1) | 0.0(±0.0) | 2.2(±2.2) | 11.1(±0.2) | 1.5 (±2.0) | 0.8 (±0.2) |
| 6° | 2.8(±3.7) | 0.1(±0.1) | 3.7(±4.1) | 11.2(±0.4) | 2.7 (±3.5) | 0.8 (±0.4) | |
| 9° | 4.2(±5.3) | 0.3(±0.3) | 5.3(±5.9) | 11.3(±0.6) | 4.0 (±5.1) | 0.8 (±0.5) | |
| 12° | 5.7(±6.8) | 0.5(±0.5) | 6.9(±7.6) | 11.5(±0.9) | 5.3 (±6.6) | 0.9 (±0.6) | |
| Lambertian (Eq. 7) | 3° | 1.4(±2.1) | 0.0(±0.0) | 3.4(±2.3) | 4.7(±0.2) | 4.8(±2.4) | 7.2(±0.2) |
| 6° | 2.8(±3.7) | 0.1(±0.1) | 4.6(±3.9) | 4.8(±0.4) | 5.6(±3.4) | 7.1(±0.4) | |
| 9° | 4.2(±5.3) | 0.3(±0.3) | 6.0(±5.6) | 4.9(±0.6) | 6.6(±4.8) | 7.1(±0.6) | |
| 12° | 5.7(±6.8) | 0.5(±0.5) | 7.4(±7.3) | 5.1(±0.9) | 7.7(±6.3) | 7.1(±0.7) | |
| θv = 40° | |||||||
| Conversion | Max. Tilt | Tilt | Total, White PTFE | Total, Grey PTFE | |||
| Clear* | OC | Clear* | OC | Clear* | OC | ||
| BRDF (Eq. 6) | 3° | 1.4(±2.1) | 0.0(±0.0) | 1.8 (±2.3) | 4.4(±0.2) | 2.3(±1.9) | 20.8(±1.6) |
| 6° | 2.8(±3.7) | 0.1(±0.1) | 3.4 (±4.1) | 4.5(±0.3) | 3.5(±3.3) | 20.8(±2.9) | |
| 9° | 4.2(±5.3) | 0.3(±0.3) | 5.0 (±5.8) | 4.7(±0.5) | 4.7(±4.7) | 20.8(±4.2) | |
| 12° | 5.7(±6.8) | 0.5(±0.5) | 6.5 (±7.5) | 4.9(±0.7) | 6.0(±6.2) | 20.7(±5.5) | |
| Lambertian (Eq. 7) | 3° | 1.4(±2.1) | 0.0(±0.0) | 2.3(±2.2) | 2.0 (±0.2) | 10.3(±5.9) | 6.0(±1.2) |
| 6° | 2.8(±3.7) | 0.1(±0.1) | 3.7(±3.9) | 2.1 (±0.3) | 11.0(±5.9) | 6.0(±2.3) | |
| 9° | 4.2(±5.3) | 0.3(±0.3) | 5.2(±5.6) | 2.2 (±0.5) | 11.8(±6.3) | 6.1(±3.1) | |
| 12° | 5.7(±6.8) | 0.5(±0.5) | 6.7(±7.3) | 2.5 (±0.7) | 12.7(±7.0) | 6.4(±3.8) | |
Clear skies for 20° ≤ θs ≤ 60°
The addition of tilt to the previous error sources does not change the best performing geometry for each plaque, θv = 40° for the white PTFE and θv = 0° for the grey. Tilt effects add a small contribution to the combined effects of BRDF and shadow for overcast conditions (cf. Tables 2 and 3). They become dominant for clear skies under the best performing geometries, adding to the effects of BRDF and shadow for the white and grey plaques. This results in the grey PTFE outperforming the white PTFE on average, for the best performing geometries of each plaque, when Eq. 6 is used for conversion from Lp to Eg (Table 3). However, if using Eq. 7, errors for the white PTFE are virtually unaffected for clear skies, while BRDF and shadowing interaction reduce the errors for overcast condition when at a θv = 40°. The lambertian assumption for the grey plaque in the presence of tilt, even for its best performing geometry, increase errors above those observed for the white plaque.
When viewed at nadir, errors for the white PTFE are only marginally higher then for its optimal geometry under clear skies, but increase by a factor of 2 under overcast conditions. When the grey plaque is observed at θv = 40°, the change in error is depend on the equation used to retrieve Eg. For Eq. 6 average errors are similar for clear conditions but rise up to 20% for OC conditions. For Eq. 7, clear skies average errors reach 13%, but decrease to 6% under OC conditions.
5.4. Field inter-comparison
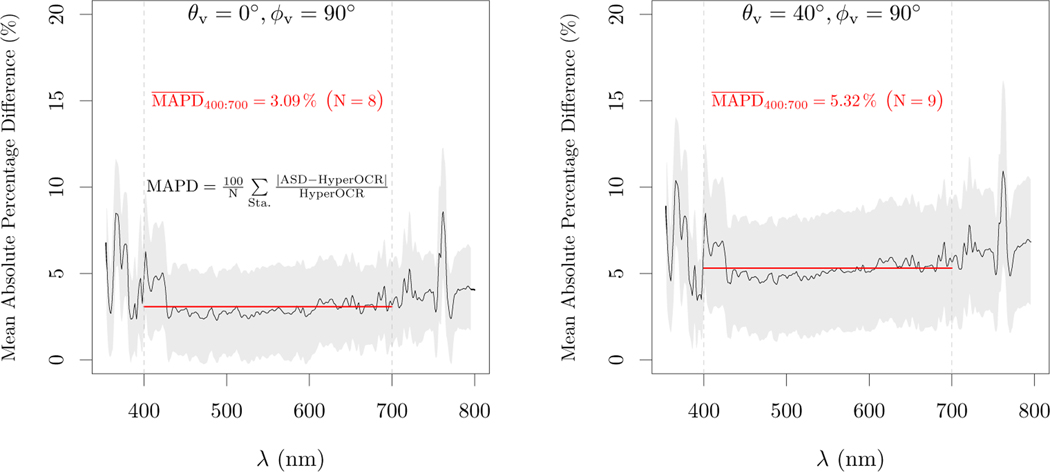
The average difference between the irradiance sensors and the plaque method in the visible range for the recommended geometry when using Eq. 7 was 3.1% (±2.8%). For the observation geometry at θv = 40°, errors average to 5.3% (±3.4%) (Fig. 8). The expected average values for a 10% grey plaque under clear skies for θs = 20° to 30° for the lambertian assumption for tilts up to 12° are 6.6% (±3.0%) and 16.7% (±3.6%), for viewing angles of nadir and 40°, respectively. The equivalent values for a white plaque, as the one used in the cross-calibration before the experiment, are 4.9% (±3.2%) and 3.7% (±3.1%), for viewing angles of nadir and 40°, respectively. The observed differences are not equivalent to the expected differences under the standard error simulation scenario. However, it will be shown in section 6 that measurements and simulation agree when the specific conditions of cross-calibration are modeled.
Fig. 8:
Results of the field inter-comparison showing the spectral mean absolute percentage difference of Eg between irradiance sensors and the plaque method for each geometry, with a grey PTFE and using Eq. 7. Grey area represents the standard deviation of the absolute percentage difference. The average over the visible range is represented by a red line.
6. Discussion
The study of isolated and incremental error sources allows us to budget their individual contributions while providing uncertainty estimates for different deployment conditions. BRDF effects alone are of interest in deployments where the plaque can be guaranteed to be horizontal and shadow can be made negligible, as in BRDF factors for terrestrial remote sensing studies. BRDF and shadow alone are of interest when the plaque can be fixed horizontally, as is the case for solar-based cross-calibration of spectrometers, solar-based calibration of spectrometers [55] or when measuring from a fixed station. And the combined effects are of interest for typical conditions where the plaque is held by hand or is fixed in a structure experiencing inclination with water surface state.
In the synthesis of results, error statistics are only calculated for the recommended sky conditions. To avoid Sun glint contamination, θs < 20° are not recommended for the classical above water method to measure Rrs [15]. A similar recommendation can be made for the newer skylight-blocked approach to measure Rrs, due to increase in self-shadowing effects [13]. The upper limit of the recommended sky conditions is set at an θs = 60°, since for higher θs even small tilts of the plaque can result in significant errors in Eg estimation. Surface roughness is also an important parameter, and rough conditions will result in increased risk of Sun glint for the above water method and hamper the deployment of skylight-blocked measurements. For Eg estimation with the plaque method, rough conditions create challenges in maintaining a level plaque.
When considering all error sources, the mean absolute percentage errors under the best performing geometries of each plaque and for recommended sky conditions show magnitudes comparable to uncertainties of irradiance sensors [35]. In fact, while their upper limit agree, estimates from the plaque can present a lower uncertainty if conditions allow minimizing tilt. Estimates under overcast conditions are also provided, and as expected for irradiance sensors [15], uncertainties in Eg will be even smaller for an appropriate deployment strategy and using the best conversion equation for each plaque under OC. Those results suggest that, under appropriate deployment as simulated in this study, Rrs estimates with the plaque method present on average equal or lower uncertainty than multiple spectrometer systems. It also suggest that Rrs calculated with plaque measurements are appropriate for all uses of in situ data, including the more stringent needs of atmospheric correction validation and sensor vicarious calibration.
While interpretation of the results is based on the average errors, it can be seen on Table 3 that standard deviations around those means can be large. This result from both a wide range of tilts included for each maximum tilt limit, but particularly from tilts in directions close to the Sun’s plane. When tilts occur with azimuths lower than ±45°, the apparent θs for the tilted plaque will be considerably lower and cosine effects will result in a large overestimation of Eg. The opposite is true for azimuths larger than ±135°. If tilt information is available for the plaque, a protocol similar to the processing of irradiance sensor data can be applied, discarding data with tilts greater than 5° [15]. However, dual axis systems should be used, to allow avoiding data close to the Sun’s plane. We note that the same consideration is also applicable to irradiance sensors, since while average errors for tilts up to 5° are 2.8%, the actual range of errors is ±18.2%, for the range of θs of the recommended sky conditions. Inclinometers are not typically used with plaques, but low cost, small weight and size commercial dual axis inclinometers are available and should be attached to the underside of the plaque structure. For both plaque and plane irradiance sensors, maximum tilt acceptance should be updated to reduce the maximum accepted tilt if tilt relative azimuth is lower than 45° or greater than 135°, and increase the maximum accepted tilt if tilt relative azimuth is between 45° and 135° (cf. Fig. 7).
The errors calculated with the simulations are accurate for the conditions they represent. Application of those estimates to ascribe error limits to actual measurements, however, require that the modeled conditions in terms of illumination, BRDF, shadowing solid angles and tilt magnitudes and direction are representative of conditions that actually occur in the field. The shadowing solid angle will be dependent on protocol and the condition simulated here represent our proposed method, as described in section 3.1. That position is proposed to minimize shadow and reflection over the plaque, while allowing eye contact with the surface of the plaque and an ergonomic position to prevent tilt. The shadow solid angle didn’t include possible surrounding superstructures as those will be variable depending on vessel and the available position on it. The situation modeled here more closely resembles deployments from small platforms (e.g., inflatable boats, small ships) or ideal positions in a larger vessel, where superstructures have a low elevation angle relative to the plaque center. Tilt was only modeled up to 12° for all azimuths and error statistics assume that every direction within that range is equally likely to occur. Ideally, a probabilistic distribution of tilt angles should be used as weights in a weighted error statistics, to account for biomechanical constraints on the combinations of azimuths and zenith tilts of a trained operator. The information necessary for this refinement, however, is not available and will not be necessary if dual axis inclinometers are routinely used with plaque measurements. Modern motorized gimbal solutions are a potential alternative that could maximize data quality, but feasibility in terms of cost and performance needs to be evaluated. We expect that under calm to moderate sea-state, a properly trained operator is able to constrain tilt angles within the limits calculated here.
Additional conditions that might diverge from the modeled ones are the presence of broken clouds and the use of aged and resurfaced plaques. The presence of broken clouds is frequent during field measurements, but remain a challenge to model. It not only requires sophisticated radiative transfer models [56] but also represent an infinite number of possible arrangement of spatial distributions and optical thickness. Empirical observations have shown that clouds can either have higher or lower radiance than equivalent clear skies directions [57]. However, resulting enhancements in Eg are small [58,59], propagating as small perturbations to and therefore to the estimated errors. More pronounced changes can occur when the net effect is to decrease Eg. Under this condition, cloud cover induced reduction of Ed will increase the relative contribution of Es to Eg and , improving the estimations with Eq. 6. If the direct beam is blocked by a cloud, it is possible that errors calculated only for the diffuse fraction are appropriate. Those values are not presented here but are available from the dataset in the Code File 1.
The measured BRDFs used in the simulations should be representative of sintered PTFE in general, as long as the BRDF properties of the reference are primarily a function of the material and its structure (i.e, little contribution from surface imperfections and organic or mineral contamination). Theory and observation support that BRDF from closely packed particulate anisotropic scattering media are primarily a function of the scattering phase function and the single scattering albedo of the particles, since the anisotropic signal from the phase function results mainly from single scattering (cf. chapter 8 in [60]). In highly reflective media, multiple scattering acts to reduce directionality of emerging photons, approaching an isotropic (Lambertian) reflectance. As a consequence, the results of our study should be general for sintered PTFE with similar material properties and small reflectance contribution from surface properties. Our estimated errors should also be applicable to aged plaques, as long as recent reflectance calibration data is available and plaque reflectance is ≈ 10% or ≈ 99%. If plaque nominal reflectance is > 10% and < 99%, the values reported here will likely represent the lower and upper boundaries [54]. Our estimation should also be applicable to resurfaced plaques, since the same surface inhomogeneities observed in those are also observed in fresh plaques. Observed inhomogeneities are small BRDF azimuthal asymmetries [37,61], that likely arise from preferential direction of sanding and small scale undulations from pressure variations. In practice, the finite solid angle of the spectrometer will result in the averaging of the BRDF and Lp from all directions within that solid angle, possibly minimizing these effects as long as inhomogeneities are small and randomly oriented. However, homogeneity of plaque reflectance properties across its surface should be tested, as recommended by [15] and plaque orientation during calibration should be used consistently in the field for accurate results.
Ultimately, the field inter-comparison experiment can be used to evaluate holistically the representativeness of the simulations to real conditions. Data presented in section 5.4 suggest disagreement between simulations and measurements, with predicted uncertainty larger than observed differences. But measurements and simulations can be brought to agreement when the specific conditions of the measurements are considered. The ρ(θv) of the grey plaque was cross-calibrated to the ρ(θv) of a white reference plaque and tilts up to 5° were allowed for the irradiance sensors. Cross-calibration between plaques are performed by calculating the ratio between exitant radiance from both plaques. If illumination conditions are appropriately stable as is necessary for a cross-calibration exercise, the result is the ratio of their fg, as expected from Eq. 8. This will under or over estimate the ρ(θv) of the grey plaque to a factor of:
| (13) |
This under- or overestimation during the cross-calibration under natural illumination can actually be advantageous, as by nature of the procedure both plaques will estimate the same Eg under illumination conditions similar to those used in the cross-calibration. This will condition the error of the grey plaque to be the same as the error of the white plaque, as long as θs of measurements is equal to the one during the cross-calibration. Our measurements represent a somewhat more challenging situation since cross-calibration at nadir view was performed at a higher θs than the inter-comparison measurements. To evaluate the effect of the cross-calibration on our data, we calculated the ratios of the of the grey and white plaques under the θs of cross-calibration for each view geometry and applied the cross-calibrated values to the estimation of Eg with Eq. 7. When considering the effects of BRDF, shadow and tilt up to 12°, errors at nadir were reduced from 6.63%(±3.01%) to 3.75%(±3.49%) while errors at θv = 40° were reduced from 16.72%(±3.58%) to 5.29%(±4.51%). The tilt induced error of the irradiance sensors for the range of θs during the experiment is 1.47%(±1.67%). Combining the average expected errors from both sensors through quadrature sum result in average expected differences of 4.03% and 5.49%, for nadir and θv = 40° respectively. Those values are in close agreement with the observed average differences of 3.09% and 5.32%, providing support for the representativeness of our error simulations.
If we consider that the past inter-comparison exercises report average differences that result in a MAPE between 6.4% and 8% [30–32] and given that the average uncertainty of an irradiance sensor is between 4.4% and 5.8% [35], quadrature sum suggest that uncertainties of the plaque estimation on those studies were between 2.7% and 6.7%, within the range of the simulation results presented here (Table 3) and of the same magnitude of the uncertainties of irradiance sensors. The higher errors observed by [32] during overcast conditions are also approximately accounted for, with our simulations for a white plaque under nadir view and using Eq. 6 resulting in MAPE of ≈ 12% (Tables 2 and 3), matching our estimation of their MAPE of ≈ 12.5%. The high range of underestimations observed by those authors under overcast conditions, however, do suggest greater shadow solid angles than the ones modeled here. This agreement with past measurements provide further support for our simulations.
Our focus with this study was on the uncertainties of Eg estimation as a normalization factor to calculate Rrs, such that absolute calibration uncertainties of the radiometer can be ignored since the same instrument is used for all necessary targets [14,15]. However, accurate determination of the BRDF or of ρ(θv) are still necessary. Uncertainty in BRDF measurements from [37] are about 0.5% and similar levels are expected for ρ(θv). This error is on the same magnitude of the BRDF and BRDF plus shadow errors when the best performing geometries are used together with recommended sky conditions (cf. Tables 1 and 2). Addition of this uncertainty through quadrature sum result in small increases to the modeled errors. If the absolute magnitude of Eg is of interest, the uncertainty on radiometer calibrations, estimated as 2.8% by [35], should also be added through quadrature sum. When this calibration uncertainty is added to the average errors under tilt for the recommended measurement protocol and retrieval method, uncertainty range increases from ≈ 1% to 6.5% to ≈ 3% to 7.1%.
The propagated error into Rrs due to possible Eg changes between the sequential acquisitions of the necessary targets with single spectrometer must also be considered. The magnitude of this error is dependent on the stability of illumination and can result in large errors under sub-optimal sky conditions represented by fast changing clouds. Limited data presented by [19] showed errors up to 10% for their study condition due to fast changing clouds. This error source represent an even bigger challenge for a model evaluation than broken clouds, as the magnitude and time scale of changes are dependent on many local and regional atmospheric parameters. As the implicit assumption on the use of Eq. 1 for the plaque method is the absence of time dependency on Eg between measurements of the necessary targets, it is recommended that measurements are only performed during stable illumination conditions.
This study included simplifications that should be clarified for a complete evaluation of the limits of its application. Pure geometrical relations were used to calculate the variables in the error simulations, meaning that no optical process (absorption or scattering) occurs in the volume of path between plaque and sensor. This assumption is reasonable considering the small path and low optical thickness of air. Additionally, a sensor with an infinitesimally small field of view was modelled, meaning that exitant radiance is sampled by direction and not averaged within a finite solid angle. This simplification is also reasonable since foreoptics with small fields-of-view are used in hydrologic research and BRDF determinations implicitly include averaging. Finally, secondary reflections from operator/instrument onto the plaque where not simulated. The suggested protocol minimizes effects of shadow and reflectance, but it is recommended that operator wear dark clothing, reducing possible influences in the visible range. Most cloth materials however, will present a red-edge and high reflectance in the near-infrared. Since atmospheric scattering at those wavelengths is small and the suggested body position avoids the direct beam reflection into the plaque, this simplification is also considered appropriate.
Finally, a word of caution is necessary on the use of uncalibrated hyperspetcral sensors with the plaque method for simulation of the Rrs signal that would be observed by another sensor (e.g., orbital sensor). While at native instrument resolution the radiance calibration factors cancels out in the reflectance calculation of Eq. 1 and do not need to be determined [15], for waveband convolution with another sensor spectral response function, the calibration factors are inside the integrals for radiance and irradiance and do not cancel out. Therefore, calculation of waveband Rrs from uncalibrated data could potentially present non-negligible bias if approximate corrections are not applied.
7. Conclusion
Weinvestigatedtheerrorsassociatedwiththeplaquemethodforestimationof Eg asanormalization factor for Rrs. Error sources included BRDF effects, shadowing of sky radiance and tilt of the plaque, both as isolated factors and with their interactions. Range of mean absolute percentage errors for both plaques are comparable to those of irradiance sensors, when best performing geometries of each plaque are used and under the recommended sky conditions. Our results therefore support the continued use of diffuse reflectance standards in hydrological optics research and monitoring. The method is particularly of interest for small research groups with constrained budgets for acquisition and maintenance of multiple spectrometer systems and the necessary periodical calibration. It is also useful for a range of applications that require greater flexibility than possible with traditional multi-spectrometer systems, such as inland water measurements from small platforms.
Based on previous protocols and considering our own findings, we propose the following recommendations for a measurement protocol from floating platforms:
Observation geometry should be at θv of 40° for white plaque and at nadir for a grey plaque, both at a 90° relative azimuth to the Sun to reduce operator shadow and secondary reflection, and plaque structure should have orientation marks for Sun and sensor sides, consistent with orientation during plaque calibration;
Operator should wear dark clothing and hold the plaque at the height of the upper chest or neck, ≈ 40 cm from the body, with sensor at distances > 20 cm from the plaque, and position on the platform should be selected as to reduce high elevation angles from surrounding structures relative to the plaque;
Plaque should have a diameter at least three times larger than the sensor field of view footprint at the used view angles and plaque-sensor distances, and operator should train to assume and hold positions and angles required for measurement, with attention to the stabilization of the plaque (the addition of a dual axis inclinometer is strongly encouraged);
Measurements should be performed under appropriate conditions represented by 20° ≤ θs ≤ 60°, stable illumination and up to moderate sea-state;
For the classical above water measurement, radiance from the necessary targets should be measured sequentially, with the cycle repeated at least 10 times. For the skylight-blocked approach, plaque radiance measurements should be performed both before and after all the replicate water measurements. Stations with Eg coefficient of variation > 6% should be flagged during quality control.
The skylight-blocked approach is mentioned here considering deployments from small platforms, such as inflatable boats and pontoons in inland water research, where the water surface is in reach of the operator and so could be used with the plaque method for irradiance [62]. Application of this protocol assumes knowledge of the ρ(θv) or of the fr(θs, 0°, θv, 90°) for the range of recommended θs. Vendors generally provide directional-hemispherical reflectance at an incidence angle of 8°. By symmetry of the BRDF, those values equal ρ(8°) and for both plaques it present negligible difference from nadir view. For a highly reflective plaque (99%), ρ(40°) will also present only a negligible difference from ρ(8°). The same is not true for a darker PTFE, with ρ(θv) increasing with θv. Measurements of darker reference plaques (e.g., 10%) should be avoided at view angles away from nadir, except if cross-calibrated ρ(θv) values against a white plaque are calculated and used under similar illumination conditions as those of the cross-calibration. This approach has been used by others (David English, University of South Florida, personal communication) and will result in similar errors as those of the white plaque at equivalent view angle. But we stress that the BRDF and ρ(θv) of the grey plaque at angles away from nadir is highly non-uniform and sensor must be carefully positioned at the nominal view angle. Specially when using a grey plaque without cross-calibration, Eq. 6 is preferred. It is also important that the plaque fills completely the field of view of the sensor, constraining the possible combinations of plaque size, foreoptics, sensor distance from plaque and view angle. For a sensor with a 8° field of view, a nadir view at a distance of 40 cm result in footprint at the plaque of 5.6 cm. The same footprint is achieved for a θv = 40° at a distance of 32 cm. For this footprint, a plaque diameter of ≈ 15 cm is recommended. Finally, the 6% limit of the coefficient of variation for quality control is based on the expected effects of tilt alone for tilts up to 12°.
Following this protocol will result in uncertainties comparable to the lowest uncertainties simulated in this study (≈ 1% to 6.5%), and so potentially provide high quality Rrs data for research and monitoring.
Supplementary Material
Acknowledgment
This research was funded by BELSPO Stereo III projects PONDER (SR/00/325) and HYPERMAQ (SR/00/335). Funding for field measurements was provided by NASA Ocean Biology and Biochemistry through the PACE project (NNX15AC32G). We are thankful to Zhehai Shang, Brandon Russell, Kaylan Randolph, Shungudzemwoyo Garaba, Emmanuel Perry and the R/V Lowell Weicker crew for their assistance in the field work. We appreciate the contributions of two anonymous reviewers for improving our manuscript. We acknowledge the R Core team and the authors of the R packages for developing and maintaining the free software used in this research.
References
- 1.Mobley CD, Light and Water: Radiative Transfer in Natural Waters (Academic Press, 1994). [Google Scholar]
- 2.Moore TS, Mouw CB, Sullivan JM, Twardowski MS, Burtner AM, Ciochetto AB, McFarland MN, Nayak AR, Paladino D, Stockley ND, Johengen TH, Yu AW, Ruberg S, and Weidemann A, “Bio-optical Properties of Cyanobacteria Blooms in Western Lake Erie,” Front. Mar. Sci. 4 (2017). [Google Scholar]
- 3.Behrenfeld MJ, Boss E, Siegel DA, and Shea DM, “Carbon-based ocean productivity and phytoplankton physiology from space,” Glob. Biogeochem. Cycles 19, GB1006 (2005). [Google Scholar]
- 4.Dogliotti A, Ruddick K, Nechad B, Doxaran D, and Knaeps E, “A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters,” Remote. Sens. Environ. 156, 157–168 (2015). [Google Scholar]
- 5.Bracher A, Vountas M, Dinter T, Burrows JP, Röttgers R, and Peeken I, “Quantitative observation of cyanobacteria and diatoms from space using PhytoDOAS on SCIAMACHY data,” Biogeosciences 6, 751–764 (2009). [Google Scholar]
- 6.Randolph K, Wilson J, Tedesco L, Li L, Pascual DL, and Soyeux E, “Hyperspectral remote sensing of cyanobacteria in turbid productive water using optically active pigments, chlorophyll a and phycocyanin,” Remote. Sens. Environ. 112, 4009–4019 (2008). [Google Scholar]
- 7.Ibrahim A, Franz B, Ahmad Z, Healy R, Knobelspiesse K, Gao BC, Proctor C, and Zhai PW, “Atmospheric correction for hyperspectral ocean color retrieval with application to the Hyperspectral Imager for the Coastal Ocean (HICO),” Remote. Sens. Environ. 204, 60–75 (2018). [Google Scholar]
- 8.Pahlevan N, Schott JR, Franz BA, Zibordi G, Markham B, Bailey S, Schaaf CB, Ondrusek M, Greb S, and Strait CM, “Landsat 8 remote sensing reflectance (Rrs) products: Evaluations, intercomparisons, and enhancements,” Remote. Sens. Environ. 190, 289–301 (2017). [Google Scholar]
- 9.Franz BA, Bailey SW, Werdell PJ, and McClain CR, “Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry,” Appl. Opt. 46, 5068 (2007). [DOI] [PubMed] [Google Scholar]
- 10.Ahmad Z, Franz BA, McClain CR, Kwiatkowska EJ, Werdell PJ, Shettle EP, and Holben BN, “New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans,” Appl. Opt. 49, 5545 (2010). [DOI] [PubMed] [Google Scholar]
- 11.Kutser T, Vahtmäe E, Paavel B, and Kauer T, “Removing glint effects from field radiometry data measured in optically complex coastal and inland waters,” Remote. Sens. Environ. 133, 85–89 (2013). [Google Scholar]
- 12.Lee Z, Pahlevan N, Ahn Y-H, Greb S, and O’Donnell D, “Robust approach to directly measuring water-leaving radiance in the field,” Appl. Opt. 52, 1693 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Shang Z, Lee Z, Dong Q, and Wei J, “Self-shading associated with a skylight-blocked approach system for the measurement of water-leaving radiance and its correction,” Appl. Opt. 56, 7033–7040 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Mobley CD, “Estimation of the remote-sensing reflectance from above-surface measurements,” Appl. Opt. 38, 7442 (1999). [DOI] [PubMed] [Google Scholar]
- 15.Mueller JL, Morel A, Frouin R, Davis C, Arnone R, Carder K, Lee Z, Steward RG, Hooker S, Mobley CD, Mclean S, Holben B, Mark M, Pietras C, Knobelspiesse KD, Fargion GS, Porter J, and Voss KJ, “Ocean Optics Protocols For Satellite Ocean Color Sensor Validation, Revision 4, Volume III: Radiometric Measurements and Data Analysis Protocols,” Tech. rep. (2003). [Google Scholar]
- 16.Carder KL and Steward RG, “A remote-sensing reflectance model of a red-tide dinoflagellate off west Florida,” Limnol. Oceanogr. 30, 286–298 (1985). [Google Scholar]
- 17.Nicodemus FF, Richmond JC, Hsia JJ, Ginsberg IW, and Limperis TL, “Geometrical considerations and nomenclature for reflectance,” Tech. Rep. October, National Bureau of Standards, Washington D.C. (1977). [Google Scholar]
- 18.Milton EJ, “Principles of field spectroscopy,” Int. J. Remote. Sens. 8, 1807–1827 (1987). [Google Scholar]
- 19.Bachmann CM, Montes MJ, Parrish CE, Fusina RA, Nichols CR, Li R-R, Hallenborg E, Jones CA, Lee K, Sellars J, White SA, and Fry JC, “A dual-spectrometer approach to reflectance measurements under sub-optimal sky conditions,” Opt. Express 20, 8959 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Knaeps E, Ruddick KG, Doxaran D, Dogliotti AI, Nechad B, Raymaekers D, and Sterckx S, “A SWIR based algorithm to retrieve total suspended matter in extremely turbid waters,” Remote. Sens. Environ. 168, 66–79 (2015). [Google Scholar]
- 21.Eleveld MA, Ruescas AB, Hommersom A, Moore TS, Peters SW, and Brockmann C, “An optical classification tool for global lake waters,” Remote. Sens. 9, 1–24 (2017). [Google Scholar]
- 22.Dierssen HM, Zimmerman RC, Drake LA, and Burdige DJ, “Potential export of unattached benthic macroalgae to the deep sea through wind-driven Langmuir circulation,” Geophys. Res. Lett. 36, 1–5 (2009). [Google Scholar]
- 23.Simis SGH, Ruiz-Verdú A, Domínguez-Gómez JA, Peña-Martinez R, Peters SWM, and Gons HJ, “Influence of phytoplankton pigment composition on remote sensing of cyanobacterial biomass,” Remote. Sens. Environ. 106, 414–427 (2007). [Google Scholar]
- 24.Wang G, Lee Z, Mishra DR, and Ma R, “Retrieving absorption coefficients of multiple phytoplankton pigments from hyperspectral remote sensing reflectance measured over cyanobacteria bloom waters,” Limnol. Oceanogr. Methods 14, 432–447 (2016). [Google Scholar]
- 25.Matthews MW, “A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters,” Int. J. Remote. Sens. 32, 6855–6899 (2011). [Google Scholar]
- 26.Lee Z, Shang S, Lin G, Chen J, and Doxaran D, “On the modeling of hyperspectral remote-sensing reflectance of high-sediment-load waters in the visible to shortwave-infrared domain,” Appl. Opt. 55, 1738–1750 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Rollin EM, Emery DR, and Milton EJ, “Reference panel anisotropy and diffuse radiation - some implications for field spectroscopy,” Int. J. Remote. Sens. 21, 2799–2810 (2000). [Google Scholar]
- 28.Epema GF, “Studies of errors in field measurements of the bidirectional reflectance factor,” Remote. Sens. Environ. 35, 37–49 (1991). [Google Scholar]
- 29.Kimes DS and Kirchner JA, “Irradiance measurement errors due to the assumption of a Lambertian reference panel,” Remote. Sens. Environ. 12, 141–149 (1982). [Google Scholar]
- 30.Dekker AG, “Detection of optical water quality parameters for eutrophic waters by high resolution remote sensing,” Ph.D. thesis, Vrije University, Amsterdam, Netherlands (1993). [Google Scholar]
- 31.Toole DA, Siegel DA, Menzies DW, Neumann MJ, and Smith RC, “Remote-sensing reflectance determinations in the coastal ocean environment: impact of instrumental characteristics and environmental variability,” Appl. Opt. 39, 456–469 (2000). [DOI] [PubMed] [Google Scholar]
- 32.Doxaran D, Cherukuru NC, Lavender SJ, and Moore GF, “Use of a Spectralon panel to measure the downwelling irradiance signal: case studies and recommendations,” Appl. Opt. 43, 5981–5986 (2004). [DOI] [PubMed] [Google Scholar]
- 33.Rhea WJ and Davis CO, “A comparison of the SeaWiFS chlorophyll and CZCS pigment algorithms using optical data from the 1992 JGOFS Equatorial Pacific Time Series,” Deep. Sea Res. Part II: Top. Stud. Oceanogr. 44, 1907–1925 (1997). [Google Scholar]
- 34.Lee Z, Carder KL, Steward RG, Peacock TG, Davis CO, and Mueller JL, “Remote sensing reflectance and inherent optical properties of oceanic waters derived from above-water measurements,” in Ocean Optics XIII, vol. 2963 Ackleson SG and Frouin RJ, eds. (1997), pp. 160–166. [Google Scholar]
- 35.Zibordi G, Ruddick KG, Ansko I, Moore G, Kratzer S, Icely J, and Reinart A, “In situ determination of the remote sensing reflectance: an inter-comparison,” Ocean. Sci. 8, 567–586 (2012). [Google Scholar]
- 36.Gregg W. and Carder K, “A simple spectral solar irradiance model for cloudless maritime atmospheres,” Limnol. Oceanogr. 35, 1657–1675 (1990). [Google Scholar]
- 37.Germer TA, “Full four-dimensional and reciprocal Mueller matrix bidirectional reflectance distribution function of sintered polytetrafluoroethylene,” Appl. Opt. 56, 9333–9340 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zibordi G. and Voss KJ, “Geometrical and spectral distribution of sky radiance: Comparison between simulations and field measurements,” Remote. Sens. Environ. 27, 343–358 (1989). [Google Scholar]
- 39.Sobolev VV, Light Scattering in Planetary Atmospheres (Pergamon, New York, 1975). [Google Scholar]
- 40.Kasten F, “A new table and approximation formula for the relative optial air mass,” Arch. für Meteorol. Geophys. und Bioklimatologie, Ser. B 14, 206–223 (1965). [Google Scholar]
- 41.Bodhaine BA, Wood NB, Dutton EG, and Slusser JR, “On Rayleigh optical depth calculations,” J. Atmospheric Ocean. Technol. 16, 1854–1861 (1999). [Google Scholar]
- 42.Rozanov A, Rozanov V, Buchwitz M, Kokhanovsky A, and Burrows J, “SCIATRAN 2.0 âĂŞ A new radiative transfer model for geophysical applications in the 175–2400nm spectral region,” Adv. Space Res. 36, 1015–1019 (2005). [Google Scholar]
- 43.Hess M, Koepke P, and Schult I, “Optical Properties of Aerosols and Clouds: The Software Package OPAC,” Bull. Am. Meteorol. Soc. 79, 831–844 (1998). [Google Scholar]
- 44.Koepke P, Gasteiger J, and Hess M, “Technical Note: Optical properties of desert aerosol with non-spherical mineral particles: data incorporated to OPAC,” Atmospheric Chem. Phys. 15, 5947–5956 (2015). [Google Scholar]
- 45.Gordon HR, “Ship Perturbation of Irradiance Measurements at Sea .1. Monte-Carlo Simulations,” Appl. Opt. 24, 4172–4182 (1985). [DOI] [PubMed] [Google Scholar]
- 46.Röttgers R, Doerffer R, McKee D, and Schönfeld W, Algorithm Theoretical Basis Document - Pure water spectral absorption, scattering, and real part of refractive index model - The Water Optical Properties Processor (WOPP), Helmholtz-Zentrum Geesthacht. Version 1.7. [Google Scholar]
- 47.R Core Team R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria: (2017). [Google Scholar]
- 48.Plate T. and Heiberger R, abind: Combine Multidimensional Arrays (2016). R package version 1.4–5. [Google Scholar]
- 49.Akima H. and Gebhardt A, akima: Interpolation of Irregularly and Regularly Spaced Data (2016). R package version 0.6–2. [Google Scholar]
- 50.Bivand RS, Pebesma E, and Gomez-Rubio V, Applied spatial data analysis with R (Springer, NY, 2013), second edition ed. [Google Scholar]
- 51.Hijmans RJ, raster: Geographic Data Analysis and Modeling (2017). R package version 2.6–7. [Google Scholar]
- 52.Castagna A, Johnson BC, Voss K, Dierssen HM, Patrick H, Germer TA, Sabbe K, and Vyverman W, “Supplementary material to: Castagna et al. 2019, Uncertainty in global downwelling plane irradiance estimates from sintered polytetrafluoroethylene plaque radiance measurements,” figshare (2019), https://osapublishing.figshare.com/s/000290376a9d41608d31 [substitute with DOI when published]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Germer TA, “Scatmech: Polarized light scattering c++ class library and the modeled integrated scattering tool (mist),” (2018). Version 7.20. [Google Scholar]
- 54.Georgiev GT and Butler JJ, “BRDF study of gray-scale Spectralon,” in Proceedings of SPIE, Earth Observing Systems XIII, Butler JJ and Xiong J, eds. (2008), p. 708107. [Google Scholar]
- 55.Cattrall C, Carder KL, Thome KJ, and Gordon HR, “Solar-reflectance-based calibration of spectral radiometers,” Geophys. Res. Lett. 29, 2–1–2–4 (2002). [Google Scholar]
- 56.Mayer B, “Radiative transfer in the cloudy atmosphere,” The Eur. Phys. J. Conf. 1, 75–99 (2009). [Google Scholar]
- 57.Weihs P, Webb AR, Hutchinson SJ, and Middleton GW, “Measurements of the diffuse UV sky radiance during broken cloud conditions,” J. Geophys. Res. Atmospheres 105, 4937–4944 (2000). [Google Scholar]
- 58.Gu L, Fuentes JD, Garstang M, Silva JTD, Heitz R, Sigler J, and Shugart HH, “Cloud modulation of surface solar irradiance at a pasture site in southern Brazil,” Agric. For. Meteorol. 106, 117–129 (2001). [Google Scholar]
- 59.Tzoumanikas P, Nikitidou E, Bais AF, and Kazantzidis A, “The effect of clouds on surface solar irradiance, based on data from an all-sky imaging system,” Renew. Energy 95, 314–322 (2016). [Google Scholar]
- 60.Hapke B, Theory of Reflectance and Emittance Spectroscopy (Cambridge University Press, 2012), 2nd ed. [Google Scholar]
- 61.Barnes PY and Early EA, “Diffuse reflectance of sintered and pressed polytetrafluoroethylene (PTFE),” in Proceedings of SPIE, Scattering and Surface Roughness II, vol. 3426 (1998), pp. 190–194. [Google Scholar]
- 62.Castagna A, Dierssen HM, Vanhellemont Q, and Vyverman W, “Monte Carlo model study of the skylight-blocked approach for measuring water-leaving radiance: self-shading and boat perturbation to the light field,” in International Ocean Color Science Meeting 2017, (2017), p. 32. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.