Estimating the High-Arsenic Domestic-Well Population in the Conterminous United States

Abstract

Arsenic concentrations from 20 450 domestic wells in the U.S. were used to develop a logistic regression model of the probability of having arsenic >10 μg/L (“high arsenic”), which is presented at the county, state, and national scales. Variables representing geologic sources, geochemical, hydrologic, and physical features were among the significant predictors of high arsenic. For U.S. Census blocks, the mean probability of arsenic >10 μg/L was multiplied by the population using domestic wells to estimate the potential high-arsenic domestic-well population. Approximately 44.1 M people in the U.S. use water from domestic wells. The population in the conterminous U.S. using water from domestic wells with predicted arsenic concentration >10 μg/L is 2.1 M people (95% CI is 1.5 to 2.9M). Although areas of the U.S. were underrepresented with arsenic data, predictive variables available in national data sets were used to estimate high arsenic in unsampled areas. Additionally, by predicting to all of the conterminous U.S., we identify areas of high and low potential exposure in areas of limited arsenic data. These areas may be viewed as potential areas to investigate further or to compare to more detailed local information. Linking predictive modeling to private well use information nationally, despite the uncertainty, is beneficial for broad screening of the population at risk from elevated arsenic in drinking water from private wells.

Graphical Abstract

INTRODUCTION

Domestic wells (private or homeowner wells) are the dominant source of drinking water for people living in rural parts of the United States.¹ Geogenic arsenic affects many domestic wells in the U.S.^2,3 and is thus a national public health concern.^4–6 Recent work in the U.S. indicates that low-level arsenic may impact fetal growth⁷ and may be related to preterm birth.⁸ In the U.S., domestic well water quality is generally not regulated. This means that it is largely up to the well owner to understand the arsenic hazard and take steps to mitigate any exposure risk. To understand the risk and to make progress on reducing exposure in a systematic way, we need better estimates of the population affected by high arsenic concentrations.

About 44.1 M people in the conterminous U.S.—14% of the total population—rely on domestic wells for household water use.⁵ The U.S. domestic well population tends to mimic the general population distribution throughout the country, serving people not connected to public supply distribution systems and people in rural areas.⁵ Because high concentrations of arsenic in water are not evident by taste or smell, the only way to know how much arsenic is in drinking water is to have it tested, a precaution utilized infrequently by domestic well owners.^2,6

Studies of arsenic in domestic wells in the U.S. commonly refer to percentages of wells with arsenic >10 μg/L, the U.S. Environmental Protection Agency (USEPA) Maximum Contaminant Level (MCL), based on observations from various databases.^2,3,7–10 National-scale maps of arsenic show either observation points or interpolated concentrations where gaps in spatial coverage are evident.^8,9,11–16 Estimates of the population in the U.S. using domestic well water with high concentrations of arsenic may not accurately represent the population at risk if they do not account for unsampled areas.

A modeling approach can directly incorporate potentially important numeric or categorical factors, such as geologic, geochemical, physical, and hydrologic/climatic data, that are available at the national scale. Although local-to regional-scale models have been developed for arsenic in groundwater in the U.S., indicating strong regional (10² to 10³ km²) to local (10° to 10¹ km²) patterns,^{10,15,17–24} and some have looked at national occurrence of arsenic,^{2,8,11–13,16} few studies have attempted to scale these factors upward to a national level,^8,10,13,15 such as has been done for nitrate^25,26 and atrazine.²⁷

Arsenic in groundwater reflects geologic sources, aquifer geochemistry, and national-to-local scale processes, such as climatic, physiochemical, and geochemical variation.^12,24 Primary geochemical factors generally include (1) reductive dissolution and desorption, (2) pH-driven desorption, (3) ion concentration in low recharge areas, and (4) ion competition.^12,24

For example, arid oxidizing environments, as in the southwest part of the U.S. are susceptible to increased likelihood of high arsenic through evaporative concentration, increasing pH, and increasing dissolved solids along flow paths, and redox differences,^17,28,29 whereas humid reducing environments also are related to increased likelihood of high arsenic, such as in the northeast U.S, where alkaline pH, reducing environments, and dissolution of sulfide minerals are important.^30–35

This understanding of the controls on high concentrations of arsenic in various parts of the U.S. can be applied to other, unsampled parts of the U.S. The extent to which these and other factors interplay across the U.S. (to produce high arsenic groundwater) is a knowledge gap that this study seeks to fill. By using a model to predict the probability of high arsenic, we take advantage of previous understanding of regional processes and apply it in a multivariate sense to areas that have not been characterized, similar to approaches used elsewhere.³⁶

There are a number of challenges associated with modeling concentrations of arsenic in private wells. Available data on concentrations of arsenic in domestic wells in the U.S. are simultaneously rich in number but spotty in geographic extent. While we understand many of the processes that control the presence of arsenic in groundwater and wells, we do not yet understand the complex interplay of factors that lead to high concentrations in some areas. For example, wells in close proximity to one another (10° to 10¹ m) may produce water with vastly different concentrations of arsenic. Another potential modeling challenge is the 3-dimensional aspect of groundwater, where adjacent domestic wells draw water from distinct aquifers, one overlying another, with differing composition and geochemical properties.^37,38

The goal of this paper is to produce estimates of the population of domestic well users with high arsenic concentrations in their drinking water at the national scale. We use a model to predict the probability of well water arsenic concentrations greater than 10 μg/L (the USEPA MCL) across the U.S. using geologic, geochemical, and hydrologic information. Information gained from model generation can improve our understanding of important spatial and physical features that contribute to high arsenic concentrations in domestic wells and will be a first attempt to geographically describe the potentially affected population based on a national-scale predictive model. Using domestic well arsenic data and a national-scale modeling approach will expand our knowledge of potential exposure to arsenic in drinking water from what is currently available only from regional- and local-scale models and will allow for comparisons between regions.

MATERIALS AND METHODS

Arsenic in Private Well Water.

Arsenic concentrations from 20 450 U.S. domestic well samples (Figure 1; Table 1) collected between 1970 and 2013 were used to develop our model. Concentrations of arsenic from 18 700 domestic wells and other ancillary data, such as latitude and longitude were obtained from the USGS National Water Information System.³⁹ Additional arsenic concentrations from domestic wells in Maine (750 wells) and Minnesota (1000 wells) were used.^40,41 The data representing arsenic concentrations are variably clustered but declustering was not applied because potential biases were unclear and well-to-well variability in arsenic concentrations was large. Also, it is assumed that, in general, the wells were not specifically installed to monitor arsenic, so the clustering is random with respect to arsenic. Further, predicting an exceedance of a threshold as was done here (arsenic >10 μg/L) has the effect of de-emphasizing high concentrations and also high-arsenic events are rare, so it is reasonable, if not desirable, to retain data.

Figure 1.

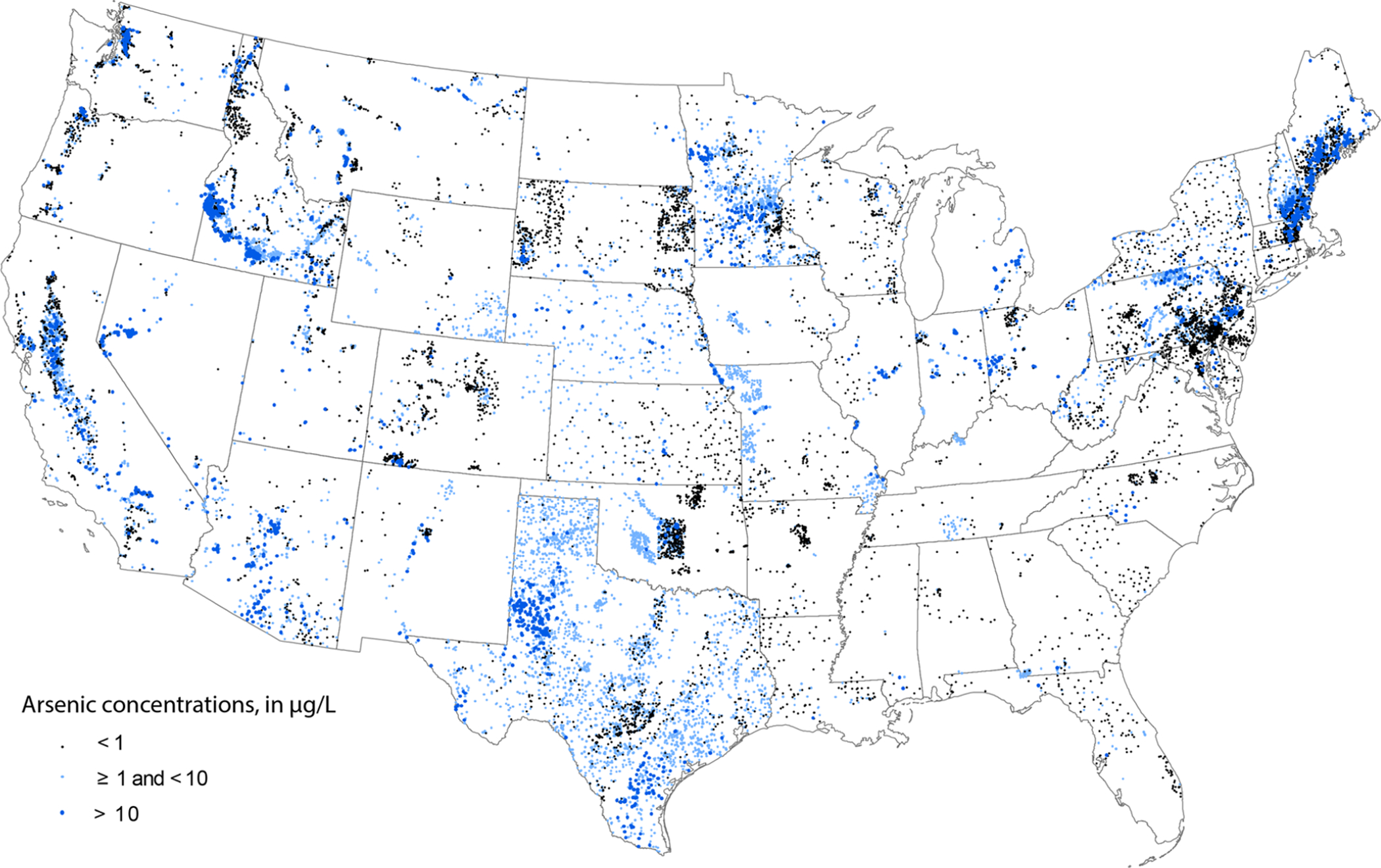
Locations of domestic wells and As concentration ranges for data used to develop the logistic regression model.

Table 1.

Summary Statistics of Arsenic Concentrations in Training and Testing Datasets Used to Develop the Arsenic >10 μg/L Logistic Regression Model

			concentrations of arsenic, μg/L
				percentiles
dataset	N	percent >10 μg/L	minimum	10th	25th	50th	75th	90th	maximum
training	17 355	10.9	<1	<1	<1	2	5	11	2900
testing	3095	10.4	<1	<1	<1	2	5	11	2140

Several preliminary data processing steps were undertaken. If a given sample had results from both filtered and unfiltered samples, the unfiltered result was preferentially retained. Where there were multiple results per site (about 15% of sites), only the maximum arsenic concentration, being the most noteworthy value, was retained. Arsenic concentrations were converted to a binary variable of less than or equal to (nonevent) and greater than (event) 10 μg/L, with 0 as a nonevent and 1 as an event for use in logistic regression models.⁴² Measurements with reporting levels higher than 10 μg/L were not used because it is not possible to determine whether they were higher or lower than the 10 μg/L threshold.

We randomly selected a “hold-out” data set (about 15%) to set aside for model testing.

Training and testing data sets used to develop the arsenic probability model had identical minimum and percentile statistics and similar maximum concentrations (Table 1). Event statistics (percent >10 μg/L) for the two data sets also were similar.

Considerable spatial variability in arsenic concentrations across the U.S. is characterized by patterns of high concentrations in coastal New England, eastern Pennsylvania, the upper Midwest, southern Idaho, West Texas, and parts of the Southwest (Figure 1), among others. Processes that affect high concentrations vary but often are a mix of factors that shift in importance depending on the area. For example, oxidation of sulfides, evaporative concentration, and pH-driven desorption may be more important in the southwest, whereas sulfide mineral sources and reductive dissolution may be more important in humid regions.^12,13,17,43 Also, specific crystalline bedrock types in New England, black shale in Ohio, and specific glacial aquifer source materials (from various Pleistocene glacial lobes in the Midwest) also have been associated with arsenic in groundwater.^{12,13,30,44–46} Sulfide enriched sandstones in Wisconsin^47,48 and geothermal sources and volcanic rocks in New Mexico can be sources of high arsenic concentrations.¹²

Source- and Process-Based Extrapolation.

Potential factors that might influence arsenic concentrations in groundwater were identified by literature review. Digital data sets for these factors that were available at the national scale were assembled to test for significance as independent variables in the logistic regression model (Supporting Information SI 1). A Geographic Information System (GIS) was used to overlay the point data set of wells with these potential independent variables resulting in the assignment of the full set of independent variables to each well. In cases where factors related to sources or processes were not available directly as variable layers, related national-scale data layers were tested as potential surrogates (e.g., areas of tile drainage to indicate aquifer hydraulic properties). Model variables fall into four major groups: (1) geologic and geochemistry variables, such as bedrock and surficial geologic units, and soil geochemistry concentrations; (2) hydrologic variables, such as precipitation, evapotranspiration, and recharge to groundwater; (3) process variables, such as position in a watershed, aquifer permeability, and water table depth; and (4) other features, such as elevation, slope, land use, and percent of areas with tile drainage.

Logistic Regression Model.

We used logistic regression (LR), a linear classifier that has been widely used in studies to simulate arsenic probability in groundwater, to generate models of arsenic concentrations greater than 10 μg/L, the USEPA MCL for arsenic.^49–51 It is well suited to use with a heavily censored response variable (groundwater arsenic) and for identifying general controlling factors, such as sources and processes. The form of the equation has been presented previously.^18,51 We used backward stepwise logistic regression and parameters were retained if they met criteria for inclusion based on Akaike’s Information Criteria and Wald p-values (p < 0.05). Although LR may have limitations with nonlinearity of independent variables, it can provide much insight into the importance of those variables⁵¹ and is not as prone to over fitting as tree-based approaches, which can reduce generality⁵² despite potential higher sensitivity.

A total of 321 potential individual variables were tested for significance as predictors in the LR models, most of which were binary geologic and other variables (Supporting Information SI 1). Independent variables were selected for inclusion by running multiple LR iterations and comparing results of automated selection procedures (backward, forward, or stepwise selections) with unspecified selection of variables. The set of variables ultimately selected had significance in most (or all) of the tested models. Potential multicollinearity was addressed by removing variables with a large variance inflation factor (generally greater than 4). In part, because few (11%) arsenic observations had concentrations greater than 10 μg/L (events), the ability to correctly predict events (sensitivity) was low. Sensitivity is mainly a function of group size (number of events), which is controlled by probability threshold; however, the receiver operating characteristics (ROC) curve integrates over all thresholds. High well-to-well arsenic variability and missing variables also contribute to low sensitivity.^18,26

Several regression model fit criteria were used to assess fit of the overall model. Classification tables for selected cut-points were used to provide information on model accuracy by showing overall correct classifications, model sensitivity, and specificity, false positives, and false negatives. The area under the ROC curve (AUC), indicated numerically by the c statistic, showed how well the model discriminated between observations at different prediction probabilities. Values of the c statistic close to 0.5 indicate no predictive power and between 0.8 and 0.9 are considered excellent.⁵¹ The pseudo r-squared value is a goodness-of-fit statistic for logistic regression, similar to the r-squared value in ordinary least-squares regression, in that larger values between 0 and 1 indicate greater improvements to the model over a model with no predictors.⁵³ R-squared values for LR are not as easy to interpret as for linear regression; for example, values can be close to 0 for models that fit well.⁵⁴ The “percent deviance explained,” as the difference between the −2 log likelihood of the specified model and the intercept-only model, divided by the −2 log likelihood of the null model, also is presented as a measure of model performance (Table 4).⁵²

Table 4.

Comparison of Modeled Estimates of Domestic Well Populations With As > 10 μg/L, and Estimates Made from Other Sources

		population likely to have arsenic concentration >10 μg/L in domestic well water
				95% confidence limit
state	domestic well population	%	model estimated number	lower	upper	estimated from other source comparison	to modeled estimate
CT	871 373	6.0	52 105	36 138	74 452	34 00066	lower
IL	1 155 342	5.9	67 709	53 347	85 636	127 00077	higher
ME	560 801	18	102 452	80 281	128 879	85 00078	same
MI	2 675 773	7.2	192 747	151 408	246 037	230 00021	same
MN	1 127 975	7.1	80 353	64 209	100 266	121 00079	higher
NC	3 303 760	3.6	119 633	76 523	187 279	76 00023	lower
NH	445 540	14	60 962	45 643	80 275	80 00080	same
NM	303 139	10	30 990	24 485	38 647	35 00067	same
TX	2 440 586	3.9	95 455	74 590	122 294	146 00081	higher
VT	181 611	5.3	9716	6988	13 363	900082	same

The influence of individual observations was assessed by using output from the influence diagnostics routine within the SAS Institute’s Logistic procedure, such as the standardized Pearson chi-squared residuals and leverage.^55,56 Model statistics were compared with and without potentially influential observations. Potential outliers were mapped and inspected; however, we did not identify a systematic influence of observations. We also examined graphical output from the Logistic procedure with influence option, as described in Supporting Information SI 5.

Layered Aquifers.

The presence of layered aquifers, such as unconsolidated sand and gravel of glacial or alluvial origin above porous or fractured bedrock might obscure the arsenic signal by aquifer type in the regression models. This is particularly true if the concentrations of arsenic in the layered aquifers are significantly different.⁵⁷ For the 82% of 20 450 wells where some kind of aquifer information was available in the USGS NWIS database, we developed a methodology (Supporting Information SI 2) to look at distributions of arsenic concentrations greater than 10 μg/L by state and generalized aquifer. Where domestic wells were located in aquifers that differed by vertical position (layered), the aquifer with the largest percentage of domestic wells with high arsenic was flagged as the potentially dominant domestic well aquifer. Areas with potentially dominant aquifers were examined visually in a GIS and evaluated based on other criteria (Supporting Information SI 2) to decide whether to take action by removing wells (that could potentially confound the arsenic “signal”) for the LR analysis. From this evaluation, we removed 208 well records from five states that met the criteria (Supporting Information SI 2) for removal. A comparison of regression results between the full data set and the data set with these 208 wells removed showed no improvement attributable to this accounting for layered aquifers, probably because the adjustment, which pertained specifically to layered aquifers, ultimately affected only about 1% of the data.

Private Domestic Water Use.

At the level of U.S. census block groups (BG), the mean probability of arsenic greater than 10 μg/L (Prob_As10; eq 1) was multiplied by the population using domestic wells (Pop_Wells) to estimate the potential population using domestic wells with high arsenic concentrations (PotentialPop_As10). The mean probability of arsenic greater than 10 μg/L was generated from the arsenic probability map using the “zonal statistics as table” tool in ArcMap (release 10.1, Environmental Systems Research Institute, Redlands, CA) where the zones were block groups with statistic type of mean. We estimated 2010 block-group populations that used domestic wells for water supply by multiplying 2010 census block-group populations⁵⁸ by the percentage of block-group populations that used well water for domestic use according to the most recently available information (1990) on that statistic from the U.S. Census Bureau.⁵⁹ Although that percentage (of block-group populations using wells for domestic use) has undoubtedly shifted over the 20 years between 1990 and 2010, the change is no more than 20% for 80% of U.S. counties (http://waterdata.usgs.gov/nwis/wu). On a statewide basis, Michigan saw the largest increase (9%) in the percentage (5 counties increased by more than 50%) and Arkansas the largest decrease (−19%; 7 counties decreased by more than 50% for domestic use). Estimates of populations with high arsenic concentrations in their well water by block groups are aggregated to county and state levels by using county and state code information in ArcMap. Uncertainty, as 95% upper and lower confidence limits for high arsenic probabilities, also was mapped and used in combination with block-group populations using well water for domestic water supplies to get upper and lower bounds on the estimates of potential high-arsenic population.

$$\text{PotentialPop\_As}{10}_{(\text{BG})}={\text{Pop\_Wells}}_{(\text{BG})}\times \text{Prob\_As}{10}_{(\text{BG})}$$ (1)

RESULTS AND DISCUSSION

Estimates of the Probability of High Arsenic.

Two models initially were developed for arsenic >10 μg/L: a complex (67 variable) model with all significant predictor variables at α = 0.05 and a simpler (42 variable) model with significant predictor variables at α = 0.001. The LR models had log likelihood ratio p-values that indicated a highly significant model (p < 0.0001) for arsenic >10 μg/L. Because the simple model performed similarly to the complex model according to nearly every metric, the simple model was used for estimating probabilities for this study (Supporting Information SI 3).

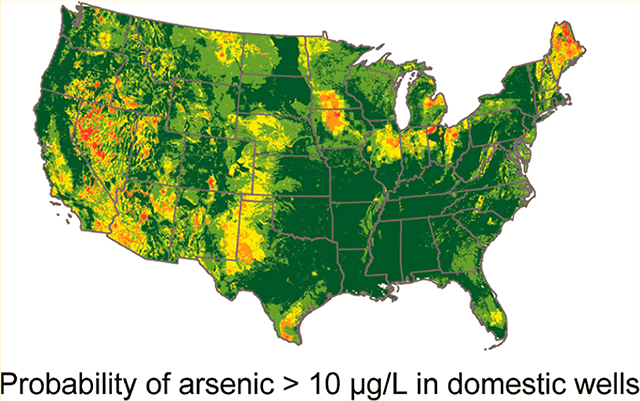
Hotspots where the probability of As > 10 μg/L in domestic well water can exceed 0.5 (Figure 2) generally reflect areas in the U.S. with high observed concentrations including New England (predominantly Maine and New Hampshire), a band in the upper Midwest, the southwest (most notably Nevada, southern Arizona, southern and central California, and isolated regions in all western states), and southern Texas.⁴² Probabilities of As > 10 μg/L are less than 0.5 throughout most of the southern Midwest and the east except for New England and coastal areas. Maps of the lower and upper confidence bounds convey additional information to support the probability estimates.⁴²

Figure 2.

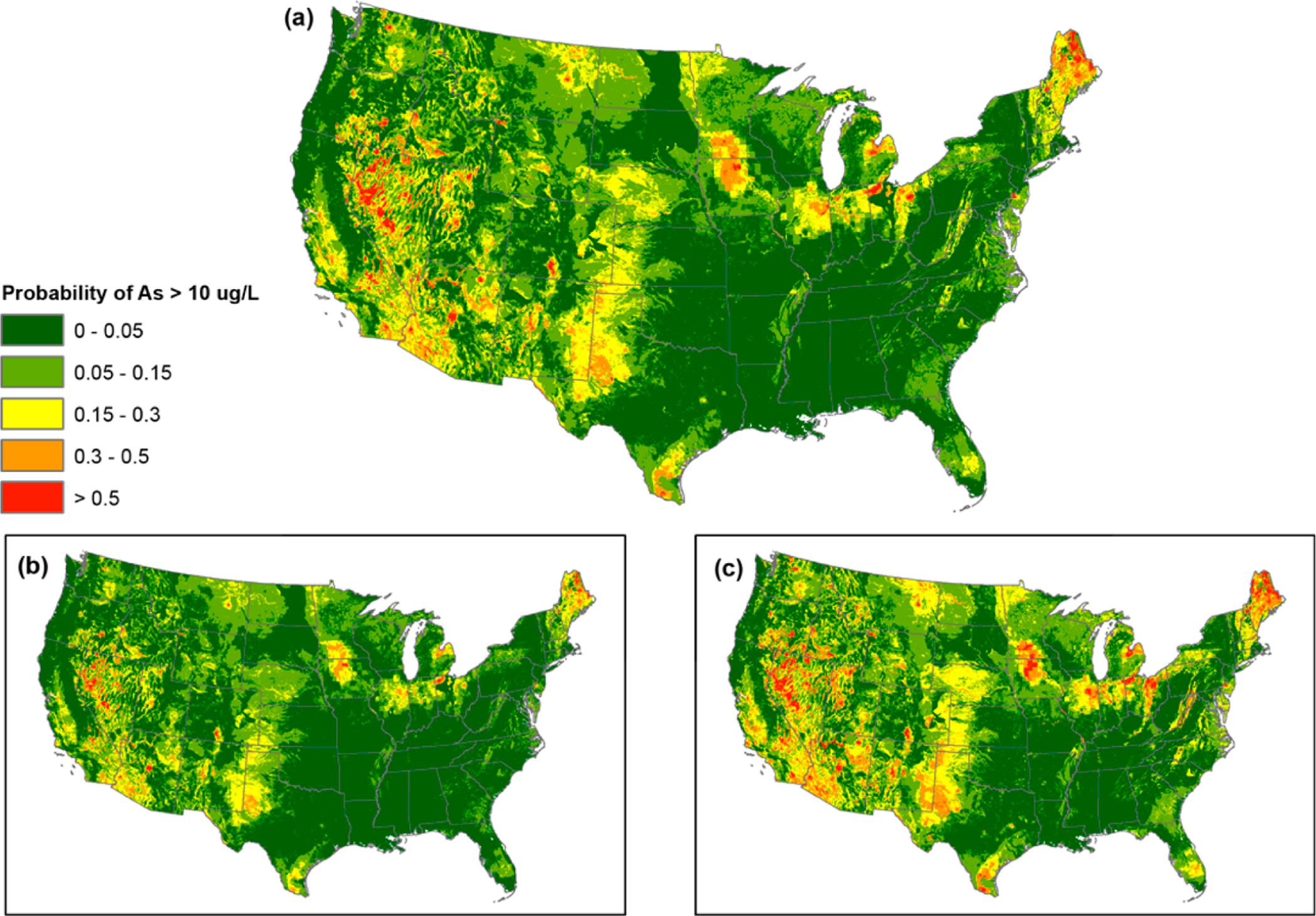
Probabilities of (a) arsenic >10 μg/L (b) 95-percent confidence lower bound for arsenic >10 μg/L; and (c) 95-percent confidence upper bound for arsenic >10 μg/L.

Predictor Variables.

Many factors predicted high concentrations of arsenic in groundwater in the U.S. At the national scale, the most fundamental were climate-related. The top two variables based on standardized coefficients were precipitation (negative coefficient) and recharge (positive coefficient) (Supporting Information Table 3), consistent with findings from national-scale occurrence studies and other work that show that arsenic is related to climate regime and that the majority of high arsenic concentrations are found in the more arid western half of the U.S.^2,3,10,15 Thus, we interpret the inverse relation with precipitation as a partial indicator of climate regime. Coupled with other factors in the models such as stream density, base-flow index, slope, and relief, we account for humid to arid climate regions. The positive relation with recharge, coupled with other model variables, is interpreted as a potential mechanism for reductive desorption and (or) dissolution of arsenic from iron oxides.¹⁵ It also may represent cycling of wetting and nonwetting conditions that can flush arsenic after periods of low or no recharge,⁶⁰ possibly more important in the eastern U.S.

As in previous studies,¹⁵ the variable precipitation minus potential evapotranspiration (PMPE) was significant in some of our models but in our best models, precipitation and recharge, as determined in model testing, produced better models. Studies that identified PMPE¹⁵ or precipitation¹⁰ as primary variables (inverse relation) also identify secondary variables such as pH (in arid regions) and iron (humid regions) or evapotranspiration as important. In our model, the positive relation with recharge (like iron) provides a mechanism for dissolution of arsenic-containing iron oxides and (or) desorption of arsenic from iron oxides. Also, because there are no national-scale models of iron in groundwater for domestic wells, we did not use that variable in our model, given that our goal was to map arsenic probabilities for the conterminous U.S. (CONUS). We use regions of glaciated terrain, bedrock geology, base-flow index, slope, relief, stream density, and other features, to further differentiate arid climate factors. Stream density (positive coefficient) is interpreted to indicate a correlation with discharge areas, and increasingly anoxic conditions, particularly in humid parts of the U.S. Anoxic conditions have been related to reductive oxyhydroxide dissolution (e.g., dissolved iron and manganese) and elevated arsenic at regional and national scales.^15,46

Additionally, other variables representing processes and mechanisms related to arsenic mobility have improved our understanding in other studies and in this one.^{10,12,15,17–20,22,23,36,43,45,61} Features such as soil hydrologic group (hga, negative coefficient), soil tile drainage (percent_ti, positive coefficient), and water table depth (wtdepave, negative coefficient) collectively suggest surrogates for long residence time, poor drainage, and areas of groundwater discharge, which are consistent with findings from other studies in the U.S.^10,15,36 and elsewhere.^10,36,62

The model used in this study also identifies geologic units⁶³ that are significant nationally as well as locally. There are geologic units where predictions of high arsenic concentrations in our national model are corroborated with observations of high arsenic concentrations, such as the Triassic marine stratified sequence (Tr) in northwestern New Jersey, and where probabilities from our model are similar to results from regional models, such as the Quaternary marine stratified sequence (Q) in the southwestern basin and range area¹⁷ and the Central Valley of California.⁴³

In one regional study, arsenic in domestic wells has been associated broadly with underlying Paleozoic sedimentary bedrock units in Illinois, Indiana, Ohio, Michigan, and Wisconsin but it was not directly associated with bedrock subcrops.³² One exception was in southwest Ohio where Silurian carbonates may be related to high groundwater arsenic.³² Although similar geologic units in Ohio were not significant in this model, areas of northern and central Ohio with low probabilities of having arsenic concentrations >10 μg/L were associated with the Upper Silurian marine stratified deposits (Supporting Information S3) unit. In other cases, local aquifers, such as the Mahomet aquifer in Illinois,^34,35,64 were not represented in our model, but the map of probabilities from our model reflects a general likelihood of having arsenic concentrations >10 μg/L in these areas. Overall, the probabilities of arsenic concentrations >10 μg/L in Illinois are similar in pattern to those published elsewhere.⁶⁵

For various reasons (data gaps or model scale), some geologic units lacked significance and were not included in the model but may be locally important at predicting high arsenic concentrations. For example, in North Carolina, the variable for Cambrian eugeosynclinal (deep marine environment) deposits,⁶³ associated with arsenic-containing slates, was not significant, but variables representing nearby rocks described as Paleozoic mafic intrusive rocks and Cambrian volcanic rocks were significant. Local model results include faults, specific rock types, and well depth as factors related to high arsenic in groundwater underlain with all three rock types in North Carolina.^20,23

The use of bedrock geologic information to help understand the groundwater arsenic hazard in unsampled areas has precedent. In New England, generalization of rock groupings had previously resulted in predictions of high arsenic in some areas that were not known to have high arsenic or where observations suggested lower concentrations of arsenic.¹⁸ A recent study of arsenic in private wells in parts of southeast and north central Connecticut indicates that there are high concentrations of arsenic in previously unsampled areas.⁶⁶ Our model predicts high arsenic in parts of eastern New Mexico and northern Wisconsin where domestic well maps indicate no or sparse data;⁶⁷ these may be areas to watch as new data become available.

Geochemical information from the National Soil Geochemical database,⁶⁸ particularly concentrations of antimony, arsenic, and beryllium, in the C-horizon, also were among the top predictors. These data indicate national-scale geochemical and mineralogical patterns that relate to underlying soil parent materials and potentially aquifer materials.⁶⁹ Antimony and arsenic commonly occur in sulfide minerals. In the model training data and in the predictor variable data for the conterminous U.S., antimony and arsenic in C-horizon soils correlated strongly (Spearman’ rho = 0.69 and 0.74, respectively). Antimony and arsenic also can substitute for sulfur in metal sulfide minerals, forming arsenides or antimonides; or can partially substitute for other metals in sulfides, as in minerals in the sulfosalt group.⁷⁰ It is possible that co-occurrence of antimony and arsenic sulfides in some areas and the potential for arsenic to dissolve in groundwater leads to the predictive power of the antimony variable. Another possibility is that iron hydroxides may contain both antimony and arsenic and that the arsenic can desorb from iron or manganese oxides coatings on aquifer materials (under reductive or alkaline pH conditions, particularly for pentavalent arsenic)⁷¹ or dissolve (under reductive geochemical conditions).²⁴ Ion competition in some areas, such as in the southwest or where road salt is used for deicing, may also support desorption.⁷² Soil arsenic concentrations align generally but not always with predicted probability of high groundwater arsenic, suggesting that although this data layer is a source indicator, there often are other variables influencing probability estimates. Bismuth and molybdenum had negative coefficients, indicating an inverse relation to arsenic probability. Although relatively coarse in scale, these features are among the most predictive (having high standardized coefficients) of the variables. These results are consistent with a recent model of the Central Valley of California.⁴³

In addition to climate, geology, and geochemical variables, other important predictor variables, as identified by standardizing (Supporting Information Table 3) regression coefficients, include variables for average water table depth, slope, and relief. Collectively, these variables capture effects of potential flow path, recharge and discharge zones, and groundwater residence time on arsenic concentrations. More specifically, important arsenic mobility processes such as pH-driven desorption and redox can be captured in a variety of surrogate variables that are predictive of high arsenic concentrations.^{10,17,43,45,46,73,74} For example, precipitation, recharge, stream density, and base flow index (long-term percentage of groundwater discharge in streamflow) suggest broad-scale (national) hydrologic conditions that relate to groundwater flux and residence time, which influences pH, which in turn influences concentrations of arsenic.^10,15,17,43

Model Performance.

Model performance information (Table 2) shows that overall accuracy (total correct predictions) at the 0.5-probability cut point was 90% for both training and testing data, indicating that the model validated well. Other cut points could be used and may be warranted. The cut point 0.2 also is shown in Table 2, indicating that lower cut points increase sensitivity but decrease specificity and overall percent correct. As expected, given the larger number of nonevents compared to events, specificity is greater than sensitivity for both cut points. The unadjusted Hosmer−Lemeshow (H−L) statistic had a low p-value (0.0182) indicating poor model fit, but this statistic is affected by large sample sizes. After adjusting (increasing) the number of groups for the H−L test because of the large number of observations used (20 450), the H−L test p-value increased to 0.1086, suggesting reasonable model fit.⁷⁵ The H−L p-value for the testing data set was 0.1601. The percent deviance explained was 20% for both training and testing data. The fact that model fit criteria were the same or similar for the testing and training data sets demonstrates that the model generalizes well to new data, which increases confidence in the mapped probabilities.

Table 2.

Summary of model fit criteria and classification tables for probability of As > 10 μg/L

metric	training data	testing data
N	17 354	3095
% deviance explained	20.3	19.2
ROC	0.81	0.82
pseudo r2	0.26	0.29
coefficient of discrimination	0.18	0.21
H–L probability	0.0035	0.1601
adjusted H–L p-value	0.1086
Cut Point = 0.2
% total correct	84.5	85.7
% sensitivity	52.3	50.5
% specificity	88.4	89.8
% false positive	64.6	63.5
% false negative	6.2	6.0
Cut Point = 0.5
% total correct	89.9	90.1
% sensitivity	12.7	13.9
% specificity	99.3	99
% false positive	29.2	37.5
% false negative	9.7	9.2

The range in Pearson residuals for the As > 10 μg/L model is −3.3 to 30.3, the 5th and 95th percentiles are −0.6 and 1.9, and the median is −0.2 (Supporting Information SI 4). Darker points (red and blue) show that values outside of the “acceptable” bounds of ±3⁵⁴ are most frequent in the northeast, with small clusters in Minnesota, Oklahoma, Idaho, Washington, and California. Very few residuals were less than −3.

Graphical results from SAS influence diagnostics reveal that two observations are consistent outliers among the influence and predicted probability diagnostic plots (Supporting Information SI 5). When the model is run without these observations, 18 points appear to be potentially influential. Because there is negligible difference between model results (Supporting Information SI 5) using (1) the full model, (2) the full model less removal of the 2 most influential observations, and (3) the full model less removal of the 20 most influential observations, the full model is used without removal of any values. Additional screening revealed that none of the numerical variable values associated with these two observations were the maximum or minimum of the full data set, which might have indicated erroneous variable assignment.

Further, the differences in logistic regression model results when some wells were removed from the data set based on the analysis of stacked aquifers were small. For predictions of arsenic >10 μg/L, differences in the total number of correct predictions and specificity were negligible; however, sensitivity increased by 1% and the overall error rate decreased by 3.6%, suggesting that this is an area of potential important improvement for future efforts.

Estimates of the Domestic Well Population with High Arsenic.

Approximately 44.1 M people in the conterminous U.S. use water from domestic wells (Figure 3a).⁵ The subset of this population with estimated arsenic concentration >10 μg/L (Figure 3b) is 2.1 M (4.8% of domestic well users); with 95-percent certainty on the arsenic probabilities, the estimate is between 1.5 and 2.9 M people (3.4−6.6% of domestic well users) (Table 3).⁴² Broadly speaking, our model shows that the parts of the U.S. with the greatest domestic well use are also likely to be the parts of the U.S. with the greatest numbers of domestic well use population with high arsenic in their well water. Exceptions occur locally where there are high probabilities of arsenic and small numbers of people using domestic wells, or low probabilities of arsenic and large numbers of people using domestic wells.

Figure 3.

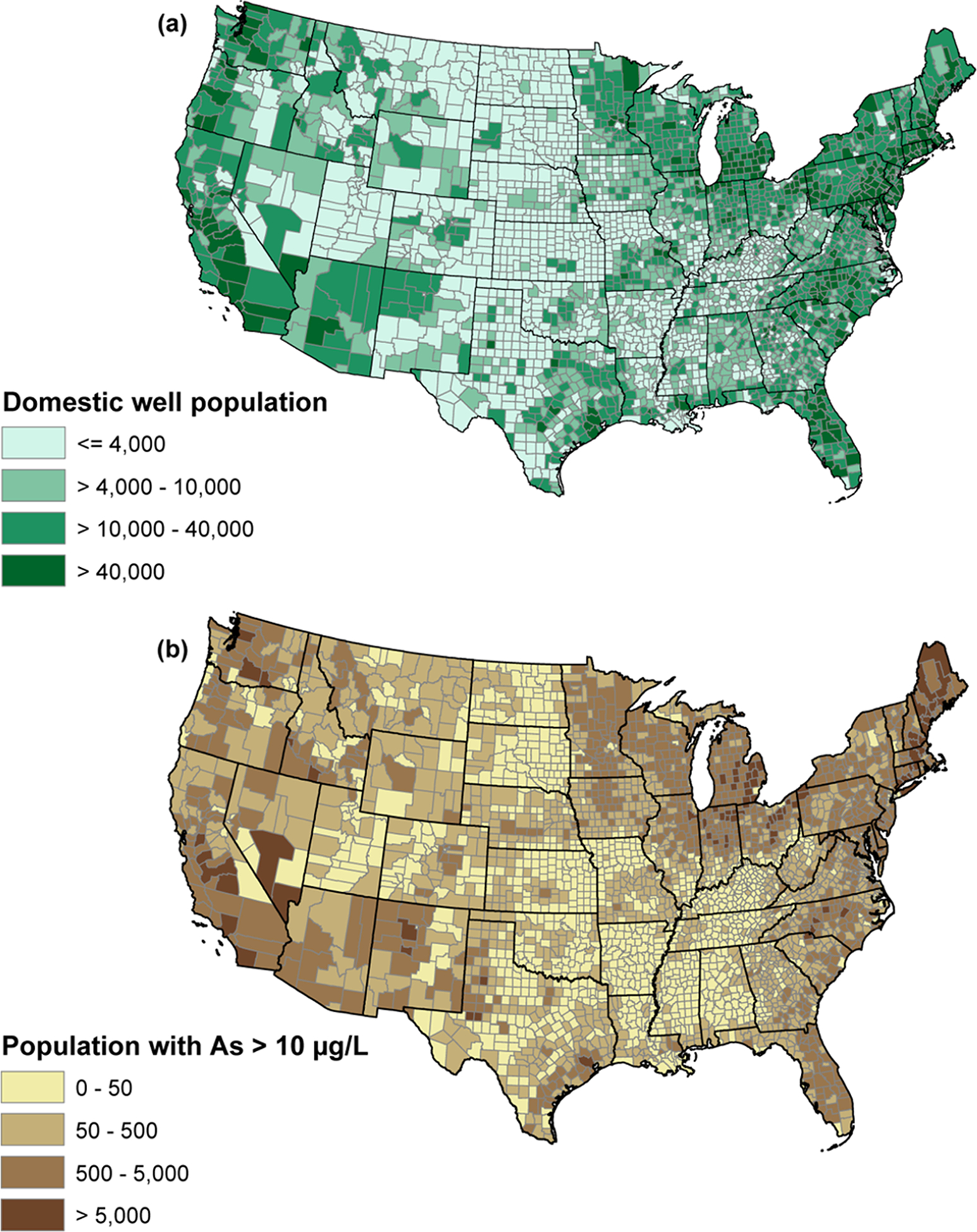
County-level (a) domestic well population and (b) domestic well population with As > 10 μg/L based on probability estimates.

Table 3.

Estimates of Populations Using Domestic Wells with Arsenic >10 μg/L, and Lower and Upper Confidence Limits, by state for the conterminous U.S.

			population likely to have arsenic concentration >10 μg/L in domestic well water
				95% confidence limit
state	domestic well population	%	estimated population	lower	upper	rank by population, descending
AL	539 394	0.5	2592	1750	3960	43
AR	144 434	0.8	1147	803	1696	48
AZ	218 170	7.8	16 979	13 637	20 902	30
CA	2 476 047	4.7	115 823	91 768	145 900	5
CO	311 619	4.6	14 339	11 705	17 607	31
CT	871 373	6.0	52 105	36 138	74 452	16
DE	185 267	5.4	9925	6643	14 737	34
FL	1 907 603	2.7	50 924	33 060	78 014	17
GA	1 530 125	2.3	34 969	23 251	53 637	22
IA	591 403	6.0	35 650	28 006	44 865	21
ID	431 945	11	47 041	38 491	57 021	18
IL	1 155 342	5.9	67 709	53 347	85 636	11
IN	1 658 685	9.1	150 858	115 385	195 482	3
KS	150 883	4.1	6168	5059	7511	39
KY	663 634	1.0	6707	4680	9744	36
LA	587 505	1.1	6464	4331	9681	37
MA	533 820	5.7	30 549	22 067	41 883	24
MD	1 069 848	3.9	41 276	27 202	63 107	19
ME	560 801	18	102 452	80 281	128 879	6
MI	2 675 773	7.2	192 747	151 408	246 037	1
MN	1 127 975	7.1	80 353	64 209	100 266	9
MO	883 261	1.2	10 242	7587	14 058	33
MS	446 129	0.6	2804	1959	4047	42
MT	285 143	8.2	23 269	18 006	30 042	27
NC	3 303 760	3.6	119 633	76 523	187 279	4
ND	49 355	4.1	2014	1591	2659	45
NE	345 966	5.0	17 399	13 593	22 252	29
NH	445 540	14	60 962	45 643	80 275	13
NJ	964 107	4.2	40 563	26 951	60 496	20
NM	303 139	10	30 990	24 485	38 647	23
NV	157 998	14	21 533	17 769	25 641	28
NY	2 046 039	3.2	66 265	47 992	92 295	12
OH	1 830 099	10	189 191	118 913	294 655	2
OK	315 670	1.4	4337	3392	5622	41
OR	606 611	4.3	26 051	20 233	33 612	26
PA	3 345 559	2.4	80 729	52 104	126 925	8
RI	112 941	1.3	1509	1145	1998	46
SC	1 152 116	2.4	28 131	18 768	42 146	25
SD	75 585	1.6	1182	900	1663	47
TN	538 259	1.0	5245	3448	8102	40
TX	2 440 586	3.9	95 455	74 590	122 294	7
UT	50 514	4.2	2131	1583	2816	44
VA	1 649 470	3.2	52 800	34 585	81 003	14
VT	181 611	5.3	9716	6988	13 363	35
WA	1 002 899	5.2	52 249	40 173	67 401	15
WI	1 644 873	4.4	72 670	58 722	90 438	10
WV	393 332	2.9	11 589	6309	20 661	32
WY	114 123	5.4	6215	5001	7761	38
Total	44 076 331		2 101 648	1 542 173	2 879 171	–

States with the largest estimated population using domestic well water with arsenic >10 μg/L are Michigan, Ohio, and Indiana with 0.193, 0.189, and 0.151 M people, respectively (Table 3). States with the largest estimated percentages of domestic well population with arsenic >10 μg/L are Maine (18%), and New Hampshire and Nevada both at 14% (Table 3), which is more than 3% of the total statewide population (Figure 4) in each of the three states. The county map of high-arsenic population distribution within these states (Figure 3b) shows that hotspots cover much of Maine except for eastern and central counties; southeastern New Hampshire; and areas of southwestern, eastern, and northern Idaho. In Maine and New Hampshire, county estimates of populations with high-arsenic domestic wells generally match those from other studies^18,76 (Figure 3a) but may overestimate the population in parts of northern Maine.⁷⁶ Some states have both relatively large estimates of statewide populations (>100 000) and comparatively higher percentages (>1%) of total state populations with arsenic >10 μg/L (Figure 4). County-level information indicates that 6 of the 10 counties with the largest number of people with high-arsenic wells are in New England; other top-10 counties are in Ohio, North Carolina, California, and Idaho.⁴² States with the estimated lowest numbers of people with high-arsenic wells are the Dakotas, Rhode Island, Utah, and southeastern and south-central states, except for Texas and those along the Atlantic coast (Figure 4; Table 3).

Figure 4.

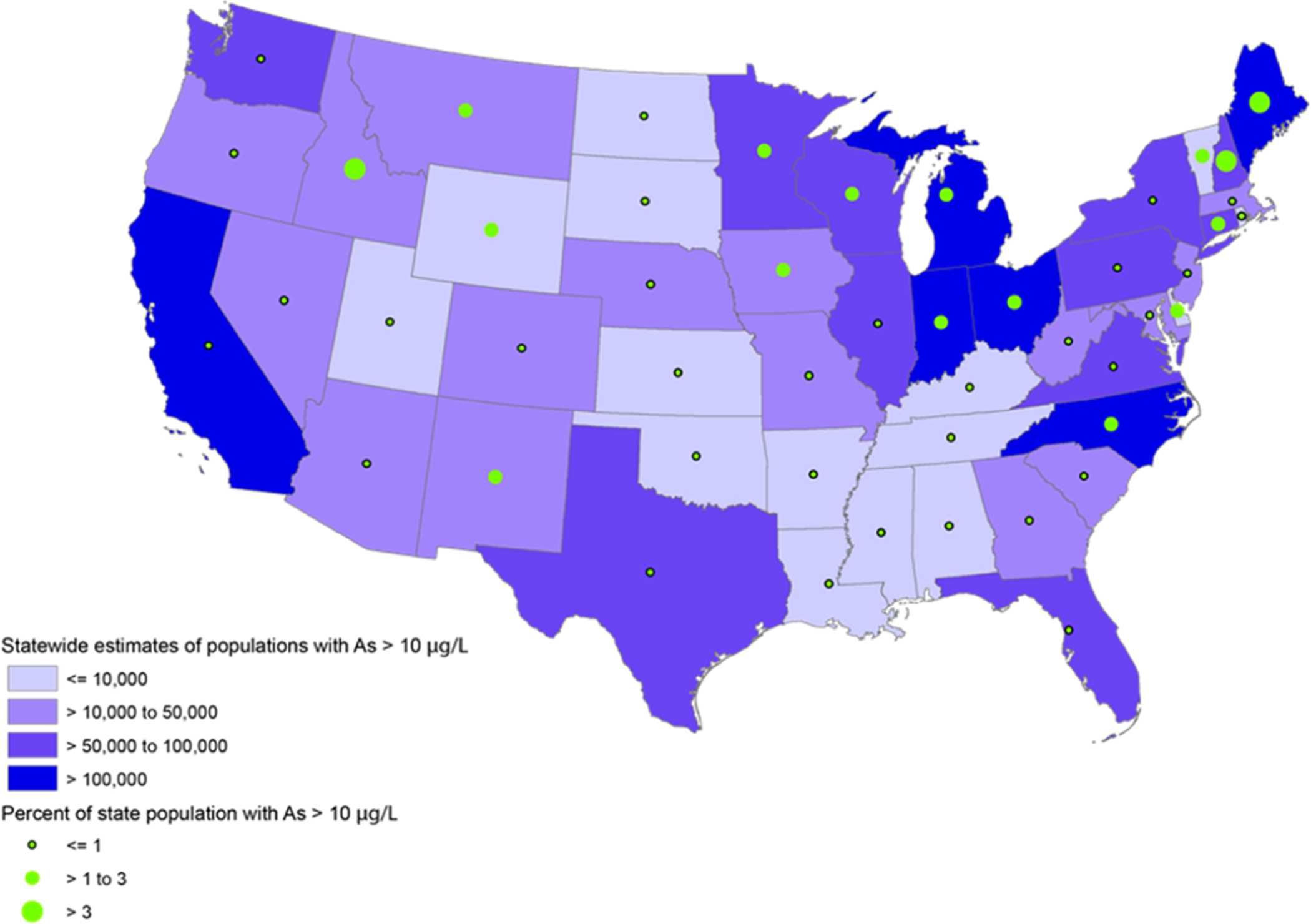
State populations and percent of state populations with arsenic >10 μg/L based on the probability modeling.

Comparing statewide estimates of populations with arsenic >10 μg/L from this model with those calculated from various published state-level information provides the opportunity to evaluate the potential arsenic hazard at different scales and to identify areas that may have been overlooked or otherwise not identified as having a high probability of high arsenic in domestic wells. In most cases, this meant multiplying statewide estimates of the percent of domestic wells with high arsenic by the domestic well population (Table 4). Some states have estimates of the proportion of domestic wells with high arsenic concentrations but generally do not provide confidence intervals on those estimates. Out of the 10 states that we found with information, 5 (Maine, Michigan, New Hampshire, New Mexico, and Vermont) were within the bounds estimated from this study, 3 (Illinois, Minnesota, and Texas) were above the upper bound, and 2 (Connecticut and North Carolina) were below but close to the lower bound. The estimates from this study of the domestic well population with high arsenic by county or state are the first nationally consistent, model-predicted look at where the potentially most affected populations are located throughout the U.S. (Table 4).

Uses and Limitations.

We emphasize that although this study resulted in estimates of the domestic well use population that may have high arsenic concentrations in their drinking water, those numbers should be viewed with an understanding of the limitations of the study. We addressed model uncertainties through use of confidence intervals on arsenic probability estimates. Estimates of county-level domestic well use are the basis for estimating the population affected by high arsenic (arsenic probability), which also carry with them uncertainty that is not easily quantified. Thus, the reported error in the estimates does not reflect all potential error.

Well depth was accounted for broadly and indirectly by selecting only domestic wells to train the model, thus constraining the model to well depths used for domestic supply. In some cases, wells may penetrate and draw water from different aquifers with different arsenic distributions; where available, we used aquifer type information (in lieu of depth) to assess the effects on the modeled probabilities and found minimal effect. The outcomes of this national-scale study include advancing our understanding of predictive factors by confirming previously reported factors,^3,8,10,15 identifying new factors (geology and geochemistry variables), and identifying gaps in predictive factors (e.g., well or aquifer depth and flow path information).^17,43 Also, a possible future refinement could include regional interaction terms or spatially varying model coefficients.

The major results of this study are estimates of the total population in the conterminous U.S. potentially exposed to high arsenic, based on a model of arsenic probability for domestic wells. Many areas of the U.S. were underrepresented with arsenic data in our study, such as parts of Iowa and New Mexico, but through extrapolation, the model also identified a potential arsenic hazard in these unsampled areas and potential hotspots that may warrant further investigation. Further, combining hazard information with data on the domestic well population shows a potential for exposure. We reiterate that these findings should be used cautiously and in conjunction with more detailed local and regional information, where they exist. These results can be used directly in future public health activities, including targeting specific areas for additional testing and national-scale ecological studies of potential human-health outcomes, as has been done in regional studies.^21,65,83,84 Anticipated future refinement of models and the methods used here will serve to provide improved estimates of the potential affected population.