Total-Body Quantitative Parametric Imaging of Early Kinetics of ¹⁸F-FDG

Abstract

Parametric imaging has been shown to provide better quantitation physiologically than SUV imaging in PET. With the increased sensitivity from a recently developed total-body PET scanner, whole-body scans with higher temporal resolution become possible for dynamic analysis and parametric imaging. In this paper, we focus on deriving the parameter k₁ using compartmental modeling and on developing a method to acquire whole-body ¹⁸F-FDG PET parametric images using only the first 90 s of the postinjection scan data with the total-body PET system. Methods: Dynamic projections were acquired with a time interval of 1 s for the first 30 s and a time interval of 2 s for the following minute. Image-derived input functions were acquired from the reconstructed dynamic sequences in the ascending aorta. A 1-tissue-compartment model with 4 parameters (k₁, k₂, blood fraction, and delay time) was used. A maximum-likelihood–based estimation method was developed with the 1-tissue-compartment model solution. The accuracy of the acquired parameters was compared with the ones estimated using a 2-tissue-compartment irreversible model with 1-h-long data. Results: All 4 parametric images were successfully calculated using data from 2 volunteers. By comparing the time–activity curves acquired from the volumes of interest, we showed that the parameters estimated using our method were able to predict the time–activity curves of the early dynamics of ¹⁸F-FDG in different organs. The delay-time effects for different organs were also clearly visible in the reconstructed delay-time image with delay variations of as large as 40 s. The estimated parameters using both 90-s data and 1-h data agreed well for k₁ and blood fraction, whereas a large difference in k₂ was found between the 90-s and 1-h data, suggesting k₂ cannot be reliably estimated from the 90-s scan. Conclusion: We have shown that with total-body PET and the increased sensitivity, it is possible to estimate parametric images based on the very early dynamics after ¹⁸F-FDG injection. The estimated k₁ might potentially be used clinically as an indicator for identifying abnormalities.

Conventional PET imaging makes widespread use of SUVs for semiquantitative analysis, especially in measurements of ¹⁸F-FDG uptake in tumors (1). However, SUV depends on the time of measurement and many other factors (2,3), which makes reliable quantitation a challenging task. On the other hand, kinetic analysis in PET has more direct physiologic meaning than does SUV and can be a more robust approach for quantifying ¹⁸F-FDG uptake and use (4,5).

Compared with volume-of-interest (VOI)–based kinetic analysis (6,7), parametric imaging enables the acquisition of voxel-level dynamics of tracer uptake by applying kinetic modeling for each individual voxel (8,9). Conventional graphical methods, including Logan analysis (10) and Patlak analysis (11), have been used for parametric imaging because of their linear properties and simplicity in acquisition protocols. Improved lesion contrast and detectability have been demonstrated by many studies (12,13). With the assumption that the dynamic activity can be described using exponentials as impulse responses, the basis function provides a possible approach for nonlinear model fitting (14,15). Recently, whole-body parametric imaging using the Patlak model has been proposed using a multipass acquisition protocol (16,17).

Even with the many added benefits of kinetic modeling, parametric imaging techniques and dynamic protocols are not widely used in clinical studies, especially in oncology (17). In some studies, the requirement for invasive arterial blood sampling for the input function makes the scan protocol impractical. Even with image-derived input functions (18,19) or population-based input functions (20,21), a minimal scan time of 30 min is often required to reveal dynamic information using Patlak analysis. Compared with state-of-the-art whole-body SUV scans, which take around 20 min and sometimes less than 10 min, the increased scan time and more complex protocol have proved to be one of the major practical factors that hinder the clinical use of dynamic analysis with whole-body imaging.

The study of early dynamics, such as first-pass studies (22,23), on the other hand, may enable much shorter scan protocols and—with ¹⁸F-FDG studies—may enable the estimation of k₁, which represents the rate of ¹⁸F-FDG transport from the arterial plasma to the intracellular space. In some studies in the literature, ¹⁸F-FDG k₁ was found to be an indicator for identifying tumor subgroups (24), gene expressions (25), and chemotherapy response (26) and could be used to assess tumor blood flow (22). ¹⁸F-FDG k₁ was found to be a valuable parameter for applications other than oncology. In the work by Sarkar et al. (27), the authors found that the k₁ value is helpful for quantifying liver inflammation in nonalcoholic fatty liver disease.

With the recently developed total-body PET system, a dramatic improvement in sensitivity has made it possible to acquire PET images with reasonable quality in scan times of 60 s or less (28,29). With this increase in sensitivity, parametric imaging with high temporal resolution becomes feasible, which in turn may allow accurate parametric imaging using only the early phases of the tracer dynamics. We have developed a method to acquire whole-body parametric images using data acquired from the total-body PET system with a temporal resolution of 1–2 s. With the much improved temporal resolution, the delay time of the input function has been shown to be an important factor in VOI-based analysis (30). In this paper, the delay time is included as a voxel-specific parameter that is jointly estimated.

MATERIALS AND METHODS

Parametric Image Reconstruction

For ¹⁸F-FDG, a 2-tissue-compartment irreversible (2Ti) model with 4 rate constants ( $k_1$ , $k_2$ , $k_3$ , and $k_4$ ) is often used to model its tracer dynamics. In the 2Ti model, $k_1$ and $k_2$ describe the forward and backward transport of ¹⁸F-FDG from plasma to tissue. $k_3$ and $k_4$ model the phosphorylation and dephosphorylation process. The accuracy of the measured kinetic parameters in dynamic analysis can be estimated by calculating the sensitivity of the model with respect to each kinetic parameter (31). Zuo et al. (32) suggested that $k_3$ and $k_4$ cannot be accurately estimated using only the first few minutes of a scan because of the low identifiability of these parameters at early times. Therefore, a 1-tissue-compartment (1T) model was used in this study. The time–activity curve for a specific voxel can be expressed as…

$$C_{}\left(t\right)=v_b{C}_b\left(t\right)+\left(1-v_b\right)\left(k_1\text{exp}\left(-k_{2}t\right)\otimes C_p\left(t\right)\right),$$ Eq. 1

where $v_b$ is the blood fraction in the tissue, $C_b\left(t\right)$ is the time–activity curve for the whole blood, $C_p\left(t\right)$ is the plasma input function, and $C_{}\left(t\right)$ is the concentration of ¹⁸F-FDG in the tissue. $\otimes$ represents the convolution operation. In the above equation, the whole-blood time–activity curve is used for the blood fraction because the intravascular activity includes that from both plasma and blood cells.

With higher temporal resolution and whole-body coverage, the delay time for different regions becomes an important factor. With the inclusion of delay time, the measured time–activity curve is…

$$C\left(t\right)=v_b{C}_b\left(t-t_d\right)+{\kappa }_1\text{exp}\left(-k_{2}t\right)\otimes C_p\left(t-t_d\right),$$ Eq. 2

where $t_d$ is the voxel-dependent delay time. For easier computation, the parameter ${\kappa }_1=\left(1-v_b\right)k_1$ is used and estimated instead of $k_1$ .

Because of the very high temporal resolution used in this study, the time–activity curve for an individual voxel is still expected to be noisy despite the much-increased sensitivity of the scanner. Therefore, it may be beneficial to develop a maximum-likelihood estimation approach that specifically models the noise of the reconstructed dynamic image. Studies in the literature indicate that the voxel values in the image approximately follow a scaled Poisson distribution (33). With this assumption, the log-likelihood function can be derived as…

$$L\left({\kappa }_1,k_2,v_b,t_d\right)={\displaystyle \sum }_t-C\left(t\right)+x_t\log \left(C\left(t\right)\right)-\log \left(x_t!\right),$$ Eq. 3

where $x_t$ are the reconstructed dynamic images and are treated as a known measurement in this case. The update equation for ${\kappa }_1$ , $k_2,$ and $v_b$ can be derived by maximizing the likelihood in the above equation (Supplemental Eqs. 1–5 show the derivations; supplemental materials are available at http://jnm.snmjournals.org):

$$\{\begin{array}{l}{\mathit{v}}_b^{p+1}=\frac{{\mathit{v}}_b^p}{{{\displaystyle \sum }}_t{C}_b\left(t-{\mathit{t}}_d\right)}{\displaystyle \sum }_t\frac{C_b\left(t-{\mathit{t}}_d\right)\mathit{C}\left(t\right)}{{\widehat{\mathit{C}}}^p\left(t\right)}\\ {\mathit{\kappa }}_1^{p+1}=\frac{{\mathit{\kappa }}_1^p}{{{\displaystyle \sum }}_t{e}^{-{\mathit{k}}_2^{\mathit{p}}t}\otimes C_p\left(t-{\mathit{t}}_d\right)}{\displaystyle \sum }_t\frac{e^{-{\mathit{k}}_2^{\mathit{p}}t}\otimes C_p\left(t-{\mathit{t}}_d\right)\mathit{C}\left(t\right)}{{\widehat{\mathit{C}}}^p\left(t\right)}\hspace{0.17em}\\ {\mathit{k}}_2^{p+1}={\mathit{k}}_2^p\frac{{{\displaystyle \sum }}_{t}t{\mathit{\kappa }}_1^p\left(\text{exp}\left(-{\mathit{k}}_2^{p}t\right)\right)\otimes C_p\left(t-{\mathit{t}}_{\mathit{d}}\right)}{{{\displaystyle \sum }}_t\frac{t{\mathit{\kappa }}_1^p\left(\text{exp}\left(-{\mathit{k}}_2^{p}t\right)\right)\otimes C_p\left(t-{\mathit{t}}_{\mathit{d}}\right)\mathit{C}\left(t\right)}{{\widehat{\mathit{C}}}^p\left(t\right)}}\hspace{0.17em}\end{array},$$ Eq. 4

where p is the iteration number and ${\widehat{C}}^p\left(t\right)=v_b^p{C}_b\left(t-t_d\right)+{\kappa }_1^p{e}^{-k_2^{p}t}\otimes C_p\left(t-t_d\right)$ are the estimated dynamic images. ${\widehat{\mathit{C}}}^p$ is the matrix version of ${\widehat{C}}^p$ ; the same is true for the other symbols as well. The multiplicative update equations imply positive constraint for ${\kappa }_1$ , $k_2,$ and $v_b$ , which is reasonable on the basis of the model. The multiplicative factors for ${\kappa }_1$ and $v_b$ are similar to that from a conventional maximum-likelihood expectation maximization approach to image reconstruction, as is the reciprocal of $k_2$ ’s update factor. This similarity makes the implementation straightforward.

A maximum-likelihood gradient-descent approach is used for the estimation of $t_d$ (Supplemental Eq. 6 shows the derivations):

$$t_d^{p+1}=t_d^p+s\frac{\partial L\left({\kappa }_1,k_2,v_b,t_d\right)}{\partial t_d},$$ Eq. 5

where $\frac{\partial L\left({\kappa }_1,k_2,v_b,t_d\right)}{\partial t_d}={\displaystyle \sum }_t\left(v_b{C}_b^{\text{'}}\left(t-t_d\right)-{\kappa }_1\text{exp}\left(-k_{2}t\right)\otimes C_p^{\text{'}}\left(t-t_d\right)\right)\left(\frac{x_t}{{\widehat{\mathit{C}}}^p\left(t\right)}-1\right)$ , and $s$ is the step size of the update. Since the range of delay times is expected to be less than 1 min based on known circulation times, to ensure convergence the absolute update for the delay time was set to a fixed value for all voxels in this paper, that is, $s=\Delta t/\left|\frac{\partial L\left({\kappa }_1,k_2,v_b,t_d\right)}{\partial t_d}\right|$ . The update value $\Delta t$ was set to be 2 s in the first few iterations and reduced to 0.2 s in later iterations.

In this study, the dynamic images were first reconstructed by applying 3 iterations with 20 subsets using time-of-flight information. The reconstruction voxel size was 4 × 4 × 2.89 mm, and attenuation, scatter, randoms, and normalization corrections and point-spread-function modeling were also included during image reconstruction. A 3-dimensinal gaussian filter of 6 mm in full width at half maximum was used for noise suppression in the reconstructed dynamic image. An alternate update approach was used to estimate the 4 parameters. In total, 18 main iterations were used. Within each iteration, ${\mathit{\kappa }}_1^{ }$ and ${\mathit{v}}_b^{ }$ were first updated with fixed ${\mathit{k}}_2^{ }$ and ${\mathit{t}}_d^{ }$ using 9 subiterations, ${\mathit{k}}_2^{ }$ was updated with fixed ${\mathit{\kappa }}_1^{ }$ , ${\mathit{v}}_b^{ }$ , and ${\mathit{t}}_d^{ }$ using 1 subiteration, followed by the update of ${\mathit{t}}_d^{ }$ with fixed ${\mathit{\kappa }}_1^{ }$ , ${\mathit{v}}_b^{ }$ , and ${\mathit{k}}_2$ using 3 subiterations. The same gaussian smoothing filter was used after every 6 main iterations for the delay-time image and ${\mathit{\kappa }}_1^{ }$ for better control of noise. With the acquired ${\mathit{\kappa }}_1^{ }$ and ${\mathit{v}}_b^{ }$ image, the k₁ image was also generated and compared with ${\mathit{\kappa }}_1^{ }$ .

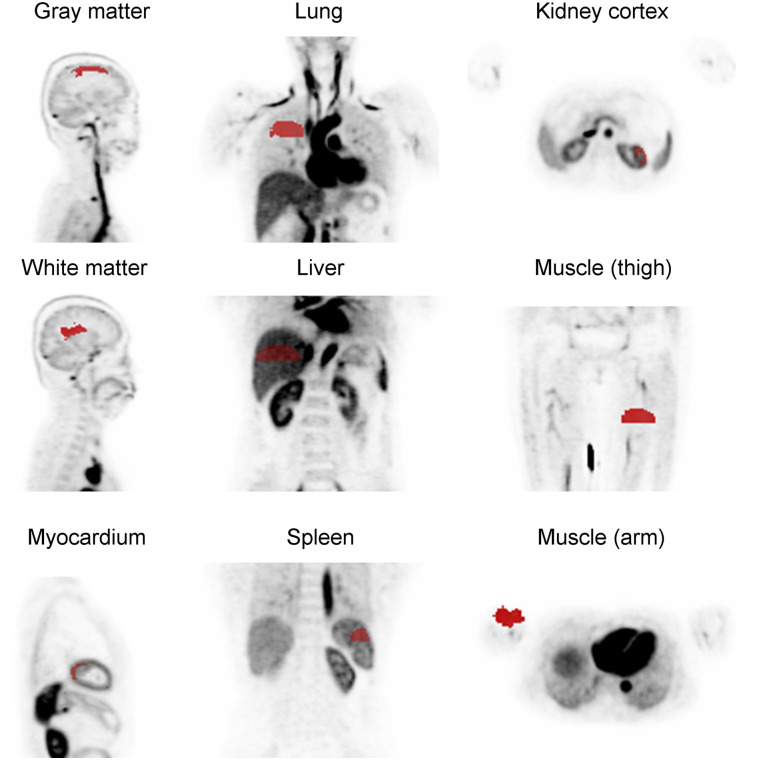
To study the accuracy of the estimated parameters, they were compared with VOI-based analysis. Nine regions were selected (gray matter, white matter, lung, liver, kidney cortex, myocardium, spleen, arm, and thighs; Fig. 1). A 2Ti model was also applied on 1-h-long data to compare the estimated k₁ values. In the 2Ti model, the same delay time as estimated using the 1T model was used because the extended time is less likely to contain information on the delay time.

FIGURE 1.

VOIs used for parameter estimation.

Patient Data and Scan Protocol

Two healthy volunteers with an injected activity of about 220 MBq were scanned using the uExplorer PET scanner (United Imaging Healthcare) with the approval of the Ethics Committee of Zhongshan Hospital and after giving informed consent. One volunteer was injected in the leg, and the other was injected in the arm. The image data obtained during the first 90 s after injection were used in this study for 1T model analysis.

To obtain an image-derived input function, VOIs over the ascending aorta and the left ventricle (Supplemental Fig. 1) were manually drawn on the PET/CT image and the time–activity curves were acquired. It has been suggested that the best location for image-derived input function is the ascending aorta (34), as it is less affected by respiratory and cardiac motion. The left ventricle is another widely used location because of the relatively large blood pool size (18). The diameter of the ascending aorta VOI was 16 mm, and the height was 40 mm. The boundaries in the left ventricle were excluded from the left ventricular VOI to reduce the effect of respiratory motion, and the total volume was about the same as for the ascending aorta VOI. Whole-blood–to–plasma correction was applied on the time–activity curve $C_b\left(t\right)$ to estimate the plasma input function $C_p\left(t\right)$ . The correction equations and values are based on the method and parameters published in the literature (Eq. 2 of Wahl et al. (35), where the hematocrit is 0.42 and the equilibration time constant is 0.23 min⁻¹).

RESULTS

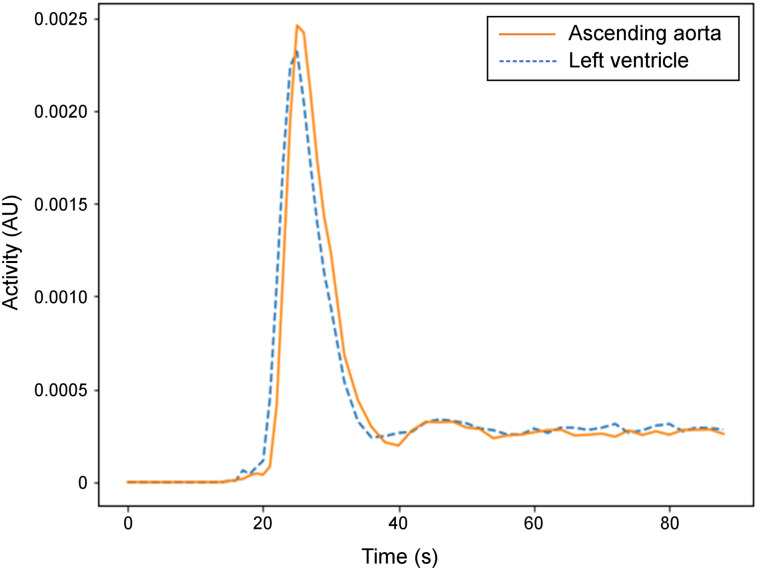
Figure 2 shows the first 90 s of the image-derived plasma input function for volunteer 1 using the reconstructed dynamic images of the ascending aorta VOI and the left ventricular VOI. Image voxel values were applied directly without calibration of activity concentrations using a well counter. The calibration scale factor cancels out in the analysis and therefore is not needed. The time–activity curves were almost identical except for the 1-s delay time. With the added delay time modeling, the results are expected to be the same with the left ventricle as the input function. The time–activity curve from the ascending aorta was used for the input function.

FIGURE 2.

Image-derived input function for first 90 s after injection. AU = arbitrary units.

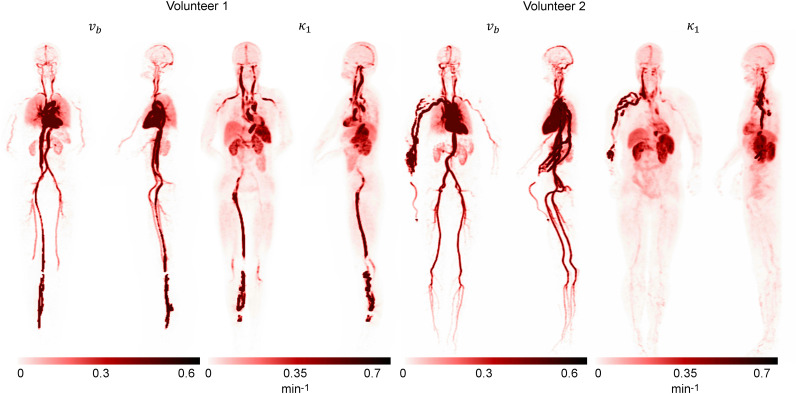
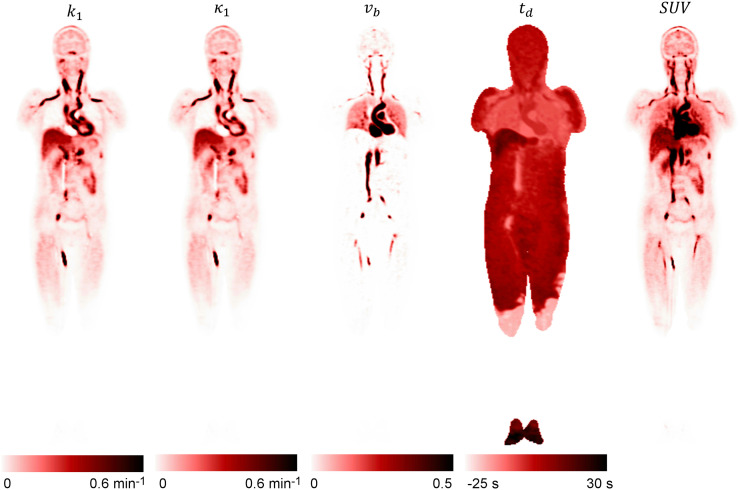
Figure 3 shows the acquired maximum-intensity projection from the reconstructed ${\kappa }_1^{ }$ and $v_b^{ }$ images. The reconstructed parametric images $v_b^{ },{\kappa }_1^{ },k_2^{ },$ and $t_d^{ }$ from volunteer 1 are shown in Figure 4. The k₁ image was also calculated using $v_b^{ }$ and ${\kappa }_1^{ }$ . The SUV image acquired from the same periods (0–90 s) is also shown for comparison. $v_b^{ }$ represents the plasma volume fraction in the tissue, which was clearly visible in the blood pool of the heart and in the aorta. The visual difference between k₁ and ${\kappa }_1^{ }$ was generally small, except for the myocardium region. High k₁ values were observed in the spleen and kidneys. Moderate k₁ values were observed in the liver and myocardium. A high k₁ was also observed in some blood vessels (mostly veins), likely the result of dispersion of the plasma input function in these vessels. The abnormal signal in the veins near the injection site suggested possible retrograde pooling in the veins. Very large $k_2^{ }$ values were also observed in some blood vessels for the same reason. Large delay times were observed in the liver (>10 s) and extremities (∼30 s) when compared with the delay time in the lungs. The large delay time in the liver region was likely caused by the dual blood supply from both the hepatic artery and the portal vein (36), and the algorithm approximated the portal vein input function with the arterial input function by means of a delay time. The delay-time image could also be used for the illustration of the circulatory system. In volunteer 1, ¹⁸F-FDG was first injected into a leg vein and then traveled to the right ventricle. From there the tracer was moved into the lungs and back to the left ventricle, where the tracer was pumped via the arterial system to other organs. The measured delay times (relative to the ascending aorta), k₁, and v _b for different organs are given in Table 1.

FIGURE 3.

Maximum-intensity projection of reconstructed parametric images ${\mathit{v}}_b^{ }$ and k₁ acquired using proposed approach.

FIGURE 4.

Coronal plane of reconstructed k₁, k₁, $v_b^{ }$ , and $t_d^{ }$ parametric images using proposed method from volunteer 1, together with SUV image.

TABLE 1.

Estimated k₁ and Delay Time (Relative to Ascending Aorta) in Different Organs

Parameter	Gray matter	White matter	Myocardium	Liver	Kidney cortex	Spleen	Lung	Arm	Thigh
k1 (min−1) VOI analysis	0.08	0.05	0.56	0.39	0.75	0.92	0.02	0.02	0.06
k1 (min−1) parametric image	0.09 ± 0.02	0.06 ± 0.01	0.45 ± 0.10	0.33 ± 0.04	0.54 ± 0.08	0.73 ± 0.13	0.02 ± 0.02	0.02 ± 0.01	0.06 ± 0.03
C b VOI analysis	0.020	0.01	0.02	0.006	0.08	0.006	0.12	0.0004	0.0
C b parametric image	0.020 ± 0.01	0.007 ± 0.005	0.05 ± 0.04	0.003 ± 0.005	0.11 ± 0.03	0.03 ± 0.02	0.12 ± 0.03	0.0009 ± 0.001	0.004 ± 0.01
Delay time (s)	3.9	3.7	−1.2	13.1	4.7	3.1	−3.8	10.8	8.6

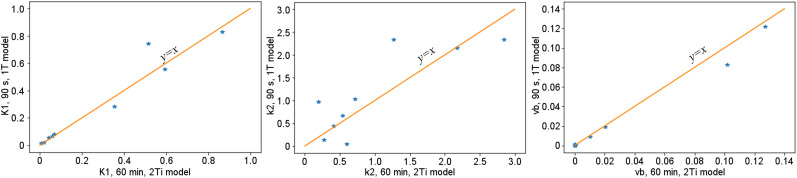
Using VOI analysis, the estimated k₁, k₂, and blood fraction v _b using the 1T model with 90 s of data were compared with the same parameters calculated using the 2Ti model with 1-h-long data. Figure 5 shows the relationships of the estimated values. For k₁ and v _b , both approaches yielded similar results (coefficient of determination of linear fitting was 0.97 for k₁ and 0.95 for blood fraction). Some large differences were observed in k₂, suggesting that k₂ cannot be accurately estimated from the 90-s data. The estimated k₁ using VOI-based analysis was also compared with the k₁ acquired from the parametric image and is given in Table 1. For most VOIs, the differences in k₁ were small. k₁ was underestimated in VOIs in the myocardium and kidney cortex, likely because of application of the gaussian filter, which introduced additional partial-volume effects and affected the quantitative values within these relatively small structures.

FIGURE 5.

Estimated k₁, k₂, and v _b for 9 VOIs using 1T model with 90 s of data (y-axis) and 2Ti model with 1 h of data (x-axis).

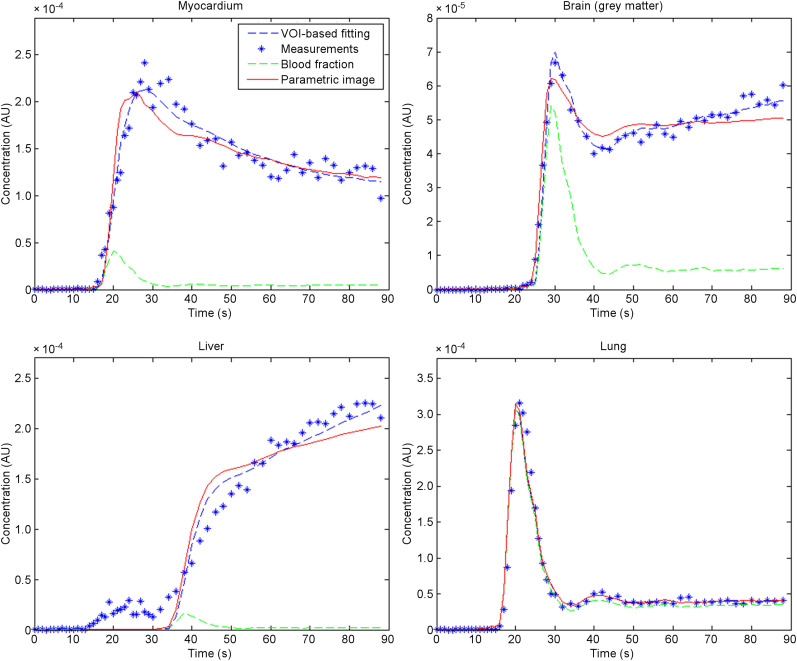
Figure 6 shows the time–activity curves for myocardium, brain, liver, and lung. The average parameters within the VOI were used to estimate the fitted curves. Because the ascending aorta was used as the input function, a positive delay time was observed in the liver and a negative delay time in the myocardium and lung, with a minimal delay time in the brain. The difference between the curves from averaged voxel-based parameters and from the VOI-based parameters was relatively small, indicating a small bias from the voxel-based analysis. Even though the model used in this paper was generally able to predict the time–activity curve from different organs with high temporal resolution, discrepancies could be observed in some organs such as the liver.

FIGURE 6.

Time–activity curve measured from dynamic frames (blue dots) and fitted curves using proposed method, and fitting based on time–activity curve from VOI in 4 different organs: myocardium, brain, liver, and lung. For better illustration of delay time, corresponding blood fraction in time–activity curve was also plotted. AU = arbitrary units.

DISCUSSION

This preliminary study showed that the k₁ estimated using 90-s data generally agrees with that derived from a much longer scan (1 h). The same agreement was not found for k₂, indicating that the estimated k₂ is less accurate in shorter scans. High k₁ values were detected in some venous blood pools, such as in the jugular veins, venous sinuses, and portal veins, whereas high blood fractions were observed in arterial blood pools such as the carotid arteries (Fig. 3). The high k₁ values in some blood-pool regions were likely caused by the dispersion effects modeled by the 1T model (37). This information may yield further physiologic insights and better kinetic modeling. For instance, the k₁ in the venous blood pools of the brain may represent the combined effects of the glucose passing through the brain’s vasculature and the small extraction of tracers within the brain. The k₁ in the portal veins may also be used to develop a more accurate model for the liver. The modeling of the delay times in the kinetic model not only enabled better model fitting but also produced a delay-time image that might provide additional information—for example, as a biomarker for assessing blood delivery and vessel occlusion.

However, our method did not model the dispersion effects of the input function for different organs. Another limitation of the proposed approach is the use of a single model for the whole body. For instance, the dual blood supplies (portal veins and arteries) in the liver region (32) were not modeled. The use of a single input function resulted in some quantitative inaccuracy, and further studies are required for more accurate parametric imaging. The image-based input function in this study was also not validated using arterial blood samples, but the feasibility has already been proven in the literature (18). Because of the very concentrated and rapidly changing tracer distribution in the first few seconds after injection, scatter corrections may not be accurate enough. One possible example is the low delay time in regions near the injection site in the delay-time image. Another example is the small increase in the liver time–activity curve around 20 s after injection, which we believe was caused by the inaccurate scatter correction from the very high activity level during the injection.

Two different injection sites were used in our study. Initially the leg was chosen so that the injection site would be closer to the end of the gantry, thus requiring a shorter tube connecting the syringe and the needle; however, a major challenge in leg injection is the difficulty in finding the appropriate vein. Subsequent to the first patient, we chose to perform all injections in the antecubital fossa, which follows conventional practice and has not led to significant difficulties (38).

Although our method was developed using ¹⁸F-FDG, the same methodology can be applied to other tracers as well. More benefit can be expected for radionuclides with a much shorter half-life, such as ¹⁵O or ⁸²Rb. The acquired ¹⁸F-FDG k₁ image can also be used to examine the relationship between blood flow and metabolism, which may help with diagnosis in some pathophysiologic conditions such as hyperemic areas of brain tissue after stroke. For ¹⁸F-FDG scans, a practical implementation of the proposed approach can still be challenging, as ¹⁸F-FDG imaging traditionally focuses mostly on the later period, when equilibrium is reached. Combination with a later scan may be the solution; however, future studies are required to address the clinical or technical challenges for that protocol.

Future studies using patient data are required for a better understanding of the full potential of the clinical significance of the proposed method.

CONCLUSION

In this study, we demonstrated that with an ultra-high-sensitivity total-body PET scanner, it is possible to achieve whole-body parametric image reconstruction using only the early stage of the scan (within the first 2 min after injection), for much easier incorporation into the daily clinical route. However, only fast parameters such as k₁ can be estimated using this ultrashort scan duration. We also showed that with the much-improved temporal resolution due to improved sensitivity, organ-dependent delay time becomes an important factor to consider in the analysis of whole-body early-stage dynamics.

DISCLOSURE

Tao Feng and Hongdi Li are employed by UIH America, Inc., and Yizhang Zhao is employed by United Imaging Healthcare. Simon R. Cherry and Ramsey D. Badawi have a research agreement with United Imaging Healthcare. The University of California Davis has a revenue-sharing agreement with United Imaging Healthcare. This work was partially supported by the National Institutes of Health under grant R01 CA206187. No other potential conflict of interest relevant to this article was reported.

KEY POINTS

• QUESTION: Can whole-body first-pass parametric imaging be achieved using an ultrashort scanning protocol?

• PERTINENT FINDINGS: We have demonstrated the possibility of generating whole-body parametric images such as k₁ (a possible indicator for tumor identification), blood fraction, and delay-time images that illustrate the circulatory system, from dynamic scans of as short as 90 s using the total-body PET scanner.

• IMPLICATIONS FOR PATIENT CARE: This protocol produces added value (a potential biomarker for identification of tumors and other diseases) with minimal added scanner time.