A neural circuit state change underlying skilled movements

SUMMARY

In motor neuroscience, state changes are hypothesized to time-lock neural assemblies coordinating complex movements, but evidence for this remains slender. We tested whether a discrete change from more autonomous to coherent spiking underlies skilled movement by imaging cerebellar Purkinje neuron complex spikes in mice making targeted arm-reaches. As mice learned the task, millimeter-scale spatiotemporally coherent spiking emerged ipsilateral to the reaching arm, and consistent neural synchronization became predictive of kinematic stereotypy. Before reach onset, spiking switched from more disordered to internally time-locked concerted spiking and silence. Optogenetic manipulations of cerebellar feedback to the inferior olive bi-directionally modulated neural synchronization and reaching direction. A simple model explained the reorganization of spiking during reaching as reflecting a discrete bifurcation in olivary network dynamics. These findings argue that to prepare learned movements olivo-cerebellar circuits enter a self-regulated, synchronized state promoting motor coordination. State changes facilitating behavioral transitions may generalize across neural systems.

In Brief

Neurons switch from predominantly autonomous spiking to synchronous spiking in preparation for movement, a state change that emerges during skill learning.

Graphical Abstract

INTRODUCTION

Inspired by phase transitions of physical matter, theoretical neuroscientists have intensively studied neural network models with transitions between different dynamical states. Akin to liquid or solid matter, collective neural activity patterns in these models often defy straightforward predictions based on attributes of the constituents. The transitions are usually between a state of ordered or coherent network activity and one of more disordered activity (Chialvo, 2010; Hopfield, 1982; Rajan et al., 2010; Schneidman et al., 2006). These states can allow individual cells to have different levels of spiking autonomy and distinct timing and coding properties, and yield different behavioral outputs (Abbott and Rohrkemper, 2007; Kelso, 2012; Poil et al., 2012). Thus, it is crucial to identify state transitions and how they may re-shape cellular activity and animal behavior.

In the motor system, the active regulation and internal synchronization of neural assemblies may help coordinate the muscles for specific actions (Churchland et al., 2010; Feige et al., 2000; Riehle et al., 1997; Welsh et al., 1995). This view suggests there should be circuitry that adjusts its internal, dynamical cohesion to serve motor control. Notably, the olivocerebellum has features that might facilitate such state changes. Inferior olivary neurons have subthreshold voltage oscillations and electrical synapses that synchronize these rhythms (De Zeeuw et al., 1998; Llinás and Yarom, 1986). The resulting synchronized spikes drive synchronized complex (Na⁺ and Ca²⁺) spikes in cerebellar Purkinje cells, each of which receives potent input from one olivary climbing fiber that, when activated, reliably evokes a complex spike (Ozden et al., 2009; Schultz et al., 2009). Inhibitory feedback from cerebellum may regulate olivary cells’ electrical coupling and spiking synchrony (Best and Regehr, 2009; Van Der Giessen et al., 2008).

Synchronous complex spiking by Purkinje cells accompanies rhythmic motor behaviors (Hoogland et al., 2015; Welsh et al., 1995), but whether this represents a transition into a coherent dynamical state to coordinate skilled movements is unknown. The mere presence of synchronous activity does not imply a discrete switch into a coherent state. By analogy, a car’s wheels and engine parts move faster when the car accelerates, but this on its own does not imply the existence of a gearbox that can abruptly alter the basic temporal relationships in how the mechanical parts interact. Likewise, rhythmic spiking by Purkinje cells during rhythmic licking or locomotion might simply reflect movement-locked rhythmic inputs, not a state transition.

We studied reaching movements and looked for hallmark features of coherent dynamics and a state transition. First, if, as proposed, coherent activity supports motor coordination, one expects this coherence to increase as animals gain motor proficiency. Second, if synchronized firing truly acts as a metronome to coordinate movement, a coherent state should be internally time-locked at a finer time-scale than movement-locked changes in spike rates. Third, in a coherent state there should be cell assemblies that encode motor kinematics via their internally synchronized dynamics, not just as independent, individual cells. Fourth, one expects a circuit with coherent dynamics should have internal mechanisms to regulate synchronization.

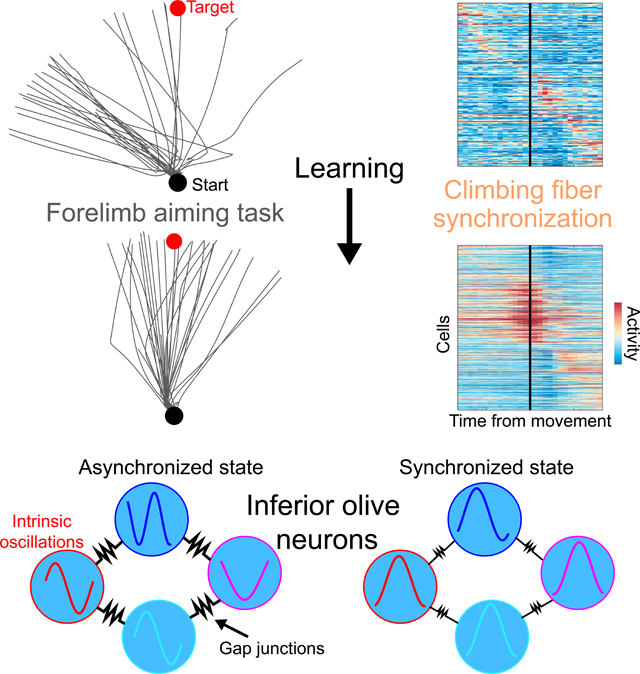
To study these facets of neural activity, we trained mice to make targeted reaches as they grasped a robotic arm. Meanwhile, we imaged Purkinje cells’ complex spiking activity in parts of the cerebellar vermis involved in forelimb control (Apps and Hawkes, 2009). As mice improved at the task, reliable neural synchronization arose across millimeter-sized areas of the vermis and was predictive of kinematic stereotypy. Starting before task execution, there was a transition into a coherent, internally time-locked state that involved a burst of synchronized complex spikes. The burst’s timing varied systematically across the cerebellar surface and was often followed by a coordinated silence among the visible Purkinje cells. When we perturbed reaching mid-trajectory, synchronized Purkinje cells signaled the disruption collectively, not as independent cells. Bi-directional manipulations of cerebellar feedback to the inferior olive led to bi-directional changes in synchronized complex spiking at reach onset, showing the olivocerebellum regulates its dynamics in a way that is gated to movement initiation.

These results argue that at onset of skilled movements the olivocerebellum switches from a baseline condition, in which Purkinje cells fire complex spikes more autonomously, to a coherent state with spatiotemporally organized activity that promotes high-quality motions. A simple model shows that this re-configuration of spiking, including enhanced synchronized spiking and concerted neural silence, likely results from a discrete bifurcation in the olivary network’s collective dynamics. This concise explanation suggests that motor circuits shift between distinct operating modes and that behavioral state changes can be triggered by more than just variations in spike rates. Instead, neural circuits can control behavioral transitions via discrete transitions in the patterning of neural activity in time and space. Such discrete transitions are analogous to those between states of physical matter, and circuits beyond the olivocerebellum may use them as a way of switching between behaviors.

RESULTS

Targeted Forelimb Reaching Task.

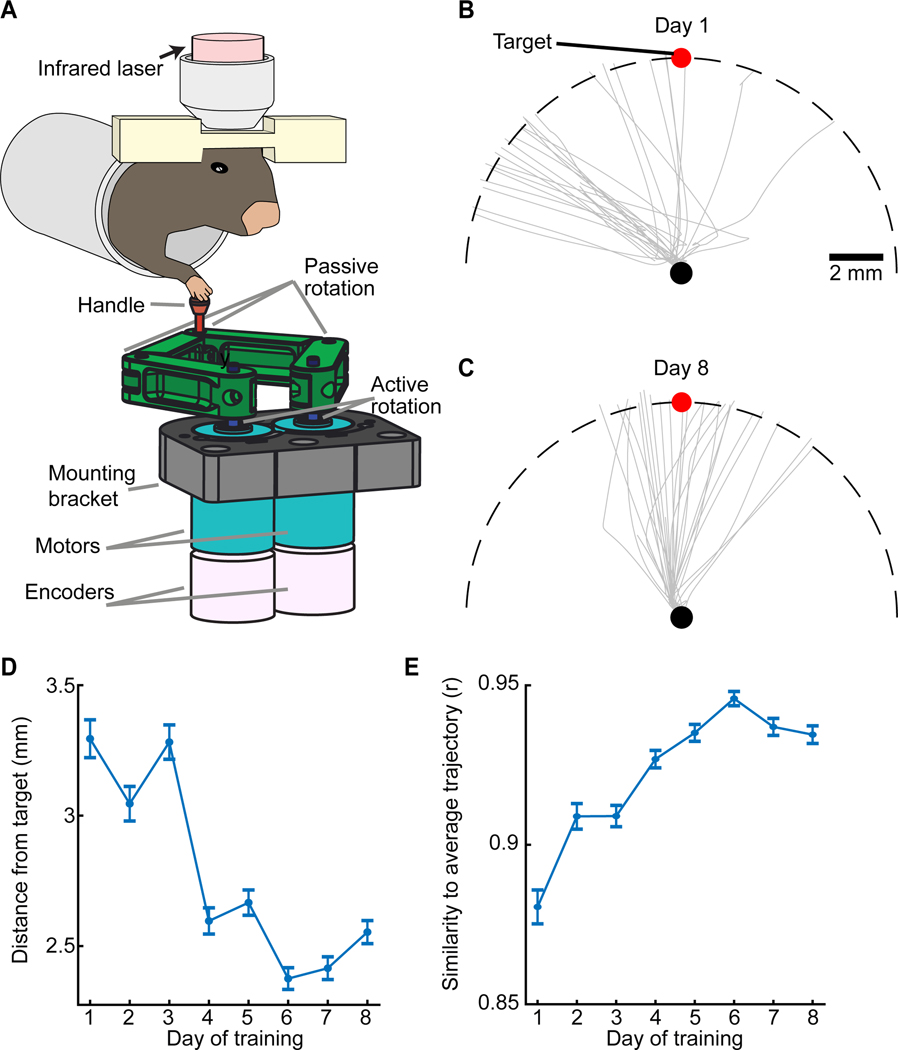
To study skilled actions, we built a robot to record (200 Hz sampling; 3–6 μm accuracy) and manipulate (1 kHz closed-loop bandwidth) movements of the robot’s handle (STAR Methods). We trained mice to direct the handle with their right forepaw from a starting position near the body to a forward target zone (Figures 1A, S1A). At first, the robot constrained reaching to a linear path. After mice trained for ~3 days, the robot allowed arbitrary motions in the forward horizontal plane (Figure 1B,C), and mice received a reward 1 s after well-targeted reaches. Early in learning, reaching was often off-target, but with training (5–11 days) targeting errors and kinematic variability declined (Figure 1B–E, S1B–G). By their last session, mice made 283±28 reaches per session (mean ± SEM; 18 mice), and reaching took 202±62 ms (mean±s.d.).

Figure 1. A Targeted Arm-Reaching Task.

(A) During Ca²⁺ imaging, mice directed a robotic manipulandum toward a target zone.

(B, C) Gray curves: Paw trajectories on 25 trials by an example mouse on training days 1 (B) and 8

(C). Black and red dots: Start and target positions, respectively. Dashed curve: 8-mm-distance at which the robot halted movement.

(D). Mean lateral displacements between reach endpoints and target location.

(E). Reaching stereotypy, assessed by the correlation coefficient of individual reaching trajectories to each day’s mean trajectory (p<10⁻⁶; rank sum test between Days 1, 8; n=8 mice; 1105–1688 total trials per day). Error bars: SEM. See Figure S1.

Millimeter-scale Synchronized Complex Spiking Emerges with Reaching Proficiency.

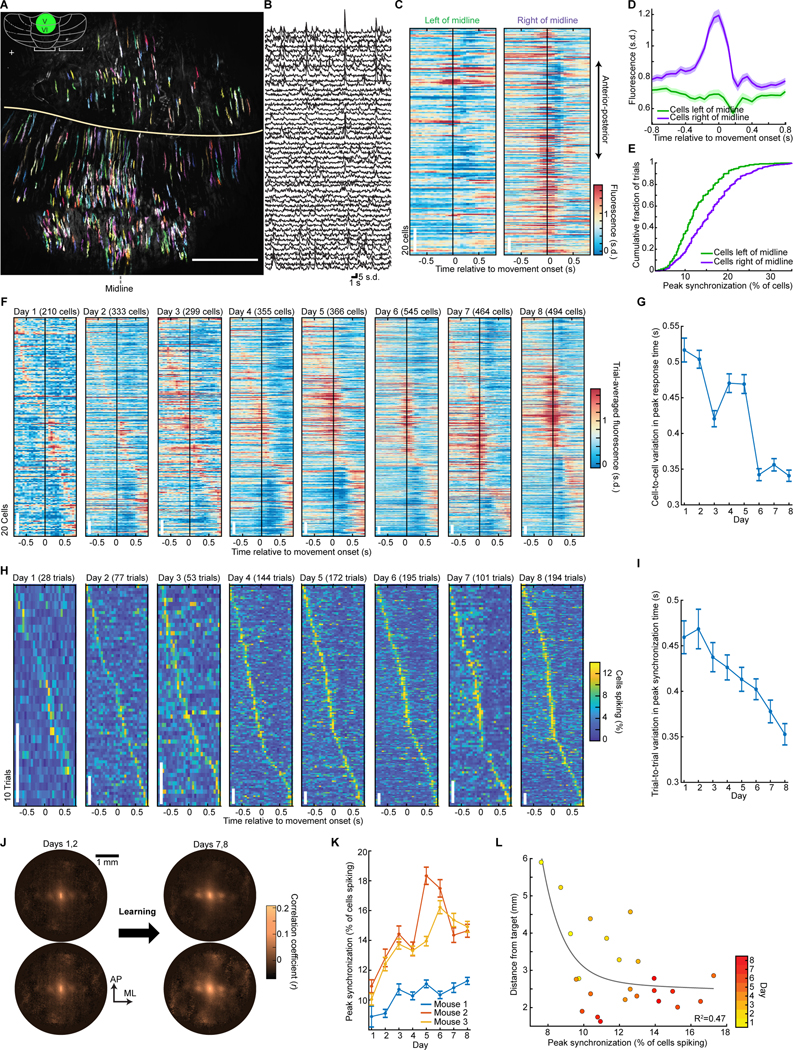
To survey Purkinje cell dynamics, we used a two-photon mesoscope with 16 laser beams (Rumyantsev et al., 2020) to image a 4-mm²-area of the vermis (lobules V and VI). While this area is likely heterogeneous, much of it receives afferents from and is activated by ipsilateral forelimb movements (Diedrichsen et al., 2005; Jörntell et al., 2000; Pasalar et al., 2006; Wagner et al., 2019). Ca²⁺-imaging in Purkinje cell dendrites reliably reports complex spikes (Mukamel et al., 2009; Ozden et al., 2009; Schultz et al., 2009), and we thereby tracked complex spiking for 8 days as mice learned the reaching task (332±19 cells per session; mean±SEM, 24 sessions; 3 mice; Figure 2A–L).

Figure 2. Ca²⁺-spiking with Millimeter-scale Coherence Arises with Motor Learning.

(A) Using a mesoscope, we imaged Purkinje cell Ca²⁺-spiking activity in lobules V and VI (area in green, inset) of PCP2-Cre/Ai148 mice. 494 cells from one mouse are shown in color.

(B) Ca²⁺ activity traces of 50 cells.

(C) For all cells in A, each row shows one cell’s activity relative to reach onset, averaged over all (194) trials.

(D) Mean Ca²⁺ activity for cells right or left of the midline, averaged across all cells and trials from the final session in 3 mice. Cells right of midline had greater peak activity (p<10⁻⁶; rank-sum test; 453 and 698 total cells left and right of midline). Shading: SEM.

(E) Cumulative distributions of the peak fraction of cells that spiked concurrently during reaching. Peak synchronization was higher right of midline (p<10⁻⁶; Kolmogorov-Smirnov test; 590 trials; 3 mice on their last session).

(F) With motor training, cells developed similar activity patterns. For an example mouse, each plot is for one day; each row shows one cell’s activity relative to reach onset, averaged across trials. Cells are sorted by time of peak activity.

(G) Variability between different cells’ dynamics declined with learning. We identified the time at which the greatest number of cells had their peak activity. We then computed the mean interval between this time and when individual cells had their peak activity. Error bars: SEM across all cells (3 mice). Timing variability was lower on Day 8 than Day 1 (p<10⁻⁶; rank-sum test; 606−1173 cells per day).

(H) With training, cells’ dynamics grew more synchronized and stereotyped. For the mouse of F, each row shows, for one trial, the percentage of cells spiking synchronously (trials sorted by time of peak synchronized activity).

(I) Across learning, trial-to-trial variations declined regarding the time at which peak synchronized activity arose. For each trial we identified the time bin with the greatest percentage of active cells. For each mouse and session, we also computed the time bin at which the greatest number of trials exhibited their peak synchrony. The differences between this identified time bin and the time of peak synchrony on single trials were lower on Day 8 than Day 1 (p<10⁻⁶; rank-sum test; n=273–655 trials per day). Error bars: SEM over trials.

(J) Spatial cross-correlations of spiking activity, averaged over all cell pairs with a given spatial separation, early or late in training and for reaching vs. inter-trial periods (24 total days; 3 mice). Millimeter-scale correlations rose with learning.

(K) Mean ± SEM peak percentages of cells that spiked concurrently in a 25 ms time bin within ±800 ms of reach onset.

(L) Mean distances between reach endpoints and the target negatively co-varied with the mean peak synchronization of Ca²⁺ spiking. Each datum is from one mouse, on one day (24 total days; 3 mice). Black curve: double exponential fit.

See Figure S2.

Early in learning, complex spiking was weakly time-locked to reaching, and there was little temporal consistency between different cells (Figure 2F). As learning progressed, cells in the right vermis gained more stereotypical and time-locked responses to the reaching motion (Figure 2C–E), consistent with their preferential control of ipsilateral body parts (Apps and Hawkes, 2009; Gao et al., 2012). Purkinje cells in the right vermis also grew more homogenous in the timing of their responses, starting before motion onset (Figure 2D,F,G). Left vermis Purkinje cells were far less synchronized (Figure 2C–E).

With motor learning, Purkinje cells’ dynamics grew more correlated with those of other cells up to ~1 mm away, especially during reaching (Figures 2J, S2A–D). The spatiotemporal coherence of complex spiking activity rose with learning, such that the mean time lag between closely timed complex spikes rose with the distance between cells, as if a wavefront of increased spiking probability propagated ~1 mm or more across cerebellar cortex (Figure S2E–J). Propagation was usually aligned within ~10° of the anterior-posterior axis (mean±SEM speed: 10±0.2 μm/ms), more commonly from anterior to posterior (Figure S2H).

To analyze synchronization on single reaching trials, we examined the fraction of visible Purkinje cells that was active at each time point. Early in learning, cells were weakly synchronized, and the timing of peak synchronization varied greatly trial-to-trial; later in learning, synchronization became stronger, more stereotyped (Figure 2H–K) and spatially organized (Figure S2I,J). Mean levels of peak synchronization rose with learning and correlated with improved reaching performance (Figure 2K,L). Thus, Purkinje cells’ task-locked and synchronized activity developed with experience and was not just a generic reflection of movement but instead reflected trained proficiency.

Neural Synchronization is Predictive of Movement Stereotypy.

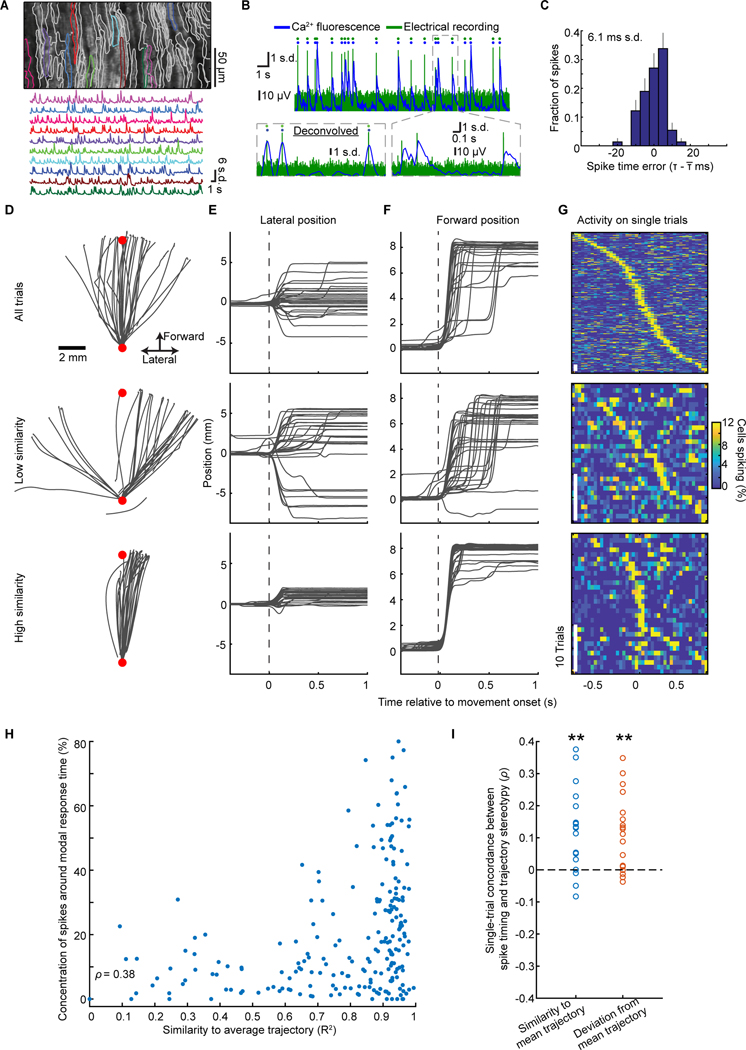
If synchronization reflects internal timing signals for motor coordination, it should be related to kinematic output. To test this idea, we studied how synchronization relates to reaching kinematics in expert mice. For these and all subsequent studies, we sought recordings of finer time-resolution and used a conventional two-photon microscope for Ca²⁺-imaging in zone AX of lobule V in the right vermis (110 μm × 270 μm fields-of-view; 46±4 Purkinje cells (mean±SEM) per session; 695 cells total in 15 mice; Figure 3A). In rodents, this area is a main recipient of forelimb-related input and is homologous to the forelimb-related X vermal and C1/C3 paravermal zones in other species (Apps and Hawkes, 2009; Buisseret-Delmas et al., 1993; Garwicz et al., 1998; Jörntell et al., 2000). To study the timing accuracy of these data, we made joint optical and electrical recordings of individual cells. There was >90% concordance across the two sets of complex spikes (5 dual recordings; Figures 3B,S3). Using sub-image-frame timing data, optical recordings yielded spikes within ±6−11 ms (s.d.) of those recorded electrically (Figure 3C). Given this accuracy, all further analyses used 25-ms-time bins, to evaluate synchrony at timescales finer than those of forelimb motion.

Figure 3. Complex Spike Synchronization Covaries with Movement Stereotypy.

(A) Top, Perimeters of Purkinje cells’ dendritic trees atop a mean two-photon image of cerebellar cortex. Bottom, Ca²⁺ traces for 10 cells colored in top panel.

(B) Example dual electrical and fast line-scanning Ca²⁺ recordings. Rasters mark identified spikes. Insets: Magnified views of 3 spikes in raw (right) and deconvolved (left) optical traces.

(C) Histogram of spike timing errors for the cell in B (s.d.:6.1 ms; 152 spikes). Error bars: s.d. estimated based on counting errors.

(D–F) Top, Example reaching trajectories, (D), chosen randomly from one mouse’s trials, and their lateral (E) or forward (F) time-dependence. Middle, bottom panels show 30 trajectories that were most dissimilar (middle) or similar (bottom) to the mean trajectory. Red dots: Start and target locations.

(G) For trials of D–F, each row shows the time-varying synchronized complex spiking on one trial. Stereotyped reaching trials were more likely to have synchronized spiking at motion onset.

(H, I) For the mouse of D–G, we assessed movement stereotypy by scoring trials (individual data points; H) by their similarity (R²) to the mean trajectory (x-axis), and the fraction of cells that spiked at the cell population’s most common response time (y-axis; p<10⁻⁶; Spearman’s ρ=0.4; 219 trials). I, Spearman’s ρ, computed as in H for 18 mice (blue points). Using the RMS-deviation from the mean trajectory (orange points) as a stereotypy metric led to nearly the same results (**p=0.002; signed-rank test for non-zero median).

See Figures S3, S4.

For each mouse, we ranked trials by how similar the reaching motion was to the mean trajectory, averaged over all trials (Figures 3D–F, S4). Trials with the most stereotyped kinematics had much greater homogeneity in the pattern and timing of neural synchronization than the lowest-ranked trials (Figures 3G, S4D,I). Across trials, greater kinematic stereotypy was predictive of increased concerted spiking at the neural ensemble’s most likely response time (Figures 3H,I and S4E,J–L). Thus, the temporal patterning of synchronization covaried with single-trial kinematics, in line with the result that neural synchronization and reaching stereotypy rose in parallel across learning (Figures 1,2).

Synchronized Spiking and Concerted Neural Silence are Associated with Reaching.

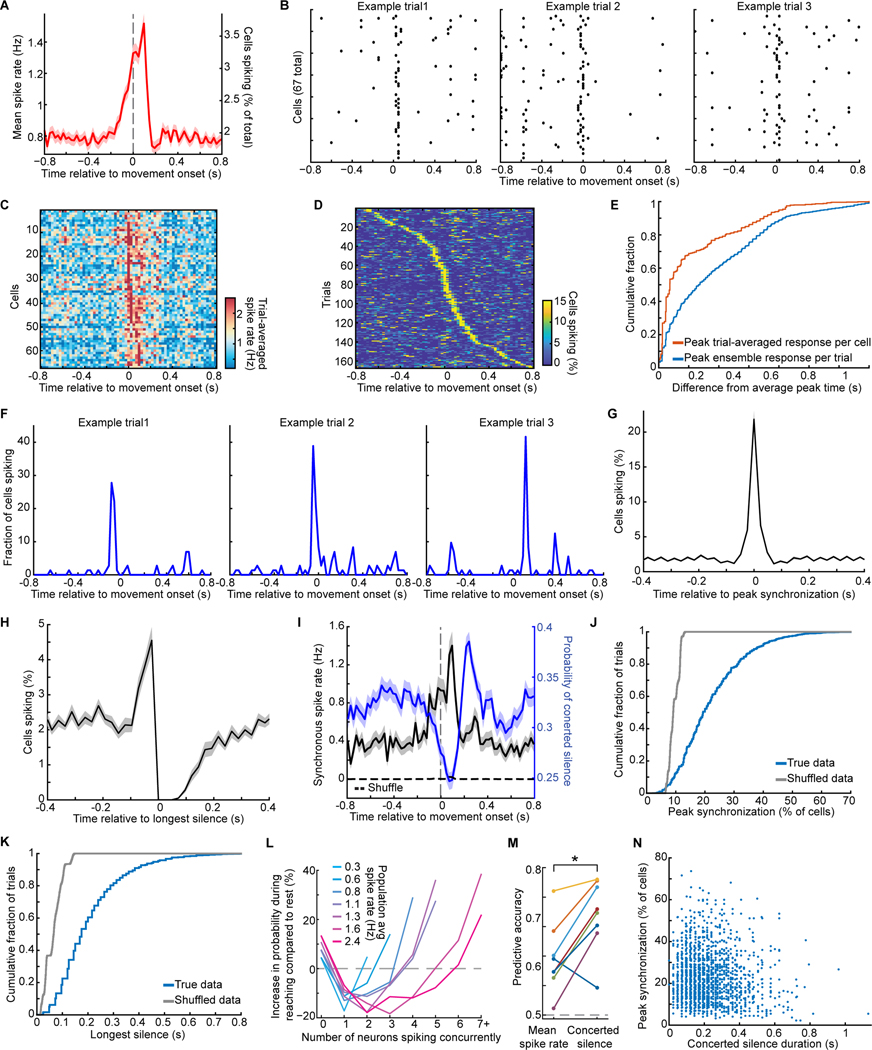
On many trials, widespread synchronized spiking arose at reach onset (Figure 4A–I), in line with reports of complex spike synchronization prior to locomotion (Hoogland et al., 2015). Different cells had similar trial-averaged spiking patterns, but there were notable trial-to-trial variations in synchronized spiking that were shared across cells (Figure 4B,D–F). Thus, cell-to-cell variations in trial-averaged activity were less than trial-to-trial variations in the timing of peak synchronized spiking, indicative of coherent spiking that arose at slightly different times on different trials but had a sharp temporal profile whenever it arose (Figure 4G).

Figure 4. Synchronized Spiking and Concerted Silence Arise During Reaching and Reflect Intrinsic Synchronization, Not Task-related Changes in Spiking.

(A) Complex spike rates rose before reach onset (averaged over 695 cells, 2552 trials by 15 mice).

Shading: SEM across trials.

(B) Spike raster plots for 67 cells and 3 trials of one mouse reveal synchronized spiking near reach onset, then a global silence.

(C, D) Trial-averaged spike rates, (C), and time-varying percentages of cells spiking synchronously on single trials, (D), for cells of B.

(E) Cumulative distributions reveal greater trial-to-trial variability in the timing of peak synchronization (blue curve) than cell-to-cell variability in the times of peak activity in trial-averaged traces (orange curve) (p<10⁻⁶; Kolmogorov-Smirnov test; 2552 trials as in A), indicative of a coherent state in which large sets of cells spike concurrently, but at times that vary trial-to-trial relative to reach onset.

(F) Example traces of the fraction of cells that spiked on different trials, with peak synchrony before, at, or after reach onset.

(G,H) Spiking synchronization within −0.4–0.4 s of each rtial’s time of peak synchronization, G, or onset of each trial’s longest concerted silence, H, averaged across all trials for each mouse, and then across mice. Shading: SEM over 15 mice.

(I) Rates of synchronous spiking (>20% of visible Purkinje cells; black trace) and full-field concerted silence (blue trace), averaged over the 2552 trials of A. Trial-shuffled data (dashed trace) had almost no synchronous spiking. Shading: SEM across trials.

(J, K) Cumulative distributions across all trials of peak synchrony levels, J, and the longest concerted silence, K. (p<10⁻⁶ for real vs. trial-shuffled datasets; Kolmogorov-Smirnov tests; 2552 trials).

(L) Percentage changes in the probabilities of 0–7 cells spiking together in the same 25-ms time bin, for reaching vs. resting epochs, in periods with different spike rates (8 mice; >2,500 time points per curve). Reaching suppressed events with 1 (p<6×10⁻⁴), 2 (p<5×10⁻⁴ for all firing rates ≥0.8 Hz), or 3 active cells (p<4×10⁻⁴ for rates ≥1.6 Hz; chi-squared test; 1,693 reaches; 302 cells; 8 mice), but boosted concerted silence and large-scale synchronized spiking.

(M) In a receiver operating characteristic analysis, concerted silence better discriminated resting epochs vs. reaching (100–400 ms after reach onset) than mean spike rates (p=0.016; signed-rank test; 8 mice).

(N) Magnitudes of concerted silence and synchronous spiking on single trials (individual points) were uncorrelated (p=0.22; 2552 reaches, 15 mice).

See Figures S5.

To characterize the mean time-dependence of synchronized spiking, we identified times at which ≥20% of all visible Purkinje cells spiked in the same 25-ms time bin. This revealed, on average, a substantial rise in synchronization starting just prior to movement (Figure 4I). Individual cells partook in ~20–40% of these synchronized events (28±12%; mean±s.d.; 695 cells), preferentially so with other nearby cells (Figure S5A,B). However, a cell’s participation in synchronized spiking depended little on its mean spike rates during rest or reaching (Figure S5C–E).

During reaching trials there also arose periods of neural silence (~200–300 ms duration) across the full field-of-view (Figures 4B,F,H and S5F). We termed this ‘concerted silence’; like synchronized spiking it arose sharply in time, without a preceding gradual change in spike rates (Figure 4H). Concerted silence was substantially more likely to arise within ±0.8 s of reach onset than in inter-trial intervals (Figure S5G; p=6×10⁻⁵; signed-rank test; 15 mice). Within this 1.6-s-interval, silence was only modestly more likely to occur ~200 ms after reach onset than beforehand (Figure 4I), suggesting it was associated with task execution but not necessarily with a specific facet of reaching motion.

Synchronized Spiking and Silence are Intrinsically Generated

To determine if concerted spiking and silence reflected intrinsic synchronization, or if cells had similar but independently modulated spike rates, we randomly shuffled cells’ activity traces across trials. This is an established way to distinguish task-driven from internally time-locked synchrony; trial-shuffling preserves the former but not the latter form of synchrony and allows one to account for the expected rise in coincident spikes that simply comes from elevated spiking (Cafaro and Rieke, 2010). In our stereotyped motor task, shuffling preserves spike timing with respect to the behavior but not single-trial correlations between cells at fine time-scales. To control for variations in motor output, we restricted shuffle analyses to reaches >6 mm in extent and <3 mm from the target.

The shuffled data showed only very weak, time-invariant synchronization (Figure 4I and S5H–J), and the maximal synchronized spiking event and longest concerted silence (Figure 4J,K), as computed on individual trials, were both far lower than in real data. We also found the rates at which Purkinje cells fired 0–5 or more complex spikes concurrently in real vs. shuffled data (Figure S5K). The real data had reduced activation of 1–2 cells at a time but more concerted silence and co-activation of ≥4 cells (increased silence and spiking by ≥4 cells, p<0.001; permutation test). Thus, nearly all coherent dynamics in the real data were intrinsic and unaccounted for by task-related spiking increases.

To check if body movements besides reaching might have influenced these results, we analyzed behavioral videos taken during Ca²⁺ imaging and found scant differences in neural synchrony between trials with varying levels of body motion (Figure S5L–S). Trial-shuffling analyses restricted to trials with very similar body motions verified that a vast majority of synchronization was internally time-locked and did not arise from movement-locked changes in spiking (Figure S5S).

Coherent Neural Dynamics Reliably Indicate the Reaching State.

Is neural synchronization specific to reaching periods? To study this question, for a subset of expert mice we identified periods between reaching trials with no visible body motion. We then matched resting and reaching epochs with comparable spike rates and compared the rates at which different numbers of Purkinje cells spiked together. Versus matched periods of rest, reaching suppressed small-scale activation involving 1, 2 or 3 co-active cells (Figure 4L; 8 mice, 302 cells, 1693 reaches). Reaching epochs also exhibited more concerted silence (p<10⁻⁷; chi-squared test) and more frequent co-activation of ≥4 cells (p<6·10⁻⁴ for all firing rates >0.8 Hz).

Given the increased concerted silence during reaching, was it a better indicator of reaching than typical metrics such as mean spike rates? We evaluated ensemble mean spike rates and the total amount of concerted silence and found the latter to be a superior marker of reaching (Figure 4M, p=0.016; signed-rank test; 8 mice). Given this and the increased synchronized spiking with reaching, we expected levels of concerted silence and synchronized spiking to be correlated trial-by-trial. Unexpectedly, this was not so (Figure 4N), ruling out a simple interpretation of concerted silence as a refractory period after synchronous spiking.

Co-Activity of Molecular Layer Interneurons Accompanies Concerted Silence in Purkinje Cells.

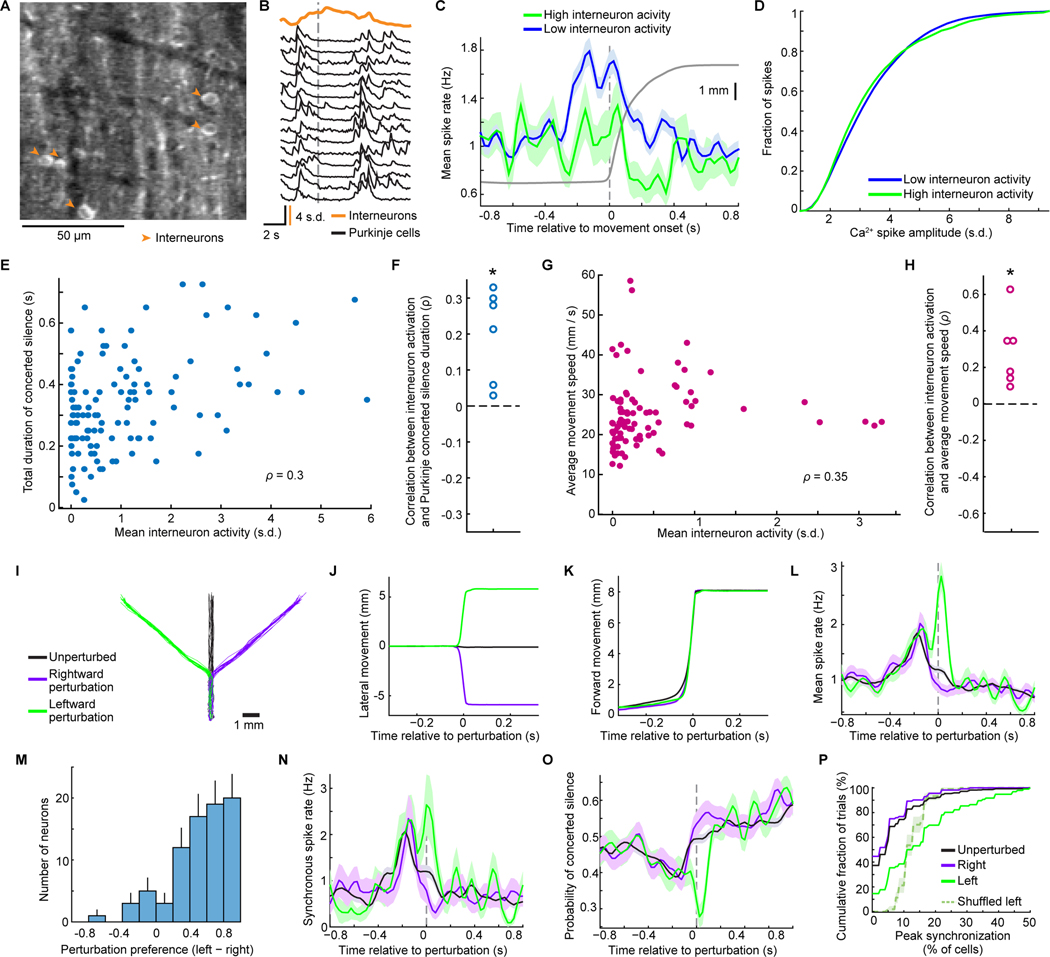
To explore mechanisms for concerted silence, we jointly imaged Purkinje cell dendrites and somatic Ca²⁺ activity in molecular layer interneurons, which inhibit Purkinje cells. On some reaching trials, activation of all visible interneurons accompanied concerted silence in Purkinje cells (Figure 5A,B). These trials also had lower complex spike rates, without affecting the magnitudes of Purkinje cells’ Ca²⁺ spikes (Figure 5C,D). Greater interneuron activity was significantly correlated with faster movement speeds and longer episodes of concerted silence (Figure 5E–H). Thus, interneuron activation and Purkinje cell concerted silence likely reflect a common aspect of network synchronization, with the inhibitory inputs likely extending Purkinje cells’ silent epochs (Discussion).

Figure 5. Interneuron Activation Accompanies Concerted Silence in Purkinje Cells and Purkinje Cell Populations Encode Movement Perturbations.

(A) In some mice, GCaMP6f expressed in both Purkinje cells and molecular layer interneurons (marked by arrowheads in a mean two-photon image).

(B) A rise in Ca²⁺ activity summed across interneurons (15 cells; orange trace) coincided with concerted silence in all 46 visible Purkinje cells in an example mouse (traces shown for 15 cells). Vertical line: onset of forelimb reaching.

(C) Mean rate of complex spiking by Purkinje cells (6 mice) on trials when interneurons were highly or weakly active (105 reaches with interneuron activity >1 s.d. above the mean, 525 reaches with interneuron activity less than the mean within −500 to 500 ms of reach onset; 62 interneurons; 219 Purkinje cells; 1048 trials).

(D) Cumulative distributions of Ca²⁺ spike amplitudes across trials with high (green) or low (blue) interneuron activity levels.

(E,F) For an example mouse, E, mean interneuron activity on individual reaching trials (points) covaried with the duration of Purkinje cell concerted silence (119 trials, p=0.0009, permutation test for Spearman correlation). F, Results for all 6 mice (*p=0.03 signed-rank test).

(G, H) Movement speed vs. mean interneuron activation on individual trials, G, for the mouse of E (p=0.008), showing that interneuron activation was predictive of faster movements. Results from 6 mice, H, (*p=0.03 signed-rank test).

(I) In the perturbation task, the robot displaced forward-constrained reaches on a random 25% of trials (12.5% each to the left or right). Traces: 20 trajectories of each type.

(J, K) Mean trajectories decomposed into lateral, J, and forward motion, K, for the mouse in I.

(L) After the perturbation, mean spike rates were greater for leftward perturbations (p<10⁻⁶comparing the 50 ms after the perturbation for 113 rightward vs. 115 leftward trials; 780 unperturbed trials; 80 cells; 3 mice in L–P; rank-sum test). Dashed vertical line: Occurrence of a 4 mm lateral deviation.

(M) Histogram of individual cells’ perturbation preferences, (R_left–R_right)/(R_left+R_right), where R is the cell’s mean spike rate from 0−50 ms after the perturbation. Error bars: s.d. estimated based on counting errors.

(N, O) Trial-averaged rates of synchronized spiking (with ≥20% of visible cells), N, and concerted silence, O. Leftward perturbations induced more synchronized spiking (p<10^–6 rank-sum test).

(P) Cumulative distributions of the largest set of cells spiking concurrently 0−50 ms after the perturbation. Trial-shuffled data had less synchrony (p=0.01; permutation test).

Shading in C,J–L,N,O: SEM over trials.

Ensemble Neural Encoding of Movement Perturbations.

To examine how internally synchronized neural dynamics might impact kinematic encoding, we tested whether cell ensembles convey signals that are not fully decipherable from single cell recordings. We studied a classic movement variable, unexpected self-motion (Brooks et al., 2015; Brooks and Cullen, 2013), by using the robot to confine arm reaches to linear paths and perturb them mid-trajectory.

On most trials, the robot enforced a forward trajectory, but on a random subset of trials, midway through the reach the robot deflected the mouse’s paw left or right (Figure 5I,J). Forward motion was indistinguishable on these 3 trial-types (peak speed: 109±3 mm/s, 105±3 mm/s and 108±2 mm/s, respectively, in 113 rightward, 115 leftward and 772 unperturbed trials by 3 mice; Figure 5K). Strikingly, most Purkinje cells in the right vermis responded preferentially to leftward perturbations, after which both spike rates and synchronized spiking rose to significantly higher levels than after rightward perturbations or on unperturbed trials (Figure 5L–N). Thus, like studies of eye movements (Herzfeld et al., 2015), our data show that complex spiking responses to unexpected perturbations can be lateralized. Apart from the brief period of elevated spiking after leftward perturbations, concerted silence was the same in all conditions (Figure 5O).

Given the high level of motion stereotypy enforced by the robot, we performed a trial-shuffling analysis. In real data, leftward perturbations evoked time-locked spikes from up to half the cells, whereas in shuffled data the perturbation-locked spiking responses led to synchronized spiking by only ~10–20% of cells (Figure 5P). Thus, Purkinje cells’ large-scale responses to an unexpected perturbation were synchronized internally, not just by the perturbation.

Cerebellum Feedback to the Olive Regulates Synchronization and Reach Targeting.

Given the evidence the olivocerebellum switches into a coherent state during skilled reaching, we examined how the network might regulate this transition. We focused on the inhibitory shunting feedback from the deep cerebellar nuclei to the olive. This pathway may modulate the synchrony of olivary spikes, and thereby of Purkinje cell complex spikes (Lefler et al., 2014), but what role this feedback has during voluntary motion has been unknown.

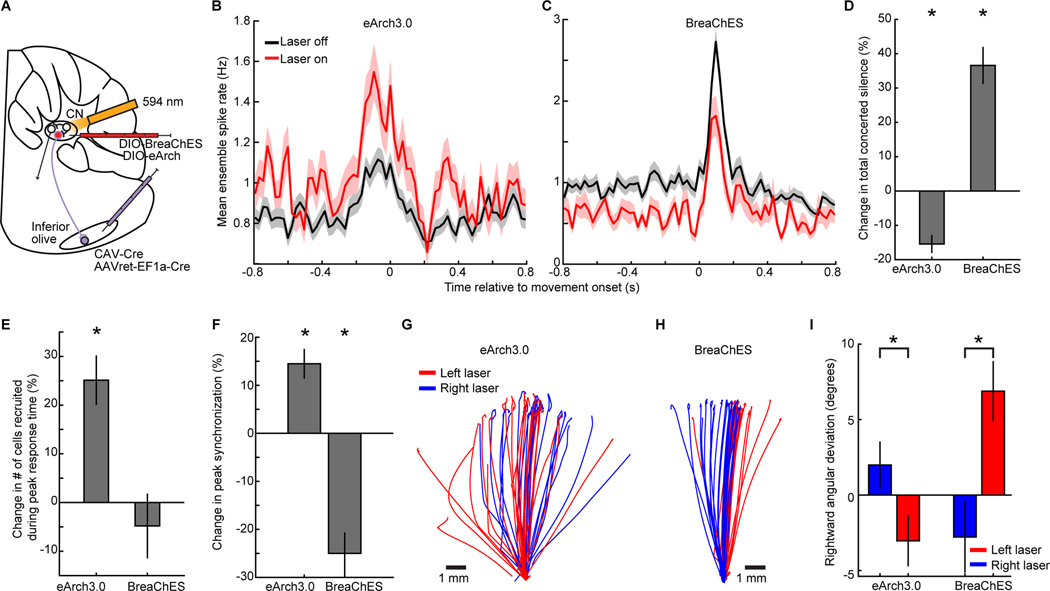
To photo-inhibit or -excite this pathway during reaching, we expressed an opsin in olive-projecting cells of the cerebellar nuclei (Figure 6A, S6A,B). On a random subset (20–30%) of trials we illuminated the cerebellar fastigial nucleus from before reaching until after its completion. Inhibition of the nucleo-olivary pathway boosted mean complex spike rates and peak levels of complex spike synchronization, in a way that was accentuated at reach onset, while decreasing the frequency of concerted silence; photo-excitation of this pathway had the opposite effects (Figure 6B–F). Photo-inhibition also led spiking to become more concentrated in time (Figure 6E).

Figure 6. Cerebellar Feedback to the Inferior Olive Regulates Purkinje Cell Synchrony.

(A) To retrogradely target axons of fastigial nuclear cells, we injected Cre-expressing virus bilaterally (7 mice) or in the left inferior olive (3 mice). To inhibit or excite feedback to the olive, fastigial nuclei received virus for Cre-dependent expression of, respectively, eArch3.0 (7 mice; 4 bilateral, 3 ipsilateral to the reaching paw) or BreaChES (3 mice bilaterally) and 594-nm-laser light.

(B,C) Mean complex spike rates in Purkinje cells on reaching trials without vs. with fastigial inhibition (B; 1268 laser-off, 374 laser-on trials; 7 mice) or excitation (C; 547 laser-off, 147 laser-on trials; 3 mice). (20–30% probability per trial of laser activation; illumination lasted across the trial).

(D,E) Inhibiting the feedback pathway reduced the total duration, D, of concerted silence; excitation increased it (*p<10⁻⁶; signed-rank tests in D–F; y-axes show changes from mean levels during laser-off trials in each mouse). Inhibiting the feedback also raised (*p=0.0006) the fraction of cells, E, that spiked on each trial at the modal response time, computed as in Figure 3.

(F) Peak levels of complex spike synchronization were boosted by inhibition and reduced by excitation of the feedback pathway (from the studies in B,C, p=0.003 for inhibition; p<10⁻⁶ for excitation).

(G–I) Right paw trajectories of mice with bilateral fiber-optic implants during inhibition (G) or excitation (H) of the left or right feedback pathway (random 20% of trials each). (I), Unilateral inhibition (excitation) biased motion in the direction ipsilateral (contralateral) to the illuminated nucleus (*p=0.01 for eArch3.0; 3×10⁻⁶ for BreaChES, for left (91 trials) vs. right (86 trials) illumination in 4 mice with eArch3.0, or 75 left vs. 68 right illumination trials by 3 mice with BreaChES; rank sum test).

Shading and error bars in B–F,I: SEM over trials.

See Figure S6.

To test if perturbing nucleo-olivary signaling would impact reaching, we unilaterally illuminated the left or right fastigial nucleus. Unilateral nucleo-olivary inhibition biased forelimb motion in the ipsilateral direction, i.e. in the direction of the illuminated nucleus; unilateral excitation led to the opposite, contralateral targeting bias (Figure 6G–I). Neither bilateral excitation nor inhibition altered reaching (Figure S6C), suggesting that reach targeting may be more sensitive to the balance of activity across the two feedback pathways than to its absolute levels. Unilateral excitation of the right (but not the left) fastigial nucleus, ipsilateral to the reaching forelimb and the Ca²⁺ imaging site, reduced complex spike synchronization (Figure S6D). Thus, the nucleo-olivary pathway regulates complex spiking and its coherence, and the bilateral balance of these effects influences reach targeting.

A Simple Model of the Olivary Network Has a Bifurcation that Re-organizes Spiking Patterns.

The discrete changes to system properties that occur at state transitions are often well described by concise mathematical models that capture the essence of a phenomenon. Well-known successes include bifurcations in predator-prey relationships, and phase transitions and critical phenomena of physical matter (Strogatz, 2015).

Given these past successes, the rhythmicity of olivary cells and their propensity to synchronize (De Zeeuw et al., 1998; Llinás and Yarom, 1986), we explored if a simple olivary network model of Kuramoto oscillator cells might capture our core results about complex spikes and their temporal re-organization during reaching. Kuramoto models have a set of phase oscillators, each with its own natural frequency, that are coupled together (Kuramoto, 1984). These models describe synchronization-desynchronization transitions in a range of systems and some versions exhibit bifurcations in their dynamics and wavelike phenomena (Acebrón et al., 2005)

In our treatment, the Kuramoto oscillators represent olivary cells, each with an intrinsic sub-threshold oscillation around 10 Hz (±2 Hz). Spiking occurs when excitatory inputs or noise drive the voltage above a threshold value. The level of phase synchronization is controlled by the coupling amplitude, κ (Figure 7A); in real olivary networks, inputs from the cerebellar nuclei modulate this coupling strength. We first modeled our data from conventional two-photon microscopy, in which the imaged Purkinje cells likely received inputs from highly coupled olivary cells (Bazzigaluppi et al., 2012a).

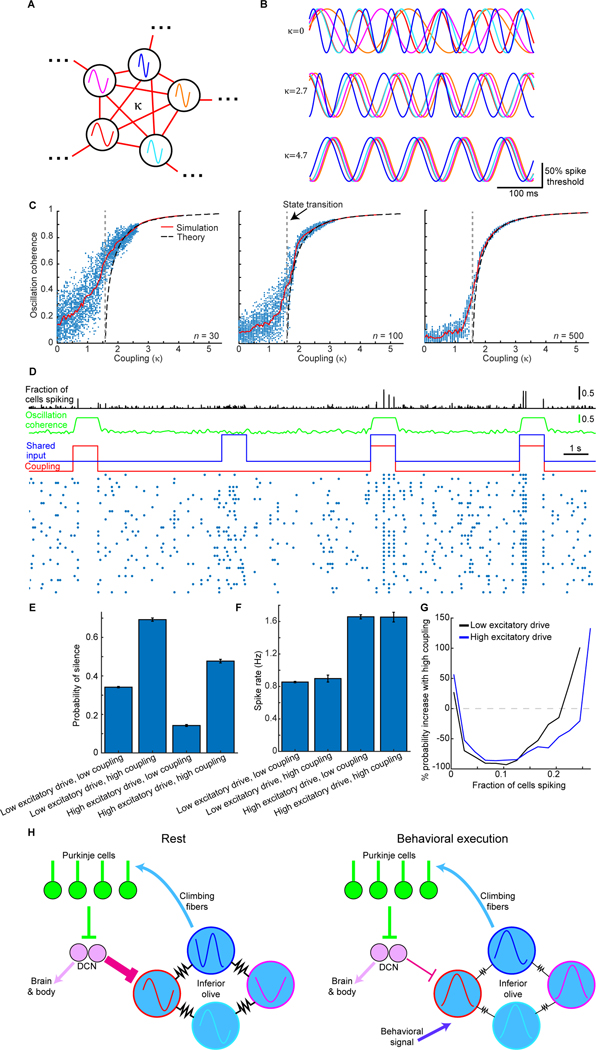
Figure 7. A Network of Kuramoto Oscillator Cells Exhibits a Dynamical Bifurcation and Captures Key Facets of Purkinje Cell Complex Spiking Before and After the State Transition.

(A) We simulated a network of olivary cells, each with a natural frequency of sub-threshold oscillation, chosen from a normal distribution (10 ± 2 Hz (s.d.)). The electrical couplings between cells, κ, sets the phase coherence and has units normalized by the frequency dispersion (2 Hz).

(B) 5 cells’ oscillations at different κ values. At high κ, cells adopt a common frequency and phase.

(C) Oscillatory coherence vs. κ, for networks of 30, 100 or 500 cells. Each datum shows the coherence at one 2-ms-time-step. Red curves: Median coherence values. Dashed black curves: Predictions from a mean field theory of the Kuramoto model (Acebrón et al., 2005). The theory has a bifurcation, in which the network switches from incoherent to coherent oscillations as κ exceeds a critical value (1.6; dashed vertical line). With finite numbers of cells, the state transition approximates the discrete bifurcation (compare red vs. black curves).

(D–F) For a spiking model (100 cells), D, with sub-threshold noise and ~1 Hz spike rates, rasters (blue dots) show spikes for 30 example cells in 25-ms-time bins. When κ (red trace) rose from a value below (0.8) to above (4.7) the bifurcation in C, mimicking how fastigial inputs would affect gap junctions, oscillatory coherence (green trace) rose. Olivary cells also shared excitatory input (blue trace) with transient rises (1.4% of spike threshold). When coupling and input changes coincided, synchronized spikes (black trace), concerted silence (75 ms periods with no spikes), E, and spike rates, F, all rose, as in real data. Acting alone, neither transient change led to all 3 rises (E,F). Concerted silence was more likely at high κ, at both high and low levels of shared input (p<10⁻⁶; rank-sum test; 200 repetitions (1 s each) per condition). Error bars: SEM.

(G) Changes in probabilities of differently sized synchronized spiking events (25 ms time bins) when κ rose from below to above its critical value, at low (black) or high (blue) shared input levels. Mimicking changes at reach onset (Figure 4L), synchronized spikes in small cell sets declined (p<10⁻⁶; rank-sum test; events with 1–15% of cells) but grew more likely in large sets (p<10⁻⁶; events with ≥30% of cells).

(H) Putative olivocerebellar dynamics at rest vs. task execution. Olivary cells share gap junctions (resistors) and send climbing fibers to Purkinje cells that inhibit deep cerebellar nuclei (DCN) cells. DCN cells shunt (magenta projection) the olivary gap junctions. At rest, when shunting is strong, olivary cells’ coupling is weak and their oscillations desynchronize. At task execution, excitatory drive (dark blue) and spike rates rise in the olive, and shunting declines, which synchronizes the oscillations.

See Figure S7.

In the model, when κ is low, olivary cells oscillate incoherently. As κ rises, the cells converge to a common frequency and phase (Figure 7B). A mean-field theory treatment shows the network has 2 operating modes: when κ exceeds a critical value there is a bifurcation inducing a switch from asynchronized to synchronized activity (Figure 7C). This state transition is one physicists term ‘second-order’, since the mean oscillatory coherence is a continuous function of κ, but its derivative is discontinuous, as seen by the steep rise in coherence as κ exceeds its critical value. Networks with a finite set of olivary cells had a transition approximating this bifurcation (Figure 7C).

To identify how a rise in κ at reach onset might alter complex spiking, we compared our model’s operating modes by transiently raising κ from below to above its critical value (Figure 7D). This increased synchronized spiking and concerted silence while leaving spike rates unchanged (Figure 7D–G). We next examined a shared excitatory input, intended to model a transient rise in motor-related input to the olive at reach onset. A rise in excitatory drive as κ stayed below its critical value raised spike rates, but not oscillatory coherence or synchronized spiking, and it suppressed concerted silence (Figure 7D–G). Concomitant rises in excitation and in κ to above its critical value led to re-organized spiking—more large-scale synchronized spiking, more concerted silence and less small-scale synchronized spiking—and higher spike rates (Figure 7D–G).

These results capture key aspects of how complex spikes are temporally re-organized during reaching and suggest the transition at reach onset reflects a bifurcation in olivary dynamics caused by joint rises in electrical coupling and excitatory input (Figure 7H). This highlights that cerebellar feedback to the olive can regulate whether the circuit operates above or below a bifurcation point. Motor-related inputs from outside the olivocerebellum could trigger the operating mode switch.

A model in which all cells are coupled may be a good approximation for studies of a local olivary compartment (De Gruijl et al., 2014), but electrical coupling declines over larger spatial scales (Vrieler et al., 2019), which is likely important for modeling the spatially varying spiking seen with our mesoscope (Figure S2E–I). Thus, we studied a model in which olivary cells lay on a grid, and κ varied with cells’ separations (Figure S7A,B). To examine the impact of coupling changes, we transiently increased all κ values in the simulation by a multiplicative scale factor and we varied this factor from low to high values. At higher values, the spatial coherence of spiking increased, and, strikingly, there were spatial gradients in the timing of complex spikes (Figure S7C,D), resembling those in the vermis during reaching (Figure S2E–J). Overall, the Kuramoto model captures observed changes in the spatiotemporal organization of spiking, supporting the idea that the olivary network undergoes a discrete switch in its collective dynamics during task execution.

DISCUSSION

Evidence for a State Transition in Olivocerebellar Dynamics.

In neuroscience, the term ‘state change’ is used to describe model networks with phase transitions between states of distinct collective properties and macroscopic attributes, e.g. ordered versus disordered activity (Chialvo, 2010; Hopfield, 1982; Schneidman et al., 2006). Neuroscientists often conceptualize different behavioral states as resulting from distinct neural activity rates, but the concept of a discrete transition or bifurcation in the dynamics leads to an alternative view in which different behavioral states stem from differences in the organization of activity, viz. the patterning of spikes in time or space. Past experiments sought features of a state transition in motor cortex (Churchland et al., 2012; Petermann et al., 2009), and theorists have modeled circuits at critical points between states (Abbott and Rohrkemper, 2007; Moretti and Muñoz, 2013; Poil et al., 2012).

We examined whether the olivocerebellum enters a state of coherent dynamics during skilled movement, which has been proposed as a way to temporally organize motor outputs (Jacobson et al., 2008). Synchronized complex spikes during rhythmic movements are consistent with a state transition, but equally so with a scenario in which no transition exists and coincident spiking reflects movement-locked inputs, not intrinsic synchrony locked at finer time scales. We found an emergence with learning of coherent spiking across millimeter spans of tissue; covariation between coherent activity and kinematic stereotypy; a temporal re-configuration of ensemble spiking during task execution; internal time-locking of neural activity at finer time-scales than movement- or perturbation locked activity changes; ensemble encoding of kinematic perturbations; and regulation of synchrony and reach targeting by the cerebellar nucleo-olivary pathway. These results support the existence of a discrete state transition at the onset of skilled reaching and show that coherent dynamics are not innate in this context, nor generic to untrained reaching, but instead relate to the acquisition of targeted reaching proficiency. A Kuramoto model explains many of our results as arising from a bifurcation in olivary network dynamics, providing a mathematical basis for the state transition and its categorization as second-order.

Past studies proposed that complex spike synchrony is modulated via shunting inhibitory inputs from the cerebellar nuclei to olivary glomeruli, structures thought to mediate synchronous spiking (Best and Regehr, 2009; De Zeeuw et al., 1997; Devor and Yarom, 2000; Lefler et al., 2014). When we optogenetically modulated nucleo-olivary feedback, even though the illumination lasted across the trial, peak synchronized spiking was gated to reach onset, presumably due to motor commands reaching the inferior olive. This effect also arose in our Kuramoto model, in which concurrent rises in excitatory drive and coupling levels led to a greater re-organization of spiking into synchronized events than a coupling rise alone; concerted silence also rose when the model entered the coherent state, even during a rise in spike rates (Figure 7E–G). These results suggest that by regulating olivary coupling the olivocerebellum can switch its dynamics into distinct regimes (Figure 7H).

With realistic numbers of olivary cells in a microcompartment, the state switch in the model is highly discrete (Figure 7C), not a progression across a continuum of states. While a model of fully connected olivary cells can describe many features of complex spiking in local patches of cerebellum, at larger scales over which olivary electrical coupling is non-uniform, coupling modulation may switch the spatiotemporal dynamics of complex spiking between coordinated and less coordinated configurations (Figure S7), potentially explaining the millimeter-scale coherence seen during reaching (Figure S2). The wavelike propagation of spiking we saw in vivo and in simulations is broadly consistent with prior olivary models showing wavelike activity under various conditions (Latorre et al., 2013; Negrello et al., 2019; Torben-Nielsen et al., 2012).

Physiological Mechanisms Underlying a Coherent state

Millimeter-scale complex spike synchrony surely reflects synchronization of olivary cells, not signals from individual climbing fibers. Each climbing fiber has ~7 collaterals (Fujita and Sugihara, 2013) that branch rostro-caudally; our conventional two-photon images spanned ~1–2 dendrites, suggesting few shared climbing fiber inputs were within view. In our mesoscope data, coincident spikes engaged ~50−100 Purkinje cells, far more than the targets of one climbing fiber.

The concerted absence of complex spiking that often arose during reaching lasted for durations that covaried with the activation of cerebellar interneurons (Figure 5E,F). A prolonged silence might result directly from interneurons’ inhibitory action, or by inhibition of Purkinje cell simple spiking and thus disinhibition of the nucleo-olivary projection, which both inhibits olivary cell bodies and shunts olivary gap junctions (Bazzigaluppi et al., 2012b; Marshall and Lang, 2009). We favor the latter possibility, as interneuron activation did not alter the magnitude of Purkinje cells’ Ca²⁺ spikes (Figure 5D). Further, photo-excitation of the nucleo-olivary pathway promoted concerted silence, showing this mechanism’s sufficiency and capacity to outweigh a decline in concerted silence that might result from a concurrent rise in shunting inhibition of olivary glomeruli (Figure 6D).

Functional Significance of a Coherent Activity State

Olivary synchronization may coordinate olivocerebellar activity by establishing an internal ‘clock’ to choreograph motor output (Jacobson et al., 2008). Here, complex spikes had more systematic timing variations across the vermis in expert than naïve mice (Figure S2J), and, in past work, mice with impaired olivary gap junctions had motor learning deficits and abnormal complex spike timing (Van Der Giessen et al., 2008). In traditional views of cerebellar learning, complex spikes signal movement or prediction errors that drive plasticity and abate as learning is achieved (Herzfeld et al., 2018; Medina and Lisberger, 2008; Yang and Lisberger, 2014). Here, learning led to more stereotyped complex spiking activity that was synchronized across greater numbers of cells, in line with findings in expert animals that complex spikes can remain synchronized and time-locked to aspects of behavior and reward expectation (Heffley and Hull, 2019; Heffley et al., 2018; Kostadinov et al., 2019; Larry et al., 2019).

In addition to Purkinje cells, climbing fibers also contact cerebellar nuclei cells, which combine these signals with Purkinje cells’ inhibitory inputs. However, large-scale synchronized complex spikes seem far more likely than ongoing asynchronous activity to silence cerebellar nuclei cells, given the convergence of many Purkinje cell inputs onto individual cerebellar nuclei cells. Synchronized complex spikes may also coordinate subsequent simple spikes from large sets of Purkinje cells, as well as the dynamics of molecular layer interneurons (Badura et al., 2013), enhancing the modulation of downstream motor areas and effectors. At least in some Purkinje cells, ~30 ms pauses in simple spiking follow each complex spike (Yang and Lisberger, 2014), so synchronized complex spikes might pause and reset simple spiking with precise temporal cohesion over an assembly of Purkinje cells. This may coordinate the timing of spikes leaving the cerebellum, while enabling a flexible patterning of these spikes that depends on the configuration of complex spike synchrony (Person and Raman, 2011).

Outlook

By identifying coherent neural activity that arises with motor skill acquisition and execution, our study highlights the importance of collective phenomena in the brain and the limits of reductionist approaches focused on single-cell properties for understanding how neural circuits drive behavior. While our Kuramoto model succinctly captures the olivocerebellar state transition, a more complete framework will be needed to understand how cell ensembles in multiple brain areas cooperate to generate a disordered-to-ordered state transition. Our data and model show that a single-cell perspective is unlikely to account for these phenomena and that it will likely be crucial to study the circuits holistically.

Limitations of the Study

This study’s chief limitations are that we only imaged Purkinje cells and that Ca²⁺ imaging reveals these cells’ complex spikes but not their simple spikes, which are just as important for olivocerebellar dynamics. Voltage imaging might allow simple spike recordings (Gong et al., 2015), but generalizing our results will require concurrent recordings of multiple cell-types, across the olivocerebellum and in other motor areas, including motor cortex, thalamus, the basal ganglia, red nucleus, and brainstem circuits like the reticular formation (Esposito et al., 2014), to reveal how dynamic states engage the entire motor system. Notably, during reaching, coherent oscillations in motor cortex may bind motor circuits across the brain via interactions with cerebellum and thalamus (Churchland et al., 2012; Groß et al., 2002). Future work should identify the inputs to the olivocerebellum that trigger and pattern concerted spiking.

While our optogenetic manipulations were anatomically precise, they involved large-scale, non-physiological patterning, so it remains untested whether physiological patterns of nucleo-olivary feedback can synchronize or de-synchronize specific olivary subdomains that might recruit and coordinate distinct cerebellar regions for different motor behaviors. Further, unlike in our model, in which κ sets the olivary coupling strength independently of excitation levels, nucleo-olivary inputs both inhibit olivary cell bodies and shunt gap junctions. Thus, one cannot conclude that the effects of our nucleo-olivary manipulations on complex spike synchrony were solely due to the coupling change, and exactly how reach targeting was altered remains unclear.

Finally, we designed our study to assay ensemble spiking dynamics, not single-cell coding properties. Complex spikes can signal intricate admixtures of kinematic variables (Fu et al., 1997; Kitazawa et al., 1998; Ojakangas and Ebner, 1992). Thus, our limited sampling of kinematic and perturbation parameters (Figures 3,5I–P) cannot reveal the exact combination of motor command, perturbation, self-generated error or feedback signals encoded in complex spiking.

STAR METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Mark J. Schnitzer (mschnitz@stanford.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

We performed analyses using publicly available software (see below and Key Resources) and custom routines written in MATLAB (Mathworks). The data of this study and the MATLAB code are available from the authors upon reasonable request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mice.

The Stanford University Administrative Panel on Laboratory Animal Care (APLAC) approved all animal experiments. For Ca²⁺ imaging in Purkinje cells, we used 11 (9 males and 2 females) PCP2-Cre driver mice with a Bl6–129 genetic background; 14 male wild-type C57/bl6 mice; and 3 (1 male and 2 female) PCP2-Cre / Ai148 (Daigle et al., 2018) transgenic mice (Figure 2). In the cerebellum, the PCP2-Cre / Ai148 mice expressed the GCaMP6f Ca²⁺ indicator selectively in Purkinje cells. However, for unknown reasons the expression was not complete; a substantial fraction of, but not all, Purkinje neurons expressed the Ca²⁺ indicator (Figure 2A). Mice were aged 6–16 weeks at the start of procedures, were in good health and normal immune status, and did not undergo any other procedures or experiments prior to those of this study. Mice were singly or group-housed in standard cages with at least weekly bedding changes.

METHOD DETAILS

Viruses.

Except for the studies of Figure 2 and S2, to express the GCaMP6f Ca²⁺ indicator (Chen et al., 2013) selectively in Purkinje cells, we used a viral strategy. Specifically, we injected AAV2/1-CAG-FLEX-GCaMP6f virus (titer: 9.4 × 10¹² GC⋅mL⁻¹) into the right cerebellar cortex of PCP2-Cre mice, or AAV2/1-CaMK2a-GCaMP6f virus (titer: 3.6 × 10¹³ GC⋅mL⁻¹) into the right cerebellar cortex of C57/bl6 mice. To express Cre-recombinase in nucleo-olivary neurons in the right cerebellar fastigial nucleus, we injected CAV2-CMV-Cre virus (Soudais et al., 2001) (titer: 4.2 × 10¹² GC⋅mL⁻¹) or AAVretro-EF1a-Cre (Tervo et al., 2016) into the inferior olive. To express eArch3.0 (Mattis et al., 2012) or BreaChES (Kim et al., 2017) in Cre-positive fastigial neurons, we injected AAV8-EF1a-DIO-eArch3.0-mCherry virus (titer: 6.5 × 10¹² GC⋅mL⁻¹) or AAV8-EF1a-dio-BreaChES-mCherry (titer: 4 × 10¹² GC⋅mL⁻¹).

Surgical procedures for two-photon imaging studies.

Following our laboratory’s published procedures (Nimmerjahn et al., 2009), we performed surgeries on isoflurane-anesthetized mice (1.25–2.5% in 0.5−1.5 L/min of O₂). Mice underwent one, two or three surgical procedures, to inject viral vectors into the brain, attach a metal head-plate to the cranium, and prepare the mice for in vivo Ca²⁺ imaging, in that order. Transgenic PCP2-Cre/Ai148 mice that expressed the GCaMP6f Ca²⁺ indicator in Purkinje cells did not undergo the first surgery.

In the first surgery, after anesthetizing the mice we cleaned the skin and made a small incision. We then drilled open a ~0.3 mm diameter craniotomy over the right vermis of cerebellar lobule V, ipsilateral to the reaching arm and ~1 mm anterior to the post-lambda fissure on the cranial midline. Using a glass pipette (30−50 μm tip diameter), we injected 400–600 nL of AAV2/1-CAG-FLEX-GCaMP6f virus in PCP2-Cre mice or AAV2/1-CaMK2a-GCaMP6f in wild-type mice, at a depth of 180–350 μm. We allowed the virus to incubate for 2−5 weeks before experiments, to allow adequate expression of GCaMP6f.

In the second surgery we attached an aluminum head-plate to the skull. We cleaned and removed skin to reveal part of the skull and centered the plate’s 6-mm-diameter opening over the cerebellum. We treated the skull with Metabond adhesive and affixed the holding plate with dental cement (Coltene Whaledent). The custom-made plate was shaped to allow the additional attachment of two stainless steel bars to the cranium. Together, these steel bars held the head in place during active mouse behavior via three attachment points, two rostral and one caudal, as we found that the use of all three clamping points was helpful for minimizing cranial motion. To the rostral part of the cranium we fixed one of the bars, oriented along the medio-lateral direction, so that during imaging experiments we could clamp it on both sides to external fixtures. To the caudal part of the cranium we fixed the other bar, angled at 45° to the horizontal plane, providing a third clamping point.

Finally, we opened a 4-mm-diameter craniotomy above cerebellar lobule V in the right vermis (100–700 μm anterior to the primary fissure, 0.3−1.2 mm lateral). In some mice, we performed this procedure prior to training during the head-plate implantation surgery described above (in these cases, the second surgery was performed 1–2 days after virus injection); in other cases, we did not open the cranial window until after the mice had successfully undergone behavioral training (in these cases, 2−5 weeks after virus injection). In some mice we also removed the dura. In some cases, we applied Kwik-Sil (World Precision Instruments) to the border of the craniotomy. We then covered the brain with a 3-mm-diameter cover slip that we had previously attached beneath a 7-mm-diameter cover slip using ultraviolet-light activated epoxy (Norland NOA81). We fixed the 7-mm-diameter cover slip to the cranium with a stainless-steel shim retaining ring and dental cement. In other cases, we directly implanted into the skull opening a 3-mm-diameter coverslip affixed to the bottom of a 1-mm-long, 3-mm-diameter stainless-steel tube. In all cases, mice recovered for 1–2 days prior to behavioral training.

Robotic manipulandum.

We built a robotic manipulandum with two degrees of mechanical freedom using two direct drive (no transmission) direct current (dc) motors (Maxon RE-max 21). During design of the robot, we took particular care to create a system capable of providing high quality force feedback to the mice, with no mechanical backlash, near-zero friction, low mechanical inertia, a broad temporal frequency bandwidth, and extreme back-drivability. The motors were arranged in a double SCARA configuration (e.g. (Figielski et al., 2007)) and coupled to two high-resolution optical rotary encoders (Gurley Precision Instruments R120B). The calculated resolution of the encoders at the mouse’s grasping point on the joystick was 0.006 mm in the lateral direction and 0.003 mm in the forward direction.

Our robotic and behavioral apparatus involved a nested hierarchy of three different levels of feedback control: two real-time controllers operating at 10 kHz and 1 kHz, respectively, and a graphical user interface controller operating at ~50–200 Hz. At the lowest level, we monitored the current drawn by each motor using an inductive sensor (Honeywell) and an analog input signal recorder (National Instruments 9215). Field programmable gate arrays (FPGAs) (National Instruments LX50 programmed in Labview) performed torque control using the current signals via a standard proportional-integrative feedback controller operating at 10 kHz. Rotational quadrature signals from the encoders entered digital input lines and allowed position control using a standard proportional-integrative-derivative (PID) feedback controller operating at 1 kHz.

The second level of control ran at 1 kHz on a real-time operating system (RTOS; National Instruments cRIO-9024, programmed in Labview), which performed kinematic transformations from the coordinates of the robot joints to Cartesian coordinates. We used the RTOS to set the physical dynamics of the robot that the mouse would experience, such as the movement friction of the robotic manipulandum. We did this by reading state variables and updating the output forces to desired values at 1 kHz. Using positional feedback control in the RTOS, we also created in software virtual walls that terminated arm-movements, external forces that perturbed reaching movements (Figure 5I–P), and virtual channels that constrained reaches to one-dimensional trajectories.

The highest level of control involved a Windows personal computer (PC) programmed in Labview. This level allowed us to specify trial parameters, compute and deliver rewards, and log data. The RTOS sampled positional data at 200 Hz, which was transferred from the RTOS buffer via network to a buffer on the Windows PC, and written to disk following experiments. We also video-recorded the animal’s behavior at a frame rate of 15 or 20 Hz using an infrared camera (Imaging Source).

Behavioral training.

Mice followed a water-restriction protocol in which they were limited to ~1 mL intake per day. Mice trained for 5−11 days for 0.5−1.5 h daily, depending on reward satiety. We monitored the animals’ weight daily, checked their coat quality, and provided supplementary saline injections as necessary. During training, the robotic manipulandum was positioned approximately 6 cm in front of and 6 cm below the shoulder, depending on the mouse’s size. Mice were allowed to initiate a reach when the robotic arm returned to the home position, provided the mice applied no appreciable force to the robot for a brief inter-trial period, as determined from the force needed for the robot to hold the handle at the start position.

As training progressed, we made the reward criteria increasingly stringent. We required longer movements (in all cases) and greater accuracy (in the planar task). We rewarded the mouse for reaches with a radial endpoint >6–7 mm. We did not reward slow or discontinuous movements, which the robot terminated before their completion. In both tasks, we used a virtual wall, as programmed in the RTOS, to constrain the arm’s maximum range of movement to 8 mm.

For the task in Figure 5I–P, in which mice were constrained to making linear movements in the forward direction, the RTOS canceled the mouse’s lateral movement using the 1 kHz PID feedback controller. For perturbation delivery, on the day of imaging only and on a random subset of trials, the robot deflected the hand after 3 mm of linear movement. These leftward or rightward perturbations then increased in amplitude (up to a maximum displacement of 4–6 mm) as a function of the mouse’s forward motion. Leftward and rightward perturbations each occurred once every eight trials, in a random order, intermixed with trials with no perturbation. On trials without a robotic perturbation of the movement, the mouse received a sugar water reward on all trials for which the arm movement was >7 mm in extent.

Body tracking.

During a subset of two-photon imaging studies, we used a pair of CMOS cameras (Imaging Source DMK 23UV024) to track the mouse’s body movements. We synchronized the two cameras to each other and to the two-photon microscope at a 20 Hz rate of image frame acquisition. One camera was positioned to capture a side view of the mouse’s body, as imaged through a transparent plastic tube that we used to restrain the mouse’s body trunk. The other camera captured a ventral view of the mouse’s body, as observed via a mirror placed beneath the plastic tube. For each reaching trial, we manually scored the behavior videos to track the motion of 6 body coordinates (anterior-posterior and dorsal-ventral positions of the right forelimb; medial-lateral and anterior-posterior positions of the left and right hindlimbs) from −1 s to +100 ms relative to forelimb movement onset, as detected by the robotic handle.

Two-photon microscopy.

For all Ca²⁺ imaging studies we used custom-built two-photon imaging instrumentation. A Ti:sapphire laser (SpectraPhysics, MaiTai) provided ultrashort-pulsed illumination of 920 nm wavelength. For the studies of Figure 2 and Figure S2, we used a custom two-photon mesoscope (Rumyantsev et al., 2020) equipped with a specialized microscope objective lens for two-photon imaging across a wide field-of-view (Sofroniew et al., 2016), which allowed us to acquire images over a 2 × 2 mm² field-of-view at a 17.5 Hz frame rate (842 × 842 pixels). For all other studies we used a custom two-photon microscope of a traditional design, equipped with a 0.95 numerical aperture (NA) 20× microscope objective lens (Olympus XLUMPlanFl), except in optogenetic experiments, for which we used a 1.0 NA 20× objective lens (Olympus XLUMPlanFl). We acquired image frames at 20 Hz across a field of view of either 110 μm × 270 μm using MPScope software (Nguyen et al., 2006) (130 × 280 pixels per frame; 2.6 kHz line scan rate) or of 130 μm × 265 μm using ScanImage software (Vidrio Technologies) (130 × 256 pixels per frame, 2.7 kHz line scan rate).

Data acquisition occurred during both the forward and backward portions of the scanning motion in both the x and y directions of the image frame, such that successive image lines and successive frames were sampled in opposite directions along the x- and y-axes, respectively. During optogenetic experiments, we placed two additional filters in the fluorescence emission pathway to block the 594-nm-wavelength laser light used for optogenetic inhibition. At the start of an imaging experiment, upon placing the mouse under the two-photon microscope, we chose a field-of-view for study with minimal curvature of the brain, few blood vessels, and bright fluorescence signals.

Electrophysiological recordings.

In mice anesthetized with 1.5–2.0 % isoflurane in ~0.6 L/min O₂, we guided a pipette filled with artificial cerebrospinal fluid (125 mM NaCl, 5 mM KCl, 10 mM D-Glucose, 10 mM HEPES, 2 mM CaCl2, 2 mM MgSO4; pH to 7.4 with NaOH) (Nimmerjahn et al., 2009) and a red fluorescent dye (Sulforhodamine-101) into the imaging field of view in the cerebellar cortex. We used dual-color two-photon microscopy to visualize the pipette in the red fluorescence channel and the GCaMP6f-labeled neurons in the green channel. We acquired electrophysiological data at 10 kHz. We placed the pipette tip ~70 μm into the brain, in the cerebellar molecular layer and just dorsal to the chosen Purkinje cell body, so that the electrical recordings generally contained only complex (Na⁺ and Ca²⁺) spikes, and not simple (Na⁺) spikes, as distinguished by their different electrical waveforms (Ekerot and Oscarsson, 1981). When we attained a stable electrical recording, we centered the field of view approximately above the tip of the pipette.

Surgical procedure for optogenetic studies of the nucleo-olivary pathway.

In mice used for combined, two-photon imaging and optogenetic studies, during the first surgery (described above) we additionally injected either CAV2-Cre virus (3 mice) into the left inferior olive (Soudais et al., 2001), or AAVretro-EF1a-Cre (7 mice) bilaterally into both inferior olives. To perform these injections, we retracted the neck muscles overlying the caudal-most aspect of the brain, where the skull has terminated and only a thick, semi-transparent dura covers the brain. We pierced a small hole in the dura and brought a glass pipette (30−50 μm tip diameter) containing viral solution to the rostro-caudal boundary between the cerebellum and brainstem, which were visible under the dura. The pipette entered the brain at this boundary (medio-lateral: 550 μm) at a 40.5° angle from the vertical axis. We inserted the pipette to a depth of 2.7 mm from the brain surface and injected 500 nL of virus.

We then injected either AAV8-EF1a-DIO-eArch3.0-mCherry into the right fastigial nucleus (3 mice) or both fastigial nuclei (4 mice), or AAV8-EFa-DIO-BreaChES-mCherry into both fastigial nuclei (3 mice). To target the fastigial nucleus, we applied saline to the thin skull overlying the posterior cerebellar cortex, which made the cerebellar lobules visible through the skull. We drilled a 0.3-mm-diameter craniotomy at the rostro-caudal boundary between cerebellar lobules VII and VIII, 900 μm to the right of the midline. We inserted a glass pipette containing viral solution into the brain at a 66° azimuthal angle from the vertical axis and to a depth of 1.75 mm beneath the brain surface. We then injected 500 nL of virus. To allow illumination of the fastigial nucleus, we implanted a multimode optical fiber (400-μm-diameter core, Thorlabs) in the right fastigial nucleus (3 mice) or both fastigial nuclei (7 mice). The fiber entered the brain at the same coordinates used for virus injection and was implanted at a depth of 1.15 mm, slightly dorsal to the locus of virus injection. The optical fiber terminated just outside the skull in a ferrule that we cemented to the skull using Metabond adhesive (Parkell). The ferrule allowed the detachable connection of a fiber optic patch cord (400-μm-diameter core) that delivered laser illumination for the optogenetics experiments.

Histology.

We verified by histological analysis that cells expressing eArch3.0 were inhibitory neurons in the deep cerebellar nuclei. We anesthetized the mice with pentobarbital (Beuthanasia) and transcardially perfused them with phosphate-buffered saline (PBS) and then 4% paraformaldehyde (PFA). We extracted the brains and kept them in 4% PFA for 24 h, followed by 24 h in 30% sucrose solution. We cut 40 μm thick tissues sections on a cryotome (Leica). We bathed the sections in blocking solution (10% normal donkey serum (NDS) in PBS) for 1 h. We labeled the sections for 24 h using the mouse monoclonal GAD67 antibody (Millipore MAB5406; 1:500 dilution in 10% NDS in PBS). We then rinsed the sections with PBS and then labeled them with the secondary antibody (Alexa−647 labeled donkey anti-mouse, Jackson Immunoresearch; 1:500 dilution in 10% NDS in PBS). Finally, to visualize cell bodies, we stained the sections with DAPI (Sigma, 0.1μg/mL of PBS for 5 min). We imaged tissue sections of the cerebellar cortex and nuclei using a confocal microscope (Leica TCS SP5).

Optogenetic manipulation studies.

We used a 594-nm-wavelength laser (Cobolt Mambo or Coherent OBIS) coupled to one or two optical fibers (400-μm-diameter core; Thorlabs) that we connected to the ferrule(s) implanted on the mouse skull. Illumination power was 15 mW at the tip of the fiber, which sufficed to activate the opsins. On trials randomly chosen for optogenetic manipulation (20% of trials for bilateral stimulation studies, 10% of trials on each side for alternating unilateral stimulation studies), a shutter opened at the start of the trial and permitted the laser light to enter the optical fiber. At ~500 ms after reach termination, the shutter closed. Thus, light exposure lasted ~1 s on trials when the mouse initiated a reach soon after trial onset.

QUANTIFICATION AND STATISTICAL ANALYSIS.

Image motion correction.

To correct for any rigid, lateral displacements of the field-of-view, first we used either TurboReg image registration software (Thevenaz et al., 1998), or NormCorre (Pnevmatikakis and Giovannucci, 2017) to align each image frame to the mean determined by averaging all image frames in the movie dataset. This registration procedure did not correct for axial displacements of the brain. However, as previously (Nimmerjahn et al., 2009) we estimated axial displacements to be <8 μm. Thus, these displacements did not impair our ability to detect the Ca²⁺ spikes that pervade Purkinje neurons’ dendritic trees, since these para-sagittally oriented dendritic arbors never left the focal plane during dorsal-ventral displacements. For spatial registration in the lateral (x-y) dimensions, images required displacements with s.d. of 2.5 μm and 3.3 μm in x and y, respectively. To temporally align the behavioral and Ca²⁺ imaging data, we programmed the RTOS to output a digital pulse each time it recorded a behavioral data sample (200 Hz acquisition rate). We used MPScope to acquire this digital pulse train concurrently with two-photon image acquisition. Alternatively, we used ScanImage to output a frame clock signal that we acquired concurrently with the behavioral data transmitted by the robot’s electronics controller.

Identification of Purkinje neurons.

To identify individual Purkinje cells in the two-photon imaging data, for all experiments, except for the mesoscope studies of Figure 2, we used an established, automated cell sorting algorithm based on principle and independent component analyses (PCA/ICA) validated previously for studies of two-photon Ca²⁺ imaging studies of Purkinje neurons (Mukamel et al., 2009).

To process the data of Figure 2, we used a cell-extraction algorithm, EXTRACT (Inan et al., 2017; Inan et al., 2021), that is based on a framework of robust statistical estimation and that provided superior speed and sensitivity for processing the large image datasets (4 mm² field-of-view) acquired on the two-photon mesoscope. Before applying EXTRACT, we first performed several pre-processing steps. We spatially filtered the raw movie data with an anisotropic high-pass filter (second-order Butterworth), for which the cutoff frequencies were 0.01 μm⁻¹ and 0.005 μm⁻¹ in the x- and y-directions, respectively. We used an anisotropic filter of this form due to the elongation of the Purkinje cell dendritic arbors in the y-direction. To remove slow time-variations in the fluorescence signals, we subtracted from each pixel in the movie a time-varying estimate of its baseline fluorescence intensity value. We computed this baseline estimate by constructing a down-sampled time trace of the pixel’s mode intensity values across successive 30-s-intervals, and then up-sampling this trace back to time bins of 57 ms via linear interpolation of the mode values.

After this pre-processing, we applied EXTRACT to identify candidate Purkinje cells. We used an automated procedure to check the attributes of the candidate Purkinje cells, including the cells’ area, solidity of the cell image, and signal-to-noise ratio of the cell’s Ca²⁺ activity trace. Candidate cells for which any of these attributes were not representative of typical Purkinje cells were automatically excluded from further analyses. Further, we visually checked all remaining candidate Purkinje cells and removed any whose shape differed from typical forms of Purkinje cell dendritic trees or that lacked clear Ca²⁺ transients.

After extracting spatial filters corresponding to individual Purkinje cells, whether from PCA/ICA or from EXTRACT, we truncated the filters by setting to zero the weights of all pixels with values less than 1.5 s.d. above the mean pixel weight, averaged across the entire spatial filter. We applied these truncated spatial filters to the raw fluorescence videos to extract fluorescence traces for each Purkinje neuron.

Identification of Ca²⁺ spikes.

To estimate the times of Ca²⁺ spikes at a temporal resolution finer than the image frame acquisition time, we made use of the anatomical arrangement of the Purkinje neurons’ dendritic trees in our images. The long axes of the dendritic trees were all approximately parallel to the slow axis of laser scanning and generally spanned many fast-scan image lines. Hence, for each dendritic tree we converted the photocurrent data from each image line into a movie with only one spatial dimension, as if we had simply performed rapid laser line-scanning across the neuron. For each line in this computed movie, we weighted the fluorescence values from all pixels according to the weights of the cell’s truncated spatial filter, determined as above.

Generally, individual dendrites had non-uniform spatial forms across the field of view. Thus, some image lines contained superior Ca²⁺ signals than others. To account for this, we designed a local smoothing function for computing each line’s signal that incorporated some signals from neighboring lines, rather than considering each line independently. To compute the signal contribution of line n (with n ranging from 1−130), we averaged lines n – W/2 through n + W/2, where W was an even integer chosen separately for each line. To determine the window W, we sought a metric of the line signal’s fidelity. An estimate of the true (free of sampling bias) line signal available to us was the raw frame signal, since it incorporated information from all lines. For each line, we therefore interpolated successive frame signals to match the line signal’s sampling times. For each line, we then chose the value of W as the minimum even integer that produced a line signal whose correlation coefficient with the interpolated frame signal was at least 0.9. In this way, lines of high fidelity used very small local smoothing windows, whereas lines in signal-poor neighborhoods of the image used large local smoothing windows. We then normalized the contributions of each line such that its largest spikes had the same average magnitude as those in the interpolated frame-averaged signal. We combined all line signals into a single time trace with a time bin corresponding to the line scan rate of 2.6 kHz.

We next corrected for drifts in fluorescence much slower than Ca²⁺ transients. To obtain an estimate of slow drifts, we computed the 10th-percentile value of each 2 s segment of the signal. We subtracted this metric of baseline drift from the signal trace and applied half-wave rectification to preclude negative deflections. To reduce the impact of noise on spike timing estimates, we smoothed the rectified trace with a low-pass Butterworth filter (–3 dB frequency: 6.5 Hz). To account for the decay kinetics of the GCaMP6f Ca²⁺ indicator, we deconvolved the smoothed trace with an exponential function (decay time: 150 ms). We determined the neuron’s spike times as the times of signal peaks in the deconvolved trace (Figure 3B and Figure S3D). By performing concurrent Ca²⁺ imaging and electrical recordings of individual Purkinje neurons, we confirmed that this cell sorting procedure correctly identifies complex spikes and their precise times of occurrence (Figure 3B,C and Figure S3).

Assessment of spike timing accuracy.

We assessed the concordance between the spike time estimates attained from the concurrently acquired optical and electrical recordings by comparing the times of peaks in the optical and electrical spike waveforms. We identified complex spikes in the electrical recordings as threshold-crossing events, using a threshold value that we manually verified to detect all visible complex spikes. We denoted the time of the electrical waveform’s first peak as the complex spike’s occurrence time. We identified complex spikes in the optical recordings and estimated the times of their occurrences as described above. Comparisons between the two sets of spike trains revealed that our procedures for analyzing the optical data resulted in >90% correct spike detection and <5% false positive detection. The paired recordings also revealed that the optical traces allowed high fidelity detection of complex spikes for inter-spike intervals as brief as ~100 ms, but could not resolve individual spikes separated by inter-spike intervals briefer than this. In mice, baseline rates of complex spiking are 0.5–2 Hz, and peak rates are generally <10 Hz (Badura et al., 2013), hence this degree of spike resolution suffices to resolve the vast majority of complex spikes in the mouse cerebellum.

We determined the systematic offset between the spike times in the paired optical and electrical datasets as the mean difference between all corresponding pairs of spike times. We determined the stochastic error in the estimation of spike times from the optical data as the s.d. of the spike time offsets (Figure 3C), which was 6.1−11 ms. This 6−11 ms timing accuracy is chiefly limited by the rise-time of the GCaMP6f Ca²⁺ indicator (~50 ms) and the finite photon flux, not the 2.6 kHz line-scanning rate, and is more than sufficient given the 25-ms time bins used for analyses throughout the paper.

Extraction of interneuron Ca²⁺ signals.

We extracted interneuron Ca²⁺ signals similarly to how we did so for Purkinje neurons. We used the PCA/ICA algorithm to extract spatial filters for the interneuron cell bodies. Due to the strongly correlated patterns of activity amongst the interneurons, the algorithm often yielded filters covering more than one interneuron. Given the uniformity of the responses seen across the visible interneurons, we analyzed interneuron dynamics based on a single time trace that reflected their collective dynamics. To attain this time trace, we first truncated all interneuron spatial filters by setting to zero the weights of all pixels with values less than 1.5 s.d. above the mean pixel weight, averaged across each spatial filter. We created a single interneuron filter by summing all of the truncated filters, and applied the resultant spatial filter to the raw video data to yield a time trace reflecting the time-dependence of aggregate, interneuron activity levels.

Due to the overlapping sets of pixels occupied by Purkinje dendrites and interneurons, and the substantially greater levels of Ca²⁺ activation in Purkinje neurons, we sometimes observed a bleed through of nearby Purkinje signals into the interneuron activity trace. To determine the level of crosstalk, we performed a least squares regression of the individual Purkinje neurons’ fluorescence traces onto the interneuron trace. This yielded a set of weights, one for each Purkinje neuron, which reflected the extent to which each Purkinje cell’s Ca²⁺ signals had contaminated the interneuron trace. To remove the cross talk, we used these weights and subtracted from the interneuron trace the weighted sum of the signals from the individual Purkinje neurons. This yielded the component of the original interneuron trace that was unaccounted for by spatial bleed through from Purkinje cells. We verified that the resultant trace reported interneuron activation at time points in the videos with visually obvious interneuron Ca²⁺ transients.

Temporal alignment of data across reaching trials.

We temporally aligned traces of neural activity across different reaching trials by first registering each arm motion trace to one of two different temporal markers and then identifying the 25-ms time bin in the Ca²⁺-imaging data closest in time to the behavioral marker. For all studies except those of perturbations, we temporally registered the traces to the time of movement onset, defined as the time at which the handle velocity rose above 5 mm · s⁻¹. This choice allowed us to reliably compare neural activity before and after reaching began. For studies of mechanically perturbed reaches (Figure 5I–P), we temporally aligned the activity traces to the time at which the perturbation had laterally deflected the handle to ±4 mm.

Determination of trial-averaged spike rates.

To compute the average reaching-evoked pattern of neural ensemble activity, we computed each cell’s reach-triggered average spiking response. We averaged the traces across all Purkinje neurons to obtain an estimate of the mean ensemble response.

Spatial cross-correlation plots of Purkinje cell Ca²⁺ spiking activity.

To construct the cross-correlation plots in Figures 2J and S2C, we took each pair of Purkinje cells and computed the pair’s anatomical displacement and the mean cross-correlation coefficient (at zero-time lag) between the two cells’ Ca²⁺ spike trains. This procedure is illustrated in Figure S2A,B. We computed the correlation coefficients using all arm-reaching trials in a recording session (79–234 trials for each mouse studied with the two-photon mesoscope). We binned the displacements between the cell pairs in spatial bins of 40 μm × 40 μm and then determined the mean correlation coefficient averaged over all cell pairs within each spatial bin (Figures 2J and S2C). We compared the results of this analysis on days early (Days 1, 2) and late (Day 7, 8) in motor learning, during reaching and inter-trial periods. (1.2 s window centered either on or −2.9 s prior to movement onset, respectively).To create the plots of Figure S2D, we took the cross-correlation maps from each mouse and session and determined the mean correlation coefficient as a function of the radial displacement from the origin point on the map. We then averaged the results over all animals and recording sessions.

Spatiotemporal coherence of Purkinje cell Ca²⁺ spiking activity.

To analyze the spatiotemporal coherence of Purkinje cell Ca²⁺ spiking activity, we applied a sliding time window (350 ms) to each cell’s raster trace of complex spiking activity (Figure S2E). Within each 350-ms-window, we identified all cells that spiked at least once, and we designated each cell’s activation time as the mean of its spike times within the window. Given N_c active cells within a specific 350-ms-interval, we performed a least-squares, bi-variate linear regression of the N_c × 2 matrix containing the x and y coordinates of each one of the cell onto the N_c × 1 vector of activation times. We used the resulting r-value from the regression as a measure of how well the linear fit was able to predict cells’ relative spike times based on their physical positions (Figure S2G).

To determine whether an r-value was statistically significant, we performed an identical analysis of shuffled datasets in which the spatial locations of the active cells within each 350-ms-window were randomly permuted. By examining many different permutations, we estimated the statistical distribution of r-values across the set of all shuffled datasets and hence the p-value of the actual r-value determined for the real data. We constructed a histogram of these p-values across all mice and all 350-ms-time windows (Figure S2I).

To assess the time-dependence of spatially coherent neural activity across the course of a reaching trial (Figure S2J), we examined all 350-ms-time-windows that had p-values <10⁻⁴ (Figure S2I). We plotted the time-dependent probability that an individual reach would evoke neural activity with such a high degree of spatial coherence, and we averaged these plots over all reaching trials and all mice within the same experimental condition. We smoothed the resulting traces with a Gaussian kernel (0.5 s time constant).

Determinations of concerted neural silence rates.

To compute the time-dependent rate of reach-triggered concerted neural silence, we scored each 25-ms-time bin according to whether or not every Purkinje neuron in the field of view was concurrently silent for the entire preceding 75 ms. We then averaged the results across behavioral trials to determine the time-dependent probability of reach-triggered concerted silence. In other cases, we computed the maximal duration of concerted silence, or the total duration of concerted silence summed over the entire trial.

Shuffled datasets.

When creating trial-shuffled datasets, for each neuron we independently and randomly permuted the cell’s spike trains across the different reaching trials. This maneuver preserved the timing of each spike with respect to the aligned behavioral data while removing within-trial correlations between neurons. For each behavioral condition we used 200−1000 distinct random permutations so as to construct shuffled data. To determine the mean rate at which synchronized spiking arose in the shuffled data, we first computed the mean rate of synchronized spiking for each shuffle and then took the mean across all shuffles. When performing permutation tests, we computed the parameter of interest (e.g. the rate of concerted silence or synchronized spiking) for each shuffled dataset and compared the resulting values to those from the actual data. If n of 1000 shuffles yielded parameter values that exceeded its value in the real data, we estimated the p value as n/1000. If n = 0, then p < 0.001 and an exact p-value could not be computed.

Determination of synchronized spiking rates.

In cases in which we discretized synchronized spiking events, we used a threshold stipulating that ≥20% of all visible Purkinje cells must have fired Ca²⁺ spikes in the same 25-ms time bin. To compute a binary time trace of the occurrences of these events, we first summed the time-varying binary spike trains of all Purkinje cells in the visible ensemble. We then binarized the resulting trace by thresholding it at a value corresponding to 20% of the total number of cells in the Ca²⁺-imaging movie. Thus, the trace of synchronized spikes had ‘1’ entries for time bins when ≥20% of the cells spiked, and ‘0’ entries in all other time bins. In other cases, we simply tabulated the fraction of cells synchronously spiking at each point in time.

Identification of active and resting behavioral epochs.

To identify epochs when the mouse was at rest, we identified all intervals lasting >1 s during which the robot detected no substantial arm motions (velocity <0.8 mm·s⁻¹ and position within 3 mm of origin) within 200 ms of the interval’s starting and ending time points. We examined the video of the mouse’s behavior for each identified resting period and retained only those during which the mouse made no overt forelimb movements. To extract epochs of arm reaching, we identified from the robot’s recordings all reaches that were >5 mm in total length, advanced >3 mm in the radial direction, and initiated <1 mm away from the manipulandum’s baseline position.

Analysis of synchronous spiking patterns.

To compute the statistical frequencies of various spiking patterns, we divided all reaching and resting epochs into data blocks of duration 325 ms. Since resting epochs did not always occur in multiples of 325 ms, we used the remainders only if the resulting blocks were 275–375 ms long. We computed the spiking rate during each block. Using the 7 spiking rate levels listed in Figure 4L, we assigned each data block to the spiking rate level to which it was closest. For all of the blocks assigned to each spiking rate level, we counted the number of concurrent spiking events that occurred with different numbers of neurons active. This allowed us to compute the statistical distribution of concurrent spiking events of different sizes.

Receiver operating characteristic analysis.

To probe the capability to discriminate reaching from resting epochs based on neural activity metrics, we used receiver operating characteristic (ROC) analysis and the above set of reaching and resting data blocks. Since the goal of this analysis was to assess the reliability of concerted neural silence as an indicator of reaching, we restricted the selection of reaching epochs to the main interval during which concerted silence occurred, [100 ms, 400 ms] relative to reaching onset. As part of the ROC analysis, we used two different methods of assigning each data block a score. The first method assigned each block a score equal to its ensemble average spike rate. The second method used as the score the duration of the longest episode of concerted silence across the data block.

For each set of scores, we then attempted to characterize each data block according to whether it occurred during a reaching or resting epoch. All blocks with a score above a minimum threshold were estimated to have occurred during reaching; blocks with scores below the threshold were estimated to have occurred during rest. For a given choice of the threshold value, the proportion of data blocks that were incorrectly estimated to have occurred during reaching was designated as the false positive rate. Similarly, the proportion of data blocks incorrectly estimated to have occurred during resting yielded the false negative rate. We varied the threshold value across the entire range of scores and tabulated the resulting true and false positive rates. The resulting plot of the true versus false positive rates equaled the ROC curve for that method of scoring.

We computed the ROC curve for each mouse and scoring method. Finally, for each mouse and scoring method we computed the area under the ROC curve (Figure 4M). This area equals the probability that an observer faced with a choice between one data block that occurred during reaching and one that occurred during resting could correctly discriminate between the two.

Frequency spectra of ensemble neural activity.

To examine synchronous activity in the frequency domain (Figure S5H–J), we computed the average power spectrum of ensemble spiking during reaching, within the interval [−1000 ms, 1000 ms] relative to reach onset. Temporal windows smaller than this generally provided an insufficient number of data points to compute accurate spectral estimates. We used the time-dependent fraction of active neurons, determined as the normalized sum of the individual spike trains, as a measure of ensemble activity. We then computed the power spectrum of ensemble spiking on each trial using the multi-taper method (Chronux toolbox in MATLAB). This method computes the power spectrum of a single, finite-length trial using multiple orthogonal windows to obtain multiple independent estimates of the spectrum. These windows, or tapers, are given by the Slepian sequence for a particular trial duration and at a particular frequency band. The Slepian sequence guarantees minimum side-lobe energy outside the frequency band of interest. We averaged the resulting spectra across all trials. To determine the contribution of correlated activity between neurons, we simulated the spectrum of an independent ensemble. We produced a shuffled data set in which single-trial correlations between neurons were absent, and we compared the resulting spectrum to that of the real data.

The spectral content of the sum of multiple signals (i.e. the ensemble spike rate) contains a component arising from the autocorrelations of the individual signals and a component arising from the pair-wise (and higher-order) correlations between the different signals. We thus examined each component individually. First we computed the mean cross-spectrum between all pairs of neurons. We then computed the power spectrum of each individual neuron’s spike train.

Analysis of movement kinematics.

To compute movement stereotypy metrics (Figure 3), for each imaging session we computed the mean movement trajectory by independently averaging across all trials the forward and lateral coordinates of the reaching motion, temporally aligned to movement onset and terminating 200 ms after the average time at which movement ended. For this analysis, we defined the end of movement as follows. For arm movements that reached the virtual wall at 8 mm from the forepaw’s point of origin, we defined the end of movement as the time at which the forepaw’s radial displacement from its starting point exceeded 7.5 mm. For movements that did not reach the virtual wall, we defined the end of movement as the first time at which the position was within 0.5 mm of the final position. For each mouse this approach yielded a net time interval, termed t_win, over which we performed the stereotypy analysis. For each movement trial, this approach yielded a pair of t_win-length vectors, one for forward and one for lateral motion. We concatenated these two into a single vector of length 2t_win. To assess the similarity of this vector on an individual trial to its trial-averaged form, we computed the Pearson correlation coefficient between the two. Alternatively, we computed the root-mean-square-difference between the corresponding elements of the two vectors. To determine the angle of each movement, we computed tan⁻¹(x_f /y_f), where (x_f, y_f) was the reach’s endpoint position.

Olivary network simulations and mean field theoretic solution.

Inferior olivary neurons have an intrinsic ~10-Hz rhythmicity in their sub-threshold membrane potential dynamics (Bazzigaluppi et al., 2012a; Khosrovani et al., 2007). Groups or ‘micro-compartments’ of these cells are interconnected by electrical gap junctions that promote synchronization of the cells’ sub-threshold oscillations (De Zeeuw et al., 1998; De Zeeuw et al., 1997). To model these dynamics, we computationally simulated a network of coupled Kuramoto phase oscillators (Kuramoto, 1984), governed by:

$$\frac{d{\theta }_i}{dt}={\omega }_i+\kappa (t)\cdot {\sum }_{j=1}^{\overline{n}}sin\left({\theta }_i-{\theta }_j\right).$$

Here ${\theta }_i(t)$ is the time-varying oscillatory phase of the subthreshold membrane voltage of the i’th cell, ${\omega }_i$is its natural frequency of oscillation, n is the total number of cells in a micro-compartment, and $\kappa (t)$ is a time-dependent parameter describing the strength of their gap junction coupling, which is physiologically modified by shunting inhibition mediated by inputs from the deep cerebellar nuclei (Bengtsson and Hesslow, 2006; Best and Regehr, 2009; Devor and Yarom, 2000; Lang et al., 1996; Lefler et al., 2014). We chose values of ${\omega }_i$ randomly from a Gaussian distribution with a mean of 10 Hz and a s.d. of 2 Hz.

These oscillator dynamics in turn determined each cell’s membrane potential dynamics,

$$V_i(t)=\sin {\theta }_i(t)+DC(t)+\epsilon (t),$$

where DC(t) is a time-varying input that is shared between all the cells and intended to model the general level of motor-related synaptic inputs. $\epsilon (t)$is a term representing input fluctuations; in practice we randomly chose values of $\epsilon (t)$ from a Gaussian-distribution with a s.d. of 4.6% of the spike threshold. This modest level of noise was set so that cells had a ~1 Hz mean spike rate and was based on intracellular electrophysiological recordings showing that the spike threshold of olivary neurons is close to the transmembrane potential value at the peak depolarization of the subthreshold voltage oscillations in these cells (Bazzigaluppi et al., 2012a). Accordingly, we set the peak-to-peak amplitude of the voltage oscillations in the simulation to be 91% of the spike threshold. The value of DC(t) was zero, except for intermittent periods when it was 1.4% of spike threshold. Figure 7 shows results from simulations (2 ms time steps) of networks of size n = 30, 100 or 500, with all cell pairs interconnected; we varied κ from 0−5 in increments of 0.06, and for each κ value we acquired data for a simulated duration of 5 s. For visual clarity, the plots of Figure 7C each show results from randomly chosen sets of 5000 time-steps.

In analytic studies of Kuramoto oscillator networks, it is common to define an order parameter that describes the network’s instantaneous level of phase coherence:

$$r=\left|\langle e^{i{\theta }_j(t)}\rangle \right|,$$

where brackets, 〈·〉, indicate an average over all n oscillators, and |·| denotes the absolute value. To plot distributions in Figure 7E–G comparably to how we treated the Ca²⁺ imaging data, we binned and binarized spikes in the simulations using 25-ms-time bins. In the unlikely event a cell fired two spikes in a single time bin, we recorded only the first spike in the bin.

In the limit of a large number of oscillators, we can analytically compute the coherence parameter, r, as a function of the coupling, κ, using the mean field theory of Kuramoto oscillators (Acebrón et al., 2005). This theory develops a Fokker-Planck equation describing the time-evolution of the distribution of oscillator phases and frequencies and then finds steady-state solutions in which the coherence, r, attains stable values. Using equation 12 from (Acebrón et al., 2005), in the case when the distribution of natural oscillation frequencies, ω_i, is a Gaussian with s.d., σ, then any non-zero value of r must obey the following relation:

$$z^{-1}={\int }_{-1}^{1}du\sqrt{\frac{1-u^2}{2\pi }}{e}^{\frac{-{(rzu)}^2}{2}}$$

where $Z=\kappa /\sigma$ is a dimensionless quantity, the coupling amplitude in units of the frequency dispersion. The right-hand side of this equation, as a function of r, achieves a maximal value of $\sqrt{\pi /8}$ when $r=0$ and decreases with increasing r. Thus, there can be no non-zero solution for r unless $z>\sqrt{8/\pi }\approx 1.6$. Indeed, the function r(𝑧) exhibits a sharp transition from $r=0$ for $z\le \sqrt{8/\pi }$, to $r>0$ for $z>\sqrt{8/\pi }$, reflecting a discrete bifurcation from zero to partial phase coherence. The numerical solution for r(z) is shown in the dashed black lines in Figure 7C, and it shows that a very small change in $z=\kappa /\sigma$ at around $z\approx 1.6$ can implement a significant state change to phase synchronization, as measured by the order parameter r. The numerical simulations confirm this prediction, particularly for large values of n.

For the studies of Figure S7, we simulated a grid of Kuramoto oscillators that were coupled locally, instead of uniformly as in Figure 7. Thus, the phase dynamics were governed by

$$\frac{d{\theta }_i}{dt}={\omega }_i+K(t)$$

where the coupling weights K_ij between neurons were 1 for nearest neighbor cells, 0.5 for next-nearest neighbors, 0.25 for next-next-nearest neighbors, and 0 otherwise, as shown in Figure S7A,B. The membrane dynamics of each cell were determined as in the model of Figure 7, using the same values of DC(t) and ε(t).

Statistical analysis.

We used MATLAB (Mathworks) to perform all statistics tests. For basic comparisons of the medians of two sample sets, we used the Wilcoxon rank-sum test, referred to as a rank-sum test in the main text. To probe whether the median difference between paired sample sets was non-zero, we used the Wilcoxon signed-rank test, termed a signed-rank test in the main text. For tests on frequency distributions, we used Pearson’s chi-squared test, an approximate test that requires relatively large sample sizes, as justified by the many thousands of spiking events in our sample sets. We used exact permutation tests to compare real and shuffled data as outlined above.

Supplementary Material

Supp.Fig7. Figure S7. A Two-dimensional Network of Kuramoto Oscillator Neurons Exhibits Spatially Dependent Patterns of Spike Timing When the Coupling Between Neurons is Strong, Related to Figure 7.

(A,B) To model an olivary cell network with spatially dependent electrical coupling between neurons, we simulated a set of Kuramoto oscillator neurons on a two-dimensional grid, in which each neuron was coupled to other nearby neurons. As in Figure 7, each neuron had its own natural frequency of sub-threshold oscillation that was chosen randomly from a Gaussian distribution with 10 Hz mean and 2 Hz s.d., shared excitatory inputs, sub-threshold voltage noise, and ~1 Hz spike rates mimicking those of real olivary neurons (STAR Methods). The amplitude of coupling, κ, between a pair of cells depended on the distance between them. The diagram, A, and map of coupling strengths, B, show the relative amplitudes of coupling between nearest neighbor, next-nearest neighbor, and next-next nearest neighbor cell pairs; cell pairs with greater separations than these were not directly coupled. As the simulations varied the value of κ, this set of relative coupling amplitudes remained invariant.

(C) We simulated the dynamics of the two-dimensional network (2 ms time-steps) over a range of coupling coefficients, κ. As in analyses of experimental data from the two-photon mesoscope (Figure S2), we examined the spatial dependence of spike timing within a sliding 350-ms-window. For each specific 350-ms-interval considered, we used linear regression to predict the time of each spike based on the two-dimensional position of the cell that fired it; we used the r-value from this regression analysis as a measure of the spatial coherence within that 350-ms-window. Blue data points show values of the spatial coherence, r, for an individual 350-ms-interval, plotted as a function of κ during that interval. For clarity, data from only 5000 randomly chosen time windows are shown. Red line shows the median value of r, as determined across all time windows with a given value of κ.

(D). Top: For zero (κ = 0), medium (κ = 80), and high levels (κ = 119) of coupling (red trace), and with no shared input beyond the shared noise fluctuations, we examined the time-varying spiking of all 121 neurons (blue dots in the raster plot), as well as the oscillatory coherence (green trace), the fraction of cells spiking concurrently (black trace), and the spatial coherence of spike timing, r, (pink trace). Bottom: We visualized the spatial pattern of spike timing in each window by coloring each oscillator by the order in which it spiked in the sequence. Shown are results from 4 different example time intervals of 350 ms. Filled circles denote cells that spiked within the interval, whereas unfilled circles mark cells that did not spike. The color of each filled circle indicates the relative time at which the cell spiked. During time windows with high spatial coherence, there were often wavelike propagations of spiking across the grid of neurons.

Supp.Fig6. Figure S6 |Optogenetic Manipulations of the Nucleo-olivary Pathway, Related to Figure 6.

(A) An image from the fastigial nucleus showing axons of GCaMP6f-expressing Purkinje neurons from lobule V intermingling with cerebellar nuclei neurons that express eArch3.0-mCherry. Thus, Cre-dependent expression of eArch3.0-mCherry was successfully enabled by uptake of CAV-Cre virus into the cerebellar nuclei neurons’ axons in the inferior olive, the site of CAV-Cre injection. A subset of the Purkinje cells that we imaged in vivo likely synapses onto the nuclear neurons that we photo-inhibited with eArch3.0. The blue label is a DAPI counterstain for cell nuclei.

(B) Cerebellar nuclei neurons (white arrows) that expressed eArch3.0-mCherry (red) were also GABAergic, as indicated by positive immunolabeling (green) with anti-GAD67. This fits with anatomical evidence that all GABAergic projection neurons in the cerebellar nuclei send their axons to the inferior olive (De Zeeuw et al., 1998).

(C) Neither bilateral inhibition nor bilateral excitation of the nucleo-olivary pathway affected reach targeting (p = 0.2 and p = 0.7 for inhibition and excitation, respectively, Wilcoxon signed rank test for non-zero median; n = 738 laser-off and 194 bilateral laser-on trials in 4 mice expressing eArch3.0, and 581 laser-off and 156 bilateral laser-on trials in 3 mice expressing BreaChES).

(D) Left, Optogenetic activation of BreaChES-expressing nucleo-olivary cells in the ipsilateral fastigial nucleus during right forelimb reaching led to significantly lower complex spike synchronization as compared to activation of the contralateral fastigial nucleus (p = 0.6 and *p = 0.03 for left and right illumination, respectively, Wilcoxon signed rank test for non-zero median; *p = 0.02 comparing left and right illumination, Wilcoxon rank sum test; trials with left or right unilateral stimulation were randomly interleaved, 20% trials each; n = 75 left and 68 right illumination trials; n = 3 mice). Right, Unlike trials with bilateral illumination (Figure 6F), unilateral inhibition using eArch3.0 had no significant effects on complex spike synchronization (p = 0.1 and p = 0.8 for left and right illumination, respectively, Wilcoxon signed rank test; p = 0.2 comparing left and right illumination, Wilcoxon rank sum test; n = 91 left and 86 right illumination trials; n = 4 mice).

Error bars in C,D: SEM across trials.

Supp.Fig5. Figure S5 | Purkinje Neuron Synchronization is Intrinsic, Preferentially Engages Subsets of Cells, and Reflects Forelimb Movement, Related to Figure 4.

(A) Histogram showing the percentages of synchronized spiking events (>20% of neurons recruited) during reaching in which each Purkinje cell participated (n = 15 mice, 695 neurons). The mean level of participation in synchronized spiking events was 28% (dashed vertical line). Error bars: s.d. estimated based on counting errors.

(B) Cells that reliably participated together in synchronous spikes (>20% of cells recruited) were located closer together than cells that spiked together less frequently. For each percentage value on the x-axis, we identified the set of cells that participated in at least that percentage of synchronous spikes; for this set of cells we then computed the ordinate value as the median separation between all cell pairs of cells in the set. Shading: SEM over 15 mice.

(C) Individual cells’ spike rates during reaching correlated only modestly (r = 0.43) with their participation in synchronous spikes (n = 296 neurons; 8 mice). Hence, differences in synchronous event participation were not fully explained by cells’ differences in spiking activity. Black lines in C–E are linear parametric fits to the data.

(D) Individual cells’ spike rates during rest and reaching were modestly correlated (r = 0.44).

(E) The extent to which individual cells participated in synchronous spiking (>20% of cells recruited) during reaching correlated well with the extent of such participation during rest (r = 0.77). This suggests synchronously spiking cell ensembles have a substantial and well-preserved anatomical structure within individual imaging sessions.

(F) Analogous to Figure 4H, but for three individual mice (from left to right, n = 255, 145, 80 trials and 31, 29, and 52 neurons). Black traces show the time-varying rate of synchronous spiking (>20% of visible Purkinje cells), blue traces show the time-varying probability of full-field concerted silence,averaged across trials, and the dashed black traces show the time-varying rate of synchronous spiking in trial-shuffled data. Shading denotes SEM across trials for the real data, and s.d. across shuffles for trial-shuffled data.

(G) For each of 15 mice (each denoted by pairs of data points with an individual color), we identified inter-trial periods as comprising those time points >2 s from the nearest period of forelimb movement and during which there was little motion (<0.1 mm · s⁻¹) of the robot manipulandum. We then computed the fraction of time that Purkinje neurons exhibited concerted silence during these inter-trial periods or during reaching trials (defined as the intervals [–0.8 s, +0.8 s] relative to a forelimb movement). Reaching trials exhibited significantly more concerted silence (*p = 6 × 10⁻⁵ Wilcoxon sign rank test; n = 15 mice).

(H–J) We computed the average power spectrum of ensemble spiking during reaching, within the interval [−1000 ms, 1000 ms] relative to reach onset. We examined individual Purkinje cells’ complex spike trains along with the time-dependent fraction of active neurons—a measure of ensemble activity. The mean power spectrum of ensemble spiking (H) (STAR Methods; n = 302 neurons in 8 mice) was markedly different from that computed using the trial-shuffled datasets, indicating correlated activity substantially contributes to the power spectrum of ensemble activity. To assess the origins of spectral features, we divided the spectrum for ensemble activity into a cross-spectrum component, (I), arising from pairwise correlated activity between cells and a component arising from individual cells’ spike trains, (J). This division confirmed that the cross-spectrum most faithfully captures the observed spectrum in H. As a control, we verified that the cross-spectrum computed from the trial-shuffled data lacked structure (I, dashed), as expected of uncorrelated cells, whereas the mean spectrum computed from the individual cells’ shuffled activity records was unchanged (J, dashed).

(K) Percentage differences between real and shuffled datasets in the probabilities of 0, 1, 2, 3, 4, or 5 or more Purkinje neurons spiking concurrently in the same 25-ms time bin during reaching trials. Both concerted silence and concurrent spiking with 4 or more Purkinje neurons active in the same time bin were enhanced in the real data. Spiking by individual neurons and the concurrent activation of 2 cells were suppressed in the real data as compared to chance expectations based on the shuffled data (p < 0.001 permutation test). Shaded areas denote SEM across n = 15 mice.

(L) To assess whether body movements other than forelimb motion affected Purkinje neuron synchronization, we manually scored the motion of 6 different body-coordinates prior to forelimb movement (STAR Methods). These 6 parameters were the medio-lateral and anterior-posterior coordinates of the left and right hindpaws, and the dorsal-ventral and anterior-posterior positions of the right forepaw. Each trace in the plot shows the time-varying rate of change in each of these 6 parameters, averaged across all trials (shading denotes the SEM over 167 trials from an example mouse). Only the right forelimb used for reaching exhibited any substantial movement on average.

(M) As a simple metric of total body motion, we averaged the time-varying speeds over all 6 body coordinates shown in L. The trace shows the mean speed, averaged across all trials (shading denotes SEM over n = 522 trials from 3 mice).

(N) In each mouse, we identified the set of 30 trials with the least preparatory body motion, prior to reaching, averaged over the time interval [–300 ms, −100 ms] relative to the onset of forelimb motion. We compared the plots of mean speed of body motion on these trials to that of all trials (shading denotes SEM over n = 167 trials for the example mouse in L).

(O) We compared the patterns of synchronous Purkinje neuron spiking on trials with low body motion (left; 30 trials per mouse; 3 mice) to the spiking patterns on the full set of trials (right). Each row in the plot shows the time-varying magnitude of synchronization on an individual trial. The two sets of trials had similar temporal distributions and levels of spiking synchrony (n = 90 low-body-motion trials; 432 trials total from 3 mice).

(P) The time-dependence of neural synchronization, averaged across trials, was similar for trials with low body motion and the set of all trials. Shading: SEM across the same 90 low-body-motion trials and 432 total trials as in panel O.

(Q) The distributions of peak synchronization levels on the trials with the least preparatory body movement (30 trials per mouse; 3 mice) and the full set of trials were indistinguishable (p = 0.8 Kolmogorov-Smirnov test; n = 432 trials total).

(R) The fractions of Purkinje cell activity that occurred in the form of synchronized spiking did not differ between trials with low body-motion (30 trials per mouse; 3 mice) and the full set of trials (p = 0.3 Kolmogorov-Smirnov test).

(S) We performed a sub-sampling analysis to determine whether trial-to-trial variations in neural synchronization were related to variations in body movement. For each mouse, we identified 50 trials with similar patterns of body motion (STAR Methods; among these trial groups, median correlations between pairs of trials in their time-varying body motion traces were 0.72, 0.66, and 0.76 in the three mice). However, we found no evidence for higher levels of neural synchronization in this subset of trials as compared to the full dataset, and trial-shuffling yielded nearly the same distribution of residual synchrony for this subset of trials and the full dataset.

Supp.Fig4. Figure S4 |Synchronization Covaries with Movement Stereotypy, Related to Figure 3.

(A–J) Analogous to Figure 3D–H, for two additional example mice (n = 250 trials for E and 242 trials for J; p < 10⁻⁶ for both Spearman correlations, permutation test).

(K, L) As in Figure 3I, for each mouse and reaching trial we computed the similarity of the kinematic trajectory to the mean trajectory for that mouse, using the Pearson correlation coefficient to the mean trajectory (blue data points) or the root-mean-square-deviation from the mean trajectory (orange data points). For each trial we also computed the level of synchronized spiking at the Purkinje neurons’ modal response time, K, and the number of Purkinje neurons that spiked at the modal response time, L. These two facets of the neural dynamics significantly covaried trial-by-trial with the movement stereotypy, as quantified using the Spearman correlation coefficient (p = 0.0005, 0.002, 0.002 and 0.003 for the 4 plots shown from left to right in K and L; Wilcoxon sign rank test for non-zero median; n = 18 mice).

Supp.Fig. Figure S3 |Accuracy of Ca²⁺ Spike Time Estimation, Related to Figure 3.

(A) Example two-photon fluorescence image of the cerebellar cortex, upon which is superposed the spatial filter of an individual Purkinje neuron dendritic tree (colored region), as determined by PCA/ICA cell sorting (STAR Methods). We used a glass pipette (outlined in white) to record the cell’s complex spikes electrically.

(B) An extracellular recording trace, annotated with detected complex spikes (dots).

(C) Multiple examples of complex spike waveforms, for each of three cells (cell in B shown in green).

(D) The electrical trace of a single Purkinje dendrite is shown overlaid on a version of the fluorescence trace that was sub-sampled and analyzed using the data in the individual line-scans (STAR Methods). The times of fluorescence peaks that rose above a minimum threshold are marked alongside times of complex spikes in the electrical data. Inset: Portions of both traces are shown on an expanded time scale. The distribution of time differences between complex spikes in the electrical data and peaks in the fluorescence traces as determined using information in the individual line-scans had a s.d. of 8.3 ms. The rate of correct spike detection using the optical data was 96%, and the false-positive detection rate was 0%.

Supp.Fig2. Figure S2. The Spatial Coherence of Purkinje Cell Activity Increases With Learning, Related to Figure 2.

(A, B) Illustration of the method used to compute a pairwise spatial correlation map, for an example Purkinje cell. Example map (A) of the correlation coefficients computed between the spike trains of each Purkinje cell and the chosen example cell that is circled in red in (A) and marked at the origin in (B). For every other individual cell, we computed its spike train correlation coefficient with and anatomical displacement from the chosen cell, thereby yielding a map (B) of spatial correlations in complex spiking activity relative to the chosen cell. The color bar applies to both (A) and (B). There are 493 neurons plus the example cell in each of the two panels.

(C) Maps of the mean spatial correlations in complex spiking activity, generated by averaging over all cells the maps created for individual cells as in (B). The maps here are for individual mice, denoted Mice 1–3, whereas Figure 2J shows maps averaged over these three mice. The spatial coherence of spiking activity during forelimb reaching and inter-trial intervals increased with motor learning (n = 108–502 cells per session), as seen by comparing maps for days early (left column, Days 1, 2) versus late in learning (right column, Days 7, 8).

(D) Mean spike correlation coefficients between pairs of cells, plotted as a function of the distance between the two cells, early (Days 1, 2) and late in learning (Days 7, 8). Shading denotes SEM (n = 108–502 cells per session).

(E–G) Analyses of spatiotemporal coherence for an example timepoint from Mouse 3, Day 8. We first generated a raster plot (E) of the complex spikes (denoted in yellow) fired by all cells within ±175 ms of the selected timepoint (n = 244 spiking neurons for the example time point, 494 cells total). Cells in the raster plot are ordered according to their time of spiking. For cells that spiked more than once, the spike time in the plot was assigned to the mean of the individual spike times. We then created a map that related cells’ relative spike times in the raster plot to the neurons’ physical locations (F) by assigning each cell a color denoting its activation time. Finally, we examined the degree to which cells’ relative times of spiking could be predicted based on the cells’ anatomical locations (G). For this analysis we performed a linear regression of cells’ relative spike times in the raster plot as a function of the neurons’ two-dimensional locations in the Ca²⁺ video. The resulting regression vector provided an approximate direction and magnitude by which spike times varied across the cerebellar surface. The scatter plot in (G) shows for each individual active cell (dots) its actual spike time relative to the selected time bin (y-axis), as a function of the predicted spike time based on the cell’s projected position along the regression vector (x-axis). The linear regression fit is shown in orange (r = 0.48; p = 10⁻⁴, obtained by comparing the real data to 10,000 different shuffled datasets in which the set of spike times was preserved for the selected time bin but cell identities were randomly permuted).

(H) Based on the regression analyses performed as in (G) to predict spike times across the two-dimensional cerebellar surface, we created histograms (right) showing the distributions of the regression vector magnitudes (i.e., the predicted difference in spike times per unit of spatial separation parallel to the regression vector), and polar histograms (left) showing the statistical distributions of the angles of the regression vectors relative to the rostro-caudal dimension. We tabulated these distributions using all time points with statistically significant regression coefficients, as determined in panel (I), for days early in motor learning (top panels, Days 1 and 2, n = 7,986 time points from 3 mice) and late in motor learning (bottom, Days 7 and 8; n = 15,630 time points). The polar plots show the spatial directions in which spike timing varied maximally within the time window used for each regression (mean ± SEM angles of deviation from the anterior-posterior axis were 5 ± 0.5 deg. early in motor learning and 7 ± 0.3 deg. late in learning), whereas the regression vector magnitudes convey the extent to which spike timing varied across the cerebellar surface in the direction of the regression vector (mean ± SEM speeds of wavefront propagation were 9.5 ± 0.5 μm/ms early in motor learning and 10 ± 0.2 μm/ms late in learning). Error bars in polar histograms and shaded regions in the linear histograms denote s.d. based on counting statistics. In the polar histograms, isocontours are spaced at radial increments of 200 counts, and the arrow-headed line denotes the anterior-posterior (AP) dimension.

(I) We performed the regression analysis of (G) for every time frame of the Ca²⁺ video and plotted a histogram of the resulting p-values, determined as in G using shuffled datasets in which cells’ identities were randomly permuted (STAR Methods; n = 580,792 timepoints). A large fraction of time points exhibited spatiotemporal coherence levels that were substantially above those found by chance in shuffled datasets. Inset: Maps in the same format as in F for 3 example timepoints with spatiotemporal coherence far above chance (p<0.0001, from the set of time points comprising the rightmost bar in the histogram).

(J) We identified time points with spatiotemporally coherent spiking activity as those at which the coherence (the r-value determined as in G) exceeded that seen in any of the 10,000 random shuffles (p<0.0001). The plot shows the time-varying, mean probability of spatiotemporal coherence relative to movement onset, for days before (Days 1,2) and after learning (Days 7,8). Shading denotes SEM over all trials (n = 908 and 1214 trials from Days 1,2 and Days 7,8, respectively, from 3 mice).

Supp.Fig1. Figure S1. Motor Learning of the Targeted Forelimb Reaching Task, Related to Figure 1.

(A) Individual video frames showing the progression of a forelimb reaching trial from initiation (t = 0 ms) to completion (t = 200 ms). Red arrows mark the forepaw’s starting position. White arrows denote the forepaw’s instantaneous position in each frame.

(B) On each trial, we quantified the maximal lateral displacement of the forepaw perpendicular to the forward direction (p < 10⁻⁶, comparing Day 1 and Day 8, Wilcoxon rank-sum test; n = 8 mice, 1105, 1284, 1375, 1567, 1688, 1504, 1606 total trials on Days 1–8, respectively). Error bars: SEM across trials.

(C–E) For individual reaching trials (dots), we plotted the displacement between the target endpoint and the actual endpoint of the movement. The plots show the resulting set of targeting errors on Day 1 and Day 8 of training for three individual mice (n = 114 and 193 trials for mouse 1, 114 and 189 trials for mouse 2, and 53 and 169 trials for mouse 3, on Days 1 and 8 respectively). On Day 8, each mouse exhibited a much greater proportion of reaching trials that ended with targeting errors in the 0– 2 mm range, as seen by the density of dots in this range within the Day 8 plots.

(F) Bar plots of the targeting errors and maximum lateral displacements in reaching trials by expert mice (n = 18 mice after 5–11 days of training; dots show individual mice).

(G) Mean position of the robot handle as a function of time relative to the onset of forelimb movement in expert mice, averaged first over individual mice and then over all mice. Shading denotes SEM (n = 18 mice).

Highlights.

• Targeted arm-reaching using a robotic manipulandum as a learned motor task for mice

• Cerebellar climbing fibers develop millimeter-scale synchronization during learning

• Cerebellum to olive feedback regulates synchronized spiking and reach targeting

• Model of coupled phase oscillators explains bifurcation in climbing fiber dynamics