Pharmacodynamics and Bactericidal Activity of Bedaquiline in Pulmonary Tuberculosis

ABSTRACT

Bedaquiline is a diarylquinoline antimycobacterial drug and a key component of several regimens in clinical development for the treatment of tuberculosis (TB) but with ongoing phase 3 trials that include assessment of simplified dosing. A pharmacokinetic-pharmacodynamic model of bedaquiline Mycobacterium tuberculosis-killing kinetics in adults with pulmonary TB was developed to inform dose selection of bedaquiline-containing regimens. The model parameters were estimated with data from the 14-day early bactericidal activity (EBA) study TMC207-CL001 conducted in Cape Town, South Africa. The study included 60 adult males and females with drug-susceptible pulmonary TB, who were administered bedaquiline with loading doses on the first 2 days followed by once-daily 100 mg, 200 mg, 300 mg, or 400 mg. The modeling results included expected values (means ± standard deviations [SDs]) for a maximum drug kill rate constant equal to 0.23 ± 0.03 log₁₀ CFU/mL sputum/day, a half-maximum effective plasma concentration equal to 1.6 ± 0.3 mg/L, and an average time to onset of activity equal to 40 ± 7 h. Model simulations showed that once-daily 200 mg, 300 mg, and 400 mg (without loading doses) attained 40%, 50%, and 60%, respectively, of an expected maximum 14-day EBA equal to 0.18 log₁₀ CFU/mL/day, or 10 h/day assessed by liquid culture time to positivity (TTP). Additional simulations illustrated efficacy outcomes during 8 weeks of treatment with the recommended and alternative dosages. The results demonstrate a general mathematical and statistical approach to the analysis of EBA studies with broad application to TB regimen development.

TEXT

The standard treatment of drug-susceptible tuberculosis (TB) requires combination chemotherapy with at least three drugs and a 6- to 9-month duration, with the prevention of acquired drug resistance as a major objective (1). Consequently, beyond short-duration phase 2a monotherapy studies, the clinical development of novel TB drugs is conducted using combination regimens. Dose selection, however, is based on single-drug pharmacokinetic-pharmacodynamic (PK-PD) target attainment, with optimal dosing chosen with reference to an exposure-based index correlated with efficacy (2, 3). While this approach can account for drug interactions that affect the dose-exposure relationship, it accounts only indirectly for antimicrobial interactions that affect efficacy, which limits the identification of multidrug dose combinations that optimize the regimen as a whole. A model-based approach to dose selection that replaces the static PK-PD index of target attainment with dynamic dose-exposure-response relationships that can distinguish the component drug effects would provide a quantitative tool for optimizing TB regimens.

Bedaquiline (BDQ) is a diarylquinoline antimycobacterial drug that is a key component of several novel regimens in clinical development for drug-susceptible and drug-resistant TB (4). The recommended dosage is 400 mg once daily for 2 weeks followed by 200 mg three times per week for 22 weeks (5). However, an alternative once-daily dosage of 200 mg for 8 weeks and then 100 mg for 18 weeks is currently being tested in two phase 3 trials of bedaquiline-based regimens (6). The phase 3 setting for dose assessment illustrates the uncertainty in transitioning results from early- to late-phase trials (7). While an acceptable dosage may be established for the regimens under current study, there are new drugs advancing through the TB drug development pipeline that can be paired with bedaquiline for entirely novel combinations (8). The challenge of identifying optimized doses for each drug in such combinations motivates an approach that starts with an accurate description of the relationships between experimental measures of exposure and efficacy in the simplest phase 2a monotherapy studies.

A PK-PD model of bedaquiline Mycobacterium tuberculosis-killing kinetics in pulmonary TB patients was developed to quantify the dose-exposure-efficacy relationship during the first 2 weeks of treatment as a basis for dose selection in subsequent testing. A structural model and prior parameter distributions were developed from previously observed time course features of bedaquiline plasma concentrations and sputum mycobacterial load. The prior distributions were updated using Bayesian hierarchical analysis with posterior distributions conditioned on observed data from the 14-day early bactericidal activity (EBA) study TMC207-CL001 (CL001) (ClinicalTrials.gov identifier NCT01215110). Model simulations were conducted to assess goodness of fit, establish once-daily dose-response parameters for the maximum 14-day EBA and half-maximum effective dose, and illustrate expected efficacy outcomes for the recommended and alternative bedaquiline dosages. The results provide a bedaquiline monotherapy limiting case for bactericidal activity that can inform the clinical development of bedaquiline-containing combination regimens.

RESULTS

CL001 participant data.

Time course data from 56 of the 60 participants randomized to the bedaquiline treatment groups were included for analysis. Individual data records, with observations collected from 2 days preceding treatment and from treatment days 1 to 14, consisted of the dosage, daily body weight, bedaquiline plasma concentrations, solid-culture CFU counts per milliliter of sputum, and liquid culture time to positivity (TTP). The baseline characteristics and data sets of the included participants are summarized in Tables 1 and 2. The four excluded participants had pretreatment bedaquiline concentrations above the lower level of quantitation (LLOQ). The missing body weights were from 3 participants, who also accounted for the 74 missing bedaquiline concentrations and for 25 missing pairs of CFU and TTP values. There were no negative culture results. There were four postdose bedaquiline concentrations below the LLOQ and were treated as missing.

TABLE 1.

Baseline characteristics of the participants included for analysis of CL001 dose groups^b

Characteristic	Value for bedaquiline dose groupa
	100 mg	200 mg	300 mg	400 mg
No. of participants	14	15	14	13
No. of male participants (%)	8 (57)	11 (73)	8 (57)	9 (69)
Age (yrs)	27 (18–48)	24 (18–61)	30 (19–47)	29 (20–58)
Body wt (kg)	53 (41–64)	53 (41–73)	50 (44–74)	51 (40–60)
BMI (kg/m2)	19 (15–24)	19 (16–23)	18 (16–27)	18 (16–24)
No. of HIV+ participants (%)	1 (7)	1 (7)	1 (8)	2 (15)
Log10 CFU/mL	6.31 (4.69–7.51)	5.77 (4.72–7.47)	6.33 (3.18–7.82)	6.70 (4.44–7.66)
TTP (days)	4.23 (2.33–7.08)	4.57 (2.90–6.81)	3.96 (2.90–10.20)	3.56 (3.00–5.42)

^aGroup labels correspond to doses on treatment days 3 to 14. Baseline CFU and TTP values are the averages from two pretreatment measurements. Data are medians (ranges) unless indicated otherwise.

^bBMI, body mass index; HIV⁺, human immunodeficiency virus positive; TTP, time to positivity.

TABLE 2.

CL001 data sets for dose groups and data counts for daily body weights, bedaquiline plasma concentrations, and sputum CFU and TTP measurements

Dose group (mg) (no. of participants)	Dosage (mg)a	Total no. of data points (no. of missing data points)b
		BW	BDQ	CFU	TTP
100 (14)	200/100/100	210 (0)	476 (0)	182 (8)	182 (20)
200 (15)	400/300/200	225 (0)	510 (3)	195 (5)	195 (29)
300 (14)	500/400/300	210 (22)	476 (48)	182 (19)	182 (27)
400 (13)	700/500/400	195 (13)	442 (26)	169 (15)	169 (33)

^aDosages are once-daily doses (milligrams) administered on day 1/day 2/days 3 to 14.

^bBW, body weight; BDQ, bedaquiline; TTP, time to positivity.

Structural model.

The PK-PD model was based on previously described features of bedaquiline plasma concentration-time profiles and the M. tuberculosis-killing effect. These features included dose-proportional plasma exposure, an absorption delay and triphasic elimination (9–11), a delayed onset of bactericidal activity followed by a log-linear CFU reduction (12, 13), and a sigmoidal drug exposure-efficacy relationship (14). The complete system of equations represented the change with time (t) of (i) drug mass in an oral absorption depot (q₀) and chain of transit compartments (q_i, i = 1, …, 5), (ii) drug concentrations in a central (C) (plasma) and two peripheral (C₂ and C₃) compartments, and (iii) the sputum CFU per milliliter (N) and TTP (T) as

plasma PK:

$$\frac{d{q}_0}{\mathit{dt}}=-k_{\mathit{tr}}{q}_0+F_{\text{max}}\cdot {\displaystyle \sum }_{n=1}^{N_D}{D}_n\text{δ}\left(t-t_n\right)$$

$$\frac{d{q}_i}{\mathit{dt}}=k_{\mathit{tr}}\left(q_{i-1}-q_i\right),i=1\text{,\hspace{0.17em}}\dots \text{,\hspace{0.17em}}5$$

$$\frac{\mathit{dq}}{\mathit{dt}}=-k_{a}q+k_{\mathit{tr}}{q}_5$$

$$V\frac{\mathit{dC}}{\mathit{dt}}=k_{a}q-Q_2\left(C-C_2\right)-Q_3\left(C-C_3\right)-\mathit{CL}\cdot C$$

$$V_2\frac{d{C}_2}{\mathit{dt}}=Q_2\left(C-C_2\right)$$

$$V_3\frac{d{C}_3}{\mathit{dt}}=Q_3\left(C-C_3\right)$$

sputum PD:

$$\frac{\mathit{dN}}{\mathit{dt}}=\left[\text{λ}\left(1-\frac{N}{K}\right)-\frac{k_d\left(1-e^{-\text{α}\cdot t}\right)C^H}{{\text{EC}}_{50}^H+C^H}\right]\cdot N$$

$$\frac{\mathit{dT}}{\mathit{dt}}=-{\text{τ}}_L\cdot \left[\text{λ}\left(1-\frac{N_0}{K}\text{exp}\left[-\left(T-T_0\right)/{\text{τ}}_L\right]\right)-\frac{k_d\left(1-e^{-\text{α}\cdot t}\right)C^H}{{\text{EC}}_{50}^H+C^H}\right]$$

where the dosage was specified by N_D discrete oral doses (D_n) and administration times (t_n) (n = 1, …, N_D), with a pulsed delta function input to the depot compartment.

The PK parameters consisted of a transit compartment rate constant (k_tr), an oral absorption rate constant (k_a), a central (V) and two peripheral (V₂ and V₃) volumes of distribution, and systemic (CL) and two intercompartmental (Q₂ and Q₃) clearances. The maximum oral bioavailability (F_max) was set equal to 1. The volume and clearance parameters were allometrically scaled with normalized body weight (BW_c) equal to BW/SBW, as V = V_c · BW_c, CL = CL_c · BW_c^3/4, V_i = V_ic · BW_c, and Q_i = Q_ic · BW_c^3/4 (i = 2, 3) (where BW [kilograms] is the total body weight and SBW [equal to 70 kg] is the standard adult body weight [15]). The coefficients V_c, V_ic, CL_c, and Q_ic are allometric normalization constants. The initial conditions for the drug masses and concentrations were equal to zero. The PD parameters consisted of a sputum mycobacterial accumulation rate constant (λ) and carrying capacity (K), a drug kill delay constant (α), a maximum drug kill rate constant (k_d), a half-maximum effective drug concentration (EC₅₀), a Hill coefficient (H), the initial conditions for CFU (N₀) and TTP (T₀), and a liquid culture time constant (τ_L) as a proportionality between the CFU and TTP kinetics.

Parameter estimates.

The unmeasured PK-PD model parameters were treated as random variables and estimated simultaneously for the study population and the CL001 participants as a joint probability distribution conditioned on the observed drug exposure and efficacy data. The PK parameters were estimated first, with the observed daily body weights included as covariates in the allometric scaling relations. The mean values of the individual posterior PK parameter distributions were used as covariates for the plasma concentration-time profiles in the subsequent estimation of the PD parameters, which were conditioned simultaneously on the corresponding individual CFU and TTP data. Missing data were ignored in all calculations, and there was no exclusion of outliers. The PK and PD posterior distributions were sampled using Markov chain Monte Carlo (MCMC) simulation, with 10 independent 60,000-iteration sampling chains and with every 20th of the last 20,000 retained and aggregated into a single 10,000-iteration sample.

The population marginal geometric means and variance distributions were summarized with an arithmetic mean and standard deviation (SD) (16) and are shown in Table 3. The geometric mean represents the central tendency, the variance expressed as a percent coefficient of variation (%CV) represents interindividual variability, and the expected value represents both measures combined as a population mean estimate. While the allometric normalization constants were estimated with the individual observed body weights, a separately generated bootstrap distribution (sample size equal to 10,000) with an expected value (mean ± SD) equal to 53 ± 0.26 kg was used to calculate population expected values for systemic clearance, CL, of 5.7 ± 0.3 L/h, and the volume of distribution at steady state, V_ss (sum of the central and peripheral compartment volumes [V_ss = V + V₂ + V₃]), of 790 ± 80 L. The drug effect terms for the maximum kill rate and liquid culture time constant were based on natural logarithms; in terms of base-10 logarithms, k_d is equal to 0.23 ± 0.03 log₁₀ CFU/mL/day, and τ_L is equal to 55 ± 4 h/log₁₀ CFU/mL. The constant τ_L has an interpretation as the liquid culture doubling time (17), with τ_double = log(2) · τ_L = 17 ± 1 h. The delay constant can be expressed as an average time to effect (t_α) and related to a half-life (t_1/2,α) as $\overline{t_{\text{α}}}$ = 1/α = 40 ± 7 h = t_1/2,α/log(2), with approximately 4 or 5 days to attain 95% of the maximum killing effect.

TABLE 3.

Summary statistics of the population marginal posterior distributions^a

Parameter (unit)	Mean value (SD)
	Geometric mean	%CV	Expected value
PK
ktr (1/h)	2.6 (0.16)	49 (4.7)	2.9 (0.19)
ka (1/h)	0.9 (0.12)	29 (11)	0.94 (0.13)
Vc (L)	120 (9.4)	51 (5.9)	140 (11)
V2c (L)	79 (13)	27 (11)	82 (14)
V3c (L)	750 (84)	45 (8.5)	820 (96)
Q2c (L/h)	6.8 (0.98)	26 (11)	7.0 (1)
Q3c (L/h)	7.3 (0.73)	59 (6.6)	8.5 (0.88)
CLc (L/h)	6.7 (0.31)	30 (4.0)	7.0 (0.33)
PD
Log10 N0 (CFU/mL)	6.2 (0.001)	14 (1.0)	6.3 (0.001)
T0 (days)	4.4 (0.15)	27 (2.9)	4.6 (0.16)
λ (1/h)	0.001 (0.0003)	—b	0.001 (0.0003)
Log10 K (CFU/mL)	8.0 (0.34)	—b	8.0 (0.34)
τL (h)	23 (1.7)	36 (8.4)	24 (1.9)
kd (1/h)	0.019 (0.0021)	53 (9.5)	0.022 (0.0025)
α (1/h)	0.022 (0.0035)	51 (18)	0.025 (0.0043)
EC50 (mg/L)	1.4 (0.24)	48 (17)	1.6 (0.28)
H	1.0 (0.092)	31 (12)	1.0 (0.1)

^aThe expected value is exp(μ + ω²/2), where exp(μ) is the geometric mean and ω² = log(CV² + 1) is the variance with CV (coefficient of variation). The sample size was 10,000.

^b—, not calculated (prior distributions for λ and K).

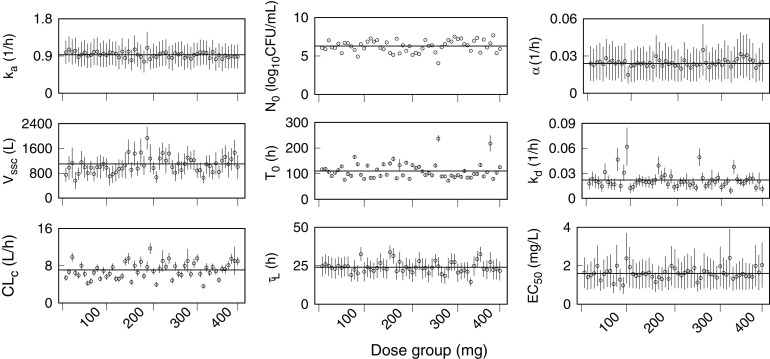
A PK-PD parameter set was determined for each participant. The marginal distributions for each parameter in a set were summarized by an arithmetic mean and SD. Figure 1 shows the mean and SD (for each participant across the four dose groups) of the absorption rate constant, the allometric constants for systemic clearance and volume of distribution at steady state, and the PD parameters for drug effect and initial conditions. Table 4 shows the combined means and their percent relative standard deviations (%RSDs) for the male, female, and total (male and female) participants, together with the observed body weights that were used as covariates for the allometric constants. Multiplication of the allometric constants by the scaled body weight factors gave mean values (%RSDs) for CL equal to 5.3 L/h (30%) for males and 6.6 L/h (20%) for females. Similarly, the V_ss values were equal to 770 L (20%) for males and 800 L (20%) for females. Separation by sex was not based on a covariate analysis but was an assignment (after the parameter estimation process) from the individual participant results to their corresponding male or female identifier. The differences between males and females were small and were consistent with previous conclusions on the CL001 study results regarding a lack of association between age, sex, or ethnicity and any efficacy variable (18). The RSD values are descriptive of interindividual variability, which is illustrated by the fluctuations of individual means about the combined means (horizontal lines) in Fig. 1. The absence of increasing or decreasing trends in the parameter values across the dose groups illustrates the independence of these parameters on drug exposure.

FIG 1.

Individual PK-PD parameter sets for each CL001 participant across the four bedaquiline dose groups. Shown are marginal posterior means (points) and SDs (error bars) of the absorption rate constant, k_a; allometric constants for the volume of distribution at steady state, V_ssc, and systemic clearance, CL_c; the initial sputum CFU per milliliter, N₀, and time to positivity (TTP), T₀; the liquid culture time constant, τ_L; the drug kill rate constant, k_d; the half-maximum effective concentration, EC₅₀; and the drug-kill delay constant, α. The horizontal lines represent the combined individual means for each parameter.

TABLE 4.

Summary statistics of the individual marginal posterior means for the total, male, and female participants^a

Parameter (unit)	Combined mean value (%RSD) for participant group
	Total (n = 56)	Male (n = 36)	Female (n = 20)
PK
BW (kg)b	53 (14)	54 (13)	51 (17)
ktr (1/h)	3.0 (46)	2.9 (43)	3.1 (52)
ka (1/h)	0.93 (7.5)	0.93 (8.0)	0.94 (6.9)
Vc (L)	140 (58)	150 (62)	110 (38)
V2c (L)	82 (4.4)	82 (3.9)	83 (5.3)
V3c (L)	840 (25)	790 (28)	910 (18)
Vssc (L)	1,100 (24)	1,000 (28)	1,100 (17)
Q2c (L/h)	7.2 (5)	7.2 (5.1)	7.2 (5.1)
Q3c (L/h)	9.8 (53)	9.7 (52)	10 (56)
CLc (L/h)	7.1 (24)	6.4 (23)	8.3 (18)
PD
Log10 N0 (CFU/mL)	6.3 (12)	6.2 (12)	6.4 (12)
T0 (days)	4.6 (29)	4.6 (27)	4.6 (32)
τL (h)	24 (15)	24 (16)	23 (13)
kd (1/h)	0.022 (44)	0.022 (45)	0.022 (43)
α (1/h)	0.024 (13)	0.025 (14)	0.024 (8.5)
EC50 (mg/L)	1.6 (18)	1.6 (17)	1.6 (20)
H	1.1 (5)	1.1 (5.1)	1.1 (4.9)

^aData represent the combined means (%RSD [percent relative standard deviation]).

^bBW, observed body weight values.

Model evaluation.

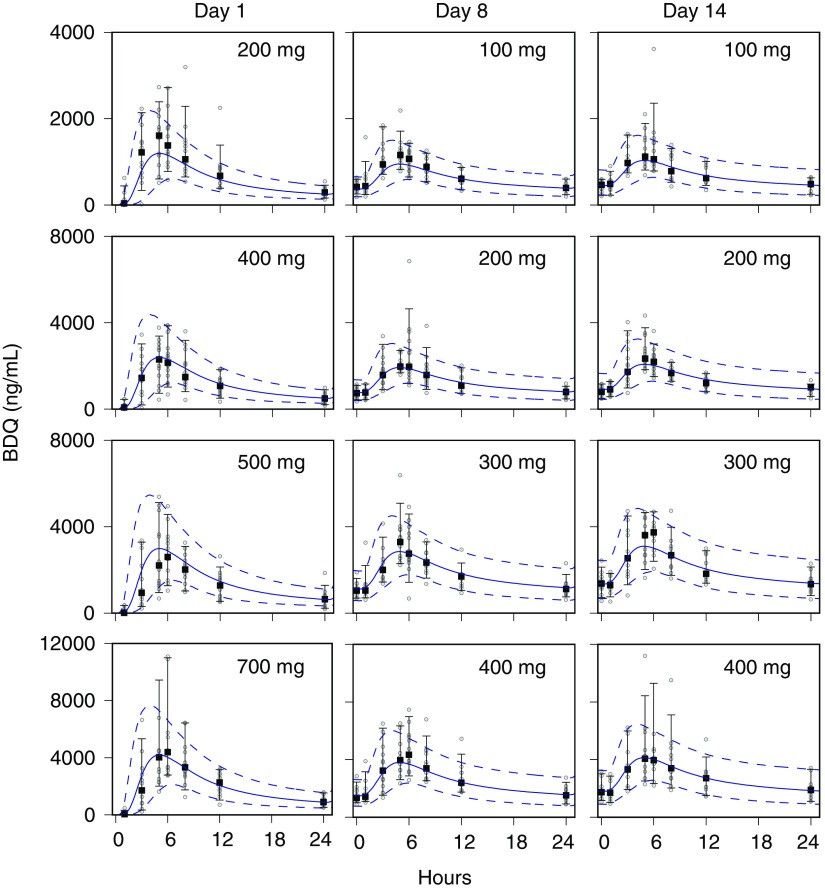
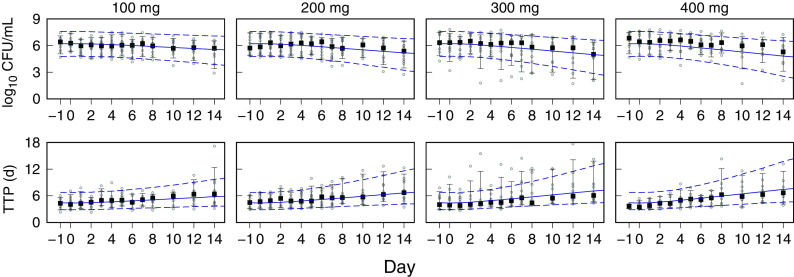
Monte Carlo (MC) simulations of the bedaquiline plasma concentrations, and the sputum CFU per milliliter and TTP, for the CL001 tested dosages are shown with the corresponding observed data in Fig. 2 and 3. The plots show the observed individual participant data points and percentile summaries (5th, median, and 95th percentiles) overlaid with the continuous model-generated distributions (sample size equal to 10,000) and the same percentile summaries. A comparison between the model output and data was made with reference to the peak values and inflection points and by the variation defined by the percentile summaries. For the observed and simulated bedaquiline concentrations shown in Fig. 2, the assumptions of dose-proportional exposure and delayed absorption accounted for the median and range of measured concentrations without clear trends in modeling errors across the four dose groups and throughout the 2-week study duration. For the CFU and TTP data shown in Fig. 3, the modeled patterns of delayed drug effect and log-linear CFU reduction are similarly descriptive of the observed data. The error in median values of the population predicted (PPRED) and observed CFU profiles for the 400-mg dose group can be accounted for as an offset due to higher measured pretreatment sputum CFU than the MC-sampled population distribution (median log₁₀ CFU equal to 6.7 [Table 1] versus 6.2 [Table 3], respectively). The outlying observed CFU and TTP data points seen in the 300-mg group were matching pairs from two participants, one with low bacterial loads throughout the study and the other with a high rate of bactericidal activity contributing points on the last days of treatment, both of whom were accounted for in the model output at the individual level.

FIG 2.

Visual predictive check for bedaquiline (BDQ) plasma concentrations. Observed and model-predicted data for the 100-mg, 200-mg, 300-mg, and 400-mg dose groups on days 1, 8, and 14 are shown. Points, observed data; square points, medians; error bars, 5th and 95th percentiles. For model-predicted Monte Carlo (MC) distributions, medians (solid lines) and 5th and 95th percentiles (dashed lines) are shown. The MC distribution sample size was 10,000.

FIG 3.

Visual predictive check for CFU and time to positivity (TTP). Observed and model-predicted data for the 100-mg, 200-mg, 300-mg, and 400-mg dose groups from study days −1 and 0 (pretreatment) and days 1 to 8, 10, 12, and 14 are shown. Points, observed data; square points, medians; error bars, 5th and 95th percentiles. For model-predicted Monte Carlo (MC) distributions, medians (solid lines) and 5th and 95th percentiles (dashed lines) are shown. The MC distribution sample size was 10,000.

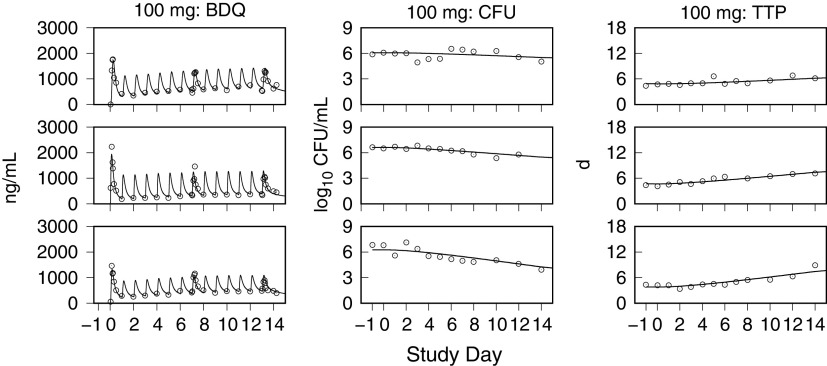
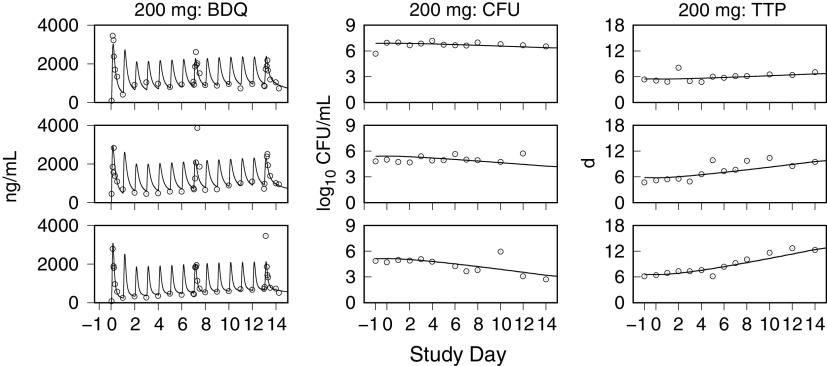
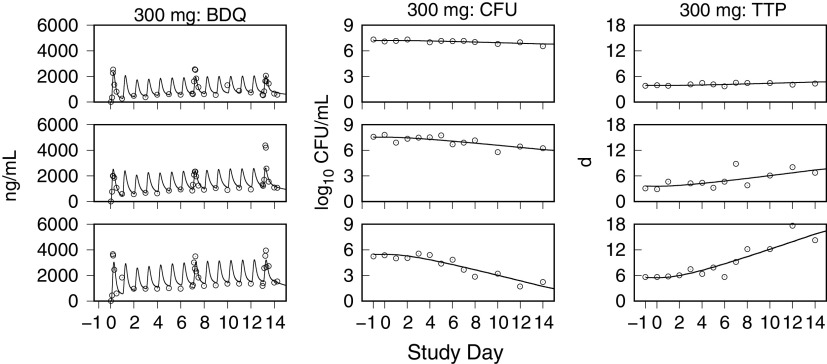
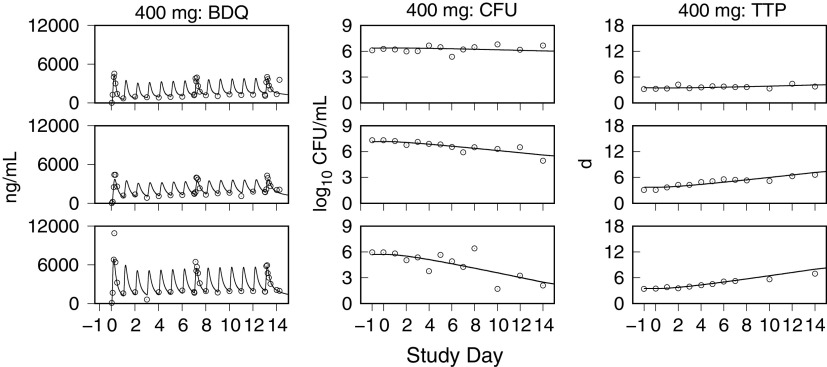
Model simulations of bedaquiline plasma concentrations and the sputum CFU and TTP using the individual PK-PD parameter means are shown together with the observed data in Fig. 4 to 7. These examples show low, intermediate, and high drug kill rates for each dose group and illustrate the correlation between the CFU and TTP profiles over the course of treatment and for the full range of kill rates.

FIG 4.

Representative exposure-response profiles for low (top row), intermediate (middle row), and high (bottom row) drug kill rates from the 100-mg dose group. For individual bedaquiline (BDQ) plasma concentrations, CFU per milliliter of sputum, and time to positivity (TTP), observed (points) and predicted (lines) values from pretreatment through day 14 are shown.

FIG 5.

Representative exposure-response profiles for low (top row), intermediate (middle row), and high (bottom row) drug kill rates from the 200-mg dose group. For individual bedaquiline (BDQ) plasma concentrations, CFU per milliliter of sputum, and time to positivity (TTP), observed (points) and predicted (lines) values from pretreatment through day 14 are shown.

FIG 6.

Representative exposure-response profiles for low (top row), intermediate (middle row), and high (bottom row) drug kill rates from the 300-mg dose group. For individual bedaquiline (BDQ) plasma concentrations, CFU per milliliter of sputum, and time to positivity (TTP), observed (points) and predicted (lines) values from pretreatment through day 14 are shown.

FIG 7.

Representative exposure-response profiles for low (top row), intermediate (middle row), and high (bottom row) drug kill rates from the 400-mg dose group. For individual bedaquiline (BDQ) plasma concentrations, CFU per milliliter of sputum, and time to positivity (TTP), observed (points) and predicted (lines) values from pretreatment through day 14 are shown.

Goodness-of-fit plots for the observed and predicted bedaquiline concentrations and the CFU and TTP are shown in Fig. S4 to S6 in the supplemental material. Statistical summaries of these plots are provided in Table S3. The PPRED values are distribution means from the MC simulations, and the individual predicted (IPRED) values are model simulations using the marginal posterior mean PK-PD parameter sets from each participant. Standardized residuals from a linear least-squares regression of the observed versus predicted values were plotted versus the predicted values and time. There were no substantial asymmetries to inform structural model bias. Also, >98% of the residuals for both population and individual predictions, in all cases, were within 3 standard deviations.

Model predictions.

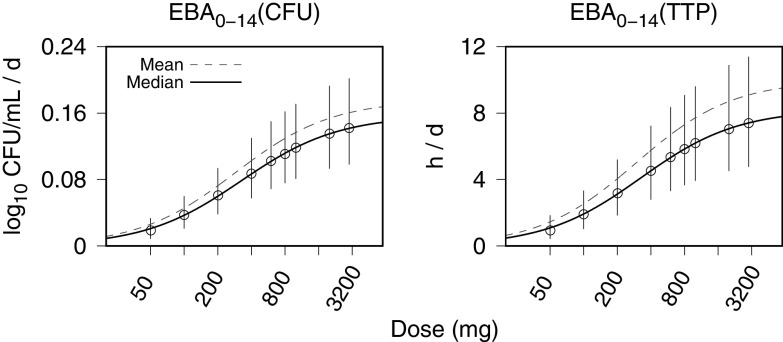
MC simulations of the PK-PD model were used to generate distributions of 14-day EBA values (calculated as the change in the model-predicted log₁₀ CFU per milliliter and TTP from the start of treatment to day 14) for once-daily doses that ranged from 50 mg to 3,000 mg. A dose-response summary of the MC simulation results was obtained using a two-parameter E_max model, E = E_max · D/(D₅₀ + D), where the response, E, is the EBA, E_max is the maximum EBA, D is the dose, and D₅₀ is the half-maximum effective dose. The model was fit (using least-squares regression) to the simulated EBA distribution mean and median values. Figure 8 shows the MC-generated EBA distributions for each simulated dosage summarized by the 5th, median, and 95th percentiles and the E_max curve fits to the mean (data points not shown) and median values. The maximum and half-maximum dose parameters are summarized in Table 5. Algebraic evaluation of the E_max equation using the mean profile parameters yielded expected 14-day EBA values for once-daily 200 mg, 300 mg, and 400 mg equal to 40%, 50%, and 60%, respectively, of the maximum of 0.18 log₁₀ CFU/mL/day, or 10 h/day assessed by TTP.

FIG 8.

Monte Carlo (MC) simulations of PK-PD model-generated 14-day EBA values, calculated for CFU and time to positivity (TTP), from once-daily bedaquiline doses of 50, 100, 200, 400, 600, 800, 1,000, 2,000, and 3,000 mg. Data points (error bars) are the population medians (interquartile ranges [IQRs]). The solid and dashed curves are E_max model fits to the population median and population mean MC simulation output, respectively. The horizontal axis for the dose is shown with logarithm-scale increments. The MC simulation sample size is equal to 10,000.

TABLE 5.

E_max model parameters for population mean and median profiles generated from Monte Carlo PK-PD model simulations of the 14-day EBA for once-daily dosing with a range of 50 to 3,000 mg^a

Population profile	Least-squares estimate for EBA0–14 (SE) using:
	CFU		TTP
	Emax (log10 CFU/mL/day)	D50 (mg)	Emax (h/day)	D50 (mg)
Mean	0.18 (0.0007)	280 (4)	10 (0.04)	290 (5)
Median	0.16 (0.001)	320 (8)	8.2 (0.1)	330 (8)

^aThe MC sample size was 10,000. EBA_0–14, day 0 to day 14 EBA calculated with CFU counts or time to positivity (TTP); E_max, maximum EBA; D₅₀, half-maximum effective dose.

Figure 9 shows PK-PD model simulations, using the population expected values in Table 3, of the time-averaged plasma concentrations, $\overline{C}$ = AUC(t_el)/t_el (where AUC is the area under the concentration-time curve and t_el is the elapsed time); log₁₀ CFU per milliliter; and TTP. The simulations show 8 weeks of treatment with once-daily 200 mg, 300 mg, and 400 mg (without loading doses) and the recommended dosage of 400 mg once daily for 2 weeks followed by dosing three times per week (repeated intervals of 48 h, 72 h, and 48 h). Comparison of the 200-mg dose with the recommended dosage shows that 200 mg underperforms the recommended dosage with respect to efficacy up to day 38 but with greater efficacy afterward. The 300-mg dose nearly matches the efficacy of the recommended dose during the first 4 weeks but continues with greater efficacy after 4 weeks.

FIG 9.

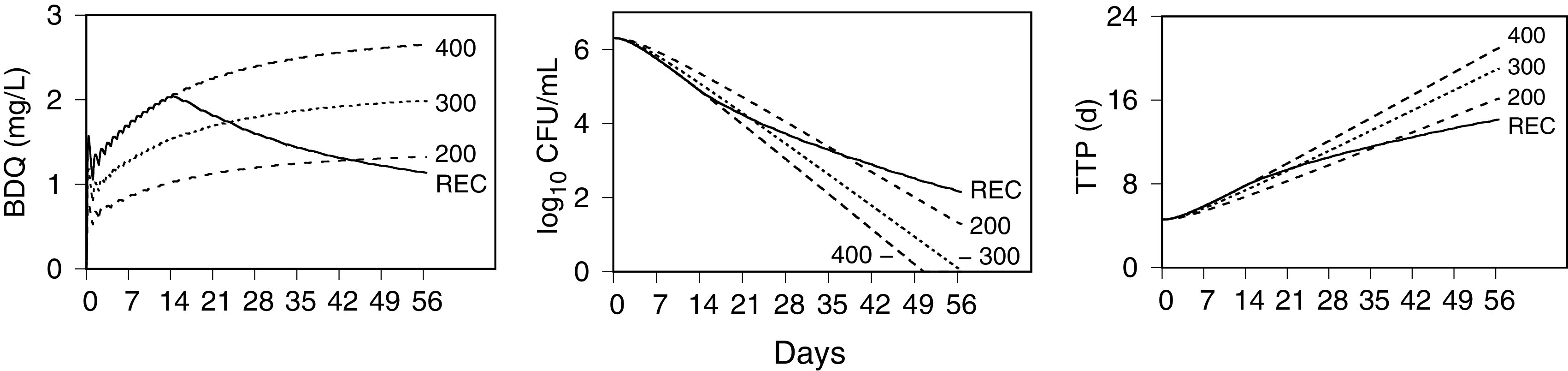
Simulated exposure-response profiles of the recommended and once-daily bedaquiline dosages during 8 weeks of treatment. PK-PD model simulations were performed for a population-typical individual of the time-average bedaquiline (BDQ) plasma concentrations, solid-culture log₁₀ CFU per milliliter of sputum, and liquid culture time to positivity (TTP) for the recommended dose (REC) (400 mg once daily for 2 weeks followed by 200 mg three times per week) and 200 mg, 300 mg, and 400 mg once daily.

The PD model relationship between CFU and TTP (17) can be expressed as

$$T=T_0+2.303\cdot {\text{τ}}_L\cdot {\text{log}}_{10}\left(\frac{N_0}{N}\right)$$

Using a computational threshold for negative solid culture, CFU = N < 1 (crossing the horizontal axis with log₁₀ CFU/ml = 0 in Fig. 9), and the population expected values from Table 3 for τ_L, T₀, and log₁₀ N₀ yields TTP = T > 460 h as the corresponding time to negative liquid culture. For the simulations with population-typical values shown in Fig. 9, culture negativity for the 300-mg and 400-mg once-daily doses is attained by approximately 8 weeks and 7 weeks, respectively.

DISCUSSION

A major challenge for TB regimen development is to quantify the contribution of each component drug to the safety and efficacy of the combination as a whole (19). Such an understanding would enhance the use of regulatory pathways for codevelopment that provide for novel regimens to be developed as a unit (20, 21). The analysis described here of bedaquiline EBA data is a starting point for an approach to dose selection based on dynamic dose-exposure-response relationships (22). For each drug in a regimen, these relationships can be combined into a multidrug PK-PD model (23) and used to identify dosage regimens that best meet the therapeutic objectives (24).

The central results are the system of model equations and the population and individual parameter distributions. Together, they provide a PK-PD model for the bactericidal activity of bedaquiline that is calibrated to the full range of CL001 drug exposure and efficacy data. The PK component was needed to define the individual drug concentration profiles as the input for the PD component, with the main focus being the exposure-efficacy relationship. The latter provided a quantitative description of the bactericidal activity with a maximum drug kill rate constant, a half-maximum effective concentration, a time delay to maximum activity, and a proportionality constant between sputum CFU and TTP rates of change. Model simulations were used to define 14-day EBA maximum- and half-maximum-effect parameters for once-daily dosing. Simulations of expected outcomes over an 8-week time frame indicate that 200 mg once daily is expected to exceed the efficacy of the recommended dosage after the first 5 weeks but with an appreciably lower rate of killing up to that point. The 300-mg once-daily dose was shown to provide a rate of killing similar to that of the recommended dosage and to exceed it by week 4 and may contribute to treatment shortening with negative cultures by week 8.

The PK model was based on typical features of plasma concentration-time profiles in phase 1 study reports (9–11). The transit compartment model for absorption was chosen as a smoothed average of a more complex pattern that resembled a mixed-order or multipeak absorption profile (25). Otherwise, the model equations were consistent with previous bedaquiline PK models (11, 26–28), with the model by McLeay et al. (28) differing in their use of a fourth volume compartment and lag times for absorption.

Bedaquiline is a mycobacterial ATP synthase inhibitor (9). The mathematically modeled pattern of activity consisted of a transient bacteriostatic effect followed by a consistently maintained dose-dependent bactericidal effect. In addition to the delayed onset of bactericidal activity observed in the 7-day EBA study by Rustomjee et al. (12), the same pattern of static and cidal activity was observed in vitro with M. tuberculosis exposure to a wide range of bedaquiline concentrations (13). Results from the latter showed a rapid decrease in the bacterial population growth rate together with metabolic remodeling that induced the dormancy regulon and enhanced the capacity of ATP-generating pathways. This enabled bacterial survival during the first 3 to 4 days of drug exposure, followed by sustained dose-dependent killing. This transient effect was modeled by an exponential decay term (29) multiplying the maximum kill rate constant (as an increasing probability for drug-induced killing with elapsed treatment time) rather than a commonly used PK effect compartment (30).

The relationship between solid-culture CFU and liquid-culture TTP was defined by a proportionality between their rates of change rather than the time course profiles themselves. The PD model parameters for the maximum kill rate constant and half-maximum effective concentration are informed by the CFU data alone, while the TTP equation requires specification of the time constant, τ_L, and the pretreatment CFU. The constant τ_L can be determined by fitting the TTP and CFU profiles simultaneously or from the sputum specimen log-phase growth rate in the liquid culture system (17). The latter is a hypothesis that requires testing. Once τ_L is specified, the TTP and pretreatment CFU may be sufficient to specify the model parameters using TTP without treatment interval CFU counts.

Other models used to describe the bedaquiline exposure-efficacy relationship have been developed (31, 32) but differ from the model presented here in the mathematical framework and the application. They included a time-to-event model of longitudinal TTP measurements and were applied to bedaquiline in combination with other TB drugs in a 24-week phase 2b trial. A comparison can be made, however, between the half-maximum effective concentrations, EC₅₀s, with point values equal to 1.42 mg/L in a study by Svensson and Karlsson (31), 1.57 mg/L in a study by Tanneau et al. (32), and 1.6 mg/L found here.

The PK-PD model was developed in the context of an EBA study as a minimal or base model without covariates (other than body weight) to characterize the relationship between an arbitrary dosage and the time course of bedaquiline plasma concentrations and the sputum CFU and TTP measures of mycobacterial load. As a descriptive model, limitations on inferences that are made in applications beyond the study population and experimental setting apply in the same manner as those based directly on the observed data. For example, the 2-week study duration did not provide enough time to reach steady-state bedaquiline concentrations. In addition to the uncertainty in extrapolating the killing kinetics beyond the observed data and the effects of other drugs in combination, the model predictions for time to negative culture are sensitive to the initial conditions, with higher pretreatment bacterial loads requiring longer treatment. Another limitation of the model is a lack of accounting for drug resistance or for multiple mycobacterial phenotypes and heterogeneous lung and lesion microenvironments (33) that could result in distinct time-kill phases.

The PK-PD model simulations (Fig. 9) of the 300-mg and 400-mg once-daily doses indicate that both may be substantially more effective at shortening treatment than the currently recommended dosage. A recent model-based analysis of bedaquiline and its N-desmethyl metabolite (M2) exposures on QT prolongation and transaminase levels found no exposure-safety relationship with the latter and suggested that dosages that lead to a doubling of M2 exposures relative to the currently approved dosage were not expected to cause QT prolongation increases beyond the recommended cutoff points (34). Modeling and simulation of the M2 exposures for the 300-mg and 400-mg once-daily doses would provide a basis for the assessment of the trade-offs between efficacy and safety.

Bedaquiline-based regimens have the potential to improve current TB treatments, but optimized dosing remains uncertain and may depend on the combination of partner drugs. The PK-PD model for bedaquiline as a single agent provides a limiting case model that can be combined with other drugs to analyze combinations as they proceed through clinical development. One challenge is to model the PD drug-drug interactions for combinations of three or more drugs within the resource constraints of clinical testing. One approach is to build up the interaction terms for a final combination from single and pairwise interactions as described previously for in vitro systems (35, 36). Analysis of EBA studies that include the testing of several single drugs together with their two-drug combinations (37) could provide a basis for such model development. As a general method of analysis, a sequential model-based approach can be tailored to any of the existing or proposed clinical trial designs (7) leading up to the identification of dose-optimized regimens for the phase 2-to-phase 3 transition. This differs from the current approaches to TB regimen development with an emphasis on individual drug component effects rather than single-drug effects in a background regimen.

MATERIALS AND METHODS

TMC207-CL001 trial data.

The CL001 data were obtained from the TB-Platform Aggregation of Clinical TB Studies (TB-PACTS) (https://c-path.org/programs/tb-pacts). Initial results were reported by Diacon et al. (18), including study design, ethics approval, analytical methods, participant characteristics, and efficacy and safety outcomes. CL001 was a phase 2a 14-day EBA study conducted during 2010 in Cape Town, South Africa, and included adult males and females (age range of 18 to 65 years and body weight range of 40 to 90 kg) with newly diagnosed, sputum smear-positive, drug-susceptible pulmonary TB. Patients with human immunodeficiency virus (HIV) infection were eligible with specified exclusion criteria.

There were 68 participants, with 60 randomized to one of four bedaquiline treatment groups (15 participants each) and 8 randomized to a standard regimen group (isoniazid, rifampin, ethambutol, and pyrazinamide) as an active comparator. Bedaquiline was administered once daily, with doses of 100 mg, 200 mg, 300 mg, or 400 mg, on treatment days 3 to 14 and loading doses on days 1 and 2. Blood samples for plasma concentrations of bedaquiline were collected predose on each treatment day, with intensive sampling on days 1, 8, and 14 (days 1 and 8 at 0, 1, 3, 5, 6, 8, and 12 h postdose and day 14 at 0, 1, 3, 5, 6, 8, 12, 24, and 30 h postdose). Drug concentrations were measured using liquid chromatography-tandem mass spectrometry, with a lower level of quantitation (LLOQ) equal to 1 ng/mL. Serial 16-h overnight sputum samples were collected for 2 days pretreatment and on treatment days 1 to 8, 10, 12, and 14. The mycobacterial load was assessed by parallel measurements of solid-culture CFU counts per milliliter of sputum and by time to liquid culture positivity (TTP). Body weights and vital signs were measured daily.

Negative cultures.

A definition and method of analysis for experimentally observed negative cultures, described previously by Diacon et al. (37), consisted of setting the log₁₀ CFU equal to 1 as the solid-medium lower limit of detection and TTP equal to 1,008 h as the longest continued period (42 days) for the liquid cultures (Bactec MGIT 960 mycobacterial growth indicator tube).

Structural model.

The bedaquiline PK-PD model (see Fig. S1 in the supplemental material) was constructed to represent the relationship between the dosage, the plasma concentrations, and the sputum CFU and TTP measurements as functions of time and to include body weight as an input parameter for drug exposure. A relationship between sputum CFU and TTP was described previously (17). The basic modeling assumption was the conservation of typical PK-PD features among individuals, with variation accounted for in differing values of the model parameters. Kinetic features of a bedaquiline dose-exposure-efficacy relationship were identified from phase 1 plasma concentration-time profiles in healthy adults (9–11) and M. tuberculosis time-kill data from TB patients (12), mice (14), and in vitro assays (13). Allometric functions of body weight for drug clearance and volume of distribution were included as physiologically based assumptions (38).

Parameter estimation.

The structural model parameters were estimated using a Bayesian hierarchical model with independent prior distributions, a log-normal (LN) likelihood, and population and individual levels (Fig. S2) (17, 39). Population and individual parameters were estimated simultaneously with a resulting joint posterior distribution conditioned on the observed CL001 data and sampled using Markov chain Monte Carlo (MCMC) simulations. The MCMC simulations consisted of multiple independent sampling chains with stopping criteria set by a Gelman-Rubin diagnostic ($\widehat{R}$) value of <1.1 and an effective sample size (n_eff) of >500 for the entire distribution (16). Parameter values were expressed as natural logarithms (log) and base-10 logarithms (log₁₀).

Each PK-PD parameter θ ∈ (θ₁, θ₂, …) was assigned an LN distribution, θ ∼ LN(μ, ω²). The parameters μ ∈ (μ₁, μ₂, …), which represented central tendency, were sampled from population distributions with geometric means, $\exp (\mu )\sim \text{LN}(M_{\mu }\text{,\hspace{0.17em}}{S}_{\mu }^2)$, where M_μ and S_μ are hyperparameters for the central value estimate and uncertainty in that estimate, respectively, and truncated with bounds defined by plausible measurement ranges. The parameters ${\omega }^2=({\omega }_1^2\text{,\hspace{0.17em}}{\omega }_2^2\text{,\hspace{0.17em}}\dots \text{)}$, which represented interindividual variability, were sampled from half-normal (HN) distributions with mean values set to the expected population variances specified by the coefficient of variation, $\text{CV}=\sqrt{\exp ({\omega }^2)-1}$. Residual-error SDs, σ, were assigned log-uniform (LU) distributions with lower bounds for limited measurement precision and upper bounds large enough to account for unspecified measurement and model error.

Prior distributions for the PK model parameters were based on a bedaquiline phase 1 study by Dooley et al. (10). Noncompartmental analysis and exponential curve peeling of the bedaquiline plasma concentration-time profile were used to specify point estimates of the absorption, volume, and clearance parameters (Table S1 and Fig. S3). A mean transit time was set as the midpoint from dose to peak concentration. Interindividual variability with %CV equal to 30% was based on the clearance and half-life interquartile ranges (IQRs). Measurement uncertainties were set with %CVs equal to 10% or 20%.

Prior distributions for the PD drug effect parameters were based on the sputum CFU-time measurements in the EBA study by Rustomjee et al. (12). The maximum kill rate was calculated from the day 4 to day 7 CFU decline for the 400-mg dose. The drug-kill delay constant was set to obtain 90% of the maximum kill rate by day 4. The half-maximum effective concentration was set to the steady-state concentration for a 200-mg dose obtained by interpolation between the observed 25-mg to 400-mg EBA results. Uncertainties for the kill rate parameters were set with %CV equal to 10%, and that for interindividual variability was set with %CV equal to 40%. The prior mean and variance estimates for the CFU and TTP initial conditions were set from bootstrap mean and SD distributions generated from the pooled pretreatment sputum measurements (16 each) from the 8 participants in the CL001 comparator group. Details of the bootstrap procedure were described previously (17). Distributions for the liquid culture time constant, the sputum mycobacterial accumulation rate, and the carrying capacity were specified from previous EBA modeling results (17).

The PK-PD prior distributions are shown in Table S2. The population distributions for mycobacterial accumulation rate and carrying capacity were not updated in the analysis. The residual errors for the bedaquiline plasma concentrations, TTP, and CFU measurements were σ_BDQ ∼ LU(1.05, 2.3), σ_TTP ∼ LU(1.05, 2.3), and σ_CFU ∼ LU(1.05, 3.6), with lower bounds corresponding to a %CV equal to 5% and upper bounds corresponding to 100% and 200%, respectively.

Model simulations.

The PK-PD model equations were evaluated numerically, with model simulations conducted for specified bedaquiline dosages using the joint posterior population distributions and individual participant PK-PD parameter sets. Monte Carlo (MC) simulations sampled the PK-PD model parameters from the posterior population distributions, with the body weights sampled with replacement from the complete set of observed values. Each MC simulation was run for 10,000 iterations, with the PK-PD model parameters sampled from the same joint posterior population distribution for all dose groups. For individual simulations, the model equations were evaluated using the observed daily body weights and individual marginal posterior means associated with each participant.

Software.

SQLite (version 3.16.2; SQLite Development Team [https://www.sqlite.org]) was used for the TB-PACTS database queries. The GNU MCSim modeling and simulation suite (40) (version 6.2.0 [http://www.gnu.org/software/mcsim]) was used for numerical evaluation of the model equations (using LSODES), including MC and MCMC (using Metropolis-within-Gibbs) simulations. R statistical software (version 3.3.3; R Development Team [https://www.R-project.org]), including the CODA package (version 0.18 [https://cran.r-project.org/web/packages/coda]), was used for statistical analysis. Data plots were generated with gnuplot (version 5.0 [http://www.gnuplot.info/]). The operating system was Linux (version 3.16.0-4-amd64; Debian distribution [https://www.debian.org]).