SAMBA: A novel method for fast automatic model building in nonlinear mixed‐effects models

Abstract

The success of correctly identifying all the components of a nonlinear mixed‐effects model is far from straightforward: it is a question of finding the best structural model, determining the type of relationship between covariates and individual parameters, detecting possible correlations between random effects, or also modeling residual errors. We present the Stochastic Approximation for Model Building Algorithm (SAMBA) procedure and show how this algorithm can be used to speed up this process of model building by identifying at each step how best to improve some of the model components. The principle of this algorithm basically consists in “learning something” about the “best model,” even when a “poor model” is used to fit the data. A comparison study of the SAMBA procedure with Stepwise Covariate Modeling (SCM) and COnditional Sampling use for Stepwise Approach (COSSAC) show similar performances on several real data examples but with a much reduced computing time. This algorithm is now implemented in Monolix and in the R package Rsmlx.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Existing model‐building methods for nonlinear mixed‐effects models have high computational time, especially for selecting the covariate model.

• WHAT QUESTION DID THIS STUDY ADDRESS?

The study describes the principle of the Stochastic Approximation for Model Building Algorithm (SAMBA) procedure, which allows to build a covariate, a correlation, and an error model automatically and compares it with Stepwise Covariate Modeling (SCM) and COnditional Sampling use for Stepwise Approach (COSSAC) procedures.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

SAMBA allows to select the best covariate model without having to fit the complete nonlinear mixed‐effects model to the data for each possible covariate model. This study confirms that it is possible to obtain relevant information on the model we are looking for, even when another model is fitted to the data. This allows to drastically reduce the computation time with respect to other existing procedures while keeping the same performances. We also show that it is possible to perform correlation and error model selection in nonlinear mixed‐effects models.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

This method will allow the practitioner to very quickly find a set of very good models in terms of data fitting and parsimony, even when the number of parameters or the number of covariates available is large.

INTRODUCTION

Construction of a complex (nonlinear) mixed‐effects model ¹ is a challenging process which requires confirmed expertise, advanced statistical methods, and the use of sophisticated software tools, but, above all, time and patience. Indeed, the success of correctly identifying all the components of the model is far from straightforward: it is a question of finding the best structural model, determining the type of relationship between covariates and individual parameters, detecting possible correlations between random effects, or also modeling residual errors. Our goal is to accelerate and optimize this process of model building by identifying at each step how best to improve some of the model components.

The procedure for constructing a model is usually iterative: one adjusts a first model to the data, and diagnosis plots and statistical tests allow to detect possible misspecifications in the proposed model. A new model must then be proposed to correct these defects and improve the predictive abilities of the model. Most of the common approaches consist in stepwise procedures consisting in testing the addition of variable forward and their elimination backward alternatively and progressing through the choice of models using a criterion derived from the log‐likelihood. A widely used approach is Stepwise Covariate Modeling (SCM), ² which consists in an exhaustive search in the covariates space. Each covariate addition or deletion is tested in turn selecting models at each step leading to the best adjustment according to the objective criterion. Approaches such as Wald Approximation Method (WAM) ³ and COnditional Sampling use for Stepwise Approach based on Correlation tests (COSSAC) ⁴ are less computationally intensive as they use, respectively, a likelihood ratio test and a correlation test to move in the covariates space, which allows the testing of less models. All these methods are nevertheless computationally intensive as they require to re‐estimate the model parameters and the likelihood many times. In particular, these methods are very sensitive to “the curse of dimensionality” when the number of covariates to test on parameters is large.

The Generalized Additive Model (GAM) method ⁵ , ⁶ is computationally appealing as it does not require as many models fitting. Indeed, it is based on a regression on the empirical Bayes estimates (EBEs). The EBEs are the modes of the conditional distributions of the individual parameters. In other words, they are the most likely value of the individual parameters, given the estimated population parameters and the data. These estimates are known to be misleading and prone to shrinkage when data are sparse. ⁷ An efficient method which can correct the bias caused by the shrinkage of the EBEs have been recently proposed for covariate analysis. ⁸ , ⁹ In this paper, we propose to develop similar method which relies on the use of random samples from the conditional distribution of each individual parameters instead of EBEs. Indeed, the random sample of the posterior distribution has been shown to correctly control the type I error when performing tests to detect misspecifications in the model. ¹⁰

As for most of the model‐building procedures, the objective of Stochastic Approximation for Model Building Algorithm (SAMBA) is to find a model that minimizes some information criterion, such as Akaike information criterion (AIC), Bayesian Information Criteria (BIC), or corrected BIC (BICc). ¹¹ The main principle of SAMBA is to use the results obtained with a wrong model to learn the right model. Then, SAMBA is an iterative procedure where a new model is used at each iteration of the algorithm. The values of the population parameters of the model are found by maximum likelihood estimation, and, then, the individual parameters are sampled from the conditional distribution defined under this estimated model. These simulated individual parameters combined with the observed data can now be used to select a new statistical model. It is important to underline that, as most of the iterative procedures for non‐convex optimization, SAMBA does not pretend to be capable of always finding the global minimum of the used criterion, but it always allows to quickly find a very good solution.

Two contributions mainly constitute the content of this paper. First, we describe the novel algorithm called SAMBA for fast automatic model building in nonlinear mixed‐effects models (section 1). Second, we benchmark its performances compared with reference methods SCM and COSSAC in real‐world examples (section 2).

METHODS

Model description

Let $y_i=\left(y_{\mathit{ij}},1\le j\le n_i\right)$ be the vector of observations for subject i, where $1\le i\le N$. The model that describes the observations y_i is assumed to be a parametric probabilistic model that depends on a vector of L (individual) parameters ${\psi }_i=\left({\psi }_{i1},\dots ,{\psi }_{\mathit{Li}}\right)$. In a population framework, the vector of parameters ${\psi }_i$ is assumed to be drawn from a population distribution $p({\psi }_i)$. Then, defining a model $\mathcal{M}$ consists in defining a joint probability distribution for the observations $y=(y_1,\cdots ,y_N)$ and for the individual parameters $\psi =({\psi }_1,\cdots ,{\psi }_N)$. For the sake of notation simplicity, we focus on models for continuous longitudinal data. However, extension to models for discrete data and time to event data is straightforward.

Let y _ij, the observation obtained from subject i at time t_ij be described as:

$$u\left(y_{\mathit{ij}}\right)=u\left(f\left(t_{\mathit{ij}},{\psi }_i\right)\right)+g\left(t_{\mathit{ij}},{\psi }_i,\xi \right){\epsilon }_{\mathit{ij}},1\le i\le N,1\le j\le n_i.$$ (1)

The structural model f is a fundamental component of the model because it defines the individual predictions of the observed kinetics for a given set of parameters. The residual errors $({\epsilon }_{\mathit{ij}})$ are assumed to be standardized Gaussian random variables (mean zero and variance 1). The residual error model is represented by function g in model (1) and may depends on some additional parameter $\xi$. Finally, one can use the function u to transform the observations, assuming for instance that they are log‐normally distributed. In the following, we will assume u to be the identity.

We assume a linear model for the individual parameters (up to some transformation h):

$$\begin{array}{c}h({\psi }_i)=h({\psi }_{\mathrm{pop}})+\beta c_i+{\eta }_i,1\le i\le N,\hfill \end{array}$$ (2)

where ${\eta }_i\sim \mathcal{N}(0,\mathrm{\Omega })$ is a vector of random effects and where $c_i$ is a vector of individual covariates used to explain part of the variability of the ${\psi }_i$'s. The ${\psi }_{\mathrm{pop}}$ and $\beta$ are fixed effects. The joint model of $y$ and $\psi$ then depends on a set of parameters $\theta =({\psi }_{\mathrm{pop}},\beta ,\mathrm{\Omega },\xi )$.

Selecting a model described by Equations 1 and 2 consists for the modeler in selecting: (i) the structural model $f$, (ii) the transformation of the individual parameters $h$, (iii) the residual error model $g$, (iv) the list of covariates that have an impact on individual parameters, and (v) the structure of the variance‐covariance matrix of the random effects in the linear model $\mathrm{\Omega }$. The selection of the two first items is problem‐specific, and their selection is out of the scope of this paper. We will therefore assume, in this paper, that $f$ and $h$ are given. The SAMBA procedure proposes solutions to address the selection of the three other components of the model.

The SAMBA procedure

Automatic model building is a difficult task because it is generally not possible to fit and compare all possible models. Moreover, it is necessary to define what is the “best model” among all the possible models. A classical approach consists in searching for the model ${\mathcal{M}}_{\ast }$, that minimizes a criterion, such as the penalized likelihood ¹² , ¹³ :

$${\mathcal{M}}_{\ast }=\text{arg}{\text{min}}_{\mathcal{M}}\left\{{\text{min}}_{\theta }(‐2\log ({\mathcal{L}}_{\mathcal{M}}(\theta ;y)))+\text{pen}(\mathcal{M})\right\}.$$ (3)

The objective of this approach is to find a model that best fits the data (by minimizing $‐2LL$) while being as simple as possible (it is the role of $\mathrm{pen}(\mathcal{M})$ to favor models with few parameters). When the space of possible models is large, an exhaustive search is clearly impossible, and an efficient minimization strategy must be implemented. It is precisely for this purpose that SAMBA was developed: to obtain very quickly the “best” model ${\mathcal{M}}_{\ast }$, or a model with an objective criterion value very close to that of ${\mathcal{M}}_{\ast }$.

SAMBA is an iterative procedure alternating three steps. Assume that model ${\mathcal{M}}_k$ was obtained at iteration $k$ of the algorithm. We first compute ${\theta }^{(k)}$, the maximum likelihood estimate of $\theta$ for model ${\mathcal{M}}_k$. We then generate a set of individual parameters ${\psi }^{(k)}$ from the conditional distribution of individual parameters $p_{{\mathcal{M}}_k}(\psi |y;{\theta }^{\left(k\right)})$. The selection step finally consists in building a new model ${\mathcal{M}}_{k+1}$ using the complete data $(y;{\psi }^{(k)})$ and minimizing the complete penalized criterion:

$${\mathcal{M}}_{k+1}=\text{arg}{\text{min}}_{\mathcal{M}}\left\{{\text{min}}_{\theta }\left(‐2\log \left({\mathcal{L}}_{\mathcal{M}}\left(\theta ;y,{\psi }^{(k)}\right)\right)\right)+\text{pen}\left(\mathcal{M}\right)\right\}.$$ (4)

As already mentioned, the statistical model to be built consists of a covariate model, a correlation model, and a residual error model. Then, the selection of model ${\mathcal{M}}_{k+1}$ is composed of three model selection procedures: the selection of the covariate model ${\mathcal{M}}_{k+1}^{\text{COV}}$, the selection of the correlation model ${\mathcal{M}}_{k+1}^{\text{CORR}}$, and the selection of the error model ${\mathcal{M}}_{k+1}^{\text{ERR}}$. Note that not all these components are necessarily selected: some may have been set arbitrarily because of existing knowledge. By noticing that ${\mathcal{L}}_{\mathcal{M}}\left(\theta ;y,{\psi }^{\left(k\right)}\right)={\mathcal{L}}_{\mathcal{M}}(\theta |y,{\psi }^{\left(k\right)})$ ${\mathcal{L}}_{\mathcal{M}}\left(y,{\psi }^{\left(k\right)}\right)$, it appears that the problem of selecting the error model is independent from the problem of selecting the covariate and correlation models. Figure 1 provides a flowchart of the complete procedure. Let us now take a closer look at what each step of the model selection process consists of.

FIGURE 1.

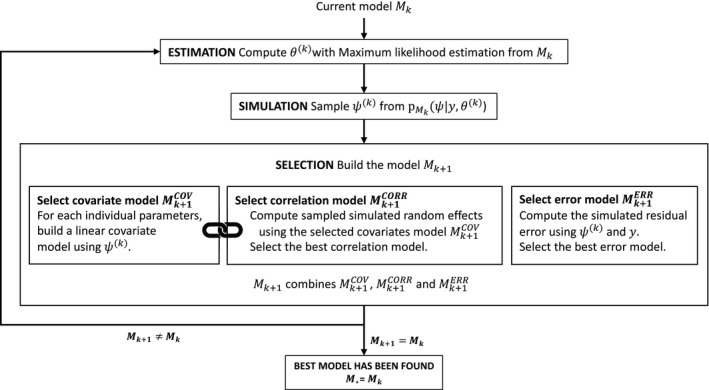
Scheme of the Stochastic Approximation for Model Building Algorithm (SAMBA)

The covariate model selection ${\mathcal{M}}_{\mathbf{k}+1}^{\mathbf{C}\mathbf{O}\mathbf{V}}$

The sample ${\psi }^{(k)}$ has been generated conditionally to the data y and the model ${\mathcal{M}}_k$. For the $\mathcal{l}$‐th parameter, we build a linear model between ${\psi }_{\ell }^{\left(k\right)}$ and covariates c, such as in Equation 2:

$$h_{\ell }\left({\psi }_{i\ell }^{\left(k\right)}\right)=h_{\ell }\left({\psi }_{\text{pop},\ell }\right)+{\beta }_{\ell }{c}_i+{\eta }_{i\ell }^{\left(k\right)},1\le i\le N,1\le \ell \le L,$$ (5)

with $h_{\ell }$ the transformation associated to the $\ell$‐th parameter and where ${\eta }_{i\mathcal{l}}^{(k)}$ is supposed normally distributed with mean zero and variance ${\omega }_{\ell }^2$. We define ${\theta }_{\ell }=\left({\psi }_{\text{pop},\ell },{\beta }_{\ell },{\omega }_{\ell }^2\right)$. Best covariate model for parameter $\ell$, denoted ${\mathcal{M}}_{k+1}^{{\text{COV}}_{\ell }}$, is selected as being the one minimizing a penalized criterion:

$${\mathcal{M}}_{k+1}^{CO{V}_{\ell }}=\text{arg}{\text{min}}_{\mathfrak{M}}\left\{{\text{min}}_{{\theta }_{\ell }}\left(‐2\log \left({\mathcal{L}}_{\mathcal{M}}\left({\theta }_{\ell };{\psi }_{\ell }^{\left(k\right)}\right)\right)\right)+{\text{pen}}^{\text{COV}}(\mathcal{M})\right\}.$$

We denote $n_{\beta }$ the number of non‐null elements in ${\beta }_{\ell }$ for model $\mathcal{M}$. The penalization depends on the criterion selected for optimization: if AIC then ${\text{pen}}^{\text{COV}}\left(\mathcal{M}\right)=2n_{\beta }$, if BIC or BICc then ${\text{pen}}^{\text{COV}}\left(\mathcal{M}\right)=\log \left(N\right)n_{\beta }$. Equation 5 tells us that the covariate selection problem has become here a classical problem of variable selection in a linear model. ¹⁴ This problem is much more easily tractable than the original one. The overall best covariate model combines the best model for each parameter such that ${\mathcal{M}}_{k+1}^{\text{COV}}=\left\{{\mathcal{M}}_{k+1}^{{\text{COV}}_1},\dots {\mathcal{M}}_{k+1}^{{\text{COV}}_L}\right\}$.

In the implemented version of package Rsmlx (R speaks Monolix), two different strategies are implemented depending on the dimension of the selection problem. If the number $d$ of available covariates is less than 11, an exhaustive search is performed over all the $2^d$ possible covariate models for each parameter. Otherwise, the stepwise variable selection procedure implemented in the function stepAIC from package MASS is used. It consists of iteratively adding and removing covariates in stepwise manner to lower the objective criterion.

The correlation model selection ${\mathcal{M}}_{\mathbf{k}+1}^{\mathbf{C}\mathbf{O}\mathbf{R}\mathbf{R}}$

Using the selected covariate model ${\mathcal{M}}_{k+1}^{\mathrm{COV}}$ and the sample of individual parameters ${\psi }_i^{(k)}$, it is possible to extract the vector of individual random effects ${\eta }_i^{\left(k\right)}=\left({\eta }_{i\ell }^{\left(k\right)},\ell =1,\dots ,L\right)$ from Equation 5. Assuming that ${\eta }_i^{\left(k\right)}\sim \mathcal{N}\left(0,\mathrm{\Omega }\right)$ where $\mathrm{\Omega }$ is a block diagonal matrix, the problem of correlation model selection consists in selecting the block structure of $\mathrm{\Omega }$. We then select the correlation model denoted ${\mathcal{M}}_{k+1}^{\text{CORR}}$ by minimizing a penalized criterion:

$${\mathcal{M}}_{k+1}^{\text{CORR}}=\text{arg}{\text{min}}_{\mathcal{M}}\left\{{\text{min}}_{\mathrm{\Omega }}\left(‐2\log \left({\mathcal{L}}_{\mathcal{M}}\left(\mathrm{\Omega };{\eta }_i^{\left(k\right)}\right)\right)\right)+{\text{pen}}^{\text{CORR}}\left(\mathcal{M}\right)\right\}.$$

We denote $n_{\mathrm{\Omega }}$ the number of non‐zero elements in the upper triangular part of the matrix $\mathrm{\Omega }$. The penalization depends on the criterion selected for global optimization: if AIC then ${\text{pen}}^{\text{CORR}}\left(\mathcal{M}\right)=2n_{\mathrm{\Omega }}$, if BIC or BICc then ${\text{pen}}^{\text{CORR}}\left(\mathcal{M}\right)=\log \left(N\right)n_{\mathrm{\Omega }}$.

In the implemented version of package Rsmlx, we limit the size of the block‐structure that can be considered at each iteration. For ${\mathcal{M}}_1$, no correlation can be added and a diagonal matrix is used for $\mathrm{\Omega }$; for ${\mathcal{M}}_2$ only blocks of size two are considered. At iteration $k$ for selection of model ${\mathcal{M}}_{k+1}^{\mathrm{CORR}}$, block size cannot be larger than $k+1$, leading to no more than $(k‐1)k/2$ non‐zero covariance terms in $\mathrm{\Omega }$.

The error model selection ${\mathcal{M}}_{\mathbf{k}+1}^{\mathbf{E}\mathbf{R}\mathbf{R}}$

For a given set of simulated individual parameters $({\psi }_i^{(k)},1\le i\le N)$, the residual errors can easily be computed:

$$e_{\mathit{ij}}^{\left(k\right)}=y_{\mathit{ij}}‐f\left(t_{\mathit{ij}},{\psi }_i^{\left(k\right)}\right),1\le i\le N,1\le j\le n_i.$$

We then fit several error models with standard deviation of the form $g\left(t_{\mathit{ij}},{\psi }_i^{\left(k\right)},\xi \right)$ for $e_{\mathit{ij}}^{\left(k\right)}$ and select the one minimizing a penalized criterion:

$${\mathcal{M}}_{k+1}^{\mathit{ERR}}={\text{argmin}}_{\mathcal{M}}\left\{{\text{min}}_{\xi }\left(‐2\text{log}\left({\mathcal{L}}_{\mathcal{M}}\left(\xi ;e_{\mathit{ij}}^{\left(k\right)}\right)\right))+{\text{pen}}^{\text{ERR}}(\mathcal{M}\right)\right\}.$$

We denote $n_{\xi }$ the length of $\xi$ (i.e., the number of parameters in model $\mathcal{M}$). The penalization depends on the criterion selected for global optimization: if AIC then ${\text{pen}}^{\text{ERR}}\left(\mathcal{M}\right)=2n_{\xi }$, if BIC then ${\text{pen}}^{\text{ERR}}\left(\mathcal{M}\right)=\log \left(N\right)n_{\xi }$, and if BICc then $\text{pen}\left(\mathcal{M}\right)=\log \left(n_{\text{tot}}\right)n_{\xi }$ where $n_{\mathrm{t}ot}$ is the total number of observations, including below the limit of quantification data.

In the implemented version of package Rsmlx, five error models (provided by function $g$in Equation 1) are tested by default: constant ($g_x\left(t_{\mathit{ij}},{\psi }_i^{\left(k\right)},\xi \right)=\xi$), proportional ($g_x\left(t_{\mathit{ij}},{\psi }_i^{\left(k\right)},\xi \right)=\xi f\left(t_{\mathit{ij}},{\psi }_i\right)$), combined₁ ($g_x\left(t_{\mathit{ij}},{\psi }_i^{\left(k\right)},\xi \right)={\xi }_1+{\xi }_{2}f\left(t_{\mathit{ij}},{\psi }_i\right)$), combined₂ ($g_x\left(t_{\mathit{ij}},{\psi }_i^{\left(k\right)},\xi \right)=\sqrt{{\xi }_1^2+{\xi }_2^{2}f\left(t_{\mathit{ij}},{\psi }_i\right)}$), or exponential in which a constant error model is fitted to the $\log (y)$ using the transformation $u=\log$ in Equation 1. Note that it is currently not possible to perform the selection on a restricted number of error models, but such a feature could be easily implemented.

Stopping rule procedure

At each iteration $k$ of the algorithm, we combine ${\mathcal{M}}_{k+1}^{\text{COV}}$, ${\mathcal{M}}_{k+1}^{\text{CORR}}$, and ${\mathcal{M}}_{k+1}^{\text{ERR}}$ to get the new selected model ${\mathcal{M}}_{k+1}$, which is passed forward on to the next estimation‐simulation run. It is important to select the covariate model before the correlation model. On the other hand, the error model can be updated before or after the other two components of the model. The algorithm stops when ${\mathcal{M}}_k$ is strictly identical to ${\mathcal{M}}_{k+1}$ for all components and the last model is the selected one.

Remark

In the above, ${\psi }_i^{\left(k\right)}$ represents a single realization of the conditional distribution $p_{{\mathcal{M}}_k}({\psi }_i|y,{\theta }^{\left(k\right)})$ for each $i=1,\dots N$. Instead of considering only one realization of this distribution, we could use a sample of size $R$ $\left({\psi }_{i\ell ,r}^{\left(k\right)},1\le r\le R\right)$. If so, the linear covariate model described in Equation 5 rewrites:

$$\overline{h_{\ell }\left({\psi }_{\ell ,i}^{\left(k\right)}\right)}=h_{\ell }\left({\psi }_{\ell ,\text{pop}}\right)+{\beta }_{\ell }{c}_i+\overline{{\eta }_{\ell ,i}^{\left(k\right)}},1\le i\le N,1\le \ell \le L,$$

where:

$$\overline{h_{\ell }\left({\psi }_{\ell ,i}^{(k)}\right)}=\frac{1}{R}\sum _{r=1}^R{h}_{\ell }\left({\psi }_{i\ell ,r}^{(k)}\right)$$

Procedures for covariate model selection and correlation model selection remains the same, but using now $\left(\overline{{\psi }_{i\ell }^{\left(k\right)}}\right)$ and $\left(\overline{{\eta }_{i\ell }^{\left(k\right)}}\right)$ at iteration k. On the other hand, the R series of residual errors $\left(e_{ij,r}^{\left(k\right)}\right)$ are used for selecting the residual error model.

RESULTS

Step‐by‐step example of the SAMBA procedure

To illustrate how SAMBA works in practice, we will describe step‐by‐step the complete procedure on the example of remifentanil. ¹⁵ We use here the SAMBA implementation in function buildmlx of the R package Rsmlx, using the default settings.

The remifentanil data

The dataset is composed of 65 healthy adults who have received remifentanil i.v. infusion at a constant infusion rate between 1 and 8 μg⁻¹ kg⁻¹ min⁻¹ for 4 to 20 minutes. Time and rate of infusion are known for each individual. The pharmacokinetic (PK) data consists in the plasma concentration of remifentanil, which is measured during and after infusion for a total of 19 to 53 observations by patients, totaling 2057 observations. A total of six covariates are available: one qualitative covariate, the sex (SEX) and five continuous covariates: the age (AGE), the height (HT), the weight (WT), the lean body mass (LBM), and the body surface area (BSA). All the latter are normalized and log‐transformed for the analysis. In the following, we adopt the notation $\log \text{AGE}=\log \left(\text{AGE}/{\text{AGE}}_{\text{pop}}\right)$, where ${\text{AGE}}_{\text{pop}}$ is a typical value to normalize on (e.g., the mean value of age in the population).

The model

The PK model for i.v. infusion has a central compartment (volume V1), two peripheral compartments (volumes V2 and V3, and intercompartmental clearances Q2 and Q3), and a linear elimination (Cl). Log‐normal distributions are used for the six individual parameters. The 2⁶ = 64 possible covariate models will be considered for each of the six individual parameters. Note that if we had to test all possible models, we would have had to test 64⁶ combinations, which would have made the problem intractable.

SAMBA iterations

We start the SAMBA procedure with a model ${\mathcal{M}}_0$ without any covariate on all parameters, with no correlation between random effects and the so‐called combined₁ error model. Figure 2 illustrates the selection steps on this specific example. One can notice that the BICc, which has been chosen as target criterion, decreases from 7186 for ${\mathcal{M}}_0$ to 6985 for ${\mathcal{M}}_1$, 6957 for ${\mathcal{M}}_2$, and 6903 for ${\mathcal{M}}_3$, which is finally selected as the best model for this example.

• Run 0 (BICc = 7185.8) + Iteration 1: Model ${\mathcal{M}}_0$ is fitted to data and individual parameters are sampled conditionally on the data and this model. Each of the 64 possible linear covariate models is fitted to each individual parameters and the one with lowest BICc is selected. Let us take the example of Cl: the three best models include (1) an effect of logAGE and logWT (BICc = −55.0), (2) an effect of logAGE and logLBM (BICc = −56.1), and (3) an effect of logAGE and logBSA (BICc = −57.5). The latter is chosen as the best model for parameter Cl as it provides the lowest BICc (${\mathcal{M}}_1^{\text{COV},Cl}$). Altogether, for all parameters, the best covariate model (${\mathcal{M}}_1^{\text{COV}}$) includes logAGE on all parameters, logBSA on Cl, and logLBM on V1 and V2. No correlation is added to the model because no correlation is allowed at first iteration. Then, ${\mathcal{M}}_1^{\text{CORR}}$ is a diagonal variance‐covariance matrix for the random effects. Among the tested error models, the three best ones are proportional (BICc = 5815.2), combined₁ (BICc = 5811.2), and combined₂ (BICc = 5807.0), which is selected for ${\mathcal{M}}_1^{\text{ERR}}$. These covariate, correlation, and error models are then passed on to run 1: ${\mathcal{M}}_1=\{\{{\mathcal{M}}_1^{\text{COV},Cl},{\mathcal{M}}_1^{\text{COV},Q2},{\mathcal{M}}_1^{\text{COV},Q3},{\mathcal{M}}_1^{\text{COV},V1},{\mathcal{M}}_1^{\text{COV},V2},{\mathcal{M}}_1^{\text{COV},V3}\},{\mathcal{M}}_1^{\text{CORR}},{\mathcal{M}}_1^{\text{ERR}}\}$}.

• Run 1 (BICc = 6984.9) + Iteration 2: Model ${\mathcal{M}}_1$ is fitted to the data and individual parameters are sampled. Again, the three best model for each covariate are provided. The best covariate model includes logAGE on all parameters except V1, logBSA on Cl, logLBM on V1, and SEX on V2 (${\mathcal{M}}_2^{\text{COV}}$). Block‐structured correlation with blocks up to size 2 are compared (i.e., up to one correlation term). The best three models are with a correlation between parameters Cl and V2 (BICc = 1082.9), between parameters Cl and Q2 (BICc = 1093.8), and between parameters V2 and Q2 (BICc = 1072.0). The latter correlation model is selected for ${\mathcal{M}}_2^{\text{CORR}}$. Residual error model combined₂ remains the best one (${\mathcal{M}}_2^{\text{ERR}}$). These covariate, correlation, and error models are then passed on to run 2.

• Run 2 (BICc = 6956.9) + Iteration 3: Model ${\mathcal{M}}_2$ is fitted to data and individual parameters are sampled. The best covariate model includes logAGE on all parameters except V1, logBSA on Cl, and logLBM on V1 and V2 (${\mathcal{M}}_3^{\text{COV}}$). Block‐structured correlation with blocks up to size 3 are compared (i.e., up to three correlation terms), a correlation block is selected between Cl, Q2, and V2 (${\mathcal{M}}_3^{\text{CORR}}$). Residual error model combined₂ remains the best one (${\mathcal{M}}_3^{\text{ERR}}$). These covariate, correlation, and error models are then passed on to run 3.

• Run 3 (BICc = 6903.4) + Iteration 4: Model ${\mathcal{M}}_3$ is fitted to data and individual parameters are sampled. Of note, regarding the correlation model selection, block‐structured correlation with blocks up to size 4 are compared (i.e., up to six correlation terms). During this iteration, the same model as the one in the previous iteration is selected (${\mathcal{M}}_4={\mathcal{M}}_3$) resulting in the stopping of the procedure. Model ${\mathcal{M}}_3$ is therefore the final model selected with the SAMBA procedure.

FIGURE 2.

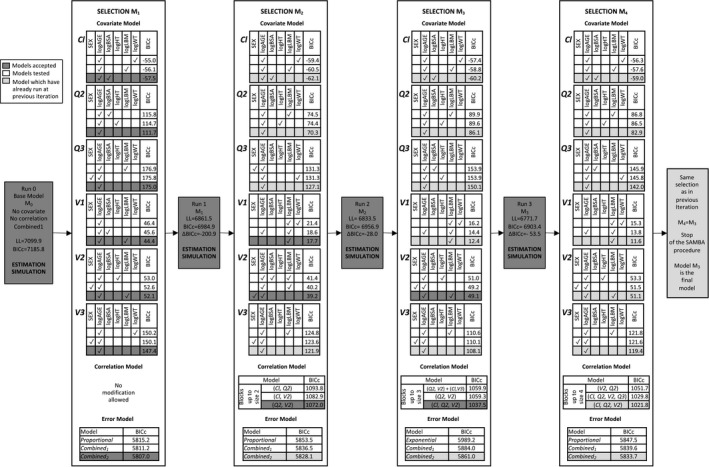
Step‐by‐step Stochastic Approximation for Model Building Algorithm (SAMBA) procedure on the remifentanil example with six covariates (SEX, logAGE, logBSA, logHT, logLBM, and logWT) and six model parameters (Cl, Q2, Q3, V1, V2 and V3). For each selection (covariate, correlation, and error model), the three best models in term of corrected Bayesian Information Criteria (BICc) are displayed. Non selected models are in white, newly accepted models are in darker grey, and models which have been already accepted at previous run are in lighter grey

Converging toward a global optimal model

Even if the selected criterion decreases at each iteration, there is no guarantee that SAMBA converges toward a global minimum of this criterion. The quality and the robustness of the convergence of SAMBA can then be assessed by running SAMBA several times from different starting models. In particular, a good practice is to: (1) launch SAMBA from several initial models, (2) compare the best models found (if there is not only one) in terms of objective criterion (e.g., BICc), and (3) make a thorough analysis and interpretation of the nearby models in order to choose the most relevant one for a given application. Regarding the choice of the starting model, similarly to the Expectation Maximization and Stochastic Approximation Expectation Maximization algorithms, there is no optimal choice. ¹⁶ , ¹⁷ We recommend to test in priority the following three starting models: (1) an empty model, (2) (when possible) a complete model, and (3) a model (or models) that make sense for the biological application. Note that this robustness assessment is standard for all non‐convex optimization algorithms and should also be performed for SCM and COSSAC in routine.

Performances on real examples, and comparison with the SCM and COSSAC procedures

To assess the performances of the SAMBA procedure compared to SCM and COSSAC procedures, we replicate the illustration provided in ref. 4. We applied the three routines to a collection of 10 representative datasets, including PKs, pharmacodynamics, and disease models. Of note, the SCM method for variable selection used here is exactly the same as the one implemented in PsN (Pearl Speaks NONMEM), differences lie in the algorithms used to estimate the parameters of a model and to calculate the likelihood. We restricted the SAMBA procedure to the covariate model selection as correlation and error model selection are not implemented in COSSAC and SCM. The results can be found in Table 1.

TABLE 1.

Comparison of the SAMBA procedure with the SCM and COSSAC procedure on 10 representative datasets

Dataset	Characteristics	SCM		COSSAC		SAMBA		$\mathrm{\Delta }$BICc
		#Runs b	Final Model a	#Runs b	Final Model 1	#Runs b	Final Model a	SAMBA‐SCM	SAMBA‐COSSAC
Warfarin	32 ind. ‐ 247 obs.	44	logtWt ‐ V, Cl	4	Identical	2	Identical	0	0
Linear PK	4 param. ‐ 3 cov.		logtAge ‐ C
	4 re ‐ 1 outcome
Remifentanil	65 ind. ‐ 1992 obs.	295	logLBM – V1	13	logLBM ‐ V1, V 2	4	logLBM ‐ V1	0.8	0.5
Linear PK	6 param. ‐ 6 cov.		logAGE ‐ Cl, Q2, $\mathbf{Q}3$, $V2$, $V3$		logAGE ‐ $\mathit{Cl}$, $Q2$, $V2$, $V3$		logAGE ‐ $\mathit{Cl}$, $Q2$, $\mathbf{Q}3$, $V2$, $V3$
	4 re ‐ 1 outcome		logBSA ‐ $\mathit{Cl}$		logBSA ‐ $\mathit{Cl}$		logBSA ‐ $\mathit{Cl}$
			logHT ‐ $\mathbf{V}2$
					SEX ‐ $\mathbf{V}3$		SEX ‐ $\mathbf{V}2$
Theophylline	12 ind. ‐ 20 obs.	12	logtWEIGHT ‐ $\mathbf{ka}$	4	Identical	2	Identical	0	0
Linear PK	3 param. ‐ 2 cov.
	4 re ‐ 1 outcome
Quinidine	136 ind. ‐ 361 obs.	22	none	11	Identical	1	Identical	0	0
Sparse PK	3 param. ‐ 2 cov.
	3 re ‐ 1 outcome
Tobramycin	97 ind. ‐ 322 obs.	22	logCLCR ‐ $\mathit{Cl}$	6	logCLCR ‐ $\mathit{Cl}$	2	logCLCR ‐ $\mathit{Cl}$	4.2	4.2
Sparse PK	3 param. ‐ 2 cov.		logWT ‐ $\mathbf{V}$		logWT ‐ $\mathbf{V}$		logWT ‐ $\mathbf{Cl}$
	2 re ‐ 1 outcome
Theophylline	18 ind. ‐ 362 obs.	98	logWT ‐ $\mathbf{Tlag}1,\mathbf{V}$	8	logWT ‐ $\mathbf{Tlag}1$	6	logWT ‐ $\mathbf{F},\mathbf{V}$	−11.7	−27
Ext. Rel.	7 param. ‐ 3 cov.				logAGE ‐$\mathbf{ka}2$		logAGE ‐$\mathbf{F}$
Linear PK	7 re ‐ 1 outcome						logHT ‐$\mathbf{ka}1,\mathbf{ka}2,\mathbf{Tlag}1,\mathbf{diffTlag}2$
Warfarin	32 ind. ‐ 247+232 obs.	92	logWT ‐ $\mathit{Cl}$	10	logWT ‐ $\mathit{Cl}$	2	logWT ‐ $\mathit{Cl}$, $\mathbf{V}$	−1.4	−1.4
PK/PD	8 param. ‐ 3 cov.						logAGE ‐$\mathbf{Cl},\mathbf{R}0$
Joint	8 re ‐ 2 outcomes
Cholesterol	200 ind. ‐ 1044 obs.	12	logAGE ‐ $Chol0$, $\mathbf{slope}$	5	logAGE ‐ $Chol0$, $\mathbf{slope}$	2	logAGE ‐ $Chol0$	13.5	13.5
Disease	2 param. ‐ 2 cov.		SEX ‐ $\mathbf{slope}$		SEX ‐ $\mathbf{slope}$
Progression	2 re ‐ 1 outcome
Alzheimer	896 ind. ‐ 3707 obs.	73	APOE ‐ $\mathit{alpha}$, $p0$	8	APOE ‐ $\mathit{alpha}$, $p0$	2	APOE ‐ $\mathit{alpha}$, $p0$	6	1.5
Sparse PK	2 param. ‐ 7 cov.		logAGE ‐ $p0$, $\mathbf{alpha}$		logAGE ‐ $p0$, $\mathbf{alpha}$		logAGE ‐ $p0$
	2 re ‐ 1 outcome		logBMI ‐ $\mathbf{alpha}$		logBMI ‐$\mathbf{alpha}$
			logWT ‐ $p0$		logWT ‐ $p0$		logWT ‐ $p0$
Tranexamic	166 ind. ‐ 817 obs.	298	GROUP ‐ $\mathit{Cl}$, $V2$	12	Identical	2	Identical	0	0
PK	4 param. ‐ 10 cov.		logBMI ‐ Cl
	4 re ‐ 1 outcome		logCOCK ‐ Cl
			logLBW ‐ Q
			logWeight ‐ V2

^a Differences of variable selection between different methods are highlighted in bold.

^b The number of runs is defined as the number of time the estimation and the simulation steps are performed (which is the most time‐consuming).

Because the datasets are real data illustrations, there is no “true” model. It is only possible to compare them in terms of BIC. Of 10 examples, the same best model was proposed by the three procedures in four examples. In two examples, the best model selected by SAMBA was better in terms of BICc than with SCM and COSSAC (Theophylline Ext. Rel. and Warfarin PK/PD). In three other examples, the model with the lowest BICc was not selected by SAMBA. However, the difference in BICc was, respectively, smaller than six in comparison with the SCM procedure and 4.2 in comparison with the COSSAC procedure. We insist on the fact that a difference in BICc does not necessarily have any biological meaning. This is an arbitrary criterion that allows to quantify the goodness of fit with respect to the sparsity of the model chosen. We thus argue that the three procedures lead to rather similar models, which all constitute very good starting points for the modeler to build a model based on biological hypothesis. Finally, in only one example discussed below, the difference in BICc was larger than 10 points of BICc both compared with the SCM and COSSAC procedures.

Regarding the cholesterol dataset, we again ran the SAMBA procedure starting from a full model in which all covariates are supposed to have an effect on all parameters. The new model selected by SAMBA is the full model with an effect of logAGE on (Chol0, slope) and SEX on (Chol0, slope) is much closer in term of BICc than the one selected starting from an empty model ($\mathrm{\Delta }$ BICc = −2). We can finally notice with this example that it is sometimes possible to improve the convergence of SAMBA by improving the convergence of SAEM. Indeed, using 10 Markov chains instead of only one, SAMBA also finds the model selected by SCM and COSSAC. Finding the optimal settings that minimizes computation time while maximizing the probability of finding the best model is an extremely difficult problem that remains open. We can claim that the default settings used in Rsmlx and Monolix give very good results in most cases, but not in all cases with absolute certainty.

In terms of computational effort, it is important to note that the SAMBA procedure completes the model‐building process in much less runs, hence much less CPU time than SCM and COSSAC. In the considered problems, the number of runs and the CPU computation time are equivalent because the other computation times are negligible in the order of a few seconds. Actually, the computation times are six to 149 smaller than for SCM and two to 11 times smaller than for COSSAC. Note that the number of evaluations required by SAMBA is always lower or equal to the number of evaluations performed by COSSAC and SCM.

Simulation study

Data generation and analysis

We simulated data from a one‐compartment PK model. The model has three population parameters ${\text{ka}}_{\text{pop}}=1$, $V_{\text{pop}}=10$ and $C{l}_{\text{pop}}=2$. All individual parameters are log‐normally distributed around the population parameters (${\omega }_{\mathit{ka}}=0.2$, ${\omega }_V=0.3$ and ${\omega }_{\mathit{Cl}}=0.3$). We simulated five individual covariates $\left(C_1,C_2,C_3,C_4,C_5\right)$ from standard normal distributions. The covariate model is such that there only exists linear relationships between $\log \left(V\right)$ and $C_1$ (${\beta }_{V,1}=0.2$), $\text{log}\left(\mathit{Cl}\right)$ and $C_1$ (${\beta }_{Cl,1}=‐0.2$), and $\text{log}\left(\mathit{Cl}\right)$ and $C_2$ (${\beta }_{Cl,2}=0.3$). The correlation model is such that there exists a linear correlation between ${\eta }_V$ and ${\eta }_{\mathit{Cl}}$ (${\rho }_{V,Cl}=0.6$). Finally, the error model is a combined₂ model with $a=2$ and $b=0.1$. A clinical trial could then be simulated by generating PK data from this model for 100 individuals and 11 timepoints (0.25, 0.5, 1, 2, 5, 8, 12, 16, 20, 24, and 30). In order to evaluate the properties of SAMBA by Monte‐Carlo, we simulated 100 replicates of the same trial and built the model for each replicate using SAMBA as implemented in Rsmlx and Monolix for minimizing BICc. The initial model did not include any covariate‐parameter relationship and any correlation between random effect. The initial residual error model was a combined₁ model. The R code used for this Monte‐Carlo study is available as Supplementary Material.

Performances

Table 2 summarizes the results obtained for the covariate model selection. On the one hand, we can see that, for this particular example, SAMBA finds the three existing covariate‐parameter relationships in 100% of the cases. On the other hand, very few spurious relationships are detected (less than 2%). Importantly, in all cases for which the final covariate model included more covariates than the true model $M^{\ast }$, the BICc of the selected model was lower than that of $M^{\ast }$ (the differences ranging from 3 to 14.7 with Rsmlx and from 2.4 to 14.6 for Monolix). In other words, SAMBA always finds a covariate model as good or better than $M^{\ast }$ in terms of BICc. Regarding the selection of the correlation model, the correct model was selected for all the replicates. Finally, the correct error model was selected in 86% of the times with Rsmlx and 85% of the times with Monolix. Note that all the wrong selected error models were all combined₁ model (instead of combined₂) with a slightly larger BICc most of the time. Actually, these two models are quite similar and difficult to distinguish on the basis of a criterion like BICc. SAMBA then may get stuck in a local minimum in such a situation. Finally, and importantly, the final selected models obtained with Rsmlx and Monolix are different in only 6% of cases. These small differences are due to small differences in the implementation of the algorithm (see the Discussion section for more details).

TABLE 2.

Performance of the SAMBA algorithm for the selection of the covariate model in a simulation study using a one‐compartment PK model

Covariates	Rsmlx			Monolix
	$\mathit{ka}$	$V$	$\mathit{Cl}$	$\mathit{ka}$	$V$	$\mathit{Cl}$
$C_1$	2	100	100	2	100	100
$C_2$	0	1	100	0	1	100
$C_3$	1	2	1	2	2	1
$C_4$	0	3	4	0	3	4
$C_5$	0	1	1	1	2	1

One hundred datasets of 100 individuals with 11 observations each have been generated. True model ${\mathcal{M}}^{\ast }$ includes an effect of $C_1$ on $V$ and $\mathit{Cl}$ and an effect of $C_2$ on $\mathit{Cl}$. The percentages of times (over 100 replicates) each covariate‐parameter relationship is selected in the final model are displayed. Implementation of SAMBA in Rsmlx and Monolix are compared.

Abbreviations: Cl, linear elimination; ka, absorption rate constant; PK, pharmacokinetic; SAMBA, Stochastic Approximation for Model Building Algorithm; V, volume.

DISCUSSION

This paper presents a novel model‐building procedure which offers covariate, correlation, and error model selection. It is fast as it requires only a limited number of runs of population parameter estimation and simulation compared to SCM and COSSAC. It allows to explore the space of models rapidly and provides to the modeler a very good model in term of the selection criterion. However, we insist on the fact that this procedure does not aim at replacing model‐building based on biological knowledge, which is, in essence, the strength of mechanistic modeling. Thus, it should not be blindly used and the best—potentially few best—models should be interpreted and compared.

SAMBA is an efficient algorithm for minimizing an objective function. In this paper, we do not aim at evaluating the quality of the criterion used for model selection. ¹⁸ What is of interest here is the convergence of SAMBA. As it is also the case for SCM and COSSAC, SAMBA may not converge to the global minimum. This is particularly the case when the amount of data is too small compared to the complexity of the model to build. This phenomenon will be particularly critical when the number of covariates is high and/or when these are highly correlated. We then strongly encourage the user to build strategies to assess the robustness of the results. Extensions of the proposed algorithm are possible but are outside the scope of this paper and constitute a possible new research direction.

When there is a large number of available covariates, COSSAC and mainly SCM often fail in finding the best model in a reasonable time. In this case, SAMBA represents a particularly appealing approach because the covariate model selection is based on a stepwise variable selection procedure for linear models, which is known to handle high‐dimension problems. Although stepwise AIC/BIC are designed to obtain a sparse estimator that works well on the training set, other methods, such as the lasso, ¹⁹ where the penalty is chosen with cross validation, is designed to obtain the sparse linear model that minimize the prediction error. A lasso type approach ²⁰ can sometimes present better performances than an approach based on an information criterion, such as AIC or BIC, in particular when the number of covariates is very high. However, it should be noted that the choice of the penalty parameter by cross‐validation can be complicated to implement and require a large number of runs. This type of method could be alternatively implemented in the covariate selection procedure and compared in further works. Note finally that it would be interesting to study the behavior of SAMBA using the EBEs (corrected as proposed in ref. 8, 9), rather than the individual simulated parameters, to build the covariate model.

The SAMBA procedure is implemented the R Package Rsmlx in the function buildmlx. ²¹ Minimal required input is a Monolix project used as initial model. Additional arguments can be used to enable specific features (all not listed): select the components of the model to optimize among the covariate, correlation, and error model, restrict the number of parameters or covariates to use, select a specific objective criterion, etc. Rsmlx is on CRAN and the R code can be modified to investigate any of the alternative implementations mentioned above for a specific problem. Note that the execution of Rsmlx requires the Monolix software, because it is only an algorithm combining tasks implemented in Monolix. The R codes allowing to replicate the analyses of this paper are available in the Supplementary Material. All the illustration datasets can be downloaded from the Supporting Information Appendix S2 of ref. 4.

Finally, the SAMBA procedure is also implemented in the Monolix‐GUI software starting from version 2019. Implementation is similar to the one in Rsmlx with two noteworthy differences. First, for the selection of covariates, a stepwise procedure is used even if the number of covariates d is small. Second, compiling differences exist between C++ and R. The full SAMBA procedure is available in the model‐building perspective, under a task called automatic statistical model building method. A single iteration of the SAMBA procedure is also proposed in the section Proposal in the tab Results after running a single estimation and simulation step for a model in Monolix. ²²

CONFLICT OF INTEREST

Marc Lavielle is chief scientist of Lixoft, the company that develops and distributes the Monolix Suite. The other author declared no competing interests for this work.

AUTHOR CONTRIBUTION

M.P. and M.L. wrote the manuscript, designed the research, performed the research, and analyzed the data. M.L. contributed new reagents/analytical tools.

Supporting information

Supplementary Material

Prague M, Lavielle M. SAMBA: A novel method for fast automatic model building in nonlinear mixed‐effects models. CPT Pharmacometrics Syst Pharmacol. 2022;11:161‐172. doi: 10.1002/psp4.12742