Modeling COVID-19 dynamic using a two-strain model with vaccination

Abstract

Multiple strains of the SARS-CoV-2 have arisen and jointly influence the trajectory of the coronavirus disease (COVID-19) pandemic. However, current models rarely account for this multi-strain dynamics and their different transmission rate and response to vaccines. We propose a new mathematical model that accounts for two virus variants and the deployment of a vaccination program. To demonstrate utility, we applied the model to determine the control reproduction number $\left(R_c\right)$ and the per day infection, death and recovery rates of each strain in the US pandemic. The model dynamics predicted the rise of the alpha variant and shed light on potential impact of the delta variant in 2021. We obtained the minimum percentage of fully vaccinated individuals to reduce the spread of the variants in combination with other intervention strategies to deaccelerate the rise of a multi-strain pandemic.

1. Introduction

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) was first reported in 2019 and has since amounted to over 388 million confirmed cases and 5.7 million confirmed deaths around the globe [1]. Much of the world struggled throughout 2020 to slow the spread of the virus by implementing non-pharmaceutical strategies (NPI's), such as partial or total lockdowns, the usage of face masks, among others [2], although these measures were sometimes insufficient to stop the pandemic. Multiple mathematical models have demonstrated that the implementation of face masks did mitigate the spread of the virus [3,4]. Since 2021, the scenario has shifted with the rollout of vaccinations campaigns mixed with the emergence of new SARS-CoV-2 variants with different transmission rates and capable of evasion from the protection provided by the vaccine [5,6].

SARS-CoV-2 is an RNA virus capable of mutagenesis, and new variants have emerged in the ongoing COVID-19 pandemic. The mutated variants are characterized by different sets of mutations and may show varying levels of infectiousness, lethality, and response to the vaccine. The most threatening ones are identified as variants of concern (VOCs) [7]. For example, the SARS-CoV-2 alpha variant, designated B.1.1.7 under the Pango lineage, is among one of the first VOCs. This variant has an N501Y mutation, for which the affected amino acid residue determines how well the virus will interact with the hosts cellular receptor angiotensin-converting enzyme (ACE2) [8]. This mutation resulted in the alpha variant having  a 75% higher transmission rate than the original strain [9]. Another important variant, delta or B.1.617.2, was identified in December 2020 and by April 2021 became the most common variant [10]. This variant is characterized by mutations in the spike protein that have the ability to affect the immune response of the host and enhance transmission. Creating a variant that is 60% more transmissible than the alpha variant and resistant to the vaccine [11].

Mass vaccination started in the US in mid-December with the deployment of BNT162b2 (Pfizer/BioNTech), followed by mRNA-1273 (Moderna) and Ad26.COV2.S (Janssen, J&J, the only vaccine of one dose). By the beginning of May 2021, 34.6 of the US population had been fully vaccinated by either one of these three vaccines [12,13]. While vaccines applied in the US are highly effective in controlling the spread of the Wild-type SARS-CoV-2 strains, they show different effectiveness against new strains like alpha and delta variant [14]. This difference implies that the trajectory of the COVID-19 pandemic will depend on several vaccine related parameters. Multiple mathematical models have been derived to evaluate the behavior of COVID-19, but not many evaluate the dynamics of the spread of a two-strain pandemic. For example Gonzalez-Parra et al, 2021 [ 15 ] derived a compartmental model based on differential equations to evaluate how a new variant can affect the behavior of the pandemic, generating more infections, hospitalizations and deaths [15]. Another important mathematical model using control theory considered multiple strain and waning immunity from natural infection [16]. Both mathematical models describe the interaction between two or more variants, but they do not evaluate the importance of vaccine to stop the spread. Model formulation by Tchoumi et al, 2021 incorporated vaccination in two strain dynamics; they showed that a variant would become dominant if it had a higher reproduction number with respect the other strain. This study only considered vaccine effectiveness for the dynamics of the spread, and the compartment for exposed population was not considered, a latent stage that is present in COVID-19.

We developed a mathematical informed approach where we depict the dynamics of two strains under one vaccination regime, applied to the US COVID-19 pandemic. We quantified the impact of SARS-CoV-2 variants and their response to the vaccination strategy on developing new infections and deaths. Our approach directly addresses the behavior of a vaccine and how it manages to reduce the spread of a virus. It also includes parameters of an imperfect vaccine [17] and three levels of transmission: low, where non-pharmaceutical intervention strategies (NPI) are heavily implemented; baseline, NPI strategies are relaxed; and high transmission where no NPI are deployed. In terms of the vaccination rate, we acknowledge three rates: 50% less than the baseline rate, baseline rate and 200% of the baseline rate. The rest of the paper is structured as follows. We formulated the mathematical model, computed the basic reproduction number, and conducted the local sensitivity analysis. We also derived the minimum percentage of vaccination and the stability of the disease-free equilibrium. In section 3 we calibrated our mathematical model using daily cumulative of infected and death individuals and the global sensitivity analysis of the set of differential equations. In Section 4 we explore the simulations of the cases in the US between variants. Lastly, we provided discussion and conclusion remarks in Section 5.

2. Mathematical Model of a two strain of SARS-CoV-2 with Asymptomatic individuals and Vaccination

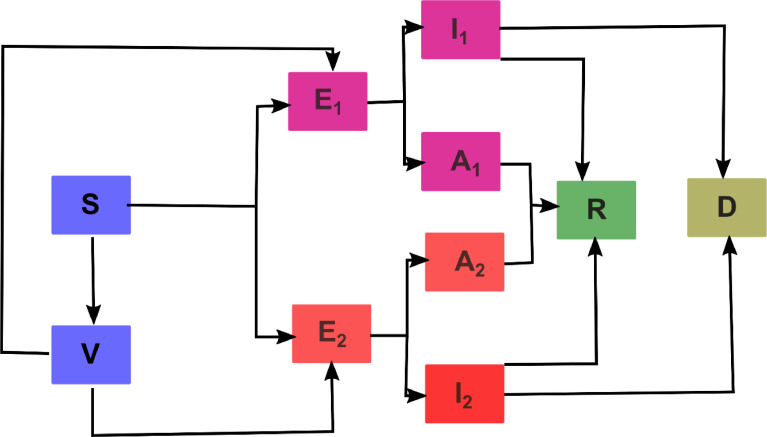
We develop and apply a compartmental differential equation to understand the dynamics of the spread of two virus variants in the US. The mathematical model contains two separate sets of equations for the virus strains that affect the same susceptible population and vaccinated subpopulation. Our SEIARD model evaluates the dynamics of ten subpopulations at any given time $t$, which are denoted as: $S\left(t\right),E_1\left(t\right)$, etc.  Fig 1 shows a diagram of the flow through the compartmentalized subpopulations. In table S1 are the value of the parameters used to evaluate the dynamics of the two strain SARS-CoV-2 in the US.

Fig. 1.

Flow diagram of the multi-strain mathematical model with vaccination to evaluate the spread of the current COVID-19 pandemic. S: susceptible, V: vaccinated with Pfizer, ${\mathit{E}}_1$: exposed to strain one, ${\mathit{I}}_1$: infected with strain one, ${\mathit{A}}_1$: infected asymptomatic with strain one, ${\mathit{E}}_2$: exposed to strain two, ${\mathit{I}}_2$: infected with strain two, ${\mathit{A}}_2$: infected asymptomatic with strain two, R: Recuperated from strain one or two and D: death by either strain one or two.

Susceptible population S(t): We do not consider any natural recruitments (births) at any time $t$. Susceptible population decreases when they interact with a symptomatic original variant infection at a rate ${\beta }_1$ and an asymptomatic original variant infection at a rate ${\beta }_2$. Also, they become exposed with a symptomatic alpha variant at a rate ${\beta }_3$ and asymptomatic at a rate ${\beta }_4$. The susceptible population may increase at a rate $\alpha$ associated with the waning rate of a vaccine, describing that protection descends over time and vaccinated individuals become fully susceptible to infection at a rate $\alpha$. Finally, the susceptible population will be vaccinated at a rate $\rho \ge 0$, multiplied by the all or nothing protection of a vaccine $(1-{\epsilon }_a)$ which means individuals who received the vaccine, but the vaccine fails to protect a fraction ${\epsilon }_a$ of individuals. The rate of change of the susceptible population is expressed in the following equation:

$$\frac{dS}{dt}=-\left(\frac{{\beta }_1{I}_1+{\beta }_2{A}_1}{N}\right)S-\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)S+\alpha V+\eta R-\left(1-{\epsilon }_a\right)\rho S.$$ (1)

Population exposed to strain 1,${\mathit{E}}_1\left(\mathit{t}\right)$: Because we are simulating an infection caused by a virus, we need to include the exposed population. This subpopulation are individuals that are infected but not infectious. It increases at a rate of infection ${\beta }_1$ and ${\beta }_2$ for symptomatic and asymptomatic infection from strain, this increase is due to unvaccinated individuals. In addition, it increases with individuals who are already vaccinated but develop a symptomatic infection at a rate $\left(1-{\epsilon }_L\right){\beta }_1$ and an asymptomatic infection at a rate $\left(1-{\epsilon }_{LA}\right){\beta }_2.$ This behavior is associated with the leakiness or vaccine efficiency, that describes when the vaccine reduces but does not eliminate the risk for infection. This population decreases at a rate $w$, which denotes the average length of the latent period. Hence,

$$\frac{d{E}_1}{dt}=\left(\frac{{\beta }_1{I}_1+{\beta }_2{A}_1}{N}\right)S+(1-{\epsilon }_L)\frac{{\beta }_1{I}_{1}V}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{A}_{1}V}{N}-w{E}_1.$$ (2)

Population infected by strain 1,${\mathit{I}}_1\left(\mathit{t}\right)$: Infected individuals that develop symptoms for the original variant are generated at a proportion $p\in \left(0,1\right)$ from the exposed subpopulation. They recover at a rate ${\gamma }_1$ and die from the disease at a rate ${\delta }_1$. Consequently,

$$\frac{d{I}_1}{dt}=pw{E}_1-\left({\delta }_1+{\gamma }_1\right)I_1.$$ (3)

Asymptomatic population infected by strain 1,${\mathit{A}}_1\left(\mathit{t}\right)$: This population is considered an infected population but do not develop symptoms of COVID-19. They are important to include in our model because they can spread the virus, they are generated at a proportion $\left(1-p\right)$ from the exposed class. This population recovers at a rate ${\gamma }_1$. This population does not die from this disease because they do develop symptoms. So,

$$\frac{d{A}_1}{dt}=\left(1-p\right)w{E}_1-{\gamma }_1{A}_1.$$ (4)

Population exposed to strain 2,${\mathit{E}}_2\left(\mathit{t}\right)$: We include the exposed population to strain 2 because we are modeling a virus and we need to include the latent period. The population enlarges at a rate ${\beta }_3$ for symptomatic infected individual and at a rate ${\beta }_4$ for asymptomatic individuals, both from strain 2 and unvaccinated individuals. Moreover, vaccinated individuals who interact with symptomatic or asymptomatic are incorporated at a rate $\left(1-{\epsilon }_{LB}\right)$, which is the vaccine efficiency associated with that strain. Also, individuals that are vaccinated and protected from strain 1 can get re-infected and develop symptoms or not at a rate ${\beta }_3$ and ${\beta }_4$ respectively from strain 2. This subpopulation deceases at a rate $w$, the length were individuals pass from infected to infected and infectious. Hence,

$$\frac{d{E}_2}{dt}=\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)S+\left(1-{\epsilon }_{LB}\right)\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)V-w{E}_2.$$ (5)

Population infected with strain 2,${\mathit{I}}_2\left(\mathit{t}\right)$: All individuals that are infected and develop symptoms at a proportion $q\in \left(0,1\right)$ who will recover at a rate ${\gamma }_2$ and die at a rate ${\delta }_2$. Consequently,

$$\frac{d{I}_2}{dt}=qw{E}_2-\left({\delta }_2+{\gamma }_2\right)I_2.$$ (6)

Asymptomatic population infected with strain 2,${\mathit{A}}_2\left(\mathit{t}\right)$: individuals that are infected but do not develop symptoms at a proportion $\left(1-q\right)$ from the exposed class. They recover at a rate ${\gamma }_2$. So,

$$\frac{d{A}_2}{dt}=\left(1-q\right)w{E}_2-{\gamma }_2{A}_2.$$ (7)

Recovered population,$\mathit{R}\left(\mathit{t}\right)$: All individuals infected with symptoms or not will recover at a rate ${\gamma }_1$ from the original variant and a rate ${\gamma }_2$ from the alpha variant. We acknowledge in this population the loss of protection from natural immunity at a rate $\eta$. As well recovered individuals vaccinated or not can get re-infected with another SARS-CoV-2 variant at a rate ${\beta }_3$ and ${\beta }_4$ for symptomatic or asymptomatic infections respectively. Consequently,

$$\frac{dR}{dt}={\gamma }_1\left(I_1+A_1\right)+{\gamma }_2\left(I_2+A_2\right)-\left(\frac{{\beta }_3{I}_{2}R}{N}+\frac{{\beta }_4{A}_{2}R}{N}+\eta R\right).$$ (8)

Deceased population,$\mathit{D}\left(\mathit{t}\right)$: Infected individuals with symptoms die at a rate ${\delta }_1$ from the original variant and ${\delta }_2$ for the alpha variant. So,

$$\frac{dD}{dt}={\delta }_1{I}_1+{\delta }_2{I}_{.2}.$$ (9)

Vaccinated population,$\mathit{V}\left(\mathit{t}\right)$: This population is vaccinated at a rate $\rho \ge 0$, multiplied by the all or nothing protection of a vaccine ${\epsilon }_a$ this parameter means individuals who received the vaccine but the vaccine fails to protect them. This population decreases due to the effectiveness of the vaccine at a rate $\left(1-{\epsilon }_L\right)$ for symptomatic strain 1 individuals. Decreases at a rate $\left(1-{\epsilon }_{LA}\right)$ for the asymptomatic strain 1 individuals, and at a rate $\left(1-{\epsilon }_{LB}\right)$ for the symptomatic or asymptomatic of the strain 2. As well, decreases due to the loss of protection from the acquired immunity (vaccine) at a rate $\alpha$. Hence,

$$\begin{array}{ccc}& & \frac{dV}{dt}=\left(1-{\epsilon }_a\right)\rho S-\hfill \\ & & \left(\left(1-{\epsilon }_L\right)\frac{{\beta }_1{I}_1}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{A}_1}{N}+\alpha +\left(1-{\epsilon }_{LB}\right)\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)\right)V.\hfill \end{array}$$ (10)

Henceforth, the system of differential equations that will simulate the dynamics of the original strain and the alpha variant with vaccination is:

$$\begin{array}{ccc}& & \frac{dS}{dt}=-\left(\frac{{\beta }_1{I}_1+{\beta }_2{A}_1}{N}\right)S-\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)S+\alpha V+\eta R\hfill \\ & & -\left(1-{\epsilon }_a\right)\rho S,\hfill \end{array}$$

$$\begin{array}{ccc}& & \frac{dV}{dt}=\left(1-{\epsilon }_a\right)\rho S\hfill \\ & & -\left(\left(1-{\epsilon }_L\right)\frac{{\beta }_1{I}_1}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{A}_1}{N}+\alpha +\left(1-{\epsilon }_{LB}\right)\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)\right)V,\hfill \end{array}$$

$$\frac{d{E}_1}{dt}=\left(\frac{{\beta }_1{I}_1+{\beta }_2{A}_1}{N}\right)S+(1-{\epsilon }_L)\frac{{\beta }_1{I}_{1}V}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{A}_{1}V}{N}-w{E}_1,$$

$$\frac{d{I}_1}{dt}=pw{E}_1-\left({\delta }_1+{\gamma }_1\right)I_1,$$ (11)

$$\frac{d{A}_1}{dt}=\left(1-p\right)w{E}_1-{\gamma }_1{A}_1,$$

$$\begin{array}{ccc}& & \frac{d{E}_2}{dt}=\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)S+\left(1-{\epsilon }_{LB}\right)\left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)V\hfill \\ & & +\frac{{\beta }_3{I}_{2}R}{N}+\frac{{\beta }_4{A}_{2}R}{N}-w{E}_2,\hfill \end{array}$$

$$\frac{d{I}_2}{dt}=qw{E}_2-\left({\delta }_2+{\gamma }_2\right)I_{2,}$$

$$\frac{d{A}_2}{dt}=\left(1-q\right)w{E}_2-{\gamma }_2{A}_2,$$

$$\frac{dR}{dt}={\gamma }_1\left(I_1+A_1\right)+{\gamma }_2\left(I_2+A_2\right)-\left(\frac{{\beta }_3{I}_{2}R}{N}+\frac{{\beta }_4{A}_{2}R}{N}+\eta R\right),$$

$$\frac{dD}{dt}={\delta }_1{I}_1+{\delta }_2{I}_2.$$

We can derive that $N\left(t\right)$ at a time $t$ is given by,

$$\begin{array}{ccc}& & N\left(t\right)=S\left(t\right)+E_1\left(t\right)+I_1\left(t\right)+A_1\left(t\right)+E_2\left(t\right)+I_2\left(t\right)\hfill \\ & & +A_2\left(t\right)+R\left(t\right)+D\left(t\right)+V\left(t\right)\hfill \end{array}$$

2.1. Control reproduction number with a disease-free equilibrium

In our mathematical model, there exists a disease-free equilibrium which happens when the vaccination rate $\rho =0.$ So $E_1=I_1=A_1=E_2=I_2=A_2=0$, and the disease-free equilibrium is:

$$x_0=\left(S^{*},0,0,0,V^{*},0,0,0,0\right)$$

Where $S^{*}\ge 0$ and $V^{*}>0$.

This equilibrium represents where the vaccination logistic program has ended, with a certain number of individuals that are vaccinated, and a population that may be susceptible to get infected. We will compute the control reproduction number $R_c$ in this disease-free equilibrium. By applying the next generation method to find $R_c$, we must solve the following equation: $R_c=\rho \left(F{V}^{-1}\right)$ [12]. Where F are the derivatives of the new infections, V is the transition matrix (flow between compartments) and $\rho$ is the spectral radius. The entire derivation of $R_c$ is as follows.

The matrix of new infections $\mathcal{F}$ is given by

$$\mathcal{F}=\left[\begin{array}{c}\left(\frac{{\beta }_1{I}_1+{\beta }_2{A}_1}{N}\right)S+\left(1-{\epsilon }_L\right)\frac{{\beta }_1{I}_{1}V}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{A}_{1}V}{N}\\ 0\\ 0\\ \left(\frac{{\beta }_3{I}_2+{\beta }_4{A}_2}{N}\right)S+\left(1-{\epsilon }_{LB}\right)\left(\frac{{\beta }_1{I}_1+{\beta }_2{A}_1}{N}\right)S+\frac{{\beta }_3{I}_{2}R}{N}+\frac{{\beta }_4{A}_{2}R}{N}\\ 0\\ 0\end{array}\right].$$

While the transition matrix $\mathcal{V}$ is given by

$$\mathcal{V}=\left[\begin{array}{c}w{E}_1\\ -pw{E}_1+\left({\delta }_1+{\gamma }_1\right)I_1\\ -\left(1-p\right)w{E}_1+{\gamma }_1{A}_1\\ w{E}_2\\ -qw{E}_2+\left({\delta }_2+{\gamma }_2\right)I_2\\ -\left(1-q\right)w{E}_2+{\gamma }_2{A}_2\end{array}\right].$$

Using the following transformations $a\prime =-pw$, $b\prime =-\left(1-p\right)w$, $c={\gamma }_1+{\delta }_1$, $d={\gamma }_1$, $e=-qw$, $f=-\left(1-q\right)w$, $g={\gamma }_2+{\delta }_2$, $h={\gamma }_2$, $u=\frac{{\beta }_1{S}^{*}}{N^{*}}+\left(1-{\epsilon }_L\right)\frac{{\beta }_1{V}^{*}}{N^{*}}$, $x=\frac{{\beta }_2{S}^{*}}{N^{*}}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{V}^{*}}{N^{*}}$, $y=\frac{{\beta }_3{S}^{*}}{N^{*}}+\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_3{V}^{*}}{N^{*}}$ and $z=\frac{{\beta }_4{S}^{*}}{N^{*}}+\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_4{V}^{*}}{N^{*}}$ consequently,

$$F=\left[\begin{array}{cccccc}0& u& x& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& y& z\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right].$$

$$V=\left[\begin{array}{cccccc}w& 0& 0& 0& 0& 0\\ a\prime & c& 0& 0& 0& 0\\ b\prime & 0& d& 0& 0& 0\\ 0& 0& 0& w& 0& 0\\ 0& 0& 0& e& g& 0\\ 0& 0& 0& f& 0& h\end{array}\right].$$

In consequence,

$$V^{-1}=\left[\begin{array}{cccccc}\frac{1}{w}& 0& 0& 0& 0& 0\\ -\frac{a\prime }{cw}& \frac{1}{c}& 0& 0& 0& 0\\ -\frac{b\prime }{dw}& 0& \frac{1}{d}& 0& 0& 0\\ 0& 0& 0& \frac{1}{w}& 0& 0\\ 0& 0& 0& -\frac{e}{gw}& \frac{1}{g}& 0\\ 0& 0& 0& -\frac{f}{hw}& 0& \frac{1}{h}\end{array}\right].$$

So that,

$$F{V}^{-1}=\left[\begin{array}{cccccc}a& \frac{u}{c}& \frac{x}{d}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& b& \frac{y}{g}& \frac{z}{h}\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right].$$

Where

$$\begin{array}{ccc}& & a=-\frac{b\prime x}{dw}-\frac{a\prime u}{cw}\hfill \\ & & =\frac{\left(1-p\right)\left[\frac{{\beta }_{2}S}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_{2}V}{N}\right]}{{\gamma }_1}+\frac{\left(p\right)\left[\frac{{\beta }_{1}S}{N}+\left(1-{\epsilon }_L\right)\frac{{\beta }_{1}V}{N}\right]}{{\gamma }_1+{\delta }_1}.\hfill \end{array}$$

$$\begin{array}{ccc}& & b=-\frac{ey}{gw}-\frac{fz}{hw}\hfill \\ & & =\frac{\left(1-q\right)\left[\frac{{\beta }_{4}S}{N}+\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_{4}V}{N}\right]}{{\gamma }_2}+\frac{\left(q\right)\left[\frac{{\beta }_{3}S}{N}+\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_{3}V}{N}\right]}{{\gamma }_2+{\delta }_2}.\hfill \end{array}$$

Since is $F{V}^{-1}$ upper triangular, we have that $F{V}^{-1}-{\lambda }_6$ is also triangular, whence its determinate is the product of the main diagonal, that is, the characteristic polynomial is given by

${\lambda }^4\left(\lambda -a\right)\left(\lambda -b\right)$, then the basic reproduction number is given by $R_c=max\left\{\left|a\right|,\left|b\right|\right\}$.

$$R_c\left(a\right)=\frac{\left(1-p\right)\left[\frac{{\beta }_{2}S}{N}+\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_{2}V}{N}\right]}{{\gamma }_1}+\frac{\left(p\right)\left[\frac{{\beta }_{1}S}{N}+\left(1-{\epsilon }_L\right)\frac{{\beta }_{1}V}{N}\right]}{{\gamma }_1+{\delta }_1},$$ (12)

$$R_c\left(b\right)=\frac{\left(1-q\right)\left[\frac{{\beta }_{4}S}{N}+\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_{4}V}{N}\right]}{{\gamma }_2}+\frac{\left(q\right)\left[\frac{{\beta }_{3}S}{N}+\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_{3}V}{N}\right]}{{\gamma }_2+{\delta }_2}.$$ (13)

As we can see in 12 and 13, we have the control reproduction number of strain 1 (12) and strain 2 (13). We can reformulate both control reproduction numbers based on the basic reproduction number and the force of infection of both symptomatic and asymptomatic for both variants, as follows:

For strain 1, the control reproduction number can be re-written based on the force of infections with or without symptoms in the absence of vaccination like in [18] . The basic reproduction numbers are: $R_{01A}=\frac{\left(1-p\right){\beta }_2}{{\gamma }_1}$ for asymptomatic; $R_{01I}=\frac{p{\beta }_1}{{\gamma }_1+{\delta }_1}$ for symptomatic infections. So,

$$R_c\left(a\right)=R_{01A}\left[\frac{S}{N}+\left(1-{\epsilon }_{LA}\right)\frac{V}{N}\right]+R_{01I}\left[\frac{S}{N}+\left(1-{\epsilon }_L\right)\frac{V}{N}\right],$$

$$R_c\left(a\right)=R_{01A}\left[\frac{S+V}{N}-{\epsilon }_{LA}\frac{V}{N}\right]+R_{01I}\left[\frac{S+V}{N}-{\epsilon }_L\frac{V}{N}\right].$$

We apply the same idea to the control reproduction number for the second strain. The reproduction numbers are: $R_{02A}=\frac{\left(1-q\right){\beta }_4}{{\gamma }_2}$; $R_{02I}=\frac{q{\beta }_3}{{\gamma }_2+{\delta }_2}$. Consequently

$$R_c\left(b\right)=R_{02A}\left[\frac{S}{N}+\left(1-{\epsilon }_{LB}\right)\frac{V}{N}+\frac{R}{N}\right]+R_{02I}\left[\frac{S}{N}+\left(1-{\epsilon }_{LB}\right)\frac{V}{N}+\frac{R}{N}\right],$$

$$R_c\left(b\right)=R_{02A}\left[\frac{S+V}{N}-{\epsilon }_{LB}\frac{V}{N}\right]+R_{02I}\left[\frac{S+V}{N}-{\epsilon }_{LB}\frac{V}{N}\right].$$

We can still rearrange the terms, to try to evaluate how the impact of vaccinations is associated with diminishing the control reproduction number. From the disease-free equilibrium defined by

$$E^{*}=\left(S^{*},\frac{\left(1-{\epsilon }_a\right)*S^{*}}{\alpha },0,0,0,0,0,0,0\right),$$ (14)

we find the following term:

$$N″*=S″*+V″*=S^{*}+\frac{\left(1-{\epsilon }_a\right)*S^{*}}{\alpha }=S″*\left(1+\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha }\right)$$ (15)

Thus,

$$R_c\left(a\right)=R_{0A}\left[1-{\epsilon }_{LA}\frac{V}{N}\right]+R_{0I}\left[1-{\epsilon }_L\frac{V}{N}\right],$$ (16)

substituting the value of $V$ and $N$ derived from Eqs. 14 and 15 respectively in Eq. 16, it follows

$$R_c\left(a\right)=\left[1-\frac{{\epsilon }_{LA}\left(\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha }\right)}{1+\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha }}\right]+\left[1-\frac{{\epsilon }_L\left(\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha }\right)}{1+\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha }}\right],$$

$$R_c\left(a\right)=R_{01A}\left[1-{\epsilon }_{LA}\left(\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha +\left(1-{\epsilon }_a\right)\rho }\right)\right]+R_{01I}\left[1-{\epsilon }_L\left(\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha +\left(1-{\epsilon }_a\right)\rho }\right)\right].$$

The vaccine impact is given by:

$$\phi =\left(\frac{\left(1-{\epsilon }_a\right)\rho }{\alpha +\left(1-{\epsilon }_a\right)\rho }\right).$$ (17)

Hence,

$$R_c\left(a\right)=R_{01A}\left[1-{\epsilon }_{LA}\phi \right]+R_{01I}\left[1-{\epsilon }_L\phi \right].$$ (18)

We follow the same calculation for the control reproduction number for strain 2. Consequently,

$$R_c\left(b\right)=R_{02A}\left[1-{\epsilon }_{LB}\phi \right]+R_{02I}\left[1-{\epsilon }_{LB}\phi \right].$$ (19)

2.2. Derivation of the minimum percentage of vaccination to reduce the spread SARS-CoV-2 variants in the US

Based on the derivation of the control reproduction numbers, we can compute the minimal fraction of the population of the US that need to be vaccinated so that they can achieve herd immunity or asymptomatic eradication of COVID-19 by placing $R_c\left(aorb\right)=1$. For strain 1 and Eq. 16 we derive the following,

$$f_v=\frac{V^{*}}{N^{*}}.$$ (20)

Is the proportion of vaccinated individuals in the US at the disease-free equilibrium. Substituting 20 in equation in 16, we obtain,

$$R_c\left(a\right)=R_{01A}\left[1+\left(1-{\epsilon }_{LA}\right)f_v\right]+R_{01I}\left[1+\left(1-{\epsilon }_L\right)f_v\right].$$ (21)

Setting $R_c\left(aorb\right)=1$ and solving $f_v$, we obtain a herd immunity threshold, or the minimum of percentage denoted as $P_{ca}$.

$$P_{ca}=\frac{1-\left(R_{01A}+R_{01I}\right)}{\left(1-{\epsilon }_{LA}\right)\left(R_{01A}\right)+\left(1-{\epsilon }_L\right)\left(R_{01I}\right)}\left(for{R}_{01A}and{R}_{01I}>1\right).$$ (22)

We apply the same derivation for the control reproduction number for the second strain, the herd immunity threshold for the second strain is

$$P_{cb}=\frac{1-\left(R_{01A}+R_{01I}\right)}{\left(1-{\epsilon }_{LB}\right)\left(R_{01A}+R_{01I}\right)}\left(for{R}_{01A}and{R}_{01I}>1\right).$$ (23)

2.3. Stability of the disease- free equilibrium

The stability of our disease-free equilibrium can be explained in the following theorem [11]: the disease-free equilibrium $NC=\left(N,0,0,0,0,0,0,0,0,0,0\right)$ of our system of differential equations is locally asymptomatically stable if $R_c<1$ and unstable if $R_c>1$. We calculate the Jacobian matrix of our system of differential equations at the disease-free equilibrium, which is given by

Let $a=\left(1-{\epsilon }_a\right)\rho S^0$, $b=\frac{{\beta }_1{S}^0}{S^0+V^0}$, $c=\frac{{\beta }_2{S}^0}{S^0+V^0}$, $d=\frac{{\beta }_3{S}^0}{S^0+V^0}$, $e=\frac{{\beta }_4{S}^0}{S^0+V^0}$, $f=\left(1-{\epsilon }_L\right)\frac{{\beta }_1{V}^0}{S^0+V^0}$, $g=\left(1-{\epsilon }_{LA}\right)\frac{{\beta }_2{V}^0}{S^0+V^0}$, $h=\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_3{V}^0}{S^0+V^0}$, $i=\left(1-{\epsilon }_{LB}\right)\frac{{\beta }_4{V}^0}{S^0+V^0}$, $j=pw$, $k={\gamma }_1+{\delta }_1$, $l=\left(1-p\right)w$, $m=qw$, $o=\left(1-q\right)w$ y $n={\gamma }_2+{\delta }_2$, we have the associated characteristic polynomial to the Jacobian matrix in infection-free equilibrium equaled to 0 is

$$0=\left|\begin{array}{ccccccccc}-a-\lambda & \alpha & 0& -b& -c& 0& -d& -e& \eta \\ a& -a-\lambda & 0& -f& -g& 0& -h& -i& 0\\ 0& 0& -w-\lambda & b+f& c+g& 0& 0& 0& 0\\ 0& 0& j& -k-\lambda & 0& 0& 0& 0& 0\\ 0& 0& l& 0& -{\gamma }_1-\lambda & 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -w-\lambda & d+h& e+i& 0\\ 0& 0& 0& 0& 0& m& -n-\lambda & 0& 0\\ 0& 0& 0& 0& 0& o& 0& -{\gamma }_2-\lambda & 0\\ 0& 0& 0& {\gamma }_1& {\gamma }_1& 0& {\gamma }_2& {\gamma }_2& -\eta -\lambda \end{array}\right|$$

$$=\left(-a-\lambda \right)\left(-\alpha -\lambda \right)\left(-\eta -\lambda \right)\left|\begin{array}{cccccc}-w-\lambda & b+f& c+g& 0& 0& 0\\ j& -k-\lambda & 0& 0& 0& 0\\ l& 0& -{\gamma }_1-\lambda & 0& 0& 0\\ 0& 0& 0& -w-\lambda & d+h& e+i\\ 0& 0& 0& m& -n-\lambda & 0\\ 0& 0& 0& o& 0& -{\gamma }_2-\lambda \end{array}\right|$$

$$-a\alpha \left(-\eta -\lambda \right)\left|\begin{array}{cccccc}-w-\lambda & b+f& c+g& 0& 0& 0\\ j& -k-\lambda & 0& 0& 0& 0\\ l& 0& -{\gamma }_1-\lambda & 0& 0& 0\\ 0& 0& 0& -w-\lambda & d+h& e+i\\ 0& 0& 0& m& -n-\lambda & 0\\ 0& 0& 0& o& 0& -{\gamma }_2-\lambda \end{array}\right|,$$

$$=\lambda \left(\lambda +a+\alpha \right)\left(-\lambda -\eta \right)\left|\begin{array}{cccccc}-w-\lambda & b+f& c+g& 0& 0& 0\\ j& -k-\lambda & 0& 0& 0& 0\\ l& 0& -{\gamma }_1-\lambda & 0& 0& 0\\ 0& 0& 0& -w-\lambda & d+h& e+i\\ 0& 0& 0& m& -n-\lambda & 0\\ 0& 0& 0& o& 0& -{\gamma }_2-\lambda \end{array}\right|$$

$$=\lambda \left(\lambda +a+\alpha \right)\left(-\lambda -\eta \right)\left|\begin{array}{ccc}-w-\lambda & b+f& c+g\\ j& -k-\lambda & 0\\ l& 0& -{\gamma }_1-\lambda \end{array}\right|\left|\begin{array}{ccc}-w-\lambda & d+h& e+i\\ j& -n-\lambda & 0\\ o& 0& -{\gamma }_2-\lambda \end{array}\right|.$$

In this way the Jacobian matrix has a null eigenvalue ${\lambda }_1=0$, two negative eigenvalues ${\lambda }_2=-a-\alpha$ y ${\lambda }_3=-\eta$. Three other eigenvalues ​​are determined by the solutions of

$$0=\left|\begin{array}{ccc}-w-\lambda & b+f& c+g\\ j& -k-\lambda & 0\\ l& 0& -{\gamma }_1-\lambda \end{array}\right|.$$

While the remaining three are the solutions of

$$0=\left|\begin{array}{ccc}-w-\lambda & d+h& e+i\\ j& -n-\lambda & 0\\ o& 0& -{\gamma }_2-\lambda \end{array}\right|$$

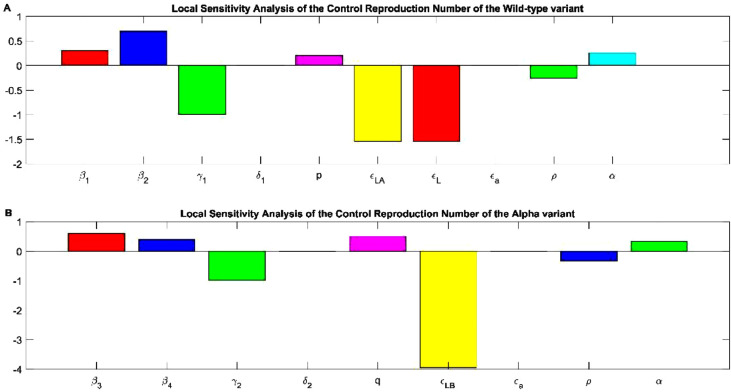
2.4. Local Sensitivity Analysis of the Control Reproduction Number

We will perform a sensitivity analysis for the control reproduction number for strain 1 (12) and strain 2 (13) to visualize the importance of each parameter in disease transmission. The values obtained from the sensitivity analysis permits us to see how $R_c\left(aorb\right)$ changes when a parameter varies. To obtain these values we use the following definition (6):

If $R_c$ is differentiable with respect to a given parameter $\theta$, the normalized forward sensitivity index of $R_c$ is defined by

$${\Gamma }_{\theta }^{R_c}=\frac{\theta }{R_c}*\frac{\partial R_c}{\partial \theta }.$$

First we will calculate the local sensitivity analysis for the control reproduction number for strain 1 $\left(R_c\left(a\right)\right)$ with respect to the following parameters ${\beta }_1,{\beta }_2,p,{\epsilon }_{LA},{\epsilon }_L,{\gamma }_1$and ${\delta }_1$. Thus,

$$\frac{\partial R_c\left(a\right)}{\partial {\beta }_1}=\frac{p\left(1-{\epsilon }_L\phi \right)}{{\gamma }_1+{\delta }_1}.$$ (24)

$$\frac{\partial R_c\left(a\right)}{\partial {\beta }_2}=\frac{\left(1-p\right)\left[1-{\epsilon }_{LA}\phi \right]}{{\gamma }_1}.$$ (25)

$$\frac{\partial R_c\left(a\right)}{\partial p}=\frac{{\beta }_1\left[1-{\epsilon }_L\phi \right]}{{\gamma }_1+{\delta }_1}-\frac{{\beta }_2\left[1-{\epsilon }_{LA}\phi \right]}{{\gamma }_1}.$$ (26)

$$\frac{\partial R_c\left(a\right)}{\partial {\epsilon }_{LA}}=-\left[\frac{\left(1-p\right){\beta }_2}{{\gamma }_1}\right]\phi .$$ (27)

$$\frac{\partial R_c\left(a\right)}{\partial {\epsilon }_L}=\frac{-{\beta }_1}{\left({\gamma }_1+{\delta }_1\right)}\left(\phi \right)$$ (28)

$$\frac{\partial R_c\left(a\right)}{\partial {\gamma }_1}=\frac{-p{\beta }_1}{{\left({\gamma }_1+{\delta }_1\right)}^2}\left[1-{\epsilon }_L\phi \right]-\frac{\left(1-p\right){\beta }_2}{{\left({\gamma }_1\right)}^2}\left[1-{\epsilon }_{LA}\phi \right].$$ (29)

$$\frac{\partial R_c\left(a\right)}{\partial {\delta }_1}=\frac{-p{\beta }_1}{{\left({\gamma }_1+{\delta }_1\right)}^2}\left[1-{\epsilon }_L\phi \right].$$ (30)

$$\begin{array}{ccc}& & \frac{\partial R_c\left(a\right)}{\partial {\epsilon }_a}=\frac{p{\beta }_1}{{\gamma }_1+{\delta }_1}\left[-\frac{\left(1-{\epsilon }_a\right){\epsilon }_L{\rho }^2}{{\left(\alpha +\left(1-{\epsilon }_a\right)\rho \right)}^2}+\frac{{\epsilon }_L\rho }{\alpha +\left(1-{\epsilon }_a\right)\rho }\right]\hfill \\ & & +\frac{(1-p){\beta }_2}{{\gamma }_1}\left[-\frac{\left(1-{\epsilon }_a\right){\epsilon }_{LA}{\rho }^2}{{\left(\alpha +\left(1-{\epsilon }_a\right)\rho \right)}^2}+\frac{{\epsilon }_{LA}\rho }{\alpha +\left(1-{\epsilon }_a\right)\rho }\right].\hfill \end{array}$$ (31)

$$\begin{array}{ccc}& & \frac{\partial R_c\left(a\right)}{\partial \rho }=\frac{p{\beta }_1}{{\gamma }_1+{\delta }_1}\left[\frac{{\left(1-{\epsilon }_a\right)}^2{\epsilon }_L\rho }{{\left(\alpha +\left(1-{\epsilon }_a\right)\rho \right)}^2}-\frac{\left(1-{\epsilon }_a\right){\epsilon }_L}{\alpha +\left(1-{\epsilon }_a\right)\rho }\right]\hfill \\ & & +\frac{(1-p){\beta }_2}{{\gamma }_1}\left[\frac{{\left(1-{\epsilon }_a\right)}^2{\epsilon }_{LA}\rho }{{\left(\alpha +\left(1-{\epsilon }_a\right)\rho \right)}^2}-\frac{\left(1-{\epsilon }_a\right){\epsilon }_{LA}}{\alpha +\left(1-{\epsilon }_a\right)\rho }\right].\hfill \end{array}$$ (32)

$$\frac{\partial R_c\left(a\right)}{\partial \alpha }=\frac{p{\beta }_1{\epsilon }_L\rho \left(1-{\epsilon }_a\right)}{\left({\gamma }_1+{\delta }_1\right){\left(\alpha +\left(1-{\epsilon }_a\right)\rho \right)}^2}+\frac{\left(1-p\right){\beta }_2{\epsilon }_{LA}\rho \left(1-{\epsilon }_a\right)}{\left({\gamma }_1\right){\left(\alpha +\left(1-{\epsilon }_a\right)\rho \right)}^2}.$$ (33)

Eqs. 24-33 will be substituted with the value of each parameter in table S1 to evaluate if they decrease or increase the control reproduction number of strain 1. The derivation of the local sensitivity analysis for the control reproduction number of strain 2 is included in the supplementary material.

3.1. Parameter Estimation for the Mathematical Model

To estimate the parameters of the two variant comparisons, it was divided into two parts: First the parameters for the original variant vs alpha variant, then the alpha variant vs delta variant. To describe the evolution of the two-strain COVID-19 pandemic in the US, taking into account the vaccination rate and the level of implemented NPI, we assumed that the infection, recovery, and death rate are time-dependent functions like described in [[18], [19]]. For estimating parameters for the original variant, we considered the data of COVID-19 infections, recovery, and death from the period of November 11th, 2020 to December 12th, 2020, the date before the vaccination period began in the United States [13]. Parameter estimation for the original variant was pursued by applying a vaccination rate equal to zero and the subpopulation associated with the alpha variant equal to cero as well. For the alpha variant, the estimation of the parameters was the same, only the subpopulation for the original variant was equal to zero. We used the global proportion of alpha infections from the CDC genomic surveillance from January 25th to May 31st. For the delta variant, we used the same approach for the alpha variant, but the time period was from June 1st to July 31st.

For this approach, there were only two fixed parameters the average length of the latent period and the proportion of symptomatic individuals. For the alpha variant, the estimation of the parameters was the same, only the subpopulation for the original variant was equal to zero. The system of differential equations was solved using Matlab R2016b and ODE45 solver. The parameters were fitted by applying two methods, first the one mentioned in [18,19].  The code and implementation can be downloaded at https://github.com/UgoAvila/Two-Strain-Covid-19-Mathematical-Model-in-the-US.

3.2. Local Sensitivity Analysis of the Parameters of the Control Reproduction Number

To perform local sensitivity analysis, we performed a one-at-a-time parameter evaluation. This approach allows us to evaluate the impact of the partial derivative of a parameter with respect to changing the input of said parameter in the control reproduction number. The sensitivity analysis of the control reproduction number was carried out using the following definition [20]:

If is differentiable with respect to a given parameter, the normalized forward sensitivity index is defined by

$${\Gamma }_{\theta }^{R_c}=\frac{\theta }{R_c}*\frac{\partial R_c}{\partial \theta }.$$ (34)

We obtained the partial derivatives of each parameter, with respect to the control reproduction number, the equations for each parameter are represented in section 2.2 of the theoretical analysis of the derivation of the mathematical model. Once we obtained the values of the parameters (Table S1), we were interested to perturb them to determine how their changes affect the reproduction number, we solved the equations using Mathematica. A positive sign of the parameter correlates with an increase of the control reproduction, meanwhile, a negative sign is associated with a decrease of the control reproduction number. Local sensitivity analysis was carried out to obtain which parameters are the most important to decrease the control reproduction number, in turn, find which are the parameters that we must avoid so that the reproduction control number does not rise.

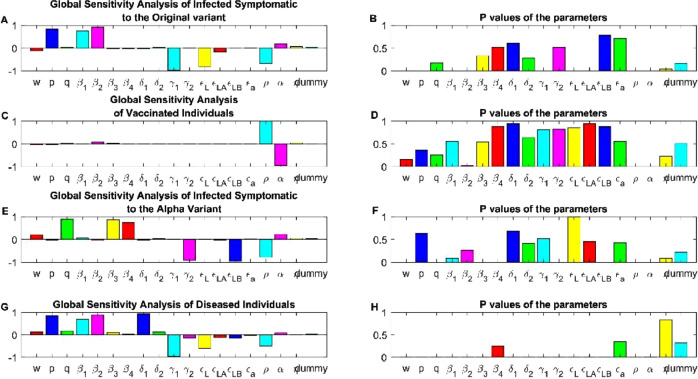
3.3. Global Sensitivity Analysis of the Mathematical Model

Unlike local sensitivity analysis, global analysis allows us to quantify the impact of the inputs (parameters) and their interaction with the outputs (for example dynamics of fully vaccinated individuals). To identify which parameters are important for the behavior of our compartmental differential equations, we applied and adaptive to our model the technique in [21] . We sampled our 17 parameters and evaluated which were important in determining the behavior of our model. All parameters were sampled 10 000 times using a Latin hypercube sampling with a uniform distribution for the probability density function.  Parameters with a p-value were used to explain the dynamics of the response function. PRCC values greater than 0.4 or -0.4 indicated a high correlation between the input and the output. Values ranging between 0.2-0.4 and -0.2- -0.4 indicate a moderate correlation and values less than 0.2 or -0.2 are not significantly different from zero, meaning that they have no correlation between the inputs and outputs.

4. Evolution of the outbreak of two strain of SARS-CoV-2 in the US

4.1. Impact of vaccination and the parameters related to an imperfect vaccine

We simulated immunity acquired by two doses of the BNT162b2 vaccine (the first FDA-approved COVID-19 vaccine) against the original virus, alpha, and delta variant. We used this vaccine because it is the vaccine most widely applied in the Us (∼60% of the US vaccinated individuals have received BNT162b2 [12]) and the availability of real-world effectiveness data [22,23] in the period during alpha was the dominant strain[22], followed by the period when delta was the dominant strain[23]. Vaccine effectiveness or leakiness occurs when the vaccine reduces but does not eliminate the risk for infection. Vaccine effectiveness may change over time as new variants carrying different mutations emerge. The effectiveness data first published in December of 2020 likely relate to strains similar to the original virus that emerged from Wuhan [24], and as new strains emerge (i.e., alpha, delta, and omicron), vaccine effectivity may reduce.  For the original strain we used the value obtained from the clinical trial, vaccine effectiveness for the original variant for two doses for the prevention of symptomatic COVID-19 is 0.913 (95% confidence interval (CI),0.89-0.932) [24]. For alpha and delta strain, we thus obtained real-world data from two different studies in the same Country. For alpha, we obtained the vaccine effectiveness from a study analyzing data between February 23 through March 18 where the value is 0.89 (CI,0.859-0.923) [22]. Finally, the vaccine effectiveness for the delta variant between the period where the delta variant was the dominant variant is 0.519 (CI, 0.47-0.564) [23]. We also included the all-or-nothing protection, which means people who received the vaccine, but the vaccine fails to protect a ${\epsilon }_a$ fraction of individuals. This value is 0.0862 (CI, 0.0689,0.10344).  Finally, waning immunity describes that protection descends over time, and vaccinated individuals become fully susceptible to infection at a rate. Parameter was assumed herein by vaccine-induced immunity being worn off after six months and represented a conservative estimate that may apply for a variant with high resistance to vaccine-induced immunity. We also obtained the transmission rates for symptomatic and asymptomatic infections by fitting the parameters using data of daily infections and deaths provided by the repository developed by Johns Hopkins University [1].

To approximate the real-world situation, we further considered vaccination rate as a function that varies in time instead of a constant.  The daily anti-SARS-CoV-2 vaccines applied in the US from December 12th to July 20th were plotted (Fig. 2 A) and used to derive a function that represented the projected vaccination rate. Based on this projection (black line), if the US maintains the baseline vaccination rate from May 1st to December 2021, over 65% of the population of the US will be vaccinated (Fig. 2B).  We also simulated the percentage of the population that will be vaccinated given a 200% or 50% project vaccination rate from May 1st. The real-world vaccination rate may vary due to a wide range of factors, and thus we simulated all three situations in subsequent models.

Fig. 2.

Fitting and projecting the vaccination rate. (A) Deriving a function that describes the behavior of the daily doses applied in the US. (B) Dynamics if the vaccination rate is doubled or diminished 50% based on the baseline vaccination rates.

4.2. Evaluating the consequence of different transmission rate and vaccination rates between the original variant and the alpha variant

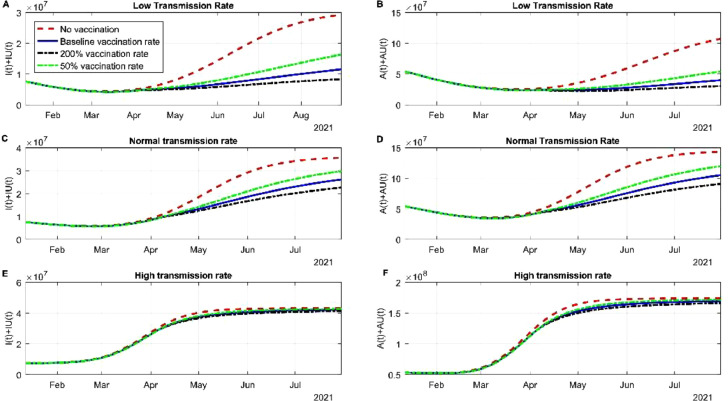
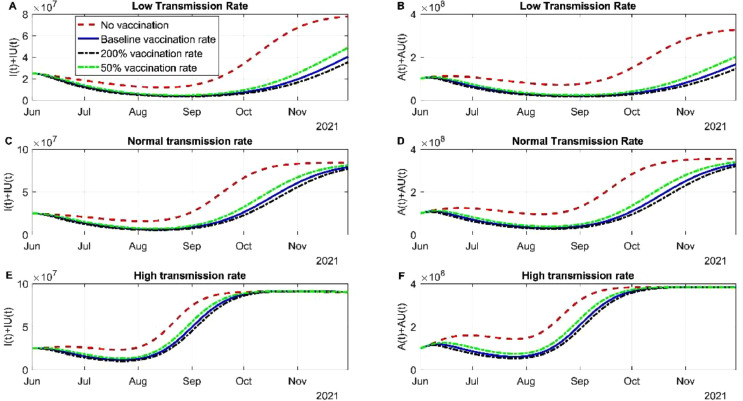
In this section we evaluated how different vaccine rate affect the spread of the virus. In the scenario of low transmission in the community the different vaccination rates stabilized the infection by the original strain and the alpha variant. The cases of infected individuals regardless of the strain was stable between June and July 2021 due to the actions of the vaccine (Fig 3 A). If a new variant is not entered or surges in this period by August 2021, the cases of SARS-CoV-2 will continue to descend (Fig 3A). The red dotted line is the scenario where no vaccines are being administered, despite the use of NPI, the US would have a fourth wave. The asymptomatic infections behave in the same manner, increasing the daily doses up to 200% it does not deaccelerate the new infections of SARS-CoV-2 (Fig 3B). The dynamics of recuperated individuals is not affected by the vaccination rate (Fig S1A) and death rate is affected and controlled significantly by the vaccines applied (Fig S1B). The latter scenario was modeled where NPI strategies are still being used, a scenario that in the US does not hold. The normal or baseline transmission does affect the dynamics of the spread. Infected SARS-CoV-2 cases nearly doubled with respect to low transmission rate. June and July 2021 will be the period with more SARS-CoV-2 cases, roughly 20 million accumulated cases and since then the cases will descend (Fig 3C). Most of the cases between this period will be from the alpha variant, the original variant was contained by the vaccine. Asymptomatic infection is detained by vaccination rate, but the difference between the rate is little but significant (Fig 3D). Recuperated individuals are not altered by vaccination rates (Fig S1C). By early July 2021, there will be around more than 600 00 deaths associated with COVID-19, if the tendency maintains by the end of July 2021 there will be 620 000 deaths. If we compare baseline transmission deaths with low transmission nearly 50 000 deaths could have been avoided if NPI had been maintained. In the scenario of high transmission of the alpha variant, the pharmaceutical intervention will not be enough to stop the spread, other strategies need to be applied (Fig 3E and F). Recuperated individuals do not change their rate despite vaccination rates, meanwhile death rate can be altered due to the amount vaccine applied (Fig S1E and F).

Fig. 3.

Simulation of different vaccine rates and different transmission rates. (A) Simulation of the dynamics of the infected subpopulation of the original variant and the alpha variant considering low transmission and different vaccination rates. (B) Simulation of the dynamics of the infected but asymptomatic subpopulation of the original variant and the alpha variant considering low transmission and different vaccination rates. (C) Simulation of the dynamics of symptomatic infected individuals for both variants considering normal transmission. (D) Simulation of the dynamics of asymptomatic infected individuals for both variants considering normal transmission. (E) Simulation of the dynamics of symptomatic infected individuals for both variants considering high transmission. (F) Simulation of the dynamics of asymptomatic infected individuals for both variants considering high transmission.

4.2.1. Varied vaccine efficiencies influence the proportions of the original vs the alpha variant

Because we are using efficiency parameters based on interim results of phase III clinical trials, there is still an unpredictability of how well the efficiency of the COVID-19 vaccine is going to behave in the real world. So, we evaluated different values for the leakiness parameters and the all or nothing protection with different vaccination rates.

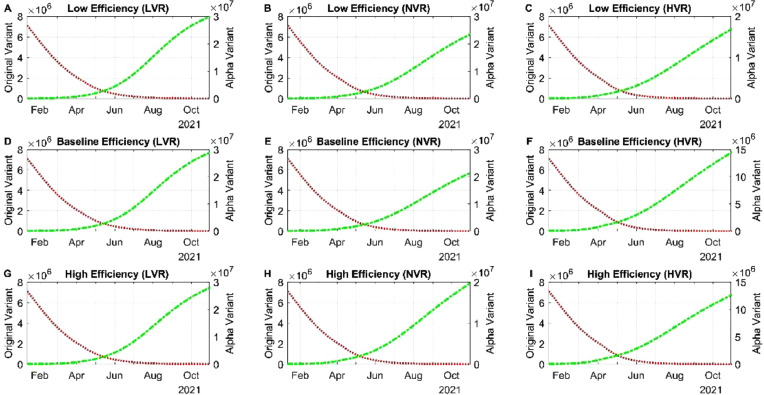
We begin with low efficiency and low vaccination rate (LVR) from both variants. From February to May 2021, the cases of infection of SARS-CoV-2 dropped drastically, this behavior is because of the action of a vaccine in lowering the infections produced by the original variant (Fig S2A). But in June 2021, the tendency shifted from a 4-month decay to a slightly growth of infections mainly because of an increase of the alpha variant (Fig 4 A). Cases from the alpha variant will still increase in the following months if no new variant is introduced, this increase is associated with a low daily dose application presented since June 2021 (). We can observe as well that regardless of the vaccine having high efficiency mixed with a low vaccination rate the cases of COVID-19 from the alpha variant will increase rapidly. The increase of cases may be due to a high population of people not vaccinated and not from breakthrough cases of individuals vaccinated (Fig 4D and G). Once transmission is little high, we can see a difference on the imperfection parameters of a vaccine, the highest number of infections will be roughly between September and October 2021 (Fig 4 D and G). There is no variation in recuperated individuals and death rate due to different efficiencies (Fig S3 A and B). For the normal vaccination rate (NVR), the valley for symptomatic and asymptomatic was reached between April and May 2021, since then a continuous but stabilized increase is happening (Fig 4B and E). This change is due to the presence of the alpha variant (Fig 4B), the imperfection of the vaccine associated with this variant and the relaxation of NPI strategies. Despite relaxation of NPI strategies, the vaccine is helping in lowering the number of infected with the alpha variant. Death toll and recuperated individuals roughly behave the same as low transmission (Fig S3 C and D). Finally, if there was a high vaccination rate (HVR), the pace of lowering will maintain between April and May 2021. In the summer of 2021, there will be a high community transmission specifically of the alpha variant (Fig 4C), even the most perfect vaccine is not going to help stop the spread of the virus and alpha as we know will become the dominant if no new variants surges (Fig 4F and I). Death toll and recuperated individuals roughly behave the same as in the other transmission rates analyzed in this subsection. This similarity can be associated that the alpha variant does not has a high death rate mixed with the protection provided by the vaccine (Fig S3E and F).

Fig. 4.

Simulation of different vaccine efficiencies with different vaccination rates. (A) Simulation the dynamics of symptomatic individuals with the lower bound of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with low vaccination rate (B) Simulation the dynamics of symptomatic individuals with the lower bound of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with normal transmission. (C) Simulation the dynamics of symptomatic individuals with the lower bound of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with high vaccination rate. (D) Simulation the dynamics of symptomatic individuals with the baseline value of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with low vaccination rate. (E) Simulation the dynamics of symptomatic individuals with the baseline value of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with normal vaccination rate. (F) Simulation the dynamics of symptomatic individuals with the baseline value of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with high vaccination rate. (G) Simulation the dynamics of symptomatic individuals with the upper bound of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with low vaccination rate. (H) Simulation the dynamics of symptomatic individuals with the upper bound of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with normal vaccination rate. (I) Simulation the dynamics of symptomatic individuals with the upper bound of the 95% confidence intervals associated with the clinical trials on the Pfizer vaccine with high vaccination rate.

4.2.2. Behavior of the control reproduction number of the original and alpha variant with the importance of the parameters of vaccination

To evaluate the behavior of the control reproduction number $R_c$ for the alpha variant and the original we substituted Eq. 12 and 13 in terms of two important populations: vaccinated (acquired immunity) and recuperated (natural immunity) to reduce the $R_c$ and achieve herd immunity. Consequently, a scenario of the disease-free equilibrium mentioned above is $x_{DF}=\left(S^{*},0,0,0,V^{*},R^{*}\right)$ and the total population is $N^{*}=S^{*}+V^{*}+R^{*}$. We can rearrange Eq. 12 in the following manner:

Because we want to define a proportion of susceptible, vaccinated and recovered individuals, we can divide Eq. 20 by the total population. So,

$$\frac{S^{*}}{N^{*}}+\frac{V^{*}}{N^{*}}+\frac{R^{*}}{N^{*}}=1,$$

$$\frac{V^{*}}{N^{*}}=xand\frac{R^{*}}{N^{*}}=y.$$

It follows that,

$$\frac{S^{*}}{N^{*}}=1-x-y.$$

We rewrite Eq. 12 with the expression mentioned above. Hence,

$$R_c\left(a\right)=R_{0A}\left[\frac{S^{*}}{N^{*}}+\left(1-{\epsilon }_{LA}\right)\frac{V^{*}}{N^{*}}\right]+R_{0I}\left[\frac{S^{*}}{N^{*}}+\left(1-{\epsilon }_L\right)\frac{V^{*}}{N^{*}}\right]$$

$$=R_{0A}\frac{S^{*}}{N^{*}}+R_{0A}\left(1-{\epsilon }_{LA}\right)\frac{V^{*}}{N^{*}}+R_{0I}\frac{S^{*}}{N^{*}}+R_{0I}\left(1-{\epsilon }_L\right)\frac{V^{*}}{N^{*}}$$

$$=\left[R_{0A}+R_{0I}\right]\left(1-x-y\right)+\left[R_{0A}\left(1-{\epsilon }_{LA}\right)+R_{0I}\left(1-{\epsilon }_L\right)\right]x$$ (35)

To investigate the control reproduction number for the alpha variant Eq. 13, we apply the same derivation used for the original strain. Hence,

$$\begin{array}{ccc}& & R_c\left(b\right)\left(x,y\right)=\left[R_{0AUK}+R_{0IUK}\right]\left(1-x-y\right)+[R_{0AUK}\left(1-{\epsilon }_{LB}\right)\hfill \\ & & +R_{0IUK}\left(1-{\epsilon }_{LB}\right)]y\hfill \end{array}$$ (36)

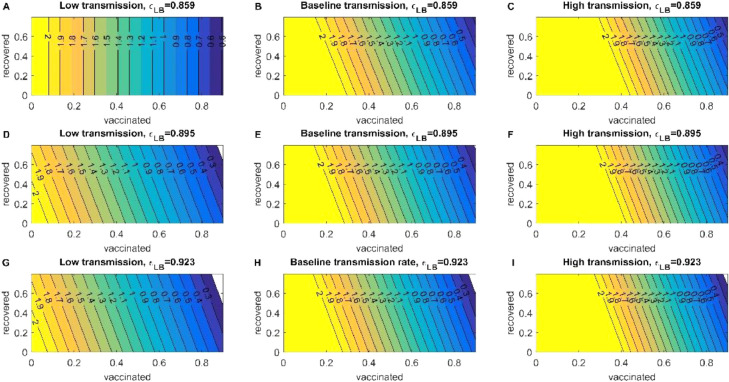
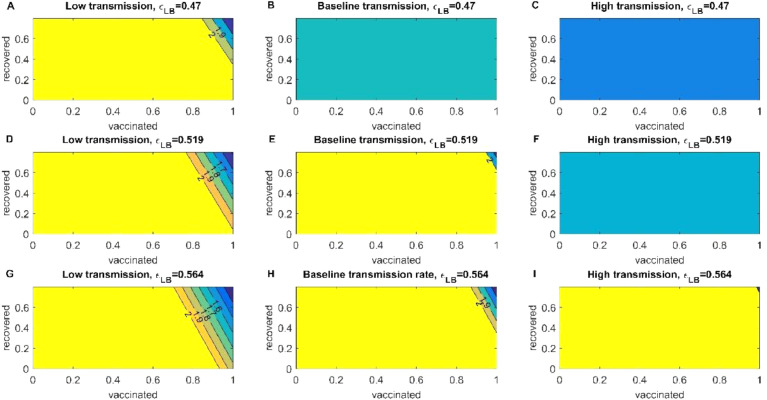
In a scenario of low transmission for the alpha variant, to reduce the value of $R_c=1$ we need 60% of fully vaccinated individuals in combination with natural immunity despite the efficiency of the vaccine. In the case of baseline transmission to reduce the value of $R_c=2$ (which is still an increasing disease) we need less than 30% of acquired immunity, we can observe that natural immunity impact in diminishing the $R_c$ is absent in this transmission. To reduce the value of $R_c=1$, we need more than 70% of individuals fully vaccinated (Fig S5). In an event of high transmission, we noticeably need more vaccinated individuals of roughly 80% to reduce the growth to a more stabilized pace of SARS-CoV-2. By the final days of July, the US has only 50% of individuals fully vaccinated, which may not be sufficient to reach herd immunity regardless of the variant. (Fig. 5 and Fig S5).

Fig. 5.

Reproduction Control Number of the alpha variant. The heatmaps of the left represent the decrease of the control reproduction number when transmission is low and different vaccination efficiencies for the Pfizer vaccine. The heatmaps of the center represent the decrease of the control reproduction number when transmission is baseline and different vaccination efficiencies for the Pfizer vaccine. And the heatmaps of the left represent the decrease of the control reproduction number when transmission is high and different vaccination efficiencies for the Pfizer vaccine.

4.3. Local Sensitivity Analysis of the control reproduction number for the original and the alpha variant

To evaluate how sensitive the $R_c$ is with respect the parameters that define it, we substituted Eqs. 24-33 with the values of the parameters in table S1 from the original variant. For the alpha variant we used the same methodology, only we replaced the parameters with the value for the alpha variant in table S1 in the equations S1-S9. The results of the change of each parameter with respect to the $R_c$ are depicted in Fig. 6 . As we can see the $R_c$ is sensible to the parameters that define it. Let us start by explaining which parameters are involved in increasing the $R_c$ and which are involved in decreasing the $R_c$ for the original variant. Asymptomatic infected individuals $\left({\beta }_2\right)$ are associated with increasing the $R_c$ the double compared with symptomatic infected individuals $\left({\beta }_1\right)$. This behavior may explain why this virus became a pandemic due to a higher infectivity from asymptomatic individuals (Fig 6A). Recovered individuals $\left({\gamma }_1\right)$ is implicated in decreasing the value of $R_c$ because these individuals are no longer susceptible to infection due to the fact of natural immunity. Increasing death is associated with decreasing the $R_c$ but not at the same pace than recuperated individuals (Fig 6A). Increasing symptomatic individuals of the original variant is associated with slightly increasing the control reproduction number. Vaccine efficiency $\left({\epsilon }_{LA}and{\epsilon }_L\right)$ of the Pfizer vaccine against the original variant regardless of developing or not symptoms is implicated in decreasing significantly the value of $R_c$. The all or nothing protection is related with increasing the $R_c$ the value is so small compared with the rest of the imperfect vaccine parameters. Not surprisingly increasing the vaccination rate $\left(\rho \right)$ is implicated in decreasing the value of $R_c$ due to the acquired immunity from the vaccine. But as neutralizing antibodies are waned over time, vaccinated individuals become susceptible individuals increasing the value of $R_c$ at the same index as the vaccination rate (Fig 6A). The alpha variant has the same behavior than the original variant but with a slight difference. Symptomatic individuals $\left({\beta }_3\right)$ are associated with increasing the $R_c$, as the asymptomatic individuals $\left({\beta }_4\right)$, but for this variant the symptomatic individuals are the carriers for augmentation the $R_c$ (Fig 6B). Increasing the recuperation rate $\left({\gamma }_2\right)$ of the alpha variant is clearly associated with a decrease of $R_c$. Increasing death$\left({\delta }_2\right)$ produced by the alpha variant is implicated in decreasing the $R_c$ but not at a significant manner. For decreasing the spread of the virus, the parameters of an imperfect vaccine are of great importance. Vaccine efficiency ${\epsilon }_{LB}$ to the alpha variant is associated with significantly decreasing the value of the control reproduction number, the double compared with the original variant. If the all or nothing protection increases, the $R_c$ increases but not as much we thought. The loss of protection provide by the vaccine has the same index as the rate of vaccination but in the opposite behavior. If we increase the vaccination rate, we can diminish the $R_c$ due to the protection of the vaccine, but if the protection wanes, the $R_c$augments in the same index (Fig 6B).

Fig. 6.

Sensitivity analysis of the control reproduction number for the original and the Alpha variant (A)${\mathit{\beta }}_1$and ${\mathit{\beta }}_2$ represent the force of infection of the symptomatic and asymptomatic individuals. ${\mathit{\gamma }}_1$ is the rate at which the individuals recuperate from the original variant. ${\mathit{\delta }}_1$ the rate at which individuals passed away from the original variant. p is the percentage of individuals that develop symptoms. ${\mathbf{\varepsilon }}_{\mathit{LA}}$ is the vaccine efficiency or leakiness to prevent asymptomatic infection by the original variant. ${\mathbf{\varepsilon }}_{\mathit{L}}$ is the vaccine efficiency or leakiness to prevent symptomatic infection by the original variant. ${\mathbf{\varepsilon }}_{\mathit{a}}$ is the all or nothing protection of the vaccine to get infected to the original variant. $\mathit{\alpha }$ is the waning rate or loss of protection provided by the vaccine to the original variant. $\mathit{\rho }$ is the rate of vaccination. (B) ${\mathit{\beta }}_3$and ${\mathit{\beta }}_4$ represent the force of infection of the symptomatic and asymptomatic individuals. ${\mathit{\gamma }}_2$ is the rate at which the individuals recuperate from the alpha variant. ${\mathit{\delta }}_2$ the rate at which individuals passed away from the alpha variant. q is the percentage of individuals that develop symptoms. ${\mathbf{\varepsilon }}_{\mathit{LB}}$ is the vaccine efficiency or leakiness to prevent being infected or not by the alpha variant. ${\mathbf{\varepsilon }}_{\mathit{a}}$ is the all or nothing protection of the vaccine to get infected to the alpha variant. $\mathit{\alpha }$ is the waning rate or loss of protection provided by the vaccine to the alpha variant. $\mathit{\rho }$ is the rate of vaccination.

4.4. Global Sensitivity Analysis of the set of differential equations for the wild-type and the alpha variant

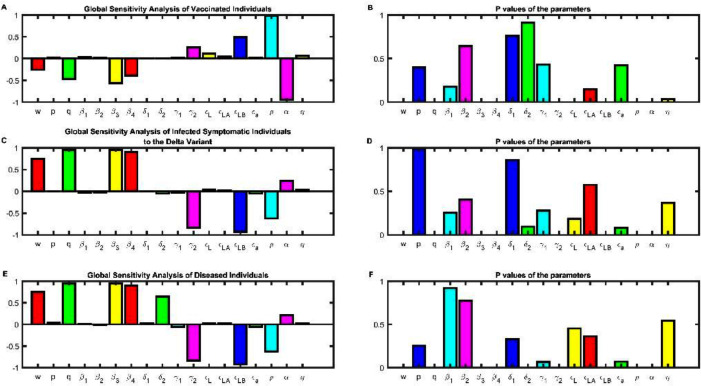
Mathematical models are vulnerable to large variations regarding social interactions that can shape the behavior of our model forecasts. To model this impact, we used a global sensitivity approach with the partial rank correlation coefficient (PRCC). We are only interested in those parameters whose p-value is less than or equal to 0.05, basically the parameters that do not have a bar height (Fig 7 B, D, F and H and the B panel for Fig S6 through S10). Exposed individuals to the original variant are affected by some parameters (Fig S6A and B). The parameter associated with time between the onset of symptoms (w) is involved in decreasing this population, this means that the latent stage is over, and the infectious period is starting to commence. The force of infection of symptomatic or asymptomatic infections $\left({\beta }_1,{\beta }_2\right)$ are implicated in increasing this population, because more individuals are entering the latent stage once they were infected by positive cases regardless of whether or not they have symptoms. Vaccine effectiveness $\left({\epsilon }_{LA},{\epsilon }_L\right)$ to this variant is associated in decreasing this population (Fig S6A), because if the acquired immunity is higher the probability of getting infected once an individual gets in contact with a positive case is lower. Enhancing the vaccination rate is involved in decreasing this population because the probability of getting in contact with a positive case is lower since most individuals are vaccinated and indirectly protecting individuals that are not (Fig S6A). Waning immunity is associated with increasing the population of exposed individuals because they become susceptible to infection again (Fig S6). Infected symptomatic individuals with the original variant are affected in growth by the force of infection of symptomatic and asymptomatic for said variant. The recuperation rate $\left({\gamma }_1\right)$ is associated in decreasing the population of infected individuals, the death rate$\left({\delta }_1\right)$ for this variant is not statistically significant (Fig 7B) in decreasing the infected symptomatic subpopulation (Fig 7A). The only parameters involved in decreasing this population are vaccine associated parameters. Vaccine effectiveness for symptomatic infections $\left({\epsilon }_L\right)$ is correlated in decreasing at the same rate as $\left({\gamma }_1\right)$ the population of infected symptomatic individuals. However, vaccine effectiveness for asymptomatic infections $\left({\epsilon }_{LA}\right)$ is associated in decreasing this population but not at the same rate as $\left({\epsilon }_L\right)$. If we increase the population of vaccinated individuals $\left(\rho \right)$ this is correlated with decreasing the population of infected individuals. Waning immunity is the only parameter of a vaccine that is positively correlated in increasing the population of infected individuals, because protection is wearing off (Fig 7A and B). Asymptomatic individuals to the wild type variant are affected by the same parameters, only at a different rate (Fig S7). For vaccinated individuals only two parameters are statistically significant (Fig 7D) in shaping the behavior. Increasing the vaccination rate is positively correlation in increasing this population, meanwhile waning immunity is strongly correlated in decreasing this population (Fig 7C and D). Exposed individuals to the alpha variant behave in the same manner as exposed to the original variant (Fig S8). Infection by the alpha variant is enhanced by the force of infection for symptomatic and asymptomatic associated with this variant (Fig 7E and F). The recuperation rate associated with this variant $\left({\gamma }_2\right)$ is correlated with decreasing this population. As well the vaccine effectiveness $\left({\epsilon }_{LB}\right)$ to this variant is correlated in decreasing at the same rate as the wild type the population of infected individuals with this variant. Increasing the vaccination rate $\left(\rho \right)$ and the waning immunity parameter $\left(\alpha \right)$ are associated in decreasing and increasing respectively this population. To decrease infected asymptomatic infections by the alpha variant the same parameters are involved as the symptomatic infections (Fig S9). For disease individuals regardless of the variant is one of the populations that is heavily influenced by the parameters. The force of infection of symptomatic individuals notwithstanding the variant is implicated in enhancing this population. The recuperation rate for both variants is implicated in reducing this population, but first you must get infected. Vaccine effectiveness regardless of the variant is positively correlated in decreasing the population of diseased individuals. Increasing the vaccination rate is associated in decreasing this population as well. Waning immunity is slightly associated with increasing this population (Fig 7G and H). Recovered individuals are positively correlated in increasing this population by the action of the force of infection regardless of the variant. Vaccine effectiveness is correlated in decreasing this population, because vaccinated individuals do not get infected by the virus, so they do not recover from it. Waning immunity is associated with increasing this population because vaccinated individuals can get infected regardless of the variant (Fig S10).

Fig. 7.

Global Sensitivity Analysis of the set of differential equations. Partial Rank Correlation Coefficient (PRCC), of the dynamic change of (A) infected symptomatic individuals, (B) Vaccinated individuals, (E) Infected symptomatic to the alpha variant and (G) Diseased individuals, -1 means negatively correlation with the response function, meanwhile value near 1 is associated with positive correlation with the response function. p- values of the PRCC values of the parameters evaluated of the response function, (B) for infected symptomatic to the wild type, (D) of vaccinated individuals, (F) infected symptomatic to the alpha variant and (H) deceased individuals.

4.5. Behavior of the alpha variant with the emergence of the delta variant in the US

4.5.1. Evaluating the consequence of different transmission rate and vaccination rates between the alpha variant and the delta variant

In this section we evaluated the behavior between the alpha and the delta variant. We assessed how different transmission rates mixed with different vaccination rate affect the behavior of the alpha variant, and how the efficiency rate may slow the pace of the either variant. Regardless of the transmission rate from June to July 2021, the infected of SARS-CoV-2 were descending because of the efficiency of the Pfizer vaccine to reduce the spread of symptomatic infected by the alpha variant. In low transmission, if individuals decided not to vaccinate the pace of increment of cases will be faster with respect to the different vaccination rates. By August 2021, there will be between 500 000 and 1 million active symptomatic cases. Despite the vaccination the tendency of increment of cases will maintained passing October 2021 for symptomatic or asymptomatic cases (Fig 8 A and B). In a normal transmission rate, the vaccination rates in slowing infected new cases still matter, by August 2021 there may be roughly two million infected individuals mixed with 5 million cases of asymptomatic cases (Fig 8C and D). For a scenario with high transmission, accelerating the vaccination rate to 200% (black line) will help diminish the cases but it would not be enough, other strategies like NPI need to be included. The recuperation increases with respect to vaccination rates and death rates pace can be diminished by the action of the vaccine (Fig S11). Overall, the efficiencies of the vaccine in preventing infection by the delta variant affects the number of infected individuals (Fig S12), but relying on the vaccine efficiency is not sufficient to halt the spread of the delta variant and other measures would be needed (Fig S13).

Fig. 8.

Simulation of different vaccine rates and different transmission rates between the alpha and the delta variant. (A) Simulation of the dynamics of the infected subpopulation of the alpha variant and the delta variant considering low transmission and different vaccination rates. (B) Simulation of the dynamics of the infected but asymptomatic subpopulation of the alpha variant and the delta variant considering low transmission and different vaccination rates. (C) Simulation of the dynamics of symptomatic infected individuals for both variants considering normal transmission. (D) Simulation of the dynamics of asymptomatic infected individuals for both variants considering normal transmission. (E) Simulation of the dynamics of symptomatic infected individuals for both variants considering high transmission. (F) Simulation of the dynamics of asymptomatic infected individuals for both variants considering high transmission.

4.5.2. The control reproduction and the parameters need to diminish the spread of the delta variant

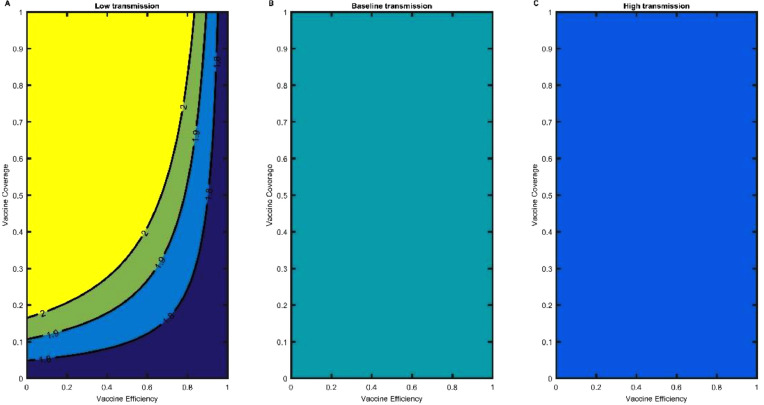
We computed the reproduction number of the delta variant. For the scenario of a low transmission (non-pharmaceutical strategies are still being used), in conjunction with low efficiency, vaccinating the entire population is not enough to decrease the value lower than $R_c=2$ (Fig. 9 A). With baseline vaccine effectiveness as in low transmission is not enough to decrease the value of $R_c$. High efficiency of the vaccine with 80% of vaccinated individuals the $R_c=2$, and 90% reduces the value of the control reproduction number to 1.5 (Fig 9G). For Baseline transmission, low and baseline efficiency will not be enough to reduce the $R_c$ (Fig 9B and E). Only high efficiency with more than 90% of the individuals vaccinated will decrease the value of $R_c$ less than 2 (Fig 9H). In a scenario of high transmission, only high efficiency will try to descend the value of the $R_c$ (Fig 9C, F and I). But other strategies need to be applied to reduce the control reproduction and descend the spread of the delta variant in the US.

Fig. 9.

Reproduction Control Number of the delta variant. The heatmaps of the left represent the decrease of the control reproduction number when transmission is low and different vaccination efficiencies for the Pfizer vaccine. The heatmaps of the center represent the decrease of the control reproduction number when transmission is baseline and different vaccination efficiencies for the Pfizer vaccine. And the heatmaps of the left represent the decrease of the control reproduction number when transmission is high and different vaccination efficiencies for the Pfizer vaccine.

4.5.3. Local Sensitivity Analysis of the control reproduction number of the delta variant

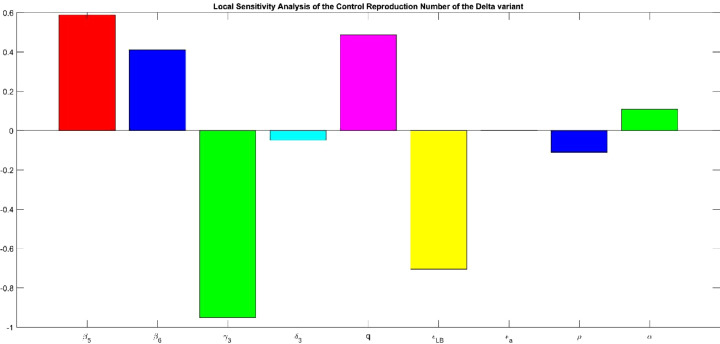
To slow the spread of the delta variant, we need to evaluate which parameters are important to diminish the $R_c\left(c\right)$. Overall, the parameters behave in the same manner as in the other evaluated variants, but we will describe the vaccine parameters to acknowledge the importance of this strategy. If we increase vaccine efficiency the $R_c\left(c\right)$ decreases significantly, this parameter is not easy to increase because it depends from other variables, but using face masks or implementing social distancing may increase vaccine efficiency because a physical barrier impedes of getting in contact with the virus. Increasing the all or nothing protection is associated with enhancing $R_c\left(c\right)$. Waning rate or loss of protection is implicated in increasing the $R_c\left(c\right)$, this parameter can be manipulated with possible doses applied annually like the influenza vaccine. The only parameter involved in the vaccination strategy that we can manage or manipulate directly is the vaccination rate. If the US increases the daily doses of COVID-19 vaccine, the $R_c\left(c\right)$ decreases, meaning less new infections of the delta variant (Fig 10 ).

Fig. 10.

Sensitivity analysis of the control reproduction number for the original variant. ${\mathit{\beta }}_5$and ${\mathit{\beta }}_6$ represent the force of infection of the symptomatic and asymptomatic individuals. ${\mathit{\gamma }}_3$ is the rate at which the individuals recuperate from the original variant. ${\mathit{\delta }}_3$ the rate at which individuals passed away from the original variant. p is the percentage of individuals that develop symptoms. ${\mathbf{\varepsilon }}_{\mathit{L}}$ is the vaccine efficiency or leakiness to prevent asymptomatic infection by the original variant. ${\mathbf{\varepsilon }}_{\mathit{L}}$ is the vaccine efficiency or leakiness to prevent symptomatic infection by the original variant. ${\mathbf{\varepsilon }}_{\mathit{a}}$ is the all or nothing protection of the vaccine to get infected to the original variant. $\mathit{\alpha }$ is the waning rate or loss of protection provided by the vaccine to the delta variant. $\mathit{\rho }$ is the rate of vaccination.

4.5.4. Global Sensitivity Analysis for the delta variant

For this section we only evaluate the global dynamics of the equation that model the behavior of the delta variant. As in the global sensitivity section of the original and alpha variant, the plots on the right-hand side are the p values ​​of each parameter. We only describe the parameters whose p value is equal to or less than 0.05, in this case those whose height of the histogram is not observed in the Fig. 11B, D and F. Exposed individuals to the delta variant are affected by $q$ which is statistically significant (Fig. S14B) the parameter associated with developing symptoms; this parameter is associated with increasing individuals of the exposed subpopulation. The force of infection of symptomatic $\left({\beta }_3\right)$ or asymptomatic $\left({\beta }_4\right)$ of the delta variant is involved in increasing this subpopulation. The recuperation rate $\left({\gamma }_2\right)$ is implicated in diminishing the population of exposed individuals. Vaccine effectiveness $\left({\epsilon }_{LB}\right)$ towards the delta variant is correlated in decreasing this subpopulation, as well the rate of vaccination $\left(\rho \right)$ is involved in decreasing this subpopulation. The waning immunity or loss of protection provided by the vaccine is correlated in increasing this population $\left(\alpha \right)$. The loss of protection provided by the antibodies after recovering from the delta variant has no relation in modifying the dynamics of the exposed population because it is not statistically significant (Fig S14A and B). For the vaccinated individuals their behavior is different with respect to the variant. The force of infection $\left({\beta }_1,{\beta }_2\right)$ of the alpha variant has no relation with the dynamics of this subpopulation because it is not statistically significant (Fig 11 A and B). Meanwhile the force of infection $({\beta }_3,{\beta }_4)$ of the delta variant are involved in decreasing this subpopulation, which means despite being vaccinated your most likely to get infected by the delta variant than the alpha. The vaccine effectiveness regardless of the variant are involved in increasing this subpopulation, but the effectiveness $\left({\epsilon }_{LB}\right)$ from the delta virus it increases at a higher pace than the effectiveness from alpha $\left({\epsilon }_L\right)$ (Fig 11A). The vaccination rate $\left(\rho \right)$ is positively correlated in increasing this subpopulation and the waning rate in decreasing this subpopulation, note that this parameter has a strong negative correlation with this subpopulation, this imperfect parameter needs to be monitored. For the infected symptomatic individuals of the delta variant, the force of infection $\left({\beta }_3,{\beta }_4\right)$ are strongly correlated in increasing this subpopulation (Fig 11C), meanwhile the recovery rate $\left({\gamma }_2\right)$ is associated in decreasing this subpopulation (Fig 11C and D). The vaccine effectiveness parameter $\left({\epsilon }_{LB}\right)$ is correlated in decreasing the subpopulation of infected individuals, this decrease has a strong correlation. The vaccination rate and waning immunity behave in the same manner as in the other subpopulation evaluated in this section. Asymptomatic individual of the delta variant behaves in the same manner as symptomatic individuals (Fig S15A and B). Diseased individuals increase by the action of the force of infection of the delta variant, alpha variants force of infection have no relation in affecting the dynamics of this subpopulation (Fig 11E and F). Vaccine effectiveness of the delta variant can decrease the population of diseased individuals at a strong correlation. The vaccination rate decreased this subpopulation, instead waning immunity increases this subpopulation, because the protection provided by the vaccine is wearing off (Fig 11E and F).

Fig. 11.

Global Sensitivity Analysis of the set of differential equations for the delta variant. Partial Rank Correlation Coefficient (PRCC), of the dynamic change of (A) Vaccinated individuals, (C) infected symptomatic individuals, (E) Diseased individuals, -1 means negatively correlation with the response function, meanwhile value near 1 is associated with positive correlation with the response function. p- values of the PRCC values of the parameters evaluated of the response function, (B) Vaccinated individuals, (D) of infected symptomatic individuals, (F) Diseased individuals.

4.6. Derivation of the minimum percentage of vaccination based on the three variants: Original, Alpha and Delta

In a population, the proportion of individuals immune against the virus sufficient to prevent the spread is considered “herd immunity” and may be achieved by a combination of natural immunity or acquired immunity (vaccination). For COVID-19, the natural immunity acquired by infection may result in a higher mortality rate (ex. Sweden relative to their neighbor countries that implemented NPI´s throughout 2020) [25], although vaccination alone may not be sufficent [26]. The theoretical derivation was obtained in section 2.2 and we used the parameters from table S1 for each variant in question.  We depicted the following results to evaluate how vaccine coverage or proportion mixed with vaccine efficiency affects the behavior of the control reproduction number of each strain. The results for the comparison between original and Alpha variants during the period between March and July 2021 are in Fig. 12 for Alpha and in Fig. S16 for original. For the original variant mixed with NPI's the control reproduction number ranges from 1.3 to 0.7 (Fig S16), where the ${\mathit{R}}_{\mathit{c}}$ decreases as vaccine coverages and efficiency increase. In the scenario of low transmission, where we explore the impact of NPI´s and 50% of the population vaccinated to decrease the value of the control reproduction number to 1.2. There is no difference in reducing the ${\mathit{R}}_{\mathit{c}}$ between a higher efficiency or higher percentage in low transmission. In the case of baseline transmission with 80% of efficiency and 60% for the population vaccinated the value of ${\mathit{R}}_{\mathit{c}}$ will be 1.5 (Fig S16B). For high transmission, we will need a higher vaccine coverage and efficiency to reduce to a value of 1.8 (Fig S16C). For the Alpha variant in 80% vaccine efficiency and 60% individuals vaccinated, the ${\mathit{R}}_{\mathit{c}}$ will only decrease to a value of 1.6. The same pattern is observed in baseline and high transmission, we need more vaccine coverage to reduce the value of ${\mathit{R}}_{\mathit{c}}$ to 1.9 and 2.5 respectively (Fig S17). For the delta variant, the only scenario where the value of ${\mathit{R}}_{\mathit{c}}$ may be less than 2 is when strict NPIs are still being used mixed with vaccination. With 80% of vaccine efficiency and a coverage of 60%, the pandemic will not decrease and reach a plateau of infected cases. For baseline and high transmission, the value will never decrease from 2. For this variant, non-pharmaceutical strategies still need to apply for the reduction of the control reproduction number (Fig 12).

Fig. 12.

Control Reproduction Number of the delta variant. (A) Low transmission, (B) Baseline Transmission and (C) High Transmission of the control reproduction number as a function of the vaccine efficiency of the delta variant and the vaccine coverage of the US population.

5. Discussion

Our mathematical model allowed us to evaluate which are the most important characteristics of the variants to become the dominant strain in a partially vaccinated population before the arrival of omicron in the US in early December 2021. Many of the variants of concern/interest have higher transmissibility than the origin variant that emerged from Wuhan, but as we can see this attribute is not sufficient to give rise to a dominant strain [27]. The alpha variant took a long duration to become the dominant strain in early 2021 despite being more transmissible [9]. This was because the immune escape of the alpha variant was not higher than the original variant. For the mRNA vaccines (BNT162b2 and mRNA-1273.211), which were being applied when the alpha variant arrived in the US, their neutralizing activity decreased only 3.3 fold compared with the original variant, and there was no evidence of immune escape [28,29]. Even the Beta and Gamma variants were better at evading the protection acquired by mRNA vaccines [30,31] but their transmissibility was not as higher compared with the alpha variant [32] . The Johnson & Johnson single-dose vaccine also had a neutralizing effect against alpha.

The delta variant was first detected in December 2020 and quickly became the common variant across many countries in 2021 [33] . This speed may be attributed to two main reasons: delta had a higher transmission rate than alpha even in vaccinated individuals. In addition, several individuals in the US population had received the full regimen of vaccination for many months, a period where the immunity waned with respect to the delta variant [34,35]. Higher transmission mixed with a decrease in the neutralization effect, demonstrating the immune escape capacity of the delta of the protection provided by vaccination [36] gave rise to delta becoming the dominant strain causing another pandemic wave in the US; this wave was slightly controlled with the application of the booster dose, which generated greater protection against infection with delta [6]. At the time of writing, the omicron variant has swiftly taken over as the dominant strain across the US and much of the world, stressing the importance of considering multi-strain dynamics in a pandemic.

Our model has several limitations, some of which are addressed in other new models developed under this pandemic. First, our model does not consider the population heterogeneity, which has shown to tamper the required number of vaccinated individuals to achieve herd immunity [37]. Other models have been used to plan the strategy of vaccination to reduce death or infections [38]. Second, we do not consider one vs two doses and the variation of immunity for individuals with different doses. Saad-Roy et al [39]. developed a mathematical approach wherein the short term having more individuals with one dose will reduce infections, but in a long term, the virus can mutate and develop characteristics to avoid elimination by the immune response [40].  We obtained the immunity parameters for the Pfizer vaccine that is the most widely used in the US, but our model can be further extended using data for other vaccines. Third, we did not consider seasonality. And lastly, we only considered two strains, although the pandemic is characterized by multiple strains each with its own transmission dynamics and associated immunity parameters. While the dominant strain has shifted in this pandemic, the model developed herein, especially considering the variant's different transmission rates and responses to vaccines, may be adapted and modified to reflect the multi-strain nature of future pandemics.

Funding

Ugo Avila Ponce de León also received a fellowship (CVU: 774988) from Consejo Nacional de Ciencia y Tecnología (CONACYT). KH received funding from ISMMS and NIH NIGMS R35GM138113. This article was supported in part by Mexican SNI under CVU 15284

Data and materials availability

The original contributions presented in the study are included in the article/Supplementary Material. All code used for analysis is available at https://github.com/UgoAvila/Two-Strain-Covid-19-Mathematical-Model-in-the-US.

CRediT authorship contribution statement

Ugo Avila-Ponce de León: Conceptualization, Methodology, Software, Formal analysis, Data curation, Writing – original draft, Writing – review & editing. Eric Avila-Vales: Conceptualization, Methodology, Supervision, Project administration. Kuan-lin Huang: Conceptualization, Methodology, Writing – review & editing, Project administration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.