Finite Element Modeling of the Complex Anisotropic Mechanical Behavior of the Human Sclera and Pia Mater

Abstract

Background and Objective:

Accurate finite element (FE) simulation of the optic nerve head (ONH) depends on accurate mechanical properties of the load-bearing tissues. The peripapillary sclera in the ONH exhibits a depth-dependent, anisotropic, heterogeneous collagen fiber distribution. This study proposes a novel cable-in-solid modeling approach that mimics heterogeneous anisotropic collagen fiber distribution, validates the approach against published experimental biaxial tensile tests of scleral patches, and demonstrates its effectiveness in a complex model of the posterior human eye and ONH.

Methods:

A computational pipeline was developed that defines control points in the sclera and pia mater, distributes the depth-dependent circumferential, radial, and isotropic cable elements in the sclera and pia in a pattern that mimics collagen fiber orientation, and couples the cable elements and solid matrix using a mesh-free penalty-based cable-in-solid algorithm. A parameter study was performed on a model of a human scleral patch subjected to biaxial deformation, and computational results were matched to published experimental data. The new approach was incorporated into a previously published eye-specific model to test the method; results were then interpreted in relation to the collagen fibers’ (cable elements) role in the resultant ONH deformations, stresses, and strains.

Results:

Results show that the cable-in-solid approach can mimic the full range of scleral mechanical behavior measured experimentally. Disregarding the collagen fibers/cable elements in the posterior eye model resulted in ~20–60% greater tensile and shear stresses and strains, and ~30% larger posterior deformations in the lamina cribrosa and peripapillary sclera.

Conclusions:

The cable-in-solid approach can easily be implemented into commercial FE packages to simulate the heterogeneous and anisotropic mechanical properties of collagenous biological tissues.

Graphical Abstract

1. Introduction

Elevated intraocular pressure (IOP) is a primary risk factor for the development and progression of glaucomatous optic neuropathy, a leading cause of blindness worldwide [1–3]. The relationship between IOP and loss of retinal ganglion cell function in glaucoma is not well understood, but has been postulated to involve both biomechanical and vascular effects in the optic nerve head (ONH) region [4–6]. It has been hypothesized that IOP-induced mechanical strain in the lamina cribrosa and resident glial cells that support the retinal ganglion cell axons in the ONH eventually leads to apoptosis of the ganglion cells and subsequent loss of vision [4, 6–10]. However, the IOP levels at which glaucomatous damage occurs are eye specific [11], which may be related to differences in ONH geometry and biomechanical properties [4, 6, 10, 12, 13]. Improving our understanding of the ONH biomechanical environment requires comprehensive knowledge of the morphology and biomechanical properties of the ONH tissues. ONH biomechanics are complex due to the interactions between heterogeneous, anisotropic tissues with markedly different mechanical properties [14–19], as well as the considerable inter-individual variability in the tissue geometry [12, 15]. Thus, the eye-specific ONH mechanical response to IOP is a function of the individual eye’s geometry and mechanical properties [4, 6, 13], which could contribute to the individual’s susceptibility to IOP. To complicate matters, IOP has been shown to be very dynamic [20, 21].

Experimental measurement of the ONH biomechanical response to date have greatly contributed in our understanding of ONH biomechanics. However, these studies have primarily reported the static planar strains or deformations of the ONH using techniques with limited resolution and/or depth of penetration [22–28]. Alternate numerical approaches that can estimate the full 3D dynamic response of the tissues, such as finite element (FE) modeling, are hence required to gain a complete understanding of the biomechanical response of the ONH to IOP elevation [15, 18, 29–33]. The mechanical properties of the ocular connective tissues play a key role in accurately simulating the mechanical response of the ONH. One of the most important load bearing components of the ONH is the sclera [34–36], a soft load-bearing tissue with a complex collagen fibril orientation in the peripapillary region [17, 37]. The collagen fibrils, together with other solid matrix constituents, are responsible for the nonlinear, anisotropic, heterogeneous material properties of ocular tissues [18, 37–44]. Many imaging modalities have been employed to measure the anisotropy of the collagen fibers in ocular load-bearing tissues, including small-angle light scattering [45, 46], X-ray scattering [37, 38, 47, 48], second harmonic imaging [26, 49, 50], electron microscopy [7, 51–53], magnetic resonance imaging [54, 55], and polarized light microscopy [17, 43, 56]. The latter technique allows for visualization and quantification of the distribution and orientation of collagen fibers in the peripapillary sclera and lamina cribrosa with micrometer-scale resolution.

Based on the imaging data, our group and others have developed models of ocular tissues that incorporate heterogeneous, anisotropic, and nonlinear mechanical properties. Zhang et al., [57] developed a human ONH and peripapillary sclera model with anisotropic collagen distribution. Campbell et al., [58] developed a porcine eye model with a generic geometry that incorporated anisotropic mechanical properties of the lamina cribrosa using eye-specific measurements of laminar cable orientation and connective tissue volume fraction. Voorhees et al., [59, 60] developed eye-specific anisotropic models of a subregion of the lamina microstructure based on polarized light microscopy. Despite these advances, the anisotropic models that have been proposed to date include major simplifications, since they typically assume a circumferential ring of collagen fibers around the ONH with a constant width through the scleral thickness. Gogola and co-workers [17] used polarized light microscopy to show that collagen fibers were distributed in circumferential, radial, and isotropic patterns depending on depth through the thickness of the peripapillary sclera. Unfortunately, most modeling studies used average measurements of the collagen fiber distribution through the scleral thickness previously reported by Pijanka et al., [37] and did not include the recently reported layer of radial collagen fibers in the anterior peripapillary sclera [17]. Our group recently [18] used the most recent depth-dependent scleral collagen orientation data reported by Gogola et al., [17] to incorporate the circumferential, radial, and isotropic collagen fibers into the scleral matrix of FE models using a mesh-free approach. While this was an improvement over prior modeling work, we used a set of complex, proprietary programs to assign these properties in CalculiX; this approach is computationally expensive and cannot be used in commercial FE packages. In addition, the distribution, density, length, and diameter of the fibers cannot be easily controlled based on simulation needs. Thus, it would be beneficial to develop a freely available alternative approach to model the complex heterogeneous and anisotropic mechanical properties of fiber-reinforced tissues that allows for control of fiber orientation, density, diameter, length, and stiffness in commercial FE packages.

Herein, we propose a mesh-free, penalty-based cable-in-solidcoupling approach to mimic complex collagenous tissues, and validate the method by comparing results from computational simulations of scleral patch behavior against previously published experimental data from biaxial scleral tensile tests [39]. We further test the method by incorporating the depth-dependent circumferential, radial, and isotropic collagen fibers into a solid scleral matrix and pia of an eye model pressurized to 45 mmHg and compare the results from models with and without scleral collagen fiber reinforcement. The proposed approach is freely available in LS-DYNA (Ansys/LST, Canonsburg, PA, US) through custom Matlab scripts (Mathworks, Natick, Massachusetts, US) that are provided as supplemental data. Although we used an eye-specific model of the posterior pole and ONH to illustrate the strengths of the proposed methodology, it can be applied to model any complex fiber-reinforced tissue, organ, or mechanical structure.

2. Materials and Methods

2.1. 3D Eye-specific FE Model of the Human Optic Nerve Head

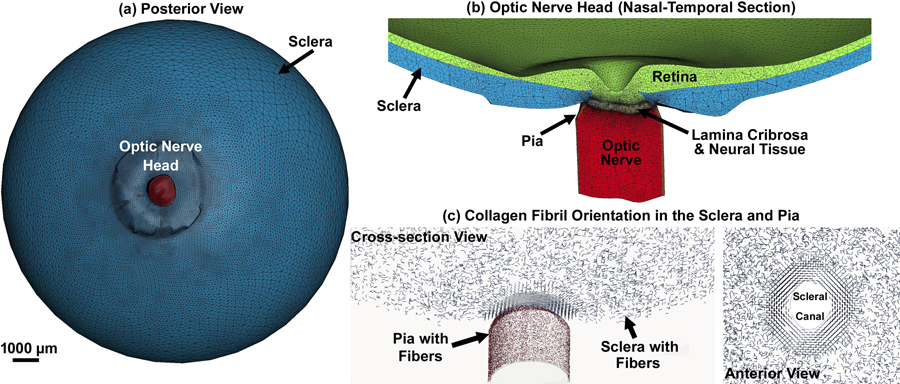
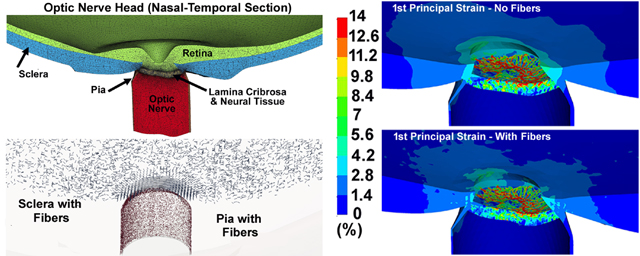
In this study, we use a single, previously published, eye-specific model of the posterior pole of a human donor eye [19, 61] to test the new fully coupled, penalty-based, mesh-free, cable-in-solid approach to modeling scleral and pia anisotropic mechanical behavior proposed herein. The construction of this model has been fully described in our previous publications. In brief, the macro-architecture of the model is first defined by 3D delineation of anatomic tissue surfaces within a high-resolution, histologic, fluorescent 3D reconstruction of the posterior eye and ONH obtained from a human donor of European descent with normality confirmed by ophthalmic clinical record review, as described previously [62]. Briefly, a human donor eye was procured from the Alabama Eye Bank within 6 hours postmortem, then fixed with aldehydes through pars plana infusion and immersion while the internal pressure was held at 10 mmHg. The ONH and surrounding peripapillary sclera were trephined, embedded in light-blocking paraffin, and then sectioned on a microtome at 1.5 μm thickness, with a fluorescent image (4096×4096 pixels at 1.5×1.5 μm pixel resolution) of the exposed block face acquired after each section is taken. The resulting image stack was aligned using laser displacement measurements of the block position after each section was taken, and combined into an image volume [62]. Custom delineation software (MultiView, courtesy of Dr. Claude F. Burgoyne) was used to digitally section the 3D fluorescent ONH reconstruction volume at forty, equally spaced, radial, sagittal planes centered on the ONH [63]. Within each radial image section, the anatomic surfaces were delineated using 2D Bezier curves to define the morphology of the neural canal, lamina cribrosa, peripapillary sclera, and pia [62, 63]. 3D surfaces are fit to the families of Bezier curves defining each anatomic surface and the resulting eye-specific geometries of the ONH and peripapillary sclera are then fit into a larger generic posterior scleral shell with anatomic shape and thickness [19]. Finally, a parameterized, anatomic surface defining the anterior surface of the prelaminar neural tissue, retina, and choroid is added [19]. These surfaces are then utilized to build the high-fidelity, eye-specific, 3D FE macro-scale mesh of the human posterior eye that includes the sclera, lamina cribrosa, pre- and retro-laminar neural tissue, retina, and pia as presented in Figs. 1a & b. A coarser mesh was generated for the anterior areas of the retina and sclera, as well as the posterior area of the optic nerve, and the mesh was more refined where more accurate estimates of stresses and strains were needed, including the peripapillary sclera, scleral flange, lamina cribrosa, neural tissue, and immediate retrolaminar optic nerve, and pia. The collagen fibril orientation in the sclera and pia are shown in Fig. 1c.

Fig. 1.

(a) Posterior view of the posterior eye FE model, (b) nasal-temporal section of the posterior eye FE model showing the ONH, and (c) anisotropic collagen fibril orientation in the sclera (circumferential, radial, and planar isotropic) and pia (planar isotropic).

To create the mesh of the lamina cribrosa microstructure [19], the lamina cribrosa was segmented from the original 12-bit grayscale images of the laminar region using a custom automated algorithm that leverages a priori knowledge of the 3D trabeculated structure of the lamina cribrosa as described previously [64]. The volume hexahedral mesh, composed of 8-noded elements, was generated using a custom Matlab script as described in our recent publication [61]. Briefly, the connectivity of the elements across tissue/geometric boundaries was maintained at their nodal interfaces using an automated mapping algorithm, which allowed us to avoid defining contacts or tying constrains between the model components [19, 61]. The final hexahedral mesh of the lamina cribrosa beams and neural tissue were incorporated into the human ONH model as shown in Fig. 1b. The FE model of the eye from donor 119 consists of 2,367,002 and 2,587,483 elements and nodes, respectively, with a minimum/maximum element edge length of 7/15 μm. To assess scleral canal deformations, a custom Matlab (Mathworks, Natick, Massachusetts, US) script was written to calculate the diameters of the anterior scleral canal opening (ASCO), posterior scleral canal opening (PSCO), anterior lamina insertion (ALI), and posterior lamina insertion (PLI) as described previously [61]. To evaluate the effects of the mesh density on different element types, the models were simulated and the results compared in terms of the average radial displacement of the scleral canal at the ALI, PLI, and PSCO, average depth of the anterior laminar surface, volumetric average 1^st principal strain in the LC, and maximum von Mises stress in the LC, as described in our recent publication [61]. Models were fully converged.

Regarding the applied boundary conditions on the ONH FE model, the nodes of the sclera and retina along the cut face of the globe at the equator were selected and assigned to allow for radial displacement only in the plane of the equator. An IOP elevation to 45 mmHg was applied to the inner surface of the retina, which is well within the physiologic range [65]. A custom Matlab script was used to detect the load surface, equivalence the nodes at the components’ interfaces, define the materials’ sections, define the element sets, and write the final LS-Dyna input file [61, 66]. A 10-core Intel® Xeon® CPU W-2155@3.30 GHz computer with 256GB RAM was used to run the simulations in explicit-dynamic LS-DYNA. The simulation was conducted by dynamic IOP elevation to 45 mmHg (500 ms) with the time step of 10 ms (50 time steps), a loading rate that is also well within the physiologic range [20, 21]. The entire simulation for the model, with and without cable-in-solid collagen fibers, took 27 and 18 hours, respectively, to run on our workstation.

2.2. Fiber Distribution and Mesh-Free Cable-in-Solid Coupling Algorithm

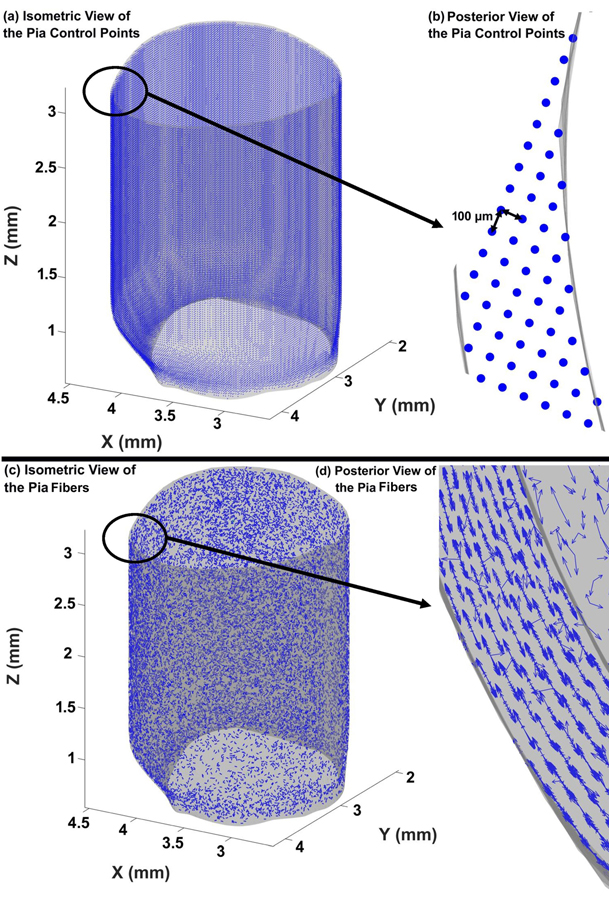
Several studies have defined collagen fiber orientations to address the anisotropic constitutive biomechanical response of the sclera [18, 34, 36, 41, 42]. Defining scleral collagen fiber directions in an eye-specific geometry is not a trivial task, as no analytical coordinate system can be identified to capture the actual eye-specific geometries of the peripapillary scleral surfaces and scleral canal, which are the morphologic basis of the collagen fiber orientation in those tissues. The cable element/collagen fiber distribution and orientation in the sclera and pia were defined based on the eye-specific surface geometries of the sclera, scleral canal, and pia, along with the central anterior-to-posterior axis through the scleral canal. These orientations are also depth-dependent in the peripapillary sclera, with a thin region of fibers anteriorly that are oriented normal to the scleral canal wall (radial fibers), and a thicker region of fibers oriented tangent to the scleral canal wall posteriorly; these anisotropic fiber orientations transition to planar isotropic fiber orientation away from the scleral canal wall [17]. The distance between the control points can be adjusted according to user needs. In this eye model, the distance between the control points was set to 100 μm to allow for an appropriate fiber distribution at a reasonable fiber diameter and length, which are restricted by dimensional limitations of the sclera and pia (more information on this is provided in Section 2–3). The distribution of the control points in the pia is shown in Figs. 2a & b. The cable elements/fibers in the pia were randomly distributed in the tangent plane, with the normal vector perpendicular to the pia’s outer surface (planar isotropic) as presented in Figs. 2c & d. When cable elements/fibers are added to the model, the scleral matrix where cable elements reside is replaced by the cable elements themselves so total scleral volume and mass is conserved. Briefly, a spherical coordinate system was employed to define the random fiber orientations in the pia. Considering the control points as the origin point of cable elements/fibers, the endpoint of the cable elements/fibers was defined by assigning the length, azimuth angle, and polar angles. The fiber orientations were only allowed in a plane with normal vector perpendicular to the nearest surface mesh. Considering the plane constraint, the inner product of cable elements/fiber orientations and normal vector of surface mesh should be zero; therefore, the equations corresponding to the end-points are as follows:

$$\theta =\arcsin \left(\frac{-c\times cot(\phi )}{\sqrt{a^2+b^2}}\right)-\arctan (\frac{a}{b})$$ (1)

$$\{\begin{array}{l}{X}_e=X_o+l_f\sin (\phi )\cos (\theta )\hfill \\ Y_e=Y_o+l_f\sin (\phi )\sin (\theta )\hfill \\ Z_e=Z_o+l_f\cos (\phi )\hfill \end{array}$$ (2)

where the origin of the cable element/fiber is located at [X_o, Y_o, Z_o], the end of the cable element/fiber is located at [X_e, Y_e, Z_e], [a, b, c] is the normal vector of nearest surface mesh to the origin position, l_f is the length of fiber, θ is the azimuth angle, and φ is the polar angle. The values of [X_o, Y_o, Z_o], [a, b, c], and l_f are known for each fiber, by selecting a random value between 0 and 2π for φ, the value of θ can be computed from Eq. (1). The Matlab scripts to define the control points and distribute the fibers in the pia are attached to the paper as supplementary material 1.

Fig. 2.

Distribution of the control points in the pia from the (a) isometric and (b) posterior views. Distribution of the planar isotropic discrete cable elements in the pia from the (c) isometric and (d) posterior views.

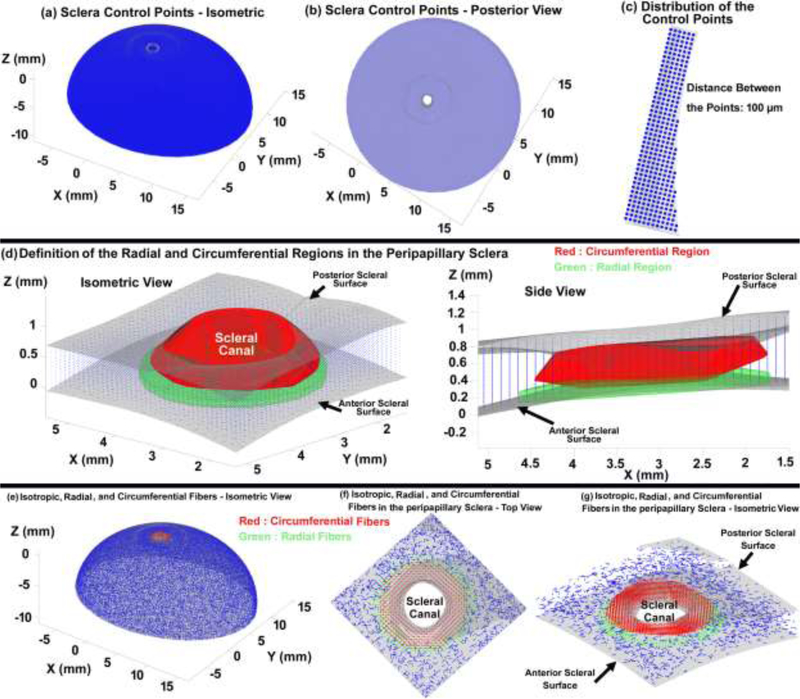
For the sclera, cable elements/fibers around the central anterior-to-posterior axis are either tangential (circumferential), radial or planar isotropic inside the solid matrix elements. The circumferential direction of the cable element/fibers in the peripapillary sclera can be defined as the tangential direction at scleral canal. However, the scleral canal geometry is complex, with a more elliptical than circular cross section that traverses the sclera at an oblique angle, and it is generally much larger at the posterior scleral boundary compared to the anterior scleral boundary. To distribute the cable elements/fibers in the sclera, the control points were distributed at a 100 μm interval as displayed in Figs. 3a–c. The regions containing circumferential, radial or planar isotropic cable elements/fibers in the peripapillary scleral region were defined as ~ 10%, 40%, and 20% of the canal diameter from the anterior scleral surface to 70% of the scleral thickness, and then from the 70% of the scleral thickness to the most posterior surface of the sclera as displayed in Fig. 3d. This was achieved using a shape function and based on the distribution of collagen fibers measured in human eyes by Gogola and colleagues using polarized light microscopy [17]. To define the circumferentially oriented cable elements/fibers, two vectors are required. The first vector is the central anterior-to-posterior axis of the scleral canal, and the second vector connects the control points to the scleral canal axis along the minimum distance path. The anterior-to-posterior axis of the scleral canal was defined by the vector between the centroid of the anterior scleral canal opening and the centroid of the posterior scleral canal opening. The cross product of these two vectors defines the circumferential direction along which the cable elements/fibers are oriented. Radial cable elements/fibers were distributed in the region from 10% to 40% of the canal diameter from the anterior scleral surface to 15% of the scleral thickness; cable elements/fibers orientation was computed by the cross product of the previously-defined circumferential direction and the vector normal to the anterior scleral surface mesh. Finally, cable elements/fibers outside of the circumferential and radial regions were randomly distributed in the solid scleral matrix (planar isotropic) based on Eqs. (1) & (2). A Gaussian function was used to provide a smooth transition in cable element/fiber direction and density from the radial and circumferential regions to the isotropic region, as shown in Figs. 3f–g. To minimize the computational cost in the eye model, 100% of the control points were used to define the circumferential, radial and planar isotropic cable elements/fibers in the peripapillary region within 2.5 mm of the scleral canal, but only 20% of the control points were used to define cable elements/fibers in the peripheral sclera farther from the ONH (see Section 2–3).

Fig. 3.

Distribution of: (a) the control points in the sclera, from the (b) posterior and (c) isometric views. Definition of the peripapillary scleral regions with radial and circumferential collagen fibers, from the (d) isometric, side and (e) posterior views. Distribution of the discrete cable elements in the peripapillary sclera from the (f) posterior and (g) isometric views.

A neo-Hookean hyperelastic material model was used to describe the mechanical response of the solid matrix of all tissues (using *MAT_027 in LS-DYNA, with B=0) as follows:

$$W_{SolidMatrix}=C_{10}\left({\overline{I}}_1-3\right)+\frac{1}{D_1}{\left(J^{el}-1\right)}^2$$ (3)

where W is the strain energy per unit of reference volume; C₁₀ and D₁ are temperature dependent material parameters; ${\overline{I}}_1$ is the first deviatoric strain invariant defined as:

$${\overline{I}}_1={{\overline{\lambda }}^2}_1+{{\overline{\lambda }}^2}_2+{{\overline{\lambda }}^2}_3$$ (4)

where the deviatoric stretches ${\overline{\lambda }}_i=J^{-\frac{1}{2}}{\lambda }_i$, J is the total volume ratio, J^el is the elastic volume ratio as defined below in thermal expansion, and λ_i are the principal stretches. The initial shear modulus, μ, and bulk modulus, K, are given by:

$${\mu }_0=2C_{10},K_0=\frac{2}{D_1}$$ (5)

where the bulk modulus is defined as 100μ for all tissues (Poisson’s ratio = 0.495). The shear moduli (μ) of the tissues are summarized in Table 1.

Table 1.

The material parameters of the eye-specific FE model of donor 119 with the age of 79-year-old male and a European ethnicity. The bulk modulus was set to κ=100μ, where μ=shear modulus for all tissues [19]. was modeled as neo-Hookean hyperelastic material model and the fibers were simulated as discrete cable/cable.

Tissue	Shear modulus, μ (MPa)	Elastic modulus, E (MPa)	Density, ρ (kg/m3)
Retina	0.01	-	1100
Sclera	1.64	-	1243
Lamina cribrosa	0.41	-	1243
Neural Tissue	0.01	-	1100
Pia	1.64	-	1100
Optic nerve	0.01	-	1100
Sclera Fibers	-	600	1100
Pia Fibers	-	600	1100

The sclera and pia were the only components with embedded fibers, modeled with discrete cable elements. The discrete cable element model allows elastic cables to be accurately modeled and no force will be induced in compression. The mass density and elastic modulus are the only assignable parameters that define the mechanical properties of the discrete cable element. The force, F, generated in the cable will be nonzero when the cable is in tension, which is given by [67]:

$$F=\max \left(F_0+K\mathrm{\Delta }L,0\right)$$ (6)

where ΔL is the change in cable element length:

$$\mathrm{\Delta }L=currentlength-\text{(}initiallength-offset\text{)}$$ (7)

And the stiffness (E>0 only) is defined as:

$$S=\frac{E\times area}{\text{(}initiallength-offset\text{)}}$$ (8)

A constant force element can be achieved through:

$$F_0>0\mathrm{and}S=0$$ (9)

The circular cross-section area of the cable element are defined in the LS-DYNA input file. A pretension was applied on the cable element at the beginning of the analysis, which was released immediately after the simulation started to allow the model to initiate and propagate the forces. The reason for prestressing is that sudden application of the cable forces at time zero may result in an excessively dynamic response during pre-tensioning. Therefore, a very negligible (very close to 0 N) force was defined immediately after pre-tensioning, so the cable force ramps up from zero at the start time to a value close to zero. Based on our experience with various simulations under dynamic loading, this provides a stable cable and solid matrix coupling throughout IOP elevation.

The collagen fibers in the sclera and pia were modeled by discrete cable elements and the matrix around the fibers were modelled by 8-noded hexahedral solid elements with an r-adaptive remeshing function based on an Element-Free-Galerkin (EFG) formulation [68]. The cable elements/fibers were embedded in the solid matrix of the sclera and pia using a penalty-based cable-in-solid coupling algorithm wherein the solid elements can be highly deformed by the 3D adaptive EFG method [69, 70]. In a penalty-based cable-in-solid coupling algorithm [71], a penalty spring is attached between coupling points on the cable and in the solid element. Penalty spring stiffness is calculated based on the geometric mean of cable and solid’s bulk modulus. Relative motion of the fibers in the solid matrix of the sclera and pia was also simulated by coupling momentum along the normal direction of each discrete cable element, so both the accelerations and velocities between the discrete cable and solid elements were constrained [67, 72]. This strong coupling interaction transfers load from the fibers to the solid matrix of the sclera and pia and vice-versa. The coupling between the cable elements and the solid is used in a way to invoke coupling not only at cable nodes, but also at coupling points between the two cable nodes of each element (along the length of the cable element). The 3D adaptive EFG used herein has several important features, including local mesh-refinement, interactive adaptive method, monotonic mesh resizing, and a pressure-smoothing scheme, which makes it a suitable choice to address the mesh-free coupling of the fibers and the solid matrix. Thus, the EFG formulation allowed us to define material properties independent of the FE mesh. After each load increment, the solid nodal velocity was updated by dividing the new momentum by new mass. Finally, the interpolated velocity was assigned back to the discrete cable nodes such that the mass at the coupling point simply takes the value of the discrete cable nodal mass. The coupling point has its velocity constrained by solid nodes during the map-back stage and it then distributes the corresponding momentum to the discrete cable nodes [73]. This results in a more uniform mechanical response of the coupled cable element/fiber-matrix under applied load due to proper mass distribution at each FE hexahedral mesh node. Solid elements of the sclera and pia were adequately remeshed with an r-adaptive function which enables large deformations and can generate complex shapes [69]. The r-adaptive approach can optimize a discretization at minimal computational costs since the relocation of nodes with invariant element connectivity as occurs in r-adaptive schemes prohibits the addition or deletion of degrees-of-freedom regardless of mesh density. Hence, r-adaptive schemes optimally use a given mesh topology, so that reasonable solutions can be obtained at minimal computational costs [74]. Another key advantage of mesh-free penalty-based cable-in-solid coupling algorithm is its independence from the FE mesh and cable elements, as the control points are defined before the volume mesh is constructed. This is especially helpful for complex geometries wherein generating a volume mesh is a challenge, as there is no need to have the geometry volume-meshed to define the control points and distribute the cable elements/fibers. Thus, remeshing the FE model for any purpose, such as mesh density analysis, will not affect the definition or distribution of the cable elements in the solid matrix and the distance between the control points can be adjusted according to simulation needs. For example, if there is a specific area that requires denser cable elements/fibers, the number of control points can be locally increased and the included Matlab script allows us to use any fraction of control points to be used for assignment of cable elements/ fibers. A Gaussian function was used to smooth the directional transition between the circumferential, radial, and isotropic fiber regions at the peripapillary sclera to match the directional distributions measured experimentally [17], which results in a stress and strain patterns in the FE model.

2.3. Scleral Patch Finite Element Model – Parametric Study and Method Validation

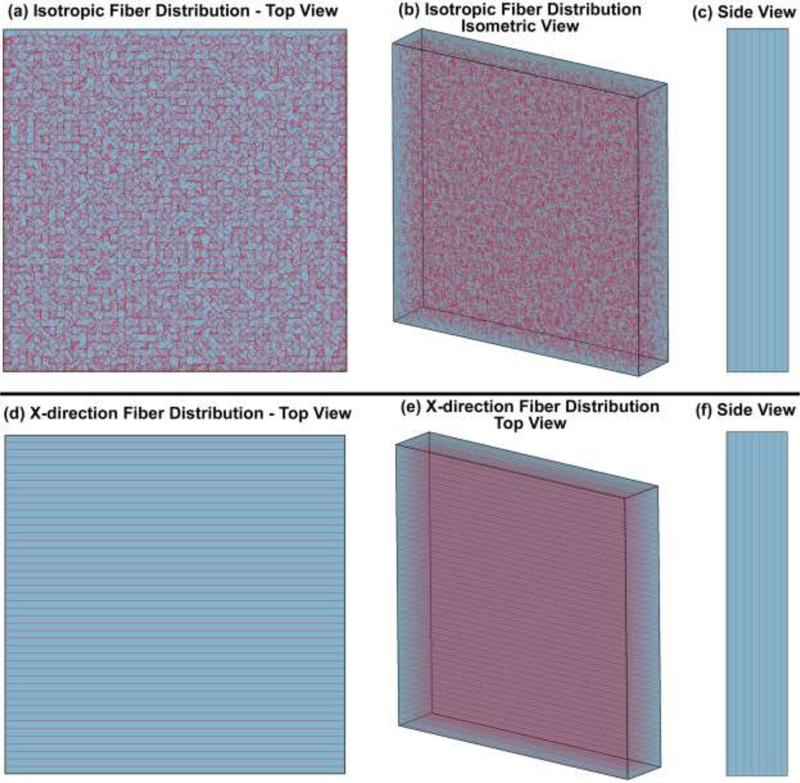
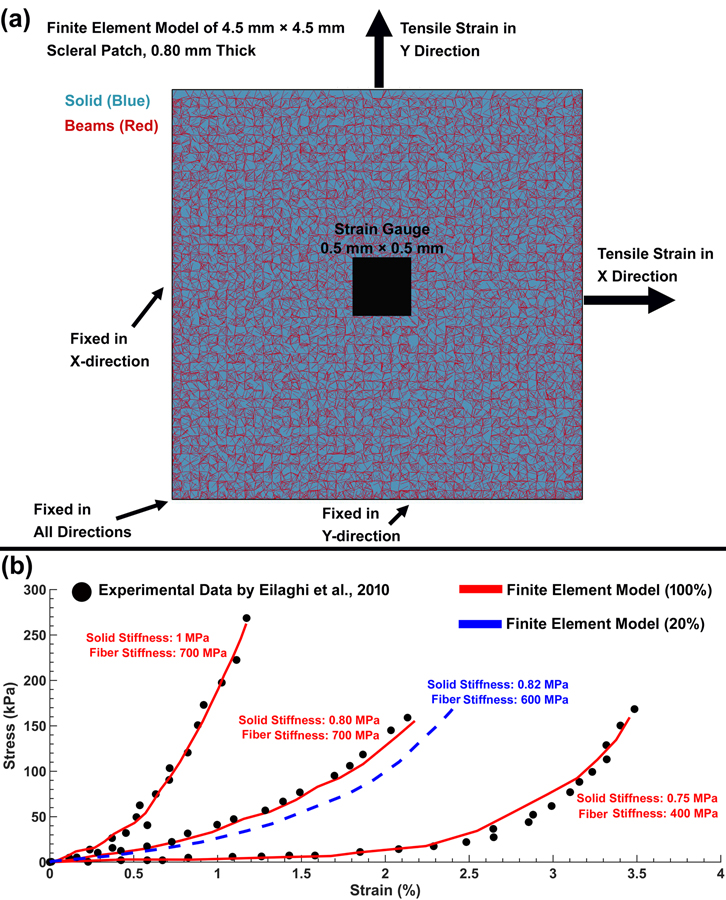
To determine the role of the density, length, diameter, solid matrix stiffness, and cable element stiffness, an FE model of a scleral patch was constructed to compare to prior experimental scleral biaxial tensile test results [39]. The FE model of the scleral patch has the length, width, and average thickness of 4.5 mm × 4.5 mm × 0.8 mm that match the experimental study, and the cable elements/fibers inside the patch were either random (isotropic, to mimic the experimental biaxial testing results) or in the X-direction (anisotropic, as a test of the cable element directional effect) as shown in Fig. 4. The control points were distributed at 100 μm intervals throughout the FE model. The solid matrix stiffness, as well as the density, length, diameter, and stiffness of the cable elements were then altered systematically to study the effects of each parameter as summarized in Table 2. Thereafter, each patch model was subjected to an equibiaxial stretch in the X and Y directions, where the displacement boundary conditions were applied to the FE model to mimic the biaxial mechanical testing of human sclera [39] as shown in Fig. 5a. The aim of the parametric study was to determine the mechanical contributions of the cable elements and solid matrix in the resultant X and Y stresses.

Fig. 4.

FE model of the scleral patch with cable elements of 100 μm length and 50 μm diameter placed at 100 μm spacing intervals in the random (planar isotropic) orientation within a solid matrix: (a) top view, (b) isometric view, and (c) side view. FE model of the scleral patch with similar cable elements oriented in the X-direction only (anisotropic) within a solid matrix: (d) top view, (e) isometric view, and (f) side view.

Table 2.

The patch parameters for the isotropic and X-direction cable distributions.

Fiber Parameters	Density (%)	Length (μm)	Diameter (μm)	Solid Stiffness (MPa)	Cable Stiffness (MPa)
Isotropic
1	100	100	50	0.8	600
2	75	100	50	0.8	600
3	50	100	50	0.8	600
4	25	100	50	0.8	600
5	100	75	50	0.8	600
6	100	50	50	0.8	600
7	100	25	50	0.8	600
8	100	100	37.5	0.8	600
9	100	100	25	0.8	600
10	100	100	12.5	0.8	600
11	100	100	50	0.6	600
12	100	100	50	0.4	600
13	100	100	50	0.2	600
14	100	100	50	0.8	450
15	100	100	50	0.8	300
16	100	100	50	0.8	150
X-Direction
1	100	100	50	0.8	600
2	75	100	50	0.8	600
3	50	100	50	0.8	600
4	25	100	50	0.8	600
5	100	75	50	0.8	600
6	100	50	50	0.8	600
7	100	25	50	0.8	600
8	100	100	37.5	0.8	600
9	100	100	25	0.8	600
10	100	100	12.5	0.8	600
11	100	100	50	0.6	600
12	100	100	50	0.4	600
13	100	100	50	0.2	600
14	100	100	50	0.8	450
15	100	100	50	0.8	300
16	100	100	50	0.8	150

Fig. 5.

(a) FE model of the scleral patch, including the strain gauge and boundary conditions. (b) Stress-strain curves representing the stiffest, most compliant, and average responses [39] from experimental biaxial tensile testing of human sclera patches (black dots), compared to identical FE cable-in-solid models of a planar isotropic scleral patch (red solid and blue dashed lines). The red line represents the fiber density of 100% used to represent the heterogeneous, anisotropic collagen fibers in the peripapillary sclera in our posterior eye FE model, and the blue dashed line represents the fiber density of 20% that represents the planar isotropic collagen fibers of the peripheral sclera and pia.

To identify the most suitable cable density and stiffness and solid matrix stiffness for the sclera and pia that both mimic the mechanical response of these tissues and result in reasonable simulation time, the stiffest, the most compliant, and the average experimental stress-strain data were extracted from the supplemental, specimen-specific biaxial scleral tensile test data published by Eilaghi and colleagues [39] and plotted in Fig. 5b. The aim of this study was to adjust the solid matrix and cable element parameters to capture the full range of mechanical responses of the sclera presented in Fig. 5b. The X and Y stresses were calculated as a function of different cable and solid matrix properties in the central strain gauge region of 0.5 mm × 0.5 mm [39].

3. Results

The stiffness of the model solid matrix and cable elements were adjusted to yield a mechanical response that matched the stiffest, average, and most compliant of the scleral specimens in previously published experimental study wherein the stress-strain data for all individual specimens tested were published as a supplemental file, [39] as shown in Fig. 5b. The cable element diameter, and length were assigned to 50 μm, and 100 μm, respectively, to conform to the requirements of the thin sclera and pia geometries. The solid matrix and cable element stiffness of 0.82 MPa (C_neo) and 600 MPa (elastic modulus), respectively, with a cable density, diameter, and length of 20%, 50 μm, and 100 μm, respectively, resulted a stress-strain curve property that fell within the experimental range (Fig. 5b). These properties were then assigned to the sclera and pia of the eye model for the dynamic FE simulations, with cable element density increased to 100% of the control points in the peripapillary sclera around the ONH where significant anisotropic collagen fiber reinforcement is known to occur.

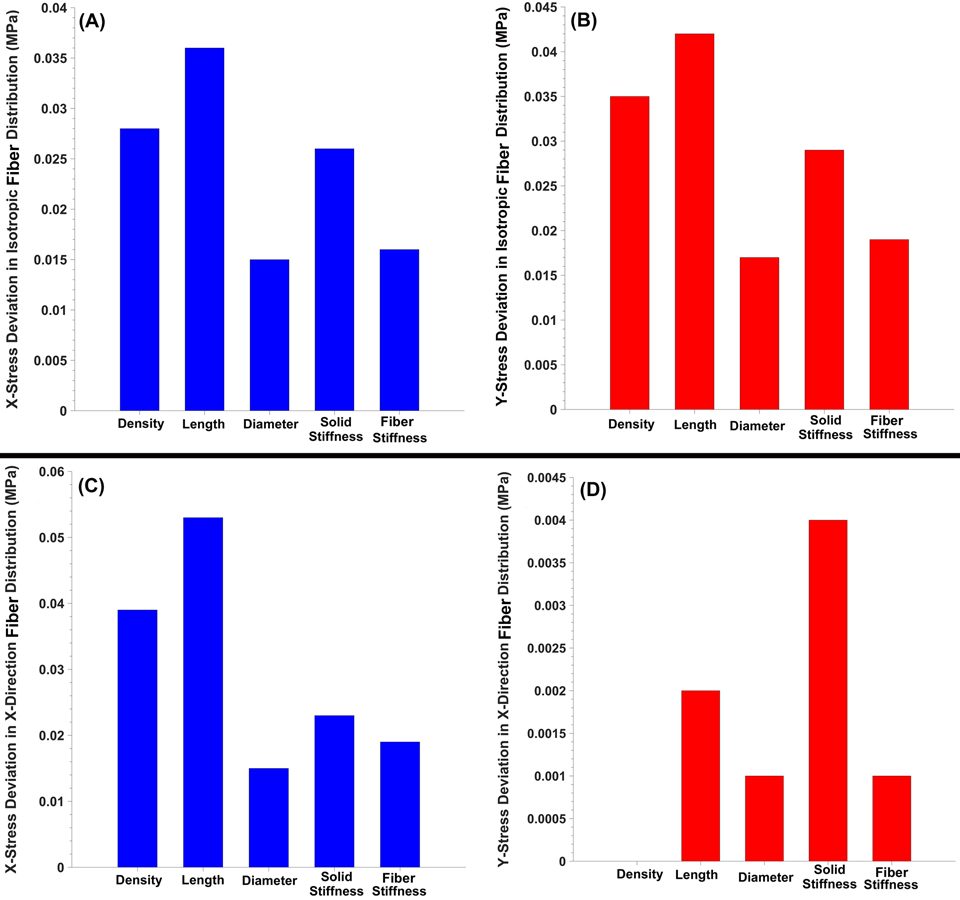
The X and Y stresses in the scleral patch FE model in both the random (isotropic) and X-direction (anisotropic) cable distributions are shown in Fig. 6. The length of the cable element exhibited the largest mechanical contribution to the resultant stresses, while the diameter of the cable element had the smallest effect.

Fig. 6.

The (a) X and (b) Y stress deviation as a function of the cable density, length, diameter, solid matrix stiffness, and cable stiffness in the planar isotropic scleral patch FE model. The (c) X and (d) Y stress deviation as a function of the cable density, length, diameter, solid matrix stiffness, and cable stiffness in the scleral patch FE model with cable elements oriented only in the X-direction.

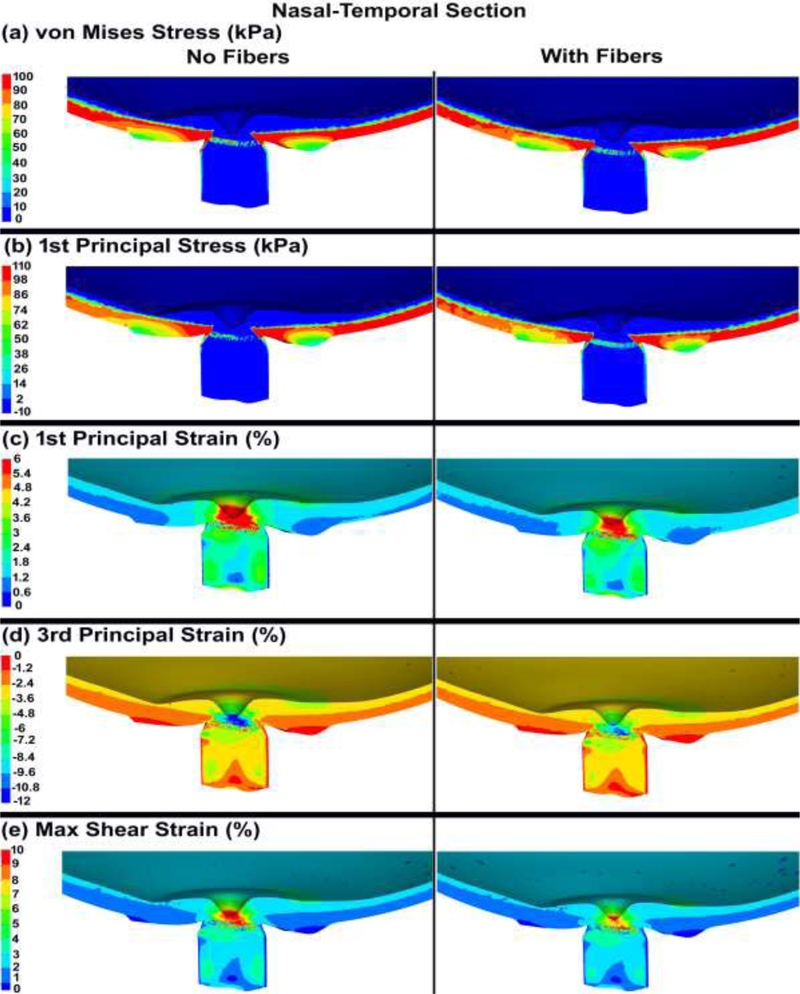
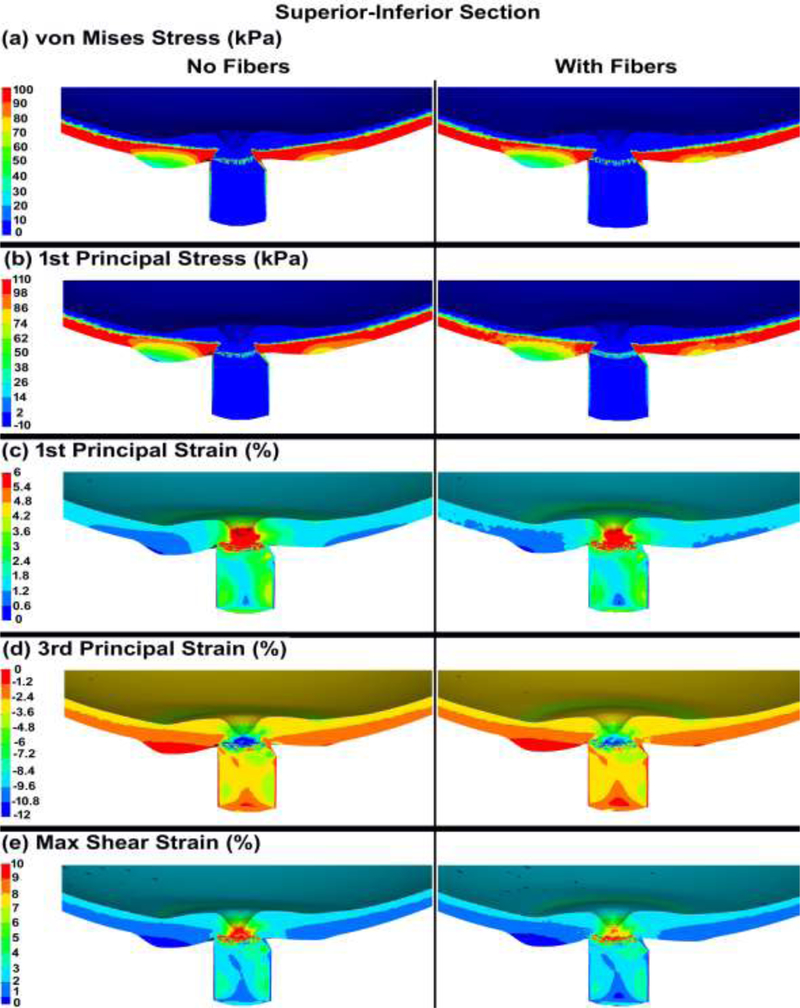
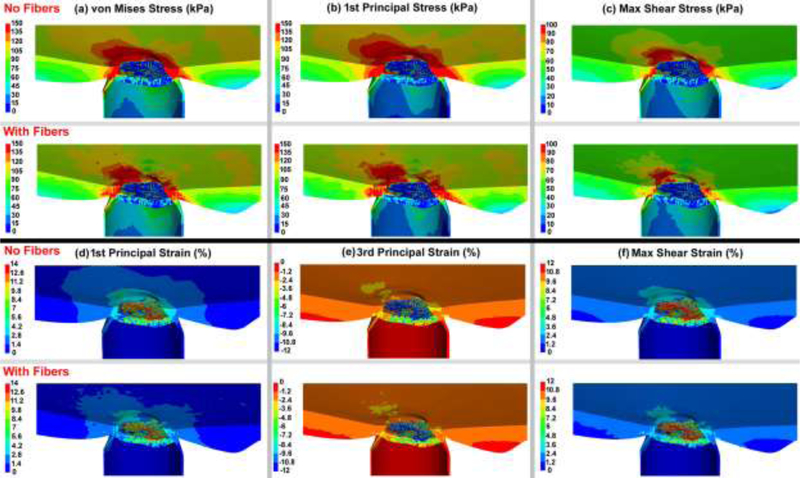
The von Mises and 1^st principal stresses, as well as the 1^st principal, 3^rd principal, and maximum shear strains in the ONH FE model, both with and without cable elements/fibers, are shown in Figs. 7 & 8 for the nasal-temporal and superior-inferior cross sections, respectively. The 1^st principal stress and strain in the nasal-temporal section of the dynamic ONH FE models, both with and without cable elements/fibers, are attached as a video clip in supplementary material 2.

Fig. 7.

The contour maps of (a) von Mises stress, (b) 1^st principal stress, (c) 1^st principal strain, (d) 3^rd principal strain, and (e) maximum shear strain in the nasal-temporal cross-sections of posterior eye models, with and without cable elements/fibers.

Fig. 8.

Contour maps of (a) von Mises stress, (b) 1^st principal stress, (c) 1^st principal strain, (d) 3^rd principal strain, and (e) maximum shear strain in the superior-inferior cross-sections of posterior eye models, with and without cable elements/fibers.

The von Mises, 1^st principal, and maximum shear stresses as well as the 1^st principal, 3^rd principal, and maximum shear strains in the nasal-temporal section through the ONH are exhibited in Fig. 9 both with and without considering the role of the cable elements/fibers. The volumetric average 1^st principal and maximum shear stresses and strains in the lamina cribrosa microstructure and the laminar region neural tissue are summarized in Table 3. In addition, the average IOP-driven radial expansion in the ASCO, PSCO, ALI, and PLI is compared in Table 4 for models with and without the cable elements/fibers.

Fig. 9.

Contour maps of (a) von Mises stress, (b) 1^st principal stress, and (c) maximum shear stress in the nasal-temporal cross-sections of posterior eye models, with and without fibers. Contour maps of (d) 1^st principal strain, (e) 3^rd principal strain, and (f) maximum shear strain in the nasal-temporal cross-sections of posterior eye models, with and without cable elements/fibers.

Table 3.

The volumetric average 1^st principal and maximum shear stresses and strains in the lamina cribrosa and neural tissue.

Tissue	1st Principal stress (kPa)	Maximum shear stress (kPa)	1st Principal strain (%)	Maximum shear strain (%)
No Fibers
Lamina cribrosa cables	75.70	49.80	7.75	8.29
Neural tissue	8.17	1.98	5.08	3.12
With Fibers
Lamina cribrosa cables	62.90	39.80	5.26	6.42
Neural tissue	6.24	1.27	3.95	1.67

Table 4.

Average radial expansion in the anterior scleral canal opening (ASCO), posterior scleral canal opening (PSCO), anterior lamina insertion (ALI), posterior lamina insertion (PLI).

Tissue	ASCO (μm)	PSCO (μm)	ALI (μm)	PLI (μm)
No Fibers	26	26	14	23
With Fibers	16	20	11	19

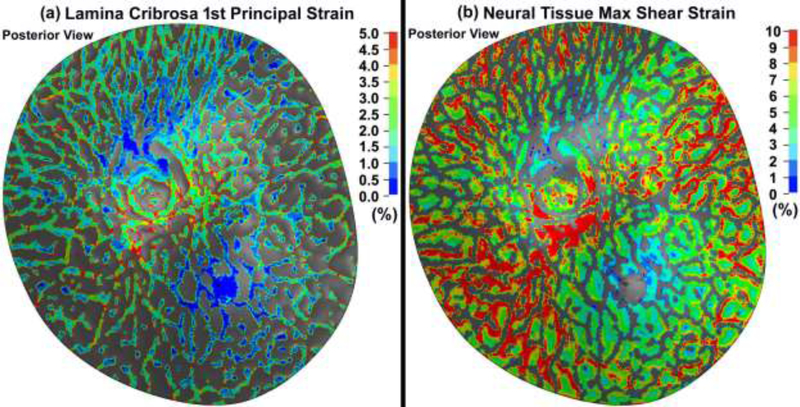
The 1^st principal and maximum shear strain in the lamina cribrosa and neural tissue considering the role of the fibers in the sclera and pia are shown in Fig. 10.

Fig. 10.

Contour maps of (a) 1^st principal strain in the lamina cribrosa (b) maximum shear strain in the neural tissue in a posterior eye model that included cable elements/fibers representing scleral and pial anisotropy.

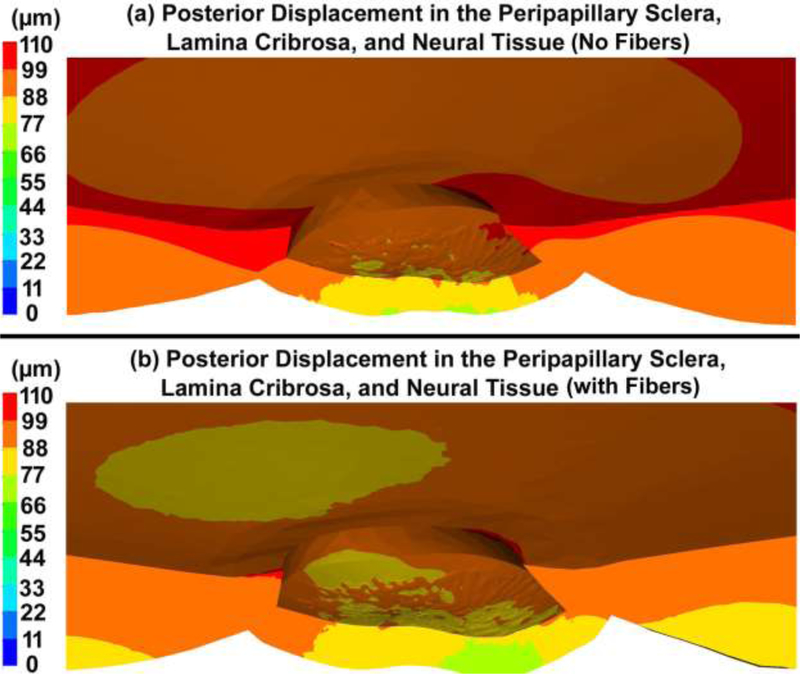
The posterior displacements of the peripapillary sclera and laminar region in the ONH FE models, with and without the cable elements/fibers, are shown in Fig. 11.

Fig. 11.

Contour maps of the posterior displacement in the peripapillary sclera, lamina cribrosa, and neural tissue (a) no cable elements/fibers and (b) with cable elements/fibers. Note that deformations are relative to the equator of the eye where the fixed boundary conditions are applied.

4. Discussion

The dominant load-bearing component of the ONH is the sclera, a collagenous tissue with a complex collagen fibril orientation in the peripapillary region [17]. The collagen fibrils and other constituents are responsible for the nonlinear, anisotropic, heterogeneous material properties of the ocular tissues [18, 37–44]. Incorporating the collagen fibers into FE models of soft biological tissues play a key role in mimicking the heterogeneous and anisotropic mechanical response of the tissues and the resultant stresses and strains. This study aimed to incorporate the complex depth-dependent circumferential, radial, and isotropic collagen fibers into a solid scleral matrix of the ONH FE model, as described in experimental measurements of collagen orientation in these tissues [17] (Fig. 1). The beam-in-solid (cable-in-solid) algorithm has been widely used for fiber reinforced thermoplastic materials [69, 70, 75], and the results were found to be in a very good agreement with the experimental data. The nerve axon fibers and volumetric ground substance of the brain has also been simulated using this technique [76], which shows that this method can satisfy the structural conditions of equilibrium, energy balance and compatibility [73] in very soft biological tissues [76].

A scleral patch FE model was constructed with random (isotropic) (Fig. 4a) and X-direction (anisotropic) (Fig. 4b) cable element distributions to investigate the parameters space and mechanical contributions of the cable elements in the proposed cable-in-solid formulation. Results were compared to that of the experimental biaxial data by Eilaghi et al., [39], and stresses were found to be in good agreement (Fig. 5b). Cable element length played the most significant role in the patch model mechanical response, while the cable element diameter had the least influence (Fig. 6). This is due to the strong coupling interaction, since a longer fiber results in more coupling points, which are located along the length of the cable element, as well as at the two end nodes. This coupling effect causes increased resistance along the length of the cable element (F is increasing while area is constant), and results in a higher mechanical stress.

The average tensile strains in the lamina cribrosa and peripapillary sclera were reported to be ~ 3% for inflation from 5 to 45 mmHg [25, 35], with local strains as large as 10% [77]. This is consistent with our eye model results, as the strain in the lamina cribrosa and peripapillary sclera was ~3% with the regional maximums as large as ~ 10% (Figs. 7 & 8 & 9). Ignoring the role of the fibers in the peripapillary sclera and pia also resulted in higher volumetric average 1^st principal and shear stresses and strains in the lamina cribrosa and neural tissue (Table 3 and Figs. 9 & 10). The addition of circumferentially oriented cable elements/fibers around the scleral canal opening significantly reduced scleral canal expansion at the ASCO, PSCO, ALI, and PLI (Table 4). This is important since scleral canal expansion at the lamina cribrosa insertion serves as the deformation boundary condition for the laminar region of the ONH, which is the probable site of damage to the retinal ganglion cell axons in glaucoma [7, 78–80]. Thus, ignoring the role of these fibers in computational models can cause an overestimation of the radial expansion in the scleral canal opening and hence laminar strain. The higher tensile and shear strains in the peripapillary sclera (Figs. 7 & 8 & 9) in models without cable elements/fibers also overestimate the resultant deformations in the ONH (Fig. 11). Higher von Mises, 1^st principal, and shear stresses were also observed at the peripapillary scleral region when the role of the fibers was ignored (Fig. 9). The contour maps of the stresses and strains in the peripapillary sclera is slightly less smooth when the role of the fibers is taken into account in the ONH FE model. This could be due to the axial resistance of the discrete cable elements along the applied load; when the resultant force is aligned with the axis of the cable, the local stress or strain may exhibit lower local magnitude [67]. The maximum tensile strain was higher in the peripheral lamina cribrosa regions (Fig. 10) compared to the adjacent peripapillary sclera (Fig. 9), which is in good agreement with the literature [25, 81]. Moreover, lamina cribrosa beams exhibited larger tensile strain compared to the peripapillary sclera (Fig. 9), which is also agrees with a prior report [25]. In addition, our model showed a lower shear strain in the peripapillary sclera (Fig. 9) compared to the central lamina cribrosa regions (Figs. 9 & 10), which agrees with observations from Midgett et al., [25]. This is due to the anisotropic collagen fibril structure that is predominantly oriented circumferentially around the ONH, which induces a larger shear strain in the peripheral region of the lamina cribrosa [24].

Including the cable elements/fibers in the peripapillary sclera and pia led to a central lamina cribrosa posterior displacement of ~66–77 μm, while ignoring the fibers caused the displacement of 88–99 μm (Fig. 11). The displacement range of ~30–80 μm has been observed in experimental inflation studies [24, 25], which matches with our modeling data when the role of the fibers is taken into account. The posterior deformation in the peripapillary sclera and lamina cribrosa varied by up to 50 μm, resulting in a variety of deformed lamina cribrosa shapes at 45 mmHg. The results showed that the lamina cribrosa displaced posteriorly relative to the peripapillary sclera by ~22 μm (Fig. 11), which is in good agreement with the 21 μm measured experimentally by Midgett, et al. [25]. They found that the ONH displaced more posteriorly after acute IOP increase than the sclera and that the posterior deformation of the lamina cribrosa was correlated with scleral canal expansion [81]. Our results showed that ignoring the role of the cable elements/fibers in the peripapillary sclera causes a 20–60% greater scleral canal expansion, depending on the reference location (Table 4) and ~30% greater posterior displacement in the lamina cribrosa, which reveals the important mechanical role of the peripapillary scleral collagen fibers in controlling lamina cribrosa deformation.

In this study, we proposed a mesh-free penalty-based cable-in-solid coupling algorithm to model anisotropic collagen fibers in soft tissues, and used that method to mimic the complex, depth-dependent, anisotropic, heterogeneous material properties of the peripapillary sclera into an eye-specific FE model. This approach, when applied to eye-specific models of the ONH, appears to provide strain estimates that more closely mimic those measured post-mortem inflation testing of the ONH. This approach can be used in future studies to investigate ONH remodeling and to elucidate the role of biomechanical factors in glaucoma pathophysiology. Moreover, this method has broad applications to biomechanical studies of other biological tissues with complex material properties, as well as collagenous tissue engineering constructs [82], collagen-based hydrogels [83–85], arterial walls [86–88], and spongy materials [89, 90].

4.1. Limitations

This study is limited by the following considerations. First, there is no validated gold standard measurement of the material properties of the lamina cribrosa we can use as a reference for the deformations, stresses, and strains presented herein. Second, although our 3D reconstruction methodology that forms the geometric basis for the lamina cribrosa microstructure, sclera, and pia has been shown to be consistent with the tissues in vivo [91], there is some artifact due to tissue pre-processing, fixation and embedding for histologic reconstruction [91]. Third, the vascular truck in the laminar region might influence the mechanics of the ONH in vivo; we include the central retinal vessel trunks in our ONH FE models but these vessels are not pressurized with blood. This will be addressed in future studies wherein we will incorporate hydrostatic pressure and compressive strain mapping as surrogates for capillary and vessel perfusion. Fourth, the element edge length of the lamina cribrosa and neural tissue in the FE model was set to ~7–15 μm although the original images of the lamina cribrosa beams had a pixel size of ~ 1.5 μm. While the remeshing led to slight alterations in the area and volume of the lamina cribrosa in the ONH FE model, our recent comparative analyses showed that these small changes of the re-meshed lamina cribrosa had negligible effects on the resultant stresses and strains [19]. This also allowed us to run the simulations in a reasonable amount of wall clock time on a workstation computer. Fifth, the length and diameter of the fibers in the scleral and pia solid matrix were held constant at 100 and 50 μm, respectively, throughout the tissues. While the cable element representation in the present study greatly improves the representation of the heterogeneous anisotropy of the tissues, the actual fibers’ length and diameter in vivo could be different at different anatomical locations in the sclera. While the loading was dynamic and solved in explicit dynamic mode in LS-DYNA, the material parameters used did not include viscoelasticity, which have been shown to be important over extended time periods in ocular tissues [92, 93]. Loading was imposed in 500 ms, which is too brief to elicit significant viscoelastic effects, but future analyses will include a viscoelastic solid matrix material formulation in cases in which the time course of the loading is longer and thus likely to involve viscoelasticity. Also, the cable element length and diameter were chosen to conform to the constraints imposed by the complex geometry of the sclera and pia, and resulted in acceptable an stress-strain response that was well within the range of biaxial experimental data [39].

In summary, we proposed a mesh-free penalty-based cable-in-solid coupling algorithm to mimic the complex heterogeneous and depth-dependent anisotropic mechanical properties of the sclera in an ONH FE model of the eye. A parametric study was carried out in a model of a scleral patch to determine the mechanical contributions of the input parameters in the cable elements and solid matrix, which matched the full range of experimental biaxial scleral tensile test data. An optimal set of parameters was identified and applied to an ONH FE model in which cable elements/fibers were embedded in the sclera and pia in the complex pattern measured experimentally. Results revealed that disregarding the role of the fibers in the peripapillary sclera causes a higher tensile and shear stresses and strains in the ONH connective tissues. The coupling algorithm is partially available in LS-DYNA and the Matlab scripts that define the control points, distribute the cable element/fibers, and generate an LS-DYNA input file are attached as supplementary material. The findings of this study will improve our understanding of the effects of collagen fibers on the resultant stresses and strains of computer simulations in soft tissue biomechanics such as the eye. This modeling approach also allows for simulation of local mechanical damage to collagen, which eventually will contribute to future studies designed to elucidate the role of biomechanical factors in glaucoma that drive the remodeling known to occur in the disease.

Highlights.

• A mesh-free penalty-based cable-in-solid coupling algorithm was proposed

• Method was validated against biaxial tensile tests of human sclera patches

• Method was used to represent complex anisotropic scleral collagen fibers in a FE model of the eye

• Ignoring anisotropy resulted in overestimation of intraocular pressure-related deformations

• Matlab code is included to allow others to leverage this approach