Predicting Diabetic Neuropathy Risk Level Using Artificial Neural Network and Clinical Parameters of Subjects With Diabetes

Abstract

Background:

A risk assessment tool has been developed for automated estimation of level of neuropathy based on the clinical characteristics of patients. The smart tool is based on risk factors for diabetic neuropathy, which utilizes vibration perception threshold (VPT) and a set of clinical variables as potential predictors.

Methods:

Significant risk factors included age, height, weight, urine albumin-to-creatinine ratio, glycated hemoglobin, total cholesterol, and duration of diabetes. The continuous-scale VPT was recorded using a neurothesiometer and classified into three categories based on the clinical thresholds in volts (V): low risk (0-20.99 V), medium risk (21-30.99 V), and high risk (≥31 V).

Results:

The initial study had shown that by just using patient data (n = 5088) an accuracy of 54% was achievable. Having established the effectiveness of the “classical” method, a special Neural Network based on a Proportional Odds Model was developed, which provided the highest level of prediction accuracy (>70%) using the simulated patient data (n = 4158).

Conclusion:

In the absence of any assessment devices or trained personnel, it is possible to establish with reasonable accuracy a diagnosis of diabetic neuropathy by means of the clinical parameters of the patient alone.

Introduction

There are approximately 4.7 million people in the United Kingdom living with diabetes and neuropathy affects up to 50% of these patients.^1,2 Diabetic neuropathy (DN) may be completely asymptomatic, but can cause numbness, tingling, or even painful burning sensations in the lower limbs, rarely affecting the upper limbs. ³ As neuropathy is a very insidious complication it may remain undiagnosed for several years, so routine regular screening is vital to identify the “at risk” foot. ⁴ Resultant foot ulceration and limb amputation are very serious complications of neuropathy with serious consequences on patients’ quality of life and survival.

Commonly used neuropathy screening tools utilize pressure/touch sensation such as the 10 g Semmes Weinstein monofilament, and vibration perception (eg,125 Hz tuning fork, biothesiometer and neurothesiometer). Devices that use vibration perception are generally considered as the gold standard for neuropathy assessment as they can quantitatively predict the onset and progression of the complication. ⁵ The 128 Hz tuning fork was the first tool to use vibration perception but its application was very limited by both observation technique and patient response. ⁶ The development of the Biothesiometer was based on mechanical and more standardized vibration perception, and was subsequently replaced by the neurothesiometer, which operates on the same principle but is battery-operated. The neurothesiometer produces mechanical vibration with a fixed frequency of approximately 100 Hz while the vibration amplitude is controlled manually using a rotatory control knob. The knob is used to adjust the voltage applied and ranges from 0 to 50 V (0-250 µm in amplitude). The operator applies the handheld probe to the pulp of the great toe and the vibration stimulus gradually increased, until the subject feels the vibration sensation. The voltage displayed on the neurothesiometer is the measured vibration perception threshold (VPT). The major drawback of such a device is its manual observer-dependent operability and its limited vibration intensity.^7,8

With the worldwide increasing prevalence of diabetes, there is a need for more intuitive, operator-independent and smarter diagnostic devices. In the absence of assessment devices or trained personnel, it may be difficult to establish the accurate level of neuropathy, bearing in mind that the clinical parameters of the patient may also play a key role in diabetes. This motivated us to develop an intelligent risk assessment tool based on patient data that can predict the risk level of DN. The software uses patient data and is shown to provide an acceptable level of accuracy, which will continue to improve in performance as quality data are collected over time. As the software is likely to perform better if trained on a larger dataset, we have interfaced it with a newly developed device (VibraScan), ⁹ which measures the subject’s VPT. With the larger integrated dataset this device can be used as a comprehensive diagnostic tool for DN, while taking into account changing patient parameters.

Methods

VPTs and various clinical measurements were used to develop a tool for automated prediction of neuropathy. VPT measurements (neurothesiometer) were used to identify the level of DN and were correlated with potential predictors obtained from a clinical diabetes database (n = 5088). Potential predictors included duration of diabetes mellitus, age, height, weight, body mass index, urinary albumin-to-creatinine ratio (ACR), blood glucose, glycated hemoglobin (HbA1c), total cholesterol, and triglyceride. These variables represented the average of a small number of measurements taken at clinic visits in a hospital setting over a 28-year period, and measured at least once a year, and if measured more frequently, averaged over a year. These data were collected repeatedly over this time period for the same subjects. The data were not specifically collected for this study, so no specific protocol was followed and we did not differentiate on the basis of demographic features. There was the possibility of unintended missing data or loss to follow-up, both of which can commonly occur in longitudinal trials. In order to provide data with properties similar to the patient data, 4158 cases were simulated with patients’ mean and covariance from the data to improve precision. A Neural Network based on a Proportional Odds Model (NNPOM) was trained using the simulated patient dataset where VPT (volts) was encoded into three categories—low, medium, and high-risk level of neuropathy.

For data classification many conventional statistical methods can be used, but for developing a risk assessment tool a classifier that can handle the data precisely should be used. In a study on 110 patients with diabetes, the Michigan Neuropathic Diabetic Score was used to differentiate normal and abnormal cases. In this study nerve conduction studies were used to assess DN and showed that age, duration of disease, gender, and quality of diabetes control all have a significant relationship with DN, but no correlation was found with hyperlipidemia, blood pressure, or smoking. ¹⁰ In another study, assessment of DN was performed using the Michigan Neuropathy Screening Instrument questionnaire-based examination. This focused on the relationship between risk factors and the prevalence of DN in youths. ¹¹

Another study was performed to identify risk factors associated with DN by comparing the prevalence of neuropathy in subjects with known diabetes mellitus and those with new-onset diabetes. In this study the 10 g monofilament test, pinprick, and VPT were used to categorize patients into normal, and into mild, moderate, and severe neuropathy. A total of 586 patients with established DN were identified. Regression analysis was used to identify the risk factors associated with DN. It was found that age, dyslipidemia, alcohol status, and macro- and microvascular complications were significant risk factors for DN. ¹²

For optimal contribution of each variable the right type of transformation should be considered, and we used Box–Cox family^13,14 transformations to identify significant variables. The analysis result (Table 1) shows that out of the 13 commonly used variables for assessment of DN, only 7 are found to be statistically significant predictors (P < .05). These are duration of diabetes, age, height, weight, glycemic control (HbA1c), ACR, and cholesterol. These can be considered as the risk factors for development of the DN tool.

Table 1.

Significant Variables for DN Prediction.

Box–Cox transformed variables (except sex)			95% confidence interval
	Coefficients	t-statistics	UB	LB
Sex	0.002	(0.14)	−0.036	0.041
Duration of diabetes	0.002*	(2.72)	0.001	0.004
Age	0.020***	(73.21)	0.019	0.021
Height	0.006***	(5.57)	0.004	0.009
Weight	0.004***	(3.55)	0.002	0.006
BMI	−0.004	(–1.38)	−0.011	0.002
HbA1c	0.032***	(6.01)	0.022	0.043
HDL	0.006	(1.04)	−0.006	0.019
LDL	0.016	(1.58)	−0.004	0.037
ACR	0.002***	(6.17)	0.001	0.002
RBG	0.002	(1.04)	−0.002	0.005
Triglyceride	−0.002	(–0.31)	−0.016	0.011
Cholesterol	0.023**	(2.78)	0.007	0.039
Observations	3691
R 2	0.656

ACR, urine albumin-to-creatinine ratio; BMI, body mass index; DN, diabetic neuropathy; HbA1c, glycated hemoglobin; HDL, high-density lipoprotein; LB, lower bound; LDL, low-density lipoprotein; RBG, random blood glucose; UB, upper bound.

^*P < .05, **P < .01, ***P < .001.

These variables can be used to obtain the point prediction of VPT or the predicted VPT within the confidence interval (Table 1). In order to simplify the interpretation of the outcome variable (VPT) for both clinicians and patients, it was useful to interpret the VPT prediction in terms of cumulative risk levels. For solving this problem in terms of classification, the first step was to divide the data into specific categories based on VPT thresholds. By considering the clinician’s expertise in the field of DN, the dataset was categorized into three classes based on VPT measurement—low risk (0-20.99 V), medium risk (21-30.99 V), and high risk (≥31 V).

The structure of the neural network classifier is shown in Figure 1 and uses a feedforward learning algorithm. It is a three-layer feed-forward neural network, which consists of the input layer, hidden layers, and output layers. These layers have 13 nodes in the input layer (as per input variables), a number of nodes in the hidden layer, and 3 nodes in the output layer (required classification).

Figure 1.

Neural network structure for diabetic neuropathy classification.

ACR, urine albumin-to-creatinine ratio; BMI, body mass index; FBG, fasting blood glucose; HbA1c, glycated hemoglobin; HDL, high-density lipoprotein; LDL, low-density lipoprotein; RBG, random blood glucose.

In order to train the network, various training algorithms are available, of which resilient backpropagation algorithms and scaled conjugate gradient algorithms are used for fast pattern classification of artificial neural network (ANN). ¹⁵ At the output node, the softmax activation function is used that yields the probability values of the classification provided by the nodes. The softmax usually takes the un-normalized vector and normalizes in terms of probability distribution over predicted output classes. Here x is the input, which incorporates the value of all the 13 attributes $=(x_1,x_2,x_3,\dots ,x_{13})$ , y is the output of the classifier and is one of the three classes of probabilities $y_i=\left(y_1,y_2,y_3\right)$ . Each $y_i$ represents the output values belonging to class i. The softmax function is applied to output probabilities of multiple output classes and can be given as the input x multiplied by weights W and added to bias b to generate the predicted output y_i as in Eq. (1).

$$y_i=softmax({\sum }_j{W}_{i.j}{x}_i+b_i)$$ (1)

The softmax function normalizes the three-dimensional vector into the range of [1, 0] and y_i is the predicted probability as the risk factor. In order to evaluate how well the classifier is working, the loss function is used to measure the inconsistency between the predicted output and actual output. The loss function is known as the performance goal. Here the cross-entropy loss function is given by Eq. (2) to get the classification success.

$$crossentropy\left(label,y\right)=-{\sum }_{i}labe{l}_i\log \left(y_i\right)$$ (2)

The neural network implementation was achieved using pattern classification feature of neural network toolbox on MATLAB platform ¹⁶ with the following steps:

1. Preprocess the medical data to achieve the class balance before using a neural network for classification.

2. Follow the file format like (labels, attr1, attr2, attr3,. . . attrN) where labels should be encoded as [1,0,0], [0,1,0], and [0,0,1] and attr means attributes for risk factors of DN.

3. Divide dataset into three sets as training (70%), testing 15% (unseen data), and validation sets (15%).

4. Adjust the important hyperparameters such as hidden neurons, hidden layers, learning rate, and iterations and measure the epochs.

5. Train the neural network using resilient backpropagation and scaled conjugate gradient algorithm.

6. Train neural network with 13 attributes using training, test, and validation set. Select the model that gives optimal result by changing the values of required hyperparameters.

7. Confusion matrix is computed to assess the neural network performance.

8. Based on the classification success of training, testing, and validation sets, calculate overall accuracy for comparison.

9. Repeat steps 2-8 to train the neural network using seven best predictors.

10. Compare the accuracies of the dataset with a different set of attributes.

Results

To the best of our knowledge, there are currently no available tools that can determine DN risk by analyzing patients’ clinical data. The focus here was to develop a risk assessment tool to help clinicians analyze a complex relationship between risk factors and the level of DN. After obtaining the results of the classical statistical analysis, which was based on summarized patient data, an accuracy of 54% was achieved. ¹⁷ However, after looking into the complexity and nonlinearity of the data, the idea of using an ANN as classifier was considered.

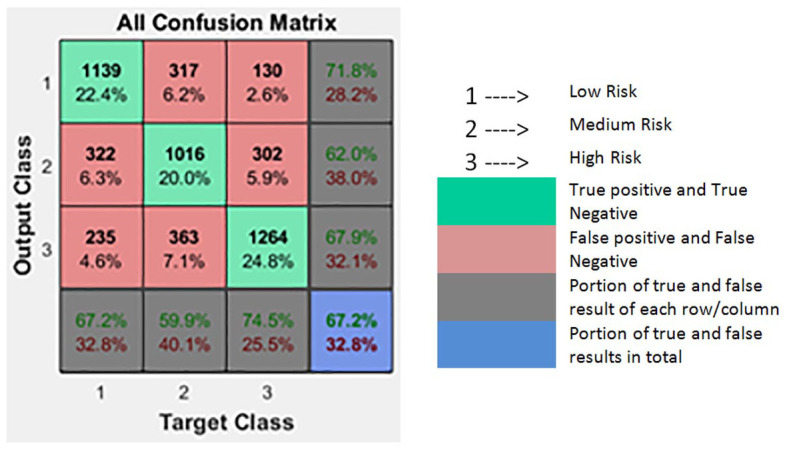
A simulation was run on the neural network with 13 attributes and some of the basic hyper-parameters were kept fixed. The confusion matrix of the overall data set (consisting of testing, validation, training sets) is shown in Table 2. The confusion matrix is the summary of prediction results on classification problems and presents the accuracy of the classifier. It gives correct classification as “true positive” or “true negative” as shown in green-colored boxes (diagonal of the square) and incorrect classification is listed by “false positive” and “false negative” as shown in red-colored boxes (adjacent to the diagonal). The numbers in the boxes are correctly classified predictions out of 5088 instances.

Table 2.

Confusion Matrix with a Dataset of 13 Attributes.

When the neural network was trained using seven attributes (the significant predictors) there was a slight decrease in classification from 67.9% to 67.4%; so the dataset with significant predictors is used for further analysis. Note that all 13 variables in Figure 1 were merely to show that all the commonly used factors for DN were considered but the simulation was done with only 7 variables in order to reduce the computational load while still achieving the equivalent results.

In order to improve accuracy, the data need to be either collected precisely or processed in a way to reduce noise. Instead of choosing the prolonged process of collecting patient data again, the second option of increasing predictor precision was to generate a simulated patient dataset. For generating simulated patient data with similar properties, the real patient data mean and covariance of each predictor were used with reduced standard error in order to increase the precision of data. By this method a larger dataset was obtained for improving prediction. The simulated data were generated using the R-code of simstudy software with genData function. ¹⁸ Using this function, it generates multivariate normal data. It requires the mean, standard error, correlation matrix, or correlation coefficient of real patient data. If data are generated by using the same standard error of the real patient data then the spread of the data may remain the same for each predictor; therefore, standard error was reduced for independent variables. By comparing the summary of the simulated data with the real patient data it was possible to reduce the skewness of the simulated data and the accuracy was significantly increased by reducing the standard error of each predictor.

Many available classifiers can predict the numerical values from labeled patterns but less consideration has been given to ordinal classification problems where labels of the dependent variables or targets have a natural ordering. In the current scenario, labels are ordered as low, medium, and high risk. While dealing with the problems of misclassification it would be more erroneous if a patient of low risk was classified as high risk rather than as medium risk. This encouraged us to use an ordinal classification model to carefully handle ordinal labels. ¹⁹ However, in order to adopt a probabilistic framework, NNPOM was considered to be more useful.^20,21 The model approaches ordinal classification by estimating the latent variable belonging to ordinal categories and is seen to perform well when classes are defined from a discretized variable. ¹⁹ This model is adjusted such that it updates the weights by minimizing the cross-entropy loss in each iteration. NNPOM is a linear combination of nonlinear basis functions, which can be adjusted by three hyper-parameters as hidden neurons (M), number of Iterations (iter), and the value of regularization parameter (λ). ²²

The training of NNPOM was performed on MATLAB framework. ¹⁶ The model was trained with prior setting of all the hyper-parameters and the range was explored using different numbers of hidden neurons M ϵ {10, 40, 60, 80, 85, 120, 130}, iter ϵ {1000, 1500} and λ ϵ {0.01, 0.001}. The accuracy of the model is calculated based on the percentage of correctly classified class. By increasing the hidden units, training time increases and by changing these hyper-parameters, the results change from 68.25% to 70.1%. However, by selecting M = 120, iter = 1500, and λ = 0.01, the highest level of correctly classified output obtained was 70.1%. This version of trained model with highest accuracy was selected for the risk assessment tool.

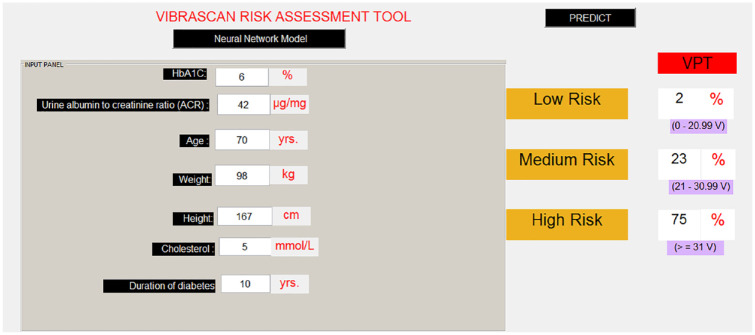
To make it user-friendly, an application was developed as shown in the example illustrated in Figure 2 using the trained neural network model. Based on the input values provided to the tool, VPT probabilities were predicted from the learnt model with 2% chance of low risk, 23% chance of medium risk, and 75% chance of high risk. The result shows that this subject is very likely to have DN.

Figure 2.

Risk assessment tool with clinical variables.

HbA1c, glycated hemoglobin.

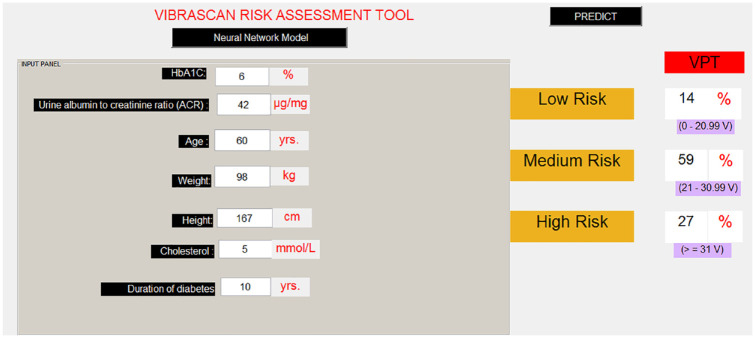
Another example was tested by keeping all the parameters the same and just decreasing the age by 10 years to determine the categories and observe the change in the risk level. As seen in Figure 3, by keeping all the other inputs (apart from age) the same, the risk level of DN is reduced from high to medium risk. Thus, based on a combination of clinical inputs, the tool can predict the subject’s VPT and determine the risk level of DN.

Figure 3.

Diabetic neuropathy prediction with changed variables.

HbA1c, glycated hemoglobin.

Discussion

This risk assessment tool is the first of its kind to provide a novel method for the reliable screening, diagnosis, and monitoring of DN. The study was conducted by using both the longitudinal data and continuous VPT measurements. Out of 13 variables, 7 variables were identified as significant predictors. For easy interpretation of the risk level of DN, VPT was divided into three categories based on VPT thresholds. We initially considered all 13 variables for training with these attributes, and the model achieved an accuracy of 67.9%. The ANN was then trained with seven best predictors and achieved an accuracy of 67.4%. This comparison gave us a good indication to use only significant predictors rather than all the attributes.

In order to improve the precision of summarized patient data (which provided only 54% accuracy due to missing data), data with similar properties were simulated with covariance and the mean value of patient data, but with reduced standard errors. The NNPOM was trained on simulated data and achieved an accuracy of 70.1% with the seven predictors. Considering the noise and imbalance in data this method worked significantly well for a risk assessment tool for DN. The limitation of quality of data was handled by using simulated patient data and the quality of data was improved by increasing the precision of variables. As a result the achieved accuracy can be further improved by collecting clinically significant patient data over time. We recognize that performance may not improve by leveraging larger datasets and may hit the ceiling; however, it is imperative that if more quality data are collected over time, the performance may increase for a particular country or population. Since the current level of accuracy is based on the summarized or simulated patient data, we found that the results were good enough when compared with the validation data. We intend to evaluate this further and this paper highlights an important step in that direction.

Conclusion

In the absence of established assessment devices or trained personnel it may prove difficult to get a diagnosis of DN. The undoubted importance of patient clinical characteristics led us to develop a risk assessment tool based on patient data alone. This intelligent software-based tool is both user-friendly and can provide the risk level of DN with reliable accuracy. As the software would perform better if trained on a larger dataset, its performance will continually improve as quality data are collected over time. We, therefore, interfaced this software with our neuropathy device (VibraScan ²³ ) in order to enrich quality patient data. The resultant larger integrated dataset enables the device to be used as a comprehensive tool for the risk assessment of DN.

Consensus for screening for DN has been historically very difficult to standardize and lags behind the much more state-of-the-art digital screening for retinopathy for example. As this intuitive artificial intelligence device aptly offers a low or noncontact patient facility, it provides a platform for the safe, quick, and effective screening of the diabetes population at large. ²⁴ With a current global prevalence of diabetes of 9.3% (just under half a billion people), and an estimation to rise by 50% in 2045, this innovative technique certainly opens a new horizon in modern diabetes care. ²⁵