Abstract
It is well established that collagen alignment in the breast tumor microenvironment provides biophysical cues to drive disease progression. Numerous mechanistic studies have demonstrated that tumor cell behavior is driven by the architecture and stiffness of the collagen matrix. However, the mechanical properties within a 3D collagen microenvironment, particularly at the scale of the cell, remain poorly defined. To investigate cell-scale mechanical cues with respect to local collagen architecture, we employed a combination of intravital imaging of the mammary tumor microenvironment and a 3D collagen gel system with both acellular pNIPAAm microspheres and MDA-MB-231 breast carcinoma cells. Within the in vivo tumor microenvironment, the displacement of collagen fiber was identified in response to tumor cells migrating through the stromal matrix. To further investigate cell-scale stiffness in aligned fiber architectures and the propagation of cell-induced fiber deformations, precise control of collagen architecture was coupled with innovative methodology to measure mechanical properties of the collagen fiber network. This method revealed up to a 35-fold difference in directional cell-scale stiffness resulting from contraction against aligned fibers. Furthermore, the local anisotropy of the matrix dramatically altered the rate at which contractility-induced fiber displacements decayed over distance. Together, our results reveal mechanical properties in aligned matrices that provide dramatically different cues to the cell in perpendicular directions. These findings are supported by the mechanosensing behavior of tumor cells and have important implications for cell-cell communication within the tissue microenvironment.
Keywords: Collagen alignment, tumor microenvironment, cell-scale modulus, fiber displacement, mechano-signaling
Graphical Abstract
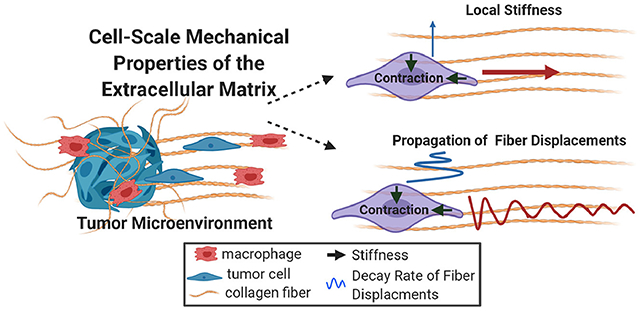
1. Introduction
Aberrant deposition and architecture of collagen in the tumor microenvironment is known to drive multiple steps in disease progression [1]. In breast cancer, a clear set of changes in collagen fiber architecture, termed Tumor Associated Collagen Signatures (TACS), have been shown to accompany tumor progression. The last stage of TACS is identified by the alignment of collagen fibers perpendicular to the tumor boundary (TACS-3) and this signature is well established as a prognostic marker of poor patient outcome [2–4]. A factor underlying the relationship between fiber alignment and disease progression is the increase in stiffness localized at the invasive front of aggressive tumors where linearized collagen fibers have been detected [5]. The behavior of invasive tumor cells as they interact with aligned collagen fibers in the native tumor microenvironment has been elucidated by intravital imaging studies. In vivo, tumor cells migrate as either single-cells or collective strands as they invade the surrounding extracellular matrix. Strands of collectively migrating tumor cells have been shown to organize along aligned collagen fibers and serve as a niche for single cell detachment [6]. Moreover, individual tumor cells traffic with macrophages along straightened collagen fibers as they migrate toward blood vessels where they disseminate to distal locations [7,8]. Together, these findings suggest that the alignment of collagen fibers (TACS-3 signatures) provide a highway for tumor cell invasion and dissemination, illuminating the importance of aligned collagen fibers in breast cancer progression. These studies also emphasize the need to better understand the dynamic interplay between tumor cells and aligned collagen in the tumor microenvironment.
Since the identification of TACS [2], numerous in vitro studies have defined mechanisms by which tumor cells sense and respond to different collagen fiber architectures. Within a 3D fibrous matrix, aligned collagen provides contact guidance cues promoting persistent cell migration through the regulation of protrusion dynamics [9–13] and the distribution and shape of focal adhesions [14–16]. Many of the signaling mechanisms driving persistent cell migration are underpinned by mechanical stiffness cues from the matrix. Indeed, aligned collagen fibers are stiffer than randomly organized fiber networks [10]. However, stiffness measurements have often been made at the macroscale and do not address local differences in matrix architecture at the cell-scale. On a subcellular scale, the stiffness of a single collagen fiber can be orders of magnitude higher than the bulk collagen gel stiffness [17,18]. Experiments demonstrated that cells respond to individual fiber stiffness and microarchitecture by organizing their contractile machinery along the axis of stiffness, indicating that mechanosensing can occur due to the anisotropy of a single collagen fiber [19]. However, the stiffness of individual fibers is not uniform throughout the matrix and cells likely sense stiffness at the scale of the local fiber network, somewhere between the bulk stiffness of the tissue and the microscale stiffness of an individual fiber. Therefore, it is important to define the anisotropic mechanical properties of an aligned collagen network at the scale of the cell to more fully understand how collagen architecture impacts disease progression.
An additional complexity of the fibrous extracellular matrix (ECM) is how the matrix responds to and deforms from the contractile forces generated by the cell. The deformation of collagen fibers and how resulting fiber displacements propagate through the tumor microenvironment has implications for mechanical communication between cells. Recently, macrophages were observed responding to the pulsatile contractions of myofibroblasts cultured on top of a 3D collagen matrix [20]. In this model of wound healing, the directed migration of macrophages was not dependent on matrix stiffness, but rather on matrix deformations produced by a myofibroblast. This observation is an example of how matrix response to the cell is equally as important as cell response to the matrix. Furthermore, it reveals a potential role for matrix deformation as a mechanism of cell-cell communication within a physiologic fibrous matrix like the tumor microenvironment. Given the significance of collagen fiber architecture within the breast tumor microenvironment, it is important to better understand whether the waves of contractile-induced fiber deformation propagate uniformly throughout an anisotropic matrix.
To improve the basic understanding of how collagen alignment is perceived at the scale of the cell there is a need to define the mechanical properties of the fibrillar matrix. Specifically, there is a critical gap in our understanding of both the local static cues (i.e., stiffness) provided by the structure of collagen fibers and the dynamic cues (i.e., matrix deformations) resulting from cellular contractile force. In this study, we addressed these gaps through intravital imaging and innovative in vitro methodology to quantify cell-scale mechanical properties of the collagen matrix. First, we observed that MMTV-PyMT and MDA-MB-231 mammary carcinoma cells not only migrate and invade through their local microenvironment but simultaneously interact with and deform aligned collagen fibers from perpendicular directions. Based on these findings, cell-scale properties of the matrix created by the local anisotropy of collagen fiber alignment were quantified through an in vitro model system that reproducibly introduced local, strain-induced alignment within a 3D collagen gel. Seeding contractile acellular pNIPAAm microspheres calibrated to the stiffness of the collagen matrix provided a method to determine the local stiffness in both random and aligned matrices. Importantly, this model also revealed a 35-fold difference in cell-scale stiffness parallel vs. perpendicular to collagen fiber alignment. In addition, both pNIPAAm microspheres and MDA-MB-231 cells clearly demonstrated how collagen alignment differentially modulates the propagation of contractile-induced fiber displacements, which has potential implications for cellular mechanosensing and cell-cell communication within the matrix. Together, our work highlights the importance of the local architecture of collagen fibers for cellular mechanosensing within the breast tumor microenvironment and provides broad implications for extracellular matrix biology during other physiologic processes.
2. Methods
2.1. In vivo imaging experiments:
Mice were maintained and bred at the University of Wisconsin under the oversight of the University of Wisconsin Animal Use and Care Committee and in compliance with an IACUC approved protocol. FVB mice expressing the MMTV-PyMT transgene were raised for 8-10 weeks until a palpable mass was detected. SCID mice (Jackson Lab) were injected with 2.5x106 MDA-MB-231 cells expressing GFP-LifeAct into the R4 mammary fat pad. Cells were allowed to grow until a palpable mass formed (10-14 days). In both the PyMT model and GFP-LifeAct-MDA-MB-231 xenografts, once the tumor was palpable and approximately 5 mm in diameter, a Mammary Imaging Window (MIW) was surgically implanted over the tumor mass [21]. The tumors grew into the window for another 3-5 days prior to imaging.
2.2. Cell culture:
The MDA-MB-231 (ATCC) cell line used in this study was maintained in DMEM (1.0 g/L glucose, L-glutamine, 110 mg/l Sodium Pyruvate) with 10% FBS under 5% CO2. The GFP-LifeAct construct (kind gift from Dr. Maddy Parsons, King’s College London) was used to create a stable cell line as previously described [10]. For the purpose of this study, GFP-LifeAct-MDA-MB-231 cells were imaged at pixel saturation to identify whole cell migration rather than actin dynamics. This allowed us to more accurately analyze protrusion dynamics in 3D collagen gels and during intravital imaging of in vivo tumors.
2.3. Generation and embedding of pNIPAAm microspheres:
As described in Burkel et al [22], microspheres of pNIPAAm were created using an oil/water emulsion [23–25]. Kerosene with 3.5% Span 80 (Tokyo Chemical Industries) was used as the solvent and 1 g N-isopropylacrylamide (Sigma 415324), 7.5 ml of 2% bis-acrylamide (Bio-Rad), 0.05 g ammonium persulfate (Bio-Rad), and 1.5 ml 1× TBS comprised the aqueous component. All components were degassed and maintained under nitrogen. The emulsion was stirred at 450 rpm with a magnetic stir bar at 22 °C. During stirring, TEMED (Bio-Rad, 0.36% final concentration) was added, and the reaction was allowed to proceed overnight. The resulting microspheres were then allowed to settle by gravity for at least 1 hr. Once the microspheres had settled, the kerosene solvent was removed and the beads were washed with series of solvents starting with hexane and then progressing through isopropyl alcohol, 100% ethanol, 70% ethanol and finally DI water. To embed the microspheres into a collagen gel, 10 mls of the washed microspheres were placed in a 40 μm cell strainer (Fisher Scientific) and washed with PBS and then 0.05 M HEPES. Sulfo-SANPAH (1 mg ml−1 final concentration in 0.05 M HEPES, Proteochem) was then added to the beads and exposed to an Osram Germicidal UV lamp (30W, UV-C 280nm) for 10 minutes. After exposure, the treated microspheres were washed with 0.05 M HEPES and 1× PBS, and then gently pelleted into an approximate volume of 100 μl with a mini tabletop centrifuge (VWR Galaxy Ministar). The treated microspheres (stock suspension) were then resuspended in a final volume of 1 ml HEPES buffer. Microspheres from this stock suspension were then mixed with unpolymerized neutralized collagen and allowed to polymerize for 60 minutes before straining the gels for imaging.
2.4. 3D collagen gel conditions:
Rat-tail collagen (Corning Inc.) was labelled with Alexa-488, neutralized, and polymerized as previously published [22]. Briefly, labeled and unlabeled collagen stock solutions were neutralized (1:1) with sterile, ice-cold 100 mM HEPES in 2x PBS, pH 7.4. The pNIPAAm microspheres (100 μl of stock suspension of microspheres) were mixed with a 1:10 ratio of fluorescent labeled collagen and unlabeled collagen to achieve a final collagen concentration of 2.0 mg/ml. For cell seeded gels, unlabeled collagen was neutralized with HEPES buffer and mixed with GFP-LifeAct-MDA-MB-231 cells (2.5x106 cells in media) to achieve a final collagen concentration of 2.0 mg/ml. The seeded collagen solution was cast in the bottom of 20 mm glass bottom dish (CellVis). The dish was placed on a thermoelectric plate (CP-061HT, TE technology) with a TC-720 temperature controller (TE technology) set at 21° C and allowed to polymerize for 60 minutes before placing in a 37° C incubator for 15 min.
2.5. Mechanical alignment of collagen gels:
A custom-built mechanical strain device was used to generate alignment of collagen fibers within a polymerized gel. The strain device, adapted from Vader et al [26], was integrated onto the lids of 20 mm dishes by mounting two cantilevers that protruded into the collagen gel. The cantilevers had cushioned ends that applied point loads to the polymerized gel, thereby producing localized strains between the cantilevers. The cantilevers were inserted with initial spacing of 2-3 mm separation and then strained another 2-3 mm until alignment of the fibers could be observed through a dissecting microscope with a 10X objective. Importantly, regions of highly aligned fibers are localized between the cantilevers with a network of random fiber architecture in surrounding regions. Thus, both fiber configurations exist within a single collagen gel. After strain was applied, the cell seeded collagen gels were maintained in culture for 18 hours to provide time for the cells to adapt to the strain event prior to image acquisition.
2.6. Microscopy and image acquisition:
All imaging was done using a Bruker Ultima Multiphoton Microscope equipped with a Coherent Chameleon Ti-Sapphire laser and Hamamatsu R3788 multi-alkali photomultipliers. For intravital imaging, mice were anesthetized on isoflurane to maintain a respiration rate of 36-40 breaths per minute. To maintain body temperature, mice were imaged within an incubation chamber set to 30° C and hydration was administered through a subcutaneous catheter (600 μl of sterile PBS every two hours). Imaging was conducted at a laser wavelength of either 780 nm or 890 nm with a Zeiss 20x NA 1.0 objective lens. Z-stack images were acquired every 15 minutes for a duration of 6-8 hours. Collagen second harmonic generation (SHG) was collected 890 nm using a (450/40) filter cube along with either GFP (525/70), FAD autofluorescence (562/30). NADH autofluorescence was captured at 780 nm with a 450/40 filter.
To measure anisotropic modulus and field displacements of the collagen network produced by contracting pNIPAAm microspheres, the Alexa-488 labelled collagen was imaged with a Nikon 20x NA .45 objective, excited at 890 nm and collected with a GFP (525/70) filter. The temperature, and therefore microsphere contraction, were controlled by an OkoLab live cell incubator. The temperature would be adjusted, allowed to stabilize for 20-30 minutes, and then imaged. Image stacks were collected such that several sections would be obtained above or below the pNIPAAm microspheres with sections collected every 5 μm.
To characterize 3D migration with GFP-LifeAct-MDA-MB-231 cells, images were collected with a Nikon 20x NA .45 objective, and the laser was tuned to 890 nm with SHG(450/40) and GFP(525/70) filters. The embedded cells were maintained in a stage top live cell incubator (Okolab) to tightly control temperature and humidity for the duration of the timelapse. Images were collected every 5 minutes for 6 hours to assess migration and collagen fiber displacements.
2.7. Quantification of Collagen Fiber Alignment with ct-FIRE
Collagen fibers were identified from the Alexa-488 labelled collagen image of gels seeded with pNIPAAm microspheres using the ct-FIRE software package (loci.wisc.edu/software/ctFIRE, v.2.0b). Briefly, single plane image (1024 x 1024 pixel resolution) taken at the widest diameter of the non-contracted microsphere were processed in ct-FIRE. To achieve maximal fiber identification for this set of images we applied threshold_img of 10, with default setting for all other parameters. The software calculated the 2D distribution of angles between fiber orientations (coefficient of alignment) for each image of random (n= 27), aligned with device (n=12), and aligned without device (n=14). A coefficient of alignment = 1 indicates perfect alignment of fibers, while a coefficient of alignment = 0 indicates completely random distribution of fibers.
2.8. Measurement of anisotropic modulus and full-field displacements with pNIPAAm microspheres:
To measure modulus, experiments were performed following the method of Proestaki et al. [27] with an additional analysis to consider the effects of anisotropy (see Supplemental Note #1). First, the thermal strain of the contractile microspheres in no-matrix (solution) was measured. Then, the modulus of the contractile microspheres was calibrated by embedding microspheres in polyacrylamide of a known modulus, measuring particle contraction upon a temperature change, and applying Eshelby’s solution [28]. Calibrated microspheres were then treated with Sulfo-SanPAH and embedded in collagen gels as described above. Upon temperature-dependent contraction of the microspheres, the strains in directions parallel and perpendicular to fiber alignment were measured, allowing for computation of the local modulus of the network as described in the Supplemental Note #2. For measurement of the vector field of displacements, an image of an unstrained reference state at the polymerization temperature was collected before increasing the temperature to induce localized contraction and collecting another image. The random fiber structure in the two images forms a high contrast pattern that can be used to quantify the displacement fields using digital image correlation (DIC). DIC was performed using the using the Fast-Iterative Digital Image Correlation (FIDIC) [29] algorithm as described in our prior work [30,31]. The code is freely available online (https://github.com/jknotbohm/FIDIC) and a sample set of images is available as described in [32].
2.9. Measurement of full-field displacements with MDA-MB-231:
To analyze full-field displacements in response to tumor cell contraction and migration, DIC was performed as described above but on time-lapse image collection. Starting with the second time-point each image is analyzed against the prior time-point. Such that time-point 1 is the reference for time-point 2, time-point 2 is the reference for time-point 3, and so on. To quantify the field displacements over time, we measured fiber displacements (in microns) at each time point with reference from the prior time point, then averaged the cell-induced displacements for all time-points. The data was then plotted as a heat map of displacement magnitude with respect to the cell centroid.
2.10. Quantification of protrusion dynamics:
Protrusions were identified using Matlab script as described in Riching et al [10]. Briefly, for each cell, the locations of the centroid and boundary pixels were identified. From the boundary pixels, the perimeter was determined, and the number of equally spaced perimeter nodes was defined as a linear function of perimeter. Once the perimeter nodes were determined, sharp convex regions in boundary curvature were identified by summing the exterior angles of the 5 subsequent nodes at each node of the enclosed polygon. Any sum of five nodes that resulted in an angle greater than 105° was considered a convex region. The starting node that resulted in the greatest maximum external angle formed between any three nodes within the identified convex region was marked at the protrusion tip. To quantify protrusion dynamics, each protrusion tip identified in Matlab was marked with a dot and transferred to a blank tiff file for each time frame in the cell migration move. A Gaussian filter was then applied using FIJI for each tiff file image. Then a particle tracking plugin from MosaicSuite in FIJI was utilized to track each dot. Dots that were tracked from one frame to the next were considered one protrusion. With this analysis we quantified the length, position relative to collagen fiber organization, and duration (lifetime) of each protrusion.
2.11. Immunofluorescence for focal adhesion identification:
Collagen gels seeded with unlabeled MDA-MB-231 cells were fixed with 4% PFA in PBS for 45 min, permeabilized using 0.2% Triton-X in PBS, and subsequently blocked overnight using 1% BSA in PBS. Cells were then incubated with primary antibody at 1:200. Anti-Phosphorylated FAK 397 (Invitrogen, catalogue #44-624G:) or Anti-vinculin (Sigma, cat #v4505:). After extensive washing, cells were incubated in secondary Alexa-488 anti-rabbit or anti-mouse antibody (Thermo Fisher Scientific) at 1:500 dilution.
2.12. Quantification of focal adhesions:
Images were gathered using z-stacks at 1 μm step size using a Nikon 40x NA 1.15 LWD objective lens. For focal adhesion identification, cell images from fluorescent channel were z projected using maximum and average intensity using FIJI. Average z projection was then subtracted from maximum z projection. The subsequent image had a background subtraction with a rolling ball radius of 5 pixels applied. A threshold was set for each image, such that only the top 0.5% pixels were included, then a binary mask was applied. Using the Analyze Particles function in FIJI, each focal adhesion coordinate was recorded and transferred to MATLAB for more in-depth characterization of the focal adhesion. Using the polygon function within MATLAB, the area and centroid of each focal adhesion were calculated. Using the fit ellipse function, the aspect ratio, angle and localization of the focal adhesion relative to collagen fiber alignment was recorded. The virtue of this methodology is that it is automated, and that it more accurately described the orientation and appearance of the adhesion, which often covered a spectrum from almost circular to highly elongated and narrow.
2.13. Statistical analysis:
GraphPad Prism v7.04 and MATLAB R2020a were used for generation of graphs and statistical analyses. All studies were performed in at least 3 independent experiments with a minimum of 2 independent events (cells or microspheres) analyzed per experiments. For all experiments, either a Wilcoxon rank sum or a Kruskal-Wallis test followed by Dunn’s post-hoc test was used to determine significance. To determine the 95% confidence intervals of moduli measured by the contracting microspheres, a Bootstrap analysis within MATLAB was performed. To perform the bootstrap, the moduli and ratio of moduli were computed by randomly sampling the data with replacement n times, where n corresponded to the number of contractile microspheres. We then computed the mean modulus or ratio of moduli over the n data points, which gave a bootstrap sample. The process was repeated for 104 bootstrap samples. The mean was computed from all bootstrap samples, and the 95% confidence interval was determined by taking the 2.5 and 97.5 percentiles of the 104 bootstrap samples.
3. Results
3.1. Migrating cancer cells physically deform and reorganize collagen fiber architecture in vivo.
To determine the nature and extent of how mechanical properties of collagen fiber networks impact cellular behavior in a physiological environment, we employed an intravital imaging system capable of visualizing cells interacting with native ECM of a MMTV-PyMT (PyMT) murine mammary tumor model [21]. Using this system, collagen fibers were visualized through second harmonic generation (SHG) while endogenous cellular fluorescence was used to track cell movement within the tumor. Initial observations of early-stage tumors imaged just after palpation (8-9 week old mice) highlighted the vast heterogeneity of the fiber network within the tumor microenvironment. Within a single tumor, different fields of view in close proximity to each other often exhibited vastly different TACS [2]. In regions of small lesions, collagen fibers had a relaxed appearance with curly, random fibers distributed throughout the field of view, indicative of a TACS-1 signature (Figure 1A). Typically, both tumor (*) and adipose (+) cells could be easily identified. Near larger tumor masses or between separate foci of the growing mass, fibers appeared straightened and aligned under tension (Figure 1A). Local regions of aligned fibers could be identified; organized either parallel (TACS-2) or perpendicular to the tumor boundary (TACS-3) (Figure 1A, arrows). Importantly, this observation was consistent with previous studies from human samples where the presence of TACS-3 was associated with poor disease-specific and disease-free survival in patients with invasive ductal carcinoma [3,4].
Figure 1: Intravital imaging of cells interacting with and deforming stromal fibers.
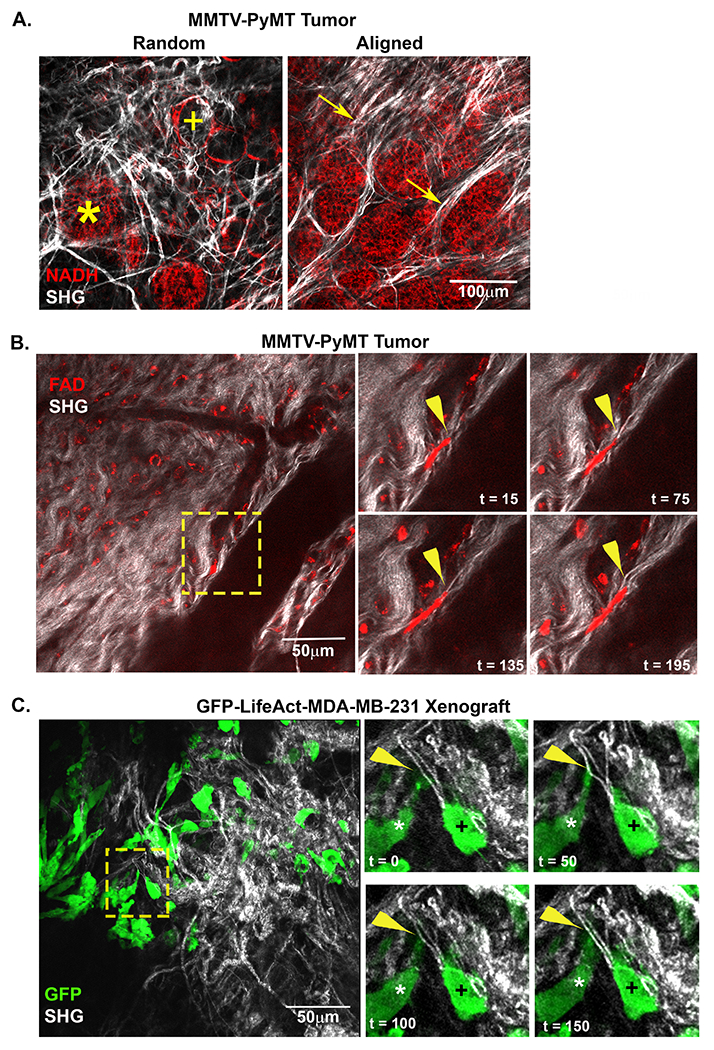
A) A representative intravital image from a MMTV-PyMT mouse mammary tumor show both random and align collagen (white) fibers within the tumor stroma. Adipose (+) and tumor (*) cells are visualized within close proximity of each other in regions of random fiber configuration while bundles of aligned fibers can be visualized extending perpendicular to tumor mass (arrow). B) Images from time lapse intravital movies show cells migrating within tumor microenvironment (TME). The inset (yellow box) highlights a migrating cell (red) deforming an individual fiber (arrowhead). C) Intravital image from a GFP-LifeAct-MDA-MB-231 tumor in the mammary fat pad. The timepoint insets (yellow box) highlight cells contacting and displacing an aligned collagen fiber from a perpendicular (*) or migrate in a parallel orientation (+) to straightened fibers within the TME. The perpendicular cell (*) extends a protrusion onto a collagen fiber and deforms the fiber. Arrowhead (yellow) indicates point of contact and deformation.
Next, we examined the architecture and displacement of collagen fibers during in vivo breast cancer cell migration. Once again, SHG was used to monitor the displacement of collagen fibers, while endogenous cellular FAD fluorescence (FAD) was used to visualize the actions of resident cells. During the course of intravital time-lapse collections, a vast majority of the cells in the PyMT tumor remained stationary, but a small population of cells could be seen undergoing both amoeboid and mesenchymal migration. In general, migratory cells, but not the stationary ones, deformed individual fibers as they contracted and moved along a region of aligned fibers (arrowheads, Figure 1B). Deformations were detected locally at the site of cell attachment and propagated away from migrating cells within a locally interconnected network of fibers (Supplemental Content - Movies 1 and 2). In addition to the PyMT tumor model, we investigated the interplay between tumor cells and collagen fibers in xenografts of MDA-MB-231 stably expressing GFP-LifeAct (Figure 1C). The behavior of the GFP-LifeAct-MDA-MB-231 mirrored that of PyMT tumor cells visualized by endogenous fluorescence with the advantage of being better able to visualize cellular protrusions. Consistent with cells visualized by endogenous fluorescence, the genetically-labeled cancer cells were also observed interacting with and displacing collagen fibers within the tumor microenvironment (Figure 1C). Moreover, cells interacted with collagen along the axis of fiber alignment (Figure 1C, cell marked with a +) as well as perpendicular to the long axis of the fiber (Figure 1C, cell marked with an *). Thus, confirming that individual cancer cells have the ability to deform individual collagen fibers in vivo. These observations inject complexity into assessments of local stiffness as determined by the cell because individual fibers are not rigid relative to the forces that the cells apply. In fact, the relative rigidity of the fiber is likely dependent on the location and orientation of the fiber relative to the local forces applied to it, evolving dynamically in direction, magnitude and location as the cell migrates. These observations motivated the need to develop methods to better characterize how different matrix architectures respond (i.e., deform) to locally applied forces.
3.2. Collagen fiber architecture relative to applied forces modulates local matrix stiffness
Our intravital investigation of mammary tumor models clearly demonstrate that migratory cells deform collagen fibers while interacting with them within the native tumor microenvironment. To investigate the role local fiber architecture plays in modulating the underlying mechanical properties of the fibrous tumor microenvironment, we adapted a mechanical strain device to reproducibly align regions of collagen fibers within a 3D matrix of random collagen architecture (Figure 2A). Using this system, we verified that local fiber alignment could be produced on-demand, and could easily be distinguished morphologically by straightened fibers with high coefficient of alignment (a measure of similarity between fiber orientations, with a coefficient of 1 representing complete alignment) as measured by an automated curvelet-based fiber analysis algorithm (Figure S1A) [33]. The average coefficient of alignment was not significantly different in collagen gels with the strain device (average coefficient = 0.73) compared to when the strain device was removed (average coefficient = 0.64) (Figure 2B). In contrast, the average coefficient of alignment in random collagen gels was 0.22 (Figure 2B). This is important because it demonstrates that any anisotropy in mechanical properties within these experiments is due to the architecture of the local fiber environment and not the transfer of forces from the embedded rigid cantilevers.
Figure 2: Mechanical strain generates reproducible fiber architecture and supports mechanosensing cell behavior.
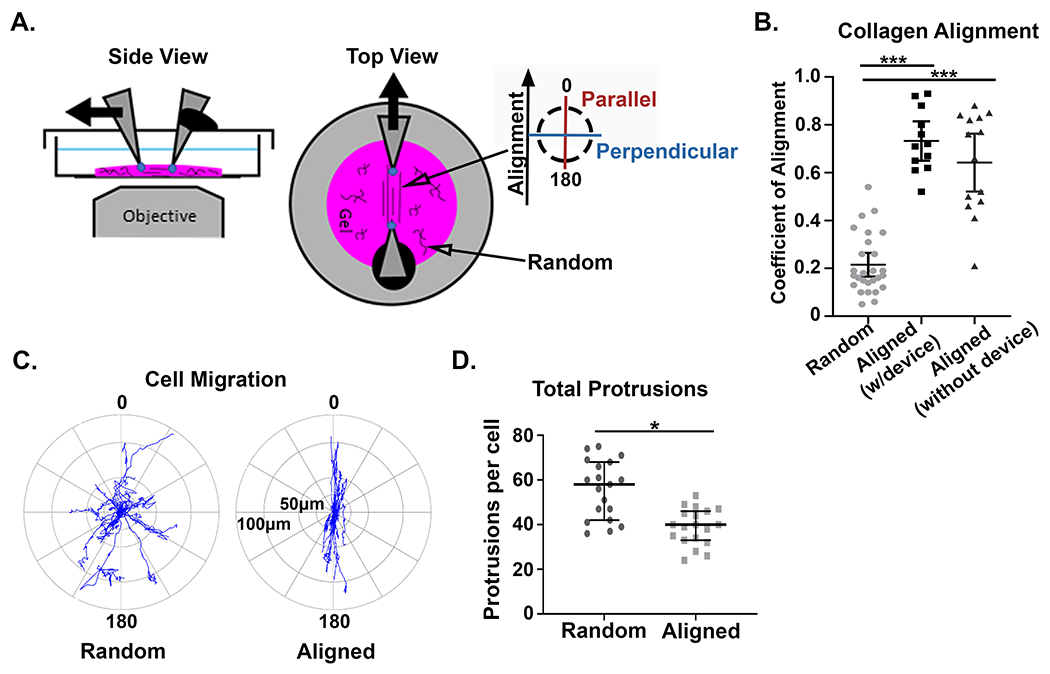
A) Alexa-488 collagen gels were strained to create fiber alignment in the central region of the gel, between the cantilevers, while the remainder of the gel had random fiber architecture. The inserted key denotes the orientation of parallel and perpendicular directions with respect to collagen fiber alignment. B) Quantification of the fiber alignment in random (unstrained) matrices (n=27), aligned (strained) matrices with the straining device inserted (n=12), and aligned (strained) matrices where the device was removed after straining (n=14). (*** p < 0.001) C) Windrose plots describe the distance and direction of GFP-LifeAct-MDA-MB-231 cell migration in aligned and random collagen architectures from four independent experiments. In aligned regions of the gel cell migration occurs +/− 30° from the axis of fiber alignment (n=20 cells). In random collagen architecture the direction of cell migration is arbitrary (n=19 cells). D) Quantification of total protrusions per cell in aligned vs random fiber architectures with the strain device inserted (n = 20 and 19, respectively). (* p < 0.05). For the coefficient of alignment, means are reported with standard deviation, and significance was determined by Kruskal Wallis test with Dunn’s correction. For total protrusions, medians and interquartile ranges were reported and significance was determined by Wilcoxon rank sum.
To compare cell migration in this system with our previous findings [10], we examined the response of cells to the localized alignment of the surrounding matrix. Consistent with previous studies, we observed that GFP-LifeAct-MDA-MB-231 cells migrated with increased directional persistence in aligned collagen matrices (Figure 2C) [10,11]. Cells generally limited their migration path to +/− 30° from the axis of fiber alignment with movements largely restricted to forward and backward motions. Additionally, cells localized to regions of aligned fibers also had significantly fewer protrusions compared to cells in random control matrices (Figure 2D and Figure S1B). Thus, our system generates significant local alignment of fibers that are sufficient to generate a directed cell response.
Using our system, we aimed to better understand the changes to mechanical cues that accompany different fiber architectures. Fibrous networks like those of the ECM stiffen under increasing strain [10,34,35] and are stiffer along the axis of alignment [10]. This characteristic underpins many of the nonlinear mechanical properties that are observed within the ECM. Our understanding of strain stiffening, however, is derived from macroscopic experiments. At the cellular scale, local mechanical properties are likely better described by the collective action of relatively small collections of fibers. It remains unclear how matrix stiffness translates to the microscopic scale where cells interact with local heterogenous networks of fibers.
To quantify the difference in stiffness between orthogonal directions in random and aligned matrices, we used an acellular approach utilizing microspheres made of temperature-sensitive poly N-isopropylacrylamide (pNIPAAm). The cell-sized microspheres were mixed with collagen solution and embedded within the 3D matrix during fiber polymerization. The microspheres were covalently attached to fibers in the random network prior to the application of strain-induced fiber alignment. Upon a precise increase in temperature, the microspheres apply controlled cell-scale contractions to the matrix (see Supplemental Note #2). This approach has been successfully used to investigate ECM micromechanics [27,30,31], and its advantages are that it can produce cell-scale deformations in 3D collagen matrices without modifying the matrix (e.g. by depositing additional matrix or degrading the existing one). We embedded the pNIPAAm microspheres into three different types of 3D collagen gels: the unstrained random controls, aligned gels with the strain device left in place, or aligned matrices with the strain device removed to ensure the device was not restraining the matrix or transferring forces (Figure 3A). At room temperature, the microspheres in all conditions were rounded and remained unstrained, serving as the experimental reference. Upon elevating the temperature, the microspheres contract, thereby exerting radial forces on the covalently attached collagen fibers. In the random collagen gels, the microspheres contracted uniformly; maintaining a spherical shape, indicating that the matrix stiffness was symmetrical in all directions. The microspheres in aligned matrices with and without the device, however, were noticeably elongated along the axis of fiber alignment, indicating an effect of collagen fiber architecture on the stiffness within the matrix. Notably, there was no significant difference between the aspect ratios of the microspheres in aligned matrices with or without the strain device, only between the aligned and random controls (Figure 3B). It should also be noted that any contracted microsphere that became detached from the fiber network was eliminated from further analysis.
Figure 3: The alignment of collagen fibers creates local anisotropy in the cell-scale modulus.
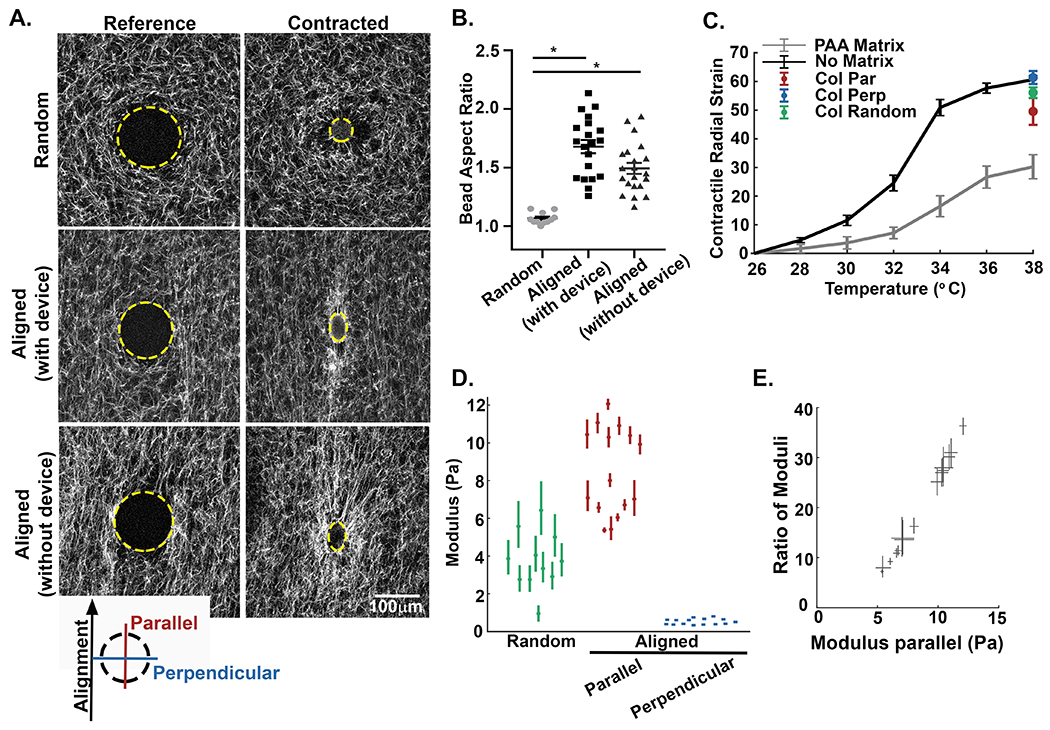
A) Alexa-488 collagen gels were seeded with inducible contractile pNIPAAm microspheres (edge of microsphere defined by yellow line) and strained to create fiber alignment. The inserted key denotes the orientation of parallel and perpendicular directions with respect to the fiber alignment. The pNIPAAm microsphere were then contracted to generate a localized displacement field. Alignment of collagen fibers results in the elongation of the spherical pNIPAAm microsphere during contraction. B) Quantification of microsphere aspect ratio for random (unstrained) matrices (n=27), aligned (strained) matrices with the straining device intact (n=12), and aligned (strained) matrices where the device was removed after straining (n=14). C) To calculate the local modulus in directions parallel and perpendicular to axis of the alignment, the bulk modulus of the pNIPAAm microspheres were calibrated to a known PAA matrix (n = 45 microspheres) and in no matrix (n = 30 microspheres). The average contraction of microspheres in random (green, n = 11 microspheres) and aligned (parallel to alignment, red; perpendicular to alignment, blue, n = 15 microspheres) matrices. Error bars indicate standard deviation. D) Plots of the directional modulus in random fiber network (green, n=11 microspheres) and in the parallel (red) and perpendicular (blue) directions in aligned collagen gels (n=15 microspheres). Means are reported with 95% confidence intervals representing uncertainty in the modulus measured by each microsphere. The data in random matrices is significantly different from aligned, in both parallel and perpendicular directions (p < 0.05 by Kruskal Wallis test with Dunn’s correction). For comparison between parallel and perpendicular directions, refer to panel E. E) Directional stiffness demonstrated by the relative ratio modulus parallel /perpendicular in aligned matrices plotted against the modulus parallel. Modulus in the direction of alignment is up to 30 to 35 times higher than the stiffness of the perpendicular axis. Width and height of each measurement correspond to the 95% confidence interval. As confidence intervals do not span 1, the modulus is statistically different between parallel and perpendicular directions.
Advances in this methodology also allow for the pNIPAAm microspheres to be calibrated to moduli of known stiffness thereby providing a quantitative measure of the local modulus at different locations within the 3D matrix [27]. Importantly, both the contraction and the bulk modulus of pNIPAAm vary with temperature, making the calibration experiment essential. First, radial strain curves are determined for non-embedded (no matrix) pNIPAAm microspheres. Next, to calibrate the stiffness of the pNIPAAm the radial strain curves are determined for microspheres embedded in a soft polyacrylamide (PAA) of a known stiffness. The difference in the curves corresponds to the resistance applied by the stiffness of the embedding medium (Figure 3C). Using the microspheres and the measurements from non-embedded (no matrix) vs PAA embedded conditions, we can then calculate the modulus of the local collagen fiber network by embedding the microspheres within the collagen matrices (Figure 3C and D). In random collagen networks we calculated the mean modulus of the matrix to be 3.7 +/− 1.5 Pa (Figure 3D, green). Adapting this concept to the different strains recorded for asymmetrically contracted microspheres in aligned matrices required that we improve upon this method to account for an anisotropic matrix, which we accomplished by using the equations for a contracting sphere in an anisotropic matrix [36] (for details, see Supplemental Note #1). Upon alignment, the mean cell-scale modulus along the axis of alignment was calculated to be 8.5 +/− 2.3 Pa, while the mean cell-scale modulus perpendicular to collagen alignment was determined to be 0.53 +/− 0.15 Pa (Figure 3D, red and blue respectively). This resulted in an average 16-fold difference in the mean directional stiffness detected at the scale of the cell. While it is not unexpected that alignment results in increased stiffness along the axis alignment, what is surprising is the magnitude of the effect. To demonstrate this point, we examined both the aspect ratios of pNIPAAm microspheres (parallel / perpendicular) (Figure 3B) and the ratio of moduli (parallel / perpendicular) from regions of aligned collagen fibers (Figure 3D). The median aspect ratio of the contracted microspheres in aligned regions was 1.71, but the difference in mean stiffness across axes is not a factor of 1.7; it is a factor of 16. Moreover, when we compared the relative measures of stiffness within a single microsphere through the ratio of their moduli across directions, the modulus in the direction of alignment could be as high as 30 to 35 times the stiffness in the perpendicular direction (Figure 3E). We also observe that the trend between ratio of moduli and the modulus in the direction parallel to alignment is linear. This linear trend indicates that regions of greater stiffness (greater parallel modulus) also have greater anisotropy (greater ratio). Together, our findings clearly demonstrate that local alignment provides a surprisingly sizeable directional cue to the cell.
3.3. Collagen fiber alignment biases matrix deformations and the propagation of fiber displacements due to uniform microsphere contraction
In addition to the differential stiffness cues that result from the architecture of collagen fibers, the dynamic behavior of the matrix in random and aligned conditions may also be different. How displacements of fibers propagate due to forces could regulate subsequent reorganization of the ECM and even cellular mechanosensing. To investigate this further, we used digital image correlation (DIC) [29], a method that provides accurate, full-field measurements of fiber displacements using only images of the fibers themselves. Contractile pNIPAAm microspheres were then embedded in collagen gels to induced localized fiber deformations (Figure 4A–D). For this set of experiments the device used to create the alignment in these experiments was removed. In the random matrices, the displacement pattern was generally uniform and circular (Figure 4B). In the aligned gels, however, the displacement fields were noticeably warped and elongated along the axis of fiber alignment (Figure 4D). That is, the displacements propagated further along the axis of alignment than perpendicular to it. This was counterintuitive, as the spherical pNIPAAm microspheres contracted less on the axis parallel to alignment due to the anisotropic moduli of the surrounding matrix. To quantify this observation, we drew 60 equally spaced lines radiating around the contractile microsphere (red, blue and gray traces, Figure 4E and G) and extending toward the edge of the image. The DIC displacements along each line were extracted and plotted over distance. In the aligned matrices, the traces measuring fiber displacement along the axis of alignment (Figure 4G, shown in red trace) show a slow decrease over distance. Conversely, displacements perpendicular to the axis of alignment (Figure 4G, blue) decrease rapidly with steeper slope, and clearly differed from the displacements parallel to fiber alignment. In random controls (Figure 4E), orthogonal measurements demonstrate that radial displacements were approximately equivalent over distance, indicating no difference in mechanical behavior.
Figure 4: The alignment of collagen fibers imparts directionality to the propagation of contraction-induced fiber displacements.
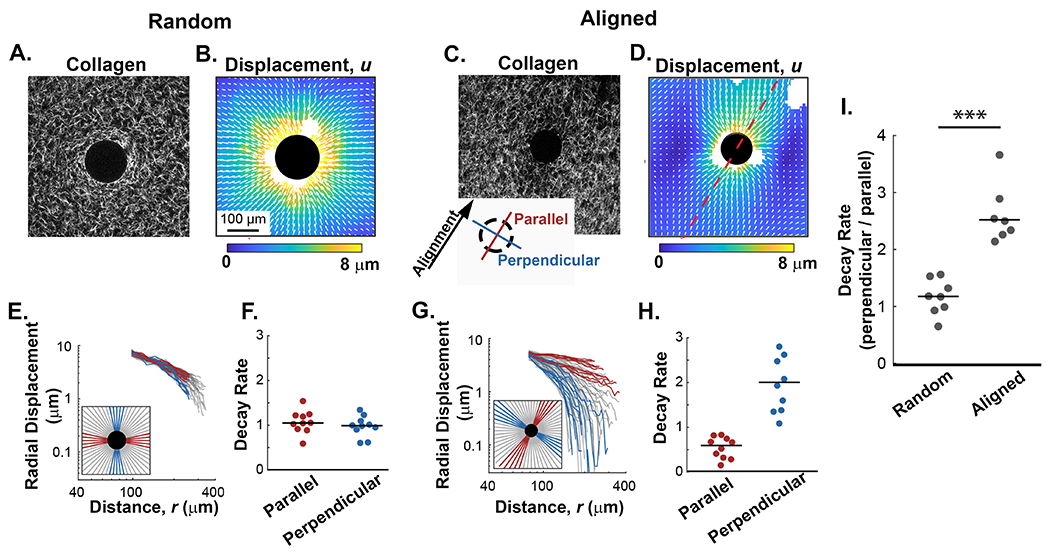
A and B) Representative example of collagen fibers (SHG) and their corresponding fiber displacement map from random collagen gels after contraction of pNIPAAm microspheres. C and D) Representative example of fibers (SHG) and their corresponding fiber displacement map from contracted pNIPAAm microspheres in an aligned collagen gel. The axis of alignment is represented by the red dashed line. E and G) Radial traces were circumferentially extracted from the displacement plots and plotted against the distance from the contractile particle as described by the key located in the lower left corner of each plot. Red lines represent traces extracted along the axis of alignment while blue lines represent traces perpendicular to alignment. In random gel the axis of alignment is arbitrarily assigned. Gray lines represent non-orthogonal angles. F and H) Quantification of fiber displacement decay rates, n, from a representative microsphere for the parallel and perpendicular directions in random and aligned matrices, respectively. I) Quantification of n (decay rates) in directions parallel and perpendicular for microspheres in random (n=8 microspheres) and aligned (n=7 microspheres) collagen fiber architectures. Lines indicate medians; significance was determined with a Wilcoxon rank sum test (*** p < 0.001).
To further quantify and characterize the fiber displacement properties observed in aligned and random matrices (Figure 4C and G), we fit the radial displacements u to distance from the center of the pNIPAAm microsphere r to the equation ur = Ar−n as in previous studies [30,37]. The fitting variable n represents how quickly the displacements diminish over distance. For reference, displacements in linear elastic materials like polyacrylamide decay rapidly with n = 2 [28]. In fibrous material like collagen, displacements decay more slowly with n ≈ 1, which results from mechanical nonlinearity [30,37]. The decay rates in matrices with random fiber organization decayed slowly with values of n near to 1 (Figure 4D). Comparisons of n in orthogonal directions, with one direction arbitrarily chosen to be defined as parallel, showed no significant difference in decay rates (Figure 4D), and the ratio of n in orthogonal directions equal to 0.91 +/− 0.31, indicating the matrices were essentially isotropic. In contrast, in aligned matrices the decay rate n was no longer uniform through the material. Perpendicular to the axis of alignment, the decay rate increased to values greater than 2 (i.e., faster decay of displacements than in linearly elastic materials), while parallel to the axis of alignment the decay rate decreased to 0.5 (i.e., slower than in random collagen networks) (Figure 4H). Under these conditions the ratio of the decay rate in directions perpendicular and parallel to fiber alignment increased to 3.32 +/− 2.18, representing a greater than 3-fold increase in the decay rate (Figure 4H). This process was repeated for multiple microspheres in both random and aligned matrices. In random matrices, the ratio of n in orthogonal directions was centered around one; however, for microspheres embedded in aligned regions of collagen the ratio was greater than 2, indicating a significant difference in decay rate due to fiber alignment (Figure 4I). The effect of alignment on the decay rates is significantly greater than expected, and this finding suggests that propagation of displacements in fibrous materials like the ECM is not homogeneous but rather variable and highly dependent on the local architecture of the fibers.
3.4. Cellular contractions in aligned collagen matrices produce bias in fiber deformations and the propagation of fiber displacements
Unlike the pNIPAAm microspheres that displace all the covalently attached fibers in the local network, cells dynamically interact with a limited number of fibers at individual protrusions and focal adhesions. To investigate the effect of this added layer of complexity on matrix behavior, GFP-LifeAct-MDA-MB-231 cells were embedded in both random and aligned collagen matrices. Cell migration and the resulting collagen fiber displacements were recorded over a 6-hour period and visualized with DIC. From this analysis, discrete pulses of fiber displacements could be observed propagating from individual protrusions instep with cell-induced contractions (Figure 5A and B and Supplemental Content - Movies 3 and 4). The displacements in the matrix did not appear as uniform plumes. Rather, they are better described as localized patches of high displacement intersperse by regions of lower displacement. This non-uniform pattern is consistent with past studies on heterogeneity within courser fiber networks and it represents the scale where the homogeneous matrix behavior breaks down and contributions from local networks of individual fibers dominates [31]. When displacement patterns arise from cells within a random fiber architecture, the fiber displacements were randomly distributed over space and time with highly variable magnitudes (Figure 5A). In contrast, the spatial localization and magnitude of cell-induced fiber displacements in aligned matrices were constrained along the axis of alignment (Figure 5B). This pattern is consistent with the presence of anisotropic decay patterns that were observed with the acellular pNIPAAm displacements.
Figure 5: The alignment of collagen affects the propagation of cell-induced fiber displacements.
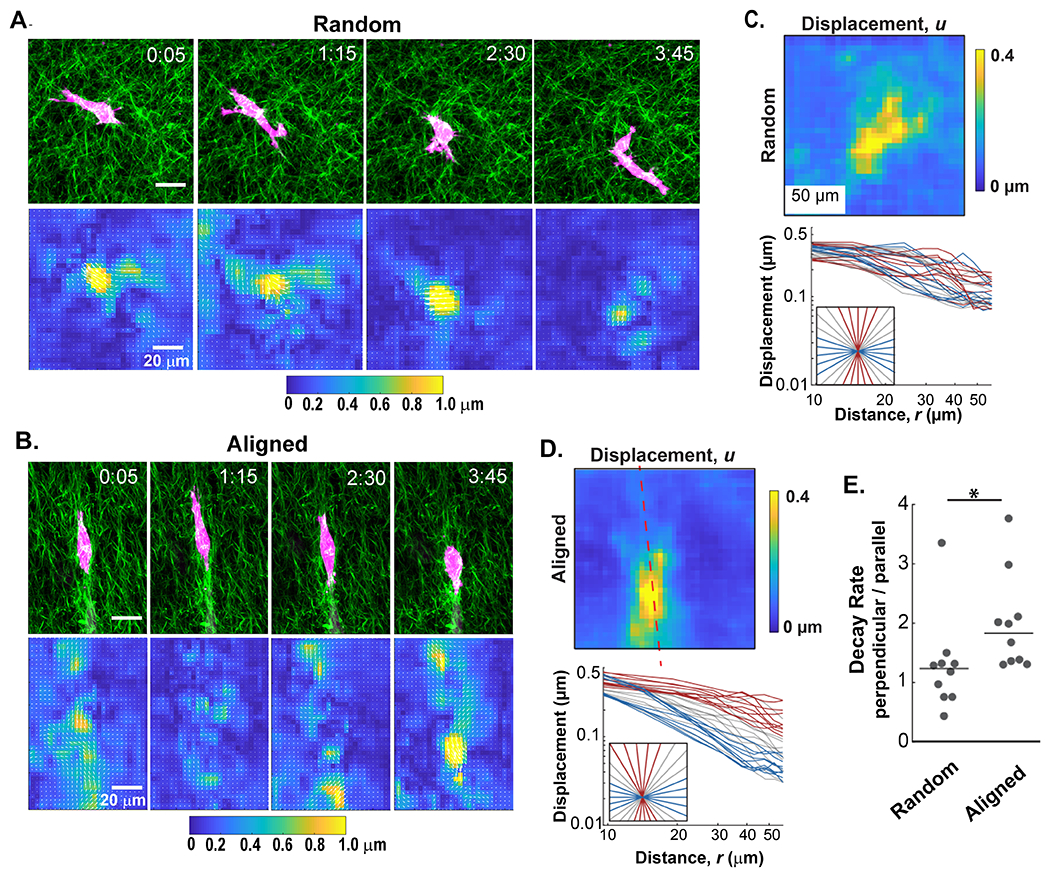
A and B) A 4 hour time course of GFP-LifeAct-MDA-MB-231 cells (red) migrating in collagen (SHG, green) gels exhibit different fiber displacement patterns in random and aligned matrices, respectively. C and D) Top panels: The fiber displacement was averaged over the 4 hour time course of cell migration for each collagen fiber architecture. Bottom panels: Graphs below each heatmap represent the radial traces extracted from the average fiber displacements plotted against the distance from the cell perimeter in random and aligned conditions. Red lines represent traces extracted along the axis of alignment while blue lines represent those that extend perpendicular. Gray lines represent non-orthogonal angles. E) Quantification of the ratio of decay rates in directions perpendicular and parallel (nperpendicular / nParallel) to fiber alignment from multiple cells (n=10 microspheres for each fiber architecture). (*p < 0.05 by Wilcoxon rank sum test)
To verify that fiber alignment also induces differential decay patterns in cell-induced displacements, an equivalent technique to that of the displacement traces measured on pNIPAAm microspheres was completed. To analyze cell-induced fiber displacement over time, we quantified displacements at each time point with reference from the prior time point, then averaged all of the cell-induced displacements and plotted them with respect to the cell centroid. Figures 5C and D represent the average fiber displacements from the 6 hour cell migration images shown in Figure 5A and B, respectively. We observed that cell-induced displacements in random fiber architectures exhibited no discernable differences in the decay rates between orthogonal directions (Figure 5C). In aligned matrices, however, the decay rates along the axis of alignment (red trace, Figure 5D) differed from the decay rates of those perpendicular to the axis of alignment (blue trace, Figure 5D), mirroring the results of the pNIPAAm microspheres. The decay rates in the matrix were calculated from a cohort of cells in both random and aligned gels, and once again, displacements propagating perpendicular to the axis of alignment decreased faster than those that propagated along the axis of alignment (Figure 5E).
3.5. Mechanical properties of the matrix correlate to changes in cellular mechanosensing behavior
Next, we sought to relate our findings on anisotropic matrix mechanics with the mechanosensing behavior of migrating tumor cells. First, we quantified the sum of cell-induced collagen fiber displacements across multiple cells relative to the cell perimeter. This was completed by circumferentially extracting the displacements from the edge of each cell, then incrementally expanding outwards to generate an average matrix displacement map with respect to the distance from the cell edge. The data was plotted on polar coordinates to give a 360-degree distribution of fiber displacements (Figure 6A and C). From this analysis, we observe many similar fiber displacement patterns to those generated by the pNIPAAm microspheres. That is, fiber displacements in random matrices varied little at different positions around the perimeter of the cell. In contrast, in aligned matrices there was a clear difference in the magnitude and propagation of fiber displacements generated along the axis of collagen alignment compared to those generated perpendicular to it. Specifically, the displacements located parallel to the axis of alignment were smaller yet propagated over a longer distance, while those generated perpendicular to the axis of alignment exhibited displacements of greater magnitude but a shorter range. This data set was then analyzed for protrusion dynamics, which were displayed on a similar 360-degree windrose plot to provide details of spatial distribution and duration of individual protrusions (Figure 6B and D). In random collagen matrices there was no significant difference in the spatial distribution of protrusion lifetimes. In contrast, within aligned matrices the protrusions orientated parallel to the axis of alignment, where local modulus is the greatest, were significantly longer lived than their perpendicular counterparts (Figure 6E). A similar result was observed by quantifying the number and spatial distribution of protrusions per cells with respect to collagen alignment (Figure S1D). The spatial dynamics of protrusions is noteworthy because even though perpendicular protrusions were short-lived, they generated very large displacements. Moreover, when we examined vinculin and phosphorylated FAK (pFAK), focal adhesion proteins known be involved in adhesion maturation and mechanosignaling signaling [38,39], we determined that in random matrices neither vinculin nor pFAK positive adhesions had any differences in size between orthogonal directions, with one direction arbitrarily chosen to be defined as parallel (Figure 6F and Figure S1E). In aligned matrices, however, both vinculin and pFAK showed a significant increase in aspect ratio when localized parallel to the axis of collagen alignment, further validating the presence of a cellular readout of a local increase in the directional stiffness due to local fiber alignment.
Figure 6: Anisotropic mechanical properties of the matrix relate to mechanosensing cellular behavior.
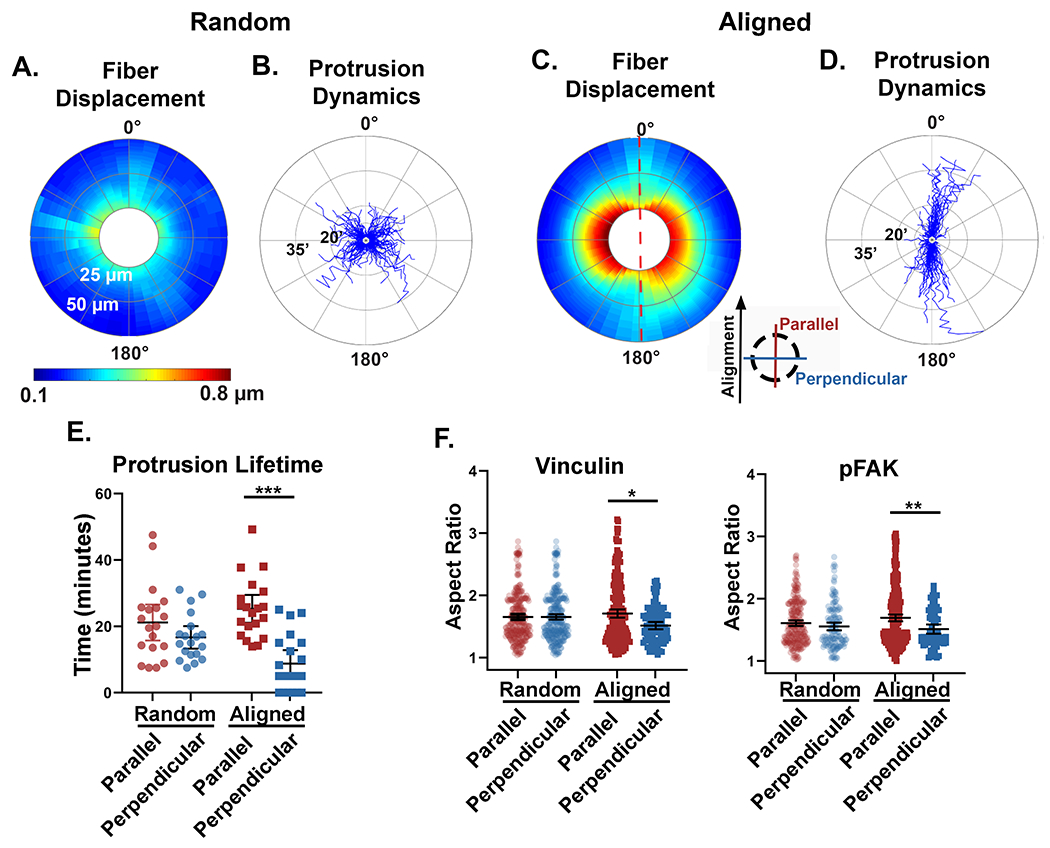
A and C) Fiber displacements were circumferentially extracted from the perimeter of multiple cells and plotted on 360° polar plots. The color scale represents the average magnitude of fiber displacements relative to the cell perimeter (n=10 cells for each fiber architecture). Fiber displacements were quantified out to 50 μm from the cell perimeter (radial axis). The red dashed line in panel C represent the axis of collagen alignment and the inserted key denotes the orientation of parallel and perpendicular directions with respect to the fiber alignment. B and D) Windrose plots described the dynamic and spatial protrusive behavior of individual cells in random (n=19 cells, 1,058 protrusions) and aligned (n=20 cells, 741 protrusions) matrices. The protrusion lifetime was measured in minutes on the radial axis. E) Quantification of the average parallel and perpendicular protrusion lifetimes per cell for random (n=19 cells) and aligned (n=20 cells) fiber architectures. Protrusions that were identified in only one timepoint were quantified as zero lifetime. F) Quantification of the aspect ratio of pFAK and vinculin positive focal adhesions oriented either parallel or perpendicular to the axis of fiber alignment. Medians and interquartile ranges were reported, and significance was determined by Mann-Whitney. (* p<0.05, ** p<0.01, *** p<0.001)
The propagation of contractile-induced fiber displacements has been suggested as a potential mechanism for cell-cell communication in fibrous networks [37]. This concept can be easily envisioned to occur within the mammary tumor microenvironment. Through intravital imaging we have identified tumor (cyan cells indicated by arrow heads) and stromal (red cells indicated by arrows) cells localized either parallel or perpendicular to each other in regions of aligned collagen fibers (Figure 7 A and B). Based on our finding of anisotropic mechanical properties of the matrix, we propose a model (Figure 7C) where stromal cells located perpendicular to collagen alignment and to a contracting tumor cell can detect fiber displacements only when the cells are in close proximity. In contrast, a stromal cell located along the axis of collagen alignment and parallel to a contracting tumor cell can detect fiber displacements when the cells are at a much greater distance from each other. Taken together, our data suggests that the anisotropic mechanical properties that result from collagen fiber alignment not only impact mechanosensing behavior of tumor cells, but potentially extend the range of cell-cell communication in the breast tumor microenvironment.
Figure 7: A model for potential cell-cell communication in the tumor microenvironment through anisotropic matrix properties.
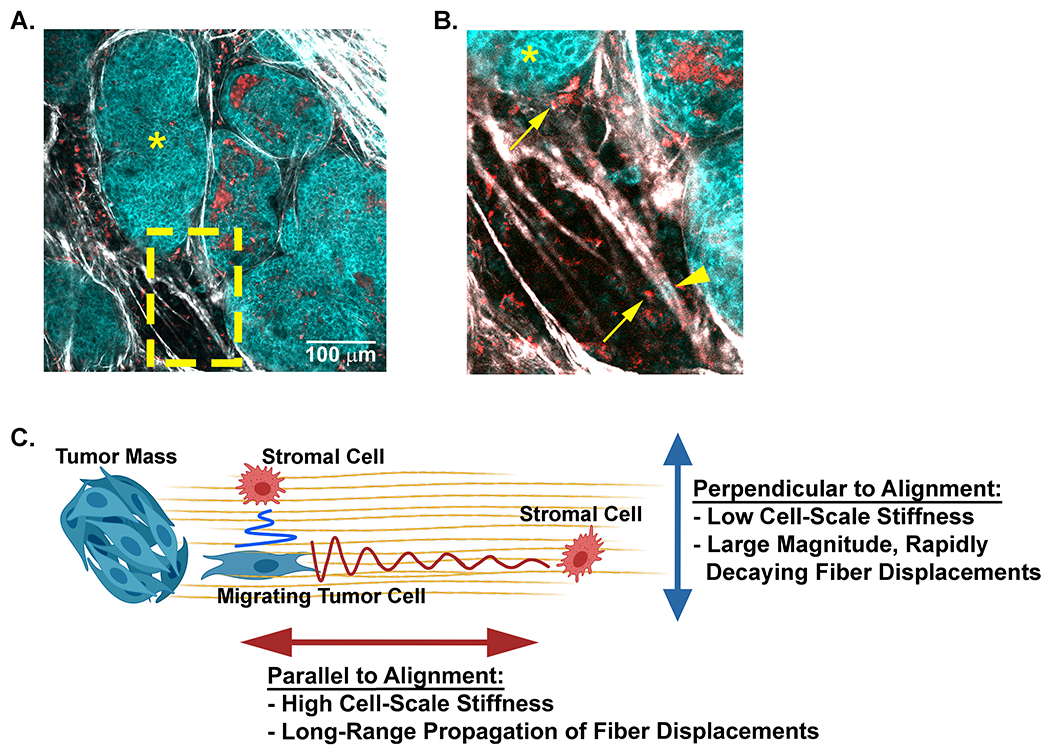
A) A representative field of view taken from intravital microscopy of a mouse mammary tumor depicts multiple cell types (cyan tumor cells and red stromal cells) within the collagen dense mammary tumor microenvironment. Collagen fibers (white) are detected with SHG. The tumors (cyan, *) and disseminating tumor cells are visualized with NADH endogenous fluorescence (cyan) while stromal cells are visualized with FAD autofluorescence (red). B) Higher magnification (yellow inset) of the tumor highlights stromal cells (arrows) and tumor cells (arrow heads) positioned parallel or perpendicular to each other along aligned collagen fibers. C) A schematic model of how collagen fiber architecture may facilitate, or bias mechanical cues used in mechanosensing. Displacements generated along the axis of alignment propagate further than those that propagate perpendicular to alignment. This may allow cells to disproportionately sense other cell types at greater distance along the axis of alignment. Artwork created with BioRender.com.
4. Discussion
This study aimed to gain a more comprehensive perspective of how the matrix responds to forces applied by the cell and how cells perceive and respond to mechanical properties of the matrix. We first used intravital imaging to evaluate the dynamic and physiological reciprocity between the cells and the matrix in vivo. From these intravital studies, we were able to visualize diverse collagen fiber configurations, both random and aligned, within the tumor microenvironment. Individual cells could be observed displacing collagen fibers as they applied contractile forces necessary for locomotion. The fiber displacement patterns varied as the tumor cells interacted with aligned fibers from orthogonal directions (i.e., parallel and perpendicular to alignment), demonstrating an underlying anisotropy that may provide cell-scale mechanosensing cues in vivo. Moreover, these findings suggested that we consider the resultant deformation from applied forces when we assess properties of the matrix in physiological tissues. To further investigate the anisotropic cues resulting from the architecture of collagen, we developed an in vitro system to generate reproducible fiber alignment. Using calibrated pNIPAAm microspheres, we determined that the local modulus, while variable, could be up to 35 times stiffer along the axis of collagen fiber alignment compared to perpendicular to alignment. In addition, fiber alignment supported the long-range propagation of fiber displacements while diminishing similar contraction-induced displacements that propagated perpendicular to the axis of alignment. Together, this encourages longer-lived protrusions with more mature, force-generating adhesions along the axis of alignment resulting in directionally persistent migration.
Initially, we focused on anisotropy in cell-scale matrix stiffness resulting from collagen fiber alignment. Through our innovative method, we directly measured dynamic cell-scale stiffness within a 3D collagen network. Our findings are in line with measurements of collagen fiber stiffness made with AFM nanoindentation, which demonstrate higher stiffness along the axis of a long flexible fiber compared to similar forces applied perpendicular to the fiber [17]. The prior study suggests that cells may sense very different stiffnesses depending on the orientation of the applied force to the fibrous network [19]. Using pNIPAAm microspheres to mimic cell-scale contractile forces within a 3D matrix, our study has given the first experimental quantification of the difference in mechanical anisotropy due to collagen alignment. This information not only fills a critical gap in our understanding of how local ECM microarchitecture impacts mechanosensing, but also opens the door to investigate how other matrix properties impact cell-scale mechanics. For example, aligned collagen in the breast tumor microenvironment is not only associated with increased stiffness [40], but associated with other matrix and crosslinking proteins [41,42]. Future studies will address the impact of additional alignment-associated proteins on cell-scale mechanics.
While quantification of cell-scale stiffness is certainly important to understanding mechanosensing in vivo, an added dimension of matrix mechanics highlighted in our study is how the local collagen architecture impinges on fiber deformations due to cellular force. Our findings on anisotropic matrix properties leads us to suggest a model for directional communication between cells in the collagen microenvironment. The concept of mechanosensing through contraction-induced fiber displacements is not new. Prior studies have demonstrated the potential of long distance cell-cell communication due to localized deformations induced by cells in a fibrin network [37,43]. Along these lines, macrophages were recently shown to respond to contractile forces from myofibroblasts at the wound site to facilitate healing [20]. It was proposed that macrophages detect fiber deformations generated by myofibroblasts at greater distances than those achievable by chemical gradients. While that study focused on wound healing and the interactions of macrophages and myofibroblasts, it is certainly plausible that a similar mechanism of force propagation through fiber displacements could occur in other cell types and fibrotic conditions. Moreover, although fibroblasts are certainly more contractile and primarily responsible for matrix reorganization, tumor cells can also contract, displace fibers, and align the matrix through cellular forces [44–46]. In the breast tumor microenvironment, aligned fibers not only enhance persistent cancer cell migration but regions of aligned fibers are enriched in macrophages [4,5,9,10]. The mechanisms by which macrophages traffic to regions of aligned collagen are not yet clear. Thus, a better understanding how contractile forces propagate through the matrix, specifically into regions of aligned collagen fibers, might shed light on a biophysical mechanism for macrophage recruitment. More specifically, tumor cells have been shown to pair with macrophages to facilitate tumor cell intravasation into blood vessels. In these situations reciprocal chemokine signaling facilitates macrophage-tumor cell trafficking along collagen fibers [47,48], but it is possible that collagen architecture may play a significant role in the initial pairing event through long-range fiber displacements driven by tumor cell contraction. This process may be further amplified because regions of local alignment may bias the detection of the contracting tumor cell by the homing macrophage at a much greater distance along the axis of alignment (Figure 7). Conversely, any cell positioned perpendicular to the axis of alignment would be effectively shielded to those same displacements. This has the broader implication that mechanosensing potential is not uniform throughout the 3D ECM, but rather is dependent on the local architecture of the matrix, thereby making mechanical signaling through the matrix very heterogenous within a tissue.
5. Conclusion
In summary, a key principle of this study is that local architecture has a dramatic effect on the cell-scale mechanical cues, which in turn impacts the stiffness sensed by a cell and the response of the matrix to cell-induced forces. Our work has defined relevant static and dynamic cell-scale mechanical cues with respect to the organization of collagen fibers, enabling investigation of how mechanical properties of the matrix impact the reciprocity in cell behavior and cell communication within the tumor microenvironment. Future studies are needed to explore whether variable compositions or specific features of the matrix will further enhance or diminish these cues, and how dynamic matrix reorganization plays a role in these processes.
Supplementary Material
Significance Statement.
It is widely appreciated that the architecture of the extracellular matrix impacts cellular behavior in normal and disease states. Numerous studies have determined the fundamental role of collagen matrix architecture on cellular mechanosensing, but effectively quantifying anisotropic mechanical properties of the collagen matrix at the cell-scale remains challenging. Here, we developed innovative methodology to discover that collagen alignment results in a 35-fold difference in cell-scale stiffness and alters contractile force transmission through the fiber network. Furthermore, we identified bias in cell response along the axis of alignment, where local stiffness is highest. Overall, our results define cell-scale stiffness and fiber deformations due to collagen architecture that may instruct cell communication within a broad range of tissue microenvironments.
6. Acknowledgments:
The authors would like to thank Drs. Anna Huttenlocher and Maria Virumbrales-Muñoz for helpful discussion and careful review of the manuscript.
7. Funding:
This work was supported by the National Institutes of Health to SMP (R01 CA179556, R01 CA216248, and R01 CA206458) and the National Science Foundation to JN (NSF CMMI-1749400).
Footnotes
Competing interests: No conflicts of interest reported.
References
- [1].Kai FB, Drain AP, Weaver VM, The Extracellular Matrix Modulates the Metastatic Journey, Dev. Cell 49 (2019) 332–346. 10.1016/j.devcel.2019.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Provenzano PP, Eliceiri KW, Campbell JM, Inman DR, White JG, Keely PJ, Collagen reorganization at the tumor-stromal interface facilitates local invasion, BMC Med. 4 (2006) 38. 10.1186/1741-7015-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Conklin MW, Eickhoff JC, Riching KM, Pehlke CA, Eliceiri KW, Provenzano PP, Friedl A, Keely PJ, Aligned collagen is a prognostic signature for survival in human breast carcinoma, Am. J. Pathol 178 (2011) 1221–1232. 10.1016/j.ajpath.2010.11.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Esbona K, Yi Y, Saha S, Yu M, Van Doorn RR, Conklin MW, Graham DS, Wisinski KB, Ponik SM, Eliceiri KW, Wilke LG, Keely PJ, The Presence of Cyclooxygenase 2, Tumor-Associated Macrophages, and Collagen Alignment as Prognostic Markers for Invasive Breast Carcinoma Patients, Am. J. Pathol (2018). 10.1016/j.ajpath.2017.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Acerbi I, Cassereau L, Dean I, Shi Q, Au A, Park C, Chen YY, Liphardt J, Hwang ES, Weaver VM, Human breast cancer invasion and aggression correlates with ECM stiffening and immune cell infiltration, Integr. Biol. (United Kingdom). 7 (2015) 1120–1134. 10.1039/c5ib00040h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Ilina O, Campanello L, Gritsenko PG, Vullings M, Wang C, Bult P, Losert W, Friedl P, Intravital microscopy of collective invasion plasticity in breast cancer, DMM Dis. Model. Mech (2018). 10.1242/dmm.034330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Leung E, Xue A, Wang Y, Rougerie P, Sharma VP, Eddy R, Cox D, Condeelis J, Blood vessel endothelium-directed tumor cell streaming in breast tumors requires the HGF/C-Met signaling pathway, Oncogene. 36 (2017) 2680–2692. 10.1038/onc.2016.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Arwert EN, Harney AS, Entenberg D, Wang Y, Sahai E, Pollard JW, Condeelis JS, A Unidirectional Transition from Migratory to Perivascular Macrophage Is Required for Tumor Cell Intravasation, Cell Rep. 23 (2018) 1239–1248. 10.1016/j.celrep.2018.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Provenzano PP, Inman DR, Eliceiri KW, Trier SM, Keely PJ, Contact guidance mediated three-dimensional cell migration is regulated by Rho/ROCK-dependent matrix reorganization, Biophys. J 95 (2008) 5374–5384. 10.1529/biophysj.108.133116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Riching KMM, Cox BL, Salick MRR, Pehlke C, Riching ASS, Ponik SM, Bass BRR, Crone WCC, Jiang Y, Weaver AM, Eliceiri KWW, Keely PJJ, 3D collagen alignment limits protrusions to enhance breast cancer cell persistence, Biophys. J 107 (2015) 2546–2558. 10.1016/j.bpj.2014.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Carey SP, Goldblatt ZE, Martin KE, Romero B, Williams RM, Reinhart-King CA, Local extracellular matrix alignment directs cellular protrusion dynamics and migration through Rac1 and FAK, Integr. Biol 8 (2016) 821–835. 10.1039/c6ib00030d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ray A, Morford RK, Ghaderi N, Odde DJ, Provenzano PP, Dynamics of 3D carcinoma cell invasion into aligned collagen, Integr. Biol. (United Kingdom) 10 (2018) 100–112. 10.1039/c7ib00152e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Fraley SI, Wu PH, He L, Feng Y, Krisnamurthy R, Longmore GD, Wirtz D, Three-dimensional matrix fiber alignment modulates cell migration and MT1-MMP utility by spatially and temporally directing protrusions, Sci. Rep 5 (2015). 10.1038/srep14580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Ray A, Lee O, Win Z, Edwards RM, Alford PW, Kim DH, Provenzano PP, Anisotropic forces from spatially constrained focal adhesions mediate contact guidance directed cell migration, Nat. Commun 8 (2017) 1–17. 10.1038/ncomms14923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Wang WY, Pearson AT, Kutys ML, Choi CK, Wozniak MA, Baker BM, Chen CS, Extracellular matrix alignment dictates the organization of focal adhesions and directs uniaxial cell migration, APL Bioeng. (2018). 10.1063/1.5052239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Kubow KE, Conrad SK, Horwitz AR, Matrix microarchitecture and myosin II determine adhesion in 3D matrices, Curr. Biol (2013). 10.1016/j.cub.2013.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Doyle AD, Carvajal N, Jin A, Matsumoto K, Yamada KM, Local 3D matrix microenvironment regulates cell migration through spatiotemporal dynamics of contractility-dependent adhesions, Nat. Commun 6 (2015) 1–15. 10.1038/ncomms9720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].An KN, Sun YL, Luo ZP, Flexibility of type I collagen and mechanical property of connective tissue, in: Biorheology, 2004. [PubMed] [Google Scholar]
- [19].Doyle AD, Yamada KM, Mechanosensing via cell-matrix adhesions in 3D microenvironments, Exp. Cell Res 343 (2016) 60–66. 10.1016/j.yexcr.2015.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Pakshir P, Alizadehgiashi M, Wong B, Coelho NM, Chen X, Gong Z, Shenoy VB, McCulloch C, Hinz B, Dynamic fibroblast contractions attract remote macrophages in fibrillar collagen matrix, Nat. Commun 10 (2019). 10.1038/s41467-019-09709-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Szulczewski JM, Inman DR, Entenberg D, Ponik SM, Aguirre-Ghiso J, Castracane J, Condeelis J, Eliceiri KW, Keely PJ, In Vivo Visualization of Stromal Macrophages via label-free FLIM-based metabolite imaging, Sci. Rep (2016). 10.1038/srep25086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Burkel B, Notbohm J, Mechanical response of collagen networks to nonuniform microscale loads, Soft Matter. 13 (2017) 5749–5758. 10.1039/c7sm00561j. [DOI] [PubMed] [Google Scholar]
- [23].Suzuki A, Tanaka T, Phase transition in polymer gels induced by visible light, Nature. (1990). 10.1038/346345a0. [DOI] [Google Scholar]
- [24].Wang Y, Qin J, Wei Y, Li C, Ma G, Preparation strategies of thermo-sensitive P(NIPAM-co-AA) microspheres with narrow size distribution, Powder Technol. (2013). 10.1016/j.powtec.2012.04.060. [DOI] [Google Scholar]
- [25].Yao C, Lei G, Li L, Gao X, Preparation and characterization of polyacrylamide nanomicrospheres and its profile control and flooding performance, J. Appl. Polym. Sci (2013). 10.1002/app.37727. [DOI] [Google Scholar]
- [26].Vader D, Kabla A, Weitz D, Mahadevan L, Strain-induced alignment in collagen gels, PLoS One. 4 (2009). 10.1371/journal.pone.0005902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Proestaki M, Ogren A, Burkel B, Notbohm J, Modulus of Fibrous Collagen at the Length Scale of a Cell, Exp. Mech 59 (2019) 1323–1334. 10.1007/s11340-018-00453-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Eshelby JD, The Elastic Field Outside an Ellipsoidal Inclusion. Proceedings of the Royal Society of London, A252 (1271), 561–569., 252 (1959) 1959. [Google Scholar]
- [29].Bar-Kochba E, Toyjanova J, Andrews E, Kim KS, Franck C, A Fast Iterative Digital Volume Correlation Algorithm for Large Deformations, Exp. Mech (2015). 10.1007/si1340-014-9874-2. [DOI] [Google Scholar]
- [30].Burkel B, Notbohm J, Mechanical response of collagen networks to nonuniform microscale loads, Soft Matter. 13 (2017). 10.1039/c7sm00561j. [DOI] [PubMed] [Google Scholar]
- [31].Burkel B, Proestaki M, Tyznik S, Notbohm J, Heterogeneity and nonaffinity of cell-induced matrix displacements, Phys. Rev. E 98 (2018) 052410. 10.1103/PhysRevE.98.052410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Saraswathibhatla A, Galles EE, Notbohm J, Spatiotemporal force and motion in collective cell migration, Sci. Data (2020). 10.1038/s41597-020-0540-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Bredfeldt JS, Liu Y, Pehlke CA, Conklin MW, Szulczewski JM, Inman DR, Keely PJ, Nowak RD, Mackie TR, Eliceiri KW, Computational segmentation of collagen fibers from second-harmonic generation images of breast cancer, J. Biomed. Opt 19 (2014) 016007. 10.1117/1.jbo.19.1.016007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Roeder BA, Kokini K, Sturgis JE, Robinson JP, Voytik-Harbin SL, Tensile mechanical properties of three-dimensional type I collagen extracellular matrices with varied microstructure, J. Biomech. Eng (2002). 10.1115/1.1449904. [DOI] [PubMed] [Google Scholar]
- [35].Motte S, Kaufman LJ, Strain stiffening in collagen i networks, Biopolymers. (2013). 10.1002/bip.22133. [DOI] [PubMed] [Google Scholar]
- [36].Yu HY, Sanday SC, Chang CI, Elastic inclusions and inhomogeneities in transversely isotropic solids, Proc. R. Soc. London. Ser. A Math. Phys. Sci 444 (1994) 239–252. 10.1098/rspa.1994.0014. [DOI] [Google Scholar]
- [37].Notbohm J, Lesman A, Rosakis P, Tirrell DA, Ravichandran G, Microbuckling of fibrin provides a mechanism for cell mechanosensing, J. R. Soc. Interface 12 (2015). 10.1098/rsif.2015.0320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Riveline D, Zamir E, Balaban NQ, Schwarz US, Ishizaki T, Narumiya S, Kam Z, Geiger B, Bershadsky AD, Focal contacts as mechanosensors: Externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism, J. Cell Biol (2001). 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Chen Y, Pasapera AM, Koretsky AP, Waterman CM, Orientation-specific responses to sustained uniaxial stretching in focal adhesion growth and turnover, Proc. Natl. Acad. Sci. U. S. A 110 (2013). 10.1073/pnas.1221637110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Acerbi I, Cassereau L, Dean I, Shi Q, Au A, Park C, Chen YY, Liphardt J, Hwang ES, Weaver VM, and Acerbil VWI 1, Cassereau L, Dean I, Shi Q, Au A, Park C, Chen YY, Liphardt J, Hwan ES, Acerbi I, Cassereau L, Dean I, Shi Q, Au A, Park C, Chen YY, Liphardt J, Hwang ES, Weaver VM, Human breast cancer invasion and aggression correlates with ECM stiffening and immune cell infiltration, Integr. Biol. (United Kingdom) 7 (2015) 1120–1134. 10.1039/c5ib00040h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Tomko LA, Hill RC, Barrett A, Szulczewski JM, Conklin MW, Eliceiri KW, Keely PJ, Hansen KC, Ponik SM, Targeted matrisome analysis identifies thrombospondin-2 and tenascin-C in aligned collagen stroma from invasive breast carcinoma, Sci. Rep 8 (2018). 10.1038/S41598-018-31126-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Grossman M, Ben-Chetrit N, Zhuravlev A, Afik R, Bassat E, Solomonov I, Yarden Y, Sagi I, Tumor cell invasion can be blocked by modulators of collagen fibril alignment that control assembly of the extracellular matrix, Cancer Res. 76 (2016) 4249–4258. 10.1158/0008-5472.CAN-15-2813. [DOI] [PubMed] [Google Scholar]
- [43].Winer JP, Oake S, Janmey PA, Non-linear elasticity of extracellular matrices enables contractile cells to communicate local position and orientation, PLoS One. 4 (2009). 10.1371/journal.pone.0006382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Wozniak MA, Desai R, Solski PA, Der CJ, Keely PJ, ROCK-generated contractility regulates breast epithelial cell differentiation in response to the physical properties of a three-dimensional collagen matrix, J. Cell Biol 163 (2003) 583–595. 10.1083/jcb.200305010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Gehler S, Baldassarre M, Lad Y, Leight JL, Wozniak MA, Riching KM, Eliceiri KW, Weaver VM, Calderwood DA, Keely PJ, Filamin A-β1 integrin complex tunes epithelial cell response to matrix tension, Mol. Biol. Cell 20 (2009) 3224–3238. 10.1091/mbc.E08-12-1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Heck JN, Ponik SM, Garcia-Mendoza MG, Pehlke CA, Inman DR, Eliceiri KW, Keely PJ, Microtubules regulate GEF-H1 in response to extracellular matrix stiffness, Mol. Biol. Cell 23 (2012) 2583–2592. 10.1091/mbc.E11-10-0876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wyckoff J, Wang W, Lin EY, Wang Y, Pixley F, Stanley ER, Graf T, Pollard JW, Segall J, Condeelis J, A paracrine loop between tumor cells and macrophages is required for tumor cell migration in mammary tumors, Cancer Res. (2004). 10.1158/0008-5472.CAN-04-1449. [DOI] [PubMed] [Google Scholar]
- [48].Goswami S, Sahai E, Wyckoff JB, Cammer M, Cox D, Pixley FJ, Stanley ER, Segall JE, Condeelis JS, Macrophages promote the invasion of breast carcinoma cells via a colony-stimulating factor-1/epidermal growth factor paracrine loop, Cancer Res. (2005). 10.1158/0008-5472.CAN-04-1853. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


