Why case fatality ratios can be misleading: individual- and population-based mortality estimates and factors influencing them

Abstract

Different ways of calculating mortality during epidemics have yielded very different results, particularly during the current COVID-19 pandemic. For example, the “CFR” has been interchangeably called the case fatality ratio, case fatality rate, and case fatality risk, often without standard mathematical definitions. The most commonly used CFR is the case fatality ratio, typically constructed using the estimated number of deaths to date divided by the estimated total number of confirmed infected cases to date. How does this CFR relate to an infected individual’s probability of death? To explore such issues, we formulate both a survival probability model and an associated infection duration-dependent SIR model to define individual- and population-based estimates of dynamic mortality measures to show that neither of these are directly represented by the case fatality ratio. The key parameters that affect the dynamics of different mortality estimates are the incubation period and the time individuals were infected before confirmation of infection. Using data on the recent SARS-CoV-2 outbreaks, we estimate and compare the different dynamic mortality estimates and highlight their differences. Informed by our modeling, we propose more systematic methods to determine mortality during epidemic outbreaks and discuss sensitivity to confounding effects and uncertainties in the data arising from, e.g., undertesting and heterogeneous populations.

INTRODUCTION

Mortality metrics are key quantities describing the severity of a viral disease [1]. During an outbreak, these metrics typically evolve in time before converging to a constant value and can be defined in a number of ways. Commonly used metrics are the case fatality ratio, case fatality rate, and case fatality risk, which are all confusingly denoted “CFR” [2, 3]. Fatality rate implies a change in deaths per unit time, risk implies an individual probability, while ratio implies a fraction of two numbers, typically populations. CFR is most often defined as the ratio of the total estimated number of deaths to date, D(t), to the estimated number of all confirmed cases to date N_c(t) [1, 4–6]. These numbers are key to estimating disease severity. Usually, antibody [7] and reverse transcription-polymerase chain reaction (RT-PCR) testing [8] is used to confirm SARS-CoV-2-positive patients. To find D(t), the number of patients who actually die of COVID-19 must also be quantified. In Italy, deaths of patients with positive RT-PCR testing for SARS-CoV-2 are reported as COVID-19 deaths, but the criteria for COVID-19-related deaths are currently not clearly defined and may vary from region to region [9].

Some studies define CFR as the “case fatality risk” and associate it with the probability of death of an individual confirmed case within “a period of time” [10]. Yet others define case fatality ratio as simply “case fatality” and reserve the term case fatality ratio to mean the ratio of the case fatalities of two different diseases [3]. Infection fatality ratios (IFR), the number of deaths to date divided by the number of all infected individuals, have also been used [11–13] although the IFR = D(t)/N(t) requires an estimate of N(t), the number of total (including unconfirmed) infected individuals. Similarly, IFR has also been called the “infection fatality risk,” the probability of an individual dying conditioned on being infected. This individual-based definition of IFR is thus equivalent to the individual-based case fatality risk. However, in nearly all practical cases, both the CFR and IFR are estimated from aggregated population data from past outbreaks [4] as well as from those of the recent SARS-CoV-2 outbreaks [1, 11, 13–17].

Since case fatality ratio is the most commonly used, we henceforth define CFR = D(t)/N_c(t). We show examples of CFR curves (orange), which typically vary significantly both by region and in time, in Fig. 1 and in the Results and Discussion section. During the severe 2003 acute respiratory syndrome (SARS) outbreak in Hong Kong, the World Health Organization (WHO) also used the aforementioned estimate to obtain an initial CFR ~ 3% while the final values, after resolution of infections, approached 17.0% [18, 19] (see Fig. 1(a)). Another population-based mortality ratio is M_p(t) = D(t)/(D(t) + R(t)), the number of deaths divided by the sum of death and recovered cases (the number of resolved cases), up to time t is shown in blue in Figs. 1(a–b). In principle, M_p(t) should be a better measure of the likelihood of death, but it is underestimated by the CFR = D(t)/N_c(t). For example, M_p(t) is currently (as of April 25, 2020) 203, 164/(203, 164 + 836, 612) ≈ 20%, significantly higher than the April 25, 2020 CFR(t) = D(t)/N_c(t) = 203, 164/2, 919, 404 ≈ 7% estimate [22]. Despite this underestimation, the CFR is still commonly used by the WHO and other health officials, such as in the ongoing SARS-CoV-2 outbreaks [1, 12, 13, 15, 17] (see Table I). As shown in Fig. 1(c), the CFR would correspond to the mortality ratio only if all tested infected individuals recover. Such underestimations by CFRs may lead to insufficient countermeasures and a more severe epidemic [23, 24].

FIG. 1. Mortality estimates.

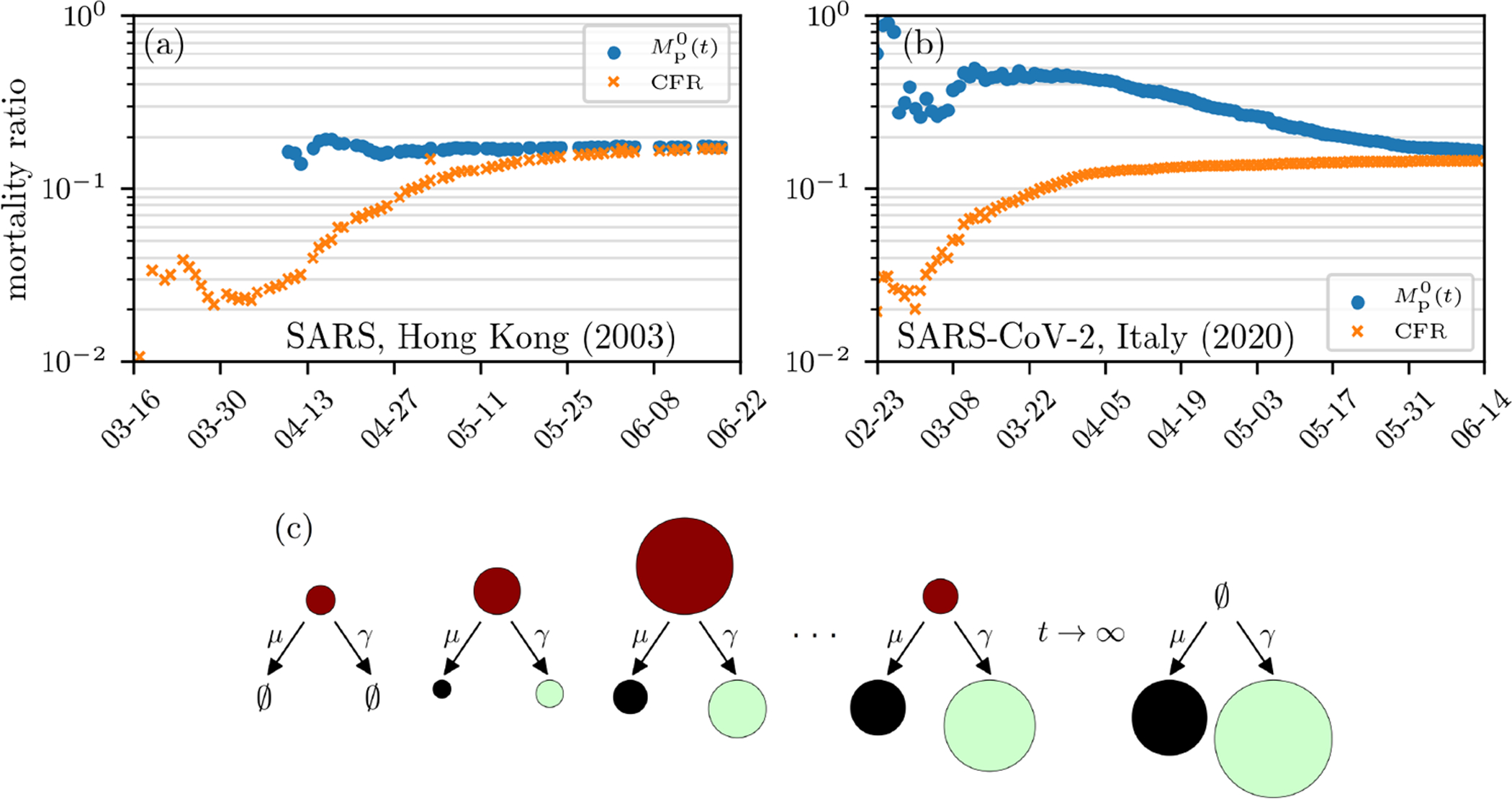
(a–b) Estimates of mortality ratios (see Eqs. (9) and (14)) of SARS-CoV infections in Hong Kong (2003) [20] and SARS-CoV-2 infections in Italy. (c) Evolution of the cumulative number of infected (red), death (black), and recovered (green) cases. The size of the circles indicates the number of cases in the respective compartments on a certain day. Note that CFR and $M_{\text{p}}^0(t)$ have exhibited qualitatively similar behavior across different epidemics. The data are based on Ref. [21].

TABLE I.

Different CFR estimates of COVID-19.

reference	CFR
Xu et al. [5, 25] and Mahase [26]	2%
Wu et al. [6]	0.1–1% (outside Wuhan)
World Health Organization [27, 28]	2–4%
Porcheddu et al. [29]	2.3% (Italy and China)
Peeri [30] et al.	2%

Since meaningful and accurate mortality metrics are critical for assessing the risks associated with epidemic outbreaks, we first unambiguously define the probability M₁(t) that a single, newly infected individual will die of the disease by a given time. This probability has also been called the case fatality risk, but without specifying its dependence on time after infection [10]. This intrinsic mortality or probability of death, can be identified as one minus the survival probability of a single infected individual. It should be an intrinsic property of the virus and the infected individual, depending on age, health, access to health care, etc., and not directly on the population-level dynamics of infected and recovered individuals. Whether this individual infects others does not directly affect his probability of eventually dying [31].

In the next section, we derive a survival probability model for M₁(t) similar to that in Ghani et al. [32]. Importantly, our individual survival model incorporates the duration of infection (including an incubation period) before a patient tests positive at time t = 0. However, the CFR and other mortality measures are typically reported based on population data. Do these population-based measures, including CFR, provide reasonable measures of the probability of death of an individual? To address these and related issues, we develop an analogous population-based mortality metric based on a disease duration-structured SIR model. While population-based estimates of CFR are typically not a meaningful measure of individual mortality, under simplifying assumptions, the population-based mortality ratio M_p(t) is more closely related to the true probability of death M₁(t) [32].

We will use the same rate parameters in our individual and population models to compute and compare the different mortality measures. By critically analyzing and comparing these estimates, the CFR, and a “delayed” case fatality ratio CFR_d, we illustrate and interpret the differences among these measures and discuss how changes or uncertainty in the data affect them. In the Results and Discussion section, we identify a correction factor to transform population-level mortality estimates into individual mortality probabilities, and discuss the effects of other possible confounding factors such as heterogeneous populations and undertesting (unconfirmed cases).

MORTALITY MEASURES

In this section, we present different mortality measures for confirmed cases and outline their underlying mathematical models.

Intrinsic individual mortality rate

Consider an individual that, at the time of positive testing (t = 0), had been infected for a duration τ₁. A “survival” probability density can be defined such that P(τ, t|τ₁)dτ is the probability that the patient is still alive and infected (not recovered) at time t > 0 and has been infected for a duration between τ and τ + dτ. Since τ₁ is unknown, it must be estimated or averaged over some distribution. The individual survival probability evolves according to [33].

$$\frac{\partial P\left(\tau ,t|{\tau }_1\right)}{\partial t}+\frac{\partial P\left(\tau ,t|{\tau }_1\right)}{\partial \tau }=-\left(\mu \left(\tau ,t|{\tau }_1\right)+\gamma \left(\tau ,t|{\tau }_1\right)\right)P\left(\tau ,t|{\tau }_1\right),$$ (1)

where the death and recovery rates, μ(τ, t|τ₁) and γ(τ, t|τ₁), depend explicitly on the duration of infection at time t and can be further implicitly stratified according to patient age, gender, health condition, etc. [1, 34]. They may also depend explicitly on time t to reflect changes in clinical policy or available health care. For example, enhanced medical care may decrease the death rate μ, giving the individual’s intrinsic physiological processes a chance to cure the patient.

If we assume an initial condition of one individual having been infected for time τ₁ at the time of confirmation, Eq. 1 can be solved using the method of characteristics shown in the Appendix. From the solution P(τ = t + τ₁, t|τ₁), one can derive the probabilities of death and recovery by time t as

$$P_{\text{d}}\left(t|{\tau }_1\right)={\int }_0^t\text{d}s\mu \left({\tau }_1+s,s\right)P\left({\tau }_1+s,t|{\tau }_1\right),P_{\text{r}}\left(t|{\tau }_1\right)={\int }_0^t\text{d}s\gamma \left({\tau }_1+s,s\right)P\left({\tau }_1+s,t|{\tau }_1\right).$$ (2)

The probability that an individual died before time t, conditioned on resolution (either death or recovery), is then defined as

$$M_1\left(t|{\tau }_1\right)=\frac{P_{\text{d}}\left(t|{\tau }_1\right)}{P_{\text{d}}\left(t|{\tau }_1\right)+P_{\text{r}}\left(t|{\tau }_1\right)}.$$ (3)

Equations (2) and (3) also depend on all other relevant patient attributes such as age, accessibility to health care, etc. In the long-time limit, when resolution has occurred (P_d(∞|τ₁) + P_r(∞|τ₁) = 1), the individual mortality ratio is simply M₁(∞|τ₁) = P_d(∞|τ₁). In order to capture the dependence of death and recovery rates on the time an individual has been infected, we propose a constant recovery rate γ and a piecewise constant death rate μ(τ|τ₁) that is not explicitly a function of time t:

$$\gamma \left(\tau ,t|{\tau }_1\right)=\gamma ,\mu \left(\tau |{\tau }_1\right)=\{\begin{array}{cc}0& \tau \le {\tau }_{\text{inc}}\\ {\mu }_1& \tau >{\tau }_{\text{inc}}\end{array}.$$ (4)

Here, τ_inc is the incubation time during which the patient is asymptomatic, has negligible chance of dying, but can recover by clearing the virus. In other words, some patients fully recover without ever developing serious symptoms.

For coronavirus infections, the incubation period appears to be highly variable with a mean of τ_inc ≈ 6.4 days [36]. We can estimate μ₁ and γ using recent individual patient data from Singapore where 178 patients (mean age: 46 years) had been tracked from the date on which their first symptoms occurred until they recovered [35], on average, after 13.7 days. We show the recovery-time distribution in Fig. 2(a). Compared to other existing datasets, the Singapore COVID-19 dataset provides complete line lists for a large number of patients and is being updated regularly.

FIG. 2. Individual mortality.

(a) Recovery time after first symptoms occurred based on individual data of 178 patients [35]. The inset shows the age distribution of these patients. (b) Death- and recovery rates as defined in Eq. (4). The death rate μ(τ₁) approaches μ₁ for τ₁ > τ_inc, where τ_inc is the incubation period and τ₁ is the time the patient has been infected before first being tested positive. (c) The individual mortality ratio M₁(t|τ₁) for τ_inc = 6.4 days at different values of τ₁. Note that the individual death probability P_d(t|τ₁) and M₁(t|τ₁) are nonzero only after t > τ_inc − τ₁. (d) The asymptotic individual mortality ratio M₁(∞) (see Eq. (3)) as a function of τ₁.

We then use the global mortality of all resolved cases (≈ 20% [22]) to determine the dependence between μ₁ and γ via μ₁/(μ₁ + γ) ≈ 1/5 (or γ/μ₁ ≈ 4). The constant recovery and post incubation death rates [37] are thus

$$\gamma \approx \frac{1}{13.7}/\text{day}=0.073/\text{day\hspace{1em}and\hspace{1em}}{\mu }_1\approx \gamma /4=0.018/\text{day}.$$ (5)

Using these numbers, the recovery and death rate functions γ(τ, t|τ₁) and μ(τ|τ₁) are plotted as functions of τ in Fig. 2(b). We show the evolution of M₁(t|τ₁) at different values of τ₁ in Fig. 2(c). The corresponding long-time limit M₁(∞|τ₁) is readily apparent in Fig. 2(d): for τ₁ ≥ τ_inc, M₁(∞|τ₁) = μ₁/(μ₁ + γ) ≈ 0.2, while M₁(∞|τ₁) < μ₁/(μ₁ +γ) when τ₁ < τ_inc. The smaller expected mortality associated with early identification of infection arises from the remaining incubation time during which the patient has a chance to recover without possibility of death. When conditioned on testing positive at or after the incubation period, the patient immediately experiences a positive death rate, increasing his M₁(∞|τ₁).

In order to infer M₁ (and also indirectly μ and γ) during an outbreak, a number of statistical issues must be considered. First, if the outbreak is ongoing, there may not be sufficient long-time cohort data. Second, τ₁ is unknown. Since testing typically occurs at the onset of symptoms, most positive patients will have been infected a few days earlier. The uncertainty in τ₁ can be represented by a probability density ρ(τ₁) for the individual. The expected mortality can then be constructed as an average over ρ(τ₁):

$${\overline{M}}_1(t)=\frac{{\overline{P}}_{\text{d}}(t)}{{\overline{P}}_{\text{d}}(t)+{\overline{P}}_{\text{r}}(t)},$$ (6)

where ${\overline{P}}_{\text{d}}(t)$ and ${\overline{P}}_{\text{r}}(t)$ are the τ₁-averaged probabilities death and cure probabilities.

Some properties of the distribution ρ(τ₁) can be inferred from the behavior of patients. Before symptoms arise, only very few patients will know they have been infected, seek medical care, and get their case confirmed (i.e., ρ(τ₁) ≈ 0 for τ₁ ≈ 0). The majority of patients will seek care when they have been infected for approximately τ_inc. We choose the gamma distribution

$$\rho \left({\tau }_1;n,\lambda \right)=\frac{{\lambda }^n}{\Gamma (n)}{\tau }_1^{n-1}{e}^{-\lambda {\tau }_1}$$ (7)

with shape parameter n = 8 and rate parameter λ = 1.25/day so that the mean n/λ is equal to τ_inc = 6.4. Note that, independent of the distribution ρ, the average ${\overline{M}}_1(t)$ is bounded from above by M₁(∞) = μ₁/(μ₁ + γ) for all times t.

Upon using the rates in Eqs. (4) and averaging over ρ(τ₁), we derived expressions for $\overline{P}(t)$, ${\overline{P}}_{\text{d}}(t)$, and ${\overline{P}}_{\text{r}}(t)$ which are explicitly given in the Appendix. Using the values in Eq. (5) we find an expected individual mortality ratio ${\overline{M}}_1(t)$ (which are subsequently plotted in Fig. 3) and its asymptotic value ${\overline{M}}_1(\infty )={\overline{P}}_{\text{d}}(\infty )\approx 0.19$ (slightly less than M₁(∞|τ₁) due to averaging over ρ(τ₁)). Of course, it is also possible to account for more complex time-dependent forms of γ and μ₁ [38], but we will primarily use Eqs. (4) in our subsequent analyses. We stress that M₁(t) tracks mortality of a cohort of individuals infected at about the same time, and does not include mortality of newly infected individuals. Thus, it can be trivially stratified according to different age groups and defined as the mortality M₁(t|μ) of each age subpopulation with death rate μ.

FIG. 3. Population-level mortality estimates.

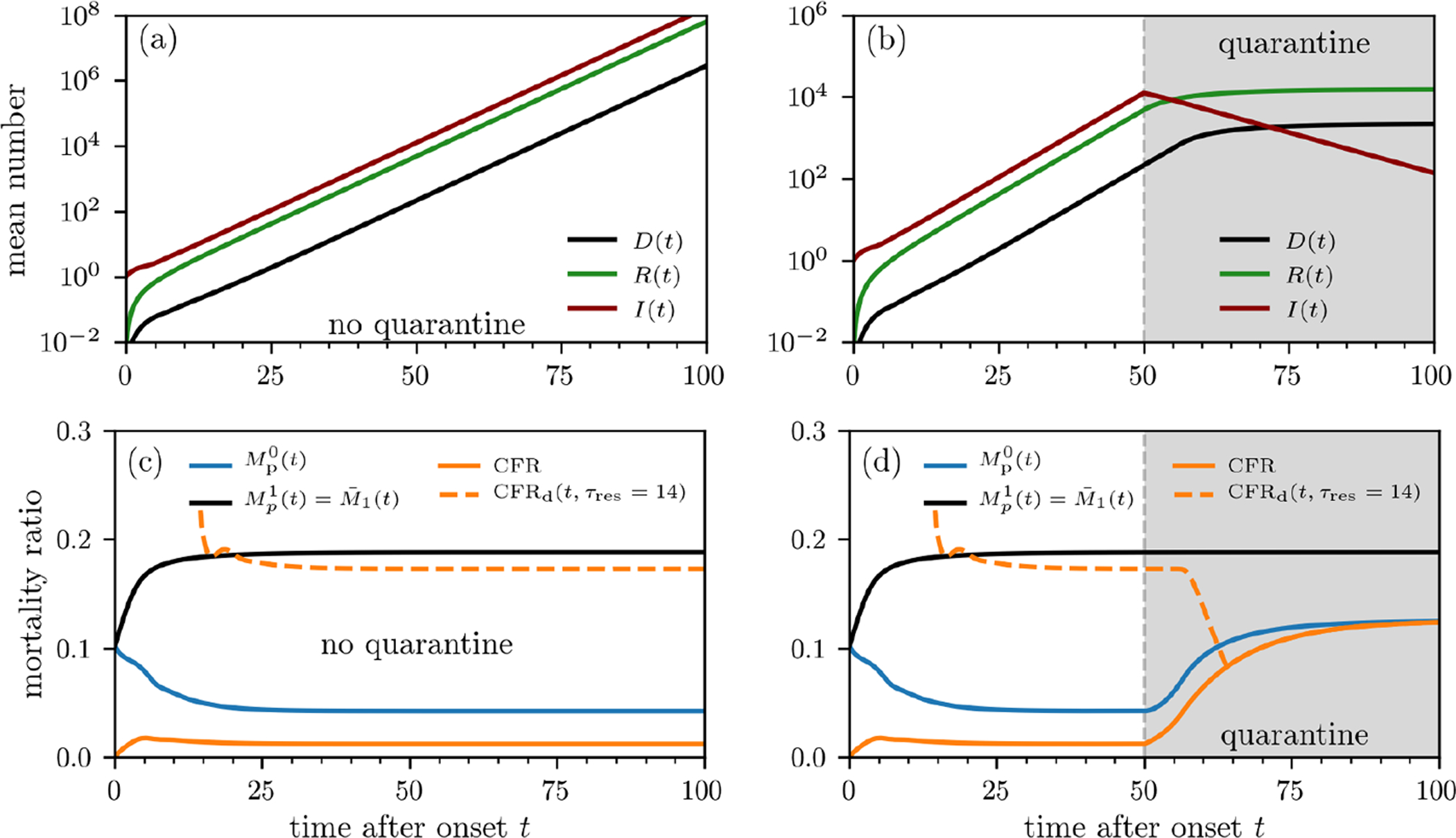
Outbreak evolution and mortality ratios without containment measures (a,c) and with quarantine (b,d). The curves are based on numerical solutions of Eqs. (10) using the initial condition I(τ, 0) = ρ(τ; 8, 1.25) (see Eq. (7)). The death and recovery rates are defined in Eqs. (4) and (5). We use an infection rate (Eq. (16)) defined by β₀S₀ = 4.64/day, which we estimated from the basic reproduction number of SARS-CoV-2 [36]. To model quarantine effects, we set β₀S₀ = 0 for t > 50 days. We show the mortality-ratio estimates $M_{\text{p}}^0(t)$ and $M_{\text{p}}^1(t)$ (see Eq. (14)) and CFR_d(t, τ_res) (see Eqs. (8), (12), and (14)). CFR_d(t, τ_res = 14 days) behaves very differently from CFR, initially decreasing for τ_res > 0 and significantly overestimating $M_{\text{p}}^0(t)$ but providing a reasonable estimate of ${\overline{M}}_1(t)=M_{\text{p}}^1(t)$ without quarantine. Note that under quarantine, CFR(∞), CFR_d(∞), and $M_{\text{p}}^0(\infty )$ approach the same value since they reflect the mortality ratio of the total cohort at the time of quarantine. On the other hand, ${\overline{M}}_1(t)=M_{\text{p}}^1(t)$ reflects the ratio of the initial cohort at the start of the outbreak and remains unchanged from the no-quarantine case.

In the next subsection, we define population-based estimates for mortality ratios, M_p(t), and explore how they can be computed using SIR-type models. By comparing ${\overline{M}}_1(t)$ to M_p(t), we gain insight into whether population-based metrics are good proxies for individual mortality ratios.

Relation to infection duration-dependent SIR model

While individual mortalities can be estimated by tracking many individuals from infection to recovery or death, often, the available data are not resolved at the individual level and only total populations are given. Typically, one only has the total number of confirmed cases accumulated up to time t, N_c(t), the number of deaths to date D(t), and the number of cured/recovered patients to date R(t) (see Fig. 1). Note that N_c(t) includes unresolved cases and that N_c(t) ≥ R(t) + D(t). Resolution (death or recovery) of all patients, N_c(∞) = R(∞) + D(∞), occurs only well after the epidemic completely passes.

A variant of the CFR commonly used in the literature is the delayed CFR [5, 6]

$${\text{CFR}}_{\text{d}}\left(t,{\tau }_{\text{res}}\right)=\frac{D(t)}{N_{\text{c}}\left(t-{\tau }_{\text{res}}\right)},$$ (8)

which uses an earlier and smaller case number to compensate for underestimation by the standard CFR

$$\text{CFR}(t)=\frac{D(t)}{N_{\text{c}}(t)}\equiv {\text{CFR}}_{\text{d}}\left(t,{\tau }_{\text{res}}=0\right).$$ (9)

The delay τ_res used is typically the time between the day symptoms first occurred and the day of death or recovery. To determine a realistic value of the delay time τ_res (which can be qualitatively interpreted as a resolution time), we use data on death/recovery periods of 36 tracked COVID-19 patients [39] and find that patients recover/die, on average, τ_res ≈ 2 weeks after first symptoms occurred. The delayed CFR_d(t, τ_res > 0) also underestimates the individual mortality in previous epidemic outbreaks of SARS [18, 32] and Ebola [40], but is highly sensitive to τ_res. If the delay between the time of infection and time of resolution were vanishingly small, we can set τ_res = 0 and find that the CFR_d and CFR are equivalent (see Eq. (9)).

Alternatively, a simple and interpretable population-level mortality is M_p(t) = D(t)/(R(t) + D(t)), the ratio of infected deaths to all resolved cases of confirmed infections. To provide a concrete model for D(t) and R(t), and hence M_p(t), we will use a variant of the standard infection duration-dependent susceptible-infected-recovered (SIR)-type model described by [41, 42]

$$\begin{array}{ccc}\hfill \frac{\text{d}S(t)}{\text{d}t}& \hfill =\hfill & -S(t){\int }_0^{\infty }\text{d}{\tau }^{\prime }\beta \left({\tau }^{\prime },t\right)I\left({\tau }^{\prime },t\right),\hfill \\ \hfill \frac{\partial I(\tau ,t)}{\partial t}+\frac{\partial I(\tau ,t)}{\partial \tau }& \hfill =\hfill & -(\mu (\tau ,t)+\gamma (\tau ,t))I(\tau ,t),\hfill \end{array}$$ (10)

and $\text{d}R(t)/\text{d}t={\int }_0^{\infty }\text{d}\tau \gamma (\tau ,t)I(\tau ,t)$, where S(t) is the number of susceptibles, I(τ, t) is density of individuals at time t who have been infected for time τ, and R(t) is the number of recovered individuals. The rate at which an individual infected for time τ at time t infects susceptibles is denoted by β(τ, t)S(t). For simplicity, we assume only community spread and neglect immigration of infected individuals, which could be straightforwardly included [42].

Note that the equation for I(τ, t) is identical to the equation for the survival probability described by Eq. (1). It is also equivalent to McKendrick age-structured models [43, 44]. In both the individual model (Eq. (1)) and population model (Eq. (10)), the death and recovery rates are insensitive to changes in age a over the ≲ 1 year epidemic timescale. In this limit, we consider only infection-duration dependence in the population dynamics. However, in contrast to the individual survival probability, new infections of susceptibles are described by the boundary condition (or renewal equation)

$$I(\tau =0,t)=S(t){\int }_0^{\infty }\text{d}{\tau }^{\prime }\beta \left({\tau }^{\prime },t\right)I\left({\tau }^{\prime },t\right),$$ (11)

which is similar to that used in age-structured models to represent birth [43]. The initial time t = 0 is arbitrary as long as the initial condition I(τ, 0) is defined. We use an initial condition corresponding to a single infected with the infection duration density given by Eq. (7): I(τ, 0) = ρ(τ; n = 8, λ = 1.25). Note that Eq. (11) assumes that all newly infected individuals are immediately identified; i.e., these newly infected individuals start with τ₁ = 0. After solving for the infected population density, we find the total number of deaths, recoveries, and total cases to date,

$$D^0(t)={\int }_0^t\text{d}{t}^{\prime }{\int }_0^{\infty }\text{d}\tau \mu \left(\tau ,t^{\prime }\right)I\left(\tau ,t^{\prime }\right),R^0(t)={\int }_0^t\text{d}{t}^{\prime }{\int }_0^{\infty }\text{d}\tau \gamma \left(\tau ,t^{\prime }\right)I\left(\tau ,t^{\prime }\right),N_0(t)=R^0(t)+D^0(t)+{\int }_0^{\infty }\text{d}\tau I(\tau ,t),$$ (12)

and use D⁰(t) and N₀(t) for D(t) and N_c(t) in definitions of CFR(t) and CFR_d(t, τ_res) (Eq. (8)). In the definitions of D⁰(t), R⁰(t), and N₀(t), we account for all possible death and recovery cases to date (see Appendix) and that newly infected individuals are immediately identified. We use these case numbers as approximations of the reported case numbers to study the evolution of mortality ratio estimates. Mortalities based on these numbers underestimate the actual individual mortality M₁ (see the previous “Intrinsic individual mortality rate” subsection) since they involve individuals that have been infected for different durations τ, particularly recently infected individuals who have not yet died.

An alternative way to compute populations is to exclude new infections and consider only an initial cohort. The corresponding populations in this case are defined as

$$D^1(t)={\int }_0^t\text{d}{t}^{\prime }{\int }_{t^{\prime }}^{\infty }\text{d}\tau \mu \left(\tau ,t^{\prime }\right)I\left(\tau ,t^{\prime }\right),R^1(t)={\int }_0^t \text{d}{t}^{\prime }{\int }_{t^{\prime }}^{\infty }\text{d}\tau \gamma \left(\tau ,t^{\prime }\right)I\left(\tau ,t^{\prime }\right).$$ (13)

Since D¹(t) and R¹(t) do not include infected individuals with τ < t, they exclude the effect of newly infected individuals and may yield more meaningful mortalities as they would be based on an initial cohort of individuals in the distant past. It is superfluous to define CFR using D¹(t)/N_c because the corresponding N_c of a cohort is a constant. The infections that occur after t = 0 contribute only to I(τ < t, t); thus, D¹(t) and R¹(t) do not depend on the transmission rate β, possible immigration of infected individuals, or the number of susceptibles S(t). Note that all the populations derived above implicitly average over ρ(τ₁; n, γ) for the first cohort of identified infected individuals (but not subsequent infections). Moreover, the population density I(τ ≥ t, t) follows the same equation as $\overline{P}\left(t|{\tau }_1\right)$ provided the same ρ(τ₁; n, λ) is used in their respective calculations.

The two different ways of partitioning populations (Eqs. (12) and (13)) lead to two different population-level mortality ratios

$$M_{\text{p}}^0(t)\equiv \frac{D^0(t)}{D^0(t)+R^0(t)}\text{\hspace{1em}and\hspace{1em}}{M}_{\text{p}}^1(t)\equiv \frac{D^1(t)}{D^1(t)+R^1(t)}.$$ (14)

Since the populations D⁰(t) and R⁰(t), and hence $M_{\text{p}}^0(t)$, depend on disease transmission through β(τ, t) and S(t), we expect $M_{\text{p}}^0(t)$ to carry a different interpretation from M₁(t) and $M_{\text{p}}^1(t)$.

In the special case in which μ and γ are constants, the time-integrated populations ${\int }_0^t\text{d}{t}^{\prime }{\int }_0^{\infty }\text{d}\tau I\left(\tau ,t^{\prime }\right)$ and ${\int }_0^t\text{d}{t}^{\prime }{\int }_{t^{\prime }}^{\infty }\text{d}\tau I\left(\tau ,t^{\prime }\right)$ factor out of $M_{\text{p}}^0(t)$ and $M_{\text{p}}^1(t)$, rendering them time-independent and

$$M_{\text{p}}^{0,1}=\frac{{\mu }_1}{{\mu }_1+\gamma }=M_1.$$ (15)

Thus, only in the special time-homogeneous case do both population-based mortality ratios become independent of the population (and transmission β) and coincide with the individual death probability.

To illustrate, in more general cases, the differences between M₁(t), $M_{\text{p}}^{0,1}(t)$ and CFR_d(t, τ_res), we use the simple death and recovery rate functions given by Eqs. (4) in solving Eqs. (1) and (10). For β(τ, t) in Eq. (11), we use a recently inferred infectiousness profile [45] which is described by a gamma distribution

$$\beta (\tau )={\beta }_0\rho (\tau ;n,\lambda )$$ (16)

with a peak that occurs shortly before the onset of symptoms at time τ_inc and coincidentally has n = 8 and λ = 1.25/day as in the testing time distribution ρ(τ₁) from a single infected (Eq. (7)). The constant dimensionless prefactor β₀ sets the amplitude of the transmission rate. For the chosen parameters n and λ, the gamma distribution ρ(τ; n, λ) reaches a maximum at τ ≈ 5.6 days, about one day before τ_inc = 6.4 days [45]. Assuming that the susceptible pool is not appreciably depleted, S(t) ≈ S₀ and Eq. (11) becomes $I(\tau =0,t)={\beta }_0{S}_0{\int }_0^{\infty }\text{d}{\tau }^{\prime }\rho (\tau ;n,\lambda )I\left({\tau }^{\prime },t\right)$. The amplitude β₀S₀ can be found by assuming a single infected for I(τ, t) in the renewal equation and using the estimated basic reproduction number. The basic reproduction number ${\mathcal{R}}_0$ is the average number of secondary infections that result from any single infected individual before he dies or recovers [37]. There are two terms to consider when determining ${\mathcal{R}}_0:(\text{i) }\beta (\tau )\text{d}\tau$ is the probability that an infection occurs in [τ, τ + dτ] and (ii) $\text{exp}\left[-{\int }_0^{\tau }\left(\mu \left({\tau }^{\prime }\right)+\gamma \right)\text{d}{\tau }^{\prime }\right]$ is the probability that a single infected individual has not died or recovered prior to time τ. If we integrate over the product of these quantities and multiply by the total susceptible population S₀ (which is equivalent to the boundary condition (11) applied to a single infected individual), we obtain the average number of susceptibles infected by one infected individual, i.e., ${\mathcal{R}}_0$. Thus, upon using Eq. (16), β₀S₀ can be found by solving

$$\begin{gathered} S_0{\int }_0^{\infty }\beta (\tau )\text{exp}\left[-{\int }_0^{\tau }\left(\mu \left({\tau }^{\prime }\right)+\gamma \right)\text{d}{\tau }^{\prime }\right]\text{d}\tau ={\beta }_0{S}_0{\int }_0^{\infty }\rho (\tau ;n,\lambda )\text{exp}\left[-{\int }_0^{\tau }\left(\mu \left({\tau }^{\prime }\right)+\gamma \right)\text{d}{\tau }^{\prime }\right]\text{d}\tau \\ ={\mathcal{R}}_0\approx \mathrm{2.91.} \end{gathered}$$ (17)

Using the death and recovery rate functions given by Eqs. 4 and 5, we find β₀S₀ ≈ 4.64/day. Using this value, we numerically solve Eqs. (10) and (11) (see Appendix for further details) and use these solutions to compute D^0,1(t), R^0,1(t), and N_0,1(t), which are then used in Eqs. (14) and CFR_d(t, τ_res).

RESULTS AND DISCUSSION

Comparison of mortalities

Here, we evaluate and compare the different mortality metrics and show how some of them qualitatively resemble the measured mortality estimates shown in Fig. 1. In Fig. 3(a), we show the unbounded subpopulations I⁰(t), D⁰(t), and R⁰(t) computed using Eqs. (10), (11), and (12) when the susceptible population is assumed constant. Fig. 3(b) shows the populations when a strict quarantine (S(t > t_q) = 0) is applied after t_q = 50 days. The mortalities plotted in Figs. 3(c) show that $M_{\text{p}}^1(t)$ approaches the individual mortality ratio ${\overline{M}}_1(\infty )\approx 0.19$ given in the “Intrinsic individual mortality rate” subsection above. This occurs because the model for P(τ, t) and I(τ, t) are equivalent and we assumed the same initial distribution ρ(τ; 8, 1.25) for both quantities. However, the population-level mortality ratios CFR_d(t, τ_res) and $M_{\text{p}}^0(t)$ also take into account recently infected individuals who may recover before symptoms. This difference yields different mortality ratios because newly infected individuals are implicitly assumed to be detected immediately and all have τ₁ = 0. Thus, the underlying infection-time distribution is not the same as that used to compute ${\overline{M}}_{\text{p}}^1(t)$ (see Appendix for further details). The mortality ratio $M_{\text{p}}^0(t)$ should not be used to quantify the individual mortality probability ${\overline{M}}_1(t)$ of individuals who tested positive, while the accuracy of CFR_d(t, τ_res) is sensitive to τ_res and quarantining. Moreover, due to evolution of the disease, D(t), R(t), and N (t) do not change with the same rates during an outbreak, the population-level mortality measures CFR_d(t, τ_res) and $M_{\text{p}}^0(t)$ reach their final steady state values only after sufficiently long times. Figs. 3(d) shows the corresponding mortalities with quarantining after t_q = 50 days.

The population-level ratios $M_{\text{p}}^0(t)$ and CFR(t) implicitly depend on new infections and the transmission rate β. Despite this confounding factor, $M_{\text{p}}^0(t)$ and CFR_d(t, τ_res) approach $e^{-\gamma {\tau }_{\text{inc}}}{\mu }_1/\left({\mu }_1+\gamma \right)$ as t → ∞, where $e^{-\gamma {\tau }_{\text{inc}}}$ is the probability that no recovery occurred during the incubation time τ_inc. Based on these results, we can establish the following connection between the different mortality ratios for initial infection times with distribution ρ(τ₁; n, λ) and mean $\overline{\tau }=n/\lambda$:

$${\text{CFR}}_{\text{d}}(\infty )=M_{\text{p}}^0(\infty )\approx e^{-\gamma \overline{\tau }}{M}_{\text{p}}^1(\infty )=e^{-\gamma \overline{\tau }}{\overline{M}}_1(\infty ).$$ (18)

According to Eq. (18), population-level mortality estimates (e.g., CFR and $M_{\text{p}}^0$), can be transformed, at least approximately, into individual mortality probabilities using the correction factor $e^{-\gamma \overline{\tau }}$ with $\overline{\tau }\approx {\tau }_{\text{inc}}$. Although population-level quarantining does not directly affect the individual mortality M₁(t|τ₁) or ${\overline{M}}_1(t)$, it can be easily incorporated into the SIR-type population dynamics equations through changes in β(τ, t)S(t). For example, we have set S(t > t_q) = 0 to represent implementation of a perfect quarantine after t_q = 50 days of the outbreak. After t_q = 50 days, no new infections occur and the estimates CFR(t) and $M_{\text{p}}^0(t)$ start to converge towards their common larger value (see Fig. 3(d)). In other words, without quarantining, the infected and recovered populations are continuously increasing, keeping CFR and $M_{\text{p}}^0(t)$ low. Since the number of deaths decreases after the implementation of quarantine measures, the delayed CFR_d(t, τ_res = 14 days) is first decreasing until t = t_q + τ_res = 64 days. For t > 64 days, the CFR_d(t, τ_res = 14 days) measures no new cases and is thus equal to the CFR.

The overall time-evolution of some of the mortalities in Fig. 3 qualitatively resembles the behavior of the mortality estimates in Fig. 1. As shown in Fig. 1, the CFR is increasing over time whereas $M_{\text{p}}^0$ provides a more stable mortality estimate for the SARS-CoV outbreak in Hong Kong (2003) and seems to follow a similar behavior in the current SARS-CoV-2 outbreak in Italy. In Fig. 4, we show additional examples of mortality-ratio estimates for China, South Korea, Spain, Germany, Switzerland, and the United Kingdom. After an initial transient, the CFR, in most cases, increases to a new asymptote after the epidemic passes. As in Fig. 1, we observe, consistent with their definitions, that the population-based mortality ratio $M_{\text{p}}^0(t)$ is larger than the corresponding CFR in all cases. $M_{\text{p}}^0(t)$ also appears to be a temporally more stable metric. Differences in the evolution of mortality ratios in different regions could result from changing practices in data collection or from explicitly time-inhomogeneous parameters μ(τ, t), γ(τ, t), and/or β(τ, t).

FIG. 4. Mortality estimates in different countries.

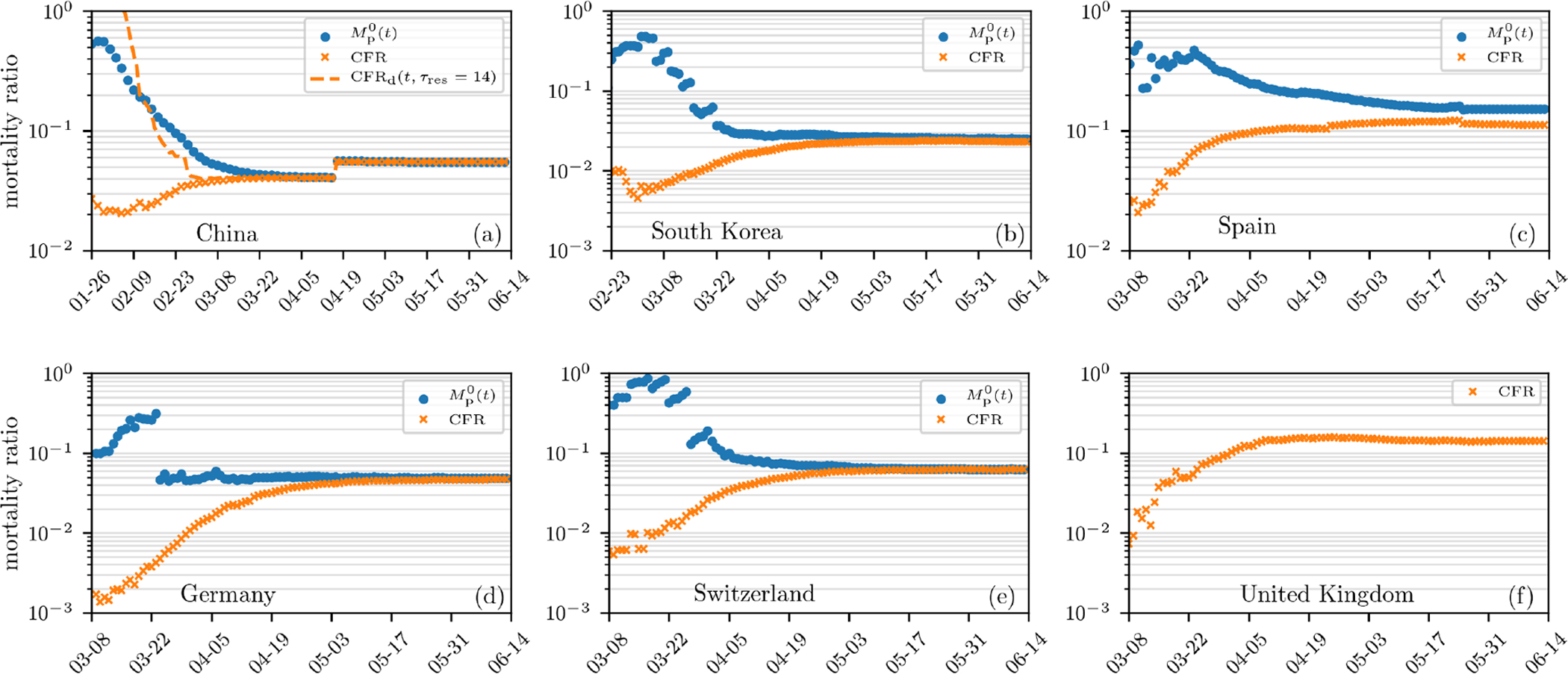
Estimates of mortality ratios (see Eqs. (8) and (14)) of SARS-CoV-2 infections in different countries. The data are derived from Ref. [21]. The case fatality rate, CFR, corresponds to the number of deaths to date divided by the total number of cases to date. The “delayed” mortality-ratio estimate CFR_d corresponds to the number of deaths to date divided by total number of cases at time t − τ_res is also shown for China. The population-based mortality ratios M_p(t) are also shown, except for the UK which has reported an inexplicable $M_{\text{p}}^0(t)~1$.

In addition to the mathematical differences between M₁(t), and $M_{\text{p}}^0(t)$, and CFR, estimating $M_{\text{p}}^0(t)$ and CFR(t) from aggregate populations implicitly incorporate a number of confounding factors that contribute to their variability. On April 25, 2020, the value of $M_{\text{p}}^0(t)$ in Sweden, Belgium, France, the US, and Italy are 2, 194/(2, 194 + 1, 005) ≈ 69%, 7, 094/(7, 094 + 10, 785) ≈ 40%, 22, 856/(22, 856 + 44, 903) ≈ 34%, 54, 941/(54, 941 + 118, 633) ≈ 32%, and 26, 384/(26, 384 + 63, 120) ≈ 29%, respectively. These $M_{\text{p}}^0(t)$ have slowly decreased (see Fig. 4) as patients resolve even if current conditions (e.g., treatment methods, age group proportion of infected individuals, etc.) have not changed. By comparison, on April 25, 2020, $M_{\text{p}}^0\approx 5\%$ and 6% in Germany and China, respectively. These differences result from delays and inaccuracies in reporting, varied guidelines for assigning cause of death, differing medical treatment strategies, and demographic heterogeneity among different countries.

Heterogeneous populations

Differences in demographics can easily be a source of variability in mortality rates measured across different regions. Older patients and those with underlying medical conditions typically have a higher death rate μ(τ, t) and/or lower recovery rate γ. Since we focus on mortality, the different subpopulations within the confirmed population matter only through their differences in μ and/or γ. For the ${\overline{M}}_1(t)$ and $M_{\text{p}}^1(t)$ metrics, no new infections are used in their determination. Thus, these metrics are associated with the mean death and recovery rates of the original group of infected individuals, i.e., the ratios ${\overline{M}}_1(t|\mu ,\gamma )$ and $M_{\text{p}}^1(t|\mu ,\gamma )$ refer to the mortality ratios of each subpopulation or individual described by μ and γ. The effective $M_{\text{p}}^1(t)$ over the entire confirmed population can be trivially constructed by population-averaging D¹(t|μ, γ) and R¹(t|μ, γ) over μ and γ before constructing $M_{\text{p}}^1(t)$.

For the other confirmed mortalities $M_{\text{p}}^0(t)$ and CFR(t), new infections are taken into account and subpopulations with different death and recovery rates can infect each other. Suppose there are two subpopulations “a” and “b” (e.g., young and old) with associated death and recovery rates μ_a,b and γ_a,b, respectively. The equations for each subpopulation are

$$\begin{gathered} \frac{\partial I_{\text{a}}(\tau ,t)}{\partial t}+\frac{\partial I_{\text{a}}(\tau ,t)}{\partial \tau }=-\left({\mu }_{\text{a}}(\tau ,t)+{\gamma }_{\text{a}}(\tau ,t)\right)I_{\text{a}}(\tau ,t), \\ \frac{\partial I_{\text{b}}(\tau ,t)}{\partial t}+\frac{\partial I_{\text{b}}(\tau ,t)}{\partial \tau }=-\left({\mu }_{\text{b}}(\tau ,t)+{\gamma }_{\text{b}}(\tau ,t)\right)I_{\text{b}}(\tau ,t), \end{gathered}$$ (19)

indicating that each subpopulation follows their own dynamics for τ > 0. However, the subpopulations interact with each other through the coupled boundary conditions

$$\begin{gathered} I_{\text{a}}(0,t)=S(t){\int }_0^{\infty }\text{d}{\tau }^{\prime }\left[{\beta }_{\text{aa}}\left({\tau }^{\prime },t\right)I_{\text{a}}\left({\tau }^{\prime },t\right)+{\beta }_{\text{ab}}\left({\tau }^{\prime },t\right)I_{\text{b}}\left({\tau }^{\prime },t\right)\right] \\ {I}_{\text{b}}(0,t)=S(t){\int }_0^{\infty }\text{d}{\tau }^{\prime }\left[{\beta }_{\text{ab}}\left({\tau }^{\prime },t\right)I_{\text{a}}\left({\tau }^{\prime },t\right)+{\beta }_{\text{bb}}\left({\tau }^{\prime },t\right)I_{\text{b}}\left({\tau }^{\prime },t\right)\right] \end{gathered}$$ (20)

that describe cross-infections between the “a” and “b” subpopulations. Thus, the infection levels in each subpopulation also depend on the transmission rates β_aa, β_ab, and β_bb. To compute the overall confirmed mortality $M_{\text{p}}^0(t)$ or CFR(t) of the entire population, we must solve Eqs. (19) and (20) for I_a and I_b, and hence D_a(t), D_b(t), and D(t) = D_a(t) + D_b(t).

In Fig. 5, we show the evolution of $M_{\text{p}}^0(t)$ for two age groups representing young and old individuals with different mortality and infection rates. The behavior of $M_{\text{p}}^0(t)$ for the entire population is qualitatively similar to, but falls in between those of each age group (see Fig. 3). Whether the overall mortality is closer to that of the young or old population depends on the relative populations of young and old infecteds, their death and recovery rates, and their cross transmission rates β_ab. For age-stratified case data, the subpopulation model outlined above, or other approaches such as scaling approximations [46] may be useful for capturing age-dependent variations in $M_{\text{p}}^0(t)$.

FIG. 5. Population-level mortality estimate for two age groups.

The mortality ratio $M_{\text{p}}^0(t)$ without containment measures (a) and under quarantining (b). The curves are based on numerical solutions of Eqs. (19) and (20) assuming constant S(t) ≈ S₀ and using the initial condition I_a(τ, 0) = I_b(τ, 0) = ρ(τ; 8, 1.25)/2 (see Eq. (7)), where the subscripts “a” and “b” denote the young and old age group, respectively. The death and recovery rates for the younger age group are defined in Eqs. (4) and (5). For the older age group, we set μ_b = 4μ_a and γ_b = γ_a. We use an infection rate (Eq. (16)) defined by β_aaS₀ = 4.64/day, which we estimated from the basic reproduction number of SARS-CoV-2 [36]. The remaining infection rates are defined via ${\beta }_{\text{aa}}=\sqrt{2}{\beta }_{\text{ba}}=\sqrt{2}{\beta }_{\text{ab}}=2{\beta }_{\text{bb}}$. To model quarantine effects, we set β₀S₀ = 0 for t > 50 days in (b).

Undertesting and unconfirmed cases

Another important confounding factor is the large number of untested and often asymptomatic infected individuals. The mortality rate often quoted in the literature ranges from < 1 – 3%, which is much smaller than the resolved mortality ratios we have used for illustration. Our estimates of $M_{\text{p}}^{0,1}(t)$ and CFR_d(t, τ_res) using I(τ, t) actually describe the mortality of the population conditioned on being tested positive. Since we used Eqs. (10) to compute infected populations, we implicitly assumed that all infected individuals have been tested/confirmed. However, the total infected population is comprised of tested and untested individuals, which may or may not carry different death and recovery rates. Typically, only a small fraction f of the total number of infected individuals might be tested and confirmed positive.

Our confirmed mortalities (derived from only the positively tested population) can be extended to the entire population, tested or untested. The “true” ${\mathcal{M}}_{\text{p}}^0$ and the fatality ratio conditioned on having been infected (the IFR) would typically be much smaller than the $M_{\text{p}}^0$ and CFR calculated using only confirmed cases. How the testing fraction f < 1 might qualitatively affect the “true” underlying mortality measures (the mortality conditioned on simply being infected) is illustrated in Fig. 6.

FIG. 6. Fractional testing.

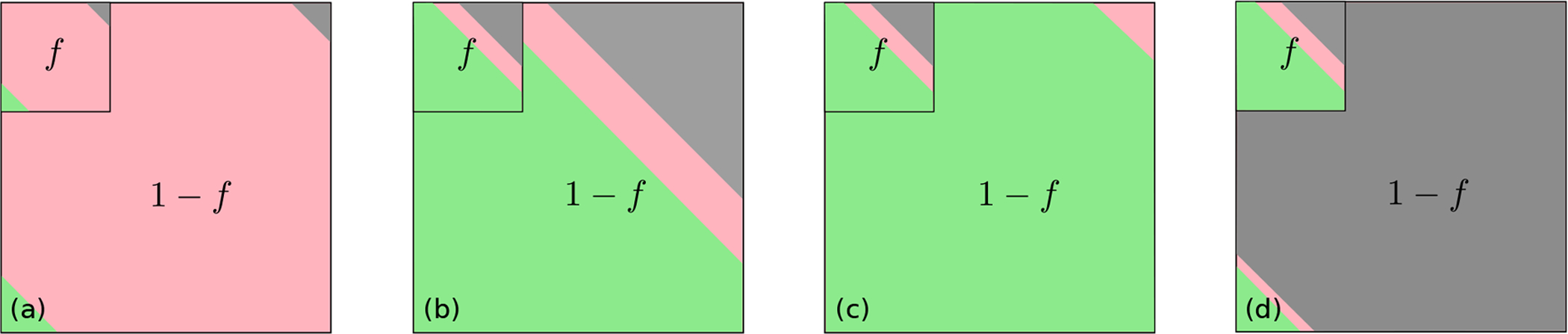
An example of fractional testing in which a fixed fraction f of the real total infected population is assumed to be tested. The remaining 1 − f proportion of infected individuals are untested. Equivalently, if the total tested fraction has unit population, then the fraction of the population that remains untested is 1/f − 1. (a) At short times after an outbreak, most of the infected patients, tested and untested, have not yet resolved (red). Only a small number have died (gray) or have recovered (green). (b) At later times, if the untested population dies at the same rate as the tested population, M_p(t) and CFR remain accurate estimates for the entire infected population. (c) If the untested population is, say, asymptomatic and rarely dies, the true mortality ${\mathcal{M}}_{\text{p}}^{0,1}(\infty )\approx f{M}_{\text{p}}^{0,1}(\infty )$ can be significantly overestimated by the tested mortality $M_{\text{p}}^{0,1}(t)$. (d) Finally, in a scenario in which untested infected individuals die at a higher rate than tested ones, $M_{\text{p}}^{0,1}(t)$ and CFR based on the tested fraction underestimate the true mortality ${\mathcal{M}}_{\text{p}}^{0,1}$.

Estimates for SARS-CoV-2 show that f is small (e.g., f ≈ 14% in China before January 23, 2020) [47]. At early times (Fig. 6(a)) most patients, tested or untested, have not yet resolved. A reported/tested fraction f < 1 would not directly affect or alter the CFRs or mortality ratios if the unreported/untested population dies and recovers in the same proportion as those tested, as depicted in Fig. 6(b). That is, undertesting would still provide a good estimate of the true mortality if the entire population were homogeneous in death and recovery rates. However, if the untested (presumably mildly or asymptomatic infected) are less likely to die than the tested infected individuals, undertesting would give rise to $M_{\text{p}}^0(t)$ and CFR(t) that overestimate the true mortality ${\mathcal{M}}_{\text{p}}^0(t)$ and the infection fatality ratio (IFR). If untested infected individuals do not die at all, as depicted in Fig. 6(c), the true long-time mortality ${\mathcal{M}}_{\text{p}}^{0,1}(\infty )\approx f{M}_{\text{p}}^{0,1}(\infty )$. In the unlikely scenario in which untested individuals do not receive medical care and hence die at a faster rate (Fig. 6(d)), ${\mathcal{M}}_{\text{p}}^{0,1}(\infty )$ and CFR based on the tested fraction would underestimate the true long-time mortality ${\mathcal{M}}_{\text{p}}^{0,1}(\infty )$ and IFR, respectively.

To quantitatively estimate the underlying mortality of the population conditioned simply on being infected, we have to quantify the number of confirmed and untested infected individuals, I_c(τ, t) and I_u(τ, t), which can be further divided into subpopulations with intrinsically different transmission, death, and recovery rates. The act of confirmation itself may change behavior and/or treatment, further changing transmission, death, and recovery parameters.

By constructing the accumulated deaths and recoveries associated with I_c(τ, t) and I_u(τ, t), $D_{\text{c},\text{u}}^{0,1}(t)$ and $R_{\text{c},\text{u}}^{0,1}(t)$, respectively, we can define true, whole population mortality ratios as listed in Table II. For example,

$$D_{\text{c},\text{u}}^0(t)={\int }_0^t \text{d}{t}^{\prime }{\int }_0^{\infty }\text{d}\tau {\mu }_{\text{c},\text{u}}\left(\tau ,t^{\prime }\right)I_{\text{c},\text{u}}\left(\tau ,t^{\prime }\right),R_{\text{c},\text{u}}^0(t)={\int }_0^t \text{d}{t}^{\prime }{\int }_0^{\infty }\text{d}\tau {\gamma }_{\text{c},\text{u}}\left(\tau ,t^{\prime }\right)I_{\text{c},\text{u}}\left(\tau ,t^{\prime }\right),$$ (21)

where μ_c,u and γ_c,u are the death and recovery rates associated with infected individuals who are confirmed and untested, respectively. Analogous expressions arise for $D_{\text{c},\text{u}}^1(t)$ and $R_{\text{c},\text{u}}^1(t)$. If the confirmed and untested populations are further subdivided, the μ_c,uI_c,u and γ_c,uI_c,u integrands would be replaced by a Hamdamard (i.e., element-wise) product of two vectors representing subpopulations and their corresponding rates. The populations I_c,u themselves can be found from a specific disease transmission model that also includes a testing process that converts I_u to I_c.

TABLE II. Definitions of the main metrics.

The superscript “0” and “1” denote quantities that are based on the total population (including new infections) and a cohort (excluding new infections), respectively. Quantities with subscript “c” and “u” denote confirmed and untested pools (for example, $N_{\text{u}}^0(t)$ is the total number of untested individuals at time t) that must be inferred using other measurements such as random testing. We have suppressed the time dependences for notational simplicity.

Subpopulation╲Metric	Fatality Ratios	Resolved Mortality w/inf	Resolved Mortality w/o inf	Individual Risk
confirmed (tested)	$\text{CFR}=\frac{D_{\text{c}}^0}{N_{\text{c}}^0}$	$M_{\text{p}}^0=\frac{D_{\text{c}}^0}{D_{\text{c}}^0+R_{\text{c}}^0}$	$M_{\text{p}}^1=\frac{D_{\text{c}}^1}{D_{\text{c}}^1+R_{\text{c}}^1}$	${\overline{M}}_1=\frac{{\overline{P}}_{\text{d}}}{{\overline{P}}_{\text{d}}+{\overline{P}}_{\text{r}}}$
total (tested+untested)	$\text{IFR}=\frac{D_{\text{c}}^0+D_{\text{u}}^0}{N_{\text{c}}^0+N_{\text{u}}^0}$	${\mathcal{M}}_{\text{p}}^0=\frac{D_{\text{c}}^0+D_{\text{u}}^0}{D_{\text{c}}^0+D_{\text{u}}^0+R_{\text{c}}^0+R_{\text{u}}^0}$	${\mathcal{M}}_{\text{p}}^1=\frac{D_{\text{c}}^1+D_{\text{u}}^1}{D_{\text{c}}^1+D_{\text{u}}^1+R_{\text{c}}^1+R_{\text{u}}^1}$	not defined

SUMMARY AND CONCLUSIONS

The CFR has been predominantly used but appears to evolve in qualitatively similar ways as epidemics evolve. Although CFR_d(t, τ_res) is based on a delay reflecting the timescales for recovery, in general, there is no clear mechanistic interpretation for using the CFR or IFR as mortality ratios.

Here, we stress that more mechanistically meaningful and interpretable metrics can be readily defined and just as easily estimated from population data as CFRs are. Our proposed mortality ratios for viral epidemics are defined in terms of (i) individual survival probabilities and (ii) population ratios using numbers of deaths and recovered individuals. Both of these measures are based on the within-host evolution of the disease, and in the case of $M_{\text{p}}^{0,1}(t)$, the population-level transmission dynamics. On a single patient level, ${\overline{M}}_1(t)$ is the metric of interest. However, to estimate this, one needs accurate cohort data, for which few exist for coronavirus. Nonetheless, cumulative population-based mortalities can provide insight.

Among the metrics we describe, $M_{\text{p}}^1(t)$ is structurally closest to the individual mortality ${\overline{M}}_1(t)$ in that both are independent of disease transmission since new infections are not counted. Both of these mortality ratios converge after an incubation time τ_inc to a value smaller than or equal to μ₁/(μ₁ + γ) and are best interpreted as approximately the mortality probability conditioned on being tested positive. The most accurate estimates of ${\overline{M}}_1$ can be obtained if we keep track of the fate of cohorts who were confirmed within a small time window in the past. By following only these individuals, one can track how many of them die as a function of time. As more cases arise, one should stratify them according to their estimated times since infection to obtain better statistics for M₁(∞). With the further spread of SARS-CoV-2 in different countries, data on more individual cases of death and recovery can also be more easily stratified according to other central factors in COVID-19 mortality: age, sex, health condition. Population heterogeneity and uncertainty in intrinsic disease parameters such as the incubation period and the time τ₁ a patient had been infected before confirmation can affect the mortality measures.

Besides demographic heterogeneity and the highly variable estimates of COVID-19 deaths due to different clinical protocols for assigning cause of death, undertesting also confounds accurate estimation of the true underlying mortality. Infected individuals in the population at large who are untested comprise an unknown population I_u which contributes to deaths and recovery, and need to be factored into the “true” mortalities ${\mathcal{M}}_{\text{p}}^{0,1}$ or the IFR.

These untested/unconfirmed populations can, in principle, be computed from a multicompartment mathematical model for disease transmission and testing. The relevant expressions for ${\mathcal{M}}_{\text{p}}^{0,1}$ are listed in Table II. Even though M_p(t) typically overestimates the true mortality, tracking ${\overline{M}}_1(t)$ or $M_{\text{p}}^1(t)$ of an initially confirmed cohort can still provide a reasonable estimate of the mortality ratio, especially if untested infected individuals die at the same rate as confirmed individuals.

APPENDIX

Numerical scheme

To numerically solve Eqs. (10) and (11), we use a uniform discretization τ_k = kΔτ, k = 0, 1, …, K. A backward difference operator [I(τ_k, t) − I(τ_k−1, t)] /(Δτ) is used to approximate ∂_τ I(τ, t) and a predictor-corrector Euler scheme is used to advance time [48]. Setting the cut-offs I(−Δτ, t) ≡ 0 and I(KΔτ, t) ≡ 0, the resulting discretized equations for the full SIR model are

$$\begin{gathered} S(t+\Delta t)=S(t)-\Delta tS(t)\sum _{k=0}^K\beta \left({\tau }_k,t\right)I\left({\tau }_k,t\right)\Delta \tau , \\ \tilde{I}\left({\tau }_k,t\right)=I\left({\tau }_k,t\right)-\Delta t\frac{I\left({\tau }_k,t\right)-I\left({\tau }_{k-1},t\right)}{\Delta \tau }-\Delta t\left(\gamma \left({\tau }_k,t\right)+\mu \left({\tau }_k,t\right)\right)I\left({\tau }_k,t\right), \\ I\left({\tau }_k,t+\Delta t\right)=I\left({\tau }_k,t\right)-\frac{\Delta t}{2}\left[\frac{I\left({\tau }_k,t\right)-I\left({\tau }_{k-1},t\right)}{\Delta \tau }+\left(\gamma \left({\tau }_k,t\right)+\mu \left({\tau }_k,t\right)\right)I\left({\tau }_k,t\right)+\frac{\tilde{I}\left({\tau }_k,t\right)-\tilde{I}\left({\tau }_{k-1},t\right)}{\Delta \tau }+\left(\gamma \left({\tau }_k,t+\Delta t\right)+\mu \left({\tau }_k,t+\Delta t\right)\right)\tilde{I}\left({\tau }_k,t\right)\right]+{\delta }_{k,0}\frac{\Delta t}{\Delta \tau }S(t)\sum _{j=0}^K\beta \left({\tau }_j,t\right)I\left({\tau }_j,t\right)\Delta \tau , \end{gathered}$$ (A1)

where $\tilde{I}$ is the initial predicted guess, and the last term proportional to δ_k,0 encodes the boundary condition Eq. (11). Note that we use $\sum _{k=0}^K\beta \left({\tau }_k,t\right)I\left({\tau }_k,t\right)\Delta \tau$ to indicate the numerical evaluation of ${\int }_0^{\infty }\text{d}{\tau }^{\prime }\beta \left({\tau }^{\prime },t\right)I\left({\tau }^{\prime },t\right)$. Quadrature methods such as Simpson’s rule and the trapezoidal rule can be used to approximate the integral more efficiently.

The total number of dead, recovered, and infected individuals at time t are found by

$$D^0(m\Delta t)=\frac{1}{2}\sum _{j=0}^m\sum _{k=0}^{K}c(k\Delta \tau ,j\Delta t)[I(k\Delta \tau ,j\Delta t)+\tilde{I}(k\Delta \tau ,j\Delta t)]\Delta \tau \Delta t,$$

$$R^0(t)=\frac{1}{2}\sum _{j=0}^m\sum _{k=0}^K\mu (k\Delta \tau ,j\Delta t)[I(j\Delta \tau ,j\Delta t)+\tilde{I}(k\Delta \tau ,j\Delta t)]\Delta \tau \Delta t,$$

$$I(m\Delta t)=\sum _{k=0}^{K}I(k\Delta \tau ,m\Delta t)\Delta \tau ,$$

with analogous expressions for D¹(mΔt) and R¹(mΔt). To obtain a stable integration scheme, the time steps Δt and Δτ have to satisfy Δt/(2Δτ) < 1. In all of our numerical computations, we thus set Δt = 0.002, Δτ = 0.02, and K = 10⁴. In the next section, we show additional plots of the magnitude of I(τ, t) in the t − τ plane.

Solutions for τ₁-averaged probabilities

Using the method of characteristics, we find the formal solution to Eq. (1):

$$P\left(\tau ,t|{\tau }_1\right)=\delta \left(\tau -t-{\tau }_1\right)e^{-{\int }_0^t\left(\mu \left(\tau -t+s,s|{\tau }_1\right)+\gamma \left(\tau -t+s,s|{\tau }_1\right)\right)\text{d}s},$$ (A2)

which can be used to construct the death and cure probabilities

$$\begin{gathered} P_{\text{d}}\left(t|{\tau }_1\right)={\int }_0^t \text{d}{t}^{\prime }\mu \left({\tau }_1+t^{\prime },t^{\prime }\right)e^{-{\int }_0^{t^{\prime }}\left(\mu \left({\tau }_1+s,s\right)+\gamma \left({\tau }_1+s,s\right)\right)\text{d}s} \\ {P}_{\text{r}}\left(t|{\tau }_1\right)={\int }_0^t \text{d}{t}^{\prime }\gamma \left({\tau }_1+t^{\prime },t^{\prime }\right)e^{-{\int }_0^{t^{\prime }}\left(\mu \left({\tau }_1+s,s\right)+\gamma \left({\tau }_1+s,s\right)\right)\text{d}s}. \end{gathered}$$ (A3)

If we now invoke the functional forms of μ and γ given in Eq. (4), we find explicitly

$$P_{\text{d}}\left(\tau ,t|{\tau }_1\right)=\{\begin{array}{ll}\frac{{\mu }_1}{{\mu }_1+\gamma }\left(1-e^{-\left({\mu }_1+\gamma \right)t}\right)\hfill & \tau >t+{\tau }_{\text{inc}}\hfill \\ 0\hfill & {\tau }_{\text{inc}}\ge \tau >{\tau }_1\hfill \\ \frac{{\mu }_1{e}^{-\gamma \left({\tau }_{\text{inc}}-{\tau }_1\right)}}{{\mu }_1+\gamma }\left(1-e^{-\left({\mu }_1+\gamma \right)\left(\tau -{\tau }_{\text{inc}}\right)}\right)\hfill & \tau >{\tau }_{\text{inc}}\ge {\tau }_1\hfill \end{array}$$ (A4)

and

$$P_{\text{r}}\left(\tau ,t|{\tau }_1\right)=\{\begin{array}{ll}\frac{\gamma }{{\mu }_1+\gamma }\left(1-e^{-\left({\mu }_1+\gamma \right)t}\right)\hfill & \tau >t+{\tau }_{\text{inc}}\hfill \\ 1-e^{-\gamma t}\hfill & {\tau }_{\text{inc}}\ge \tau >{\tau }_1\hfill \\ 1-e^{-\gamma \left({\tau }_{\text{inc}}-{\tau }_1\right)}+\frac{\gamma e^{-\gamma \left({\tau }_{\text{inc}}-{\tau }_1\right)}}{{\mu }_1+\gamma }\left(1-e^{-\left({\mu }_1+\gamma \right)\left(\tau -{\tau }_{\text{inc}}\right)}\right)\hfill & \tau >{\tau }_{\text{inc}}\ge {\tau }_1.\hfill \end{array}$$ (A5)

FIG. A1. Phase plot for P (τ > t, t) and I(τ > t, t).

The regions delineate the different forms for the solution (Eq. (A6)). Here, we have included an incubation time τ_inc before which no death occurs. The solution for $\overline{P}(\tau ,t)$ or I(τ, t) in the τ < t region must be self-consistently solved using the boundary condition Eq. (11). At any fixed time, the integral of I(τ, t) over t < τ ≤ ∞ captures only the initial population, excludes newly infected individuals, and is used to compute D¹(t), R¹(t), and $M_{\text{p}}^1(t)$. To compute D⁰(t), R⁰(t), and $M_{\text{p}}^0(t)$, we integrate across all infected individuals (including the integral over t > τ ≥ 0 shown in magenta).

Finally, we can also find the τ₁-averaged probabilities for τ ≥ t by weighting over ρ(τ₁; n, λ). For example,

$$\overline{P}(\tau ,t)=\{\begin{array}{ll}\rho (\tau -t;n,\lambda )e^{-\left({\mu }_1+\gamma \right)t}\hfill & \tau \ge t+{\tau }_{\text{inc}}\hfill \\ \rho (\tau -t;n,\lambda )e^{-\gamma t}\hfill & {\tau }_{\text{inc}}\ge \tau >t\hfill \\ \rho (\tau -t;n,\lambda )e^{-\gamma t}{e}^{-{\mu }_1\left(\tau -{\tau }_{\text{inc}}\right)}\hfill & t+{\tau }_{\text{inc}}\ge \tau >{\tau }_{\text{inc}}\hfill \end{array}.$$ (A6)

These solutions hold for the different regions shown in the phase plot of Fig. A1 and are equivalent to those for I(τ > t, t). Corresponding expressions for ${\overline{P}}_{\text{d}}(t)$ and ${\overline{P}}_{\text{r}}(t)$ can be found and used to construct $M_{\text{p}}^1(t)$. Fig. A2(a) shows the magnitude of I(τ, t) in the t − τ plane when we use Eq. (16), set S(t) = S₀ constant (so that the first equation in Eq. (A1) does not apply) and assign β₀S₀ = 4.64/day. In this case, the epidemic continues to grow in time, but the mortality rates $M_{\text{p}}^{0,1}(t)$ nonetheless converge as t → ∞. In Fig. A2(b), we set β₀S₀ = 0 for t > t_q to model strict quarantining after t_q = 50 days. We observe no new infection after the onset of strict quarantine measures. In both cases (quarantine and no quarantine), we use ρ(τ; n = 8, λ = 1.25) (see Eq. (7) in the main text) to describe the initial distribution of infection times τ. As time progresses, more of the distribution of τ moves towards smaller values until quarantine measures take effect (see Fig. A2(c) and (d)).

FIG. A2. Density plots of I(τ, t) in the t − τ plane.

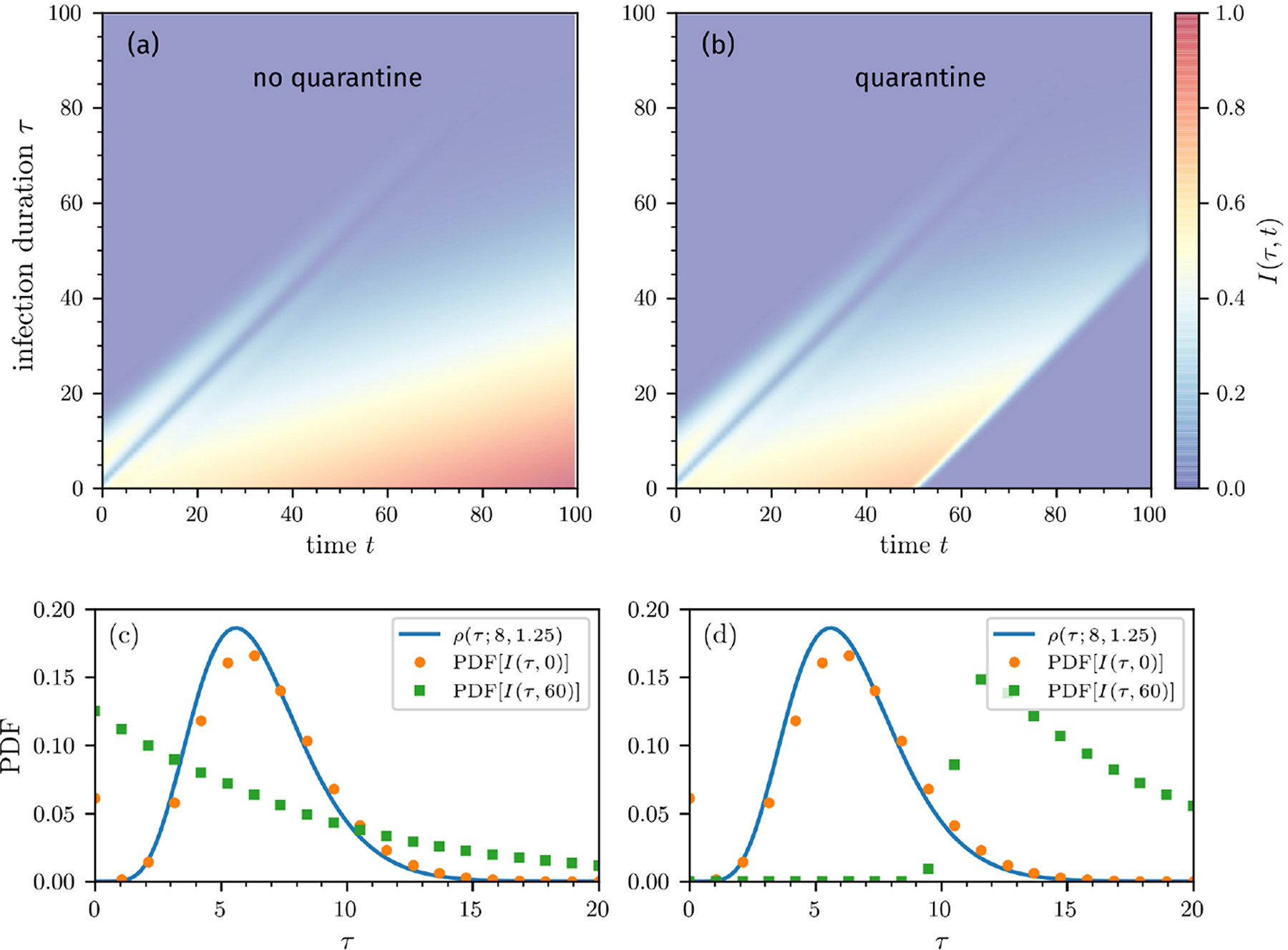
Numerical solution of the equation for I(τ, t) in Eqs. (10) under the assumption of a fixed susceptible size and β₀S₀ = 4.64/day. (a) The density without quarantine monotonically grows with time t in the region τ < t as an unlimited number of susceptibles continually produces infections. (b) With quarantining after t_q = 50 days, we set β₀S₀ = 0 for t > t_q, which shuts off new infections. Both plots were generated using the same initial density ρ(τ₁) defined in Eq. (7). In both cases, the density I(τ > t) is identical to P(τ > t) if the same ρ(τ₁) is used and is independent of disease transmission, susceptible dynamics, etc. (c-d) Probability-density functions (PDFs) of the number of infected individuals I(τ, t) for t = 0, 60 days (b) without and (c) with quarantine. The blue solid line corresponds to the initial distribution ρ(τ; n = 8, λ = 1.25) (see Eq. (7)).