Back to school or … back to lockdown? The effects of opening schools on the diffusion of COVID-19 in Italian regions

Abstract

The opening of schools that coincided with the beginning of fall 2020 and the arrival of the second wave of COVID-19 in continental Europe has fostered significant debate in several countries. Some contributions have suggested that youngsters play a minor role in the spread of the virus, given the specific characteristics of this infection; other scholars have raised concerns about the necessary movement that involves keeping schools open, and the consequent potential spread of the virus. In this study, we focus on the Italian case, an interesting setting in which to test the impact of opening schools on the spread of COVID-19, because of the different dates at which schools have opened in the various Italian provinces, and because of the different rates at which the virus has spread across Italy. Our results suggest that open schools have a positive impact on COVID-19 cases, whose spread occurs between 10 and 14 days after opening. While closing schools or using distance learning have other social and economic consequences, making it necessary for policymakers to adopt a holistic evaluation, it should be taken into account that open schools have an impact on the spread of the pandemic.

1. Introduction

In December 2019, starting from Hubei province in China, a coronavirus infectious disease (COVID-19) spread rapidly across the world. On March 11, 2020, the World Health Organization (WHO) declared “[its] assessment that COVID-19 can be characterized as a pandemic”.1 In order to fight the spread of the virus, national governments began to adopt different containment measures. In particular, as has been pointed out by several scholars, along with health policies aimed at strengthening the capacity of the hospital system, so-called non-pharmaceutical interventions were introduced. Their objective was to reduce the probability of people contracting the virus, and they included social distancing [1], school closures [[2], [3]], and lockdown policies [[4], [5], [6]].

During the first wave of the pandemic, Italy was an interesting case study. Indeed, between February and March 2020, Italy was the Western country that was worst hit by COVID-19, and the second most badly affected country in the world. The diffusion of the virus was especially severe in Northern Italy, and in particular in the regions of Lombardy, Emilia-Romagna, and Veneto. During the first days of the diffusion of the virus, different regions implemented different strategies, mainly characterized by a mixture of school closures, enforcement of social distancing behaviour, and some lockdowns, at first localized in ten municipalities in Lodi province (in the region of Lombardy), and one municipality in Padua province (in the region of Veneto) [7]. On March 11, 2020, the central government decided to extend the lockdown to the entire country, a measure that was put into action the very next day.

While in some countries the levels of transmission and diffusion of the virus have never been reduced, in Italy and other countries, thanks to the combination of pharmaceutical and non-pharmaceutical interventions (NPIs), governments have been able to control the pandemic[6], significantly reducing its diffusion. Nevertheless, in these countries too, after a number of months characterized by a general reduction in cases, we again observed an upward trend in the infection rate, after a period in which the trend had been stable. These are the so-called second and third waves. It is worth noting that in these subsequent waves national governments have seemed less willing to impose full lockdowns, probably due to the negative effect they have had on national economies, which are often still trying to recover from the previous complete lockdowns. It may also be due to the fact that most of these countries, thanks to increased expenditure in their health budgets during the first wave, have now increased the number of beds in intensive care units, and thus feel more prepared to cope with a new, temporary increase in COVID-19 cases. Of the NPIs, school closures are among the most controversial measures due to the social impact for pupils and their family.

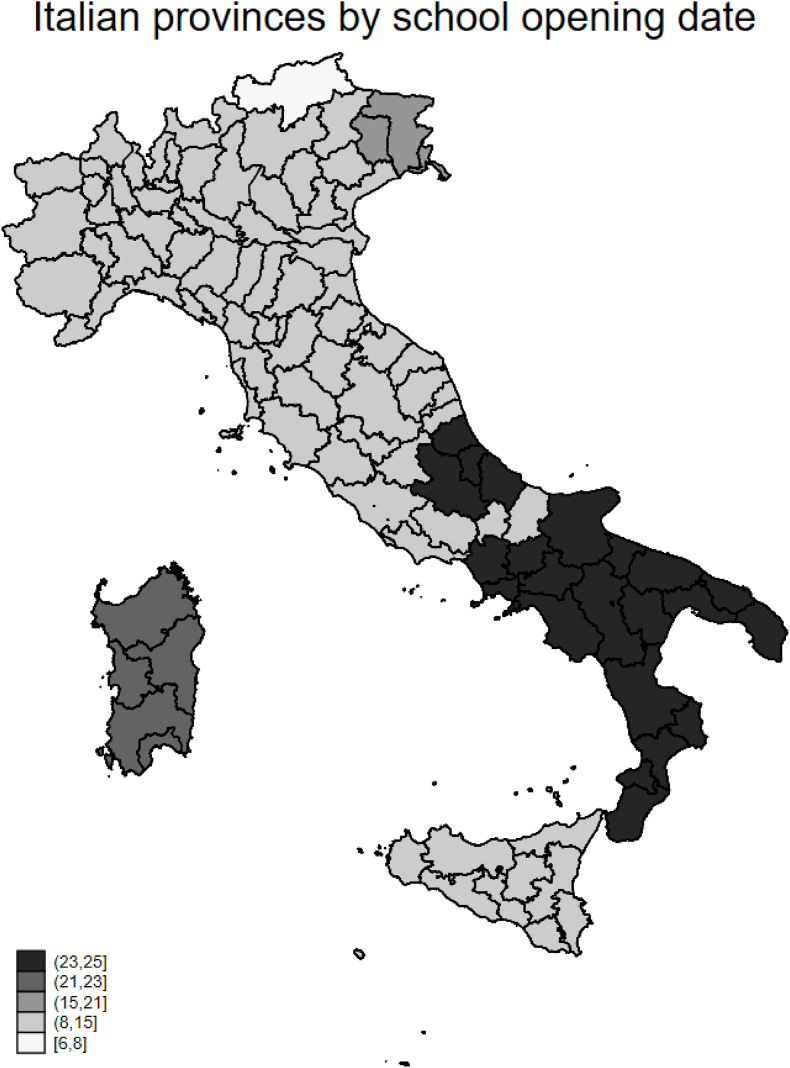
In the Italian case, this debate has generated political conflicts between the central government and some of the regional governments. In terms of school organization, while the central government is responsible for determining the number of days in the school year, regional governments are responsible for determining the calendars for schools within their borders. For this reason, some regions may decide to bring forward or delay the opening date suggested by the central government or decide to close the schools for certain periods. This is exactly what occurred in September 2020 in the Italian regions for the beginning of the 2020/21 school year. While most regions opened their schools on 14 September, some regions decided to postpone openings: specifically Friuli (delayed to 16 September), Sardinia (to 22 September), and Abruzzo, Basilicata, Calabria, Campania and Puglia (to 24 September). One autonomous province, Bolzano, brought forward the opening date to 7 September. A summary of the different dates on which schools opened in each Italian province is reported in Fig. 1 . This heterogeneity of opening dates, united with the fact that Italy has been severely, but heterogeneously, affected by the virus, makes it a very good set for us to test whether school openings are associated with an increase in COVID-19 infections.

Fig. 1.

Dates of school openings in the different Italian provinces.

The aim of the present paper is to provide some indications with regard to the school closures measures observed in the Italian case, by means of a quantitative analysis based on regional data. More specifically, we estimate a model aimed at measuring the correlation between re-opening schools and the spread of COVID-19 in the various Italian regions. We employed different estimators in different specifications, namely a Feasible-Generalized Least Square (F-GLS) with fix effects, along with an ANalysis Of Variance (ANOVA) model, and found that the re-opening of schools is associated with an increase in COVID-19 cases. This effect begins between 10 and 15 days after school openings.

The remainder of the paper is organized as follows. Section 2 reports the main contributions that deal with the topic and the research question of the present manuscript; section 3 describes the data and methodology used in the quantitative analysis, while section 4 reports and discusses the results of the quantitative estimations. Section 5, finally, highlights the main conclusions of the study.

2. Background and research questions

The adoption of NPIs has led various scholars to measure their efficacy in terms of containing the pandemic. In the Chinese case, according to Ref. [8]; lockdowns have been able to decrease the growth of new COVID-19 cases significantly. [9]; on the other hand, analysing the Indian case, conclude that the positive effects of the lockdown seem to be observable only in some provinces. [4]; evaluating the efficacy of lockdown in a cross-country perspective, find that a lockdown works in reducing the number of new COVID-19 cases: countries that implement it have significantly fewer new COVID-19 cases than those that do not.

The efficacy of lockdown has been investigated by scholars, with attention paid specifically to the Italian case. In particular, according to the study proposed by Ref. [7]; the introduction of non-pharmacological control measures is an effective way to reduce transmission of COVID-19.

During the first wave of the pandemic, NPI were adopted in a step-by-step approach. As a matter of fact, after the introduction of social distancing measures, in most countries the second measure to be introduced was school closures. Only when the trend of the diffusion of the virus had reached significant growth rates did the governments adopt lockdown measures[6]. This is probably due to the fact that this type of policy involves making a difficult choice between people's health and the nation's economy [10].

In light of this, in order to avoid a new generalized lockdown and the accompanying negative effects, a growing debate is emerging about what other non-pharmaceutical measures are able to contain, or at least slow down, the diffusion of the virus. Among these measures, the most widely discussed and adopted seems to be school closures [11]. Despite the centrality of in-person, face-to-face teaching in the return to a regular learning process for students, school openings are also correlated with two important facts: i) the presence of numerous people in classrooms, and thus in relatively small places; and ii) the increase in people using local public transport to reach schools [2]. These elements are possibly drivers of an increase in the diffusion of the virus.

According to Ref. [12]; the adoption of such measures is based on evidence from previous epidemics, where young people (and especially children) were the major transmitters of the virus. Following this reasoning, as suggested elsewhere in the literature [13]), school closures have been considered as one of the first non-pharmaceutical measures to be adopted in order to control the spread of the virus.

According to a report of the European Center for Disease Prevention and Control, despite the negative impact of school closures on the physical and mental health of children, this measure can contribute to a reduction in virus transmission. However, in the same report, the authors highlight the importance of complementary NPIs to make school closures effective [14]. This result is consistent with the findings reported in a very recent study conducted by the Centers for Disease Control and Prevention [15].

The empirical contributions focused on school closures present mixed evidence. [16]; by means of a meta-analysis, suggest that there is limited evidence available to quantify the extent of SARS-CoV-2 transmission in schools, but the same authors highlights the importance of implementing coordinated and effective NPIs to mitigate and prevent a possible acceleration of contagion during the re-opening of schools [11]. suggest that confounding issues could be one of the main factors that studies focused on school closures have to deal with. In fact, by means of a systematic review they found that “school closure studies were at risk of confounding and collinearity from other non-pharmacological interventions implemented around the same time as school closures, and the effectiveness of closures remains uncertain” [11]: p. 3). Despite the increase in the number of contributions focused on the impact of school openings on COVID-19 [13,[17], [18], [19]][3], as pointed out by Ref. [12]; the possibility of confounding factors suggests the importance of new studies able to contribute to this important topic.

Looking at the Italian case, a topical debate about the appropriateness of school closures is emerging. Indeed, the region of Campania, one of those most affected by the second wave of the pandemic, decided on October 15, 2020 to close in-person teaching activities in primary and secondary schools, as well as in universities. Among the reasons declared in support of the decision by the governor of Campania, Vincenzo De Luca, to impose this measure, the regional ordinance refers to the “level of contagion registered in families derived from individual contacts in the schools”.2 Nevertheless it is important to note that a part of the literature suggests that the idea that COVID-19 is spread through schools derives mainly from previous experiences with influenza [20], and that this should not matter very much in the case of COVID, given the lower susceptibility of children to the virus. At the same time, another study focused on the island of Sicily in Italy suggests that in the areas where schools opened earlier, a significant increase in the number of new cases is observed [19]. The present paper, by means of an empirical analysis based on Italian provincial data, contributes to the cited literature by trying to answer the following research questions:

RQ1

Does the opening of schools increase COVID-19 contagion?

RQ2

If it does, how long does this effect take to become manifest?

We consider Italy to be the perfect case to test these hypotheses. Other than the reasons previously explained, such as heterogeneity in school openings and in COVID-19 cases, at the start of September Italy had essentially no strict non-pharmaceutical policy to prevent the spread of the virus, and saw none up to October 15, 2020, when it was decreed that a mask had to be worn in open spaces across the national territory. For this reason, and given the absence of other policies that may act in this relationship as possible confounding factors, the period between 1 September, when Italians traditionally come back from the summer break and return to regular life and work, and 14 October, is a very good natural experiment setting in which to test the impact of school openings on the pandemic.

3. - Data and methodology

In order to measure the impact of school openings on the pandemic in a cross-provincial perspective, following [4] we chose to test this relationship in a cross-provincial analysis utilizing a panel dataset with daily data from the different Italian provinces as the basic statistical unit of observation. In more formal terms, we model the problem as the following equation:

$$\Delta i_{pt}=\alpha +{\beta }_1{i}_{pt-1}+{\beta }_{2}S{C}_{pt}+{\beta }_{3}DS{O}_{pt}+\epsilon$$ (1)

where $\Delta i$ are new COVID-19 cases at time t (with respect to t-1) in province p. In other words, this measures the daily increase in the spread of infection in each Italian province. It is modelled as a function of the infections measured the previous day ($i_{t-1}$) in the same province. The equation also includes the daily total of provincial schools closed because of COVID, in the SC variable. Indeed, after the start of the school year, some schools were closed in each province because there were some COVID-19 positives among their students or teachers. Since this is of course a notable variable that plays a role in the relationship, because it indicates the number of local clusters, we consider it useful to include a measure of the schools closed because of COVID in the equation as well. Therefore, this measure is included as the variable SC, which measures the total number of schools closed so far in the province because of COVID-19.

Finally, the last term is DSO, a dichotomous dummy variable signalling whether or not on day t province p had open schools (i.e. the school year already began). Alternatively, in order to measure the impact on the spread of COVID-19 of the timing of school openings, in alternative specifications DSO may also signal whether schools were open for x days (more details on this later on).

As usual, the equation also includes an error term $\epsilon$.

3.1. - operationalization of the variables

To estimate equation (1), we need two kinds of information: data on the daily number of COVID-19 cases, and the number of closed schools in each province and day. The former are gathered from the Italian Ministry of Health dataset, reporting official data for each province and day, from 1 September, the first day after the summer break that typically takes place in August in Italy, to 14 October, the day of a decree from the Prime Minister implementing other restrictive measures, specifically to wear a mask even in open spaces across Italy, from 15 October onwards. Given that it is very likely that these policies may also play a role in the trend of new COVID-19 cases, and thus may affect the relationship we are studying, we consider it better to conclude the analysis at this date, to avoid biased estimates. Data are gathered from the latest version of the Italian Ministry of Health document available at the time of writing (namely that for October 16, 2020). This allows us to create a dataset with a total of 45 days observed for the 107 Italian provinces described in the Italian Ministry of Health dataset. From this source, we computed New cases, the operationalization of $\Delta i$, as the first difference between the cases of day $i_t$ and $i_{t-1}$, and also YCases, the operationalization of $i_{pt-1}$, which is the absolute value of cases in province p at time $t-1$.

Given the lack of any official governmental information, data about schools closed because of COVID-19 are gathered from Scuole COVID 19 Italia, a dataset compiled by Ref. [21].3 This is a dataset reporting a list of the schools closed due to the testing of a COVID-19 positive, for all Italian municipalities, on a daily basis. From this source we computed the variable SchoolsClosed, the operationalization of SC, as the total number of schools closed, on a given date, in each Italian province.

Finally, there is the operationalization of DSO. As already pointed out, this is a dichotomous dummy variable that assumes the value of 1 if on day t province p had open schools (i.e. the school year already began), and of 0 otherwise. Once again following [4]; in order to measure the impact on the spread of COVID-19 of the timing of school openings, in alternative specifications DSO may also signal whether schools were open for x days. Indeed, we cannot expect that the opening of schools will have an impact on contagion rates immediately. On the contrary, given that 97.5% of those who develop symptoms do so within 11.5 days of infection [22], we should expect its impact to increase over time, since, under the assumption that people with symptoms are more likely to be tested, the infections reported in time t are likely to be due to transmissions of the virus that happened 7–14 days beforehand. DSO may thus assume different values on the same day for different provinces, given the fact that the regions decided to open schools at several different times.

3.2. Empirical strategy

Considering that data have several observations for each p and t, the best estimator to employ is a Feasible–Generalized Least Square (F-GLS) [23,24]. Moreover, given the heterogeneity of socio-economic characteristics in Italian regions [25], which may play a role in this relationship [26,27][28], meaning that the spread of the virus may be due to factors specific to each province, we employed as main estimator a fixed effects (FE) estimator, which captures heterogeneity between provinces. It is widely recognized by the econometric literature that fixed effects models have an advantage over random-effects models when analysing panel data because they control for all level 2 characteristics, whether measured or unmeasured [[29], [30], [31]]. In other words, by employing this strategy we estimate the average effects with respect to a single province, assuming that the heterogeneity among them does not change in the 45 days of our timespan. Please note in this regard that estimating a regression with fixed effects means controlling for all the time-invariant variables, since characteristics that do not vary in time are automatically taken into account in the within province estimation. Nevertheless, setting aside the theoretical importance of using this estimator to provide a meaningful estimation in such an innovative context, for which much information about the important covariates are not yet available, in order to test the appropriateness of employing a fixed effects estimator we performed a Hausman test [32] on this sample, which confirmed that a fixed effects estimate is to be preferred to a random effects estimate (results in Table 1 ).4

Table 1.

Hausman test for Fix versus Random Effects.

Complete sample – complete model (with controls)
Ho: difference in coefficients not systematic
chi2 (3) = (b-B)' [(V_b-V_B)^(-1)](b-B) = 100.93
Prob > chi2 = 0.0000

The final sample is composed of 44 daily observations, from 1 September to October 14, 2020, for 107 Italian provinces, with a total of 4708 observations. Descriptive statistics of the variables are presented in Table 2 a, while Table 2b presents the matrix of correlation between the variables.

Table 2a.

Descriptive statistics.

Label	Variable	Mean	Sample	Std. Dev.	Min	Max	Observations
NewCases	New COVID-19 infection reported in the province on the day	21.37829	overall	88.58754	−3679	3803	N = 4708
			between	31.85305	.5	214.6591	n = 107
			within	82.71883	−3687.894	3794.106	T = 44
YCases	Total number of COVID cases reported in the province on the day before	2783.829	overall	4060.269	0	32,663	N = 4708
			between	4056.618	93.81818	28515.25	n = 107
			within	424.2257	−505.0578	8723.874	T = 44
SchoolsClosed	Number of schools closed in the province per COVID-19 infection at the date	.9,256,585	overall	2.487785	0	26	N = 4708
			between	1.516826	0	8.295455	n = 107
			within	1.977203	−7.369796	19.92566	T = 44
DSO	Dichotomous dummy variable, equal to 1 if schools were open on the day, to 0 otherwise	.6,425,234	overall	.4,793,077	0	1	N = 4708
			between	.1,157,425	0	.8,636,364	n = 107
			within	.4,652,547	-.221,113	1.165251	T = 44

Table 2b.

Correlation matrix.

	NewCases	YCases	SchoolsClosed	DSO
NewCases	1.0000
YCases	0.2473	1.0000
SchoolsClosed	0.2515	0.1008	1.0000
DSO	0.0689	0.0801	0.2654	1.0000

4. Results

Our main finding suggests that on average, in the Italian provinces, after opening schools there was a statistically significant increment in the number of COVID-19 cases. Results of the estimates through an F-GLS-FE are presented in analytical form in Table 3 (without controlling for SchoolsClosed, the variable controlling for the number of schools closed) and Table 4 (which also includes this control), and graphically in Fig. 2 .

Table 3.

F-GLS Fixed Effects - New cases after school opening - with SchoolsClosed.

	(3.1)	(3.2)	(3.3)	(3.4)	(3.5)
	NewCases	NewCases	NewCases	NewCases	NewCases
YCases	0.0242***	0.0232***	0.0221***	0.0203***	0.0187***
	(6.26)	(5.96)	(5.64)	(5.15)	(4.71)
SchoolsClosed	3.555***	3.401***	3.286***	3.295***	3.506***
	(4.34)	(4.14)	(4.01)	(4.06)	(4.34)
DSO	−0.941
	(-0.33)
7 days		2.068
		(0.75)
11 days			5.002*
			(1.77)
15 days				8.994***
				(3.03)
19 days					13.31***
					(4.06)
Constant	−48.62***	−47.35***	−45.06***	−41.06***	−36.89***
	(-4.81)	(-4.65)	(-4.39)	(-3.96)	(-3.53)
Observations	4708	4708	4708	4708	4708

t statistics in parentheses * p < 0.1, **p < 0.05, ***p < 0.01.

Table 4.

F-GLS Fixed Effects - New cases after school opening - without closed schools.

	(4.1)	(4.2)	(4.3)	(4.4)	(4.5)
	NewCases	NewCases	NewCases	NewCases	NewCases
YCases	0.0343***	0.0327***	0.0313***	0.0300***	0.0295***
	(11.15)	(10.36)	(9.89)	(9.52)	(9.53)
DSO	1.023
	(0.36)
7 days		4.126
		(1.51)
11 days			6.770**
			(2.42)
15 days				10.05***
				(3.40)
19 days					13.33***
					(4.06)
Constant	−74.80***	−71.54***	−68.48***	−65.28***	−63.78***
	(-9.21)	(-8.56)	(-8.10)	(-7.69)	(-7.55)
Observations	4708	4708	4708	4708	4708

t statistics in parentheses * p < 0.1, **p < 0.05, ***p < 0.01.

Fig. 2.

Betas of several Schools Opening dummies, computed at the date of implementation, 1 days after, 2 days after, and so on, up to 21 days after. Lines and lighter colours represent 95% and 90% confidence intervals. Betas are estimated through the F-GLS-FE model, with the SchoolsClosed variable included. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

As explained previously, YCases is the operationalization of $i_{ct-1}$, and is the total number of COVID-19 cases registered in province p on t-1 (i.e. yesterday). It has, as expected, a positive and statistically significant coefficient, suggesting that the more cases were reported in province p yesterday, the more New Cases of COVID-19 there will be today.

SchoolClosed, the operationalization of $S{C}_{pt}$, is also positive and statistically significant in all the specifications. This is due to the fact that the more coronavirus cases there are in a province, the more likely it will be that one of those who tests positively will be in a school, causing that school's subsequent closure.

Finally, the variables of greatest interest for the present work are included in the regression (DSO): the various dichotomous dummies discriminating for how many days the schools have been open. As already explained while commenting the construction of the dataset, these variables may assume different values on the same day for different provinces, given the fact that the regions decided to open schools at several different times. For this reason, the dummy variable discriminating for a province that has schools opened for x days may have a different value on the same day across different provinces. For instance, on day t for provinces p1 and p2, 7 days may assume the value of 0 for p1 and 1 for p2, given that the former may have opened the schools nine days prior, while the latter opened them only one day prior.

As explained previously, we prefer not to include in our analysis observations that refer to days after 14 October, given the imposition of a new decree from the national government with new restrictions, which may have had an effect on the dynamic of the spread of cases. Of course, with our data it is impossible to disentangle this effect from that due to school openings; for this reason, we prefer to limit the analysis to a homogeneous period; homogeneous, that is, in terms of non-pharmaceutical measures imposed on the population. This also implies that we may not control the effect of school openings for more than 21 days after the date on which the schools open, at least in the complete sample. Indeed, the group of regions that opened schools last did so on 24 September; they thus opened the schools 21 days before the 14 of October, which is, as we have seen, the last useful day for capturing the effect of school openings in this natural experiment.

The coefficients of the different operationalizations of DSO suggest that there is a positive effect for the opening of schools on NewCases, which becomes statistically significant at 90% from 11 days after opening. Both the magnitude and the statistical significance of this effect grow over time, becoming statistically significant at 99% 15 days after opening.

This is possibly even clearer when looking at Fig. 2, which plots the different betas of the same regression, including operationalizations of DSO for each day after opening up to 21 days after. While the growth of NewCases is irrelevant in the initial days after school openings, and is in any case statistically insignificant, it has a turning point about 7 or 8 days after the school opening. Please note that this is the bottom threshold that the literature suggests as the average time to observe symptoms after a COVID-19 infection: a 95% confidence interval of between 8.2 and 15.6 days [22]. This trend keeps growing as the days elapse, becoming statistically significant at 10% 11 days after opening, at 5% 14 days after, and at 1% 15 days after. All these findings suggest that school openings do indeed have a positive effect on COVID-19 cases, and that it is considerable.

In order to test the robustness of our results, we decided to complete the analysis with a hierarchical linear random effects analysis of variance (ANOVA) model, which is presented in Table 5 . This model allows us to analyze the degree of variance due to cross-regional differences. The levels of aggregation in the model are the 21 Italian regions (19 regions and 2 autonomous provinces) into which the peninsula is administratively divided, and to which the provinces belong. As expected, the likelihood ratio test statistics for the null hypothesis that there is no cross-regional variation in NewCases have a p-value below the threshold of 1%, suggesting that there is indeed variation between the different regions that we identified. Looking at the different coefficients, these results are in line with the previous estimates and also have a higher statistical significance, which is likely due to the fact that through this model we take into account certain structural regional characteristics that apparently play a role in the pandemic dynamic. This also adds some robustness to our findings.

Table 5.

ANOVA Multilevel (Region) - New cases after school opening - without closed schools.

	(5.1)	(5.2)	(5.3)	(5.4)	(5.5)
	NewCases	NewCases	NewCases	NewCases	NewCases
YCases	0.00684***	0.00680***	0.00677***	0.00676***	0.00676***
	(18.48)	(18.37)	(18.33)	(18.30)	(18.31)
DSO	10.35***
	(3.93)
7 days		13.61***
		(5.43)
11 days			16.11***
			(6.30)
15 days				19.25***
				(7.09)
19 days					22.67***
					(7.43)
Constant	−1.856	−1.913	−1.610	−1.059	−0.0390
	(-0.48)	(-0.52)	(-0.44)	(-0.29)	(-0.01)
lns1_1_1	2.630***	2.632***	2.639***	2.648***	2.660***
	(14.50)	(14.56)	(14.61)	(14.69)	(14.79)
lnsig_e	4.437***	4.435***	4.434***	4.433***	4.433***
	(429.69)	(429.55)	(429.44)	(429.33)	(429.27)
Observations	4708	4708	4708	4708	4708

t statistics in parentheses * p < 0.1, **p < 0.05, ***p < 0.01.

4.1. - Limitations

The analysis presented in the previous section tries to measure the general effect due to schools being open on the rate of contagion, which is also due to side effects such as public transportation congestion and all the other activities needed to keep students in schools. More precisely, we catch this general effect simply by analysing whether it is possible to observe an increase in new cases of COVID-19 in Italian provinces after the opening of schools.

As already pointed out, it is worth noting that our analysis cannot be simply interpreted in terms of direct causation, since available data do not allow us to know where the contagion happened. It is nonetheless important to highlight, especially given the impossibility of having such granular data, that the aim of this paper is different. We aim to empirically investigate a robust ceteris paribus correlation between opening schools and the spread of the virus, using Italy as a specific case study, given its relevance as a setting. We are aware that our results do not detect a direct community transmission mechanism due to the existence of confounding issues [11].

Moreover, our results do not deal with the issue of COVID-19 transmission that happens specifically in schools.

Despite the possible limitations of the present study, the main findings can contribute to shedding some light on a growing debate that, as pointed out by previous contributions [11,12], requires further research able to control more thoroughly for other confounding factors.

5. Conclusions and discussion

The present paper has presented an empirical estimation, based on provincial data from Italy, that can contribute to the important debate about the effects associated with opening schools on the spread of COVID-19. It is worth noting that the aim of the paper is not to measure the level of contagion generated within schools, but the more general effect due to schools being open, which is also due to side effects such as public transportation congestion and all the other activities needed to keep students in schools. On the basis of our results, one can derive that school openings seem to be correlated with an increase in new COVID-19 cases. More precisely, we observe an increase in contagion 11 days after the opening of schools, which continues to grow up to 21 days afterwards (at which point we had to interrupt our analysis, given the occurrence of other measures to reduce the spread). These results seem to confirm the findings of a recent study based on Sicilian census data, where an increase in COVID-19 cases is observed in those zones where schools opened earlier [19].

From a policymaker's perspective, opening schools could be a very important choice for national governments, due to the centrality of face-to-face teaching activities in defining a regular learning path for students. Nevertheless, despite the fact that in the case of COVID-19 younger people seem to show a lower probability of contracting the virus, this choice triggers several social circumstances that may be possible drivers for the diffusion of COVID-19, the most obvious of which is the increase in people in the street, and especially on local public transport. Moreover, with schools open, it is likely that adults also tend to stay home less, doing risky activities that may contribute to furthering the community spread of the virus.

Following this reasoning, it should be stressed that our results do not suggest that schools are a place where the virus is spread. Nevertheless, it is worth noting that the fact that people of school-going age often remain asymptomatic, and that the increase in social interaction among students is also triggered by opening schools, are two factors that may easily contribute to the spread of the virus among students’ families and other social networks outside the school (as confirmed by Ref. [19]. For this reason, if opening schools is a central political objective, national and local governments should have the capacity and effective possibility to plan mitigation measures to keep the increase in interactions between citizens after school openings under control. Some accompanying measures, like the implementation of shifts in schools, or the limitation of face-to-face teaching activities to just a few students (for example the decision taken by numerous universities to limit activities to first year undergraduates only) could help to reduce the probability of contracting the virus, thus slowing down the spread of the pandemic. According to a recent study carried out in some Italian schools, good mechanical ventilation may also be able to reduce indoor viral concentration and the effectiveness of facemasks even when these are not being used, as is often the case among students [33]. If we look at the possibility of asymptomatic cases among the student population, an important control measure may be a focused testing policy.

We are aware that our results present various limitations, and we have tried to discuss these in the previous subsection. At the same time, we hope our paper has contributed usefully to this important and on-going debate, which, as pointed out by several contributions, requires further research that is able to control more thoroughly for other confounding factors [11,12]. In conclusion, our findings suggest that when a government decides to open schools, it is crucial to make the public aware of the threats involved and plan accompanying measures, in order to be able to prevent community transmission correlated with opening schools.

Biographies

Vincenzo Alfano (corresponding author - vincenzo.alfano@unina.itvalfano@wiut.uz) is Assistant Professor in Applied Economics at the University of Messina, and affiliated fellow at Center for Economic Studies - CESifo. His research focus on institutions and the structure of incentives created by them in a variety of contexts. He has published in several journals, including Journal of Sports Economics, Applied Health Economics and Health policy, The BE Journal of Economic Analysis and Policy, and Political Studies Review.

Salvatore Ercolano is Assistant Professor of Political Economy at the University of Basilicata (Italy), where he currently teaches Economics and Political Economy. His research interests are focused on Public economics, Environmental Economics, Political Economy and Cultural Economics.