Treatments of Differential Item Functioning: A Comparison of Four Methods

Abstract

Test fairness is critical to the validity of group comparisons involving gender, ethnicities, culture, or treatment conditions. Detection of differential item functioning (DIF) is one component of efforts to ensure test fairness. The current study compared four treatments for items that have been identified as showing DIF: deleting, ignoring, multiple-group modeling, and modeling DIF as a secondary dimension. Results of this study provide indications about which approach could be applied for items showing DIF for a wide range of testing environments requiring reliable treatment.

Introduction

Test fairness is critical to the validity of group comparisons involving gender, ethnicities, culture, or treatment conditions. Ensuring test fairness includes the detection and prevention of unfairness in all aspects of the testing program (e.g., test design and development, test administration, and test scoring; Camilli, 2006; Dorans & Cook, 2016). Differential item functioning (DIF) procedures are one component of these efforts that are used to address test fairness in scoring across subgroups of interest. A variety of procedures for detecting DIF have been proposed, and a large body of literature exists on the relative effectiveness of these methods. However, relatively less attention has been given to the question of how to handle items that show DIF.

Cho et al. (2016) reviewed 27 articles that treated DIF items by various approaches. Four DIF treatment methods were commonly reported in these studies: ignoring DIF items, deleting DIF items, multiple-group calibration, and modeling DIF items using a multidimensional model. Across the articles reviewed, only one used the modeling approach.

Modeling DIF is a novel approach for treating DIF that arises from the notion that multidimensionality of items is the general cause of DIF (e.g., Ackerman, 1992, 1994; Camilli, 1992; Roussos & Stout, 1996; Shealy & Stout, 1991, 1993). Ackerman (1992) investigated DIF from the perspective of multidimensional item response theory (IRT). From this point of view, items that are flagged as showing DIF measure multiple dimensions—the intended measured construct, which is the primary dimension, and the nuisance construct, which is the secondary dimension. DIF occurs when there is a difference in the distributions on the secondary dimension between reference and focal groups. For example, reading proficiency can be seen as a nuisance dimension that would influence item scores on a mathematics test for certain items. Students with high levels of reading proficiency would have a higher probability of a correct response on such math items. When groups differ in reading proficiency distributions, DIF occurs. Camilli (1992) explored a mathematical model for approximating parameters for items measuring multiple dimensions by one-dimensional estimates. The results indicated a confounding effect of the secondary dimension with the item parameters, which manifested as DIF. Shealy and Stout (1993) presented a multidimensional model for DIF (MMD) to formalize the occurrence of DIF. Under this model, DIF occurs when two conditions are met:

(a) DIF items elicit at least one secondary dimension, η, in addition to the primary dimension the test is intended to measure, θ, and (b) a difference exists between the two groups of interest in their conditional distributions on the secondary dimension η, given a fixed value on the primary dimension, θ (i.e., η|θ). (Gierl, 2005, p. 5)

Based on MMD, Shealy and Stout (1993) developed a multidimensional IRT-based approach, which they called the simultaneous item bias test, for detecting DIF. Roussos and Stout (1996) adopted Shealy and Stout’s (1993) simultaneous item bias test method and proposed a multidimensionality-based DIF analysis paradigm that integrated substantive content and statistical DIF analysis for test development. Based on the root cause of DIF investigated by previous studies, Walker and Sahin (2017) used Shealy and Stout’s (1993) framework to investigate the magnitude of the difference in secondary ability distributions between reference and focal groups that would influence the power of DIF detection procedures. The study found that when the mean difference in the secondary dimension between the two groups was at least 0.5, the DIF detection techniques had adequate power to identify DIF.

Multigroup calibration within the IRT framework is one approach to modeling DIF that does not explicitly rest on the conceptualization of DIF as undesired multidimensionality. Under this approach, the parameters of non-DIF items are constrained to be equal across groups and the parameters of DIF items are allowed to vary across groups. In an alternative framework to that of IRT, several researchers have explored the issue of DIF using multiple-group confirmatory factor analysis (MG-CFA), which is more firmly rooted in a multidimensional framework. Although both frameworks allow modeling of group differences, the focus of MG-CFA is typically on examining the difference in factor structures between groups, whereas the goal of IRT multiple-group methods is to recover the item and latent person parameters for test-takers. Fleishman et al. (2002) used the MG-CFA approach to examine the performance of two strategies—statistical adjustment of DIF items and deleting DIF—on group comparisons. Millsap and Kwok (2004) evaluated the impact of different levels of partial invariance on the accuracy of test-taker comparisons and selection. Steinmetz (2013) and Zumbo (2003) investigated the impact of partial invariance on other perspectives of group comparisons, such as observed composite scores and the relation between item- and test-level DIF. The current study uses the IRT approach and investigates the multiple-group method under the IRT framework.

A recently proposed alternative to multigroup calibration for DIF items is to explicitly model the secondary dimension and allow group differences in loadings on that dimension. Currently, there are only two studies that have investigated the treatment of DIF using this approach (i.e., Cho et al., 2016; Liaw, 2015).

Cho et al. (2016) compared the performance of the DIF modeling approach with other commonly used methods (deleting, ignoring, and multiple-group methods) in calibrating and scoring simulated responses with items previously flagged as showing DIF. Item responses for items with DIF were generated using a unidimensional IRT model. They found that the multiple-group and DIF modeling approaches resulted in the most accurate trait parameter estimates, with the multiple-group approach providing better results under most conditions. The deleting and ignoring DIF methods performed worse than the multiple-group and modeling approaches.

Similarly, Liaw (2015) investigated the impact of the magnitudes of primary and secondary item discrimination on the accuracy of calibration of the primary ability for tests with DIF items by comparing the modeling DIF approach to deleting and ignoring DIF item methods within the two-parameter IRT model. The multiple-group approach was not incorporated in the comparison of methods for handling DIF. In this study, item responses were generated differently than Cho et al. (2016). The item responses were produced by a noncompensatory two-dimensional model for DIF items, while non-DIF items were generated with a unidimensional model. The results showed that ignoring DIF resulted in the least accurate primary trait estimates and modeling DIF did not perform better than deleting DIF.

Although both of these studies investigated the performance of DIF treatments by comparing the approach of modeling DIF as the secondary dimension to other commonly used methods within the two-parameter IRT model, there are several distinctions between them, and each of them has some limitations.

First, the fitted models and results differ. The two studies fitted different models in the reference group when applying the modeling approach. Cho et al. (2016) constrained the loadings on the secondary dimension to be zero for the reference group on DIF items, while Liaw (2015) freed the secondary dimension to be estimated for the reference group on DIF items. In addition, Liaw (2015) did not incorporate the multiple-group treatment into the comparison and did not compare the accuracy of item parameter estimates among different DIF treatments. Moreover, Cho et al. (2016) found that the multiple-group and modeling DIF approaches performed the best among the four treatments, while Liaw (2015) concluded that deleting DIF was the best for estimating person scores.

Second, the two studies employed different methods of data generation for items with DIF. Liaw (2015) generated two-dimensional item responses for items with DIF, while Cho et al. (2016) simulated responses with a unidimensional model. As mentioned in Walker and Sahin (2017), data generated with a unidimensional IRT model do not perfectly align with the multidimensional framework that is treated as the cause of DIF. Therefore, whether the modeling DIF approach does perform the best among the four methods under the two-dimensional item response framework is not explored in Cho et al. (2016).

Third, the two studies employed different test lengths in the experimental design. Liaw (2015) used a 40-item test, while Cho et al. (2016) adopted a 20-item test in the study. Neither included test length as a factor into the DIF treatment comparison.

Based on the different models employed, conflicting results, and limitations of the previous research, the current study investigated the accuracy of scoring and item calibration for the four DIF treatments with DIF generated using a MMD. Additionally, test length is included as a factor in the comparison for the four DIF treatments. Furthermore, the current study extended the testing context from a two-parameter model to a three-parameter IRT model. Therefore, the purpose of the current study is to extend the studies of Cho et al. (2016) and Liaw (2015) by comparing the four DIF treatment methods (deleting, ignoring, multiple-group, and modeling DIF) within a two-dimensional framework, across a wider range of test length conditions, and with data that fit a three-parameter IRT model. The outcomes of interest are the accuracy, precision, and bias of trait and item parameter estimates.

Differential Item Functioning Treatment Approaches

We employed four DIF treatment approaches, which were used and compared in Cho et al. (2016). The DIF treatment methods investigated in the current study include the following.

Deleting Differential Item Functioning Items

DIF items were deleted and only non-DIF items were used during item calibration and scoring with the unidimensional three-parameter IRT model. This method is easy to implement but it may lead to low reliability and content validity (Cho et al., 2016; Fleishman et al., 2002).

Ignoring Differential Item Functioning Items

DIF items were treated as non-DIF items and were used in item calibration and scoring with the unidimensional three-parameter IRT model. Accuracy of estimates with this method may be good when the magnitude of DIF is small and there are few DIF items, but parameter estimates are likely biased when DIF is more substantial (Cho et al., 2016). This method is generally not acceptable in practice but was included for comparison purposes.

Multiple-Group Differential Item Functioning Method

Item parameters were constrained to be equal across groups for items not showing DIF and allowed to differ across groups for items with DIF. Unidimensional three-parameter IRT models were fitted. Reference and focal groups were calibrated simultaneously in the current study, in contrast to the two-step multiple-group method of Cho et al. (2016). Cho et al. (2016) found that this method produced more accurate parameter estimates.

Confirmatory Multiple-Group Multidimensional Item Response Theory Model

Multidimensional three-parameter IRT models were fitted. Both the primary dimension and the secondary dimension due to DIF were modeled. In both reference and focal groups, discriminations on the secondary dimension were fixed at zero for non-DIF items and estimated for DIF items. This method can be expected to provide more accurate parameter estimates when DIF arises as a result of a common secondary dimension. More details about the advantages and disadvantages for each method are provided in Cho et al. (2016).

Method

Simulation Design

Data were generated using a two-dimensional IRT framework with a primary dimension measured by all items and a common secondary dimension measured by DIF items with group differences on the secondary dimension. All DIF items were simulated to favor the reference group.

A fully crossed design was employed where the factors were the level of item discrimination for the two dimensions, correlation between the dimensions, test length, and percentage of DIF items. We chose factors that may have an impact on the performance of the four DIF treatment methods based on the experimental design and results of previous research. Given a two-dimensional IRT framework, the level of item discrimination on each dimension and the correlation between dimensions are important factors that should be included in the design to determine their impacts on the treatment of DIF items. These factors are commonly manipulated in simulation studies using multidimensional item response data (e.g., Finch, 2010; Gosz & Walker, 2002; Liaw, 2015; Tate, 2003; Walker & Sahin, 2017). Percentage of DIF items was varied since both Cho et al. (2016) and Liaw (2015) found that this factor had an impact on the estimation of person and item parameters under different treatments for DIF. Test length was manipulated because Cho et al. (2016) and Liaw (2015) used different test lengths in their simulations and obtained conflicting results. More details about the simulation conditions and their levels in previous research are offered in the following paragraphs.

Item Discrimination

For DIF items, Liaw (2015) fixed the primary discrimination parameter at either 0.5 or 0.8 and the secondary discrimination parameter at either 0.2 or 0.5. However, Walker and Sahin (2017) generated DIF by putting higher loadings, in the range (0.997, 1.649), on the second dimension for items with DIF. In the current study, we integrated the conditions in Liaw (2015) and Walker and Sahin (2017) and selected 0.4, 0.8, and 1.2 to represent low, moderate, and high discrimination parameters, respectively. Three conditions were generated: (1) low discrimination parameter on the primary dimension (α = 0.4) with high discrimination parameter on the secondary dimension (α = 1.2), (2) high discrimination parameter on the primary dimension (α = 1.2) with low discrimination parameter on the secondary dimension (α = 0.4), and (3) moderate discrimination parameter on both dimensions (α = 0.8). The three combinations of discrimination parameters in our design reflect three different types of DIF items: items that mainly load on the primary dimension, items that mainly load on the secondary dimension, and items with similar loadings on both dimensions. Our design extends Liaw (2015) and Walker and Sahin (2017) by exploring the effect of different combinations of item loadings on methods for treating DIF items. The multidimensional discrimination (MDISC) parameter ${\alpha }_j$ was defined as $\sqrt{\sum _{k=1}^n{({\alpha }_{\mathrm{jk}})}^2}$ (Reckase, 2009), where ${\alpha }_{\mathrm{jk}}$ is discrimination parameter on each dimension k for item j. MDISCs for the three conditions are 2.15, 2.15, and 1.92, respectively. We fixed discrimination parameters to be the same across DIF items for each test to avoid the confounding effect of varying values of discrimination parameters.

Correlation Between Dimensions

Three different correlations between dimensions were used: 0, 0.3, and 0.7. Previous studies have used $\rho =0$ and 0.3 to represent no and low correlations (Finch, 2010; Liaw, 2015). For high correlation, prior research used 0.6 (Tate, 2003), 0.75 (Walker & Sahin, 2017), 0.8 (Finch, 2010), or 0.9 (Gosz & Walker, 2002). The current study used 0.7 as the strong correlation.

Test Length

Test length was 20 or 40 items. These test lengths are commonly used in DIF research (Klockars & Lee, 2008) and reflect relatively short and moderate test lengths in most testing contexts. Many tests have subscales of 20 items or fewer, and numerous instruments have short forms (e.g., health-related quality of life instruments, Advanced Progressive Matrices–Short Form; Chiesi et al., 2012; Scott et al., 2010). Standardized achievement tests are often considerably longer. Based on previous DIF detection research (e.g., Fidalgo et al., 2000; Swaminathan & Rogers, 1990), we did not expect that increasing the test length beyond 40 items would produce substantial changes in the results.

Percentage of Differential Item Functioning Items

Ten percent and 30% were selected as low and high percentages of DIF items, respectively, similar to those of Finch and French (2007) and Liaw (2015).

Sample sizes for the reference and focal group are 1,500 and 500, respectively. Sample sizes of 2,000 in total are widely employed in simulating response patterns for DIF studies (Cho et al., 2016; Liaw, 2015; Walker & Sahin, 2017). The current study did not include balanced–unbalanced sample size as a manipulated factor since the unbalanced condition was a more realistic one and balanced and unbalanced conditions had similar patterns on the performance of DIF treatment methods in the earlier results (Cho et al., 2016).

Four different DIF treatment procedures were used: (1) deleting DIF items, (2) ignoring DIF items, (3) a multiple-group DIF method, and (4) a confirmatory multiple-group multidimensional IRT model. For the fourth method, discriminations on the secondary dimension were fixed at zero for non-DIF items and were estimated for DIF items for both reference and focal groups. FlexMIRT3.5 was used for item calibration and scoring (Cai, 2017).

Trait Distributions, Item Parameters, and Data Generation

For DIF items, person parameter values on the secondary dimension for the reference group were drawn from a N(0, 1) distribution. The focal group values were drawn from a N(−1, 1) distribution. Both reference and focal groups had N(0, 1) distributions for the primary dimension.

The current study employed Liaw’s (2015) method for generating responses on DIF items and their method in fitting models since the same structures of latent constructs are tested for both reference and focal groups when examinees take the same DIF items. Therefore, responses of DIF items were generated with the compensatory multidimensional three-parameter model for both reference and focal groups (Reckase, 2009). The probability of answering an item correctly is

$$\mathrm{\Phi }(x_{\mathrm{ij}}=1|{\theta }_i,{\alpha }_j,d_j,{\gamma }_j)={\gamma }_j+\frac{(1-{\gamma }_j)}{1+\exp [-D({\alpha }_j^T{\theta }_i+d_j)]},$$ (1)

where $x_{\mathrm{ij}}$ is the response of student i on item j, ${\theta }_i$ is a vector of the latent factor of student i, ${\alpha }_j$ is the vector of item slopes for multiple dimensions, $d_j$ and ${\gamma }_j$ are the intercept and lower asymptote parameter for item j, respectively. The multidimensional difficulty (MDIFF) parameter was defined as $d_j/(-\sqrt{\sum _{k=1}^n{({\alpha }_{\mathrm{jk}})}^2})$ , where ${\alpha }_{\mathrm{jk}}$ is the item loading for item j dimension k (Reckase, 2009). The intercepts of DIF items were generated based on the definition of MDIFF. In the current study, ${\alpha }_j=({\alpha }_1,{\alpha }_2)$ for two dimensions and values of ${\alpha }_1$ and ${\alpha }_2$ were manipulated with the three conditions: low ${\alpha }_1$ and high ${\alpha }_2$ , high ${\alpha }_1$ and low ${\alpha }_2$ , and moderate ${\alpha }_1$ and ${\alpha }_2$ . In addition, since the existence of the ability differences on the nuisance dimension were assumed as one of the causes of DIF in the current study, two components need to be considered in the generation of DIF item responses: differences of theta distributions on the secondary dimension between reference and focal groups and the multidimensional item structure. Discrepancies between groups in discrimination and difficulty parameters were not the components for DIF response generation. Therefore, DIF items cannot be categorized as uniform or nonuniform types of DIF.

DIF-free item responses were generated using a unidimensional three-parameter item response model. Discrimination parameters were drawn from a N(1, 0.2) distribution and difficulty parameters were drawn from a standard normal distribution. Values for the lower asymptote parameters were drawn from a uniform distribution of (0, 0.2) for both DIF and non-DIF items. Five hundred replications were performed. We chose a normal distribution of discrimination parameters to reflect the fact that most items are moderately discriminating with fewer that are very low and very high. Responses were generated for both DIF and non-DIF items using R 4.0.3.

Evaluation Criteria

Bias and root mean square error (RMSE) were used to measure the accuracy of latent trait and item parameter estimates. Standard errors of estimates were examined to assess estimate precision. Bias and RMSE were defined as

$$\mathrm{Bias}({\theta }_j)=\overline{{\hat{\theta }}_j-{\theta }_j};\mathrm{RMSE}(\theta )=\sqrt{\sum _{r=1}^{500}{({\hat{\theta }}_j-{\theta }_j)}^2},$$ (2)

where ${\theta }_j$ is the true value of the parameter and ${\hat{\theta }}_j$ is the estimated value for individual or item j. Average bias and RMSE of θ estimates were calculated across all students in each group. Average bias and RMSE of discrimination, difficulty, and lower asymptote parameters were computed across non-DIF items. While there is no established criterion for these indices, lower values of bias and RMSE represent more accurate estimation of parameters and better performance of a DIF treatment method.

Results

Expectation of Four Differential Item Functioning Treatment Methods and Simulation Conditions

Based on previous results of the comparison of the four methods, we expected that ignoring DIF would produce the worst performance with respect to trait estimation since it included contaminated information in the analysis. Modeling DIF was expected to perform better than other methods with respect to trait estimation since it was the same model that generated the data. The multiple-group method was expected to outperform deleting items since there would be less information available for trait estimation under the deleting DIF items method. The two prior studies investigating DIF treatment methods had conflicting results with respect to trait estimates. Cho et al. (2016) found that deleting DIF items performed the worst among the four methods. The multiple-group method and modeling DIF as the secondary dimension outperformed the other two methods. However, Liaw (2015) found that deleting DIF items and modeling DIF performed similarly. Both studies found that ignoring DIF items results in lower average accuracy of trait estimates than the modeling approach.

For item parameter estimation, ignoring DIF and modeling DIF were expected to perform better than the multiple-group method and deleting DIF items for conditions with fewer DIF items. Cho et al. (2016) pointed out that ignoring DIF may work well when the magnitude of DIF is low and when there a small number of DIF items. Again, we expected that modeling DIF would perform the best for conditions with a larger percentage of DIF items since it was the same model that generated the data.

Both Cho et al. (2016) and Liaw (2015) expected that a larger percentage of DIF items would decrease the estimation accuracy of trait parameters for the focal and reference groups. Liaw (2015) also found that a higher correlation between the two dimensions, lower primary discrimination and higher secondary discrimination, would decrease the estimation accuracy of the trait parameter for the focal group as well. Based on the earlier results, we expected that a higher percentage of DIF items, the combination of higher loadings on the second dimension and lower loading on the primary dimension of DIF items, and higher correlation between the two dimensions would result in lower estimation accuracy. We also expected that a shorter test length would produce higher values of bias and RMSEs since the shorter the test the less the information available for the analysis.

Trait Estimation

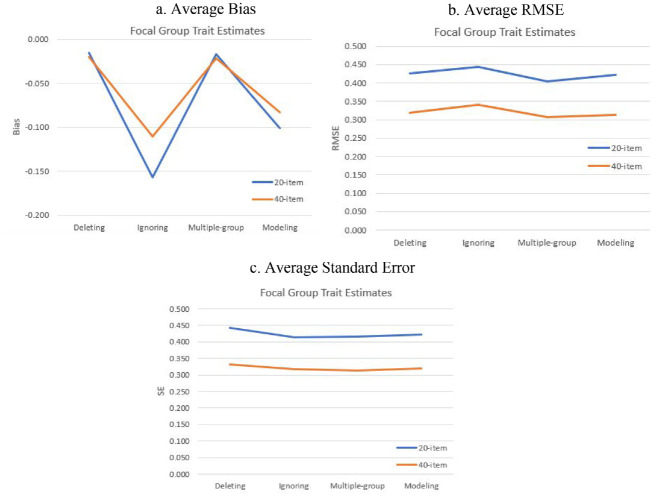
Average bias, RMSE, and standard error of the primary dimension trait estimates for the focal group are presented in Tables 1 and 2. A positive value of bias means that on average the trait parameter estimate is higher than the true value (i.e., overestimated). A negative value of bias means that on average the trait parameter estimate is lower than the true value (i.e., underestimated). Generally, all four DIF treatments underestimated the primary dimension for both 20- and 40-item tests. The multiple-group method and modeling DIF outperformed deleting and ignoring DIF methods for the trait estimates as expected. Ignoring DIF items resulted in the highest absolute values of average bias for the focal group. Deleting DIF items yielded the lowest average negative bias of all the conditions. The multiple-group approach had slightly higher bias values than those of the deleting DIF method. However, unexpectedly, the modeling approach performed worse with respect to average bias than deleting DIF items and the multiple-group method, but better than ignoring DIF. Figure 1a shows the graph of average bias of the four DIF treatment methods.

Table 1.

Average Bias, RMSE, and Standard Error of Focal Group Trait Estimates for 20-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item discrimination for two dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	−0.027	−0.017	−0.005	−0.078	−0.102	−0.135	−0.027	−0.017	−0.006	−0.059	−0.075	−0.103
	Low α2 high α1	−0.025	−0.016	−0.003	−0.065	−0.057	−0.045	−0.026	−0.017	−0.004	−0.063	−0.055	−0.044
	Moderate α1 and α2	−0.026	−0.017	−0.006	−0.089	−0.089	−0.087	−0.026	−0.017	−0.005	−0.078	−0.077	−0.047
30%	Low α1 high α2	−0.023	−0.015	−0.003	−0.238	−0.369	−0.397	−0.021	−0.025	−0.007	−0.082	−0.127	−0.202
	Low α2 high α1	−0.025	−0.016	−0.004	−0.139	−0.130	−0.117	−0.029	−0.020	−0.009	−0.125	−0.117	−0.109
	Moderate α1 and α2	−0.026	−0.014	−0.009	−0.227	−0.236	−0.232	−0.023	−0.016	−0.006	−0.136	−0.148	−0.173
	Average	−0.025	−0.016	−0.005	−0.139	−0.164	−−0.169	−0.026	−0.019	−0.006	−0.091	−0.100	−0.113
RMSE
10%	Low α1 high α2	0.402	0.402	0.403	0.408	0.412	0.418	0.400	0.397	0.389	0.405	0.405	0.406
	Low α2 high α1	0.401	0.401	0.402	0.389	0.386	0.384	0.385	0.383	0.381	0.389	0.386	0.383
	Moderate α1 and α2	0.402	0.402	0.402	0.405	0.402	0.399	0.394	0.391	0.386	0.402	0.399	0.481
30%	Low α1 high α2	0.451	0.451	0.452	0.518	0.588	0.577	0.458	0.389	0.438	0.457	0.460	0.464
	Low α2 high α1	0.450	0.451	0.452	0.423	0.415	0.403	0.402	0.397	0.388	0.416	0.409	0.399
	Moderate α1 and α2	0.450	0.452	0.452	0.494	0.490	0.470	0.440	0.432	0.412	0.454	0.448	0.440
	Average	0.426	0.426	0.427	0.439	0.449	0.442	0.413	0.398	0.399	0.420	0.418	0.429
SE
10%	Low α1 high α2	0.415	0.417	0.419	0.417	0.418	0.414	0.410	0.408	0.402	0.418	0.418	0.414
	Low α2 high α1	0.415	0.416	0.418	0.397	0.396	0.394	0.400	0.399	0.399	0.397	0.395	0.393
	Moderate α1 and α2	0.415	0.417	0.421	0.410	0.408	0.402	0.406	0.404	0.402	0.412	0.409	0.412
30%	Low α1 high α2	0.466	0.467	0.469	0.467	0.450	0.403	0.457	0.464	0.429	0.472	0.470	0.449
	Low α2 high α1	0.466	0.467	0.470	0.406	0.399	0.391	0.414	0.410	0.406	0.412	0.404	0.392
	Moderate α1 and α2	0.465	0.465	0.469	0.439	0.422	0.399	0.439	0.431	0.418	0.456	0.444	0.421
	Average	0.440	0.441	0.444	0.423	0.415	0.401	0.421	0.419	0.409	0.428	0.424	0.414

Note. RMSE = root mean square error; DIF = differential item functioning.

Table 2.

Average Bias, RMSE, and Standard Error of Focal Group Trait Estimates for 40-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item discrimination for two dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	−0.031	−0.022	−0.009	−0.071	−0.092	−0.117	−0.030	−0.022	−0.010	−0.051	−0.060	−0.075
	Low α2 high α1	−0.031	−0.022	−0.010	−0.060	−0.052	−0.042	−0.033	0.022	−0.011	−0.057	−0.049	−0.039
	Moderate α1 and α2	−0.031	−0.023	−0.010	−0.076	−0.076	−0.074	−0.031	−0.024	−0.011	−0.064	−0.063	−0.061
30%	Low α1 high α2	−0.029	−0.020	−0.007	−0.226	−0.326	−0.007	−0.026	−0.022	−0.013	−0.063	−0.086	−0.130
	Low α2 high α1	−0.028	−0.020	−0.008	−0.147	−0.137	−0.008	−0.034	−0.025	−0.014	−0.118	−0.110	−0.106
	Moderate α1 and α2	−0.029	−0.021	−0.008	−0.238	−0.242	−0.008	−0.031	−0.025	−0.041	−0.107	−0.126	−0.132
	Average	−0.030	−0.022	−0.009	−0.136	−0.154	−0.042	−0.031	−0.016	−0.017	−0.077	−0.082	−0.090
RMSE
10%	Low α1 high α2	0.304	0.303	0.304	0.311	0.316	0.321	0.303	0.301	0.299	0.307	0.307	0.307
	Low α2 high α1	0.304	0.304	0.304	0.300	0.297	0.294	0.297	0.238	0.293	0.300	0.297	0.294
	Moderate α1 and α2	0.304	0.303	0.304	0.309	0.307	0.304	0.301	0.299	0.295	0.307	0.304	0.301
30%	Low α1 high α2	0.334	0.334	0.335	0.417	0.482	0.335	0.348	0.368	0.350	0.339	0.341	0.343
	Low α2 high α1	0.335	0.334	0.334	0.333	0.323	0.334	0.303	0.298	0.289	0.317	0.310	0.301
	Moderate α1 and α2	0.334	0.333	0.334	0.412	0.408	0.334	0.340	0.338	0.263	0.340	0.276	0.331
	Average	0.319	0.318	0.319	0.347	0.355	0.320	0.315	0.307	0.298	0.318	0.306	0.313
SE
10%	Low α1 high α2	0.314	0.315	0.317	0.315	0.314	0.306	0.311	0.310	0.308	0.318	0.318	0.313
	Low α2 high α1	0.315	0.316	0.318	0.303	0.302	0.302	0.307	0.304	0.308	0.304	0.303	0.302
	Moderate α1 and α2	0.315	0.316	0.317	0.310	0.307	0.303	0.310	0.310	0.308	0.314	0.311	0.306
30%	Low α1 high α2	0.347	0.348	0.349	0.347	0.327	0.349	0.338	0.338	0.321	0.351	0.350	0.339
	Low α2 high α1	0.347	0.348	0.350	0.301	0.296	0.350	0.305	0.302	0.299	0.312	0.306	0.295
	Moderate α1 and α2	0.348	0.348	0.350	0.328	0.313	0.350	0.326	0.321	0.330	0.345	0.350	0.323
	Average	0.331	0.332	0.334	0.317	0.310	0.327	0.316	0.314	0.312	0.324	0.323	0.313

Note. RMSE = root mean square error; DIF = differential item functioning.

Figure 1.

(a) Bias, (b) RMSE, and (c) standard error of trait estimates of focal group.

Note. RMSE = root mean square error.

The average RMSE of primary trait parameter estimates for the focal group under the multiple-group approach was the lowest among methods across all the conditions. As expected, the modeling approach outperformed both the deleting and ignoring DIF methods. Ignoring DIF resulted in the highest values for RMSE of the primary trait estimate. The average standard error of the trait estimates was the lowest under the ignoring DIF and multiple-group methods. Deleting DIF items resulted in the largest average standard error among the four methods, presumably because excluding DIF items resulted in a shorter test length with less information. Figures 1b and 1c show the graph of average RMSE and standard error of the four DIF treatment methods.

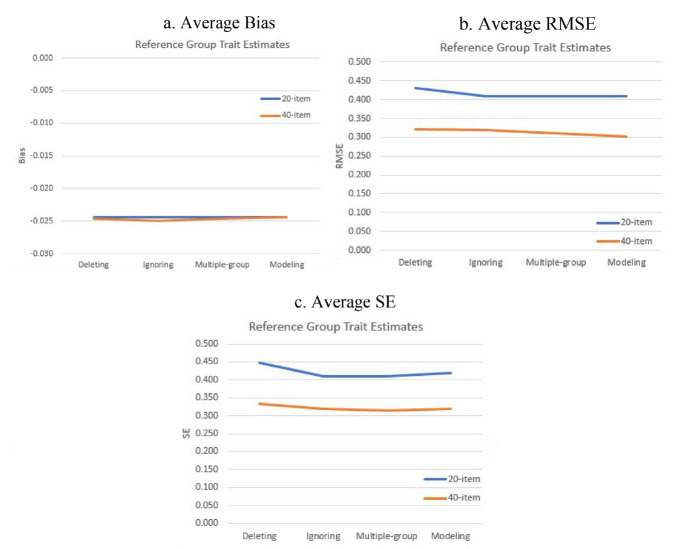
Average bias, RMSE, and standard error of trait estimates for the reference group are presented in the appendix (Tables A1 and A2). The four methods show very similar values with respect to average bias. Average RMSE and standard error show some discrepancies. For 20-item tests, ignoring DIF and the multiple-group method performed similarly and better than deleting DIF. The modeling approach also had good performance with respect to bias and RMSE, but it had slightly higher average standard errors than ignoring DIF and the multiple-group procedure. For 40-item tests, the multiple-group and modeling approaches outperformed the other methods with respect to the accuracy of trait estimates and average standard errors in the reference group. In sum, the multiple-group method always performed well for both short and moderate test length conditions. Deleting DIF items performed the worst in the reference group, likely because deleting items lost information for scoring. Figure A1 shows the graphs of average bias, RMSE, and standard error for the reference group. It is interesting to see that ignoring DIF, multiple-group and modeling approaches behaved similarly for scoring the reference group, while the multiple-group approach outperformed other methods for the focal group. This may be a result of the misfit between the ability distribution of the focal group and the item difficulty distribution of the test. In this situation, different scoring approaches showed different performances in scoring. However, when the ability distribution and item difficulty distribution were matched (i.e., in the reference group), all three scoring methods performed well.

As expected, conditions of more DIF items in the test and shorter test length produced higher RMSEs of the trait estimates. For shorter tests, estimation accuracy was similar across different correlations between the two dimensions, while for longer tests, a higher correlation between dimensions produced higher estimation accuracy, an unexpected result. Higher loadings on the second dimension resulted in lower estimation accuracy as expected. This is in line with Camilli’s (1992) finding that there is a confounding effect of the secondary dimension on item parameters that causes DIF.

Item Parameter Estimation

Average bias, RMSE, and standard error of item discrimination and difficulty estimates for non-DIF items for 20- and 40-item tests are presented in Tables 3, 4, 5, and 6. A positive value of bias means that on average the item parameter estimate is higher than the true value (i.e., overestimated). In contrast, a negative value of bias means that on average the item parameter estimate is lower than the true value (i.e., underestimated). As expected, modeling DIF and multiple-group methods performed better than deleting for item parameter estimation. However, ignoring DIF worked well in shorter test length conditions. Ignoring DIF did not outperform other methods for the few DIF items conditions, which was found in the previous studies.

Table 3.

Average Bias, RMSE, and Standard Error of Item Discrimination for 20-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item Discrimination for Two Dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	0.070	0.060	0.047	0.070	0.054	0.034	0.076	0.061	0.042	0.068	0.056	0.041
	Low α2 high α1	0.073	0.060	0.048	0.069	0.058	0.045	0.067	0.055	0.042	0.071	0.060	0.048
	Moderate α1 and α2	0.071	0.060	0.043	0.068	0.055	0.041	0.071	0.058	0.043	0.069	0.058	0.069
30%	Low α1 high α2	0.066	0.054	0.043	0.028	−0.059	−0.068	0.047	−0.029	−0.033	0.062	0.048	0.034
	Low α2 high α1	0.064	0.053	0.041	0.046	0.035	0.024	0.044	0.031	0.018	0.059	0.048	0.035
	Moderate α1 and α2	0.062	0.056	0.041	0.028	0.005	0.000	0.039	0.015	0.005	0.061	0.051	0.037
	Average	0.068	0.057	0.044	0.052	0.025	0.013	0.057	0.032	0.020	0.065	0.053	0.044
RMSE
10%	Low α1 high α2	0.115	0.109	0.101	0.115	0.105	0.093	0.119	0.109	0.097	0.114	0.106	0.097
	Low α2 high α1	0.116	0.108	0.101	0.113	0.106	0.098	0.112	0.104	0.097	0.115	0.107	0.099
	Moderate α1 and α2	0.115	0.109	0.097	0.113	0.105	0.097	0.115	0.107	0.098	0.114	0.107	0.114
30%	Low α1 high α2	0.121	0.113	0.109	0.108	0.108	0.107	0.113	0.093	0.093	0.118	0.108	0.101
	Low α2 high α1	0.119	0.113	0.108	0.103	0.098	0.093	0.102	0.096	0.091	0.110	0.104	0.098
	Moderate α1 and α2	0.120	0.114	0.107	0.101	0.093	0.089	0.105	0.094	0.089	0.116	0.108	0.100
	Average	0.118	0.111	0.104	0.109	0.102	0.096	0.111	0.100	0.094	0.114	0.107	0.101
SE
10%	Low α1 high α2	0.181	0.179	0.176	0.179	0.175	0.170	0.180	0.176	0.170	0.178	0.175	0.171
	Low α2 high α1	0.181	0.179	0.177	0.175	0.173	0.170	0.175	0.172	0.169	0.176	0.173	0.170
	Moderate α1 and α2	0.181	0.179	0.176	0.177	0.174	0.170	0.178	0.174	0.170	0.177	0.174	0.177
30%	Low α1 high α2	0.195	0.192	0.190	0.185	0.169	0.160	0.190	0.172	0.164	0.194	0.189	0.180
	Low α2 high α1	0.194	0.191	0.189	0.177	0.173	0.169	0.177	0.173	0.168	0.180	0.176	0.172
	Moderate α1 and α2	0.193	0.192	0.189	0.181	0.173	0.168	0.183	0.175	0.169	0.190	0.185	0.177
	Average	0.187	0.185	0.183	0.179	0.173	0.168	0.180	0.174	0.169	0.183	0.179	0.175

Note. RMSE = root mean square error; DIF = differential item functioning.

Table 4.

Average Bias, RMSE, and Standard Error of Item Discrimination for 40-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item Discrimination for Two Dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	0.070	0.057	0.044	0.071	0.058	0.039	0.074	0.061	0.037	0.072	0.062	0.050
	Low α2 high α1	0.073	0.054	0.041	0.063	0.054	0.040	0.058	0.057	0.033	0.073	0.064	0.050
	Moderate α1 and α2	0.071	0.057	0.043	0.067	0.057	0.042	0.067	0.054	0.036	0.072	0.064	0.051
30%	Low α1 high α2	0.060	0.052	0.038	0.034	−0.051	−0.062	0.053	−0.025	−0.044	0.078	0.069	0.058
	Low α2 high α1	0.059	0.049	0.037	0.041	0.030	0.019	0.038	0.025	0.011	0.078	0.069	0.055
	Moderate α1 and α2	0.058	0.049	0.036	0.022	−0.001	−0.005	0.033	0.005	−0.023	0.076	0.045	0.057
	Average	0.065	0.053	0.040	0.049	0.024	0.012	0.054	0.029	0.008	0.075	0.062	0.053
RMSE
10%	Low α1 high α2	0.122	0.117	0.110	0.126	0.117	0.106	0.128	0.119	0.105	0.118	0.111	0.104
	Low α2 high α1	0.119	0.113	0.106	0.118	0.112	0.104	0.115	0.080	0.101	0.117	0.111	0.102
	Moderate α1 and α2	0.121	0.115	0.107	0.122	0.114	0.106	0.122	0.113	0.103	0.118	0.112	0.104
30%	Low α1 high α2	0.135	0.132	0.123	0.136	0.113	0.107	0.144	0.109	0.100	0.120	0.113	0.106
	Low α2 high α1	0.134	0.128	0.121	0.119	0.112	0.105	0.117	0.109	0.102	0.118	0.110	0.101
	Moderate α1 and α2	0.133	0.126	0.121	0.116	0.102	0.098	0.120	0.103	0.080	0.118	0.077	0.104
	Average	0.127	0.122	0.115	0.123	0.112	0.104	0.124	0.105	0.099	0.118	0.106	0.104
SE
10%	Low α1 high α2	0.192	0.190	0.189	0.192	0.190	0.187	0.195	0.191	0.187	0.181	0.179	0.177
	Low α2 high α1	0.191	0.190	0.189	0.189	0.188	0.186	0.189	0.188	0.185	0.179	0.178	0.175
	Moderate α1 and α2	0.192	0.191	0.189	0.191	0.190	0.187	0.192	0.190	0.186	0.180	0.179	0.176
30%	Low α1 high α2	0.188	0.186	0.184	0.181	0.167	0.164	0.187	0.173	0.167	0.176	0.174	0.170
	Low α2 high α1	0.188	0.186	0.184	0.178	0.176	0.174	0.179	0.176	0.173	0.170	0.167	0.164
	Moderate α1 and α2	0.187	0.186	0.184	0.179	0.174	0.171	0.182	0.176	0.168	0.174	0.169	0.167
	Average	0.190	0.188	0.186	0.185	0.181	0.178	0.187	0.182	0.178	0.177	0.174	0.171

Note. RMSE = root mean square error; DIF = differential item functioning.

Table 5.

Average Bias, RMSE, and Standard Error of Item Difficulty for 20-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item Discrimination for Two Dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	0.077	0.079	0.084	0.065	0.059	0.052	0.079	0.081	0.084	0.068	0.064	0.058
	Low α2 high α1	0.081	0.082	0.087	0.069	0.070	0.076	0.079	0.079	0.085	0.071	0.071	0.077
	Moderate α1 and α2	0.080	0.081	0.086	0.065	0.063	0.064	0.081	0.081	0.085	0.067	0.066	0.067
30%	Low α1 high α2	0.081	0.084	0.092	0.034	−0.001	−0.016	0.090	0.087	0.083	0.065	0.054	0.039
	Low α2 high α1	0.080	0.083	0.091	0.047	0.049	0.055	0.073	0.074	0.080	0.051	0.053	0.059
	Moderate α1 and α2	0.073	0.084	0.087	0.031	0.025	0.028	0.082	0.080	0.083	0.050	0.047	0.046
	Average	0.079	0.082	0.088	0.052	0.044	0.043	0.081	0.081	0.083	0.062	0.059	0.058
RMSE
10%	Low α1 high α2	0.119	0.120	0.121	0.114	0.111	0.105	0.121	0.121	0.120	0.115	0.112	0.108
	Low α2 high α1	0.122	0.121	0.122	0.117	0.115	0.115	0.120	0.119	0.120	0.118	0.116	0.116
	Moderate α1 and α2	0.121	0.120	0.119	0.114	0.112	0.111	0.121	0.120	0.121	0.114	0.113	0.114
30%	Low α1 high α2	0.128	0.127	0.130	0.120	0.110	0.103	0.137	0.130	0.124	0.121	0.114	0.107
	Low α2 high α1	0.126	0.126	0.128	0.112	0.110	0.108	0.119	0.118	0.118	0.114	0.112	0.111
	Moderate α1 and α2	0.126	0.127	0.125	0.116	0.108	0.104	0.130	0.124	0.123	0.117	0.113	0.110
	Average	0.124	0.124	0.124	0.116	0.111	0.108	0.125	0.122	0.121	0.117	0.113	0.111
SE
10%	Low α1 high α2	0.182	0.181	0.180	0.180	0.177	0.173	0.182	0.179	0.176	0.181	0.178	0.174
	Low α2 high α1	0.183	0.181	0.180	0.178	0.177	0.176	0.180	0.178	0.177	0.179	0.177	0.176
	Moderate α1 and α2	0.183	0.181	0.180	0.179	0.177	0.175	0.181	0.179	0.177	0.179	0.177	0.179
30%	Low α1 high α2	0.196	0.194	0.194	0.190	0.183	0.175	0.197	0.189	0.184	0.198	0.193	0.184
	Low α2 high α1	0.195	0.194	0.193	0.182	0.180	0.178	0.185	0.183	0.181	0.184	0.181	0.179
	Moderate α1 and α2	0.194	0.194	0.192	0.186	0.181	0.178	0.192	0.187	0.184	0.192	0.187	0.182
	Average	0.189	0.188	0.186	0.183	0.179	0.176	0.186	0.183	0.180	0.186	0.182	0.179

Note. RMSE = root mean square error; DIF = differential item functioning.

Table 6.

Average Bias, RMSE, and Standard Error of Item Difficulty for 40-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item discrimination for two dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	0.077	0.071	0.081	0.059	0.056	0.054	0.069	0.074	0.080	0.061	0.060	0.061
	Low α2 high α1	0.081	0.070	0.079	0.058	0.063	0.070	0.065	0.074	0.079	0.059	0.062	0.070
	Moderate α1 and α2	0.080	0.069	0.080	0.056	0.057	0.062	0.067	0.071	0.079	0.058	0.060	0.065
30%	Low α1 high α2	0.099	0.103	0.111	0.080	0.040	0.016	0.130	0.122	0.109	0.084	0.080	0.071
	Low α2 high α1	0.101	0.104	0.113	0.075	0.076	0.080	0.102	0.103	0.107	0.073	0.074	0.077
	Moderate α1 and α2	0.100	0.102	0.113	0.063	0.049	0.052	0.114	0.105	0.129	0.074	0.082	0.070
	Average	0.090	0.086	0.096	0.065	0.057	0.056	0.091	0.092	0.097	0.068	0.070	0.069
RMSE
10%	Low α1 high α2	0.116	0.115	0.123	0.115	0.115	0.113	0.128	0.139	0.119	0.108	0.105	0.103
	Low α2 high α1	0.113	0.112	0.116	0.117	0.125	0.111	0.113	0.106	0.116	0.108	0.107	0.107
	Moderate α1 and α2	0.115	0.114	0.128	0.113	0.120	0.107	0.118	0.123	0.115	0.108	0.106	0.105
30%	Low α1 high α2	0.139	0.140	0.144	0.149	0.127	0.107	0.172	0.156	0.143	0.123	0.119	0.112
	Low α2 high α1	0.142	0.142	0.152	0.127	0.138	0.123	0.140	0.142	0.139	0.119	0.117	0.114
	Moderate α1 and α2	0.155	0.145	0.157	0.136	0.114	0.118	0.156	0.141	0.129	0.119	0.100	0.112
	Average	0.130	0.128	0.137	0.126	0.123	0.113	0.138	0.134	0.127	0.114	0.109	0.109
SE
10%	Low α1 high α2	0.226	0.230	0.227	0.244	0.223	0.294	0.249	0.225	0.293	0.197	0.195	0.193
	Low α2 high α1	0.226	0.226	0.232	0.262	0.222	0.226	0.224	0.224	0.227	0.195	0.194	0.194
	Moderate α1 and α2	0.226	0.232	0.230	0.223	0.224	0.240	0.279	0.237	0.225	0.195	0.195	0.193
30%	Low α1 high α2	0.214	0.216	0.214	0.202	0.198	0.198	0.210	0.208	0.208	0.180	0.177	0.173
	Low α2 high α1	0.215	0.215	0.232	0.206	0.205	0.205	0.210	0.210	0.209	0.172	0.170	0.168
	Moderate α1 and α2	0.214	0.214	0.214	0.204	0.203	0.202	0.211	0.210	0.201	0.176	0.174	0.171
	Average	0.221	0.222	0.225	0.223	0.212	0.228	0.230	0.219	0.227	0.186	0.184	0.182

Note. RMSE = root mean square error; DIF = differential item functioning.

Item Discrimination

Generally, the four DIF treatment approaches overestimated item discrimination parameters except in the conditions of 30% DIF items with high loadings on the secondary dimension for ignoring DIF and multiple-group approaches. The four DIF treatment approaches performed differently with respect to accuracy of item parameter estimates for shorter and longer test length conditions.

For 20-item tests, ignoring DIF items during calibration resulted in the lowest average positive bias in discrimination parameter estimates and deleting DIF items produced the highest average positive bias. Average bias values of the multiple-group method were slightly higher than those of the ignoring DIF method. The modeling approach did not outperform ignoring DIF and the multiple-group method. The multiple-group and ignoring DIF methods showed the best performance with respect to average RMSE and standard error of discrimination parameter estimates. Deleting DIF items produced the highest values of average RMSE and standard error of discrimination parameter estimates and the modeling method did not outperform ignoring DIF and the multiple-group method.

For 40-item tests, however, the modeling approach outperformed other methods with respect to average RMSEs and standard errors, but had higher values of average positive bias. Ignoring DIF resulted in the lowest values of average positive bias but relatively high values of average RMSEs and standard errors. The multiple-group method outperformed other methods for both average positive bias and RMSE, but had higher standard errors. As in the 20-item condition, deleting DIF items performed the worst.

Lower correlation between the two dimensions and higher loadings on the secondary dimension led to lower estimation accuracy for item discrimination parameters. However, the condition of a short test length (20-item) showed slightly lower values of average bias and RMSE than other conditions. This pattern is different from that for trait estimation. The percentage of DIF items did not have a substantial influence on the results.

Item Difficulty

Generally, the four DIF treatment approaches overestimated non-DIF item difficulty parameters, except in the conditions of 30% DIF items with higher loadings on the secondary dimension for the ignoring DIF approach in the 20-item test. Again, the four DIF treatment approaches performed differently with respect to accuracy of item difficulty parameter estimates for shorter and longer test length conditions.

For 20-item tests, ignoring DIF produced the most accurate item difficulty estimates. However, the modeling approach performed better than deleting DIF and the multiple-group method with respect to average bias, RMSE, and standard error.

For 40-item tests, the modeling method performed the best among the four approaches with respect to average RMSE and standard error. Deleting DIF and the multiple-group method performed worse than ignoring DIF and the modeling approach.

In addition, a higher number of DIF items and longer test length led to lower estimation accuracy for item difficulty. The magnitude of the loadings on the secondary dimension and the correlation between the two dimensions did not have a consistent effect on the accuracy of difficulty estimates.

Figure 2 shows graphs of average bias, RMSE, and standard error of the four DIF treatment methods for both discrimination and difficulty parameters. All four approaches performed well with respect to lower asymptote parameter estimation. Average bias, RMSE, and standard error of estimation for the lower asymptote parameters are shown in the Tables A3 and A4.

Figure 2.

Bias, RMSE, and standard error of item parameters

Note. RMSE = root mean square error

Discussion

Proper treatment of DIF is essential to test fairness. This study compared four DIF treatment methods (deleting, ignoring, multiple-group calibration, and modeling DIF) within a two-dimensional framework for items with DIF. Based on the mixed results, none of the DIF treatments has a dominant advantage over other treatments. Table 7 shows a summary of the performance of the four DIF treatment approaches under different conditions. The criterion for the best and worst methods was based on overall accuracy (i.e., RMSE) and precision (i.e., average standard error) across all conditions.

Table 7.

Summary of Performance of DIF Treatment Approaches Under Different Conditions.

Parameters	Conditions	Best	Worst
Trait	Focal group	Multiple-group	Ignoring
	Reference group	Multiple-group	Deleting
Discrimination	20-Item	Ignoring and multiple-group	Deleting
	40-Item	Modeling	Deleting
Difficulty	20-Item	Ignoring	Deleting
	40-Item	Modeling	Deleting and multiple-group

Overall, the multiple-group approach performed the best in estimating trait values for both the focal and the reference groups. This result agrees with the conclusion of Cho et al. (2016). The modeling approach worked well in estimating trait values for the reference group with respect to overall accuracy but had lower precision than other methods. However, the modeling method in the current study did not show as good performance as in Cho et al. (2016). Ignoring DIF performed the worst for estimating trait values in the focal group and deleting DIF yielded the least accurate estimates for trait values in the reference group.

The modeling approach has the best overall estimation accuracy and precision for longer test length conditions for non-DIF item parameter estimates, while ignoring DIF always performed the best for short test length conditions. Deleting DIF also performed the worst for estimating item parameters. These results are not consistent with those of Cho et al. (2016), who found that the multiple-group method worked the best in item parameter estimation for short test length conditions. This difference may be due to different calibration methods for the multiple-group approach. Cho et al. (2016) used the reference group only for calibrating, whereas the current study used both reference and focal groups and allowed the DIF item parameters to vary for the two groups.

Deleting DIF method performed the worst for most conditions with respect to trait and item parameters. This may be due to the loss of information after removing DIF items, especially when many DIF items are detected. Furthermore, deleting DIF leads to lower reliability and content validity, and would shorten the number of items with a certain level of difficulty (Fleishman et al., 2002). Therefore, this method is not recommended.

The conclusions of the current study mostly agree with the suggestions offered by Cho et al. (2016) that the multiple-group and modeling methods outperform deleting and ignoring DIF items for trait estimation. Importantly, the current study extended the previous studies by investigating the impact of test length, which does have an impact on the estimation of trait and item parameters. Surprisingly, ignoring DIF produced the best results with respect to non-DIF item parameter estimation for shorter test length conditions, while the modeling approach performed best for longer test length conditions.

Practical Recommendations

Based on the present results, different treatments should be selected for different assessment purposes. If trait estimation is of greatest interest, the multiple-group approach should be chosen. If item parameter calibration is of greatest interest for a short test, ignoring DIF would not hurt for this purpose. If the test is longer, however, the modeling approach is the best choice. Deleting DIF items is not recommended since it always performed the worst in scoring and item calibration.

One point of note for choice of DIF treatment is the computational load. Deleting DIF, ignoring DIF, and the multiple-group method used only a few seconds when running the analysis with flexMIRT 3.5. However, the modeling approach used approximately 2 minutes for the current study with samples of 1,500 for the reference group and 500 for the focal group, and it would be more time-consuming when a larger data set is analyzed.

Limitations and Future Directions

The current study presumes DIF items were known rather than identified using a preliminary DIF detection procedure. In reality, DIF detection is not perfect and failure to correctly identify the DIF/non-DIF items may affect the relative efficacy of the DIF treatments. The impact of imperfect DIF detection should be taken into account in comparing different DIF treatment approaches for future studies. In addition, all DIF items were assumed to measure the same secondary dimension, which may not be the case in a real test, and which may give a spurious advantage to the DIF modeling approach. Different secondary dimensions that cause DIF should be studied as a factor affecting the efficiency of DIF treatments. Furthermore, the current study used a multidimensional item response model to generate DIF items and applied the same MMD in the modeling treatment, which may also advantage this method.

Appendix

Table A1.

Average Bias, RMSE, and Standard Error of Reference Group Trait Estimates for 20-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item discrimination for two dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	−0.034	−0.026	−0.013	−0.034	−0.026	−0.012	−0.034	−0.026	−0.012	−0.034	−0.026	−0.012
	Low α2 high α1	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.012
	Moderate α1 and α2	−0.034	−0.026	−0.013	−0.034	−0.026	−0.012	−0.034	−0.026	−0.013	−0.034	−0.026	−0.012
30%	Low α1 high α2	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013
	Low α2 high α1	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.012
	Moderate α1 and α2	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013
	Average	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013	−0.034	−0.026	−0.013
RMSE
10%	Low α1 high α2	0.407	0.407	0.408	0.405	0.400	0.390	0.405	0.401	0.391	0.405	0.400	0.390
	Low α2 high α1	0.407	0.407	0.407	0.388	0.386	0.383	0.388	0.386	0.383	0.388	0.385	0.383
	Moderate α1 and α2	0.407	0.407	0.407	0.398	0.394	0.386	0.398	0.394	0.387	0.398	0.394	0.486
30%	Low α1 high α2	0.456	0.456	0.456	0.469	0.483	0.438	0.470	0.483	0.438	0.452	0.442	0.414
	Low α2 high α1	0.455	0.455	0.456	0.400	0.392	0.380	0.400	0.393	0.380	0.399	0.391	0.379
	Moderate α1 and α2	0.454	0.456	0.453	0.442	0.431	0.402	0.444	0.433	0.404	0.433	0.422	0.398
	Average	0.431	0.431	0.431	0.417	0.414	0.396	0.418	0.415	0.397	0.413	0.406	0.408
SE
10%	Low α1 high α2	0.420	0.421	0.422	0.416	0.412	0.403	0.416	0.411	0.401	0.418	0.415	0.406
	Low α2 high α1	0.421	0.421	0.423	0.401	0.400	0.398	0.401	0.400	0.398	0.401	0.400	0.398
	Moderate α1 and α2	0.421	0.421	0.423	0.410	0.406	0.401	0.409	0.406	0.400	0.411	0.408	0.411
30%	Low α1 high α2	0.472	0.473	0.474	0.455	0.433	0.396	0.455	0.433	0.395	0.467	0.458	0.433
	Low α2 high α1	0.471	0.472	0.474	0.403	0.397	0.390	0.404	0.398	0.391	0.410	0.403	0.392
	Moderate α1 and α2	0.471	0.472	0.473	0.431	0.417	0.397	0.431	0.416	0.397	0.448	0.437	0.415
	Average	0.446	0.447	0.448	0.419	0.411	0.397	0.419	0.411	0.397	0.426	0.420	0.409

Table A2.

Average Bias, RMSE, and Standard Error of Reference Group Trait Estimates for 40-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item discrimination for two dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013	−0.035	−0.026	−0.013	−0.035	−0.026	−0.013
	Low α2 high α1	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013	−0.035	−0.026	−0.013	−0.034	−0.026	−0.012
	Moderate α1 and α2	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013	−0.035	−0.026	−0.013	−0.034	−0.026	−0.013
30%	Low α1 high α2	−0.034	−0.026	−0.013	−0.035	−0.027	−0.013	−0.034	−0.026	−0.013	−0.035	−0.027	−0.013
	Low α2 high α1	−0.034	−0.026	−0.013	−0.035	−0.027	−0.013	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013
	Moderate α1 and α2	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013
	Average	−0.035	−0.026	−0.013	−0.035	−0.027	−0.013	−0.035	−0.026	−0.013	−0.034	−0.026	−0.013
RMSE
10%	Low α1 high α2	0.307	0.306	0.306	0.306	0.303	0.297	0.306	0.304	0.298	0.306	0.303	0.296
	Low α2 high α1	0.307	0.306	0.306	0.296	0.294	0.291	0.296	0.231	0.292	0.297	0.294	0.292
	Moderate α1 and α2	0.307	0.306	0.307	0.302	0.299	0.294	0.302	0.299	0.295	0.302	0.299	0.295
30%	Low α1 high α2	0.338	0.338	0.338	0.367	0.395	0.338	0.371	0.397	0.360	0.337	0.331	0.315
	Low α2 high α1	0.339	0.338	0.338	0.301	0.295	0.338	0.303	0.296	0.285	0.298	0.292	0.282
	Moderate α1 and α2	0.339	0.338	0.338	0.349	0.342	0.338	0.353	0.345	0.264	0.326	0.260	0.302
	Average	0.323	0.322	0.322	0.320	0.321	0.316	0.322	0.312	0.299	0.311	0.297	0.297
SE
10%	Low α1 high α2	0.318	0.318	0.319	0.314	0.310	0.303	0.314	0.311	0.304	0.317	0.315	0.309
	Low α2 high α1	0.318	0.318	0.320	0.306	0.305	0.304	0.307	0.306	0.305	0.307	0.306	0.304
	Moderate α1 and α2	0.318	0.318	0.319	0.310	0.308	0.304	0.311	0.308	0.305	0.313	0.311	0.307
30%	Low α1 high α2	0.351	0.351	0.352	0.335	0.319	0.352	0.335	0.320	0.295	0.349	0.344	0.329
	Low α2 high α1	0.351	0.351	0.352	0.296	0.292	0.352	0.298	0.294	0.289	0.308	0.303	0.293
	Moderate α1 and α2	0.351	0.351	0.353	0.317	0.307	0.353	0.317	0.308	0.300	0.338	0.337	0.317
	Average	0.334	0.335	0.336	0.313	0.307	0.328	0.314	0.308	0.300	0.322	0.319	0.310

Note. RMSE = root mean square error; DIF = differential item functioning.

Table A3.

Average Bias, RMSE, and Standard Error of Lower Asymptote for 20-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item Discrimination for Two Dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	0.060	0.057	0.055	0.060	0.058	0.056	0.060	0.058	0.055	0.060	0.057	0.054
	Low α2 high α1	0.061	0.058	0.055	0.060	0.057	0.055	0.060	0.057	0.055	0.060	0.057	0.055
	Moderate α1 and α2	0.060	0.058	0.055	0.060	0.058	0.055	0.060	0.058	0.055	0.060	0.058	0.060
30%	Low α1 high α2	0.069	0.067	0.065	0.074	0.074	0.066	0.074	0.072	0.066	0.069	0.067	0.064
	Low α2 high α1	0.068	0.066	0.064	0.068	0.065	0.062	0.068	0.065	0.062	0.067	0.064	0.062
	Moderate α1 and α2	0.067	0.067	0.063	0.072	0.068	0.063	0.072	0.067	0.063	0.069	0.066	0.063
	Average	0.064	0.062	0.059	0.066	0.063	0.059	0.066	0.063	0.059	0.064	0.061	0.060
RMSE
10%	Low α1 high α2	0.096	0.094	0.092	0.097	0.095	0.094	0.097	0.095	0.093	0.096	0.094	0.093
	Low α2 high α1	0.097	0.095	0.093	0.097	0.095	0.093	0.097	0.095	0.093	0.097	0.095	0.093
	Moderate α1 and α2	0.096	0.095	0.092	0.097	0.095	0.093	0.097	0.095	0.093	0.097	0.095	0.097
30%	Low α1 high α2	0.092	0.090	0.088	0.098	0.097	0.088	0.097	0.092	0.089	0.092	0.090	0.088
	Low α2 high α1	0.091	0.089	0.088	0.092	0.090	0.087	0.092	0.089	0.087	0.091	0.089	0.087
	Moderate α1 and α2	0.091	0.090	0.086	0.095	0.091	0.088	0.095	0.091	0.088	0.092	0.089	0.087
	Average	0.094	0.092	0.090	0.096	0.094	0.090	0.096	0.093	0.090	0.094	0.092	0.091
SE
10%	Low α1 high α2	0.340	0.343	0.346	0.338	0.339	0.339	0.338	0.339	0.340	0.339	0.341	0.341
	Low α2 high α1	0.339	0.343	0.346	0.336	0.340	0.342	0.336	0.340	0.342	0.336	0.339	0.342
	Moderate α1 and α2	0.340	0.343	0.347	0.336	0.339	0.341	0.336	0.339	0.341	0.337	0.339	0.337
30%	Low α1 high α2	0.325	0.327	0.329	0.334	0.342	0.345	0.332	0.335	0.336	0.338	0.337	0.334
	Low α2 high α1	0.326	0.328	0.330	0.324	0.327	0.329	0.324	0.327	0.329	0.326	0.328	0.329
	Moderate α1 and α2	0.327	0.327	0.330	0.330	0.335	0.335	0.329	0.333	0.333	0.333	0.334	0.333
	Average	0.333	0.335	0.338	0.333	0.337	0.339	0.333	0.335	0.337	0.335	0.336	0.336

Note. RMSE = root mean square error; DIF = differential item functioning.

Table A4.

Average Bias, RMSE, and Standard Error of Lower Asymptote for 40-Item Tests.

		Deleting			Ignoring			Multiple-group			Modeling
No. of DIF items	Item Discrimination for Two Dimensions	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7	0	0.3	0.7
Bias
10%	Low α1 high α2	0.060	0.045	0.043	0.048	0.046	0.043	0.048	0.047	0.043	0.050	0.047	0.044
	Low α2 high α1	0.061	0.045	0.043	0.047	0.045	0.043	0.047	0.044	0.043	0.049	0.047	0.044
	Moderate α1 and α2	0.060	0.045	0.043	0.048	0.046	0.043	0.048	0.046	0.043	0.050	0.048	0.045
30%	Low α1 high α2	0.061	0.058	0.056	0.068	0.060	0.052	0.069	0.064	0.056	0.059	0.057	0.054
	Low α2 high α1	0.060	0.058	0.055	0.063	0.059	0.056	0.063	0.059	0.055	0.060	0.057	0.054
	Moderate α1 and α2	0.060	0.058	0.056	0.067	0.060	0.055	0.067	0.061	0.064	0.060	0.060	0.054
	Average	0.060	0.052	0.049	0.057	0.053	0.048	0.057	0.053	0.051	0.055	0.053	0.049
RMSE
10%	Low α1 high α2	0.084	0.082	0.081	0.084	0.083	0.081	0.084	0.083	0.081	0.086	0.085	0.083
	Low α2 high α1	0.084	0.082	0.081	0.084	0.082	0.081	0.084	0.078	0.081	0.086	0.084	0.083
	Moderate α1 and α2	0.084	0.083	0.081	0.085	0.083	0.081	0.085	0.083	0.081	0.086	0.085	0.083
30%	Low α1 high α2	0.084	0.082	0.080	0.092	0.085	0.078	0.092	0.088	0.080	0.083	0.082	0.080
	Low α2 high α1	0.084	0.082	0.080	0.086	0.084	0.081	0.086	0.083	0.080	0.084	0.082	0.080
	Moderate α1 and α2	0.083	0.082	0.080	0.089	0.084	0.080	0.089	0.084	0.079	0.084	0.077	0.080
	Average	0.084	0.082	0.080	0.087	0.083	0.080	0.087	0.083	0.081	0.085	0.083	0.081
SE
10%	Low α1 high α2	0.293	0.295	0.298	0.291	0.292	0.296	0.292	0.292	0.296	0.298	0.299	0.301
	Low α2 high α1	0.294	0.296	0.298	0.293	0.295	0.298	0.293	0.295	0.298	0.297	0.300	0.302
	Moderate α1 and α2	0.293	0.295	0.298	0.292	0.294	0.298	0.292	0.294	0.297	0.296	0.299	0.302
30%	Low α1 high α2	0.306	0.309	0.311	0.297	0.317	0.326	0.295	0.306	0.314	0.315	0.315	0.315
	Low α2 high α1	0.306	0.309	0.312	0.294	0.299	0.303	0.296	0.300	0.303	0.305	0.308	0.310
	Moderate α1 and α2	0.307	0.309	0.312	0.298	0.308	0.312	0.297	0.305	0.301	0.311	0.313	0.315
	Average	0.300	0.302	0.305	0.294	0.301	0.305	0.294	0.299	0.302	0.304	0.306	0.308

Note. RMSE = root mean square error; DIF = differential item functioning.

Figure A1.

Average Bias, RMSE, and standard error of reference group.

Note. RMSE = root mean square error.