Abstract
Background
Escalation With Overdose Control (EWOC) designs are increasingly used to ensure dose-toxicity curve of investigational oncology drugs is efficiently characterized during dose escalation steps. We propose a novel EWOC-based method that integrates the longitudinal pharmacokinetic (PK) data of individual patients in a Bayesian forecasting exposure-safety framework.
Methods
The method, called exposure-driven EWOC (ED-EWOC), relies on a population PK model coupled with a Bayesian logistic regression model to make dose recommendation for the next cohort of patients.
Results
We applied ED-EWOC to a real oncology clinical trial in parallel to a traditional EWOC approach. We found that for comparable priors, ED-EWOC dose recommendations were equivalent to the one suggested by EWOC when PK is dose proportional with low inter-individual variability.
Conclusion
This case example demonstrates that ED-EWOC is logistically feasible during a trial conduct when PK bioanalysis can be expedited in the dose escalation phase. Overall, we anticipate that exposure-guided Bayesian designs could benefit patients and drug developers to identify the optimal dose steps of novel compounds entering the clinic with suspected liability in PK or that exhibit large inter-individual variability.
Keywords: Adaptive designs, Escalation with overdose control (EWOC), Bayesian inferences, Population pharmacokinetic modeling, Exposure
Abbreviations: Escalation With Overdose Control, EWOC; exposure-driven EWOC, ED-EWOC; pharmacokinetic, PK; maximum tolerated dose, MTD; Continual Reassessment Method, CRM; dose limiting toxicity, DLT; pharmacodynamic, PD; area under the concentration-time curve, AUC; Bayesian logistic regression model, BLRM; once every 3 weeks, Q3W; First Order Conditional Estimation, FOCE
Highlights
-
•
Formally leverage pharmacokinetic data and modeling in dose escalation studies.
-
•
Suitable for molecules with potential non-linear pharmacokinetic.
-
•
Smarter dose escalation and more informative recommended phase 2 dose.
1. Introduction
Phase I dose escalation in oncology aims at finding the maximum tolerated dose (MTD) and Recommended Phase 2 dose (RP2D) for further development, based on pharmacokinetics, safety data, and early signs of efficacy. This is a critical step in oncology early clinical development that consists of evaluating a therapeutic intervention in small cohorts of patients covering a spectrum of doses and ensuring that safety data is accrued while controlling dose-limiting toxicity risk in future patients being tested. Typically, two main classes of clinical trial designs are implemented: rule-based designs originally described by Dixon and Mood's work [1], and model-based designs introduced by O'Quigley et al. [2]. Rule-based designs have been the gold standard over the last few decades and comprises a variety of empirical approaches to effectively escalate patients to the next dose cohort according to pre-specified criteria utilizing data generated at the previous dose level. While simulations have shown that rule-based designs identify the right maximum tolerated dose less frequently than model-based designs [[3], [4], [5]], adoption of model-based designs in early clinical trials remain relatively low although prevalence is gradually increasing [6]. Model-based designs referred to as Continual Reassessment Method (CRM) [2] possess attractive operating characteristics, including good efficiency relative to the sample size of patients and dose steps required, ultimately resulting in more efficient dose escalation [7]. CRM is relying on a model relating dose to probability of toxicity (typically either a 1-parameter power model or a 2-parameter logistic model) from which forecasting of the probability of dose limiting toxicity (DLT) at subsequent dose levels can be inferred. Escalation With Overdose Control (EWOC) designs [[8], [9], [10], [11]] are a more advanced CRM design in which integration of the totality of toxicity data from all patients enrolled up to a certain point is complemented by an additional probabilistic adjustment to prevent excessive overdose. Overall, model-based designs based on robust statistical framework present significant advantages over algorithmic design [[12], [13], [14]] and their use is accepted by health authority agencies (FDA guideline on Adaptive Designs for Clinical Trials [15]). However, from a pharmacological standpoint and in light of the variability observed in biological systems, the underlying paradigm upon which a direct association of dose and toxicity is clinically questionable. Indeed, while the occurrence of a toxicity or safety event could be a function of the concentration of drug in the body, the dose may not be an appropriate surrogate of the drug pharmacokinetics (PK) when the latter exhibit a large variability or when drug pharmacology or disease progression follows non-linear processes. We postulate that an accurate specification of the MTD capturing the relationship between drug exposure and dose limiting events would allow for a better discrimination of patients with high likelihood of experiencing events. This is echoed by recent EMA guidelines [16] that recommend integration of all available and relevant non-clinical and clinical data (such as PK and pharmacodynamic (PD) endpoints) in dose-escalation studies.
Precedents of accounting for drug exposure levels in dose escalation oncology trials have been proposed. A variation of the standard 3 + 3 rule-based design called pharmacologically guided dose escalation was implemented [17]. Other model‐based approaches incorporating PK or PD information into early phase dose‐finding trials have been suggested by Piantadosi and Liu [18], Patterson et al. [19], Whitehead et al. [20,21], and O'Quigley et al. [22]. However, it has been shown by Ursino et al. [23] in a simulation study that none of these approaches has a significant edge over previous methods. Ursino et al. [23] and more recently Takeda et al. [24] have proposed more elaborate methods with attempts of a better integration of the PK. However in both manuscripts simple estimation of the drug exposure were used while the between patients variability was not appropriately characterized. For instance, the drug is assumed to follow a one-compartment dose-linear kinetics and only the variability of the clearance is accounted for. The potential variability in bioavailability or of absorption in case of flip-flop kinetics [25,26] are ignored. Takeda et al. [24] considered simplified non-linear kinetics not reflecting what is observed in case of saturated absorption for instance or for target mediated drug disposition antibody. Furthermore, the authors used inflated measurement errors in lieu of between patients variability. Moreover, none of the approach consider inclusion of adjustment for potential overdose and all proposed methodologies lack application to a real clinical trial setting. In parallel to our work, two new approaches were proposed recently. Günhan et al. [27,28] offer an elegant solution to support dose-escalation relying on a drug exposure-time to event model. This approach requires prior knowledge (or assumptions) on the PK profiles of the IMP, and uses time to DLT as an endpoint to drive the dose escalation. We believe that this method is a promising venue to support the design and dose-related decisions in Phase 1a studies. The other approach, by Gerard et al. [29,30], further incorporate PK/PD knowledge into the determination of the MTD regimen (i.e. a set of doses inducing acceptable tolerability/toxicity). The proposed solution recapitulates a possible causal pathway going from dose to concentration to cytokine release syndrome (CRS). This model-based exercise is addressing a clear need in immunotherapy where DLTs are often immune-related. However, it may not apply to other setting. Besides, it can be implemented only when enough data has been collected to support the development of the dose-exposure-cytokine levels and related CRS models.
In the present paper, we report the implementation of a new Bayesian adaptive design utilizing exposure metrics in the dose allocation of a dose escalation clinical study evaluating an anonymized drug. Instead of the dose, our approach incorporates secondary PK parameters (e.g., maximum concentration levels (Cmax) or area under the concentration-time curve (AUC)) as dependent variable of the Bayesian logistic regression model. We refer to this approach as Exposure-Driven Escalation With Overdose Control (ED-EWOC) since the dose allocation process incorporates the updated dose-exposure relationship, the variability observed in PK, and an overdose control implementation. The ED-EWOC approach is presented as an integrated process enabling estimation of the posterior predictive probability of DLT occurrence while accounting for both the variability in drug exposure and the uncertainty in the exposure-DLT relationship. We then describe implementation of ED-EWOC statistical framework during the dose-escalation conduct of a phase 1 clinical trial operated with a conventional EWOC design, and draw direct comparison of its relative performance in dose recommendation for the next cohorts of patients.
2. Material and method
2.1. ED-EWOC principle
Conceptually, ED-EWOC is a Bayesian adaptive design enabling a dose recommendation for a subsequent cohort of patients based on the assessment of the interplay between dose, exposure, and toxicity and with an overdose control. The dose escalation rule is based on the predictive probability of dose limiting toxicity (DLT) which is the product of two models: a population PK model relating dose to exposure and a model relating exposure to toxicity. Let call the observed dose limiting toxicity (DLT) occurrence of patient in response to treatment at the end of cycle 1, where cycle 1 is defined as the DLT observation period. The predictive probability of DLT at dose , noted , on which the ED-EWOC decision rule is based, is defined as follows:
| (1) |
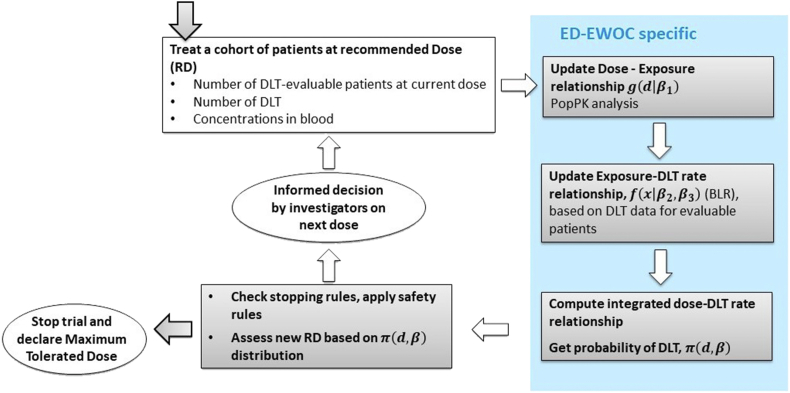
The proposed ED-EWOC design is an iterative stepwise process, which adapts at each iteration of the dose escalation, as new observations become available (Fig. 1). For each candidate dose, the distribution of an exposure metric of interest (e.g. AUC over a given treatment duration) accounting for the inter-individual variability in PK is computed based on a population compartmental PK model fitted to emerging PK data. This model is denoted in Equation (1). For each likely exposure level, a probability of DLT is computed using a Bayesian model. In this work, we used a Bayesian logistic regression model (BLRM), denoted in equation (1) but the method is applicable to any model structure. A more detailed description of the method is provided below.
Fig. 1.
Adaptive decision process of the ED-EWOC design.
2.2. Population PK model
In ED-EWOC, the dose-exposure relationship is defined by a population PK model which is assumed available at the start of the clinical trial. This model is updated at each escalation step as new pharmacokinetic data become available. The population model can be written according to equations (2), (3), (4) below.
It is assumed that the drug kinetics can be well described by a compartmental pharmacokinetic model. The population model can be written as follows.
Let note the concentration of drug X in patient at -th sample time :
| (2) |
is the residual error associated with a concentration at the -th time for patient . The residual error variability was described by a proportional model, with mean 0 and variance matrix .
is the vector of PK model parameters for patient . Inter-individual variability in parameters is incorporated on all model parameters when supported by the data assuming a lognormal distribution:
| (3) |
| (4) |
where is the population typical value for the vector of PK parameter (of dimension K), and is the random inter-individual variability of PK parameter for patient that is assumed to follow a normal distribution with mean zero and variance governed by the multivariate covariance matrix . Note that, for any given dose, the drug kinetic is completely characterized by the set of population PK parameters denoted .
After completion of each cohort of patients, the population PK model is re-evaluated based on the observed data in a stepwise manner without performing covariate analysis since the desired output is a predicted measure of exposure that would serve as regressor for the BLRM prediction. When necessary, the model structure (e.g., number of compartments, inclusion of a nonlinear component of the drug clearance or absorption mechanism) can be updated from one cohort to another if supported by the data.
Once a population PK model is available, emerging data from the dose escalation phase can be processed to quantify individual exposure of each patient based on a relevant metric choice without the need of re-estimation or additional model building. In this work, AUC over the first cycle of the treatment period was used as the relevant exposure metric and was derived based on integration of blood concentration levels predicted by the model according to equation (5):
| (5) |
where represents the exposure of the patient (here, AUC) after having received the dose events across the DLT time period.
2.3. Bayesian exposure toxicity model
Let be the predicted exposure metric obtained from the population PK model and explaining the DLT event occurrence. Let call the observed DLT occurrence of patient in response to treatment at the end of cycle 1. A Bernoulli distribution with parameter is used to model depending on the administered dose and on parameter vector .
| (6) |
where is the vector of parameters of both PK and pharmacodynamics (PD) relationships. It is assumed that the occurrence of a DLT is explained by exposure, then equation (6), can be written:
| (7) |
where represents the probability of DLT after exposure . While PK parameter is specific to each subject since it incorporates inter-individual variability, PD related parameters are common for the whole population. The inference is performed in a Bayesian framework, here assuming a logistic regression structural model (BLRM). The BLRM of exposure DLT rate can be written as a logit function:
| (8) |
where and are the intercept and slope of the logit function respectively, represents a reference exposure allowing for the interpretation of parameters and prior setting, and are the parameters of the prior bivariate Normal distribution.
As prior distributions can significantly influence Bayesian model based designs, the ones used in this work to compare ED-EWOC and EWOC method were defined based on current knowledge.
The joint posterior distribution of exposure-DLT rate relationship was obtained via Monte Carlo Markov chain (MCMC). Parameters of the logistic exposure-probability of DLT relationship are updated at each dose escalation step.
2.4. Dose recommendation rules
Dose recommendation for the next patient i+1, was based on the probability of DLT:
| (9) |
where represents the density of (DLT rate) given and (exposure-DLT rate relationship), is the distribution of according to the population model, is the joint prior distribution for and is the likelihood of the DLT endpoint after the i first patients. The function is the density of (exposure metric) given (dose-exposure relationship), and is the expectation of the density f.
After each cohort of patients has been completed, the posterior distribution is assessed to quantify, for each candidate dose, the following risks: (i) under-dosing: , (ii) targeted toxicity: , and (iii) overdosing: .
The recommended dose for the next patient is the one maximizing the probability of targeted toxicity while controlling the overdosing risk at a pre-specified level inferior to 25%:
| (10) |
This rule and the cut-offs for the bands of targeted toxicity and overdosing can be accommodated to each new therapeutic modality but they are frequently set to the values proposed by Neuenschwander et al. [10].
2.5. Stopping rules
In this work, the process of dose escalation continues until stopping rules are fulfilled. Stopping rules consist of reaching a maximum sample size (for instance, 60 patients) or concomitantly fulfilling all the below criteria: (i) at least 6 subjects observed a dose close to the new recommended dose (i.e., a dose within a 20% range of the estimated MTD), (ii) at least 3 dose cohorts have been enrolled (to allow PK/PD model being early evaluated), and (iii) the maximal posterior probability of a dose being in the target toxicity interval exceeds 40%.
The stopping rule can also be accommodated and we refer to Neuenschwander et al. [10] for examples which can also handle the risk of underdosing.
If the predicted DLT rate at a given dose matched the stopping rule criteria, the MTD is declared. If not, the safety rule of overdosing is assessed to decide the maximum increment for the next cohort recommended dose. This process was repeated until MTD was declared according to the operating mode described in Fig. 1.
2.6. Clinical trial design settings and choice of priors
Both EWOC and ED-EWOC designs were evaluated with similar settings in an early phase oncology clinical study run at F. Hoffmann‐La Roche, for a molecule that cannot be disclosed for confidentiality reasons. The study was carried out in accordance with The Code of Ethics of the World Medical Association (Declaration of Helsinki), and was approved by the ethics committee of the local investigator sites. Informed consents were obtained from all participants. A modified CRM-EWOC design Neuenschwander et al. [10] was formally implemented to guide the dose escalation phase of a multi-center, open label phase I dose finding study in patients with late stage cancer. ED-EWOC design was run in parallel, prospectively, as a feasibility exercise. In the clinical trial, the Maximum Tolerated Dose (MTD) was defined as the dose maximizing the posterior probability that the DLT rate belongs to [0.20, 0.35], while keeping the probability of overdose below 0.25.
In this trial, the investigational medicinal product (IMP) was administered orally once every 3 weeks (Q3W) with a flat dose possibly ranging from 2.5 mg to 16.25 mg. The starting dose of 2.5 mg Q3W derived from predictions from a pre-existing translational PK/PD model was projected to be safe. The planned maximum dose of 16.25 mg Q3W was extrapolated from a PK/PD model predicting Grade 4 thrombocytopenia events. Reference dose in the EWOC logistic regressions was set to 2.5 mg. The reference exposure in the ED-EWOC, was set to the median exposure following a dose of 2.5 mg, predicted using the pre-existing population PK model.
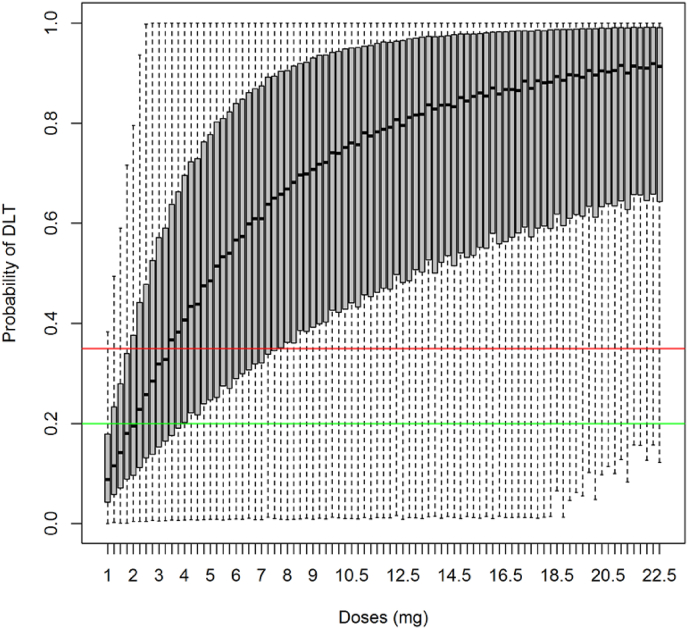
A minimally informative multivariate normal prior [10] was used in the dose-escalation. A quantile based non-informative prior approach was used to assess the parameters of the BLRM in both EWOC and ED-EWOC. It was conservatively assumed that it would be very unlikely (with a 95% confidence) that a 50% or higher DLT rate is associated with the starting dose and that a 10% or lower DLT rate could be associated with the planned maximum dose. These assumptions allowed deriving prior parameters used in the EWOC and ED-EWOC designs (Fig. 2). For ED-EWOC, the mean predicted exposure (AUC over cycle 1) estimates obtained from the population PK model was considered as the driver of BLRM while for EWOC, the dose administered was used. Using the quantile based non-informative prior approach for the ED-EWOC, logistic parameters for the prior and were respectively estimated to −1.808 and 0.032 with a variance-covariance matrix of (1.172, 0.142, 0.142, 0.365). The predictive prior distributions of probability of DLT implemented in both ED-EWOC and EWOC approaches were inspected and showed comparable uncertainty based on visual inspection.
Fig. 2.
Dose-probability of DLT relationship based on the prior model For each dose, the assessed integrated probability of DLT rate has been summarized a using box plot. Grey boxes indicate the interquartile range and whiskers provide the minimum and maximum values. Each candidate dose (on the x-axis) has then a given probability of being underdosing, in the target range of DLT or overdosing based on the position of this distribution in regard to the toxicity thresholds. Horizontal green and red lines correspond respectively to the probability thresholds for Target (0.20) and Overdosing intervals (0.35). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
2.7. Data collection and operational aspects
Data were sequentially collected in cohorts of three individuals who were treated at the same dose level. To support the dose recommendation of the next cohort, the data collected in each patient included the actual dosing schedule over time, the observed drug concentrations (in blood), and the occurrence (yes or no) of a toxicity event. Blood samples were collected for analysis of plasma concentrations at the following time-points: 1, 2, 4, 6, 8, 24, 72, 96, 168, 264, 336, 432 h, following the first dose at cycle 1 and 2 and pre-dose on the following cycles. DLT were collected at the end of cycle 1 to estimate the BLRM parameters of EWOC and ED-EWOC. The DLT period was defined as a 3-week window (duration of one cycle).
2.8. Computations and software
Prior population PK model and following updates of the model were implemented using the nonlinear-mixed effect model software NONMEM, version 7.2.0 (ICON development solutions, Ellicott City, MD [31]. The joint posterior distribution of exposure-DLT rate relationship was obtained via MCMC method imbedded in the Bayesian R package crmPack [32].
3. Results
3.1. Population PK model and exposure assessment
3.1.1. Population PK model developed on anterior data
Before study start, a population PK model from a previous clinical study evaluating the same compound was available. A total of 361 blood concentrations measured from 15 patients receiving the same IMP constituted the dataset upon which a population PK model was developed based on the assumed model structure derived from legacy data. The PK model consisted of a 2-compartment disposition model with linear mechanism. The First Order Conditional Estimation (FOCE) method with interaction was used to derive the population PK model parameters.
3.1.2. Population PK model fitted on current cumulative data
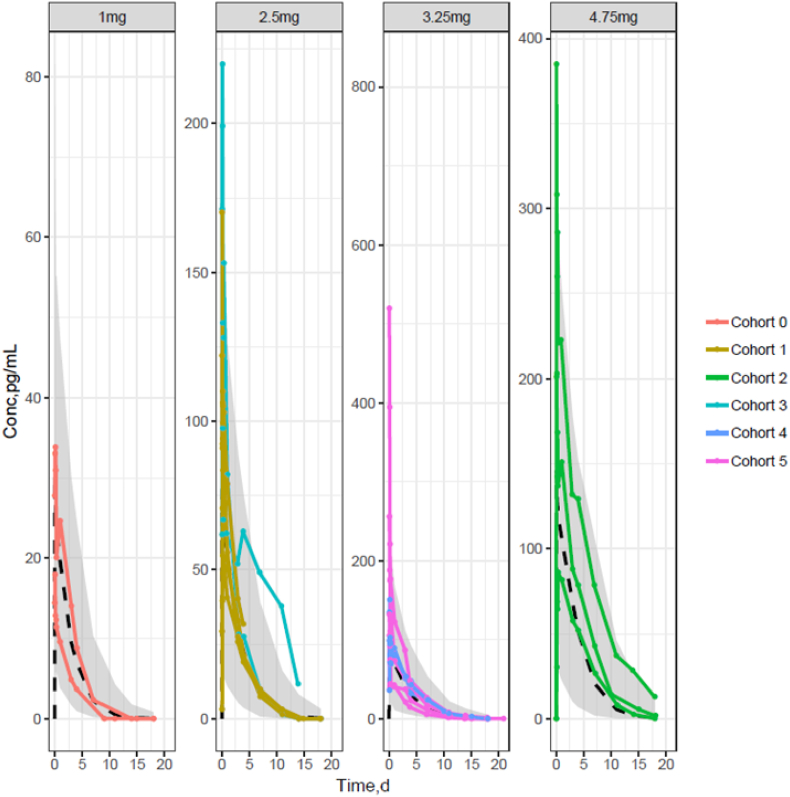
Upon receipt of new data from the current dose escalation study, drug concentrations measured during the first cycle of treatment and any other subsequent PK samples were used to update the population PK model. During the course of the trial, the PK model structure was updated to describe emerging PK data. After cohort 2 received 4.75 mg, a non-linear clearance mechanism based on Michaelis-Menten equation was incorporated to account for non-proportional exposure increase with dose. Observed individual PK profiles by dose level tested across the 6 cohorts of patients with population PK model prediction overlaid are presented in Fig. 3.
Fig. 3.
Observed individual PK profiles by dose level tested across the 6 cohorts of patients with population PK model prediction overlaid The shaded area represents the 90% prediction interval of the PK model predictions and the dashed line the median predicted exposure level for each dose. The individual PK profiles are represented by solid lines joining the dots, when PK observations were obtained.
Overall, the PK model was able to predict with good accuracy all individual PK profiles at each dose tested. Individual AUC estimates after cycle 1 were computed by integration of the concentration time-profile predicted for each patient by the NONMEM software.
The PK parameter estimates evaluated on the PK data collected during the trial at each dose escalation step were used to provide ED-EWOC dose recommendations and the latest population PK model parameter estimates obtained from pooled data accrued up to cohort 5 and comprising a total of 17 patients and 289 PK observations are provided in Table 1.
Table 1.
Parameter estimates of the population PK model after completion of cohort 5.
| Model parametersa | Interpretation | Typical values (median) | Inter-individual variability (variance) |
|---|---|---|---|
| Vmax (pg/mL/h) | Maximum elimination rate of the Michaelis-Menten nonlinear clearance pathway | 0.418 | Fixed to 0 |
| Km (pg/mL) | Michaelis-Menten constant of the nonlinear clearance mechanism | 76.1 | 215% |
| CL (L/h) | Linear clearance | Fixed to 0 | Fixed to 0 |
| V1 (L) | Distributional volume in central compartment | 11.7 | 16% |
| V2 (L) | Distributional volume in peripheral compartment | 3.86 | 3.7% |
| Q (L/h) | Inter-compartmental clearance | 0.383 | 35% |
| Ka (h−1) | First-order absorption rate constant | 0.67 | 142% |
| Ε | Residual error | 44%b | Fixed to 0 |
Note: No relative standard error of model parameters was estimated and bioavailability was not estimated since no intravenous data were available. Inter-individual variability of parameters (η) and residual error (ε) were assumed normally distributed with mean 0 and variance Ω2 and σ2 respectively. Variances are expressed as coefficient of variation (%).
Estimates based on 17 patients and 289 PK observations after oral administration of IMP up to cohort 5.
Residual error was estimated on a coefficient of variation scale (%).
3.2. ED-EWOC dose recommendation process (example of cohort 3 to cohort 4)
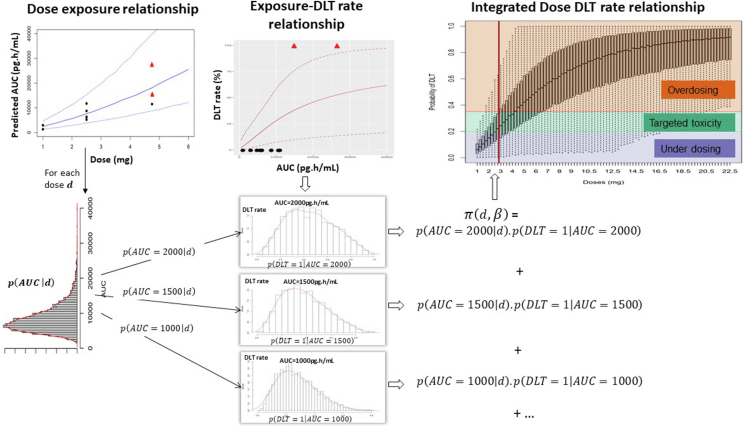
To illustrate practically how dose recommendation is obtained following ED-EWOC, an example of emerging data obtained after completion of the fourth cohort's DLT period is presented in Fig. 4. Eleven patients were treated at three different dose levels: 1 mg Q3W (cohort 0), 2.5 mg Q3W (cohort 1), and 4.75 mg Q3W (cohort 2) with a dose de-escalation to 2.5 mg Q3W for the cohort 3. Ten patients out of 11 were evaluable for DLT, i.e. they received at least the first treatment cycle or discontinued due to DLT. Two patients out of three experienced a DLT in cohort 2, explaining the dose de-escalation phase at cohort 3.
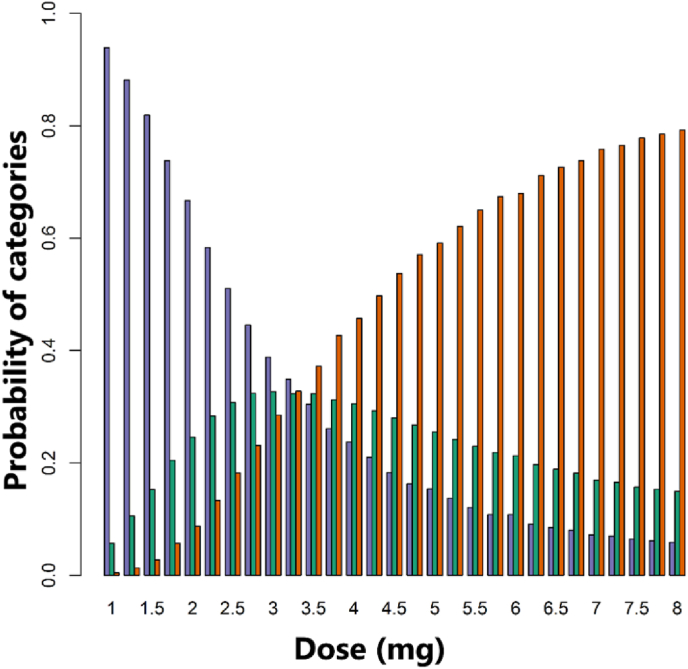
Fig. 4.
Bayesian Logistic Regression ED-EWOC dose recommendation process after completion of the fourth dose cohort. Left panel: (top) predictions of individual AUC estimates after the first cycle from the population PK model at each dose evaluated. Dots correspond to patients' data with black dots and red triangles respectively representing patients without and with DLT respectively, plain line is for the median AUC estimate, and dashed lines represent the 95% prediction interval. (bottom) Distribution of predicted population AUC for a given dose (here, for d = 2.75 mg). Middle panel: (top) Estimated posterior probability of DLT, defined as a function of exposure (AUC over first cycle). Dots correspond to patients' data, plain line is for the median DLT rate estimate and dashed lines represent the 95% prediction interval. (bottom) Histograms of the estimated distribution of DLT rates for different exposures. Right panel: Boxplot of the posterior integrated probability of DLT for each candidate dose according to the ED-EWOC approach. The DLT rate was assessed by Monte Carlo integration using the distribution of AUCs, as indicated. The pre-specified intervals of interest which PUD, PT, and POD relied upon and defining decision rules for the recommendation have been overlaid. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Individual longitudinal PK data emerging from the cohort 0 to cohort 3 were used to update the population PK model and estimate the individual PK parameters and population PK parameters (exponent index corresponding to current cohort 3). These estimates were respectively used (i) to compute AUCs for each patient and (ii) to assess, for each dose, the distribution of likely AUCs in the overall population (Fig. 4 left panel top row illustrates the dose-AUC relationship and left panel bottom row illustrates the AUC distribution for dose 2.75 mg). Then, the Bayesian logistic AUC-DLT rate model was updated based on emerging DLT data from cohort 0 to 3 and the individual predicted AUCs. In this step, the PD parameters and estimated after cohort 3 were used to derive the posterior distribution of DLT rate for each value of likely AUC (Fig. 4 middle panel). For a given dose d, the distribution of DLT rate is computed by reweighting the DLT rate distribution according to the probability of AUC (corresponding to equation (9) above). In order to reconstruct the overall dose-DLT rate relationship and obtain the predictive probability of DLT, the calculation of was performed by Monte Carlo integration. The updated dose-DLT rate relationship and related uncertainty is presented in Fig. 4 right panel.
The dose for cohort 4, , was recommended on the basis of (i) the probability that the dose would be in the target toxicity range (), and (ii) the probability of over-dosing (). The recommended dose for the cohort 4 is:
The dose = 2.75 mg Q3W is recommended for cohort 4 based on ED-EWOC at the end of cohort 3 as it maximized , while maintaining below 25%. At this dose level, is estimated to 33.0% and to 22.6%. At dose 2.75 mg, the median AUC level is 8500 pg h/mL according to the population PK model. However, this AUC level is not defining the recommended dose on its own because the dose recommendation results from the integration of (i) the probability of exposure conditionally to dose and (ii) the probability of DLT conditionally to exposure. The probabilities , and for each dose previously tested and for the next recommended dose are provided in Fig. 5. The probability of underdosing, ,
is also provided in Fig. 5 for completeness. Fig. 5 allows to visually identify the doses leading to excessive risk of potential toxicities (red bar exceeding the consented level of risk of 25%), and the recommended dose, corresponding to the highest green bar in the tolerated doses.
Fig. 5.
Predictive posterior probability obtained from the ED-EWOC model for each dose to fall in the pre-specified toxicity categories: (i) under-dosing (blue), (ii) target toxicity (green), (iii) overdosing (red), after the cohort 3 completion. As seen in Fig. 4 (dose-DLT rate relationship), the uncertainty in the DLT rate translates into a probability for each dose to fall in the pre-specified toxicity categories. To report these probabilities, a barplot is provided for each dose keeping colors consistent with Fig. 4. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
The predicted DLT rate at dose 2.75 mg did not match the stopping rule criteria for 2 reasons: (i) only five (less than 6) subjects were observed at a dose close to 2.75 mg (between 2.2 mg and 3.3 mg), and (ii) the maximal posterior probability for a dose being in the target toxicity interval does not exceed 40%. Indeed, 3 mg is the dose that is predicted to maximize the posterior probability of target toxicity which is equal to 33.5%.
Because the stopping rule criterion is not fulfilled, the MTD could not be declared and a new cohort was recommended to be treated according to ED-EWOC at the dose 2.75 mg. This process was continuing iteratively until MTD was declared (see Fig. 1).
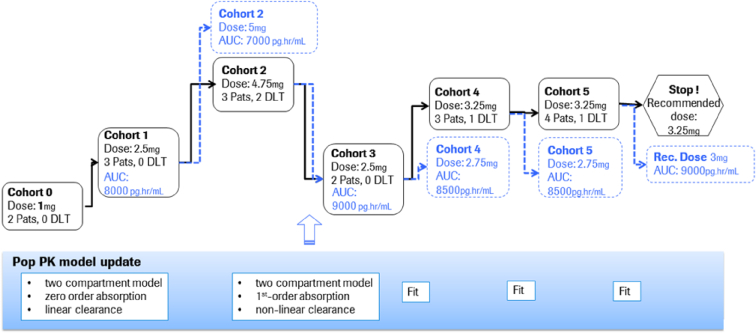
3.3. Overall study outcomes from EWOC and ED-EWOC
The execution of the trial was completed successfully with the EWOC design while ED-EWOC dose recommendation was performed in parallel (Fig. 6). The trial design specified that dose escalation step was initiated when a minimum of three patients at the current dose level were evaluable for DLT. In total, 18 patients were treated in six different cohorts. Only 17 patients were DLT-evaluable and four dose levels were explored: 1 mg (cohort 0), 2.5 mg (cohorts 1 and 3), 4.75 mg (cohort 2), and 3.25 mg (cohort 4 and 5). A total of four patients experienced a DLT: two out of three at dose level 4.75 mg (cohort 3) and two out of 7 at the dose level 3.25 mg (cohort 4).
Fig. 6.
Dose escalation paths explored with EWOC (solid lines, black outcomes) and ED-EWOC (dotted lines and blue outcomes) AUC = area under the concentration-time curve; DLT = dose limiting toxicity; Pats = patients; PK = pharmacokinetics. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
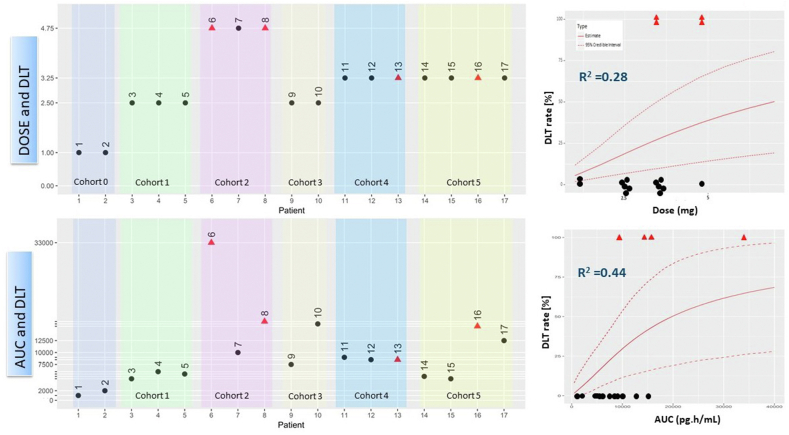
When comparing the outcomes of DLT event for each of the 17 DLT-evaluable patients with the EWOC and ED-EWOC design (Fig. 7), a clearer relationship is observed with exposure (AUC) compared to dose, suggesting that ED-EWOC is a more reliable model for predicting DLT. A clearer relationship between AUC-DLT than dose-DLT is observed (Fig. 7 left panels). This was supported by a larger measure of association between DLT rate and the respective predictor with ED-EWOC than EWOC BLR models (McFadden's pseudo-R2 = 0.44 vs. 0.28, Fig. 7 right panels). Moreover, the ED-EWOC BLR model showed a more clinically meaningful relationship of DLT event when compared to EWOC BLR model with a quicker plateauing of DLT event, suggesting that AUC is a better predictor of DLT risk than dose.
Fig. 7.
Comparison of EWOC (top row) and ED-EWOC (bottom row) predictive outcomes for each patient tested across the 6 dose cohorts (left panels) and their respective Bayesian logistic regression model (right panels) Red triangles represent patients having experienced a DLT and black dots, patients who did not. On the left side graphs, patients are ordered by cohort as they entered the study (numbers above dots corresponding to rank of patient inclusion in the study). The reported R2 are the McFadden's pseudo-R2. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
4. Discussion
In this work, we have proposed a novel Bayesian EWOC-derived method integrating the PK of an IMP during the conduct of dose escalation study in oncology. Instead of solely relying on the nominal dose administered in dose escalation cohorts to inform the safety of the next dose as typically performed in a classical EWOC design, the observed concentration data available at the time of decision-making are processed within the framework of nonlinear mixed-effects modelling to better establish the dose-exposure-toxicity relationship through Bayesian forecasting. Conceptually, this approach is expected to provide superior performance to the EWOC design in terms of determining an MTD by enabling quantification of the variability observed in PK within patients at any dose but also by accounting for potential non-proportional increase in exposure relative to the dose administered.
In our case example, dose recommendations obtained with EWOC and ED-EWOC were similar. While the EWOC design was pre-specified in the study protocol to guide decision for dose escalation, the ED-EWOC design was run in parallel for comparison purposes. The result of this work shows that fitting a population PK on emerging PK data in a Bayesian forecasting decision framework is practically feasible. It also shows that PK data availability and other considerations relating to the timeframe for model building and interpretation are not incompatible with decision-making within a trial conduct, although the timelines between DLT observation period and dose escalation decision are typically very short. From an operational standpoint, the ED-EWOC implementation required a predefined process and study team coordination. However, thanks to a semi-automated process, the recommendations of a dose from EWOC and ED-EWOC were delivered simultaneously. In our example, and despite taking into consideration the longitudinal PK data observed in this trial, the similarity of results between EWOC and ED-EWOC was expected for two main reasons. First, the dose-exposure relationship of the drug under investigation is not departing drastically from linearity since the nonlinear component is starting at the top dose tested. In this case, the recommendation of both designs would not be expected to diverge since the exposure-DLT rate relationship of ED-EWOC would use a proportional metric of the dose-DLT rate relationship used by EWOC. Secondly, the low-to-moderate inter-individual variability observed in the blood concentration levels of the drug investigated (20–30% CV in clearance, and volume estimates in dose escalations) does not allow a zone of overlap in concentration levels from one dose to another for patients with extreme PK properties. For example, with large variability in PK, a patient with a low clearance tested at dose 2.5 mg could exhibit similar exposure levels as a patient with a high clearance who received a 2-fold higher dose, and this would have impacted the Bayesian forecasting and recommended dose for the next cohort.
In our work, we assume that AUC is a reliable predictor of toxicity as opposed to dose. The choice of AUC during the first treatment cycle as the predictor for DLT was motivated by the time of DLT occurrence. Indeed, the time of DLT was not correlated with the time of observed Cmax within the dosing interval, suggesting that toxicity was not triggered by an acute exposure but more probably was correlated with the accumulated exposure over the first cycle period. However, the ED-EWOC can accommodate any choice of PK metrics, and could be adapted to any driving function of clinical relevance for the DLT predictions. For instance, one could consider predicted concentration levels in a tissue based on a physiologically based PK predictions instead of systemic exposure levels.
In our case study, the recommendations of designs started to be slightly different (15% difference in recommended dose in cohort 4) when sign of nonlinear PK was identified. Emerging PK data of cohort 3 suggested a sub-proportional increase in exposure with dose that necessitated an update of the population PK model structure that was initially assumed dose-proportional since the nonlinearity trend in the PK data was small and did not significantly affect the dose recommendation. In the case of biologic drugs with high specificity for a target tested in an indication with known overexpression of the target (e.g, trastuzumab, an anti-HER2 monoclonal antibody in breast cancer), the ED-EWOC design is expected to provide more accurate dose recommendation at lower dose cohorts compared to an EWOC design due to the antigen sink effect. Likewise, a drug with saturable absorption or elimination pathways known to result in nonlinear PK observations would benefit from an ED-EWOC design.
One limitation of using ED-EWOC is mainly of practical considerations since it is customary to have PK data lagging behind decision making due to the complex logistics required to ensuring availability of PK data in the clinical database. Typically, PK samples generated per study protocol are first shipped from the investigational site to a central lab prior to being routed to a lab vendor for bioanalysis. After sample reconciliation and storage, PK data are sent back to the external data facilitator for data reconciliation and cleaning. Once the raw PK data are available in the clinical database, the clinical pharmacologist or pharmacometrician is accountable for generating a model-ready dataset to process in PK modeling software. Only after all these steps can model-derived AUC estimates be obtained. One complication pertaining to the implementation of the ED-EWOC design resides therefore in ensuring that PK data, PK modeling, estimation of an exposure-derived risk and dose recommendation is available at the time of dose escalation committee and monitoring safety review board meetings.
Another time consuming component that could prevent implementation of ED-EWOC design on an industrial scale is the population PK model building process that necessitates a stepwise procedure to test hierarchical candidate models without the possibility yet for automation, even for simple PK models. In our work, a prior population PK/translational model was available for IMP. Exploring the impact of structural PK model misspecification and distributional assumptions of PK parameters used to inform DLT probabilities was not performed in this work and could be considered for future work to further understand the operating characteristics of ED-EWOC designs.
We are confident that such approach will be endorsed by regulatory authorities since the concept underpinning ED-EWOC fits within the new EMA guideline [16] in which estimation of exposure and exposure-response relationships by sponsors is encouraged. The population PK model embedded in the ED-EWOC procedure allows the assessment of drug exposures by accounting for relevant variability and handling any nonlinearity of exposure even when very few patients are observed at each dose level. Therefore, as exposure may be a better predictor of DLT than dose, a good characterization of the PK may reduce the uncertainty surrounding the DLT rate. This is particularly true in the context of small sample size when the observed exposures do not encompass the large range of overlapping exposures of different doses predicted by the PK model. In addition, assessing the impact of some common covariates such as body weight association on PK during the escalation trial when possible may lead to better MTD. For instance, if the explored regimen is a flat dosing regimen while the true MTD is body weight dependent, the ED-EWOC design may be more appropriate as the body weight effect on exposure can be quantified using the PK model. In a MTD paradigm, an ED-EWOC design would therefore instill confidence in the identification of a safe and better-tolerated dose. As a pharmacology driven design, ED-EWOC approach may be adapted to allow the opportunity to explore and evaluate alternative dosing regimens. This is of major interest in some program where step-up increasing administrations during the first cycle is considered to minimize the risk of adverse events. Handling dosing regimen in the dose escalation design allows identifying a relevant Maximum Tolerated Dosing Regimen, which is not possible with current designs that reduce “dosing regimen” to “dose level”.
Our approach shared some similarities with the PKLOGIT model presented in Ursino et al. [23]. Instead of a simple Gaussian model for the AUC, we use a full population PK model and instead of a simple logistic regression for the DLT-AUC relationship, a BLRM inspired design with overdose control [10] is implemented. A similar approach was also recently proposed by Gerard et al. [29,30] but it does not incorporate the iterative use of a population PK model estimation to guide the dose escalation process.
Should a ED-EWOC design be considered to guide a dose escalation, simulations would have to be performed before the study start, in order to assess the operating characteristics of the design under some likely scenarios, as usually done for model based designs. This would support the protocol writing and justify the selected design options to the health authorities and ethic committees. In our case, the EWOC (with associated operating characteristics) was pre-specified in the study protocol to guide decision for dose escalation; the ED-EWOC procedure was run in parallel for comparison purpose. ED-EWOC was built so that it would match the EWOC specification (a priori probability, escalation rules and stopping rules), but no simulation was performed as it was not required for the purpose of our study. One challenge for such an investigation would be the simulation of the population PK model building process at each escalation step based on emerging PK data that, in real life, requires the intervention of a modeler. ED-EWOC simulations would require assumption on population PK model fitting at each dose escalation step of each simulated trial from each scenario of interest. We encourage the reader to evaluate the simulation assumptions and scenarios based on the molecule specificities.
Overall, this work illustrates the attractiveness of ED-EWOC design since it combines the PK knowledge and mixed-effects modeling with Bayesian forecasting for assessment of the MTD, and minimize the risk of a patient to experience a DLT or an overdose following treatment irrespective of the PK properties of a drug while gaining efficiency in dose increment if the risk of DLT is projected to be marginal. The concept of ED-EWOC could also be extended to an exposure-PD/efficacy assessment, with a model-based approach to guide establishment of an optimal dose for dose recommendation of phase 2 initiation as done by Alam et al. [33] or Colin et al. [34] in a dose-response framework. From a practical point of view, drug development in oncology is gradually pivoting from an all-comer MTD dogma to a patient-centric personalized health care paradigm focused on early sign of efficacy. By accounting for PK in the decision-making process of dose escalation in early oncology trials, drug developers are able to integrate more complex dose strategy within dose escalation designs. For example, one could consider a conversion in the route of administration (from intravenous to subcutaneous for biologics, or from intravenous to oral for small molecules), or handle mitigation strategy related to the tolerability of drugs or immunogenicity such as step-up dosing or dose fractionation within the DLT observation period. Another opportunity where ED-EWOC can provide significant benefit is in the context of dose escalation of a new drug administered in combination with a standard therapy where exposure predictions and exposure-response relative to safety and efficacy of the drug is already partially known in single agent and could serve as informative prior information within the ED-EWOC design. We believe ED-EWOC is a step in the direction towards a precision dosing vision of drug development that would benefit patients through the synergistic use of advanced statistical concepts, basic drug pharmacology principles, and PK/PD modeling.
Financial support
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. During the conduct of this study, all authors were employees of Roche.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Dixon W.J., Mood A.M. A method for obtaining and analyzing sensitivity data. J. Am. Stat. Assoc. 1948;43:109–126. [Google Scholar]
- 2.O'Quigley J., Pepe M., Fisher L. Continual reassessment method: a practical design for phase 1 clinical trials in cancer. Biometrics. 1990;46:33–48. [PubMed] [Google Scholar]
- 3.Thall P.F., Lee S.J. Practical model-based dose-finding in phase I clinical trials: methods based on toxicity. Int. J. Gynecol. Cancer. 2003;13:251–261. doi: 10.1136/ijgc-00009577-200305000-00001. [DOI] [PubMed] [Google Scholar]
- 4.O'Quigley J., Zohar S. Experimental designs for phase I and phase I/II dose-finding studies. Br. J. Cancer. 2006;94:609–613. doi: 10.1038/sj.bjc.6602969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Iasonos A., Wilton A.S., Riedel E.R., Seshan V.E., Spriggs D.R. A comprehensive comparison of the continual reassessment method to the standard 3+ 3 dose escalation scheme in Phase I dose-finding studies. Clin. Trials. 2008;5:465–477. doi: 10.1177/1740774508096474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Le Tourneau C., Lee J.J., Siu L.L. Dose escalation methods in phase I cancer clinical trials. JNCI: J. Natl. Cancer Inst. 2009;101:708–720. doi: 10.1093/jnci/djp079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van Brummelen E.M., Huitema A.D., van Werkhoven E., Beijnen J.H., Schellens J.H. The performance of model-based versus rule-based phase I clinical trials in oncology: a quantitative comparison of the performance of model-based versus rule-based phase I trials with molecularly targeted anticancer drugs over the last 2 years. J. Pharmacokinet. Pharmacodyn. 2016;43:235–242. doi: 10.1007/s10928-016-9466-0. [DOI] [PubMed] [Google Scholar]
- 8.Babb J., Rogatko A., Zacks S. Cancer phase I clinical trials: efficient dose escalation with overdose control. Stat. Med. 1998;17:1103–1120. doi: 10.1002/(sici)1097-0258(19980530)17:10<1103::aid-sim793>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 9.Tighiouart M., Rogatko A., Babb J.S. Flexible Bayesian methods for cancer phase I clinical trials. Dose escalation with overdose control. Stat. Med. 2005;24:2183–2196. doi: 10.1002/sim.2106. [DOI] [PubMed] [Google Scholar]
- 10.Neuenschwander B., Branson M., Gsponer T. Critical aspects of the Bayesian approach to phase I cancer trials. Stat. Med. 2008;27:2420–2439. doi: 10.1002/sim.3230. [DOI] [PubMed] [Google Scholar]
- 11.Tighiouart M., Rogatko A. Dose finding with escalation with overdose control (EWOC) in cancer clinical trials. Stat. Sci. 2010;25:217–226. doi: 10.1214/10-STS333. [DOI] [Google Scholar]
- 12.Chevret S. Wiley; New York: 2006. Statistical Methods for Dose-Finding Experiments. [Google Scholar]
- 13.Jaki T., Clive S., Weir C.J. Principles of dose finding studies in cancer: a comparison of trial designs. Cancer Chemother. Pharmacol. 2013;71:1107–1114. doi: 10.1007/s00280-012-2059-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Conaway M.R., Petroni G.R. The impact of early-phase trial design in the drug development process. Clin. Cancer Res. 2019;25:819–827. doi: 10.1158/1078-0432.CCR-18-0203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.FDA Adaptive Designs for Clinical Trials of Drugs and Biologics Guidance for Industry. U.S. Department of Health and Human Services Food and Drug Administration; 2019. https://www.fda.gov/media/78495/download [Google Scholar]
- 16.EMA Guideline on Strategies to Identify and Mitigate Risks for First‐in‐human and Early Clinical Trials with Investigational Medicinal Products. 2017. https://www.ema.europa.eu/en/documents/scientific-guideline/guideline-strategies-identify-mitigate-risks-first-human-early-clinical-trials-investigational_en.pdf [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collins J.M., Grieshaber C.K., Chabner B.A. Pharmacologically guided phase I clinical trials based upon preclinical drug development. JNCI: J. Natl. Cancer Inst. 1990;82:1321–1326. doi: 10.1093/jnci/82.16.1321. [DOI] [PubMed] [Google Scholar]
- 18.Piantadosi S., Liu G. Improved designs for dose escalation studies using pharmacokinetic measurements. Stat. Med. 1996;15:1605–1618. doi: 10.1002/(SICI)1097-0258(19960815)15:15<1605::AID-SIM325>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 19.Patterson S., Francis S., Ireson M., Webber D., Whitehead J. A novel Bayesian decision procedure for early-phase dose-finding studies. J. Biopharm. Stat. 1999;9:583–597. doi: 10.1081/BIP-100101197. [DOI] [PubMed] [Google Scholar]
- 20.Whitehead J., Patterson S., Webber D., Francis S., Zhou Y. Easy-to-implement Bayesian methods for dose-escalation studies in healthy volunteers. Biostatistics. 2001;2:47–61. doi: 10.1093/biostatistics/2.1.47. [DOI] [PubMed] [Google Scholar]
- 21.Whitehead J., Zhou Y., Hampson L., Ledent E., Pereira A. A Bayesian approach for dose-escalation in a phase I clinical trial incorporating pharmacodynamic endpoints. J. Biopharm. Stat. 2007;17:1117–1129. doi: 10.1080/10543400701645165. [DOI] [PubMed] [Google Scholar]
- 22.O'Quigley J., Hughes M.D., Fenton T., Pei L. Dynamic calibration of pharmacokinetic parameters in dose-finding studies. Biostatistics. 2010;11:537–545. doi: 10.1093/biostatistics/kxq002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ursino M., Zohar S., Lentz F., Alberti C., Friede T., Stallard N., Comets E. Dose‐finding methods for Phase I clinical trials using pharmacokinetics in small populations. Biom. J. 2017;59:804–825. doi: 10.1002/bimj.201600084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Takeda K., Komatsu K., Morita S. Bayesian dose‐finding phase I trial design incorporating pharmacokinetic assessment in the field of oncology. Pharmaceut. Stat. 2018;17:725–733. doi: 10.1002/pst.1890. [DOI] [PubMed] [Google Scholar]
- 25.Honma T., Min K.Y., Yoneda S., Yoshida S., Fujigaki M., Komiya I., et al. Pharmacokinetics of a new antitumor antibiotic, neothramycin, after intrapleural administration. Gan to Kagaku Ryoho. 1983;10:1504–1510. [PubMed] [Google Scholar]
- 26.Yáñez J.A., Remsberg C.M., Sayre C.L., Forrest M.L., Davies N.M. Flip-flop pharmacokinetics - delivering a reversal of disposition: challenges and opportunities during drug development. Ther. Deliv. 2011;2:643–672. doi: 10.4155/tde.11.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Günhan B.K., Weber S., Friede T. A Bayesian time-to-event pharmacokinetic model for phase I dose escalation trials with multiple schedules. Stat. Med. 2020;39:3986–4000. doi: 10.1002/sim.8703. [DOI] [PubMed] [Google Scholar]
- 28.Günhan B.K., Weber S., Seroutou A., Friede T. Phase I dose-escalation oncology trials with sequential multiple schedules. BMC Med. Res. Methodol. 2021;21 doi: 10.1186/s12874-021-01218-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gerard E., Zohar S., Lorenzato C., Ursino M., Riviere M.K. Bayesian modeling of a bivariate toxicity outcome for early phase oncology trials evaluating dose regimens. Stat. Med. 2021;40:5096–5114. doi: 10.1002/sim.9113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gerard E., Zohar S., Thai H.T., Lorenzato C., Riviere M.K., Ursino M. Biometrics; 2021. Bayesian Dose Regimen Assessment in Early Phase Oncology Incorporating Pharmacokinetics and Pharmacodynamics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bauer R. NONMEM Tutorial Part I: description of commands and options, with simple examples of population analysis. CPT Pharmacometrics Syst. Pharmacol. 2019;8:525–537. doi: 10.1002/psp4.12404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sabanes-Bové D.S., Yeung W.Y., Palermo G., Jaki T. Model-based dose escalation designs in R with crmPack. J. Stat. Software. 2019;89:1–22. doi: 10.18637/jss.v089.i10. [DOI] [Google Scholar]
- 33.Alam M.I., Coad D.S., Bogacka B. Combined criteria for dose optimisation in early phase clinical trials. Stat. Med. 2019;38:4172–4188. doi: 10.1002/sim.8292. [DOI] [PubMed] [Google Scholar]
- 34.Colin P., Delattre M., Minini P., Micallef S. An escalation for bivariate binary endpoints controlling the risk of overtoxicity (EBE-CRO): managing efficacy and toxicity in early oncology clinical trials. J. Biopharm. Stat. 2017;27:1054–1072. doi: 10.1080/10543406.2017.1295248. [DOI] [PubMed] [Google Scholar]