Abstract
Background: Standardized and concise data presentation forms the base for subsequent analysis and interpretation. This article reviews types of data, data properties and distributions, and both numerical and graphical methods of data presentation.
Methods: For the purposes of illustration, the National Inpatient Sample was queried to categorize patients as having either emergency general surgery or non-emergency general surgery admissions.
Results: Variables are categorized as either categorical or numerical. Within the former, there are ordinal and or nominal subtypes; within the latter, there are ratio and interval subtypes. Categorical data are typically displayed as number (%). Numerical data must be assessed for normality as normally distributed data behave in certain patterns that allow for specific statistical tests to be used. Several properties exist for numerical data, including measurements of central tendency (mean, median, and mode), as well as standard deviation, range, and interquartile range. The best initial assessment of the distribution of numerical data is graphical with both histograms and box plots.
Conclusion: Knowledge of the types, distribution, and properties of data is essential to move forward with hypothesis testing.
Keywords: data description, data science, statistics
Counting and measurement is the basis of all research and accurate representation of numeric data ensures that research is systematic and reproducible. After the design of a research study, the most critical juncture in a project is a complete and accurate description of the data and the methods used to obtain the results. Utilizing a systematic description of the data as a first step not only ensures transparent reporting of results, but helps the investigator identify potential problems in their analytic process or data sources to guide analytic decisions. Examining the distribution and structure of data ensures that the test and analyses chosen are the most appropriate and statistically valid. In addition to aiding the investigator, a clear description of the methods and data will aid in peer review and the study's utility in the broader research enterprise. Specifically, the description helps readers to understand external validity of a particular study, in other words, are findings generalizable to other populations? When drafting a manuscript, the description of data presentation and analysis should be standardized to the point where, after reading it, an independent party could reproduce your results exactly.
There are two cornerstones to an appropriate description of data: (1) a well-developed and presented table that describes your population, often referred to as a demographics table or Table 1 and (2) data visualization with appropriately chosen graphics. In this article, we provide examples of how to describe and visualize data using a nationally representative database, the Nationwide Inpatient Sample, to demonstrate a robust and thorough description of the methods and data used, while also highlighting specific pitfalls. We also demonstrate how weighted databases may add an extra layer of complexity to describing your study population. It is our goal that this work provides a road map for investigators seeking to utilize best practices in describing and presenting their data.
Table 1.
Types of Quantitative Data
| Data type | Subtype | Description | Example | Attributes |
|---|---|---|---|---|
| Categorical | Nominal | Named group | Race: black, white, Asian, other Gender: Male, female, non-binary, other |
Describe as n (%) |
| Ordinal | Groups with a clear order | Education level: Low, middle, high income Satisfaction ratings |
Describe as n (%) | |
| Numerical | Discrete | Numbered items which can be counted | Number of coin flips Population count |
Can be described as mean, median, mode |
| Continuous | Numbers that represent measurements and are usually rounded | Age, height, weight White blood cell count |
Can be described as mean, median, mode | |
| Interval | Numbers where the distance between numbers is standard and equal | Temperature pH |
Describe as mean, median, mode Can be added or subtracted Cannot be multiplied or divided |
|
| Ratio | Has all properties of interval data and uses the reference of a true zero (i.e., no negative numbers) | Age, weight, length Pulse rate |
Describe as mean, median, mode Can be added, subtracted, multiplied or divided |
Methods
To demonstrate these data science statistical practices and pitfalls, we used data from the 2017 Nationwide Inpatient Sample (NIS) from the Healthcare Cost and Utilization Project (HCUP). The NIS is an approximately 20% sample of all-payer hospitalizations that are included as part of HCUP that are then weighted to provide national estimates. This weighting means that each observed hospitalization in the sample represents a specific number of hospitalizations in the population. With this, the sample of 7.1 million hospitalizations represents more than 35.7 million hospitalizations. It includes parameters covering patient demographics (race, gender, age, payer, etc.), admission and discharge status, diagnoses, procedures, length of stay (LOS), and cost. All data are at the discharge-level and the NIS does not provide patient identifiers to be able to link hospitalizations. In this study we identified patients who underwent emergency general surgery (EGS) in 2017. Here, EGS is defined as appendectomy, colectomy and colostomy, laparotomy, laparoscopy, lysis of adhesions, small bowel resection, ulcer repair, and gallbladder procedures, as previously described by Smith et al. [1]. Specifically, we required that the hospitalization contain both a diagnosis and procedure code for EGS.
Of note, NIS data are structured to be able to perform a weighted adjustment to establish a nationally representative sample. For this article, however, the only weighted analysis we present is for the overall number of EGS procedures. This weighting followed guidelines from the Agency for Healthcare Research and Quality (AHRQ) using the given weights, cluster, and strata. Because of this weighting, the national estimates are presented with standard errors. Data cleaning was done via SAS, version 9 (SAS Institute, Cary, NC) with visualizations made in R version 3.6.1 using the tidyverse and patchwork packages [2,3]. Sample data available online were also used to build the skewed distributions in Figure 1 [4].
FIG. 1.
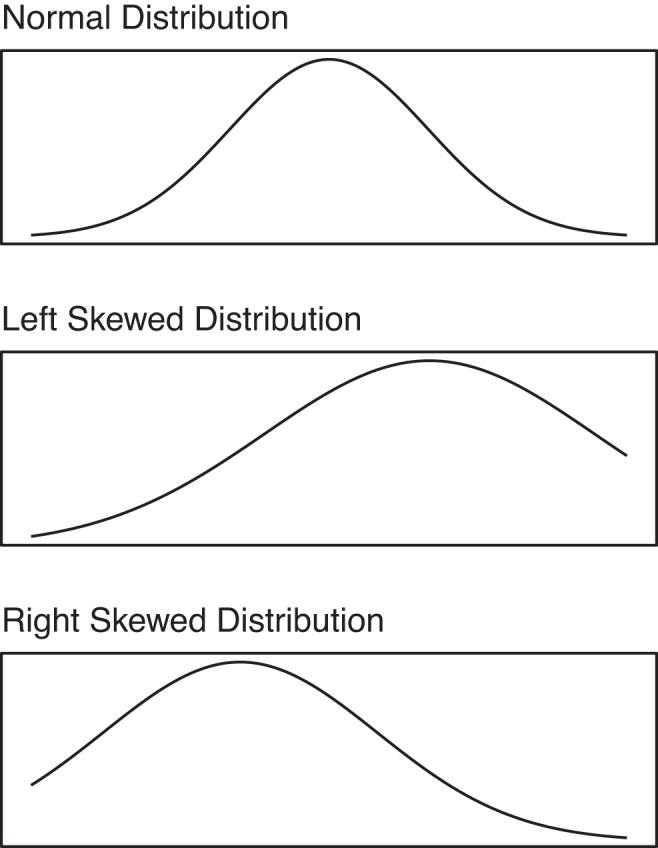
Example of normal and skewed distributions, using simulated data.
Using these data, we demonstrate how to construct a demographics table or Table 1 while also showing the value of graphical visualization of data to illustrate the distribution of age and LOS. The 2017 NIS contained 7,159,694 admissions that, when weighted, represent a national estimate of 35,798,453 hospitalizations. There was a total of 11,034 (1.6%) hospitalizations for emergency general surgery (EGS), representing an estimated 555,170 ± 5,969 (1.6% ± 0.01) nationally in 2017.
Data Cleaning and Categorization for Analysis
Data types
Data collection is typically organized via a data table, spreadsheet, or data frame. These datasets are typically organized such that each row of data represents one observation or unit to be studied (such as a single patient, one admission, or a hospital) and each column of data is a collected parameter (such as age or sex). Broadly, there are two types of variables: categorical (nominal and ordinal) and numeric (interval and ratio) (Table 1). Categorical data represent named groups of observations and are not quantitative. Categorical data can be ordered (ordinal) or not ordered (nominal). In our example below, represented by Table 2, gender, race, payer, and disposition are examples of categorical nominal variables. In the below example, the age categories (<18 years, 18–34, 35–49, etc.) are examples of ordered categorical variables.
Table 2.
Table of Demographics
| Non-EGS |
EGS |
|
|---|---|---|
| n = 7,048,660 | n = 111,034 | |
| Gender n (%) | ||
| Female | 3,975,703 (55.5) | 61,549 (55.4) |
| Race/ethnicity n (%) | ||
| White | 4,375,714 (62.1) | 69,306 (62.4) |
| Black | 1,039,483 (14.8) | 10,465 (9.4) |
| Hispanic | 836,059 (11.9) | 20,111 (18.1) |
| Asian Pacific Islander | 210,608 (3.0) | 3,091 (2.8) |
| Native American | 43,609 (0.6) | 697 .6) |
| Other | 240,386 (3.4) | 3,833 (3.5) |
| Missing | 302,712 (4.3) | 3,530 (1.2) |
| Payer n (%) | ||
| Medicare | 2,866,436 (40.7) | 36,350 (32.8) |
| Medicaid | 1,632,996 (23.2) | 21,151 (19.1) |
| Private insurance | 2,047,129 (29.1) | 42,481 (38.3) |
| Self-pay | 272,578 (3.9) | 7,190 (6.5) |
| No charge | 20,261 (0.3) | 600 (0.5) |
| Other | 196,537 (2.8) | 3,052 (2.8) |
| Age | ||
| Mean (SD) | 49.5 (27.5) | 51.4 (21.3) |
| Median (IQR) | 56 (29–72) | 54 (36–68) |
| <18 years old | 1,066,298 (15.1) | 8,870 (8.0) |
| 18–34 | 1,130,528 (16.0) | 17,410 (15.7) |
| 35–49 | 848,116 (12.0) | 21,106 (19.0) |
| 40–64 | 1,411,924 (20.0) | 29,158 (26.3) |
| 65–79 | 1,601,174 (22.7) | 24,808 (22.3) |
| 80+ | 990,282 (14.1) | 9,678 (8.7) |
| Admission type n (%) | ||
| Non-elective | 5,550,479 (78.9) | 92,878 (83.8) |
| Elective | 1,485,303 (21.1) | 17,982 (16.2) |
| LOS | ||
| Mean (SD) | 4.6 (6.9) | 5.1 (6.2) |
| Median (IQR) | 3 (2–5) | 3 (2–6) |
| Total charges | ||
| Mean (SD) | $49,442.52 ($96,256.50) | $71,664.93 ($86,774.56) |
| Median (IQR) | $26,443 ($12,800–$53,971) | $50,688 ($33,422–$81,303) |
| Disposition n (%) | ||
| Routine | 4,791,116 (68.0) | 90,324 (81.4) |
| Transfer to short-term | 140,316 (2.0) | 818 (0.7) |
| Transfer other (SNF, ICF, other) | 993,680 (14.1) | 8,285 (7.5) |
| Home health care | 884,954 (12.6) | 10,219 (9.2) |
| Against medical advice | 93,840 (1.3) | <300 |
| Died | 138,701 (2.0) | 1,037 (0.9) |
| Alive, destination unknown | 1,280 (0.02) | <11 |
Description of the study population, comparing those hospitalization not for EGS and those for EGS. These data come from the 2017 Nationwide Inpatient Sample. Note that two cells are presented as “<” (less than); this is due to data restrictions of displaying cells less than 11.
EGS = emergency general surgery; SD = standard deviation; IQR = interquartile range; LOS = length of stay; SNF = skilled nursing facility; ICF = intermediate care facility.
Numerical data are collected as numbers. Length of stay is an example of numerical data. Length of stay is a continuous variable, meaning that it is a measure of length, represented by the unit “days” and usually rounded to the nearest integer. Length of stay is also an example of “ratio” data, whereby the numbers are meaningfully related and zero is an absolute number. In other words, a person who had a LOS of 6 days was in the hospital twice as long as a person in the hospital for 3 days, and no one has a negative LOS. This differs from interval data. Interval data are characterized by numbers that have equal distances between values but there is no fixed beginning. An example of this is time in a 12-hour clock. These distinctions are important because some numbers should not be added or subtracted, and only ratio data can be interpreted as multiples of each other. Some numeric data should not be treated as continuous, such as injury severity scale (ISS) because an ISS of 20 is not twice as bad as an ISS of 10. Furthermore, other seemingly numeric data do not even represent numbers, such as medical record number or zip code, which should be considered categorical data because the numbers are really only assigned labels.
Numerical data can be converted to categories if the researchers believe this conversion is appropriate. However, it is important to remember that converting data from continuous to categorical necessarily results in loss of information granularity. This may limit future analyses. Age is a continuous numerical variable that consists of ratio data. In Table 2, age is described multiple ways. As continuous numerical data, age can be represented as a distribution with a mean and standard deviation, or a median and interquartile range. Alternatively, age was also converted into a categorical ordinal variable. We elected to present standard groups, namely, <18, 18–34, 35–49, 40–64, 65–79, 80+. These groups are not even intervals but are socially representative of groups that have similar attributes (child, young adult, etc.); another way to categorize age might be by deciles. Yet another way to group numerical data would be into those either above or below the median value for that parameter. Finally, numerical data may be grouped into categories to replicate findings from previous research, in which certain groupings were found to be meaningful. The researchers can decide which data presentation is most appropriate for their study and study question, and whether “cutting” numeric data into categories is useful or advantageous to demonstrate specific concepts being studied.
Data distribution and properties
When visualizing data, we are often seeking some conclusion regarding the distribution of the data, that is the shape of the data. Frequently, researchers try to determine if data follow a normal (or bell-shaped) distribution but often encounter data that is either left-skewed or right-skewed. Figure 1 demonstrates a normal distribution as well as distributions that are both left-skewed and right-skewed. The normal distribution is often desired because it allows for a number of powerful statistical tests to be conducted with the data, such as a Student t-test and linear regression, whereas skewed distributions violate important statistical assumptions of these tests. Another common distribution found in medical research is a bimodal distribution that as two peaks, which may occur, for example, if we saw the highest frequencies of a disease or condition in young adulthood and then again in older adulthood. Whereas the normal distribution is the most commonly discussed, it is actually found in only the minority of cases. It is important to note that there are numerous other statistical distributions with their own assumptions and analyses that are beyond the scope of this article but that researchers may encounter in the literature.
Mean, median, and mode are called measures of central tendency and are the simplest way to describe where the middle of numerical data distribution lies. The arithmetic mean is the average of all the numbers (the sum of numbers divided by the total count of items that were included in the sum). Technically, numeric scales such as Likert scales or injury severity scores that are not ratio data should not be presented as means. In a 10-point Likert scale, a value of eight is not twice as large as a level of four, nor is it four times as bad as a value of two, and thus a mean value cannot really be interpreted. A mean is most appropriate when a ratio continuous variable is normally distributed, or the values are shaped like a classic bell curve. Means can also be used more confidently when sample sizes are large and are therefore more likely to follow a normal distribution.
The median value is the middle number if all numerical values are lined up sequentially. A median and range is less affected to outliers than a mean and standard deviation, which makes the median a better choice for variables with a skewed distribution, a large number of outliers, or small sample size. Because no arithmetic is used to calculate them, median values are more interpretable for things such as scales or scores that cannot be added or subtracted. The mode is the value observed frequently. For a parameter that is distributed normally, the mean, median, and mode are all the same.
In addition to measurements of central tendency, the range, interquartile range, and standard deviation are useful properties. The range is displayed as the minimum and maximum value for the variable. Reviewing the minimum and maximum values can often help identify data entry errors, for example, an age of 510 years entered by mistake when the actual age was 51 years. The interquartile range represents the 25th percentile to the 75th percentile for the variable and is typically listed after the median. Mean values are typically displayed with a standard deviation, which indicates how wide the spread of numbers is around the average value.
Demographics table example
In the example demographics table (Table 2), categorical variables such as gender, race, payer, admission type, and disposition are presented as n (%) and these are relatively straightforward. Important groupings here are dependent on the researcher's aims. For example, race groups or disposition can be combined or separated.
We present multiple ways to show numerical data. Looking first at age, there is a small difference between mean and median, where the mean age for EGS and non-EGS groups is slightly lower than the median age, suggesting that there are young outliers that skew the mean age with a leftward tail. Grouping by age categories may provide extra detail about age distribution, showing more than one-half of all EGS and non-EGS admissions occur in adults over the age of 40, whereas hospitalizations for EGS occurs in a lower proportion of pediatric patients.
Alternatively, the mean values for LOS as well as total charges are much larger than the median values, suggesting that there are outliers with long LOS that skew the data to have a long rightward tail. This is common for hospital and intensive care unit LOS data. For total charges, the standard deviations are larger than the value of the means, suggesting that there is a wide variation in charges and utilizing the mean for this variable is likely not the best approach for further analysis. Thus, without even seeing the actual data, the reader can make inferences about their shape based on the differences between mean and median calculations and also on the relative size of the standard deviation compared with the mean. Familiarity with the most common shapes of data such as age and LOS will also draw attention to unusual patterns and alert readers when the incorrect statistical test is being applied.
Data description and visualization using histograms
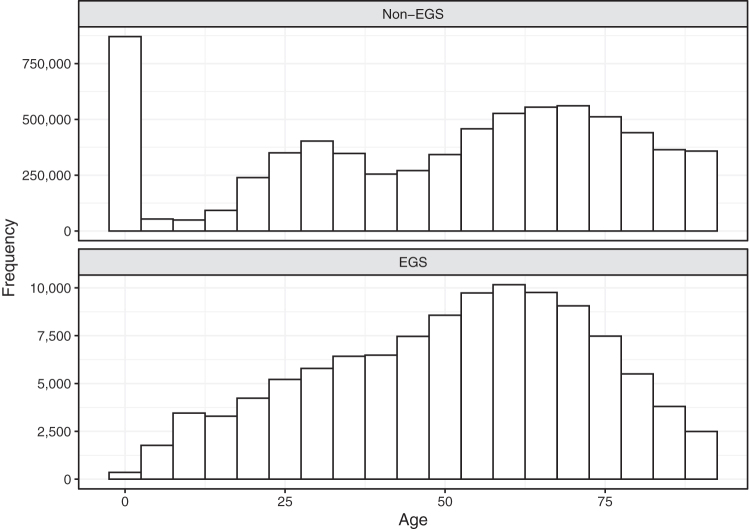
Although there are several statistical tests to assess for normality of a certain parameter, often the most obvious method is visual interpretation of a histogram. A histogram is a visual representation of the distribution of the data, where the frequency of a value is plotted on the y-axis, typically as bars, against the value of the variable on the x-axis. We present several histograms below, overlaying the normal distribution to highlight skewness. Of note, the y-axis here is not the frequency (the number of individuals in each bin) but rather the density. The density is a re-scaling of the frequency to accommodate a true normal distribution, where the area under the curve and the sum of the area of the bars equals one. The visual shape of the distribution will be identical with either frequency or density on the y-axis. Formal comparisons of these data are presented in a follow-up article [5]. Figure 2 highlights the distribution of age between non-EGS cases and EGS hospitalizations. As suggested by the demographics table, there is a large number of young non-EGS admissions, which leads to skewing of the age data; the histogram shows this more clearly than simply the presentation of the means and medians. Note also that the non-EGS age has a tri-modal distribution, with three peaks of frequency compared with only a single peak in the EGS group.
FIG. 2.
Distribution of age (in years) stratified by those hospitalizations that were not for emergency general surgery (EGS) and those that were for EGS.
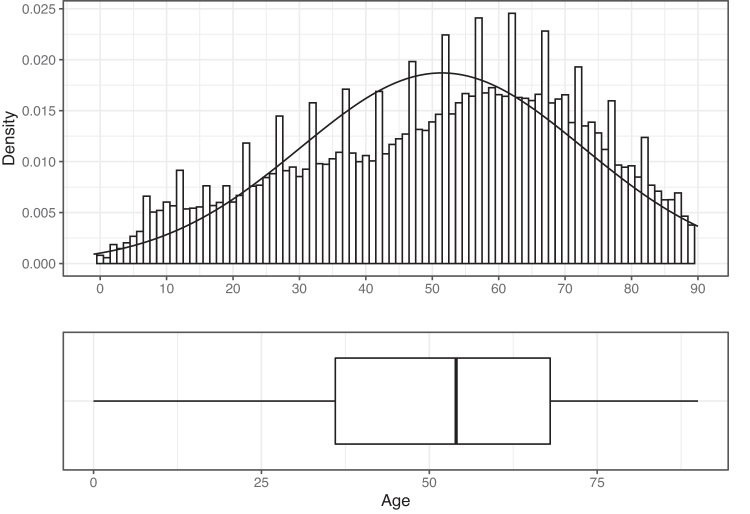
Another commonly used figure is the boxplot, seen in the lower half of Figure 3. This is another way to demonstrate the distribution of the data and is a very efficient method of communicating data. The middle bar represents the median, the edges of the box are the first and third quartiles, and the lines (commonly called whiskers) represent the data extending to 1.5 times the interquartile range. Points outside this are displayed and represent the most extreme outliers. They are another useful visualization, especially when presenting the distribution of a value across groups (e.g., LOS stratified by race). Figures 2 and 3 demonstrate the distribution, and particularly the skewness, of two of the continuous variables of interest: age (Fig. 3) and LOS. In particular, LOS shows a skewed distribution and inflation of the mean but arriving at these conclusions can be much easier using well-developed data visualizations such as Figure 3. In these figures we can clearly see the outliers in the boxplots, whereas the histograms confirm that the distributions do not follow a normal distribution (the black curve overlaid). Additionally, we would likely want to present the median and interquartile range when describing these variables because we know the mean and standard deviation are highly sensitive to these outliers. Although we present these figures in this article, in a study we would likely include them as a supplement for reviewers and fellow researchers to reference if needed.
FIG. 3.
Distribution, both histogram and boxplot, of the age (in years) of those hospitalizations for emergency general surgery (EGS). The y-axis of the histogram represents the density (not frequency), and the normal curve for these data is overlaid to highlight the skew in age data for this population.
Example of data description for a methods section of an article
Ideally, the methods section of an article will be comprehensive enough that would allow for your work to be reproduced. In addition to the overview, data source(s), study population, inclusion/exclusion criteria, and variables of interest (as we do in our own methods section), it is important to describe how data will be displayed. The portion of the methods that includes this information, from a hypothetical study, could be as follows: “Numerical data are expressed as median (interquartile range) and were assessed for normality using both the XXX test and visually using both histograms and boxplots. Categorical data are expressed as number (%). Because age was not distributed normally, and rather followed a bimodal distribution, this variable was converted to categorical and dichotomized around the median. Time to surgery was also not distributed normally and so converted into three categories: <24 hours, 24–72 hours, and >72 hours, based on our prior study (appropriate citation).”
Discussion
The complete description of our data, as the first step of the analysis stage, is crucial to understanding the study population as well as informing our later statistical decisions. This process of describing the data can also serve as a mechanism for study validity and ensure that earlier parts of the study (e.g., data cleaning, processing, and management) did not introduce any errors. One example of this may be if we were studying a condition primarily prevalent in older adults but identified younger adults in the exploratory analysis. This would either suggest a data or coding error, which should be investigated thoroughly, or unique cases of the condition of study that may warrant exclusion.
This ability to spot errors also links to the ability to make additional study cohort restrictions to better refine the study population or remove heterogeneity. In our example of EGS, there are two key areas in our data exploration that could influence future analytic decisions: age and admission type. Of our EGS population, 8% of hospitalizations were children and 31% were 65 years old or older (Table 1). In our study we would first, perhaps, exclude children from the analysis by considering potential heterogeneity or differences, in disease presentation and management across later age groups. If our study question was to examine only the geriatric population, we might restrict our analysis to the 31% that are 65 years old or older. Furthermore, although termed emergency general surgery, we identified that 16.2% of hospitalizations for EGS were labelled elective (Table 1), which highlights a limitation of administrative data and use of diagnosis codes. For that reason, and in hopes of creating the most accurate case definition, we could consider restricting on both age and admission type, to focus on older adults who were non-elective admissions.
Once the study cohort has been identified and the initial descriptive statistics have been conducted, data visualization is an important next step. This visualization of the data, much like the description of the data, serves two important purposes: first it provides a way to convey important information about your study population and second it aids decisions for subsequent statistical analyses. In addition to these important principles to convey your data and findings, these visualizations can help assess the normality of variables that identifies skewness and informs the validity of statistical comparisons and regression models, discussed in more detail elsewhere. Lack of normality and distributions, would require us to utilize non-parametric analyses, which again are detailed in a follow-up article [5].
Another important consideration in the creation of a Demographics Table is whether or not to include p values. Historically, these tables have included p values as a way to identify statistically significant differences between the two groups efficiently, with a threshold of significance to be 0.05 (that is, only p values <0.05 are considered statistically significant). This statistical value was introduced to prominence by statistician Ronald Fisher in 1925 as a mechanism to assess the probability that the result obtained is as or more extreme than what was observed due to chance alone [6,7]. In recent years, however, there has been a shift away from the reliance on p values because of a myriad of factors, including the increasing emphasis on the threshold to determine significance or results, and the often misleading interpretation or reasoning surrounding these cut points [6–8]. One additional limitation of an arbitrary p value is that in large datasets such as the NIS, statistical significance is easily achieved even when differences between groups are small and likely not clinically or meaningfully significant. For these reasons, we have chosen not to display them and, instead, focus our description of the data on meaningful differences while leaving hypothesis testing to specific questions in comparing the data.
The final important point to raise in this article is our analysis of the unweighted data. The NIS, and many other federal and nationally representative datasets, includes weighting information, which makes it possible to create national estimates. We did present the national estimate for the number of hospitalizations, but the rest of our description was on the unweighted and thus cannot be taken as national estimates. One must think critically about the intention of the study and its goals when deciding on weighting, as weighting adds another layer of complexity to describing the data, conducting the analyses, and reporting the results. Primarily, weighting results in standard errors for each estimate and its proportion. This standard error helps capture the complex survey design elements but makes reporting the results much more challenging. As the point of this article was not to produce national estimates but to demonstrate statistical principles, we chose not to account for weight.
In conclusion, accurately describing data in tables and figure helps to make important decisions on study inclusion criteria, present and convey results to readers, and make decisions regarding which statistical approach is valid. Although the field has previously emphasized including p values in tables, recent advancements have de-emphasized this and, instead, descriptions of data should focus on meaningful differences not just those that may be statistically significant.
Funding Information
Dr. Ho is supported by the Case Western Reserve University Clinical and Translational Science Collaborative of Cleveland (KL2TR002547).
Author Disclosure Statement
Dr. Ho's spouse is a consultant for Zimmer Biomet, Sig Medical, Atricure, and Medtronic.
This publication was made possible by the Clinical and Translational Science Collaborative of Cleveland, KL2TR002547 from the National Center for Advancing Translational Sciences (NCATS) component of the National Institutes of Health and NIH roadmap for Medical Research. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
References
- 1. Smith JW, Knight Davis J, Quatman-Yates CC, et al. . Loss of community-dwelling status among survivors of high-acuity emergency general surgery disease. J Am Geriatr Soc 2019;67:2289–2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. patchwork: The Composer of Plots [computer program]. Version R package version 1.0.12020. [Google Scholar]
- 3. Wickham H, Averick M, Bryan J, et al. . Welcome to the tidyverse. J Open Source Softw 2019;4:1686. [Google Scholar]
- 4. Héroux M. Verify if data are normally distributed in R: Part 1. Scientifically Sound. 2018. https://scientificallysound.org/2018/06/07/test-normal-distribution-r/ (Last accessed January 12, 2021).
- 5. Bensken WP, Ho VP, Pieracci FM. Basic introduction to statistics in medicine, part 2: Comparing data. Surg Infect 2021;22:597–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Greenland S, Senn SJ, Rothman KJ, et al. . Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol 2016;31:337–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Kennedy-Shaffer L. Before p <0.05 to beyond p <0.05: Using history to contextualize p-values and significance testing. Am Stat 2019;73(Suppl 1):82–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. McShane BB, Gal D, Gelman A, Robert C, Tackett JL. Abandon statistical significance. Am Stat 2019;73(Suppl 1):235–245. [Google Scholar]