Basic Introduction to Statistics in Medicine, Part 2: Comparing Data

Abstract

Background: Comparison of parameters between two or more groups forms the basis of hypothesis testing. Statistical tests (and statistical significance) are designed to report the likelihood the observed results are caused by chance alone, given that the null hypothesis is true.

Methods: To demonstrate the concepts described, we utilized the Nationwide Inpatient Sample for patients admitted for emergency general surgery (EGS) and those admitted with non-EGS diagnoses. Depending on the type and distribution of individual variables, appropriate statistical tests were applied.

Results: Comparison of numerical variables between two groups is begun with a simple correlation, depicted graphically in a scatterplot, and assessed statistically with either a Pearson or Spearman correlation coefficient. Normality of numerical variables is then assessed and in the case of normality, a t-test is applied when comparing two groups, and an analysis of variance (ANOVA) when comparing three or more groups. For data that are not distributed normally, a Wilcoxon rank sum (Mann-Whitney U) test may be used. For categorical variables, the χ² test is used, unless cell counts are less than five, in which case the Fisher exact test is used. Importantly, both the ANOVA and χ² test are used to assess for overall differences between two or more groups. Individual pair comparison tests, as well as adjusting for multiple comparisons must be used to identify differences between two specific groups when there are more than two groups.

Conclusion: A basic understanding of statistical significance, and the type and distribution of variables is necessary to select the appropriate statistical test to compare data. Failure to understand these concepts may result in spurious conclusions.

After a thorough data description and examination of variables in a dataset, it is then possible to begin to make formal statistical comparisons for the purpose of testing a hypothesis. This is where the researchers start to understand whether two groups are different from each other, and whether those differences are large enough that it would be unlikely that those differences could have occurred by chance. The results of formal statistical comparisons between groups typically form the basis of a research study's conclusions. These comparisons may be related to the primary outcome, such as disparities in diagnosis or procedure use, but more often provide a first look at potential differences in groups and areas for adjustment in regression models or other statistical techniques. The choice of which statistical test to use is dependent on the distribution and structure of the data, and thus a clear description and presentation of the initial results is critical, as detailed previously [1].

In this article we build upon this previous description by making a number of formal statistical comparisons, including comparisons of normally and non-normally distributed data as well as the distribution of categorical variables and proportions between groups. These comparisons can be made both as the primary focus of an article or as a step along the way toward additional analyses to identify variables for which to adjust. We discuss in more detail a number of statistical tests including Pearson and Spearman correlation, Student t-test, analysis of variance (ANOVA), Wilcoxon rank sum test, Kruskal-Wallis test, Fisher exact test, and χ² test, as well as some important considerations when making these comparisons.

Data Source and Analysis Methods

The Nationwide Inpatient Sample (NIS) inpatient hospitalizations for emergency general surgery (EGS) was used to illustrate the various statistical tests [1]. This analysis is conducted on the unweighted sample but weighting to produce national estimates is possible following guidelines from the Agency for Healthcare Research and Quality (AHRQ) using the given weights, cluster, and strata. The data presented here expand on the previous data by also reporting comorbidity prevalence estimates for the Elixhauser comorbidities. The Elixhauser comorbidities are a list of comorbidities that are used frequently in health services research, and have previously been documented to have associations with negative outcomes [2]. We made the following comparisons: the correlation between length of stay and cost among EGS hospitalizations, demonstrated using Pearson and Spearman correlation coefficients; differences in length of stay and age between non-EGS and EGS hospitalizations using Wilcoxon rank sum test; differences in length of stay among racial groups for EGS hospitalizations using Kruskal-Wallis with a post hoc Dunn test with Bonferroni correction to examine pairwise comparisons; and differences in proportion of hypertension, valvular disease, and coagulopathy between non-EGS and EGS hospitalizations. Non-parametric tests were used due to the clear non-normal distribution of continuous variables, as discussed previously [1]. The level of significance for these tests was 0.05, and p values that were <0.001 were reported as p < 0.001. Data cleaning, which is preparing the data for analysis from its raw format, was done via SAS version 9 (SAS Institute, Cary, NC), with visualizations made in R version 3.6.1 using tidyverse and dunn.test [3,4].

There were a total of 7,159,694 hospitalizations in the 2017 Nationwide Inpatient Database, of which 111,034 or 1.6% were for EGS (Table 1) [1]. Although demographic comparisons have been reported previously, in this article we expand on that by further presenting comorbidities present in each group (Table 1) using standard Elixhauser comorbidity classifications [2]. The most common comorbidity, regardless of whether or not the hospitalization was for EGS, was hypertension with 41.2% and 42.5% of non-EGS and EGS hospitalizations, respectively (Table 1).

Table 1.

Elixhauser Comorbidities, in Descending Order of Prevalence for Non-Emergency General Surgery

Comorbidity n (%)	Non-EGS	EGS
	n = 7,048,660	n = 111,034
Hypertension	2,901,879 (41.2)	47,224 (42.5)
Fluid and electrolyte disorders	1,641,744 (23.3)	24,755 (22.3)
Chronic pulmonary disease	1,213,890 (17.2)	15,879 (14.3)
Deficiency anemias	1,085,535 (15.4)	10,731 (9.7)
Obesity	947,881 (13.5)	22,628 (20.4)
Diabetes with complications	892,591 (12.7)	7,954 (7.2)
Renal failure	885,531 (12.6)	7,091 (6.4)
Depression	760,152 (10.8)	9,636 (8.7)
Hypothyroidism	751,633 (10.7)	10,851 (9.8)
Diabetes without complications	640,714 (9.1)	10,399 (9.4)
Weight loss	368,451 (5.2)	6,286 (5.7)
Coagulopathy	364,868 (5.2)	3,341 (3.0)
Peripheral vascular disease	331,946 (4.7)	3,942 (3.6)
Drug abuse	284,829 (4.0)	1,843 (1.7)
Alcohol abuse	280,015 (4.0)	2,217 (2.0)
Liver disease	255,254 (3.6)	6,335 (5.7)
Psychoses	235,455 (3.3)	2,419 (2.2)
Valvular disease	232,061 (3.3)	3,198 (2.9)
Paralysis	206,274 (2.9)	1,338 (1.2)
Rheumatoid arthritis	178,571 (2.5)	2,348 (2.1)
Chronic blood loss anemia	174,036 (2.5)	784 (0.7)
Metastatic Cancer	139,246 (2.0)	1,832 (1.7)
Solid tumor without metastasis	132,561 (1.9)	1,446 (1.3)
Peptic ulcer disease	46,575 (0.7)	1,141 (1.0)
Lymphoma	45,702 (0.7)	408 (0.4)
Other neurologic disorders	45,452 (0.6)	179 (0.2)
Pulmonary circulation disease	43,052 (0.6)	475 (0.4)
AIDS	15,278 (0.2)	138 (0.1)

Prevalence of Elixhauser comorbidities between hospitalizations not for emergency general surgery (EGS) and those for EGS in the 2017 Nationwide Inpatient Sample (NIS).

AIDS = acquired immune deficiency syndrome.

Statistical significance

The concept of statistical significance in the medical literature is often oversimplified. Specifically, a p value <0.05, in and of itself, is thought to be sufficient to believe the validity of a study's conclusions. To understand the meaning of a p value, one must begin with the concept of hypothesis testing. Most studies test a null hypothesis, which states that there is no difference between groups in an outcome of interest. For example, our null hypothesis may be that there is no difference in age between two groups of patients. The next point is that, given enough attempts (repeated sampling), a difference between groups will be found by chance alone, even when a true difference does not actually exist. For example, one could imagine that with enough repetitions of tossing a coin, a string of five consecutive “heads” flips would arise by chance. Using this framework, the p value is the probability of observing results as or more extreme than what we observed, given that the null hypothesis is true. In our prior example, consider the mean ages of the two patient groups to be 42 and 44 years, respectively, and the p value was 0.04. If our experiment were repeated 100 times, and the null hypothesis were true, we would observe age differences as or more extreme as in only four of 100 cases.

A basic understanding of statistical significance results in an appreciation of several additional concepts. The first is that the threshold for statistical significance, although reasonable, is ultimately arbitrary. However, once this threshold is set, it must be honored. For example, if statistical significance is defined as 0.05, a calculated p value of 0.06 must not be considered statistically significant, even though based on our prior discussion, it represents a relatively low likelihood that the observed results are the result of chance alone. Next, p values are not binary, and are continuous measures of evidence. That is, a p value of 0.001 indicates a lower probability of the observed result being the result of chance compared with a p value of 0.04. Finally, statistical significance, which is determined solely by the p value, should not be confused with clinical significance. Consider if in our previous example because of a large sample size, a mean age difference of 0.02 years between the two groups is found to be statistically significant with a p value of 0.04. If the primary outcome is mortality, it would be highly unlikely that such a miniscule age difference contributed to mortality risk. Thus, statistical significance must always be interpreted in the context of clinical significance.

Correlation

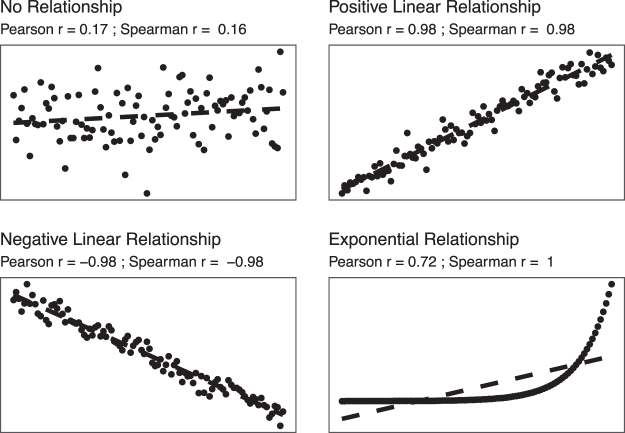
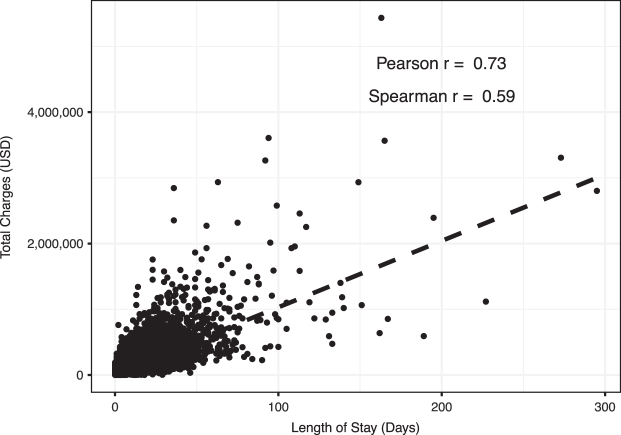
When comparing two continuous numerical variables, the first step undertaken is to apply a simple correlation test. The first analysis conducted was to examine the relation between total charges and length of stay (LOS) among those hospitalization for emergency general surgery (EGS). The relation between two numerical variables can be assessed graphically with a scatterplot (Figs. 1 and 2). In Figure 1 we demonstrate four relations with their corresponding Pearson and Spearman correlation coefficients, to illustrate their assessment of strength and direction. In Figure 2, each dot represents a single hospitalization that also aides in identifying potential outliers that may have a strong influence on the relation. The dashed line in the figure represents the result if we were to use a linear model on these data. This comparison demonstrates a positive correlation, wherein as the LOS increases so do the total charges. As we can see, this linear trend does not fit our data well, largely because of the skew and variation in the data. The correlation between total charges (in U.S. dollars) and LOS (in days) was 0.73 using the Pearson correlation coefficient, and 0.59 using the Spearman correlation coefficient.

FIG. 1.

Scatterplots showing various correlation strength and direction including no relationship, a positive and negative linear relation, and an exponential relation. Included with each are the Pearson and Spearman correlation coefficients to demonstrate their strength of association as well as direction (positive or negative), and how the Spearman correlation is more appropriate for non-linear relations.

FIG. 2.

A scatterplot and the correlation, both Pearson and Spearman correlation coefficients, between length of stay, in days, and total charges, in U.S. dollars, for hospitalizations for emergency general surgery (EGS) in the 2017 Nationwide Inpatient Sample (NIS).

The Pearson's correlation coefficient models the linear correlation between the variables and ranges from −1 to 1; −1 represents a perfectly correlated (all observations on the line) in the downward direction where 1 represents that the data are perfectly correlated in the positive direction [5 − 7]. Meanwhile, a coefficient of 0 would represent no linear correlation between the two variables of interest [5 − 7]. These correlation coefficients are often split into categories to qualify the strength of the relation. You may find typical ranges for the coefficient are: 0.7–1 (highly correlated); 0.4–0.7 (moderately correlated), and <0.4 (weak/no correlation). Other approaches include more categories: 0–0.1 (negligible), 0.1–0.39 (weak), 0.40–0.69 (moderate), 0.70–0.89 (strong), 0.90–1 (very strong) [6]. However, these cut points are still somewhat arbitrary and should be approached with caution.

A few important notes about this measure. First, the size of the correlation does not measure the slope of the line but rather demonstrates how close the relation is to being linear. Second, a weak Pearson correlation does not mean that the two variables are not correlated; rather, if simply means that there is not a linear correlation. Non-linear patterns, such as a bimodal relation, would result in a Pearson correlation coefficient being close to zero, exemplifying the importance of visualizing the data with a scatterplot to recognize non-linear patterns more easily. Our coefficient of 0.73 means that there is a fairly strong (closer to 1) positive (greater than 0) linear correlation between LOS and total charges, as we would expect.

The second correlation coefficient presented, Spearman correlation, does not require that the relation between the two variables be a linear relation and is generally less sensitive to outliers [8,9]. The Spearman coefficient will be more helpful when it appears, via a scatterplot, that the relation is not linear [8,9]. In our example presented here, the Pearson coefficient is higher than the Spearman, which may be partially explained by the large number of observations relatively close to the linear relation, as well as the skew, but overall, these results suggest that LOS and total charges are positively correlated, and we could model them using a linear relation.

Two-group (or more) comparisons of categorical variables

Often, the key comparisons between groups aims to perform two-group comparisons of a categorical variable. For example, are patients with EGS more likely to have hypertension than patients without EGS? Here what we are trying to demonstrate is whether the proportion of individuals in one group with a specific attribute is larger than the proportion of individuals in a comparator group. Is that proportion different than what would be expected by chance alone? In our analysis, we wanted to compare three comorbidities which we believe would be particularly important when considering a study on EGS: hypertension, coagulopathy, and valvular disease.

These comparisons use one of the most common tests, namely the χ² test, specifically Pearson χ² test. Although this test is commonly presented as comparing the proportion between two groups, technically this compares the observed and expected frequencies between groups, and also can be used across more than two groups [10–12]. The main caveat of using the χ² test is that for any study with very small sample sizes, a χ² test is inappropriate and may yield misleading results. The general rule of thumb is if you have an expected cell count less than five, a Fisher exact test should be used instead [10,11].

In our example data, each of these comparisons were significant: hypertension (χ² [degrees of freedom: 1] = 83.64; p < 0.001); coagulopathy (χ² [1] = 1052.2; p < 0.001); and valvular disease (χ² [1] = 58.28; p < 0.001). If we were to continue with further analysis or modeling, these results suggest that these would be variables we should include, control, or for which to adjust. One final point about the χ² test is that when more than two groups are being compared, a statistically significant result implies that there are overall significant differences between groups but cannot inform the question of which specific groups are different from the others.

Two-group comparisons of numerical variables

Comparisons of numerical variables are also key for identifying key differences between groups. Here, we use the example of examining differences in age or LOS between hospitalizations that were not for EGS compared with those that were for EGS. Here, the choice of test to use depends largely on distribution of the variables. A rule of thumb here is that if your data are normally distributed, then you can describe the data with means (and standard deviations) and compare data using parametric tests such as the Student t-test [13]. The Student t-test tests a hypothesis that the two groups were drawn from the same population with the same distribution by comparing the means of the two groups. If the means are substantially different, then it is unlikely that the two groups came from the same distribution. Although there are a few approaches within the framework of a t-test, the most prominent is independent versus paired t-tests. Independent samples t-tests are used when the two groups are independent of each other or not related. On the other hand, a paired samples t-test would be used if you were comparing two groups who had been matched or paired to each other or if you were comparing the same individuals across two time-points (which can be thought of as being matched to themselves). This decision should be reliant upon the design of your study.

For non-normally distributed data, or data that should not be described with a mean, non-parametric tests should be used. Our data were not normally distributed, and therefore we needed a non-parametric test, which in this case was the Wilcoxon rank-sum test which is also known as the Mann-Whitney-Wilcoxon, or Mann-Whitney U test [8,14–17].^7,13–16 The Wilcoxon rank sum test does not truly compare the medians, as is sometimes thought. Rather it compares the “ranks” of the two samples. What this means, practically, is that the data is ranked from smallest to largest, and then split between the two samples (non-EGS and EGS) and then the sum of the ranks calculated and compared [8]. With this understanding, we can now evaluate our results to see that both age and length of stay were significantly different (p = 0.02 and p < 0.001, respectively) between those hospitalizations for EGS and those which were not for EGS. Non-EGS hospitalizations had a mean LOS of 4.6 days (standard deviation [SD], 6.9) and a median of 3 (interquartile range [IQR], 2–5), whereas EGS hospitalizations had a mean LOS of 5.1 (SD, 6.2), and a median of 3 (IQR, 2–6). These differences were statistically significant using the Wilcoxon rank sum test (p < 0.001). The mean age of non-EGS hospitalizations was 49.5 (SD, 27.6) years with a median of 56 (IQR, 29–72) years whereas EGS hospitalizations had a mean of 51.4 (SD, 21.3) years and a median of 54 (IQR, 36–68) years. Again, these differences were statistically significant (p = 0.02).

More than two-group comparisons of numerical variables

Pushing these initial analyses further, sometimes we want to compare differences in means within a sample that have more than two groups, for example, race versus LOS. If our outcome (LOS in this example) is normally distributed we would consider an ANOVA that would yield one p value and tell us, globally, if there were significant differences [18,19]. We could then follow this test with a post hoc test, such as Tukey honestly significant differences (HSD) for example, that then conducts pairwise comparisons to evaluate which are significantly different [20]. A post hoc test is simply a way of referring to a statistical analysis that would follow after obtaining a global p value. Another approach one could take in lieu of Tukey HSD would be to simply do multiple pairwise-comparisons between each group using Student t-test. When you conduct this type of post hoc analysis with multiple statistical testing you would need to consider a statistical correction, such as the Bonferroni correction [21]. Simply, this increases our threshold for statistical significance by decreasing our cutoff below 0.05 to minimize the risk of a false discovery. For example, when three groups are compared to each other, the corrected p value would be 0.05/3, or 0.017. Because performing multiple comparisons increases the likelihood that one of the comparisons will be significant simply by chance, and by changing this threshold for significance we can reduce the risk of a false-positive. Refer to the article by Gelbard and Cripps [22] in this issue.

Because our data on LOS are non-normally distributed (as they usually are for LOS), we can use the non-parametric alternative: Kruskal-Wallis one-way ANOVA on ranks followed by the Dunn test (with Bonferroni correction) for the post hoc pairwise comparisons [23]. Similar to the Wilcoxon rank sum test, this analysis is using ranks instead of the mean. In a study on racial disparities or inequities, this first analysis is revealing but it would also only be a first look, and we would want to consider potential confounders and other techniques, such as regression models, which would help account for this.

To demonstrate these principles, we show an analysis of the relation between race and LOS that would demonstrate racial disparities among EGS hospitalizations (Table 2). Here, we used the Kruskal-Wallis test. This test was statistically significant (p < 0.001), suggesting that LOS differs between racial groups. Interpreting these results, we now know that at least one group significantly differs from the others but cannot identify which group or groups are different. To investigate further which comparisons were significant, we used a post hoc Dunn test with Bonferroni correction, which identified significant differences (p < 0.001) in LOS between all comparisons except: Asian or Pacific Islanders and Native Americans; Asian or Pacific Islanders and Other; Native Americans and Other; and Native American and those with missing race data (Table 3).

Table 2.

Length of Stay (in days) by Race

	Length of stay
Race/ethnicity	Mean (SD)	Median (IQR)
White	5.3 (6.2)	4 (2–6)
Black	6.7 (8.6)	4 (6)
Hispanic	3.9 (4.5)	3 (3)
Asian Pacific Islander	4.9 (7.2)	3 (4)
Native American	4.8 (5.7)	3 (3)
Other	4.3 (5.0)	3 (3)
Missing	5.0 (5.8)	3 (4)

Length of stay (in days) stratified by race among those hospitalizations for emergency general surgery (EGS) in the 2017 Nationwide Inpatient Sample (NIS).

SD = standard deviation; IQR = interquartile range.

Table 3.

Dunn Pairwise Comparisons

	White	Black	Hispanic	Asian Pacific Islander	Native American	Other
Black	<0.001
Hispanic	<0.001	<0.001
Asian Pacific Islander	<0.001	<0.001	<0.001
Native American	<0.001	<0.001	<0.001	1.0
Other	<0.001	<0.001	<0.001	0.147	0.111
Missing	<0.001	<0.001	<0.001	<0.001	0.462	<0.001

Results of the Dunn test pairwise comparisons, with Bonferroni correction, for length of stay. Displayed are the p values for each comparison.

Discussion

In this article, we present a number of analyses and comparisons using data from the NIS, specifically looking at those hospitalizations for EGS. The goal of this work is to demonstrate a number of approaches in comparing data, that may either be the focus of a manuscript or analysis or may represent only one step along the way to identifying important covariates, for example using a regression model. See also the article by Rattan et al. [24] in this issue.

The understanding of these results, and results from any study that compare data, is not complete without a discussion on spurious correlations, the role of confounders, and acknowledgement of the substantial limitations of the p value. In the first analysis we presented the correlation between LOS and total charges. Conceptually, this makes sense and our observed correlation coefficients are unsurprising given this context. However, caution should be taken when interpreting these correlations, and ensuring that conceptually the correlation makes sense. In fact, there are numerous instances where unrelated things produce nearly perfect correlations [25]. These spurious correlations underscore the importance of having a clear conceptual model and approach when conducting these analyses, or else findings may be unfortunately spurious.

In our analysis we presented an example using Kruskal-Wallis analysis on LOS by race to identify potential racial disparities for EGS patients. This analysis can be considered an unadjusted analysis in that it only demonstrates the relation between race and LOS, without adjusting for any other factors. It is imperative to consider the role of confounders, or variables that are associated with both the exposure and outcome, and their role in this relation, particularly for retrospective, non-randomized data, such as those available in administrative databases [26]. In fact, we would not suggest that conclusions should be drawn based on these analyses because no confounders were considered. Any study that evaluates an outcome such as LOS would most certainly want to include other variables that may explain an increased LOS, such as comorbidities or complications. This adjustment is most often done through regression models that help to tease out the complex relations that underplay these relations.

The final important note to contextualize these findings is the role of the p value in these analyses. It is important to note that, as a whole, the field is largely moving away from a reliance on p values to determine what is considered to be significant and what is not [27–29]. Indeed, in our previous article we outlined how excluding p values in a Table 1 is becoming more common practice [1]. However, we recognize that many of the methods, their teaching, and interpretation in clinical research center around a resulting p value. However, the p value is an imperfect measure and is fraught with limitations. In the results we present here, because of the large sample size, it is unsurprising that all of our findings were statistically significant, such as our significant difference in LOS even though the median was the same. In fact, most comparisons we could or would make using these data would yield statistically significant findings, in some regard defeating the purpose of the p value. Although we do not discuss alternatives to p values here, investigators should be aware of this shift in the field and understand that much like any other field, statistics continues to evolve and develop.

Conclusion

In conclusion, we have presented and illustrated the tests used most commonly to compare data and demonstrated the results of these comparisons using data on EGS from the NIS. This article should help guide investigators in how to plan and perform their own analyses as well as interpret the findings of statistical tests performed by others. Any analysis and comparison should be strongly rooted in a conceptual framework, wary of potentially spurious correlations and confounders, and consider not just the statistical significance of the result, but the clinical and meaningful significance of the findings. As the field continues to develop, these tests may rise or fall in prominence, but nonetheless provide a strong foundation.

Funding Information

Dr. Ho is supported by the Case Western Reserve University Clinical and Translational Science Collaborative of Cleveland (KL2TR002547) from the National Center for Advancing Translational Sciences (NCATS) component of the National Institutes of Health and NIH roadmap for Medical Research).

Author Disclosure Statement

Dr. Ho's spouse is a consultant for Zimmer Biomet, Sig Medical, Atricure, and Medtronic.