Casting a bright light on Ostwald’s rule of stages

Crystallization, which is a ubiquitous process in both natural and technological settings, follows a rich set of pathways as crystallizing systems evolve from dispersed monomers to condensed solids in their equilibrium, ordered state. While sound theoretical frameworks for both nucleation (1) and subsequent growth (2) via direct assembly of monomers into ordered phases were established in the 19th and 20th centuries, over the past two decades the advent of experimental methods capable of probing the atomic structure of crystals during the early stages of formation have placed the limitations of those frameworks in stark relief (3). In particular, initial appearance of poorly ordered, amorphous, or liquid precursors that then (re)crystallize to form the final phase is now recognized as widespread. Ostwald’s rule of stages (4), which states that the phase that nucleates is not necessarily the most thermodynamically stable, rather it is the one closest in free energy to the mother phase, is often invoked to explain the appearance of these precursors. However, an a priori rationale for the universal validity of this rule does not exist (5). Moreover, the structural pathways by which disordered phases transform to well-ordered crystals and the relative roles of kinetic and thermodynamic controls over both their appearance and conversion remain poorly understood. In PNAS, Niozu et al. (6) exploit the brightness of X-ray free electron laser pulses to probe the structure of more than a million individual Xe nanoparticles formed in supercooled jets within the timescale required for initial disordered precursors to transform to the ordered, equilibrium phase. In doing so, the authors reveal an unexpected structural state composed of hexagonally close packed (hcp) layers that are randomly stacked. They attribute the appearance of this random hcp (rhcp) phase to a size-dependent free energy that initially favors random stacking, before eventually shifting to favor the regular ABC stacking of the bulk face-centered cubic (fcc) phase. Thus, the findings provide insight into Ostwald’s rule.

The genesis of Ostwald’s rule was a set of empirical observations in a wide range of solution-based crystallizing systems showing that metastable phases typically appeared first and were then replaced by increasingly stable phases, leading eventually the appearance of the equilibrium phases (4). The original argument put forth by Ostwald for the generality of this observation was that less-stable phases more closely resemble the solution itself and thus are easier to form. This rationale can be cast in terms of classical nucleation theory (CNT) by recognizing that there is a rough inverse scaling between the equilibrium solubility C_e of a phase and its interfacial free energy α (7). Less-soluble phases are inherently more stable, but higher interfacial free energy implies a greater energetic “mismatch” with the surrounding solution. This inverse relationship leads naturally to Ostwald’s rule. To understand why, consider two common crystals with very different solubilities. For KDP (KH₂PO₄), which has a solubility at room temperature of ∼3 M, α ≈ 20 mJ/m², while, for a sparingly soluble crystal such as gypsum (BaSO₄) with a solubility of about 8E⁻⁶ M, α ≈ 150 mJ/m². This difference in α has a profound impact on the free energy barrier to nucleation ΔG*, which is proportional to the cube of α—i.e., ΔG* ∝ α³—and, thus, on the nucleation rate, which is ∝ e^−(ΔG*kT) where k is Boltzmann‘s constant and T is the temperature (1). Suppose, for example, that the supersaturation σ of a KDP solution is chosen to create a ΔG* of 2 kT—i.e., it is just twice the thermal energy of the ions in the solution so that nucleation is rapid and widespread. If a gypsum solution is set to the same value of σ, then ΔG* will be >800 kT. Ignoring differences in kinetic factors, the rate of gypsum nucleation is then reduced from that of KDP by a factor of e⁻⁸⁰⁰, or about 1E-365. To put this in perspective, if a KDP nucleation event occurred every second, a gypsum nucleation event would be unlikely to occur within a time period equal to 1E347 times the age of the universe.

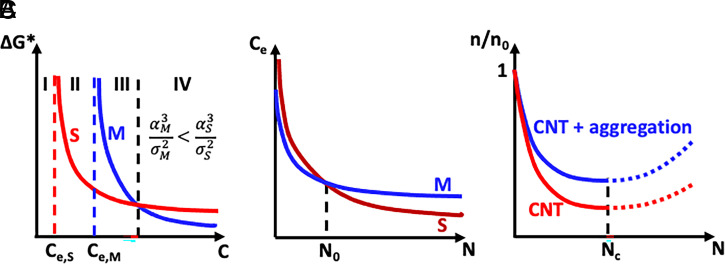
As the above example illustrates, even small differences in interfacial free energy can provide a rationale for the initial appearance of less-stable phases. However, unlike that example, which compares barriers for two distinct materials in separate solutions set to the same σ, in a single solution from which two phases can form the value of σ with respect to each cannot be equal. The value relative to the more stable, lower-solubility phase will be larger than that for the less stable, higher-solubility phase. Because ΔG* ∝ σ⁻² (1), this difference acts to counter the impact of the difference in α on ΔG*. In fact, the scaling of ΔG* with α³/σ² leads to an expectation of four distinct regimes, with Ostwald’s rule manifest in only one (Fig. 1A). For values of the solute concentration below C_e for the stable phase C_e,S, no crystallization can take place. Above that concentration, but below C_e for the metastable phase C_e,M, only the stable phase can form. In the range of concentration above C_e,M but below the concentration for which σ_S²/σ_M² = α_S³/α_M³, both phases can form, but ΔG* for the stable phase is still smaller than that of the metastable form, so Ostwald’s rule would not be expected to apply, at least not for reasons based in CNT. Instead, Ostwald’s rule is only expected to apply once the concentration is raised above this so that σ_S²/σ_M² < α_S³/α_M³.

Fig. 1.

Three distinct mechanisms can lead to the apparent observation of Ostwald’s rule of stages. (A) Schematic dependence of free energy barrier to nucleation ΔG* on solute concentration C for a system with one stable phase (S) and one metastable phase (M). On average, Ostwald’s rule will be observed only in region IV. (B) Schematic dependence of equilibrium solubility C_e on the number of growth units N in a particle for the stable and metastable phases, where the cross-over in stability occurs at N₀. (C) Schematic dependence of cluster number density n normalized to the monomer density n₀ on N for a cluster distribution predicted by CNT and one that also includes cluster aggregation.

The above analysis based on CNT makes two assumptions that have been shown, over the past 20 y, to be invalid for many crystalizing systems. The first is that the relative stability of two phases is given by their bulk solubilities and is independent of particle size. This assumption is generally expected to fail precisely because, typically, α_M < α_S. The reason why is easily seen by considering the free energy per growth unit (e.g., atom or molecule) ΔG vs. particle radius R (Fig. 1B). As R is reduced, the proportion of growth units that lie within the particle relative to those on the surface decreases, with the ratio ∝ R. Consequently, as shown for a wide range of materials, at sufficiently small particle size, ΔG, which is the sum of surface and bulk contributions, is smaller for the metastable phase (8). In other words, the relative stabilities are reversed. The consequence is that, as the nucleus begins to form, both C_e,M and α_M are lower than C_e,S and α_S, respectively; thus, ΔG* is less for all values of σ. As discussed by Navrotsky (9), Ostwald’s rule now becomes a near certainty as the pathway of crystallization coincides with the appearance of the most stable nanoscopic phase, which eventually becomes large enough to transform to the most stable macroscopic phase (Fig. 1B). This analysis even applies to amorphous precursors, which do not lie on any phase diagram, because, at macroscopic length scales, they are always less stable than the ordered phases. Recently, this scenario was beautifully demonstrated by direct imaging of atomic arrangements in metallic particles nucleating from the vapor phase using atomically resolved transmission electron microscopy (10).

In PNAS, Niozu et al. exploit the brightness of X-ray free electron laser pulses to probe the structure of more than a million individual Xe nanoparticles formed in supercooled jets within the timescale required for initial disordered precursors to transform to the ordered, equilibrium phase.

The findings of Niozu et al. (6) add a twist to the above mechanism of Ostwald’s rule. For particles exhibiting hcp packing, the entropy of mixing associated with the random layer stacking of the rhcp phase provides a negative term in ΔG that scales with the number of layers and hence is linear in particle dimension. For large particles, this contribution is small compared to the excess free energy of the bulk rhcp phase over that associated with the ordered ABC stacking of the fcc phase, which is cubic in particle dimension, and thus the fcc phase is more stable. However, at sufficiently small size, this linear term wins out over the cubic term and, hence, the rhcp phase is most stable. As both phases have the same value of α—or nearly so—the higher σ relative to the rhcp phase ensures that it appears first. Once particle size crosses the threshold at which the relative phase stabilities revert to their bulk relationship, recrystallization to the fcc phase leads to periods in which the two phases coexist within individual particles.

The second assumption that underlies the view of Ostwald’s rule rooted in CNT, but is violated in numerous systems, is that nuclei form by repeated addition of monomers. For a number of systems, there is substantial evidence that higher-order species, such as multi-ion complexes or oligomers, aggregate to form the first stable nuclei (Fig. 1C) (3). These species may be unstable relative to the free monomers and thus represent only a small fraction of the species (11), but their aggregation, which may be favored due to attractive interactions, can enable them to leap-frog the classical free energy barrier and thus provide a low-barrier route to stability. The handful of simulations that have modeled cluster formation prior to nucleation predict unstructured and highly solvated clusters (12). Thus, any aggregates that form are likely to initially be amorphous and highly solvated, leading once again to a multistep process of crystallization. Such predictions are consistent with the few cases in which such precursors have been directly observed (11).

Even when the cluster size distribution in the absence of aggregation follows the predictions of CNT, aggregative pathways may lead to a higher rate of creating clusters that exceed the critical size—i.e., the size at which ΔG = ΔG* and beyond which further growth is spontaneous—than would be possible simply through monomer-by-monomer growth (Fig. 1C). However, the result is a nonequilibrium distribution that arises from dynamic processes of diffusion, collision, and attachment. Thus, the distribution cannot be calculated within the framework of CNT, which is rooted in the free energy of cluster formation. Developing a comprehensive framework that integrates aggregation dynamics into the analysis of cluster populations is a challenge for future research.

While much of the research into multiphase crystallization pathways has focused on atomic and molecular systems, research into colloidal systems points toward a degree of universality in occurrences of Ostwald’s rule and underlying mechanisms. Experiments that probed nucleation of two-dimensional colloidal crystallization found that formation of amorphous clusters preceded the appearance of an hcp layer (13). Moreover, as discussed by Niozu et al. (6), for the case of three-dimensional systems of hard sphere colloids, the rhcp phase has been observed to nucleate under conditions of rapid crystallization—i.e., high σ—before the appearance of the fcc phase and the two phases can coexist as the transformation process proceeds. Thus, the same progression and underlying mechanism of Ostwald’s rule seen for Xe atoms is manifest for colloids despite five orders of magnitude discrepancy in the size of the growth unit and 12 orders of magnitude difference in the timescale for recrystallization.

Due to the complex nature of molecular systems in solution for which multiple types of species and hydration states are possible, a wider range of potential structural pathways is expected than in the case of monoatomic noble gasses or noninteracting spherical colloids. Nonetheless, key factors in multistage nucleation pathways are common across such diverse systems, such as the existence of metastable structures, a tendency toward higher interfacial free energy with higher stability, and both the dominance of surface energy over bulk energy and the stabilizing impact of disorder due to entropic contributions at sufficiently small particle size. This commonality combined with the progress made in the past 20 y in observing and explaining instances where Ostwald’s rule occurs holds promise for reaching a predictive understanding of multistep nucleation that enables the design of crystallization pathways across the full set of materials classes.