Self-healing codes: How stable neural populations can track continually reconfiguring neural representations

Significance

The brain is capable of adapting while maintaining stable long-term memories and learned skills. Recent experiments show that neural responses are highly plastic in some circuits, while other circuits maintain consistent responses over time, raising the question of how these circuits interact coherently. We show how simple, biologically motivated Hebbian and homeostatic mechanisms in single neurons can allow circuits with fixed responses to continuously track a plastic, changing representation without reference to an external learning signal.

Abstract

As an adaptive system, the brain must retain a faithful representation of the world while continuously integrating new information. Recent experiments have measured population activity in cortical and hippocampal circuits over many days and found that patterns of neural activity associated with fixed behavioral variables and percepts change dramatically over time. Such “representational drift” raises the question of how malleable population codes can interact coherently with stable long-term representations that are found in other circuits and with relatively rigid topographic mappings of peripheral sensory and motor signals. We explore how known plasticity mechanisms can allow single neurons to reliably read out an evolving population code without external error feedback. We find that interactions between Hebbian learning and single-cell homeostasis can exploit redundancy in a distributed population code to compensate for gradual changes in tuning. Recurrent feedback of partially stabilized readouts could allow a pool of readout cells to further correct inconsistencies introduced by representational drift. This shows how relatively simple, known mechanisms can stabilize neural tuning in the short term and provides a plausible explanation for how plastic neural codes remain integrated with consolidated, long-term representations.

The cellular and molecular components of the brain change continually. In addition to synaptic turnover (1), ongoing reconfiguration of the tuning properties of single neurons has been seen in parietal (2), frontal (3), visual (4, 5), and olfactory (6) cortices and the hippocampus (7, 8). Remarkably, the “representational drift” (9) observed in these studies occurs without any obvious change in behavior or task performance. Reconciling dynamic reorganization of neural activity with stable circuit-level properties remains a major open challenge (9, 10). Furthermore, not all circuits in the brain show such prolific reconfiguration, including populations in primary sensory and motor cortices (11–13). How might populations with stable and drifting neural tuning communicate reliably? Put another way, how can an internally consistent “readout” of neural representations survive changes in the tuning of individual cells?

These recent, widespread observations suggest that neural circuits can preserve learned associations at the population level while allowing the functional role of individual neurons to change (14–16). Such preservation is made possible by redundancy in population codes because a distributed readout allows changes in the tuning of individual neurons to be offset by changes in others. However, this kind of stability is not automatic: Changes in tuning must either be constrained in specific ways (e.g., refs. 17 and 18), or corrective plasticity needs to adapt the readout (19). Thus, while there are proposals for what might be required to maintain population codes dynamically, there are few suggestions as to how this might be implemented with known cellular mechanisms and without recourse to external reference signals that recalibrate population activity to behavioral events and stimuli.

In this paper, we show that the readout of continuous behavioral variables can be made resilient to ongoing drift as it occurs in a volatile encoding population. Such resilience can allow highly plastic circuits to interact reliably with more rigid representations. In principle, this permits compartmentalization of rapid learning to specialized circuits, such as the hippocampus, without entailing a loss of coherence with more stable representations elsewhere in the brain.

We provide a simple hierarchy of mechanisms that can tether stable and unstable representations using simple circuit architectures and well-known plasticity mechanisms, Hebbian learning, and homeostatic plasticity. Homeostasis is a feature of all biological systems, and examples of homeostatic plasticity in the nervous system are pervasive (e.g., see refs. 20 and 21 for reviews). Broadly, homeostatic plasticity is a negative-feedback process that maintains physiological properties such as average firing rates (e.g., refs. 22 and 23), neuronal variability (e.g., ref. 24), distributions of synaptic strengths (e.g., refs. 25 and 26), and population-level statistics (e.g., refs. 27 and 28).

Hebbian plasticity complements homeostatic plasticity by strengthening connectivity between cells that undergo correlated firing, further reinforcing correlations (29, 30). Pairwise correlations in a population provide local bases for a so-called task manifold, in which task-related neural activity resides (31). Moreover, neural representations of continuous variables typically exhibit bump-like single-cell tuning that tiles variables redundantly across a population (2, 7). We show how these features can be maintained to form a drifting population. We then show how Hebbian and homeostatic mechanisms can cooperate to allow a readout to track encoded variables despite drift, resulting in a readout that “self-heals.” Our findings thus emphasize a role for Hebbian plasticity in maintaining associations, as opposed to learning new ones.

Finally, we show how evolving representations can be tracked over substantially longer periods of time if a readout population encodes a stable predictive model of the variables being represented in a plastic, drifting population. Our assumptions thus take into account, and may reconcile, evidence that certain circuits and subpopulations maintain stable responses, while others, presumably those that learn continually, exhibit drift (32).

Background

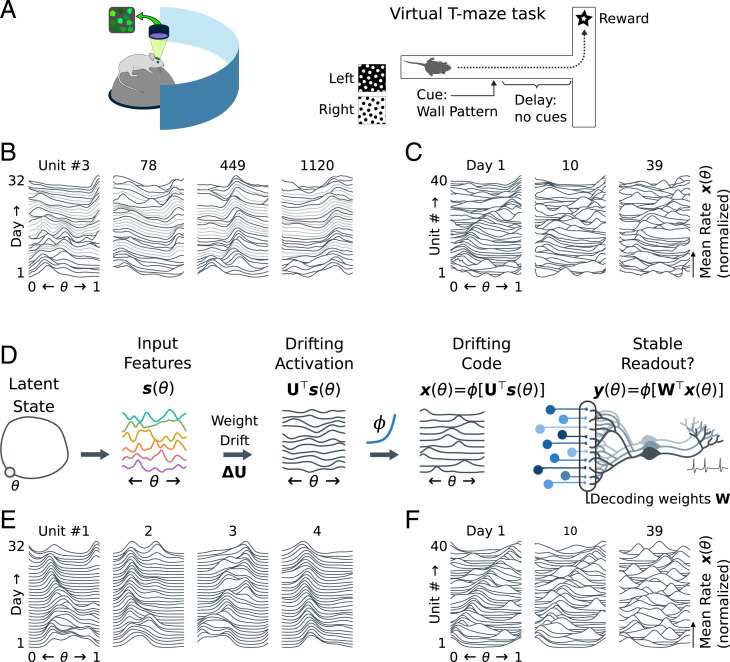
We briefly review representational drift and important recent work related to the ideas in this manuscript. Representational drift refers to ongoing changes in neural responses during a habitual task that are not associated with behavioral change (9). For example, in Driscoll et al. (2), mice navigated to one of two endpoints in a T-shaped maze (Fig. 1A), based on a visual cue. Population activity in Posterior Parietal Cortex (PPC) was recorded over several weeks by using fluorescence calcium imaging. Neurons in PPC were tuned to the animal’s past, current, and planned behavior. Gradually, the tuning of individual cells changed: Neurons could change the location in the maze in which they fired or become disengaged from the task (Fig. 1B). The neural population code eventually reconfigured completely (Fig. 1C). However, neural tunings continued to tile the task, indicating stable task information at the population level. These features of drift have been observed throughout the brain (4, 5, 8). The cause for such ongoing change remains unknown. It may reflect continual learning and adaptation that is not directly related to the task being assayed or unavoidable biological turnover in neural connections.

Fig. 1.

A model for representational drift. (A) Driscoll et al. (2) imaged population activity in PPC for several weeks, after mice had learned to navigate a virtual T maze. Neuronal responses continued to change even without overt learning. (B) Tunings were often similar between days, but could change unexpectedly. Plots show average firing rates as a function of task pseudotime (0 = beginning, 1 = complete) for select cells from ref. 2. Tuning curves from subsequent days are stacked vertically, from day 1 up to day 32. Missing days (light gray) are interpolated. Peaks indicate that a cell fired preferentially at a specific location (Data and Analysis). (C) Neuronal tunings tiled the task. Within each day, the mouse’s behavior could be decoded from population activity (2, 19). Plots show normalized tuning curves for 40 random cells, stacked vertically. Cells are sorted by their preferred location on day 1. By day 10, many cells have changed tuning. Day 39 shows little trace of the original code. (D) We model drift in a simulated rate network (Simulated Drift). An encoding population $\mathbf{x}(\theta )$ receives input $\mathbf{s}(\theta )$ with low-dimensional structure, in this case, a circular track with location θ. The encoding weights $\mathbf{U}$ driving the activations ${\mathbf{U}}^{\top }\mathbf{s}(\theta )$ of this population drift, leading to drifting activations. Homeostasis preserves bump-like tuning curves. (E) As in the data in A–C, this model shows stable tuning punctuated by large changes. (F) The neural code reorganizes, while continuing to tile the task. We will examine strategies that a downstream readout could use to update how it decodes $\mathbf{x}(\theta )$ to keep its own representation $\mathbf{y}(\theta )$ stable. This readout is also modeled as linear–nonlinear rate neurons, with decoding weights $\mathbf{W}$.

Previous work shows how downstream readouts could track gradual drift using external error feedback to relearn how to interpret an evolving neural code, e.g., during ongoing rehearsal (19). Indeed, simulations confirm that learning in the presence of noise can lead to a steady state, in which drift is balanced by error feedback (33–36). Previous studies have shown that stable functional connectivity could be maintained despite synaptic turnover (33, 37, 38). More recent work has also found that discrete representations can be stabilized using neural assemblies that exhibit robust, all-or-nothing reactivation (39, 40).

Our work extends these results as follows. Rather than using external learning signals (19, 33–35), we show that drift can be tracked using internally generated signals. We allow the functional role of neurons in an encoding population to reconfigure completely, rather than just the synaptic connectivity (33, 37, 38). Previous work has explored how to stabilize point attractors using neuronal assemblies, both with stable (39, 41) and drifting (40) single-cell tunings. Key insights in this previous work include the idea that random reactivation or systematic replay of circuit states can reinforce existing point attractors. However, to plausibly account for stable readout of drifting sensorimotor information and other continuous variables observed experimentally (2, 7, 42), we require a mechanism that can track a continuous manifold, rather than point attractors.

Our other main contribution is to relate these somewhat abstract and general ideas to concrete observations and relevant assumptions about the nature of drift. Representational drift is far from random (19), and this fact can be exploited to derive stable readouts. Specifically, the topology and coarse geometry of drifting sensorimotor representations appear to be consistent over time, while their embedding in population activity continually changes (2, 7, 43, 44). Thus, the statistical structure of external variables is preserved, but not their neuron-wise encoding. Notably, brain–machine interface decoders routinely confront this and apply online recalibration and transfer learning to track drift in (e.g., see refs. 45 and 46 for review). We argue that neural circuits may do something similar to maintain “calibration” between relatively stable circuits and highly plastic circuits. Early sensory or late motor populations that communicate directly with sensory receptors or muscle fibers necessarily have a consistent mapping between neural activity and signals in the external world. Such brain areas need to communicate with many other brain areas, including circuits that continually learn and adapt and thus possess more malleable representations of behavioral variables.

Results

We first construct a model of representational drift, in which homeostatic plasticity stabilizes the capacity of a “drifting” population to encode a continuous behavioral variable, despite instability in single-neuron tunings. We then derive plasticity rules that allow single downstream neurons to stabilize their own readout of this behavioral variable, despite drifting activity. Finally, we extend these ideas to show how comparatively stable neural populations that encode independent, predictive models of behavioral variables can actively track and stabilize a readout of drifting neural code.

A Model for Representational Drift.

We have previously used the data from Driscoll et al. (47) to assess how much plasticity would be required to track drift in a linear readout (19). However, these data contain gaps of several days, and the number of high signal-to-noise units tracked for over a month is limited. To explore continual, long-term drift, we therefore construct a model inspired by the features of representational drift seen in spatial navigation tasks (2, 7).

We focus on key properties of drift seen in experiments. In both refs. 2 and 7, neural populations encode continuous, low-dimensional behavioral variables (e.g., location), and exhibit localized “bump-like” tuning to these variables. Tuning curves overlap, forming a redundant code. Over time, neurons change their preferred tunings. Nevertheless, on each day, there is always a complete “tiling” of a behavioral variable; thus, the ability of the population to encode task information is conserved.

To model this kind of drifting code, we consider a population of N neurons that encode a behavioral variable, θ. We assume θ lies on a low-dimensional manifold and is encoded in the vector of firing rates in a neural population with tuning curves ${\mathbf{x}}_d(\theta )={\{x_{d,1}(\theta ),\mathrm{..},x_{d,N}(\theta )\}}^{\top }$. These tunings change over time (day d).

We abstract away some details seen in the experimental data in Fig. 1C. We focus on the slow component of drift and model excess day-to-day tuning variability via a configurable parameter. We assume uniform coverage of the encoded space, which can be ensured by an appropriate choice of coordinates. We consider populations of 100 units that encode θ and whose tunings evolve independently. Biologically, noise correlations and fluctuating task engagement would limit redundancy, but this would be offset by the larger number of units available.

To model drift, we first have to model an encoding “feature” population, whose responses depend on θ and from which it is possible to construct bump-like tuning with a weighted readout (Fig. 1D). To keep our assumptions general, we do not assume that the encoding population has sparse, bump-like activity and simply define a set of K random features (tuning curves), sampled independently from a random Gaussian process on θ. These features have an arbitrary, but stable, relationship to the external world, from which it is possible to reconstruct θ by choosing sufficiently large K:

$$\begin{array}{ll}\mathbf{s}(\theta )\hfill & ={\{s_1(\theta ),\mathrm{..},s_K(\theta )\}}^{\top }\hfill \\ s_i(\theta )\hfill & \sim \mathcal{G}\mathcal{P}[0,\mathrm{\Sigma }(\theta ,\theta \prime )].\hfill \end{array}$$ [1]

In the above equations, $\mathrm{\Sigma }(\theta ,\theta \prime )$ denotes the covariance between the values of $s(\theta )$ at two states θ and $\theta \prime$.

We next define an encoding of θ driven by these features with a drifting weight matrix ${\mathbf{U}}_d=\{{\mathbf{u}}_{d,1},\mathrm{..},{\mathbf{u}}_{d,N}\}$, where ${\mathbf{u}}_{d,i}={\{u_{d,i,1},\mathrm{..},u_{d,i,K}\}}^{\top }$ reflects the encoding weights for unit $x_{d,i}(\theta )$ on day d. Each weight $u_{d,i,j}$ evolves as a discrete-time Ornstein–Uhlenbeck (OU) process, taking a new value on each day (Simulated Drift). The firing rate of each encoding unit is given as a nonlinear function of the synaptic activation $a_{d,i}(\theta )={\mathbf{u}}_{d,i}^{\top }\mathbf{s}(\theta )$:

$$\begin{array}{ll}{x}_{d,i}(\theta )\hfill & =\varphi [{\gamma }_i\hspace{0.17em}{a}_{d,i}(\theta )+{\beta }_i],\hfill \end{array}$$ [2]

where γ_i and β_i are vectors that set the sensitivity and threshold of each unit. To model the nonlinear response of the readout and prevent negative firing rates, we use an exponential nonlinearity $\varphi (·)=\exp (·)$.

In this model, the mean firing rate and population sparsity of the readout can be tuned by varying the sensitivity γ and threshold β in Eq. 2, respectively. In the brain, these single-cell properties are regulated by homeostasis (24). Stabilizing mean rates ${\langle x_{d,i}(\theta )\rangle }_{\theta }\approx {\mu }_0$ ensures that neurons remain active. Stabilizing rate variability ${\text{var}}_{\theta }[x_{d,i}(\theta )]\approx {\sigma }_0^2$ controls population code sparsity, ensuring that ${\mathbf{x}}_d(\theta )$ carries information about θ (48). This is achieved by adapting the bias β_i and gain γ_i of each unit $x_{d,i}(\theta )$ based on the errors ${ϵ}_{\mu },{ϵ}_{\sigma }$ between the statistics of neural activity and the homeostatic targets μ₀, σ₀:

$$\begin{array}{ll}\mathrm{\Delta }\gamma \hfill & \propto {\epsilon }_{\sigma }={\sigma }_0-{\sigma }_x\hfill \\ \mathrm{\Delta }\beta \hfill & \propto {\epsilon }_{\mu }={\mu }_0-{\mu }_x.\hfill \end{array}$$ [3]

Fig. 1 shows that this model qualitatively matches the drift seen in vivo (2). Tuning is typically stable, with intermittent changes (Fig. 1E). This occurs because the homeostatic regulation in Eq. 3 adjusts neuronal sensitivity and threshold to achieve a localized, bump-like tuning curve at the location of peak synaptic activation, θ₀. Changes in tuning arise when the drifting weight matrix causes the encoding neuron to be driven more strongly at a new value of θ. The simulated population code reconfigures gradually and completely over a period of time equivalent to several weeks in the experimental data (Fig. 1F).

Hebbian Homeostasis Improves Readout Stability Without External Error Feedback.

Neural population codes are often redundant, with multiple units responding to similar task features. Distributed readouts of redundant codes can therefore be robust to small changes in the tuning of individual cells. We explored the consequences of using such a readout as an internal error signal to retrain synaptic weights in a readout population, thereby compensating for gradual changes in a representation without external feedback. This re-encodes a learned readout function $\mathbf{y}(\theta )$ in terms of the new neural code ${\mathbf{x}}_d(\theta )$ on each “day” and improves the tuning stability of neurons that are driven by unstable population codes, even in single neurons. We first sketch an example of this plasticity and then explore why this works.

Using our drifting population code as input, we model a readout population of M neurons with tuning curves ${\mathbf{y}}_d(\theta )={\{y_{d,1}(\theta ),\mathrm{..},y_{d,M}(\theta )\}}^{\top }$ (Fig. 1D). We model this decoder as a linear–nonlinear function, using decoding weights $\mathbf{W}$ and biases (thresholds) $\mathbf{b}$ (leaving dependence on the day d implicit):

$$\begin{array}{ll}\mathbf{y}(\theta )\hfill & =\varphi [{\mathbf{W}}^{\top }\mathbf{x}(\theta )+\mathbf{b}].\hfill \end{array}$$ [4]

On each simulated day, we retrain the decoding weights using an unsupervised Hebbian learning rule (c.f. ref. 49). This potentiates weights $w_{i,j}$, whose input $x_j(\theta )$ correlates with the postsynaptic firing rate $y_i(\theta )$. We modulate the learning rate by an estimate of the homeostatic error in firing-rate variability $(\tilde{\delta })$. Thresholds are similarly adapted based on the homeostatic error in mean-rate $(\tilde{\beta })$. We include a small baseline amount of weight decay “ρ” and a larger amount of weight decay “c” that is modulated by $\tilde{\delta }$. For a single readout neuron $y(\theta )$, the weights and biases evolve as:

$$\begin{array}{ll}\mathrm{\Delta }\mathbf{w}\hfill & \propto \tilde{\delta }\left[{\langle \mathbf{x}(\theta )y{(\theta )}^{\top }\rangle }_{\theta }-c\mathbf{w}\right]-\rho \mathbf{w}\hfill \\ \mathrm{\Delta }b\hfill & \propto \tilde{\beta }{\langle \mathbf{x}(\theta )\rangle }_{\theta }.\hfill \end{array}$$ [5]

We apply Eq. 5 for 100 iterations on each simulated day, sampling all θ on each iteration. We assume that the timescale of Hebbian and homeostatic plasticity is no faster than the timescale of representational drift. The error terms $\tilde{\delta },\hspace{0.17em}\tilde{\beta }$ are leaky integrators of instantaneous errors (Eq. 3) for each cell, ${\epsilon }_{\sigma },\hspace{0.17em}{\epsilon }_{\mu }$, respectively: ${\tilde{\delta }}_{t+1}=0.5\hspace{0.17em}{\tilde{\delta }}_t+{\epsilon }_{\sigma }$ (analogously for $\tilde{\beta },\hspace{0.17em}{\epsilon }_{\mu }$). For the readout $\mathbf{y}(\theta )$, the homeostatic targets $({\mu }_0,{\sigma }_0)$ are set to the firing-rate statistics in the initial, trained state (before drift has occurred). Eq. 5 therefore acts homeostatically. Rather than scale weights uniformly, it adjusts the component of the weights most correlated with the postsynaptic output, $\mathbf{y}(\theta )$. Plasticity occurs only when homeostatic constraints are violated. Further discussion of this learning rule is given in Synaptic Learning Rules.

To test whether the readout can tolerate complete reconfiguration in the encoding population, we change encoding features one at a time. For each change, we select a new, random set of encoding weights ${\mathbf{u}}_i$ and apply homeostatic compensation to stabilize the mean and variability of $x_i(\theta )$. Eq. 5 is then applied to update the decoding weights of the readout cell. This procedure is applied 200 times, corresponding to two complete reconfigurations of the encoding population of $N=100$ cells (Single-Neuron Readout).

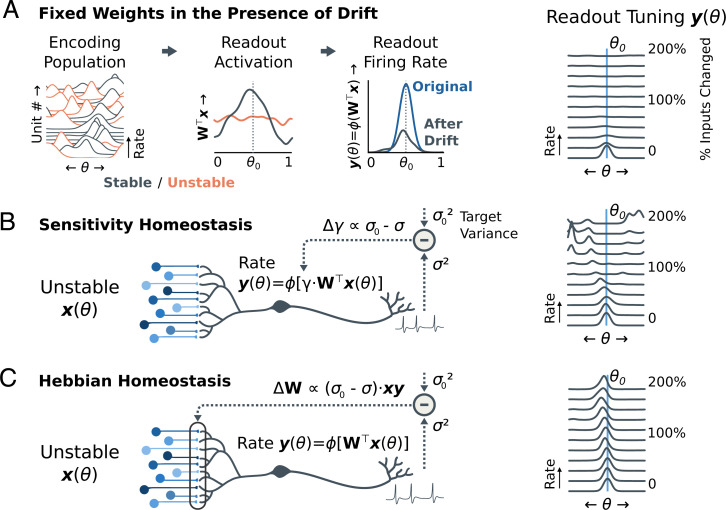
With fixed weights, drift reduces the readout’s firing rate without changing its tuning (Fig. 2A). This is because the initial tuning of the readout requires coincident activation of specific inputs to fire for its preferred θ₀. Drift gradually destroys this correlated drive and is unlikely to spontaneously create a similar conjunction of features for some other θ. For small amounts of drift, homeostasis Eq. 3 can stabilize the readout by compensating for the reduction in drive (Fig. 2B). Eventually, however, no trace of the original encoding remains. At this point, a new (random) θ will begin to drive the readout more strongly. Homeostasis adjusts the sensitivity of the readout to form a new, bump-like tuning curve at this location.

Fig. 2.

Homeostatic Hebbian plasticity enables a stable readout from unstable populations. (A) Simulated drift in a redundant population causes a loss of excitability, but little change in tuning, to a downstream linear–nonlinear readout neuron. Since the cell is selective to a conjunction of features, it loses excitatory drive when some of its inputs change. Since most drift is orthogonal to this readout, however, the preferred tuning θ₀ does not change. The rightmost plot shows that the excitability diminishes as a larger fraction of inputs change. Two complete reconfigurations of an encoding population of 100 cells are shown. (B) Homeostatic adjustments to increase the readout’s sensitivity can compensate for small amounts of drift. As more inputs reconfigure, the cell compensates for loss of excitatory drive by increasing sensitivity (“gain”, γ). However, the readout changes to a new, random location once a substantial fraction of inputs have reconfigured (B, Right). This phenomenon is the same as the model for tuning curve drift in the encoding population (c.f. Fig. 1E). (C) Hebbian homeostasis increases neuronal variability by potentiating synaptic inputs that are correlated with postsynaptic activity or depressing those same synapses when neuronal variability is too high. This results in the neuron relearning how to decode its own tuning curve from the shifting population code, supporting a stable readout despite complete reconfiguration (C, Right) (Single-Neuron Readout).

Fig. 2C shows the consequences of Hebbian homeostasis (Eq. 5). Drift in the encoding $\mathbf{x}(\theta )$ decreases the excitatory drive to the readout, activating Hebbian learning. Because small amounts of drift have minimal effect on tuning, the readout’s own output provides a self-supervised teaching signal. It relearns the decoding weights for inputs that have changed due to drift. Applying Hebbian homeostasis periodically improves stability, despite multiple complete reconfigurations of the encoding population. In effect, the readout’s initial tuning curve is transported to a new set of weights that estimate the same function from an entirely different input (for further discussion, see SI Appendix, Weight Filtering). In the long term, the representation degrades, for reasons we dissect in the next section.

Hebbian Homeostasis with Network Interactions.

In the remainder of the manuscript, we show how Hebbian homeostatic principles combine with population-level interactions to make readouts more robust to drift. Generally, a mechanism for tracking drift in a neural population should exhibit three features:

• 1)The readout should use redundancy to mitigate error caused by drift.
• 2)The readout should use its own activity as a training signal to update its decoding weights.
• 3)The correlations in input-driven activity in the readout neurons should be homeostatically preserved.

We explore three types of recurrent population dynamics that could support this: 1) population firing-rate normalization; 2) recurrent dynamics in the form of predictive feedback; and 3) recurrent dynamics in the form of a linear–nonlinear map. Fig. 3 summarizes the impact of each of these scenarios on a nonlinear population readout, and we discuss each in depth in the following subsections.

Fig. 3.

Self-healing in a nonlinear rate network. Each plot shows a population readout $\mathbf{y}(\theta )$ from a drifting code $\mathbf{x}(\theta )$ of $N=100$ cells (Left); a schematic of the readout dynamics (Center); and a plot of readout tuning after applying each learning rule if 60% of the encoding cells were to change to a new tuning (Right) (Population Simulations). (A) Drift degrades a readout with fixed weights. Drift is gradual, with $\tau =100$. The simulated time frame corresponds to 10 complete reconfigurations. (B) Homeostasis increases sensitivity to compensate for loss of drive, but cannot stabilize tuning (${\sigma }^2$: firing-rate variance; ${\sigma }_0^2$: target variance; ${ϵ}_{\sigma }$: homeostatic error; $\mathrm{\Delta }\gamma$: gain adjustment). (C) Hebbian homeostasis (Eq. 5) restores drive using the readout’s output as a training signal. Error correction is biased toward θ that drive more variability in the encoding population. ($\mathrm{\Delta }\mathbf{W}$: weight updates.) (D) Response normalization (Eq. 6) stabilizes the population statistics, but readout neurons can swap preferred tunings ($\widehat{\mathbf{y}}$: normalized response). (E) A recurrent linear–nonlinear map (Eq. 8) pools information over the population, improving error correction (${\mathbf{y}}_f$: feed-forward estimates; $\mathbf{A}$: recurrent weights). (F) Predictive coding (Eq. 7) corrects errors via negative feedback (τ indicates dynamics in time). All simulations added 5% daily variability to $\mathbf{x}(\theta )$ and applied 1% daily drift to the decoding weights $\mathbf{W}$. SI Appendix, Fig. S2 evaluates readout stability for larger amounts of variability and readout-weight drift; SI Appendix, Fig. S3 quantifies readout stability for each scenario.

Population competition with unsupervised Hebbian learning.

In Fig. 2C, we saw that Hebbian homeostasis improved stability in the short term. Eq. 5 acts as an unsupervised learning rule and pulls the readout $y(\theta )$ toward a family of bump-like tuning curves that tile θ (36). Under these dynamics, only drift $\mathrm{\Delta }\mathbf{x}(\theta )$ that changes the peak of $y(\theta )$ to some new, nearby $\theta {\prime }_0$ can persist. All other modes of drift are rejected. If the encoding population is much larger than the dimension of θ, there is large null space in which drift does not change the preferred tuning. However, in the long run Hebbian homeostasis drives the neural population toward a steady state, which forgets the initial tuning (Fig. 3C). This is because Hebbian learning is biased toward a few salient θ₀ that capture directions in $\mathbf{x}(\theta )$ with the greatest variability (30, 50, 51).

Models of unsupervised Hebbian learning address this by introducing competition among a population of readout neurons (50, 51). Such rules can track the full covariance structure of the encoding population and lead to a readout population of bump-like tuning curves that tile the space θ (52–55). In line with this, we incorporate response normalization into a readout population (56). This serves as a fast-acting form of firing-rate homeostasis in Eq. 3, causing neurons to compete to remain active and encouraging diverse tunings (54, 57).

Because it is implemented via inhibitory circuit dynamics, we assume that this normalization acts quickly relative to plasticity and model it by dividing the rates by the average firing rate across the population. If ${\mathbf{y}}_f(\theta )$ is the forward (unnormalized) readout from Eq. 4, we define the normalized readout ${\mathbf{y}}_n(\theta )$ by dividing out the average population rate, ${\langle {\mathbf{y}}_f(\theta )\rangle }_{\text{M}}$, and multiplying by a target mean rate μ_p:

$$\begin{array}{l}{\mathbf{y}}_n(\theta )={\mu }_p·{\mathbf{y}}_f(\theta )/{\langle {\mathbf{y}}_f(\theta )\rangle }_{\text{M}}.\hfill \end{array}$$ [6]

We found that response normalization improves readout stability (Fig. 3D). However, it does not constrain individual readout neurons to any specific preferred θ₀. The readout thus remains sensitive to noise and perturbations, which, in the long run, can cause neurons to swap preferred tunings (Fig. 3D; PopulationSimulations).

Error-correcting recurrent dynamics.

The error-correction mechanisms explored so far use redundancy and feedback to reduce errors caused by incremental drift. However, there is no communication between different readouts $y_i(\theta )$ to ensure that the correlation structure of the readout population is preserved. In the remainder of the paper, we explore how a readout with a stable internal model for the correlation structure of $\mathbf{y}(\theta )$ might maintain communication with a drifting population code.

Where might such a stable internal model exist in the brain? The dramatic representational drift observed in, e.g., the hippocampus (7, 58) and parietal cortex (2) is not universal. Relatively stable tuning has been found in the striatum (59) and motor cortex (60–62). Indeed, perineuronal nets are believed to limit structural plasticity in some mature networks (63), and stable connections can coexist with synaptic turnover (14). Drift in areas closer to the sensorimotor periphery is dominated by changes in excitability, which tends not to affect tuning preference of individual cells (3, 5). Thus, many circuits in the brain develop and maintain reliable population representations of sensory and motor variables. Moreover, such neural populations can compute prediction errors based on learned internal models (64), and experiments find that neural population activity recapitulates (65) and predicts (66) input statistics. Together, these findings suggest that many brain circuits can support relatively stable predictive models of the various latent variables that are used by the brain to represent the external world.

We therefore asked whether such a stable model of a behavioral variable could take the form of a predictive filter that tracks an unstable, drifting representation of that same variable. To incorporate this in our existing framework, we assume that the readout $\mathbf{y}(\theta )$ contains a model of the “world” (θ) in its recurrent connections, which change much more slowly than $\mathbf{x}(\theta )$. These recurrent connections generate internal prediction errors. We propose that these same error signals provide error correction to improve the stability of neural population codes in the presence of drift.

We consider two kinds of recurrent dynamics. Both of these models are abstract, as we are not primarily concerned with the architecture of the predictive model, only its overall behavior. We first consider a network that uses inhibitory feedback to cancel the predictable aspects of its input, in line with models of predictive coding (67–69). We then consider a linear–nonlinear mapping that provides a prediction of $\mathbf{y}(\theta )$ from a partially corrupted readout.

Recurrent feedback of prediction errors.

Some theories propose that neural populations retain a latent state that is used to predict future inputs (67–69). This prediction is compared to incoming information to generate a prediction error, which is fed back through recurrent interactions to update the latent state. This is depicted in the schematic in (Fig. 3F). Here, we assume that the network contains a latent state “$\mathbf{z}$” and predicts the readout’s activity, $\widehat{\mathbf{y}}=\varphi (\mathbf{z})$, with firing-rate nonlinearity $\varphi$ as defined previously. Inputs provide a feed-forward estimate ${\mathbf{y}}_f(\theta )$, which is corrupted by drift. The prediction error is the difference between ${\mathbf{y}}_f(\theta )$ and $\widehat{\mathbf{y}}$. The dynamics of $\mathbf{z}$ are chosen as:

$$\begin{array}{ll}{\tau }_z\stackrel{.}{\mathbf{z}}\hfill & =-\mathbf{z}+{\mathbf{A}}_p[{\mathbf{y}}_f-\widehat{\mathbf{y}}].\hfill \end{array}$$ [7]

We set the weight matrix ${\mathbf{A}}_p$ to the covariance of the activations $\mathbf{z}={\mathbf{W}}^{\top }\mathbf{x}$ during initial training (motivation for this choice is in SI Appendix, Predictive Coding as Inference). In making this choice, we assume that part of the circuit can learn and retain the covariance of $\mathbf{z}$. This could, in principle, be achieved via Hebbian learning (refs. 49, 50, and 70; Learning Recurrent Weights).

Assuming that a circuit can realize the dynamics in Eq. 7, the readout $\widehat{\mathbf{y}}$ will be driven to match the forward predictions ${\mathbf{y}}_f$. We assume that this converges rapidly relative to the timescale at which ${\mathbf{y}}_f(\theta )$ varies. This improves the tracking of a drifting population code when combined with Hebbian homeostasis and response normalization (Fig. 3F). The readout continuously realigns its fixed internal model with the activity in the encoding population. We briefly discuss intuition behind why one should generally expect this to work.

The recurrent weights, ${\mathbf{A}}_p$, determine which directions in population-activity space receive stronger feedback. Feedback through larger eigenmodes of ${\mathbf{A}}_p$ is amplified, and these modes are rapidly driven to track ${\mathbf{y}}_f$. Due to the choice of ${\mathbf{A}}_p$ as the covariance of $\mathbf{z}$, the dominant modes reflect directions in population activity that encode θ. Conversely, minor eigenmodes are weakly influenced by ${\mathbf{y}}_f$. This removes directions in population activity that are unrelated to θ, thereby correcting errors in the readout activity caused by drift.

In summary, Eq. 7 captures qualitative dynamics implied by theories of predictive coding. If neural populations update internal states based on prediction errors, then only errors related to tracking variations in θ should be corrected aggressively. This causes the readout to ignore “off manifold” activity in $\widehat{\mathbf{y}}(\theta )$ caused by drift. However, other models of recurrent dynamics also work, as we explore next.

Low-dimensional manifold dynamics.

Recurrent dynamics with a manifold of fixed-point solutions (distributed over θ) could also support error correction. We model this by training the readout to make a prediction $\widehat{\mathbf{y}}$ of its own activity based on the feed-forward activity ${\mathbf{y}}_f$, via a linear–nonlinear map, (c.f. ref. 71):

$$\begin{array}{l}\widehat{\mathbf{y}}[t+1]\leftarrow \varphi \left({\mathbf{A}}_r^{\top }{\mathbf{y}}_f[t]+\mathbf{v}\right),\hfill \end{array}$$ [8]

with timestep, t, and recurrent weights and biases ${\mathbf{A}}_r$ and $\mathbf{v}$, respectively (Learning Recurrent Weights). We chose this discrete-time mapping for computational expediency, and Eq. 8 was applied once for each input $y_f(\theta )$ alongside response normalization. In simulations, the recurrent mapping is also effective at correcting errors caused by drift, improving readout stability (Fig. 3F).

We briefly address some caveats that apply to both models of recurrent dynamics. The combination of recurrent dynamics and Hebbian learning is potentially destabilizing, because leaning can transfer biased predictions into the decoding weights. Empirically, we find that homeostasis (Eq. 3) prevents this, but must be strong enough to counteract all destabilizing influences. Additionally, when the underlying θ has continuous symmetries, drift can occur along these symmetries. This is evidenced by a gradual, diffusive rotation of the code for, e.g., a circular environment. Other manifolds, like the T-shaped maze in ref. 2, have no continuous symmetries and are not susceptible to this effect (SI Appendix, Fig. S5). Overall, these simulations illustrate that internal models can constrain network activity. This provides ongoing error correction, preserves neuronal correlations, and allows neural populations to tolerate substantial reconfiguration of the inputs that drive them.

Discussion

In this work, we derived principles that can allow stable and plastic representations to coexist in the brain. These self-healing codes have a hierarchy of components, each of which facilitates a stable readout of a plastic representation: 1) single-cell tuning properties (bump-like tuning and redundant tiling of encoded variables) that make population codes robust to small amounts of drift; 2) populations that use their own output as a training signal to update decoding weights; and 3) circuit interactions that track evolving population statistics using stable internal models. All of these components are biologically plausible, some corresponding to single-cell plasticity mechanisms (Hebbian and homeostatic plasticity), others corresponding to circuit architectures (response normalization and recurrence), and others corresponding to higher-level functions that whole circuits appear to implement (internal models). As such, these components may exist to a greater or lesser degree in different circuits.

Hebbian plasticity is synonymous with learning novel associations in much of contemporary neuroscience. Our findings argue for a complementary hypothesis that Hebbian mechanisms can also reinforce learned associations in the face of ongoing change—in other words, prevent spurious learning. This view is compatible with the observation that Hebbian plasticity is a positive-feedback process, where existing correlations become strengthened, in turn promoting correlated activity (72). Abstractly, positive feedback is required for hysteresis, which is a key ingredient of any memory-retention mechanism, biological or otherwise, because it rejects external disturbances by reinforcing internal states.

Homeostasis, by contrast, is typically seen as antidote to possible runaway Hebbian plasticity (72). However, this idea is problematic due to the relatively slow timescale at which homeostasis acts (73). Our findings posit a richer role for homeostatic (negative) feedback in maintaining and distributing responsiveness in a population. This is achieved by regulating the mean and the variance of neural activity (24).

We considered two populations: a drifting population that encodes a behavioral variable and another that extracts a drift-resilient readout. This could reflect communication between stable and plastic components of the brain or the interaction between stable and plastic neurons within the same circuit. This is consistent with experiments that find consolidated stable representations (12, 16) or with the view that neural populations contain a mixture of stable and unstable cells (74).

By itself, Hebbian homeostasis preserves population codes in the face of drift over a much longer timescale than the lifetime of a code with fixed readout (Fig. 2). Even though this mechanism ultimately corrupts a learned tuning, the time horizon over which the code is preserved may be adequate in a biological setting, particularly in situations where there are intermittent opportunities to reinforce associations behaviorally. However, in the absence of external feedback, extending the lifetime of this code still further required us to make additional assumptions about circuit structures that remain to be tested experimentally.

We found that a readout population can use an internal model to maintain a consistent interpretation of an unstable encoding population. Such internal models are widely hypothesized to exist in various guises (64, 66, 67, 69). We did not address how these internal models are learned initially, nor how they might be updated. By setting fixed recurrent weights, we are also assuming that population responses in some circuits are not subject to drift. This may be reasonable, given that functional connectivity and population tuning in some circuits and subpopulations is found to be stable (11–13).

The recurrent architectures we studied here are reminiscent of mechanisms that attenuate forgetting via replay (e.g., refs. 75 and 76). The internal models must be occasionally reactivated through rehearsal or replay to detect and correct inconsistencies caused by drift. If this process occurs infrequently, drift becomes large, and the error correction will fail.

The brain supports both stable and volatile representations, typically associated with memory retention and learning, respectively. Artificial neural networks have so far failed to imitate this and suffer from catastrophic forgetting, wherein new learning erases previously learned representation (77). Broadly, most proposed strategies mitigate this by segregating stable and unstable representations into distinct subspaces of the possible synaptic weight changes (c.f. ref. 18). These learning rules therefore prevent disruptive drift in the first place. The mechanisms explored here do not restrict changes in weights or activity: The encoding population is free to reconfigure its encoding arbitrarily. However, any change in the code leads to a complementary change in how that code is read out. Further exploration of these principles may clarify how the brain can be simultaneously plastic and stable and provide clues to how to build artificial networks that share these properties.

Materials and Methods

Data and Analysis.

Data shown in Fig. 1 B and C were taken from Driscoll et al. (2) and are available online at Dryad (47). Examples of tuning-curve drift were taken from mouse 4, which tracked a subpopulation of cells for over a month using calcium fluorescence imaging. Normalized log-fluorescence signals ($\ln [x/\langle x\rangle ]$) were filtered between 0.3 and 3 Hz (fourth-order Butterworth, forward–backward filtering), and individual trial runs through the T maze were extracted. We aligned traces from select cells based on task pseudotime (zero, start; one, reward). On each day, we averaged log-fluorescence over all trials and exponentiated to generate the average tuning curves shown in Fig. 1B. For Fig. 1C, a random subpopulation of 40 cells was sorted based on their peak firing location on the first day. For further details, see refs. 2 and 19.

Simulated Drift.

We modeled drift as a discrete-time OU random walk on encoding weights $\mathbf{U}$, with time constant τ (in days) and per-day noise variance α. We set the noise variance to $\alpha =2/\tau$ to achieve unit steady-state variance. Encoding weights for each day are sampled as:

$$\begin{array}{ll}{u}_{d+1,i,j}\hfill & =u_{d,i,j}\sqrt{1-\alpha }+\xi \sqrt{\alpha },\hspace{1em}\hspace{1em}\xi \sim \mathcal{N}(0,1).\hfill \end{array}$$ [9]

These drifting weights propagate the information about θ available in the features $\mathbf{s}(\theta )$ (Eq. 1) to the encoding units $\mathbf{x}(\theta )$ in a way that changes randomly over time.

This random walk in encoding-weight space preserves the population code statistics on average: It preserves the geometry of θ in the correlations of ${\mathbf{a}}_t(\theta )$ and the average amount of information about θ encoded in the population activations (SI Appendix, Stability of Encoded Information). This implies that the difficulty of reading out a given tuning curve $y(\theta )$ (in terms of the L2 norm of the decoding weights, $\left|\right|{\mathbf{w}}_j|{|}^2$) should remain roughly constant over time. This assumption, that $\mathbf{x}(\theta )$ encodes a stable representation for θ in an unstable way underlies much of the robustness we observe. We discuss this further in Synaptic Learning Rules.

Because the marginal distribution of the encoding weights on each day is Gaussian, ${\mathbf{U}}_d\sim \mathcal{N}(0,I_N)$, the synaptic activations ${\mathbf{a}}_d(\theta )={\mathbf{U}}_d^{\top }\mathbf{s}(\theta )$ are samples from a Gaussian process on θ, with covariance inherited from $\mathbf{s}(\theta )$ (SI Appendix, Gaussian-Process Tuning Curves). In numerical experiments, we sampled the synaptic activation functions ${\mathbf{a}}_d(\theta )$ from this Gaussian process directly. We simulated $\theta \in [0,1)$ over a discrete grid with 60 bins, sampling synaptic activations from a zero-mean Gaussian process on θ with a spatially low-pass squared-exponential kernel ($\sigma =0.1$). The gain and threshold (Eq. 2) for each encoding unit was homeostatically adjusted for a target mean rate of ${\mu }_0=5$ and rate variance of ${\sigma }_0^2=25$ (in arbitrary units). This was achieved by running Eq. 3 for 50 iterations with rates ${\eta }_{\gamma }=0.1$ and ${\eta }_{\beta }=0.2$ for the gain and bias homeostasis, respectively.

To show that the readout can track drift despite complete reconfiguration of the neural code, we replace gradual drift in all features with abrupt changes in single features in Fig. 2. For this, we resampled the weights for single encoding units one-at-a-time from a standard normal distribution. Self-healing plasticity rules were run each time 5 out of the 100 encoding features changed. SI Appendix, Fig. S1 confirms that abrupt drift in a few units is equivalent to gradual drift in all units. Unless otherwise stated, all other results are based on an OU model of encoding drift.

We modeled excess variability in the encoding population that was unrelated to cumulative drift. This scenario resembles the drift observed in vivo (9; SI Appendix, Fig. S4). We sampled a unique “per-day” synaptic activation ${\tilde{a}}_{d,i}(\theta )$ for each of the encoding units, from the same Gaussian process on θ used to generate the drifting activation functions $a_{d,i}(\theta )$. We mixed these two functions with a parameter r = 0.05 such that the encoding variability was preserved (i.e., 5% of the variance in synaptic activation is related to random variability):

$$\begin{array}{ll}a{\prime }_{d,i}(\theta )\hfill & =a_{d,i}(\theta )\sqrt{1-r}+{\tilde{a}}_{d,i}(\theta )\sqrt{r}.\hfill \end{array}$$ [10]

SI Appendix, Fig. S2A shows that the readout can tolerate up to 30% excess variability with modest loss of stability. SI Appendix, Fig. S4 shows that neuronal recordings from Driscoll et al. (47) are consistent with 30% excess variability and that the qualitative conclusions of this paper hold for this larger amount of day-to-day variability (SI Appendix, Calibrating the Model to Data).

We also applied drift on the decoding synapses $\mathbf{W}$. This is modeled similarly to Eq. 10, with the parameter n controlling the percentage of variance in synapse weight that changes randomly at the start of each day:

$$\begin{array}{l}w{\prime }_{d,i,j}=w_{d,i,j}\sqrt{1-n}+{\sigma }_d·\xi \sqrt{n}\hspace{0.17em}\hspace{1em}\hspace{1em}\xi \sim \mathcal{N}(0,1),\hfill \end{array}$$ [11]

where σ_d is the empirical SD of the decoding weights on day d. Unless otherwise stated, we use $n=1\%$. Larger values of drift on the decoding weights is destabilizing for Hebbian homeostasis (with or without response normalization), but readouts with stable internal recurrent dynamics can tolerate larger ($\sim 8\%$) amounts of readout-weight drift (SI Appendix, Fig.S2B).

Synaptic Learning Rules.

The learning rule in Eq. 5 is classical unsupervised Hebbian learning, which is broadly believed to be biologically plausible (49, 50, 70). However, it has one idiosyncrasy that should be justified: The rates of learning and weight decay are modulated by a homeostatic error in firing-rate variability. The simplest interpretation of Eq. 5 is a premise or ansatz: Learning rates should be modulated by homeostatic errors. This is a prediction that will need to be experimentally confirmed. Such a learning might be generically useful, since it pauses learning when firing-rate statistics achieve a useful dynamic range for encoding information. The fact that weight decay is proportional to learning rate is also biologically plausible, since each cell has finite resources to maintain synapses.

Eq. 5 may also emerge naturally from the interaction between homeostasis and learning rules in certain scenarios. When Hebbian learning is interpreted as a supervised learning rule, it is assumed that other inputs bias the spiking activity y of a neuron toward a target $y^{*}$. This alters the correlations between presynaptic inputs $\mathbf{x}$ and postsynaptic spiking. Hebbian learning rules, especially temporally asymmetric ones based on spike timing (78), adjust readout weights $\mathbf{w}$ to potentiate inputs that correlate with this target. In the absence of external learning signals, homeostatic regulation implies a surrogate training signal ${\tilde{y}}^{*}$. This ${\tilde{y}}^{*}$ is biased toward a target mean rate and selectivity. For example, recurrent inhibition could regulate both population firing rate and population-code sparsity. This could restrict postsynaptic spiking, causing Hebbian learning to adjust readout weights to achieve the desired statistics. Cells may also adjust their sensitivity and threshold homeostatically. Hebbian learning could then act to adjust incoming synaptic weights to achieve the target firing-rate statistics, but in a way that is more strongly correlated with synaptic inputs.

In SI Appendix, Hebbian Homeostasis as an Emergent Property, we verify the intuition that Eq. 5 should arise through emergent interactions between homeostasis and Hebbian learning in a simplified, linear model. In the remainder of this section, we use a linear readout to illustrate why one should expect Eq. 5 to be stabilizing.

The decoder’s job is to generate a stable readout from the drifting code $\mathbf{x}(\theta )$. This is a regression problem: The decoding weights $\mathbf{W}$ should map $\mathbf{x}(\theta )$ to a target $\mathbf{y}(\theta )$. Since small amounts of drift are akin to noise, $\mathbf{W}$ should be regularized to improve robustness. The L2-regularized linear least-squares solution for $\mathbf{W}$ is:

$$\begin{array}{l}\mathbf{W}={[{\mathrm{\Sigma }}_x+{\rho }_2\mathbf{I}]}^{-1}{\mathrm{\Sigma }}_{xy}.\hfill \end{array}$$ [12]

The regularization ${\rho }_2\mathbf{I}$ corresponds to the assumption that drift will corrupt the activity of $\mathbf{x}(\theta )$ by an amount $\mathrm{\Delta }\mathbf{x}\sim \mathcal{N}(0,{\rho }_2\mathbf{I})$.

Can drift be tracked by reinferring $\mathbf{W}$ on each day? We lack the ground-truth covariance ${\mathrm{\Sigma }}_{xy}^d$ to retrain $\mathbf{W}$, but could estimate it from decoded activity ${\mathbf{y}}_d(\theta )$:

$${\widehat{\mathrm{\Sigma }}}_{xy}^d={\langle {\mathbf{x}}_d(\theta ){\mathbf{y}}_d{(\theta )}^{\top }\rangle }_{\theta }.$$ [13]

Since ${\mathbf{y}}_d(\theta )$ is decoded from ${\mathbf{x}}_d(\theta )$ through weights ${\mathbf{W}}_d$, the estimated covariance is ${\widehat{\mathrm{\Sigma }}}_{xy}^d={\mathrm{\Sigma }}_x^d{\mathbf{W}}_d$, where ${\mathrm{\Sigma }}_x^d={\langle {\mathbf{x}}_d(\theta ){\mathbf{x}}_d{(\theta )}^{\top }\rangle }_{\theta }$ is the covariance of the inputs ${\mathbf{x}}_d(\theta )$. The regularized least-squares weight update is therefore:

$$\begin{array}{ll}{\mathbf{W}}_{d+1}\hfill & ={[{\mathrm{\Sigma }}_x^d+{\rho }_2\mathbf{I}]}^{-1}{\mathrm{\Sigma }}_x^d{\mathbf{W}}_d.\hfill \end{array}$$ [14]

This update can be interpreted as recursive Bayesian filtering of the weights (SI Appendix, Weight Filtering).

Because $\mathbf{x}(\theta )$ continues to encode information about θ, we know that variability in the decoded $\mathbf{y}(\theta )$ should be conserved. Each readout $y_i(\theta )$ homeostatically adjusts its sensitivity to maintain a target variability ${\sigma }_0^2$. As introduced earlier, this multiplies the firing rate by a factor $\gamma ={\sigma }_0/{\sigma }_1=1+\delta$, where δ is a small parameter, and σ₁ is the SD of the readout’s firing rate after drift, but before normalization. Accounting for this in Eq. 14 and considering the weight vector $\mathbf{w}$ for a single readout neuron yields:

$$\begin{array}{ll}{\mathbf{w}}_{d+1}\hfill & ={[{\mathrm{\Sigma }}_x^d+{\rho }_2\mathbf{I}]}^{-1}{\mathrm{\Sigma }}_x^d\mathbf{w}·(1+\delta ).\hfill \end{array}$$ [15]

To translate this into a plausible learning rule, the solution Eq. 15 can be obtained via gradient descent. Recall the loss function $\mathcal{L}(\mathbf{w})$ for optimizing regularized linear least squares:

$$\begin{array}{ll}\mathcal{L}(\mathbf{w})\hfill & =\frac{1}{2}\langle \left|\right|{\mathbf{w}}^{\top }\mathbf{x}-\mathbf{y}|{|}^2\rangle +\frac{1}{2}{\rho }_2|\left|\mathbf{w}\right|{|}^2.\hfill \end{array}$$ [16]

Gradient descent $-{\nabla }_{\mathbf{w}}\mathcal{L}(\mathbf{w})$ on Eq. 16 implies the weight update

$$\begin{array}{ll}\mathrm{\Delta }\mathbf{w}\hfill & \propto \langle \mathbf{x}{(\mathbf{y}-{\mathbf{w}}^{\top }\mathbf{x})}^{\top }\rangle -{\rho }_2\mathbf{w}.\hfill \end{array}$$ [17]

After matching terms between Eqs. 12–15 and Eq. 17 and simplifying, one finds the following Hebbian learning rule:

$$\begin{array}{ll}\mathrm{\Delta }\mathbf{w}\hfill & \propto \delta {\langle {\mathbf{x}}_d(\theta )y_d(\theta )\rangle }_{\theta }-{\rho }_2\mathbf{w}.\hfill \end{array}$$ [18]

Eq. 18 is equivalent to Eq. 5 for a certain regularization strength ρ₂ (now taking the form of weight decay). The optimal value of ρ₂ depends on the rate of drift. Since drift drives homeostatic errors, it follows that ${\rho }_2\propto \delta$ for small δ. Here, we set ${\rho }_2=\delta$, corresponding to c = 1 in Eq. 18.

Single-Neuron Readout.

In Fig. 2, we simulated a population of 100 encoding neurons ${\mathbf{x}}_d(\theta )$ that changed one at a time (Simulated Drift). We initialized a single readout $y(\theta )=\varphi [{\mathbf{w}}^{\top }\mathbf{x}(\theta )]$ to decode a Gaussian bump $y_0(\theta )$ (σ = 5% of the track length) from the activations ${\mathbf{x}}_0(\theta )$ on the first day. We optimized this via gradient descent using a linear–nonlinear Poisson loss function.

$$\begin{array}{l}\mathrm{\Delta }\mathbf{w}\propto {\langle {\mathbf{x}}_0(\theta ){[{\mathbf{y}}_0(\theta )-y(\theta )]}^{\top }\rangle }_{\theta }-{\rho }_r\mathbf{w},\hfill \end{array}$$ [19]

with regularizing weight decay ${\rho }_r={10}^{-4}$. In this deterministic firing-rate model, the Poisson error allows the squared norm of the residuals to be proportional to the rate. We simulated 200 time points of drift, corresponding to two complete reconfigurations of the encoding population. After each encoding-unit change, we applied 100 iterations of either naïve homeostasis (Fig. 2B and Eq. 3) or Hebbian homeostasis (Fig. 2C and Eq. 5). For naïve homeostasis, the rates for gain and threshold homeostasis were ${\eta }_{\beta }={10}^{-3}$ and ${\eta }_{\gamma }={10}^{-5}$, respectively. For Hebbian homeostasis, the rates were ${\eta }_{\beta }={10}^{-1}$ and ${\eta }_{\gamma }={10}^{-3}$.

Homeostatic regulation requires averaging the statistics over time (48). To model this, we calculated the parameter updates for the gain and bias after replaying all θ and computing the mean and variance of the activity for each neuron. Since the processes underlying cumulative changes in synaptic strength are also slower than the timescale of neural activity, weight updates were averaged over all θ on each iteration. We applied additional weight decay with a rate $\rho =1\times {10}^{-4}$ for regularization and stability and set $c=1$ in Eq. 5 such that the rate of weight decay was also modulated by the online variability error $\tilde{\delta }$.

Learning Recurrent Weights.

For recurrent dynamics modeled as feedback in Eq. 7, supervised, linear Hebbian learning implies that the recurrent weights should be proportional to the covariance of the state variables $\mathbf{z}$. To see this, consider a linear Hebbian learning rule, where $\mathbf{z}$ has been entrained by an external signal and serves as both the presynaptic input and postsynaptic output:

$$\begin{array}{l}\frac{d}{dt}{\mathbf{A}}_p={\langle \mathbf{z}{\mathbf{z}}^{\top }\rangle }_{\theta }-\alpha {\mathbf{A}}_p\hfill \end{array},$$ [20]

where α is a weight decay term. This has a fixed point at ${\mathbf{A}}_p=\langle \mathbf{z}{\mathbf{z}}^{\top }\rangle /\alpha$. In our simulations, we ensure that $\mathbf{z}$ is zero-mean such that the second moment, $\langle \mathbf{z}{\mathbf{z}}^{\top }\rangle$, is equal to the covariance.

For the linear–nonlinear map model of recurrent dynamics Eq. 8, neurons could learn ${\mathbf{A}}_r$ by comparing a target ${\mathbf{y}}_0$ to the predicted ${\mathbf{y}}_r$ at the same time that the initial decoding weights ${\mathbf{W}}_0$ are learned. For example, ${\mathbf{y}}_0$ could be an external (supervised) signal or the forward predictions in Eq. 4 before drift occurs, and ${\mathbf{y}}_r$ could arise though recurrent activity in response error to ${\mathbf{y}}_0$. A temporally asymmetric plasticity rule could correlate the between these signals with the recurrent synaptic inputs to learn ${\mathbf{A}}_r$ (78). This plasticity rule should update weights in proportion to the correlations between synaptic input ${\mathbf{y}}_f^{\top }$ and a prediction error ${\mathbf{y}}_0-{\mathbf{y}}_r$:

$$\begin{array}{l}\mathrm{\Delta }{\mathbf{A}}_r\propto {\langle {\mathbf{y}}_f{({\mathbf{y}}_0-{\mathbf{y}}_r)}^{\top }\rangle }_{\theta }-{\rho }_r{\mathbf{A}}_r,\hfill \end{array}$$ [21]

where ${\rho }_r={10}^{-4}$ sets the amount of regularizing weight decay.

Eq. 8 is abstract, but captures the two core features of error correction through recurrent dynamics. It describes a population of readout neurons that predict each other’s activity through recurrent weights. Eq. 21 states that these weights are adapted during initial learning to minimize the error in this prediction. We assume ${\mathbf{A}}_r$ is fixed once learned.

Population Simulations.

In Fig. 3, we simulated an encoding population of 100 units. Drift was simulated as described in Simulated Drift with τ = 100. In all scenarios, we simulated M = 60 readout cells tiling a circular θ divided into L = 60 discrete bins. Learning and/or homeostasis was applied every five iterations of simulated drift. The readout weights and tuning curves were initialized similarly to the single-neuron case, but with tuning curves tiling θ.

For the predictive coding simulations (Eq. 7), we simulated a second inner loop to allow the network activity $\mathbf{z}$ to reach a steady state for each input $\mathbf{x}(\theta )$. This loop ran for 100 iterations, with time constant of ${\tau }_z=100$. The recurrent weights ${\mathbf{A}}_p$ were initialized as the covariance of the synaptic activations on the first day (${\mathrm{\Sigma }}_z$, where $\mathbf{z}(\theta )={\mathbf{W}}^{\top }\mathbf{x}(\theta )$), and held fixed over time. The final value $\widehat{\mathbf{z}}$ was used to generate a training signal, $\widehat{\mathbf{y}}=\varphi (\widehat{\mathbf{z}})$ to update the readout weights. For the recurrent map, recurrent weights were learned initially by using Eq. 21 and held fixed through the simulations.

For both the linear–nonlinear map and the recurrent feedback models, weights were updated as in Eq. 5, where the output of the recurrent dynamics was used to compute homeostatic errors and as the signal $\widehat{\mathbf{y}}$ in Hebbian learning. For naïve homeostasis (Fig. 3B) and Hebbian homeostasis (with and without response normalization; Fig. 3 C and D), learning rates were the same as in the single-neuron simulations (Fig. 2; Single-Neuron Readout). For the linear–nonlinear map (Fig. 3E), learning rates were set to ${\eta }_{\gamma }={10}^{-4}$ and ${\eta }_{\beta }={10}^{-1}$. For recurrent feedback (Fig. 3F), the learning rates were ${\eta }_{\gamma }=5\times {10}^{-3}$ and ${\eta }_{\beta }=5$. Learning rates for all scenarios were optimized via grid search.

Response normalization was added on top of Hebbian homeostasis for Fig. 3D and was also included in Fig. 3 E and F to ensure stability. The population rate target μ_p for response normalization was set to the average population activity in the initially trained state.

Different parameters were used to generate the right-hand column of Fig. 3 to show the effect of a larger amount of drift. After training the initial readout, 60% of the encoding features were changed to a new, random tuning. Learning rates were increased by $50\times$ for naïve homeostasis to handle the larger transient adaptation needed for this larger change. The other methods did not require any adjustments in parameters. Each homeostatic or plasticity rule was then run to steady-state (1,000 iterations).

Data Availability

Source code for all simulations have been deposited in GitHub (https://github.com/michaelerule/selfhealingcodes). Previously published data were used for this work (47).