Abstract
As an important chemical raw material, styrene has a high price because of its high energy consumption for separation. This article focuses on the styrene separation unit in a practical propylene oxide/styrene monomer process, and divided wall columns (DWC) are used for process optimization. Four DWC models are evaluated in terms of both economics based on the minimum total annual cost (TAC) and operability based on degrees of freedom. Differential evolutionary (DE) algorithms are used to optimize the parameters for each case study. In the process of finding the minimum TAC, the traditional DE often falls into local solutions and has low efficiency. In order to solve this problem, we propose chaotic sequences in DE algorithms to generate variables with ergodicity, which improves the optimization efficiency. Compared with the conventional process, Wright’s fully thermally coupled DWC (FTC) and Agrawal’s liquid-only transfer DWC (ALT) can save 21.36 and 10.14% TAC, respectively, but ALT has 2 more degrees of freedom than FTC. The FTC has the best economic efficiency, while the ALT strikes a balance between operability and economics.
1. Introduction
As one of the most fundamental upstream raw materials in polymer science and technology, styrene monomer (SM) is widely employed for synthesizing various resins, such as acrylonitrile butadiene styrene resin, high-impact polystyrene, and styrene maleic anhydride resin.1 In recent research studies, the ethylbenzene (EB) dehydrogenation process has an outlet stream with a close ratio of EB and SM after the feed flow passes through the reactor.2,3 It can be predicted that the reflux ratio (RR) in an EB/SM distillation column will be enormous due to the close boiling point of this binary system.4−7 A higher RR means more energy loss, so finding an energy-efficient process is of great significance.
EB co-oxidation is a new process for producing SM and another high-value product propylene oxide (PO). The difference between the EB co-oxidation process and other SM processes is that EB has a high single-pass conversion rate, so trace EB needs to be separated from SM. Meanwhile, other substances like α-methyl styrene (AMS) and methylbenzyl alcohol (MBA) with boiling points slightly higher than that of SM will also be present.8−11 A comparison of the feed composition between the two process separation units is shown in Table 1.
Table 1. Separation Unit Feed Composition in the EB Co-oxidation Process and the PO/SM Process.
| composition | EB co-oxidation (%) | PO/SM (%) |
|---|---|---|
| EB | 17–32 | 2.7 |
| SM | 67–72 | 79 |
| AMS | ∼7 | 4.2 |
| MBA | <0.5 | 10.6 |
| heavy oils | 3 | 3.5 |
Conventional distillation columns (CDiC) were utilized in the current separation unit. With more than 99.7% mass purity, the SM product was accessed at the top of the second column (SM column) after EB distillation in the first column (prefractionation column). A high RR and massive theoretical stages were still present in this process; however, it costs much less energy than the EB dehydrogenation process. Thus, the potential for saving energy and cost was highly predictable.
Various technologies, such as multi-effect distillation (MED),12,13 heat pump-assisted distillation (HPAD),14−16 and internally heat-integrated distillation column (HDiC),17−19 are expected to substantially reduce energy consumption for the closing-boiling system and have constantly been studied during the last few decades. Li et al.20 performed a comprehensive economic evaluation of the CDiC, double-effect distillation (DED, the simplest type of MED), self-heat recuperation technology (SHRT), and DED-SHRT for the EB/SM separation to obtain a configuration with a minimum separation cost, thus with potential for saving energy and cost. According to their research, the total annual cost (TAC) reduction can be improved up to ∼28% with a larger capacity (100 kmol/h) owing to the scaling effects. Primarily, SHRT was the best choice from the perspective of economics.
The divided wall column (DWC) is another distillation energy-saving technology. Petlyuk et al.21 proposed a fully coupled distillation column structure that aimed to address the shortcomings of conventional distillation sequences in energy utilization. In this unit, after the ternary mixture is fed, it first passes through the prefractionation column for preliminary separation, with the gas-phase mixture of components A and B at the top of the column and the liquid-phase mixture of components B and C at the bottom, before entering the central column for further separation. At the same time, a liquid phase is taken out from the main column near the gas-phase feed tray as the liquid-phase reflux of the prefractionation column, while a gas phase is taken from the liquid-phase feed tray near the prefractionation column as the gas-phase reflux of the prefractionation column. Thus, the purpose of complete thermal coupling can be achieved by a fully thermally coupled (FTC) distillation column, which is thermodynamically equivalent.22 DWC combines two columns into one shell and divides the middle section into two zones by inserting vertical interstices. The wall divides the column into four sections. The left side of the wall, which has a feed flow, is similar to the prefractionator of an FTC distillation column. The other sections are identical to the central column. Compared with the FTC distillation column, the DWC further reduces the equipment investment and plant space and avoids the pressure balance between the prefractionator and the central column.23 Chen and Agrawal24 classified DWC into five types based on the following three parameters: (1) the location of the ends of the divided wall with respect to the top and bottom ends of the column shell, (2) the number of condensers and reboilers associated with the divided wall, and (3) the number and types of transfer streams across the divided wall. Based on certain simplifying assumptions, in their article, the minimum total vapor duty usage for each type of DWC was compared for different representative relative volatility systems. Furthermore, we would like to comprehend which type of DWC is better for EB/SM systems based on a rigorous calculation using TAC as the evaluation method.
In this article, the actual PO/SM production process is used as a benchmark, and DWC is adopted as a process optimization approach. Four different DWC models are utilized for comparison with CDiC in terms of both operability and economics. A DE algorithm introducing chaotic sequences is also employed to find the optimal parameters with the lowest TAC. In addition, several chaotic sequences have been introduced in this research to increase the efficiency of the optimization, and each result has been compared separately.
2. Process Design
2.1. Process Specification
To better identify the most economical DWC, a real working condition from an SM separation unit in a PO/SM plant in southern China was selected as the source. The specific composition of the feed is exhibited in Table 2.
Table 2. Feed Flow Profiles in the PO/SM Process.
| parameters | unit | value |
|---|---|---|
| temperature | °C | 40.8 |
| pressure | kPaG | 260 |
| SM | kg/h | 59447.3 |
| EB | kg/h | 2200.1 |
| AMS | kg/h | 3158.3 |
| MBA | kg/h | 8058.1 |
| H60 (benzyl alcohol) | kg/h | 2150.9 |
| H50 (2-phenyl ethanol) | kg/h | 800.4 |
The product (SM) extraction was kept consistent for all scenarios during the optimization process to ensure the rigor of the various compared strategies. At the same time, the mass fraction of SM was set to 99.7% according to product quality, and the concentration of EB in the product was less than 100 ppm. The EB/SM column was operated under high vacuum conditions with a low-pressure drip tray to suppress the SM polymerization. The vacuum system was realized as a separate package in the original process. In the original design data, the top stage pressure for the two columns was 14.67 kPa (absolute). Thus, the pressure of the column was set to 14.67 kPa in all configurations. Instead of using the column operating pressure as an optimization variable, we focused on the impact of tray distribution and feed position on economic efficiency in this study. Cooling water at 30–40 °C served as the cold utility, and medium-pressure steam at 5 bar served as the hot utility.
All the process simulations were performed in the Aspen Plus V11.0 environment with the Peng–Robinson thermodynamic model.20
2.2. Process Configurations
2.2.1. Configuration 1: CDiC
CDiC has been leveraged to separate EB, SM, and heavies in the actual process in recent years.9 As shown in Figure 1, the number of trays in the distillation and fractionation sections (NT1, NT2, NT3, and NT4) and the RR of the two columns (RR1 and RR2) were selected as optimization variables, using design specifications in Aspen Plus to ensure a product mass fraction of 99.7% while fixing the flow rate of the three product streams to be consistent with the actual process. The CDiC was used as the baseline case for comparison with other configurations.
Figure 1.
Flowsheet of the CDiC.
2.2.2. Configuration 2: Wright’s DWCFTC
FTC, which is the most traditional type of DWC, was constructed by inserting a divided wall into the tower’s interior.25 In the cross-sectional view, the divided wall was “suspended” inside the tower and did not intersect with the top and bottom of the tower. The mixture ABC was fed from the left side of the divided wall and was roughly divided into two streams (liquid AB and vapor BC). These two streams crossed the divided wall. We finally obtained A in the condenser, C in the reboiler, and B from the right side of the divided wall.
The superiority of FTC over CDiC in terms of energy and economic savings has been demonstrated in numerous papers, not only by saving a condenser and a reboiler but also by increasing the thermodynamic efficiency of the column. The thermodynamic equivalence of this type of column is revealed in Figure 2. The flow rates of the three product streams are aligned with the baseline. The number and distribution of trays (NT1, NT2, NT3, NT4, NT5, and NT6), RR, gas-phase distribution flow rate (Vapor), and liquid phase distribution flow rate (Liquid) are selected as optimization variables.
Figure 2.
Flowsheet and thermodynamic equivalence model of the FTC.
2.2.3. Configuration 3: Agrawal’s Side-Stripper DWC
Despite the fact that FTC shows significant advantages over CDiC in terms of economic and energy consumption, it has a fatal flaw in operation. When the divided wall position is fixed, the gas-phase distribution ratio is also determined, which is a crucial variable in the column design. As a result, the lack of an effective control scheme has been one of the constraints in the large-scale industrialization of FTC.
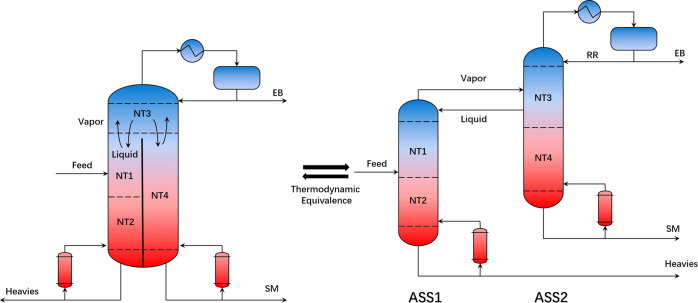
The divided wall can be extended to the bottom of the tower to solve this problem, while another reboiler can be added. In that case, the amount of rising steam on either side of the wall can be determined by varying the heat load of the two reboilers, which is mostly at the expense of thermal efficiency but significantly enhances the robustness of the equipment. This equipment is named the side-stripper DWC, which was synthesized by Agrawal et al. in 2001.26 The actual equipment model of Agrawal’s side-stripper (ASS) and its thermodynamic equivalent can be observed in Figure 3. Mass and energy exchange can occur only above the divided wall. Similar to FTC, the number and distribution of trays (NT1, NT2, NT3, NT4, and NT5), RR, gas-phase distribution flow rate (Vapor), and liquid-phase distribution flow rate (Liquid) were selected as optimization variables.
Figure 3.
Flowsheet and thermodynamic equivalence model of ASS.
2.2.4. Configuration 4: Madenoor Ramapriya’s DWC
Granted that ASS is beyond the limitation of the FTC in terms of control scheme, it still has a strict demand for the relative volatility of the components to be separated. The left side of the divided wall takes up too much of the separation duty. More theoretical stages are often required to ensure the purity of the heavy component extracted from the left reboiler.
The pure heavy component can be directly obtained if the mixture from the left reboiler is sent to the right side for separation. The corresponding DWCs were synthesized by Madenoor Ramapriya et al.27 As shown in Figure 4, a reboiler substitutes a thermal coupling in the Madenoor Ramapriya’s DWC (MR) compared to the FTC. Although fluid transfer costs rise in MR, improvements in operability make it highly attractive for new applications. The same variables (NT1, NT2, NT3, NT4, NT5, NT6, RR, Liquid, and Vapor) were chosen for optimization as FTC and ASS.
Figure 4.
Flowsheet and thermodynamic equivalence model of MR.
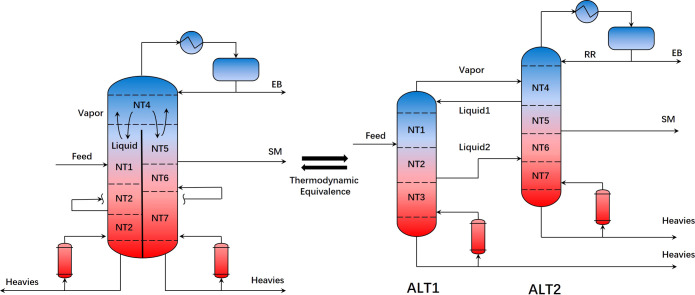
2.2.5. Configuration 5: Agrawal’s Liquid-Only Transfer DWC
In MR, all of the left reboiler extraction was sent to the right side of the divided wall for clear separation. The thermal efficiency of MR was improved compared with that of ASS but was still lower than that of FTC. A new fully thermally coupled model can be obtained by shifting the extraction position on the left side of MR upward, as revealed in Figure 5. Agrawal’s liquid-only transfer (ALT) converts a complete thermal coupling in the FTC to a liquid transfer without increasing too much cost of equipment and losing additional thermal efficiency.28 The choice among FTC, ASS, MR, and ALT requires a compromise between heat consumption and economic losses.
Figure 5.
Flowsheet and thermodynamic equivalence model of ALT.
3. Optimization Design
3.1. Framework Design
Three elements need to be identified to solve optimization problems: variables, constraints, and the function (objective).29
The variables are specified in Section 2.2. Although each configuration variable differs slightly in form, they are essentially the number and distribution of trays (NT1, NT2, ...), the fluid distribution flow rate (Liquid, Vapor), and RR. Some of these variables are discontinuous integers, and some are continuous real numbers.
The three products need to be of the same quality, while the purity of the main product, SM, was 99.7%. All configurations were fairly compared under this baseline. The constraint can be mathematically expressed as eq 1
 |
1 |
Economic efficiency is a more important indicator for assessing different configurations than heat consumption. That is why we adopted the economic indicator as an optimization target. We generally used TAC as the indicator that best reflects economic efficiency. TAC is related to the capital cost, operating cost, and payback period. The relationship among these parameters, the equipment parameters, and the operating parameters is concretely described in Section 3.2. In the construction of the framework, we consider TAC to be a function of equipment and operating parameters that can be mathematically expressed as eq 2.
 |
2 |
Some of these parameters are variables, and others need to be calculated by the process. After assigning all the variables and setting the data in Aspen, Aspen offers the remaining parameters. As shown in eqs 3 and 4, we can then assume that all the parameters required by the TAC are supplied by a black-box function named “Aspen”.
 |
3 |
 |
4 |
Eq 4 is a very
complex
nonlinear function. In this analysis, we abstracted the DWC optimization
problem to a Mixed-Integer Nonlinear Programming (MINLP) problem,
which can be mathematically expressed as eq 5. As shown in eq 5, TAC(x1, x2, ..., xn) describes the optimization objective, and g(xi) describes the equation constraints
as shown in eq 1.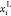 
and 
describe the upper and lower bounds of
the variables, respectively, and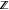 
refers to the set of integer variables.
 |
5 |
 |
 |
 |
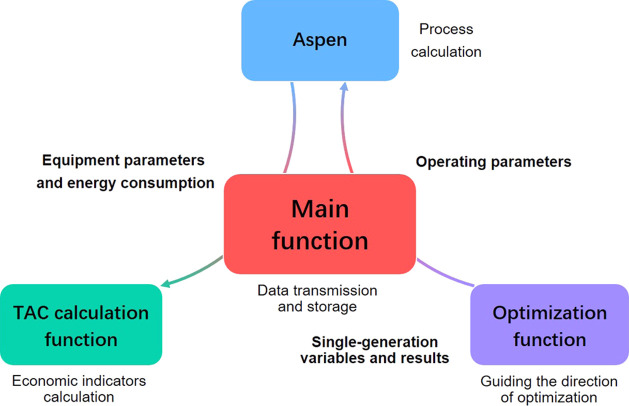
As shown in Figure 6, the main function generates the initial values of the variables and then assigns the variables to the Aspen software for process calculation. Aspen transfers the calculated equipment parameters and operating parameters to the TAC calculation function. The TAC calculation function returns the calculation results together with the initial values of the variables to the optimization function, which evaluates the results of the TAC calculation and transfers the next generation of variable values via the main function to the TAC calculation function. The next generation of variable values is then transferred to Aspen for the next generation of calculations.
Figure 6.
Framework of the function.
3.2. TAC
As shown in eq 6, OPEX is the operational expenditures (US$/year), CAPEX is the capital expenditures (US$/year), PBP is the payback period, and PBP of 3 years for capital investment is the initially considered parameter.
 |
6 |
Here, OPEX includes hot utility (QR) for the reboiler and cold utility (QC) for the condenser; in this case of optimization, distillation operation at external pressures (<10 kPa) is required to prevent SM self-polymerization at high temperatures, so the operating costs of the vacuum system (Qv) are also an aspect that cannot be ignored.
The CAPEX calculation is relatively simple, that is, the construction costs of the distillation column, condenser, reboiler, and vacuum system. It is worth mentioning that the CAPEX for the distillation column includes both the main column cost and the tray cost.
The relationship between the cost of each component and the values of the operating and equipment parameters is revealed in Table 3.
Table 3. Basis of Economics.
| parameter | formulas or data | units |
|---|---|---|
| Column | ||
| θ | 1.1 | |
| H | (NT2) × 1.2 × 0.61 | m |
| Ccol | 17,640 × D1.066 × H0.802 × θ | $ |
| Ctray | D1.55 × (NT-2) × 229 | $ |
| Condenser | ||
| U | 0.852 | kW/m2/K |
| LMTD | 15 | K |
| Ac | Qc/U/LMTD | m2 |
| Chexc | 7296 × Ac0.65 | $ |
| CW | 0.354 | $/GJ |
| Ccon | Qc × CW | $ |
| Reboiler | ||
| U | 0.568 | kW/m2/K |
| LMTD | 20 | K |
| Ar | QR/U/LMTD | m2 |
| Chexr | 7296 × Ar0.65 | $ |
| MP | 8.22 | $/GJ |
| Creb | QR × MP | $ |
| Vacuum system | ||
| Vc | D2× H × 0.785 | m3 |
| M | 5 + (0.028 + 0.03088 × ln(7602× P)-0.0005733 × ln(7602× P)2× (Vc/0.0283168)0.66) | |
| Cvs | 1640 × (M/P/7602)0.41 | $ |
Table 3 summarizes economic parameters and formulas for the separation system.
The CAPEX mainly considers the column shells (Ccol), trays (Ctray), reboilers (Chexr), condensers (Chexc), and vacuum systems (Cvs).
The cost of column shells and trays is a function of both the column height (H) and tower diameter (D). Different compositions lead to different factors for the cost of column shells (θ). For compositions with close boiling points, θ takes the value 1.1.
Both condensers and reboilers are heat exchangers, and their costs are calculated in almost the same way, as a function of the heat exchange area (Ac and Ar). The heat exchange area can then be determined by heat duty (Qc and QR), the overall heat-transfer coefficient (U), and the logarithmic mean temperature difference (LMTD). For condensers, LMTD takes the value 15 °C, and for reboilers, 20 °C.
Vacuum systems are an uncommon piece of equipment, but for styrene, which tends to self-polymerize at high temperatures, vacuum distillation is the process that must be adopted. The cost of the vacuum system is related to the volume of the tower (Vc) and the operating pressure (P), which can be related as a factor (M), making the formula simpler.
OPEX includes the hot utility (Creb) for the reboiler and the cold utility (Ccon) for the condenser. Strictly speaking, a certain amount of steam is also required for the operation of the vacuum system, but the amount of steam used for this is much less than that for the two utilities mentioned above, so we ignore it in our calculations. The utility calculation is very simple; just multiply the unit price by the heat duty. The specifications for cooling water (CW) and steam (MP) are the same in all configurations and therefore the unit prices are the same.30
3.3. Degrees of Freedom and Optimization Variables
Determination of the number of independent variables (degrees of freedom) for chemical engineering objects can be viewed as a separate area of chemical engineering science. This area is very important for the design and optimization of technological complexes.
Based on basic mathematical principles, a system of equations consisting of n independent equations can and can only be solved for n variables. When the number of independent equations is greater than the number of variables, the system of equations will have multiple solutions. The difference between the number of variables and the number of independent equations is therefore the degrees of freedom of the model.31 If the number of variables is m, the number of independent equations is n, and the degrees of freedom is f, then the mathematical relationship can be expressed as eq 7
 |
7 |
In the following, we analyze the number of variables, the number of independent equations, and the degrees of freedom of the specific FTC model as an example.
The top-stage pressure, the composition flow rate and state of the feed stream, the distillation flow rate, and the side stream flow rate are all given variables.
The independent variables for the FTC model with six components are enumerated in Table 4.
Table 4. Independent Variables of the FTC Model.
| variable name | number of variables |
|---|---|
| feed flow rate | 1 |
| feed composition | 6 |
| feed temperature | 1 |
| feed enthalpy | 1 |
| distillation flow rate | 1 |
| side stream flow rate | 1 |
| gas- and liquid-phase distribution ratio | 2 |
| pressure of each tray | NT1 + NT2 + NT3 + NT4 + NT5 + NT6 |
| temperature of each tray | NT1 + NT2 + NT3 + NT4 + NT5 + NT6 |
| gas- and liquid-phase flow rate of each tray | 2 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| gas- and liquid-phase composition of each tray | 2 × 6 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| enthalpies of gas and liquid phases for each tray | 2 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| phase equilibrium constants for each tray | 6 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| number of theoretical trays | 6 |
| condenser and reboiler heat duty | 2 |
| total | 21 + 24 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
The independent equations of the FTC model are enumerated in Table 5.
Table 5. Independent Equations of the FTC Model.
| equation name | number of equations |
|---|---|
| material balance equations | 6 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| vapor–liquid equilibrium equations | 6 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| enthalpy balance equations | NT1 + NT2 + NT3 + NT4 + NT5 + NT6 |
| summation equations | 2 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| phase equilibrium constant equations of trays | 6 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| enthalpy of the liquid-phase and gas-phase equations of trays | 2 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
| pressure drop equations of trays | NT1 + NT2 + NT3 + NT4 + NT5 + NT6 |
| feed enthalpy equation | 1 |
| total | 1 + 24 × (NT1 + NT2 + NT3 + NT4 + NT5 + NT6) |
For the FTC model with six components, the degrees of freedom can be calculated using eq 8
 |
8 |
Table 6 shows the independent variable scheme for the FTC model.
Table 6. Independent Variable Scheme for the FTC Model.
| name of independent variables | number of independent variables |
|---|---|
| feed flow rate | 1 |
| feed composition | 6 |
| feed temperature | 1 |
| top-stage pressure | 1 |
| distillation flow rate | 1 |
| side stream flow rate | 1 |
| reflux flow rate | 1 |
| gas- and liquid-phase distribution flow rate | 2 |
| number of theoretical trays | 6 |
| total | 20 |
The top-stage pressure, the composition flow rate and state of the feed stream, the distillation flow rate, and the side stream flow rate are all given variables. Thus, the final number of optimized variables is 9.
The number of independent equations, the number of variables, the degrees of freedom, the number of optimization variables, and the selection of optimization variables for five process configurations are shown in Table 7.
Table 7. Selection of Optimization Variables.
| equation | variables | degrees of freedom | selection of optimization variables | |
|---|---|---|---|---|
| CDiC | 1 + 24 × NT | 25 + 24 × NT | 24 | number of trays(NT1, NT2, NT3, NT4) |
| reflux ratio(RR1, RR2) | ||||
| FTC | 1 + 24 × NT | 21 + 24 × NT | 20 | number of trays(NT1, NT2, NT3, NT4, NT5, NT6) |
| reflux ratio(RR1) | ||||
| distribution flow rate(Vapor, Liquid) | ||||
| ASS | 1 + 24 × NT | 20 + 24 × NT | 19 | number of trays(NT1, NT2, NT3, NT4, NT5) |
| reflux ratio(RR1) | ||||
| distribution flow rate(Vapor, Liquid) | ||||
| MR | 1 + 24 × NT | 21 + 24 × NT | 20 | number of trays(NT1, NT2, NT3, NT4, NT5, NT6) |
| reflux ratio(RR1) | ||||
| distribution flow rate(Vapor, Liquid) | ||||
| ALT | 1 + 24 × NT | 23 + 24 × NT | 22 | number of trays(NT1, NT2, NT3, NT4, NT5, NT6, NT7) |
| reflux ratio(RR1) | ||||
| distribution flow rate(Vapor, Liquid1, Liquid2) |
3.4. Optimization Algorithm
Optimization is a field of applied mathematics that involves finding the extreme value of a function in a defined domain based on various restrictions of the important variables. Historically, optimization techniques first appeared in problems related to the logistics of people and transport management. Typically, these problems were modeled as finding the minimum cost provided such that all constraints were satisfied. However, as optimization problems become more and more complex, the variables change from linear to nonlinear and from continuous real numbers to discontinuous integers. The optimization objective also changes from linear to nonlinear functions, even in equations and their complex non-differentiable functions. The generalized MINLP problem has not been solved by a universal polynomial-time algorithm.32,33
Hence, common search algorithms are applied to find a better solution in the defined domain of given variables when the state space is not large. However, the search algorithm efficiency will substantially decline when the state space is vast and not predicted. It is too inefficient to complete the optimization task where heuristic search algorithms come into play.
The heuristic search algorithms evaluate each position in the state space before each generation of calculation. Therefore, a large number of unnecessary search paths can be omitted. Different evaluation methods cause different results.
Common heuristic search algorithms include ant colony (AC),34 simulated annealing (SA),35 and DE algorithms.36,37
3.4.1. Differential Evolution Algorithm
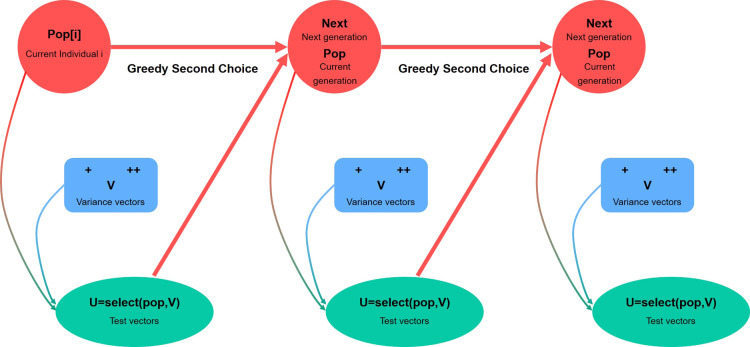
The DE algorithm is mainly utilized to solve global optimization problems, and its main working steps are the same as those of other evolutionary algorithms. Figure 7 illustrates a basic DE algorithm flow. The basic idea of the algorithm is to start with a randomly generated initial population, using the difference vector of two randomly selected individuals from the population as the source of random variation for the third individual, weigh the difference vector, and sum it with the third individual according to specific rules to produce a mutated individual. The variant is then mixed with a predetermined target individual to create a test individual, a process known as crossover. If the fitness value of the test individual is better than that of the target individual, the test individual will replace the target individual in the next generation. Otherwise, the target individual remains the same. In each generation of evolution, each body vector is used as the target individual once, and the algorithm iterates through the computation, keeping the suitable individuals and eliminating the poorly performing ones, guiding the search process toward a global optimization solution.
Figure 7.
Flowchart of the DE algorithm.
3.4.2. Chaos and Random
The initial values of variables in the DE algorithm are generated randomly according to a uniform distribution. The initial values and iterative process developed by this method are not ergodic, which results in the cruising efficiency of the algorithm, strongly dependent on the initial values. The algorithm needs to find an optimum with the traversal of the initial values.38
Chaos theory represents the interplay among bifurcation and periodic and non-periodic motions in a nonlinear system, leading to non-periodic and ordered movements under specific parameters.39−41 According to the law, chaotic variables can pass through all states of existence within a given category without repeating themselves. Due to the ergodic nature of chaotic variables, the chaotic search can escape locally optimal solutions compared to random search, so it is widely employed in optimization problems. A chaotic map represents some chaotic behaviors, and some standard chaotic maps are logistic map,42 sinusoidal map,43 tent map,44 and piecewise map.45
Logistic map, also known as single-peaked map, is a quadratic polynomial map often leveraged as a typical example of how complex, chaotic phenomena can arise from elementary nonlinear dynamic equations. It can be mathematically expressed as
Other common chaotic sequence generation algorithms are shown in Table 8.
Table 8. Chaotic Sequence Generation Algorithms.
| name | definition | |
|---|---|---|
| circle map |
|
|
| Gauss map |
|
|
| Henon map |
|
|
| sinusoidal iterator | xi+1 = sin(πxi) | |
| sinus map |
|
|
| tent map |
|
3.4.3. Chaos Differential Evolution Algorithm
Here, we chose the population size NP = 60, the variation factor CR = 0.5, and the generation of iterations Gmax = 400 as optimization parameters.
A chaotic sequence was generated for the differential weight parameter F to ensure the ergodicity of the variation. Different chaotic sequences were compared according to their optimization speed to derive a suitable chaotic sequence for this problem. Therefore, when designing the optimization algorithm, we introduced multiple chaotic sequences under the same configuration for a cross-sectional comparison.
Figure 8 shows the algorithm’s specific arithmetic process for eq 9.
 |
9 |
Figure 8.
lowchart of the chaos differential evolution algorithm. Rand(a,b) means to take a random number between a and b, and Randi(a) means to take a random integer between 1 and a.
Different f(x) corresponds to different chaotic sequences. In particular, f(x) = c,c ∈ [0,1] means a standard DE algorithm DE. We chose the standard DE algorithms, logistic map chaos differential evolution algorithm (LMCDE), Gauss map differential evolution algorithm (GMCDE), and sinusoidal iterator chaos differential evolution algorithm (SICDE) for comparison. The corresponding f(x) for these algorithms is shown in Table 3.
4. Results and Discussion
4.1. Process Optimization Results
First, we simulated a CDiC process with the original design data. The simulation results were compared with the design data for the following parameters: the temperature at key locations, heat duty of condenser and reboiler, and RR of the columns. Table 9 shows the results of the comparison in detail.
Table 9. Comparison of CDiC Original Design Data and Simulation Results.
| column | parameters | design data | simulation result | tolerance (%) |
|---|---|---|---|---|
| CDiC1 | number of stages | 118 | 118 | |
| feed stage | 57 | 57 | ||
| distillate rate (kg/h) | 2202.36 | 2202.36 | ||
| RR | 106.00 | 102.464 | 3.34 | |
| top-stage temperature (°C) | 74.50 | 76.06 | 2.09 | |
| bottom-stage temperature (°C) | 99.60 | 97.55 | 2.06 | |
| condenser duty (GJ/h) | 81.52 | 83.26 | 2.13 | |
| reboiler duty (GJ/h) | 88.56 | 90.71 | 2.43 | |
| CDiC2 | number of stages | 70 | 70 | |
| feed stage | 42 | 42 | ||
| distillate rate (kg/h) | 59620.2 | 59620.2 | ||
| RR | 1.41 | 1.40 | 0.71 | |
| top stage temperature (°C) | 84.50 | 84.29 | 0.25 | |
| bottom stage temperature (°C) | 138.20 | 135.34 | 2.07 | |
| condenser duty (GJ/h) | 54.65 | 54.62 | 0.06 | |
| reboiler duty (GJ/h) | 58.10 | 54.19 | 6.73 |
The simulated results fit the design data well, with most of the parameters having a tolerance of less than 3%. The reason for the higher tolerance in the CDiC2 reboiler is that some heavy oils are removed from the feed flow composition. The results of the Peng–Robinson thermodynamic model selected for the simulations are reliable.
The process parameters optimized for the five types of configurations optimization are exhibited in Figure 9. As observed from the optimization results, the improvement in thermal efficiency can significantly reduce the theoretical stages and the utility duty, resulting in economic and energy advantages.
Figure 9.
Optimum (a) CDiC, (b) FTC, (c) ASS, (d) MR, and (e) ALT configurations. Qc is the heat duty of the condensers, and Qr is the heat duty of the reboilers.
Figure 10 shows the cost proportion of each equipment and system in CAPEX and OPEX, as well as the ratio of these two in TAC. In CAPEX, a more significant proportion is taken up by the cost of the tower, while in OPEX, the economic cost is almost determined by the energy consumption of the reboiler. Because OPEX accounts for the majority of the TAC, we can assume that the key to the optimization mainly depends on the degree of optimization of the reboiler heat load.
Figure 10.
Comparison of the operating cost (a), capital cost (b), and TAC (c) for the optimum configuration.
Table 10 exhibits a more precise analysis in conjunction with the economic indicators demonstrated. As the type with the highest degree of thermal coupling, the FTC tower is only 73.63% and 79.82% of the CDiC in terms of CAPEX and OPEX, respectively, saving more than 20% of the cost. Thus, the superiority of thermal coupling in a distillation tower process design is further demonstrated. Compared with the results of Li’s experiment in 2019,20 which constructed a complex DED–SHRT process with a 28% saving in TAC, the results of our optimization are considered credible and exceptional.
Table 10. Economic Results for the CDiC, FTC, ASS, MR, and ALT Designs.
| CDiC | FTC | ASS | MR | ALT | ||
|---|---|---|---|---|---|---|
| NT1 | 57 | 11 | 31 | 37 | 59 | |
| NT2 | 61 | 37 | 36 | 24 | 11 | |
| NT3 | 42 | 29 | 46 | 26 | 11 | |
| NT4 | 28 | 48 | 15 | 38 | 35 | |
| NT5 | 9 | 41 | 40 | |||
| NT6 | 9 | 16 | 11 | |||
| NT7 | 36 | |||||
| RR1 | 102.46 | 149.30 | 253.43 | 183.21 | 189.38 | |
| RR2 | 1.40 | |||||
| Ccol | 106$ | 4.66 | 3.61 | 4.50 | 4.80 | 4.39 |
| Ctray | 106$ | 0.34 | 0.26 | 0.34 | 0.35 | 0.31 |
| Chexc | 106$ | 1.68 | 1.22 | 1.73 | 1.40 | 1.44 |
| Chexr | 106$ | 2.07 | 1.37 | 2.44 | 2.00 | 2.05 |
| CAPEX | 106$ | 8.76 | 6.45 | 9.01 | 8.56 | 8.18 |
| Cvs | $/h | 298.95 | 267.53 | 316.46 | 307.36 | 322.64 |
| Creb | $/h | 1370.56 | 1059.47 | 1781.12 | 1306.62 | 1153.44 |
| Ccon | $/h | 48.84 | 42.82 | 73.45 | 53.19 | 55.19 |
| OPEX | $/h | 1718.36 | 1369.83 | 2171.03 | 1667.16 | 1531.27 |
| TAC | 106$ | 16.67 | 13.11 | 20.37 | 16.19 | 14.98 |
Somewhat unexpectedly, the optimization results of ASS are much less favorable than those revealed by CDiC, especially with a 26.34% increase in OPEX. A hypothesis for explaining this result is that the boiling points among EB, SM, and heavies are close to each other, especially the tiny difference between EB and SM. Therefore, ASS1 takes on only a minimal amount of the separation between EB and SM, resulting in the ASS2 tower being overloaded with the separation task. Instead of reducing the SM back-mixing, the gas–liquid exchange between the two parts further aggravates it.
MR optimization resulted in a slight improvement (∼3%) over CDiC. The possible reason is that this set of CDiC process parameters has been optimized for many years and is in a relatively good operation state. Another explanation is that the structure of MR is similar to CDiC, except that the upper space of MR2 replaces the condenser of MR1.
In 2012, Nikačević et al. presented a view that process intensification reduces the number of control degrees of freedom of a process.46 Furthermore, they argued that the number of degrees of freedom directly relates to decrease in actuation options. In 2015, Baldea led to the first rigorous justification for existing empirical arguments concerning the loss of control degrees of freedom caused by process intensification.47 Therefore, we can consider the number of degrees of freedom to be a measure of the operability of similar models. Degrees of freedom of four different DWC configurations have been listed in Table 7. Consequently, based on the operability analysis, ALT is better than FTC and MR, while ASS is the worst option. Unfortunately, operability cannot be measured quantitatively in the same way as economics. Further research in the future could concretely demonstrate the difference in operability by way of dynamic simulations.
As mentioned earlier, MR is thermodynamically closer to CDiC, while ALT is thermodynamically closer to FTC. ALT transforms a full thermal coupling of FTC into a liquid transport across the divided wall. Therefore, it is expected that the optimization of ALT is roughly half that of FTC (10.14%). Except for ASS, FTC, MR, and ALT achieved some optimization improvements. FTC achieved the most impressive results. Nevertheless, its shortcomings in degrees of freedom and operability cannot be ignored. MR made minimal progress, and ALT gave the most counterbalanced optimization solution due to its economic efficiency and operability advantages.
4.2. Algorithm Comparison Result
Figure 11 exhibits the optimization trajectory produced by our four similar optimization algorithms for the most complex structure of the ALT tower. The number of generations that reached the minimum TAC for each algorithm is marked by data points in the same color.
Figure 11.
Comparison of the different algorithms.
The optimization trajectory is expected to be a smoother curve similar to GMCDE and SICDE, which means that the optimization process can steadily jump out of a locally optimal solution. In contrast, a more extended plateau appears for the indicated DE line. As we have suggested, if the variational parameters are simply random values generated by a uniform distribution, then there will be a risk of falling into a luck-based optimization process, with the ability to jump out of the local optimum depending on probability or a large-scale computational method.
Computation time is an important metric to evaluate the performance of an algorithm. However, for algorithms such as DE, which specify the generations, the running time of the full program does not allow for an accurate comparison among different algorithms. Replacing the full-program computation time with the computation time when the optimum point is touched is a fairer solution. The computation time of the program is listed in Table 11.
Table 11. List of the Computation Time of Four Different DE Algorithms.
| algorithm | full-program computation (time/h) | optimum-point computation (time/h) |
|---|---|---|
| DE | 60.45 | 49.63 |
| LMCDE | 58.37 | 21.50 |
| GMCDE | 62.18 | 18.57 |
| SICDE | 56.48 | 12.46 |
The results fully justify the necessity of introducing variables with iterative properties. Even for the most basic chaotic sequential logistic map, the variables generated can significantly improve the optimization efficiency, demonstrating the superiority of chaotic differential evolutionary algorithms.
5. Conclusions
This study focuses on the EB/SM separation unit based on the PO/SM production process, which has high energy consumption and poor economic efficiency and proposes a DWC optimization method. This process is followed by an analysis of different types of DWC and a systematic investigation of thermal efficiency and operability.
A heuristic search algorithm is then adopted to search for economically optimal operating points for different DWCs. In response to the defects of the DE algorithm to generate algorithm ergodic parameters, chaotic sequences are proposed to improve optimization efficiency.
TAC is used to measure economics, while degrees of freedom are used to assess operability. The final FTC exhibits the best economic efficiency (−21.36%), while the ALT retains a significant portion of the financial savings (−10.14%) with a substantial improvement in degrees of freedom and operability. In addition, the concrete operational and control issues of the optimal configuration are worth further exploration with dynamic simulation in future research.
This article introduces DWC to the PO/SM process for the first time based on actual industrial design data. The simulation results are highly achievable and have a potential application in guiding the pilot scale-up directly. It also focuses on the operational difficulties of the DWC and aims to balance economic efficiency and operability, providing a practical idea for distillation optimization..
Acknowledgments
The authors gratefully acknowledge the financial support by the National Natural Science Foundation of China under grant number 21506007.
Glossary
Nomenclature
- Ac
condenser heat exchange area (m2)
- Ar
reboiler heat exchange area (m2)
- Ccol
cost of tower vertical vessels ($)
- Ccon
cost of condensers ($)
- Chexc
cost of cold utility ($/h)
- Chexr
cost of hot utility ($/h)
- Creb
cost of reboilers ($)
- Ctray
cost of trays ($)
- Cvs
vacuum system cost ($/h)
- CW
unit price of cooling water ($/GJ)
- FEB
mass flow rate of EB product flow (kg/h)
- FHeavies
mass flow rate of heavies’ product flow (kg/h)
- FSM
mass flow rate of SM product flow (kg/h)
- H
height of the tower (m)
- Liquid
mass flow rate of liquid transmission
- LMTD
limited minimum temperature difference
- M
vacuum system cost factor
- MP
unit price of middle pressure steam ($/GJ)
- NT
total number of trays
- NT1
the number of trays in area 1
- NT2
the number of trays in area 2
- NT3
the number of trays in area 3
- NT4
the number of trays in area 4
- NT5
the number of trays in area 5
- NT6
the number of trays in area 6
- NT7
the number of trays in area 7
- NT8
the number of trays in area 8
- RR
reflux ratio
- SMmass
mass fraction of styrene in SM product flow
- θ
tower vertical vessel cost factor
- U
heat transfer coefficient
- Vapor
mass flow rate of vapor transmission
- Vc
volume of column (m3)
Appendix
Author Contributions
Z.L.: data curation, software, visualization, methodology, and writing—original draft, X.Z.: investigation and supervision, J.Z.: formal analysis, Z.D.: conceptualization, project administration, and writing—review and editing, J.W.: resources.
The authors declare no competing financial interest.
References
- Nederlof C.Catalytic dehydrogenations of ethylbenzene to styrene. Doctoral Thesis; Delft University of Technology, 2012. [Google Scholar]
- Cavani F.; Trifirò F. Alternative processes for the production of styrene. Appl. Catal., A 1995, 133, 219–239. 10.1016/0926-860x(95)00218-9. [DOI] [Google Scholar]
- Welch V. A.Cascade reboiling of ethylbenzene/styrene columns. US Patent 6,171,449 B1, 2001.
- Cui C.; Li X.; Guo D.; Sun J. Towards energy efficient styrene distillation scheme: From grassroots design to retrofit. Energy 2017, 134, 193–205. 10.1016/j.energy.2017.06.031. [DOI] [Google Scholar]
- Yang D.; Li T.; Leng B. Energy-saving technology of styrene unit based on mechanical vapor recompression coupled with organic Rankine cycle process. Energy Sources, Part A 2020, 1–14. 10.1080/15567036.2020.1821127. [DOI] [Google Scholar]
- Jongmans M. T. G.; Hermens E.; Raijmakers M.; Maassen J. I. W.; Schuur B.; de Haan A. B. Conceptual process design of extractive distillation processes for ethylbenzene/styrene separation. Chem. Eng. Res. Des. 2012, 90, 2086–2100. 10.1016/j.cherd.2012.05.019. [DOI] [Google Scholar]
- Jongmans M. T. G.; Luijks A.; Maassen J.; Schuur B.; de Haan A. B.. Extractive distillation of ethylbenzene and styrene using sulfolane as solvent: Low pressure isobaric VLE data. Proceedings of Distillation Absorption, 2010; pp 337–342.
- Sheldon R.Catalytic Oxidations: An Overview. Catalytic Oxidation: Principles and Applications: A Course of the Netherlands Institute for Catalysis Research (NIOK); World Scientific, 1995, pp 1–15. [Google Scholar]
- Nijhuis T. A.; Makkee M.; Moulijn J. A.; Weckhuysen B. M. The production of propene oxide: catalytic processes and recent developments. Ind. Eng. Chem. Res. 2006, 45, 3447–3459. 10.1021/ie0513090. [DOI] [Google Scholar]
- Buijink J. K. F.; Lange J.-P.; Bos A. N. R.; Horton A. D.; Niele F. G. M., Chapter 13 - Propylene Epoxidation via Shell's SMPO Process: 30 Years of Research and Operation. In Mechanisms in Homogeneous and Heterogeneous Epoxidation Catalysis. Oyama S. T., Ed. Elsevier: Amsterdam, 2008; pp 355−371. 10.1016/b978-0-444-53188-9.00013-4 [DOI] [Google Scholar]
- Cavani F. Catalytic selective oxidation: The forefront in the challenge for a more sustainable chemical industry. Catal. Today 2010, 157, 8–15. 10.1016/j.cattod.2010.02.072. [DOI] [Google Scholar]
- Al-Shammiri M.; Safar M. Multi-effect distillation plants: state of the art. Desalination 1999, 126, 45–59. 10.1016/s0011-9164(99)00154-x. [DOI] [Google Scholar]
- Sayyaadi H.; Saffari A. Thermoeconomic optimization of multi effect distillation desalination systems. Appl. Energy 2010, 87, 1122–1133. 10.1016/j.apenergy.2009.05.023. [DOI] [Google Scholar]
- Annakou O.; Mizsey P. Rigorous investigation of heat pump assisted distillation. Heat Recovery Syst. CHP 1995, 15, 241–247. 10.1016/0890-4332(95)90008-x. [DOI] [Google Scholar]
- Fonyo Z.; Benkö N. Comparison of various heat pump assisted distillation configurations. Chem. Eng. Res. Des. 1998, 76, 348–360. 10.1205/026387698524776. [DOI] [Google Scholar]
- Leo M. B.; Dutta A.; Farooq S. Process synthesis and optimization of heat pump assisted distillation for ethylene-ethane separation. Ind. Eng. Chem. Res. 2018, 57, 11747–11756. 10.1021/acs.iecr.8b02496. [DOI] [Google Scholar]
- Nakaiwa M.; Huang K.; Endo A.; Ohmori T.; Akiya T.; Takamatsu T. Internally heat-integrated distillation columns: a review. Chem. Eng. Res. Des. 2003, 81, 162–177. 10.1205/026387603321158320. [DOI] [Google Scholar]
- Suphanit B. Design of internally heat-integrated distillation column (HIDiC): uniform heat transfer area versus uniform heat distribution. Energy 2010, 35, 1505–1514. 10.1016/j.energy.2009.12.008. [DOI] [Google Scholar]
- Suphanit B. Optimal heat distribution in the internally heat-integrated distillation column (HIDiC). Energy 2011, 36, 4171–4181. 10.1016/j.energy.2011.04.026. [DOI] [Google Scholar]
- Li X.; Cui C.; Li H.; Gao X. Process synthesis and simulation-based optimization of ethylbenzene/styrene separation using double-effect heat integration and self-heat recuperation technology: A techno-economic analysis. Sep. Purif. Technol. 2019, 228, 115760. 10.1016/j.seppur.2019.115760. [DOI] [Google Scholar]
- Petlyuk F. B. Thermodynamically optimal method for separating multicomponent mixtures. Int. Chem. Eng. 1965, 5, 555–561. [Google Scholar]
- Kolbe B.; Wenzel S. Novel distillation concepts using one-shell columns. Chem. Eng. Process. 2004, 43, 339–346. 10.1016/s0255-2701(03)00133-8. [DOI] [Google Scholar]
- Lestak F.; Collins C. Advanced distillation saves energy and capital. Chem. Eng. 1997, 104, 72–76. [Google Scholar]
- Chen Z.; Agrawal R. Classification and Comparison of Dividing Walls for Distillation Columns. Processes 2020, 8, 699. 10.3390/pr8060699. [DOI] [Google Scholar]
- Wright R. O.Fractionation apparatus. US Patent 2,471,134 A, 1949.
- Agrawal R. Multicomponent distillation columns with partitions and multiple reboilers and condensers. Ind. Eng. Chem. Res. 2001, 40, 4258–4266. 10.1021/ie000315n. [DOI] [Google Scholar]
- Madenoor Ramapriya G.; Tawarmalani M.; Agrawal R. A systematic method to synthesize all dividing wall columns for n -component separation-Part I. AIChE J. 2018, 64, 649–659. 10.1002/aic.15964. [DOI] [Google Scholar]
- Ramapriya G. M.; Tawarmalani M.; Agrawal R. Thermal coupling links to liquid-only transfer streams: An enumeration method for new FTC dividing wall columns. AIChE J. 2016, 62, 1200–1211. 10.1002/aic.15053. [DOI] [Google Scholar]
- Rangaiah G. P.; Bonilla-Petriciolet A.. Multi-objective optimization in chemical engineering: developments and applications; John Wiley & Sons, 2013. [Google Scholar]
- Luyben W. L.Principles and case studies of simultaneous design; John Wiley & Sons, 2012. [Google Scholar]
- Gilliland E. R.; Reed C. E. Degrees of freedom in multicomponent absorption and rectification columns. Ind. Eng. Chem. 1942, 34, 551–557. 10.1021/ie50389a008. [DOI] [Google Scholar]
- Viswanathan J.; Grossmann I. E. A combined penalty function and outer-approximation method for MINLP optimization. Comput. Chem. Eng. 1990, 14, 769–782. 10.1016/0098-1354(90)87085-4. [DOI] [Google Scholar]
- Adjiman C. S.; Androulakis I. P.; Floudas C. A. Global optimization of MINLP problems in process synthesis and design. Comput. Chem. Eng. 1997, 21, S445–S450. 10.1016/s0098-1354(97)87542-4. [DOI] [Google Scholar]
- Dorigo M.; Di Caro G.. Ant colony optimization: a new meta-heuristic. Proceedings of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406); IEEE, 1999; pp 1470–1477.
- Van Laarhoven P. J. M.; Aarts E. H. L.. Simulated annealing. In Simulated annealing: Theory and applications; Springer, 1987, pp 7–15. [Google Scholar]
- Price K. V.Differential evolution: a fast and simple numerical optimizer. Proceedings of North American fuzzy information processing; IEEE, 1996; pp 524–527.
- Lampinen J.; Zelinka I.. Mixed integer-discrete-continuous optimization by differential evolution. Proceedings of the 5th international conference on soft computing, 1999; pp 71–76.
- Chua L. O.; Itoh M.; Kocarev L.; Eckert K. Chaos synchronization in Chua’s circuit. J. Circ. Syst. Comput. 1993, 03, 93–108. 10.1142/s0218126693000071. [DOI] [Google Scholar]
- Levy D. Chaos theory and strategy: Theory, application, and managerial implications. Strat. Manag. J. 1994, 15, 167–178. 10.1002/smj.4250151011. [DOI] [Google Scholar]
- Murphy P. Chaos theory as a model for managing issues and crises. Publ. Relat. Rev. 1996, 22, 95–113. 10.1016/s0363-8111(96)90001-6. [DOI] [Google Scholar]
- Bing L.-L.; Weisun J. Chaos optimization method and its application. Control Theory & Appl. 1997, 4, 613–615. [Google Scholar]
- Phatak S. C.; Rao S. S. Logistic map: A possible random-number generator. Phys. Rev. E 1995, 51, 3670. 10.1103/physreve.51.3670. [DOI] [PubMed] [Google Scholar]
- Nakagawa M. A chaos associative model with a sinusoidal activation function. Chaos, Solit. Fractals 1999, 10, 1437–1452. 10.1016/s0960-0779(98)00121-0. [DOI] [Google Scholar]
- Hasler M.; Maistrenko Y. L. An introduction to the synchronization of chaotic systems: coupled skew tent maps. IEEE Trans. Circ. Syst. 1997, 44, 856–866. 10.1109/81.633874. [DOI] [Google Scholar]
- Tsubone T.; Saito T. Manifold piecewise constant systems and chaos. Trans. Inst. Electron., Inf. Commun. Eng., Sect. E 1999, 82, 1619–1626. [Google Scholar]
- Nikačević N. M.; Huesman A. E.; Van den Hof P. M.; Stankiewicz A. I. Opportunities and challenges for process control in process intensification. Chem. Eng. Process. 2012, 52, 1–15. [Google Scholar]
- Baldea M. From process integration to process intensification. Comput. Chem. Eng. 2015, 81, 104–114. 10.1016/j.compchemeng.2015.03.011. [DOI] [Google Scholar]