Modified Red Blood Cells as Multimodal Standards for Benchmarking Single-Cell Cytometry and Separation Based on Electrical Physiology

Abstract

Biophysical cellular information at single-cell sensitivity is becoming increasingly important within analytical and separation platforms that associate the cell phenotype with markers of disease, infection, and immunity. Frequency-modulated electrically driven microfluidic measurement and separation systems offer the ability to sensitively identify single cells based on biophysical information, such as their size and shape, as well as their subcellular membrane morphology and cytoplasmic organization. However, there is a lack of reliable and reproducible model particles with well-tuned subcellular electrical phenotypes that can be used as standards to benchmark the electrical physiology of unknown cell types or to benchmark dielectrophoretic separation metrics of novel device strategies. Herein, the application of red blood cells (RBCs) as multimodal standard particles with systematically modulated subcellular electrophysiology and associated fluorescence level is presented. Using glutaraldehyde fixation to vary membrane capacitance and by membrane resealing after electrolyte penetration to vary interior cytoplasmic conductivity and fluorescence in a correlated manner, each modified RBC type can be identified at single-cell sensitivity based on phenomenological impedance metrics and fitted to dielectric models to compute biophysical information. In this manner, single-cell impedance data from unknown RBC types can be mapped versus these model RBC types for facile determination of subcellular biophysical information and their dielectrophoretic separation conditions, without the need for time-consuming algorithms that often require unknown fitting parameters. Such internal standards for biophysical cytometry can advance in-line phenotypic recognition strategies.

The phenotypic heterogeneity displayed by cellular systems¹ has motivated the need for robust platforms for single-cell analysis and separation,² to enable disease diagnostics based on cellular markers³ and to control cellular compositions for transplant applications. While fluorescently stained cell surface markers that provide identifying biochemical information on each cell type are widely adopted for this purpose,⁴ there is an increasing recognition that complementary biophysical information is essential to identify subpopulations associated with key functions.⁵ Specifically, methods for reliable multiparametric biophysical identification of cellular subpopulations, without the need to label or lyse them, can enable longitudinal temporal studies that are often not possible using fluorescently stained surface markers. Microfluidic single-cell electrical measurements by impedance-based flow cytometry^6,7 and electrically driven separations by dielectrophoresis⁸ (DEP) are able to sensitively quantify the cellular biophysical information at high sample throughput (300–500 cells/s) and utilize this through frequency-modulation to distinguish cellular subpopulations. While impedance magnitude at low frequencies (<0.5 MHz) provides highly sensitive size information on each measured cell, the polarization of cell membrane at successively higher frequencies (1–10 MHz) provides information on membrane capacitance, and polarization of the interior at even higher frequencies (>10 MHz) can provide valuable information on cytoplasmic contents,⁹ including the nucleus size.¹⁰ In this manner, impedance cytometry has been used to quantify subpopulations from heterogeneous samples, including infected red blood cells,¹¹ activation of various leukocyte subtypes,^12,13 tumorigenicity of pancreatic cancer cell types,¹⁴ drug sensitivity of cancer cells,¹⁵ bacterial germination from spores,¹⁶ apoptotic bodies generated by drug-sensitive cancer cells,¹⁷ and to monitor the cell density of spheroids.¹⁸ Also, dielectrophoresis has been applied to isolate cells of a particular phenotype from heterogeneous samples,¹⁹ including circulating tumor cells,^20,21 stem cell progenitors,²² cells based on mitochondrial phenotype,²³ bacterial strain discrimination,^24,25 and isolate secreted exosomes.^26,27 However, while standard particles with known signal characteristics are used in flow cytometry and fluorescently activated cell sorting for benchmarking each measured cell and to trigger sorting, similar tools are lacking for dielectrophoresis and impedance cytometry.

Currently, in impedance cytometry, polystyrene beads of well-controlled sizes are used to benchmark the impedance magnitude at low frequencies (<0.5 MHz) for enabling accurate determination of cell size.²⁸ However, such plastic beads bear little resemblance to living cells that possess a high capacitance plasma membrane of varying composition and morphology, and a conductive interior that reflects the cytoplasmic organization. Hence, polystyrene beads that are opaque to the electric field at higher frequencies cannot be used for benchmarking of cell membrane capacitance and cytoplasmic conductivity. On the other hand, yeast cells are often used to validate novel cytometry²⁹ and separation platforms,³⁰ but they are not well-suited to function as standard particles due to their wide range of size and shape distributions. Standardized coflowing particles of well-tuned subcellular phenotypes can enable benchmarking of electrical physiology (henceforth, electrophysiology) of unknown cell types during impedance cytometry and provide systems with a well-defined DEP frequency response for facile assessment of separation metrics (collection efficiency and separation purity) within novel microfluidic device designs. To address this vision, we explore the modification of red blood cells (RBCs) to create standard particles with modulated subcellular properties (i.e., membrane capacitance and interior cytoplasmic conductivity), that can also be identified by their fluorescence level.

RBCs or erythrocytes are the predominant cell type in blood,³¹ with the function of carrying oxygen to tissues and carbon dioxide away from tissues. Their functional outcomes are strongly linked to their biophysical properties, such as the relationship of cellular dielectric properties to oxygen carrying capacity,³² glucose homeostasis,³³ and age^34,35 or that of their cellular biomechanical properties to oxygen transport,³⁶ infection³⁷ and disease.³⁸ Hence, their modification to create standardized coflowing particles during impedance cytometry or dielectrophoretic separation can lead to facile stratification of subcellular electrophysiology of disease-modified RBC phenotypes.

The availability of coflowing standard particles for impedance cytometry and dielectrophoresis can enable accurate comparison of data sets across sample types, device platforms and machine learning assisted phenotypic recognition models, leading to a more holistic workflow for biophysical phenotyping.³⁹ In the field of biomechanical cytometry, for instance, wide divergences in the measured cell stiffness on identical cells by different techniques⁴⁰ led to an interest in reference particles with well-characterized mechanical properties to calibrate the elastic modulus of cells across cytometry platforms.⁴¹ Analogously, we explore methods to modulate the RBC membrane capacitance by altering glutaraldehyde fixation to create fixed RBCs and to modulate cytoplasmic conductivity by penetrating RBCs with buffers of varying conductivity and fluorescence⁴² prior to membrane resealing to create ghost RBCs. While prior work has reported on creating fixed⁴³ and ghost RBCs,⁴⁴ our innovation is the systematic modulation of the subcellular electrical physiology, as validated by impedance metrics from single-cell cytometry, and the generation of multimodal standard particles for coupling fluorescence-based identification to cell distinction based on cytoplasmic conductivity. To enable their application as standard coflowing particles in impedance cytometry and dielectrophoretic separation devices, we illustrate how single-cell impedance data from unknown cell types can be compared to those from a progression of modified RBC types with known subcellular physiology. As a result, the DEP crossover frequency and relative dielectric property differences for unknown cell types can be determined, without the need for time-consuming algorithms that often require unknown fitting parameters and off-line computation. In this manner, we seek to advance the vision of internal standards for biophysical cytometry and for in-line phenotypic recognition.⁴⁵

Methods

RBC Sample Preparation

Human red blood cells (RBCs) from multiple batches of blood type A+ (Valley Biomedical, Winchester, VA) were suspended in RPMI 1640 HEPES (Sigma-Aldrich, St. Louis, MO) after supplementing with 0.5% Albumax II Lipid-Rich BSA (Sigma) and 50 mg/L hypoxanthine (Thermo Fisher Scientific) for storage and dilution, as needed (1.13 × 10⁸ cells/mL). The control sample of unmodified healthy RBCs was prepared by washing diluted RBCs in 1× PBS, three times. The fixed RBC samples were prepared by washing diluted unmodified RBCs in 1× PBS, three times, and resuspending the packed cells in 1 mL of 1× PBS, mixed with 0.01%, 0.1%, or 1% glutaraldehyde (Sigma), followed by incubation at room temperature for an hour. Samples were then centrifuged at 400 g for 5 min, and the cell pellet was resuspended in 1 mL of 1× PBS for measurement. For preparing ghost RBCs, the diluted unmodified RBCs were washed three times in 1× PBS. Then, one volume of packed RBC was incubated with 4 volumes of hypotonic buffer, composed of 0.1× PBS in the fridge at 4 °C for 30 min to obtain RBC ghosts. The ghost cells were centrifuged at 1400 g for 10 min and washed three times with 0.1× PBS, until the supernatant was colorless, with a light pink cell pellet.⁴⁶ The ghost RBCs were then resuspended in different buffers of differing conductivities (1.57, 1.91, and 2.12 S/m), followed by room temperature incubation for 4 h, so that the cell membrane can reseal after the buffer penetration. The samples were centrifuged at 1400 g for 10 min and the cell pellet was resuspended in the respective buffers. After resealing, the ghost RBCs (i.e., filled with respective buffer) were fixed with 0.1% glutaraldehyde, by incubation in their respective buffer at room temperature for 1 h. After centrifuging at 1400 g for 10 min, the cell pellet was resuspended in 1× PBS (1.57 S/m). For fixed ghost samples, the resealed ghost RBCs were fixed with glutaraldehyde, by incubation at room temperature for an hour. Then, the cell pellet after centrifuging at 1400 g for 10 min was resuspended in 1× PBS (1.57 S/m) for analysis.

Impedance Cytometry

For impedance cytometry, cells were measured in 1x PBS buffer after dilution to ∼2 × 10⁵ cells/mL, with coflowing 10 μm sized polystyrene beads (Sigma) at ∼1.2 × 10⁵ beads/mL. A syringe pump was used to introduce the respective sample into a microfluidic chip (fabrication per prior report¹⁴) with a detection region 30 μm (width) × 30 μm (height) and the measurement was carried out using an impedance analyzer (Amphasys AG, Switzerland), per Figure 1. Four simultaneous frequencies were used: 0.5, 2, and 30 MHz, and a probe frequency that is swept in the 2 to 20 MHz range. Acquisition settings were optimized for signal-to-noise based on levels of signal modulation, amplification, and demodulation of the trigger voltage level. Processed signal data were stored as impedance magnitude and phase, exported as CSV files, and processed with Python.

Figure 1.

Schematic of (a) RBC modification to prepare fixed, ghost, and fixed ghost RBCs and (b) their impedance detection. RBCs in 1× PBS flow through a microchannel with two sets of facing top-bottom detection electrodes. AC signals are applied at simultaneously differing frequencies to the top electrodes and the respective differential current at the bottom electrodes is used to determine single-cell impedance signals. (c) Depending on frequency of the applied AC signal, cellular biophysical properties corresponding to different cell components interacting with the AC field can be measured.

Impedance Data Processing and Statistical Analysis

The impedance phase and magnitude for RBCs were normalized based on division to those obtained for polystyrene beads to account for any temporal variations during the measurement and to enable quantitative comparison between measurements. Due to normalization, impedance phase is reported in arbitrary units (with respect to impedance phase of beads indexed at zero). The RBC populations were gated from reference beads in normalized impedance data at 30 MHz and the normalized impedance for gated RBCs was analyzed at each probe frequency (0.5–30 MHz; SI, section B). All statistical analyses were performed using a custom script in Python. Significance level was defined as p < 0.05. Comparisons between any two groups were done using a student’s two-tailed t test, while comparisons between multiple groups were performed using a one-way ANOVA with a Tukey’s multiple comparisons test. All results are representative of at least three repetitions, with error bars indicating standard deviation between sample triplicates.

Flow Cytometry

Resealing of ghost RBCs was tested with FITC–dextran (Fluorescein isothiocyanate–dextran, Sigma) with an average molecular weight of 40000. Different FITC–dextran concentrations (0.25, 0.5, and 1 mg/mL) were added to the ghost during resealing. The samples were then washed twice in 1× PBS. Following imaging, flow cytometry was performed using a CytoFLEX (Beckman Coulter) and analyzed using CytExpert (Beckman Coulter).

DEP Spectral Measurement

RBCs samples (normal and fixed [1%] RBCs) were centrifuged and resuspended in 8.8% sucrose water, with media conductivity of 400 μS/cm for DEP spectral measurements performed on the 3DEP analyzer (DepTech, Uckfield, U.K.) with a recording interval set to 30 s at 10 V_pp, with data collected over 20 points between 100 kHz and 30 MHz. In this 3DEP reader, the electric field is applied to gold-plated conducting electrode stripes inside the wall of each well, with the DEP response measured at 20 different frequencies applied individually within each well. The relative DEP force at each frequency is obtained by analyzing spatiotemporal variations in light intensity from particle scattering using particular bands in each of the 20 wells, after normalization to the background at zero field (time = 0). The maximum nDEP (negative DEP) force level for each cell line was used as the basis to normalize the measured DEP level for each cell type.²³

Results and Discussion

Modulating Membrane Capacitance of RBCs

Glutaraldehyde is an agent that cross-links proteins in the cell membrane and cytoplasm, which is often utilized to simulate the pathological state of RBCs.⁴⁷ Herein, we investigate the effect of the reduced ion mobility due to this treatment, on impedance metrics of single RBCs measured over large event numbers (∼10000 per cell type). Presence of the lipid cell membrane typically causes biological cells to behave as insulators at low frequencies (<1 MHz), therefore, allowing for an estimation of cell volume. The electrical diameter is estimated based on the cube root of impedance magnitude at a frequency level of 0.5 MHz, which is just below that required for cell membrane-induced field dispersion: 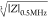. At increasing frequencies, the cells become increasingly conductive due to capacitive coupling across the membrane, until the stabilization of the electric field dispersion at a cutoff frequency, beyond which the field short-circuits the cell membrane (>10 MHz). Focusing our data analysis on this frequency range, wherein the membrane capacitance is responsible for field dispersion (1–10 MHz), we compute the so-called electrical opacity as the impedance magnitude at each probe frequency versus that at 0.5 MHz: |Z|_{probe_freq}/|Z|_0.5MHz. Since size-controlled insulating polystyrene beads continue to screen the electric field, even at successively higher frequencies, their electrical opacity remains constant at unity. In this manner, the electrical opacity can be used as a size-normalized impedance metric that varies inversely to the membrane capacitance for comparison versus beads of invariant opacity. Based on Figure 2a, while the respective RBC phenotypes cannot be distinguished solely based on their electrical diameter, due to the wide distributions for each cell type, their respective opacity distributions show systematic differences, especially at frequency levels of 5 MHz and beyond (Figure 2b; vs insulating beads normalized at unity opacity) The histograms (Figure 2c) and bar plots (Figure 2d) for opacity at 5 MHz indicate gradually increasing opacities (i.e., lower membrane capacitance) with fixation level, with significant differences (Figure 2d). It is noteworthy that based on the impedance metrics at higher frequencies (>10 MHz) that correspond to properties of the cell interior, there are no significant differences for the respective cell types (SI, Figure S1). This confirms the ability to generate model particles with modulated membrane capacitance, but with minimal differences within the cell interior. These modified RBCs are reliable model particles for quantifying functionality of novel DEP designs. Per work in SI, Figure S2 and video, the separation metrics of a novel design with a set of sequential field non-uniformities was validated using normal and fixed RBCs.¹⁹ Fixed RBCs of lower membrane capacitance exhibit higher crossover frequencies versus unmodified RBCs. Hence, by utilizing frequency ranges wherein unmodified RBCs exhibit pDEP (positive DEP or translation toward the high field) and fixed RBCs exhibit nDEP (negative DEP or translation away from the high field), the DEP separation was validated.

Figure 2.

Impedance data for unmodified RBCs (control) and for fixed RBCs, with different levels of glutaraldehyde fixation (0.01%, 0.1%, and 1%) represented as (a) a single-cell event scatter plot of electrical opacity (|Z|_5MHz/|Z|_0.5MHz) vs electrical diameter (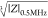); (b) Frequency response of the electrical opacity in the 2–8 MHz range (points connected by lines to guide the reader); (c) Histogram distributions of electrical opacity (|Z|_5MHz/|Z|_0.5MHz) (based on 10000 events for each cell type); (d) Bar plot of electrical opacity (|Z|_5MHz/|Z|_0.5MHz) to indicate significance level of the differences (**p < 0.01 level; ***p < 0.001 level).

Modulating Interior Conductivity and Fluorescence

Considering ghost RBCs prepared by membrane resealing in media of differing conductivity, we expect no significant differences in membrane capacitance for well-sealed membranes but anticipate systematic differences in interior conductivity. The varying RC time constant (τ_RC) arising from an increase in interior conductivity is expected to upshift the frequency dispersion in impedance phase (ϕ(Z)), while the impedance phase level would be systematically altered to be shifted further away from insulating beads that are normalized to ϕ(Z) = 0. In fact, this is apparent in Figure 3a, with the successively higher interior conductivity of each type of ghost RBC causing a phase dispersion that is shifted to progressively higher frequencies, while the impedance phase levels are also gradually increased to become shifted further away from that of the insulating beads. The single-event scatter plot of ϕ(Z) versus electrical diameter (Figure 3c) shows the successive alteration of ϕ(Z) at high frequency for each ghost RBC type. The averaged ϕ(Z) level for each ghost RBC type at 30 MHz, which reflects property alterations at the interior of each cell type, shows statistical significance of their distinction based on this impedance phase metric (Figure 3b). To assess effectiveness of the resealing protocol, the ghost RBCs were resealed in buffers of different conductivity that also include different FITC-dextran levels (0.25, 0.5, and 1 mg/mL), as confirmed by fluorescence images (SI, Figure S3). The flow cytometry results (Figure 3d) confirm a similar level of FITC in the ghost RBCs, regardless of the buffer conductivity used to reseal. The small differences between the fluorescence level of the ghost RBC types is attributed to alterations in the kinetics of resealing for the ghost RBCs in 1.57 S/m versus in 2.12 S/m buffers. However, the mean fluorescence levels within each ghost RBC type can be linearly modulated based on the FITC level in the buffer during resealing. Hence, by adding differing levels of FITC into the respective penetrating conductive PBS media, each type of ghost RBC modification can be identified based on a fluorescence level that is correlated to the interior conductivity of the ghost RBC type. For instance, ghost RBCs penetrated with media of 1.57 S/m conductivity can be differentiated from those penetrated with media of 2.12 S/m conductivity, simply by using a differing FITC level in the penetrating media (e.g., 0.5 mg/mL for the former and 1 mg/mL for the latter). This ability to independently alter the fluorescence and interior conductivity levels for each ghost RBC type enables them to be used in tandem for distinctions based on their fluorescence or high frequency impedance phase (>10 MHz) or both. The fluorescence level of the FITC-penetrated RBCs is in the range of intensities from standard beads used in flow cytometry (SI, Figure S3c). Furthermore, these FITC-penetrated ghost RBCs with a well-defined DEP frequency response that arises due to their interior conductivity can be utilized together with fluorescence imaging or cytometry for facile determination of DEP separation metrics within heterogeneous samples composed of different ghost RBC types. Such model cells could be utilized for optimization of microfluidic geometries and the resulting separation force fields (voltages, frequency, media conductivity, flow rate, etc.). In summary, ghost RBC modification by membrane resealing to modulate cytoplasm conductivity with minimal alteration in electrical diameter and membrane capacitance can be used to independently modulate their fluorescence level, thereby enabling multimodal identification and optimization of DEP separation strategies to aid in microfluidic device design.

Figure 3.

Impedance data of ghost RBCs prepared by membrane resealing in media of differing conductivity (1.57, 1.91, and 2.12 S/m) and of differing levels of FITC–dextran (0.25, 0.5, and 1 mg/mL). (a) Frequency dispersion of the normalized impedance phase (ϕZ; points connected by lines to guide the reader); (b) Mean phase at 30 MHz (ϕ_30MHz) indicates the significant differences (***p < 0.001) between the cell types; (c) Scatter plot of normalized impedance phase (30 MHz) vs electrical diameter; (d) Fluorescence of ghost RBCs after membrane resealing in buffers with differing conductivity (S/m) and FITC levels.

Modulation of Membrane and Cytoplasmic Properties

Finally, each ghost RBC type is fixed with differing levels of glutaraldehyde, so that the membrane capacitance can be varied for cells of differing interior conductivity. This is apparent from differing opacity levels (inverse of the membrane capacitance) for ghost RBCs that are first penetrated with 1.57 S/m PBS media and then fixed by differing levels of glutaraldehyde (Figure 4a), as per the significance plot (Figure 4b). Difference between fixed ghost (0.1%) and fixed RBC (0.1%) is apparent within the high frequency impedance phase response (>10 MHz in Figure 4c) that shows statistical significance (Figure 4d).

Figure 4.

RBCs with modulated membrane capacitance (a, b) and with modulated interior conductivity (c, d) measured based on frequency region for the impedance analysis of ghost RBCs after membrane resealing in buffer of media conductivity of 1.57 S/m and after fixing with different levels of glutaraldehyde (0.1%, 0.3%, and 0.5%). (a) Systematically differing frequency dispersions in opacity, with (b) statistically significant differences in |Z|_5MHz/|Z|_0.5MHz. (c) The interior conductivity of these fixed ghost RBCs vs similarly fixed RBCs without electrolyte penetration shows differences in frequency dispersion of normalized impedance phase at 30 MHz that show statistically significant differences (d). The statistical significance is indicated by *p < 0.05 level; **p < 0.01 level; ***p < 0.001 level (points on the frequency dispersion connected by lines to guide the reader).

Benchmarking Unknown Phenotypes versus Modified RBCs of Known Dielectric Properties

The impedance spectra from each RBC type are fit to standard single-shell dielectric models⁴⁸ (refer to SI, section B and Figure S4 for further details) for the computation of their dielectric parameters (Table 1) of cell membrane capacitance and cytoplasmic conductivity, based on subcellular geometric parameters for RBCs obtained from prior work (fixed membrane thickness 5 nm and fixed membrane conductivity ≤10^–8 S/m).¹¹ Cell radius estimation from the single shell model is ∼2.6–2.7 μm for all modified RBCs.

Table 1. Dielectric Parameters for Each RBC-Type Based on Fitting of Their Impedance Spectra to a Single-Shell Model^a.

sample	membrane capacitance (Cmembrane; mF/m2)	cytoplasm conductivity (σcytoplasm; S/m)
control RBCs	8.85 ± 0.23	0.5 ± 0.01
fixed RBCs [0.01%]	5.66 ± 0.36	0.5 ± 0.03
fixed RBCs [0.1%]	4.95 ± 0.14	0.5 ± 0.01
fixed RBCs [1%]	4.07 ± 0.25	0.5 ± 0.03
unfixed ghost (1.57 S/m)	8.85 ± 0.35	1.2 ± 0.03
fixed ghost [0.1%] (1.91 S/m)	7.08 ± 0.22	1.4 ± 0.04
fixed ghost [0.1%] (2.12 S/m)	7.08 ± 0.35	1.6 ± 0.05
fixed ghost [0.1%] (1.57 S/m)	7.08 ± 0.2	1.2 ± 0.06
fixed ghost [0.3%] (1.57 S/m)	6.70 ± 0.18	1.2 ± 0.02
fixed ghost [0.5%] (1.57 S/m)	6.20 ± 0.25	1.2 ± 0.04

^aThe square bracket indicates the glutaraldehyde level for fixation and the rounded bracket indicates conductivity of the penetrating buffer prior to resealing.

As expected, in comparison to control RBCs that are unmodified, the RBCs that are fixed to successively higher levels show successively lower membrane capacitance and no alteration to their cytoplasmic conductivity. Similarly, ghost RBCs penetrated with successively more conductive media, prior to resealing, show successively higher interior conductivity in comparison to control RBCs that are unmodified. It is noteworthy that the interior conductivity of ghost RBCs gradually increases to become close to that of the penetrating media, with 1.57 S/m penetrating media reaching an interior conductivity of 1.2 S/m, 1.9 S/m penetrating media reaching an interior conductivity of 1.4 S/m, and 2.12 S/m penetrating media reaching an interior conductivity of 1.6 S/m. The efficacy of the resealing process is confirmed based on their high membrane capacitance and low membrane conductivity values (see Table S1, Supporting Information). The fixed ghost RBCs show alterations only in membrane capacitance, while maintaining their cytoplasmic conductivity level. Hence, not only are the phenomenological impedance metrics of each RBC type altered in characteristic manners, but their fitted inherent biophysical properties also span over a broad range. This relationship between the phenomenological and biophysical properties for each RBC type is shown in Figure 5, wherein the position of each RBC type is plotted with respect to solid lines that indicate varying membrane capacitance levels and the dashed lines that indicate varying cytoplasmic conductivity levels. Based on this, for an unknown RBC type (indicated as X in green font in Figure 5a), the impedance opacity at 5 MHz (=0.86) and the normalized impedance phase at 30 MHz (=0.2) that are obtained from the impedance spectra can be located on the map, so that the solid/dashed lines can be followed for determining the cytoplasm conductivity (∼0.5 S/m) and membrane capacitance (∼4.1 mF/m²) values for the unknown RBC type (Figure 5b), without the need to fit its full impedance spectra. In fact, spectra from this unknown RBC type (control RBC fixed with 1% glutaraledhyde) fit by the shell model to a comparable cytoplasm conductivity (= 0.5 S/m) and membrane capacitance (=4.07 mF/m²), indicating high accuracy of such a mapping approach.

Figure 5.

Translating from phenomenological impedance metrics, such as the opacity vs phase contrast plot (a) to cellular biophysical properties of cytoplasm conductivity vs membrane capacitance (b), as obtained from shell-model fits is accomplished for unknown RBCs without the need to do a shell model fit. Instead, the impedance metrics for the unknown RBCs are mapped on the respective plot for the known modified RBCs, so that their biophysical properties can be determined by projection onto the colored solid lines that show contours of differing membrane capacitance values and colored dashed lines that show contours of differing cytoplasm conductivity, with each color indicating specific levels.

Fitting of impedance spectra to dielectric shell models usually requires certain fixed parameters (geometric properties like cell size and membrane thickness, for instance) and other “fitting” parameters (for instance: interior permittivity or membrane conductance) to go from phenomenological impedance metrics to biophysical properties. While these are known for model cells, like the modified RBC types in this work, the same is not the case for unknown RBC types. Hence, utilization of this approach (Figure 5) to go from the phenomenological parameters to biophysical properties for unknown cell types can be conducted by simply comparing their phenomenological metrics versus those of the model RBC types, with no need for arbitrary geometric properties or “fitting” parameters for these unknown cell types. The associated off-line computation time is also not needed, thereby allowing for in-line biophysical recognition. Furthermore, based on membrane capacitance values (C_membrane) determined from the map of Figure 5, the spread in crossover frequency (f_crossover) at a particular media conductivity (σ_media), for individual cells of a given hydrodynamic radius (r) can be calculated.^49,50

1

For instance, the map suggests that the C_membrane for the unknown sample (1% fixed control RBC) is about 4.1 mF/m², while that for an unmodified sample of control RBCs is about 9 mF/m². The computed f_crossover values of 813293 and 370500 Hz, respectively, agrees well for the respective RBC types with their validated levels determined using the 3DEP reader (SI, Figure S5).

Conclusions and Outlook

To address the need in impedance-based flow cytometry and in dielectrophoresis, for standard particles with well-modulated subcellular electrical physiology to benchmark unknown samples and to normalize for temporal device-level deviations, we present a class of modified RBC types. Glutaraldehyde fixation at varying levels is able to generate a class of fixed RBCs with well-modulated membrane capacitance, as measured by electrical opacity, but with no alterations to their interior conductivity. RBC membrane resealing after electrolyte penetration from the media to vary cytoplasmic conductivity inside each cell is able to generate ghost RBCs with well-modulated interior conductivity, as measured by normalized impedance phase, but with minimal alterations in membrane capacitance. Along similar lines, by penetrating the RBCs with differing FITC levels in the electrolyte prior to resealing, ghost RBCs with well-modulated fluorescence can be generated. Interestingly, the fluorescence and interior conductivity levels can be independently altered for each ghost RBC type so that the respective values can be correlated to identify translation of particular ghost RBC types in microfluidic devices. Such model ghost RBCs of differing interior conductivity levels that lead to well-defined DEP frequency responses can be utilized together with fluorescence imaging or cytometry as coflowing cells within heterogeneous samples for facile determination of DEP separation metrics. Such model cells could be utilized for optimization of microfluidic geometries and the resulting separation force fields (voltages, frequency, media conductivity, flow rate, etc.). To illustrate the application of these model RBC types for the purpose of benchmarking unknown RBC types, we present a map that allows facile translation from phenomenological impedance metrics to inherent biophysical properties for each RBC type. In this manner, single-cell impedance data from unknown RBC types can be mapped versus these model RBC types for the facile determination of subcellular biophysical information and the spread of their dielectrophoretic crossover frequency, without the need for time-consuming algorithms that often require unknown fitting parameters. RBCs are the simplest model cell, and future work will investigate the extension of the approach to other cell types with a more complex internal structure. Such standards for biophysical cytometry can enable inline phenotypic recognition strategies.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.1c04739.

• A: Supplementary Results include: impedance metrics of modified RBCs (Figure S1), application of modified RBCs to benchmark DEP separation devices (Figure S2a–e), fluorescence images and intensity comparisons of FITC penetrated ghost RBCs (Figure S3), impedance spectrum (real and imaginary components) for each modified RBC type (Figure S4), and validation of determined membrane capacitance from impedance cytometry for each modified RBC type by correlation to DEP crossover frequency (Figure S5). B: Supplementary Methods include the following: gating of each RBC population (Figure S6) and details of the single shell model (Table S1 and Figure S7) (PDF)

• Video of RBC separation (AVI)

Author Contributions

The manuscript was written through contributions of all authors and all authors approved the final version.

Funding from U.S. AFOSR Contracts FA2386-21-1-4070 & FA2386-18-1-4100, NCI Cancer Center Support Grant P30 CA44579, and the University of Virginia’s Cancer Centre are acknowledged. We also thank graduate student Audrey Brown, in the lab of Prof. Jennifer Güler, for advice on handling of the RBC samples.

The authors declare no competing financial interest.