Forecasting ATM Cash Demand Before and During the COVID-19 Pandemic Using an Extensive Evaluation of Statistical and Machine Learning Models

Abstract

The overarching goal of this paper is to accurately forecast ATM cash demand for periods both before and during the COVID-19 pandemic. To achieve this, first, ATMs are categorized based on accessibility and surrounding environmental factors that significantly affect the cash withdrawal pattern. Then, several statistical and machine learning models under different algorithms and strategies are employed. In aiming to provide the feature matrix for machine learning models, some new influential variables are added to the literature. Finally, a modified fitness measure is proposed for the first time to correctly choose the most promising model by considering both the prediction errors and accuracy of direction’s change simultaneously. The results obtained by a comprehensive analysis—a statistical analysis together with grid search and k-fold cross-validation techniques—reveal that (i) category-wise prediction enhances forecasting quality; (ii) before COVID-19 and in times when there are only minor disturbances in withdrawal patterns, forecasting quality is higher, and in general, the machine learning models can more appropriately forecast ATM’s cash demand; (iii) despite studies in the literature, sophisticated models will not always outperform simpler models. It is found that during COVID-19 and in times when there is a sudden shock in demand and massive volatility in withdrawal patterns, the statistical models of the autoregressive integrated moving average (ARIMA) and seasonal ARIMA (SARIMA) can mainly provide better forecasting likely due to high performance of such models for short-term prediction, while minimizing overfitting.

Supplementary Information

The online version contains supplementary material available at 10.1007/s42979-021-01000-0.

Introduction

Automated Teller Machines (ATMs) provide convenience to the customers and support various financial services round the clock without the need for a human clerk. Because of this, over the past years, the number of ATMs in the world has increased, reaching over 3 million machines [7]. Financial institutions (e.g., banks, credit unions, and stock brokerages) might have thousands of ATMs and, in turn, millions of transactions over the course of a year. In the case of Iran, for example, the number of ATMs and debit cards are about 60 thousand and 23 million, respectively [14]. Aiming to maximize income from transactions and satisfy customer demand for cash, some banks might store as much as 40% more banknotes in ATMs than they actually need [38]. However, loading excess cash in ATMs, rather than only loading in what the demand roughly is, will increase operational and opportunity costs [9, 20, 21]. Conversely, if there is not enough cash loaded into ATMs, there will be “out of cash” transactions, resulting in the bank’s reputation being damaged, as well as lowered income and customer satisfaction. Thus, a more accurate prediction of ATM currency demand can help financial institutions avoid being tempted to fill ATMs with too many notes and earn more profit by mobilizing idle cash and generating additional revenue through investments—specifically in countries with high-interest rates and overnight interest rates.

Much effort has been devoted to the context of predicting ATM cash demand by considering different features (e.g., historical patterns, geographical location, and seasonal factors) as well as predictive models (e.g., parametric or non-parametric). However, choosing the most efficient model to appropriately forecast an ATM’s cash demand is one of the most important activities. According to an extensive study in time series prediction conducted by Parmezan et al. [33], no unique model can always be considered the best, because each model has its own benefits and limitations. More specifically, different problems have different components and attributes that need to be tackled separately. One primary assumption of models in the literature is that the amount of cash demand and withdrawal patterns are not overly volatile (though some studies have investigated chaos time series and uncertainty in demand). However, forecasting demand during a disaster and unprecedented challenges (e.g., earthquake, hurricane, and pandemic) substantially differs from the norm. The ongoing coronavirus (COVID-19) pandemic and the measures (e.g., total or partial lockdown) taken to prevent its outbreak have sharply decreased cash demand and significantly changed cash withdrawal patterns. In this context—a sudden shock in demand and massive volatility in the withdrawal pattern—selecting the most efficient model with appropriate diagnostic performance is of paramount importance as it relates to accurately predicting ATM cash demand.

Motivated by a real-world case in a private bank, this paper precisely addresses this gap in the literature by proposing an extensive evaluation that can forecast ATM cash demand before and during the COVID-19 outbreak. To accomplish this, first, we collected real data from three different categories of ATMs, based on their accessibility and environmental factors that substantially affect both the daily cash demand and the withdrawal pattern. Next, several predictive models (i.e., parametric and non-parametric) are applied to the collected data and compared systematically. Parametric models include a moving average (MA), simple exponential smoothing (SES), Holt’s exponential smoothing (HES), autoregressive integrated moving average (ARIMA), and seasonal autoregressive integrated moving average (SARIMA), while non-parametric models include an artificial neural network (ANN, also known as a multi-layered perceptron or MLP), support vector machines (SVM), random forest (RF), and k-nearest neighbors (KNN). Two algorithms are used to generate the feature matrix of non-parametric models. In the first algorithm, a named data-sequence—the cash withdrawal of the preceding days (i.e., prior 7 days)—is used as the input variables to forecast any new observation's cash withdrawal data. However, the second algorithm, named regular-features, utilizes features such as day-of-the-week, month, season, holidays, and even some new and influential time-related independent variables as the input variables to predict cash withdrawal for further observations. To recursively include each new observation in the learning process, two strategies (namely approximate and updated) are employed [33]. It should be mentioned that the improvement of the performance of these models is not possible without finding the optimal combination of hyperparameters. That being said, the main hyperparameters of all models are selected and tuned through an exhaustive grid search algorithm. The evaluation metric is set to be the Fitness measure proposed for the first time in this study. The presented metric simultaneously considers the difference between the predicted and the actual values, as well as the accuracy of direction’s changes—particularly when the pattern abruptly changes. Finally, all tuned models are trained and tested to best forecast the cash withdrawal for all three categories of ATMs for periods both before and during the COVID-19 pandemic to select the most promising model through a comprehensible analysis.

The rest of this paper can be summarized as follows. In Section “Literature Review”, previous relevant studies are reviewed. Section Methodology introduces the methodology and research process, followed by the results and discussion in Section “Results and Discussion”. Finally, Section “Conclusion” reports the conclusion and possible directions for future work.

Literature Review

Different approaches have been researched in forecasting ATM cash demand; among them, the most commonly used methods are time series modeling and machine learning algorithms [21]. In the following section, we review the literature on modeling and analyzing ATM cash withdrawal predictions.

Simutis et al. [38] derived daily predictions using 3 years of data from a bank in Lithuania. They employed the Levenberg–Marquard algorithm for training neural networks (NNs) and then applied Artificial Neural Networks (ANN) to estimate the daily and weekly ATM cash demand. They used MAPE (mean absolute percentage error) as a performance criterion and obtained prediction errors for simulated and real-case data equal to 5–10% and 25–30%, respectively. Simutis et al. [37] employed both ANN and support vector regression (SVR) on a 2-year dataset. They boosted the prediction quality by modeling days of the month, labeling each day from 1 to 31.

The ATM demand forecasting problem became more popular after the “Forecasting Competition for Artificial Neural Networks and Computational Intelligence” (NN5 Competition) in [17]. The competition had some rules and assumptions, such as using the same model for all ATMs; using the same performance measure of symmetric MAPE (SMAPE); 2-year time frame data of 111 empirical ATM daily cash withdrawal series in England; and a demand prediction for the next 56 days. Andrawis et al. [4] were ranked first among the computational intelligence models in the competition. Their approach consisted of two essential components, including a combination of forecasts from different models (i.e., ANN, linear models, and regression) and seasonality modeling, which achieved 18.95% of SMAPE. Ramirez and Acuna [35] obtained the second place in the NN5 competition using an MLP neural networks model with a high degree of accuracy—over 85% for long-term predictions. Some other works for NN5 Competition data were presented by Coyle et al. [16] and Wichard [46]. The former utilized self-organizing fuzzy neural networks and obtained 21.5% SMAPE, while the latter predicted time series with recurring seasonal periods and developed a model based on a combination of forecasting methods via a simple average of forecasts, achieving 22.2% SMAPE. Teddy and NG [40] incorporated local learning to model the complex dynamics of heteroscedastic time series effectively. Later, using the same dataset, Taieb et al. [39] obtained the best results with a multi-input, multi-output forecasting strategy that selected autocorrelation selection criteria using input variable selection, deseasonalization, and average weight combination. The end result was an SMAPE accounting for 18.81%. Venkatesh et al. [43] yielded an average SMAPE of 18.44% via clustering ATMs and employing general regression NNs (GRNNs).

Forecasting the amount of money that must be placed in ATMs was also conducted on other ATM data. For instance, Broda et al. [12] presented a model based on time series and regression using the 3-year data from a bank in Serbia. The modeling approaches were ARIMA and exponential smoothing. Gurgul and Suder [24] modeled daily withdrawals from selected ATMs of the “Euronet” Network using switch ARIMA. Moreover, a hybrid of NN with a genetic algorithm created to predict cash withdrawal was proposed by Bhandari and Gill [11]. Recently, Ekinci et al. [21] investigated optimal ATM replenishment policies for a bank in Turkey and introduced linear programming to minimize both the holding cost and customer dissatisfaction.

Some researchers studied the uncertainty and chaos in an ATM’s daily cash demand. For instance, Darwish [18], Zandevakili, and Javanmard [47] incorporated fuzzy logic in models to deal with individual features of uncertainty and cover noise data by employing an Interval Type-2 Fuzzy NN (IT2FNN) method. Additionally, Arora and Saini [6] applied the Fuzzy ARTMAP Network to approximate the ATM currency demand using selected parameters for the simulated data, and Ekinci et al. [21] used robust optimization to forecast the uncertain demand using prediction intervals. Venkatesh et al. [43] stated that chaos was present in the NN5 Competition dataset; therefore, to appropriately estimate the cash demand, they used the TISEAN tool to calculate the optimal lag and embedding dimension of each series. In a more recent example, Vangala and Vadlamani [42] modeled chaos in the ATM cash withdrawal time series and predicted the money demand using deep learning methods.

In the literature, many studies examined time-related independent variables to capture the seasonality in the data. However, some significant features, such as the number of consecutive holidays ahead, have not been included in the previous studies. Besides, only a few papers considered both time- and location-related variables (e.g., [20, 21]), though the location of ATMs can meaningfully affect the amount of daily cash withdrawn from these ATMs. For instance, Ekinci et al. [20] included a location feature as an independent variable of the model and proposed grouping ATMs into nearby-location clusters. However, using a more meticulous outlook, the nearby-location and/or the same geographical location of ATMs do not necessarily indicate a similar withdrawal pattern, since the points of interest in the ATM’s vicinity might be different. For example, two ATMs located on different floors of a mall have the same geographical location, but if ATM 1’s vicinities are company offices, and those of ATM 2 are recreation and shopping centers, the daily withdrawal pattern might be completely different. The reason for this is that the withdrawal of cash from ATM 1 is conducted mainly on weekdays throughout the year, while the money withdrawal from ATM 2 is made mostly on weekends and during specific months. Thus, to better capture the seasonality in the data and apprehend inherently different established usage patterns, we have categorized the ATMs based on their accessibility and surrounding environments.

Furthermore, to the best of the authors' knowledge, the studies cited above mostly predicted the ATM cash demand with normal volatility in the withdrawal pattern, utilized a few prediction models—mainly non-parametric methods—and employed only one performance measure (e.g., MSE, SMAPE, and R²) to compute the error. Moreover, none of the previous ATM cash withdrawal time series contains a huge amount of volatility that stemmed from a disaster or unprecedented challenge (e.g., pandemic). Alongside the contributions already mentioned, this study aims to fill the gap and propose a comprehensive evaluation for ATM cash demand prediction both before and during the COVID-19 pandemic (i.e., just after a disruption in demand) to choose the most promising algorithms based on a new performance metric that simultaneously takes both the error and accuracy of direction’s change into account.

Methodology

Dataset

The purpose of this study is to propose an extensive evaluation that accurately predicts ATM cash demand both before and during the COVID-19 pandemic for different categories of ATMs. With that aim, we first identify three different categories for ATMs based on their accessibility and environmental factors, which significantly affect both the daily cash demand and the withdrawal pattern. These categories are comprised of ATMs that are located in one of the following districts: (i) residential districts—ATMs where the environment is dominated neither by office companies nor by shopping centers; (ii) business districts—characterized by high cash withdrawal on weekdays and low cash withdrawal on the weekend; and (iii) shopping and recreation districts—cash withdrawals mostly on weekends and in particular months.

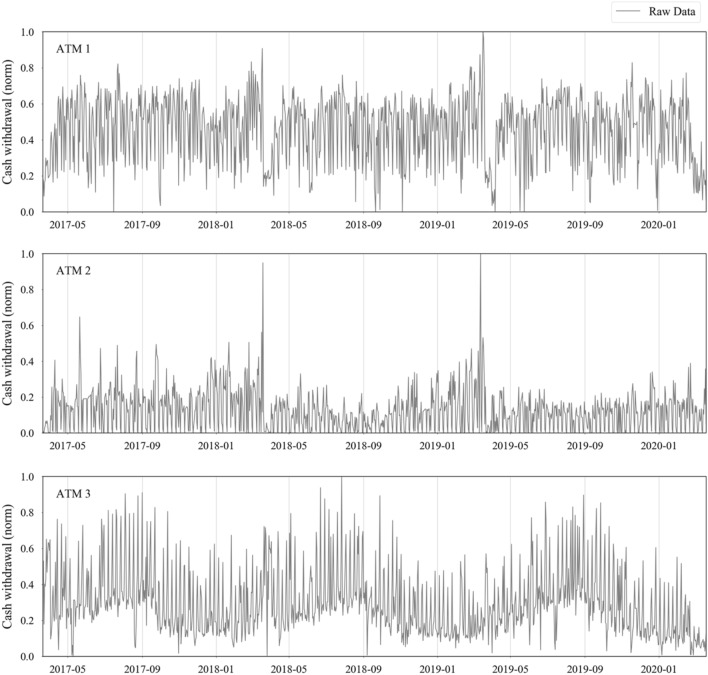
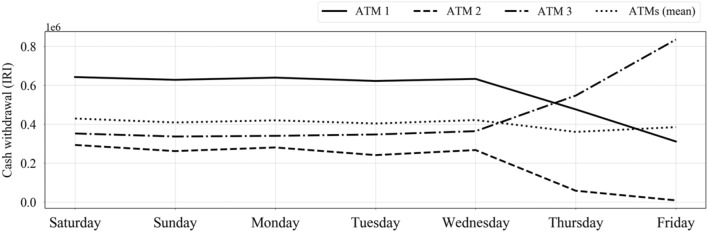
The collected data show the daily cash withdrawal from each category of ATMs (i.e., ATM 1 in the residential district, ATM 2 in the business district, and ATM 3 in the shopping and recreation district) for three consecutive years from 03/21/2017 to 03/19/2020, according to the solar calendar used in the studied case, a private bank in Tehran, Iran. ATMs in each category have a similar distribution, and ATMs used in this study are the most representative of their group. The datasets are publicly available at https://github.com/af551515/Forecasting_ATM_Cash_Demand. Figure 1 illustrates the time series of cash withdrawals from ATMs 1, 2, and 3, while Fig. 2 depicts the effect of the day-of-the-week on the cash withdrawal pattern. For each ATM, the reported values are averaged over all 3 years and normalized accordingly. It should be noted that in Iran, the weekdays are Saturday to Wednesday, and weekends are Thursday and Friday. Generally, as is shown in Fig. 1, in the last month of the first 2 years, the cash demand has an upward trend for all ATMs. However, the last month of the third year has a contrary trend because of the beginning of the COVID-19 pandemic and the announcement of a stay-at-home order. Furthermore, as can be seen in Fig. 2, ATMs 1 and 2 have a high cash demand during weekdays, followed by a low amount of money withdrawn on weekends. However, the cash demand from ATM 2 (located in business districts) is lower because fewer people—mostly personnel of the companies/agencies in the vicinity—have access to such ATMs. ATM 3 has an opposite trend, with a huge cash withdrawal on weekends rather than on weekdays. The ATMs are compared with other time-related features (i.e., day-of-the-month and number of consecutive holidays ahead) in Fig. S1B, C of the supplementary material.

Fig. 1.

Daily normalized cash withdrawal from ATMs 1, 2, and 3. The mean of the three ATMs’ daily cash demand, named the ATM mean, is shown in Fig. S1A

Fig. 2.

The day-of-the-week withdrawal pattern from different types of ATMs. Note that, in Iran, the weekdays are from Saturday to Wednesday, while the weekend days are Thursday and Friday. See Fig. S1B, C for more comparison of ATMs in terms of time-related features

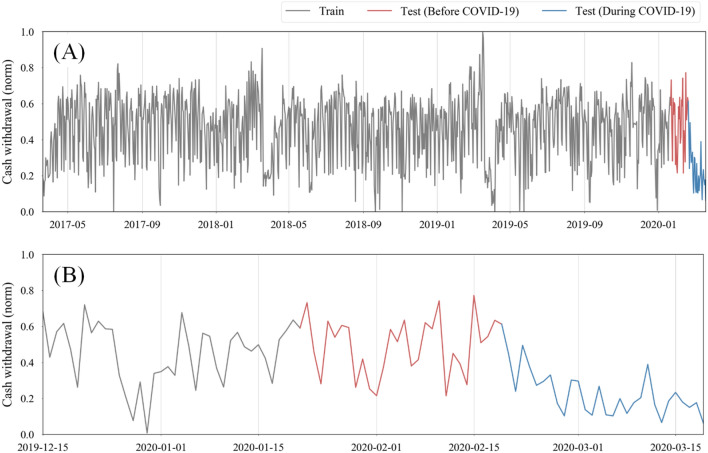
The given time frame of 3 years is split by the period that the COVID-19 pandemic was observed in society. From 02/20/2020 to 03/19/2020 (i.e., the last month of the available data) is the period in which the pandemic and preventive measures (e.g., stay-at-home-orders) began; thus, this period is selected as the during the COVID-19 testing set (the entire month 12 on the solar calendar), in which the cash demand decreased remarkably followed by significant volatilities in the withdrawal pattern just after implementing prevention. To be consistent with the length of testing sets, the before COVID-19 testing set was selected between 1/21/2020 and 02/19/2020 (the entire month 11 on the solar calendar). The training set comprises the balance of the data, which starts from 03/21/2017 and ends 01/20/2020 (1036 days in total). The aim is to choose the most promising predictive model in two different situations in times when there is a minor disturbance in the pattern (here called as before COVID-19) or a significant disturbance in demand and radical changes in the withdrawal pattern (here named as during COVID-19). It is important to note that we first analyzed ATMs 1, 2, and 3 separately due to their inherently different established usage patterns; then, we took the mean of these three machined, analyzed the ATM mean completely independently, and compared the results. Figure 3 represents the splitting of the data for ATM 1. The same splitting approach was used for the other ATMs (see Figs. S2–S4).

Fig. 3.

Splitting data into training and testing sets for ATM 1. A shows all available data, while B magnifies the last 3 months of the dataset for the sake of clarity. The length of the testing set is 30 days, while the training set is 1036 days long. Figures S2–S4 contains the same information for other ATMs

Prediction Approaches

Time series are ordered sequences of datapoints at equally spaced time intervals. Before applying any prediction method on a time series, one should ensure is that the data are discrete and uniformly sampled [22]. Figure 1 shows that the given data in this study satisfy such a requirement. In general, there are two types of time series prediction approaches, namely, (i) parametric and (ii) non-parametric. Parametric techniques are statistical methods that require some prior knowledge about the distribution of data [33]. In contrast, non-parametric approaches, known as machine learning (ML) prediction methods, have no such limitations and are ready to be applied to any non-linear series, as the distribution of data is not an issue [28, 33].

The parametric models used in this study are MA, SES, HES, ARIMA, and SARIMA. A thorough explanation of each of these models is given elsewhere [8, 15, 19, 41], but each model will be briefly discussed here. The MA model uses the arithmetic mean of the last n values of datapoints to predict future datapoints [30]. The SES model behaves similarly, but unlike MA, it uses exponentially decreasing weights for past datapoints. This model emphasizes the more recent observations by giving higher weights to them compared to datapoints from the more distant past. Compared to the SES, the HES model employs both weight and trend parameters to avoid the methodical error (underestimation/overestimation of the actual data) that often occurs in the SES [32]. The ARIMA model makes its prediction using the difference between the values of datapoints, rather than their actual values. In this model, the number of lags observed in the data (p), the number of times datapoints are subtracted to make the series stationary (d), and the size of the moving average window (q) are the substantial hyperparameters that should be carefully chosen based on some statistical analysis [27, 33]. To compensate the ARIMA limitation for the series with seasonality, the SARIMA model plays a prominent role by taking the seasonal autoregressive order (P), seasonal difference order (D), seasonal moving average order (Q), and the number of time-steps for a single seasonal period (s) into account [33].

The non-parametric models employed in this study are well-known ML regressors, namely MLP, SVM, RF, and KNN. The description of each model is beyond the scope of the current study, but each is briefly discussed here for context. The MLP, well known as a class of feedforward artificial neural network, is a popular stochastic technique used for forecasting purposes via performing a non-linear mapping from previous datapoints to future datapoints [33, 43]. The structure of the network (number of layers: n-hidden-layers and number of neurons in each layer: n-nodes) is the critical part of this model required to obtain the highest possible accuracy. MLP is a self-adaptive method, using interconnected nodes called neurons, which are placed in multiple layers. The nodes of adjacent layers are linked by the edges of weights that are adjusted continuously as learning proceeds [10]. The SVM has been successfully applied to a variety of different classification and regression problems [2, 25, 36]. The SVM model accomplishes its prediction by optimizing hyperplanes as well as a support vector’s positions to minimize the number of generalization errors. The cost and gamma are the two main hyperparameters that control the hyperplanes’ and support vectors’ functionality, which are required to be tuned before any further investigation [2, 3]. Another well-known ML regressor is RF, which constructs a combination of multiple decision trees for regression purposes [34]. The number of trees (n-trees) and the fraction of features used to grow each tree (max-features) are the primary hyperparameters that need to be tuned for this method [29]. The KNN regressor, unlike the stochastic models, looks for the k most similar samples that have been observed in the training set for each new sample. By taking the weighted average of their values, the regressor then reports a predicted value for that new sample. The weighting average can be dependent or independent of the distance. Thus, the number of neighbors (n-neighbors) and the method of averaging (avg-method) are the two main hyperparameters of the KNN algorithm considered in this study [21, 23].

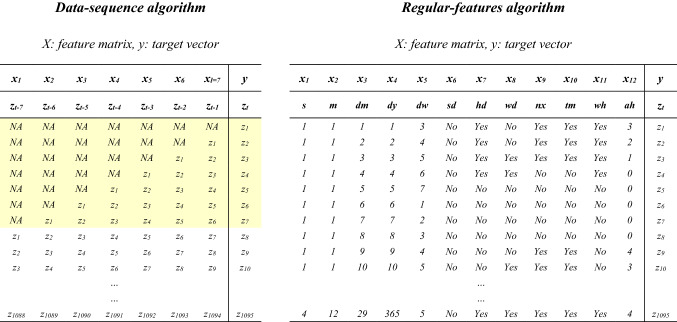
The non-parametric models require an attribute-value table (X, also known as a feature matrix) along with the target vector (y: cash withdrawal). Two different algorithms, namely, data-sequence and regular-features, are used in this study to generate the feature matrix. The models suffixed “_DS” constitute ML models in which a data-sequence algorithm was used to build their feature matrix. In contrast, ML prediction models without any suffix are non-parametric models in which a regular-features algorithm was applied to generate their feature matrix. The hierarchy of all employed prediction models in the current study is displayed in Fig. 4.

Fig. 4.

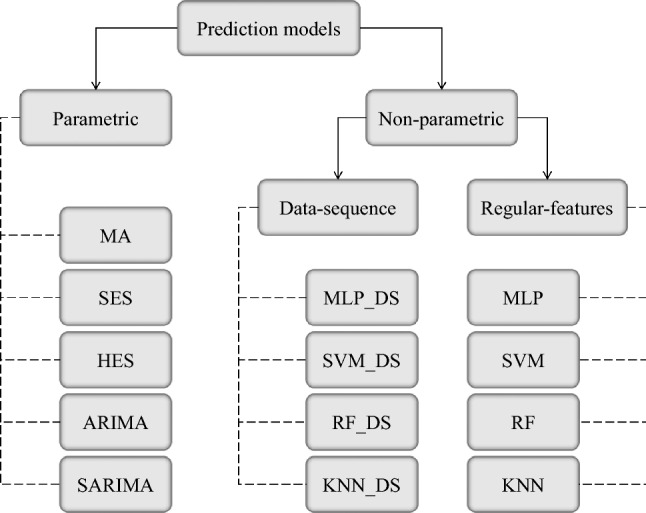
Hierarchy of employed time series prediction models in this study

In the data-sequence algorithm, the feature matrix is constructed via the transposition of the data-sequence with the sliding window of length 7 (the yellow-shaded rows in Fig. 5). However, in the regular-features algorithm, the feature matrix is described by 12 input variables represented in Table 1

Fig. 5.

Data-sequence algorithm (left) vs. regular-features algorithm (right) to build a feature matrix of non-parametric models. The shaded rows on the left panel show the window of length 7 for the data-sequence algorithm based on the autocorrelation matrix results that report a lag of 7 for the available data

Table 1.

Selected input variables (features) considered in the regular-features algorithm

Description	Symbol	Range	Type
Season	s	[1, 2, 3, 4]	Numerical
Month	m	[1–12]	Numerical
Day of month	dm	[1–30]	Numerical
Day of year	dy	[1–365]	Numerical
Day of week	dw	[1–7]	Numerical
Special day	sd	{yes, no}	Categorical
Holiday	hd	{yes, no}	Categorical
Weekend	wd	{yes, no}	Categorical
The next 3 days includes special day or holiday	nx	{yes, no}	Categorical
Tomorrow is a special day or holiday	tm	{yes, no}	Categorical
Weekend is a special day or holiday	wh	{yes, no}	Categorical
Number of consecutive holidays ahead	ah	[1–5]	Numerical

The first eight features were considered in the previous studies [20, 21], while the last four features were added to accurately model the cash withdrawal pattern (Table 1). Importantly, the last feature of the table is a new influential independent variable, which denotes how many consecutive holidays (including weekends) are ahead of each day. Figures S1C and 8 show the influence of this feature on the cash withdrawal pattern. Note that the special days are “Mother’s Day”, “Father’s Day”, “Teacher’s Day”, “Student’s Day”, “College Day”, “Valentine’s Day”, “Love Day”, and “Yalda (national day).” However, the exact types of special days are not considered; instead, “yes” or “no” values are employed. The same approach was employed for the categories of holidays that are “New Year (4 days)”, “Religious Holidays (17 days)”, and “National Holidays (6 days).”

Fig. 8.

(ATM 1) The importance of employed features in non-parametric-regular-feature models. The results of other ATMs are reported in Fig. S8

Iteration Strategies

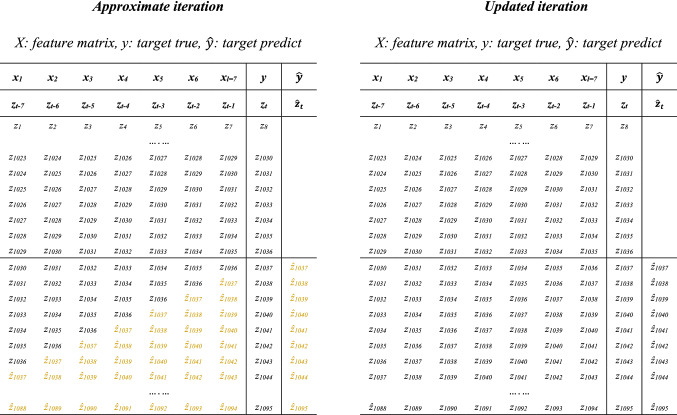
The multi-step prediction approach is an intuitive method used in the prediction of the sequence of values in time series problems via using observed values in the past [7]. One of the well-known strategies in multi-step time series forecasting is a recursive strategy (also known as walk-forward). This approach provides a forecast using either the previous forecast (approximate iteration) or respective actual value (updated iteration) based on the single constructed model. The approximate iteration is a recursive strategy that uses the previous predicted value in determining the estimation of the next forecast value, while the updated iteration adopts the actual values in predicting the next value recursively [33]. Figure 6 schematically compares these two iteration strategies. For both strategies, a history of feature matrix and target vectors have been constructed to generate the future observations’ (next days’) input variables; however, to prevent the forecasted observations from entering into the learning process, this history was not added to the training set when the model was fitted. The approximate iteration was only applied to the parametric and non-parametric with data-sequence algorithm methods, because the non-parametric models with regular-features algorithms (MLP, SVM, RF, and KNN) are independent of previously predicted values, and the history is not required to generate the input variables. Thus, the results of approximate and updated iterations are the same for these models.

Fig. 6.

Approximate iteration (left) vs. updated iteration (right) used to build the feature matrix as well as the target vector. The first 1,036 datapoints are in the training set, so no target-predicted values are shown for them

Performance Measurement Metrics

Mean squared error (MSE) is a common metric used to evaluate the performance of predictions. The MSE, as formalized by Eq. (1), is calculated by the average squared difference (error) between the actual values and prediction values

$$\text{MSE}=\frac{1}{N}\sum _{t=1}^N{\left({\widehat{y}}_t-y_t\right)}^2,$$ 1

where N is the number of observations in the testing set, and $y_t$ and ${\widehat{y}}_t$ represent the actual and predicted values at time t, respectively. The MSE is computed to figure out how far the prediction values are from the actual values in terms of quantity. The lower MSE, the higher accuracy of the predictor. However, this metric’s limitation is that the prediction trend in time series is not clear—specifically when the pattern abruptly changes. The prediction of the change in direction (POCID) metric, denoted by Eqs. (2) and (3), addresses the issue by mapping the prediction trend and estimating the accuracy of the direction’s changes

$$\text{POCID}=100\frac{{\sum }_{t=1}^N{D}_t}{N}$$ 2

$$D_t=\left\{\begin{array}{cc}1,& \left({\widehat{y}}_t-{\widehat{y}}_{t-1}\right)\left(y_t-y_{t-1}\right)>0\\ 0,& \text{otherwise ,}\end{array}\right)$$ 3

where $y_t\text{and}{y}_{t-1}$ are the actual values at times t and t-1, while ${\widehat{y}}_t\text{and}{\widehat{y}}_{t-1}$ are the predicted values obtained at times t and t − 1. POCID is applied to examine the trend of the prediction set compared with the actual testing set. The higher value of POCID, the better the mapping of the trend. However, the POCID metric does not consider the exact closeness of the prediction to the actual values. Therefore, considering the metric’s limitations, it is not advisable to use either measure solely for time series forecasting. In this paper, we propose a new measure to properly evaluate predictors’ performance by considering both MSE and POCID in one metric. The proposed metric modifies the fitness function evaluations in the literature [29] by giving more weight to the MSE in the denominator to make the Fitness a more inclusive measurement of both POCID and MSE. The fitness metric is expressed in Eq. (4) as follows:

$$\text{Fitness}=\frac{\text{POCID}}{1+10\times \text{MSE}}.$$ 4

The min and max possible values of the Fitness metric are 0 and 100, respectively. The greater Fitness value indicates better forecasting of fluctuations in time series and better accuracy of the prediction model. In the denominator, the MSE is multiplied by a factor of 10 to give some weight to it compared to the number 1 that it was added to. Since 1 is much greater than the MSE values, if MSE is not multiplied by the factor of 10, the Fitness value would become relatively the same as POCID, which is not desired.

Experimental Setup

All predictive models were implemented in Python 3.8 using numerous Python libraries. The algorithms were performed on a computer with a Windows 10 operating system and a CPU Core i7-6700 with 16 GB of memory.

Design of Elements

The performance of the prediction algorithms was quite sensitive to the value of the hyperparameters [45] and thus needed to be tuned before comparing their performance. First, three statistical analyses, including a fuller test, autocorrelation function (ACF) plot, and partial autocorrelation function (PACF) plot, were employed to initially estimate an acceptable range of required parameters for the parametric models. Then, the grid search method with a fivefold cross-validation algorithm was utilized to tune the hyperparameters of all of the models.

The fuller test is a test that is known to ensure the data are stationary. This test reports the p value and test statistics of the given time series. By definition, stationary time series hold the p value and test statistics lower than 0.05 and critical values, respectively (see Table 2 for more details). As is shown, ATM 1, ATM 2, and ATM (mean) are stationary, while ATM 3 requires a transformation to become stationary. Our results suggest that the first-order differencing was enough to make ATM 3 stationary (see Fig. S6). Thus, the differentiation order (d) of 0 or 1 has been selected for the range of d parameter for the ARIMA and SARIMA models.

Table 2.

Fuller test results for the ATMs time series

	ATM 1	ATM 2	ATM 3	ATM (mean)
Test statistic	– 6.19	– 4.44	– 2.26	– 3.88
p Value	6.0e– 8	2.5e– 4	1.8e– 01	2.1e– 3
Critical values:1%	– 3.43	– 3.43	– 3.43	– 3.43
Critical values:5%	– 2.86	– 2.86	– 2.86	– 2.86
Critical values: 10%	– 2.56	– 2.56	– 2.56	– 2.56

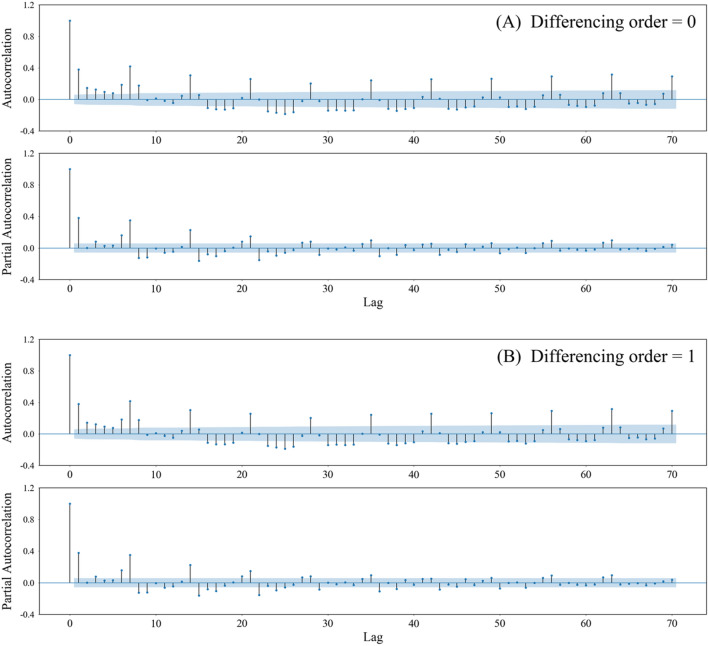
The ACF and PACF plots are the key analysis when it comes to approximating the autoregression, moving average, and other seasonality parameters of non-parametric models. To obtain a decent range for other parameters of the non-parametric models, we estimated the ACF and PACF plots of cash withdrawal data for both d values of 0 and 1 (Fig. 7). Looking at the ACF, a seasonal lag of 7, 14, 21, etc. (every week) is clear and means that the number of time-steps for a single seasonal period (s) is 7. Giving the significant non-seasonal lag of 1, 6, 7, 8, and 9 suggests that the autoregressive order (p) is in this range. The moving average (q) of 0 or 1 is good enough to be applied. The positive value of s indicates that the seasonal autoregressive order (P) is greater than or equal to 1 [13], and since P + Q should not exceed 2 [13], the seasonal moving average order (Q) was found to be either 0 or 1.

Fig. 7.

The ACF and PCF plots for ATM 1 time series with differencing orders of A 0, and B 1

Consequently, this initial analysis suggests that a possible model for ATM 1 is an ARIMA (7,1,0) and SARIMA (1,1,0) (1,1,0)₇. These models, along with some variations, have been used to find the best models according to the Fitness metric. The same statistical analysis for the other ATMs was performed, and the results are presented in Figs. S5–S7.

For the tuning process, a range of values for the hyperparameters of all models is considered, and accordingly, several sub-models are then constructed. Afterward, these sub-models are compared thoroughly, based on the proposed fitness metric. \* MERGEFORMAT

Table 3 summarizes the utilized hyperparameters of each model, coupled with their designed range of values. The selected values corresponding to each category of ATMs are presented in Tables S1–S4. In addition, the full comparison of the sub-models of each employed model for all ATMs alongside the corresponding Fitness scores is available in Tables S5–S14. The selected best models from Tables S1 to S4 are used hereafter for further comparisons and predictions.

Table 3.

Description and range of values of the hyperparameters for the employed models

Method	Hyperparameters’ description	Abbreviation	Values’ range
ARIMA	Autoregressive order	AR (p)	[1, 6, 7, 8, 9]
	Differentiation order	I (d)	[0, 1]
	Moving average order	MA (q)	[0, 1]
SARIMA	Autoregressive order	AR (p)	[1]
	Differentiation order	I (d)	[0, 1]
	Moving average order	MA (q)	[0, 1]
	Seasonal autoregressive order	P	[0, 1]
	Seasonal difference order	D	[0, 1]
	Seasonal moving average order	Q	[0, 1]
	The number of t-steps for a single seasonal period	s	[7]
MLP_DS	Number of hidden layers	n-hidden-layers	[1, 2, 3]
	Number of neurons per hidden layer	n-nodes	[2, 4, 6, 8, 10]
SVM_DS	Regularization parameter	Cost	[1, 5, 10, 100, 1000]
	Kernel coefficient	Gamma	[1.0, 0.1, 0.01, 0.001, 0.0001]
RF_DS	Number of trees (estimators) in the forest	n-trees	[10, 50, 100, 200, 500]
	Number of features to consider for best splitting	Max-features	[0.6, 0.7, 0.8, 0.9, 1.0]
KNN_DS	Number of neighbors	n-neighbors	[3, 4, 5, 6, 7]
	Weight function	Weights	[“uniform”, “distance”]
MLP	Number of hidden layers	n-hidden-layers	[1, 2, 3]
	Number of neurons per hidden layer	n-nodes	[2, 4, 6, 8, 10]
SVM	Regularization parameter	Cost	[1, 5, 10, 100, 1000]
	Kernel coefficient	gamma	[1.0, 0.1, 0.01, 0.001, 0.0001]
RF	Number of trees (estimators) in the forest	n-trees	[10, 50, 100, 200, 500]
	Number of features to consider for best splitting	Max-features	[0.6, 0.7, 0.8, 0.9, 1.0]
KNN	Number of neighbors	n-neighbors	[3, 4, 5, 6, 7]
	Weight function	Weights	[“uniform”, “distance”]

It is necessary to mention that the employed MA method is set to always have a window of 7, since we observed the seasonal lag of 7, 14, 21, etc. As suggested, the default parameters of the corresponding packages are used for the SES and HES models.

Results and Discussion

Features Importance

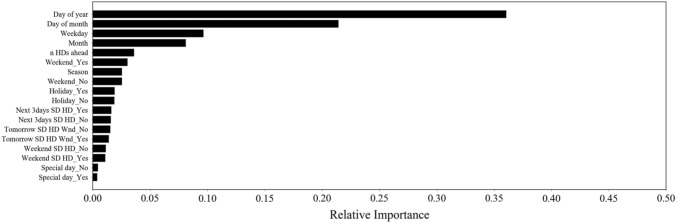
To evaluate the importance of features in the non-parametric models embedded with the regular-features algorithm, we estimated the importance of features using random forest (RF) regressor. Figure 8 depicts the results and produces the rank of features in such a way features, including “day of year,” “day of month,” “weekday,” “month,” and “n HDs ahead” are the most influential attributes selected for ATM 1. The latter feature that stands for the number of consecutive holidays ahead is one of the proposed attributes in this paper for the first time. As shown, such a feature is among the factors with the greatest impact in estimating the amount of cash withdrawal for all ATMs (see Fig. S8).

Comparison of Models

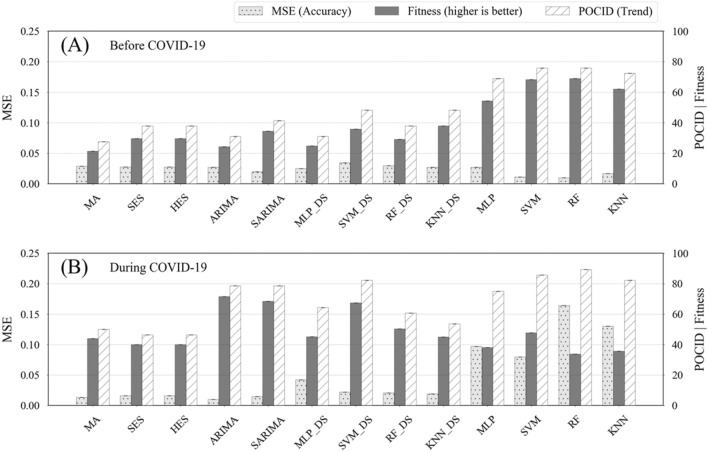
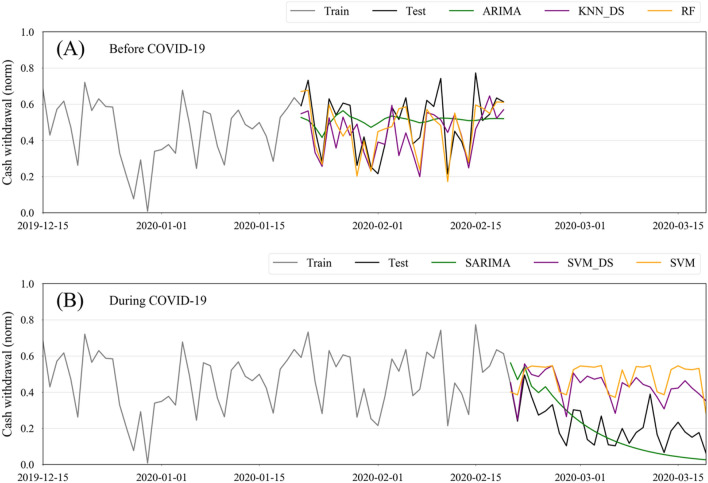
In this study, the performance of predictive models on forecasting the cash demand for different ATMs both before and during the COVID-19 pandemic with approximate and updated iteration strategies are extensively evaluated. Figure 9 reports the performance of predictors (i.e., parametric, non-parametric with data-sequence, and regular-features) on ATM 1 with an approximate iteration strategy both before COVID-19 (Fig. 9A) and after COVID-19 (Fig. 9B). Results obtained with the approximate iteration strategy in Fig. 9 show that the overall performance of predictive models before COVID-19 was significantly better than those during COVID-19. This observation was expected, since the predictive algorithms perform better when there is a more stable pattern, not only in time series forecasting but also in other prediction fields. Before COVID-19 (Fig. 9A), in which there is only a minor disturbance in the pattern, generally, non-parametric models overshadowed the parametric models, demonstrating the better performance of machine learning models than the statistical models (see the same results in [5, 26, 42]). More specifically, non-parametric models with regular-features, including SVM, RF, and KNN, outperformed the others. Among all models, RF reported the highest performance, with a Fitness equal to 68.87 computed by MSE and POCID at 0.0101 and 75.86, respectively. However, during COVID-19, in which the ATM cash withdrawal pattern sharply went into a downward trend, the performance of non-parametric models with regular-features notably decreased; however, performance loss in parametric models and non-parametric models with data-sequences were insignificant, and in some cases (i.e., SARIMA and KNN_DS), the Fitness rate improved. As shown in Fig. 9B, the parametric method of SARIMA has the highest Fitness during COVID-19 at 55.53 with respect to MSE and POCID at 0.0158 and 64.28, respectively. The reasons for such results might be mainly related to the high performance of ARIMA and SARIMA for short-term prediction [44], while avoiding or minimizing overfitting.

Fig. 9.

(ATM 1) Comparison of performance measures for different models (parametric: MA, SES, HES, ARIMA, and SARIMA; non-parametric-data-sequence: MLP_DS, SVM_DS, RF_DS, and KNN_DS; and non-parametric-regular-features: MLP, SVM, RF, and KNN) in the prediction of cash demands with “approximate” iteration. A Before and B during the COVID-19 pandemic. Figures S9–S11 report the results of other ATMs

Comparing Fig. 9A with Fig. 9B, generally, all predictors performed more accurately before COVID-19 than during COVID-19 in terms of MSE. During COVID-19, although the error (MSE) increased, the trend prediction rate (POCID) stayed the same and, in some cases, improved. These results indicate that during a pandemic, ML models are capable of capturing the trend of cash withdrawal; however, the Fitness rate worsens due to an increase in the number of errors. Moreover, the results show that during an unprecedented challenge, when a sudden change in the withdrawal pattern occurs, by utilizing preceding days’ data—instead of features such as day-of-the-week, month, or year—we can better map the following datapoints and, in turn, boost the prediction outcome. However, in case there is normal volatility in the time series, these features play a more pivotal role than the preceding days’ cash withdrawal information.

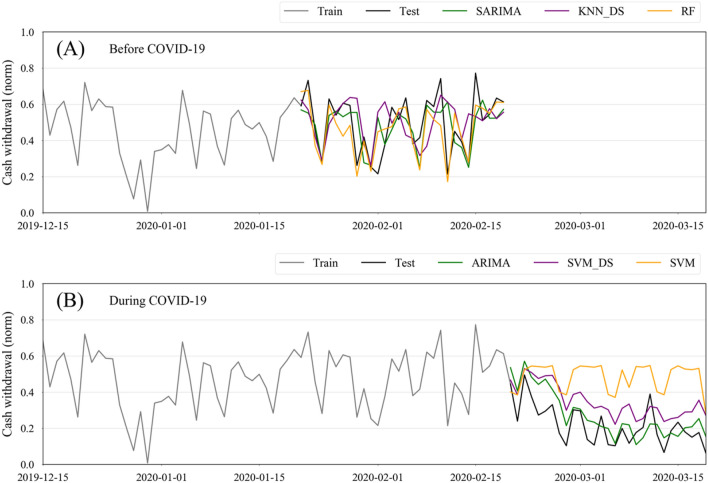
Likewise, Fig. 10 illustrates the results with the updated iteration strategy on ATM 1. As is shown, the maximum Fitness before and during COVID-19 was observed for RF and ARIMA, respectively. The former obtained a Fitness at 68.87, and the latter achieved 71.57. According to the results represented in Figs. 9 and 10, the updated iteration strategy has a better predictive performance compared to the approximate iteration strategy. However, the approximated approach seems to be a more reasonable strategy when it comes to forecasting ATM cash demand in the following days due to using the previously estimated values, and not adopting the actual values.

Fig. 10.

(ATM 1) Comparison of performance measures for different models (parametric: MA, SES, HES, ARIMA, and SARIMA; non-parametric-data-sequence: MLP_DS, SVM_DS, RF_DS, and KNN_DS; and non-parametric-regular-features: MLP, SVM, RF, and KNN) in the prediction of cash demands with “updated” iterations. A Before and B during the COVID-19 pandemic. See Figs. S12–S14 to see the results of other ATMs

Comparison of the Best Models

To visually compare the performance of the three categories of employed models (i.e., parametric, non-parametric with data-sequence, and regular-features) before and during COVID-19, the prediction of the best predictive model of each category versus the actual data are plotted in Figs. 11 and 12. The former depicts the prediction quality in forecasting cash withdrawals from ATM 1 with the approximate iteration, and the latter shows the results with the updated iteration strategy. The best predictive model in each class is reported with different colors (i.e., the parametric model in green, non-parametric-data-sequence in purple, and non-parametric-regular-features in orange). As illustrated in Fig. 11, non-parametric models can reliably predict the changes in the withdrawal pattern both before and during COVID-19. According to Fig. 11A, before COVID-19, ARIMA, KNN_DS, and RF are the best representatives of the parametric, non-parametric with data-sequence, and non-parametric with regular-features models, respectively; among them, the stochastic method of RF showed the highest performance, thanks to its lowest prediction error. However, during COVID-19 (Fig. 11B), the quality of prediction—specifically MSE in non-parametric models with regular-feature—substantially declines. In this context, SARIMA, SVM_DS, and SVM are the best models for each category. SARIMA represented the highest performance among all predictive models owing to its closest prediction to the actual data (small prediction error). Thus, the pandemic condition is perfectly observed and captured with SARIMA, and it can better map further withdrawal patterns from ATMs during COVID-19. Note that before COVID-19, ARIMA has shown to be the best predictor of parametric models, while during the pandemic, SARIMA was the best in terms of overall Fitness among parametric models.

Fig. 11.

(ATM 1) Comparison of different ML methods to predict cash demand with “approximate” iteration strategy. A Before and B during the COVID-19 pandemic. (Colors code—green: best parametric model, purple: best non-parametric-data-sequence model, and yellow: best non-parametric-regular-feature model.) See Figs. S15–S17 to see the results of other ATMs

Fig. 12.

(ATM 1) Comparison of different ML methods to predict cash demand with “updated” iteration strategy. A Before and B during the COVID-19 pandemic. (Colors code—green: best parametric model, purple: best non-parametric-data-sequence model, and yellow: best non-parametric-regular-feature model.) See Figs. S18–S20 to see the results of other ATMs

Similarly, Fig. 12 reports the quality of the best-fitted models when compared with the updated iteration strategy. Overall, the updated iteration fits the models better than the approximate iteration, as expected, especially when there is a huge change in a trend. As can be seen, before COVID-19 (Fig. 12A) the RF learning predictor has the highest performance both in terms of prediction error and the accuracy of direction’s changes, while during COVID-19 (Fig. 12B), the parametric method of ARIMA outperformed the other predictors with high performances in both MSE and POCID.

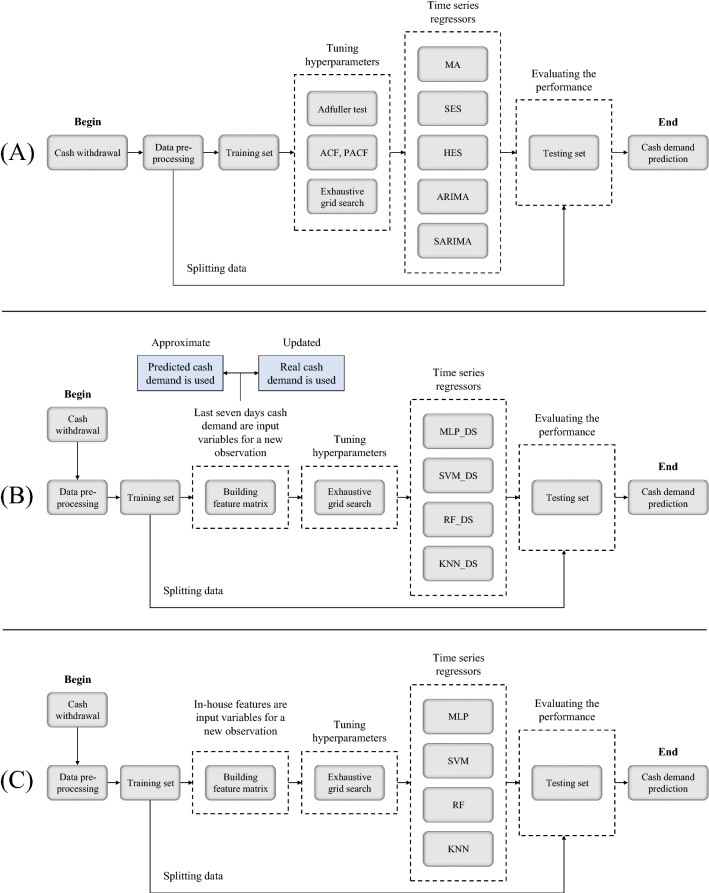
The schematic architecture of employed statistical and machine learning models is described in Fig. 13. The four main stages for the parametric models, as shown in Fig. 13A, included data preprocessing, tuning hyperparameters, predictive regressors, and evaluating the performance of models. For the non-parametric models with data-sequence and regular-features iteration (respectively, shown in Fig. 13B, C), constructing a feature matrix was also required.

Fig. 13.

The architecture of built A parametric models, B non-parametric-data-sequence models, and C non-parametric-regular-features models

Comparison of ATMs

Our last comparison constitutes all of the datasets (i.e., different cash withdrawal patterns based on different environments and levels of accessibility around the ATMs). Apart from an exhaustive hyperparameter tuning, we extensively evaluated a total of 192 configurations (including 12 predictors, 2 iteration strategies, 2 statuses of before/during COVID-19, and 4 ATMs with different time series). Table 4 reports the results of such a comprehensive evaluation of the best predictors for forecasting cash withdrawal in terms of MSE, POCID, and Fitness metrics. Overall, the quality of prediction before COVID-19 is higher than during COVID-19, and the updated iteration strategy does a better job in mapping the trend during the pandemic. According to the results, before COVID-19, non-parametric models outperform the parametric methods in all eight configurations. However, during COVID-19, the performance of the parametric methods of ARIMA and SARIMA mostly overshadows the non-parametric models. Another highlighted takeaway from the table is that analyzing and forecasting ATMs’ cash demand based on their withdrawal patterns (i.e., three different types) compared to researching them in a single class resulted in higher predictive performance. Generally, ATM means that contains the average daily cash withdrawal for all three ATMs has a higher MSE, as well as a lower POCID and Fitness, in all associated configurations, resulting in lower overall performance. For instance, when using an approximate iteration before COVID-19, the performance measures of MSE, POCID, and Fitness for ATM (means) were 0.0105, 75.86, and 68.62, while ATM 1, ATM 2, and ATM 3 had the better performance individually for all three metrics. This result shows that category-wise forecasting based on the accessibility, environment factors, and different withdrawal patterns—rather than taking the average of daily cash demand from different ATMs—significantly enhances the prediction quality.

Table 4.

Comparison of ATMs in terms of MSE, POCID, and Fitness metrics

Iteration	Time interval	ATM	Best method	MSE	POCID	Fitness
Approximate iteration	Before COVID-19	ATM 1	RF	0.0101	75.86	68.87
		ATM 2	KNN_DS	0.0044	86.20	82.57
		ATM 3	KNN_DS	0.0046	79.31	75.82
		ATM (mean)	SVM	0.0105	75.86	68.62
	During COVID-19	ATM 1	SARIMA	0.0158	64.28	55.53
		ATM 2	KNN	0.0169	85.71	73.31
		ATM 3	SES	0.0158	75.00	64.77
		ATM (mean)	SARIMA	0.0576	78.57	49.84
Updated iteration	Before COVID-19	ATM 1	RF	0.0101	75.86	68.87
		ATM 2	RF	0.0065	82.75	77.68
		ATM 3	MLP_DS	0.0098	79.31	72.21
		ATM (mean)	SVM	0.0105	75.86	68.62
	During COVID-19	ATM 1	ARIMA	0.0098	78.57	71.57
		ATM 2	KNN	0.0042	78.57	75.38
		ATM 3	ARIMA	0.0055	64.28	60.92
		ATM (mean)	SARIMA	0.0105	67.85	61.39

Details of performance measures for each model are reported in Tables S5–S14

The results also showed that the comprehensive analysis conducted in this study led to a high level of accuracy in estimating cash withdrawal from ATMs. As shown in Table 4, the category-wise prediction can enhance the forecasting by at least 4%. Additionally, the maximum mean squared errors before and during COVID-19 are about 1% and 5%, respectively. Such a significant prediction can help bank managers to mobilize idle cash and generate additional revenue—rather than load excess banknotes in ATMs, which increases operational and opportunity costs, especially when there are thousands of ATMs.

Conclusions

This study presented a comprehensive analysis when it came to forecasting ATM’s cash demand both before and during the COVID-19 pandemic, using an extensive evaluation of statistical and machine learning models. Several parametric models (MA, SES, HES, ARIMA, and SARIMA) and non-parametric models (MLP, SVM, RF, and KNN), followed by the data-sequence and regular-features algorithms were employed in the analysis of the collected datasets. The models were evaluated for three groups of ATMs having different accessibility and withdrawal pattern. Applying the predictive models on diverse (not a single) time series datasets can reduce the raising of questions regarding the statistical significance of our results and generalization [31]. Moreover, we applied the approximate and updated iteration strategies to incorporate each new datapoint in the learning process recursively.

In previous studies in this context, different research papers came up with varying conclusions regarding the performance of machine learning models (non-parametric predictors) compared to the statistical models (parametric predictive models). For example, Adebiyi et al. [1] claimed that statistical methods such as ARIMA underperform machine learning models, while Makridakis et al. [31] concluded that machine learning models underperform the counterpart in terms of accuracy and thereby might be upsetting from a scientific perspective. This paper strived to conduct a trustful comparison approach and perform different models equally well. With that aim, the models were implemented and compared after performing an exhaustive statistical analysis, coupled with grid search and k-fold cross-validation techniques that led to the highest performance of models. On the other hand, in the literature, the performance of models has been mainly compared in terms of accuracy measures such as MSE, SMAPE, and R², representing the error of prediction. In this study, it has been revealed that error measure (e.g., MSE) alone cannot be the best evaluation metric in comparing the performance of the predictors on ATM cash demand—especially when the withdrawal pattern drastically changes as a result of preventive measures such as a stay-at-home order or partial lockdowns that are taken to reduce the spread of COVID-19. To address this issue, we proposed a modified fitness metric that simultaneously considers both prediction error (MSE) and trend (POCID).

Our findings demonstrated that the extensive evaluations performed in this study resulted in a high accuracy when it came to forecasting ATM cash demand. The maximum mean squared errors before and during COVID-19 were about 1% and 5%, respectively. Additionally, category-wise forecasting led to improving forecasting quality by at least 4%. Before the COVID-19pandemic—in times when there were only minor disturbances in withdrawal patterns—forecasting quality was higher, and generally, the non-parametric models could more accurately predict the ATM’s money demand. However, the results showed that despite earlier studies in the literature of forecasting ATM cash demand, sophisticated non-parametric methods will not always have higher performance when compared to parametric methods. It was revealed that during COVID-19, in which there was a sudden shock in demand followed by abnormal volatility in withdrawal patterns, the parametric models of ARIMA and SARIMA could mostly provide better predictions based on the Fitness evaluation metric. Taking comprehensive hyperparameter tuning into account, the reasons for such impressive results might be mainly related to the high performance of ARIMA and SARIMA for short-term prediction [44] and the fact that we aimed to predict the demand just after the occurrence of the pandemic, while avoiding or minimizing overfitting.

From a managerial perspective, such a high prediction accuracy level can help the bank’s top management keep cash at the right levels instead of excessive cash storage, allow the bank to save a large sum on operational costs, protect the bank’s reputation, and increase its profitability through investments. Although this paper addressed some gaps in the literature, some limitations still need to be tackled in the future to further enhance the forecasting performance. For instance, the results of this study were discussed based on short-term forecasting horizon during pandemic (30 days period for before and during COVID-19) to determine the most appropriate models in forecasting cash demand. However, it is beneficial to use long-term horizon forecasting to achieve more accurate discussion. Furthermore, other methods, such as deep learning, hybrid AI, and metaheuristics optimization algorithms, can be utilized and compared.

Supplementary Information

Below is the link to the electronic supplementary material.

Authors Contributions

AF: conceptualization, methodology, data curation, formal analysis, software, writing—original draft, and writing—review & editing. MA: conceptualization, methodology, software, formal analysis, writing—original draft, and writing—review & editing. SA: methodology, software, formal analysis, and writing—original draft. GRW: writing—review & editing, and supervision.

Funding

No funding was received.

Availability of Data and Materials

The data are available and submitted.

Code Availability

The Python source code is available if needed.

Declarations

Conflicts of Interest/Competing Interests

The authors hereby declare that they have no conflict of interest that would have affected the work presented in this article.

Ethical Approval

The authors affirm that they followed professional, ethical guidelines in preparing this work.

Consent to Participate

Not applicable.

Consent for Publication

Not applicable.