An Investigation of Multileaf Collimator Performance Dependence on Gantry Angle Using Machine Log Files

Abstract

Background:

Quality assurance of linear accelerators (linacs) is an important part of ensuring accurate radiotherapy treatment deliveries. The aim of this study is to investigate the role of gravity on the positional accuracy of multileaf collimator (MLC) leaves during complex radiotherapy treatments on linacs. This investigation is based on the analysis of the machine log files from five different linacs in multiple centers.

Materials and Methods:

Three main categories of deliveries were considered: Picket fence, volumetric modulated arc therapy (VMAT) (both delivering with continuous gantry rotation), and sliding gap tests delivered at cardinal gantry angles, to determine the error of the MLC in relation to the gantry angle.

Results:

Analysis of picket fence tests revealed a dependence of the error upon the gantry angle. For the majority of deliveries, the MLC showed greater error at gantry angles 270 and 90. The errors computed for the cardinal angles for sliding gap tests were all statistically different with greatest error arising at gantry angle 270 and least error at gantry 90. For picket fence, sliding gap, and VMAT cases, MLC errors were dependent on the gantry angle.

Conclusions:

The errors in leaf positioning were found to be dependent on the gantry angle. For sliding gap tests, the error was greater at gantry angle 270° and 90° and less when the leaf motion was perpendicular to the force of gravity.

INTRODUCTION

Volumetric modulated arc therapy (VMAT) treatments rotate the gantry of a linear accelerator (linac) around the patient while constantly extending and retracting the MLC leaves to provide a highly conformal dose to the treatment area and to minimize dose to the surrounding organs at risk.[1] VMAT treatments also vary; the gantry rotation speed, dose rate, and the collimation set for each VMAT arc.[2,3,4,5]

With the dawn of intensity modulated radiation therapy (IMRT) and VMAT treatments, concerns facing the dependence of the error of the deliveries upon the gantry angle at which they were delivered at were raised. As a result, there has been ample research into assessing the effect of gravity on the gantry head of the linear accelerator[6,7,8,9] and its MLC.[7,10,11,12,13]

In 2005, Wijesooriya et al. used electronic portal imaging devices to discover that gravity can affect the speed of the MLC leaves. When the MLC leaf motion is parallel to the force of gravity, the outer leaves fighting against gravity move 6% slower and the leaves moving with gravity move 2.3% faster than MLC leaves moving perpendicular to gravity.[12]

Analysis of head and neck IMRT treatments using a 2D ion chamber array, radiochromic film, and Varian log files, Buckey et al. observed no gravity effects.[14]

Sharma et al. also researched into the gravity effect on a high definition MLC (HDMLC). They delivered a sliding window IMRT test at different gantry angles and found no gravity effect from measurement of film.[15]

This is in contrast to the numerous papers who all accept the effect of gravity on the MLC, attributing errors, and discrepancies to this effect as well as simulating and warning of it.[12,16,17,18,19,20,21] Lee et al. used a MatriXX ion chamber to measure the dose distribution at different gantry angles. Their research “conclusively reveals that the DMLC gravity definitely affects IMRT dose distribution.”[22] Furthermore, the manual for the Varian (Varian Medical Systems, Palo Alto, CA) MLC suggests preforming tests at different gantry angles so that “the leaves have to fight gravity.”

Varian log files have been in use for over the past decade as a part of quality assurance (QA) programs.[23,24,25,26,27,28,29,30,31,32,33]

These files are created by Varian machines and log at regular time step intervals important information. Some examples include the normalized MUs delivered, the beam state, the gantry angle, and the expected and actual location of each individual leaf of the MLC. From here, the error of the leaves can be calculated. However, it should be noted that, due to the dependent nature of the Varian log files on the system, the error calculated does not take into account external forces that act on the whole system, for example, gravity which causes the entire gantry head to shift.

The aim of this research was to calculate and compare the error of MLC leaves to their corresponding gantry angles through the analysis of Varian log files with the goal to see if there is an innate gantry angle dependence on the leaves of the MLC. To the author's knowledge, this has not been the subject of any research. Five Varian linear accelerators of different models including, Clinac iX, Trilogy, and Truebeam, from multiple centers have been utilized to deliver standard plans used in the quality assurance of MLCs as well as clinical VMAT treatments for analysis. The resulting Varian log files were analyzed by an in-house program.

MATERIALS AND METHODS

Treatment machines

Five Varian linear accelerator treatment machines, including Trilogy (1), Clinac iX (2), and Truebeam (3) models were analyzed as a part of this study.

Each machine is equipped with a Millennium 120 leaf MLC. This MLC is comprised two banks (bank A and bank B) each with 60 tungsten alloy rounded-end leaves mounted on a carriage. The 40 central leaves in each bank are 0.5 cm thick (at the isocenter level) and are known as inner leaves. The peripheral leaves which are known as outer leaves are 1.0 cm thick (except for the first and last leaf pairs which are 1.4 cm thick). Each leaf is equipped with a motor and encoder and is driven by the MLC controller (VxWorks^® Real-time operating system) which drives the leaf along the carriage. Each of the MLC carriage assemblies weighs approximately 36 kg.

Throughout this paper, all angle measurements of the Varian treatment machines conform to IEC-61217 convention.[34]

Five linacs were used in this study. Their code names, models, and number of years in service are listed in Table 1.

Table 1.

The code name each linac used in this study and their number of years in service

Code name	Model	Age
iX-1	Varian - Clinac iX	7
iX-2	Varian - Clinac iX	6
Tri-1	Trilogy	5
True-1	Truebeam v1.5	2
True-2	Truebeam v1.5	2

Calculating error from Varian log files

The trajectory log files were converted into DynaLog format before analysis by a third party software.

Using these files, the error of each leaf, n, at each time step, t, was calculated by equation 1.

Error (n, t) = Expect (n, t) − Actual (n, t) (Equation 1)

Where Expect is the expected position of the MLC leaf and actual is the actual position of each leaf as denoted by the Varian log files. The error is computed for both bank A and bank B of the MLC.

The leaf gap error was computed by equation 2.

GapError (n, t) = (ExpectA [n, t] + ExpectB [n, t]) – (ActualA [n, t] + ActualB [n, t]) (Equation 2)

Where ExpectA is the expected position of the MLC leaf for bank A, ExpectB is the expected position of the MLC leaf for bank B, ActualA is the actual position of the MLC leaf for bank A, and ActualB is the actual position of the MLC leaf for bank B.

Picket fence test

In the picket fence test, also known as Ling's test 1,[35] the 60 MLC leaf pairs were swept across a 200 × 390 mm² (X × Y) field collimated by the jaws. The MLC stopped every 20 mm, irradiating a 1 mm gap while rotating the gantry 28.6°, resulting in ten strips of narrow gaps acquired during a 352° gantry rotation.[36] All tests were performed with collimator angle 0° and each delivery took approximately 70 s to run.

Ling's test 1 was routinely delivered as a part of a quality assurance program on the five linacs. The log files were retroactively collated and analyzed to compute the error of each leaf through equation 1. The error for each leaf at each time step was tagged with its corresponding gantry angle also pulled from the log files. A total of 13, 14, and 732 log files were collated for the iX-1, Tri-1, and True-1 machines, respectively.

Each delivery was split into 176, 2° control point windows for analysis. The errors of the leaves were averaged over these control point windows to investigate the dependence of error upon the gantry angle. Data were only logged in the log files when the leaves were stationary and the beam was delivering. As such there exists control points, when the leaves are moving and the beam is off, that have no corresponding data. The error was computed for bank A, bank B, and the leaf gap between the two banks.

Sliding gap

In the sliding gap test, the 60 MLC leaf pairs were swept unidirectionally at a constant velocity, across a 200 mm × 390 mm (X × Y) field collimated by the jaws. Each leaf pair was separated by a gap of 5 mm with the collimator at 0° for the fixed-gantry measurements.

Sliding gap tests was performed on iX-2 a total of four times each at the cardinal gantry angles of 0°, 90°, 180°, and 270°. This was repeated for leaf velocities, 10 mm/s and 20 mm/s. Delivery times ranged from 7.6 s for leaf velocity 20 mm/s to 15 s for leaf velocity 10 mm/s. Varian log files were extracted for each of these tests and analyzed to extract the error of the leaves which were then amalgamated based on their gantry angle and leaf velocity.

Volumetric modulated arc therapy deliveries

A total of 1126 VMAT deliveries were performed on Truebeam machines, True-1 and True-2. Among 1126 deliveries, 724 were delivered with a collimator angle of 30° and the remaining 402 were delivered with collimator angle 330° (−30°). The collimator angle was fixed during delivery. This has the consequence that at gantry angle 90° or 270° the motion of the MLC leaves will not be parallel to the force of gravity.

The collimator angles were chosen due to the abundance of data available for analysis. These collimator angles are commonly used in deliveries to combat the tongue and groove effect. All deliveries with collimator angle 30° were delivered on a gantry rotating clockwise, and all deliveries with collimator angle 330° were delivered on a gantry rotating counter clockwise.

The deliveries were split into 180, 2° control point windows for analysis. The error of all the leaves for all the deliveries for both treatment machines was then averaged inside of these control points. Due to the range of the gantry angle for different treatment deliveries, some of the control points did not contain any data. The error was computed for bank A and bank B of the MLC.

Statistical analysis

Statistical analysis was undertaken using MATLAB programming language and software (The Mathworks Inc., Natick, MA, USA). Statistical analysis was performed on Ling's Test 1 as well as Sliding Gap QA.

In the case of Sliding Gap QA analysis of variance (ANOVA), tests were performed to assess the difference between errors present at gantry angles 0°, 90°, 180°, and 270°. A multiple comparison test was then performed to determine if any similarities were shared between the different errors (P < 0.05). This was performed for both bank A and bank B of the MLC.

In the case of Ling's Test 1, where the gantry was constantly rotating during delivery, ANOVA tests were performed to assess the difference between the control point averaged error located in a 40° arc centered on gantry angles 0°, 90°, 180°, and 270°. The arc length of 40° was experimentally chosen to give the best graphs. A multiple comparison test was then performed to determine if any similarities were shared between the different errors (P < 0.05). The statistical analysis was performed for error on bank A, bank B, and error present in the leaf gap.

RESULTS

Results of investigations into Ling's Test 1, Sliding Gap QA, and VMAT treatments regarding the error of the MLC at different gantry angles are given separately in this section. All angles present are given in IEC convention.

Ling's test 1

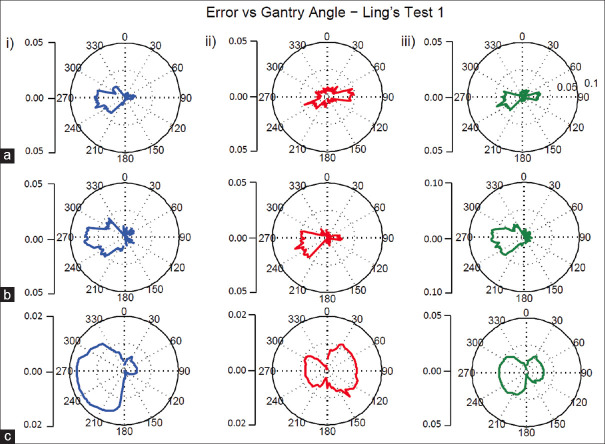
Ling's Test 1 for True-1, iX-1, and Tri-1 was analyzed to assess the effect of gravity on the positional error of the leaves. Data were only recorded when the leaves were stationary. The error of all the leaves for each treatment machine was averaged over multiple 2° control points [Table 2]. The absolute error of these results, iX-1, Tri-1, and True-1 is presented graphically in Figure 1.

Table 2.

The absolute error (microns) at the cardinal gantry angles of Ling Test 1 for bank A, bank B, and the leaf gap

Gantry angle	iX-1			Tri-1			True-1
	Absolute error (μm)			Absolute error (μm)			Absolute error (μm)
	Bank A	Bank B	Leaf Gap	Bank A	Bank B	Leaf Gap	Bank A	Bank B	Leaf Gap
	0°	3.25	9.17	12.4	0.643	1.48	0.839	1.98	14.17	6.16
90°	4.98	21.1	26.1	0.255	12.0	11.4	4.70	10.8	15.5
180°	2.23	3.78	4.21	5.85	3.69	10.6	2.73	6.50	3.78
270°	17.6	7.12	33.4	34.2	20.8	58.0	17.4	8.05	25.4

Figure 1.

Polar plots of the error (mm) versus the gantry angle of multiple treatment machines and leaf banks. Polar plot of the error (mm) in the radial component that has been averaged over 2° control points, versus the gantry angle (IEC convention) for (a) iX-1 (13 tests) (b) Tri-1 (14 tests) and (c) True 1 (732 tests). This was further split into the error present on (i) bank A, (ii) bank B, and (iii) the leaf gap width. Please note the different scales present on the polar plots. These graphs serve to help us understand the error distribution for each individual bank of each machine

There is a trend present on bank A for a greater error to be present at gantry angle 270° when compared with gantry angle 90°. Conversely, on bank B, iX-1, and True-1 both have marginally greater error at gantry angle 90° although Tri-1 still possesses greater error at gantry angle 270°.

The error present in the leaf gap width also shows dependence on the gantry angle with greater error at gantry angles 90° and 270° save for the data collected for Tri-1, which shows minimal change in error for gantry angle 90° when compared with gantry angle 0°.

A table collating the maximum error of each graph and their corresponding gantry angle is collated in Table 3.

Table 3.

The absolute maximum error (mm) and the corresponding gantry angles of Ling Test 1 for bank A, bank B, and the leaf gap delivered on iX-1, Tri-1, and True-1

Machine	Measurement site	Maximum error (mm)	Gantry angle (degree)
iX-1	Bank A	0.028	251
	Bank B	0.024	85
	Leaf gap	0.050	251
Tri-1	Bank A	0.037	265
	Bank B	0.031	247
	Leaf gap	0.060	277
True-1	Bank A	0.018	251
	Bank B	0.013	139
	Leaf gap	0.025	261

Statistical analysis was undertaken to determine if the error located inside 40° control point arcs centered on gantry angles 0°, 90°, 180°, and 270° was different to each other.

For treatment machine iX-1, the mean error was statistically different between each gantry angle pair except for gantry angle pair, 0° and 180°. We cannot reject the null hypothesis that the mean error between gantry angles 0° and 180° for bank A are dissimilar. For bank B of the MLC gantry angles, the only gantry angle statistically dissimilar is gantry angle 270°. All other gantry angles are statistically similar to each other, 0° to 90°, 90° to 180°, and 0° to 180°. For the leaf gap error, all angles were statistically different.

For bank A of treatment machine Tri-1, all gantry angle windows were statistically different. For bank B, we could not reject the null hypothesis between gantry angles 0° and 180°. Moreover, for the leaf gap error, we could not reject the null hypothesis between gantry angles 0° and 180° or 90° and 270°.

For bank A of True-1, the mean error of gantry angles 0° and 90° is statistically similar. For bank B, the mean error of gantry angles 0° and 180° is statistically similar. Moreover, for the leaf gap error, gantry angles 180° and 270° were statistically similar.

Sliding gap

Sliding gap tests from iX-2 were analyzed to compare the error of the MLC to its corresponding gantry angle. The test was performed four times at cardinal gantry angles 0°, 90°, 180°, and 270°. This was repeated for two discrete leaf velocities.

One such result, for when the leaves were travelling at 10 mm/s is represented graphically in Figure 2. The analysis of leaves travelling at 20 mm/s is represented graphically in Figure 3. This analysis is also tabulated in Tables 4 and 5 for sliding gap 10 mm/s and 20 mm/s, respectively. Statistical analysis comparing the error at different gantry angles was also carried out.

Figure 2.

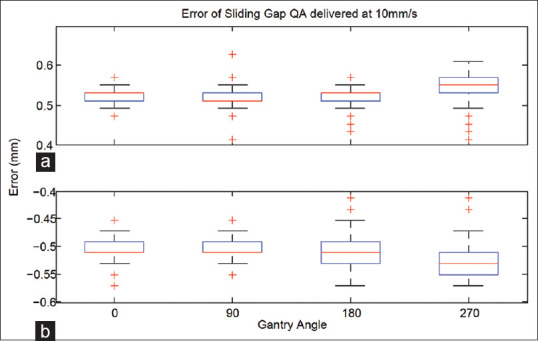
Box and whisker plots of the multileaf collimator error of Sliding Gap QA (10 mm/s) performed at cardinal gantry angles. The error (mm) for sliding gap QA delivered at four different gantry angles on iX-2 for (a) bank A, and (b) bank B. Leaves moved with velocity 10 mm/s. The box and whisker plot represents the data as follows: The top line (or whisker) is the maximum value, the next line is the 3^rd quartile, the red line is the median, the next line is the 1^st quartile, and the last line is the minimum value. The red crosses are outliers

Figure 3.

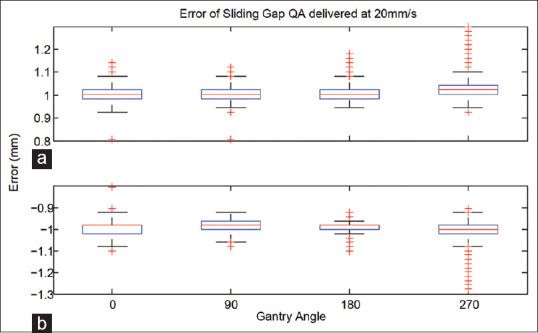
Box and Whisker plots of the multileaf collimator error of Sliding Gap QA (20 mm/s) performed at cardinal gantry angles. The error (mm) for Sliding Gap QA delivered at four different gantry angles on iX-2 for (a) bank A, and (b) bank B. Leaves moved with velocity 20 mm/s. The box and whisker plot represents the data as follows: The top line (or whisker) is the maximum value, the next line is the 3^rd quartile, the red line is the median, the next line is the 1^st quartile, and the last line is the minimum value. The red crosses are outliers

Table 4.

The error for Sliding Gap quality assurance (10 mm/s) delivered at cardinal gantry angles on iX-2 on bank A and bank B

Leaf bank	Gantry angle (degree)	Mean (mm)	SD (mm)
Bank A	0	0.520	0.037
	90	0.518	0.037
	180	0.524	0.036
	270	0.544	0.039
Bank B	0	−0.506	0.037
	90	−0.503	0.038
	180	−0.508	0.038
	270	−0.523	0.040

Results are displayed as mean error and SD. SD: Standard deviation

Table 5.

The error for sliding gap quality assurance (20 mm/s) delivered at cardinal gantry angles on iX-2 on bank A and bank B

Leaf bank	Gantry angle (degree)	Mean (mm)	SD (mm)
Bank A	0	0.995	0.119
	90	0.991	0.117
	180	0.993	0.120
	270	1.01	0.097
Bank B	0	−0.980	0.122
	90	−0.971	0.120
	180	−0.975	0.121
	270	−0.995	0.094

Results are displayed as mean error and SD. SD: Standard deviation

As an aside, there is a small 50 ms delay inherent in older Varian treatment machines.[37] Varian Truebeam machines have a supervisor module installed which eradicates this delay.

Due to the nature of the Sliding Gap deliveries, that is the leaves on bank A are extending unidirectionally and the leaves on bank B are retracting unidirectionally, the expected positions of the leaves of bank A will always be greater than the actual positions. Furthermore, the expected positions of the leaves of bank B will always be less than the actual positions. This explains why the error for the leaves on bank A is always be positive and the error for the leaves on bank B is always negative.

In both banks, gantry angle 270° had the greatest mean error. Conversely, gantry angle 90° had the least mean error in both banks.

Each gantry angle on each bank was analyzed to determine if it was statistically significant from other gantry angles residing on the same bank. For the sliding gap delivered at 10 mm/s, all gantry angles were found to be statistically different from each other.

For the sliding gap delivered at 20 mm/s, the delivery at gantry angle 270° had the greatest error and gantry angle 90° had the least. All gantry angles were statistically different from one another except for gantry angles 180° and 0° on bank A, as well as gantry angles 180° and 90° on bank A. In addition on bank B, the errors found at gantry angles 90° and gantry angle 180° were statistically similar.

Volumetric modulated arc therapy treatments

A total of 1126 VMAT deliveries performed on Truebeam machines, True-1 and True-2, with either collimator angle 30° or 330°, were analyzed to calculate the error of the MLC at different gantry angles. This is shown graphically in Figure 4. The standard deviation for collimator angle 30° is 0.007 mm for both bank A and bank B. The standard deviation for collimator angle 330° is 0.008 mm for bank A and 0.007 mm for bank B.

Figure 4.

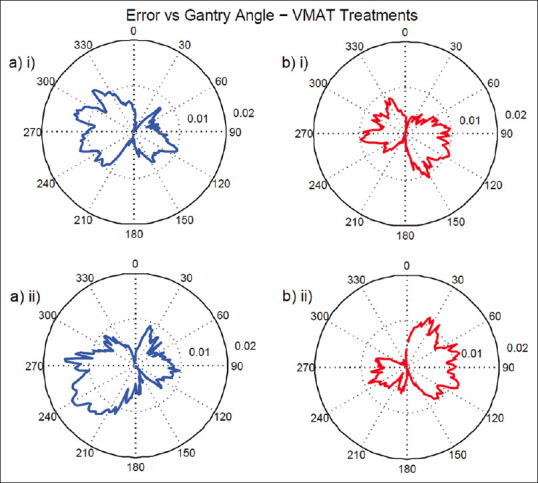
Polar plot of the error (mm), averaged over 2° control points, in the radial component versus the gantry angle (IEC convention) for treatments with collimator angle (IEC convention) (i) 30 and (ii) 330. These were also split into (a) bank A and (b) bank B. There were 798 and 402 treatments for collimator angles 30 and 330, respectively

The polar plots possess the same basic structure as the polar plots created from Ling Test 1 data from the Truebeam machines [Figure 1]. However, it is interesting to note that the distribution of the average positional errors is dependent on the collimator angle. The polar plot of collimator angle 30° and 330° rotates the distribution found at collimator angle 0° of Ling's Test 1.

DISCUSSION

The magnitude of the errors that were calculated from the Varian log files is clinically insignificant. However, though the calculated error from the Varian log files may be clinically insignificant, due to their nature, one where they lack independence from the machine, the errors will be magnified and contribute to larger issues. As such it is important to take note of the general trends that arise from the analysis as they give us a deeper understanding of the system and will help us in our future endeavors to minimize error.

Ling's test 1

This study looked into the affect gravity played on the positional errors of the MLC. Results from Ling's Test 1 tests indicate that, on bank A, there is a trend toward greater error present at gantry angle 270° when compared with gantry angles 0°, 90°, and 180°. There is also an increase in error at gantry angle 90° but to a lesser extent. This trend is similar in bank B except the error at gantry angle 90° is more pronounced. The increase in error can be explained due to the presence of gravity. The error is greater at angles where the MLC motion is parallel to the force of gravity and less when it is perpendicular to the force of gravity.

The asymmetric distribution of errors toward 270° instead of 90° could be a result of a number of factors. At gantry angle 270° and collimator angle 0°, for Ling's Test 1, the MLC is positioned as in Figure 5.

Figure 5.

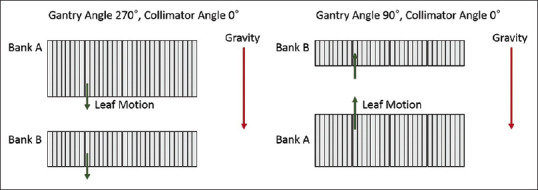
Schematic of multileaf collimator banks at different orientations. The position of the multileaf collimator at gantry angles 90° and 270° for Ling's test 1. The collimator angle is 0°

At gantry angle 270°, the leaves on bank A are travelling in the direction of the force of gravity. At gantry angle 90°, the leaves on bank A are travelling in a direction opposing the force of gravity. The fact that the motion of the leaves on bank A is assisted by gravity at gantry angle 270°, whereas the motion of the leaves on bank B is retarded by gravity at gantry angle 90° may lead to the asymmetric distribution of positional error.

However, this effect is not mirrored for bank B. The position of bank B is inverted such that at gantry angle 90° the leaves are moving opposite to the force of gravity and at gantry angle 270° the leaves are moving in the same direction as the force of gravity. However, the distribution of the positional error of bank B changes depending on the machine. For iX-1, the positional error of bank B for gantry angle 90° is slightly larger than the error at gantry angle 270°. For Tri-1, the error for gantry angle 90° is smaller than the error found at 270° and for True-1 the error at gantry angle 90° is of the same order as the error at gantry angle 270°. None of the distributions of bank B mirror those of bank A where the positional error at 270° is significantly larger than the error at gantry angle 90°. The error of bank B at gantry angle 90° is either smaller, of the same order, or slightly larger than the error at gantry angle 270° based on the treatment machine.

The fact that this is not restricted to one machine is interesting. Bank A has consistently greater error at gantry angle 270° when compared to gantry angle 90° in all treatment machines, whereas the structure present in bank B is completely different. Ling's Test 1 was performed for both clockwise and counter clockwise rotations which erases dependence on any errors arising from a temporal standpoint.

If gravity is the only force that is acting on the system then we would assume the distribution of errors on bank B to mirror those of bank A. As this is not the case, then it is safe to assume that other factors are in play. More research needs to be done in this area to understand this phenomenon, focusing on delivering Ling's Test 1 at different collimator rotations, most importantly 180°, to see if the direction of motion of the leaves, that is whether they are extending or retracting, affects the outcome or if the error of the MLC is solely dependent on the gantry angle.

Sliding gap

The results obtained from sliding gap deliveries at cardinal gantry angles suggest a dependence of the positional errors on the gantry angle. For both bank A and B the error was more pronounced at gantry angle 270°. Interestingly, the positional error at gantry angle 90° was less than the error of the control gantry angles, 0° and 180°. The same error distribution for both bank A and bank B suggests that there is not a dependence on the direction of motion of the leaves but instead purely on the gantry angle. Again, the asymmetry of gantry angle 270° having greater error than gantry angle 90° for both banks suggests that there are other factors besides gravity that are coming into play. Further research has to be done to ascertain what these factors are and whether or not this effect is localised to Clinac iX treatment machines or not.

The positive error found in bank A and the negative error found in bank B is a consequence of how the error is calculated, the MLC system delay, and the movement of the leaves. The aforementioned 50 ms delay inherent in older Varian treatment machines[37] along with the unidirectional motion of the leaves on both bank A and bank B, ensure the leaves of bank A will always have positive error and the leaves of bank B will always have negative error.

Volumetric modulated arc therapy treatments

Finally, the analysis of actual VMAT treatments delivered by Truebeam machines further supports the hypothesis that the gantry angle affects the positional accuracy of the leaves. Treatments delivered with a collimator angle of 30° and treatments delivered with a collimator angle of 330° had different distributions for the positional accuracy versus the gantry angle. When the collimator angle is set to 0° the motion of the leaves are subjected to the full force of gravity at gantry angles 90° and 270°. However, this changes when the collimator rotates. The rotation of the collimator ensures that the direction of motion of the leaves is never parallel to the force of gravity. As such one would expect the distribution of the positional errors to change with different collimator angles as each collimator angle would have a corresponding gantry angle that provides the least resistance to the force of gravity. As the collimator rotates, gravity will then start acting on the leaves such that they are pushed into one another causing interleaf friction to come into play however this was not investigated in this study.

It should be noted that the error difference of the leaves at different gantry angles is quite small. In Clinac iX and Trilogy machines the maximum error difference between gantry angles 270° or 90°, and 0° or 180° of the leaves when they were stationary during Ling's Test 1 is <0.03 mm. For sliding gap tests, the maximum error difference between gantry angle 270° and 0° or 180° is 0.0245 mm. Of course, these discrepancies may be magnified during real treatments where the leaves are not moving with routine patterns. It should be noted the differences of error found in VMAT treatments delivered on Truebeam machines were <0.0200 mm however these results do not translate across to Clinac iX or Trilogy machines as the Truebeam machine “significantly reduced leaf position error” when compared with 2100CD linacs,[38] that is Clinac iX machines.

To clarify, the Varian log files only record the effect upon the leaf position. The actual gantry head, as well as the MLC carriages themselves, do sag throughout the treatment by a significant amount[39] however, the Varian log files do not pick up on this discrepancy due to the MLC controller system being located inside of the gantry head. The gantry head can sag up to 0.82 mm and the MLC carriage can sag up to 0.99 mm throughout the course of a treatment.

There is a dependence of the positional error of the leaves upon the gantry angle; however, it is clear that there are other factors in play from the dissimilar error distributions of bank A and bank B of Ling's Test 1 and sliding gap tests.

One such factor may arise from loose t-nuts connecting the motor to each individual leaf. If the t-nut connecting the motor to the leaf is loose then even though the motor is rotating, the leaf would not move. As such, the Varian log file would record that the leaf has extended a set distance even though it has not moved. Calvo-Ortego et al. raised concerns over DynaLog files pointing out that “DynaLog files do not reflect leaf positional errors related to a miscalibration (offset)” and that they are not sensitive to errors pertaining to the absolute calibration of the linac.[40]

CONCLUSIONS

The study concludes that the error of the leaves is dependent on the gantry angle. For Ling's Test 1, the positional error is greater at gantry angles where the leaf motion is parallel to the force of gravity. For sliding gap tests, the error is greatest at gantry angle 270°, followed by 90°, but less when the leaf motion is perpendicular to the force of gravity. In addition, the positional errors of VMAT treatments were also affected by gravity which is evidenced in the different distributions based on the collimator angle.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.