A 200 nanoseconds all-atom simulation of the pH-dependent EF loop transition in bovine β-lactoglobulin. The role of the orientation of the E89 side chain

Abstract

In silico molecular dynamics (MD) using crystallographic and NMR data was used to simulate the effects of the protonation state of E89 on the pH-dependent conformational rearrangement of the EF loop, also known as the Tanford transition, in a series of apo-β-lactoglobulin (BLG) structures. Compared to existing studies these simulations were carried out over a much longer time scale (200 ns where the stability of the transition can be evaluated) and used an explicit water model. We considered eight different entries from the Brookhaven Protein Data Bank (PDB) separated into two groups. We observed that fixing the protonation state of E89 prompts the transition of the EF loop only when its side chain is oriented under the loop and into the entrance of the interior cavity. The motion of the EF loop occurs mostly as a step-function and its timing varies greatly from ~ 20 ns to ~170 ns from the beginning of the simulation. Once the transition is completed, the protein appears to reach a stable conformation as in a true two-state transition. We also observed novel findings. When the transition occurs, the hydrogen bond between E89 and S116 is replaced with a salt bridge with Lys residues in the βC-CD loop-βD motif. This electrostatic interaction causes the distortion of this motif as well as the protrusion of the GH loop into the aperture of the cavity with the result of limiting the increase of its contour area despite the rotation of the EF loop.

1. Introduction

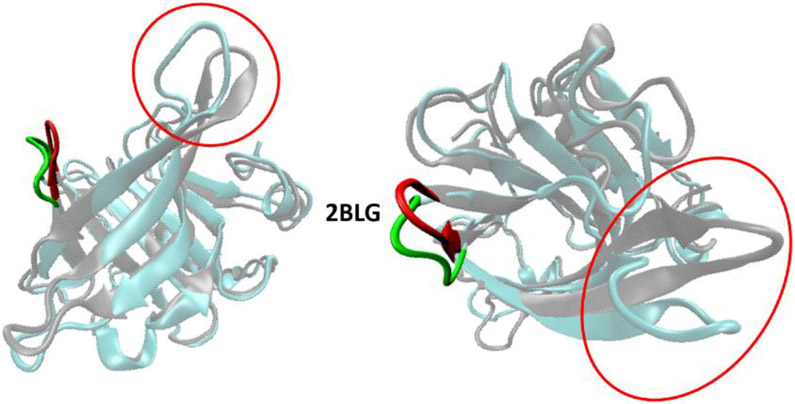
Under physiological conditions proteins undergo several internal motions that span large time (from to s (Eaton & Wolynes, 2017; Englander & Mayne, 2017)) and spatial scales (from local librations, to collective folding transitions (Kubelka et al., 2006; Henzler-Wildman et al., 2007; Eaton & Wolynes, 2017; Englander & Mayne, 2017; Xie et al., 2019)). Often these motions are not mere fluctuations of microstates but are reversible events (frequently aided by other factors such as ligands, chaperones, etc.) that are essential to the function of polypeptides (Freedman et al., 2017; Guo & Zhou, 2016; Henzler-Wildman et al., 2007). Among the dynamic segments of proteins, loops, i.e. regions that connect highly repetitive structures (such as α-helices and β-sheets), undergo crucial folding transitions. Loops can be short and structured (e.g. hairpins (Blanco et al., 1998)) or develop over longer and apparently unstructured conformations (Martin et al., 1995). They often provide flexible motifs that contribute to an array of fundamental biophysical properties (Amacher et al., 2015; Deryusheva et al., 2018; Herr, 2018; Jupin et al., 2017; Kreß et al., 2018) such as the regulation of catalytic activity (Devanand et al., 2018; Papaleo et al., 2016), the gating of transmembrane channels (Uthoff & Baumann, 2018), the control of folding patterns (Fukuchi et al., 2006; Weng & Wang, 2019) and the access of ligands to binding sites (Kaneko et al., 2010; Mokaberi et al., 2020). Conformational changes of loops can be triggered by many mechanisms that include, among others, the binding of specific ligands (Dellisanti et al., 2013), structural changes of other regions of the protein (Sagermann et al., 2003) or the protonation/deprotonation of residues (Mollaaghababa et al., 2000). The prominent role played by loop mobility is evident in lipocalins (Flower, 1996), a ubiquitous family of transport proteins. Within this family one important motion is represented by the pH-dependent conformational change (also known as the Tanford transition (Tanford & Nozaki, 1959)) involving the loop that connects β-strands E and F (EF loop) in bovine β-lactoglobulin (BLG). Although the detailed functional role of this transition (and indeed of the entire protein) is still not completely characterized, the leading hypothesis for the EF loop conformational change is the regulation of the access to the single interior cavity (β-barrel) of the protein which is the major binding site for fatty acids and other molecules (Kontopidis et al., 2002; Konuma et al., 2007; Loch et al., 2011). The EF loop is located at the rim of the cavity and experimental studies have revealed that at pH < 7.5 it folds over the entrance of the cavity and limits access to its interior(Qin et al., 1998). Conversely, at pH > 7.5 the loop undergoes a rotation that increases access to the cavity. Since BLG is found in the milk of most mammals, the evidence for the EF loop transition has led to the hypothesis that the mechanism is used to ‘trap’ fatty acids inside the cavity as milk travels through the acidic upper GI tract, whereas the nutrients are released in the lower GI tract, where the pH is alkaline. This sequence of events may make the nutrients more digestible in suckling animals (Sawyer & Kontopidis, 2000). The event that regulates the transition has been postulated to be the deprotonation of a glutamic acid residue (E89) at the end of the loop. This residue appears to have an unusually large pK_a of the side chain (~ 7.0, compared to an expected value of ~ 4.4) which has been attributed to the formation of a hydrogen bond with the S116 residue on the GH loop adjacent to the EF loop(Eberini et al., 2004; Harms et al., 2009). The correlation between this unusual pK_a and the pH at which the conformational change of the loop occurs, makes E89 the likely culprit of the structural change of BLG. Crystallographic data has provided the evidence of the conformational change but it has not elucidated whether the deprotonation of E89 is the cause or has provided dynamic information about the transition. Such hypothesis can be tested using computational methods that have been used to simulate protein folding as well as the association of biomolecules with ligands either alone or in support of experimental data (Hu et al., 2017; Noinaj et al., 2017; Hu et al., 2019; Shakibapour et al., 2019; Sharifi-Rad et al., 2020). Surprisingly, only few examples of computational simulation of the EF loop of BLG can be found. One study by Bello et al. showed that the loop participates in the binding of fatty acids (Bello & Garcia-Hernandez, 2014) (highlighting the role that loop flexibility plays in modulating the binding of ligands). Two other studies by Fogolari et al. Fogolari et al., Fogolari et al., (2005) and Eberini et al. Eberini et al., Eberini et al., (2004) investigated the Tanford transition in a short time window (3 ns) using an implicit water model. In addition, the structures used in those studies (2BLG and 3BLG) have starting coordinates that orient the side chain of E89 in the direction away from the cavity (Figure 1 and Figure S1, supplementary material). The study we carried, on the other hand, is an all-atom study that uses an explicit water model and extends the simulation to a time window of 200 ns, which is sufficiently long to observe the step-wise conformational transition of the EF loop. In addition, we investigated simulation results among a larger group of starting BLG structures (different BLG entries in the Protein Data Bank, PDB) to compare the effects of the initial orientation of E89 relative to the loop as well as the influence of the initial conformation of the EF loop (open vs closed) (Figure 1 and Figure S1, supplementary material). The results show that the initial orientation of the side chain of E89 is crucial to prompt the conformational changes. Only PDB entries in which the side chain of E89 is located underneath the EF loop (Figure 1 and Figure S1, supplementary material) show a significant transition upon changing the net charge of the residue.

Figure 1.

Starting of representative PDB entries for group 1 (2BLG) and group 2 (1CJ5). In gray is the ribbon structure of the protein while in orange is the EF loop (also represented as a ribbon structure). The E89 residue is represented as balls-and-sticks in CPK colors. In 2BLG ((A) and (B)) the EF loop is rotated and stretched in a conformation approximately perpendicular to the entrance of the cavity (open conformation) consistent with the alkaline condition used to collect its structure. Moreover, the side chain of E89 is oriented outside the EF loop. In 1CJ5 ((C) and (D)) the EF loop is folded over the entrance of the cavity in a closed conformation consistent with the structure obtained under acidic conditions. Also, the side chain of E89 is oriented towards the center of the entrance of the cavity under the EF loop.

The closed open transition itself appears to occur mostly as a step-function and more rarely as a gradual rearrangement. Our simulations also reveal some additional effects that influence the accessibility of the cavity: 1) the protrusion of a the AB loop into the entrance of the cavity, 2) the formation of a salt bridge between the deprotonated E89 and one of two Lys residues (K60 or K69) on the CD-loop and the βD strand and (as a result) the protrusion of the CD and GH loop into the entrance of the cavity. These interactions, limit the increase of the accessible area of the cavity when the conformational transition of the EF loop occurs.

2. Materials and methods

2.1. Structural models

Molecular structures were entries from the Brookhaven Protein Data Bank (PDB) (Kuwata et al., 1999; Loch et al., 2011; Qin et al., 1998; 1999; Sauter et al., 2014; Uhrinova et al., 2000). We selected eight entries summarized in Table 1. Of the eight entries 6 were obtained by X-ray diffraction and two by solution NMR, one was recorded at alkaline pH, three with pH slightly above neutral and four at slight or strong acidic pH. In five of the structures (all the ones obtained at pH < 7.0 and one, 1BSQ, recorded at pH 7.1) the EF loop was folded over the entrance of the interior cavity of the protein (‘closed’ conformation) while three assumed an ‘open’ conformation with the EF loop stretched perpendicular to the entrance of the cavity (Figure 1 and Figure S1, supplementary material). We separated the entries in two groups: group 1, that contains the entries at neutral or slightly alkaline pH and present the EF loop in open configuration and group 2 that contains the entries that are experimentally obtained at acidic pH (Table 1) as well as 1BSQ which was obtained at neutral pH but which shows the closed conformation of the EF loop common to the structures at acidic pH.

Table 1.

Summary of the relevant structural features of the PDB entries.

PDB Entry	pH	Experimental Method	Initial Position EF Loop	Position of the ionizable group of E89
2BLG	8.2	X-ray diffraction	open	exterior
1BSY	7.1	X-ray diffraction	open	exterior	Group 1
3NPO	7.5	X-ray diffraction	open	exterior
1BSQ	7.1	X-ray diffraction	closed	interior close to S116
3BLG	6.2	X-ray diffraction	closed	interior close to S116
1DV9	2.7	Solution NMR	closed	interior close to S116	Group 2
4LZU	6.0	X-ray diffraction	closed	interior under N88
1CJ5	2.0	Solution NMR	closed	interior under N88

One of the most relevant parameters for our discussion is the orientation of the side chain of E89 compared to the rest of the EF loop when is folded in the closed conformation. One notices that in all three entries of group 1 (2BLG, 1BSY, 3NPO) the side chain of E89 is directed outward and its ionizable group is therefore positioned away from the residues of the EF loop (Figures 1 and S1). In three of the entries of group 2 (3BLG, 1BSQ and 4LZU) the side chain of E89 is directed towards the interior of the protein but to the side of the loop in a conformation that forms a hydrogen bond with S116 (postulated to be the reason for the unusual pK_a for E89 (Qin et al., 1998)). In the remaining two entries (1CJ5 and 1DV9) the side chain of E89 is directed towards the interior of the cavity with the ionizable group positioned underneath the N88 residue of the EF loop when it is folded in closed configuration (Figures 1, Figures S1 and S2, supplementary material).

2.2. Molecular dynamics simulations

2.2.1. Protein preparation and structure minimization

MD simulations were carried out using version 2.11 of NAMD Scalable Molecular Dynamics (Phillips et al., 2005) and utilizing the CHARMM36 force field (Vanommeslaeghe et al., 2010). Each protein was prepared using the psfgen structure building tool of Visual Molecular Dynamics (VMD 1.9.3). For each PDB structure we carried out two simulations at fixed protonation state for E89: one with the protonated E89 (E89⁽⁰⁾, fixed 0 net charge of the side chain reproducing the native condition at pH < 7.4) and one with the deprotonated E89 (E89⁽⁻¹⁾, fixed −1 charge of the side chain reproducing native condition at pH > 7.4). By default the PDB files contain E89⁽⁻¹⁾ for all glutamic acid residues. Therefore, E89⁽⁰⁾ had to be introduced by applying the force field parameters of CHARMM for protonated glutamic acid (GLUP patch) at position 89. The molecule was solvated in a 80 × 80 × 80 cubic box using the explicit TIP3P water model. Sodium atoms were added to neutralize the system and additional sodium and chloride atoms were added to reproduce a 150 mM salt concentration (these steps were carried out using the autoionize function in VMD). Each systems contained ~ 48,200 atoms. The energy of each system was initially minimized for 1000 steps (1 ps) using the conjugate gradient algorithm.

2.2.2. Molecular dynamic settings

Simulations used the CHARMM36 force field with Langevin stochastic dynamics to reproduce a constant temperature of 310 K and a constant pressure of Pa. Electrostatic interactions were implemented by means of particle mesh Ewald (PME) with grid size 1.0. Time steps were set at 2 fs (rigid bonds). The PME was evaluated every 4 fs and the Langevin damping was set at 1 ps⁻¹. Bonded and non-bonded interactions were updated every time-step while the long-range forces were updated every two time-steps. The covalent bonds of hydrogens were not fixed. The van der Waals interactions were smoothly switched off at 12 (starting at 10). Simulations without constraints were carried out for 200 ns with trajectory and energy parameters recorded every 0.1 ns.

2.2.3. Molecular dynamic analysis

2.2.3.1. Secondary structure analysis.

Secondary structure comparisons were carried out using the sequence viewer plugin in VMD. The percentages of secondary structures were determined using the assignments generated by sequence viewer (categorized according to the dihedral and angles of consecutive peptide bonds).

2.2.3.2. Conformation of the EF loop.

The conformational change of the EF loop was determined by measuring the distance between of W19 and of L87 (W19-L87). The L87 residue is located at the apex of the EF loop and is therefore the one that undergoes the larger backbone motion during the Tanford transition. On the other hand W19 (which is the only conserved residue in the lipocalin family (Katakura et al., 1994)) is located at the bottom of the cavity and possesses one the smallest RMSD values within the protein (< 0.8). The W19-L87 distance was calculated using the bond label plugin of VMD and plotted as a function of the number of steps (time).

2.2.3.3. Rmsd analysis.

The RMSD analysis was carried out using the RMSD trajectory tool of VMD. RMSD analysis was performed on consecutive sequences of 5 residues throughout the entire protein using the initial frame as reference. The RMSD was calculated only on the backbone atoms since the conformational transition of the EF loop is foremost a rotation of the backbone atoms. The rationale for this analysis is to establish whether the 5-residue-long EF loop has an intrinsically larger mobility compared to any other sequence of 5 residues within each BLG entry.

2.2.3.4. Hydrogen bonds (HB) and salt bridges (SB).

HB were counted using the hydrogen bonds plugin of VMD and tracked during the trajectories. HB were limited to OH pairs with a distance cutoff of 3.2 and cutoff angle of 60°. We tracked both the total number of HB as well as the number of HB formed or broken by the residues in the EF loop throughout its trajectory. In particular we recorded the distance between E89 and S116 that are known to form a HB which is key to the unusual deprotonation pK_a of E89. The SB between E89 and K60 or K69 was monitored using the hydrogen bonds plugin of VMD and tracked during the trajectory. The SB distance cutoff was set at 5.5.

2.2.3.5. Area of the entrance to the interior cavity.

The area of the entrance to the interior cavity was calculated by visually identifying the atoms forming the rim of the cavity and assigning their coordinates using the atoms label plugin in VMD. The coordinates were imported into Matlab and the contour of the entrance was determined by the polygonal line that joined the coordinates of these atoms. The area of the polygon was calculated using the polyarea command in Matlab.

3. Results and discussion

Experimentally, the most important effect observed in BLG between acidic and alkaline pH is the movement of the EF loop prompted by the unusual pK_a of E89. (Qin et al., 1998) Deprotonation of the carboxylic group of E89 causes changes in the boundary of the electrostatic field and prompts the rotation of the EF loop. The major focus of this work was to compare the effect of the deprotonation of E89 on the conformational transition of the EF loop and the consequent access to the interior cavity of BLG. More specifically, we investigated what is the effect of the starting location of the side chain of E89 relative to the EF loop and to the entrance of the cavity. We first present some general structural results among the various proteins and we subsequently focus the analysis on the major conformational changes associated with the EF loop transition.

3.1. Comparison of secondary structures

3.1.1. Initial structure

We analyzed the initial secondary structures of the various entries in order to rule out major initial structural differences that may lead to the changes that we observed. Although some degree of variability occurs, the features of the secondary conformations are conserved across the proteins in the two groups (Table S1, supplementary material) and a more detailed discussion is available in the supplemental information. The percentage of residues in β-sheet conformation ranges from 35% to 43% and is only slightly more consistent (38% to 41%) in entries of group 1. All entries have between 20 and 25% of the structure in turns and they all show the long helical motif (10 to 12 residues long) between β-strands H and I. The only remarkable feature among the entries is provided by 1CJ5 which has a shorter βE and a disrupted βI (Table S1, supplementary material). In addition, 3NPO is the only entry that does not have any additional attempt at helical folding throughout the sequence, whereas all other entries have short helical attempts of 1 turn or less.

3.1.2. Structure changes

The simulations does not show any remarkable changes in the secondary structure. Because changes are small, effects of the E89 protonation state are not evident. The most common events are elongation or shortening of the secondary structure by no more than one or two residues as well as the disruption of the existing short helical folding attempts or the formation of equally short helical motifs, which however appear as fluctuations of the main structure and not as permanent features.

3.1.2.1. E89⁽⁰⁾.

The suppression and formation of short helical motifs can be seen in 1DV9, 4LZU and 1BSQ (group 2). In 1DV9, however a short helix is formed in the AB loop while in 1BSQ the EF loop ‘attempts’ to fold into a single turn helical motif (Table S2A, supplementary material; see Section 3.4.1). In 4LZU one notices the restoration of the EF loop which starts as a 2 residues-long segment and returns to the expected length of 5 residues at the end of the simulation. As was the case for 1BSQ in 2BLG (group 1) the EF loops also attempts to fold into a single turn helical motif.

3.1.2.2. E89⁽⁻¹⁾.

Compared to the simulations with E89⁽⁰⁾ (Section 3.2.1), there are two more remarkable effects. In 4LZU (group 2) there is an elongation of the EF loop by two residues on each side. This reduces the length of both the βE and the βF strand. More remarkable is the fact that in 1CJ5 (group 2) the βE strand reduces to just two residues (Tables S2A and S2B, supplementary material) while the integrity of βI is re-established. Thus, in both cases there is a substantial disruption of the βE strand. As will be discussed later, this effect appears to be correlated not only to the transition of the EF loop but also to a distortion of the βC-CD loop-βD motif whereby the twisting of βD breaks the contact with βE and prompts this strand to partially unfold.

Overall, the analysis of the secondary structure reveals that the various entries have nearly identical conformation and that effects of the protonation of E89 on the secondary structure of the various lactoglobulin entries show only minor effects. The only noticeable one appears to be the partial disruption that occurs for the E89⁽⁻¹⁾ in strand βE of 1CJ5, 1DV9 and 4LZU caused by the combination of the EF loop transition and the distortion of the βC-CD loop-βD motif that affect the contact between βD and βE and cause the latter to partially unfold.

3.2. Analysis of RMSD of 5-residue long sequences

The EF loop is a sequence of five residues (from D85 to E89). In order to characterize its conformational change we analyzed the mobility of consecutive segments of five amino acids throughout the sequence of each entry, measured by the RMSD of their backbone atoms during the simulations. This analysis was carried out to determine whether the backbone atoms in the EF loop shows intrinsic mobility properties compared to other equally long sequences in the protein. We established that across all entries the behavior was very similar. The N- and C-terminals have, on average, larger RMSD () than the rest of the protein (as it would be expected). In general the regions of the AB loop and the CD loop have RMSD values that are larger than other regions outside of the terminals (and occasionally even larger than these) as shown in Figure 2 and Figure S2 (supplementary material). The EF loop has larger RMSD than its immediate surrounding, but it does not have an intrinsically larger mobility than other loops in the protein. The protonation state of E89 does not affect this general analysis. In the entries where the Tanford transition (or its reverse) occurs (see discussion below) the RMSD of the EF loop is larger but but does not intrinsically affect the other regions. Overall, the analysis of the 5-residue mobility does not indicate special intrinsic mobility of the backbone of the EF loop compared to other consecutive segments of equal number of residues. Moreover, there is no larger mobility of the EF loop in group 1 entries compared to those of group 2 other than in cases where the EF loop undergoes the conformational transition. In fact transitions of the EF loop occur in both groups. It is noticeable, however that both the residues of the AB and the CD loop have large mobility which is correlated with the distortion of these regions discussed in section 3.4. Nevertheless, since we did not determine any unique intrinsic mobility of the residues in this loop compared to the rest of the protein we left the detailed description of these results in the supplemental information.

Figure 2.

Backbone RMSD values for consecutive sequences of consecutive 5 amino acids during the 200 ns simulations. The comparison shows the results of simulations with E89 deprotonated (red) vs. E89 protonated (blue). The sequence regions of AB, CD and EF loop are also shown. (Top) Values for 3BLG as representative of group 1. (Bottom) Values for 2BLG as representative of group 2.

3.3. Hydrogen bond (HB) network

We investigated how the HB network formed by the residues in the EF loop (D85 to E89) changes during the simulations. The observations compared the interactions between non-adjacent residues. The HB formed between residues of EF loop and residues of other regions are detailed in Table S3 (supplementary material). The majority of the HB are formed by the two residues at the beginning (D85) and the end (E89) of the loop. Residues 86 to 88 form mostly intra-loop HB and rarely participate in forming HB with residues outside the loop. A discussion of general findings can be found in the supplemental information, however, in the next section (3.4) we will discuss in detail the HB that has been postulated to be the most significant in terms of the Tanford transition (Qin et al., 1999): the one formed between E89 and S116.

3.4. Analysis of the EF loop transition

The main focus of the current study was to investigate whether the modification of the fixed charge of E89 from 0 to −1 prompts a conformational change of the EF loop that reproduces the experimentally observed Tanford transition. The paradigm of the transition involves a collective motion of the EF loop that can be schematically described as a rotation around an axis that connects (approximately) the Cσυβ > ὰ/συβ> of residues D85 and E89 and generally lies parallel to the aperture of the interior cavity (Figure 3).

Figure 3.

Representative motion of the EF loop in the Tanford transition relative to the entrance of the cavity. The figure was created using the 2BLG entry, but is representative of all the other entries investigated in this study. (Left) The EF loop is represented in purple and while the rest of the protein is represented in cyan. In balls and sticks are represented respectively the D85 and the E89 residues at the beginning and the end of the loop. The dashed black line represents an approximate axis of rotation for the EF loop during the Tanford transition. The axis of rotation crosses approximately the Cα atoms of D85 and E89. (Right) The side view shows the dashed line approximately parallel to the entrance of the cavity and the vector that approximately represents the direction of an ideal plane parallel to the entrance of the cavity.

To analyze the movement of the EF loop and its effects on the various entries we focus on four elements that reflect the novel information obtained by our simulations: i) the distance between the carbonyl oxygen of the side chain of E89 and the hydrogen of the side chain of S116 (postulated to form a HB that may be the cause for the unusually large pK_a of E89), ii) the distance between the carboxylic carbon of the side chain of E89 with the nitrogen of the side chains of K69 and K60), iii) the approximate area of the entrance of the interior cavity (calculated as explained in section 2.2.3.5 and iv) the distance between the C_α of L87 and the C_α of W19. According to the paradigm for the Tanford transition the more extensive backbone excursion within the EF loop is experienced by L87 at the apex of the loop. Conversely, the bottom of the cavity (as discussed in section 3.3) represents one of the most stable portions of the protein (Figure 2 and Figure S2, supplementary material). Within this motif W19, located at the bottom of the cavity, is also the most conserved amino acid across all lipocalins (Brownlow et al., 1997)) and shows one of the smallest RMSD among the amino acid of these proteins.

3.4.1. Group 1

The experimental starting structure for the entries in this group were obtained at alkaline and neutral pH, and present the EF loop in open conformation (Figure S1, supplementary material) (Qin et al., 1998; Sauter et al., 2014; Uhrinova et al., 2000). Although the pdb files do not contain information about the charges of the amino acids, one assumes that, experimentally they were obtained under conditions where E89 is deprotonated (E89⁽⁻¹⁾). Thus, the simulations obtained with E89⁽⁻¹⁾ reproduce the experimental conditions while the simulations with E89⁽⁰⁾ reproduce non-experimental conditions. A comparison of the two ionization conditions would inform us on whether, upon protonation of E89, the entries spontaneously transition back to a closed conformation. In 2BLG one notices substantial differences only in the W19-L87 distance whereby around 140 ns the distance appears to increase from 25.7 0.4 to 27.3 0.5 (Figure 4) indicating a further distancing of the apex of the EF loop to the its bottom.

Figure 4.

Time traces for relevant parameters of the simulations. In blue are the traces with E89⁽⁰⁾ in red are the traces with E89⁽⁻¹⁾. Left Panel. 2BLG. The vertical line represents the time point where the W19-L87 distance shows a marked further increase. Right Panel. 4LZU. The vertical line represents the time point where the W19-L87 distance increases and the conformational change reproducing the Tanford transition occurs. (A) Distance between C_α of W19 (bottom of the cavity) and C_α of L87 (apex of the EF loop). (B) Distance between the carboxylate oxygen of the side chain of E89 and the hydrogen of the hydroxyl side chain of S116. When this distance is near or below 3.5 Å (gray horizontal line) one assumes the formation of a hydrogen bond. (C) Distance between the carboxylic group of the side chain of E89 and ammonium group of K69. When this distance is near or below 5.5 Å (gray horizontal line) one assumes the formation of a salt bridge. (D) Contour area of the entrance of the interior cavity calculated according to the method in section 2.2.3.5.

The E89-S116 and the E89-K69 distance are basically unchanged by the protonation state of E89 and remain much larger than the threshold required to form a HB (E89-S116) or a salt-bridge (E89-K69) (Figure 4). This is consistent with the fact that E89 starts (Figure S1, supplementary material) and remains to the outside of the cavity for the duration of the simulation. With E89⁽⁰⁾ the contour area of the interior cavity progressively decreases in the first 50 ns of the simulation from an initial value of ~ 611 44 to 250 29. This 2.4-times decrease appears consistent with the Tanford transition (i.e. the protonation of E89 of an experimentally deprotonated entry causes the closure of the entrance of the interior cavity), and with the decrease the W19-L87 distance. However, Figures S6 and S10 (supplementary material) suggest, the closure of the cavity is prompted mostly by the side chain of L87 rotating from perpendicular to parallel to the entrance of the cavity, rather than by a rotation of the entire EF loop. With E89⁽⁻¹⁾ the last 20 ns show a slight increase (~12%) of the area in correlation to the increased W19-L87 distance which follows a further rotation of the EF loop away from the entrance of the interior cavity (Figures 4 and 5). In the same group, 1BSY shows a sharper effect of the W19-L87 distance whereby changing the protonation state from E89⁽⁻¹⁾ to E89⁽⁰⁾ prompts the distance to decrease in a stepwise profile at ~ 160 ns (Figure S3A, supplementary material). This step corresponds to the rotation of the EF loop in a closed configuration which can be clearly seen in Figure S6 (supplementary material). Nevertheless, this step does not appear to produce any other major effects since E89 remains on the side of the surface of the protein and does not participate in the HB with S116 or the salt bridge with the Lys residues (K60 or K69) of the βC-CD loop-βD motif. The area of the entrance of the cavity reduces substantially (from 682 81 with E89⁽⁻¹⁾ to 400 28 with E89⁽⁰⁾) but the transition is gradual and does not follow the same dramatic step as the W19-L87 distance. The behavior of 3NPO is peculiar. A transition occurs that appears to be opposite to the Tanford transition. The deprotonation of E89, in fact, prompts the EF loop to assume a closed instead of open conformation. This transition proceeds in two steps that occur at ~ 110 ns and ~ 125 ns as shown by the profile of the W19-L87 distance with E89⁽⁻¹⁾ (Figure S3A, supplementary material). The first step seems to be the one that causes the aperture of the cavity to partially shut (Figure S3, supplementary material A) from 832 80 with to 400 44. The conformational change of the EF loop can also be clearly observed in Figures S7 and S10 (supplementary material). Conversely, no effects are noticed with the position of E89 relative to S116 or K60 and K69 (Figure S3A, supplementary material). E89 remains on the outside of the protein and the distance between its side chain and the one of S116 or the two lysine residues remains well above the threshold to form HB or a SB.

Figure 5.

Overlapped structures of at (start of the simulation) and (end of the simulation) for 2BLG and 3BLG (group 2) entries and E89⁽⁻¹⁾. The ribbon structure of BLG at the start of the simulation () shows the protein in translucent cyan with the EF loop (green), while the structure at the end of the simulation () is shown in translucent grey with the EF loop (red). The overlap shows that the final conformation of the EF loop () does not change substantially from its initial configuration. The red circle highlights the region of the βC-CD loop-βD motif which undergoes conformational modifications(twists counterclockwise and extends in 2BLG whereas it bends towards the EF loop in 3BLG).

3.4.2. Group 2

The starting structures for the members of this group are obtained at acidic and neutral pH, and show the inital EF loop in closed conformation (Figure 1 and Figure S1, supplementary material). The results of the simulations provide two different sets of observation. Entry 3BLG shows that for the last 40 ns of the simulation the W19-L87 distance is basically identical between the E89⁽⁰⁾ and E89⁽⁻¹⁾ forms of the protein (Figure S3B, supplementary material). Before that, E89⁽⁻¹⁾ appears to transiently destabilize the EF loop which attempts to transition to at least a partially open conformation for periods of < 10 ns each time. Entry 3BLG is one in which the initial configuration includes the HB between E89 and S116. With E89⁽⁰⁾ this HB appears to break and re-form constantly throughout the simulation with a distance ranging from below the threshold for HB (<3.2) and substantially above the threshold (up to 6). The deprotonation of E89 eliminates the constant fluctuation of the E89-S116 distance (Figure S3B, supplementary material, left panel, red trace) but large fluctuations still occur for several time intervals increases, however when the distance falls below the threshold the fluctuation decreases drastically (0.12 with E89⁽⁻¹⁾ vs. 0.68 with E89⁽⁰⁾) (Figure S3B, supplementary material). The distance between E89 and the Lys residues on the βC-CD loop-βD motif is virtually unaffected by the protonation of E89 (Figure S3B, supplementary material). This is because the relatively stable formation of the HB with S116 prevents E89⁽⁻¹⁾ from forming the SB with the lysine residues. The combination of these results does not fully explain the effects on the contour area of the aperture of the interior cavity. This area remains small and substantially closed (Figure S3B, supplementary material), but the deprotonation of E89 increases its values significantly (from 150 11 to 386 31). This effect is not prompted by a transition of the EF loop. Instead, it appears to be prompted by a movement of the CD loop (Figure S5, supplementary material) which undergoes a similar transition to the one expected for the EF loop whereby the top of the loop goes from parallel to the entrance of the cavity to rotating to a position perpendicular to it. The increase in this area can also be observed in Figure S10 (supplementary material). In summary, the deprotonation of E89 in 3BLG does not prompt conformational changes that reproduce the postulated Tanford transition (Qin et al., 1998).

The 1BSQ entry shows a different behavior. Throughout the 200 ns simulation the W19-L87 distance with E89⁽⁰⁾ fluctuates around its initial value (Figure S3B, supplementary material, blue trace) and has an average value of 18.9 ± 0.6 Å (range 16.6-21.4 Å). Conversely, with E89⁽⁻¹⁾ 1BSQ shows a step-wise (< 1 ns) change at approximately ~ 2.5 ns into the simulation. The transition changes the W19-L87 distance from an average value of 19.5 ± 0.8 Å to an average value of 22.6 ± 0.7 Å. This conformation is maintained for the remainder of the simulation (Figure S3B, supplementary material, red trace). However, as one observes in Figure S5 (supplementary material) the change in distance is not caused by the expected hinging motion of the EF loop around the D85-E89 axis (Figure 3). Instead, the EF loop twists clockwise while maintaining its folding parallel to the entrance of the cavity (Figure S5, supplementary material). Remarkably, but not unexpectedly, the profile of the E89-S116 HB distance shows the same step-wise profile at the same time points of the W19-L87 distance (Figure S3B, supplementary material, red trace). This clearly indicates that the changes are due to the breaking of the HB between E89 and S116 which allows the EF loop to rotate clockwise (Figure S5, supplementary material). As Figure S3B (supplementary material) shows, the E89-K69 distance shows a dramatic change transitioning from a fluctuating distance (14.4 1.1) well above the threshold for the formation of a salt bridge (established at 5.5 according to the parameters used by VMD) to locking into a distance near or below the threshold for salt a bridge (average 4.1 0.8) (Figure S3B, supplementary material, red trace). It is interesting to notice that this salt bridge does not immediately replace the HB. A step-wise transition in the E89-K69 distance is observed at the same point (~ 2.5 ns) where the transition of the E89-S116 distance occurs (Figure S3B, supplementary material, red trace), however the step only decreases the E89-K69 distance from an average distance of 18.4 1.2 to and average distance of 8.6 1.4 which is above the threshold for the formation of the salt bridge and (as the standard deviation indicates) is still subject to large fluctuation (Figure S3B, supplementary material, red trace). The formation of the salt bridge is delayed until ~ 53 ns into the simulation (Figure S3B, supplementary material, red trace). The combination of these changes does not appear to modify the area of the aperture to the interior cavity. With E89⁽⁰⁾ the area gradually decreases even further from the initial conditions (which already represented a closed conformation) (Figure S3B, supplementary material, blue trace). With E89⁽⁻¹⁾ one notices an abrupt decrease in the accessible area at the time the E89-K69 salt bridge is formed (Figure S3B, supplementary material, red trace). Thus when E89 is deprotonated the clockwise rotation of the EF loop that would increase the aperture of the interior cavity is compensated by the formation of the E89-K69 salt bridge causing effectively causing a decrease of the entrance area to ~ 0.6 of the value of the aperture with protonated E89. Therefore, 1BSQ also does not show the conformational modification postulated for the Tanford transition upon deprotonation of E89.

The remaining three entries 1DV9, 1CJ5 and 4LZU, however, are the ones showing the most interesting results and features that are consistent with the Tanford transition as it has been postulated (Qin et al., 1998). The W19-L87 distance increases substantially upon deprotonation of E89 (red traces in Figure 4 right panel and Figure S3C, supplementary material) whereas with E89⁽⁰⁾ the values fluctuate around the starting distance (blue traces in Figure 4 right panel and Figure S3C, supplementary material). In 1CJ5 the transition (from 20.0 ± 0.2 Å to 30.2 ± 0.7 Å) (Figure S3C, supplementary material, red trace) occurs gradually over a period of ~ 50 ns and the new configuration is maintained until the end of the simulation. In 1DV9 the transition is instead sharp (< 2 ns) and occurs at ~15 ns into the simulation (Figure S3C, supplementary material, red trace). The L87-W19 distance transitions from 22.9 ± 0.7 Å to 26.2 ± 0.8 Å and maintains such configuration until the end of the simulation. Contrary to the other cases, 4LZU shows a late transition of the L87-W19 distance. The transition is sharp (~ 1 ns) and occurs at ~ 170 ns from the start (Figure 4, right panel, red trace). Before the transition occurs L87-W19 = 19.5 ±0.8 Å while immediately after the transition L87-W19 = 23.2 ±0.8 Å and the distance slowly drifts to plateau at 26.7 ±0.7 Å for the rest of the simulation.

In 1CJ5 and 4LZU the behavior observed for the W19-L87 correlates with the observation of the E89-S116 HB. As the W19-L87 distance gradually increases in 1CJ5, so does the E89-S116 distance. Unlike the E89⁽⁰⁾ case (Figure S3C, supplementary material, left panel, blue trace) where the HB is maintained throughout the simulation, E89⁽⁻¹⁾ disrupts the HB from the start (Figure S3C, supplementary material, left panel, red trace) as the distance remains well above the threshold for the formation of HB and further increases in lockstep to the increase of the W19-L87 distance. In 4LZU the sharp transition of the W19-L87 distance is mirrored by the increase in the E89-S116 distance. As seen in Figure 4 (left panel) in this case the increase also implies the breaking of the HB between E89 and S116. Unlike the case of 1BSQ discussed earlier, the swap of the HB with S116 with the salt bridge with K69 is immediate. This correlation exists in 1CJ5 as well. However while the increase of the W19-L87 distance and the E89-S116 HB breakage occurs gradually, the formation of the E89-K60 (not K69) salt bridge is sudden and occurs simultaneously with the start of the increase of the W19-L87 distance. In 1DV9 the transition of the W19-L87 distance correlates with a large fluctuation of the E89-S116 HB (Figure S3C, supplementary material, right panel). However, the HB is re-established and is not broken until ~ 60 ns after the transition of the W19-L87 (Figure S3C, right panel).

The effects of the deprotonation of E89 on the area at the entrance of the interior cavity are quite significant. With E89⁽⁰⁾ the area remains substantially unchanged in 4LZU (Figure 4, right panel, blue trace) at 380 40 consistent with the EF maintaining its closed conformation over the entrance of the interior cavity (Figure 6). In 1CJ5 one notices a drift in the value of the area from 288 31 in the first 2 ns to 353 16 in the last 2 ns of the simulation which could be due to a movement of the base of the EF loop which maintains its closed conformation but distances from the AB loop across the entrance of the cavity (Figure S4, supplementary material). A similar drift can also be noticed in 1DV9 whereby the area increases from 234 42 in the first 2 ns to 380 37 in the last 2 ns (Figure S3C, supplementary material). Conversely, in all entries the presence of E89⁽⁻¹⁾ causes a significant increase of the area at the entrance of the interior cavity. In 1CJ5 the increase is gradual and mirrors the time profile of the W19-L87 distance. The effect is to increase the area from 395 24 in the 5 ns before the slow transition to 695 49 in the last 5 ns of the simulation (Figure S3C, supplementary material, bottom, left panel), a 76% increase. Figure S5 (supplementary material) clearly shows the EF loop that rotates and stretches orthogonal to the entrance of the cavity. However, this conformational change is accompanied by the twisting of the βC-CD loop-βD motif (Figure S5, supplementary material, circled in red) which is due to the formation of the E89-K60 salt bridge. These effects can be better appreciated in Figure S9 where one observes that the increase in the accessibility of the interior cavity prompted by the transition of the EF loop is moderated by the formation of the E89-K60 salt bridge. The effect of E89⁽⁻¹⁾ on the accessibility of the interior cavity is displayed also by 4LZU. In this case the area transitions in a step-wise manner at the same time as the E89-S116 HB breaks and the E89-K69 salt bridge is formed. The increase in the area is very dramatic, from 525 32 in the 5 ns before the slow transition to 728 41 in the last 5 ns of the simulation (Figure 4, right panel, red trace). The rotation of the EF loop is clearly seen in Figure 6 where one also notices that, unlike 1CJ5, the βC-CD loop-βD motif remains virtually unaffected by the conformational transition. On the other hand Figure 7 shows the clear increase in accessibility of the interior cavity. In 1DV9 the increase in area is similar between the entry with E89⁽⁰⁾ and the entry with E89⁽⁻¹⁾ (Figure S3C, supplementary material, right panel, Figures S8 and S9, supplementary material) despite the evident transition of the EF loop (Figure 6). With E89⁽⁰⁾ the increase is not due to a conformational transition of the EF loop and is entirely due to the movement of the side chain (not the backbone) of L87 which moves perpendicular to the entrance of the cavity (Figure S8, supplementary material). With E89⁽⁻¹⁾ the contour area shows a more complex behavior. At the step-wise transition of the W19-L87 distance (the EF loop conformational transition) with E89⁽⁻¹⁾ there is a corresponding sudden increase in the contour area of the interior cavity (Figure S3C, supplementary material, right panel) from 301 67 to ~ 864 83. However, this initial step-wise decrease which corresponds to a first breaking of the E89-S116 HB, is then followed by a gradual decrease when the E89-K69 salt bridge is formed (Figure S3C, supplementary material, right panel). The formation of the salt bridge leads to a final contour area to 472 27. One also notices another contribution to the gradual decrease of the contour area. The formation of the E89-K69 bridge (Figure S9 vs. Figure S8, supplementary material) prompts a large distortion of βC-CD loop-βD motif (Figure 5) which is ‘pulled’ closer to both the AB loop and the βE-EF loop-βF motif across from the entrance of the cavity.

Figure 6.

Overlapped structures of at (start of the simulation) and (end of the simulation) for 1DV9 and 4LZU (group 1) entries and E89⁽⁻¹⁾. The ribbon structure of BLG at the start of the simulation () shows the protein in translucent cyan with the EF loop (green), while the structure at the end of the simulation () is shown in translucent grey with the EF loop (red). The overlap shows that the final conformation of the EF loop (red) assumes and open conformation after starting (green) from a closed configuration. The red circle highlights the region of the βC-CD loop-βD motif which undergoes a large counterclockwise swing.

Figure 7.

Van der Waals representation of the residues delimiting the rim of the interior cavity with E89⁽⁻¹⁾. The point of view is from the entrance of the cavity towards its bottom. The residues at the rim are represented in various colors and labeled, whereas the residues at the bottom of the cavity are represented in yellow and include residues 15 to 20 as well as 98 to 102. The structures on the left represent the conformation at, The structures on the right represent the conformation at. (Top) Entry 4LZU from group 1. (Bottom) Entry 3NPO from.

The results of our simulations show some novel and interesting results in both groups. Group 1 includes entries at alkaline or neutral pH that have the backbone of the EF loop oriented nearly perpendicular to the entrance of the interior cavity and have adopted an open conformation. In this case one expects that the neutralization of E89 would prompt a transition from the open to the closed conformation of the EF loop. This, however appears to occur only with the 1BSY entry (Figures S6, supplementary material & S3A, left panel). The 2BLG entry does not show any substantial transition, whereas 3NPO shows a peculiar transition. In fact, it is E89⁽⁻¹⁾, not E89⁽⁰⁾, that causes the EF loop to undergo a transition to the closed conformation (Figure S3A, supplementary material, right panel and Figure S7, supplementary material). This is opposite to what is expected from the postulated mechanism of the Tanford transition. Conversely, group 2 includes entries at acidic or neutral pH with the EF loop rotated towards the middle of the entrance of the interior cavity in a closed conformation. One expects that in this case the deprotonation of E89 triggers the Tanford transition that involves the rotation of the EF loop. This is indeed the case with, however, a noteworthy exception: 3BLG. In this entry, the substitution of E89⁽⁰⁾ with E89⁽⁻¹⁾ does not produce remarkable transitions in any of the key parameters associated with the rotation of the EF loop to an open conformation (W19-L87, E89-S116 and E89-K69/K60 distance or the area at the entrance of the cavity). On the contrary, albeit to various extents, in the other entries of this group (1CJ5, 1DV9, 4LZU and 1BSQ) deprotonation of E89 does prompt the rotation of the EF loop that one associates with the Tanford transition. Why is 3BLG the outlier in this group? We propose that the reason for the isolated behavior of 3BLG is the position of the side chain of E89 with respect to the EF loop. In this group, 3BLG is the only entry where the side chain of E89 is outside the interior cavity (Figure S1, supplementary material) and away from the EF loop. This probably causes the structure to be less sensitive to the changes in the net charge of this amino acid. In the other entries, instead, the position of the side chain of E89 is either closer or directly below the EF loop (Figure 1 and Figure S1, supplementary material) so that the presence of a net negative charge in the amino acid may induce electrostatic repulsion that prompts the EF loop to distance itself from the entrance of the cavity.

Other time traces provide key novel information related to the conformational transition of the EF loop. In all cases in which the EF loop undergoes a rotation from a closed to an open configuration the HB between E89-S116 breaks. Given the evidence that this event can occur with some delay (up to 65 ns) from the rotation of the loop, indicates that the breaking of this bond is not the trigger to the Tanford transition. A novel finding is that the cleavage of the HB with S116 prompts E89 to ‘lock’ into a salt bridge with K69 or K60 across the entrance of the bridge. This effect is only possible in the entries where the side chain of E89 is oriented inward and does not occur when the side chain is oriented outward (Figure 1 and Figure S1, supplementary material). Although replacing the HB with the salt bridge is energetically favorable (~ 1.25 kcal/mol) the replacement does not always happen simultaneously with the cleavage of the E89-S116 HB. The formation of the salt bridge has two consequential effects: 1) the distortion of the βC-CD loop-βD motif and 2) the limitation of the opening of the interior cavity. The first effect includes a twisting of the motif that rotates the CD loop counterclockwise and moves it into the entrance of the interior cavity (Figure 5, top and Figure S5, supplementary material). This movement also loosens the contact between βD and βE and cause the disruption of the latter (as seen in 1CJ5, but also to some extent in 1DV9 and 4LZU Table S2A and S2B, supplementary material). The area of the accessible entrance to the cavity increases when the EF loop rotates into an open conformation, however the movement of the CD loop as well as the creation of the bridge across the entrance of the interior cavity limit the aperture of the cavity. Therefore, even though the EF loop transition upon deprotonation of E89 would open the entrance of the cavity the salt bridge between E89 and the lysines in the CD loop and βD as well as the ensuing distortion of the βC-CD loop-βD motif effectively moderate the extent of the area of the entrance of the cavity that is actually available. These findings have not been reported before and we are in the process of investigating the effects on the binding of fatty acids as well as whether the salt bridge and the distortion of the βC-CD loop-βD motif occur if a ligand is present within the interior cavity.

3.5. Contour to the interior cavity

As mentioned in the Introduction, it is currently postulated that the pH-dependent conformational change of the EF loop regulates access to the interior cavity by changing the accessible area of its entrance (Qin et al., 1998). In the previous section we discussed how an approximation of this area changes throughout the trajectory of the simulation. A general analysis of all the entries reveals that the residues that most often delimit the rim of the cavity include S27, L31, P38, L39 (AB loop), K60, E62, K69, I71 (βC-CD loop-βD), L87, E89 (EF loop), N109 and S116 (GH loop).

3.5.1. Group 1: E89⁽⁰⁾

A survey of the entrance of the cavity reveals that at the beginning of the simulation one can identify an aperture (Figure 7 and Figure S10, supplementary material) with contour areas (ranging from ~ 320 to ~ 570, in agreement with these alkaline structure to be in an open conformation). The details of the trajectory for the area have been discussed above and one observes (Figures S6 and S10, supplementary material) that at the end of the simulation L87 is protruding over the entrance of the cavity in all three entries. In 1BSY and 2BLG this causes a decrease of the contour area of the entrance of the cavity to values < 400. In 3NPO the folding of the top of the EF loop into a closed conformation establishes a contact between L87 and P38/L39 which restricts the contour area to ~ 150.

3.5.2. Group 1: E89⁽⁻¹⁾

The starting conformations of the entries with E89⁽⁻¹⁾, yield conformations and contour areas that are larger than with E89⁽⁰⁾ (Figure S11, supplementary material) and range from ~ 480 for 2BLG to ~ 650 for 1BSY. These values are still consistent with the alkaline condition under which the structures were obtained. At the end of the changes are not substantial. The most remarkable effect (as discussed before) is the ‘reverse’ Tanford transition showed by 3NPO. In this case the contour area transitions from a large (~ 500) to a smaller opening of 173 (Figure 7). The ‘reverse’ Tanford transition creates contact between L87 and P38/L39 (Figure 7) which is aided by a protrusion of the AB loop into the entrance of the interior cavity.

3.5.3. Group 2: E89⁽⁰⁾

The survey at the beginning of the simulation reveals contour areas that range from ~ 228 to ~ 395, in agreement with the closed conformation of structures obtained under acidic conditions (Figure 7 and Figure S9, supplementary material). The only exception is 1BSQ where the contact between the AB loop and the GH loop is less compact so that the contour area extends to include the P144 residue of the C-terminal (Figure S8, supplementary material). As a result, despite the contact between the AB and the EF loops, a relatively large contour area (~ 560) remains (Table 2 and Figure S8, supplementary material). In the 3BLG entry the AB loop protrudes into the entrance of the cavity to the point of interacting with the EF loop (Figure S10, supplementary material) and is reflected by this entry having the lowest starting contour area (228). Figures S4 and S8 (supplementary material) show that, although the EF loop maintains a closed conformation throughout the simulations, the P38/L39 and the L87/N88 residues separate. The separation, however does not provide a substantial increase of the entrance to the cavity. In 1BSQ, the contact between the AB loop and the GH loop is re-compacted and, in addition, a HB is formed between E89 and K60 that brings the βC-CD Loop-βD closer to the AB and EF loops with the effect of decreasing the contour area of the interior cavity (~ 200, Figure S8, supplementary material). In 1CJ5 the P38:N88 contact is replaced with a A37:N88 contact that maintains the AB loop protruded and in contact with the EF loop maintaining a small contour area (~280) of the cavity. In 4LZU the protrusion of the AB loop remains, but the K60:E89 contact breaks, creating an increase in the contour area of the entrance of the cavity (to ~ 400, Figure S8, supplementary material and Table 4).

3.5.4. Group 2: E89⁽⁻¹⁾

The starting conformations of 1BSQ shows an increased distancing between the AB loop and the EF loop compared to the case of E89⁽⁰⁾. This creates a narrow opening of the interior cavity with a contour area of ~ 470 (Figure S9, supplementary material). Similar to the protonated conditions, the other entries (Figures 7 and S9) show the contact between L39 or P38 and L87 (or N88 for 3BLG and 1DV9) and contour areas ranging between 220 and 470. As we discussed earlier, in this group two of the entries (1BSQ and 3BLG) do not undergo the conformational change of the EF loop postulated by the Tanford transition whereas the other entries do (Figures S3B and S5, supplementary material) and these changes can be observed in the contour area of the entrance of the interior cavity. As shown earlier, in 1BSQ the EF loop rotates clockwise but remains basically parallel to the entrance of the cavity, thus in a closed conformation (Figures S5 and S9, supplementary material). The rotation increases the distance between L87 (EF loop) and P38 (AB loop). However, the formation of the salt bridge with K60 which is at the base of the CD loop effectively contributes to reduce the contour area of the interior cavity. This is further decreased by the rotation of the GH loop that allows N109 to protrude into the entrance of the cavity (Figure S9, supplementary material). This rotation is likely the effect of the cleavage of the E89-S116 HB followed by the formation of the salt bridge between E89 and K60. Cleaving the HB allows S116 to distance from the EF loop and at the same time the formation of the salt bridge causes E89 to ‘pull’ βG and effectively cause N109 at the base of the GH loop to protrude into the entrance of the cavity. In 3BLG the changes are even more subtle. Only notable are the distancing of P38 in the AB loop from L87 in the EF loop and the rotation of the side chain of N88 from a position parallel to the entrance of the cavity to one that is nearly perpendicular to it. In 1CJ5 the conformational transition of the EF loop (Figure 7 and Figure S9, supplementary material) breaks the contact between the AB and the EF loops and creates a larger opening. However, the increase in contour area of the entrance of the cavity is affected by the formation of the K60:E89 salt bridge and the rotation of the GH loop into towards the interior of the cavity which limits the increase in access area. Thus, although the conformational change of the EF loop occurs and produces an open conformation with the loop oriented perpendicular to the entrance of the cavity, the contour area only increases by ~ 100 which is less than the other two entries 4LZU and 1DV9 that undergo the same transition. In 1DV9 the EF loop undergoes the same transition (Figure 5) which also does not translate into a large increase of the opening of the entrance of the cavity. In part this is an effect of the formation of the K69:E89 salt bridge but for this entry another effect occurs. The conformational change of the EF loop includes a clockwise rotation that allows contact between L31 in the AB loop and N109 in the GH loop (Figure S9) which can be explained by the ‘swap’ between the E89-S116 HB with the E89-K60 salt bridge discussed for 1BSQ. Thus the contour of the cavity becomes delimited by the K69-E89 and the L31-109 pairs (Figure S9). The 4LZU entry is the one that shows the most dramatic effect. As discussed section 3.4.2 (Figure 5) 4LZU with E89⁽⁻¹⁾ shows the same conformational change of the EF loop as the other entries of this group, but the increase in the contour area of the rim of the cavity is much more significant. (Figures 4 and 7). In this case E89 forms a salt bridge with K69 (not K60) allowing for the larger increase in the contour area because K69 is located in βD instead of the end of βC. The formation of this salt bridge also contributes to make the rotation of the GH loop less extensive because βG does not have to move as much to ‘follow’ the pull of the E89 residue towards the opposite side of the cavity.

4. Conclusion

Overall, this works presents a detailed analysis of the simulated effects of the protonation state of E89 on the pH-dependent conformational change of the EF loop of several PDB entries of BLG as a function of its orientation relative to the entrance of the cavity. We believe this the first example of reproducing the details of the transition using an in silico approach over a time scale that allows to observe the transition of the protein from one stable conformation to another. Two groups of entries were investigated: group 1 where the entries include structures collected under slight or strong alkaline conditions with the initial conformation of the EF loop perpendicular to the entrance of the interior cavity (Figure 1 and Figure S1, supplementary material) (i.e. an open conformation according to the paradigm of the Tanford transition (Qin et al., 1998)), and group 2 where the entries include structures obtained at neutral or acidic pH with the initial conformation of the EF loop parallel to the entrance of the interior cavity (Figure 1 and Figure S1, supplementary material) (i.e. a closed conformation according to the paradigm of the Tanford transition (Qin et al., 1998)). Experimentally resolved structures, such as the ones used in this study, have allowed to postulate that the protonation state of E89 regulates the access to the interior cavity (β-barrel) of BLG by prompting the rotation of the EF loop from the closed to the open conformation (Qin et al., 1998) (Figure 3). These ‘snapshots’, however do not provide evidence for the dynamics of the changes or for the actual role of the net charge of E89 in triggering the transition. Our simulations show that E89⁽⁻¹⁾ indeed provides the trigger to the transition of the EF loop and that the rearrangement of the loop reproduces the Tanford transition. However we have also shown that the transition only occurs under certain circumstances and involve other motifs within the protein. The most important finding of our simulations is that deprotonation of E89 is not a sufficient condition for the transition to occur. In fact only three of the five entries among the acidic group (1CJ5, 1DV9 and 4LZU) undergo the transition when E89 becomes negatively charged. What is the common feature among these three structures that is not occurring in the other two (3BLG and 1BSQ)? Our results reveal that the orientation of the side chain of E89 is key to prompt the transition. When the side chain of E89 is located underneath the closed EF loop (1CJ5, 1DV9 and 4LZU, Figure 1 and Figure S1, supplementary material) the transition occurs. Conversely, when the side chain is positioned to the outside of the protein (3BLG Figure 1 and Figure S1, supplementary material) or towards the GH loop (3BLG Figures 1 and S1) E89⁽⁻¹⁾ does not prompt the rearrangement of the EF loop (Figure 7 and Figure S7, supplementary material). In the alkaline group one would expect that the opposite change, from E89⁽⁻¹⁾ to E89⁽⁰⁾, would trigger the reverse transition (i.e. from open to closed). This appears to occur only in 1BSY while in 3NPO the opposite of the expected effect occurs. In this entry is E89⁽⁻¹⁾ that causes the EF loop to rotate to a closed configuration (Figures S3A and S7, supplementary material).

As mentioned above, our simulations confirm postulated mechanisms but also reveal novel findings.

1. Our results confirm that the cleavage of the HB between E89 and S116 is involved in the Tanford transition. The cleavage occurs in all the acidic entries where the conformational transition of the EF loop from closed to open occurs (Figure 4 and Figure S3C, supplementary material). However, as 1DV9 shows, the cleavage does not always occur simultaneously with the rotation of the EF loop but can occur after a significant delay (>60 ns).

2. A novel finding of our simulation which is also related to the cleavage of the E89-S116 HB is the rotation of the GH loop. When the HB between E89 and S116 breaks, the serine residue distances from the EF loop with a consequent clockwise rotation of the GH loop which brings N109 (at the N-terminal end of the loop) to protrude into the aperture of the interior cavity and contribute to limit the increase in its contour area.

3. Equally novel is the observation that, when the simulations reproduce the Tanford transition (i.e., entries 1CJ5, 1DV9 and 4LZU with E89⁽⁻¹⁾) the deprotonated E89 replaces the HB with S116 with a more energetically favorable salt bridge with K69 or K60 residues located in the βC-CD loop-βD motif (Figure 4 and Figure S3C, supplementary material).

4. The formation of this salt bridge then creates two additional effects on the aperture of the interior cavity: i.) it directly decreases the contour area of the aperture of the cavity (Figure 7 and Figure S9, supplementary material), and ii.) it twists the βC-CD loop-βD motif closer to the EF loop, thus also contributing to limit the aperture of the interior cavity. In the case of 1CJ5, the distortion of this motif is sufficiently large to disrupt the contact between βD and βE and cause the partial unfolding of the latter (Table S2A, supplementary material).

Although many of our observations are novel, they could help explain some pH-dependent binding effects observed in the past by our group and others (Ragona et al., 2000, 2003; Tian et al., 2006) as well as some unusual folding patterns of BLG. (Papiz et al., 1986) In addition, our results confirm, on a longer time scale (~ 2000-fold longer) that the AB loop (and not just the EF loop) may play a pivotal role in regulating access to the interior cavity of BLG, as was suggested almost three decades ago by Gu and Brady (1992).