Effects of handle orientation, gloves, handle friction, and elbow posture on maximum horizontal pull and push forces

Abstract

Biomechanical models were evaluated for effects of handle orientation, handle material, gloves, and arm posture on maximum pull/push force. Eight healthy subjects performed maximum pull/push exertions on handles of two different orientations and materials, using three glove conditions and two arm postures. Empirical data supported the biomechanical models: Pull/push forces for the bare hand on a rubber handle decreased 10% when the handle was parallel to the pull/push direction, compared to when perpendicular to it. For parallel handles, pull/push forces further decreased with decreasing hand-handle friction coefficient (simulated by different handle materials and gloves). Pull force exerted by the bear hand was 29% greater when the elbow was extended than flexed. Pull force was greater than push (with bare hand and flexed elbow). The biomechanical models suggest that friction between the hand and handle limits pull/push forces for parallel handles. Elbow strength may be responsible for decreased pull force for the flexed elbow posture and decreased force for pull compared to push in the postures examined.

1. INTRODUCTION

1.1. Significance

Pull/push activities are frequently performed to move an object from one location to another, join two parts together, support the body, or propel a wheelchair. Pushing and pulling tasks contribute to 20% of all industrial back injuries in the United States (NIOSH, 1981). In addition, an individual’s limited pull/push capability can pose safety risks in many situations, such as climbing a ladder (Christensen & Cooper, 2005) or propelling a wheel chair (Richter et al., 2006). Knowledge of factors and models concerning maximum pull/push force are needed for analysis and design of workstations and tasks to prevent hand slippage, overexertion, and repetitive stress injury.

Among other body parts, hand and arm are of interest, as they are often the weakest link in the chain during force exertions, and thus a “limiting factor.” Therefore, understanding of pull/push force in relation to handle features such as handle orientation and hand-handle friction and upper extremity posture is important for analysis of upper extremity injury and design of grip objects. The aim of this study was to develop and evaluate biomechanical models of pushing and pulling for a seated worker that account for the effects of handle orientation and handle material on maximum pull/push forces, and effects of arm posture and gloves on maximum pull force, as described below.

1.2. Handle Orientation

One of the handle design guidelines that is commonly found violated in handles and objects around us is to allow the hand to exert force to a handle through compression rather than shear (Pheasant & Haslegrave, 2006). Maximum voluntary pull/push forces have been studied mostly using handles that produced mechanical interference to prevent the hands from slipping, so that the full force of the body could be transferred to the work object (e.g., pushing against a wall) (Chaffin et al., 1983; Daams, 1993; Davis & Stubbs, 1977a; Peebles & Norris, 2003; Snook & Ciriello, 1991). Though helpful in some situations, these data may not be appropriate when pull/push forces applied to an axial handle can be limited by friction. Empirically, maximum push forces exerted at parallel to the long axis of cylindrical handles were found to be, on average, 30% lower compared to those exerted at the right angles to the handle (Okunribido & Haslegrave, 2008). However, an explanation for these results was not offered. These results may be explained biomechanically as detailed below.

Force exertions perpendicular to the long axis of a cylindrical handle have previously been thought as pure compression force generation. In this paper, pull/push force exerted perpendicular to the long axis of a cylindrical handle is considered as an outcome of both normal and shear force components at the hand-handle interface: Figure 1a shows forces acting between the hand and a handle that is oriented at the right angle to the forearm. Normal contact forces between the hand and handle are produced by flexing the fingers and thumb or pressing with the palm and base of the thumb. Friction forces are produced by the normal forces acting between the hand and handle as the hand begins to slip. The total pull/push force can be computed by integrating the normal force (f_n(θ)) and friction force (f_t(θ)) acting in the direction of interest. If the z-axis is arbitrarily defined as the pull/push direction and it is assumed that friction force on one half of the cylinder (θ from 0° to 180° in Figure 1a) is applied by the fingers and the other half (θ from 0° to −180° in Figure 1a) is applied by the thumb, an equation for the resultant pull/push force can be written as:

$$\begin{gathered} {\mathrm{F}}_{\mathrm{z}}\left(\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{l}\mathrm{e}\right)=\underset{\text{0}}{\overset{\text{2π}}{\int }}\left\{{\text{f}}_{\text{n}}\left(\text{θ}\right)\text{sinθ}+{\text{f}}_{\text{t}}\left(\text{θ}\right)\left|\text{cosθ}\right|\right\}\text{dθ} \\ =\underset{\text{0}}{\overset{\text{2π}}{\int }}\left\{{\text{f}}_{\text{n}}\left(\text{θ}\right)\text{sinθ}+{\text{μf}}_{\text{n}}\left(\text{θ}\right)\left|\text{cosθ}\right|\right\}\text{dθ} \end{gathered}$$ (1)

where μ is the coefficient of friction between the hand and handle.

Figure 1.

Different handle orientations examined in the study: (a) Top view of the hand pulling/pushing a handle that is oriented perpendicular to the pull/push direction. (b) Side view of the hand pulling/pushing a handle whose long axis is parallel to the pull/push direction. (F_n: normal force, F_t: friction force, μ: coefficient of friction)

Force exertions parallel to the long axis of a cylindrical handle have been modeled previously: Figure 1b shows how pull/push forces are transmitted between the hand and a cylindrical handle when the pull/push forces are acting parallel to the long axis of the handle. In this case, only friction forces are transmitted to the handle. The axial pull/push force can be calculated as follows, in accordance with previous literature (MacKenzie & Iberall, 1994; Pheasant & O’Neill, 1975; Seo et al., 2008; Smaby et al., 2004):

$${\mathrm{F}}_{\mathrm{z}}\left(\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{l}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{l}\mathrm{e}\right)=\underset{\text{0}}{\overset{\text{2π}}{\int }}{\text{μ}\text{f}}_{\text{n}}\left(\text{θ}\right)\text{dθ}$$ (2)

Maximum pull force that can be generated for the handle surface from θ = 0 to 90° (see Figure 1a) is for a perpendicular handle (using Equation 1), and for a parallel handle (using Equation 2) if a constant normal force (f_n) is assumed over the handle surface. Accordingly, maximum pull force may be greater for a perpendicular handle than for a parallel handle when hand-handle friction coefficient is less than 1.75, which is the case for most conventional objects (Buchholz et al., 1988). For push, a perpendicular handle provides mechanical interference that prevents the hands from slipping and allows the upper-body push force to be applied directly against the handle (as F_n in Equation 1). On the other hand, pushing on a parallel handle relies on friction for coupling between the hand and handle (Equation 2). In summary, comparison of Equations 1 and 2 suggests that greater pull/push force may be exerted at right angles to the handle than parallel to it for a conventional handle.

1.3. Hand-Handle Friction: Handle Material and Gloves

Friction coefficient between the hand and handle can influence maximum pull/push forces for a parallel handle, based on Equation 2 (MacKenzie & Iberall, 1994; Pheasant & O’Neill, 1975; Seo et al., 2008; Smaby et al., 2004), and for a perpendicular handle, based on Equation 1. Factors that affect the friction coefficient, such as handle materials and gloves, can be expected to affect pull/push strength. It has been shown that jar lid opening capability increased when rubber gloves were worn, and decreased for cotton gloves, compared to the bare hand (Nagashima & Konz, 1986). This is probably because the coefficient of friction between the hand and an object changes with the use of gloves, affecting friction force and maximum torque. The present study examined the relationship between hand-handle friction and maximum pull/push force. Specifically, effects of two commonly used handle materials on maximum pull/push forces and the relationship between glove friction and maximum pull force for three common glove conditions for parallel handles were quantified.

1.4. Arm Posture

Pull and push require not only force exertions in the direction of the pull and push, but also stabilization of the joints during the exertions (Bober et al., 1982; Kornecki et al., 2001). Use of a fixed handle (as opposed to an unstable handle) may reduce the muscular burdens for joint stabilizations, resulting in increased maximum voluntary push force (Kornecki et al., 2001). In this study, it was investigated whether change of the arm posture could vary the extent of the required joint stabilization during pull.

Two typical arm postures – extended elbow posture vs. flexed elbow posture – are investigated using biomechanical analysis for isometric maximum pull exertions as follows. In particular, vertical forces (that are not required by the pull task, but may be beneficial for joint stabilizations) are examined in the present study. This was done so because during pull, workers can apply forces in the directions other than the pull direction (e.g., upward/downward (y-direction) specified in Figure 2) if a handle is fixed.

Figure 2.

Postures used in the study: All handles were adjusted to the vertically rested elbow height (when the arm was resting vertically by the side of the body). Subjects were seated and grasped a handle (a). Different arm postures (flexed (a) vs. extended (b) elbow) for pull were examined. Pull and vertical force exertions at the hand (F_z and F_y, respectively) result in external moments applied at each joint (M_{elbow, external}, M_{shoulder, external}) via moment arms (y_elbow-hand, y_{shoulder-hand}, z_elbow-hand,, z_{shoulder-hand}). All three direction forces (F_x, F_y, F_z) were measured using a lode cell.

Application of external pull force (F_z) and vertical force (F_y) in Figure 2 generates reaction forces to the hand in the opposite directions. These reaction forces produce an external moment about the elbow (M_{elbow, external}) and shoulder (M_{shoulder, external}). These external moments cannot be greater than the internal joint strength generated by the muscles crossing the elbow and the shoulder (Andres & Chaffin, 1991).

Therefore, maximum pull force for the extended elbow posture (Figure 2a), limited by the shoulder and elbow joint strengths, can be expressed as follows:

$$\begin{gathered} {\text{F}}_{\text{z}\text{(extended}\text{elbow)}}\le \text{min}(\frac{{\text{M}}_{\text{shoulder}\text{extension}\text{strength}}+{\text{z}}_{\text{shoulder}-\text{hand}}{\text{F}}_{\text{y}}}{{\text{y}}_{\text{shoulder-hand}}} \\ ,\frac{{\text{M}}_{\text{elbow}\text{extension}\text{strength}}+{\text{z}}_{\text{elbow}-\text{hand}}{\text{F}}_{\text{y}}}{{\text{y}}_{\text{elbow-hand}}}) \end{gathered}$$ (3)

where M_{shoulder extension strength} is the internal shoulder joint strength, z_{shoulder-hand} is the horizontal distance between the shoulder and the hand, y_{shoulder-hand} is the vertical distance between the shoulder and the hand, M_{elbow extension strength} is the internal elbow joint strength, z_elbow-hand is the horizontal distance between the elbow and the hand, and y_elbow-hand is the vertical distance between the elbow and the hand. Equation 3 suggests that application of upward force (F_y) can increase pull force (F_z) limited by the shoulder and elbow joint strengths. In other words, with enough upward force, maximum pull force may not be limited by the upper extremity strength, but by torso extension strength or whole-body pull strength. In that case, joints in the upper extremity are under tensile loads and ligaments can contribute to the strength of the joints (Basmajian & De Luca, 1985).

Similarly, maximum pull force for the flexed elbow posture (Figure 2b) can be expressed as follows:

$${\text{F}}_{\text{y}\text{(flexed}\text{elbow)}}\le \frac{{\text{M}}_{\text{elbow}\text{flexion}\text{strength}}}{{\text{z}}_{\text{elbow-hand}}}$$ (4)

$${\text{F}}_{\text{z}\text{(flexed}\text{elbow)}}\le \frac{{\text{M}}_{\text{shoulder}\text{extension}\text{strength}}+{\text{z}}_{\text{shoulder}-\text{hand}}{\text{F}}_{\text{y}\text{(flexed}\text{elbow)}}}{{\text{y}}_{\text{shoulder-hand}}}$$ (5)

It can be seen that for the flexed elbow posture, upward force (F_y) is limited by the elbow flexion strength (M_{elbow flexion strength}) in Equation 4. Consequently, pull force (F_z) may be limited by the elbow and shoulder strengths for the flexed elbow posture (Equation 5). Therefore, it was hypothesized that straightening the arm by extending the elbow will result in increased maximum pull force compared to a flexed elbow posture.

1.5. Hypotheses

To augment knowledge concerning handle features that can assist industrial designers and ergonomists with safe and efficient design of pull/push tasks, following hypotheses were put forward: 1) greater pull/push force can be produced at right angles to the handle than parallel to it; 2) maximum pull/push force for a parallel handle is related to hand-handle friction. Specifically, maximum pull/push force is related to handle materials and maximum pull force varies with gloves. Lastly, it was hypothesized that 3) the flexion of the elbow results in reduced maximum pull force compared to that for the straight arm with the extended elbow.

2. METHODS

2.1. Procedure

A repeated measures experiment was conducted to test effects of handle orientation and handle material on maximum pull/push force and effects of gloves and arm posture on maximum pull force. Subjects were seated on a chair that supported the back and feet to stabilize the balance and minimize slip (Figure 2a). The handle height was adjusted to each subject’s elbow height when the arm was resting vertically on the side of the body. Subjects grasped a cylindrical handle with the right hand in a power grip. Subjects were instructed to build up to their maximum pull/push force without jerking and then maintain the maximum pull/push force for 4 seconds, according to the static strength testing procedure recommended by earlier investigators (Caldwell et al., 1974).

Independent variables were handle orientation (long axis of the handle perpendicular to the pull/push direction as shown in Figure 1a vs. parallel to the pull/push direction as shown in Figure 1b), handle material for the parallel handle (smooth aluminum, smooth rubber), arm posture during pull (elbow flexed at 90° as shown in Figure 2a vs. elbow extended as shown in Figure 2b), and gloves during pull with the extended elbow (bare hand, cotton glove: GoldKnit™ Mediumweight 70–227 as shown in Figure 3a, PVC dot glove which is a cotton glove covered with 3-mm diameter PVC dots which are 5.5 mm apart from center to center: Performers Extra™ Knit Series D2–09 as shown in Figure 3b). Complete test conditions are listed in Table 1. Aluminum and rubber surfaces with the two gloves were examined as they were the combinations often used in automotive assembly plants. Different sizes of gloves were provided to accommodate different hand sizes of subjects. Gloves were tightly seated on the hand via an elastic band around the wrist.

Figure 3.

Cotton glove (a) and PVC dot glove (b) were used for pull in addition to the bare hand condition.

Table 1.

Mean ± SE coefficient of friction (COF) and orthogonal-direction forces (F_x: + for lateral, - for medial direction, F_y: + for upward, - for downward) during the maximum pull/push force exertions (F_z: + for pull, - for push) for 2 arm postures, 3 glove conditions, 2 handle orientation, and 2 handle materials (8 subjects’ data pooled; See Figure 2 for illustration of the arm postures and force directions, Figure 1 for handle orientations, and Figure 3 for gloves)

Direction & arm	Glove	Handle orientation	Handle Material	COF	Fx (N)	Fy (N)	Fz (N)
Pull w/elbow extended	Cotton	Parallel	Aluminum	0.40±0.04	−29±11	30±5	111±13
			Rubber	0.61±0.03	−52±13	83±10	326±35
	PVC dot	Parallel	Aluminum	0.72±0.04	−39±12	63±7	247±24
			Rubber	0.78±0.06	−56±14	94±10	370±43
	Bare hand	Parallel	Aluminum	0.80±0.06	−40±11	97±10	339±40
			Rubber	1.10±0.06	−56±13	90±9	416±47
		Perpendicular	Rubber	1.10±0.06	−47±9	93±17	472±57
Pull w/elbow flexed	Bare hand	Parallel	Aluminum	0.80±0.06	−36±9	82±9	274±32
			Rubber	1.10±0.06	−43±9	84±12	329±33
		Perpendicular	Rubber	1.10±0.06	−46±8	66±14	345±42
Push w/elbow flexed	Bare hand	Parallel	Aluminum	0.80±0.06	−23±22	−109±16	−212±26
			Rubber	1.10±0.06	−17±19	−108±15	−250±28
		Perpendicular	Rubber	1.10±0.06	11±5	−79±11	−290±35

The dependent variable was maximum pull/push force (F_z). Additionally, orthogonal-direction forces (upward (+y), downward (-y), lateral (+x), and medial forces (-x) as shown in Figure 2) were measured. Force data were measured using a 6-axis load cell (AMTI MC3A, Watertown, MA; shown in Figure 2a), amplified (using 6-Channel Load Cell Amplifier and Display, Measurement Systems Inc., Livonia, MI), and recorded in a computer via data acquisition system (U12, LabJack Corp., Lakewood, CO, and LABVIEW, National Instruments Corp., Austin, TX). Force data were collected at 5 Hz. Force data were averaged over 2 seconds during which the mean pull/push force was maximal.

Each condition was tested twice. Conditions were randomly presented to subjects. A two-minute break was given between successive trials. Subjects washed their hands with soap, rinsed with water, and dried with paper towels 10 minutes prior to testing, to eliminate artifacts due to contaminants (Buchholz et al., 1988; Comaish & Bottoms, 1971). The cylindrical handle diameter was 38 mm for the aluminum handle, and 40 mm for the rubber handle. The handle attachment to the transducer was constrained to prevent any rotation or displacement of the handle.

After completing the pull/push exertions, friction coefficients were measured using the method evaluated in Seo et al. (2009): A flat object was placed on each subject’s palmar side of the hand with the forearm horizontal. Subjects tilted the forearm until the object slid from the hand, while the sequence was videotaped using a digital video camera at 29.97 frames per second. The angle at which the object started slipping was measured from the video. Friction coefficient was calculated as the tangent of the angle. The object weight was 30 N. The object surface in contact with the hand was covered with the rubber or aluminum. The bare hand as well as the hand wearing the two gloves was tested. All six combinations (3 glove conditions × 2 handle materials) were tested with two replicates for each subject.

2.2. Subjects

Eight healthy subjects (4 male, 4 female, average age = 26 ± 5 yrs, ranging from 19 to 35 yrs) participated in the experiment. Their grip strength ranged from 11^th to 90^th percentile for males, and 8^th to 83^rd percentile for females according to population strength data reported previously (Mathiowetz et al., 1985). The protocol for the experiments was approved by the University of Michigan Institutional Review Board. Subjects gave written informed consent prior to testing.

2.3. Analysis

Three major repeated measures analyses of variance were performed using MINITAB®. The first ANOVA was to determine whether maximum force in the z-direction in the absolute value (|F_z|) was significantly affected by the handle orientation (perpendicular vs. parallel) and the three posture and force direction conditions (pull with extended elbow, pull with flexed elbow, and push with flexed elbow) for the bare hand and rubber handle combination. The second ANOVA was to determine whether absolute maximum push/pull force was significantly affected by the handle material (aluminum vs. rubber) and the three posture and force direction conditions for the bare hand and parallel handle condition. The third ANOVA was to determine if maximum pull force varied significantly with the 6 friction conditions (2 handle materials × 3 glove conditions) for the parallel handle orientation with the extended elbow posture. After the three posture and force direction conditions were found significant, the effects of elbow posture and force direction (push vs. pull) were then examined using Tukey post-hoc analysis. Secondary analyses were performed to determine the effect of elbow posture on orthogonal-direction forces (F_x, F_y). The p-value of .05 was considered significant.

3. RESULTS

Mean maximum pull/push forces and orthogonal-direction forces during the maximum pull/push exertions for each condition are summarized in Table 1. In addition, the coefficients of friction measured for all combinations of three glove conditions (bare hand, PVC dot glove, cotton glove) and two handle materials (rubber, aluminum) are summarized in Table 1. Repeated measures analyses of variance showed that maximum pull/push force (|F_z|) was significantly affected by all independent variables tested: handle orientation (perpendicular vs. parallel), elbow posture (extended vs. flexed), coefficient of friction (6 different combinations of handle materials and glove conditions), and force exertion direction (pull vs. push) (p<0.01 for all independent variables). The specific effects of each independent variable on |F_z| are described in detail as follows.

Change of the handle orientation from the parallel to the perpendicular orientation increased the mean maximum pull/push force 11% (elbow posture pooled; rubber handle and bare hand only; p<0.01; Figure 4; Table 1). Mean maximum pull/push force decreased as the handle material changed from rubber to aluminum (decreasing friction coefficient) as shown in Figure 4 and Table 1 (bare hand and parallel handle only; p<0.01). The PVC dot glove and cotton glove resulted in, on average, 18% and 46% reduced coefficient of friction, respectively, compared to the bare hand (handle material pooled; Table 1). Maximum pull force decreased with decreasing coefficient of friction (p<.01; see Figure 5 for the parallel handle with the extended elbow posture). Mean maximum pull force decreased 18% and 42% for the PVC dot glove and cotton glove, respectively, compared to the bare hand (handle material pooled; Table 1). A linear relationship between maximum pull force and the coefficient of friction was found as shown in Figure 5 (r² = .76).

Figure 4.

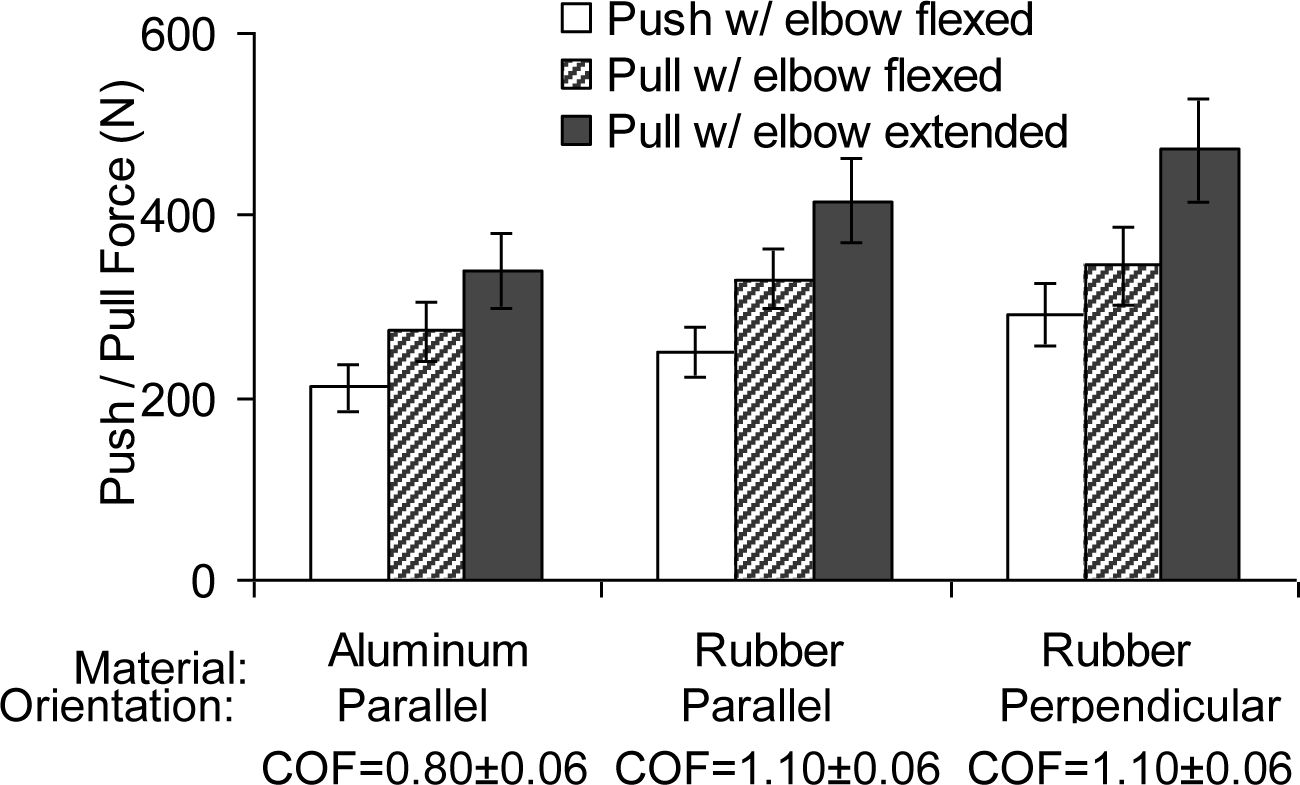
Mean ± SE maximum push/pull force in absolute values (|F_z|) for the two force directions (push vs. pull), elbow postures (flexed vs. extended, only for pull), handle materials (coefficient of friction (COF) = 0.80 ± 0.06 between the aluminum handle and the bare hand, and 1.10 ± 0.06 between the rubber handle and the bare hand), and handle orientations (parallel vs. perpendicular) (bare hand only).

Figure 5.

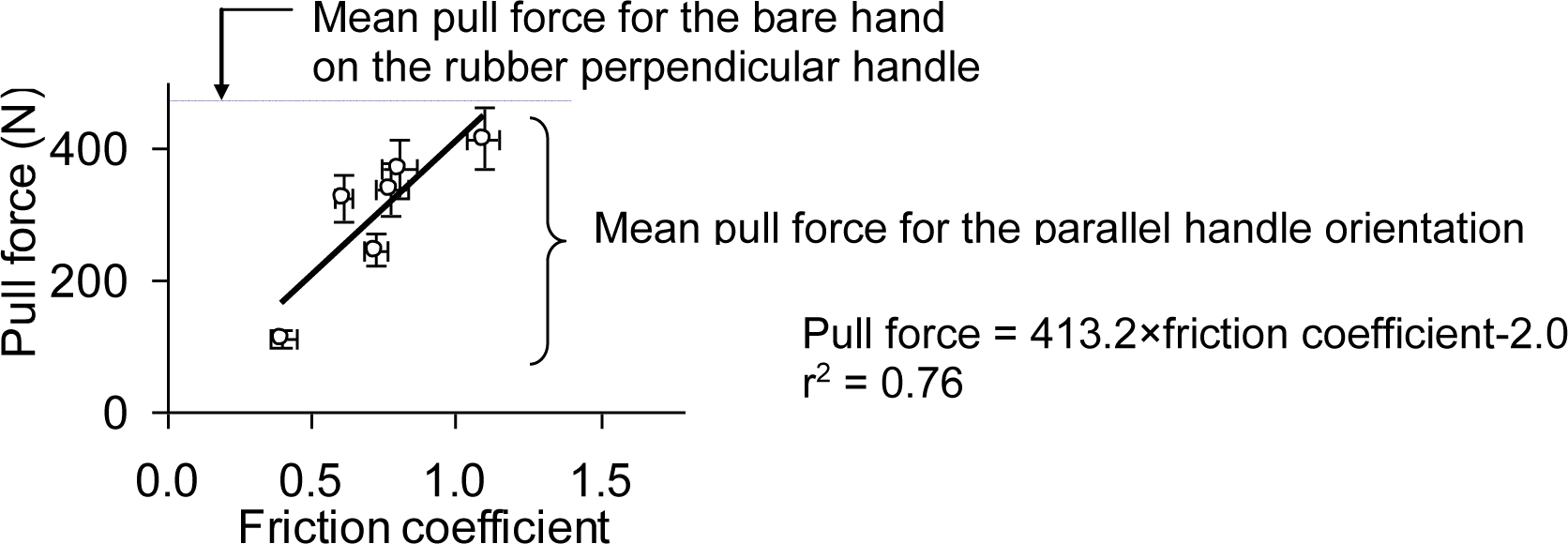
The relationship between maximum pull force and the coefficient of friction (shown in mean ± SE). Mean friction coefficient = 0.40 for cotton glove-aluminum, 0.61 for cotton glove-rubber, 0.72 for PVC dot glove-aluminum, 0.78 for bare hand-aluminum, 0.80 for PVC dot glove-rubber, 1.10 for bare hand-rubber. (Pull and extended elbow posture only.)

Maximum pull force was, on average, 29% greater when the elbow was extended, compared to when the elbow was flexed (the handle material and handle orientation conditions pooled; bare hand only; Figure 4; Table 1). The effect of elbow posture was found significant (p<0.01). The extended elbow posture was accompanied with 12% greater upward force (positive F_y), compared to the flexed elbow posture (p<0.05; Table 1). Lateral force (F_x) did not change significantly with the arm posture. Maximum pull force was, on average, 26% greater than maximum push force (handle materials and orientations pooled; bare hand and flexed elbow posture only; p<0.01; Figure 4; Table 1). Pull exertions were accompanied by upward force (positive F_y), whereas push exertions were accompanied by downward force (negative F_y) (Table 1).

4. DISCUSSION

4.1. Handle orientation

Data support the hypothesis that greater pull/push force can be produced at right angles to the handle than parallel to it. Maximum pull/push force was, on average, 11% greater for the perpendicular handle than for the parallel handle, when the same rubber handle with the bare hand was used (Table 1; Figure 4). This is consistent with a previous study that reported greater push force for a perpendicular handle than for a parallel handle (Okunribido & Haslegrave, 2008).

For the parallel handle, previous studies (MacKenzie & Iberall, 1994; Pheasant & O’Neill, 1975; Seo et al., 2008; Smaby et al., 2004) and Equation 2 explain that pull/push force is solely dictated by and limited by friction force. In contrast, modeling of the shear and normal force application by the hand to a perpendicular handle performed in the present study (Equation 1) suggests that both normal and friction forces from the hand could contribute to pull/push forces, resulting in greater maximum voluntary pull/push forces for the perpendicular handle than for the parallel handle. In addition, for push, the perpendicular handle provides mechanical interference that prevents the hand from slipping and allows the upper-body push force to be applied directly against the handle, which may contribute to greater push force for the perpendicular handle compared to the parallel handle.

4.2. Hand-handle friction: Handle Material and Glove

Data support the hypothesis that maximum pull/push force for the parallel handle is related to the hand-handle friction simulated by handle materials and gloves. As the handle material changed from rubber to aluminum, the coefficient of friction decreased from 1.10 to 0.80. With this decreasing hand-handle friction coefficient, maximum pull/push force decreased 17% on average for the parallel handle (Table 1; Figure 4). The data agree to the prediction from Equation 2 and to previous studies (MacKenzie & Iberall, 1994; Pheasant & O’Neill, 1975; Seo et al., 2008; Smaby et al., 2004), suggesting that pull/push force was limited by hand-handle friction when pull/push force was applied parallel to the cylindrical handle’s long axis.

The bare hand-rubber handle combination yielded the highest friction coefficient (1.10) and average maximum pull force, whereas the cotton glove-aluminum handle combination resulted in the lowest friction coefficient (0.40) and lowest average maximum pull force (only 27% of bare hand-rubber handle combination). As shown in Figure 5, maximum pull force decreased linearly with decreasing coefficient of friction (r² = .76). This linear relationship between maximum pull force and friction coefficient further validates the model in Equation 2.

The gloves investigated in this study displayed lower friction coefficients on the rubber and aluminum handles compared to the bare hand. Specifically, the PVC dot glove and cotton glove resulted in, on average, 18% and 46% reduced coefficient of friction compared to the bare hand, respectively. Likewise, two gloves resulted in 18% and 42% reduced maximum pull force compared to the bare hand, respectively. Although the gloves investigated in this study resulted in lower friction force, other gloves such as a rubber glove (Nagashima & Konz, 1986) or surgical glove (Shih & Wang, 1997) have been shown to increase friction force compared to the bare hand. The coefficient of friction can either decrease or increase depending on the glove material. Gloves can also reduce finger/hand dexterity and comfort (Havenith & Vrijkotte, 1994). Reduced tactile sensitivity and/or low hand-handle friction coefficient may lead to elevated grip force exertions than necessary (Kinoshita, 1999), which, when repeated, can contribute to fatigue and musculoskeletal disorders (Armstrong et al., 1993).

4.3. Arm Posture

Mean maximum pull force was 29% greater for the extended elbow than for the flexed elbow (Table 1; Figure 4; p<0.01). This result is consistent with the previous empirical data (Davis & Stubbs, 1977b). As analyzed in Equations 4 and 5, maximum pull force for the flexed elbow posture may have been limited by the elbow flexion and shoulder extension strengths. For the extended elbow posture, maximum pull force may not be limited by shoulder and elbow strengths as long as enough upward force (positive F_y) is applied (Equation 3) to keep the joint external moment low. Indeed, 12% greater upward forces, on average, were applied by the subjects for the extended elbow posture than for the flexed elbow posture (Table 1). Based on Equation 3, it appears that this greater upward force for the extended elbow could reduce the extent of the required joint stabilizations, resulting in increased maximum pull force, compared to the flexed elbow posture.

4.4. Pull vs. Push

Consistent with previous studies (Das & Wang, 2004; Davis & Stubbs, 1977b; Keyserling et al., 1980; Kumar, 1995; Kumar et al., 1995), mean maximum pull force was 26% greater than mean maximum push force for the flexed elbow posture (Table 1; Figure 4). Equations 4 and 5 describe that pull exertions utilize upward force exertion (positive F_y) and elbow flexion strength. Similar analysis can be applied to push exertions to show that downward force exertion (negative F_y) and elbow extension strength are used in push exertions. In fact, downward force was empirically observed in the present study (Table 1). Elbow flexion strength has been shown to be approximately 25% greater than elbow extension strength (Holzbaur et al., 2007). Thus, greater pull force than push force may be related to greater elbow flexion strength than elbow extension strength for the posture examined in this study (Figure 2a). Other factors such as torso strength may be involved in other pull/push postures where the arm strength is not limiting.

4.5. Future work

For a perpendicular handle, only rubber handle surface was examined. However, the model presented in Figure 1a and Equation 1 suggests that the maximum pull force on a perpendicular handle can also be affected by hand-handle friction conditions. Measurement of maximum pull force for varying handle surface friction coefficients may reveal relative contributions of friction force and normal force in pulling on a perpendicular handle.

In addition, the model presented in Figure 1a and Equation 1 does not consider that each segment of the hand (e.g., contributing to F_n(θ_i)) are connected to neighboring segments (e.g., contributing to F_n(θ_i-1) and F_n(θ_i+1)). For example, friction force at θ = 0 is not used for estimation of pull/push force in the current model. However, if the hand wrapping around the handle in Figure 1a is thought as a pulley or a rope, this friction force at θ = 0 can be delivered to the whole link of the hand and it could contribute to pull/push force. Modeling of the hand as a link system could improve the current model presented in this paper.

Friction between the skin and the inner material of the glove was not considered, as gloves were tightly seated on the hand via an elastic band around the wrist in this study. For gloves that do not provide firm contact with the skin, friction between the skin and the inner surface of the glove can limit force exertion, especially for pull. In that case, friction in both inside and outside the glove needs to be examined and considered.

5. Conclusions/Application

This study used biomechanical models to analyze effects of handle orientation, handle material, gloves, and arm posture on maximum pull/push force. Empirical data obtained in the study supported the proposed biomechanical models. Specifically, the present study demonstrated that maximum pull/push force decreased when a cylindrical handle was parallel to the pull/push direction, compared to when the handle was perpendicular to the pull/push direction. This is because the parallel handle relies on friction for the coupling between the hand and handle during pull/push force exertions (Equation 2), whereas both normal and friction forces from the hand contribute to pull/push force for the perpendicular handle (Equation 1). For the parallel handle, maximum pull/push forces further decreased with decreasing hand-handle friction coefficient (simulated by different handle materials and gloves). It indicates that friction between the hand and handle limited maximum pull/push forces for parallel handles, supporting Equation 2. For design of work objects that involve pull/push, simply installing handles perpendicular to the pull/push direction may increase workers’ capability to produce pull/push forces. Increasing the friction coefficient between the hand and handle by changing the handle material or gloves may also increase workers’ capability to produce pull/push forces.

Mean maximum pull force exerted by the bare hand against the two handle materials in both handle orientations was 29% greater when the elbow was extended than flexed. Maximum pull force was, on average, 26% greater than push, when the bare hand was used against the two handle materials in both handle orientations with the flexed elbow. These effects of arm posture and force direction (pull vs. push) may be attributed to limited elbow strength based on the biomechanical analysis performed for the postures examined in the present study. It should be noted that these findings can be sensitive to postures, as the geometry given for a posture (e.g., moment arms in Figure 2 and Equations 3–5) affects the results of the analyses. Different postures would require new biomechanical analyses such as the one performed in the present study.

Biomechanical models and analyses presented in this paper provide insights for causality of upper extremity strength limitations during pull/push. Findings in this paper can be directly used in workstation design to reduce fatigue and musculoskeletal disorders. It is to be noted that the pull/push force data presented here do not represent the population data, but rather demonstrate the consistent effects of the handle orientation, handle material, glove, and arm posture on maximum pull/push forces across individuals with different strengths. By carefully designing pull/push tasks and workstations in regards to handle orientation, handle material, glove, and arm posture, maximum pull/push capabilities can be increased for a person with a given strength as demonstrated and analyzed in this paper. As a result, occurrence of fatigue and upper extremity injuries can be reduced.

Statement of Relevance.

Upper extremity injuries associated with push/pull tasks have recently increased. Biomechanical models presented in this paper provide insights for causality of upper extremity strength limitations during pull/push. Findings in this paper can be directly used in design of workstation and work objects to reduce fatigue and musculoskeletal disorders.