Highlights
-
•
A closed-loop controller based on PL regulation to sustain temporal stability of SC.
-
•
Three proportional factors were optimized to improve performance of the controller.
-
•
Rise time and temporal stability of SC of circulating MBs were improved.
-
•
A transition from SC to IC was reduced by the controller.
Keywords: Ultrasound, Circulating microbubbles, Stable cavitation, Closed-loop controller, Pulse length
Abstract
Stable cavitation (SC) has shown great potential for novel therapeutic applications. The spatiotemporal distribution of the SC activity of microbubbles circulating in a target region is not only correlated with the uniformity of treatment, but also with some undesirable effects. Therefore, it is important to achieve controllable and desirable SC activity in target regions for improved therapeutic efficiency and biosafety. This study proposes a closed-loop feedback controller based on pulse length (PL) regulation to improve the temporal stability of SC activity. Microbubbles circulating in a physiological flowing phantom were exposed to a 1 MHz focused transducer. The SC signals produced were initially received by another 7.5 MHz plane transducer, followed by high-speed signal acquisition and real-time processing. Based on the real-time-measured SC intensity excited by the current acoustic pulse, the proposed closed-loop feedback controller used three proportional coefficients to regulate the peak negative pressure (PNP) and PL of the next acoustic pulse during the acceleration and stable stages, respectively. The results show that the rise time and the temporal stability of the SC intensity of the microbubbles circulating in these two stages were improved significantly by the optimized proportional coefficients used in the proposed controller. Importantly, when compared with the traditional closed-loop feedback controller based on PNP regulation, the proposed closed-loop feedback controller based on PL regulation reduced the probability of a transition between stable and inertial cavitation, thus avoiding the risk of disadvantageous bioeffects in practical applications. These results demonstrate the effectiveness of the proposed PL-based closed-loop feedback controller and provide a feasible strategy for realization of controllable cavitation activity in applications.
1. Introduction
During the rarefaction and compressional phases of incident acoustic waves, preformed artificial gas cores (i.e., microbubbles) are driven into radial oscillation in a periodic manner; this phenomenon is known as stable cavitation (SC) [1], [2]. These oscillating microbubbles produce direct radiation forces and stimulate the ambient fluid into micromotion; this leads to the formation of microstreaming in the surrounding microenvironment, which then produces shear stress on adjacent objects [3], [4], [5]. It is accepted that when SC interacts with biological tissues, the direct forces and the secondary physical effects can induce certain advantageous bioeffects for therapeutic applications [6], [7]. For example, the reversible perforation of plasma membranes and the reversible opening of blood–brain barriers by SC ease the delivery of impermeable therapeutic agents into the cells or target tissues [8], [9], [10], [11], [12]. However, other undesirable bioeffects, e.g., hemorrhages and cell lysis, can also be induced by oscillating microbubbles with large amplitudes [13], [14]. In particular, when flowing microbubbles circulate in in vivo vascular networks, the spatial and temporal distributions of the SC activity produced in the target region are not only correlated with the uniformity of the macromolecule delivery distribution, but also cause some unwanted and undesirable effects [15], [16]. Therefore, to improve efficiency while ensuring the biosafety of cavitation-based therapies, it is important to achieve controllable and desirable SC activity within the target region [6], [17].
Different microbubble activities are generated depending on the acoustic parameters [18], [19]. By pre-determining the relationship between the acoustic pulse parameters and shapes and the expected cavitation activity, previous studies mainly used open-loop strategies to achieve the cavitation dynamics required in the target region. For the acoustic pulse parameters, a pre-determined peak negative pressure (PNP) that corresponded to the radial oscillation amplitude of the microbubbles (i.e., the expected SC intensity (SCI)) was generally applied throughout the experiments in most studies [18], [20]. To obtain a uniform temporal distribution of the SC activity in the focal region, based on the blood fluid velocity and the −6 dB bandwidth of the transducer used, the pulse repetition frequency (PRF) is selected to ensure that the same number of flowing microbubbles replenishes the target region when every acoustic pulse is received [21], [22]. Longer pulse length (PL) are reported to increase the primary and secondary acoustic radiation forces, thus influencing the translational dynamics of microbubbles and resulting in unwanted bioeffects [23], [24]. In terms of the acoustic pulse shapes, rapid short-pulse sequences (PL of the order of microseconds emitted at kHz-order PRFs) were used to extend the persistence of microbubble acoustic emissions and thus enhance the spatiotemporal distribution of the cavitation activity that leads to the desired bioeffect [11], [15], [16].
Besides the incident acoustic pulse parameters and shapes, the properties of the circulating microbubbles within the focused region, including their numbers, size distributions, and shell features (i.e., the stability, surface tension, and gas compressibility), also dominate the spatiotemporal distribution of the cavitation activity [6], [25]. On the one hand, either physiological dissolution or acoustically-driven diffusion, which the flowing microbubbles experienced during blood circulation, caused the difference between the numbers and the properties of the microbubbles that were replenished into the focal region between two successive acoustic pulses [26], [27], [28]. On the other hand, the inherent polydispersity and aggregation of the preformed microbubbles resulted in a heterogeneous spatial distribution for the microbubbles population within the focal region [6], [29]. Therefore, nonuniform spatiotemporal distributions of the cavitation activity over the exposure time were unavoidably generated, even if the same incident acoustic pulses were applied. In previous studies, via real-time monitoring of the acoustic emission from flowing microbubbles, some closed-loop feedback controllers were developed to regulate the PNP of incident acoustic pulses to sustain the SC activity with the exposure time[20], [30], [31], [32], [33], [34].Through observation of the subharmonic emission level, a recent study regulated the PNP of an incident acoustic pulse using a ultrafast FPGA-based feedback loop to sustain relatively stable cavitation activity within a pulse and achieved a high level of reproducibility over the exposure time [35]. Further, on the basis of passive acoustic mapping, a feedback loop controller using non-linear control law was designed to achieve uniform spatiotemporal distribution of cavitation activity [36]. We noted that almost all the proposed closed-loop controllers in these studies used harmonic, ultra-harmonic, or sub-harmonic emissions as the observer and regulated the PNP of the incident pulse using the expected state and the previous state of the system to improve the spatiotemporal distribution of the cavitation activity. However, with the reduction in the number of microbubbles flowing in the focal region over the exposure time, the PNP applied during the later stages of exposure may be regulated to be high enough to sustain the expected SC activity, causing it to be beyond the threshold pressure for inertial cavitation and producing some undesirable bioeffects [20], [31], [34]. For example, erythrocyte extravasation was found in the target or off-target regions when regulating the PNP in the closed-loop controller, and higher median values of the cavitation intensities induced by PNP feedback control could cause lesions [30].
To improve the temporal stability of SC activity and also suppress the occurrence of large-scale stable cavitation during ultrasound exposure, this study aims to develop a novel closed-loop feedback controller using PL regulation. Based on use of a physiological-flow phantom for microbubble circulation and a high-speed acquisition and processing system for SCI measurement, the proposed controller used the difference between the measured SCI and the expected SCI to modulate the rising velocity and the temporal stability of SC activity by PNP and PL regulation in two stages. When compared with the traditional feedback controller based on PNP regulation, three performance metrics and two safety parameters were used to evaluate the effectiveness, stability, and safety of the proposed closed-loop controller.
2. Materials and methods
2.1. Microbubbles and tissue-mimicking phantom fabrication
Before each experiment, SonoVue microbubbles (Bracco Research, Switzerland), which are preformed artificial gas nuclei, were freshly reconstituted using a mixture of lyophilisate with 5 mL of a physiological saline solution. The suspension formed in this manner contains approximately 2–5 × 108 microbubbles per milliliter. To ensure relevance for clinical applications, the original microbubble solution was diluted to 1% (2–5 × 106 microbubbles per milliliter) of this concentration for the experiments. Note that the bubbles concentration used was approximately equal to the acceptable dose in clinical applications [37].
A tissue-mimicking phantom (60 mm 42 mm 40 mm), in which a 2.4-mm-diameter channel was formed to simulate vasculature, was self-fabricated from a 1.5% degassed agarose gel solution. The fabrication process details were presented in our previous reports [22], [38]. The acoustic properties of this phantom were similar to those of human soft tissues, therefore making the phantom suitable for simulation of physiological tissues.
2.2. Acoustic emission and detection in experimental platform
-
1)
Physiological flow circulation system in vitro
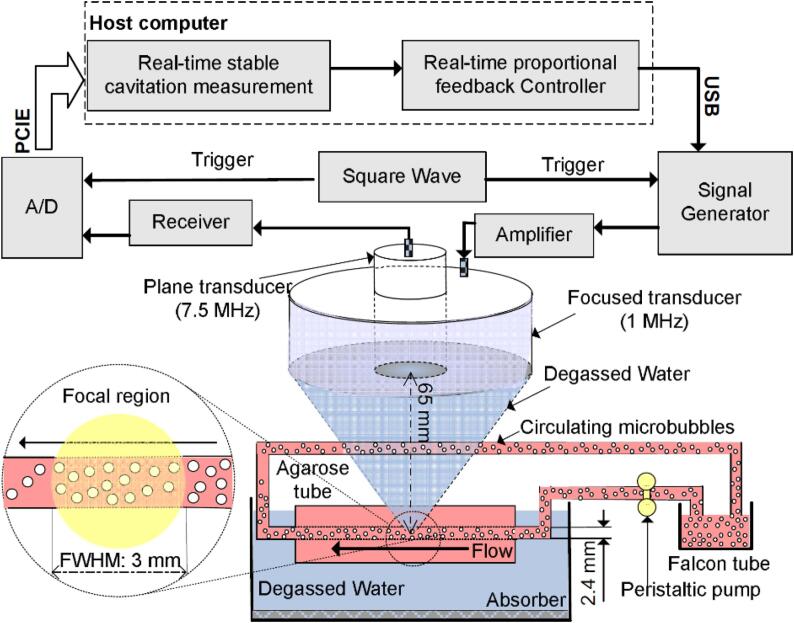
A physiological flow platform, as shown schematically in Fig. 1, was established to imitate the circulation of microbubbles flowing in blood vessels in vivo. The agarose gel tissue-mimicking phantom was installed horizontally in the tank with degassed and deionized water, and the channel inside the phantom was submerged into the water. The preformed microbubble suspension in a Falcon tube was driven and circulated through the agarose gel phantom using a peristaltic pump (BT100-2J, Longer Pump, China), which provides known fluid velocities ranging from 0 to 100 mm/s. An acoustic absorber (UA-1, Institute of Acoustics, Chinese Academy of Sciences, China) was adhered to the bottom of the tank to minimize acoustic reflections and to form a travelling wave field during ultrasound exposure.
-
2)
Ultrasound emission and calibration
Fig. 1.
Schematic diagram of the physiological flow phantom for imitating the circulation of microbubbles flowing in blood vessels in vivo and the real-time measurement and closed-loop control system for stable cavitation activity. A spherical, focused transducer (1 MHz) and a plane transducer (7.5 MHz) were used to sonicate and passively detect cavitation signals, respectively. The dashed box is the cavitation measurement and feedback controller modules operated in the host computer. The enlarged yellow region in the dashed circle is the focal region of 1-MHz focused transducer, in which the lateral FWHM is ∼3.0 mm. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
As illustrated in Fig. 1, a single-element, annular-shaped focused transducer (center frequency: 1 MHz; active diameter: 65 mm; focal length: 65 mm) (Advanced Devices, Wakefield, MA) was fixed in a holder to ensure that its active surface was at a distance of 65 mm from the center axis of the channel in the agarose gel phantom; it was then coupled with the top surface of the agarose gel phantom via a bottom-sealed cone cover filled with degassed water. A 1 MHz sinusoidal signal with regulated PLs, fixed voltage amplitudes, and a fixed PRF was first output by an arbitrary waveform generator (33320A, Agilent Technologies, USA), which was triggered using a square wave signal, and was then amplified using a 50 dB radio-frequency amplifier (E&I 2100L; Electronics &Innovation Ltd, USA) to drive the transducer to generate acoustic signals. Before the experiments, using a capsule hydrophone (HGL-0200, ONDA, USA), various voltage amplitudes were calibrated to determine the free-field peak negative pressures within its focal zone. The details of the calibration procedure were introduced in our previous reports [18], [22].
-
3)
Acoustic emission detection of flowing microbubbles
Under excitation by incident acoustic signals, the acoustic emission properties of the circulating microbubbles were detected passively using another single-element, plane-shaped unfocused transducer (center frequency: 7.5 MHz; active diameter: 13 mm) (Advanced Devices, Wakefield, MA), which was aligned to be coaxial with the transmitting transducer through physical positioning (via a hole at the center of the transmitting transducer). The electrical signals converted from the acoustic emissions were initially amplified by a receiver (5077PR, Olympus, USA) with 9 dB gain, and were then acquired at a rate of 65 million samples per second using a 16-bit digitizer (Spectrum, M4i.4410, Germany) before being transmitted into a host computer through a Peripheral Component Interconnect Express (PCIe) bus interface. The digitizer was triggered by the rising edge of an external square wave signal, which was synchronized with the incident acoustic signal and controlled using a self-built Python-based controller in the host computer. Note that the number of sampling points was set at 32,768 (far greater than the maximal pulse period) to prevent loss of the acoustic signals.
2.3. Real-time closed-loop controller design
-
1)
Acoustic parameters used and the expected SCI
The acoustic parameters, including the PRF and the PNP, required to produce the expected SCI were determined first. To ensure that the same number of circulating microbubbles is presented in the focal region before receiving each acoustic pulse, the focal region should be completely filled with the new microbubbles during the off-time between successive acoustic pulses. Therefore, theoretically, the PRF used in the experiments should be less than the critical PRF (CPRF) [21], [22], which is calculated as v/FWHM (note here that the fluid velocity v (corresponding to the velocity of the circulating microbubbles) was 50 mm/s and the lateral full-width at half maximum (FWHM) of the focused transducer was 3.0 mm, corresponding to CPRF = 16.7 Hz). Therefore, a PRF of 5 Hz (less than the CPRF) was used in this study. A PNP of 0.25 MPa, which was above the PNP threshold for SC of the SonoVue microbubbles, was used to elicit SC of the flowing microbubbles in the focal region. The average value of the SCI (please see the SCI calculation below) caused by 100 single acoustic pulses with a PNP of 40 mV, a PL of 100 µs, and a PRF of 5 Hz were used as the expected values.
-
2)
SCI calculation
After the microbubbles circulating in the focal zone were excited using a single acoustic pulse, the sampled signal X(i) (where i = 0, 1, ···, N − 1, and N is the number of sampling points) within a sampling period T was first processed using a fast Fourier transform to determine the frequency spectrum of the signal.
| (1) |
where k is a frequency point in the frequency spectrum. To quantitate the intensity of the ultra-harmonic components, the power spectrum (P) of the signal was obtained by
| (2) |
The ultra-harmonic components with the fixed 0.1 MHz bandwidth, which were centered at odd multiples of half the driving frequency, were separated from the whole frequency. Then, the ultra-harmonic intensity, as the SCI was calculated within a sampling period T using
| (3) |
where a and b are the numbers of ultra-harmonics in the 2–10 MHz bandwidth and the number of frequency points in each ultra-harmonic component, respectively. Note that the ultra-harmonic components were and that the total number of frequency points in each ultra-harmonic component can be calculated to be . In Eq. (3), the coefficient (fs: Sampling frequency) is the sampling time for the SC signals. The measured SCI ( in each acoustic pulse can thus be calculated using:
| (4) |
where and are the intensities of the ultra-harmonics from the circulating microbubbles and the control saline solution, respectively.
2.4. Real-time proportional feedback controller
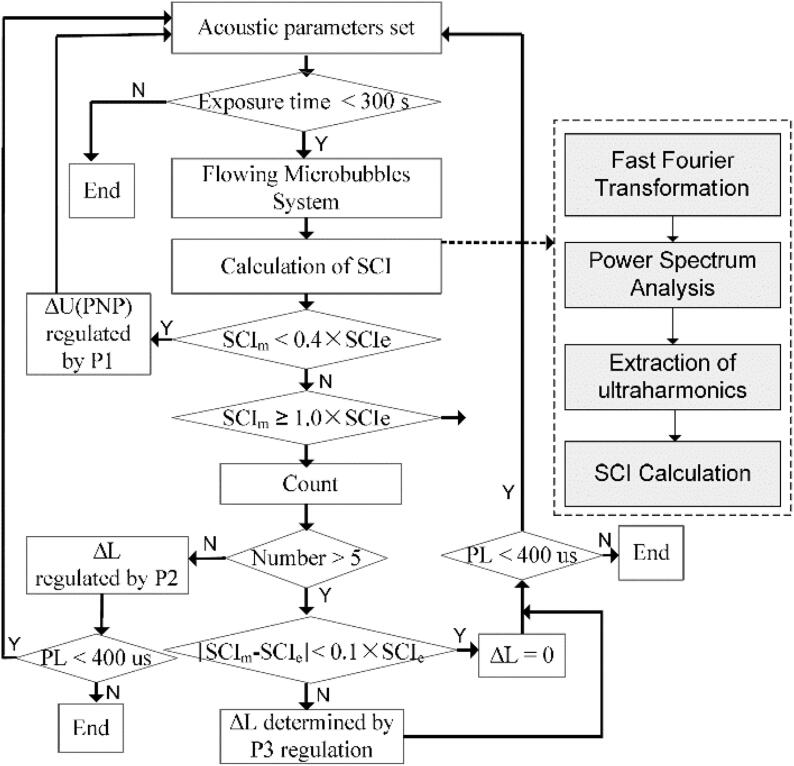
To regulate the temporal distribution of the SCI during ultrasound exposure, based on the SCIm generated by the current acoustic pulse, a real-time closed-loop feedback controller with three proportional factors was designed to regulate the PNP or the PL of the next acoustic pulse during two stages. The corresponding flowchart for this controller is presented in Fig. 2.
-
1)
PNP and PL regulation in the acceleration stage
Fig. 2.
Flowchart of the proposed closed-loop feedback controller based on pulse length regulation. The procedure in the dotted-line block is the method for stable cavitation intensity measurement.
If a large PNP was applied directly at the beginning of the ultrasound exposure, some unpredictable bioeffects could easily be caused. It is thus better to apply a minimal PNP (for the system used in this case, the minimum was a PNP of 0.03 MPa, corresponding to a voltage amplitude of 10 mV) when starting the exposure. Therefore, the aim during this stage is to accelerate the SCI from the minimum up to the expected value. Note that the PNP has a greater influence on the SCI than the PL. In this stage, to achieve the expected SCI of 40% rapidly, the PNP (corresponding to the amplitude of the input voltage) was first regulated using the term
| (5) |
where U(t) represents the voltage amplitude of the current acoustic pulse input, and U(t + T) is the regulated voltage amplitude of the next acoustic pulse. P1 is the proportional factor. Subsequently, when SCIm reached the expected SCIe of 40%, to prevent SCI overshoot when using PNP regulation and to ensure relatively smooth elevation of SCIm to SCIe, the PL was regulated using equation (6) as follows:
| (6) |
where PL(t) represents the length of the current acoustic pulse, PL(t + T) is the regulated length of the next acoustic pulse, and P2 is the proportional factor. When the real-time measured SCI reached the SCIe of 100% during the next five consecutive acoustic pulse periods, the controller would then complete the regulation in this stage.
-
2)
PL regulation in stable stage
During this stage, the effects of the fluid conditions and acoustic excitation on the stability of the microbubbles meant that the numbers and the stability of the microbubbles changed gradually (decreased and became worse, respectively) with increasing exposure time. To maintain the temporal stability of the SCI in the focal region, P3 in Eq. (7) was used as a third proportional factor to regulate the PL during this stage.
| (7) |
Note that all measurement and control processes, including the acoustic emission, signal acquisition and processing, and adjustment calculations using the proportional algorithm, were performed in the closed-loop controller. These processes should be completed during the off-time between two successive pulses, and the regulated PNP or PL could then be input in the subsequent pulse.
2.5. Evaluation of controller performance
-
1)
Rise time for the acceleration stage
The rise time (, which is used to determine how quickly SCIe can be achieved during the acceleration stage, is associated with PNP and PL regulation by the parameters and . Tr was calculated as the time () taken for SCIm to reach an SCIe of 90% minus the time () taken for SCIm to reach an SCIe of 10%, i.e., .
-
2)
Stability ratio and concentration ratio for the stable stage
The stability ratio () and the concentration ratio (δ) were proposed to evaluate the stability and dispersion of the controller during the stable stage. , which measures the frequency of SCIm within the error band of SCIe, can be calculated using the following equation:
| (8) |
where and N are the number of SCIm over the range from an SCIe of 90% to an SCIe of 110%, and the total number of SCIm, respectively.
δ, which evaluates the degree of deviation of SCIm within the error band relative to SCIe, is the standard variation of SCIm with respect to SCIe during the stable stage, and can be calculated as follows:
| (9) |
-
3)
Parameters for safety evaluation
-
a)
Broadband emission intensity
To determine the degree of broadband emission during the stable stage, after the power spectrum (P) of the acquired acoustic signal was calculated using Eq. (2), the broadband emission intensity (BEI) within a sampling period was calculated as follows:
| (10) |
where c and d are the number of broadband components within the 2–10 MHz bandwidth and the number of frequency points in each broadband component, respectively. Note that the broadband components were and that the total number of frequency points in each broadband component can be calculated using . Therefore, the measured can be calculated as follows:
| (11) |
where and are the intensities of the broadband emissions from the circulating microbubble solution and the control saline solution, respectively. Here, the cumulative broadband emission intensity from the last 200 acoustic excitation pulses (during the stable stage) was used to evaluate the safety of the controller.
-
b)
Ratio of SCI to BEI
Because the ultra-harmonics could be elevated to enhanced levels by increments in the broadband emissions (particularly during the transition from stable to inertial cavitation), the ratio of SCI to BEI was used to provide an accurate evaluation of the enhancement of the ultra-harmonics. Note here that the numbers of frequency points for SCI and BEI were different in Eqs. (3), (10). Here, the number of frequency points used to calculate the BEI was adjusted to be the same as the number used to calculate the SCI. The adjusted can be calculated by
| (12) |
Therefore, the ratio of the SCI to the BEI can be calculated using
| (13) |
3. Results
3.1. SCI dynamics of non-circulating and circulating microbubbles under open-loop system conditions
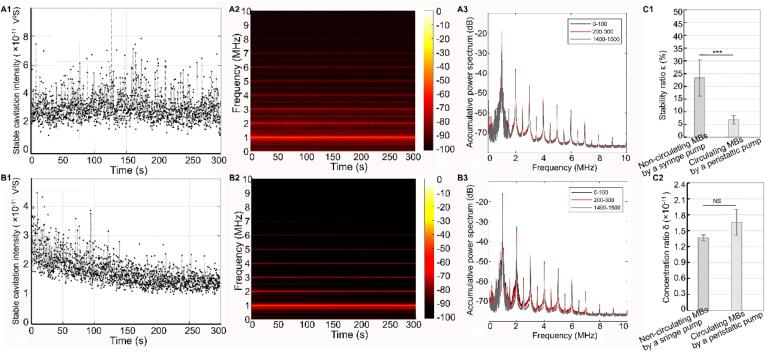
To illustrate the effects of the number and properties of the flowing microbubbles on the temporal distribution of the SCI within the target region under open-loop system, we first investigated the dynamics of the SCI of the non-circulating microbubbles when driven using a syringe pump. (Noted that under this situation, the focal region is theoretically replenished by the newly flowing microbubbles before receiving every acoustic pulse) The microbubbles were exposed to acoustic pulses with a fixed PNP of 0.25 MPa, a PL of 100 µs, and a PRF of 5 Hz. As shown in Fig. 3A1, the SCI was maintained at a relatively stable level (∼2.9 × 10−11 V2S) throughout the entire exposure time. Corresponding ultra-harmonics were observed throughout the exposure time and were maintained at ∼−65 dB, as shown in the time–frequency domain curve in Fig. 3A2. Fig. 3A3 shows that the cumulative spectra produced by excitation by the first 100 pulses, by excitation by the third 100 pulses, and by excitation by the final 100 pulses almost coincided and were maintained at the same level. These results suggest that for the non-circulating microbubbles driven using the syringe pump, where the focal region can be perfused completely by the newly flowing microbubbles before acoustic pulse emission, the same number of flowing microbubbles in the focal region with the same properties were exposed to the acoustic pulses used during acoustic exposure, thereby achieving the uniform temporal distribution of the SCI throughout the exposure time.
Fig. 3.
SCI temporal distribution and spectrum characteristics of non-circulating and circulating microbubbles under open-loop system. The non-circulating microbubbles driven using a syringe pump were exposed to pulsed ultrasound (0.25 MPa PNP, 100 µs PL,5 Hz PRF and 300 s), A1-A3 shows that the obtained temporal distribution of SCI, time–frequency spectrum, and the accumulative spectrum produced by the first 100 pulses, the third 100 pulses and the last 100 pulses excitation. The circulating microbubbles driven using a peristaltic pump were exposed to pulsed ultrasound (0.25 MPa PNP, 100 µs PL, 5 Hz PRF and 300 s), B1-B3 shows that the obtained temporal distribution of SCI, time–frequency spectrum, and the accumulative spectrum produced by the first 100 pulses, the third 100 pulses and the last 100 pulses excitation. C1-C2. Statistical comparison of stability ratio and concentration ratio between SCI dynamics of the non-circulating and circulating microbubbles under open-loop system. ***Statistically significant difference (p < 0.001). NS: no statistical significance.
However, when the circulating microbubbles that were driven using a peristaltic pump were exposed to the same acoustic pulses (fixed PNP of 0.25 MPa, PL of 100 µs and PRF of 5 Hz), a different temporal distribution of the SCI in the focal region was observed in Fig. 3B1. As Fig. 3B1 shows, within the first ∼30 s (corresponding to excitation by the first 100 acoustic pulses), a stable SCI was maintained at approximately 2.8 × 10−11 with a relatively uniform temporal distribution. This time was longer than the time required for the microbubbles to flow through their first circulation (the fluid velocity was 50 mm/s, and the tube length was 100 cm). Note that during the first circulation, the same amounts of initial microbubbles with the same properties were theoretically perfused into the focal region before receiving the acoustic pulse. Therefore, the temporal distribution of the SCI within the first 30 s showed a relatively stable level. However, during the subsequent 30–300 s, the SCI decreased gradually with a relatively fast decay ratio, ultimately reaching a relatively low level (∼1.4 × 10−11 V2S). The time–frequency spectrum shown in Fig. 3B2 showed that the amplitude of the ultra-harmonic components decreased gradually with increasing time. Comparison of the cumulative spectra obtained from excitation by the first 100, third 100, and final 100 acoustic pulses, showed an obvious reduction in the amplitudes of the ultra-harmonics, as observed in Fig. 3B3. Fig. 3C1 also showed that although no significant difference was observed in the SCI concentration ratio between the non-circulating and circulating microbubbles, the stability ratio of the SCI in the circulating microbubbles was significantly lower than that in the non-circulating microbubbles. These results indicate that the number and the properties of the perfused microbubbles passing into the focal region continued to vary with the fluid circulation after the first circulation, and a uniform temporal SCI distribution cannot be achieved in the open-loop system.
3.2. SCI rapid increment in acceleration stage by P1 and P2 regulation in the proposed controller
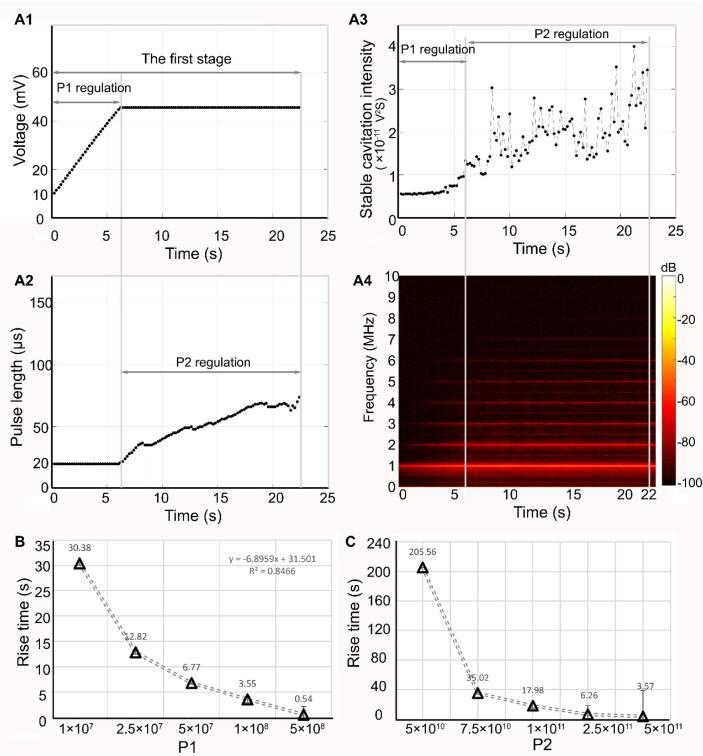
To elevate the SCI rapidly to the desired level while avoiding the occurrence of large amplitude oscillations of the microbubbles, the proportional factors P1 and P2 in the proposed controller were initially designed to regulate the voltage amplitude (PNP) and the PL during the acceleration stage, respectively. The region on the left (t < 6.67 s) of the gray line in Fig. 4A1–A3 shows a representative temporal distribution of SCI with respect to the change in voltage amplitude and the PL of the incident acoustic pulse when P1 was 1 × 108. Fig. 4A1 shows that the voltage amplitude increased linearly from 10 mV to ∼43 mV (Corresponding PNP increased 0.03 MPa to 0.27 MPa) in the first 6.67 s. However, the PL remained unchanged within this period, as shown in Fig. 4A2. Fig. 4A3 shows that the controller took approximately 6.67 s to raise the SCI from its initial level to the SCIe of 40%. The time–frequency domain change in Fig. 4A4 shows that the ultra-harmonic components grew to ∼−70 dB at 6.67 s. The relationship between the rise time for the initial stage and P1 is shown in Fig. 4B. As Fig. 4B indicates, the rise time for the SCI was approximately positively correlated with P1 (R = 0.92). Although a larger value of P1 could produce faster rise times, there was a risk of overshoot when P1 exceeded 1 × 108, which would lead to the occurrence of large amplitude oscillations. Therefore, P1 was optimized at 5 × 107 during this stage.
Fig. 4.
SCI temporal distribution regulated by the amplitude (corresponding to peak negative pressure) and pulse length of the acoustic pulse (corresponding to proportional coefficients P1 and P2, respectively) in acceleration stage for achieving fast rise time. When proportional coefficients P1 and P2 were 1 × 108 and 1 × 1011 respectively, A1-A3 shows the temporal change of the amplitude (corresponding to peak negative pressure) and pulse length of the acoustic pulse, and SCI in the acceleration stage. A4. Time-frequency spectrum of SC signal in the acceleration stage. B. The relationship between proportional coefficient P1 and the rise time in the acceleration stage. C. The relationship between proportional coefficient P2 and the rise time in the acceleration stage.
Subsequently, the PL (but not the PNP) was regulated using another proportional factor P2 in the controller. The middle region between the two gray lines in Fig. 4A1–A3 shows the temporal distribution of the SCI with respect to the changes in the voltage amplitude (PNP) and the PL for a typical P2 (1 × 1011). Fig. 4A1 and 4A2 show that from 6.67 s to ∼22.4 s, the PL increased by ∼ 250% (from 20 µs to ∼70 µs), while the voltage amplitude (PNP) remained constant. With this increase in PL, the SCI exhibited an increasing trend, and reached its expected level at ∼22.4 s, as shown in Fig. 4A3. Fig. 4A4 shows that the ultra-harmonic components were enhanced notably from −70 dB to ∼−66 dB during this period. These results illustrated the effectiveness of PL regulation during this period. Fig. 4C shows that the rise time of SCI improved from 205.56 s to 3.57 s when P2 increased from 5 × 1010 to 5 × 1011, and the rise time was approximately positively correlated with P2 (R = 0.86). Similar to the influence of P1 on the increments in the SCI, the higher P2 (e.g., 5 × 1011) also caused an overshoot of the SCI. Furthermore, the time taken for the microbubbles to circulate in the first cycle was approximately 22 s, which was approximately equal to the total rise time (22.4 s) during the acceleration stage (where P1 and P2 were optimized at 5 × 107 and 1 × 1011 with 6.67 s and 17.9 s rise times, respectively). Therefore, the SCI was regulated to the expected level within the first circulation and avoided the influence of the number of circulating microbubbles and their properties on the SCI.
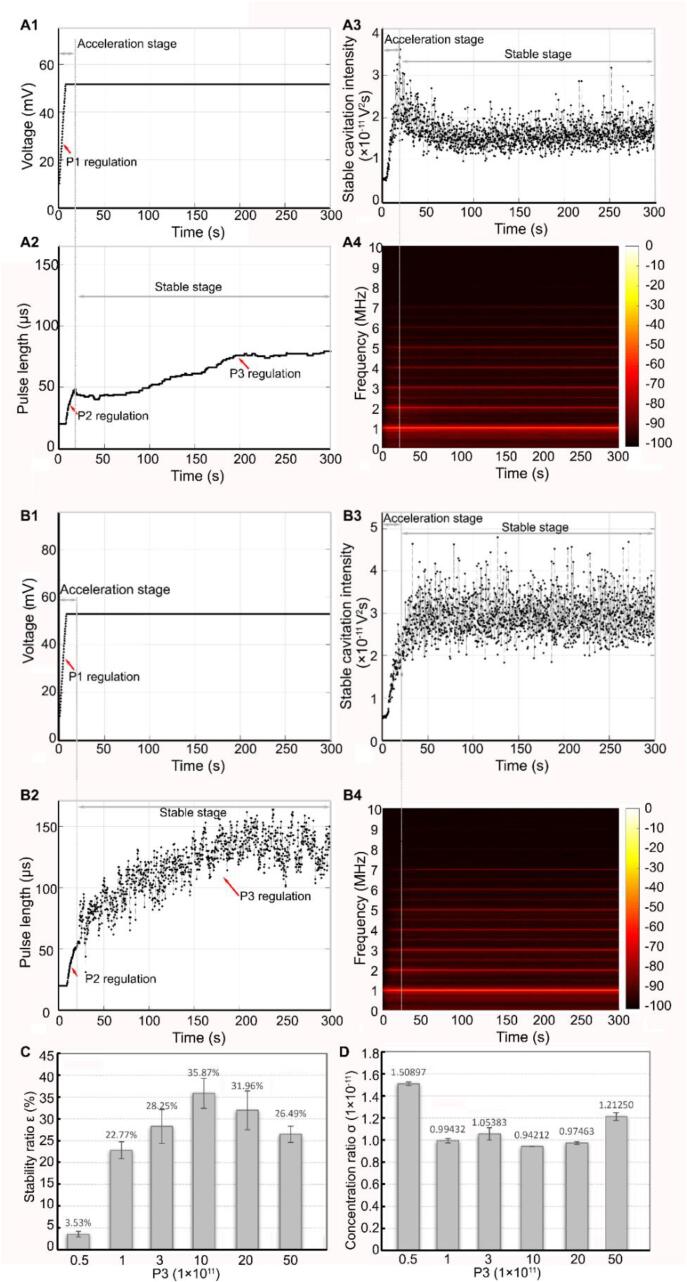
3.3. SCI maintaining stability in the stable stage by P3 regulation in the proposed controller
When the expected value of the SCI was achieved five times consecutively, the proportional factor P3 was used to regulate to maintain the temporal stability of the SCI during the stable stage. Two representative sets of SCI dynamics and the corresponding regulated PL characteristics are shown in Fig. 5. For the smaller P3 (5 × 1010) case, as shown in Fig. 5A1–5A3, the PL was regulated continuously during the stable stage (the region to the right of the gray dotted line), and the voltage amplitude (PNP) remained unchanged. However, the SCI initially showed a moderate reduction over the period from ∼24.65 s to ∼75 s, subsequently raising slowly to a relatively high level (∼1.5 × 10−11 V2S) that was still below the expected SCI level within the subsequent ∼225 s. Fig. 5A4 showed that the intensity of the ultra-harmonic components was maintained at a small but stable value (∼−68 dB). These results suggest that, with the reduction in the numbers and the stability of the circulating microbubbles during this period, using the smaller P3, the SCI could not be maintained at the expected level. However, for the case where P3 was equal to 1 × 1012, Fig. 5B1–5B2 show that the PL exhibited an increasing trend with increasing exposure time (from ∼24.65 s to 300 s), while the voltage amplitude (PNP) remained constant. Fig. 5B3 shows that the SCI maintained a relatively uniform temporal distribution at the expected level during this period. Fig. 5B4 shows that the intensity of the ultra-harmonics was maintained at ∼−65 dB throughout this period. These results indicate that the SCI can be maintained at a stable level when using the appropriate value of P3.
Fig. 5.
SCI temporal distribution regulated by the pulse length of the acoustic pulse (corresponding to proportional coefficient P3) in the stable stage for sustaining stability. For proportional coefficients P3 (5 × 1010), A1-A3 shows the temporal change of the amplitude (corresponding to peak negative pressure) and pulse length of the acoustic pulse, and SCI in the stable stage. A4. Time-frequency spectrum of SC signal with this period. For proportional coefficients P3 (1 × 1012), B1-B3 show the temporal change of the amplitude (corresponding to peak negative pressure) and pulse length of the acoustic pulse, and SCI in the stable stage. B4. Time-frequency spectrum of SC signal in the stable stage. C. The relationship between proportional coefficient P3 and the stability ratio in the stable stage. D. The relationship between proportional coefficient P3 and the concentration ratio in the stable stage.
The effects of the different P3 values on the temporal distribution of the SCI during the stable stage are shown in Fig. 5C–5D. Fig. 5C shows that the stability ratio increased gradually with increasing P3 values below 1 × 1012, but it then decreased rapidly when P3 exceeded 1 × 1012. Fig. 5D shows that the concentration ratio rapidly reduced at P3 values below 1 × 1012 but increased gradually at P3 values above 1 × 1012. These results indicate that the larger P3 values might cause a larger PL, resulting in the occurrence of large-amplitude oscillations of the microbubbles and large deviations. Therefore, 1 × 1012 can be considered to be the optimal P3 value required to achieve a relatively uniform SCI distribution.
3.4. Performance comparison between the closed-loop controllers based on PL regulation and PNP regulation
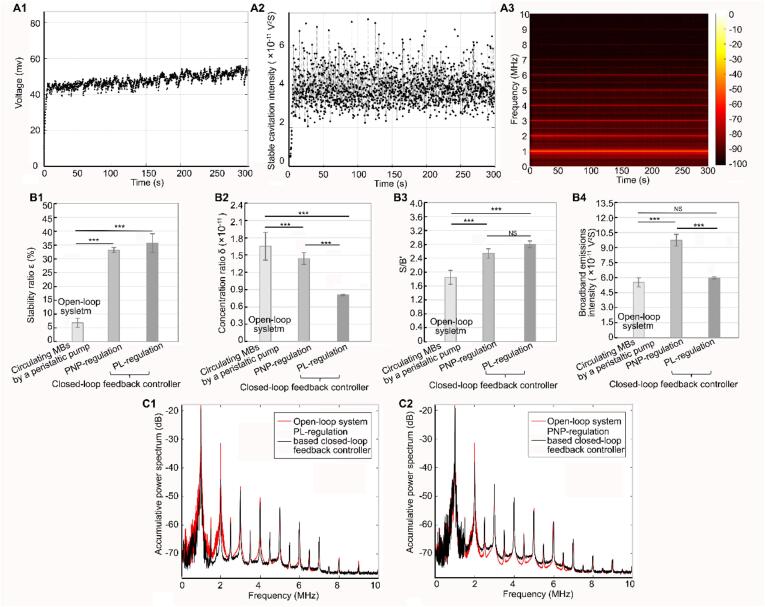
Fig. 6A1–6A2 show the temporal distribution of the SCI when only the PNP (corresponding to the voltage amplitude of the pulse) was regulated during the acceleration and stable stages using the optimal proportional factor in the PNP-regulation-based controller (details of the regulation strategy are presented in the Supplementary Materials). As shown in Fig. 6A1–6A2, using the optimized proportional factor P1 (5 × 107), within the first 10 s of the acceleration stage, in which the the voltage amplitude (PNP) increased quickly, the SCI rose rapidly to the expected value, similar to the increment trend during the acceleration stage in the proposed PL-regulation-based controller. (Note that the P1 was optimized based on the rise time for this stage.) Within the subsequent period from 10 to 300 s, where the voltage amplitude (PNP) was regulated using another optimized proportional factor P2 (1 × 108), the SCI was maintained at a relatively stable level. Fig. 6A3 shows that apart from the ultra-harmonic components, some additional broadband components with low intensity were generated throughout this period. Fig. 6B1 illustrates that the SCI of ∼33% reached the expected level, thus indicating the effectiveness of this controller.
Fig. 6.
SCI temporal distribution regulated by the amplitude (corresponding to peak negative pressure) of the acoustic pulse in PNP-based closed-loop feedback controller. A1-A3. shows the temporal change of the amplitude of the acoustic pulse, SCI and the spectrum of SC signal when using PNP-based closed-loop feedback controller. B1-B4. Performance comparison of open-loop system, PNP-based closed-loop feedback controller and PL-based closed-loop feedback controller (B1. stability ratio; B2. concentration ratio; B3. S/B’; B4. broadband emissions). ***Statistically significant difference (p < 0.001). NS: no statistical significance. C1. Comparison of the accumulative spectrum produced by the first 100 pulses between open-loop system and PL-based closed-loop controller. C2. Comparison of the accumulative spectrum produced by the first 100 pulses between open-loop system and PNP-based closed-loop controller.
Fig. 6B1–6B2 show a performance comparison between the open-loop system (in which the circulating microbubbles were driven using a peristaltic pump) and the closed-loop controllers based on PNP regulation or PL regulation during the stable stage. The stability ratios in the closed-loop controllers based on PL regulation and PNP regulation were significantly higher than the corresponding ratio in the open-loop system, while the concentration ratios were significantly lower, thus suggesting that the temporal stability of the SCI can be improved by use of the closed-loop controller. Furthermore, the concentration ratio in the closed-loop controller based on PL regulation was significantly lower than that in the closed-loop controller based on PNP regulation. Importantly, as shown in Fig. 6B3–6B4, by analyzing the frequency spectra of the signals, we found that although the value of S/B’ in the two controllers was significantly higher than that in the open-loop system, the broadband noise intensity in the closed-loop controller based on PNP regulation was significantly higher than the corresponding intensities in the closed-loop controller based on PL regulation and the open-loop system. Additionally, the amplitudes of the broadband signals in the PL regulation-based controller were observed to be similar to those in the open-loop system, but the amplitudes in the PNP regulation-based controller were higher than those in the open-loop controller, as shown in Fig. 6C1–6C2. These results indicated that the proposed PL regulation controller could eliminate the risks of inertial cavitation or large amplitude oscillation of the circulating microbubbles.
4. Discussion
4.1. Summary of the proposed method and application relevance
Through monitoring of the ultra-harmonic emissions, the proposed closed-loop feedback controller based on PL regulation used three proportional factors to regulate the temporal distribution of the SCI throughout two stages. The initial acceleration stage, which should be completed within the first cycle of circulation of the microbubbles, aimed to reach the expected SCI rapidly using a combination of PNP and PL regulation. To achieve a fast rise time and prevent overshoot, the proportional factors P1 and P2 for PNP and PL regulation were optimized during this stage to obtain the expected SCI values of 40% and 100%, respectively. The second stable stage, in which the number and the stability of the flowing microbubbles both gradually decreased and degraded because of the influence of the fluid environment and acoustic excitation, was intended to sustain a uniform temporal distribution of the SCI via PL regulation using the proportional factor P3. The results validated the effectiveness of the proposed controller.
When compared with the proposed controller, previous closed-loop controllers have similarly used the difference between the measured ultra-harmonics or harmonic emissions and the expected emissions as observers to calculate the required regulation [30], [31], [32], [33], [34]. In contrast, most of these controllers were designed to regulate the PNP of the acoustic pulse. This adds the probability of a transition between stable and inertial cavitation. This transition can be observed based on the increase in large amplitude oscillations and increased broadband noise. Our results also verified this conclusion. Additionally, previous studies have shown that when inertial cavitation was monitored or a larger SC occurred, certain undesirable bioeffects, such as hemorrhage or cell necrosis, would occur [20], [30], [31], [34]. To eliminate the probability of occurrence of large-scale SC or inertial cavitation, a nonlinear proportional coefficient was used in the PNP regulation-based controller [36]. However, our results preliminarily show that the proposed PL regulation-based controller could achieve ultra-harmonic emission control successfully while also reducing the broadband noise emission. This is because the SCI was approximately positively correlated with the PL [18]. Furthermore, in contrast to the PNP, the PL has a relatively weak influence on the SCI [27]. Therefore, when compared with the coarse tuning of the PNP regulation-based controller for the SCI, the PL regulation-based controller exhibited a fine-tuning characteristic.
From an application viewpoint, because the proposed PL regulation-based controller can achieve a relatively uniform temporal distribution of the SCI, application of this controller could enable uniform bioeffects to be achieved within the target region and reduce the risk of undesirable bioeffects, thus improving both therapeutic efficiency and biosafety. These points will require further validation in future experiments in vivo. Furthermore, to achieve controllable bioeffects and minimize any undesirable results, some specific bioeffects induced by SC, after being quantitated using advanced imaging technologies, can act as state observers and be combined with the proposed controller to regulate the PL of the incident acoustic waves. For example, in sonoporation-based therapy, certain biomarkers (e.g., calcein) could be used as sonoporation tracers [39], [40], [41]. The intracellular calcein determined via real-time imaging could act as a state observer to regulate the emitted PL, thus producing the desired bioeffects.
4.2. Limitations and improved strategies
We also noted that the improved temporal distribution of the SCI was characterized by a fluctuating temporal stability. These random fluctuations may occur for the following reasons. The proposed control strategy was based on a theoretical assumption that emphasized that the number of microbubbles used to replenish the focal region and their properties were the same before two successive acoustic pulses were received. However, on the one hand, due to the polydisperse or aggregate nature of the microbubbles and the effects of acoustic excitation and liquid circulation on the stability of the microbubbles [6], [29], it was difficult to ensure that the number of microbubbles used to replenish the focal region and their properties were the same before receiving each incident acoustic pulse [11], [15], [16]. On the other hand, the proposed controller requires approximately 100 ms to complete all calculations and obtain the parameters for regulation of the closed-loop adjustment in the host computer, including times for acoustic signal propagation (∼85 µs), signal acquisition and transmission to the host PC via the PCIe bus (∼85 µs), SCI and adjustment calculations (∼20 ms), and the signal generator response (∼40 ms). Therefore, at least 100 ms of off-time was required between two successive pulses. However, throughout this long off-time, the focused region would be filled with the new flowing microbubbles, and the number and properties of these microbubbles would be different to those that previously replenished the focal region. Therefore, when the proposed method used the measured SCI caused by the current acoustic pulse to regulate the PL of the next acoustic pulse, fluctuations in the temporal distribution of the SCI were unavoidable.
Some possible strategies to eliminate these fluctuations are available. One method is to pre-measure the temporal change in the concentration (corresponding to the number and properties) of the circulating microbubbles with respect to the exposure time, and then determine the relationship between the expected SCI and the incident acoustic parameters (PNP or PL) for the given concentration of flowing microbubbles. Based on the results, the time-varying acoustic parameters obtained during exposure were programmed into the controller beforehand to improve the temporal stability of the SCI. Another possible method is to use the real-time SCI caused by the first few cycles of the current acoustic pulse to regulate the PNP or the PL of the remaining cycles of the current pulse. This method, in which it is necessary to complete the SCI measurement and PL regulation calculations within a short time (≪PL), requires higher real-time performance capabilities from the measurement and control systems. The current system could not meet these fast calculation and response requirements. Previous studies used a field-programmable gate array (FPGA) system to perform ultrafast (<250 µs) monitoring and control of the subharmonic emissions via PNP regulation during long pulse exposure [35], [42]. The proposed system will be improved to validate the feasibility of this strategy in future studies.
In addition, although the PRF selected here can ensure replenishment of the new microbubbles in the focal region, the emitted signals in the active field were recorded using only a single channel and were then processed in the controller. Therefore, it is difficult to achieve a uniform spatial distribution of SC because of the polydispersion or aggregation of the microbubbles. Recently, passive cavitation mapping to obtain spatiotemporal information about the cavitation activities has been realized in practical applications [6], [43]. Combining passive cavitation mapping with the proposed system could provide spatial information about the cavitation, enable early identification of undesirable cavitation activities at the target region, and allow adjustment of the exposure to achieve the desired outcome.
5. Conclusion
In this study, a closed-loop feedback controller is proposed that uses the difference between the measured ultra-harmonic or harmonic emissions and the expected emissions as observers to regulate the PNP and PL via two proportional factors and thus accelerate the SCI to the expected level during the acceleration stage; the PL is then regulated using a third proportional factor to maintain the temporal stability of SCI during the stable stage. The results confirmed that temporal stability of the SCI of the circulating microbubbles was improved significantly by use of the proposed controller. Specifically, in contrast to traditional controllers based on PNP regulation, the proposed PL-based closed-loop controller reduced the probability of a transition between stable and inertial cavitation, thus avoiding the risk of disadvantageous bioeffects in practical applications. The proposed controller provides a feasible strategy to achieve controllable cavitation activity in these applications.
CRediT authorship contribution statement
Chunjie Tan: Investigation, Data curation, Software. Bo Yan: Data curation, Software. Tao Han: Methodology. Alfred C.H. Yu: Methodology. Peng Qin: Conceptualization, Funding acquisition, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research is funded by the National Natural Science Foundation of China (Nos. 12074255, 31630007), Program of Medicine and Engineering Cross Fund of Shanghai Jiao Tong University (YG2019ZDA27, ZH2018QNA21).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ultsonch.2021.105882.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Apfel R.E. Sonic effervescence: A tutorial on acoustic cavitation. J. Acoust. Soc. Am. 1997;101(3):1227–1237. [Google Scholar]
- 2.Church C.C., Carstensen E.L. “Stable” inertial cavitation. Ultrasound Med. Biol. 2001;27:1435–1437. doi: 10.1016/s0301-5629(01)00441-0. [DOI] [PubMed] [Google Scholar]
- 3.Kooiman K., Vos H.J., Versluis M., de Jong N. Acoustic behavior of microbubbles and implications for drug delivery. Adv. Drug. Deliv. Rev. 2014;72:28–48. doi: 10.1016/j.addr.2014.03.003. [DOI] [PubMed] [Google Scholar]
- 4.Ferrara K., Pollard R., Borden M. Ultrasound microbubble contrast agents: fundamentals and application to gene and drug delivery. Annu. Rev. Biomed. Eng. 2007;9:415–447. doi: 10.1146/annurev.bioeng.8.061505.095852. [DOI] [PubMed] [Google Scholar]
- 5.VanBavel E. Effects of shear stress on endothelial cells: Possible relevance for ultrasound applications. Prog. Biophys. Mol. Biol. 2007;93(1-3):374–383. doi: 10.1016/j.pbiomolbio.2006.07.017. [DOI] [PubMed] [Google Scholar]
- 6.Stride E., Coussios C. Nucleation, mapping and control of cavitation for drug delivery. Nat. Rev. Phys. 2019;1:495–509. [Google Scholar]
- 7.Kooiman K., Roovers S., Langeveld S.A.G., Kleven R.T., Dewitte H., O'Reilly M.A., Escoffre J.-M., Bouakaz A., Verweij M.D., Hynynen K., Lentacker I., Stride E., Holland C.K. Ultrasound-Responsive Cavitation Nuclei for Therapy and Drug Delivery. Ultrasound Med. Biol. 2020;46(6):1296–1325. doi: 10.1016/j.ultrasmedbio.2020.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Qin P., Han T., Yu A.C.H., Xu L. Mechanistic understanding the bioeffects of ultrasound-driven microbubbles to enhance macromolecule delivery. J. Control Release. 2018;272:169–181. doi: 10.1016/j.jconrel.2018.01.001. [DOI] [PubMed] [Google Scholar]
- 9.Qin P., Xu L., Han T., Du L., Yu A.C.H. Effect of non-acoustic parameters on heterogeneous sonoporation mediated by single-pulse ultrasound and microbubbles. Ultrason. Sonochem. 2016;31:107–115. doi: 10.1016/j.ultsonch.2015.12.001. [DOI] [PubMed] [Google Scholar]
- 10.Konofagou E.E. Optimization of the ultrasound-induced blood-brain barrier opening. Theranostics. 2012;2(12):1223–1237. doi: 10.7150/thno.5576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Choi J.J., Selert K., Vlachos F., Wong A., Konofagou E.E. Noninvasive and localized neuronal delivery using short ultrasonic pulses and microbubbles. Proc. Natl. Acad. Sci. U. S. A. 2011;108(40):16539–16544. doi: 10.1073/pnas.1105116108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deng C.X. Targeted drug delivery across the blood-brain barrier using ultrasound technique. Therapeut. Deliv. 2010;1(6):819–848. doi: 10.4155/tde.10.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Baseri B., Choi J.J., Tung Y.-S., Konofagou E.E. Multi-modality safety assessment of blood-brain barrier opening using focused ultrasound and definity microbubbles: a short-term study. Ultrasound Med. Biol. 2010;36(9):1445–1459. doi: 10.1016/j.ultrasmedbio.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu H.-L., Wai Y.-Y., Chen W.-S., Chen J.-C., Hsu P.-H., Wu X.-Y., Huang W.-C., Yen T.-C., Wang J.-J. Hemorrhage detection during focused-ultrasound induced blood-brain-barrier opening by using susceptibility-weighted magnetic resonance imaging. Ultrasound Med. Biol. 2008;34(4):598–606. doi: 10.1016/j.ultrasmedbio.2008.01.011. [DOI] [PubMed] [Google Scholar]
- 15.Pouliopoulos A.N., Li C., Tinguely M., Garbin V., Tang M.-X., Choi J.J. Rapid short-pulse sequences enhance the spatiotemporal uniformity of acoustically driven microbubble activity during flow conditions. J. Acoust. Soc. Am. 2016;140(4):2469–2480. doi: 10.1121/1.4964271. [DOI] [PubMed] [Google Scholar]
- 16.Pouliopoulos A.N., Bonaccorsi S., Choi J.J. Exploiting flow to control the in vitro spatiotemporal distribution of microbubble-seeded acoustic cavitation activity in ultrasound therapy. Phys. Med. Biol. 2014;59:6941–6957. doi: 10.1088/0031-9155/59/22/6941. [DOI] [PubMed] [Google Scholar]
- 17.Gorick C.M., Sheybani N.D., Curley C.T., Price R.J. Listening in on the Microbubble Crowd: Advanced Acoustic Monitoring for Improved Control of Blood-Brain Barrier Opening with Focused Ultrasound. Theranostics. 2018;8:2988–2991. doi: 10.7150/thno.26025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lin Y., Lin L., Cheng M., Jin L., Du L., Han T., Xu L., Yu A.C.H., Qin P. Effect of acoustic parameters on the cavitation behavior of SonoVue microbubbles induced by pulsed ultrasound. Ultrason. Sonochem. 2017;35:176–184. doi: 10.1016/j.ultsonch.2016.09.016. [DOI] [PubMed] [Google Scholar]
- 19.Yasui K., Tuziuti T., Lee J., Kozuka T., Towata A., Iida Y. Numerical simulations of acoustic cavitation noise with the temporal fluctuation in the number of bubbles. Ultrason. Sonochem. 2010;17:460–472. doi: 10.1016/j.ultsonch.2009.08.014. [DOI] [PubMed] [Google Scholar]
- 20.O'Reilly M.A., Hynynen K. Blood-Brain Barrier: Real-time Feedback-controlled Focused Ultrasound Disruption by Using an Acoustic Emissions-based Controller. Radiology. 2012;263:96–106. doi: 10.1148/radiol.11111417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Choi J.J., Coussios C.C. Spatiotemporal evolution of cavitation dynamics exhibited by flowing microbubbles during ultrasound exposure. J. Acoust. Soc. Am. 2012;132:3538–3549. doi: 10.1121/1.4756926. [DOI] [PubMed] [Google Scholar]
- 22.Cheng M., Han T., Yu A.C.H., Qin P. Effects of ultrasound pulse parameters on cavitation properties of flowing microbubbles under physiologically relevant conditions. Ultrason. Sonochem. 2019;52:512–521. doi: 10.1016/j.ultsonch.2018.12.031. [DOI] [PubMed] [Google Scholar]
- 23.Palanchon P., Tortoli P., Bouakaz A., Versluis M., de Jong N. Optical observations of acoustical radiation force effects on individual air bubbles. IEEE T Ultrason. Ferr. 2005;52:104–110. doi: 10.1109/tuffc.2005.1397354. [DOI] [PubMed] [Google Scholar]
- 24.Dayton P.A., Allen J.S., Ferrara K.W. The magnitude of radiation force on ultrasound contrast agents. J. Acoust. Soc. Am. 2002;112:2183–2192. doi: 10.1121/1.1509428. [DOI] [PubMed] [Google Scholar]
- 25.Stride E., Segers T., Lajoinie G., Cherkaoui S., Bettinger T., Versluis M., Borden M. Microbubble Agents: New Directions. Ultrasound Med. Biol. 2020;46(6):1326–1343. doi: 10.1016/j.ultrasmedbio.2020.01.027. [DOI] [PubMed] [Google Scholar]
- 26.Smith D.A., Porter T.M., Martinez J., Huang S., MacDonald R.C., McPherson D.D., Holland C.K. Destruction thresholds of echogenic liposomes with clinical diagnostic ultrasound. Ultrasound Med. Biol. 2007;33:797–809. doi: 10.1016/j.ultrasmedbio.2006.11.017. [DOI] [PubMed] [Google Scholar]
- 27.Radhakrishnan K., Bader K.B., Haworth K.J., Kopechek J.A., Raymond J.L., Huang S.L., McPherson D.D., Holland C.K. Relationship between cavitation and loss of echogenicity from ultrasound contrast agents. Phys. Med. Biol. 2013;58:6541–6563. doi: 10.1088/0031-9155/58/18/6541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Borden M.A., Longo M.L. Dissolution behavior of lipid monolayer-coated, air-filled microbubbles: Effect of lipid hydrophobic chain length. Langmuir. 2002;18:9225–9233. [Google Scholar]
- 29.Segers T., Lohse D., Versluis M., Frinking P. Universal Equations for the Coalescence Probability and Long-Term Size Stability of Phospholipid-Coated Monodisperse Microbubbles Formed by Flow Focusing. Langmuir. 2017;33:10329–10339. doi: 10.1021/acs.langmuir.7b02547. [DOI] [PubMed] [Google Scholar]
- 30.Kamimura H.A., Flament J., Valette J., Cafarelli A., Aron Badin R., Hantraye P., Larrat B. Feedback control of microbubble cavitation for ultrasound-mediated blood-brain barrier disruption in non-human primates under magnetic resonance guidance. J. Cereb. Blood Flow Metab. 2019;39:1191–1203. doi: 10.1177/0271678X17753514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tsai C.H., Zhang J.W., Liao Y.Y., Liu H.L. Real-time monitoring of focused ultrasound blood-brain barrier opening via subharmonic acoustic emission detection: implementation of confocal dual-frequency piezoelectric transducers. Phys. Med. Biol. 2016;61:2926–2946. doi: 10.1088/0031-9155/61/7/2926. [DOI] [PubMed] [Google Scholar]
- 32.Bing C., Hong Y., Hernandez C., Rich M., Cheng B., Munaweera I., Szczepanski D., Xi Y., Bolding M., Exner A., Chopra R. Characterization of different bubble formulations for blood-brain barrier opening using a focused ultrasound system with acoustic feedback control. Sci. Rep. 2018;8:7986. doi: 10.1038/s41598-018-26330-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sun T., Zhang Y., Power C., Alexander P.M., Sutton J.T., Aryal M., Vykhodtseva N., Miller E.L., McDannold N.J. Closed-loop control of targeted ultrasound drug delivery across the blood-brain/tumor barriers in a rat glioma model. Proc. Natl. Acad. Sci. U. S. A. 2017;114(48):E10281–E10290. doi: 10.1073/pnas.1713328114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Arvanitis C.D., Livingstone M.S., Vykhodtseva N., McDannold N., Muñoz-Barrutia A. Controlled ultrasound-induced blood-brain barrier disruption using passive acoustic emissions monitoring. PLoS ONE. 2012;7(9):e45783. doi: 10.1371/journal.pone.0045783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cornu C., Guedra M., Bera J.C., Liu H.L., Chen W.S., Inserra C. Ultrafast monitoring and control of subharmonic emissions of an unseeded bubble cloud during pulsed sonication. Ultrason. Sonochem. 2018;42:697–703. doi: 10.1016/j.ultsonch.2017.12.026. [DOI] [PubMed] [Google Scholar]
- 36.Patel A., Schoen S.J., Arvanitis C.D. Closed-Loop Spatial and Temporal Control of Cavitation Activity With Passive Acoustic Mapping. IEEE T Bio-Med. Eng. 2019;66:2022–2031. doi: 10.1109/TBME.2018.2882337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Unger E.C., Porter T., Culp W., Labell R., Matsunaga T., Zutshi R. Therapeutic applications of lipid-coated microbubbles. Adv. Drug. Deliver. Rev. 2004;56:1291–1314. doi: 10.1016/j.addr.2003.12.006. [DOI] [PubMed] [Google Scholar]
- 38.Li Y., Tan C., Yan B., Han T., Yu A.C.H., Qin P. Evaluation of the properties of daughter bubbles generated by inertial cavitation of preformed microbubbles. Ultrason. Sonochem. 2021;72:105400. doi: 10.1016/j.ultsonch.2020.105400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jia C., Shi J., Yao Y., Han T., Yu A.C., Qin P. Plasma Membrane Blebbing Dynamics Involved in the Reversibly Perforated Cell by Ultrasound-Driven Microbubbles. Ultrasound Med. Biol. 2021;47:733–750. doi: 10.1016/j.ultrasmedbio.2020.11.029. [DOI] [PubMed] [Google Scholar]
- 40.Jia C., Xu L., Han T., Cai P., Yu A.C., Qin P. Generation of Reactive Oxygen Species in Heterogeneously Sonoporated Cells by Microbubbles with Single-Pulse Ultrasound. Ultrasound Med. Biol. 2018;44:1074–1085. doi: 10.1016/j.ultrasmedbio.2018.01.006. [DOI] [PubMed] [Google Scholar]
- 41.Qin P., Xu L., Hu Y., Zhong W., Cai P., Du L., Jin L., Yu A.C.H. Sonoporation-induced depolarization of plasma membrane potential: analysis of heterogeneous impact. Ultrasound Med. Biol. 2014;40(5):979–989. doi: 10.1016/j.ultrasmedbio.2013.11.024. [DOI] [PubMed] [Google Scholar]
- 42.Desjouy C., Poizat A., Gilles B., Inserra C., Bera J.C. Control of inertial acoustic cavitation in pulsed sonication using a real-time feedback loop system. J. Acoust. Soc. Am. 2013;134:1640–1646. doi: 10.1121/1.4812973. [DOI] [PubMed] [Google Scholar]
- 43.Coviello C., Kozick R., Choi J., Gyongy M., Jensen C., Smith P.P., Coussios C.C. Passive acoustic mapping utilizing optimal beamforming in ultrasound therapy monitoring. J. Acoust. Soc. Am. 2015;137:2573–2585. doi: 10.1121/1.4916694. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.