Optimized NMR Experiments for the Isolation of I=½ Manifold Transitions in Methyl Groups of Proteins

Abstract

Optimized NMR experiments are developed for isolating magnetization belonging to the I=1/2 manifolds of ¹³CH₃ methyl groups in proteins, enabling the manipulation of the magnetization of a ¹³CH₃ moiety as if it were an AX (¹H-¹³C) spin-system. These experiments result in the same ‘simplification’ of a ¹³CH₃ spin-system that would be obtained from the production of {¹³CHD₂}-methyl-labeled protein samples. The sensitivity of I=1/2 manifold-selection experiments is a factor of approximately 2 less than that of the corresponding experiments acquired on {¹³CHD₂}-labeled methyl groups. The methodology described here is primarily intended for small-to-medium sized proteins, where the losses in sensitivity associated with the isolation of I=1/2 manifold transitions can be tolerated. Several NMR applications that benefit from simplification of the ¹³CH₃ (AX₃) spin-systems are described, with an emphasis on the measurements of methyl ¹H-¹³C residual dipolar couplings in a {¹³CH₃}-methyl-labeled deletion mutant of the human chaperone DNAJB6b, where modulation of NMR signal intensities due to evolution of methyl ¹H-¹³C scalar and dipolar couplings follows a simple cosine function characteristic of an AX (¹H-¹³C) spin-system, significantly simplifying data analysis.

The design of multinuclear, multi-pulse experiments has been critical to the development of NMR spectroscopy as a powerful tool for studying protein structure and dynamics. NMR experiments targeting methyl groups as unique probes of molecular structure and motion, play a special role in these developments yielding considerable insights into numerous biochemical processes.^[1] The degree of sophistication of NMR experiments is to a large extent predicated on the complexity of targeted spin-systems. The eigenstates of complex spin systems containing magnetically equivalent nuclei such as AX₃ or AX₂ groups in protein side-chains, are usually divided onto several classes (manifolds) using the standard rules of angular momentum theory.^[2] For example, in the case of an AX₃ (¹³CH₃) methyl moiety, the energy level diagram contains one manifold with spin I=3/2 and two with I=1/2. The magnetization of each of the two I=1/2 manifolds, as well as their sum, behave in a manner analogous to that of a simple AX spin system. Thus, the ability to manipulate the magnetization in a manner that enables separation of I=3/2 and I=1/2 manifolds would reduce the complexity of the ¹³CH₃ spin-system to the simple AX case. The problem of separation of ¹³CH₃ methyl transitions belonging to I=3/2 and I=1/2 manifolds was tackled previously,^[3] where NMR experiments were designed that allow the ¹H coherences of the two manifolds to be separated using extensive phase-cycling of radio-frequency (RF) pulses. This earlier work was primarily geared towards the measurement of Carr-Purcell-Meiboom-Gill (CPMG)^[4,5] relaxation dispersion profiles, targeting the isolated ¹H magnetization of the I=1/2 manifolds of ¹³CH₃ methyls in protein systems undergoing chemical exchange.

Here, we address the problem of simplification of the ¹³CH₃ spin-system in a more comprehensive manner. Making use of a simpler and more sensitive method for isolation of the ¹H magnetization of the I=1/2 manifolds, we design optimized NMR experiments aimed at the sequestration of both ¹H and ¹³C single quantum coherences of the I=1/2 manifolds, allowing one to manipulate the magnetization of a ¹³CH₃ methyl as if it were an AX spin-system, not unlike that available via {¹³CHD₂}-labeling of methyl groups. The methodology is tested on two {¹³CH₃}-methyl-labeled proteins: {U-[²H]; Ileδ1-[¹³CH₃]; Leu,Val-[¹³CH₃,¹²CD₃]}-labeled human ubiquitin (8.5 kDa; 5 and 25°C) and {U-[²H]; Alaβ-[¹³CH₃]}-labeled malate synthase G (MSG; 82 kDa; 37°C). We show that the I=1/2 manifold-selection experiments are only a factor of ~2 less sensitive than the (same) NMR experiments acquired on {¹³CHD₂}-methyl-labeled proteins, {U-[²H]; Ileδ1-[¹³CHD₂]; Leu,Val-[¹³CHD₂,¹²CD₃]}-ubiquitin and {U-[²H]; Alaβ-[¹³CHD₂]}-MSG. Finally, the application of I=1/2 manifold selection to the measurement of methyl ¹H-¹³C residual dipolar couplings (RDCs) in a {U-[²H]; Ileδ1-[¹³CH₃]; Leu,Val-[¹³CH₃,¹²CD₃]}-labeled deletion mutant of the human DNAJB6b chaperone, ΔST-DNAJB6b (25 kDa; 25°C), is described. The resulting modulation of NMR signal intensities due to evolution of methyl ¹H-¹³C scalar and dipolar couplings follows that of an AX (¹H-¹³C) spin-system, significantly simplifying data analysis.

An energy level diagram of a spin system consisting of three magnetically equivalent nuclei in a methyl group (H₃) is shown in Figure 1. Although a ¹³CH₃ methyl group is considered in practice, the transitions of ¹³C nuclei have been omitted from the figure for simplicity, as the state of the density matrix of a ¹³CH₃ group can be represented as a tensorial product of the ¹³C spin operator and the density matrix containing ¹H states. The I=3/2 and two I=1/2 manifolds are independent of each other under the effect of RF pulses or any coherent NMR interactions but can be coupled through spin relaxation. In the macro-molecular limit, transverse spin relaxation of the inner ¹H transitions of the I=3/2 manifold and the ¹H transitions of the I=1/2 manifold occurs with slower rates (red arrows), while the outer transitions of the I=3/2 manifold are characterized by faster rates of decay (blue arrows).^[6]

Figure 1.

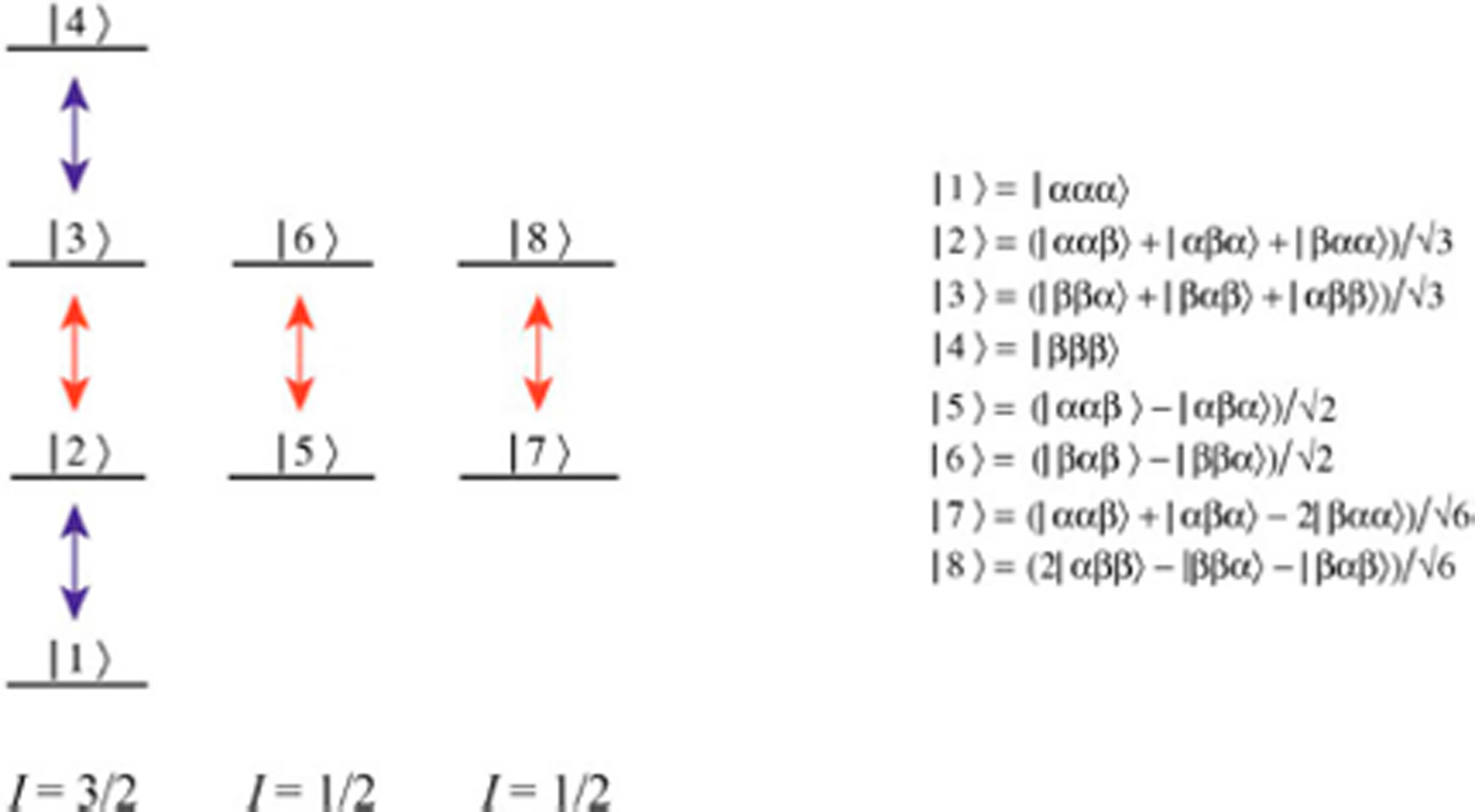
Energy level diagram for the X₃ spin-system of a methyl group. Slow and fast relaxing single-quantum ¹H transitions are shown by the red and blue arrows, respectively. The eight ¹H eigenstates are depicted by |i,j,k>(i,j,k ∈ {α,β}). The spin quantum numbers, I, of the three manifolds are specified below the diagram. For simplicity, only the ¹H part of the ¹³CH₃ spin-system is shown.

The optimized pulse schemes that have been developed to sequester the coherences belonging to the I=1/2 manifolds are shown in Figure 2. A detailed description of these schemes ‘tracking’ how each of the transitions illustrated in Figure 1 evolves during the course of the experiment using single transition spin operators is provided in the SI. Briefly, the ¹³CH₃ methyl magnetization is prepared first in a state in which only the slowly relaxing coherences (shown with red arrows in Figure 1) are present. Subsequent application of a ¹H pulse of flip-angle α =sin⁻¹(2/3)=41.81° (shown in green in Figure 2) is central to the approach developed here. This pulse eliminates the slow-relaxing 1H transitions of the I=3/2 manifold, ‘recreates’ some fast-relaxing ¹H coherences (shown with blue arrows in Figure 1), and produces a mixture of methyl ¹H coherences: double quantum, ‘DQ’, triple-quantum, ‘TQ’, and zero-quantum, ‘ZQ’ (see SI for details). The cycling of the phase of the ¹H pulse of flip-angle α with concomitant retention of the receiver phase eliminates all the ¹H coherences of even order (ZQ and DQ), while the fast-relaxing ¹H coherences of the I=3/2 manifold are eliminated by the second application of the element of duration 2τ_b and the associated phase-cycling of the subsequent ¹³C 90° pulse, so that after the elements of the scheme enclosed in dashed boxes in Figure 2, the state of the density matrix of methyl ¹H magnetization, σ_H can, to within a multiplication factor, be described by,

$${\sigma }_H=(\sqrt{5}/3)(|5><6|+|6><5|)+(\sqrt{5}/3)(|7><8|+|8><7|)-2(\sqrt{5}/9)(|1><4|+|4><1|)$$ (1)

Figure 2.

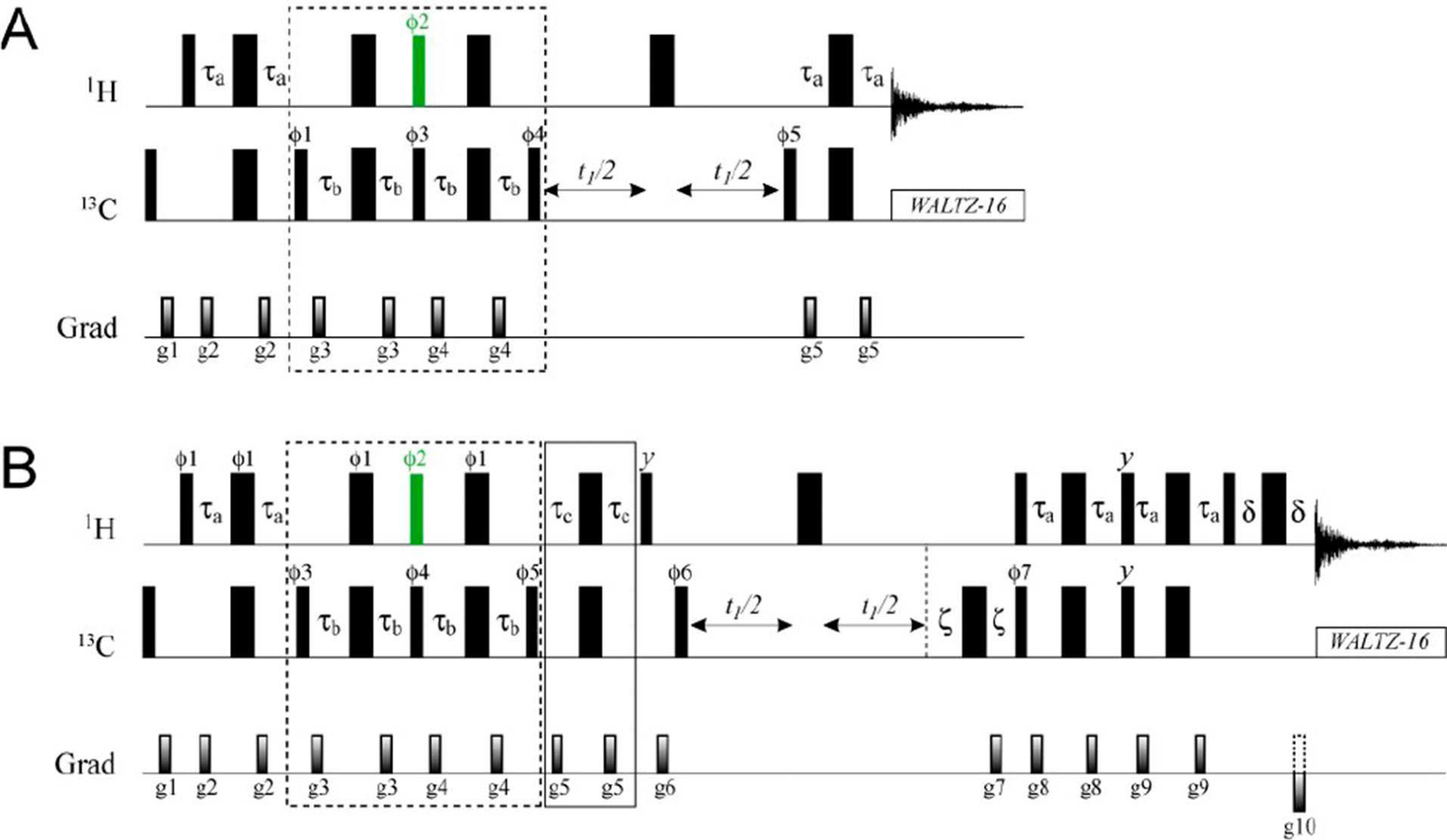
Pulse sequences for separation of I=1/2 manifold transitions in ¹³CH₃ methyl groups with (A) a HMQC-’read-out’, and (B) active elimination of ¹H TQ coherences and a gradient-selected sensitivity enhanced HSQC ‘read-out’ scheme.^[7,8] Details of experimental parameters are provided in the Supplementary Information (Figure S1).

If the order of ¹H coherences is not ‘perturbed’ in the rest of the experiment as is the case, for example, in HMQC-type ‘read-out’ schemes,^[9,10] the selection of the I=1/2 manifold transitions (the first two terms in Eq. (1)) occurs ‘naturally’, as the third term containing ¹H TQ coherences will not lead to observable magnetization at the end of the experiment. An example of such a scheme is presented in Figure 2A. The ratio of sensitivity of the I=1/2 selection in Figure 2A, where, according to Eq. (1), √5/3 of the I=1/2 magnetization is recovered in a single scan, to the previously published scheme^[3] (where 3/5 of the I=1/2 magnetization is recovered per scan) is 5√5/9=1.24. We have been able to verify this gain in sensitivity on a sample of {¹³CH₃}-labelled ubiquitin: the average ratio of signal intensities was 1.26±0.02 for the two experiments. In addition, using a straightforward extension of the scheme in Figure 2A to measure methyl ¹H transverse spin relaxation rates, R₂, we verified that the I=1/2 ¹H coherences in ubiquitin relax slower (6.3±1.7 s⁻¹ at 25°C) than the slow relaxing ¹H coherences of the I=3/2 manifold (7.6±1.7 s⁻¹; selected as described earlier^[3]) by ~20% on average - in agreement with expectations based on earlier predictions that the I=1/2 ¹H coherences relax 2.2-times slower than the inner transitions of the I=3/2 manifold due to interactions with external proton spins.^[3] Note the contribution of external protons to methyl ¹H transverse relaxation rates is relatively small in perdeuterated proteins, where methyl ¹H-¹³C dipolar interactions constitute the main relaxation mechanism.

Many NMR applications require that the selected I=1/2 magnetization be manipulated as a ‘standalone’ AX spin-system. In particular, if isolation of single-quantum (SQ) ¹³C coherences of the I=1/2 manifolds is desired and/or gradient-selected sensitivity enhancement schemes^[7,8] are employed, the third term of Eq. (1), containing ¹H TQ coherences, will unavoidably lead to generation of SQ ¹³C coherences of the I= 3/2 manifold. Depending on the details of the NMR pulse-scheme employed, these coherences will be either directly observable during the indirect and direct acquisition periods of a 2D experiment or will generate detectable magnetization due to large differences in transverse relaxation properties of individual ¹³C transitions. It is important, therefore, to achieve ‘clean’ selection of I=1/2 magnetization by active elimination of any terms belonging to the I=3/2 manifold. Such a scheme is shown in Figure 2B, where elimination of ¹H TQ coherences is achieved via their selective refocusing with respect to ¹³C spins (the element of duration 2τ_c =1/(6J_CH) enclosed in the solid box in Figure 2B; see SI for details). Of note, only when ¹H SQ magnetization deriving from the I=1/2 manifold is completely isolated and not ‘contaminated’ by ¹H TQ coherences, sensitivity enhancement by preservation of equivalent pathways (PEP),^[11] employed in the scheme of Figure 2B, provides the expected gain of √2 in signal-to-noise (39±2 % on average measured for {¹³CH₃}-ubiquitin). The theoretical efficiency E of the elements that ensure the proper isolation of the I=1/2 manifold, which we define as the fraction of the I=1/2 magnetization that is recovered at the end of the experiment in the absence of losses due to relaxation and pulse imperfections, is equal to (√5/3) cos(π/6) = 0.645. This loss in signal is largely compensated for by the sensitivity enhancement used in the scheme of Figure 2B. The measured average sensitivity ratios of 0.165±0.015 and 0.283±0.022 obtained for ubiquitin (25°C) in the experiment of Figure 2B compared to [¹H-¹³C]-HMQC spectra without and with selection of slow-relaxing transitions,^[6] respectively, are therefore in good agreement with expectations considering that the total amount of detectable ¹H magnetization contained in the I=1/2 manifolds is 1/6 of that in the whole of the (¹³C)H₃ group and 1/3 if only slow-relaxing transitions are selected.

Since the magnetization from I=1/2 manifolds isolated by the scheme in Figure 2B is equivalent to that of an AX (¹H-¹³C) spin-system with respect to any coherent NMR interactions, it is of interest to compare the sensitivity attainable in this experiment with that of its counterparts targeting {¹³CHD₂}-methyl-labeled samples. In the absence of relaxation, the total amount of ¹H magnetization contained in I=1/2 manifolds of a ¹³CH₃ group is one half that available in a ¹³CHD₂ spin-system. As the selection for the I=1/2 manifolds can only be performed with a given efficiency E (defined as above), any deviations from a factor of ~E/2=0.32 in sensitivity ratios between the experiment of Figure 2B recorded on the {¹³CH₃}-labeled samples and the sensitivity-enhanced HSQC on the {¹³CHD₂}-labeled samples (the scheme in Figure 2B excluding the elements enclosed in boxes), under otherwise identical experimental conditions, must arise from relaxation and pulse imperfections. Indeed, the recovery of methyl ¹H magnetization to equilibrium between the scans of NMR experiments is much slower in {¹³CHD₂}-methyls^[12] (Figure 3A), and the results of sensitivity comparisons will therefore depend on the scan repetition rate. Figure 3B shows average ratios of 2D cross-peak intensities obtained in the experiment of Figure 2B recorded on a sample of {¹³CH₃}-ubiquitin and the sensitivity-enhanced HSQC acquired on the {¹³CHD₂}-labeled sample of the same protein concentration (1.3 mM) as a function of inter-scan delay. From almost 50% of {¹³CHD₂} intensity at an inter-scan delay of 1 s, the ratio slowly approaches the value of E/2 for slower repetition rates. The same comparison performed between Alaβ-{¹³CH₃}- and Alaβ-{¹³CHD₂}-labeled samples of MSG (0.6 mM; 37°C; 33 peaks) yields somewhat higher ratios (0.62±0.12 for an inter-scan delay of 1 s) as the ¹H longitudinal relaxation rate (R₁) in both methyl isotopomers is slower on average in alanines of MSG. We note that alternative methyl isotope labeling schemes of Val and Leu residues can be expected to provide somewhat different results in sensitivity comparisons between the experiments targeting {¹³CHD₂}-labeled samples and those performed on ¹³CH₃ methyls with I=1/2 manifold selection. For example, if both methyl groups of isopropyl moieties of Val and Leu are labeled with {¹³CHD₂} methyl isotopomers, one would expect a substantial increase in ¹H R₁ rates due to spatial proximity of the two prochiral methyl groups.

Figure 3.

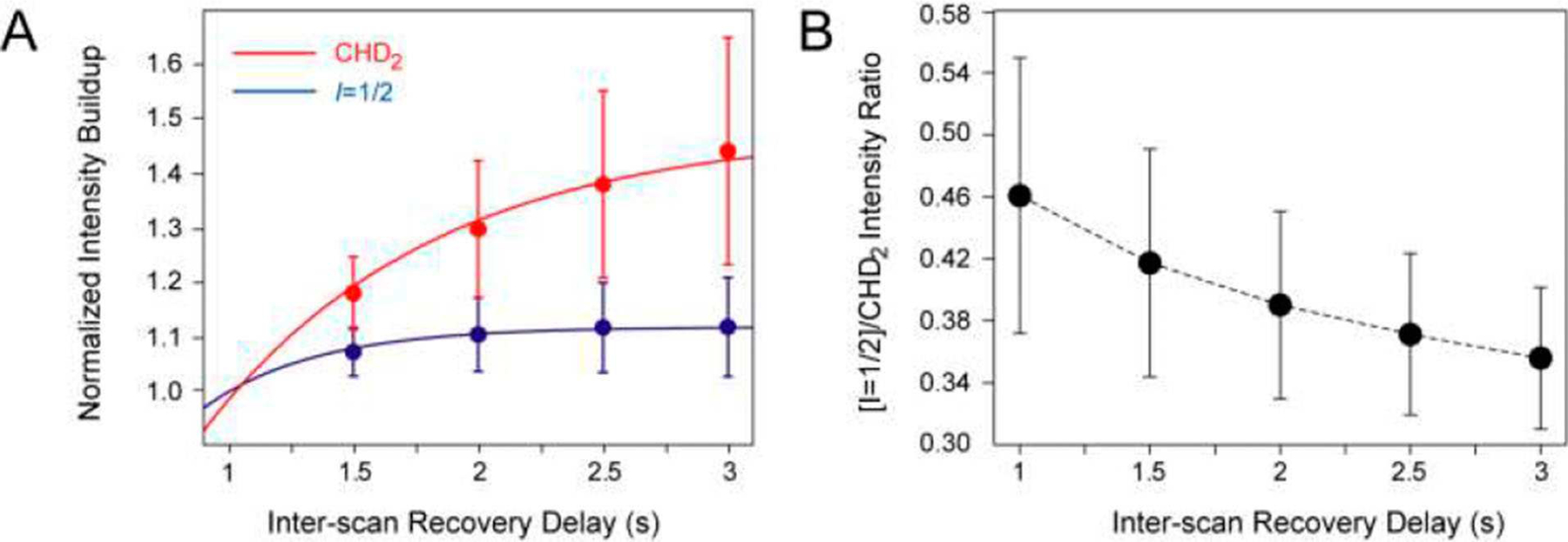
(A) Build-up of an average 2D cross-peak intensity normalized to the intensity at an inter-scan delay equal to 1 s (y-axis) versus the inter-scan delay duration (x-axis) in the gradient-selected sensitivity enhanced HSQC acquired on 1.3 mM {U-[²H]; Ileδ1-[¹³CHD₂]; Leu,Val-[¹³CHD₂,¹²CD₃]}-ubiquitin (red filled circles) and the I=1/2 manifold selection experiment in Figure 2B acquired on 1.3 mM {U-[²H]; Ileδ1-[¹³CH₃]; Leu,Val-[¹³CH₃,¹²CD₃]}-ubiquitin (blue filled circles). The error bars derive from the r.m.s.d. of the intensities of 29 methyl cross-peaks. Least-squares best-fits of the data to the function I₀[1 - exp(−R₁d₁)], where I₀ is the intensity at equilibrium, R₁ is the average longitudinal methyl ¹H spin relaxation rate and d₁ is the duration of the inter-scan delay (shown with red and blue curves), provide R₁ rates of 1.09±0.20 s⁻¹ and 2.23±0.25 s⁻¹ for the {¹³CHD₂}- and {¹³CH₃}-labeled samples, respectively. (B) Average ratios of 2D cross-peak intensities obtained in the experiment of Figure 2B recorded on {¹³CH₃}-labeled ubiquitin and the gradient-selected sensitivity-enhanced HSQC acquired on {¹³CHD₂}-labeled ubiquitin (y-axis) as a function of the inter-scan delay duration (x-axis). The error bars derive from the r.m.s.d. of the ratios of intensities over 29 cross-peaks. The dashed curve connecting the experimental ratios is drawn to guide the eye. All the spectra were recorded at 500 MHz and 5°C. Very similar values are obtained at 25°C.

Methyl-{¹³CHD₂}-labeled samples can be used to estimate the experimental losses of magnetization at each stage of I=1/2 selection in the scheme of Figure 2B. Comparisons of 2D signal intensities obtained using this experiment with and without each of the elements enclosed in boxes in Figure 2B using {¹³CHD₂}-labeled ubiquitin (25°C) provided the following average efficiencies associated with each successive element: 0.73 for the first element (enclosed in the dashed box; Figure 2B) compared with the theoretical factor (√5/3) = 0745, and 0.84 for the second element (enclosed in the solid box) compared with the theoretical factor of (√3/2) = 0.866. Each of the two experimental values and their product (0.61; to be compared with the value of I=1/2 selection efficiency E=0.64) are slightly lower than the corresponding theoretical estimates reflecting minor losses of magnetization due to relaxation and pulse imperfections.

A number of NMR applications can be envisaged that would benefit from the simplification of the ¹³CH₃ spin-system achieved using the approach described above. For example, using the I=1/2 manifold selecting elements of the scheme in Figure 2B, we developed a SQ ¹H CPMG relaxation dispersion experiment (SI, Figure S2) that was tested on {¹³CH₃}-labeled ubiquitin providing flat dispersion profiles for all methyl sites, as well as on a sample of {¹³CH₃}-labeled ΔST-DNAJB6b, where relaxation dispersions were observed for the methyl sites that participate in chemical exchange with sparsely-populated, oligomeric states of the protein. The experiment in Figure S2 is on average ~2.5-fold more sensitive than that developed previously with I=1/2 manifold selection,^[3] due to the use of gradients to eliminate ¹H TQ coherences in the latter, and the use of more efficient I=1/2 manifold selection and sensitivity enhancement in the former. However, a much more sensitive methyl-TROSY-based SQ methyl-¹H CPMG experiment, developed recently by Kay and co-workers^[13] for ¹³CH₃ methyls, largely eliminates the need for the simplification of the ¹³CH₃ spin-system in NMR studies that use methyl protons as probes of chemical exchange on the micro-to-millisecond timescale. Likewise, more sensitive SQ ¹³C CPMG experiments exist that target ¹³CH₃ methyls directly.^[14] With these considerations in mind, we choose to focus in more detail on applications that benefit from a reduction in the complexity of a ¹³CH₃ spin-system that is not achievable without isotopic labeling of methyl moieties in proteins with ¹³CHD₂ groups that (if deuterons are treated as ‘silent’ nuclei) effectively represent fast-rotating AX spin-systems.^[15–17]

One such application is the measurement of methyl ¹H-¹³C scalar (J_CH) and residual dipolar couplings (RDCs; D_CH) in the indirect (¹³C) dimension of 2D methyl ¹H-¹³C correlation spectra of proteins. Figure 4A shows the pulse-scheme that makes use of the I=1/2 selecting elements of the experiment in Figure 2B to effectively reduce the ¹³CH₃ spin-system to a ¹H-¹³C one with respect to the evolution of magnetization due to J_CH and D_CH couplings. Aiming at determination of methyl-containing side-chain rotamer distributions and refinement of side-chain conformations, we measured methyl ¹H-¹³C RDCs in a {¹³CH₃}-labeled ΔST-DNAJB6b first using a simplified version of the constant-time HSQC-based experiment of Ottiger et al.^[18] In the absence of relaxation, the modulation of the methyl signal intensity I occurring during the evolution delay t₂, is given by, I(t₂)=I₀{3 cos(3π[J_CH+D_CH]t₂) + cos(π[J_CH+D_CH]t₂)}, where I₀ is initial intensity, the first term accounts for evolution of the two outer (fast-relaxing) lines of the HSQC ¹³C quadruplet, and the second term describes that of the two inner (slow-relaxing) transitions (shown with the dashed red curves in the upper row of Figure 4B). Due to very different transverse relaxation rates of the inner and outer ¹³C transitions, the experimental modulation patterns (black filled circles in the upper row of Figure 4B) show considerable deviations from ‘relaxation-free’ predictions - especially so for well-ordered methyl sites located deep in the hydrophobic core of the protein structure as is the case, for example, for Val^11γ1 (see Figure 4C for location of the corresponding methyl groups in the structure of ΔST-DNAJB6b). Spin relaxation cannot be accounted for in a rigorous manner in these measurements, and approximate approaches have to be devised. However, in the measurements performed with the scheme in Figure 4A, the signal modulation patterns are reduced to a simple cosine function I(t₂)=I₀cos(π[J_CH+D_CH]t₂) as shown in the lower row of panels in Figure 4B, where all the effects of relaxation during the constant-time period are contained in I₀. Although the experiment in Figure 4A is on average a factor of ~4.5 less sensitive than that targeting the whole of ¹³CH₃ moiety in ΔST-DNAJB6b, the analysis of the I=1/2 manifold selected data is significantly simplified without compromising the accuracy of the derived RDC values. The robustness of the experiment in Figure 4A with respect to deviations of the couplings (J_CH+D_CH) from the nominal value of 125 Hz is estimated in the SI (Figure S4).

Figure 4.

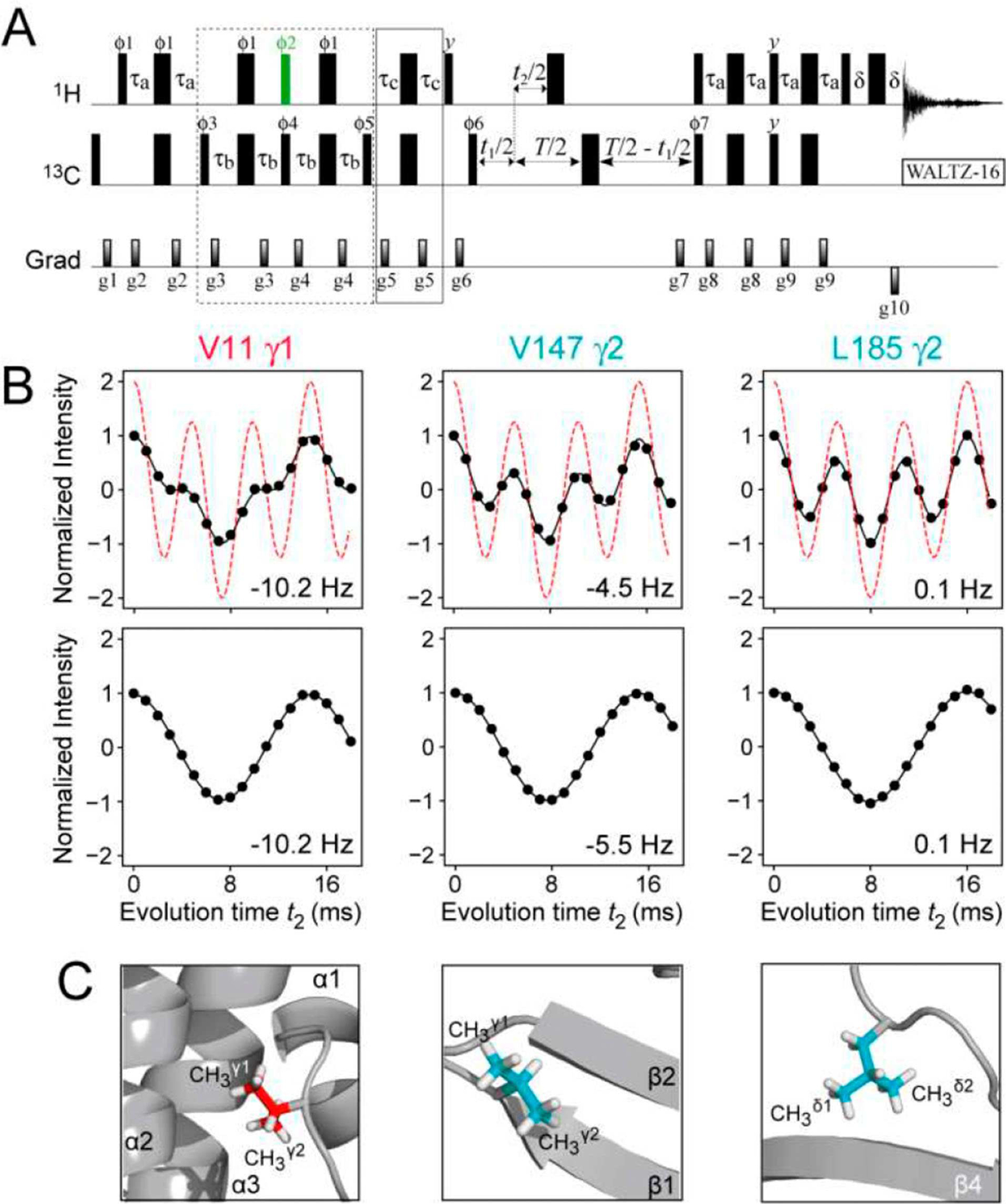
(A) Pulse scheme for the measurement of ¹H-¹³C scalar and residual dipolar couplings in methyl groups of proteins with I=1/2 manifold selection in ¹³CH₃ methyl groups. See SI, Figure S1B, for experimental parameters. A constant-time (CT) delay T=28 ms was used, although sensitivity permitting, any value of T can be used in selectively {¹³CH₃}-labeled protein samples. (B) Plots showing the modulation of the intensity of the ¹³CH₃ correlations in the spectra of {U-[²H]; Ileδ1-[¹³CH₃]; Leu,Val-[¹³CH₃,¹²CD₃]}-labeled ΔST-DNAJB6b (600 MHz; 25°C) recorded using the scheme in panel (A) as a function of the coupling evolution period (t₂) without (top row) and with (bottom row) I=1/2 manifold selection. The plot of intensity modulation in the absence of relaxation and without I=1/2 manifold selection is shown with red dashed lines (top row). The data in upper and lower rows are best-fit to the functions, I(t₂)=I₀{3cos(3πJ_CHt₂)exp(−7R^ST)+cos(πJ_CHt₂) exp(−R^ST)} and I(t₂)=I₀cos(πJ_CHt₂), respectively, where the initial intensity I₀, the coupling constant J_CH, and the transverse relaxation rate of slow-relaxing carbon coherences R^S, are optimized parameters. This function approximately accounts for relaxation of ¹³C magnetization during the period T. The values of D_CH derived from the fits are indicated in each panel. The sample was aligned in 10 mg/mL phage pf1 (see SI for experimental conditions). (C) The locations of the corresponding methyl groups in the structure of ΔST-DNAJB6b are shown in ‘ball-and-stick’ representations.

Using the approach for I=1/2 manifold selection described here, experiments have been designed for the measurement of methyl ¹H-¹³C RDCs directly from the ¹H-¹³C splitting in the indirect (¹³C) dimension of 2D spectra. As the I=1/2 manifold selection scheme in Figures 2B and 4A effectively converts the ¹³C quadruplet in HSQC-type correlation maps of ¹³CH₃ groups to a ¹³C-¹H doublet, conventional in-phase/anti-phase (IPAP)^[19,20] acquisition scheme developed for AX spin systems, can be applied in these experiments circumventing the need for more complicated signal manipulation schemes,^[21] or the use of {¹³CHD₂} methyl isotopomers.^[22] We note, however, that for large proteins, the IP/AP scheme for methyl 1H-¹³C RDC measurements in the acquisition (¹H) dimension of 2D spectra developed by Sprangers and Kay,^[23] is expected to provide much higher sensitivity since no losses associated with the (unnecessary) simplification of the ¹³CH₃ spin-system would be incurred in this case.

In conclusion, we present optimized NMR experiments for complete isolation of the magnetization belonging to the I=1/2 manifolds of ¹³CH₃ methyl groups, enabling the manipulation of the magnetization of a ¹³CH₃ moiety as if it were an AX (¹H-¹³C) spin-system, thereby avoiding the need for production of {¹³CHD₂}-methyl-labeled samples of small-to-medium sized proteins, where the losses in sensitivity associated with the isolation of the I=1/2 manifold can be tolerated. The sequestration of the I=1/2 manifold coherences described here can be used in practically any NMR applications that benefit from simplification of the ¹³CH₃ (AX₃) spin-system, commonly achieved by labeling of methyl sites with ¹³CHD₂ isotopomers. In addition to the examples of such applications provided above, NMR experiments can also be developed for the measurement of ¹³C R₂(R_1ρ) and R₁ relaxation rates of SQ ¹³C coherences of the I=1/2 manifold. It is worth noting that these relaxation rates will be equal to those of analogous ¹³C SQ coherences in ¹³CHD₂ methyl groups only in the limit where the local motions of a methyl group (including rotation around the three-fold symmetry axis) are infinitely fast compared to the rate of global molecular tumbling^[24] (i.e. when the auto-relaxation spectral density function is equal to that of cross-correlated relaxation). In methyl groups of small-to-medium sized proteins for which the methodology described here is mainly primarily intended, this condition is likely to be violated resulting in significant differences between the measured ¹³C relaxation rates. These differences are currently a subject of further investigation.