Abstract
A generic torque model for various handle shapes has been developed and evaluated using experimental data. Twelve subjects performed maximum isometric torques using circular and elliptic cylinders in medium and large sizes (circular: r=25.4, 38.1mm; elliptic: semi-major/minor axes=30.9/19.3, 47.1/27.8mm) finished with aluminum and rubber, in two opposite directions. Torque, grip force distribution, and finger position were recorded. Maximum torques were 25%, 7%, and 31% greater for the elliptic, large-size, and rubber-finished cylinders than for the circular, medium-size, and aluminum-finished cylinders, respectively. Greater torque for the elliptic cylinders was associated with 58% greater normal force subjects could generate for the elliptic than circular cylinders. The model suggests that greater torques for the large-size and rubber cylinders are related to long moment arms and greater frictional coupling at the hand-cylinder interface, respectively. Subjects positioned their hands differently depending on torque direction to maximize their normal force and torque generation.
Statement of Relevance:
Desirable handle features for torque generation may be different from those for grip only. Design of handles per advantageous handle features (e.g., shape, size, surface) may help increase people’s torque strength and contribute to increased physical capacity of people.
Keywords: friction, torque direction, normal force distribution, moment arm
1. INTRODUCTION
Knowledge on how handle features affect the way people squeeze and twist a work object with their hand is essential to improve design of handles and reduce acute and chronic hand injuries (Kong et al. 2007; Kuo et al. 2009). Previously, investigators have shown that maximum torque capacity is affected by diameter of cylinder handles (Pheasant and O'Neill 1975; Adams and Peterson 1988; Imrhan and Loo 1988; Crawford et al. 2002), handle material (Nagashima and Konz 1986), handle surface texture (Pheasant and O'Neill 1975), handle surface area (Crawford et al. 2002), a person’s grip strength (Imrhan and Loo 1988; Crawford et al. 2002), and the direction to which torque is applied (Seo et al. 2008b). In the present study, the effect of handle shape on a person’s maximum torque capacity was examined.
A generic isometric torque model has been developed as an extension of the previous torque model (Seo et al. 2007) to account for different handle shapes (Figure 1). For circular cylinder handles, torque about the long axis of the handle is produced by friction force applied on the surface of the handle with a moment arm equal to the radius, while normal force is needed to support friction force generation so that the hand does not slip on the handle during torque exertion (Pheasant and O'Neill 1975; Seo et al. 2007; Seo et al. 2008b). For cylindrical handles with non-circular cross-sections, however, both friction force and normal force can directly contribute to torque generation. Figure 1 illustrates that contact force can be resolved into normal (fn) and friction force (ff) components, both of which contribute to torque generation as depicted in Equation 1.
| (1) |
where T is torque about the center of rotation, fn is normal force applied by the hand at a point on the handle surface, ff is friction force applied by the hand at that point, is a vector (magnitude = r) from the center of the handle cross-section to normal force application point, ө is the angle about the handle center, and α is the angle between and fn. Both r and α are functions of the handle shape and ө (Figure 1).
Figure 1.
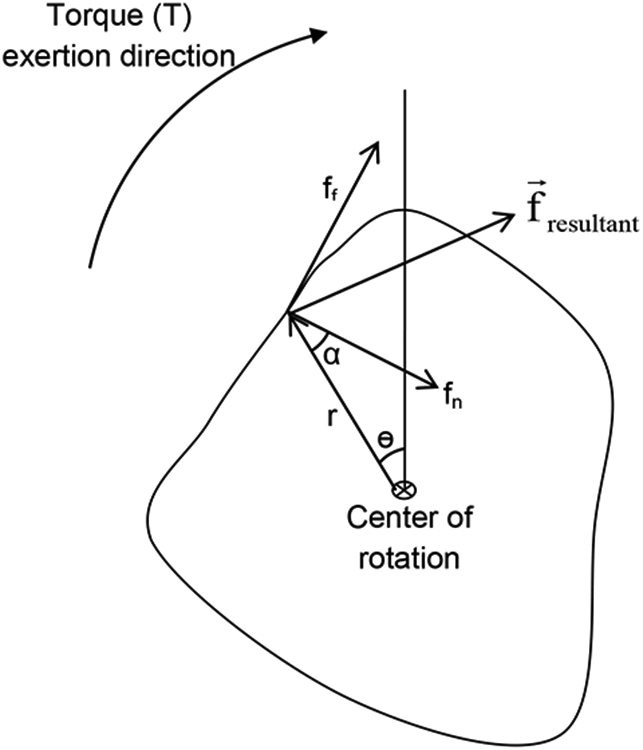
A cross-sectional area of a generic cylinder handle for torque (T) generation. A contact force can be resolved into a normal force (fn) and friction force (ff). Not only friction force but also normal force applied to the handle surface by the hand can contribute to torque generation about the center of the handle. The extent of each force’s contribution to torque is dependent on the moment arm (rcosα for friction force, rsinα for normal force) (0 ≤ ө ≤ 2π) (see Equation 1).
Previously we presented experimental results evaluating an earlier torque model for circular cylinders (Seo et al. 2007; Seo et al. 2008b). In the present paper, we present experimental results to evaluate this generic torque model for elliptic cylinders. The generic model (Equation 1) can be simplified for elliptic cylinders as shown below, assuming people generate maximum allowable friction force at all points of the handle to maximize torque.
| (2) |
| (3) |
| (4) |
| (5) |
where μ is the coefficient of friction between the hand and handle, and a and b are the lengths of the semi-major and semi-minor axes of the ellipse (cross-sectional area of the elliptic cylinder), respectively (Figure 2).
Figure 2.
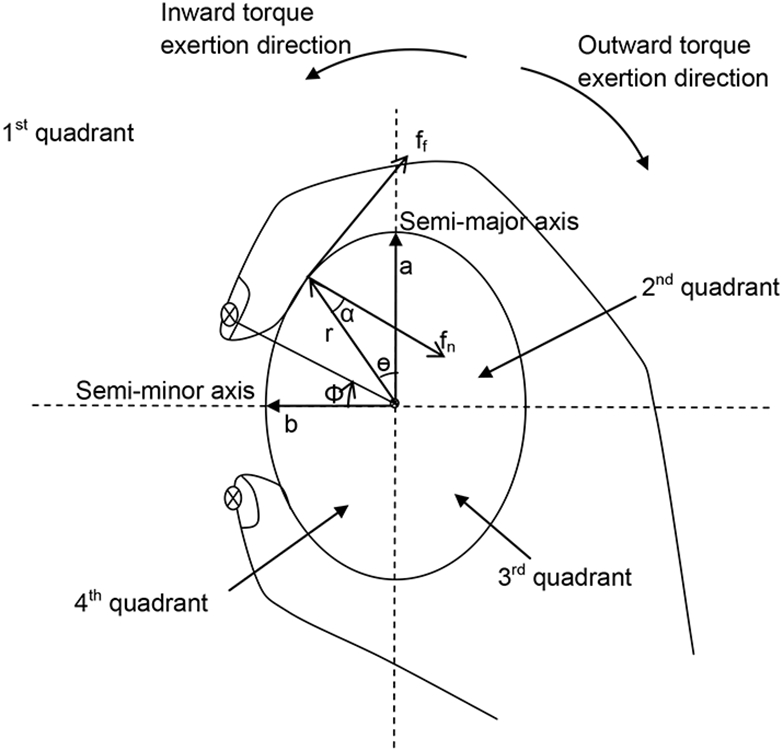
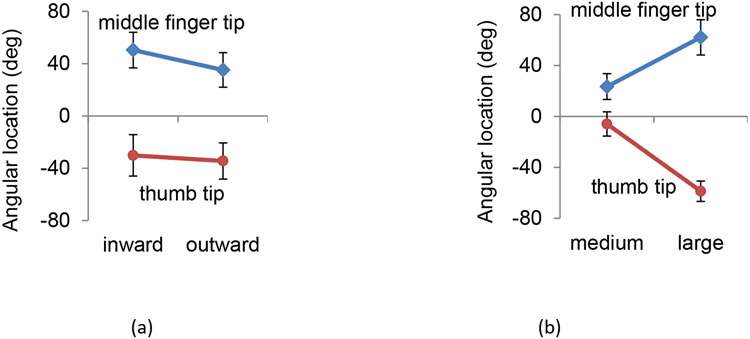
An elliptic cylinder handle grasped by the hand viewed from the top of the handle. Both normal force (fn) and friction force (ff which can be up to μ fn, where μ is the coefficient of friction between the hand and handle) contribute to torque generation, via moment arms (rcosα for friction force, ff, rsinα for normal force, fn). The elliptic cross-section area with a semi-major axis length of a and semi-minor axis length of b can be divided into four quadrants to examine force distribution along the handle circumference. Fingertips’ angular locations from the semi-minor axis (ϕ) were found for the thumb tip and the middle fingertip separately. The finger shown on the top represents the middle finger.
Based on this elliptic cylinder model (Equation 5), effects of cylinder shapes, sizes, and friction on torque can be predicted by examining the ratio of maximum possible torque (output) to a given total normal force (input). The ratios for a few selected cylinder shape, size, and friction conditions are summarized in Table 1a, assuming uniform normal force distribution along the handle circumference. The ratios predict greater torque for large-size than medium-size handles, and greater torque for a high-friction than low-friction condition. Under the assumption of uniform normal force distribution, the ratios are smaller for the elliptic than circular cylinders, indicating that elliptic cylinders’ elongated cross-section does not necessarily provide increased overall moment arm. However, concentrating normal force close to the semi-major axis to utilize long moment arms in that handle region may help torque generation.
Table 1.
The ratio of maximum torque (output) to a given total normal force (input) for different handle surfaces, sizes, and shapes (mm) predicted by the model (a) and observed during the experiment (b). The model prediction was performed using Equation 5, assuming a uniform normal force distribution along the handle circumference (i.e., constant fn = total normal force/(2π) in Figure 2) and the coefficient of friction of 0.85 between the aluminum and the hand skin and of 1.43 between the rubber and the hand skin (Seo et al. 2009) to examine the combined effects of friction, handle shape (circular vs. elliptic), and handle size (medium size with the circumference of 160 mm vs. large size with the circumference of 239 mm) on torque generation.
| Estimated torque to total normal force ratio (mm) | ||||
|---|---|---|---|---|
| Handle surface | Handle size | Circular cylinder handle | Elliptic cylinder handle | |
| (a) Model Prediction | Aluminum μ = 0.85 |
Medium | 21.6 | 19.4 |
| Large | 32.4 | 28.3 | ||
| Rubber μ = 1.43 |
Medium | 36.3 | 32.7 | |
| Large | 54.5 | 47.6 | ||
| (b) Empirical Observation | Aluminum μ = 0.85 |
Medium | 17.6 | 12.9 |
| Large | 26.9 | 23.9 | ||
| Rubber μ = 1.43 |
Medium | 27.9 | 19.1 | |
| Large | 39.2 | 34.5 | ||
The aim of this study was to evaluate the model proposed in Equation 5 by testing the following hypotheses. First, a person’s maximum torque is greater for circular, high-friction, and large-size cylinders than for elliptic, low-friction, and medium-size cylinders, respectively (based on the prediction in Table 1a). Second, people concentrate their grip force close to the semi-major axis to maximize torque for elliptic cylinders.
2. METHOD
To test the proposed hypotheses, maximum torque and normal force applied to the handle during torque generation were compared for circular vs. elliptic, low- vs. high-friction, and medium- vs. large-size cylinders. To gauge how deviation from the uniform normal force distribution assumption is related to increased torque output per grip normal force, the ratios of torque to normal force experimentally observed were compared to those predicted by the model (Table 1a). Torque exertions in two directions were tested to examine how people applied normal force differently depending on the torque direction. The two torque directions tested were outward (clockwise direction when the right hand’s power grip of a vertical cylinder is viewed from the top) and inward (counterclockwise, towards the direction the fingers point) directions. In addition, hand positions relative to the handle were recorded to examine how people positioned their hand differently depending on the handle size and torque direction.
2.1. Procedure
Six healthy individuals (3 female and 3 male college students, 23 to 34 years of age) grasped a vertical cylinder with the right hand in power grip with the elbow flexed approximately at 90°. Subjects were instructed to apply maximum isometric torque exertions about the long axis of a cylinder for 5 seconds, while (i) torque (ii) normal force applied to the cylinder by the hand, and (iii) the hand position on the cylinder were recorded. Subjects decided for themselves where on the cylinder to position their fingers. Subjects did not have training/practice trials. Subjects did not receive feedback on their torque output. Subjects were naïve about the study hypotheses.
Torque was recorded using a 6-axis load cell to which the cylinder was connected via universal joints. The universal joints minimize lateral force (Drury 1980) by subjects. Normal force was recorded using a 0.15 mm-thick sheet of pressure sensors (Tekscan, Inc., South Boston, MA) that was placed on the cylinder surface and measured normal force on each 5.08 by 5.08 mm sensor. The thumb and the middle finger’s tip locations relative to elliptic cylinders during torque exertions were recorded using infrared emitting markers (OptoTrak Certus, NDI, Waterloo, ON).
A full factorial experiment with four independent variables of handle cross-section (circular vs. elliptic), size (circumference = 160 vs. 239 mm), surface (aluminum vs. rubber), and torque direction (inward vs. outward, verbally instructed to subjects) was conducted. The circular cross-sections had radii of 25.4 and 38.1 mm for the medium- and large-size, respectively. The elliptic cross-sections’ semi-major and minor axes were 30.9 and 19.3 mm, respectively, for the medium-size, and 47.1 and 27.8 mm, respectively, for the large-size. To change the cylinder surface, a thin smooth sheet of aluminum (0.2 mm-thick) and rubber (2 mm-thick) was placed on top of the pressure sensors. The independent variables were presented to subjects in a random order. Each condition was tested twice. All data were collected at 30 Hz. A minimum of two minutes of break was given between consecutive exertions to minimize muscle fatigue (Caldwell et al. 1974). All participants gave written informed consent prior to the experiment.
2.2. Analysis
For each torque trial, torque, normal force, and finger position data were averaged over a 2-second window during which the mean isometric torque was the highest. As primary analysis, two analyses of variance (ANOVA) were performed to determine if handle shape, size, surface, torque direction, and their second-order interactions (shape × size, shape × surface, shape × direction, size × surface, size × direction, surface × direction) significantly affected maximum torque and total normal force, separately. Total normal force was determined as the sum of all normal forces recorded on the pressure sensors covering the cylinder surface. A significance level of .05 was used.
As secondary analysis, normal force distribution across the four quadrants of elliptic cylinders (Figure 2) was examined. Specifically, another ANOVA was performed to determine if the sum of normal forces on each quadrant significantly varied for handle size, surface, torque direction, quadrant (first, second, third, and fourth), and their second-order interactions, only for elliptic cylinders. In addition, subjects’ chosen hand position during torque exertion on the elliptic cylinders was examined. The middle fingertip and thumb tip locations were projected to a cross-section of the elliptic cylinder and expressed as the angle from the semi-minor axis of the cross-sectional area about the ellipse center (denoted by ϕ in Figure 2). Multivariate ANOVA was performed to determine if the thumb and middle finger’ angular locations (ϕ) significantly varied for handle size, surface, torque direction, and their second-order interactions, only for elliptic cylinders. Lastly, the ratios of measured torque to measured normal force ratios were computed for each torque trial. The empirically-observed torque to normal force ratios were compared to those predicted by the model.
3. RESULTS
3.1. Maximum torque
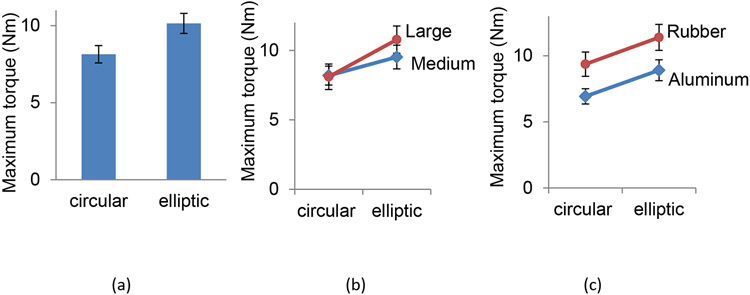
Maximum torque significantly varied for handle shape, size, and surface (Figure 3). Mean maximum torque was, on average, 25% greater for the elliptic cylinders than for the circular cylinders (p<.01, Figure 3a), 7% greater for the large-size than for the medium-size cylinders (p=.04, Figure 3b), and 31% greater for the rubber-than for the aluminum-finished cylinders (p<.01, Figure 3c). Maximum torque did not significantly vary for torque direction and any second-order interactions (p>.05). An interaction between shape and size was seen (p=.06, Figure 3b).
Figure 3.
Maximum torque a person could produce on a handle significantly varied for the handle shape (circular vs. elliptic cylinder handle, a), handle size (cross-section circumference of 160 vs. 239 mm or medium vs. large, b), and handle surface (aluminum-finished vs. rubber-finished, c). For each figure, all other conditions including subject and torque direction were pooled.
3.2. Normal force
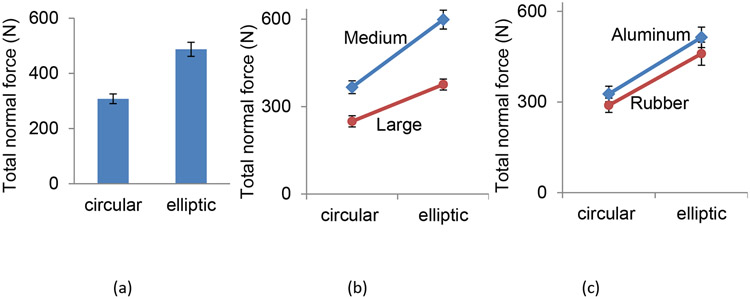
Total normal force subjects applied during torque exertion significantly varied for handle shape, size, surface (Figure 4), torque direction, and the interaction between shape and size (p<.05). Other second-order interactions were not found to be significant (p>.05). Mean total normal force was 58% greater for the elliptic than for circular cylinders (p<.01, Figure 4a), 54% greater for the medium-size than for the large-size cylinders (p<.01, Figure 4b), 11% greater for the inward than for the outward torque generation (p<.01), and 12% greater for the aluminum- than for the rubber-finished cylinders (p<.01, Figure 4c). Increase in total normal force for the elliptic cylinder compared to the circular cylinder was greater for the medium-size (63%) than for the large-size cylinders (51%) (p<.01, Figure 4b).
Figure 4.
Total normal force a person applied to a handle during torque exertion significantly varied for the handle shape (circular vs. elliptic cylinder handle, a), handle size (cross-section circumference of 160 vs. 239 mm or medium vs. large, b), and handle surface (aluminum-finished vs. rubber-finished, c). For each figure, all other conditions including subject and torque direction were pooled.
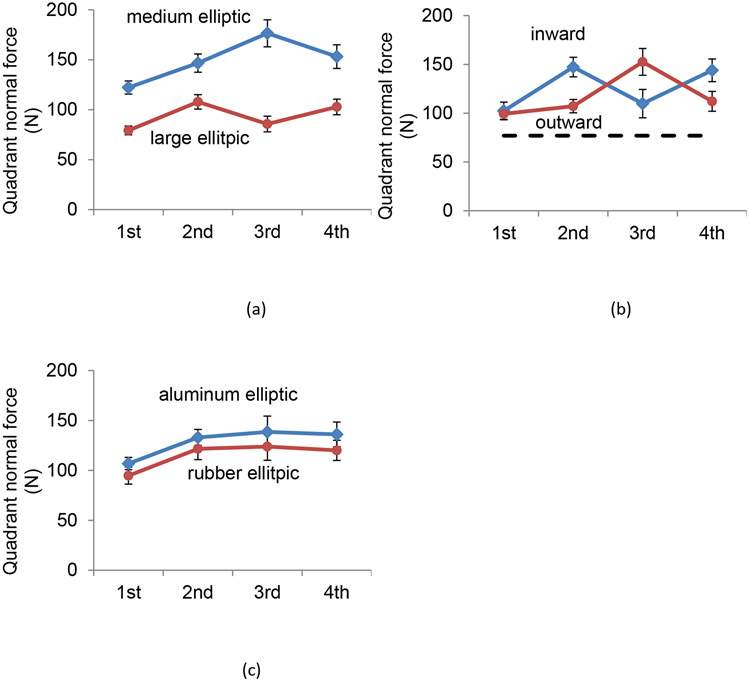
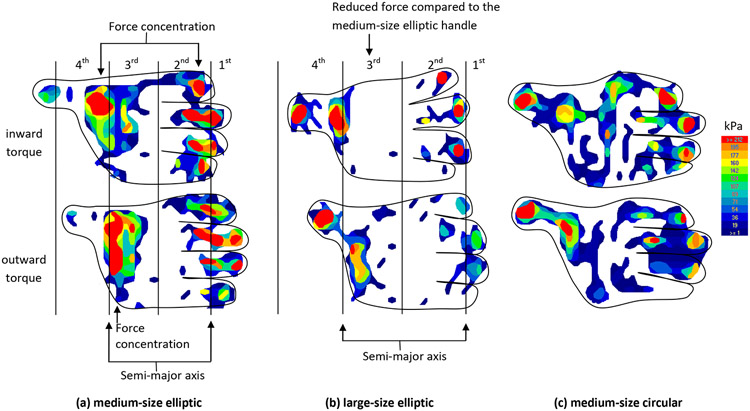
Normal force in each quadrant during torque exertions on elliptic cylinders significantly varied for handle size, surface, torque direction, quadrant, and interactions between handle size and quadrant and between torque direction and quadrant (p<.05; Figure 5). Other interactions were not found to be significant (p>.05). The 3rd quadrant (where the palm and thenar eminence contact the cylinder) had high normal force concentration relative to other quadrants for the medium-size cylinder, but not for the large-size cylinder (Figure 5a, Figure 6a,b). During inward torque generation, normal forces were concentrated on the 2nd (by the phalanges) and 4th quadrants (by the thumb/thenar eminence) (Figure 6a-top). For outward torque, normal forces were concentrated on the 3rd quadrant by the thenar eminence (Figure 5b, Figure 6a-bottom). Normal force for all quadrants was, on average, 12% greater for the aluminum- than for the rubber-finished elliptic cylinders (Figure 5c), as expected from the finding that the total normal force was 12% greater for the aluminum- than for the rubber-finished cylinders (Figure 4c).
Figure 5.
Normal force in a quadrant observed during torque exertion on elliptic cylinder handles significantly varied for the interaction between handle size and quadrant (a) and for the interaction between torque direction and quadrant (b). Normal force in each quadrant was, on average, 12% greater for the aluminum- than rubber-finished elliptic cylinders (c). The quadrant forces on elliptic cylinder handles were, in general, higher than the average quadrant force on circular cylinder handles (total normal force divided by 4) denoted by the segmented line in b. Only elliptic cylinder handle data are shown. For each figure, all other conditions not specified were pooled.
Figure 6.
Sample force distribution on the hand across four quadrants (1st through 4th) for one subject during the inward (top) and outward (bottom) torque direction for the medium-size elliptic cylinder handle (a), the large-size elliptic cylinder handle (b), and the medium-size circular cylinder handle (c). Outlines of the hands are estimated to illustrate locations of forces on the hand. Rubber surface only.
3.3. Fingertip location
Mean fingertip angular location on elliptic cylinders (ϕ) was −32° for the thumb tip and 43° for the middle fingertip. The subjects significantly varied the thumb tip and middle fingertip’s locations on the handles (ϕ) depending on torque direction and handle size (p<.05; Figure 7), but not depending on other factors (p>.05). The middle fingertip was further away from the semi-minor axis and the thumb tip was closer to the semi-minor axis during inward torque generation, compared with outward torque (Figure 7a). The middle finger and thumb tips became further away from the semi-minor axis when grasping a large-size cylinder, compared with a medium-size cylinder (Figure 7b).
Figure 7.
Angular locations of the thumb tip and the middle finger tip on elliptic cylinder handles (ϕ in Figure 2) significantly varied for torque direction (a) and handle size (b). Only elliptic cylinder handle data are shown. For each figure, all other conditions not specified were pooled.
3.4. Ratio of torque to total normal force
To facilitate the comparison with the model prediction (Table 1a), the ratios of measured maximum torque to measured total normal force were computed and summarized in Table 1b. As for the handle shape effect, the ratio of measured torque to measured total normal force was, on average, 19% less for the elliptic than circular cylinders (Table 1b). As for the size effect, the empirically-observed ratio of torque to total normal force was, on average, 61% greater for the large-size than for medium-size cylinders. As for the surface effect, the empirically-observed ratio was, on average, 48% greater for the rubber-finished than aluminum-finished cylinders. These trends for the shape, size, and surface were similar with the model predictions. The empirically-observed ratios were, on average, 26% lower than the predicted ratios.
4. DISCUSSION
The present study demonstrated that handle features and intended direction of motion significantly affected the way subjects gripped and generated torque. Specifically, maximum torque was greater for the elliptic, large-size, and rubber-finished cylinders than for circular, medium-size, and aluminum-finished cylinders, respectively (Figure 3). Greater torque for the elliptic cylinders was associated with greater total normal force subjects could generate for the elliptic than circular cylinders. Greater torque for the large-size cylinders appears to be due to greater moment arms provided for the large- than medium-size cylinders. Greater torque for the rubber-finished cylinders appears to be due to greater coefficient of friction available for the rubber- than aluminum-finished cylinders. Subjects concentrated hand normal force close to the semi-major axis during torque generation on the elliptic cylinders (Figure 6). Biomechanical descriptions and ergonomic implications for each handle feature are discussed below.
4.1. Handle shape
Mean maximum torque was 25% greater for the elliptic than circular cylinders (Figure 3a). Greater maximum torque for the elliptic than circular cylinders was associated with 58% greater total normal force that subjects could apply for the elliptic than circular cylinders (Figure 4a), rather than with changes in the torque to normal force ratio (Table 1b). It was anticipated that subjects would concentrate the hand force close to the semi-major axis to utilize the long moment arms around the semi-major axis, increase the torque output per given total normal force, and maximize torque for elliptic cylinders. Subjects adjusted their hand position and concentrated force close to the semi-major axis (Figure 6). However, empirically-observed ratios of torque to normal force were not greater for the elliptic than circular cylinders (Table 1b).
The way that subjects could apply 58% greater normal force across quadrants (Figure 5b) for the elliptic than for the circular cylinders is postulated as follows. First, the hand grip postures for the elliptic cylinders could have allowed the biomechanical parameters such as the long finger flexor muscle length and moment arms to be closer to optimum for grip force production, compared to those for the circular cylinders (Amis 1987; O'Driscoll et al. 1992; Kamper et al. 2006). Varying finger postures could result in 60% changes in maximum joint moments (Kamper et al. 2006). Second, the subjects could have generated greater total normal force for the elliptic than circular cylinders, by wedging the elliptic cylinders between the finger joints and the palm to secure the handle position in the space, and by counterbalancing large forces from the distal and middle phalanges with the reaction force on the thumb/thenar eminence on the opposite quadrant (Figure 6a). For circular cylinders, forces that people could generate using the fingers were limited by the availability of sufficient reaction force by the palm (Seo et al. 2007; Enders and Seo 2011).
Another reason for greater total normal force observed for the elliptic than for the circular cylinders could be that elliptic cylinders allow not only friction force but also normal force to directly contribute to torque generation (Equation 1), encouraging normal force generation. In contrast, torque about the circular cylinders is produced by friction forces, while normal force prevents hand slippage on the handle during torque generation. Performing two tasks simultaneously (gripping to generate normal force and twisting to generate torque) may reduce a person’s force capacity as evidenced by reduction in maximum push force when torque generation is simultaneously required (Seo et al. 2008a), reduction in digit strength when multiple fingers are working simultaneously (Ohtsuki 1981b), and reduction in hand grip strength when the contralateral hand is simultaneously gripping (Ohtsuki 1981a).
4.2. Handle size
Large-size handles resulted in 13% greater mean maximum torque compared with medium-size handles for the elliptic cylinders (Figure 3b), likely due to increased overall moment arms as computed by the model (Table 1a). With 53% increase in a and 44% increase in b, the model computes, on average, 48% increase in r (Equation 3) and 11% increase in α (Equation 4). These increases in r and α lead to 48% and 1% increase in torque, respectively (Equation 5). Overall, the model predicts 48% increase in maximum torque for the large- than medium-size handles, assuming a constant normal force for both handle sizes. Experimentally-observed maximum torque increased only 13% for the large- than medium-size handles (as opposed to 48% increase in the model prediction), probably because increase in the moment arm (48%) was canceled out by decrease in total normal force (35%).
Mean total normal force was 35% less for the large-size handles than for the medium-size handles for both shapes (Figure 4b). Decreased total normal force with increased handle size is probably due to changes in the finger posture leading to (i) lengthened long finger flexor muscle (exceeding the optimal length) reducing muscle force output (accounting for less than 9% changes in grip force output) (Amis 1987; O'Driscoll et al. 1992; Kamper et al. 2006), (ii) reduced muscle moment arm (Peebles and Norris 2003; Greig and Wells 2004; Kong et al. 2004; Kamper et al. 2006; Lee et al. 2008), and (iii) difficulty in strategically placing the fingertips and thenar eminence for maximizing reaction force (Seo et al. 2007). For example, with the large separation between the thumb and middle finger tips for the large-size cylinders (Figure 7b), the four fingers were barely on the first quadrant (Figure 6b-bottom), reducing the reaction force on the thenar eminence on the third quadrant (Figure 5a). Despite this reduction in total normal force, the advantage in the moment arm (as predicted in Table 1a) resulted in greater maximum torque for the large-size than for the medium-size handles. On a similar note, the handle whose size allows maximum grip force such as 38 mm-diameter circular cylindrical handles (Ayoub and Presti 1971; Grant et al. 1992; Hall 1997; Edgren et al. 2004) may not provide maximum torque due to limited moment arm.
4.3. Handle surface & torque direction
The rubber-finished handles resulted in, on average, 31% greater maximum torque compared with the aluminum-finished handles for both shapes (Figure 3c, 35% and 28% increases for the circular and elliptic cylinders, respectively), likely due to increase in the coefficient of friction for the rubber surface. Mean total normal force was 11% less for the rubber handles than for the aluminum handles (Figure 4c), probably due to slightly greater handle size and subsequent reduction in grip strength from the 2 mm-thick rubber sheet compared to 0.2 mm-thick aluminum sheet (Seo et al. 2008a). Despite reduced total normal force, increased coefficient of friction and hand-handle frictional coupling resulted in greater maximum torque for the rubber than for the aluminum handles, as anticipated in Equation 5. This finding is consistent with previous studies that demonstrated that increased coefficient of friction between the hand and handle can increase hand strength that utilizes friction force such as push/pull along the long axis of handles or holding onto a handle until the hand slips (Kong et al. 2007; Seo et al. 2008a; Seo et al. 2008b; Seo 2009; Young et al. 2009; Seo et al. 2010).
Torque direction did not significantly affect the subjects’ maximum torque. However, torque direction affected how the subjects gripped the handle and distributed the hand force. Specifically, during inward torque generation, subjects shifted the hand position relative to the handle clockwise when viewed from the top (Figure 7a) so that the thenar eminence could contact the fourth quadrant near the semi-major axis and the four fingers’ major forces could be applied to the second quadrant near the semi-major axis (Figure 6a-top). During outward torque generation, subjects shifted the hand position counterclockwise so that the thenar eminence could contact the third quadrant and the four fingers’ major forces could be applied to the first quadrant (Figure 6a-bottom). Any obstructions to placement of the hand and distribution of hand force accordingly may lead to reduced torque strength for workers.
4.4. Comparison to model prediction
The effects of handle shape, size, and surface on the ratio of maximum torque (output) to total normal force (input) empirically observed (Table 1b) compared favorably with the model predictions (Table 1a). Both the empirical data and models suggest that torque output per given normal force is greater for the circular, large-size, and rubber-finished cylinders than for the elliptic, medium-size, and aluminum-finished cylinders. Our anticipation that non-uniform normal force distribution might lead to greater torque to normal force ratios for the elliptic than circular cylinders was not supported by the experimental results. Rather, the observed 25% increase in torque for the elliptic cylinders appears to be related to 58% increase in total normal force the subjects could generate on the elliptic than circular cylinders. The empirically-observed torque to normal force ratios were, on average, 26% lower than the predicted ratios. The consistently lower ratios for empirical observations than model predictions may be because the predicted ratios are for maximal possible torque per given normal force, assuming that people apply maximum possible friction forces (up to slippage) at all points of the contact, which is unlikely in reality.
The model can predict only the ratio of maximum possible torque to uniform normal force. The model, however, does not predict how much grip force people can apply for different handle shapes and size. For instance, the total normal force varied, on average, 58% between the two handle shapes, and 54% between the two handle sizes in the present study (Figure 4a, b). Such large variations in the total normal force significantly affected the subjects’ maximum torque. Without the knowledge of grip force that people can apply for varying grip conditions, the model is currently limited in its ability to predict maximum torque. Further studies that aim to predict grip force capability for varying handle shapes and corresponding hand postures (Kong et al. 2007; Domalain et al. 2008; Seo and Armstrong 2008; Lee et al. 2009) would help improve the torque prediction capacity.
4.5. Future studies
Future studies may look into designing handles with irregular cross-sections that achieve the best balance between maximizing grip force and maximizing torque. For example, asymmetric handles may be investigated to identify their significant advantages for climbing, body support, tools and package opening (Rowson and Yoxall 2011), which may have a high impact on handle design to maximize efficiency in force/torque application in daily living. A further systematic investigation of various semi-major vs. semi-minor axis length ratios of elliptic shapes and associated hand postures could improve our understanding of the handle shape effects on grip force and torque exertions. In addition to maximizing torque capabilities, user discomfort associated with high force concentration with varying handle shapes need to be considered in determining the optimum handle shapes, especially for tasks that require prolonged or repetitive exertions. Consideration of the effect of handle shape on people’s grasping strategy, movement speed, and speed of force application to handles could also assist improving safety of products or tools for particular tasks (Chang et al. 2008; Kuo et al. 2009; Carse et al. 2011; Rowson and Yoxall 2011).
The present study investigated torque exertion on an unconstrained vertical handle in an unconstrained manner only. Other gripping situations such as fixed handles (Seo and Armstrong 2009), horizontally- or obliquely-oriented handles (Kong et al. 2007; Okunribido and Haslegrave 2008), and presence of obstruction in the way of gripping (Grieshaber et al. 2009) may be further examined to evaluate the model. In the present study, only normal force distribution was examined. Since friction force is limited by the product of the coefficient of friction and normal force, normal force distribution provides insight into possible friction force distribution. Upon availability of technology for a thin sensor measuring friction force, friction force distribution information may provide a complete picture of how people apply torque.
5. CONCLUSIONS
The present study demonstrated that people adjusted their hand position on elliptic cylinders depending on the direction of torque application and increased hand normal force by 58% and maximum torque by 25% for the elliptic cylinders compared to circular cylinders. Increased maximum torque with the elliptic cylinders could be achieved by allowing people to position their hands as they think optimally. In addition, the present study demonstrated that longer moment arms for the large-size than for the medium-size handles resulted in increased maximum torque, although total normal force was greater for the medium-size than for the large-size handles. This finding illustrates that a handle size that allows for maximum torque is different from that for maximum grip force. Greater frictional coupling at the hand-handle interface resulted in greater maximum torque for the rubber-finished than for the aluminum-finished handles. Handle shape, size and surface can be modified to help increase a person’s torque capacity. Such handle redesign has the potential to contribute to ease of performing activities, efficient torque generation in daily living, and reduced risk of musculoskeletal injuries.
Contributor Information
Na Jin Seo, Department of Industrial Engineering, University of Wisconsin-Milwaukee, 3200 N. Cramer St., Milwaukee, WI 53211 USA.
Thomas J. Armstrong, Department of Industrial & Operations Engineering, University of Michigan, 1205 Beal Ave., Ann Arbor, MI 48109 USA
REFERENCES
- Adams SK, Peterson PJ (1988) Maximum voluntary hand grip torque for circular electrical connectors. Hum Factors 30: 733–745 [DOI] [PubMed] [Google Scholar]
- Amis AA (1987) Variation of finger forces in maximal isometric grasp tests on a range of cylinder diameters. J Biomed Eng 9: 313–320 [DOI] [PubMed] [Google Scholar]
- Ayoub MM, Presti PL (1971) The determination of an optimum size cylindrical handle by use of electromyography. Ergonomics 14: 509–518 [DOI] [PubMed] [Google Scholar]
- Caldwell LS, Chaffin DB, Dukes-Dobos FN, Kroemer KH, Laubach LL, Snook SH, Wasserman DE (1974) A proposed standard procedure for static muscle strength testing. Am Ind Hyg Assoc J 35: 201–206 [DOI] [PubMed] [Google Scholar]
- Carse B, Thomson A, Stansfield B (2011) A novel device for evaluating forces during the dynamic jar opening action--do older and younger adults do things differently? Med Eng Phys 33: 521–525 [DOI] [PubMed] [Google Scholar]
- Chang JH, Ho KY, Su FC (2008) Kinetic analysis of the thumb in jar-opening activity among female adults. Ergonomics 51: 843–857 [DOI] [PubMed] [Google Scholar]
- Crawford JO, Wanibe E, Nayak L (2002) The interaction between lid diameter, height and shape on wrist torque exertion in younger and older adults. Ergonomics 45: 922–933 [DOI] [PubMed] [Google Scholar]
- Domalain M, Vigouroux L, Danion F, Sevrez V, Berton E (2008) Effect of object width on precision grip force and finger posture. Ergonomics 51: 1441–1453 [DOI] [PubMed] [Google Scholar]
- Drury CG (1980) Handles for manual materials handling. Appl Ergon 11: 35–42 [DOI] [PubMed] [Google Scholar]
- Edgren CS, Radwin RG, Irwin CB (2004) Grip force vectors for varying handle diameters and hand sizes. Hum Factors 46: 244–251 [DOI] [PubMed] [Google Scholar]
- Enders LR, Seo NJ (2011) Phalanx force magnitude and trajectory deviation increased during power grip with an increased coefficient of friction at the hand-object interface. Journal of Biomechanics 44: 1447–1453 [DOI] [PubMed] [Google Scholar]
- Grant KA, Habes DJ, Steward LL (1992) An analysis of handle designs for reducing manual effort: The influence of grip diameter. International Journal of Industrial Ergonomics 10: 199–206 [Google Scholar]
- Greig M, Wells R (2004) Measurement of prehensile grasp capabilities by a force and moment wrench: methodological development and assessment of manual workers. Ergonomics 47: 41–58 [DOI] [PubMed] [Google Scholar]
- Grieshaber DC, Armstrong TJ, Chaffin DB, Keyserling WM, Ashton-Miller J (2009) The effects of insertion method and force on hand clearance envelopes for rubber hose insertion tasks. Hum Factors 51: 152–163 [DOI] [PubMed] [Google Scholar]
- Hall C (1997) External pressure at the hand during object handling and work with tools. International Journal of Industrial Ergonomics 20: 191–206 [Google Scholar]
- Imrhan SN, Loo CH (1988) Modelling wrist-twisting strength of the elderly. Ergonomics 31: 1807–1819 [DOI] [PubMed] [Google Scholar]
- Kamper DG, Fischer HC, Cruz EG (2006) Impact of finger posture on mapping from muscle activation to joint torque. Clin Biomech (Bristol, Avon) 21: 361–369 [DOI] [PubMed] [Google Scholar]
- Kong YK, Freivalds A, Kim SE (2004) Evaluation of handles in a maximum gripping task. Ergonomics 47: 1350–1364 [DOI] [PubMed] [Google Scholar]
- Kong YK, Lowe BD, Lee SJ, Krieg EF (2007) Evaluation of handle design characteristics in a maximum screwdriving torque task. Ergonomics 50: 1404–1418 [DOI] [PubMed] [Google Scholar]
- Kuo LC, Chang JH, Lin CF, Hsu HY, Ho KY, Su FC (2009) Jar-opening challenges. Part 2: estimating the force-generating capacity of thumb muscles in healthy young adults during jar-opening tasks. Proc Inst Mech Eng H 223: 577–588 [DOI] [PubMed] [Google Scholar]
- Lee SJ, Kong YK, Lowe BD, Song S (2009) Handle grip span for optimising finger-specific force capability as a function of hand size. Ergonomics 52: 601–608 [DOI] [PubMed] [Google Scholar]
- Lee SW, Chen H, Towles JD, Kamper DG (2008) Estimation of the effective static moment arms of the tendons in the index finger extensor mechanism. J Biomech 41: 1567–1573 [DOI] [PubMed] [Google Scholar]
- Nagashima K, Konz S (1986) Jar lids: Effect of diameter, gripping materials and knurling. Proceedings of the human Factors Society thirtieth annual meeting. The Human Factors Society, Santa Monica [Google Scholar]
- O'Driscoll SW, Horii E, Ness R, Cahalan TD, Richards RR, An KN (1992) The relationship between wrist position, grasp size, and grip strength. J Hand Surg Am 17: 169–177 [DOI] [PubMed] [Google Scholar]
- Ohtsuki T (1981a) Decrease in grip strength induced by simultaneous bilateral exertion with reference to finger strength. Ergonomics 24: 37–48 [DOI] [PubMed] [Google Scholar]
- Ohtsuki T (1981b) Inhibition of individual fingers during grip strength exertion. Ergonomics 24: 21–36 [DOI] [PubMed] [Google Scholar]
- Okunribido OO, Haslegrave CM (2008) Ready steady push--a study of the role of arm posture in manual exertions. Ergonomics 51: 192–216 [DOI] [PubMed] [Google Scholar]
- Peebles L, Norris B (2003) Filling 'gaps' in strength data for design. Appl Ergon 34: 73–88 [DOI] [PubMed] [Google Scholar]
- Pheasant S, O'Neill D (1975) Performance in gripping and turning -a study in hand/handle effectiveness. Appl Ergon 6: 205–208 [DOI] [PubMed] [Google Scholar]
- Rowson J, Yoxall A (2011) Hold, grasp, clutch or grab: consumer grip choices during food container opening. Appl Ergon 42: 627–633 [DOI] [PubMed] [Google Scholar]
- Seo NJ (2009) Dependence of safety margins in grip force on isometric push force levels in lateral pinch. Ergonomics 52: 840–847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ (2008) Investigation of grip force, normal force, contact area, hand size, and handle size for cylindrical handles. Hum Factors 50: 734–744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ (2009) Biomechanical analysis for handle stability during maximum push and pull exertions. Ergonomics 52: 1568–1575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ, Ashton-Miller JA, Chaffin DB (2007) The effect of torque direction and cylindrical handle diameter on the coupling between the hand and a cylindrical handle. J Biomech 40: 3236–3243 [DOI] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ, Chaffin DB, Ashton-Miller JA (2008a) The effect of handle friction and inward or outward torque on maximum axial push force. Hum Factors 50: 227–236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ, Chaffin DB, Ashton-Miller JA (2008b) Inward torque and high-friction handles can reduce required muscle efforts for torque generation. Hum Factors 50: 37–48 [DOI] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ, Drinkaus P (2009) A Comparison of Two Methods of Measuring Static Coefficient of Friction at Low Normal Forces: A Pilot Study. Ergonomics 52: 121–135 [DOI] [PubMed] [Google Scholar]
- Seo NJ, Armstrong TJ, Young JG (2010) Effects of handle orientation, gloves, handle friction, and elbow posture on maximum horizontal pull and push forces Ergonomics 53: 92–101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young JG, Woolley C, Armstrong TJ, Ashton-Miller JA (2009) Hand-handhold coupling: effect of handle shape, orientation, and friction on breakaway strength. Hum Factors 51: 705–717 [DOI] [PubMed] [Google Scholar]