International stock market risk contagion during the COVID-19 pandemic

Abstract

This paper examines the risk contagion among international stock markets during the COVID-19 pandemic by using the realized volatility information from sixteen major stock markets in the world. The empirical evidence based on the connectedness methods of Diebold and Yilmaz (2012) and Baruník and Křehlík (2018) shows that the COVID-19 epidemic significantly increases the risk contagion effects in international stock markets. Besides, the risk spillovers from stock markets in European and American regions increase rapidly but those in Asian markets decrease obviously after the outbreak of COVID-19 pandemic. Finally, the risk contagion among international stock markets caused by the pandemic can last for about 6 to 8 months. These results provide important implications regarding to financial risk management and macroprudential design.

1. Introduction

The COVID-19 pandemic deeply affects global economy activities (Janiak et al., 2021; Tisdell, 2020; Yang et al., 2021). Governments have released many precautionary measures (such as city lockdown, flight ban and work suspension) to prevent the further spread of the COVID-19 epidemic, which result in heavy global economy recession and huge fluctuations in international stock markets (Contessi and De Pace, 2021; Frezza et al., 2021), as well as stronger market risk contagion (spillover effects) among them (Davidovic, 2021; Wei et al., 2019).

Recent studies about the impacts of the COVID-19 epidemic on financial contagion have been very popular (Bai et al., 2020, Bai et al., 2021; Goodell, 2020; Liang et al., 2021, 2020a). Several researchers (Akhtaruzzaman et al., 2021; Bouri et al., 2021; Corbet et al., 2020; Gharib et al., 2021; Le et al., 2021) find that the correlations among various financial markets increase significantly during the COVID-19 pandemic. For example, Guo et al. (2021) indicate that the COVID-19 epidemic enlarges contagion channels in the international financial system. Li et al. (2021b) use the causal forest and complex network methods to analyze the characteristics of industry risk contagion before and after the pandemic. Contessi and De Pace (2021) find the evidence of instable transmission from the Chinese stock market to other stock markets. Sharif et al. (2020) employ wavelet method and unveil the unprecedented impact of COVID-19 on the geopolitical risk, economic policy uncertainty and stock market volatility over the low frequency bands. Davidovic (2021) indicates international financial markets are more integrated and risk contagion increases during the pandemic. Fassas (2020) investigates the dynamic connectedness of variance risk premium among developed and emerging stock markets and calculates the total investors' risk aversion connectedness.

Investigating the international risk contagion is of great importance for international investors to allocate their portfolios and for policy makers to propose relevant policies (Bai et al., 2019; Coroneoet al., 2020; Daly et al., 2019; Gkillas et al., 2019; Li and Wei, 2018; Li et al., 2021a; Park and Shin, 2020; Wang et al., 2021). However, there are few researches focusing on the risk contagion effects among international stock markets during the COVID-19 epidemic by using the realized volatility (RV) information in these markets.

For highly liquid stocks, using RV as market risk measurement has clear advantages. First of all, RV is a nonparametric estimator of intraday price fluctuations (Nielsen and Shephard, 2002), and it is very easy to calculate and free from functional form assumptions. Secondly, the distribution of daily logarithm RV appears to be very close to normal distribution, which means that it meets most of assumptions in risk analyzing models (e.g., GARCH-type or HAR-type volatility models). Thirdly, RV measurement ignores the overnight variations in stock price and sometimes the variations in the first few minutes of the trading day when recorded prices may contain large errors (Liang et al., 2020b, 2019; Ma et al., 2018; Wei et al., 2020, Wei et al., 2021). Thus, based on the connectedness methods of Diebold and Yilmaz (2012) and Baruník and Křehlík (2018), this paper aims to explore the risk contagion effects across international stock markets by utilizing the RV measurements released by Oxford-Man Institute of Quantitative Finance, and provide some implications relative to financial risk management.

2. Methodology

2.1. Spillover analysis in time domain

To analyze the risk spillover effect among different stock markets, this paper firstly employs the connectedness method proposed by Diebold and Yilmaz (2012), hereafter labelled as DY method. This approach is based on a forecast generalized variance decomposition (FGVD) process in vector auto-regression (VAR) models, and it can not only measure the spillover index in time domain but also identify the risk contagion direction of this spillover index. The method starts from a covariance stationary N-variate generalized VAR framework with lag p:

$$Y_t={\varphi }_1{Y}_{t-1}+{\varphi }_2{Y}_{t-2}+...+{\varphi }_p{Y}_{t-p}+{\epsilon }_t,$$ (1)

where Y_t = (y _1t,y _2t,..., y_Nt) represent volatilities in various stock markets 1, 2, …, N. φ_i is the ith coefficient matrix, ${\epsilon }_t\sim N\left(0,{\Sigma }_{\epsilon }\right)$ is white noise with possibly non-diagonal covariance matrix Σ_ε. Assuming that Y_t is a covariance stationary process, which means that the roots of |φ_i|,i = 1, 2, ..., p are outside the unit circle. This VAR(p) can be organized as the following vector moving average representation:

$$Y_t={\epsilon }_t+M_1{\epsilon }_{t-1}+M_2{\epsilon }_{t-2}+...+M_{\infty }{\epsilon }_{t-\infty },$$ (2)

where M_h = φ₁ M _i − 1 + φ₂ M _i − 2 + ... + φ_p M _i − p, i = 1, 2, ..., ∞ is in a recursive form. .. is N-dimensional unit matrix. Eq. (2) can measure contribution of market y_k to the forecast error variance of y_j at h = 1, 2, ..., H horizons.

DY method decomposing the forecast error variance of Eq. (2) is based on the researches of Koop et al. (1996); Pesaran and Shin (1998), which are invariant to variable ordering. The proportion of the forecast error variance in forecasting y_j due to shocks from market y_k at H-horizon is (Θ_H)_j,k. When j ≠ k, (Θ_H)_j,k denotes the pairwise directional spillover from market k to j, and it can be computed as

$${\left({\Theta }_H\right)}_{j,k}=\frac{{\sigma }_{kk}^{-1}{\sum }_{h=0}^{H-1}{\left({\left(M_h{\Sigma }_{\epsilon }\right)}_{j,k}\right)}^2}{{\sum }_{h=0}^{H-1}{\left(M_h{\Sigma }_{\epsilon }{M_h}^{\prime }\right)}_{j,j}},$$ (3)

where σ_kk = (Σ)_kk is the standard error of the k th equation in VAR framework, M_h is an N × N matrix of moving average coefficients with lag h. Σ_ε is the non-diagonal covariance matrix of VAR error term ε_t. Based on (Θ_H)_j,k, the standardized pairwise spillover from market k to j is

$${\left({{\Theta }^{\prime }}_H\right)}_{j,k}={\left({\Theta }_H\right)}_{j,k}/{\sum }_k{\left({\Theta }_H\right)}_{j,k}.$$ (4)

Furthermore, the total volatility spillover index is constructed as

$$S_H=100\frac{{\sum }_{j\ne k}{\left({{\Theta }^{\prime }}_H\right)}_{j,k}}{\sum {\left({{\Theta }^{\prime }}_H\right)}_{j,k}}=100\left(1-\frac{Tr\left\{{{\Theta }^{\prime }}_H\right\}}{N}\right),$$ (5)

where Tr{ • } indicates the trace operator. The total spillover index measures the contribution of spillovers of volatility shocks across all markets to the total forecast error variance. Additionally, the directional spillover received by market j from all other markets k is defined as

$$S_{H,j\leftarrow •}=100\frac{{\sum }_{k,k\ne j}{\left({{\Theta }^{\prime }}_H\right)}_{j,k}}{\sum {\left({{\Theta }^{\prime }}_H\right)}_{j,k}}=100\frac{{\sum }_{k,k\ne j}{\left({{\Theta }^{\prime }}_H\right)}_{j,k}}{N}.$$ (6)

Similarly, the directional spillover transmitted by market j to all other markets k is

$$S_{H,•\leftarrow j}=100\frac{{\sum }_{k,k\ne j}{\left({{\Theta }^{\prime }}_H\right)}_{k,j}}{\sum {\left({{\Theta }^{\prime }}_H\right)}_{k,j}}=100\frac{{\sum }_{k,k\ne j}{\left({{\Theta }^{\prime }}_H\right)}_{k,j}}{N}.$$ (7)

In addition, to measure the net directional spillover of market j, we can simply calculate the difference between Eq. (6) and Eq. (7) as

$$S_{H,j}=S_{H,•\leftarrow j}-S_{H,j\leftarrow •}.$$ (8)

2.2. Spillover analysis in frequency domain

In order to analyze the risk spillovers in different time horizons, Baruník and Křehlík (2018) further develop a frequency response function based on DY method (hereafter labelled as BK mehtod). By applying Fourier transformation on the impulse response M_i, we can get (f(ω))_j,k, which is the ratio of the spectrum of jth market at frequency ω (ω ∈ ( − π, π)) due to shocks in kth market, and the equation is shown as follows:

$${\left(f\left(\omega \right)\right)}_{j,k}\equiv \frac{{\sigma }_{kk}^{-1}{\left|{\left(M\left(e^{-i\omega }\right)\Sigma \right)}_{j,k}\right|}^2}{{\left(M\left(e^{-i\omega }\right)\Sigma M^{\prime }\left(e^{+i\omega }\right)\right)}_{j,j}}.$$ (9)

In order to apply the forecast error variance decomposition for different frequencies, (f(ω))_j,k needs to be weighted by the frequency share of variance of the jth market. The weighting function is defined as

$${\Gamma }_j\left(\omega \right)=\frac{{\left(M\left(e^{-i\omega }\right)\Sigma M^{\prime }\left(e^{+i\omega }\right)\right)}_{j,j}}{\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{\left(M\left(e^{-i\lambda }\right)\Sigma M^{\prime }\left(e^{+i\lambda }\right)\right)}_{j,j}d\lambda },$$ (10)

which indicates the power of jth market at a given frequency over the sum through frequencies in the frequency band ( − π, π). Therefore, the FEVD on the frequency band h = (a, b), a, b ∈ ( − π, π) and a < b  is

$${\left({\Theta }_h\right)}_{j,k}=\frac{1}{2\pi }{\int }_h{\Gamma }_j\left(\omega \right){\left(f\left(\omega \right)\right)}_{j,k}d\omega .$$ (11)

When h → ∞, (Θ_∞)_j,k is equal to (Θ_h)_j,k in time domain, Eq. (11) can be transformed as

$${\left({\Theta }_{\infty }\right)}_{j,k}=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{\Gamma }_j\left(\omega \right){\left(f\left(\omega \right)\right)}_{j,k}d\omega .$$ (12)

So the GFEVD on the frequency band h = (a, b), a, b ∈ ( − π, π) and a < b can be further standardized as

$${\left({\tilde{\Theta }}_h\right)}_{j,k}={\left({\Theta }_h\right)}_{j,k}/{\sum }_k{\left({\Theta }_{\infty }\right)}_{j,k}.$$ (13)

${\left({\tilde{\Theta }}_h\right)}_{j,k}$ measures the spillover from market k to market j in frequency band h. Then, the frequency spillover effect on the frequency band h can be defined as

$$C_h^F=100\left(\frac{{\Sigma }_{j\ne k}{\left({\tilde{\Theta }}_h\right)}_{j,k}}{{\left({\tilde{\Theta }}_h\right)}_{j,k}}-\frac{Tr\left({\tilde{\Theta }}_h\right)}{{\left({\tilde{\Theta }}_h\right)}_{j,k}}\right)=100\left(1-\frac{Tr\left({\tilde{\Theta }}_h\right)}{N}\right).$$ (14)

In a similar way, we can calculate the directional spillover and net spillover in the same way indicated in Eqs. (6)-(8).

3. Data

The 5-min realized volatilities (RV5) data in our analysis are obtained from Oxford-Man Institute of Quantitative Finance, which are also commonly used in recent researches (Liang et al., 2020b, 2019; Ma et al., 2018; Wei et al., 2020, Wei et al., 2021). The dataset spans from 24th January 2019 to 30th December 2020, with a total 326 daily observations. The dataset is divided equally into two parts by the date of 13th January 2020, when the first cross-border coronavirus transmission of infection was reported by the World Health Organization, and both pre- and post-epidemic sub-datasets have 163 observations. Table 1 exhibits some representative regions (classified by continents) with their respective stock exchanges and indices labels. The summation of market capitalization of these regions accounts for almost 70% global stock market value, and the chosen regions incorporates both developed and developing stock markets across the three continents.

Table 1.

Stock markets and corresponding stock indexes.

Continent	Region	RegionSymbol	Exchange Name	IndexSymbol	Index Name
Europe	England	UK	LSE Group	FTSE	FTSE 100
	Eurozone	EURO	Euronext	STOXX50E	EURO STOXX 50
	Norway	NOR	Euronext Oslo	OSEAX	Oslo Exchange All Share Index
	Germany	DEU	Deutsche Boerse AG	GDAXI	DAX
	Spain	ESP	BME Spanish Exchanges	IBEX	IBEX 35 Index
	Swiss	CHE	SIX Swiss Exchange	SSMI	Swiss Stock Market Index
Asia	Australia	AUS	ASX Australian Securities Exchange	AORD	All Ordinaries
	China	CHN	Shanghai Stock Exchange	SSEC	Shanghai Composite Index
	Hong Kong	HK	Hong Kong Exchanges and Clearing	HSI	HANG SENG Index
	India	IND	National Stock Exchange of India	NSEI	NIFTY 50
	Korea	KOR	Korea Exchange	KS11	Korea Composite Stock Price Index
	Japan	JPN	Japan Exchange Group	N225	Nikkei 225
America	Brazil	BRA	Brasil Bolsa Balcão	BVSP	BVSP BOVESPA Index
	Canada	CAN	TMX Group	GSPTSE	S&P/TSX Composite Index
	United States	US	New York Stock Exchange	SPX	S&P 500
	Mexico	MEX	Bolsa Mexicana de Valores	MXX	IPC Mexico

Notes: According to the World Federation of Exchange market capitalization, the summation capitalization of these sixteen stock markets accounts for almost 70% global stock market capitalization.

Table 2 presents the descriptive statistics of RV5 for all the stock indices. The results show that all the stock RV5 series are stationary, right-skewed, leptokurtic and non-normally distributed. The Q-statistics suggest significant autocorrelation within 5-, 10- and 20-day lags in these time series.

Table 2.

Descriptive Statistics.

Region	Market	Mean	Std. Dev.	Skewness	Kurtosis	Jarque-Bera	ADF	Q(5)	Q(10)	Q(20)
Europe	England	1.64E-04	4.81E-04	9.39	113.491	170,095.45***	−11.833***	293.23***	397.85***	425.072***
	Eurozone	1.59E-04	3.87E-04	6.324	48.983	30,798.549***	−7.752***	585.17***	757.50***	781.755***
	Norway	2.01E-04	1.14E-03	15.674	266.102	950,701.314***	−16.23***	42.20***	53.11***	54.419***
	Germany	1.16E-04	2.29E-04	5.470	37.124	17,388.94***	−6.374***	767.33***	1002.06***	1033.941***
	Spain	1.50E-04	3.35E-04	8.546	93.877	115,791.278***	−6.728***	416.56***	482.50***	487.059***
	Swiss	1.20E-04	4.32E-04	8.693	92.762	113,202.074***	−10.62***	390.62***	482.46***	493.388***
Asia	Australia	1.08E-04	3.28E-04	8.67	100.972	134,050.596***	−9.406***	400.51***	544.55***	560.272***
	China	7.70E-05	8.72E-05	3.469	18.976	4108.360***	−9.481***	260.57***	340.28***	376.466***
	Hong Kong	7.03E-05	1.43E-04	13.427	211.115	596,276.977***	−13.846***	75.94***	79.46***	80.874***
	India	1.36E-04	5.81E-04	13.007	197.692	522,461.149***	−13.23***	145.51***	166.81***	169.225***
	Korea	9.02E-05	2.01E-04	8.873	96.466	122,563.015***	−10.655***	387.17***	423.40***	426.621***
	Japan	7.79E-05	2.46E-04	11.72	172.191	395,079.245***	−11.515***	224.48***	289.76***	297.167***
America	Brazil	1.64E-04	4.10E-04	6.451	51.048	33,516.874***	−6.663***	568.33***	749.57***	818.095***
	Canada	7.92E-05	2.77E-04	8.645	97.608	125,256.361***	−9.933***	460.26***	589.49***	601.777***
	America	1.32E-04	3.88E-04	6.466	52.373	35,275.144***	−7.486***	585.60***	787.64***	805.063***
	Mexico	7.90E-05	9.53E-05	5.957	58.792	44,073.449***	−12.091***	272.71***	473.82***	603.242***

Notes: *, ** and *** denote rejections of the null hypothesis at the 10%, 5% and 1% significance levels, respectively. The Jarque-Bera statistic is used to test the null hypothesis of the normal distribution. Q(5), Q(10) and Q(20) are the Ljung-Box Q statistics with lag order of 5, 10 and 20, respectively. ADF refers to the statistics from the augmented Dickey-Fuller unit root tests. This table calculated based on the entire sample period span from 24 January 2019 to 30 December 2020.

4. Empirical results

In this section, we present estimation results from the DY and BK methods, based on both pre- and post-COVID-19 epidemic sub-samples, with a focus on the risk spillover in international stock markets and its changes in different time horizons during the COVID-19 pandemic.

4.1. International spillover effects in time domain

According to Akaike information criterion (Chen et al., 2020; Tao et al., 2018; Wei et al., 2010), we choose lag of 2 for pre-pandemic sub-sample and lag of 1 for post-pandemic sub-sample in the VAR estimations. Table 3 reports the results from the DY method.

Table 3.

International stock market spillovers estimated by DY method.

		Before pandemic				After pandemic
Overall spillover		64.7				88.2
	REGION	FROM	TO	NET		FROM	TO	NET
Europe	UK	3.99	4.36	0.367		5.42	6.36	0.945
	EURO	4.79	8.21	3.42		5.45	10.3	4.82
	NOR	4.06	2.51	−1.55		5.11	4.99	−0.122
	DEU	4.89	5.65	0.752		5.49	9.33	3.84
	ESP	4.21	2.73	−1.48		5.52	7.95	2.43
	CHE	4.85	6.61	1.76		5.44	8.17	2.73
Asia	AUS	4.76	1.62	−3.15		5.74	6.22	0.481
	CHN	2.91	2.06	−0.855		3.98	0.171	−3.81
	HK	4.06	3.57	−0.482		6.15	0.373	−5.78
	IND	2.56	1.37	−1.19		6.22	0.095	−6.12
	KOR	3.99	4.39	0.400		5.94	0.712	−5.22
	JPN	4.11	2.87	−1.24		6.02	2.79	−3.23
America	BRA	2.91	1.10	−1.81		5.61	5.89	0.285
	CAN	4.52	7.53	3.01		5.49	9.93	4.44
	US	4.69	6.78	2.10		5.47	9.79	4.32
	MEX	3.44	3.39	−0.050		5.14	5.14	−0.002

Notes: This table reports both on the pre- and post- COVID-19 sub-samples stock markets’ risk spillover based on DY method. The ‘FROM’ column provides directional spillover from all others to market j. The ‘TO’ column provides directional spillover to all others from market k. The ‘Overall spillover’ is the sum of directional spillover. The bold figure highlights the biggest risk contributor or transmitter, and underlined figure indicate the biggest risk receiver.

Table 3 presents several interesting results. Firstly, the overall stock markets’ risk spillover effect leaps from 64.7% to 88.2% after the outbreak of COVID-19 pandemic. This significant increase indicates that international stock markets is more integrated and risk contagion is easier to transfer among different markets. Secondly, from the ‘TO’ column, we find that the outbreak of COVID-19 enhances the risk spillover of European and American regions but reduces those of most Asian regions. Before the COVID-19 pandemic, the Eurozone, US, Canada, Swiss and Germany, are major contributors of risk spillover with almost 34.8% share (sum of the ‘TO’ column values in these regions). After the pandemic, the contribution share of these regions increases to 47.5%. On the contrary, the total spillover share of all Asian regions except for Australia decreases from 15.9% before pandemic to 10.4% after that. In terms of risk spillover received from others (the ‘FROM’ column results), the situations are similar among the regions. All the stock markets receive more risk spillovers from others comparing to the cases before the pandemic. In specific, India is the most affected country as it receives the largest proportion of spillover among all regions. Thirdly, the ‘NET’ column of Table 3 exhibits that Eurozone is the biggest net risk transmitter in both pre- and post- pandemic periods with transmission shares of 3.42% and 4.82%, respectively. While, Asian regions, especially India and Hong Kong, are major net risk receivers. The biggest net risk receiver changes from Australia with 3.15% to India and Hong Kong with 6.12% and 5.78%, respectively after the pandemic. Other Asian countries, such as China and Korea, also receive more risk spillover shares than before.

4.2. International spillover effects in frequency domain

For policy makers, international investors and speculators, they are more likely interested in the risk contagion effects in different time horizons(Liu et al., 2020; Zhang et al., 2019). To investigate the spillover changes in different time frequencies, we extend our analysis further by using BK method. Tables 4 , 5 , 6 exhibit risk spillover estimates in a framework of frequency domains.

Table 4.

Short term stock markets spillover (Weekly).

		Before epidemic				After epidemic
Overall spillover		27.6				39.3
	REGION	FROM	TO	NET		FROM	TO	NET
Europe	UK	1.27	0.66	−0.62		1.63	3.84	2.21
	EURO	1.25	7.20	5.95		1.08	3.73	2.65
	NOR	2.04	0.77	−1.27		2.94	7.77	4.83
	DEU	1.35	3.41	2.06		2.14	1.85	−0.290
	ESP	2.72	0.45	−2.27		2.57	0.426	−2.14
	CHE	1.08	2.87	1.79		1.04	10.2	9.21
Asia	AUS	4.07	0.901	−3.17		3.05	0.140	−2.91
	CHN	0.787	0.699	−0.088		2.49	0.032	−2.46
	HK	1.77	2.00	0.236		3.81	0.143	−3.68
	IND	1.31	0.185	−1.12		3.32	0.060	−3.26
	KOR	2.25	1.57	−0.675		3.63	0.380	−3.25
	JPN	2.24	0.962	−1.28		2.90	0.270	−2.63
America	BRA	1.31	0.850	−0.461		1.99	1.36	−0.631
	CAN	1.59	2.97	1.38		1.92	6.33	4.41
	US	1.30	1.33	0.032		1.99	2.38	0.389
	MEX	1.28	0.781	−0.498		2.75	0.314	−2.44

Notes: This table reports both on pre- and post- epidemic sub-samples stock markets’ risk connectedness based on BK method. The ‘FROM’ column provides directional connectedness or spillover from all others markets to markets j. The ‘TO’ column provides directional spillover to all others markets from market k. The overall spillover is the sum of directional spillover. The bold figures highlight the biggest risk contributor or transmitter, and underlined figures indicate the biggest risk receiver.

Table 5.

Medium term stock markets spillover (Monthly).

		Before epidemic				After epidemic
Overall spillover		11.4				22.7
	REGION	FROM	TO	NET		FROM	TO	NET
Europe	UK	0.748	0.317	−0.432		0.972	5.94	4.97
	EURO	0.770	1.19	0.424		1.70	2.27	0.569
	NOR	0.974	0.083	−0.892		1.02	1.19	0.169
	DEU	0.850	0.917	0.067		1.71	0.901	−0.808
	ESP	0.553	0.146	−0.407		1.88	0.137	−1.75
	CHE	0.685	1.77	1.08		0.931	5.52	4.59
Asia	AUS	0.731	0.197	−0.534		1.45	0.155	−1.29
	CHN	0.649	0.533	−0.116		1.43	0.075	−1.36
	HK	0.420	0.696	0.276		1.43	0.117	−1.31
	IND	0.375	0.080	−0.295		1.46	0.049	−1.41
	KOR	0.905	1.40	0.490		1.10	0.577	−0.523
	JPN	0.692	0.678	−0.014		1.55	0.173	−1.38
America	BRA	1.04	0.372	−0.666		1.58	1.86	0.283
	CAN	0.724	1.94	1.22		1.55	1.83	0.280
	US	0.863	0.614	−0.249		1.65	1.69	0.040
	MEX	0.410	0.459	0.048		1.29	0.211	−1.07

Notes: This table reports both on pre- and post- epidemic sub-samples stock markets’ risk connectedness based on BK method. The ‘FROM’ column provides directional connectedness or spillover from all others markets to markets j. The ‘TO’ column provides directional spillover to all others markets from market k. The overall spillover is the sum of directional spillover. The bold figures highlight the biggest risk contributor or transmitter, and underlined figures indicate the biggest risk receiver.

Table 6.

Long-term stock markets spillover (Longer than one month).

		Before epidemic				After epidemic
Overall spillover		7.09				23.2
	REGION	FROM	TO	NET		FROM	TO	NET
Europe	UK	0.434	0.215	−0.219		1.14	7.42	6.29
	EURO	0.532	0.505	−0.027		2.12	1.87	−0.246
	NOR	0.637	0.026	−0.611		0.713	0.928	0.215
	DEU	0.595	0.365	−0.230		2.02	1.07	−0.946
	ESP	0.327	0.071	−0.257		1.62	0.083	−1.54
	CHE	0.475	1.22	0.748		1.12	5.66	4.55
Asia	AUS	0.282	0.102	−0.180		1.56	0.193	−1.36
	CHN	0.673	0.538	−0.134		0.771	0.095	−0.675
	HK	0.237	0.619	0.382		0.913	0.069	−0.844
	IND	0.226	0.058	−0.168		1.42	0.053	−1.37
	KOR	0.450	1.09	0.644		1.21	0.688	−0.523
	JPN	0.395	0.341	−0.054		1.64	0.181	−1.46
America	BRA	0.676	0.192	−0.484		1.86	2.20	0.340
	CAN	0.412	1.25	0.843		1.97	0.675	−1.29
	US	0.544	0.258	−0.286		1.94	1.82	−0.121
	MEX	0.197	0.232	0.035		1.17	0.154	−1.02

Notes: This table reports both on pre- and post- epidemic sub-samples stock markets’ risk connectedness based on BK method. The ‘FROM’ column provides directional connectedness or spillover from all others markets to markets j. The ‘TO’ column provides directional spillover to all others markets from market k. The overall spillover is the sum of directional spillover. The bold figures highlight the biggest risk contributor or transmitter, and underlined figures indicate the biggest risk receiver.

We find that the results from BK method are consistent with those from DY method. On the one hand, the overall spillover effects among international stock markets increase significantly for all time frequencies after the pandemic. The total spillover effects increase sharply from 27.6% to 39.2% in short-term, 11.4% to 22.7% in medium-term and 7.09% to 23.2% in long-term. These results reveal that the COVID-19 pandemic has deep impacts on stock markets worldwide, and these influences of the pandemic may last for months or even years. On the other hand, similar to the DY results, we also find that the total spillover share from Asian countries falls quickly after the COVID-19 pandemic in all time frequencies.

At short term frequency, Swiss and Norway replace the Eurozone and become the top two risk contributors in the post-COVID-19 period with a spillover shares of 10.2% and 7.77%, respectively. While the major risk receivers are still in Asian regions, such as Hong Kong and Korea. However, the situation has changed in the medium- and long-term cases. At medium- and long-term frequencies, Canada is the dominant risk contributor and Brazil is the biggest risk receiver before the COVID-19 pandemic. After the pandemic, UK turns to the largest risk contributor, and the Eurozone, Germany, Canada and the US become the major four risk receivers. Moreover, the ‘NET’ results show that the largest net risk transmitter is Swiss with 9.21% spillover share after the pandemic at short-term frequency. While UK becomes the biggest net risk transmitter over the medium-term and long-term horizons, which is in line with the finding of ‘TO’ results of Tables 4, 5, 6. Asian countries are still the main net risk receivers for all time frequencies, further confirming the results from DY method in Section 4.1. In addition, the change of regions’ transmission direction is irregular for these regions (signs of ‘NET’ column values are not fixed), indicating that the net risk spillover transmitters and receivers are unexpected, and the impacts of the COVID-19 pandemic on risk spillovers in international stock markets change rapidly.

4.3. Dynamic spillover effects in time and frequency domains

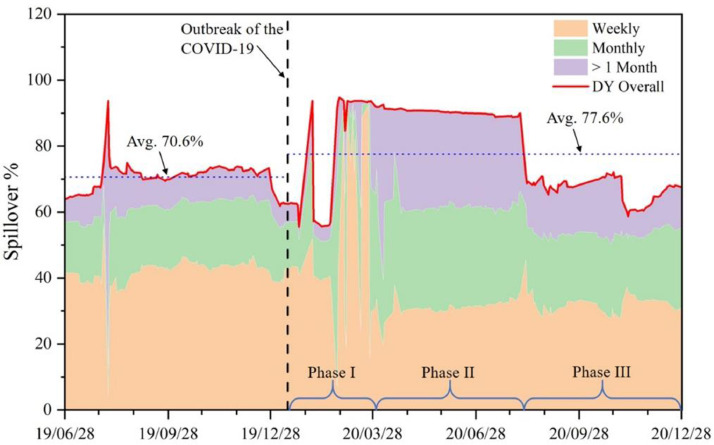
The analyses on pre- and post-pandemic sub-samples in Section 4.1 and 4.2 only offer us the static pictures for risk spillovers in international stock market. In this section, we further investigate the dynamic spillover effects by using a rolling-window estimation method (Li et al., 2020; Liu et al., 2020; Wei et al., 2017). We choose several different window sizes and expand the pre-pandemic sub-sample in the estimation processes for robustness check, and find that these results are similar to those reported in previous examinations. To save place, we present the results of robustness checks in the Appendices. Fig. 1 only reports the dynamic results of the overall spillovers with a rolling-window size of 70 days in both time and frequency domains across all the sixteen markets.

Fig. 1.

Dynamic overall spillover based on rolling-window size of 70 days.

In terms of time domain results by DY method, Fig. 1 indicates that the average overall spillover index measured rises from 70.6% before the pandemic to 77.6% after that, indicating the enhancement in risk contagion among the international stock markets. With regarding to frequency domain outcomes by BK approach, we can see that the risk spillover after the pandemic may be roughly divided into three phases: I) Between 13th January and the end of March 2020, weekly and monthly risk spillovers occupy a large proportion of the DY overall spillover index, implying that the COVID-19 impacts are primarily responded in the short- and mid-term stock market spillovers. II) From April to July 2020, the long-term spillover index increases more sharply than others. However, the mid-term spillover comes the second, and the short-term spillover falls. III) After July 2020, both the DY overall spillover and the BK spillovers in different frequencies almost drop back to pre-pandemic level. These findings reflect the time-varying fluctuations in the risk spillover across international stock markets, and the impacts induced by the pandemic on international stock markets may last for about 6 to 8 months. For international investors and speculators, they should realize how their portfolio's risk is altered and timely manage their portfolio risk. Policy makers can also improve regulation decisions in preventing larger risk contagion and maintaining financial market stability according to these dynamic spillovers.

5. Conclusions

This paper investigates risk contagion among sixteen major stock markets across three continents, and compares the spillover effects before and after the outbreak of COVID-19 pandemic in both time and frequency domains. The major empirical results show that, firstly, after the burst of COVID-19 pandemic at the beginning of 2020, the integration of international stock markets enhances greatly and the market risk contagion among them also increases significantly. Therefore, in order to maintain international stock markets stability, policy makers should focus on the risk spillovers directions and make timely policies to prevent the spread of risks across borders. Secondly, the pandemic-induced shocks in international stock markets may last for 6–8 months and come through three phases. In severe phases I) and II) of the epidemic, stock market regulators should strengthen supervision measures, and improve market accountability and transparency. In phase III), the epidemic-induced risks would be incorporated in stock prices, therefore, market supervisors can gradually relax the epidemic response restrictions. Additionally, the results indicate that the epidemic strengthens the spillover contributions of European and American markets but reduces those in most Asian markets. For international investors and portfolio managers, their portfolio risks may be heavily influenced by the pandemic. Thus, they are suggested to hedge the portfolio risks by increasing the investment weights in Asian stock markets and actively managing their portfolios during the pandemic.

Declaration of interest statement

Yuntong Liu, Yu Wei, Qian Wang, and Yi Liu declare no conflicts of interest in this manuscript.

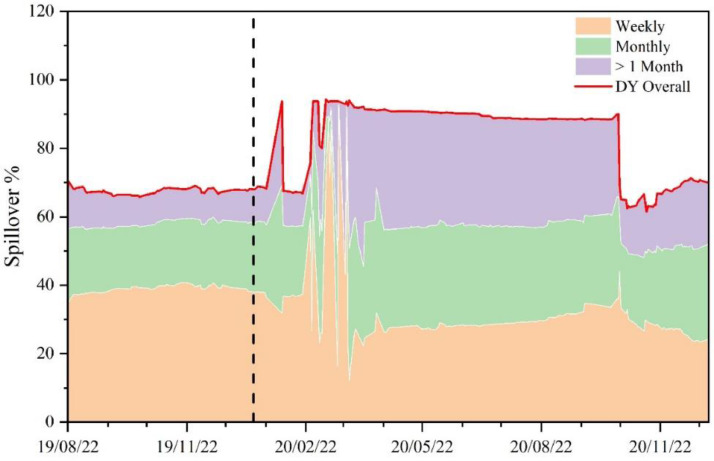
Appendix

Fig. A1, A2, A3

Fig. A1.

Dynamic overall spillover based on rolling-window size of 100 days.

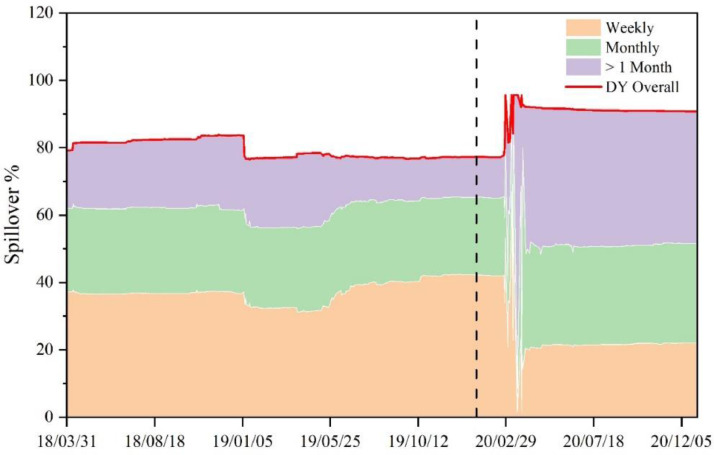
Fig. A2.

Dynamic overall spillover based on rolling-window size of 130 days.

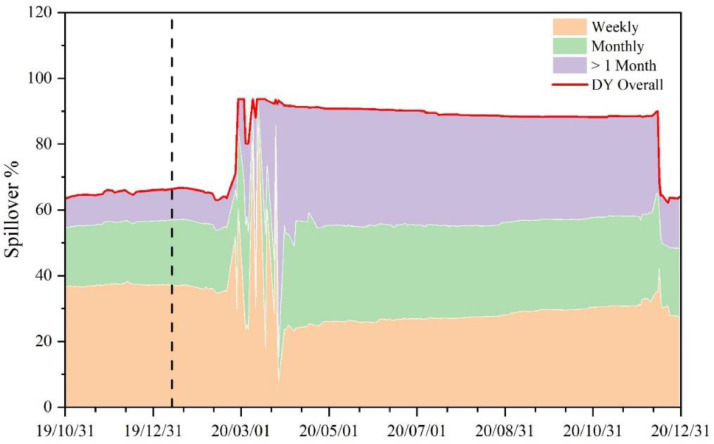
Fig. A3.

Dynamic overall spillover based on rolling-window size of 550 days.