Extrinsic control and intrinsic computation in the hippocampal CA1 circuit

SUMMARY

In understanding circuit operations, a key problem is the extent to which neuronal spiking reflects local computation or responses to upstream inputs. We addressed this issue in the hippocampus by performing combined optogenetic and pharmacogenetic local and upstream inactivation. Silencing the medial entorhinal (mEC) largely abolished extracellular theta and gamma currents in CA1, while only moderately affecting firing rates. In contrast, CA3 and local CA1 silencing strongly decreased firing of CA1 neurons without affecting theta currents. Each perturbation reconfigured the CA1 spatial map. Yet, the ability of the CA1 circuit to support place field activity persisted, maintaining the same fraction of spatially tuned place fields, and reliable assembly expression as in the intact mouse. Thus, the CA1 network can induce and maintain coordinated cell assemblies with minimal reliance on its inputs, yet these inputs can effectively reconfigure and assist in maintaining stability of the CA1 map.

Graphical Abstract

eTOC BLURB

Zutshi et al. perform simultaneous silencing of major afferents into hippocampal CA1 to address whether CA1 spiking can be sustained by local computations. These manipulations reveal that coordinated CA1 place cell assemblies persist with minimal input, but that each input has distinct effects on spatial tuning and field potentials.

INTRODUCTION

In contrast to the modularly organized neocortex, the vast majority of synaptic connections in the hippocampus are supplied from its own neurons, most notably by the extensive collaterals of the CA3 pyramidal neurons (Witter, 2007). Its most important extrinsic afferents arrive from the entorhinal cortex and other retrohippocampal and thalamic structures, supplemented by subcortical inputs (Amaral and Lavenex, 2007). The entorhinal inputs provide communication with the rest of the neocortex and the outside world, whereas the subcortical neuromodulators toggle the hippocampal physiological dynamic between two fundamental computational modes: an interactive mode, characterized by theta oscillations (5-9 Hz) and an intrinsic, self-organized sharp wave ripple mode. Interfering with theta oscillations, typically brought about by manipulating the septal ‘pacemaker’ results in behavioral impairments comparable with surgical damage of the hippocampus (Winson, 1978). During explorative behavior and learning, theta oscillations organize the temporal structure of neurons, as amply illustrated by the relationship between the spatial position of the animal and the phase of the theta waves at which place cells spike ("phase precession"; O’Keefe and Recce, 1993) and by the relationship between the distances of place fields and the theta phase offsets of place field spikes (Dragoi and Buzsáki, 2006). Several previous studies have been devoted to understand the relationship between behavior on the one hand and the contribution of mesoscopic theta waves and the spiking activity of neurons on the other. A key question that remains is to what extent hippocampal neuronal activity reflects intrinsic local computation as opposed to “inheritance” from upstream inputs (Mizuseki et al., 2009). This is a particularly relevant question in the CA1 region, in which connections between the pyramidal neurons are very sparse (Amaral and Lavenex, 2007; Bezaire and Soltesz, 2013; Deuchars and Thomson, 1996)

Early studies used lesions and pharmacological inactivation of various structures to evaluate the relative contribution of the intrinsic versus extrinsic afferents on physiology and behavior. Damaging CA3 neurons (Brun et al., 2002), their chemogenetic silencing (Keinath et al., 2020) or suppressing their spiking by inhibiting the septum yielded only minor changes in CA1 place responses (Mizumori et al., 1989). Selectively blocking vesicle release at CA3 terminals by a molecular approach did not affect firing rates but altered place field sizes (Middleton and McHugh, 2016; Nakashiba et al., 2008, 2009). In contrast, local optogenetic silencing of CA3 to CA1 afferents decreased both the firing rate and spatial properties of CA1 place cells (Davoudi and Foster, 2019). Yet, in a related optogenetic silencing study, an increase in CA1 firing rates was reported, accompanied by a decrease in theta-modulated slow gamma oscillation (El-Gaby et al., 2021).

The discovery of grid cells in the dorso-medial entorhinal cortex (mEC; (Hafting et al., 2005)) boosted the investigation of the impact of mEC on hippocampal physiology. Large lesions of the entorhinal cortex, including the medial and lateral parts, reduced theta/gamma oscillations (Bragin et al., 1995; Kamondi et al., 1998; Ormond et al., 2015; Schlesiger et al., 2015), decreased the fraction of hippocampal CA1 place cells and affected various features of place field properties (Brun et al., 2008; Chenani et al., 2019; Hales et al., 2014; Miller and Best, 1980; Ormond et al., 2015; Sabariego et al., 2019; Schlesiger et al., 2015, 2018). More recent studies used optogenetic and pharmacogenetic techniques to readdress the role of the entorhinal inputs on hippocampal circuits. Optogenetic suppression of entorhinal inputs, by either directly suppressing the spiking activity of superficial layer neurons or activating the inhibitory neuronal population, affected the temporal properties of neuronal spiking, induced partial or major remapping of place representation in the hippocampus, although often without major disruption of the spatial firing properties of individual neurons (Fernández-Ruiz et al., 2021; Miao et al., 2015; Rueckemann et al., 2016), leading to the suggestion that mEC is responsible for remapping of hippocampal place cells (Latuske et al., 2018; Miao et al., 2015) but see (Schlesiger et al., 2018). In contrast, another study (Robinson et al., 2017) reported that mEC inactivation produced a deficit in temporal coding in CA1 neurons, associated with impairment in memory across a temporal delay, while spatial and object coding remained intact. Spike suppression of mEC neurons by pharmacogenetic perturbation induced remapping in CA3 (Miao et al., 2015). Relatively selective excitation, but not inhibition, of layer 2 mEC neurons by pharmacogenetic means was sufficient to induce partial remapping and affect the spatial firing correlates of CA1 pyramidal neurons (Kanter et al., 2017).

Despite the intense and careful work in this research area, the magnitudes and types of the reported physiological and spatial correlation impairments, and the interpretations of the mechanisms of the experimental interventions vary widely across experiments. At least part of the existing variability and conflicts is due to the different behavioral paradigms, designs and evaluation methods used by different investigators. Simultaneous manipulations in the same animal or even separate manipulations of the different inputs to the hippocampal circuits in the same experiment are rare (Fernández-Ruiz et al., 2021). Most studies focusing on spiking activity of neurons used recordings from the cell body layers, precluding the evaluation of layer-specific effects of the applied perturbations. Conversely, experiments dedicated to studying mesoscopic network effects, lacked single neuron resolution to address the importance of neuron-circuit interactions. Therefore, the goals of our experiments were to examine and compare the contribution of local hippocampal circuits and major inputs on the temporal organization of neurons at the mesoscopic and microscopic scales by selective targeted perturbations and to relate the observed network changes to the ensuing spatial “representations” (inheritance vs local induction) of CA1 hippocampal neurons. Each manipulation was performed in the same hippocampus-dependent spatial alternation paradigm (Ainge et al., 2007) and during rest/sleep, allowing head-to-head comparison of the consequences of separate and combined interventions. To achieve these goals, we used combinations of optogenetic silencing of unilateral and bilateral mEC and local CA1 region and bilateral pharmacogenetic silencing of the entire CA3 region, combined with high spatial resolution recording of local field potentials (LFP) in the CA1-dentate axis and simultaneously collecting firing pattern data from thousands of single neurons. Our study revealed a much higher input-independent computation in the CA1 region than predicted by previous studies.

RESULTS

Transient functional deafferentation of the hippocampus

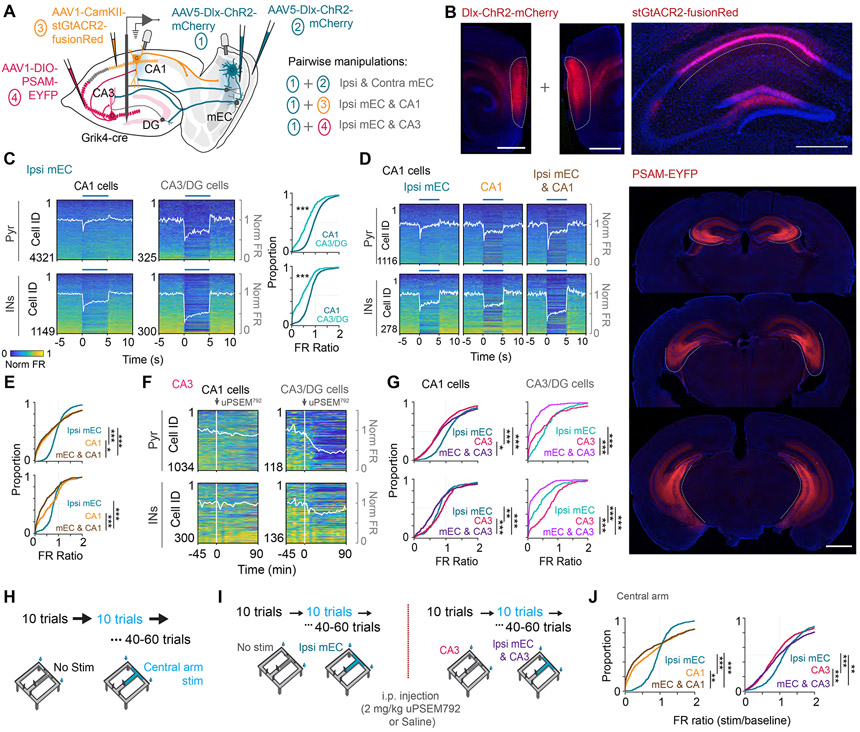
To quantitatively assess the physiological contribution of the various inputs to the CA1 circuit, we used a combination of optogenetic and pharmacogenetic manipulations. These transient manipulations (“functional deafferentation”) allowed us to compare the impact of specific inputs on both LFP and spiking of the same neuronal populations within the same animal and session. To silence the medial entorhinal cortex (mEC), we infected all types of GABAergic interneurons by AAV5-mDlx-ChR2- mCherry virus in one or both hemispheres (n = 18 and n = 3 mice, respectively; Figure 1A). The virus evenly infected large populations of interneurons throughout the dorsal and mid parts of the superficial layers of mEC, as well as interneurons within the deep layers(Figures 1B; S1A; (Fernández-Ruiz et al., 2021). To address the contribution of local circuit computations, CA1 pyramidal neurons were infected with a virus expressing the inhibitory opsin stGtACR2-fusionRed (Mahn et al., 2018) under the control of a CamKII promoter. The virus labeled almost the entire CA2-subicular axis of the CA1 region, confined to the dorsal hippocampus (Figures 1B; S1E-G), with occasional labeling of dentate gyrus neurons. Because CA3 pyramidal neurons contribute both widely divergent afferents to CA1 neurons bilaterally (Li et al., 1994) and because our mEC silencing also affected the CA3/DG region, we chose bilateral pharmacogenetic suppression to examine their control of the CA1 circuit. PSAM⁴-GlyR (Pharmacologically Selective Actuator Modules) was used as a neuronal silencer, with uPSEM792 as the agonist (Magnus et al., 2019). PSAM-EYFP expression was homogeneous throughout the septotemporal axis of the CA3 region, with sparse labeling of granule cells (Figures 1B; S1E-G).

Figure 1. Transient functional deafferentation of CA1 region by optogenetic and pharmacogenetic manipulations.

(A) Schematic for the approach used for pairwise silencing of mEC, CA3 and local CA1 pyramidal cells. AAV-Dlx-ChR2 was bilaterally or unilaterally injected into the mEC to express ChR2 in all inhibitory interneuron types and optic fibers were implanted bilaterally, or unilaterally over the mEC. For CA3 silencing, AAV-DIO-PSAM was injected bilaterally along the entire dorso-ventral CA3 axis of Grik4-cre mice, which express Cre in CA3 and DG neurons. For local CA1 inhibition, AAV-CamKII-stGtACR2 was injected unilaterally into CA1, and an optic fiber was implanted over CA1. A single or multiple-shank silicone probe was implanted into the hippocampus. (B) Representative histology for each of the described manipulations. Left, sagittal sections showing virus expression labeling interneurons with ChR2 across all layers of the mEC. Right, coronal section showing spread of stGtACR2 largely restricted to CA1. Bottom, Coronal sections with bilateral expression of PSAM along the entire extent of CA3. (C) Left, Firing rate changes of pyramidal cells and putative interneurons in CA1 and CA3/DG regions in response to 5-s long optogenetic inhibition of the ipsilateral mEC in the home cage (Blue bar). Each row of the heatmap is a cell normalized by its peak firing rate. White trace, average population firing rate. Right, CDF plots comparing the firing rate ratio between stimulation and baseline epochs for CA1 and CA3/DG pyramidal cells (top, Wilcoxon rank sum test, Z=12.92, p < 0.001) and interneurons (bottom, Wilcoxon rank sum test, Z = 12.27, p<0.001). (D) Plots as described in C, but for cells recorded from CA1 in response to ipsilateral mEC, CA1, and combined ipsi mEC and CA1 silencing. (E) CDF plots showing effective inhibition of pyramidal cells by the CA1 manipulation (top, Friedman test followed by Tukey-Kramer posthoc tests, Chi-square(2,2236) = 96.79, p<0.001) and interneurons by combined ipsi mEC and CA1 silencing (bottom, Chi-square(2,554) = 88.46, p<0.001). (F) Firing rate responses of CA1 and CA3/DG pyramidal cells and interneurons before and after injection of μPSEM⁷⁹². White trace, average population firing rate. (G) Cumulative density function plots showing the firing rate changes after ipsi mEC, CA3 and combined ipsi mEC and CA3 silencing for CA1 and CA3/DG pyramidal cells (Friedman test followed by Tukey-Kramer posthoc tests, CA1: top-left, Chi-square(2,2146) = 152.73, p<0.001, CA3/DG: top-right, Chi-square(2,306) = 155.77, p<0.001) and interneurons (CA1: bottom-left, Chi-square(2,604) = 63.29, p<0.001, CA3/DG: bottom-right, Chi-square(2,348) = 139.70, p<0.001). (H) Recordings were also performed as the mice ran on a delayed spatial alternation task (10s delay). Optogenetic stimulation was performed in blocks of 10 trials, interleaved with 10-trial blocks of no stimulation, restricted to the central arm of the maze (region highlighted in blue). (I) The mice used for CA3 silencing were first run on a morning session with ipsilateral mEC silencing on the central arm, followed by an i.p.. injection of either μPSEM792 or saline. They were subsequently run on a second session with ipsilateral mEC silencing targeted to the central arm, but now with simultaneous pharmacogenetic CA3 manipulation. (J) Left, CDF plot of firing rate ratios of CA1 pyramidal cells during CA1 and ipsi mEC manipulation in the central arm of the maze revealed similar effects as that observed in the home cage (Kruskal wallis test followed by Tukey-Kramer posthoc tests, n[ipsi mEC, CA1, ipsi mEC & CA1] = 617, 899, 640 cells from 5 mice, Chi-square(2,2153) = 77.66, p<0.001). Right, CDF plot of firing rate ratios during CA3 and ipsi mEC manipulation on the central arm of the maze (Kruskal wallis test followed by Tukey-Kramer posthoc tests, n[ipsi mEC, CA1, ipsi mEC & CA1] = 1082, 1085, 1086 cells from 6 mice, Chi-square(2,3250) = 65.02, p<0.001). *p<0.05, **p<0.01, ***p<0.001. See also Figures S1 and S2.

Before examining the impact of the various functional deafferentation of hippocampal LFP, we assessed their effects on the firing rates of hippocampal neurons first in the home cage during rest/sleep (including periods of quiet wake, NREM and REM sleep), and then during maze behavior. Unilateral optogenetic stimulation of inhibitory interneurons in mEC (5-s pulses on, 25-s off) exerted a large effect on DG/CA3 neurons but, unexpectedly only a small effect on the firing rate of the CA1 pyramidal neuron population (a stronger effect though on CA1 interneurons; Figure 1C). The magnitude of the effect on the mean population firing rate depended on the light intensity delivered to mEC (Figure S1B). Optogenetic suppression of CA1 pyramidal neurons brought about a stronger reduction of firing rates of both CA1 pyramidal cells and interneurons (Figure 1D, 1E, S1C). As expected, PSAM⁴-GlyR activation suppressed CA3 and dentate excitatory cells and dis-facilitated interneurons, and removal of the bilateral physiological excitation by CA3 neurons decreased CA1 firing rates (Figures 1F, G, S1D). Combined perturbation of mEC and CA1 regions and mEC and CA3/DG regions brought about a larger decrease of CA1 neuron firing rates than the respective single region manipulations (Figures 1E, G). Bilateral stimulation of mEC also had a larger effect on firing rates than unilateral stimulation (Figure S2B). These firing rate changes were not observed in control sessions where the mice were injected with the vehicle instead of the agonist uPSEM792 (Figure S3A).

Optogenetic stimulation during maze performance was restricted to the central arm of the maze (including a small section of the maze after the animal makes a turn) and was triggered by the opening of the delay area gate and terminated by the mouse’s crossing the photobeam in front of the water port. (Figure 1H). Blocks of control and stimulated trials (10 trials per block) alternated until the mouse ran 50 to 60 trials in a session. LFP and unit firing in the (non-stimulated) side arms served as additional controls. For sessions with CA3/DG silencing, the first session with ipsilateral mEC silencing was followed by a second, identical session after i.p. injection of the agonist or vehicle (Figure 1I). Optogenetic and pharmacogenetic manipulations on the maze induced qualitatively similar firing rate changes as those observed in the home cage (Figure 1J, S6B).

Anchoring mesoscopic patterns to anatomical landmarks

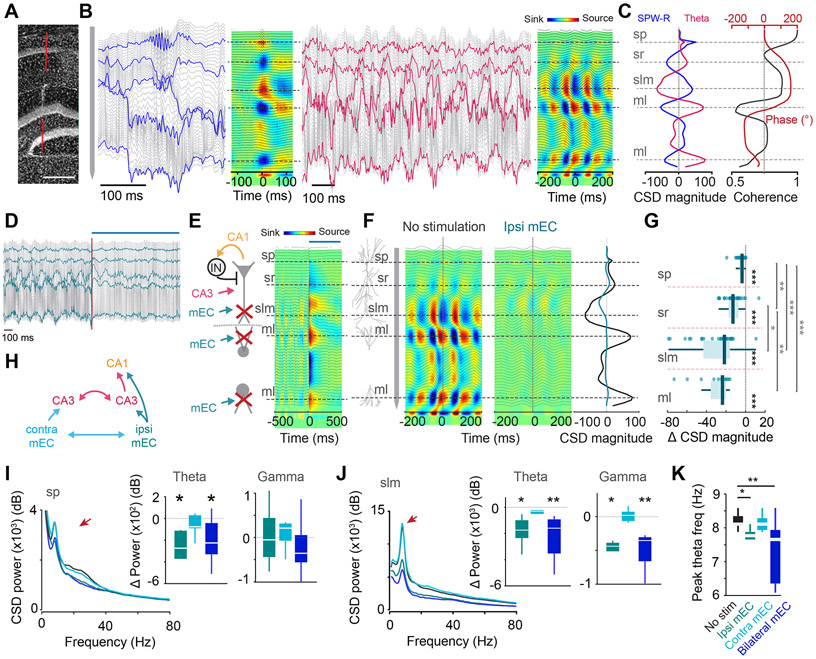
Mice were implanted with 64-site linear silicon probes (single shank or double shank) or a 5-shank probe (for many-neuron recordings; STAR Methods) in the dorsal hippocampus. The local field potential (LFP) traces were converted to current source density (CSD) maps to relate the domain-specific transmembrane potentials of pyramidal neurons brought about by the afferent activity to layer-specific extracellular current flow (Brankačk et al., 1993; Buzsáki et al., 1986; Fernández-Ruiz et al., 2021; Mitzdorf, 1985). The characteristic depth distribution of CSD and unit firing was used to identify three physiological patterns that reliably anchored the recording sites to CA1, CA3 and DG sublayers across animals. In unstained histological sections (Figure 2A), the distance between the mid-pyramidal layer and the hippocampal fissure along the silicon probe track was measured and related to the recording sites. The recording site with the largest amplitude sharp wave ripple (SPW-R) marked the middle of the CA1 pyramidal layer. This site also corresponded to the largest magnitude of the sharp wave source and the largest density of discriminated spikes (Mizuseki et al., 2011; Valero et al., 2017). In turn, the sink of the sharp wave marked the middle of the str. radiatum. The prominent sink during walking-related theta oscillations served as the third physiological marker and identified the str. lacunosum-moleculare (sLM; Figure 2B; (Buzsáki, 2002)). An additional large theta sink, phase reversed with the one in sLM, was used to identify the mid-molecular layer of the dentate gyrus in mice with more medial probe implantation (Figure 2A). These landmarks were highly consistent across mice, allowing for group analyses (Figure S1E-G). Theta waves were highly coherent within and across layers and regions, with a gradual phase shift of theta waves starting below the CA1 pyramidal layer, reaching 180° in sLM and continuing to approximately 90°/270° in the dentate hilus (Figure 2C; (Brankačk et al., 1993; Buzsáki et al., 1986)).

Figure 2. Ipsilateral mEC silencing led to a profound decrease in CA1 CSD power.

(A) Track of the 64-site linear silicone probe spanning across the hippocampus. (B) LFP traces recorded across all channels. Left, Example LFP traces and the resultant CSD map during a CA1 SPW-R. Horizontal dashed lines correspond to str. pyramidale (sp), radiatum (sr), lacunosum-moleculare (slm) and molecular layers (ml) of the inner and outer dentate blades. Right, Example theta waves and the resultant CSD map during maze running. (C) Left trace, CSD depth profile during SPW-Rs (blue) and theta oscillations (pink) show opposing sinks and sources. Right trace, Theta band coherence magnitude (black) and phase (red) of LFP as a function of depth along the CA1-DG axis. (D) 2s-long LFP traces during ipsi mEC silencing. Red line and blue bar indicates onset of stimulation. Blue highlighted traces indicate sp, sr, slm and ml channels respectively. (E) Left, schematic highlighting expected effects of mEC silencing along the CA1-DG axis. Red X, reduced inputs. Right, LFP traces, black and CSD map in response optogenetic silencing of the ipsilateral mEC, showing prominent sources at the mEC terminal zones due to disfaciliation. Blue bar on top indicates optogenetic stimulation. (F) Reduction of theta sinks and sources pairs along the CA1-DG axis during ipsilateral mEC silencing. Right, CSD plot at time zero. Black, control; blue, mEC silencing. (G) Theta CSD magnitude decreased across all hippocampal layers, with the greatest reduction in slm and ml (each dot represents one session from one animal, n = 32 sessions across 13 mice, Within layer:, Wilcoxon signed rank test against 0, all p <0.001, Across layers: Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square(3,105) = 56.81, p < 0.001). (H) Schematic depicting potential pathways affected by contralateral versus ipsilateral mEC manipulation. (I, J) Left, Average power spectra of CSD across all mice upon ipsi, contra, and bilateral mEC stimulation shows a decrease in theta and gamma CSD power in CA1 pyramidal layer (sp; I), and str. lacunosum-moleculare (slm; J). Red arrows, theta peak. Right, Change in theta (6-12 Hz) and gamma (25-90 Hz) CSD power for each manipulation compared to baseline in sp and slm (n[Ipsi, contra, bilateral mEC] = 6, 7 and 9 sessions from 3 mice, Wilcoxon two sided signed rank test against 0. sp: Theta, p = 0.03, 0.47, 0.02 respectively, Gamma, p = 1, 0.37, 0.36 respectively. slm: Theta, p = 0.03, 0.22, 0.004 respectively, Gamma, p = 0.03, 0.81, 0.004 respectively). Color legend as in H. (K) Ipsi and bilateral but not contra mEC silencing led a decrease in theta frequency (n = 7-9 sessions across 3 mice, Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square(3,40) = 14.45, p = 0.0024). *p<0.05, **p<0.01, ***p<0.001. All box plots show median ± interquartile; whiskers show range excluding outliers. See also Figures S2, S4.

Optogenetic suppression of the entorhinal cortex reduces hippocampal theta oscillations

To maintain comparable behavioral states across manipulations, the effects of all optogenetic and pharmacogenetic silencing were tested specifically in the central arm, while mice performed the memory task in the maze (Figure 2D-K). Optogenetic pulse onset in mEC, triggered by opening of the start area door, induced prominent current sources (representing a removal of excitation) in CA1 sLM and the mid-molecular layer of the dentate gyrus (Figure 2E). In contrast to the relatively small effect of mEC silencing on the spiking activity of CA1 pyramidal cells, theta currents, as measured during the entire stimulation period, were dramatically reduced in both CA1 and dentate gyrus (Figures 2D, F; Movie S1) and the reduced sink maximum in sLM shifted upward significantly (Figure S2D). The largest changes were present in the dentate molecular layer and sLM followed by str. radiatum, and a minor decrease of theta current was also observed in the CA1 pyramidal layer (Figures 2G). The magnitude of theta suppression varied with the strength of light power delivered to mEC (Figure S1B).

Optogenetic suppression of the contralateral mEC output induced a negligible effect on the power of theta oscillations and the effect of concurrent ipsilateral and contralateral stimulation was largely additive (Figures 2H-K; S2G). In addition to theta, the power in the gamma frequency band was also reduced (Figures 2I-J). Ipsilateral, but not contralateral suppression of mEC also reduced the frequency of theta oscillations by approximately 0.5 Hz (Figure 2K), and this reduction was not due to change in running speed, which remained mostly unaffected by optogenetic stimulation (Figure S4). In addition, the theta phase coherence between oriens and molecular layer, and radiatum and molecular layer, both increased during stimulation (Figures S2E, F). The gradual theta phase-shift in the str. radiatum became steeper, and the coherence minimum between str. oriens and str. radiatum theta shifted closer to the pyramidal layer Figure S2E-F, 4E)), similar to results reported previously after surgical removal of the entire entorhinal cortex (Bragin et al., 1995). As an additional control, CSD activity remained mostly unchanged in the (non-stimulated) side arms of the maze between control and stimulation trials (Figure S2C). Optogenetic inactivation of ipsilateral mEC led to a small but significant deterioration of choice behavior in the maze (Figure S4A).

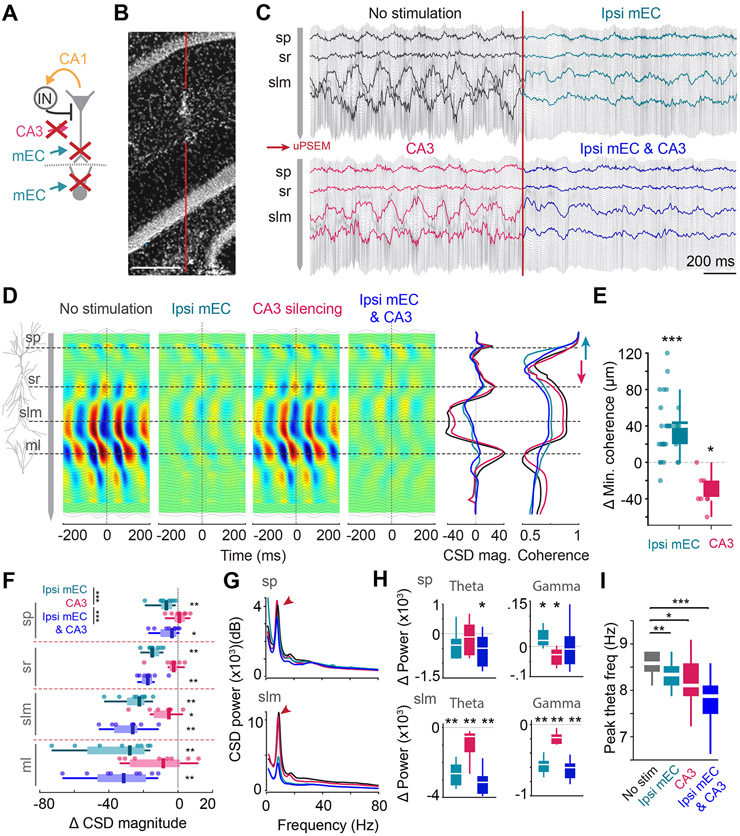
Figure 4. CA3 silencing exerts a minor effect on theta amplitude.

(A) Silencing strategy for combined ipsi mEC and bilateral CA3 manipulations. (B) Track of the linear silicone probe. (C) 2 s-long LFP traces during ipsi mEC, bilateral CA3 and combined silencing. Highlighted traces correspond to sp, sr, slm and ml. (D) Average CSD maps of theta oscillations during each manipulation. Note only minor decreases in the CSD magnitude upon CA3 silencing. Right-middle, average CSD magnitude at time 0, overlaid across all 4 conditions. Right, Coherence magnitude along the depth of CA1 with respect to the LFP at stratum oriens during each of the manipulations. The minima of LFP coherence between sp and sr shifted upwards during ipsi mEC silencing and downwards during CA3 silencing (E) Ipsi mEC silencing led to an upward shift of ~40μm of coherence minimum (each dot represents one session from one animal, n = 29 sessions from 12 mice, Wilcoxon two-sided signed rank test against 0; p<0.001), while CA3 silencing led to a downward shift of ~40μm (n = 8 sessions from 3 mice, Wilcoxon two-sided signed rank test against 0; p = 0.0156) (F) Average change in CSD magnitude in different hippocampal layers for each of the manipulations (each dot represents one session from one animal, n = 8 sessions across 3 mice; within layer: Wilcoxon signed rank test against 0; across layers: 2-way ANOVA followed by Tukey-Kramer posthoc tests, layer*manipulation interaction, F(6,84) = 1.14, p =0.35, manipulation, F(2,84) = 18.12, p < 0.001, layer, F(3,84) = 18.49, p < 0.001). CA3 silencing only led to a significant reduction in slm. (G) Average power frequency spectra of sp and slm CSD across mice (n = 3) upon ipsi mEC, CA3 and combined silencing. Color legend in E. (H) Change in theta (6-12 Hz) and gamma (25-90 Hz) CSD power for each manipulation compared to baseline in sp and slm (n[Ipsi mEC, CA3, ipsi mEC & CA3] = 8, 8 and 8 sessions from 3 mice, Wilcoxon two sided signed rank test against 0. sp: Theta, p = 0.07, 0.46, 0.04 respectively, Gamma, p = 0.04, 0.015, 0.74 respectively. slm: Theta, p = 0.008, 0.008, 0.008 respectively, Gamma, p = 0.008, 0.008, 0.008 respectively) (I) CA3 and ipsi mEC silencing led to a ~0.5 Hz decrease in the peak theta oscillation frequency (n = 15 sessions across 6 mice, Friedman test followed by Tukey-Kramer posthoc tests, Chi-square(3,42) = 25.33, p<0.001). *p<0.05, **p<0.01, ***p<0.001. All box plots show median ± interquartile; whiskers show range excluding outliers. See also Figures S3, S4.

Effect of local suppression of CA1 pyramidal cells on LFP

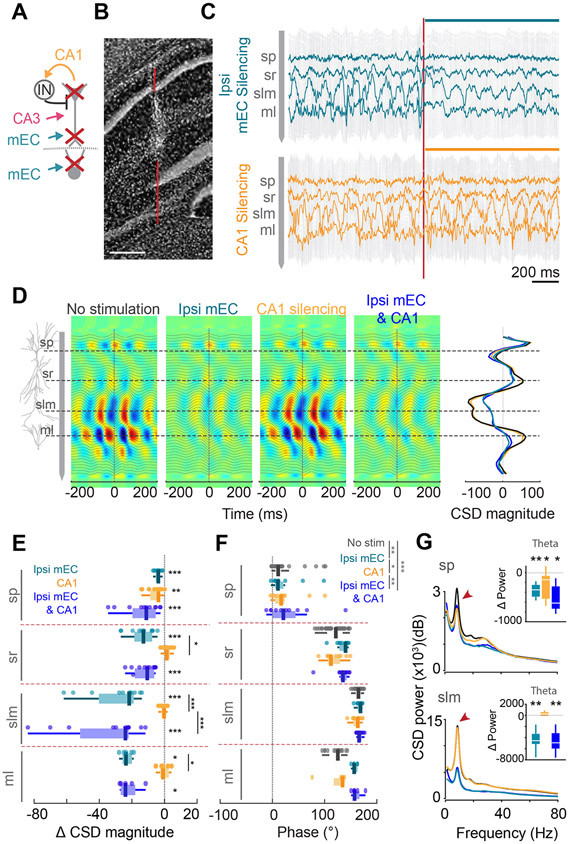
Direct optogenetic suppression of CA1 pyramidal cells did not exert a significant effect on the depth distribution of theta currents, except in the pyramidal layer (Figures 3A-E; n = 4 mice), despite the strong reduction of the discharge frequency of CA1 neurons (Figures 1D, E, S1C). The depth profile of theta phase was not significantly affected (Figure 3F), although a significant decrease in high gamma power (150-300 Hz) was observed (Figures S2L, M). When local suppression was combined with simultaneous suppression of mEC neuronal spiking, the effect of the combined optogenetic manipulation on CSD power was largely similar to mEC suppression alone (Figure 3G). Overall, these findings show that firing rates and the magnitude of synaptic currents, as measured by CSD, are dissociable.

Figure 3. Minimal effect of local CA1 silencing on theta oscillations.

(A) Schematic of silencing strategy.(B) Track of the linear silicone probe. (C) 2s-long LFP traces during ipsi mEC (top) and local CA1 (bottom) silencing. An immediate decrease in theta power was observed upon ipsi mEC silencing. Vertical red line is light onset. LFP traces recorded from sp, sr, slm and ml are highlighted. (D) Average theta CSD profiles during control, ipsi mEC, CA1 and combined silencing. Reduction of sink-source pairs was observed only for manipulations with ipsi mEC silencing. Right, average CSD magnitude at time 0, overlaid across all 4 conditions. (E) Average change in CSD magnitude across different hippocampal layers for each of the manipulations (each dot represents one session from one animal, n = 11 sessions across 4 mice; within layer: Wilcoxon signed rank test against 0; across layers: 2-way ANOVA followed by Tukey-Kramer posthoc tests, layer* manipulation interaction, F(6,102) = 5.33, p < 0.001; only within-layer post-hoc results shown). (F) Theta phase reversal (with respect to so theta phase) across sp to ml was preserved during all manipulations (n = 11 sessions across 4 mice, 2 way ANOVA followed by Tukey-Kramer posthoc tests, layer*manipulation interaction, F(9,212) = 1.83, p = 0.065, manipulation, F(3,212) = 8.44, p < 0.001, layer F(3,212) = 461.07, p < 0.001. Each layer was different from each other, p<0.05). (G) Left, Average power frequency spectra of CSD across all mice (n = 4) upon ipsi mEC, CA1 and combined ipsi mEC and CA1 silencing for sp and slm. Red arrows, theta peak. Right, Change in theta (6-12 Hz) CSD power for each manipulation compared to baseline in sp and slm (n[Ipsi mEC, CA1, ipsi mEC & CA1] = 9, 9 and 9 sessions from 4 mice, Wilcoxon two sided signed rank test against 0. sp: Theta, p = 0.004, 0.02, 0.02 respectively, slm: Theta, p = 0.004, 0.16, 0.004 respectively). Color legend in E. *p<0.05, **p<0.01, ***p<0.001. All box plots show median ± interquartile; whiskers show range excluding outliers. See also Figures S2, S4.

Effect of CA3 inactivation on LFP

Because mEC silencing also affected the CA3 region, which in turn can influence the CA1 region, we next examined the selective effects of the CA3 input in mice with PSAM⁴-GlyR expression in CA3 pyramidal cells, infected with AAV5-mDlx-ChR2-mCherry in mEC. We tested the effect of optogenetic silencing of mEC versus CA3 PSAM⁴-GlyR silencing and their combined effects on alternate days. In contrast to optogenetic pulses, PSAM⁴-GlyR-induction was sustained, thus affected hippocampal networks in all aspects of the task. PSAM⁴-GlyR-induced suppression of CA3 neuronal activity visibly increased motor activity in the home cage and drastically reduced memory performance in the maze (Figures S4 D, H). Despite the large spatial extent of the silenced CA3 region, demonstrated by the robust suppression of neuronal firing of CA3 and dentate neurons (Figures 1B, F, S1D), theta currents were not significantly affected, except for a small reduction of the sink in sLM (Figure 4A-E). Yet, phase and phase coherence measures demonstrated a clear effect of CA3 manipulation. Theta phase, relative to str. oriens signal, remained unchanged in the CA1 layers but the phase shift between sLM and the dentate molecular layer in the intact animal was abolished by PSAM⁴-GlyR treatment (Figure S3I). Opposite to the effect of mEC silencing, the theta coherence minimum between str. oriens and str. radiatum theta signals shifted deeper in CA1 str. radiatum (Figures 4D, E, S3H). In PSAM⁴-GlyR sessions, theta frequency was reduced by approximately 0.5 Hz (Figure 4I), and this reduction could not be explained by a change of locomotion speed (Figure S4I-M). The combined effects of PSAM⁴-GlyR on CA3 and optogenetic silencing of mEC were additive on the reduction of both theta current magnitude and theta frequency (Figure 4F-I, S4L, M). In contrast to PSAM⁴-GlyR sessions, vehicle injection (control sessions) did not induce changes in physiological or behavioral measures (Figures S3B-C, S4D-H).

Input-unique effects of transient functional deafferentation on network-embedded firing

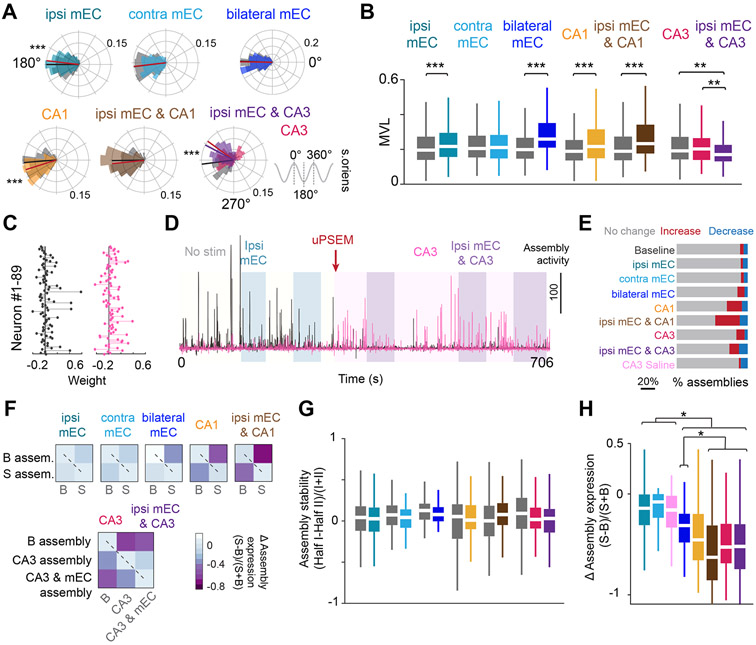
The theta phase preference of CA1 pyramidal neurons depends on the relative strength of several phase-shifted theta-modulated inputs (Fernández-Ruiz et al., 2017; Mizuseki et al., 2009). Optogenetic suppression of mEC slightly advanced the phase preference of CA1 pyramidal cells (Figure 5A) and interneurons (Figure S5A). An opposite direction small shift of theta phase preference of spiking was observed during local suppression of the CA1 circuits (Figure 5A). In the PSAM⁴-GlyR group, pyramidal cells, as a group, advanced their preferred phase by 30° but many cells shifted as much as 120° from the trough toward the peak of the theta cycle (Figure 5A). With each type of manipulation, the spike-theta phase modulation (‘mean vector length’) increased (Figure 5B), implying a reduced distribution of spikes in the theta phase space. A similar effect on preferred theta phase firing was observed for interneurons (Figure S5B). No phase shift was induced in vehicle control sessions (Figure S3G).

Figure 5. Theta phase preference of spiking is controlled distinctly by inputs.

(A) Distribution of theta phase angle preferences of all CA1 pyramidal cells during no stimulation in the central arm, compared to each respective manipulation. Radial axis represents probability for each bin. Small but opposite shifts in the phase preference were observed during ipsi mEC and CA1 silencing, whereas CA3 silencing led to an ~30 degree shift in preferred phase angle. Only cells that were significantly modulated by theta (Rayleigh test, p < 0.05) were included in the analysis (Wilcoxon ranksum test, ipsi mEC, Z = 3.65, p <0.001, contra mEC, Z = 0.145, p = 0.885, bilateral mEC, Z = −0.316, p = 0.752, CA1, Z = −3.91, p < 0.001, ipsi mEC & CA1, Z = −1.24, p = 0.216, CA3, ipsi mEC & CA3, Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square(2,1054) = 52.06, p<0.001, baseline is significantly different from CA3 and ipsi mEC and CA3, p <0.001). Gray shaded areas (and black line) are baseline, colored shaded areas (and lines) are stimulation. (B) Most manipulations resulted in an increase in the mean vector length (MVL) of locking to theta phase for individual cells (Wilcoxon ranksum test, ipsi mEC, Z = −5.185, p < 0.001, contra mEC, Z = 0.115, p = 0.908, bilateral mEC, Z = −9.57, p < 0.001, CA1, Z = −4.185, p < 0.001, ipsi mEC & CA1, Z = −5.45, p< 0.001, CA3, ipsi mEC & CA3, Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square(2,1054) = 14.84, p<0.001). (C) The relative weights of each neuron for two example assemblies. (D) Assembly expression over time of the two assemblies shown in C. The black assembly is highly expressed during no stimulation and ipsi mEC silencing but is diminished after PSAM inactivation of CA3. The opposite effect is observed for the pink assembly. (E) Bilateral mEC, CA1, and CA3 manipulations either increased or decreased cell assemblies identified during baseline runs (see STAR Methods). (F) Assemblies were defined separately for the first and second halves of baseline and stimulation sessions, and the change in assembly expression was quantified. Both baseline and stimulation assemblies had minimal changes in expression between the two halves (i.e., diagonal, dashed line), but assembly expression decreased across conditions (i.e., anti-diagonal). (G) Assembly stability (comparisons along the diagonal from F) was preserved within all manipulations (Wilcoxon two-sided signed rank test, ipsi mEC, p = 0.51, contra mEC, p = 0.42, bilateral mEC, p = 0.155, CA1, p = 0.70, ipsi mEC & CA1, p = 0.26, CA3, ipsi mEC & CA3, Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square(2,402) = 5.75, p= 0.06). Color legend in B. (H) Bilateral mEC, CA1 and CA3 manipulations led to the largest change in assembly expression across baseline versus manipulated runs (quantification of the top-right boxes from each heatmap in F) (Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square (7,949) = 244.85, p<0.001). Color legend in E. *p<0.05, **p<0.01, ***p<0.001. All box plots show median ± interquartile; whiskers show range excluding outliers. See also Figure S5.

Spikes of place cells within their place fields oscillate faster than the simultaneously recorded LFP theta and the consequence of this frequency difference-induced interference is ‘phase precession’ of spikes (O’Keefe and Recce, 1993). Bilateral mEC and CA3 manipulations both led to a 40-50% decrease in the proportion of significantly precessing place fields (Figures S5C-E), suggesting that both these inputs are required by CA1 pyramidal cells for effective phase precession (Davoudi and Foster, 2019; Fernández-Ruiz et al., 2017; Schlesiger et al., 2015). The slope of the remaining fraction of precessing cells was impacted only by the bilateral mEC, and not by the CA3 manipulation, and furthermore continued to be significantly negative despite all manipulations, suggesting that the deafferented CA1 circuit is capable of supporting some level of phase precession (Figures S5F-G).

To measure whether any of these manipulations affected the timing and synchrony of CA1 neural populations, we quantified the expression of CA1 spike assemblies (Lopes-dos-Santos et al., 2013) while the mice were crossing the central arm of the maze. First, assemblies were defined in 25 ms bins (Harris et al., 2003) across no stimulation and stimulation trials, and the stability of assembly expression was compared between baseline and stimulation epochs (Figure 5C-E). Assemblies detected over the entire session were affected during bilateral mEC, CA1 and CA3 manipulations, with several assemblies either increasing or decreasing their expression strength (Figure 5D, E, S5H). To examine whether these manipulations reduced the ability of the CA1 region to form assemblies or whether different assemblies were formed, we identified assemblies independently during baseline and stimulation trials. There was no change in the number of assemblies, nor the fraction of highly contributing neurons per assembly during any of the manipulations (Figure S5I, J), suggesting that despite functional deafferentation, the CA1 circuit continued to express cell assemblies. To quantify this effect further, baseline and stimulation trials were divided into halves and the expression between the two halves demonstrated that assemblies expressed during stimulation were also stable (Figure 5F, G). In contrast, the expression of baseline assemblies changed drastically during bilateral mEC, CA1 and CA3 manipulations, suggesting reorganization of co-firing populations of cells (Figure 5H). This result was further supported by examining the pair-wise correlation of pyramidal cells, and clustering co-firing cells separately during baseline and stimulation sessions (STAR Methods). While these clusters were maintained between the two halves of both baseline and stimulation conditions, there was a complete reorganization of these clusters during bilateral mEC, CA1, and CA3 manipulations (Figure S5K, L). Together, these results demonstrate that afferent inputs are valuable in selecting populations of co-firing neurons and that local CA1 manipulation can also reconfigure neuronal assemblies.

Spatial firing of CA1 pyramidal neurons is differentially affected by specific afferents

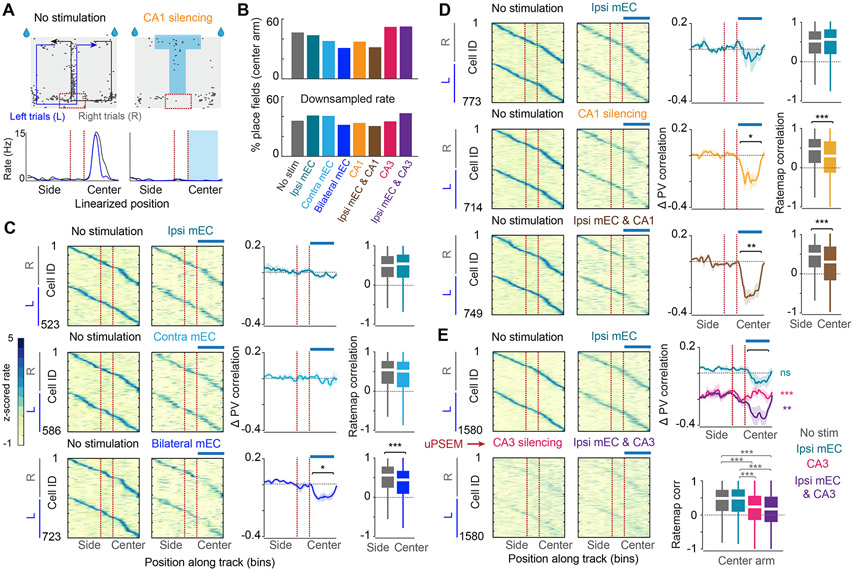
For maintaining the relationship between CA1 neuronal assemblies and environmental/body cues, we reasoned that at least some input is needed to update the mouse’s position in the maze. To address this, we examined how the transient deafferentation perturbations affected the place map. Linearized maps of stimulation and control trials were generated, and maps in the central (stimulated) and side (non-stimulated, control) arm sections of the maze were analyzed separately (Figure 6A). Before and during any of the perturbations, a similar fraction of neurons expressed place fields in the center arm (Figure 6B), suggesting that place field expression is a robust phenomenon and that the CA1 circuit is sufficient to generate place field dynamics with minimal external drive. Optogenetic suppression of the ipsilateral mEC input had a relatively small effect on the stability of place cells, as quantified by the population-vector correlation (i.e., bin-by-bin correlation of the firing rate of all cells across conditions) and rate-map correlation of individual neurons during control and stimulation trials (Figure 6C-E). Yet, the importance of the mEC was clearly revealed when mEC silencing was combined with other perturbations. Combined ipsilateral and contralateral mEC stimulation resulted in a larger decrease than the algebraic sum of the separate manipulations (“supralinear” effect; Figure 6C; Figure S6C). Local CA1 suppression exerted a larger perturbation on place map stability, which was supralinearly enhanced by MEC co-stimulation (Figure 6D, Figure S6C). These changes can be contrasted to persisting place field stability in the side arms (within-run control of side arms and delay area, Figure 6D). PSAM⁴-GlyR-induced suppression of the CA3 region had a profound effect on place field stability across conditions, which was present throughout the maze, due to the continuous presence of the pharmacogenetic ligand (Figure 6E). The strongest remapping of place fields was observed when optogenetic silencing of mEC was co-applied during CA3 suppression sessions (Figure 6E). However, the remapped field locations on the non-mEC stimulated (side) arm remained stable throughout the recording session despite ongoing CA3 silencing (Figure S3J). These changes were not observed in the vehicle control sessions (Figures S3D-F). These profound changes in place field correlations could be dissociated from firing rates since downsampling of spikes in the control conditions (see STAR Methods) before constructing the rate maps and population vectors yielded comparable within-session map stability differences between control and perturbation conditions (Figures S6 E, H, K). PSAM⁴-GlyR CA3 perturbation and bilateral mEC silencing reduced place field stability, while other spatial properties, such as place field size and information (bits/spike), remained largely unaltered even after examining downsampled maps (Figures S6F-K).

Figure 6. Spatial firing persists after all manipulations despite remapping of fields.

(A) Schematic of the spatial alternation task with spikes overlaid (black dots) from an example CA1 pyramidal cell that was targeted during CA1 silencing. The maze was linearized into left and right trials as depicted by the paths superimposed on the maze. Below, average linearized rate map for the same example cell for left and right trials with and without stimulation. Light blue, zone of light stimulation, Red dashed lines, delay zone. (B) Top, Percentage of place fields defined in the center arm during baseline and each of the 7 manipulations. Bottom, to account for the rate changes during manipulations, each cell was downsampled during baseline to match the rate during manipulation, and the percentage of place fields was determined in the downsampled maps. (C) Left, Z-scored rate maps sorted separately for left versus right trials during baseline and the corresponding ipsi mEC, contra mEC, and bilateral mEC silencing trials. Blue bar above indicates the targeted stimulation zone (central arm). Place fields are sorted by their position during baseline and the order is maintained for stimulation sessions. Middle, the entire duration of each baseline and stimulation session was divided into two halves, and a position bin-by-bin correlation across all cells (PV correlation) was calculated between the half-session baseline maps. The same value was calculated between baseline and stimulation trials and normalized to the baseline PV correlation. A significant deterioration in the PV correlation was observed during bilateral mEC silencing (One sample t-test against 0, n = 3 mice, ipsi mEC, p = 0.37, contra mEC, p = 0.83, bilateral mEC, p = 0.045). Right, Cell-by-cell rate map correlation for the center arm during baseline (gray), and baseline versus stimulation (colored) revealed significant remapping during bilateral mEC silencing (Wilcoxon signed rank test, ipsi mEC, p = 0.21, contra mEC, p = 0.06, bilateral mEC, p <0.001). (D) Same as C, but for ipsi mEC, CA1 and combined silencing. There was a significant decrease in the PV correlation during CA1 and combined silencing (n = 5 mice, ipsi mEC, p = 0.57, CA1, p = 0.023, ipsi mEC and CA1, p = 0.003). A significant change in the rate map correlation was observed during all manipulations (Wilcoxon signed rank test, ipsi mEC, p = 0.10, CA1, p < 0.001, bilateral mEC, p <0.001). (E) Same as C,D,but for ipsi mEC, bilateral CA3, and combined manipulations. The CA3 manipulation was targeted to the entire maze due to the continuous nature of the pharmacogenetic manipulation. Strong remapping was observed during CA3 silencing, which was further altered by additional ipsi mEC silencing (Central arm, n = 6 mice, One sample t-test against 0, ipsi mEC, p = 0.21, CA3, p <0.001, ipsi mEC and CA3, p = 0.0012). A significant change in the rate map correlation was also observed during all manipulations (central arm, Kruskal-Wallis test followed by Tukey-Kramer posthoc tests, Chi-square(3,6289) = 358.4882, p<0.001). *p<0.05, **p<0.01, ***p<0.001. All box plots show median ± interquartile; whiskers show range excluding outliers. See also Figure S6.

DISCUSSION

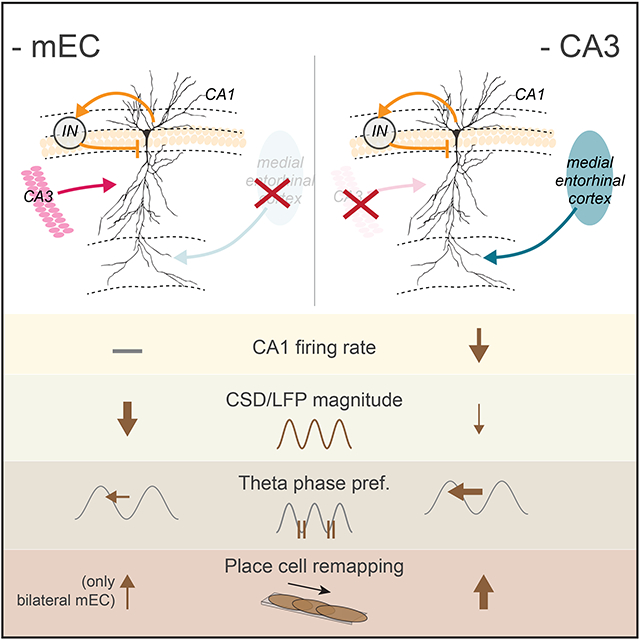
Using a combination of physiological recordings, CSD analyses of the LFP, and optogenetic/pharmacogenetic perturbations, we found that transient deafferentation of the hippocampal network induced differential effects on subthreshold collective activity, as reflected by the LFP, and the firing patterns of individual neurons. mEC was the main current generator of hippocampal theta oscillations. Both input (bilateral CA3 and bilateral mEC) and local (CA1) perturbations resulted in remapping of the CA1 population. Yet, the fraction of place fields and the ability of the CA1 circuit to support place field activity and express assemblies remained largely intact, even during double deafferentations. These findings suggest that the CA1 network can give rise to substantially more self-organized dynamics that hitherto suspected.

LFP and neuronal spiking are dissociable

LFP is composed of the summed transmembrane potential changes in synchronously active neurons, brought about mainly by excitatory and inhibitory postsynaptic potentials (EPSPs, IPSPs) and intrinsic currents of neurons (Buzsáki et al., 2012). As such, it characterizes the subthreshold activity of neuronal populations, as opposed to their output spiking. Excitatory activity impinges upon the dendrites of pyramidal neurons, whereas the somatic region is contacted by inhibitory synapses (Buhl et al., 1994; Gulyas et al., 1999; Halasy et al., 1996). Of the three manipulations, mEC silencing had the largest impact on LFP, though we would like to add a cautionary note that it is impossible for the efficacy of silencing in each brain region to be identical, and some of the differences in the scale of effects observed may arise from this mismatch. CA3/DG neurons strongly decreased their firing rates, coupled with decreased theta power in the molecular layer and hilus. Stellate cells in layer 2 of MEC, but not other mEC neurons, are tuned to resonate at theta frequency in vivo (Quilichini et al., 2010) mainly due to a prominent HCN1 channel-mediated h current (Alonso and Llinás, 1989; Giocomo and Hasselmo, 2009; Giocomo et al., 2011; Isomura et al., 2006). Electric stimulation of mEC axons induces large extracellular PSPs and population spikes of granule cells (Andersen et al., 1971). Overall, these observations suggest that the main current source of theta activity in the dentate gyrus is AMPA receptor-mediated fast transmission dominantly from mEC stellate cells.

In contrast to the dentate area, optogenetic silencing of mEC brought about a small effect on the overall firing rates of CA1 pyramidal cells, yet exerted a dramatic reduction of theta currents, particularly in sLM, the target of layer 3 mEC pyramidal cells (Amaral and Lavenex, 2007). The depth profile of the theta waves, coherence and phase in the intact mouse was similar to those previously described in rats (Brankačk et al., 1993; Buzsáki et al., 1983, 1986; Fernández-Ruiz et al., 2021; Kamondi et al., 1998; Lasztoczi and Klausberger, 2016). Although entorhinal synapses on the distal dendrites of pyramidal neurons are larger than excitatory synapses in other layers (Megías et al., 2001), single pulse stimulation of this path induces only a weak sink in sLM and fails to elicit spiking in pyramidal cells because of the strong feed-forward inhibition (Isomura et al., 2006). On the other hand, repetitive stimulation of mEC or pairing it with CA3 stimulation is effective, due to potentiation of synapses on the distal apical dendrites, depression of the entorhinal–interneuron spike transmission (Buzsáki, 2002) and induction of large Ca²⁺ spikes in the distal dendrites of CA1 pyramidal cells (Kamondi et al., 1998; Larkum et al., 1999; Magee and Carruth, 1999; Schiller et al., 1997). Thus, the mechanisms of theta current generation in CA1 are different than in the dentate gyrus.

Direct projections from deep layers of mEC to the CA1 regions have been described (van Groen et al., 2003; Witter and Amaral, 1991). This weak projection targets the basal dendrites of CA1 pyramidal cells and interneurons in str. oriens. Because our viral infections also targeted interneurons in the deep layers of mEC, some of the changes we observed in CA1 str. oriens may have been brought about by this complementary input. In addition to excitatory inputs, mEC also sends direct inhibition to the hippocampus (Melzer et al., 2012; Ye et al., 2018) and to the medial septum (Gulyás et al., 2003). These long-range GABAergic neurons arise mainly in the lateral EC and less so in mEC (Basu et al., 2016) but are unlikely to contribute significantly to the LFP changes we observed due to their sparsity and because stimulation of their CA1 terminals did not bring about detectable changes in LFP (Figure S2J, K). The large differences between ipsilateral and contralateral mEC stimulation indicates further that the impact of mEC-septal projection was not an important contributor to the LFP effects we observed.

In addition to mEC, afferents from the lateral entorhinal cortex, perirhinal cortex and thalamic reuniens neurons also project to sLM (Amaral and Lavenex, 2007). Furthermore, the ratio of inhibitory to excitatory synapses is 1 to 4 in sLM, which is eight-fold higher than in other dendritic layers (Megías et al., 2001). Therefore, the surviving small theta sink-source in the proximal part of the layer (Figure 2) may reflect the activity of extrahippocampal inputs (Witter, 1997) and/or inhibitory currents from O-LM and sLM-targeting neurogliaform interneurons.

Local silencing of CA1 pyramidal neurons further supports the dissociability of dendritic currents and spiking activity. Although firing rates of local neurons substantially decreased, local silencing reduced theta currents only in the pyramidal layer, leaving the rest of the layers unperturbed, corroborating previous observations in rats, in which pyramidal neurons were strongly silenced pharmacogenetically, yet theta LFP was not affected (Rogers et al., 2021). Surprisingly, widespread and bilateral suppression of CA3 spiking activity induced only a minor effect on the theta CSD profile, although it had a significant effect on coherence measures. This finding indicates that the LFP/CSD changes in CA1 during mEC suppression was not mediated dominantly by the layer 2-dentate-CA3-CA1 path but by the direct layer 3 to CA1 projection. A possible explanation for the weak effect of CA3 silencing on the theta sink in str. radiatum is that the reduced excitation similarly affected CA1 pyramidal neurons and the layer-matching bistratified interneurons. In turn, the relatively preserved ratio of excitation and inhibition could produce a comparable transmembrane drive in the CA1 pyramidal cells. The additional role of local interneurons are supported by two findings. First, the gradual phase shift of theta waves from str. oriens to sLM, assumed to be the result of phase shifted inputs (Brankačk et al., 1993; Buzsáki, 2002; Buzsáki et al., 1986) was only minimally affected even by combined CA3 and mEC inactivation (Figure S3K), implying that local circuit mechanisms are at play. Second, during local CA1 inactivation, the theta phase preference of the remaining active CA1 pyramidal cells shifted significantly. To identify the exact mechanisms of CSD and coherence changes will require further experiments, targeting the different interneuron types.

Our results also suggest that cell assemblies in the entorhinal cortex-hippocampus regions contribute to theta frequency as well. Suppression of both mEC and CA3 inputs reduced theta frequency (Ormond et al., 2015; Schlesiger et al., 2015). A potential mechanism of this effect is the hippocampo-septal feedback. Assemblies of place cells, oscillating at the same frequency, may enslave their associated long-range inhibitory interneurons, whose septal collaterals (Gulyás et al., 2003) can adjust the frequency of septal theta pacemaker neurons. This way the oscillation frequency of place cell assemblies may adjust the global LFP theta rhythm (Geisler et al., 2010).

Intrinsic computation in the CA1 network

The most surprising finding of our experiments is the contrast between the robust reconfiguration of the relationship between neuronal assemblies and the animal’s spatial position by perturbations (i.e., the case of “remapping”) versus the continued ability of the CA1 network to induce and maintain a new map during various forms of functional disconnections. This conclusion is in contrast with suggestions that CA1 neurons largely inherit their firing patterns and spatial features from their upstream CA3 and EC networks (Ahmed and Mehta, 2009; Brun et al., 2008; Franzius et al., 2007; Rolls et al., 2006; Savelli and Knierim, 2010; Solstad et al., 2006; Steffenach et al., 2005) and that the contribution of the CA1 circuit is mainly to refine the place fields (Mizumori et al., 1989).

Local CA1 silencing, CA3 inactivation and bilateral mEC inactivation altered cell assembly configurations (Figure 5), decreased population vector correlations and spatial correlations of individual CA1 neurons (Figure 6), independent of firing rate reductions (Figure S6). CA3 inactivation and local CA1 perturbation exerted a larger effect on the spatial map than mEC silencing. Yet, the importance of mEC (Fernández-Ruiz et al., 2021; Hales et al., 2014; Miao et al., 2015; Miller and Best, 1980; Ormond et al., 2015; Robinson et al., 2017; Rueckemann et al., 2016; Schlesiger et al., 2015) was clearly demonstrated when ipsilateral mEC perturbation was combined with additional perturbation. The large differences between the impact of mEC and CA3 inactivation on both LFP/CSD and place map reorganization is surprising in light of our finding that mEC silencing was accompanied by a strong disfacilitation of the dentate/CA3 regions.

mEC silencing may be viewed as a combined deafferentation of CA1 neurons from both mEC and CA3 inputs (i.e., direct and indirect paths). Yet, our results do not support such interpretation for either theta currents (Figures 2-4) or neuronal firing. This apparent paradox may be explained by assuming two parallel pathways from mEC to CA1. Previous research has shown that there are two distinct types of CA3 pyramidal neurons, one that receives mossy synapses from granule cells (‘thorny’ type), whereas the other type (‘athorny’ pyramid cell) lacks mossy-fiber input but gives rise to extensive recurrent and association path collaterals, and the subcircuits formed from these respective populations antagonize each other (Hunt et al., 2018). Whereas our pharmacogenetic manipulation may have equally affected both CA3 neurons types, mEC inactivation more likely impacted thorny CA3 pyramidal cells with granule cell contacts. This hypothesis is supported by the larger effect of the combined mEC and CA3 silencing on DG/CA3 firing rates than their individual manipulations (Figure 1G, J) and that mEC and CA3 manipulations affected different sets of CA3/DG neurons (Figure S3K). We hypothesize that the subnetwork of CA3 neurons with strongly interconnected recurrent collaterals is more critical in maintaining the place representation of CA1 pyramidal cells than the mEC input. This result is supported by our observation that stability of the reconfigured CA1 map after CA3 inactivation was diminished. In simple situations, such as walking on the center arm of the maze, environmental cues might not be critical to maintain cell assembly sequences. Only occasional realignment of the internally generated map may be needed, which may be accomplished by mEC or other inputs from retrohippocampal structures (Van Strien et al., 2009; Zhang et al., 2014). On the other hand, the outcome may be different in more complex environments when the animal has to rely heavily on multiple landmarks and their relationships. The magnitude of dependence from environmental cues may be one key source of the variability observed across studies examining the impact of mEC on CA1 neuronal firing patterns (Hales et al., 2014; Ravassard et al., 2013; Robinson et al., 2017; Rueckemann et al., 2016; Schlesiger et al., 2015, 2018; Sharif et al., 2021).

In contrast to the remapping effects of the input and local perturbations (Kanter et al., 2017; Miao et al., 2015; Rueckemann et al., 2016), the transiently deafferented CA1 continued to induce and maintain place fields. These findings suggest that the CA1 region possesses the necessary circuit dynamic to create and maintain sequentially organized neuronal assemblies, a prerequisite for place field sequences. This suggestion is supported by previous observation showing that the participating neurons and their sequences in hippocampal sharp wave ripples are largely created by local CA1 circuits, without the need of extrinsic inputs (Stark et al., 2015). Further, when animals are tested in novel environments, CA1 neurons remap faster than CA3 neurons (Dong et al., 2021; Frank et al., 2004; Roth et al., 2012), again suggesting that operations in CA3 and CA1 circuits can be independent. Place fields have been suggested to emerge as a result a hypothetical “attractor” based on extensive excitatory recurrency in the CA3 region (Hunt et al., 2018; Samsonovich and McNaughton, 1997). However, recent computational efforts demonstrated that such property can also emerge in a model layer 2 mEC network with no recurrent excitation but mutual lateral inhibition (Couey et al., 2013; Pastoll et al., 2013), a requirement present in the CA1 circuit (Freund and Buzsáki, 1996). Overall, our findings suggest that the CA1 circuit is endowed with the computational capacity to generate assembly sequences, detected as sequentially active place fields during maze performance.

STAR METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, György Buzsáki (gyorgy.buzsaki@nyumc.org)

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

• All the data of this study is publicly available in the Buzsaki Lab Databank: https://buzsakilab.com/wp/public-data/.

• All custom code for preprocessing the data is freely available on the Buzsaki Laboratory repository: https://github.com/buzsakilab/buzcode (DOI: 10.5281/zenodo.5668715) and scripts specific for analyzing this dataset can be found on https://github.com/IpshitaZutshi/Zutshi_Neuron2021 (DOI: 10.5281/zenodo.5668669

• Any additional information required to reanalyze the data reported in this work paper is available from the Lead Contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experiments were approved by the Institutional Animal Care and Use Committee at New York University Langone Medical Center. Mice were kept in the vivarium on a 12-hour light/ dark cycle and were housed 2-3 per cage before surgery. Following surgery, the mice were moved to a 12-hour reverse light cycle (lights on/off at 7 pm/am) and housed individually. Prior to behavior training, mice were provided food and water ad libitum, but were water restricted to maintain 85% of their weight during and after behavioral training. We used heterozygous male C57B1/6 transgenic mice (n = 21 mice, Tg(Grik4-cre)G32-4Stl/J, Jax Stock No. 006474), weighing 22-39g, and aged between 4-12 months old.

METHOD DETAILS

Subjects and surgical procedures

Of the 21 mice used in this study, 6 mice were unilaterally (right hemisphere) injected with AAV5-mDlx-ChR2-mCherry (titer, 1.4x10¹³, custom prepared from Addgene, plasmids were a gift from Dr. Gord Fishell, (Fernández-Ruiz et al., 2021)) in the mEC, 3 mice were bilaterally injected with AAV5-mDlx-ChR2-mCherry in the mEC, 6 mice were injected with AAV5-mDlx-ChR2-mCherry in the mEC right hemisphere along with AAV1-CamKIIα-stGtACR2-FusionRed in the right dorsal CA1 (titer: 1.3x10¹¹, gift from Ofer Yizhar, Addgene viral prep #105669-AAV1; http://n2t.net/addgene:105669; RRID:Addgene_105669), and 6 mice were injected with AAV5-Dlx-ChR2-mCherry in the mEC right hemisphere along with AAV5-Syn-DIO-PSAM4-GlyR-IRES-GFP (titer: 2x10¹², gift from Scott Sternson, Addgene viral prep #119741-AAV5; http://n2t.net/addgene:119741:RRID:Addgene_119741) in bilateral CA3. For the CA3 silencing cohort of mice, mice were given an i.p. injection of either 0.9% saline (Lifeshield Diluent NaCl), or 1.5-3 mg/kg μPSEM792 hydrochloride (Tocris, #6865) diluted in 0.9% saline (working concentration 1 mg/ml, volume injected: 0.04-0.06 ml).

For viral vector injections, mice were anesthetized with isoflurane (1.5-2.5% in O₂) and mounted in a stereotaxic frame (David Kopf Instruments). Craniotomies were made over the injection sites, and a glass pipette containing virus was slowly lowered into the brain. The following coordinates and viral volumes were used – (a) mEC: 0.2 mm AP from the transverse sinus, ±3.75 mm from lambda, 150 nl injections each at −1.7mm DV,−1.3mm DV and −0.9 mm DV from the surface of the brain, angled at 6° toward anterior, (b) CA1: 2 injection sites at −1.6mm AP, +1.2mm ML, −1.1mm DV from bregma, and - 2.0mm AP, +1.8mm ML, −1.2mm DV from the bregma, 250nl at each site, (c) CA3: 6 injection sites at - 1.7mm AP, ±1.9mm ML, −2.0mm DV, −2.3mm AP, ±2.5mm ML, −2.2mm DV, and −2.8mm AP, ±3.0mm ML, −3.2mm DV from bregma, 250nl, 350nl and 500nl at each site respectively. After each injection, the pipette was left in place for atleast 10-15 minutes. The injections were administered at a flow rate between 25-50 nl/min using a microsyringe pump (World Precision Instruments, UMP3 UltraMicroPump). The constructs were allowed to express for at least 2-3 weeks before the mice were implanted with silicon probes. Following surgery, an opioid analgesic was injected (Buprenex at 0.06 mg/kg, 0.015 mg/ml, IM).

Animals were implanted with 64 or 128 channel silicon probes into CA1 (6 mice were implanted with Neuronexus A5x12-16-Buz-Lin-5mm-100-200-160-177 probes, 9 mice were implanted with Cambridge NeuroTech H2 probes, 4 mice were implanted with Cambridge NeuroTech H3 probes, 2 mice were implanted with Diagnostic Biochips ASSY-INT128, P128-2 probes). The coordinates used for CA1 implants was either −1.8mm AP, +1.5 mm ML from bregma, or −2.0 AP, +1.7mm ML from bregma. A ground screw coupled with a 0.005” stainless steel wire (A-M Systems, #792800) was implanted in the skull above the cerebellum, and a grounded copper mesh hat was constructed, shielding the probes. Metabond was used to cement the base to the skull of the animal (C&B Metabons, #S380). The probes were mounted on custom-made 3D-printed micro-drives to allow precise adjustment of vertical position of sites after implantation (Vöröslakos et al., 2021). Local CA1 silencing was achieved by attaching a 100 μm optic fiber glued to a ceramic ferrule (0.22 NA, Thorlabs, FG105LCA and Thorlabs, 30126L9) to the shanks of the silicon probe. mEC silencing was achieved by implanting a 200 μm optic fiber glued to a stainless-steel ferrule (0.50 NA, Thorlabs, FP200URT and Thorlabs, SFLC230) unilaterally or bilaterally over the mEC (+0.2 mm AP from the transverse sinus, ±3.75 mm from lambda, −0.6 mm DV from the surface of the brain, angled 6° toward anterior). Light was delivered by coupling the optic fiber to a laser diode (450 nm blue, Osram) and stimulation pulses were delivered using an isolated current driver (Thorlabs, LDC205C). Light intensity was calibrated across animals to achieve maximal reduction in theta power with the least power and was between (2 mW to 8 mW for the mEC optic fiber, and 0.5mW to 1.5 mW for the CA1 optic fiber). Light output was measured using a power meter (Thorlabs, PM100D).

Viral expression and the position of the probe was confirmed at the end of each experiment. The mice were perfused with cold saline solution (0.9%) followed by pre-made 4% paraformaldehyde (PFA) in in phosphate-buffered saline (PBS) solution (Affymetrix USB). Brains were post-fixed for 24h in 4% PFA and sectioned coronally and sagitally to visualize both the hippocampus (coronal) and mEC (sagittal). Sections were obtained with 40-50 μm thickness using a vibrating blade microtome (Leica, VT1000S), mounted on electrostatic slides, coverslipped with DAPI Fluoromount-G (Southern Biotech, 0100-20), and imaged using a virtual slide microscope (Olympus, VS120). No additional immunohistochemistry or tissue processing was done to visualize viral fluorescence.

Recordings and behavior

Animals ran on the delayed spatial alternation task for 40-60 laps (approximately 40 minutes) and were then recorded from in their home cage for 3-4 hours. Within the homecage, stimulation was provided randomly for up to three different manipulations (individual and combined manipulations) for atleast 30 trials (5 seconds ON, 25 seconds OFF for 15 minutes, followed by 15 minutes of no stimulation). Therefore all homecage manipulations lasted for atleast 180 minutes, and the median total time spent in the home cage was approximately 2.5 hours. On most days, the mice subsequently ran a second spatial alternation task session with a different stimulation. For sessions with CA3 silencing, mice were injected with μPSEM792 or saline mid-way through the home cage recording session, and always ran the second behavioral session. Animals were handled daily and accommodated to the experimenter, recording room and cables, and trained to obtain a minimum performance of 80% in the delayed version of the alternation task before the start of experiments (training lasted 7-10 days). The maze was custom-built in the lab with dimensions 70cm x 40 cm (1 m above the floor) and 3.7 mm high walls (McMaster-Carr, PVC U-Channel #85065K55). Water was delivered by solenoids (Cole-Parmer, EW-98302) and activated by the animal crossing infrared beams (NOYITO E180D80NK) at the reward and delay zones. Maze doors, water delivery, and optogenetic stimuli were controlled by a custom-made Arduino-based circuit (Valero et al., 2015).

Electrophysiological data were acquired using an Intan RHD2000 system (Intan Technologies) digitized at 30-kHz. The wideband signal was downsampled to 1250 Hz and used the LFP. A pulley system was designed to counteract the weight of the tether and headstage. In the home cage, optogenetic stimulation was delivered as 5s-long square pulses, repeated every 30 seconds for 30-50 trials, using PulsePal2 (Sanworks, v2) connected with MATLAB. On the maze, stimulation was triggered by TTLs from the IR sensors, using PulsePal2. The animal’s position was monitored using a Basler camera (acA1300-60 gmNIR, Graftek Imaging) sampling at 30Hz to detect a head-mounted red LED. Position was synchronized with neural data with TTLs signaling shutter position.

Unit clustering and neuron classification

Spikes were extracted and classified using Kilosort (Pachitariu et al., 2016) using a custom pipeline KilosortWrapper (https://github.com/brendonw1/KilosortWrapper). Automated sorting was followed by manual curation of the waveform clusters using Phy (https://github.com/cortex-lab/phy) and custom plugins for Phy (https://github.com/petersenpeter/phy1-plugins). Kilosort clustering was performed with the following parameters: ops.Nfilt:6*numberChannels, ops.nt0:64;ops. whitening:’full’;ops.nSkipCov:1;ops.whiteningRange:64;ops.criterionNoiseChannels:0.00001 ; ops.Nrank: 3; ops.nfullpasses: 6; ops.maxFR: 20000; ops.fshigh: 300; ops.ntbuff: 64; ops.scaleproc: 200; ops.Th: [4 10 10]; ops.lam: [5 20 20]; ops.nannealpasses: 4; ops.momentum: 1./[20 800]; ops.shuffle clusters: 1. Units were separated into putative pyramidal cells and narrow waveform interneurons using their autocorrelograms, waveform characteristics and firing rate. This classification was performed using CellExplorer (Petersen et al., 2020). Units were defined as CA1 or CA3/DG cells based on their recording position on the silicon probe and after confirming the location of the probe with histology.

Ripple detection

Ripples were detected as described previously (Tingley and Buzsáki, 2020), and the code is available at the Buzsaki lab github repository (bz FindRipples). Briefly, the raw LFP (1250 Hz) was filtered (130-200 Hz; Butterworth; order = 3) and was transformed to a normalized squared signal (NSS). This signal was used to identify peaks that were beyond 5 standard deviations above the mean NSS. The beginning/end cutoff of the ripple was defined by a threshold of 2 standard deviations above the mean NSS. Ripple duration limits were between 20ms and 100ms. In addition, estimated EMG from the LFP (Schomburg et al., 2014) was used to exclude EMG related artifact. The peak of the ripple (max power value > 5 standard deviations) was defined as time 0 for the ripple. Ripples were defined across the entire duration of a day, including both periods in the maze and the homecage.

CSD and coherence analysis

The second spatial derivative of the LFP profile was used to calculate the CSD (Makarov et al., 2010; Mitzdorf, 1985). The CSD power spectra was calculated using a custom written script (bz_PowerSpectrumSlope), which calculates the FFT using the MATLAB function ‘spectrogram’ (window size, 1 s; dt, 0.1 s). Theta CSD magnitude was calculated using the script bz_eventThetaCSD2. First, periods of LFP while the mouse was running on the central arm of maze (either baseline or stimulation) were extracted. This LFP from oriens was filtered (6-12 Hz; Butterworth; order = 3) and the instantaneous phase was estimated using a Hilbert transform. Theta peaks greater than 2 standard deviations from the LFP squared signal were determined. Segments of the LFP signal on each channel along the depth of the shank were subsequently aligned with reference to the peak, and the differential between successive average aligned channels was used to generate the CSD magnitude. Unless mentioned otherwise, all analysis was restricted to the central arm of the figure 8 maze.

LFP coherence was measured using the script bz_lfpCoherence. The coherogram was calculated using a multi-taper estimation using the chronux function ‘cohgramc’ (window, 2s; overlap,1s; step, 1;padding, 0), and the magnitude and phase of the resultant coherogram was examined. Unless mentioned otherwise, all analysis was restricted to the central arm of the figure 8 maze.

Theta phase locking, phase precession, and oscillation frequency analysis

LFP from oriens was filtered and the instaneous phase was determined using a Hilbert transform. Theta phase locking was determined by calculating the phase angles for each timestamp where an action potential occurred, restricted to the defined central arm of the figure-8 maze (bz_PhaseModulation). A histogram of phase angles was calculated, and the circular mean and resultant vector (Berens, 2009) were calculated for each neuron. Only neurons that were significantly modulated (Rayleigh test) were included in the analysis. Phase locking was estimated separately for no stimulation and stimulation trails.

To measure phase precession, theta phase was first estimated as described above. Next, place fields were normalized between 0 and 1 to the beginning to end of the field. A circular-linear regression was generated for spikes occurring within the bounds of the fields, and the slope and significance of the regression line is reported. Significance was achieved by a p<0.05. Boundaries of ±1.5 cycles were used to constrain the circular-linear regression.

Assembly analysis

Cell assemblies were defined using an unsupervised statistical framework based on a hybrid PCA followed by ICA (Lopes-dos-Santos et al., 2013; van de Ven et al., 2016). Spike trains of each neuron were binned in 25-ms intervals by concatenating spikes only in the central arm of the maze and z-scored rates were calculated for each bin. Assemblies were defined in two ways – first by combining baseline and stimulation trials, but also by examining baseline and stimulation trials independently. To define assemblies, spike trains from periods of interest were convolved with a Gaussian kernel (SD =10 ms), and the matrix of firing correlation coefficients for all pairs of neurons was constructed. Principal components with eigenvalues that exceeded the threshold for random firing correlations (using the Marcenko-Pastur law) were used to determine the number of assemblies. Next, using the fast-ICA algorithm (Ritchey et al., 2015), we determined the vector of weights (contribution of each neuron) for each assembly (component). High contributing neurons were defined as cells that had weights > 2 standard deviations from the mean weight of all neurons. The strength of each assembly’s activation as a function of time was determined by multiplying the convolved z-scored firing rate of a given neuron at a given time by the weight of that neuron’s contribution to the assembly. The product of these weighted spike counts was then summed for all nonidentical pairs of neurons to generate the instantaneous activation strength. For each assembly, irrespective of which period it was defined in, the average activation strength during baseline, and stimulation conditions was subsequently compared, and a measure of change in activation strength (Δ assembly activity) was defined as - (Stim-baseline)/(stim+baseline). For within baseline, and within stimulation stability measures, Δ assembly activity was calculated by dividing baseline or stimulation trials into half and calculating Δ assembly activity between the two halves.

The fraction of assemblies increasing or decreasing in expression during each manipulation was defined by calculating a threshold of mean±2*std. dev of the stability during baseline sessions, and measuring the fraction of assemblies whose expression changed greater than, or less than this threshold during stimulation (Figure 5E).

We also implemented a cell-by-cell correlation analysis to quantify pairs of co-active cells. As described above, spike train matrices for spikes within the center arm were generated, but in this case by using 125 ms (theta timescale) bins. Periods of either baseline or stimulation trials were extracted, and further divided into halves. Subsequently, the spike trains between all cell pair combinations were correlated (Spearman correlation) with each other for each baseline or stimulation half. Cell pair correlation values were clustered into groups of co-firing neurons (matlab function linkage, followed by cluster, ‘maxCluster’,5) for the first half of each session type, and the same order was maintained for the second half. Cell pair correlation matrices were next generated by sorting according to clustered neurons for baseline and stimulation sessions separately, and the stability of cell pair correlations was measured by correlating between the two half session matrices for baseline and stimulation separately. Changes in co-firing pairs between baseline and stimulation was measured by sorting cell-pair correlation values during stimulation by cell clusters defined during baseline, and correlating between the baseline versus resorted stimulation matrix (Figure S5K, L). Because the correlation matrix is symmetric around the diagonal, only the bottom half of each matrix was correlated to each other (excluding the diagonal, which is equal to 1). Only sessions with atleast 5 active CA1 pyramidal cells were included in these analyses.

Place field analysis

Rate maps were generated by first binning spiking data into 1.75 cm wide-bins, generating maps of spike counts and occupancy for periods when the animal’s speed was > 1 cm/s. Maps for left and right bound trials, and stimulation and non-stimulation trials were generated separately. A smoothed rate map (smoothing size: 2 bins) was constructed by dividing the spike map by the occupancy map. Place fields were defined from these rate maps by finding peaks in the rate map. The field boundaries were defined till the rate was above 20% of the peak firing rate. Place fields cleared all criteria if they were between 8.75 cm and 75 cm wide, had a minimum peak firing rate of 2 Hz. Additional fields were defined if they cleared the above-described criterion. Spatial rate-map correlations for individual cells between trials was calculated as the average pixel-by pixel Spearman correlation of the smoothed-averaged firing rate maps. PV correlations were defined by stacking the rate maps of all cells in the same order and calculating the bin-by-bin Spearman correlation across all cells for a single bin. Baseline PV correlations were calculated by dividing baseline sessions into halves and measuring the PV correlation of each half against each other. Rate map stability was defined by generating rate maps for the first and second halves of each trial type (e.g., no stim, left trials), and correlating these half-session rate maps. Because the within baseline comparison was on session halves, i.e., fewer trials to generate the ratemap, the baseline versus stimulation comparisons were also performed on correlations between the first half of baseline, and first half of stimulation trials.

Spatial information was calculated in bits per spike (Skaggs and McNaughton, 1992) as,

$$\text{SPI}=\sum _i{p}_i\frac{{\lambda }_i}{\lambda }\log 2\frac{{\lambda }_i}{\lambda }$$

where λ_i is the mean firing rate of a unit in the i^th bin, λ is the overall mean firing rate, and p_i is the probability of the animal being in the i_th bin (ocuupancy in i_th bin/total time).

Downsampled maps were generated by first detecting the number of spikes in the center versus side arms for each cell separately for baseline and stimulation trials. Spikes in the baseline trials were randomly subsampled to match the number of spikes during stimulation, separately for the center and side arms of the maze. Rate maps were constructed using these downsampled spike matrices, and all subsequent analyses were conducted as described above.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical analysis

Data collection was not performed blinded to the subject conditions, but data analysis or behavior experiments did not require manual scoring. All stimulation conditions were performed randomly, and animals from different experiments were run in parallel cohorts. No specific analysis was used to estimate minimal population sample, but the number of animals, trials and recorded cells were larger than or similar to those employed in previous studies (McKenzie et al., 2021; Senzai et al., 2019; Valero et al., 2021; Zhang et al., 2021). All statistical tests were conducted using MATLAB R2021a, and the details of the tests used are described with the results. Unless otherwise noted, all tests used non-parametric comparisons of means and variance (Wilcoxon paired signed rank tests, Wilcoxon ranksum test, Kruskal-Wallis one-way analysis of variance, and Friedman tests). When parametric tests were used, the data satisfied the criteria for normality (Kolmogorov-Smirnov test) and equality of variance (Bartlett test for equal variance). All posthoc tests were performed using Tukey honest significant differences and correcting for multiple comparisons. Boxplots represent the median and 25^th and 75^th percentiles, and the whiskers represent the data range. In box plots without datapoints, outliers were excluded from the plots, but always included in the statistical analysis.

Supplementary Material

2

Movie S1. CSD profile and spiking activity during behavior with mEC optogenetic silencing in the center arm. Related to Figure 2.

Data from a 64-site recording session (the same as that shown in Fig. 2B) along the CA1-DG axis as the mouse is running on a delayed spatial alternation task. Bottom-left, current position of the mouse on the alternation task. The delay zone (10s) is at the bottom center of the maze, while the reward ports are at the top-left and top-right corners. Top-right, Spike rasters from CA1 interneurons (dark purple), CA3/DG interneurons (light purple), CA1 pyramidal cells (dark yellow) and CA3/DG pyramidal cells (light yellow). Bottom-right, CSD, calculated from the LFP. mEC optogenetic silencing starts immediately after the delay at 1s and 33s timepoints (marked by a solid blue line, and a ‘Stim ON’ label), and ends after the animal makes a choice on the center arm. Notice near-complete inhibition of CA3/ DG cells, and a huge decrease in the CSD theta amplitude upon mEC silencing

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
AAV5-mDlx-ChR2-mCherry	Plasmid gift from Dr. Gord Fishell, Virus custom prepared by Addgene	N/A
AAV1-CamKIIα-stGtACR2-FusionRed	Mahn et al, Nat Commun. 2018	RRID:Addgene_105669
AAV5-Syn-DIO-PSAM4-GlyR-IRES-GFP	Magnus et al, Science, 2019	RRID:Addgene_119741
Chemicals, peptides, and recombinant proteins
μPSEM792 hydrochloride	Tocris	Cat#6865
C&B Metabond	Parkell	Cat#S380
Experimental models: Organisms/strains
Mouse: B6.Tg(Grik4-cre)G32-4Stl/J	Jackson Laboratories	RRID: IMSR_JAX: 006474
Software and algorithms
KiloSort (template based spike sorting MATLAB software)	Pachitariu M & Cortex-lab	https://github.com/cortex-lab/KiloSort
KilosortWrapper	Peter C. Petersen & Brendon Watson	https://github.com/petersenpeter/KilosortWrapper
Phy (Python GUI for manual spike curation)	Cyrille Rossant, Ken Harris et al.	https://github.com/cortex-lab/phy
Phy plugins	Peter C. Petersen	https://github.com/petersenpeter/phy-plugins
CellExplorer (Cell classification pipeline and graphical interface)	Peter C. Petersen & Gyorgy Buzsaki	http://cellexplorer.org / DOI: https://doi.org/10.1016/j.neuron.2021.09.002.
MATLAB	MathWorks	https://www.mathworks.com/
Buzcode (MATLAB analysis tools)	Buzsaki Lab	https://github.com/buzsakilab/buzcode (DOI: 10.5281/zenodo.5668715)
Custom MATLAB scripts	Ipshita Zutshi	https://github.com/IpshitaZutshi/Zutshi_Neuron2021 (DOI: 10.5281/zenodo.5668669).
FMA Toolbox (MATLAB toolbox for Freely Moving Animal (FMA))	Michael Zugaro	https://fmatoolbox.sourceforge.net/
Chronux toolbox	Mitra lab	http://chronux.org/
Other
Silicon probes	Neuronexus, Cambridge Neurotech, Diagnostic Biochips	A5x12-16-Buz-Lin, H2, H3, P128-2
RHD2000 USB Interface Board	Intan Technologies	C3100
64 channel digital amplifies	Intan Technologies	C3314
PulsePal v2	Sanworks	N/A
3D printed microdrives	Mihály Vöröslakos & Gyorgy Buzsaki	Voroslakos et al, 2021

HIGHLIGHTS.

• Unilateral or bilateral silencing of the mEC decreases theta and gamma currents.

• Bilateral, but not unilateral mEC silencing causes remapping in CA1 cell assemblies.

• CA3 silencing decreases CA1 firing rates and leads to place cell remapping.

• CA1 place cells and assemblies persist despite combined mEC and CA3 silencing.