Abstract
Neurons in primate lateral prefrontal cortex (LPFC) play a critical role in working memory (WM) and cognitive strategies. Consistent with adaptive coding models, responses of these neurons are not fixed, but flexibly adjust based on cognitive demands. However, little is known about how these adjustments affect population codes. Here, we investigated ensemble coding in LPFC while monkeys implemented different strategies in a WM task. Although single neurons were less tuned when monkeys used more stereotyped strategies, task information could still be accurately decoded from neural populations. This was due to changes in population codes that distributed information among a greater number of neurons, each contributing less to the overall population. Moreover, this shift occurred for task-relevant, but not irrelevant, information. These results demonstrate that cognitive strategies that impose structure on information held in mind rearrange population codes in LPFC, such that information becomes more distributed among neurons in an ensemble.
Keywords: working memory, cognitive strategy, population coding, neural ensemble, dimensionality, lateral prefrontal cortex, macaque monkey
eTOC
Strategies are commonly used to improve working memory performance, but whether they change the information held in mind is less clear. Using a self-ordered selection task, Chiang et al. show that adopting sequencing strategies shifts information from single, highly tuned neurons to more distributed population codes in lateral prefrontal cortex.
Introduction
Higher-order cognitive abilities, such as planning and problem solving, require online organization of information. This includes cognitive strategies that impose structure on information held in mind, such as creating lists or categories. For example, servers in a restaurant might remember customers’ drink orders in a sequence so they can serve the right drink to the right person later on (Ericsson and Kintsch, 1995). Organizing information in this way allows us to overcome natural constraints on the capacity of working memory (WM). WM is the ability to hold information temporarily in mind, allowing it to be manipulated for cognitive processes (D'Esposito and Postle, 2015; Miller, 1956), but is restricted to approximately four units of stored information (Cowan, 2001; Luck and Vogel, 1997). Both WM and implementing cognitive strategies are well known to rely on intact function of the dorsolateral prefrontal cortex (dlPFC) (Bor et al., 2003; Miller, 2000; Nichelli et al., 1994), but the neural mechanisms that organize WM information online are not well understood. This is in part because it is challenging to capture the flexible, self-generated aspects of cognitive strategies that are most dependent on prefrontal function.
Cognitive strategies are deployed in many cognitive tasks, and a hallmark of prefrontal cortex function is flexible neural responses that adapt to encode relevant information under varying task demands (Duncan, 2001). Indeed, at the single neuron level, the selectivity of prefrontal neurons is not fixed, but changes depending on the task being performed (Asaad et al., 1998, 2000; Funahashi et al., 1989; Rao et al., 1997). Dynamic coding is also observed at the population level in prefrontal cortex (Meyers, 2018; Rigotti et al., 2013; Sigala et al., 2008; Stokes et al., 2013), but how this relates to changing task demands and single unit selectivity is not well understood. In some cases, it has been found that task information can be decoded from subsets of prefrontal ensembles as reliably as from the whole population (Leavitt et al., 2017; Meyers et al., 2008), suggesting that neurons provide either unequal or redundant contributions to the overall population code. More recently, empirical (Bartolo et al., 2020) and theoretical (Gao et al., 2017) approaches have shown low dimensionality of population activity obtained from large-scale recordings, suggesting constraints on the diversity of activity patterns generated by a population of neurons. However, to date, it remains unclear how these properties of population activity relate to adaptive coding commonly observed in prefrontal cortex. One possibility is that the flexible changes in single neuron responses are part of larger changes in neuronal ensembles that optimize population coding under different cognitive demands. Here, we investigated this in a WM task, by examining how ensemble encoding changes when subjects use strategies that impose structure on mnemonic information, thus changing the cognitive demands of the task.
Recently, we found that monkeys spontaneously adopt sequencing strategies in a spatial self-ordered target selection task that taxes their WM capacity (Chiang and Wallis, 2018b). Despite improved task performance, the strength of spatiotemporal tuning among neurons in the LPFC decreased with more sequential behavior. Given the involvement of prefrontal cortex in strategy implementation, the apparent loss of information from LFPC is not intuitive. To assess how changes in single unit selectivity contribute to ensemble coding under different cognitive demands, we decoded task information, including target locations, orders, and colors, from ensembles of LPFC neurons. We found that, even though the individual neurons were less tuned, the accuracy of decoding task-relevant information remained the same or increased when subjects performed more sequenced selection patterns. Further analyses revealed that the sizes of the neural ensembles that yielded optimal decoding increased with sequencing strategies, suggesting that information became more distributed within the population, but less efficiently coded at a single neuron level. Lastly, behavior that was less stereotyped lead to more diverse activity patterns, with higher dimensionality. Together, these results demonstrate that using a cognitive strategy to structure behavior systematically changes neural codes in LPFC, shifting information from single, highly-tuned neurons to populations. This additionally suggests that online adaptations of population-level codes may underlie flexible cognitive abilities.
Results
Single neuron spatial tuning is modified by self-ordered search strategies
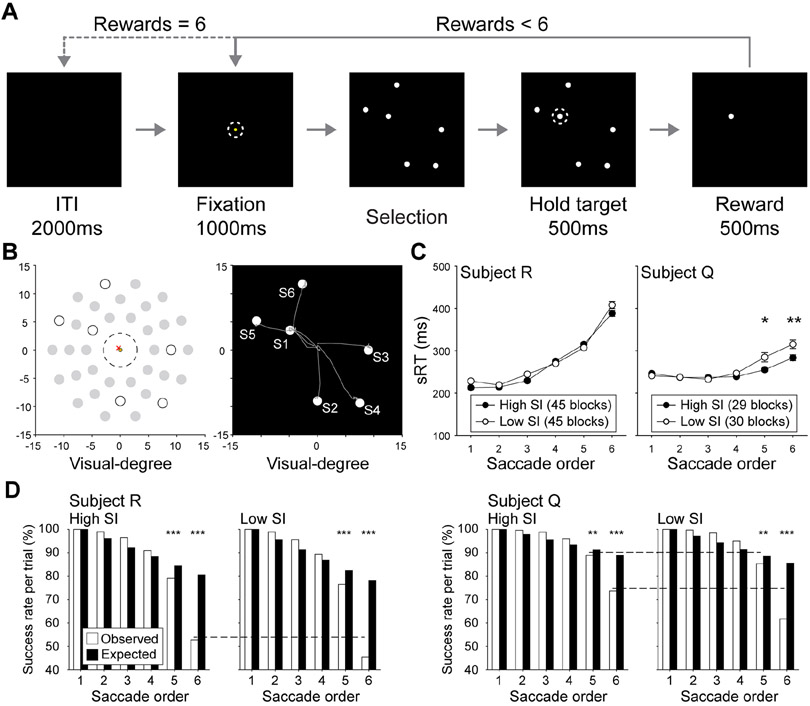
When faced with a task that exceeds the capacity limits of WM, humans and animals tend to employ mnemonic strategies. For animals, we operationally define ‘strategies’ by patterns of behavior that indicate a superordinate organization, which may or may not be deliberately selected by the subject. For instance, a previous study showed that monkeys spontaneously adopt sequencing strategies to accomplish a target selection task that required them to track the self-ordered selections of six identical visual targets (Chiang and Wallis, 2018b). In the task, two monkeys were presented with spatial configurations of targets, represented by colored circles on a computer screen. Starting from a central fixation point, they had to saccade to one target at a time to obtain a juice reward, and then return gaze to fixation before the next selections (Figure 1A and 1B). If a target was revisited within a trial, the monkey received a time-out and no reward. After each of the six targets were selected once, a new trial started after an inter-trial interval, signaled by a change in target color. Therefore, to perform well, the monkeys had to use WM to remember which targets had been visited, and update this information after each selection.
Figure 1.
Spatial self-ordered search task. (A) On each trial, monkeys fixated a yellow point in the center of the screen and were shown a configuration of 6 identical targets (white circles). They made a selection (dashed line) by saccading to and holding fixation on one target. If the target had not been visited on that trial, a reward was delivered, and the monkey had to move his eyes back to the central fixation point before making another selection. This continued until all targets were visited once, at which point the trial ended and was followed by an intertrial interval (ITI). (B) An example trial with the target selection pattern. Gray trajectories indicate saccade paths starting from fixation to each target. S1 to S6 indicates target selection order. (C-D) Blocks were divided into high and low SI groups by a median split of each session. (C) A multiple linear regression model predicted RTs from saccade order, high/low SI block, and order x block interaction. In both subjects, RTs increased across saccades, suggesting later selections were more difficult (main effect of order p < 0.001 for both). For subject R, RTs during high SI blocks were faster than low SI blocks (main effect of SI block p < 0.05), and for subject Q, there were faster RTs during high SI blocks on the last two saccades (order x SI block interaction p < 0.001, post-hoc comparisons, *p < 0.05, **p < 0.01). (D) Monkeys make more errors than expected later in selection sequences. Expected success rates were calculated as a linear function of the number of potentially incorrect saccades possible at each selection (see STAR Methods), and observed rates were the number of correct selections divided by the total number of trials (Chiang and Wallis, 2018b). Monkeys performed better than the expected when WM loads were low, but performance declined precipitously when capacity was exceeded (binominal tests, **p < 0.01, ***p < 0.001). Performance was enhanced on high SI blocks specifically during later target selections, when WM began to falter (Chi-square tests, dashed lines indicate p ≤ 0.01).
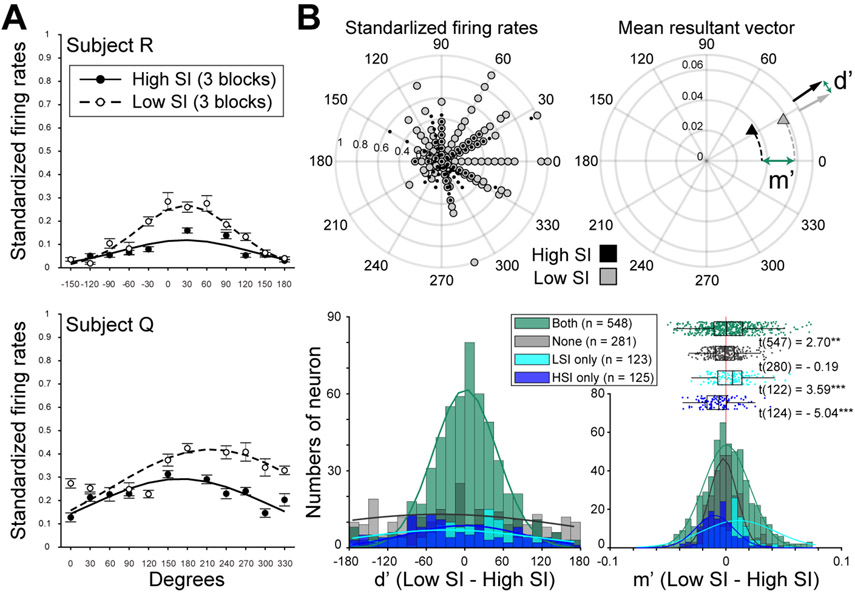
Each recording session consisted of six blocks of 40 trials, with target configurations held constant within a block. This allowed target selection patterns to be quantified within each block. Previously, a measure of target sequencing, termed stereotyped index (SI), was defined to quantify the similarity of target selection patterns in a given block (see STAR Methods). Higher SIs indicated blocks in which targets tended to be visited in the same order, and lower SIs indicated blocks with more diversity in selection orders. Using this approach, SIs varied block to block, but there was no evidence for systematic changes in SI depending on the configuration of targets, the block number within a session, or the session number (Chiang and Wallis, 2018b) (Supplemental Table S1). However, behavior patterns indicated that sequencing strategies improved WM performance. Revisit errors were not equally distributed across six target selections, but occurred predominantly in the last two selections. This pattern suggests that monkeys used WM to complete the task (see STAR Methods), and the final targets exceeded a limited WM capacity (Chiang and Wallis, 2018b). Importantly, employing a sequencing strategy improved both errors and reaction times (RTs) in these last two selections, suggesting the strategy augmented WM performance (Figure 1C and 1D). In addition, it was shown that LPFC neurons encode the spatial and sequential information required to perform the target selection task (Chiang and Wallis, 2018b), but the amplitude of spatial tuning significantly decreased as target selection patterns became more stereotyped (Figure 2). This feature of stable spatial tunning with amplitudes modulated by task demands has previously been found in primate dIPFC in another self-organized behavioral task (Procyk and Goldman-Rakic, 2006).
Figure 2.
Sequencing strategies decrease spatial tuning among single neurons. (A) Two single-neuron examples, recorded from subject R (left) and Q (right), showing the effects of the sequencing strategies on spatial tuning. The x-axis refers to the angle, in polar coordinates, of the selected target on the screen. Filled circles are from the three blocks in an exemplar session with higher SIs. Empty circles are from the three blocks in the same session with lower SIs. Flatter tuning curves were observed when the animal was searching through the targets using a more stereotyped strategy (Chiang and Wallis, 2018b). (B) Changes in spatial tuning were quantified by the change in direction (d’) and magnitude (m’) of resultant vectors for standardized firing rates in high and low SI blocks. The first circular plot shows standardized firing rates for one example neuron. The second shows the end points of the resultant vectors for each group (triangles), with m’ and d’ measures. Histograms show d’ and m’ for each single unit, grouped according to when they exhibited spatial selectivity: in both high and low SI blocks (green), low SI only (teal), high SI only (blue), or neither (gray). The direction of spatial tuning shifted slightly in the high SI group (deviation from zero degrees t124 = −2.51, p = 0.013), when directional tuning was weak. Other groups showed no shift in tuning direction (p > 0.05). In contrast, there was consistently stronger tuning in low SI blocks (positive m’) among neurons that exhibited spatial tuning in low SI only or both low and high SI blocks, constituting the majority of recorded neurons. Those with spatial tuning in high SI blocks only had significantly negative m’ distributions, and those with no tuning had distributions centered at zero. **p < 0.01. ***p < 0.001.
No loss of task information in LPFC ensembles with stereotyped behavior patterns
Populations of approximately 40 LPFC neurons were simultaneously recorded during task performance (47.27 ± 2.72 for subject R and 36.80 ± 2.14 for subject Q; Supplemental Table S1), allowing us to assess how task information is represented at the ensembles level. We created three decoders to examine representations of target locations (target A to F), saccade orders (correct saccade 1 to 6, excluding revisits), and target colors (green, blue, and white). Each variable was decoded from ensembles of simultaneously recorded LPFC neurons using linear discriminant analysis (LDA) with leave-one-saccade-out cross validation (Supplemental Figure S1, see STAR Methods). Classifier performance was assessed separately for each block of 40 trials. The feature matrices used for the three decoders were identical, with columns consisting of each recorded unit, and six correct saccade responses (revisit errors excluded) x 40 trials comprising the rows. The elements of the feature matrix were the mean firing rates in a given epoch.
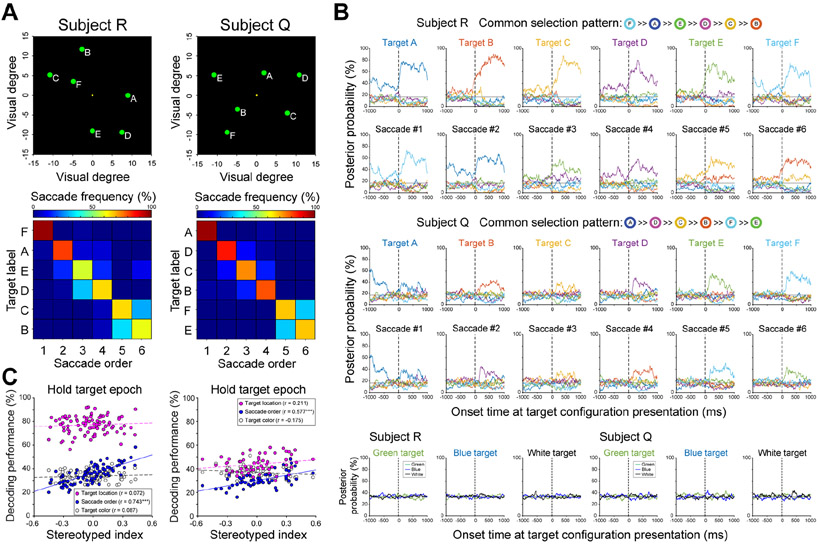
We found that neural ensembles in LPFC represented both target locations and saccade orders (Figure 3B). These were decoded as categorical variables that changed across selections within a trial according to the onset time of the 6-target configuration. In Figure 3B, the posterior probability of the selected target or current saccade number, but not target color, increased as the monkey initiated each saccade response. That is, when ‘target A’ was selected, the posterior probabilities for A were high, and this pattern switched to B then C, et cetera as each was subsequently selected (Figure 3B, top panel). Similarly, the posterior probabilities of the current saccade number also increased on each successive saccade (Figure 3B, middle panel). Overall, in a 500ms time window after the monkey selected a target, the posterior probabilities for the correct target location and saccade order were 0.33 ± 5x10−3, 0.184 ± 3.7x10−3 for subject R, and 0.25 ± 3.7x10−3, 0.183 ± 3.3x10−3 for subject Q, respectively (for held-out data), significantly higher than those for the non-selected targets or incorrect saccade numbers [0.134 ± 0.001, 0.163 ± 7.4x10−4 for subject R and 0.15 ± 7.5x10−4, 0.163 ± 6.7x10−4 for subject Q, respectively. Wilcoxon signed-rank test p = 1.4x10−86, 0.01 for subject R; p = 1.6x10−58, 3.0 x 10−4 for subject Q]. Therefore, both target location and saccade number could be decoded from LPFC ensembles. In contrast, posterior probabilities for target colors were close to chance level (Figure 3B, bottom panel) [0.333 ± 1.1x10−3 and 0.334 ± 5.7x10−4 for subject R; 0.348 ± 1.8x10−3 and 0.326 ± 8.9x10−4 for subject Q, chance = 33.3%]. This is likely because different colors were only used to indicate the beginning of a new trial and were not themselves relevant to performance of the WM task.
Figure 3.
Target location and saccade order, but not target color, can be decoded from LPFC ensembles. (A) Two sample target configurations with saccade frequency matrices from two subjects. Targets at unique locations were arbitrarily assigned a letter for analysis. The matrices show the proportion of trials within a block that each target was selected first, second, etc. These example blocks show strong sequencing behavior, with high frequencies on the main diagonal. (B) Posterior probabilities calculated for each of six target selections, across 40 trials from the same blocks shown in A. Top and middle panels show posterior probabilities of target locations and saccade orders from both subjects, and the bottom panel shows target color. Dotted lines indicate the onset time of the target configurations, and gray line indicates the chance level. The common saccade order was defined by the sorted saccade frequencies in A. Color labels indicate different targets or target colors. (C) The decoding performance during the hold target epoch for target location (pink circles), saccade order (blue circles) and target color (empty circles) decoders, as a function of SI in each block. Person correlation, ***p < 0.001. Left panel: subject R (n = 90 blocks). Right panel: subject Q (n = 59 blocks).
Next, we examined how stereotyped selection patterns interact with our ability to decode the three task variables during the epoch of highest decoder performance (hold target epoch, 500ms following each saccade. Supplemental Figure S2). Based on the earlier finding that single neurons were less spatially tuned when behavior was more stereotyped, we anticipated poorer decoding of target locations in higher SI blocks. However, this was not the case. Figure 3C shows that decoding performance for each variable was unaffected or improved in higher SI blocks. To quantify this, we performed a two-way ANCOVA on decoding performance with continuous variable SI and categorical variable decoder type. There were significant main effects of decoder type [F(2,264) = 1670.55, p < 0.001 for subject R; F(2,171) = 87.96, p < 0.001 for subject Q], and SI [F(1,264) = 36.61, p < 0.001 for subject R; F(1,171) = 11.07, p = 0.0011 for subject Q], with better decoding of target locations compared to the saccade orders and target colors in both monkeys. In addition, there were significant interactions between SI and decoder type in both subjects [F(2,264) = 22.59, p < 0.001 for subject R; F(2,171) = 8.76, p < 0.001 for subject Q], with performance of the saccade order decoder improving with higher SI, but target location and color decoders remaining unchanged. This was confirmed by post-hoc comparisons, showing that target location decoding did not depend on SI in either subject [Pearson correlation, r = 0.07, p = 0.502, for subject R; r = 0.21, p = 0.108, for subject Q], but saccade order decoding improved with higher SI [Pearson correlation, r = 0.74, p < 0.001, for subject R; r = 0.58, p < 0.001, for subject Q]. More sequenced behaviors did not appear to activate multiple target representations simultaneously. When blocks were pooled into high and low SI groups by a median split of behavior in each session (HSI, LSI respectively), there was consistently better decoding of the current target location or saccade position on HSI blocks, but no changes in information about the immediately preceding or following selections (Supplemental Figure S3). Finally, there were no correlations between performance of target color decoder and SI [Pearson correlation, r = 0.08, p = 0.414, for subject R; r = −0.18, p = 0.184, for subject Q]. Together, results from both subjects showed equal or better decoding of task variables as behavior became more stereotyped, despite loss of spatial tuning among single neurons.
Given these results, one possibility is that as SI increases, target identities and saccade orders become more correlated so that a decoder for either variable could improve by relying on information about both categories rather than just one. Despite this correlation, however, the performance of the two task-relevant decoders did not converge at higher SIs, suggesting that the representations were not completely overlapping (Figure 3C). Further analyses using partial correlations revealed that better saccade order decoding at higher SIs was largely accounted for by correlations with target location, but the accuracy of target location decoding increased with higher SIs after controlling for the actual X,Y position and saccade order (Supplemental Figure S4 and Supplemental Table S3). We also examined each unit’s mean firing rate as the independent variable rather than decoder performance and found no tendencies toward weaker or stronger relationships between firing rate and saccade order or target identity as SI increased (Supplemental Figure S4), meaning that changes in mean firing rate do not explain how decoder performance was maintained during more stereotyped performance.
Shared variability among neurons has been shown to impact information decoding, either positively or negatively (Ben Hadj Hassen and Ben Hamed, 2020; Cohen and Kohn, 2011; Nogueira et al., 2020; Tremblay et al., 2015), so we tested whether there were systematic changes in noise correlations in blocks where monkeys’ behavior was more stereotyped. We assessed whether the proportion of neuron pairs with correlated variability changed across blocks with different SIs, but did not find reliable evidence for consistent effects (Supplemental Table S4). Therefore, it’s unlikely that decoding accuracy was impacted by systematic changes in noise correlations across blocks.
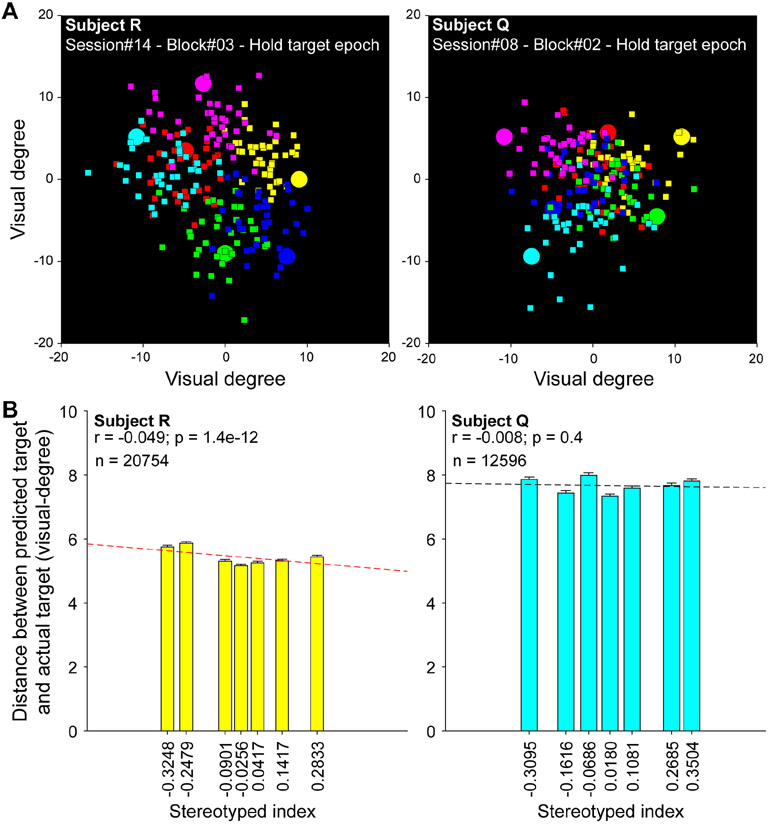
Finally, because LDA classifiers may have been subject to ceiling effects in target decodability (Figure 3C), we assessed a more sensitive measure of spatial information in LPFC ensembles that is independent of saccade order. We decoded two-dimensional spatial coordinates for each target from the same neural activity feature matrix including all trials in a recording session (i.e., across blocks with different SIs) (Astrand et al., 2016). To define decoding performance, we found the Euclidean distance between predicted and actual target locations. A small distance indicated a prediction that was close to selected target, and therefore accurately decoded. We found that performance of the 2-D spatial decoder improved as SI increased in subject R, and there was no change with SI in subject Q [Pearson correlation, r = −0.049, p < 0.001, for subject R; and r = −0.008, p = 0.399, for subject Q] (Figure 4). Therefore, despite reductions in spatial tuning at the single neuron level, there was again no loss of accuracy in decoding target locations from ensembles of the same neurons.
Figure 4.
Two-dimensional spatial decoding. (A) Example target configurations, in which each target (circles) is color-coded, to show the corresponding locations of the predicted targets (squares). Different color labels were used for visualization only; targets in the task were identical. Note that the decoder was trained and tested across blocks with different SIs and target configurations, but the same neuron ensemble. (B) Decoding performance was quantified for each target selection as the Euclidean distance between actual and predicted targets and plotted as a function of SI. Performance improved with SI in subject R and was unaffected subject Q, demonstrating no loss of spatial information at the population level with more stereotyped behaviors. For data visualization, the original scatter plots (Supplemental Figure S5) were binned by SI into 7 subgroups with an equal number of observations in each. The SI value on x-axis for each bar is the mean of SIs within the subgroup.
Single units make different contributions to ensemble codes
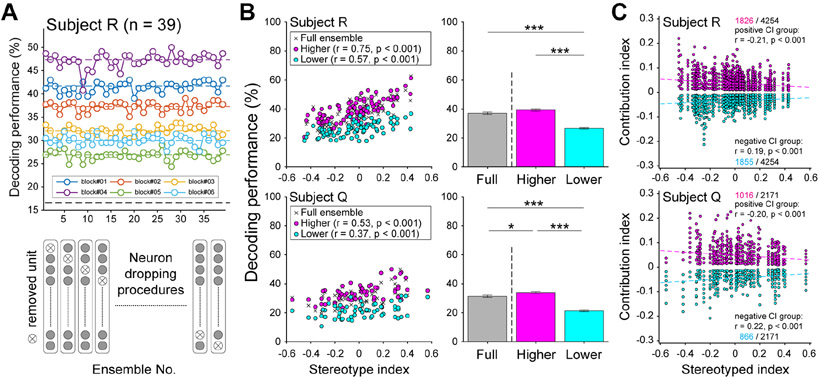
To understand how population coding changed when monkeys used sequencing strategies, we assessed the contributions of each unit to the ensemble’s decoding performance using a neuron dropping procedure (Narayanan et al., 2005; Nicolelis, 1998). First, we found the accuracies of LDA classifiers trained and tested on N-1 ensembles, where one unit was iteratively removed from a full ensemble of size N. A unit’s unique contribution was quantified by the difference in performance between the full and N-1 ensembles, with reductions in decoding accuracy corresponding to positive contributions and improvements in decoding accuracy corresponding to negative contributions. This approach takes interactions between neurons into account, since neurons providing redundant information would have approximately zero contribution.
Six exemplar blocks in the top panel of Figure 5A show decoding of saccade order using N-1 ensembles, where the horizontal line is the median performance in that block, and each circle is performance with a different held-out neuron. These blocks were recorded from the same session, so the ensemble remained constant, illustrating how the contributions of the same neuron can vary across blocks with different target configurations. In the full data set, only rare neurons [16 out of 1077, 1.5%] kept the same type of informative contribution consistently across blocks. In addition, there were differences in median decoding performance across blocks within a recording session, implying that decoding depends on the target configurations and/or block-wise changes in behavior.
Figure 5.
Units make smaller contributions to the ensemble when behavior is more sequenced. (A) Diagram of the neuron dropping procedure in a sample recording session. Six blocks from the same session are labeled by different colors. Average performance from a saccade order decoder (y-axis) varied across blocks. In the neuron dropping procedure, the same decoder was run while iteratively removing one unit from the ensemble (bottom schematic). (B) Scatter plots show block-wise mean saccade order decoding as a function of SI for the full ensemble (+), higher contribution (magenta), and lower contribution (cyan) subgroups. Decoding performance corresponds to the proportion of target selections accurately classified. Bar plots show the overall means, collapsed across SI. (Pairwise t-tests, ***p < 0.001, *p < 0.05). (C) Population data showing CI as a function of SI. Each point is the contribution of one neuron to one block. Neurons making positive contributions (magenta) improved decoder performance, while those making negative contributions (cyan) reduced it. The contributions of the positive groups decreased as SI increased, and contributions of the negative groups increased as SI increased.
To determine whether some neurons consistently contribute more to population decoding, we separated each full ensemble into two sub-ensembles. If a given neuron’s contribution was greater than or equal to the median decoding performance in at least 3 out of 6-blocks in a session, then that neuron was included in the higher contribution subgroup, and the remainder were included in the lower contribution subgroup. Consistent with our earlier results, we found that decoding improved in blocks where selection patterns were more sequenced, and the higher contribution subgroup performed similarly to the full ensemble (Figure 5B). In addition, decoding performance was lower among the low contribution group, but still tended to increase with SI [SI x contribution group ANCOVA; main effect of SI: F(1, 176)= 151.86, p < 0.001, for subject R; F(1, 114) = 30.4, p < 0.001, for subject Q. Main effects of contribution groups: F(1, 176) = 343.6 , p < 0.001 for subject R; F(1, 114) = 205.43, p < 0.001, for subject Q; interaction: F(1,176) = 17.02, p < 0.001, for subject R; F(1,114) = 2.61, p = 0.109, for subject Q]. In post-hoc comparisons, both contribution groups were positively correlated to the SI [Pearson correlations, higher contributions: r = 0.75, 0.53, both p < 0.001, for subject R and Q; lower contributions: r = 0.57, 0.37, p < 0.001, 0.004 for subject R and Q]. In comparison to the full ensemble, the higher contribution groups achieved similar or higher accuracies, while the lower contribution group performed worse [ means ± SEM 0.39 ± 0.008 full, 0.37 ± 0.008 high, 0.27 ± 0.005 low for subject R; 0.31 ± 0.008 full, 0.34 ± 0.008 high, 0.21 ± 0.006 low for subject Q]. One-way ANOVA on decoding performance with post-hoc comparisons confirmed these results [F(2, 269) = 85.83, p < 0.001, for subject R; F(2, 176) = 81.63, p < 0.001 for subject Q. Bonferroni corrected post-hoc comparisons: Full versus high: p = 0.078, 0.034; Full versus low: both p < 0.001; High versus low: both p < 0.001, subject R, Q]. Thus, the neural representations of saccade orders could be extracted from subsets of the full recorded population, and removing the less informative neurons had little effect on accuracy. We found similar results from the target location decoder (Supplemental Figure S6). This emphasizes that there is variability and potentially redundancy in the contributions individual neurons make to population codes (Hung et al., 2005; Meyers et al., 2008; Narayanan et al., 2005)
Next, we wanted to determine whether the contributions of neurons changed as the monkeys’ target selection patterns became more sequenced. To better understand this question, we created a standardized contribution index (CI) for each unit in each block, defined as the ratio of the difference between the mean decoding performance from the full ensemble (N) and the N – i ensemble after removing neuron i (see STAR Methods). Positive or negative CIs indicate that neuron i improved or reduced the decodability, respectively, and zero CI indicated that the neuron provided redundant information and made no contribution to decoding. Using this approach, we found that the proportion of positive or negative CI units did not vary with SI (Pearson correlations all p > 0.05), but the magnitude of both positive and negative CIs decreased as behavior became more stereotyped (Figure 5C). In the target location decoder, this effect was stronger for positive compared to negative CIs (Supplemental Figure S6). This was confirmed by significant interactions in two-way ANCOVAs (SI x contribution type) predicting CI in both monkeys [F(1, 3677) = 148.67, p < 0.001, for subject R; F(1,1878) = 85.56, p < 0.001, for subject Q]. Post-hoc comparisons found that, for the saccade decoder, neurons with positive contributions were negatively correlated with SI, while those with negative contributions were positively correlated [n = 1826, 1016 positive, 1855, 886 negative out of 4254, 2171 neurons for subject R, Q; Pearson correlations, positive: r = −0.21, −0.20, both p < 0.001 for subject R, Q; negative: r = 0.19, 0.22, both p < 0.001 for subject R, Q], and similar results were found for the target location decoder (Supplemental Figure S6). Therefore, the contributions of single neurons to an ensemble’s decoding performance consistently decreased in magnitude as behavior became more stereotyped. This suggests fundamental changes in the population codes for task-relevant information in LPFC under different self-generated cognitive strategies. In addition, the data indicate that the diversity of contributions among both positively and negatively contributing neurons became smaller during the routine behavioral strategies. This is consistent with smaller, more homogenous contributions to decoding performance, and may reflect loss of strong tuning among single neurons as previously described (Chiang and Wallis, 2018b). Together, these analyses show that units make unequal contributions to the overall representation, and these contributions can change under varying behavioral patterns. With this in mind, we next address the question of why task-relevant decoders perform equally well or better when individual neurons make smaller contributions under more stereotyped behavioral strategies.
Optimal ensemble sizes varied by behavioral strategy
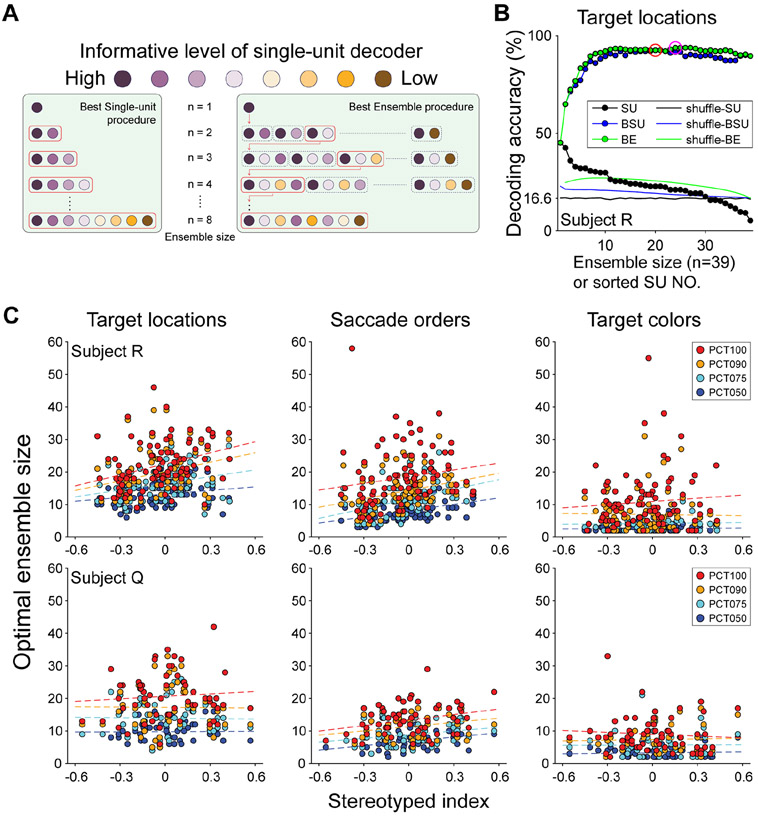
Our findings so far show that, when decoding task information, some neurons in an ensemble are redundant or non-contributing. This means that in a given recorded population, the best decoding accuracies can be achieved with less than the full ensemble. To better understand ensemble coding and how it changes, we determined the optimal ensemble size for maximum decoding in each trial block. We used two approaches: best single-unit (BSU) and best ensemble (BE) procedures to assess how decoding performance changes as ensemble size gradually increases (Backen et al., 2018; Leavitt et al., 2017). Both BSU and BE add units one at a time into the ensemble to build feature decoders (Figure 6A), but differ in how they select which neuron to add. The BSU procedure rank orders the decoding performance of all single-unit (SU) decoders, and then adds units one at a time by descending rank into the ensembles. In contrast, the BE procedure takes all possible combinations of units into account and increases the ensemble size by adding whichever unit leads to the maximum decoding performance. Both procedures are performed iteratively until all units have been added.
Figure 6.
Optimal ensemble sizes increase with SI. (A) Schematic of BSU and BE procedures adapted from (Backen et al., 2018; Leavitt et al., 2017). In the BSU procedure, the information carried by each neuron is determined by a single-unit decoder, and the ensemble size is gradually increased by iteratively adding units based on their information rank. The BE procedure starts with the most informative neuron then tests all possible combinations of neurons to iteratively select one that produces the maximum decoding performance at that step. (B) Performance of the target location decoder from subject R in an example block. Black symbols show ordered single-unit decoders. Filled circles show BSU (Blue) and BE (Green) accuracies as neurons are added to the ensemble. Red and magenta circles indicated the ensemble size with maximum decoding accuracies for each approach. The same procedures were also used on shuffled data sets (BSU in blue, BE in green, and single unit in black lines, see STAR Methods). Note that BSU and BE procedures selected ensembles optimized to decode real or shuffled data, so that shuffled accuracies are slightly above theoretical chance, as observed in other studies (Backen et al., 2018; Leavitt et al., 2017). The chance level for target location and saccade order decoders was 16.6%, and for target color decoder was 33.3%. (C) Optimal ensemble sizes increase with sequencing. Optimal ensemble sizes at each PCT as a function of SI for target location, saccade order, and target color decoders from two subjects. Ensemble sizes were higher with high SI for task-relevant (location and order), but not irrelevant (color) information.
Following both BSU and BE procedures, we decoded three variables for each block - target location, saccade order, and target color. Decoding was conducted with LDA, and accuracies were based on leave-one-out cross validation. Decoding accuracies improved and eventually asymptoted as ensemble sizes increased under either the BSU or BE procedure (Figure 6B, Supplemental Figure S7). Optimal ensemble sizes were defined as the smallest size to achieve maximum (100 percentile, PCT100) decoding performance. Because accuracy curves fluctuated slightly around the plateau, we also identified the ensemble sizes corresponding to 50th, 75th, and 90th percentile of the maximum decoding performance (PCT50, PCT75, and PCT90 respectively) in each block for further analyses. Compared to the BSU, BE produced higher maximum performance in all three types of decoders because it takes into account how redundant or complimentary the units in the ensemble are. The color decoders performed closest to shuffled baselines, indicating that color information is weakly represented compared to the target locations or saccade orders, likely because color is less relevant to task performance (Supplemental Figure S7A). Optimal ensemble sizes for target location and saccade order tended to be positively correlated (Supplemental Figure S7B), indicating that blocks in which more neurons were required to reach maximum accuracy in spatial decoding also required more neurons to accurately decode saccade order. Interestingly, these co-varying ensemble sizes also appeared to correlate with SI, such that lower SI blocks tended to have smaller optimal ensemble sizes. To quantify this observation, we performed two-way ANCOVAs with categorical factor PCT and continuous factor SI predicting optimal ensemble size, and found that ensemble sizes increased with SI for the saccade decoder in both animals (Figure 6B) [significant main effect of SI: F(1, 352)= 32.77, p < 0.001, for subject R; F(1, 228) = 20.98, p < 0.001, for subject Q], and for the target decoder in one animal [F(1, 352) = 33.70, p < 0.001, for subject R; F(1, 228) = 0.10, p < 0.76, for subject Q]. In contrast, decoding of color, which was less relevant to the working memory component of the task, did not vary with SI in either animal [F(1, 352)= 0.41, p = 0.52, for subject R; F(1, 228) = 0.02, p = 0.88, for subject Q]. Overall, these data demonstrate that optimal ensemble sizes for decoding task-relevant, but not irrelevant, information increased as the SI increased, so that more neurons were required to accurately decode task-relevant information when behavioral strategies became more stereotyped.
Neural dimensionality varies by behavioral strategy
According to the results above, strategy use in the self-ordered WM task decreased single neuron contributions to ensemble coding and increased optimal ensemble sizes for task-related decoding. In a final analysis, we focused on whether these changes are reflected in the dimensionality of LPFC activity under different behavioral strategies. We specifically investigated dimensionality over the time course of the six correct saccades in each trial and determined how it varied with SI across successive saccades.
Our previous results showed that reaction times increased and success rates decreased across saccades (Chiang and Wallis, 2018b), suggesting that WM loads increased as the monkey progressed through six target selections and kept track of which had already been selected. Thus, dimensionality of neural responses may be affected by WM load as well sequencing strategies that impose structure on that information held in mind. Different measurements of dimensionality in neural populations have been used in different experimental systems (Abbott et al.; Ganguli and Sompolinsky; Gao and Ganguli; Rigotti et al.). Here, we used the participation ratio (PR) (Dąbrowska et al., 2021; Gao et al., 2017) that finds the number of dimensions needed to explain around 80-90% of the total variance in a population covariance matrix (Dąbrowska et al., 2021; Gao et al., 2017). We computed the covariance matrices from average firing rates in 20 ms non-overlapping bins that spanned four trial epochs around each correct saccade (Supplemental Figure S1). Therefore, the resulting PR reflects similarities in the pattern of firing rates across neurons on each saccade, and a low PR can be interpreted as a more homogenous firing rate profile.
To determine how PR varied across saccades, we created a multiple linear regression model to predict PR from saccade number (1 to 6) and SI in the corresponding block for each monkey. Only correct saccades were included, and PRs within each session were z-scored to make different recording sessions comparable. In addition, a third predictor indicated the number of simultaneously recorded signals in the corresponding recording session, since this can affect PR values (Mazzucato et al., 2016). Overall, this model significantly explained dimensionality changes across target selections in both subjects [p < 0.001, for subject R and Q]. The PR was positively correlated with saccade number [b1 = 0.027, 0.019, both p < 0.001, for subject R, Q], and negatively correlated with SI [b2 = −0.081, −0.088, both p < 0.001, for subject R, Q]. Therefore, as the WM load increased across saccades, patterns of firing rates become more diverse (i.e., more eigenvectors were needed to capture the same amount of variance). Note that this result does not imply that saccade order is encoded as dimensionality, but rather that the diversity of firing rate patterns increases as the monkey proceeds through six target selections in a trial. On the other hand, when monkeys enlist sequencing strategies, this diversity is reduced, consistent with the notion that these strategies reduce WM load. Together, these dynamic changes of dimensionality suggest that firing patterns in neural ensembles become more diverse when more information is needed for successful performance (e.g. remembering selected targets), and return to their initial status when a new trial begins and the information held in WM resets. In addition, dimensionality was modulated by a cognitive strategy that improved WM performance. Therefore, neural dimensionality reflects not only behavior-related states such as motor preparation (Churchland et al., 2006) and resting state (Dąbrowska et al., 2021), but also task demands such as rule learning (Bartolo et al., 2020; Durstewitz et al., 2010), cognitive strategies, and WM loads.
Discussion
When a cognitive task exceeds the limits of our WM abilities, performance can be improved with mnemonic strategies that organize the information held in mind. One common strategy is to remember lists that arrange items in an arbitrary sequence (Desrochers et al., 2015; Desrochers et al., 2010; Ericsson and Kintsch, 1995; Lashley, 1951). This process likely relies on the LPFC, an area that plays a role in both WM and the use of mnemonic strategies. Supporting this, previous studies have found that LPFC neurons demarcate boundaries of well-learned sequences (Fujii and Graybiel, 2003), and BOLD signals in human LPFC increased when structured sequences were recognized (Bor et al., 2003). However, little is known about how an organizing structure such as a sequence changes coding of mnemonic information. In this study, we found that self-generated sequencing strategies reorganize ensemble-level coding of task information in LPFC, such that more stereotyped behaviors were governed by more distributed codes. Distributed coding that relies less on strongly tuned neurons may be more robust and generalizable (Morcos et al., 2018), and our results suggest that distributed codes are also used to optimize performance of capacity-limited WM networks.
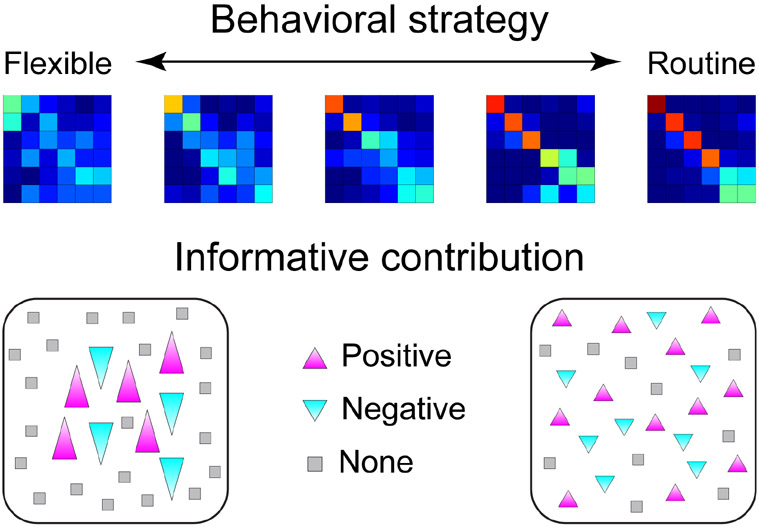
To summarize empirical findings from behavior, single-units, and ensembles in this task, we propose a schematic of how representations change with the implementation of sequencing strategies (Figure 7). Behaviorally, monkeys appear to use WM to perform the task, making fewer errors on early saccades, when visited targets can be held in mind, but many more errors on the last saccades, when the list of visited targets exceeded WM capacity. To solve this task, subjects were able to generate flexible or routine (i.e., sequenced) target selection patterns, and the latter improved behavioral performance, measured as fewer target revisits per trial. This benefit occurred primarily on the final saccades, when WM begins to falter, indicating that sequencing behavior allowed the monkeys to overcome capacity limits on WM. We found that task-relevant information, including target locations and saccade orders, could be decoded from LPFC neural ensembles, and decoding accuracy tended to improve when monkeys’ selection patterns were more stereotyped. However, this improvement was not intuitively explained by previous work showing that, in the same neurons, the amplitude of spatial tuning decreased when the monkeys used more routine strategies (Chiang and Wallis, 2018b). To reconcile these seemingly contradictory results, we showed that individual neurons made smaller contributions to ensemble decoding when the monkey’s behavior was more sequenced, while at the same time the ensemble sizes that optimized decoding performance increased. These results explain how decoding accuracy was maintained despite reduced spatial tuning among individual neurons. As the monkeys followed a more routine sequence, task information at the population level consisted of smaller contributions from a greater number of units. Consistent with this, we found that dimensionality of firing rates decreased when more routine strategies were adopted, meaning that the activity patterns became more homogenous across the population. Overall, we conclude that representations of task information become more distributed in LPFC ensembles when monkeys use a sequencing strategy. These distributed representations may overcome WM constraints, perhaps by increasing the fidelity of information critical for task performance.
Figure 7.
Sequencing strategies shift information from single units to populations. (Top) Self-generated strategies varied across blocks, from flexible to routine. Selection frequencies for example blocks are similar to Figure 2, with warm colors on the diagonal indicating that selections frequently occur in the same order. (Bottom) Schematic of neural ensembles from the extremes of the flexible-routine spectrum. Triangle size indicates the amplitude of each neuron’s contribution. When strategies are more routine, larger group of units with smaller individual contributions are recruited; otherwise, task information is represented by smaller groups of units with larger individual contributions.
Our results emphasize how single units and populations provide different views of neural coding (Stokes et al., 2013). It is generally, if tacitly, assumed that information encoded by an ensemble must be present in the tuning properties of the component neurons when they are examined in isolation. However, there is accumulating evidence that classic tuning curves do not convey a full picture of the information present at an ensemble level (Pouget et al., 1999; Zhang and Sejnowski, 1999). For instance, ensemble codes for WM are affected by correlated variability among constituent neurons, with optimal coding commonly relying on units that are poorly tuned in a classical sense (Leavitt et al., 2017). Similar population interactions also change ensemble representations of visual space, independent of individual neuron tuning (Dehaqani et al., 2018). In simulations, the presence of non-classical value-related responses in a population improves value decoding (Enel et al., 2021), and at the level of fMRI, adding non-selective voxels that appear irrelevant to stimulus coding nonetheless improves performance of a stimulus decoder (Yamashita et al., 2008). Thus, the stimulus-related tuning of individual units does not necessarily dictate their importance to population-level codes.
Beyond simply representing information, distributed codes may play other important roles in network functions. For instance, artificial neural networks have suggested that distributed codes are more robust and generalizable. Compared to networks that used rote memorization to recognize images, those that learned generalizable concepts relied less on units that were selective for individual features (Morcos et al., 2018). The networks that developed fewer classically tuned units not only generalized better to new images, but were also more robust to noise or unit ablation. Therefore, the selectivity of individual units is often a poor predictor of network performance, and this is echoed in our finding that monkeys tended to perform better in blocks where single units exhibited less spatial tuning.
An open question is what benefit less tuned, more distributed representations might confer compared to other possibilities, such as populations that maintain single unit selectivity but distribute the information among more tuned neurons. One consideration is that the latter coding scheme may be metabolically costly. Theoretical work has emphasized that neural codes likely evolved to optimize the trade-off between representational capacity and energy expenditure (Levy and Baxter, 1996). Since metabolic costs per bit of information increase with bit rate (Laughlin et al., 1998), distributing information across populations should favor lower activity among individual neurons, which might manifest as reduced tuning. Another possibility is that reduced tuning could arise if neurons increasingly multiplex information as behavior becomes more routine. Neurons with mixed selectivity appear less classically tuned for single variables (Rigotti et al., 2013), and such mixing of task variables increases with task training in LPFC neurons (Dang et al., 2021). In our data, we found no evidence that past or future targets or saccades are increasingly represented with routine behavior, but it remains possible that other contextual or environmental information could mix with target information as selection order becomes more fixed, making neurons appear less tuned. Indeed, the context-dependence of habitual behaviors (Thrailkill and Bouton, 2015) suggests that task and environmental information could become linked with repetition.
We found that distributed neural codes not only correlated with improved behavioral performance, but were also implemented on the fly, as the monkey generated different strategies in a challenging task. This emphasizes the adaptability of prefrontal neurons under different conditions and goals. Although distributed coding led to better behavioral performance, different patterns of behavior, and their concomitant neural codes, are desirable under different conditions. Flexibility and exploration are frequently important, so we would not want to organize all behavior into structured sequences. If distributed coding is part and parcel of more stereotyped behavior, it may be observed more commonly when behaviors become routine or overtrained, or when facing familiar situations. Indeed, as monkeys were trained on multi-item WM or association tasks over several weeks, more LPFC neurons became selective, but with lower average firing rates, suggestive of a more distributed code (Asaad et al., 1998; Tang et al., 2019). Different mnemonic strategies may also be employed to overcome WM constraints. We commonly group a series of items into “chunks” or subgroups (Chiang and Wallis, 2018a), for instance when remembering telephone or social security numbers, and it remains to be seen whether these strategies also depend on distributed neural codes. Beyond behavioral circumstances that might promote more flexible or strategic behaviors, the underlying neuronal responses themselves may be constrained by metabolic costs, as discussed above (Levy and Baxter, 1996). For instance, increased BOLD signals have been found in human LPFC when subjects performed sequenced responses that lowered WM loads (Bor et al., 2003), suggesting that imposing structure on mnemonic representations entails an energetic cost. Thus, a balance of biological and behavioral benefits may ultimately influence how LPFC codes WM information.
In summary, implementing a cognitive strategy in a self-ordered WM task improved performance and shifted information from highly-tuned single units to distributed ensemble representations. These results provide a novel view of how WM information is internally manipulated, without changes in external stimuli or task requirements. The mechanisms that dictate when and how information is distributed among a population remain to be investigated further, but could involve online adjustments in synaptic weights, as proposed under the “activity-silent” model of WM (Stokes, 2015). The current results provide the first step toward such investigations, and reveal important insights into the mechanisms underlying advanced cognitive abilities such as implementing mnemonic strategies.
STAR * Methods
Resource Availability
Lead Contact and Materials Availability
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Erin L. Rich (erin.rich@mssm.edu). This study did not generate any new unique reagents.
Data and Code Availability
All data reported in this paper will be available by the lead contact upon request.
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOI are listed in the key resources table.
Key Resources Table
| REAGENT or RESOURCE | ||
|---|---|---|
| Experimental models: Organisms/strains | SOURCE | |
| Non-human primate (Macaca mulatta) | California National Primate Research Center | |
| Software and algorithms | SOURCE | IDENTIFIER |
| MATLAB | The Mathworks | https://www.mathworks.com/products/matlab.html |
| The Multichannel Acquisition Processor (MAP) Neurophysiology System | Plexon | http://plexon.com/ |
| Offline Sorter | Plexon | http://plexon.com/ |
| MonkeyLogic Toolbox for MATLAB | NIH | https://www.brown.edu/Research/monkeylogic/ |
| Custom analysis code | This paper | https://doi.org/10.5281/zenodo.5708963 |
| ISCAN | ISCAN | http://iscaninc.com/home.html |
| Adobe Illustrator | Adobe Inc. | https://www.adobe.com/ |
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Experimental Model and Subject Details
All procedures were in accord with the National Institute of Health guidelines and the recommendations of the University of California, Berkeley Animal Care and Use Committee. Subjects were two male rhesus monkeys (Macaca mulatta), Q and R, aged 5 and 6 years, and weighing approximately 7 and 9 kg at the time of recording. Monkeys worked for diluted fruit juice rewards and daily fluid intake was regulated to maintain motivation. Subjects sat head-fixed in a primate chair and viewed a computer screen. MonkeyLogic software (Asaad and Eskandar, 2008) controlled the behavior interface and subjects’ eye movements were tracked with an infrared camera (ISCAN). Subjects each had two circular recording chambers (Crist instrument, Inc.) situated over the bilateral prefrontal cortex.
Method Details
Spatial self-ordered search task
We analyzed data from two monkeys performing a spatial self-ordered search task with six identical visual targets. Behavior and single unit data were previously reported in (Chiang and Wallis, 2018b). On each trial, subjects were presented with a configuration of six targets and were required to saccade to each target, one at a time in any order, returning their eyes to the center after each target (Figure 1A and 1B). Reward was only delivered the first time each target was selected within a trial. Any revisited target resulted in a 500ms time-out with a red square presented on a full screen. Therefore, subjects had to use WM to track and update which targets had already been selected and prepare for the next target selection. A trial was completed when all six targets had been selected. To avoid frustration, the trial was terminated as incomplete if there were 10 consecutive time-outs within a trial. On average, numbers of completed trials per block were 38.4 ± 0.2 and 34.8 ± 0.7 for subject R and Q, respectively. For each new trial, the target-reward contingency was reset after the inter-trial interval (2s). The target color was the same within a trial, but changed in sequence of green-blue-white at the onset of a new trial to ensure that subjects realized reward contingencies were reset. Target configurations remained the same for blocks of 40 trials (>=240 selections), enabling us to quantify selection patterns. The spatial configuration of targets used for each block was pseudorandomly chosen from a pool of 20 a priori designed spatial configurations. We ensured that targets were distributed relatively evenly across the display so that the centroid of each target configuration was located within ± 3° of the window around the fixation cue. The same configuration was presented repeatedly within a block but used only once per session. Subjects were able to complete 6 blocks per session (240 trials, or >=1440 selections). Only one block of data with less than 20 complete trials in subject Q was removed from analysis. In total, we analyzed 90 blocks in 15 recording sessions from subject R and 59 blocks in 10 recording sessions from subject Q (Supplemental Table S1). Only completed trials were included in the analyses.
We calculated SI as previously described (Chiang and Wallis, 2018b) to quantify the subject’s target selection patterns. For each block of trials, we counted how often each target (target A to F) was selected first, second, etc. and created a matrix of selection frequencies (e.g. Figure 2A), with dimensions of six selections by six targets. These matrices were sorted according to the most common sequence in which the targets were selected. SI quantified the extent to which the subject searched through the targets in the same sequence for all completed trials within a block and was defined as:
| Equation (1) |
where a is the sum of the entries on the main diagonal of the matrix and b is the off-diagonal sum of the matrix. Our previous results had shown that higher SIs significantly improved behavioral performance, evident as a reduction in the number of revisited targets for both subjects (Chiang and Wallis, 2018b).
We compared behavior between high and low SI blocks, defined by a median split of observed SIs within session for each monkey. Common selection patterns were followed more frequently on high SI compared to low SI blocks (Two-way ANOVAs: H/LSI blocks, p < 0.001 for both subjects), and the pattern is clearly present throughout all 6 selections, indicating that high SI’s aren’t exclusively driven by first or last target effects (Supplemental Figure S2C). RTs were calculated as the time from configuration presentation to target selection. A multiple linear regression model predicted RTs from saccade order, high/low SI block, and the order x block interaction. Errors with respect to sequence position were previously analyzed by determining the difference between observed and expected success rates (Chiang and Wallis, 2018b). Expected success rates were calculated by assuming that errors are a linear function of the number of potentially incorrect saccades that are possible. That is, it’s impossible to make a mistake on the first target selection, and highly unlikely on the second (1/6, or 16.7% chance), etc., so that success rates should show a linear decline with each target selected if errors are randomly distributed. The other possibility is that monkeys use WM and memory strategies, so that they perform better than the expected success rates when WM loads are low, but performance suffers when WM capacity is exceeded. Therefore, the expected success rates were calculated by fitting a linear function to the average success rate across all target selections, such that there is a consistent decrease at each target selection. This calculation assumes that there is a baseline error rate and the only factor distributing these errors is task statistics that change the probability of selecting a correct target by chance.
Neurophysiological Procedures
Our methods for neurophysiological recording have been reported in detail previously (Chiang and Wallis, 2018b). In brief, both subjects were implanted with a titanium head positioner and recording chambers over each hemisphere. Chamber position was determined from previously acquired 1.5-T MRI scans to target the dorsal and ventral banks of the principal sulcus. Neurons were recorded from bilateral LPFC with 12–16 tungsten microelectrodes (FHC Instruments), advanced with custom built, manual microdrives in each recording session. Electrodes were placed in the target area by mapping the position of sulci and gray and white matter boundaries during recordings. Within the target area, we randomly sampled neurons and did not attempt to filter neurons based on selectivity. In total, 1077 units were collected from both monkeys (Subject R: 709; subject Q: 368), the majority of which were within the principal sulcus. The number of recording units per session are listed in Supplemental Table S1. Waveforms were digitized (Plexon Inc.) and stored for offline spike sorting (Offline Sorter, Plexon Inc.) and analysis.
Quantification and Statistical Analysis
We conducted all statistical analyses using custom MATLAB (Mathworks) scripts. Data included in the analyses were from six correct saccades in completed trials. For each neuron, we calculated its mean firing rate (FR) during the hold target epoch, which comprised the 500ms period of fixation required to select a target, or during the sliding epochs of 200ms windows stepped forward by 10ms. The size of the neural ensembles corresponded to the number of neurons recorded per session (Supplemental Table S1). In decoding analyses, we treat each simultaneously recorded ensemble as independent and do not pool neurons into a pseudo-population.
Spatial tuning
Responses of single neurons are described in detail in Chiang and Wallis (2018b). Briefly, the firing rate of each neuron was computed in a 500 ms window during the hold-target epoch, and fit with a linear model that included the following predictors: X and Y coordinates of the selected target, saccade order position, target distance from fixation, SI in the block, X and Y coordinates of the previous target selected, X and Y coordinates of the next target selected, and target color (Supplemental Table S2). To quantify changes in spatial tuning across the population, we used the same analysis windows and converted target locations to polar coordinates to compute the magnitude and direction of the resultant vectors for standardized firing rates in response to each target selection. Changes in spatial tuning were quantified by splitting each session into high and low SI blocks (median spit), and calculating one resultant vector for each block type, then finding the change in direction (d’) and magnitude (m’) of these vectors (Figure 2).
Categorical Decoders
We used LDA with leave-one-out cross validation to decode task features, as implemented by the Matlab function classify. A diagram in Supplemental Figure S1 illustrates the decoders we used to classify target locations, saccade orders, and target colors, separately. The feature matrix consisted of average firing rates in a given epoch observed during each correct saccade (rows) from each neuron (columns), and labels were target identity, as determined by its spatial location (e.g. target A, B, etc.), saccade number (e.g. saccade#1, #2, etc.), or target color (green, blue, and white). Classifiers were separately trained and tested on each block of 40 trials (<= 240 correct saccades). Performance was quantified as either the percent of saccades accurately classified when held out from the training set, or the decoding accuracy of the correct category for the held-out observation (Supplemental Figure S2). Mean decoding performance was calculated as the mean number of held-out trials classified correctly from all saccades. To examine whether decoding was affected by SI, we performed two-way ANCOVAs on mean decoding performance with continuous variable SI and two categorical variables: target location and saccade order. Significance was evaluated at p < 0.05 unless otherwise specified.
Two-dimensional Spatial Decoder
The LDA tested whether neural activity distinguished different targets categorically, but cannot determine whether these codes are based on spatial coding or other distinctions. To examine how well target locations could be predicted, we used a regularized general linear model with 10-fold cross validation as a continuous variable decoder to predict the locations of selected targets (Astrand et al., 2016). A diagram in Supplemental Figure S1 illustrates the data structure. The feature matrices were the same as those of categorical decoders, and labels were either X- or Y-coordinates corresponding to each selected target. Regularization was implemented with the Matlab function ridge. Ridge regression is a regularization method to prevent overfitting (James et al., 2013). In order to find the optimal ridge parameter, k, we calculated the mean square error (MSE) between predicted and actual values (Supplemental Figure S5). We used a 2-step grid search procedure for optimization. First, we searched a wide parameter space that was coarsely sampled (k = 10t, t = −8:1:8), to find the parameter that most frequently minimized MSE in 100 iterations, each using 10-fold cross validation. We used these results to narrow the search space and sample more precisely. We repeated the above procedure with 100 evenly spaced parameters t’, where k = 10t’, and 10t−2 ≤ t’ ≤ 10t+2. Optimal k was again based on the minimum MSE. Accuracies were quantified as the Euclidean distance between actual and predicted targets in 2-D space (Supplemental Figure S5).
Noise Correlations
Noise correlations are defined as shared variability among neurons that can be detected across repeated presentations of identical stimuli (Cohen and Kohn, 2011). Our task design is somewhat unconventional for calculating noise correlations, since there is variability in both saccade order and target location so there are few repeated presentations of stimuli that could be considered both perceptually and cognitively identical. Therefore, we approximated noise correlation measures separately for each selected target location or sequence position, as if it were repeated measures of an identical stimulus. To calculate correlated activity at each sequential position, we performed pair-wise Pearson correlations separately on all first saccades, second saccades, etc. across all trials with each block. These analyses removed signal correlations due to saccade order, since each saccade was examined separately, and shuffled signal correlations due to target location, since the data were sorted with respect to saccade number, not target. Likewise, to calculate correlated activity across saccades to the same target location, we performed pair-wise Pearson correlations separately on all selections target A, B, etc., across all trials within each block. These analyses removed signal correlations due to target location, since each selection was examined separately, and shuffled signal correlations due to saccade order, since the data were sorted with respect to target, not saccade number. Further, we minimized the risk of falsely inflating the correlation values by excluding correlations between units on the same electrode from analysis (Leavitt et al., 2013). After applying this exclusion criterion for each recording session, on average we had 1118.1 ± 131.1 and 658.2 ± 71.1 pairs of noise correlation from 47.3 ± 2.7 and 36.8 ± 2.1 simultaneously recorded neurons on subject R and Q, respectively. Fisher’s r-to-z transformation was applied to the correlation coefficients in order to normalize variance for hypothesis testing. As previously reported (Leavitt et al., 2013; Tremblay et al., 2015), we found different pairs of neurons had positively and negatively correlated activity. We reasoned that positive and negative noise correlations may be differentially related to sequencing strategies, so we separately calculated the proportion of neurons with significant positive or negative noise correlations as a function of SI in each block (Pearson correlations). This was carried out in four different epochs: early and late fixation (500ms non-overlapping bins from the 1s fixation window), the hold target epoch, and the reward delivery epoch (Supplemental Table S4).
Neuron Dropping Procedure
To determine the contribution of each neuron to ensemble decoding, we reran the LDA analyses with a neuron dropping procedure (Narayanan et al., 2005). We removed one neuron at a time from the whole neural ensemble (N), ran the classifier with the remaining ensemble (N-1), and found the change in decoding performance between ensembles N and N-1. Performance was quantified by calculating the decoding accuracy between actual and predicted classes across saccades in a given block. Thus, removing an informative neuron will decrease decoding performance, but removing a noisy or redundant neuron will have little effect or even increase performance. A median baseline performance was also calculated from all N-1 ensembles in a block (Figure 3A), and used to define high and low contribution subgroups of neurons as those that produced performance drops below or above the median respectively. To further quantify each neuron’s contribution, we created a standardized contribution index for each unit in each block.
| Equation (2) |
The contribution index of the i-th neuron is defined as the ratio of the difference between the mean decoding accuracy from the full ensemble (N) and the remaining ensemble (N − i) after removing neuron i. In Eq. 2, Prob(N) denotes the mean decoding performance from the full ensemble, Prob(N-i) denotes the same mean decoding performance from the N-i ensemble. If the contribution index was positive, the N-i ensemble had lower decoding accuracy compared to the full ensemble, and the i-th single neuron improved decoding. More positive CIs indicated a bigger drop in performance, so that the neuron made a larger contribution to the ensemble. On the other hand, if the CI was negative, then neuron i reduced decoding, and if it equaled 0, there was no difference between the full and reduced ensemble. In the latter case, the i-th unit either provided redundant information or made no contribution. CIs were calculated separately for each block, resulting in 4254 data points for subject R and 2171 data points for subject Q. We then excluded data points with zero contribution indices [573 out of 4254 for subject R; 289 out of 2171 for subject Q] for the further analysis.
Optimal Ensemble Size Measures
To assess the optimal ensemble size for each decoder in trial blocks, we adopted BSU and BE procedures from previous work (Backen et al., 2018). First, we decoded each feature (target identity, saccade number, target color) from each single unit within a block, and sorted the neurons according to descending accuracy. Then, for the BSU procedure, we iteratively added each neuron to an accumulating ensemble in the sorted order, starting with the most informative, and ran the LDA as previously described to determine accuracy at each step. The BE procedure was similar, starting with the most informative neuron, but considered all possible combinations of neurons with each new addition, keeping the unit that yielded the highest accuracy for that ensemble size. After either BSU or BE, the optimal ensemble size was defined by how many neurons were included in the neural ensemble to reach the maximum decoding accuracy (PCT100), or 90%, 75%, or 50% of maximum (PCT90, PCT75, PCT50).
Dimensionality Measurement
Dimensionality can be quantified by different measurements in different tasks and neural systems (Abbott et al., 2011; Ganguli and Sompolinsky, 2012; Gao and Ganguli, 2015; Rigotti et al., 2013). Here, we used the PR, calculated as a continuous measurement of dimensionality by using the population activity patterns from every correct saccade in each trial, to assess variability. The PR is closely related to the concept of explained variance from principal component analysis (Dąbrowska et al., 2021; Gao et al., 2017) and is defined as:
| Equation (3) |
Where μi are the eigenvectors of a covariance matrix for i = 1 to M simultaneously recorded units. To calculate PR, we first created spike-count arrays from simultaneously recorded units, consisting of 20ms non-overlapping bins in four 500ms epochs (early fixation, late fixation, hold target, and reward epochs), for each correct saccade in a given trial (Supplemental Figure S1). Then, we calculated the covariance (COV) for each array, which indicated how the population covaries across epochs (Gao, et al., 2017), and calculated the vector μ containing the eigenvalues of the square matrix COV. The size of the square matrix COV is equal to M simultaneously recorded units. Lastly, we created a vector of PR values for each correct saccade in blocks of complete trials to assess changes in dimensionality across saccades. In general, the PR corresponds to the number of dimensions required to explain about 80% ~ 90% of the total population variance (Gao et al, 2017). In other words, the diversity of firing patterns in the neural ensembles increased with PR. To compare PR values across recording sessions, we normalized vectors of PR within a session before further analyses. The linear model was calculated for each monkey as follows:
| Equation (4) |
where Saccades is the saccade number within a trial, SI is calculated from behavior in each block, and nSigs is the number of neurons in each ensemble (Supplemental Table S1).
Supplementary Material
Highlights.
Sequencing strategies improve performance in a self-ordered working memory task
Strategies distribute information from tuned LPFC neurons to population codes
Less routine behavior and higher memory loads increase neural dimensionality
Acknowledgements
The authors thank P. Viswanathan, A.Q. Perkins, and J. Simon for feedback on a previous draft of the manuscript, and P. Enel for technical support with the computing server. This work was funded by National Institute of Mental Health Grant R01 MH121480 (to E.L.R), National Institute of Mental Health Grant R01 MH097990, NINDS R01 NS116623, NIMH R01 MH117763 (to J.D.W.) and by Taiwan Top University Strategic Alliance Graduate Fellowship USA-UCB-100-S01 (to F.-K.C.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no conflicts of interest.
Inclusion and Diversity
One or more of the authors of this paper self-identifies as a member of the LGBTQ+ community.
References
- Abbott LF, Rajan K, and Sompolinsky H (2011). Interactions between intrinsic and stimulus-evoked activity in recurrent neural networks. The dynamic brain: an exploration of neuronal variability and its functional significance, 1–16. [Google Scholar]
- Asaad WF, and Eskandar EN (2008). A flexible software tool for temporally-precise behavioral control in Matlab. J Neurosci Methods 174, 245–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asaad WF, Rainer G, and Miller EK (1998). Neural activity in the primate prefrontal cortex during associative learning. Neuron 21, 1399–1407. [DOI] [PubMed] [Google Scholar]
- Asaad WF, Rainer G, and Miller EK (2000). Task-specific neural activity in the primate prefrontal cortex. J Neurophysiol 84, 451–459. [DOI] [PubMed] [Google Scholar]
- Astrand E, Wardak C, Baraduc P, and Ben Hamed S (2016). Direct Two-Dimensional Access to the Spatial Location of Covert Attention in Macaque Prefrontal Cortex. Curr Biol 26, 1699–1704. [DOI] [PubMed] [Google Scholar]
- Backen T, Treue S, and Martinez-Trujillo JC (2018). Encoding of Spatial Attention by Primate Prefrontal Cortex Neuronal Ensembles. eNeuro 5, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolo R, Saunders RC, Mitz AR, and Averbeck BB (2020). Dimensionality, information and learning in prefrontal cortex. PLoS Comput Biol 16, e1007514. doi.org/1007510.1001371/journal.pcbi.1007514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben Hadj Hassen S, and Ben Hamed S (2020). Functional and behavioural correlates of shared neuronal noise variability in vision and visual cognition. Current Opinion in Physiology 16, 85–97. [Google Scholar]
- Bor D, Duncan J, Wiseman RJ, and Owen AM (2003). Encoding strategies dissociate prefrontal activity from working memory demand. Neuron 37, 361–367. [DOI] [PubMed] [Google Scholar]
- Chiang FK, and Wallis JD (2018a). Neuronal Encoding in Prefrontal Cortex during Hierarchical Reinforcement Learning. J Cogn Neurosci 30, 1197–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang FK, and Wallis JD (2018b). Spatiotemporal encoding of search strategies by prefrontal neurons. Proc Natl Acad Sci U S A 115, 5010–5015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Ryu SI, Santhanam G, and Shenoy KV (2006). Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci 26, 3697–3712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Kohn A (2011). Measuring and interpreting neuronal correlations. Nat Neurosci 14, 811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N (2001). The magical number 4 in short-term memory: a reconsideration of mental storage capacity. Behav Brain Sci 24, 87–114; discussion 114-185. [DOI] [PubMed] [Google Scholar]
- D'Esposito M, and Postle BR (2015). The cognitive neuroscience of working memory. Annu Rev Psychol 66, 115–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dąbrowska PA, Voges N, von Papen M, Ito J, Dahmen D, Riehle A, Brochier T, and Grün S (2021). On the Complexity of Resting State Spiking Activity in Monkey Motor Cortex. Cerebral Cortex Communications 2, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang W, Jaffe RJ, Qi XL, and Constantinidis C (2021). Emergence of Nonlinear Mixed Selectivity in Prefrontal Cortex after Training. J Neurosci 41, 7420–7434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaqani MA, Vahabie AH, Parsa M, Noudoost B, and Soltani A (2018). Selective Changes in Noise Correlations Contribute to an Enhanced Representation of Saccadic Targets in Prefrontal Neuronal Ensembles. Cereb Cortex 28, 3046–3063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desrochers TM, Amemori K, and Graybiel AM (2015). Habit Learning by Naive Macaques Is Marked by Response Sharpening of Striatal Neurons Representing the Cost and Outcome of Acquired Action Sequences. Neuron 87, 853–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desrochers TM, Jin DZ, Goodman ND, and Graybiel AM (2010). Optimal habits can develop spontaneously through sensitivity to local cost. Proceedings of the National Academy of Sciences 107, 20512–20517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan J (2001). An adaptive coding model of neural function in prefrontal cortex. Nat Rev Neurosci 2, 820–829. [DOI] [PubMed] [Google Scholar]
- Durstewitz D, Vittoz NM, Floresco SB, and Seamans JK (2010). Abrupt transitions between prefrontal neural ensemble states accompany behavioral transitions during rule learning. Neuron 66, 438–448. [DOI] [PubMed] [Google Scholar]
- Enel P, Perkins AQ, and Rich EL (2021). Heterogeneous value coding in orbitofrontal populations. Behav Neurosci 135, 245–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ericsson KA, and Kintsch W (1995). Long-term working memory. Psychol Rev 102, 211–245. [DOI] [PubMed] [Google Scholar]
- Fujii N, and Graybiel AM (2003). Representation of action sequence boundaries by macaque prefrontal cortical neurons. Science 301, 1246–1249. [DOI] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ, and Goldman-Rakic PS (1989). Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. J Neurophysiol 61, 331–349. [DOI] [PubMed] [Google Scholar]
- Ganguli S, and Sompolinsky H (2012). Compressed sensing, sparsity, and dimensionality in neuronal information processing and data analysis. Annu Rev Neurosci 35, 485–508. [DOI] [PubMed] [Google Scholar]
- Gao P, and Ganguli S (2015). On simplicity and complexity in the brave new world of large-scale neuroscience. Curr Opin Neurobiol 32, 148–155. [DOI] [PubMed] [Google Scholar]
- Gao P, Trautmann E, Yu B, Santhanam G, Ryu S, Shenoy K, and Ganguli S (2017). A theory of multineuronal dimensionality, dynamics and measurement. BioRxiv, p.214262. doi:214210.211101/214262. [Google Scholar]
- Hung CP, Kreiman G, Poggio T, and DiCarlo JJ (2005). Fast readout of object identity from macaque inferior temporal cortex. Science 310, 863–866. [DOI] [PubMed] [Google Scholar]
- James G, Witten D, Hastie T, and Tibshirani R (2013). An introduction to statistical learning, Vol 112 (Springer; ). [Google Scholar]
- Lashley KS (1951). The problem of serial order in behavior, Vol 21 (Oxford, United Kingdom: Bobbs-Merrill; ). [Google Scholar]
- Laughlin SB, de Ruyter van Steveninck RR, and Anderson JC (1998). The metabolic cost of neural information. Nat Neurosci 1, 36–41. [DOI] [PubMed] [Google Scholar]
- Leavitt ML, Pieper F, Sachs A, Joober R, and Martinez-Trujillo JC (2013). Structure of Spike Count Correlations Reveals Functional Interactions between Neurons in Dorsolateral Prefrontal Cortex Area 8a of Behaving Primates. PLOS ONE 8, e61503. doi:61510.61371/journal.pone.0061503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leavitt ML, Pieper F, Sachs AJ, and Martinez-Trujillo JC (2017). Correlated variability modifies working memory fidelity in primate prefrontal neuronal ensembles. Proc Natl Acad Sci U S A 114, E2494–E2503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy WB, and Baxter RA (1996). Energy efficient neural codes. Neural Comput 8, 531–543. [DOI] [PubMed] [Google Scholar]
- Luck SJ, and Vogel EK (1997). The capacity of visual working memory for features and conjunctions. Nature 390, 279–281. [DOI] [PubMed] [Google Scholar]
- Mazzucato L, Fontanini A, and La Camera G (2016). Stimuli Reduce the Dimensionality of Cortical Activity. Front Syst Neurosci 10:11, doi: 10.3389/fnsys.2016.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyers EM (2018). Dynamic population coding and its relationship to working memory. J Neurophysiol 120, 2260–2268. [DOI] [PubMed] [Google Scholar]
- Meyers EM, Freedman DJ, Kreiman G, Miller EK, and Poggio T (2008). Dynamic population coding of category information in inferior temporal and prefrontal cortex. J Neurophysiol 100, 1407–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK (2000). The prefrontal cortex and cognitive control. Nat Rev Neurosci 1, 59–65. [DOI] [PubMed] [Google Scholar]
- Miller GA (1956). The magical number seven plus or minus two: some limits on our capacity for processing information. Psychol Rev 63, 81–97. [PubMed] [Google Scholar]
- Morcos AS, Barrett DGT, Rabinowitz NC, and Botvinick M (2018). On the importance of single directions for generalization. p. arXiv:1803.06959v06954. [Google Scholar]
- Narayanan NS, Kimchi EY, and Laubach M (2005). Redundancy and synergy of neuronal ensembles in motor cortex. J Neurosci 25, 4207–4216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichelli P, Grafman J, Pietrini P, Alway D, Carton JC, and Miletich R (1994). Brain activity in chess playing. Nature 369, 191. [DOI] [PubMed] [Google Scholar]
- Nicolelis MA (1998). Methods for Neural Ensemble Recordings (Boca Raton, FL: CRC.). [PubMed] [Google Scholar]
- Nogueira R, Peltier NE, Anzai A, DeAngelis GC, Martinez-Trujillo J, and Moreno-Bote R (2020). The Effects of Population Tuning and Trial-by-Trial Variability on Information Encoding and Behavior. J Neurosci 40, 1066–1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouget A, Deneve S, Ducom JC, and Latham PE (1999). Narrow versus wide tuning curves: What's best for a population code? Neural Comput 11, 85–90. [DOI] [PubMed] [Google Scholar]
- Procyk E, and Goldman-Rakic PS (2006). Modulation of dorsolateral prefrontal delay activity during self-organized behavior. J Neurosci 26, 11313–11323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SC, Rainer G, and Miller EK (1997). Integration of What and Where in the Primate Prefrontal Cortex. Science 276, 821–824. [DOI] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang XJ, Daw ND, Miller EK, and Fusi S (2013). The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigala N, Kusunoki M, Nimmo-Smith I, Gaffan D, and Duncan J (2008). Hierarchical coding for sequential task events in the monkey prefrontal cortex. Proc Natl Acad Sci U S A 105, 11969–11974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes MG (2015). 'Activity-silent' working memory in prefrontal cortex: a dynamic coding framework. Trends Cogn Sci 19, 394–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, and Duncan J (2013). Dynamic coding for cognitive control in prefrontal cortex. Neuron 78, 364–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Qi XL, Riley MR, and Constantinidis C (2019). Working memory capacity is enhanced by distributed prefrontal activation and invariant temporal dynamics. Proc Natl Acad Sci U S A 116, 7095–7100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thrailkill EA, and Bouton ME (2015). Contextual control of instrumental actions and habits. J Exp Psychol Anim Learn Cogn 41, 69–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay S, Pieper F, Sachs A, and Martinez-Trujillo J (2015). Attentional filtering of visual information by neuronal ensembles in the primate lateral prefrontal cortex. Neuron 85, 202–215. [DOI] [PubMed] [Google Scholar]
- Yamashita O, Sato MA, Yoshioka T, Tong F, and Kamitani Y (2008). Sparse estimation automatically selects voxels relevant for the decoding of fMRI activity patterns. Neuroimage 42, 1414–1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, and Sejnowski TJ (1999). Neuronal tuning: To sharpen or broaden? Neural Comput 11, 75–84. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data reported in this paper will be available by the lead contact upon request.
All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOI are listed in the key resources table.
Key Resources Table
| REAGENT or RESOURCE | ||
|---|---|---|
| Experimental models: Organisms/strains | SOURCE | |
| Non-human primate (Macaca mulatta) | California National Primate Research Center | |
| Software and algorithms | SOURCE | IDENTIFIER |
| MATLAB | The Mathworks | https://www.mathworks.com/products/matlab.html |
| The Multichannel Acquisition Processor (MAP) Neurophysiology System | Plexon | http://plexon.com/ |
| Offline Sorter | Plexon | http://plexon.com/ |
| MonkeyLogic Toolbox for MATLAB | NIH | https://www.brown.edu/Research/monkeylogic/ |
| Custom analysis code | This paper | https://doi.org/10.5281/zenodo.5708963 |
| ISCAN | ISCAN | http://iscaninc.com/home.html |
| Adobe Illustrator | Adobe Inc. | https://www.adobe.com/ |
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.