Skip to main content
NCBI home page
Heliyon logoLink to Heliyon
. 2022 Feb 12;8(2):e08949. doi: 10.1016/j.heliyon.2022.e08949

Thin-layer modelling of sweet potato slices drying under naturally-ventilated warm air by solar-venturi dryer

Siyabonga Gasa a,∗, Sipho Sibanda a, Tilahun S Workneh b, Mark Laing b, Alaika Kassim b
PMCID: PMC8857478  PMID: 35243071

Abstract

The drying of agricultural produce is an important food preservation measure. However, high energy requirements for drying, limited access to energy sources, small-medium scale farmers experience high post-harvest losses of their produce. Therefore, there is a need to develop and optimize low-cost food preservation technologies. In this study, eleven mathematical models were used to estimate the drying coefficients following non-linear regression method, in hot-air oven and naturally-ventilated solar-venturi drying to find the best fit of the moisture ration models. Sweet potato tubers were sliced at 3, 5 and 7 mm thickness sizes with and without pre-drying treatments. The prepared sweet potato slices were dried in a hot-air oven dryer at a constant temperature of 70 °C in comparison to the naturally-ventilated solar-venturi dryer with a heated ambient air that varied according to the outside environmental conditions. The drying rate of the samples in a hot-air oven dryer was higher than for those in the naturally-ventilated solar-venturi dryer. The results showed that the drying time was significantly (P < 0.05) affected by the thickness size of sweet potato slices (SPS) and that the drying took place at the falling rate period and a constant drying time. The Midilli et al. model was the best fit for predicting the moisture ratio of SPS dried in hot-air oven dryer and naturally-ventilated solar-venturi dryer based on statistical analysis (R2 = 0.982–0.999, χ2 = 4.60 × 10−6-5.56 × 10−5 and RMSE = 0.011–0.067). The Deff was 3.32 × 10−9- 6.31 × 10−9 m s−1 for the naturally-ventilated solar-venturi dryer and 1.02 × 10−8 - 2.19 × 10−8 m s−1 for the hot-air oven dryer. According to the results obtained, naturally-ventilated, solar-venturi dryer and lemon juice pre-drying treatment are the suitable application for small-medium scale drying of SPS under Pietermaritzburg conditions.

Keywords: Drying, Modelling, Thin-layer drying, Drying kinetics

Drying; Modelling; Thin-layer drying; Drying kinetics.

1. Introduction

Sweet potato tubers are amongst a group of crops that feed the world and are regarded as an excellent source of vitamins and starch (Doymaz, 2011; Sanginga, 2015; Sanoussi et al., 2016). Sweet potato tubers can be grown all year round under suitable climatic conditions and they are highly resistant to adverse climatic conditions (Chandrasekara & Kumar, 2016; de Souza et al., 2021). Freshly-harvested sweet potato tubers have a moisture content of 48.0–53.3% (Titus and Janet, 2016). Such high moisture content makes sweet potatoes highly perishable and difficult to transport from one place to another (Nwakuba et al., 2016; Seidu et al., 2012). Hence, appropriate preservation technologies that can increase shelf life are required (Oyebanji et al., 2013; Vivek et al., 2021). The study proposed development of low cost drying technologies with little or no energy input for them to be attractive to small-to medium-scale farmers with no capital and access to conventional electricity.

Drying method and equipment have an impact on the quality of the final product; hence there is a need to study the effect of the drying method on the quality of dried food material (Mewa et al., 2018; Javed et al., 2019). Drying of food involves heat and mass transfer accompanied by changes in the structure, shape, and biological quality of the product (Nasri and Belhamri, 2018; Dasore et al., 2020). Therefore, to produce a good quality dried product, it is important to understand the drying characteristics of different food materials. Doymaz (2011) and Nurkhoeriyati et al. (2021) reported that heat and mass transfer during the drying process cause browning of the product resulting in the reduction of quality compared to the original food. Mathematical models, known as thin-layer drying models are tools used to better understand the thermal process and to develop and improve the existing drying systems (Akoy, 2014; Miraei Ashtiani et al., 2017; Oke and Workneh, 2014). These models describe both the microscopic and macroscopic drying behaviour of the heat and mass transfer of the drying material (Ayadi et al., 2014; Doymaz, 2011). Thin-layer drying models provide the basis for understanding the drying characteristics of any food material (Babiker et al., 2016) by depicting its drying kinetics at any given time when subjected to certain drying conditions (da Silva et al., 2014; Naderinezhad et al., 2015; Oke and Workneh, 2014). These drying conditions (relative humidity, air temperature and air velocity) have an impact on the quality of the final dried product (Ertekin and Firat, 2015; Meher and Nayak, 2016; Onwude et al., 2016). Therefore, there is a need to model and analyse their effects on drying performance and further look at physical and microstructure changes after drying.

Olawale and Omole (2012) studied thin-layer drying models for blanched and unblanched sweet potato slices (SPS) drying in a tray dryer. Amongst these models, the Page model was found to be the best model for all samples. Other researchers have studied thin-layer drying models using different types of dryers since the 1990s (Khanal and Lei, 2011). However, the study of thin-layer models using a naturally-ventilated, solar-venturi dryer (NSD) to dry SPS in South Africa has not been investigated and reported. Therefore, this study investigated the effect of solar-venturi drying on thin-layer drying characteristics of SPS, modelled the heat and mass transfer of these samples and evaluated the effect of drying on dried SPS.

2. Materials and methods

2.1. Study site description and climatic data

The study was conducted at the Ukulinga Research Farm, at the University of KwaZulu-Natal, Pietermaritzburg, South Africa (29.7o S and 30.4o E at an altitude of 721 m above sea level). The area has a mean long-term minimum and maximum temperatures of 6.0–16.4 °C and 20.6–27.4 °C, respectively, and a relative humidity of 61.1–75.3%. The area receives mean solar radiation of 15.1–27.8 MJ m−2.day−1, which is sufficient for solar drying applications (Schulze and Maharaj, 2007).

The study was conducted in September 2018. The mean long-term minimum and maximum temperature in September is 10.0–17.1 °C and 12.0–27.0 °C, respectively, while the relative humidity is 61.1–68.1%. The mean solar radiation, wind speed and mean sunshine hours for September are 15.1–27.8 MJ m−2.day−1, 0.8–9.7 m s−1 and 7 h, respectively (Schulze and Maharaj, 2007). The weather data (temperature, relative humidity, solar radiation and wind speed) recorded during the study period was obtained from the weather station at the Ukulinga Research Farm.

2.2. Sample preparation and treatments

A batch of fresh sweet potato storage roots was purchased from a local supermarket in Hayfields, Pietermaritzburg, South Africa. Sweet potato storage roots with no physical damage and no sign of fungal or microbial infection were selected. The selected storage roots were peeled, using a carbon steel blade potato peeler, after which they were washed, using deionized water. The peeled sweet potato storage roots were dabbed, using paper towels to remove water on their surface. Thereafter, the sweet potato storage roots were sliced into rectangular shapes with the dimensions of, 50 by 20 mm, using a stainless steel kitchen knife (Oke and Workneh, 2014). The thickness sizes of the slices were 3, 5 and 7 mm. The slices were pre-treated by either:

  • •

    dipping in an iodate table salt solution (0.1 % w/v concentration for 20 min);

  • •

    a lemon juice solution (1 % w/v concentration for 20 min);

  • •

    blanched in a water bath at 70 °C for 10 min (using Labotech water bath, Thermo Fisher Scientific, Waltham, Massachusetts, United States); and

  • •

    the batch of control samples was not pre-treated.

The treated samples were dabbed using paper towels to remove any free liquid from their surface (Olawale and Omole, 2012).

2.3. Experimental design and drying procedure

A factorial experimental (Factor A, B and C) design was followed with each experiment replicated three times; Factor A at three levels, Factor B at four levels, and Factor C at two levels as shown in Figure 1. The factors (A, B, and C) were the thickness of SPS (3, 5, and 7 mm); the pre-drying treatments (salt, lemon juice, blanching and control), and drying method (HAD and NSD), respectively. Air-drying was performed using a hot-air oven dryer (HAD) set at 70 °C and a naturally-ventilated solar-Venturi dryer (NSD).

Figure 1.

Figure 1

Open in a new tab

Schematic presentation of the experimental treatment structure with three factors (factor A = thickness size, factor B = drying pre-treatment, factor C = drying method).

The weight loss was monitored at fixed intervals of 5-minute for the first 45 min, a 15-minute interval for the following three hours, and an hourly interval for the rest of the drying process until there was a negligible change in the weight of slices (Oke and Workneh, 2014). The weight loss measured during drying was used to calculate the different moisture contents, namely; (i) the initial moisture content (mi), (ii) the moisture content at a time, t (mt), and (iii) the equilibrium moisture content (me). The weight loss of SPS dried in the NSD and HAD driers was measured using a digital mass balance (Avery Berkel, Model TB151-C4ZA10AAR, United Kingdom) with an accuracy of ±0.1. The equilibrium moisture content was determined in the HAD by drying the samples for 48 h at 105 °C (AOAC, 1984).

2.4. Drying characteristics analysis

2.4.1. Moisture ratio

The moisture ratio, (MR) (dimensionless) at the time, t, was calculated using Eq. (1) by Onu et al. (2016), where mt (in %) is the moisture content at the time, t, me(in ​%) is the equilibrium moisture content and mi (in %) is the initial moisture content. The data obtained was used to generate drying curves in Microsoft Office Excel (2016).

MR=Mt−MeMi−Me (1)

2.4.2. Drying rate

The drying rate, DR, (in kg.hr−1) was calculated using Eq. (2) by Onwude et al. (2016), where Mt+dt (in %) is the moisture content of the sample at a time, (t + dt in hrs), Mt (in %) is the moisture content at a time, t (in hrs) and dt (in hrs) is the change in drying time. Drying rate curves were generated using Microsoft Office Excel (2016).

DR=Mt+dt−Mtdt (2)

2.5. Modelling of sweet potato slices drying curves

Non-linear regression was used to determine the goodness of fit of thin-layer drying models summarised in Table 1 to the experimental moisture ratio.

Table 1.

Selected thin-layer drying models commonly used in drying of fruits and vegetables.

Model name Model References
1. Henderson and Pabis MR=aexp(−kt) Hashim et al., 2014
2. Modified Henderson and Pabis MR=aexp(−kt)bexp(−gt)+nexp ​(−ct) Meisami-asl & Rafiee 2009
3. Logarithmic MR=a ​exp(−kt) + b Kaur and Singh (2014)
4. Two-term MR=aexp(−kt)+b ​exp ​(−kt) Demiray and Tulek (2012)
5. Two-term exponential MR=aexp(−kt)+(1−a) ​exp ​(−kat) Thompson
6. Midilli et al. MR=aexp(−(ktn)+bt Kucuk et al. (2014)
7. Modified Midilli MR=exp(−ktn)+bt Xiao and Gao, 2012
8. Hii et al. MR=aexp(−ktn)+cexp(− gtn) Hii et al. (2009)
9. Demir et al., MR=aexp(−ktn)+b Demir et al., (2007)
10. Verma et al., MR=aexp(−kt)+(1−a)exp(−gt) Verma et al., (1985)
11. Sigmoid MR=a+b1+ ​ek(t−c) Süfer et al. (2017)
Open in a new tab

∗a, b, = empirical model constant (dimensionless), k = drying constant obtained from experimental data (s−1), n = empirical model constant (dimensionless) and t = time (s).

The experimental data was fitted on the selected models, which have been successfully used to describe the drying characteristics of fruits and vegetables and has produced good fits with fewer assumptions in predicting drying of various food materials (Khaled et al., 2020). Further, these models have been observed as important tools for establishing empirical relationships (Toğrul and Pehlivan, 2004). R2017b Matlab and Simulink – Math Works was used to estimate the drying coefficients and the coefficient of determination (R2), root mean square error (RMSE), shown as Eq. (3) by Onwude et al. (2016), where MRpre, is the predicted moisture ratio and MRexp, is the experimental moisture ratio, N is the number of observations. The chi-squared (χ2) was determined using Microsoft Office Excel (2016) shown as Eq. (4) after Onwude et al. (2016) with z being the number of constants. These statistical parameters were then used to assess the goodness of fit for each model (Asiru et al., 2013; Hussein et al., 2016). The criterion for selection of the best model in describing the drying kinetics would be according to the highest R2 mean values, and the lowest RMSE and chi-squared mean values (Taheri-Garavand et al., 2011).

RMSE=(∑i=1N(MRpre,i−MRexp,iN)12 (3)
χ2=(∑i=1N(MRpre,i−MRexp,iN−z)2 (4)

2.6. Determination of effective moisture diffusivity

Fick's law of diffusion is widely used to describe drying in the falling rate, where diffusion is the dominant drying mechanism of fruits and vegetables (Onu et al., 2016; Zhu and Feiyan, 2014). Fick's equation was developed, by Crank (1975) and assumes that in the drying period there is uniform initial moisture distribution; moisture migration is by diffusion, negligible external resistance and shrinkage, constant diffusivity, and temperature. In this study, Fick's law of diffusion and the Arrhenius-type model determined the moisture diffusion during drying and the activation energy for the SPS with 3, 5, and 7 mm thickness. Therefore, this study assumes that the initial moisture concentration was uniform and the mean moisture ratio at time t can be calculated using Eq. (5) by Aregbesola et al. (2015), where MR (dimensionless) is the instantaneous moisture content, H is the half-thickness of a thin-layer sample (in m), Deff(m2.s−1) is the effective moisture diffusivity and t (s) is the drying time.

MR=8π2 ​exp(−π2Defft4H2) (5)

The slope, Ko (dimensionless) of the ln (MR) versus time graph was used to estimate the Deff using Eq. (6) by Doymaz (2007) and Hussein et al. (2016).

Deff=−4KoH2π2t (6)

2.7. Physical and microstructure changes

The morphology of starch grains in the SPS was analyzed using a scanning electron microscope (SEM), Zeiss Evo LS15 (Zeiss, Germany), which was used to take micrographs of fresh and dried sweet potato chips. The samples were mounted on aluminium double-sided stubs and gold-coated before taking micrographs. The SEM magnification was set at a 124 x high vacuum and the extra high-tension (EHT) voltage was set at 20 kV. Micrographs were taken of the surfaces of dried and fresh SPS using standard SEM procedure by Xiao and Gao (2012).

3. Results and discussions

3.1. Drying kinetics of sweet potato slices in hot-air oven drier and a naturally-ventilated solar-venturi dryer

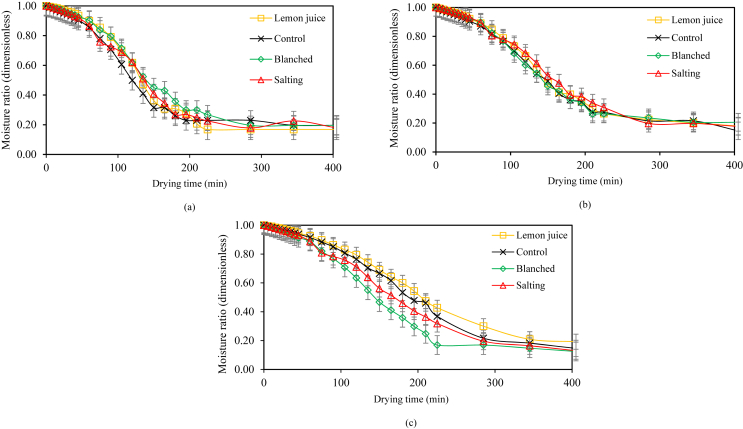
The dimensionless moisture ratio decreased with the increase in the drying time as shown in Figure 2 (HAD) and Figure 3 (NSD) for SPS samples with and without pre-drying treatments at 3, 5 and 7 mm thickness size. The graphs indicate that the drying time increased significantly (P < 0.05) with the increase in thickness size (from 3 to 7 mm) for both HAD and NSD having a longer total drying time. Other studies reported that the thickness of drying sample has a significant influence on the drying time (Vivek et al., 2021; Raut et al., 2021). The shorter drying time in HAD was a result of constant and higher drying air temperature compared to NSD drying temperature. Asiruet al. (2013) also reported that as temperature increased, the drying time was decreased in the drying of cashew kernels and Hussein et al. (2016) reported similar findings in the drying of tomato slices. In both HAD and a NSD, SPS pre-treated with lemon juice had shorter drying times.

Figure 2.

Figure 2

Open in a new tab

Moisture ratio of (a) = 3 mm, (b) = 5 mm and (c) = 7 mm thickness sweet potato slices drying in a hot-air oven dryer at 70 °C.

Figure 3.

Figure 3

Open in a new tab

Moisture ratio of (a) = 3 mm, (b) = 5 mm and (c) = 7 mm thickness sweet potato slices drying in a naturally-ventilated solar-venturi dryer.

The time taken to reach constant moisture for SPS at 3, 5 and 7 mm thickness under the HAD was 225 min (4 h), 285 min (5 h), and 345 min (6 h), respectively, and 11–13 h for the same thickness sizes under NSD. The drying rates in HAD and NSD were higher at the beginning of the drying process and gradually decreased as the drying process progressed. The results showed that the drying rate was rapid at the start of the drying process and decreased with time. The higher drying rates at the start of the process are a result of more radiation energy being absorbed by the water at the product surface initially, resulting in faster drying (Doymaz, 2011; Jabeen et al. (2015). The drying of SPS in NSD was observed to vary with the time of the day, due to varying environmental conditions of air temperature, relative humidity, and air velocity over the length of the day. Similar observations were made by Khanal and Lei, 2011; Afriyie and Bart-Plange (2012). The shorter drying times for HAD resulted in higher mass transfer and a higher drying rate. The drying curves depict that at the start of drying, the drying process occurred in the falling-rate drying period (Jabeen et al., 2015; Naderinezhad et al., 2015).

There was almost no constant-rate drying period though moisture was evaporating from the surface as internal moisture moved towards the surface at the same rate as that of moisture vaporization. This is analogous to results reported by Diamante and Munro (1991) and Mbegbu et al. (2021). Therefore, it is safe to assume that internal moisture diffusion occurs. Sweet potato slices at 3 mm thickness had a faster drying rate compared to 5 and 7 mm thick SPS for both drying methods. The reason is that there was a greater distance travelled by moisture to the surface of the SPS with a larger thickness size compared to smaller thickness size. The observed drying rate showed dependency on the drying temperature and thickness size in both the HAD and NSD. Similar observations were made by Hashim et al. (2014) and Akpinar (2008) when modelling the drying process of pumpkins using a convective hot air dryer and when investigating open sun and solar drying respectively.

3.2. Modelling of sweet potato slices drying curves

The experimental moisture ratios were then fitted to the selected thin-layer drying models presented in Table 1. The results obtained gave statistical parameters of each model as shown in Table 2 and Table 3.

Table 2.

Statistical parameters of selected thin-layer drying models under a naturally-ventilated solar-venturi dryer.

T [mm] Model Blanching
 Lemon juice
 Salting
 Control
R2 RMSE χ2 R2 RMSE χ2 R2 RMSE χ2 R2 RMSE χ2
3 Henderson and Pabis 0.937 0.078 2.16 × 10−3 0.848 0.121 2.71 × 10−2 0.920 0.091 1.56 × 10−3 0.912 0.102 2.11 × 10−3
Modified Henderson and Pabis 0.975 0.060 4.87 × 10−4 0.924 0.104 1.86 × 10−3 0.953 0.085 1.02 × 10−4 0.968 0.075 3.05 × 10−4
Logarithmic 0.957 0.067 8.32 × 10−3 0.916 0.094 1.46 × 10−3 0.942 0.080 1.56 × 10−3 0.952 0.078 1.88 × 10−4
Two-term 0.937 0.081 1.84 × 10−3 0.848 0.126 2.71 × 10−2 0.920 0.095 1.86 × 10−3 0.912 0.106 2.11 × 10−3
Two-term exponential 0.980 0.044 4.32 × 10−4 0.950 0.069 8.80 × 10−4 0.974 0.051 8.25 × 10−4 0.937 0.085 2.16 × 10−4
Midilli et al. 0.989 0.014 2.08 × 10−5 0.988 0.042 3.15 × 10−5 0.984 0.044 3.14 × 10−5 0.992 0.033 1.75 × 10−6
Modified Midilli 0.985 0.042 3.04 × 10−5 0.974 0.053 4.95 × 10−5 0.983 0.042 3.37 × 10−5 0.992 0.031 1.77 × 10−6
Hii et al., 0.981 0.049 4.00 × 10−5 0.981 0.049 4.83 × 10−5 0.986 0.047 1.39 × 10−5 0.988 0.043 5.41 × 10−5
Demir et al., 0.984 0.046 3.11 × 10−5 0.977 0.051 4.93 × 10−4 0.984 0.045 3.57 × 10−5 0.994 0.030 4.63 × 10−6
Verma et al., 0.981 0.045 4.00 × 10−5 0.954 0.069 5.23 × 10−4 0.974 0.054 5.44 × 10−4 0.985 0.044 2.48 × 10−5
Sigmoid 0.964 0.068 1.42 × 10−4 0.979 0.052 1.29 × 10−4 0.982 0.050 3.68 × 10−5 0.991 0.038 3.48 × 10−5
5 Henderson and Pabis 0.877 0.119 5.09 × 10−2 0.870 0.114 3.26 × 10−2 0.862 0.137 4.67 × 10−2 0.906 0.110 2.58 × 10−3
Modified Henderson and Pabis 0.976 0.051 3.75 × 10−3 0.903 0.120 2.65 × 10−3 0.976 0.039 3.69 × 10−4 0.970 0.076 7.55 × 10−4
Logarithmic 0.947 0.081 1.63 × 10−3 0.957 0.068 1.52 × 10−4 0.927 0.104 3.94 × 10−3 0.940 0.092 3.15 × 10−4
Two-term 0.876 0.124 1.29 × 10−2 0.870 0.119 3.27 × 10−2 0.862 0.143 4.08 × 10−2 0.906 0.115 3.05 × 10−3
Modified Two-term 0.968 0.060 8.85 × 10−4 0.951 0.070 1.34 × 10−4 0.958 0.075 1.65 × 10−4 0.977 0.055 7.45 × 10−4
Midilli et al. 0.992 0.031 2.39 × 10−6 0.987 0.047 2.26 × 10−5 0.985 0.049 4.14 × 10−5 0.992 0.038 2.44 × 10−6
Modified Midilli et al., 0.985 0.042 4.19 × 10−5 0.977 0.981 3.17 × 10−5 0.985 0.025 4.10 × 10−5 0.990 0.037 2.39 × 10−6
Hii et al., 0.984 0.049 3.78 × 10−5 0.984 0.039 2.87 × 10−5 0.978 0.063 1.22 × 10−4 0.983 0.054 1.08 × 10−5
Derma et al., 0.982 0.050 4.29 × 10−5 0.987 0.057 5.40 × 10−5 0.985 0.049 4.21 × 10−5 0.991 0.038 2.49 × 10−6
Verma et al., 0.981 0.049 1.27 × 10−4 0.957 0.068 2.87 × 10−4 0.964 0.073 1.52 × 10−4 0.978 0.055 3.23 × 10−4
Sigmoid 0.980 0.055 1.92 × 10−4 0.983 0.020 3.75 × 10−5 0.985 0.052 4.37 × 10−5 0.970 0.069 4.76 × 10−5
7 Henderson and Pabis 0.925 0.093 4.43 × 10−4 0.885 0.121 3.27 × 10−4 0.905 0.111 2.71 × 10−4 0.915 0.104 2.40 × 10−4
Modified Henderson and Pabis 0.955 0.088 1.06 × 10−4 0.951 0.097 1.57 × 10−4 0.986 0.053 4.72 × 10−4 0.967 0.079 8.98 × 10−4
Logarithmic 0.976 0.055 6.52 × 10−4 0.885 0.127 2.69 × 10−4 0.946 0.087 2.77 × 10−4 0.942 0.089 2.30 × 10−4
Two-term 0.925 0.097 4.43 × 10−4 0.963 0.069 3.13 × 10−4 0.905 0.147 2.81 × 10−4 0.915 0.108 2.40 × 10−3
Modified Two-term 0.979 0.049 1.42 × 10−4 0.978 0.058 1.18 × 10−5 0.978 0.054 5.83 × 10−4 0.969 0.062 8.34 × 10−4
Midilli et al. 0.989 0.033 3.36 × 10−6 0.987 0.056 6.74 × 10−6 0.987 0.051 3.44 × 10−5 0.982 0.067 5.56 × 10−5
Modified Midilli et al., 0.984 0.046 6.86 × 10−5 0.981 0.058 6.16 × 10−5 0.983 0.052 5.33 × 10−4 0.980 0.064 6.43 × 10−5
Hii et al., 0.983 0.047 9.53 × 10−5 0.966 0.068 5.01 × 10−5 0.992 0.037 1.54 × 10−4 0.984 0.051 1.78 × 10−5
Demir et al., 0.983 0.047 1.41 × 10−4 0.980 0.059 6.46 × 10−5 0.981 0.054 5.55 × 10−5 0.971 0.067 8.98 × 10−4
Verma et al., 0.981 0.049 1.89 × 10−4 0.979 0.057 5.12 × 10−5 0.980 0.054 1.51 × 10−4 0.970 0.065 2.57 × 10−4
Sigmoid et al., 0.973 0.065 2.03 × 10−4 0.978 0.059 1.18 × 10−3 0.973 0.074 2.03 × 10−3 0.969 0.072 1.16 × 10−4
Open in a new tab

∗T [mm] = Slice thickness (in mm), R2 = coefficient of determination, RMSE = root mean square error and χ2 = Chi-squared.

Table 3.

Statistical parameters of selected thin-layer drying models under hot-air oven drying.

T [mm] Model Blanching
 Lemon juice
 Salting
 Control
R2 RMSE χ2 R2 RMSE χ2 R2 RMSE χ2 R2 RMSE χ2
3 Henderson and Pabis 0.989 0.030 5.03 × 10−5 0.990 0.037 2.39 × 10−5 0.991 0.035 7.42 × 10−6 0.992 0.032 5.93 × 10−6
Modified Henderson and Pabis 0.996 0.025 4.28 × 10−6 0.999 0.013 2.34 × 10−6 0.998 0.016 5.33 × 10−6 0.999 0.007 5.94 × 10−6
Logarithmic 0.993 0.030 2.20 × 10−5 0.990 0.037 2.61 × 10−6 0.991 0.036 7.67 × 10−6 0.992 0.032 5.93 × 10−6
Two-term 0.993 0.031 3.93 × 10−5 0.991 0.036 2.38 × 10−6 0.992 0.034 4.92 × 10−6 0.991 0.032 5.55 × 10−6
Modified Two-term 0.989 0.038 3.93 × 10−5 0.990 0.036 2.87 × 10−6 0.985 0.046 7.54 × 10−5 0.990 0.036 5.06 × 10−6
Midilli et al. 0.999 0.012 2.69 × 10−6 0.999 0.012 2.40 × 10−6 0.998 0.016 3.71 × 10−6 0.999 0.013 2.51 × 10−6
Modified Midilli 0.999 0.013 3.31 × 10−6 0.999 0.013 2.40 × 10−6 0.998 0.016 7.46 × 10−6 0.998 0.016 5.57 × 10−6
Hii et al., 0.986 0.045 5.12 × 10−5 0.999 0.010 2.39 × 10−6 0.997 0.017 7.54 × 10−6 0.997 0.018 5.54 × 10−6
Demir et al. 0.988 0.040 4.89 × 10−5 0.999 0.011 2.80 × 10−6 0.998 0.016 6.54 × 10−6 0.999 0.013 5.48 × 10−6
Verma et al., 0.989 0.038 4.39 × 10−5 0.999 0.013 2.95 × 10−6 0.996 0.018 7.46 × 10−6 0.990 0.037 5.67 × 10−5
Sigmoid 0.989 0.013 4.94 × 10−5 0.929 0.182 2.65 × 10−3 0.879 0.183 7.71 × 10−3 0.998 0.014 5.80 × 10−6
5 Henderson and Pabis 0.993 0.030 4.62 × 10−5 0.995 0.026 4.25 × 10−5 0.994 0.028 1.85 × 10−6 0.997 0.021 1.67 × 10−6
Modified Henderson and Pabis 0.998 0.017 2.36 × 10−6 0.998 0.016 4.17 × 10−6 0.998 0.017 1.83 × 10−6 0.996 0.022 2.13 × 10−6
Logarithmic 0.993 0.030 2.33 × 10−5 0.995 0.026 4.47 × 10−6 0.994 0.028 1.86 × 10−6 0.997 0.021 1.95 × 10−6
Two-term 0.993 0.025 4.62 × 10−5 0.994 0.027 4.07 × 10−6 0.985 0.046 1.67 × 10−5 0.995 0.023 2.01 × 10−6
Modified Two-term 0.990 0.037 2.63 × 10−5 0.996 0.023 4.16 × 10−6 0.985 0.046 1.98 × 10−5 0.996 0.023 2.05 × 10−6
Midilli et al. 0.999 0.012 4.33 × 10−6 0.999 0.011 4.52 × 10−6 0.998 0.016 1.79 × 10−6 0.999 0.012 2.91 × 10−6
Modified Midilli et al., 0.999 0.013 4.64 × 10−6 0.998 0.013 4.50 × 10−6 0.998 0.016 1.90 × 10−6 0.999 0.013 2.00 × 10−6
Hii et al., 0.999 0.011 4.83 × 10−6 0.999 0.010 4.56 × 10−6 0.998 0.017 1.92 × 10−6 0.998 0.012 1.93 × 10−6
Demir et al., 0.890 0.070 4.53 × 10−3 0.999 0.012 3.54 × 10−6 0.998 0.017 1.87 × 10−6 0.999 0.012 1.98 × 10−6
Verma et al., 0.999 0.012 4.61 × 10−5 0.993 0.031 4.30 × 10−6 0.990 0.038 1.90 × 10−6 0.996 0.023 2.02 × 10−6
Sigmoid 0.890 0.126 4.60 × 10−3 0.870 0.185 4.09 × 10−3 0.880 0.127 1.79 × 10−3 0.935 0.095 1.98 × 10−3
7 Henderson and Pabis 0.995 0.025 3.37 × 10−6 0.997 0.021 3.33 × 10−6 0.995 0.025 3.10 × 10−6 0.996 0.023 5.27 × 10−6
Modified Henderson and Pabis 0.999 0.011 3.59 × 10−6 0.998 0.010 3.36 × 10−6 0.999 0.014 3.04 × 10−6 0.998 0.018 4.88 × 10−6
Logarithmic 0.995 0.025 3.49 × 10−6 0.997 0.021 3.72 × 10−6 0.995 0.026 3.11 × 10−6 0.996 0.023 5.01 × 10−6
Two-term 0.995 0.023 1.62 × 10−6 0.996 0.020 3.43 × 10−6 0.992 0.033 3.13 × 10−5 0.996 0.024 5.10 × 10−6
Modified Two-term 0.993 0.031 9.32 × 10−5 0.995 0.026 3.42 × 10−6 0.989 0.036 3.01 × 10−5 0.998 0.012 4.84 × 10−6
Midilli et al. 0.999 0.011 2.14 × 10−6 0.999 0.011 3.38 × 10−6 0.999 0.014 3.61 × 10−6 0.999 0.011 4.60 × 10−6
Modified Midilli et al., 0.998 0.012 1.68 × 10−6 0.998 0.016 3.42 × 10−6 0.998 0.015 7.52 × 10−6 0.999 0.014 4.91 × 10−6
Hii et al., 0.997 0.010 2.69 × 10−6 0.998 0.010 3.04 × 10−6 0.999 0.014 3.11 × 10−6 0.998 0.015 4.94 × 10−6
Demir et al., 0.998 0.011 1.61 × 10−6 0.997 0.016 3.42 × 10−6 0.997 0.018 2.87 × 10−6 0.988 0.041 4.94 × 10−5
Verma et al., 0.996 0.023 1.58 × 10−6 0.995 0.027 3.50 × 10−6 0.998 0.016 3.21 × 10−6 0.999 0.011 5.05 × 10−6
Sigmoid 0.966 0.070 1.37 × 10−5 0.879 0.183 3.51 × 10−3 0.879 0.127 2.78 × 10−3 0.923 0.106 4.92 × 10−3
Open in a new tab

∗T (mm) = Thickness (in mm), R2 = coefficient of determination, RMSE = root mean square error and χ2 = Chi-squared.

From Table 2 and Table 3 the highest values of R2 and the lowest values of χ2 were obtained from Midilli et al. model for both NSD and HAD, hence, the model was selected as the best model in predicting the drying behaviour of SPS for all thickness sizes. The highest R2 for Midilli et al. model was obtained in drying samples pre-treated with lemon juice for both the NSD and HAD. This shows the suitability of the model in describing the drying kinetics of SPS for both drying methods. Various researchers in the drying of fruits and vegetables obtained similar results. Taheri-Garavand et al. (2011) and Isa and Oyerinde (2020) reported similar results and the Midilli et al. model was selected as the best model in describing the drying kinetics of tomatoes and milled carrots respectively.

3.3. Estimation of effective moisture diffusivity and activation energy

The variation of ln (MR) with drying time, for the Midilli et al. model indicates that the moisture transfer during drying was governed by diffusion in both HAD and NSD, hence, Fick's second law of diffusion and Midilli et al. model was used to predict the effective moisture diffusion rate of lemon juice pre-treated SPS at different thickness size. The effective moisture diffusivity (Deff) determined using Eq. (4) varied with SPS thickness and the values were 1.02 × 10−8 and 3.32 × 10−9 m2 s−1 for both HAD and NSD respectively. The 3 mm thickness slices had higher moisture diffusivity than the 5 mm and 7 mm ones as shown in Table 4.

Table 4.

Effective moisture diffusivities of sweet potato slices in different thickness sizes.

Drying method Thickness [mm] Deff [m2.s−1]
HAD 3 2.19 × 10−8
5 1.56 × 10−8
7 1.02 × 10−8
NSD 3 6.31 × 10−9
5 4.16 × 10−9
7 3.32 × 10−9
Open in a new tab

∗HAD – hot air oven dryer, NSD – solar venturi dryer, Deff – effective moisture diffusivity.

Hot-air drying showed a higher effective moisture diffusivity (Deff) than the NSD. This could be as a result of a relatively high temperature in HAD compared to the NSD. The diffusivity values obtained from the experimental data fell within the 10−11 – 10−6 m2 s−1 range reported by Demiray and Tulek (2011) for hot-air drying methods. Dinrifo (2012) found a moisture diffusivity range of 7.76 × 10−9 to 1.2 × 10−8 m s−1 in the drying of SPS using the hot-air drying method, which is within the range for most dried food materials.

3.4. Physical and microstructure changes

The physical appearance and colour is one of the most important parameters with a major influence on the buyers’ choice (Nazmi et al., 2018; Oyebanji et al., 2013). The difference in colour images taken after drying shows that the pre-drying treatment, drying method and drying temperature influenced the physical characteristics of the SPS as shown in Figures 4 and 5. Naturally-ventilated, solar-venturi dried SPS were darker compared to HAD treated samples. This was presumed to be the result of the drying temperature and time, and formation of browning pigments, which inhibited change in colour of SPS. The presence of oxygen and polyphenol oxidase activity causes enzymatic browning in low-temperature drying (Sehrawat et al., 2018). Blanched SPS had the worst lightness values for both drying methods when compared with the other treatments. This indicates that blanching did not improve the colour of the dried samples and hot water treatment influenced the physical characteristics of dried samples.

Figure 4.

Figure 4

Open in a new tab

Naturally-ventilated solar dried SPS (A1 = Control, A2 = Salting, A3 = Blanching, A4 = Lemon juice).

Figure 5.

Figure 5

Open in a new tab

Hot-air oven dried SPS (B1 = Control, B2-Salting, B3 = Blanching, B4 = Lemon juice).

Scanning electron micrographs (SEM) were used for comparing the surface microstructure of fresh and dried SPS using micrographs of fresh and dried SPS, as shown in Figures 6 and 7. This investigation was done to determine the effect of pre-treatments and drying method on final dried SPS. Starch morphological images were taken at the centre of each SPS. Fresh SPS starch granules were observed to have regular oval and spherical structures.

Figure 6.

Figure 6

Open in a new tab

Solar dried SPS (NSD1 = Control, NSD2 = Salted, NSD3 = Blanched, NSD4 = Lemon juice) and Oven dried SPS (OVD1 = Control, OVD2 = Salted).

Figure 7.

Figure 7

Open in a new tab

HAD dried SPS (OVD3 = Blanched, OVD4 = Lemon juice) and Fresh SPS (SPS1 = Control, SPS2 = Salting, SPS3 = Blanched, SPS4 = Lemon juice).

Dried SPS had varying sizes of starch granules, depending on the treatments and drying methods (Hartiningsih et al., 2020). However, most of the starch granules were oval-shaped, and in various sizes. Blanched SPS were observed to have flat deformed starch surface granules after both drying methods (HAD and NSD), as a of result hydrothermal treatment which alters the starch properties of sweet potatoes by causing modified starch granules. This is analogous to a study by Babu et al. (2015) and Iheagwara (2012). Control, salted and lemon juice treated samples dried in the HAD displayed an oval shape, while SPS dried in the NSD had oval-flat shape starch granules. Lemon juice pre-treated samples dried using both HAD and NSD retained oval-shaped starch granules after drying; hence, the lemon juice treatment was found to be the best pre-drying treatment method for the dehydration of SPS.

4. Conclusions

Selected thin-layer models were evaluated to illustrate the drying characteristics of SPS under HAD and NSD, select the drying models that best fit the drying data, and estimate the effective moisture diffusivity. Hot air drying took a shorter drying time compared to NSD, as the temperature of the HAD was relatively higher than that of NSD. The thickness of the SPS influenced the drying characteristics (drying time and drying rate). The 3 mm slices dried faster in both HAD and NSD, compared to 5 and 7 mm thickness slices. Consequently, the moisture diffusivity in 3 mm thick SPS was relatively higher. Although the drying of SPS in NSD had a longer drying time, the moisture removal rate was relatively high and drying occurred at the falling-rate drying period, enabling moisture removal by diffusion, and this resulted in better product quality. Therefore, the drying conditions (temperature and relative humidity) in NSD are suitable for drying SPS together with lemon juice as pre-drying treatment to maintain the chemical properties of SPS. However, an increase in drying air velocity is recommended to eliminate challenges resulting from energy-intensive methods. Naturally-ventilated solar-venturi drying is, therefore, a practical method for use in the drying of large quantities of a product and it allows for the use of renewable energy as an alternative to electricity. This study found Midilli et al. model to be the best fit for experimental moisture ratio data that can be used to estimate the moisture ratio of SPS during drying. Furthermore, the study showed that NSD is a practical solution for small-scale farmers. However, the study recommends an increase in airflow velocity to increase the drying rate, hence effectiveness for the use of the NSD.

Declarations

Author contribution statement

Siyabonga Gasa: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Sipho Sibanda, Mark Laing, Alaika Kassim: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Tilahun S. Workneh: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by the Agricultural Research Council.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

References

  1. Afriyie J.K., Bart-Plange A. Vol. 2012. International Scholarly Research Network (ISRN) Renewable Energy; 2012. Performance Investigation of a Chimney-dependent Solar Crop Dryer for Different Inlet Areas with a Fixed Outlet Area; p. 194359. [Google Scholar]
  2. Akoy E. Experimental characterization and modeling of thin-layer drying of mango slices. Int. Food Res. J. 2014;21(5):1911–1917. [Google Scholar]
  3. Akpinar E.K. Mathematical modelling and experimental investigation on sun and solar drying of white mulberry. J. Mech. Sci. Technol. 2008;22(8):1544–1553. [Google Scholar]
  4. AOAC . fourteenth ed. Association of Official Agricultural Chemists; Washington: 1984. Official Methods of Analysis. [Google Scholar]
  5. Aregbesola O.A., Ogunsina B.S., Sofolahan A.E., Chime N.N. Mathematical modeling of thin layer drying characteristics of dika (Irvingia gabonensis) nuts and kernels. Niger. Food J. 2015;33(1):83–89. [Google Scholar]
  6. Asiru W., Raji A.O., Igbeka J., Elemo G.N. Mathematical modelling of thin layer dried cashew kernels. Niger. Food J. 2013;31(2):106–112. [Google Scholar]
  7. Ayadi M., Mabrouk S.B., Zouari I., Bellagi A. Kinetic study of the convective drying of spearmint. J. Saudi Soc. Agric. Sci. 2014;13(1):1–7. [Google Scholar]
  8. Babiker A., Osman O., Mohammed B., Abdalla E., Nourain J., Aboshora W. Mathematical modelling of thin layer solar drying of fish (Bagrusbayad) Int. J. Med. Clin. Res. 2016;4:259–264. March/April 2016) [Google Scholar]
  9. Babu A.S., Parimalavalli R., Jagannadham K., Rao J.S. Chemical and structural properties of sweet potato starch treated with organic and inorganic acid. J. Food Sci. Technol. 2015;52(9):5745–5753. doi: 10.1007/s13197-014-1650-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chandrasekara A., Kumar T. Roots and tuber crops as functional foods: a review on phytochemical constituents and their potential health Benefits. Int. J. Food Sci. 2016;2016:3631647. doi: 10.1155/2016/3631647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Crank J. second ed. Oxford University Press; London, UK: 1975. The Mathematics of Diffusion. Clarendon Press. [Google Scholar]
  12. da Silva W.P., eSilva C.M.D.P.S., Gama F.J.A., Gomes J.P. Mathematical models to describe thin-layer drying and to determine drying rate of whole bananas. J. Saudi Soc. Agric. Sci. 2014;13(1):67–74. [Google Scholar]
  13. Dasore A., Konijeti R., Puppala N., Polavarapu T. A novel empirical model for drying of root vegetables in thin-layers. Int. J. Scient. Technol. Res. 2020;9:2639–2642. [Google Scholar]
  14. de Souza D.M., Coelho S.R.M., Christ D., Kottwitz L.B.M., Lewandoski C.F., Kowaleski J.…Gurgacz F. Optimization of the drying process for production of biofortified sweet potato flour. J. Food Process. Preserv. 2021;45(1) [Google Scholar]
  15. Demir V., Gunhan T., Yagcioglu A.K. Mathematical modelling of convection drying of green table olives. Biosyst. Eng. 2007;98(1):47–53. [Google Scholar]
  16. Demiray E., Tulek Y. Thin-layer drying of tomato (Lycopersicum esculentum Mill. cv. Rio Grande) slices in a convective hot air dryer. Heat Mass Tran. 2012;48(5):841–847. [Google Scholar]
  17. Diamante L., Munro P. Mathematical modelling of hot air drying sweet potato slices. Int. J. Food Sci. Technol. 1991;26(1):99–109. [Google Scholar]
  18. Doymaz İ. The kinetics of forced convective air-drying of pumpkin slices. J. Food Eng. 2007;79(1):243–248. [Google Scholar]
  19. Doymaz İ. Thin-layer drying characteristics of sweet potato slices and mathematical modelling. Heat Mass Tran. 2011;47(3):277–285. [Google Scholar]
  20. Dinrifo R.R. Effects of pre-treatments on drying kinetics of sweet potato slices. Agric. Eng. Int.: CIGR J. 2012;14(3):136–145. [Google Scholar]
  21. Ertekin C., Firat M. A comprehensive review of thin layer drying models used in agricultural products. Crit. Rev. Food Sci. Nutr. 2015;57(4):1–71. doi: 10.1080/10408398.2014.910493. [DOI] [PubMed] [Google Scholar]
  22. Hashim N., Daniel O., Rahaman E. A preliminary study: kinetic model of drying process of pumpkins (cucurbita moschata) in a convective hot air dryer. Agric. Agric. Sci. Proc. 2014;2:345–352. [Google Scholar]
  23. Hartiningsih S., Pranoto Y., Supriyanto Structural and rheological properties of modified sago starch (Metroxylon sagu) using treatment of steam explosion followed by acid-hydrolyzed as an alternative to produce maltodextrin. Int. J. Food Prop. 2020;23(1):1231–1242. [Google Scholar]
  24. Hii C.L., Law C.L., Cloke M. Modelling using a new thin layer drying model and product quality of cocoa. J. Food Eng. 2009;90(2):191–198. [Google Scholar]
  25. Hussein J., Filli K., Oke M. Thin layer modelling of hybrid, solar and open sun drying of tomato slices. Res. J. Food Sci. Nutr. 2016;1:15–27. [Google Scholar]
  26. Iheagwara M. Isolation, modification and characterization of sweet potato (Ipomoea batatas L (lam)) starch. J. Food Process. Technol. 2012;4 [Google Scholar]
  27. Isa J., Oyerinde A. Vol. 20. 2020. Modelling of the Drying of Milled Carrot Using Microwave and Laboratory Oven; pp. 268–280. [Google Scholar]
  28. Jabeen R., Aijaz T., Gul K. Drying kinetics of potato using a self-designed cabinet dryer. Cogent Food Agric. 2015;1(1):1036485. [Google Scholar]
  29. Javed I.M., Waseem A.M., Rawal A., Ibrar Y., Umer J. Heat and mass transfer modeling for fruit drying: a review. Food Process. Technol. 2019;7(3):69–73. [Google Scholar]
  30. Kaur K., Singh A.K. Drying kinetics and quality characteristics of beetroot slices under hot air followed by microwave finish drying. Afr. J. Agric. Res. 2014;9(12):1036–1044. [Google Scholar]
  31. Khaled A.Y., Kabutey A., Mizera Hrab P., Herak D. Modelling of hot-air and vacuum drying of persimmon fruit (Diospyros kaki) using computational intelligence methods. Agron. Res. 2020;18:1323–1335. [Google Scholar]
  32. Khanal R., Lei C. Solar chimney—a passive strategy for natural ventilation. Energy Build. 2011;43(8):1811–1819. [Google Scholar]
  33. Kucuk H., Midilli A., Kilic A., Dincer I. A review on thin-layer drying-curve equations. Dry. Technol. 2014;32(7):757–773. [Google Scholar]
  34. Mbegbu N.N., Nwajinka C.O., Amaefule D.O. Thin layer drying models and characteristics of scent leaves (Ocimum gratissimum) and lemon basil leaves (Ocimum africanum) Heliyon. 2021;7(1) doi: 10.1016/j.heliyon.2021.e05945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Meher J., Nayak P.K. Effect of pre-drying and frying kinetics of sweet potato chips. Int. Quart. J. Life Sci. 2016;10(2):521–525. [Google Scholar]
  36. Meisami-asl E., Rafiee S. Mathematical modeling of kinetics of thin-layer drying of apple (var.Golab) Agric. Eng. Int.: CIGR J. 2009;XI(2009):1185–1196. [Google Scholar]
  37. Mewa E.A., Okoth M.W., Kunyanga C.N., Rugiri M.N. Effect of drying air temperature and slice thickness on the physical and microbiological quality of dried beef. LWT - Food Sci. Technol. 2018;92:484–489. [Google Scholar]
  38. Miraei Ashtiani S.H., Salarikia A., Golzarian M.R. Analyzing drying characteristics and modeling of thin layers of peppermint leaves under hot-air and infrared treatments. Info. Proc. Agric. 2017;4(2):128–139. [Google Scholar]
  39. Naderinezhad S., Etesami N., Poormalek N.A., Ghasemi F.M. Mathematical modeling of drying of potato slices in a forced convective dryer based on important parameters. Food Sci. Nutr. 2015;4(1):110–118. doi: 10.1002/fsn3.258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Nasri M.Y., Belhamri A. Effects of the climatic conditions and the shape on the drying kinetics, Application to solar drying of potato-case of Maghreb's region. J. Clean. Prod. 2018;183(2018):1241–1251. [Google Scholar]
  41. Nazmi I., Gokcen I., Onur T. Impact of different drying methods on the drying kinetics, color, total phenolic content and antioxidant capacity of pineapple. CyTA - J. Food. 2018;16(1):213–221. [Google Scholar]
  42. Nurkhoeriyati T., Kulig B., Sturm B., Hensel O. The effect of pre-drying treatment and drying conditions on quality and energy consumption of hot air-dried celeriac slices: optimisation. Foods. 2021;10(8):1758. doi: 10.3390/foods10081758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Nwakuba N., Asoegwu S., Nwaigwe K. Energy requirements for drying of sliced agricultural products: a review. Agric. Eng. Int. CIGR J. 2016;18(2):144–155. [Google Scholar]
  44. Oke M.O., Workneh T.S. Convective hot air drying of different varieties of blanched sweet potato slices. Int. J. Agric. Biosyst. Eng. 2014;8(12):1–7. [Google Scholar]
  45. Olawale A., Omole S. Thin layer drying models for sweet potato in tray dryer. Agric. Eng. Int.: CIGR J. 2012;14(2) [Google Scholar]
  46. Onu C., Philomena I., Nwabanne J., Onu E., Nwabanne J.T. Effective moisture diffusivity, activation energy and specific energy consumption in the thin-layer drying of potato. Int. J. Novel Res. Eng. Sci. 2016;3(2):10–22. [Google Scholar]
  47. Onwude D.I., Hashim N., Janius R.B., Nawi N.M., Abdan K. Modeling the thin-layer drying of fruits and vegetables: a review. Compr. Rev. Food Sci. Food Saf. 2016;15(3):599–618. doi: 10.1111/1541-4337.12196. [DOI] [PubMed] [Google Scholar]
  48. Oyebanji A.O., Ajani A.O., Adeize A., Oyelakin M.O., Ikotun I., Agboola A.A., Awoite T. Effect of pre-drying treatments on utilizability of sweet potato tubers for production of chips for confectionery flour. Afr. J. Food Sci. 2013;7(9):258–263. [Google Scholar]
  49. Raut S., Md Saleh R., Kirchhofer P., Kulig B., Hensel O., Sturm B. Investigating the effect of different drying strategies on the quality parameters of daucus carota L. Using dynamic process control and measurement techniques. Food Bioprocess Technol. 2021;14(6):1067–1088. [Google Scholar]
  50. Sanginga N. 2015. Root and Tuber Crops (Cassava, Yam , Potato and Sweet Potato) Roots and Tubers Paper Presented at the Feeding Africa, Dahar, Senegal. [Google Scholar]
  51. Sanoussi F., Alexandre D., Ahissou H., Abdul-Rasaq A., Sanni L., Orobiyi A., Sanni A. Possibilities of sweet potato [Ipomoea batatas (L.) Lam] value chain upgrading as revealed by physico-chemical composition of ten elites landraces of Benin. Afr. J. Biotechnol. 2016;15(13):481–489. [Google Scholar]
  52. Schulze R., Maharaj M. 2007. Daily Maximum Temperatures. Pretoria, South Africa. [Google Scholar]
  53. Sehrawat R., Nema P.K., Kaur B.P. Quality evaluation and drying characteristics of mango cubes dried using low-pressure superheated steam, vacuum and hot air drying methods. LWT - Food Sci. Technol. 2018;92:548–555. [Google Scholar]
  54. Seidu J., Kwenin W., Tevor W.J., Mahama A., Agbeven J. Drying of sweet potato (ipomoea batatas) (chipped and grated) for quality flour using locally constructed solar dryers. Asian Res. Publish. Netw. (ARPN) - J. Agric. Biol. Sci. 2012;7(6):466–473. [Google Scholar]
  55. Süfer O., Sezer S., Demir H. Thin layer mathematical modelling of convective, vacuum and microwave drying of intact and brined onion slices. Food Process. Preserv. 2017;41(6) [Google Scholar]
  56. Taheri-Garavand A., Rafiee S., Keyhani A. Mathematical modeling of thin layer drying kinetics of tomato influence of air dryer conditions. Int. Trans. J. Eng. Manag. Appl. Sci. Technol. 2011;2(2):147–160. [Google Scholar]
  57. Titus P., Janet L. 2016. Cassava and Sweet Potato. Inter-American Institute for Cooperation on Agriculture (IICA). From VirtualPRO Magazine.https://www.bibliotecadigitaldebogota.gov.co/resources/2211563/ [Google Scholar]
  58. Toğrul İ.T., Pehlivan D. Modelling of thin layer drying kinetics of some fruits under open-air sun drying process. J. Food Eng. 2004;65(3):413–425. [Google Scholar]
  59. Verma L., Bucklin R., Endan J., Wratten F. Effects of drying air parameters on rice drying models. Trans. ASAE (Am. Soc. Agric. Eng.) 1985;28(1):296–301. [Google Scholar]
  60. Vivek K., Subbarao K.V., Srivastava B. Effect of thin-layer drying on the quality parameters of persimmon slices. Int. J. Fruit Sci. 2021;21(1):587–598. [Google Scholar]
  61. Xiao H.W., Gao Z.J. In: Scanning Electron Microscopy. Kazmiruk V., editor. InTech; Beijing, China: 2012. The application of scanning electron microscope (SEM) to study the microstructure changes in the field of agricultural products drying; pp. 213–226. [Google Scholar]
  62. Zhu A., Feiyan J. Modeling of mass transfer performance of hot-air drying of sweet potato (Ipomoea Batatas L.) slices. Chem. Ind. Chem. Eng. Q. 2014;20(2):171–181. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

Data will be made available on request.

Articles from Heliyon are provided here courtesy of Elsevier

RESOURCES