Abstract
Stereotactic radiosurgery (SRS) is now the standard of care for brain metastases (BMs) patients. The SRS treatment planning process requires precise target delineation, which in clinical workflow for patients with multiple (>4) BMs (mBMs) could become a pronounced time bottleneck. Our group has developed an automated BMs segmentation platform to assist in this process. The accuracy of the auto-segmentation, however, is influenced by the presence of false-positive segmentations, mainly caused by the injected contrast during MRI acquisition. To address this problem and further improve the segmentation performance, a deep-learning and radiomics ensemble classifier was developed to reduce the false-positive rate in segmentations. The proposed model consists of a Siamese network and a radiomic-based support vector machine (SVM) classifier. The 2D-based Siamese network contains a pair of parallel feature extractors with shared weights followed by a single classifier. This architecture is designed to identify the inter-class difference. On the other hand, the SVM model takes the radiomic features extracted from 3D segmentation volumes as the input for twofold classification, either a false-positive segmentation or a true BM. Lastly, the outputs from both models create an ensemble to generate the final label. The performance of the proposed model in the segmented mBMs testing dataset reached the accuracy (ACC), sensitivity (SEN), specificity (SPE) and area under the curve (AUC) of 0.91, 0.96, 0.90 and 0.93, respectively. After integrating the proposed model into the original segmentation platform, the average segmentation false negative rate (FNR) and the false positive over the union (FPoU) were 0.13 and 0.09, respectively, which preserved the initial FNR (0.07) and significantly improved the FPoU (0.55). The proposed method effectively reduced the false-positive rate in the BMs raw segmentations indicating that the integration of the proposed ensemble classifier into the BMs segmentation platform provides a beneficial tool for mBMs SRS management.
Keywords: Brain metastases, Stereotactic radiosurgery, Classification
1. Introduction
Brain metastases (BMs) are diagnosed in up to 40% of cancer patients. Current data estimates that ~200,000 new patients develop BMs annually (Nayak et al., 2012; Langer and Mehta, 2005), and these numbers will continue to rise due to the advances in systemic therapy and improved primary cancer control (Barnholtz-Sloan et al., 2004). The treatment regimens for BMs include surgical resection, whole brain radiation therapy (WBRT) and stereotactic radiosurgery (SRS). Recently, SRS has become the standard for patients with 1–3 BMs due to its efficacy and reduced toxicity (Sturm et al., 1987; Chang et al., 2009). Further, evidence from several clinical trials has demonstrated that for patients with multiple (>4) BMs (mBMs), compared to WBRT, SRS reduced the neurocognitive decline and improved quality of life (QoL) outcomes with no difference in overall survival (Thomas et al., 2014; Brown et al., 2016). Therefore, SRS is now increasingly favored for mBMs patients in the contemporary clinical practice.
High quality SRS treatment requires accurate target delineation for treatment planning as well as post-treatment follow-up. However, in the current clinical practice, BMs delineation is usually done manually by physicians, which can be very time-consuming especially for mBMs cases. Therefore, the automation of mBMs segmentation has become an urgent need in the clinic. Various algorithms have been proposed for this task recently. However, most algorithms cannot be directly applied into SRS for clinical applications either due to the requirement of imaging modalities or manual interactions (Geremia et al., 2012; Bagci et al., 2013; Buendia et al., 2013; Bauer et al., 2013; Gordillo et al., 2013; Bousabarah et al., 2020; Rudie et al., 2021; Xue et al., 2020).
The T1-weighted MRI with Gadolinium contrast (T1c) sequence is the current clinical standard and the most used sequence for the BMs SRS simulation in many institutions. The benefit of the Gadolinium contrast is that tumors can present with high intensity, which helps the diagnosis and contouring process. Recently, our group has developed a convolutional neural network-based BMs segmentation platform using T1c images as the input (Liu et al., 2017; Yang et al., 2020), which can segment BMs with high sensitivity and segmentation accuracy compared to other related works (Cao et al., 2021; Charron et al., 2018; Dikici et al., 2020). However, the false positive (FPs) contours in the segmentation are common due to intake of the contrast agent in cerebral vessels during the T1c MRI acquisition, as shown in Figure 1. Therefore, to further improve the performance and workflow automation without compromising the segmentation accuracy, a post-processing strategy is needed to reduce the FPs, which can be treated as a classification task separating true BMs and FPs in the auto-segmentation results.
Figure 1.
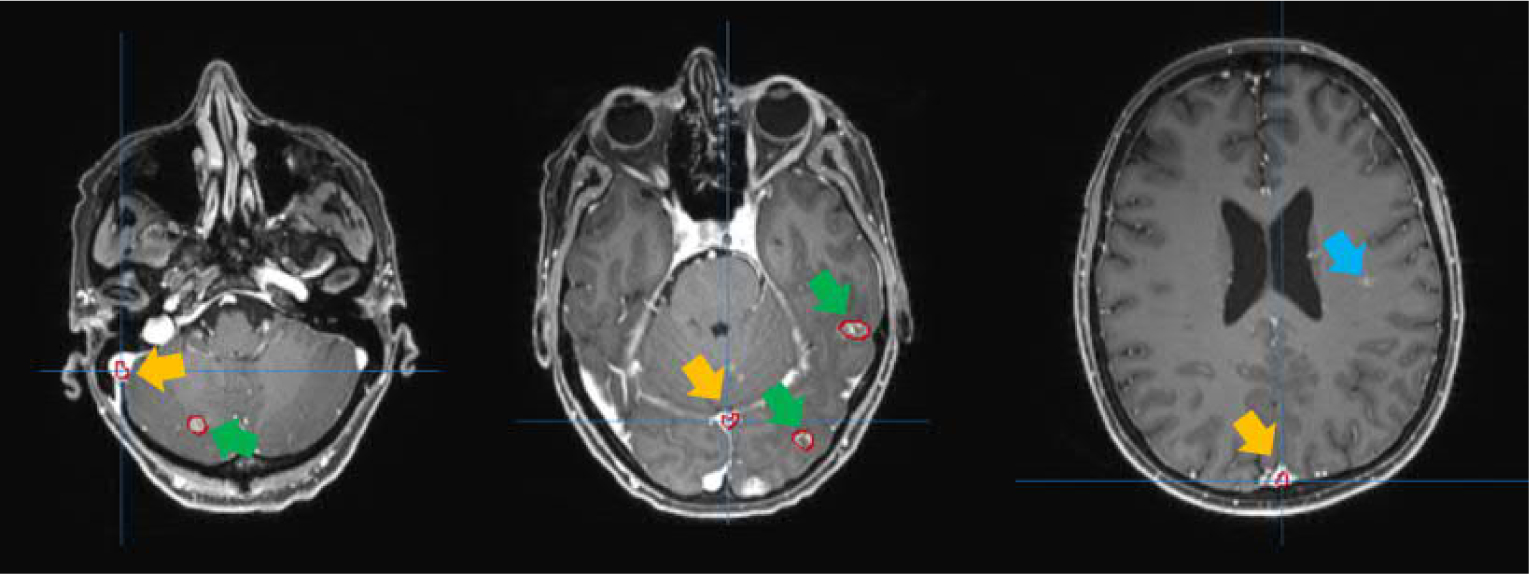
Examples of the segmentation results shown in red contours. The segmentations pointed to by yellow arrows are FPs. The blue arrow indicates the missed BM by segmentation. And the segmented true BMs are indicated by the green arrows.
Conventional classification approaches in the field of medical imaging usually utilize handcrafted feature together with suitable machine learning (ML) models. The most popular handcrafted features nowadays are radiomic features, referring to high-throughput quantitative features extracted from a large number of radiographic images (Nie et al., 2016); and the commonly used ML methods include K-means clustering (Huang, 1998), support vector machine (SVM) (Cortes and Vapnik, 1995), random forest (RF) (Svetnik et al., 2003), etc. For instance, Zacharaki et al. (Zacharaki et al., 2009) proposed a support vector machine recursive feature elimination (SVM-RFE) algorithm to distinguish different types of brain tumors, such as primary gliomas or BMs. Zhang et al. (Zhang et al., 2018) proposed a novel random forest approach for the classification of different types of high-grade gliomas using T1-weighted MR images. These ML methods usually do not require high computational cost and have been proved to provide effective performance for medical image datasets.
In recent years, deep learning (DL)-based classification approaches are shown to be accurate and robust for medical image processing (Khoshdeli et al., 2017; Roth et al., 2015; Liu et al., 2019; Pan and Yang, 2009). The automatic feature learning performed by DL models effectively learns complicated patterns in the image data, thus no longer requiring manual feature extraction. Moreover, in recent studies, there is an emerging application of the Siamese network, whose architecture design can help to expand the richness of the dataset in a manner of pair-wise learning (Norouzi et al., 2012). Therefore, the Siamese network is considered to be powerful at discovering interclass differences and has been applied to a wide range of studies such as object tracking (Bertinetto et al., 2016), face recognition (Chopra et al., 2005), and other matching tasks (Perek et al., 2018), which can be essentially considered as classification problems. For example, in the applications of medical imaging field, Fu et al. (Fu et al., 2020) employed a Siamese network to classify and assess the viable and necrotic tumor regions in osteosarcoma. In addition, Liu et al. (Liu et al., 2019) proposed a Siamese network with a margin ranking loss for automated lung nodule analysis.
To solve the FP reduction problem, we proposed a deep learning and radiomics ensemble model to take advantage of both methods. The radiomic features are designed and calculated from 3D volumes to describe the geometry and texture characteristics, and the deep learning features are automatically extracted from the 2D images. These two approaches provide independent but complementary information to identify FPs.
2. Methods & Materials
2.1. Patient Data
This study was approved by the University of Texas Southwestern Medical Center review board. Two datasets were collected: one was for training/validating the FP reduction model, and the other was for testing the overall segmentation platform performance after the integration of the FP reduction model.
To prepare the dataset for training/validating the FP reduction model, we retrospectively identified and collected a total of 242 mBMs patients treated with Gamma Knife (GK) SRS. All patients had T1-weighted MRI with Gadolinium contrast (T1c) (TR=2260 ms, TE=3.4 ms, FA=8°, 256*256 acquisition matrix, 0.98 mm in-plane resolution, 1 mm slice thickness) available as the baseline for treatment planning. The BMs in the baseline MRIs were delineated by physicians as the ground truth contours. All MRI volumes were then segmented by a CNN-based BMs segmentation platform En-DeepMedic (Yang et al., 2020). As an embedded workflow prior to the segmentation, the platform first automatically preprocessed the input T1c MRI images which included the intensity normalization and resampling to 1 mm3 isotropic resolution. The segmentation results (raw segmentations) were compared to the ground truth contours to identify FPs and true positive (TPs). In total, the raw segmentations contained 11890 volumes, among which 10832 volumes were FPs and 1058 volumes were TPs.
To test the segmentation platform after integrating the FP reduction model, a total of 10 mBMs patient data were collected with similar data availability as the FP reduction dataset. Patients were chosen to have a wide range of BMs counts (11–69) to test the overall performance of the platform. Table 1 shows the demographic summary of patients enrolled into this dataset.
Table 1.
The demographic summary of patient cohort
| Characteristic | Value |
|---|---|
|
| |
| Number | 10 |
| Mean age [years] | 60.5±8.1 |
| Sex: | |
| Male | 6 |
| Female | 4 |
| No. of lesions diagnosed | 38 ± 24 |
2.2. Model Design
As shown in Figure 2, the proposed FP reduction model, designed to classify FPs and TPs in the raw segmentation results, consists of two sub-models, a Siamese network-based classification model (branch (b) in Figure 2) and an SVM -radiomics model (branch (a) in Figure 2). The Siamese network-based model takes 2D images of the segmentation volumes as the input, next it generates a class label and a probability score along one cardinal axis, and then all three cardinal axes outputs are combined via majority voting. The SVM-radiomics model takes the radiomic features extracted from the 3D volumes with different dilations as the input and outputs a class probability score.
Figure 2.
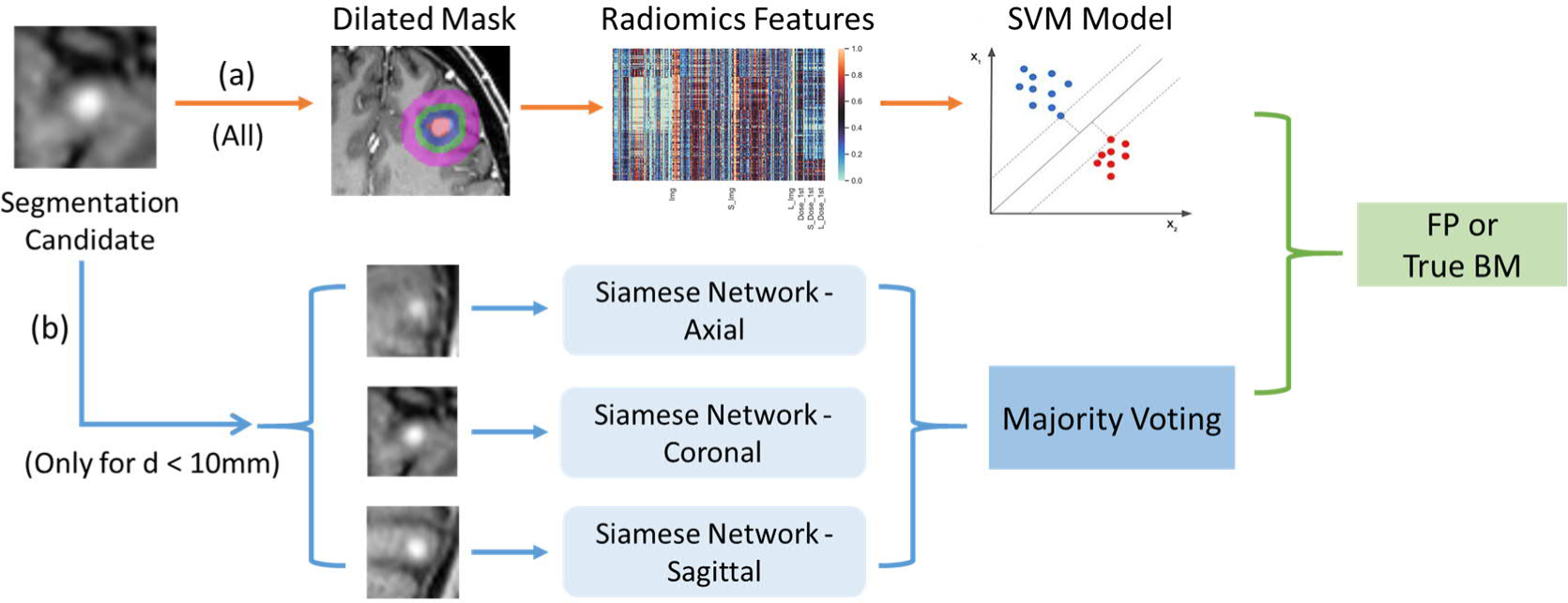
Workflow of the false-positive reduction process
Note that the Siamese network-based model only takes BMs candidates that have the largest dimension < 10 mm. This threshold is designed for accommodating the size for the majority of BMs while satisfying consistent input size requirement of the deep learning network. We found more than 95% of the total raw segmentations of the collected data had the largest dimension <10 mm. This is not surprising since large number of mBMs clinically often manifest as small, and the BM candidates, mainly the contrast-agent-enhanced vessels, are also small in size.
Thus, in this FP reduction model, the segmentation candidates with size less than 10 mm will go through the Siamese network and SVM-radiomics ensemble model, in which the final classification is fused using outputs from both models with the fusion weighted by the corresponding area under the curve (AUCs). For the segmentation candidates with the size larger than 10 mm, only the SVM model will be utilized for the classification process.
2.2.1. Siamese Network Model
2.2.1.1. Methods
The proposed Siamese network model, as shown in Figure 3, consists of two consecutive modules. The first module is a feature extractor (green boxes in Figure 3), which utilizes a pair of fine-tuned truncated ResNet50 structure as branches with shared weighs (He et al., 2016). Each branch starts with a single convolutional layer, followed by a series of residual blocks (Residual block 1 and Residual block 2) as shown in Figure 3. The residual block 2 contains a 1*1 down-sampling convolutional layer added to the shortcut path to match the dimensions (He et al., 2016). This feature extractor enables the model to efficiently extract complex and representative high-level features from low-level image features. The second module is a classifier (red box in Figure 3), which uses three fully connected layers to convert the extracted high-level features to the final class label. The entire Siamese network consists of two identical sub-network branches, and trains both branches conjointly. The updating of weight parameters is mirrored in both branches. Based on the output pair from these the two weight-shared branches, similarity or difference between the two inputs can be explored by implementing appropriate losses with the feature vector outputs.
Figure 3.
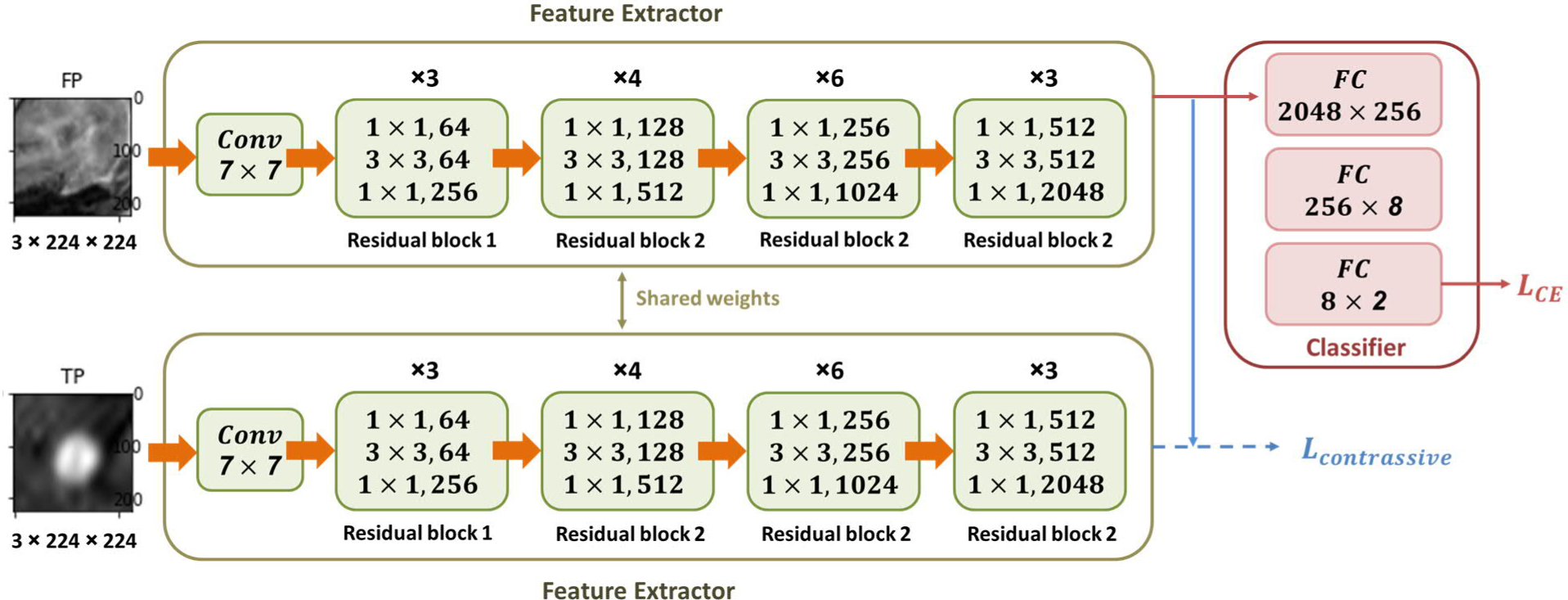
Architecture of the Siamese network for FP reduction
To address the classification problem in raw BMs segmentations, we chose the contrastive loss together with this Siamese network design to investigate the differences between true BMs and FPs. Specifically, during the forward propagation process, these two parameter-mirrored branches take a pair of images of the segmentation candidate as the inputs, and output the corresponding feature vectors, respectively. These two feature maps will be directly used to calculate the contrastive loss Lcontrastive measuring the similarity of the two feature maps:
| [1] |
| [2] |
| [3] |
where d(X1, X2)i is defined as the euclidean distance between the output feature maps and of the Siamese networks for the ith input pair and . The latent variable is zero, Yi = 0, if the input pair (X1, X2)i have the same class; otherwise, it is one, Yi = 1. In addition, the margin λ is introduced to the Lcontrastive. Dissimilar input pairs that are beyond this margin will not contribute to the loss. The classifier will randomly pick one feature map to conduct TP/FP classification and calculate the cross-entropy loss LCE in the equation below, where lc is the ground truth label and pc is the probability of the cth class.
| [4] |
During the network training, the total loss is the weighted sum of these two complementary losses, the cross-entropy loss and the contrastive loss, plus an L2 regularization term R where w represents the corresponding weights of the model:
| [5] |
| [6] |
Here, α and γ are weighting parameters. During the back propagation process, the Lcontrassive only affects the feature extractor, while the LCE affects the entire network. Those two sub-networks update the parameters simultaneously. As a consequence of the Ltotal and the LCE formulations, the output of the feature extractor enables discovering the interclass differences.
2.2.1.2. Training Data Preparation
As described in the above session, the Siamese model only considers segmentation candidates with size less than 10 mm. Therefore, in total we collected 9038 segmentation volumes for the Siamese network, among which 8357 volumes were FPs, and 681 volumes were TPs.
The proposed Siamese network takes advantage of the pre-trained ResNet50 structure, which has a required input size of 224*224*3. This 2D-based model requires moderate computational cost while providing benefits from parameters pre-trained with a large non-medical image dataset. To prepare the input, we identified all such candidates in the pre-processed MRI and cropped a square region of interest (ROI) with a size of 20 mm in three consecutive slices at the center of the candidate volume which included the surrounding tissues. Therefore, the cropped ROI had a size of 20*20*3. Since the segmentation candidates were less than 10 mm, a 20 mm size ROI included the peritumoral edema, normal brain and other critical structures. Next, the cropped ROI images were resampled into 224*224*3 to meet the network input requirement. We used 10% of the dataset for testing, while 80% was utilized for training and 10% for validation.
In the training stage, the number of true BMs and FPs were highly imbalanced. For that reason, data augmentation was applied for true BMs in training and validation dataset by flipping (horizontal & vertical) and rotation. During the training process, two images were randomly selected as the paired input. If the first input candidate was a FP segmentation, then the probability of the second image to be a true BM was increased to 0.6. The final ratio in training and validation dataset was TP/FP = 7300/7348.
2.2.1.3. Model Training and Testing
The implementation of the proposed model was based on Pytorch library. To alleviate the amount of data requirement for the Siamese network, we adopted a transfer learning strategy and initialized the parameters of the feature extractor pair in the network by applying the parameters of the pre-trained ResNet 50. In addition, the “Xavier” algorithm was implemented for the parameter initialization of the classifier. The two hyper-parameters of the total loss function α, and γ are selected using the grid search.
The entire model was trained for 100 epochs with a batch size of 32 in a single NVIDIA RTX-2080ti GPU. And during the training process, we chose the Adam algorithm to update the model parameters with the initial learning rates as 1×10−3 in the feature extractor pair and 1×10−4 in the classifier.
In the testing stage, only half of the Siamese network architecture was utilized. Specifically, only one branch of the feature extractor was kept together with the classifier. Therefore, the model only takes one segmentation candidate as the input during testing. The single input candidate was processed through the single branch of the feature extractor following with the classifier to get the final prediction.
Since the model only takes three slices of the 2D images as the inputs, which only contain information along a specific axis, we generated 2D inputs in all three axes (axial, coronal, and sagittal) and trained three Siamese models separately. The final classification of the Siamese network was generated by combining these three models via majority voting.
2.2.2. SVM-Radiomics Model
The SVM-radiomics model takes the radiomic features that are extracted from the 3D volume of interest (VOI) as the input. Prior to the radiomic feature extraction, four VOI masks were generated for each segmentation volume, including the masks of the original tumor and three ring-volume masks obtained by dilation of 3, 6, and 12 mm from the tumor boundary. The reason to include the dilated masks with different margins in the feature extraction was to include the sensitive regions like peritumoral edema. Figure 4 shows one example of the generated VOI masks, in which the red volume in (a) was the original tumor volume mask, the blue region in (b) was the 3 mm dilation margin mask, the green region in (c) was the 6 mm dilation margin mask and the pink region in (d) was the 12 mm dilation margin mask. Personalized skull-stripped brain masks were utilized to exclude the skull and outside brain regions in the dilation masks (Iglesias et al., 2011).
Figure 4.
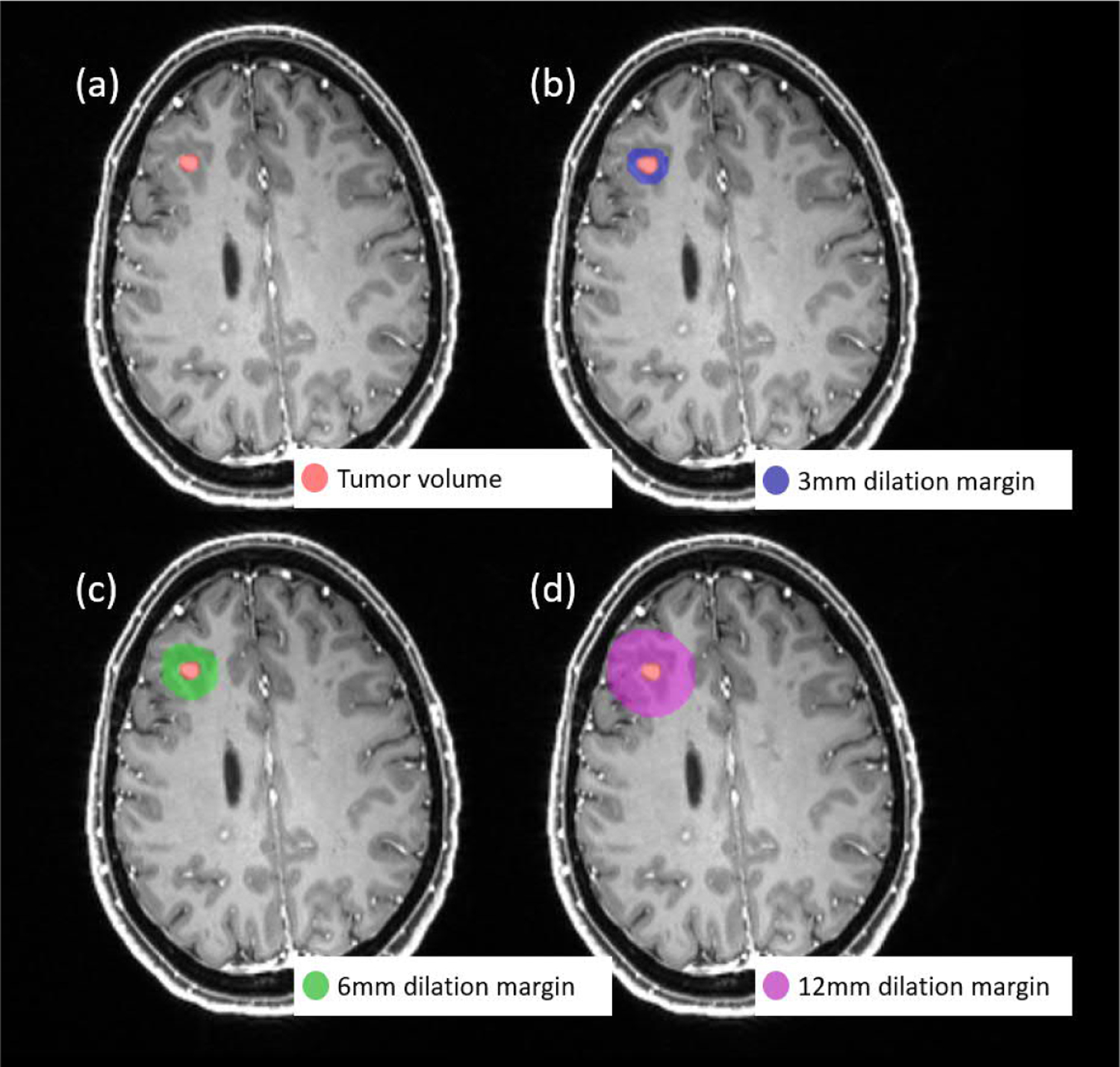
Example of the VOI masks used for radiomic feature extraction: (a) the original tumor volume mask, (b) 3 mm dilation from the tumor boundary mask, (c) 6 mm dilation from the tumor boundary mask, (d) 12 mm dilation from the tumor boundary mask
After the VOI mask generation, we extracted radiomic features for each segmentation subject with MATLAB program (Vallières et al., 2015). To ensure reliability and stability of the radiomic features, we utilized the pre-processed images generated from the platform for the extraction process, since they are intensity-normalized and have isotropic resolution. We first measured twelve morphological features with the original segmentation mask. The morphological features described the geometry-related characteristics of the VOI, thus, extracting morphological features with other dilated masks can be meaningless. Moreover, for each type of the dilated VOI masks, we extracted six first-order features and forty texture features from the pre-processed T1c MRI images. The first-order features measure the statistics of the intensity histogram within the VOI, and the higher order texture features measure the texture characteristics of the VOI derived from the gray-level co-occurrence matrix (GLCM), gray-level run-length matrix (GLRLM), and gray level size zone matrix (GLSZM), neighboring gray tone difference matrix (NGTDM), and gray level dependence matrix (GLDM). In total, 150 features were collected from both the tumor volume and the dilated regions surrounding the tumor volume. All features were normalized with z-scores normalization. Then a SVM was trained using all 150 normalized radiomic features to classify the segmented volumes as true BMs or FPs.
2.3. Evaluation
For the classification problem, model’s accuracy (ACC), sensitivity (SEN), specificity (SPE) and area under the curve (AUC) are the primary metrics to comprehensively evaluate the performance of a model. These evaluation metrics are defined as follows:
| [7] |
| [8] |
| [9] |
| [10] |
where TP, TN, FP, and FN denote the number of true positive, true negative, false positive, and false negative samples, respectively. P, N are the numbers of positive samples and negative samples, respectively. In addition, ranki is the rank of the ith positive example, and i ∈ p denotes the ith example from the positive sample. We applied the metrics above to evaluate the performance of the Siamese model, SVM model, and the ensemble model.
In addition, we integrated the developed FP reduction models into the BMs segmentation platform to improve the effectiveness of the auto-segmentation, and then tested the overall segmentation performance on ten individual patient data. Same as the evaluation method applied in our previous publication regarding the BMs segmentation platform (Yang et al., 2020), the overall segmentation performance was evaluated by the following metrics, false-negative rate (FNR) and false-positive over Union (FPoU), before and after the false-positive reduction process:
| [11] |
| [12] |
3. Results
Since the proposed ensemble model was built upon the Siamese model and the SVM-radiomic model, in this session the individual performance of both models will be presented first followed by the results of the combined ensemble model.
To test the proposed ensemble FP reduction models, we used a testing set of 1074 BMs raw segmentations from the FP reduction dataset, in which 70 were true BMs and the other 1004 were FP segmentations. No data augmentation was applied in the testing set. The testing dataset did not contain any segmentation candidates with size larger than 10 mm as the Siamese network only takes candidates with size less than 10 mm. For each model, a confusion matrix was recorded during the testing stage. In addition, as mentioned in session 2.1, a total of 10 mBMs patient were collected to test the overall performance after integrating the ensemble FP reduction model with the segmentation platform. For this dataset, the candidates included all raw segmentations regardless of size.
3.1. Siamese Network Model
Since the proposed Siamese network only takes three slices of the 2D images as the input, we separately trained three Siamese models using 2D image inputs from axial, coronal, and sagittal planes with one model for each plane. The predictions from all three models were then combined through majority voting to generate a final label. Figure 5 shows the confusion matrix of each model, where (a), (b) and (c) correspond to the models trained with the coronal, sagittal and axial images, respectively, and (d) is the result generated by majority voting from all three models. In the confusion matrix, class 0 represents the FPs, and class 1 represents the true BMs segmentations. It was found, see Figure 5, that the majority voting provided the best performance compared with models trained in a specific plane.
Figure 5.
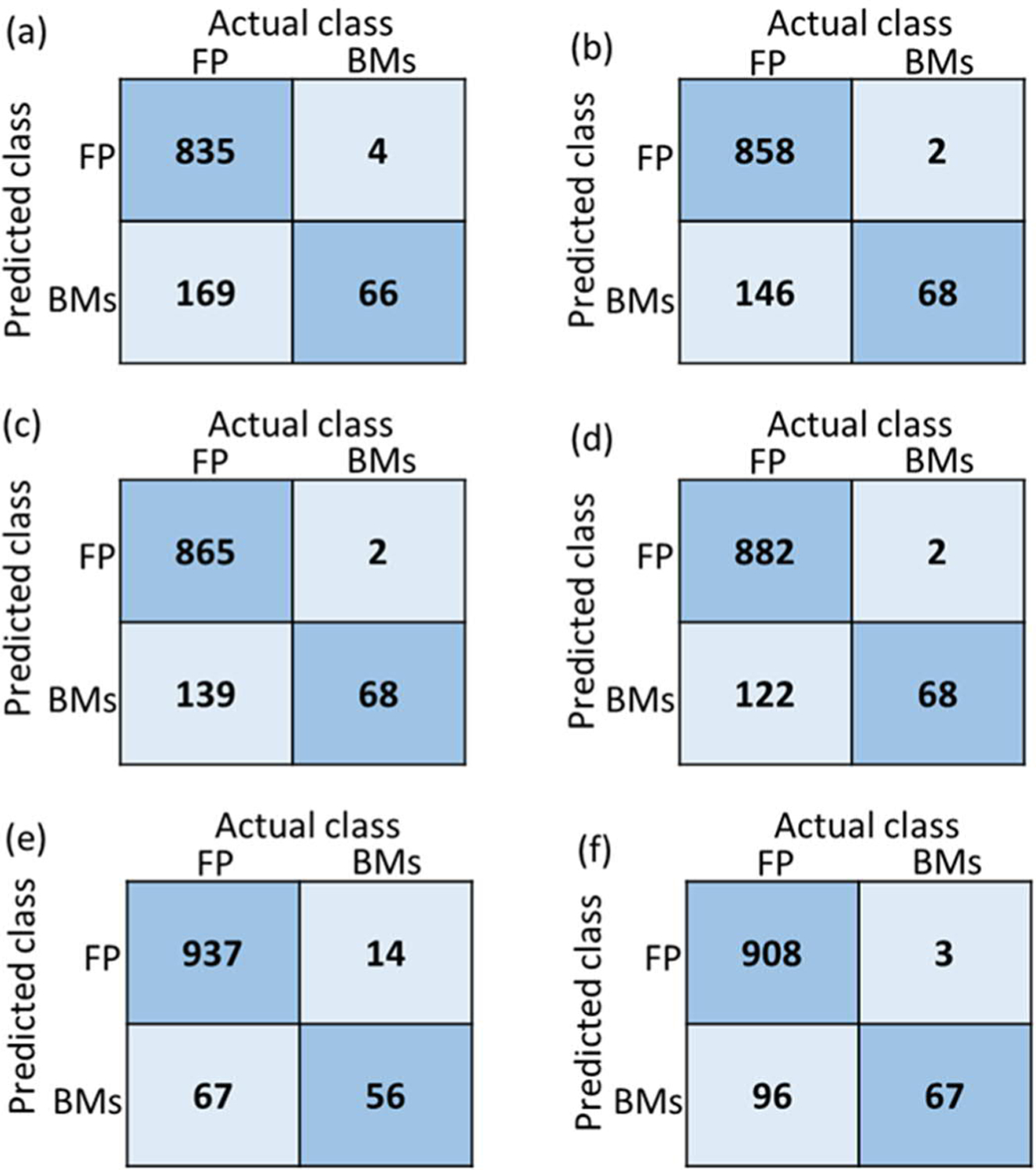
Confusion matrix of all tested models: the Siamese network model trained with (a) coronal, (b) sagittal and (c) axial images, and (d) majority voting from the above 3 models; (e) the SVM model using radiomics feature; (f) the proposed ensemble FP reduction model combining SVM with Siamese model. FP represents the false-positive segmentations, and BMs represents the true brain mets segmentations.
As mentioned in the section 2.3, we also employed four commonly used metrics for the performance comparison: accuracy (ACC), sensitivity (SEN), specificity (SPE) and area under the curve (AUC). Table 2 lists the detailed performance of all these above 4 Siamese network models. In this table, Siamese_cor, Siamese_sag, and Siamese_axial represent the models trained using coronal, sagittal and axial images, respectively, while Siamese_majority corresponds to the model combining predictions of each cardinal plane via majority voting. It was found that the majority voting model had the best performance compared to the individual models trained with images from a specific plane.
Table 2.
Detailed performance of all tested models. Siamese_cor, Siamese_sag, and Siamese_axial represent the models trained with coronal, sagittal and axial views respectively, and Siamese_majority is the model representing majority voting. SVM-radiomic represents the SVM model utilizing only radiomic features, and the ensemble model combines the SVM-radiomics and Siamese models.
| Models | ACC | SEN | SPE | AUC | |
|---|---|---|---|---|---|
|
| |||||
| Siamese-network models | Siamese_cor | 0.83 | 0.94 | 0.83 | 0.89 |
| Siamese_sag | 0.86 | 0.97 | 0.85 | 0.91 | |
| Siamese_axial | 0.87 | 0.97 | 0.86 | 0.92 | |
| Siamese_majority | 0.88 | 0.97 | 0.88 | 0.93 | |
| SVM-Radiomics model | 0.92 | 0.80 | 0.93 | 0.92 | |
| Ensemble model | 0.91 | 0.96 | 0.90 | 0.93 | |
3.2. SVM-Radiomics Model
Figure 5(e) shows the confusion matrix of the SVM-radiomics model for the testing dataset. In addition, the corresponding ACC, SEN, SPE, and AUC were 0.92, 0.80, 0.93, and 0.92, respectively.
3.3. Ensemble Model
Figure 5(f) presents the final performance of the ensemble FP reduction network. Table 2 shows the detailed evaluation scores of the above models. The proposed ensemble model had the best AUC among all the models. In addition, both the sensitivity and specificity of the ensemble model were above 0.9, thus providing a more balanced FP reduction results compared with the other models.
3.4. Performance of BMs segmentation platform with the FP reduction model
The overall BMs segmentation platform performance was tested with ten testing patients. First, the baseline segmentation performance was established without any FP reduction process, and then the data was processed with the platform integrated with the ensemble FP reduction model. In addition, to demonstrate the effectiveness of the ensemble FP reduction model, we also compared the performance with a simple FP reduction approach using geometric sphericity metric as the removal threshold. Table 3 lists the platform performance for these ten patients before and after post-processing, where “Org-” represents the raw results generated by the segmentation algorithm, and “-Geo” indicates post-processing using geometric threshold to update segmentation results, and “-ES” indicates the proposed FP reduction ensemble models.
Table 3.
The segmentation platform performance on 10 individual patient cases comparing raw segmentations), post-processing by geometric threshold FP reduction (-Geo), and post-processing by the ensemble FP reduction model (-ES).
| Patient | Number of BMs | Number of TP-Org | Number of FP-Org | Number of TP-Geo | Number of FP-Geo | Number of TP-ES | Number of FP-ES | FNR-Org | FPoU-Org | FNR-Geo | FPoU-Geo | FNR-ES | FPoU-ES |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||
| 1 | 11 | 9 | 48 | 7 | 10 | 8 | 6 | 0.18 | 0.81 | 0.36 | 0.17 | 0.27 | 0.11 |
| 2 | 61 | 60 | 84 | 49 | 34 | 54 | 14 | 0.02 | 0.58 | 0.20 | 0.23 | 0.10 | 0.10 |
| 3 | 69 | 69 | 74 | 34 | 12 | 63 | 13 | 0.00 | 0.52 | 0.51 | 0.08 | 0.09 | 0.09 |
| 4 | 12 | 12 | 96 | 8 | 40 | 12 | 12 | 0.00 | 0.89 | 0.33 | 0.37 | 0.00 | 0.11 |
| 5 | 44 | 44 | 106 | 39 | 44 | 41 | 19 | 0.00 | 0.71 | 0.11 | 0.29 | 0.07 | 0.13 |
| 6 | 55 | 51 | 13 | 33 | 9 | 49 | 3 | 0.07 | 0.19 | 0.40 | 0.13 | 0.11 | 0.04 |
| 7 | 58 | 52 | 8 | 41 | 8 | 47 | 2 | 0.10 | 0.12 | 0.29 | 0.12 | 0.19 | 0.03 |
| 8 | 11 | 10 | 26 | 9 | 12 | 9 | 5 | 0.09 | 0.70 | 0.18 | 0.32 | 0.18 | 0.14 |
| 9 | 11 | 9 | 15 | 8 | 3 | 9 | 2 | 0.18 | 0.58 | 0.27 | 0.12 | 0.18 | 0.08 |
| 10 | 43 | 41 | 33 | 34 | 5 | 39 | 4 | 0.05 | 0.43 | 0.21 | 0.07 | 0.09 | 0.05 |
| Mean | 38±24 | 36±23 | 50±37 | 26±26 | 18±15 | 33±21 | 8±6 | 0.07±0.07 | 0.55±0.25 | 0.29±0.12 | 0.19±0.11 | 0.13±0.08 | 0.09±0.04 |
From formula [10]-[11]: the smaller values of FPoU and FNR, the better performance. Among these ten patient cases, the proposed ensemble model can help reduce the FPoU from 0.55±0.25 to 0.09±0.04, while keeping the FNR around 0.1. This means that the ensemble network can help effectively remove the FP segmentations in the platform without sacrificing the true BMs segmentations.
As indicated in Figure 2, for large BMs, i.e., with size larger than 10 mm, only the SVM-radiomic model was used for the FP/true BM classification. Figure 6 shows the confusion matrix of the classification result for large BMs (d >10 mm) for ten patient cases. The corresponding ACC, SEN, SPE, and AUC were 0.97, 0.95, 0.97, and 0.98, respectively.
Figure 6.
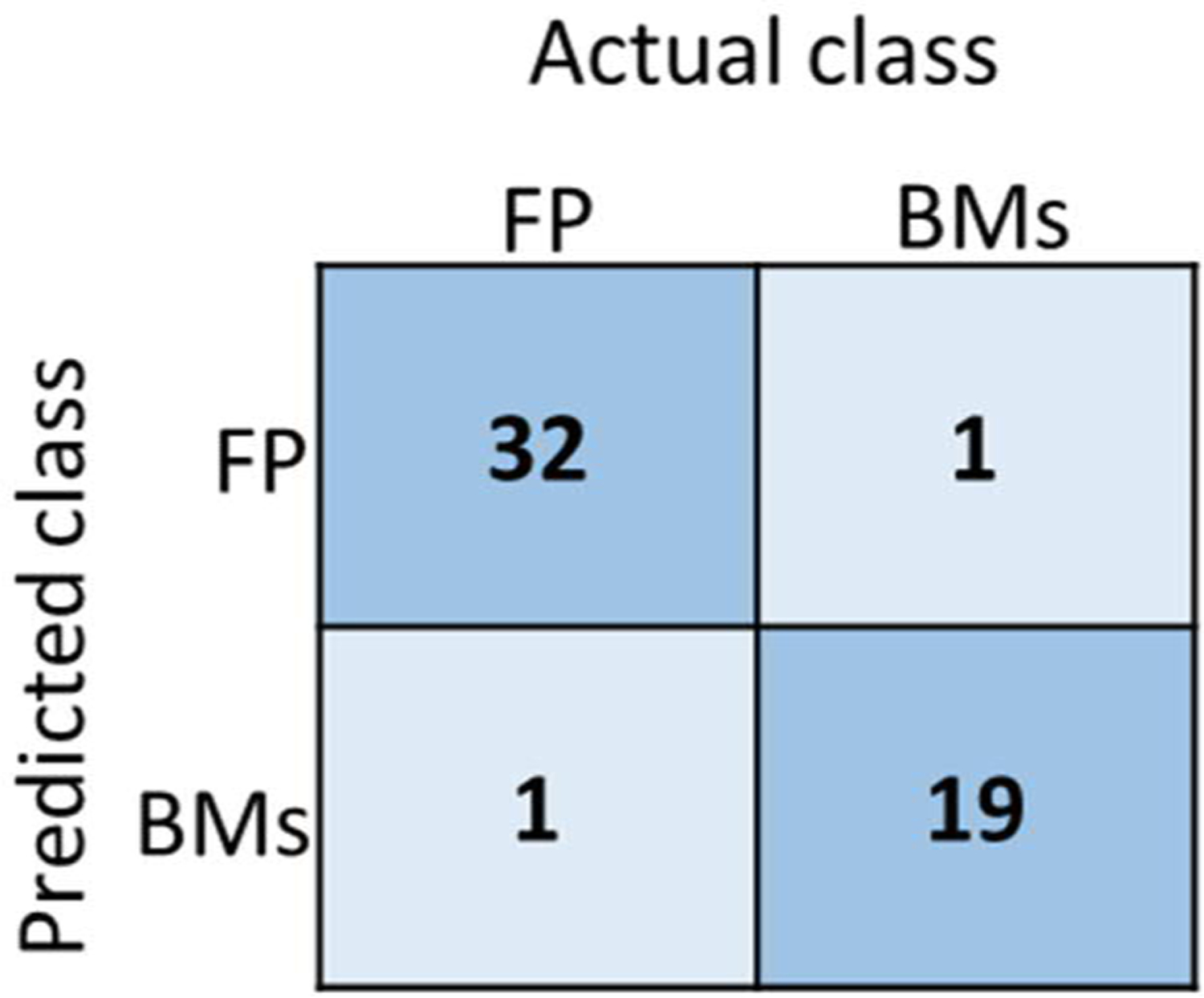
The confusion matrix of the SVM-radiomic model for large BMs (d >10mm) for 10 patient testing cases. FP represents the false-positive segmentations, and BMs represents the true brain mets segmentations.
4. Discussion
The BM segmentation platform for SRS applications provided promising segmentation accuracy (Yang et al., 2020; Liu et al., 2017). However, the T1c MRIs utilized in the platform with the injected contrast agents can cause the vessels to become bright in the images causing FPs as shown in Figure 1. Two possible approaches were considered to tackle this issue. The first choice was to modify the segmentation algorithm to reduce the generation of FPs at the segmentation stage, and the other choice was to add a post-processing step after the segmentation to reduce the FP volumes. Since our original BMs segmentation platform can detect BMs with high sensitivity and segment BMs volumes with high segmentation accuracy, the second approach was preferred to assist the overall segmentation workflow.
In our initial investigation, we had implemented simple post-processing strategies for the raw segmentation results (Yang et al., 2020; Liu et al., 2017). The BMs segmentation algorithm is sensitive to intensity variations in the T1c images, causing the FP volumes to be more likely to occur in certain anatomical regions such as the superior sagittal sinus. However, utilizing anatomical masks in the removal process introduces extra steps and additional uncertainty as it requires supplementary segmentation of the brain structures to generate a personalized mask (Chen et al., 2019). As an alternative approach, we adopted the sphericity metric calculated by the contoured volume, the radius and the axis ratio of volume as the thresholds to remove the FPs. The underlying idea was that the BMs usually resemble rounded objects, whereas the segmented sinuses present more irregular shapes. In particular, the FP volume was removed if its sphericity was smaller than the desired threshold, or the axis ratio was larger than the desired threshold. However, this approach requires additional user interaction, since the physicians need to test different numbers to find out the best personalized variables to rule out most of the FPs, which is not efficient for the clinical application.
Over the past decades, the Siamese networks using CNNs contributed significantly to the progress made in natural language processing, recognition, and classification tasks (Rubin et al., 2019; Rao et al., 2017). The Siamese network’s dual branch architecture design in combination with the contrastive loss can benefit the classification task by exploiting the inter-class differences. We chose the Siamese network architecture to solve our FP reduction problem since the geometry characteristics of the segmentation candidates as well as their surrounding tissue can provide important information for the classification problem. However, considering the computational cost, the Siamese model we proposed takes 2D image as the input instead of 3D volumes. Therefore, we generated 2D inputs from three cardinal planes to train three different models and then combined the outputs via majority voting to obtain the classification results, which takes more texture information into consideration for classification tasks. Figure 5 shows the classification results of these three models and the majority voting model in the confusion matrix. Among these three models of different planes, the model with axial images as the input had the best performance. This might be due to the original T1c acquisition being in the axial plane, which can thus provide the best consistent quality of information among these three planes. Overall, the majority voting model provided the best performance among these four models as it integrates information from the three different planes.
The traditional machine learning methods combined with radiomic hand-crafted features have been widely used in many classification studies, and these approaches can provide satisfying performance in many tasks with small computational cost (Jordan and Mitchell, 2015). In this study, we chose the SVM model combined with radiomics features. The model we proposed to solve FPs reduction problem was designed using both the Siamese network and the radiomic-based SVM model. The radiomic features were directly calculated from 3D volumes capturing geometry and texture features in a relatively large VOI without much computational cost, while the Siamese network extracted deep learning features from the 2D images in specific planes and in a relatively smaller ROIs to keep computational cost manageable. Therefore, our proposed ensemble model takes advantages of the complementary information and balanced computational cost of these two models.
Figure 5 shows the confusion matrix of the radiomic model, majority voting based Siamese model and the ensemble model, and Table 2 listed their corresponding evaluation matrix including ACC, SEN, SPE and AUC. It was found that the radiomic SVM approach can greatly detect the FP segmentations, but the sensitivity was not satisfying compared with the Siamese model. The proposed ensemble model are shown to have the best AUC performance with a balance between sensitivity and specificity. In clinical practice, missing true BMs requires detailed inspection and additional manual contouring, while removing FP segmentation would be easier as it simply requires deleting selected structures. Therefore, the sensitivity of the FP reduction tasks can be weighted more than the specificity when the overall accuracy and AUC performance are relatively close among different models. The proposed ensemble model is thus preferred in this problem setting.
As shown in Table 3, we tested ten patient cases after integrating the FP reduction model into the segmentation platform. The original segmentation results have an average FPoU of 0.55±0.25 and FNR of 0.07±0.07, which indicates the platform can segment almost all BMs. After the FP reduction process, the FPoU can be effectively reduced to 0.09±0.04, indicating most of the FP segmentation can be removed, while the FNR can still be kept at 0.13±0.08 to maintain the achieved sensitivity.
The effectiveness of the proposed ensemble model was compared to our previous approach which utilized the geometry threshold metrics to remove the FPs for the above mentioned 10 patient cases. In particular, we implemented the following threshold criteria for all 10 patient cases: sphericity larger than 0.6, axis ratio smaller than 1.6, and radius larger than 2 mm. These numbers were the default values for the removal thresholds in our platform, which were statistically defined by analyzing the distribution of all BMs contours from 242 mBMs patients. Users can also personalize these thresholds for each patient case, but in this study, we only applied the default values as the baseline to compare with the proposed ensemble model. The results are listed in Table 3. We found that the ensemble model can improve the FPoU to 0.09±0.04 and FNR to 0.13±0.08, while the original geometric threshold approach with default settings provided the FPoU of 0.19±0.11 and FNR of 0.29±0.12.
In our proposed ensemble model, we mainly focused on the segmentation candidates with size smaller than 10 mm since the FP segmentations caused by vessels are often small. As introduced in Figure 2, for segmentations larger than 10 mm, only the SVM model was used in our workflow since the radiomic features take the geometry information into consideration by design. In figure 6 we presented the performance of the SVM model for large segmentation candidates for 10 patient cases. It was found that the SVM model was effective to classify the large segmentation candidates.
The limitation of this study was that the FP reduction model only relied on a single modality MRI, i.e., the T1c MRI. A possible improvement direction is to add other MRI modalities, such as vessel suppression sequences (Wang et al., 2010), which could provide multi-modality information in separating the true lesion from the FPs. In addition, the entire segmentation platform including the segmentation model and the FP reduction model were trained on data from a single institution and single modality. Therefore, for the future application in clinic, the generalization problem of this model needs to be taken into consideration.
5. Conclusion
In this study, we developed an ensemble model combining the Siamese network with radiomics for false-positive BMs segmentation reduction. The proposed method can effectively reduce the false-positive rate of the raw segmentation candidates. The integration of the FP reduction models with the BMs segmentation platform can improve the efficiency of the SRS treatment planning and provide beneficial tool for an improved mBMs SRS workflow.
Acknowledgement
This work was supported by the National Institutes of Health under Grant No. R01-CA235723.
References
- Bagci U, Udupa JK, Mendhiratta N, Foster B, Xu Z, Yao J, Chen X and Mollura DJ 2013. Joint segmentation of anatomical and functional images: Applications in quantification of lesions from PET, PET-CT, MRI-PET, and MRI-PET-CT images Medical image analysis 17 929–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnholtz-Sloan JS, Sloan AE, Davis FG, Vigneau FD, Lai P and Sawaya RE 2004. Incidence proportions of brain metastases in patients diagnosed (1973 to 2001) in the Metropolitan Detroit Cancer Surveillance System Journal of clinical oncology 22 2865–72 [DOI] [PubMed] [Google Scholar]
- Bauer S, Lu H, May CP, Nolte LP, Büchler P and Reyes M 2013. Integrated segmentation of brain tumor images for radiotherapy and neurosurgery International journal of imaging systems and technology 23 59–63 [Google Scholar]
- Bertinetto L, Valmadre J, Henriques JF, Vedaldi A and Torr PH European conference on computer vision,2016), vol. Series): Springer; ) pp 850–65 [Google Scholar]
- Bousabarah K, Ruge M, Brand J-S, Hoevels M, Rueß D, Borggrefe J, Hokamp NG, Visser-Vandewalle V, Maintz D and Treuer H 2020. Deep convolutional neural networks for automated segmentation of brain metastases trained on clinical data Radiation Oncology 15 1-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown P, Ballman K, Cerhan J, Anderson S, Carrero X and Whitton A 2016. N107C/CEC. 3: A phase III trial of post-operative stereotactic radiosurgery (SRS) compared with whole brain radiotherapy (WBRT) for resected metastatic brain disease Int J Radiat Oncol Biol Phys 96 937 [Google Scholar]
- Buendia P, Taylor T, Ryan M and John N 2013. A grouping artificial immune network for segmentation of tumor images Multimodal Brain Tumor Segmentation 1 [Google Scholar]
- Cao Y, Vassantachart A, Jason CY, Yu C, Ruan D, Sheng K, Lao Y, Shen ZL, Balik S and Bian S 2021. Automatic detection and segmentation of multiple brain metastases on magnetic resonance image using asymmetric UNet architecture Physics in Medicine & Biology 66 015003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang EL, Wefel JS, Hess KR, Allen PK, Lang FF, Kornguth DG, Arbuckle RB, Swint JM, Shiu AS and Maor MH 2009. Neurocognition in patients with brain metastases treated with radiosurgery or radiosurgery plus whole-brain irradiation: a randomised controlled trial The lancet oncology 10 1037–44 [DOI] [PubMed] [Google Scholar]
- Charron O, Lallement A, Jarnet D, Noblet V, Clavier J-B and Meyer P 2018. Automatic detection and segmentation of brain metastases on multimodal MR images with a deep convolutional neural network Computers in biology and medicine 95 43–54 [DOI] [PubMed] [Google Scholar]
- Chen H, Lu W, Chen M, Zhou L, Timmerman R, Tu D, Nedzi L, Wardak Z, Jiang S and Zhen X 2019. A recursive ensemble organ segmentation (REOS) framework: application in brain radiotherapy Physics in Medicine & Biology 64 025015. [DOI] [PubMed] [Google Scholar]
- Chopra S, Hadsell R and LeCun Y 2005. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05),2005), vol. Series 1): IEEE; ) pp 539–46 [Google Scholar]
- Cortes C and Vapnik V 1995. Support-vector networks Machine learning 20 273–97 [Google Scholar]
- Dikici E, Ryu JL, Demirer M, Bigelow M, White RD, Slone W, Erdal BS and Prevedello LM 2020. Automated brain metastases detection framework for T1-weighted contrast-enhanced 3D MRI IEEE journal of biomedical and health informatics 24 2883–93 [DOI] [PubMed] [Google Scholar]
- Fu Y, Xue P, Ji H, Cui W and Dong E 2020. Deep model with Siamese network for viable and necrotic tumor regions assessment in osteosarcoma Medical Physics 47 4895–905 [DOI] [PubMed] [Google Scholar]
- Geremia E, Menze BH and Ayache N 2012. Spatial decision forests for glioma segmentation in multi-channel MR images MICCAI Challenge on Multimodal Brain Tumor Segmentation 34 14–8 [Google Scholar]
- Gordillo N, Montseny E and Sobrevilla P 2013. State of the art survey on MRI brain tumor segmentation Magnetic resonance imaging 31 1426–38 [DOI] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S and Sun J Proceedings of the IEEE conference on computer vision and pattern recognition,2016), vol. Series) pp 770–8 [Google Scholar]
- Huang Z 1998. Extensions to the k-means algorithm for clustering large data sets with categorical values Data mining and knowledge discovery 2 283–304 [Google Scholar]
- Iglesias JE, Liu C-Y, Thompson PM and Tu Z 2011. Robust brain extraction across datasets and comparison with publicly available methods IEEE transactions on medical imaging 30 1617–34 [DOI] [PubMed] [Google Scholar]
- Jordan MI and Mitchell TM 2015. Machine learning: Trends, perspectives, and prospects Science 349 255–60 [DOI] [PubMed] [Google Scholar]
- Khoshdeli M, Cong R and Parvin B 2017. IEEE EMBS International Conference on Biomedical & Health Informatics (BHI),2017), vol. Series): IEEE; ) pp 105–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langer CJ and Mehta MP 2005. Current management of brain metastases, with a focus on systemic options J Clin Oncol 23 6207–19 [DOI] [PubMed] [Google Scholar]
- Liu L, Dou Q, Chen H, Qin J and Heng P-A 2019. Multi-task deep model with margin ranking loss for lung nodule analysis IEEE transactions on medical imaging 39 718–28 [DOI] [PubMed] [Google Scholar]
- Liu Y, Stojadinovic S, Hrycushko B, Wardak Z, Lau S, Lu W, Yan Y, Jiang SB, Zhen X and Timmerman R 2017. A deep convolutional neural network-based automatic delineation strategy for multiple brain metastases stereotactic radiosurgery PloS one 12 e0185844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nayak L, Lee EQ and Wen PY 2012. Epidemiology of brain metastases Curr Oncol Rep 14 48–54 [DOI] [PubMed] [Google Scholar]
- Nie K, Shi L, Chen Q, Hu X, Jabbour SK, Yue N, Niu T and Sun X 2016. Rectal cancer: assessment of neoadjuvant chemoradiation outcome based on radiomics of multiparametric MRI Clinical cancer research 22 5256–64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norouzi M, Fleet DJ and Salakhutdinov RR Advances in neural information processing systems,2012), vol. Series) pp 1061–9 [Google Scholar]
- Pan SJ and Yang Q 2009. A survey on transfer learning IEEE Transactions on knowledge and data engineering 22 1345–59 [Google Scholar]
- Perek S, Hazan A, Barkan E and Akselrod-Ballin A 2018. Image Analysis for Moving Organ, Breast, and Thoracic Images: Springer; ) pp 55–63 [Google Scholar]
- Rao DJ, Mittal S and Ritika S 2017. Siamese neural networks for one-shot detection of railway track switches arXiv preprint arXiv:1712.08036 [Google Scholar]
- Roth HR, Lu L, Liu J, Yao J, Seff A, Cherry K, Kim L and Summers RM 2015. Improving computer-aided detection using convolutional neural networks and random view aggregation IEEE transactions on medical imaging 35 1170–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin M, Stein O, Turko NA, Nygate Y, Roitshtain D, Karako L, Barnea I, Giryes R and Shaked NT 2019. TOP-GAN: Stain-free cancer cell classification using deep learning with a small training set Med Image Anal 57 176–85 [DOI] [PubMed] [Google Scholar]
- Rudie JD, Weiss DA, Colby JB, Rauschecker AM, Laguna B, Braunstein S, Sugrue LP, Hess CP and Villanueva-Meyer JE 2021. Three-dimensional U-Net Convolutional Neural Network for Detection and Segmentation of Intracranial Metastases Radiology: Artificial Intelligence 3 e200204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturm V, Kober B, Hover K-H, Schlegel W, Boesecke R, Pastyr O, Hartmann GH, Schabbert S, Karl zum Winkel M and Kunze S 1987. Stereotactic percutaneous single dose irradiation of brain metastases with a linear accelerator International Journal of Radiation Oncology* Biology* Physics 13 279–82 [DOI] [PubMed] [Google Scholar]
- Svetnik V, Liaw A, Tong C, Culberson JC, Sheridan RP and Feuston BP 2003. Random forest: a classification and regression tool for compound classification and QSAR modeling Journal of chemical information and computer sciences 43 1947–58 [DOI] [PubMed] [Google Scholar]
- Thomas EM, Popple RA, Wu X, Clark GM, Markert JM, Guthrie BL, Yuan Y, Dobelbower MC, Spencer SA and Fiveash JB 2014. Comparison of plan quality and delivery time between volumetric arc therapy (RapidArc) and Gamma Knife radiosurgery for multiple cranial metastases Neurosurgery 75 409–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallières M, Freeman CR, Skamene SR and El Naqa I 2015. A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities Physics in Medicine & Biology 60 5471. [DOI] [PubMed] [Google Scholar]
- Wang J, Yarnykh VL and Yuan C 2010. Enhanced image quality in black-blood MRI using the improved motion-sensitized driven-equilibrium (iMSDE) sequence Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine 31 1256–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue J, Wang B, Ming Y, Liu X, Jiang Z, Wang C, Liu X, Chen L, Qu J and Xu S 2020. Deep learning–based detection and segmentation-assisted management of brain metastases Neuro-oncology 22 505–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z, Liu H, Liu Y, Stojadinovic S, Timmerman R, Nedzi L, Dan T, Wardak Z, Lu W and Gu X 2020. A web-based brain metastases segmentation and labeling platform for stereotactic radiosurgery Medical physics 47 3263–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zacharaki EI, Wang S, Chawla S, Yoo DS, Wolf R, Melhem ER and Davatzikos C 2009. IEEE International Symposium on Biomedical Imaging: From Nano to Macro,2009), vol. Series): IEEE; ) pp 1035–8 [Google Scholar]
- Zhang L, Zhang H, Rekik I, Gao Y, Wang Q and Shen D Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR),2018), vol. Series): Springer; ) pp 14–21 [Google Scholar]


