Learning to Disentangle Inter-subject Anatomical Variations in Electrocardiographic Data

Abstract

Objective:

This work investigates the possibility of disentangled representation learning of inter-subject anatomical variations within electrocardiographic (ECG) data.

Methods:

Since ground truth anatomical factors are generally not known in clinical ECG for assessing the disentangling ability of the models, the presented work first proposes the SimECG data set, a 12-lead ECG data set procedurally generated with a controlled set of anatomical generative factors. Second, to perform such disentanglement, the presented method evaluates and compares deep generative models with latent density modeled by non-parametric Indian Buffet Process to account for the complex generative process of ECG data.

Results:

In the simulated data, the experiments demonstrate, for the first time, concrete evidence of the possibility to disentangle key generative anatomical factors within ECG data in separation from task-relevant generative factors. We achieve a disentanglement score of 92.1% while disentangling five anatomical generative factors and the task-relevant generative factor. In both simulated and real-data experiments, this work further provides quantitative evidence for the benefit of disentanglement learning on the downstream clinical task of localizing the origin of ventricular activation. Overall, the presented method achieves an improvement of around 18.5%, and 11.3% for the simulated dataset, and around 7.2%, and 3.6% for the real dataset, over baseline CNN, and standard generative model, respectively.

Conclusion:

These results demonstrate the importance as well as the feasibility of the disentangled representation learning of inter-subject anatomical variations within ECG data.

Significance:

This work suggests the important research direction to deal with the well-known challenge posed by the presence of significant inter-subject variations during an automated analysis of ECG data.

I. Introduction

Deep neural networks are most successful in supervised learning that relies on a large amount of data with quality annotations. Unsupervised learning presents an appealing alternative for the domains where labeling can be expensive and challenging (e.g., clinical domains) for learning robust and generic latent representations in a task-agnostic manner [1]–[3]. Within unsupervised learning, disentangled representations are often desirable as they explain the factors of variations in observed data in a compact, mutually independent, and semantically interpretable manner [4], [5], such as the factors of identity, pose, and lighting conditions in facial images. Disentangled representations have been demonstrated to be useful for downstream tasks including semi-supervised [6], [7], zero-shot learning [8], transfer learning [9], and life-long learning [10].

Advances in unsupervised disentangled learning have been mostly made in the domain of computer vision, especially in synthesized or natural images with clear and interpretable generative factors [11], [12]. Extension to clinical data has been limited, where emerging efforts have mostly focused on separating a task-irrelevant representation from a task-relevant representation in visual images, often with some level of weak supervision [13], [14]. In comparison, many non-visual clinical data such as physiological signals are generated with a physics-based process with physically-meaningful factors. These generative factors may be of tremendous value in explaining the observed data, such as those contributing to inter-subject variations within the data. However, they are potentially more difficult to learn or disentangle, as their contribution to the data is not visual but follows an indirect physical process. To date, very limited work has considered fully unsupervised disentangling of physically-meaningful generative factors in non-visual physiological signals.

Electrocardiographic (ECG) signals are one type of such physiological signals of which the key generative factors are well understood by the underlying physics: ECG signals are generated by electrical activation and relaxation pattern of the heart muscle, modulated by other anatomical and physiological factors such as the geometrical relationship between the heart and the electrode positioning on the body surface, the anatomical and conduction characteristics of the heart, and the structural remodeling of the myocardium [15]. The latter generative factors are sources of inter-subject variations that influence the generated ECG data but are often irrelevant to the factors of clinical interest (e.g., sites of the origin or the pattern of abnormal activation in the heart). This presence of significant inter-subject variations is a major challenge in automated ECG analysis [4].

The potential of modern deep learning, as in many other domains, has increasingly been shown in mining important information from ECG data for a variety of tasks, such as arrhythmia detection [16] and atrial fibrillation classification [17], [18]. Limited work has considered the potential of unsupervised learning for disentangling anatomical and physiological factors of inter-subject variations in ECG data. While our earlier work demonstrated the benefit of disentangling inter-subject variations in ECG data on downstream classification tasks [19], two primary challenges hinder the progress of disentangling representation learning in ECG data. First, unlike visual images where the generative factors are often finite and directly visible from the data, the physics underlying the generation of ECG data is complex and the number of generative factors (geometry, tissue property, etc) is potentially unbounded. Second, knowledge of the generative factors in real ECG data is limited and often absent, preventing a quantitative evaluation of disentangled learning as in other visual benchmarks. For instance, in computer vision literature, procedurally generated data sets like dSprites [12] and 3DShapes [20] serve such purpose.

In this paper, we demonstrate the possibility of disentangled representation learning of inter-subject anatomical variations within ECG data. To this end, we first present the SimECG data set, a 12-lead ECG data set procedurally generated with a controlled set of generative factors involving the geometry of the heart. This creates to our knowledge the first ECG data set that will allow systematic and quantitative evaluation of disentangled representation learning in non-visual physiological signals. Second, we evaluate and compare deep generative models with latent representations modeled by a standard parametric Gaussian density versus a nonparametric Indian Buffet Process (IBP), investigating the importance of an improved modeling capacity of the latent distributions for disentangled representation learning as the complexity of the data grows. On the simulated ECG data, we present detailed and quantitative evaluations of our ability to disentangle factors of anatomical variations from the ECG data. On both the simulated and a clinical ECG data set, we then demonstrate the benefit of such unsupervised representation learning on the down-stream task of localizing the origin of ventricular activation from ECG data. The main contributions of the paper include:

1. Using inter-subject anatomical variations in ECG data as an example, we investigate the ability of disentangled representation learning in non-visual physiological data that are generated from a complex physics-based process with physically-meaningful generative factors that are not directly visible from the data.

2. We present a 12-lead ECG data set, SimECG, simulated with a controlled set of generative factors involving the geometry of the heart.

3. We demonstrate the benefit of increasing the modeling capacity of the latent distributions, via an IBP, in disentangled representation learning of data with an unknown and potentially infinite number of generative factors.

4. We provide quantitative evidence for the benefit of disentanglement learning on downstream clinical tasks in both simulated and clinical ECG data sets.

II. SimECG: Disentanglement testing ECG data set

In this section, we describe our approach for building the presented ECG data set with controlled generative factors. For brevity, we refer to this data set as “SimECG”.

We initially consider a combined bi-ventricular and torso model made available through the EDGAR data base [21]. As illustrated in Fig. 1, the torso is represented as a homogeneous conductor with 352 surface triangles and the 3D ventricular mass is represented by 1665 mesh points. On the 3D bi-ventricular model, we used a mono-domain two-variable AlievPanfilov (AP) [22] model to simulate spatiotemporal action potential propagation:

$$\begin{gathered} \frac{\partial u}{\partial t}=\Delta (D\Delta u)-cu(u-a)(u-1)-uz \\ \frac{\partial z}{\partial t}=ϵ(u,z)(-z-cu(u-a-1)) \end{gathered}$$ (1)

where u represents a normalized action potential [0,1], z represents recovery current, D is the diffusion tensor, c, ϵ and a are the parameters controlling the shape of the action potential. The relationship between the cardiac action potential in the heart and body-surface ECG can be defined by the quasi-static approximation of electromagnetic theory [15]. Using a coupled meshfree-boundary element method (BEM) as described in [23] on the given heart-torso geometry, we can generate a set of ECG data corresponding to ventricular activation originating from locations throughout the ventricular myocardium at a 5-mm resolution.

Fig. 1:

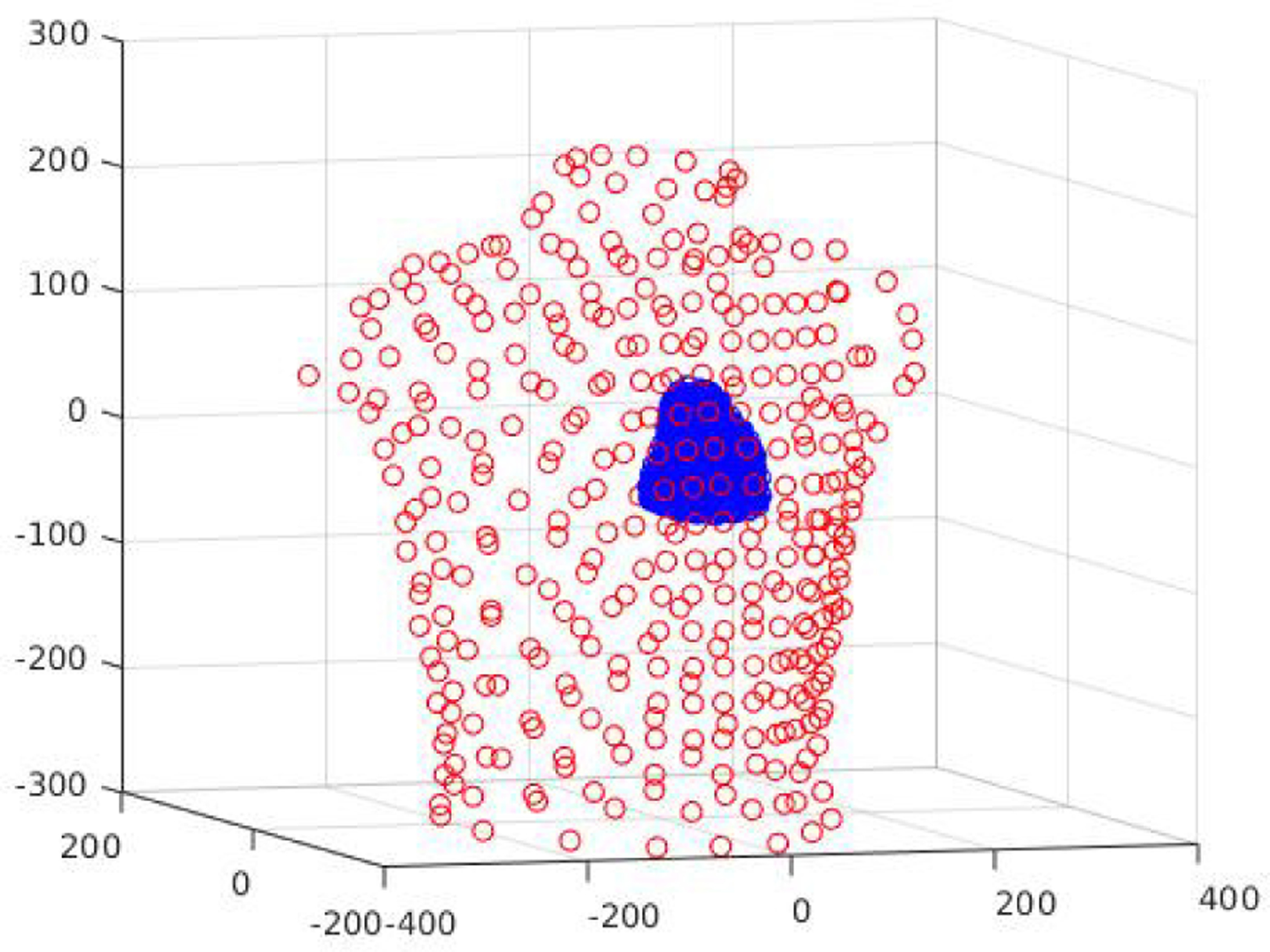
Personalized heart-torso structure where the heart is represented with a cloud of 1666 points and the torso with 352 points.

While there is a large number of anatomical parameters that affect the generation of ECG data such as the position, orientation, and shape of the heart as well as the shape of the torso, in this work we consider six significant factors of variations: rotation and translation of the ventricles along the X-, Y- and Z-axis, where the X-axis corresponds to the dorsal/ventral direction, the Y-axis to the lateral direction, and the Z-axis to the cranio-caudal direction. For rotation, we perform swing about X- and Y-axis which represents swing around center of mass in the axial plane restricted to a maximum deviation of less than 6 cm, and rotation about the Z-axis which represents rotational pivoting of the heart about a vertical axis, limited to a deviation of 20°. For translation, we limit the deviation to less than or equal to 2 cm along all three axes. As suggested in [24], these transformations curb the heart within the regions on the body surface, where the potentials are sensitive to the relative position between the heart and the surface electrodes. In Fig. 2, we present the schematic illustration of some of these geometrical transformations. For simplicity, we consider three values for each of these transformations, resulting in 729 variants of the heart-torso models. These transformations as summarized in Table I generated the SimECG data set with known values of the underlying anatomical factors of variations. With simulated action potential originated at 1665 different locations on each of these 729 hearts, we were able to generate more than a million unique ECG samples. In Fig. 3, we present some examples of ECG signals from the given SimECG data set. There are several ways to extend the variations within the SimECG dataset, which we discuss later in V-B. For understanding the effect of other variations, we created SimECG-torso where besides heart variations as used in SimECG, we also introduced variations in the torso geometry. The torso variation represents expansion (or reduction) of the torso with three different ratios (0.9, 1, 1.1), and for the heart variations, we used translation factors along the three-axis, same as SimECG. Both SimECG and SimECG-torso are publicly available at https://github.com/Prasanna1991/SimECG.

Fig. 2:

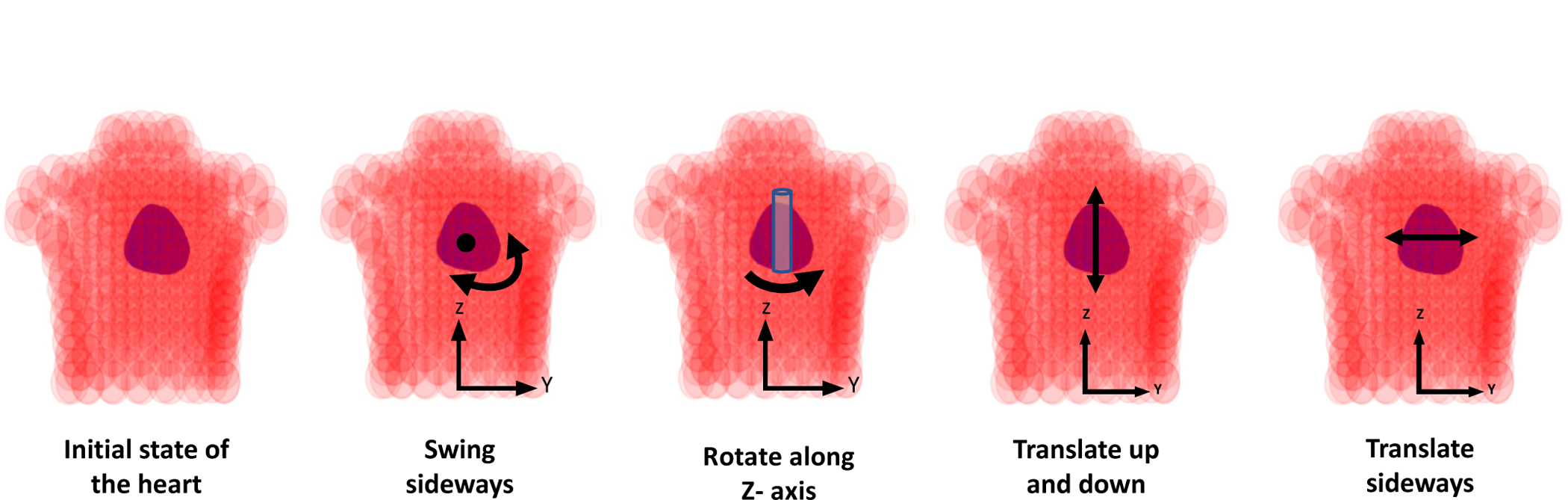
Schematics of the four different geometric transformations of the heart with respect to the torso for producing SimECG data set.

TABLE I:

The values for different factors involved in the generation of the presented SimECG data set.

Factor (fi)	$l_{f_i}=3$	end-to-end deviation
Swing X-axis	{−10°, 0°, 10°}	< 6 cm
Swing Y-axis	{−10°, 0°, 10°}
Rotate Z-axis	{−20°, 0°, 20°}	20°
Translation X-axis	{−10mm, 0mm, 10mm }	≤ 2 cm
Translation Y-axis	{−5mm, 0mm, 5mm }
Translation Z-axis	{−20mm, 0mm, 20mm }

Fig. 3:

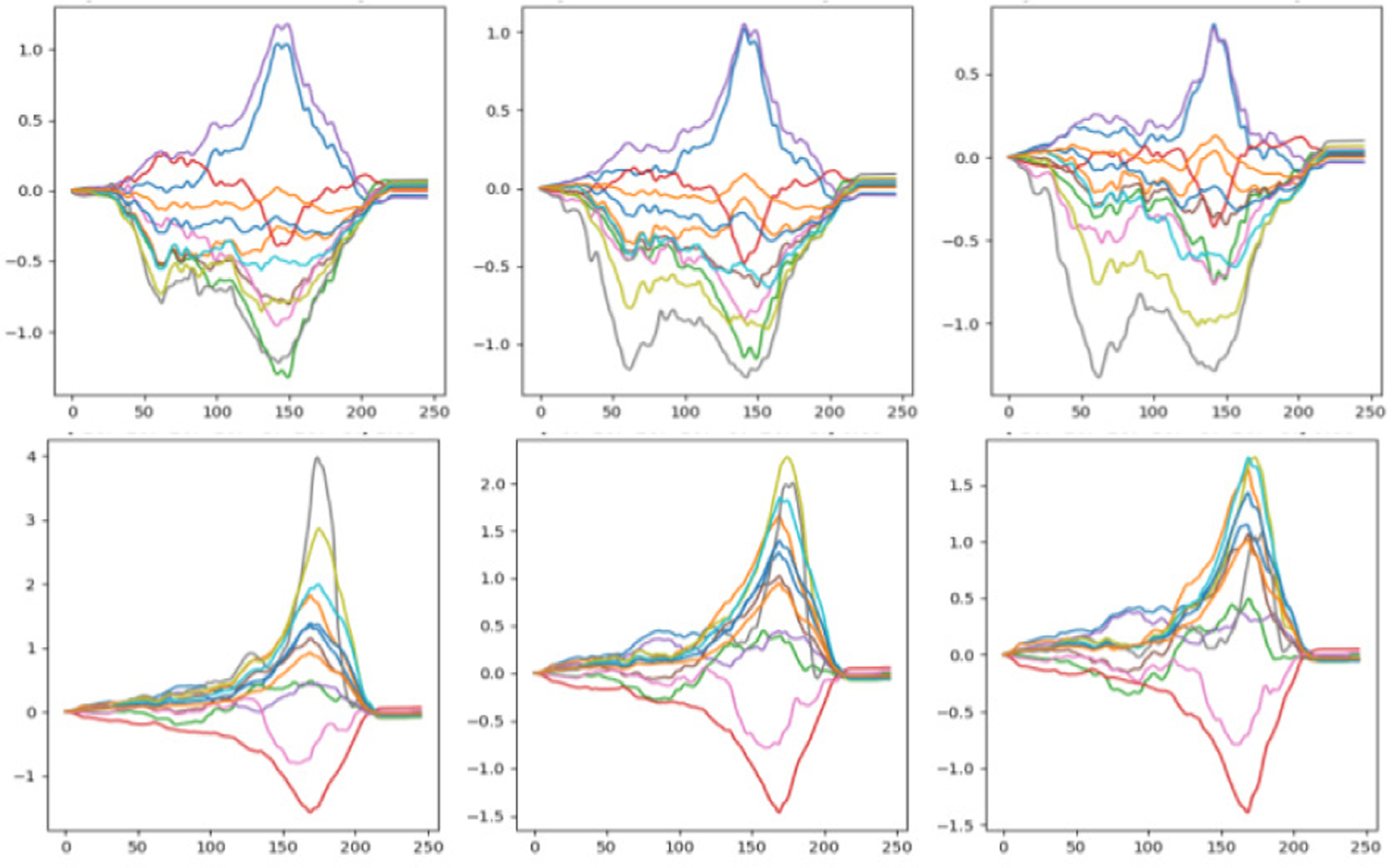
Sample data from SimECG data set where changes in a single factor is presented. Top: Rotation about z-axis with values −20°, 0°and 20°, respectively, in three columns. Bottom: Swinging about x-axis for −10°, 0°and 10°, respectively, in three columns.

III. Methods

In this section, we first give the background of disentangled representation learning and then provide technical details of the disentangled methods considered in this work. We then discuss an approach to supervise the disentanglement of a task-relevant representation from unobserved generative factors.

A. Learning disentangled representation

Consider a setup where the data x are generated by the generative distribution p(x|y) involving a set of latent variables y from k independent sources y₁,...,y_k. The generative model takes the following form:

$$p(\mathbf{x},\mathbf{y})=p(\mathbf{x}\mid \mathbf{y}){\prod }_{i}p\left(y_i\right)$$

Disentanglement learning aims to find a representation with independent components such that a change in one component corresponds to the change in a single dimension of y. Other formal definition of disentanglement is discussed in [25]. Most of the state-of-the-art approaches for unsupervised disentanglement learning are based on the representations learned by variational autoencoders (VAEs) [26].

B. Variational autoencoder (VAE)

The variational autoencoder (VAE) [26], [27] models the generative distribution of data x, p_θ(x|y), with a decoding neural network parameterized by θ. It then models the approximated posterior distribution of the latent variable y, q_ϕ(y|x_n), by another encoding neural network parameterized by ϕ. This gives rise to a encoding-decoding architecture that can be optimized by maximizing the evidence lower bound (ELBO) of the marginal likelihood of the observed data ${\left\{x_n\right\}}_{n=1}^N$:

$$\mathcal{L}=\frac{1}{N}\sum _{n=1}^N{\mathbb{E}}_{q_{\varphi }\left(\mathbf{y}\mid {\mathbf{x}}_n\right)}\left[\log p_{\theta }\left({\mathbf{x}}_n\mid \mathbf{y}\right)\right]-KL\left[q_{\varphi }\left(\mathbf{y}\mid {\mathbf{x}}_n\right)\Vert p(\mathbf{y})\right]$$ (2)

where p(y) defines the prior distribution of y and KL(||) stands for the non-negative Kullback-Leibler divergence between the prior and the approximate posterior. In standard practice, the prior p(y) is often assumed to be an isotropic Gaussian $\mathcal{N}(0,1)$, and the posterior q_ϕ(y|x) distributions are parametrised as Gaussians with a diagonal covariance matrix.

To promote learning of disentangled representation, β-VAE [28] is a variant of the VAE that increases the penalty on the the KL term in the ELBO objective (2):

$${\mathcal{L}}_{\beta }=\frac{1}{N}\sum _{n=1}^N{\mathbb{E}}_{q_{\varphi }\left(\mathbf{y}\mid {\mathbf{x}}_n\right)}\left[\log p_{\theta }\left({\mathbf{x}}_n\mid \mathbf{y}\right)\right]-\beta KL\left[q_{\varphi }\left(\mathbf{y}\mid {\mathbf{x}}_n\right)\Vert p(\mathbf{y})\right]$$ (3)

where β > 1. In practice, a higher degree of disentanglement is obtained by a stronger regularization for the learned posterior q_ϕ(y|x) to match a factorised Gaussian prior p(y).

C. IBP-VAE

When modeling the posterior density of the latent distribution q_ϕ(y|x) as a factorized Gaussian and constraining it to follow an isotropic Gaussian prior, the increased disentangling ability obtained through the objective (3) is obtained at the expense of a decreased modeling capacity of the latent distribution and thus a decreased reconstruction ability of the VAE. This is especially a problem as the complexity of the data, in terms of the complexity of the underlying generative factors, increases.

In an earlier work [29], we have demonstrated that, by using an independent latent factor model with increased modeling capacity, we can simultaneously improve disentangled learning of generative factors and the reconstruction accuracy of the VAE when the complexity of the data increases. In specific, we considered modeling the latent variable by an Indian Buffet Process (IBP), a stochastic Beta-Bernoulli Process that defines a probability distribution over sparse binary matrices indicating feature activation for K features and taking the limit K → ∞ [30]. The infinite binary sparse matrix $\mathbf{Z}\in {\{0,1\}}^{\left\{NX{K}^{+}\right\}}$ represents latent feature allocations where z_n,k is 1 if feature k is active for the n^th sample and 0 otherwise. We presented the IBP-VAE, where the latent representations $\mathbf{Y}={\left\{{\mathbf{y}}_n\right\}}_{n=1}^N$ are modeled as:

$$\begin{gathered} \mathbf{Y}=\mathbf{Z}\odot \mathbf{A} \\ p(\mathbf{A})=\prod _{n=1}^N\mathcal{N}\left(0,{\mathbf{I}}_{K^{+}}\right); \\ p(\mathbf{Z}\mid \nu )=\prod _{k=1}^{K\to \infty }\prod _{n=1}^{N}Bernoulli\left({\pi }_k\right),{\pi }_k=\prod _{i=1}^k{\nu }_i \\ p(\nu )=Beta(\alpha ,1) \end{gathered}$$ (4)

where $\mathbf{Z}={\left\{{\mathbf{z}}_n\right\}}_{n=1}^N$, $\mathbf{A}={\left\{{\mathbf{a}}_n\right\}}_{n=1}^N$, ⊙ is element-wise product, and N is the number of data samples. The Beta parameter α in (4) controls how quickly the probabilities π_k decay which influence how many latent dimensions are required for the generative model. Formally, the representation learned in this manner essentially allows the model to infer which latent features captured by a_n,k, k ∈ {1,..K → ∞} is active for the observed data x_n. As the active factors for each data point are inferred and not fixed, this non-parametric model is able to grow with the complexity of the data.

Similar to VAE, IBP-VAE is optimized by maximizing the ELBO loss:

$$\begin{gathered} \log p(\mathbf{X})\ge \mathcal{L}={\mathbb{E}}_q\left[\log \frac{p(\mathbf{X},\mathbf{Z},\nu ,\mathbf{A})}{q(\mathbf{Z},\nu ,\mathbf{A}\mid \mathbf{X},a,b)}\right] \\ ={\mathbb{E}}_q\left[\log \frac{p(\mathbf{X}\mid \mathbf{Z},\mathbf{A})p(\mathbf{A})p(\mathbf{Z}\mid \nu )p(\nu )}{q(\mathbf{A}\mid \mathbf{X})q(\mathbf{Z}\mid \mathbf{X},\nu )q(\nu \mid a,b)}\right] \\ ={\mathbb{E}}_q[\log p(\mathbf{X}\mid \mathbf{Z},\mathbf{A})]-\beta KL(q(\nu \mid a,b)\Vert p(\nu )) \\ -\beta KL(q(\mathbf{Z}\mid \nu ,\mathbf{X})\Vert p(\mathbf{Z}\mid \nu ))-\beta KL(q(\mathbf{A}\mid \mathbf{X})\Vert p(\mathbf{A})) \end{gathered}$$ (5)

where β > 1 promotes the learning of disentangled representation by increasing the KL penalty similar to β-VAE [28]; we refer such version as β-IBP-VAE. This objective function can be interpreted as minimizing a reconstruction error along with minimizing the KL divergence between the variational posteriors and the corresponding priors in the remaining terms.

D. Learning task representation

The VAE variants presented in Section III-B and III-C are unsupervised models. To facilitate the clinical task of localizing ventricular activation from the 12-lead ECG data set, we then distill the task-specific representation from the disentangled representation using the supervisory signals from the training data. In specific, we append the encoder of the VAE with fully-connected linear layers that take the sample from the latent distribution and output class logit $\mathbf{t}\in {ℝ}^m$, where m is the number of classes involved in the classification task and t is wrapped with a softmax function to be converted into class probability. This classification network $q_{{\varphi }_t}(\mathbf{t}\mid \mathbf{x})$, composed of the VAE encoder and the appended classification layers as described above, is fine-tuned with a cross-entropy classification loss:

$${\mathcal{L}}^{\text{supervised}}={\mathbb{E}}_{p(\mathbf{x},\mathbf{t})}\left[-\log q_{{\varphi }_t}(\mathbf{t}\mid \mathbf{x})\right]$$ (6)

The process of unsupervised learning and the subsequent fine-tuning are illustrated in Fig. 4A.

Fig. 4:

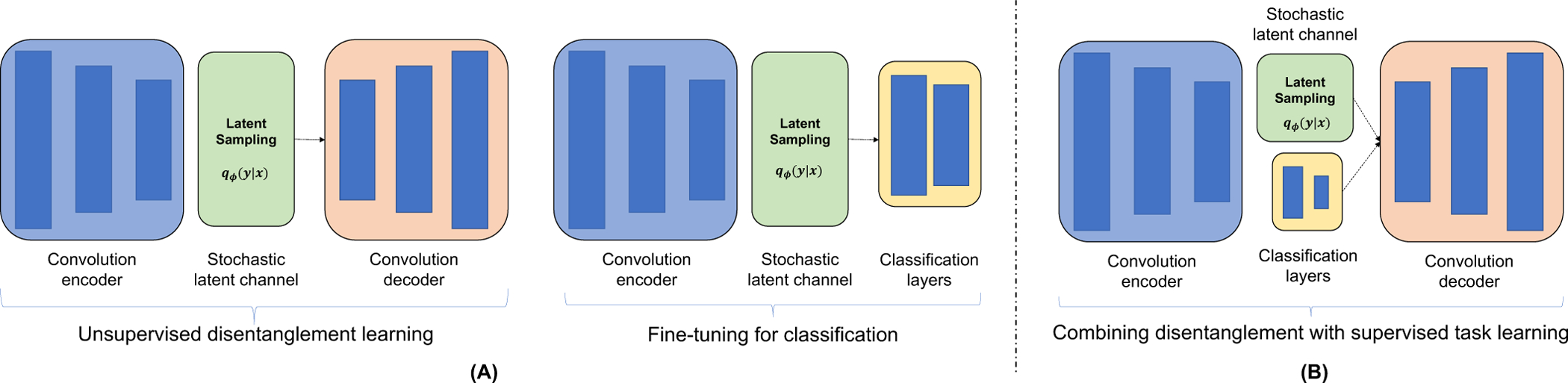
Schematic diagram of the presented model. (A) A two-step process: (Left) disentangled representations are learned in an unsupervised manner and (Right) encoder network is fine-tuned with added classification layers. (B) Combined learning of disentangled and task representation as in [29]. Both VAE and IBP-VAE models follow the same architecture except the stochastic latent channel block.

IV. Experiments

We studied disentangled learning of ECG data from two primary aspects. First, on the simulated ECG data with controlled anatomical variations, we present both qualitative and quantitative evaluations of the unsupervised β-VAE and β-IBP-VAE models in disentangling the anatomical generative factors from the ECG data. Second, on both the simulated and a clinical ECG data set, we evaluate the effect of this disentangled learning on the subsequent supervised task of localizing the origin of ventricular activation from ECG data.

A. Experimental data & data processing

We primarily consider three different data sets in this work: the simulated SimECG and SimECG-torso data set as described in Section II, and a private 12-lead clinical ECG data set as described in [19].

1) SimECG and SimECG-torso data: The generation of these simulated data sets is presented in Section II. In the experiment results presented below, SimECG data was split into three groups based on the degree of swing along the X-axis: group 1 (−10°), group 2 (0°) and group 3 (+10°). Each group consists of one-third, i.e., 404595, samples of the entire data set. For experiments to investigate unsupervised disentaglement, we also consider SimECG-torso which similar to SimECG is split into three groups based on the three values of translation along X-axis: group 1 (−10 mm), group 2 (0 mm) and group 3 (10 mm), with group consisting of one-third, i.e., 44955, samples of the entire data set. Unless otherwise specified, the models were trained on group 1, validated on group 2, and tested on group 3 in the results presented below for both data sets.

2) 12-lead clinical ECG data:: The clinical ECG data described in [19] was collected from routine pace-mapping procedures on 39 patients who underwent ablation of scar-related ventricular tachycardia (VT). Study protocols were approved by the Nova Scotia Health Authority Research Ethics Board. On each patient, 15-second 12-lead ECG recordings resulting from 19 ± 11 different simulation locations were collected. The study protocols for this data set were approved by the institutional research ethics board. Following the preprocessing procedure as described in [19], the data set consists of 16848 ECG beats across 1012 distinctive pacing sites on the left-ventricular (LV) endocardium; each ECG beat is in the form of 12 leads with 100 temporal samples in each lead. The entire data set was split into training (10292 beats from 22 patients), validation (3017 beats from 5 patients), and test sets (3539 betas from 12-patients) making sure that no data from the same patient are shared between any two sets.

B. Network architecture and comparison

For unsupervised disentangling of anatomical variations, we compared β-VAE and β-IBP-VAE at different values of β including β = 1. For the supervised task of localizing ventricular activation, we compared the fine-tuned IBP-VAE model, the fine-tuned VAE model, and a CNN baseline. Since all the considered models have CNN as building blocks, we first describe the architecture of these CNN blocks, followed by descriptions of each specific model:

• CNN (encoder): The CNN encoder consisted of five convolution blocks for feature extraction. Each convolution block consisted of a 1D convolution layer, 1D batch normalization layer, dropout layer, and rectified linear unit (ReLU) as an activation function. The kernel size of 7 was used in all these five convolution layers and stride of 5 except for the last convolution layer. The input channel size for these five convolution layers was 1, 32, 64,128 and 200, respectively.

• CNN (decoder): The CNN decoder consisted of four convolution blocks of transpose convolution (with kernel size of 7 and stride length of 5), batch normalization, and a ReLU activation function. The input channel size for these four convolution layers was 100, 200, 128 and 64, respectively. Finally, in order to decode the signal, we further added a 1D transpose convolution layer (kernel size of 7, stride of 5 and input channel size of 32) without any batch-norm or non-linear activation function.

• VAE (unsupervised): The unsupervised VAE consisted of the CNN encoder followed by two linear layers to obtain the mean and log-variance of the latent Gaussian distribution, each with an output dimension of 100. From a re-parameterization of the mean and log-variance, latent samples were drawn as the input to the CNN decoder.

• IBP-VAE (unsupervised): The IBP-VAE consisted of the CNN encoder followed by three linear layers to obtain the parameters of the latent IBP, i.e., z_n for the Beta-Bernoulli distribution and the mean and log-variance for the Gaussian distribution a_n. The dimension for each of these parameters are of size 100. From the re-parameterization of these parameters, latent samples were drawn as the input for the CNN decoder.

• IBP-VAE/VAE (fine-tuned): For the supervised task of localizing ventricular activation, the trained encoder of the unsupervised IBP-VAE or VAE was appended with two additional fully-connected layers with an output of ten dimensions representing the ten LV segments to be classified. This output was wrapped with the softmax function for the classification loss.

• IBP-VAE/VAE (conditional): For completeness, we compared the fine-tuned IBP-VAE/VAE with the conditional networks presented in [29] for the task of localizing ventricular activation. As described in [29] and as illustrated in 4B, we appended two heads to the CNN encoder: a stochastic latent channel and a separate classifier network. The former followed the same architecture as described for unsupervised IBP-VAE/VAE and the latter followed the same architecture as those appended to the trained encoder for fine-tuned IBP-VAE/VAE. The output of both heads were combined as inputs to the decoder network. The task related representation was learned through the classifier network, simultaneously with disentangling of the rest of the disentangled generative factors through the IBP-VAE/VAE head, where only the classifier network received supervision.

• CNN (supervised): For the supervised task of localizing ventricular activation, we further considered a supervised CNN trained end-to-end as the baseline. The network had the same architecture with the CNN encoder, the output of which was flattened and passed onto fully connected layers (with dropout and batch normalization layer) to output a final prediction of 10 dimensions and wrapped with a soft-max function for the supervised loss.

For SimECG dataset, we also perform analysis for supervised localization of ventricular activation using electrocardiographic imaging (ECGi), a non-invasive multi-lead ECG-type imaging tool [31].

C. Results: unsupervised disentanglement of anatomical variations from ECG data

In this section, we analyze the ability of the presented unsupervised VAE/IBP-VAE models to disentangle inter-subject anatomical variations in both SimECG and SimECG-torso data sets. Fig. 5 shows the change of the overall ELBO loss (left) as well as the individual reconstruction loss (middle) and KL-divergence loss (right) of the presented IBP-VAE on the training and validation data. Fig. 6 shows examples of reconstructed ECG data by the unsupervised IBP-VAE model.

Fig. 5:

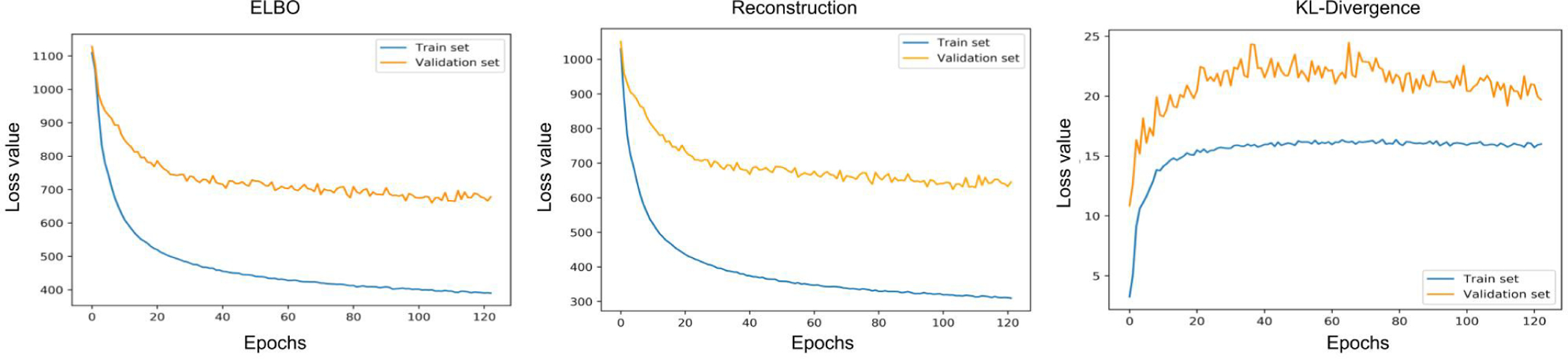
Training and validation loss over training epochs for IBP-VAE. Left: ELBO of IBP-VAE as defined in (5). Middle: Loss curve for the reconstruction error. Right: Loss curve for the combined KL-Divergence between variational posteriors and the corresponding priors.

Fig. 6:

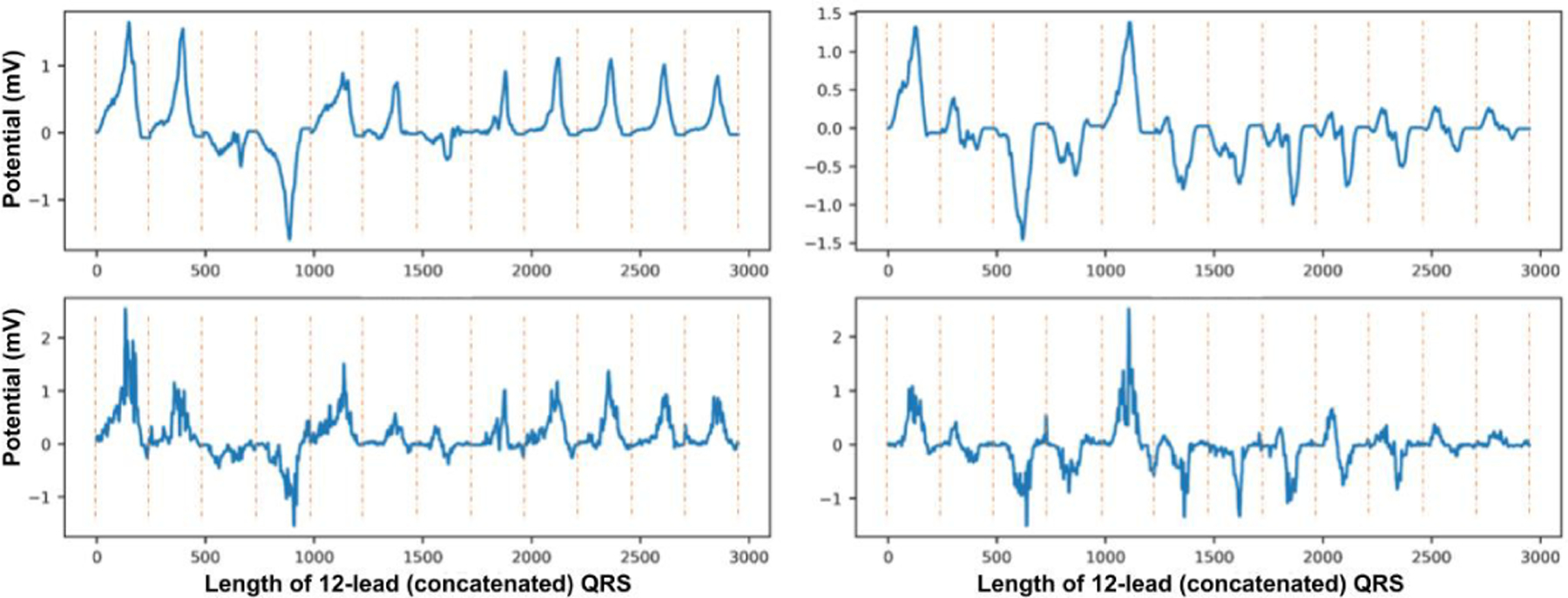
Reconstruction examples (bottom) for the consecutive two original samples (top) from SimECG data set. Note that the QRS signals from each lead are concatenated to form a single 1D signal. The vertical dotted lines demonstrate the separation of signals in each lead.

We consider the ability of the presented models to disentangle eight generative factors in the SimECG data: two related to the orientation of the heart in the torso (swing around Y-axis and swing around Z-axis), three related to the position of the heart in the torso (translation along the X-, Y-, and Z-axis), and three related to the origin of the ventricular activation in the heart (position along the X-, Y-, and Z-axis). For SimECG-torso, we consider the models to disentangle six generative factors: one related to the variation in the torso, two related to the the position of the heart in the torso (translation along the Y- and Z-axis), and three related to the origin of the ventricular activation in the heart (position along the X-, Y-, and Z-axis). For both data sets, the first two groups of factors represent anatomical variations underlying the ECG data, whereas the last group represents task-related factors. Note that, for SimECG, swing around the X-axis was not considered because, as described earlier, the value of this swing was used to divide the training, validation, and test data: i.e., the training data do not include variations in the orientation of the heart around the X-axis. For SimECG-torso, translation around X-axis was used for such division.

For quantitative evaluation of the disentanglement results, we adopted the metric proposed by [28] that measures both the independence and interpretability of the inferred latent representation. It is obtained by training a linear classifier¹ to identify which dominant generative factor has changed between a pair of given data. Here, we used a support vector machine (SVM) with linear kernel for the linear classifier [32]. The SVM was trained on group-2 data and tested on group-3 data to ensure fair assessment of disentanglement. The result for different models is presented in Table II. As shown, IBP-VAE, owing to its increased modeling complexity in the latent space, was able to achieve a higher disentanglement score when compared to VAE. When the value of β was increased to 5, the disentanglement scores of both β-VAE and β-IBP-VAE were increased where the β-IBP-VAE still delivered a higher score close to ~ 80%.

TABLE II:

Beta-VAE disentanglement metric [28] for VAE and IBP-VAE for β = 1 and β = 5 for SimECG data set.

Model	SimECG
VAE	67.82
VAE (β = 5)	76.24
IBP-VAE	73.32
IBP-VAE (β = 5)	79.99

For a closer look at how well the presented β-IBP-VAE model was disentangling among the eight generative factors under consideration, in Fig. 7(A) we present the confusion matrix of the SVM in classifying the contributing generative factor using the latent representation obtained by the β-IBP-VAE (β = 5). As shown, there was minimal confusion in the generative factors among the group of heart orientation, heart position, and origin of ventricular activation, indicating a clear separation between the task-irrelevant anatomical variations and the task-relevant factors in the learned latent representations. The main confusion occurs when separating the three task-related position factors: the position of the origin of the ventricular activation along the X-, Y- and Z-axis, while some minor confusion occurred among separating the three anatomical factors related to the position of the heart along the X-, Y-, and Z-axis within the torso. When we re-trained the SVM model for the disentanglement metric by considering the same five anatomical factors when grouping the three task-related position factors into one factor, a disentanglement score of 92.81% could be achieved, demonstrating an excellent separation between the task-relevant representation and the task-irrelevant factors of anatomical variations: the corresponding confusion matrix is presented in Fig. 7(B). For SimECG-torso, among two β values, we obtained the best result of 88.99% for β = 1. The better disentangling performance that we achieved, compared to the SimECG data set, stems from the fact that SimECG-torso has fewer generative factors (six vs. eight). Also, the variations due to the torso may be more discernible against the variations due to heart geometry. We present the corresponding confusion matrix of the SVM in Fig. 7(C).

Fig. 7:

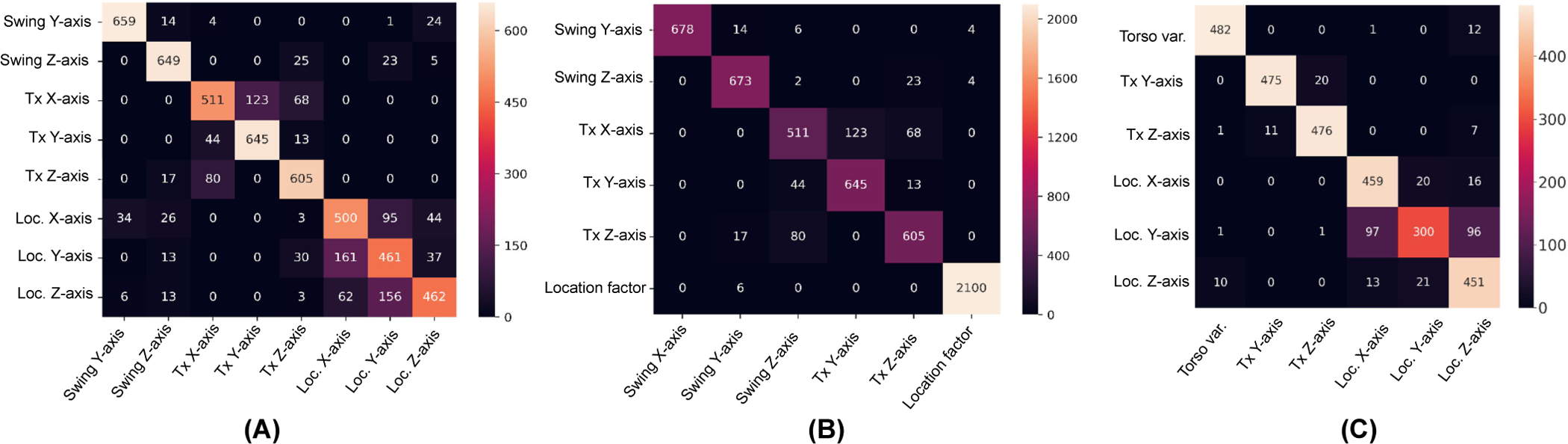
Confusion Matrix for the disentanglement of representations learned via IBP-VAE (β = 5) for SimECG data set in (A) (5 anatomical factors and 3 location factors) and (B) (5 anatomical factors and a single location factor), and for SimECG-torso data set in (C) (3 anatomical factors, including torso variations and 3 location factors).

In addition, Fig. 8 provides a t-SNE [33] visualization of the latent representation learned by the unsupervised IBP-VAE using β = 5 for SimECG data set. Consistent with the observation from the confusion matrix in Fig. 7 (A), a clear separation among the five anatomical factors and the task-related factor (dotted circle) was seen, whereas the specific task-related position factor along each axis is less separated among themselves.

Fig. 8:

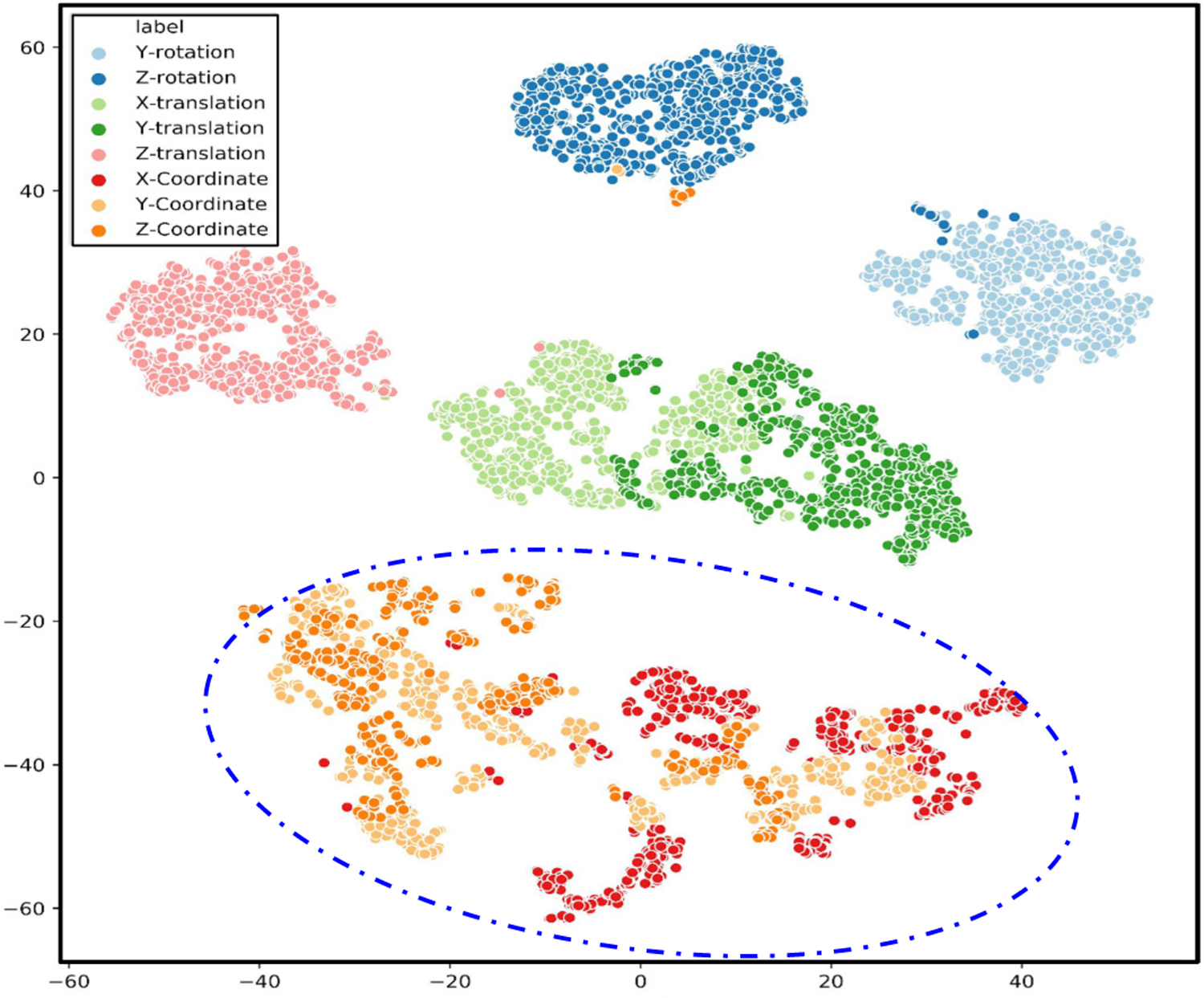
t-SNE visualization for disentangled latent representation for SimECG data set. The blue dotted line is manually added to highlight task-related factors specific to the location of the origin of ventricular activation.

Finally, to identify which unit(s) in the latent code are most responsive to the changes in each of the five anatomical generative factors, we analyze the mean fluctuations in the latent code corresponding to changes in each anatomical factor. To do so, from pairs of input data where only one factor is changing, we calculate the average standard deviation of mean values between inferred latent codes from the pair of data. We find the most active units for each factor and, for that unit, we calculate the mean fluctuation (standard deviation of mean values) of all factors. The results for both β-VAE and β-IBP-VAE are presented in Fig. 9. The identified latent units are ordered such that the first two units, as presented, are the most responsive to changes in the rotation factors, while the last three units are the most responsive to changes in the position factors. The separation between these two groups of factors are in general clear in both models. Among the individual factors within each group, swing around the Y-axis (red triangle) and translation along the Z-axis appear to be better disentangled than the other factors, especially by the β-IBP-VAE mode.

Fig. 9:

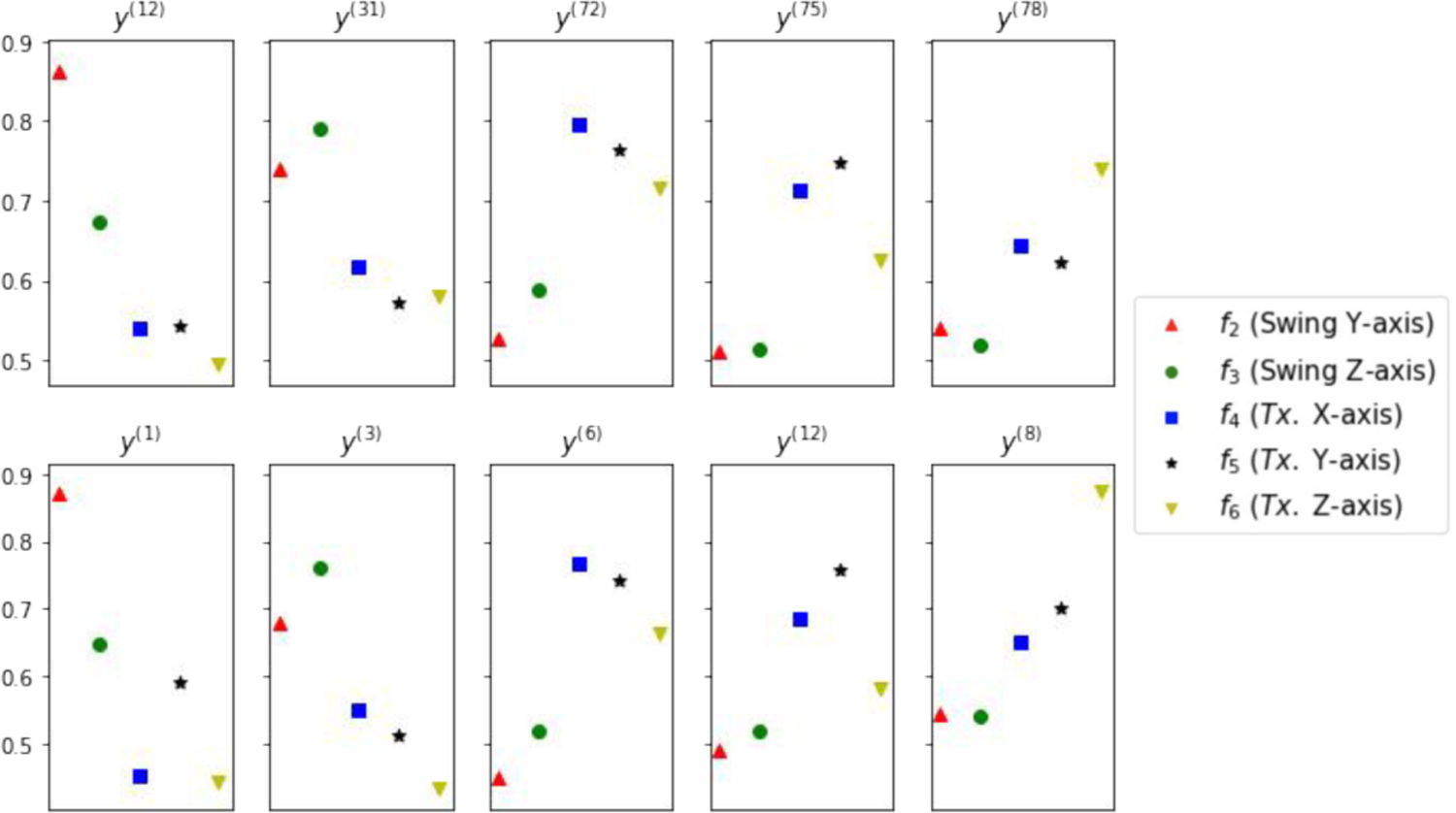
Average mean fluctuations corresponding to changes in each of the five geometrical generative factors f_i in each of the five high ranking latent units. Top: β-VAE. Bottom: β-IBP-VAE.

D. Results: supervised localization of the origin of ventricular activation

In this section, we evaluated the effect of disentangled representation learning on the downstream task of localizing the origin of ventricular activation from both the simulated and clinical ECG data. In specific, we considered the task of classifying the origin of ventricular activation into 10 anatomical segments of the LV [34]. The nomenclature of these segments is provided in the Fig 10(A), and the distribution of training data among the ten segments for both data sets are shown in Fig. 10 (B)–(C).

Fig. 10:

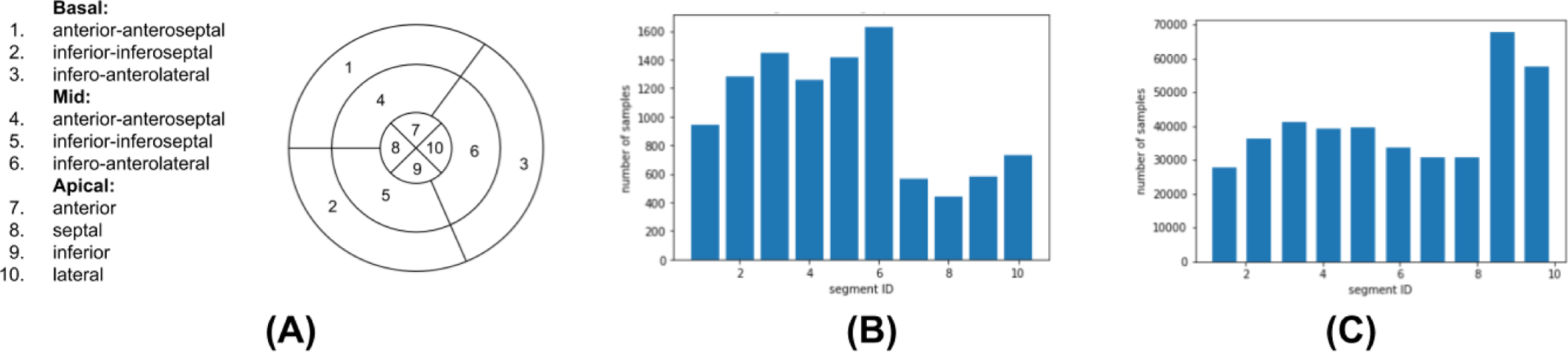
(A) Schematics of the 10-segment division of the left ventricle. (B–C) Training data distribution in bar diagrams for 12-lead Clinical ECG and SimECG, respectively, showing the number of samples in each segment class.

Table III summarizes the accuracy of the presented fine-tuned IBP-VAE model along with the various comparison models as described in section IV-B on both data sets. As shown, the presented fine-tuned IBP-VAE achieves an improvement of around 18.5% and 7.2% over baseline CNN for the SimECG and clinical ECG, respectively. Similarly, due to the effect of increased modeling capacity, via IBP-VAE (fine-tuning), over standard VAE (fine-tuning), at β = 5, we can see the improvement of around 11.3% and 3.6% for the SimECG and clinical ECG, respectively. Finally, considering the effect of disentanglement (from β = 1 to β = 5), we can see the improvement of 3.7% and 1.5% for the SimECG and clinical ECG, respectively. Fig. 11 and Fig. 12 presents the Receiver Operating Characteristics (ROC) curves of the different models on the SimECG data set and clinical data set, respectively. As shown, on both data sets, disentangled representation via the fine-tuned IBP-VAE achieved higher classification accuracy and AUC scores, with the best performance achieved at β = 5.

TABLE III:

Segment localization accuracy of the presented models under different settings.

Model	Segment classification (in %)
	SimECG	12-lead clinical ECG
CNN (Baseline)	61.81	50.23
VAE (conditional)	65.82	49.25
VAE (fine-tuning)	59.06	52.33
VAE (conditional) (β = 5)	65.97	47.33
VAE (fine-tuning) (β = 5)	65.81	51.96
IBP-VAE (conditional)	63.98	47.10
IBP-VAE (fine-tuning)	70.63	53.02
IBP-VAE (conditional) (β = 5)	68.07	46.82
IBP-VAE (fine-tuning) (β = 5)	73.27	53.83

Fig. 11:

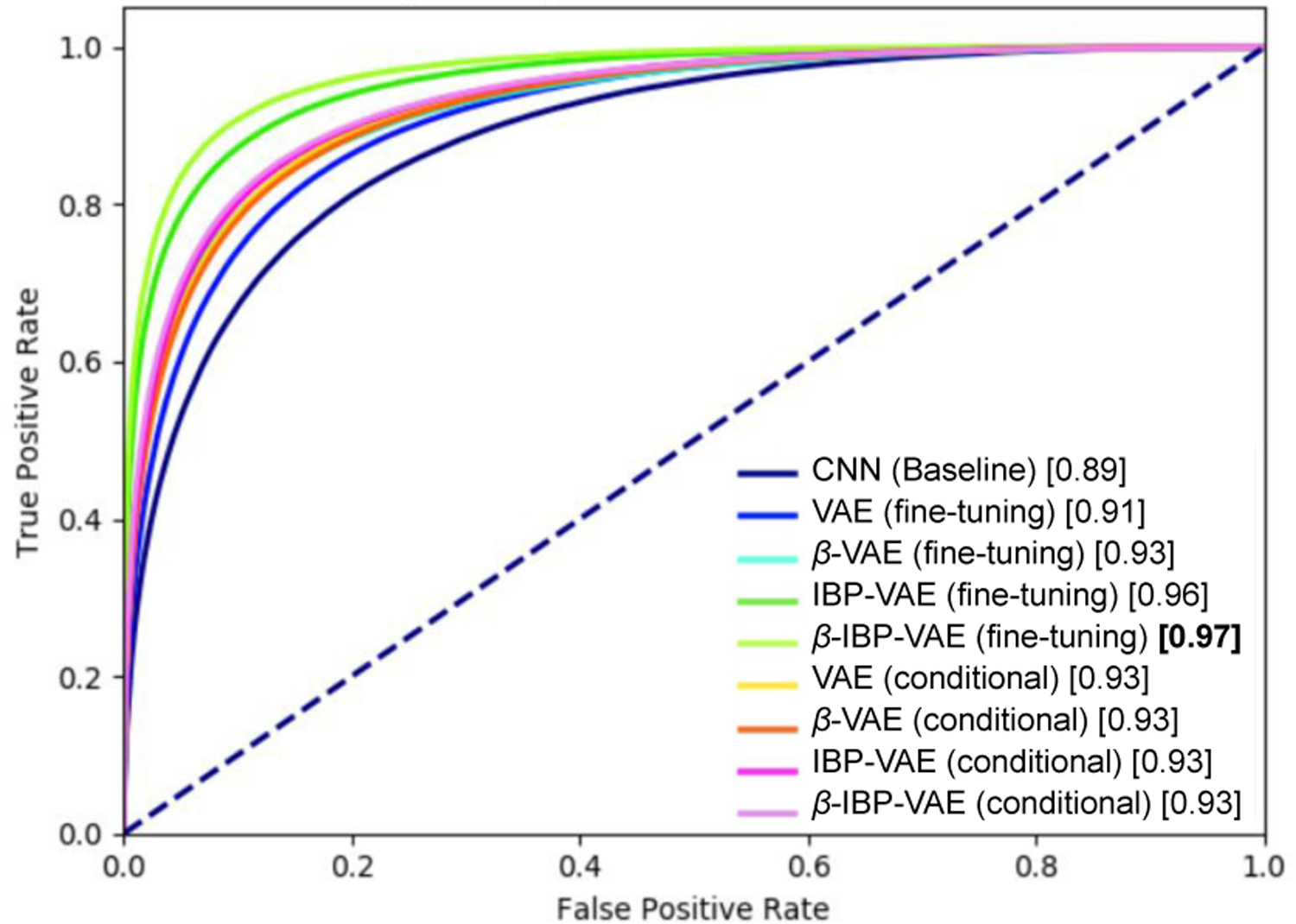
ROC plot of different models on the SimECG data set.

Fig. 12:

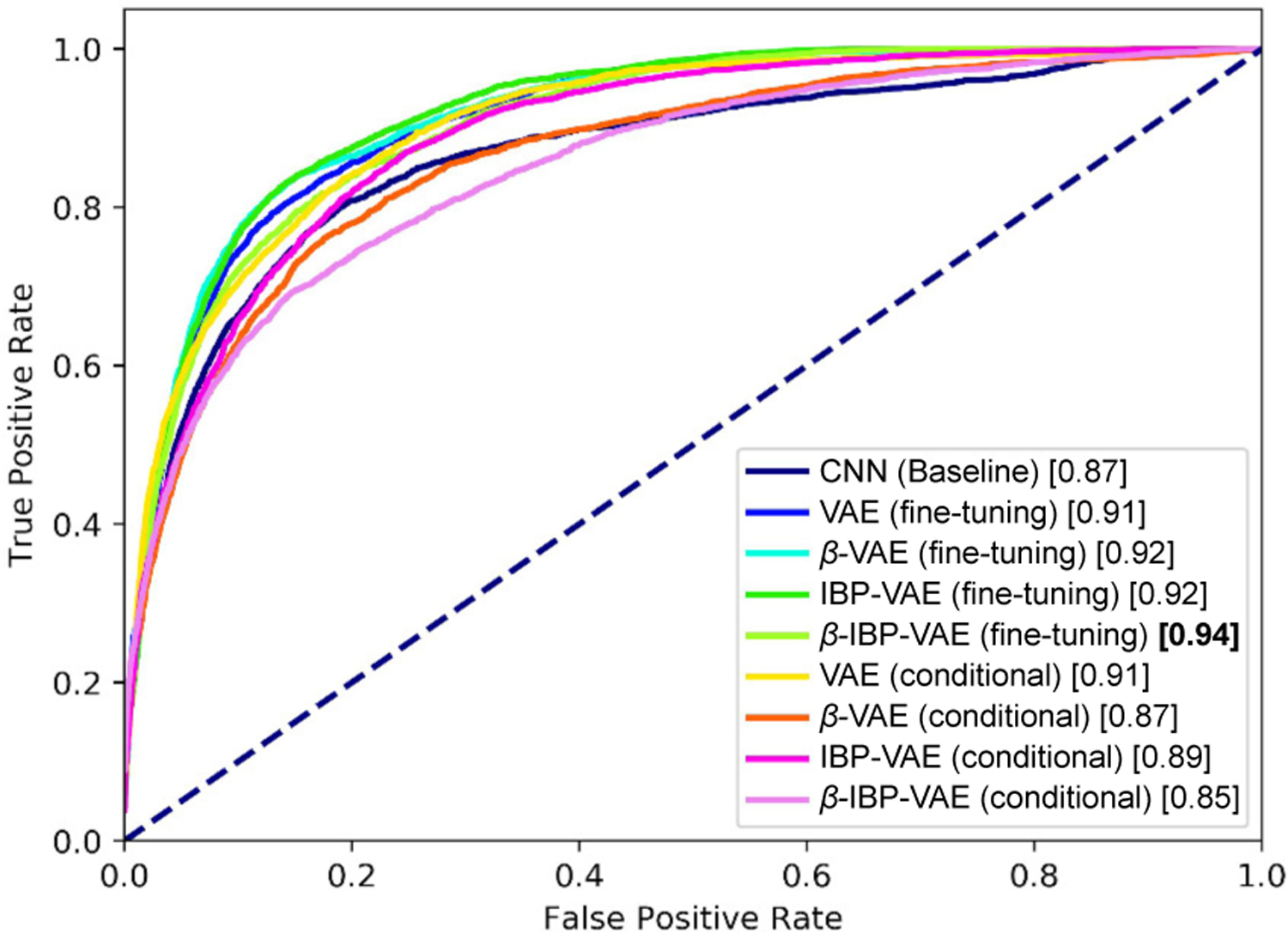
ROC plot of different models on the clinical data set.

E. Results: comparison with ECGi

We performed ECGi analysis for supervised localization of ventricular activation for the SimECG dataset. The results are presented in Table IV. In specific, we selected 10 geometries from the whole dataset (i.e., among 729 geometries) with large anatomical variations among these geometries, and for each selected geometry we randomly picked the activation sites for the analysis such that the selected sites cover all 10 anatomical segments of the LV, totaling 50 activation sites. Among these 50 activation sites, ECGi method was able to accurately classify only 13 cases (26%). When we augment the neighborhood (i.e., if the predicted segment is adjacent to the ground-truth segment) cases, the percentage increases to 70% (i.e., 33 out of 50 cases). In this analysis, for the geometries (4) within the test set (of Table III), the top-1 accuracy was only 20% and with neighborhood, the accuracy was 70%. Overall, the presented method achieved significantly higher results compared to the ECGi-based approach.

TABLE IV:

Segment localization accuracy for randomly selected sites using electrocardiographic imaging (ECGi).

Group (number of sites)	top-1	top-1 and neighbors
All dataset (50)	26%	70%
Test dataset (20)	20%	70%

V. Discussion

A. Disentangling anatomical variations from ECG data

Via simulated data generated with controlled factors of anatomical variations, we provided concrete evidence – to our knowledge for the first time – that it is possible to tease apart anatomical generative factors from ECG data and that this disentangling can benefit downstream tasks confounded by such anatomical variations. As the first work of this kind, we considered a small number of representative anatomical factors including the orientation and position of the heart. In practice, there is a much larger variety of factors of anatomical and physiological variations among individual that affect ECG data. For instance, inaccurate ECG electrodes placement can cause change in morphology of the signal introducing substantial variations [35]. Detailed investigation of the feasibility and benefit of disentangling these inter-subject variations require a more comprehensive study with a larger simulation data set.

With the primary objective to demonstrate the feasibility and benefit of disentangle anatomical generative factors from ECG data, we considered the state-of-the-art VAE [26], β-VAE [28], and our previously presented (β)-IBP-VAE [29] for the purpose of disentangled representation learning in this work. A large number of alternative models for disentangled representation learning, such as TC-VAE [5] and FactorVAE [36] using VAE [26], or InfoGAN [37] and SC-GAN [38] using GAN [39], can be investigated for the same tasks in the future, although it was not the intent of this study to present the best-performing model but to demonstrate the feasibility and importance of disentangling learning in ECG data that has not been considered before. Note that, in a recent large-scale study in disentanglement learning, disentanglement scores of unsupervised models were shown to be heavily influenced by randomness (random seed) and the choice of the hyperparameter (regularization strength) compared to the objective function (choice of model) [3].

B. Value and limitation of SimECG data

Much of the recent success in machine learning comes at the cost of a large amount of well-labeled data samples, and thus, among many other challenges in machine learning, data management (collecting, cleaning, analyzing, etc.) is becoming one of the critical steps [40]. In the clinical or medical imaging domain, the issue of data availability for testing machine learning algorithms is further critical due to a wide variety of constraints. SimECG, owing to its large sample size, is well suited for training deep learning models, much deeper and wider than the one presented in this work. Here, we demonstrated the usages of the SimECG data set in supervised learning (classification) and unsupervised learning (disentanglement). Beside these there are other machine learning areas where SimECG data set can be used to study or compare different competitive models. Since the SimECG data set also has 1665 coordinate labels, this data set can be used for the regression problem of predicting the coordinate of the VT sites [41]. Transfer learning [42] and domain adaptation [43] are other exciting fields of machine learning and medical imaging where the SimECG data set can be used. Below we provide a brief example scenario for the domain adaptation.

Domain adaptation is the task of adapting models between different domains. An example in medical imaging could be an adaptation of a model trained on X-ray images from one hospital to X-ray images from another hospital [44]. Since SimECG has the ground truth geometrical variations, we can re-group the data set to simulated different domains. The model trained on some particular group for the clinical task of localizing ventricular tachycardia has to be adapted to perform well on other configurations of the data set. To demonstrate this, we created nine different data sets from nine different combinations of two geometrical factors (instead of one considered in this work): rotation along Y-axis and Z-axis; and train the presented IBP-VAE along with VAE on one group. The result for other groups is presented in Fig. 13. The trend for both the models is similar: the performance is decreased as the test data lies further away from the training set. This demonstrates the necessity of specialized domain adaptation techniques or models in this setup. Hence, the SimECG data set can be rearranged in a different way to understand or build the models for domain adaptation.

Fig. 13:

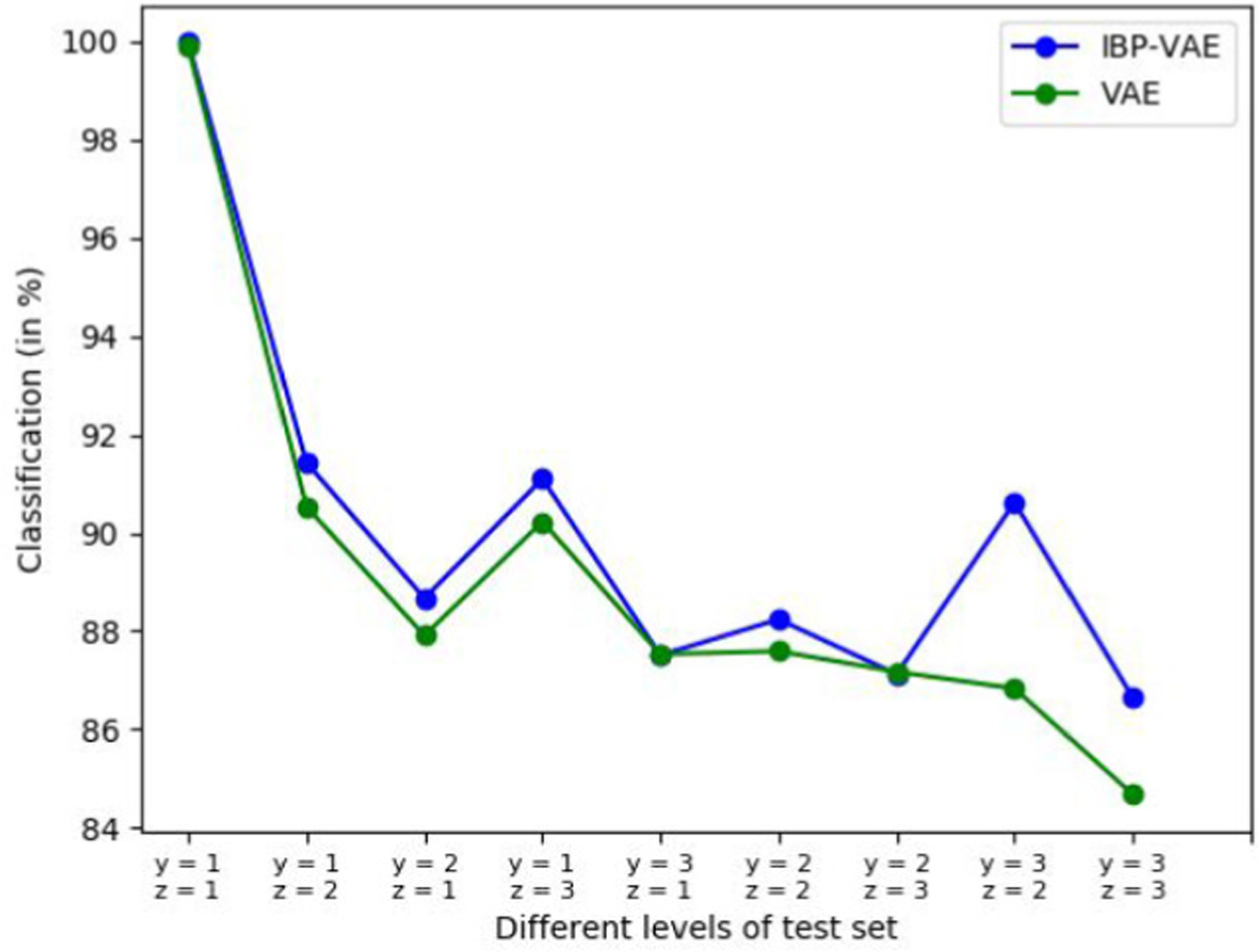
Localization accuracy for nine combinations of geometrical variations (rotation factors). Y-axis represents the classification accuracy, and the X-axis represents the performance for each data set, including a training set (in the left).

The generation of the SimECG data can be improved in several aspects. First, to simulate the spatiotemporal action potential propagation for constructing the SimECG data set, we relied on two-variable AlievPanfilov (AP) model. There are many different models to simulate cardiac electrophysiology, grouped into two main approaches: phenomenological and biophysical or iconic models. The AP model considered in this work belongs to the former group of phenomenological models built using a simpler system of equations to compute the cell potential without computing the concentrations of ion. These models are computationally very efficient but lack electrophysiological detail. On the other hand, ionic models (e.g., a human cardiac cell model [45]), unlike phenomenological models, may be able to both reproduce and predict a wide range of cardiac electrophysiological dynamics observed experimentally. However, these electrophysiological details come at the price of expensive computation. Some intermediate approaches like [46] could be a useful alternative to the AP model as these models are efficient enough for whole organ arrhythmia simulations yet detailed enough to capture the effects of cell-level processes such as current blocks and channelopathies. Second, we consider translation and rotation of the heart as geometrical variations in the SimECG dataset. These variations affect the ECG propagation in a homogenous way. However, other variations may exist due to factors like deposition of fat in the heart whose effect isn’t captured proportionately, and such obesity can significantly lower ECG sensitivity for detecting various diagnostic conditions [47]. Our current setup doesn’t handle such non-homogeneous anatomical factors, and incorporating real-world data along with the SimECG may reduce the effect of such variations to a certain extent. Finally, our assumption of homogeneous torso model could be relaxed to include conductive inhomogeneity among different torso tissues. Finally, current SimECG data consists of a limited number of anatomical variations which could be extended by including other anatomical variations such as the deformation of the heart and the shape of the torso.

C. Potential of using Electrocardiographic imagining

In this study, we primarily focused on ECG use to localize the origin of ventricular activation. But it has been argued that although the 12-lead ECG is fundamental for assessing heart diseases, it cannot always reveal the underlying mechanism or the location of the arrhythmia origin [31]. Alternatively, electrocardiographic imaging (ECGi), a non-invasive multi-lead ECG-type imaging tool, has seen a recent upsurge from both research and industry communities due to its potential for clinical application in diagnosis and treatment planning of cardiac arrhythmias, including atrial fibrillation and VT. Specifically, there is evidence from previous studies (e.g., [48]) that suggests that ECGi can be used to provide diagnostic insights regarding the location of arrhythmia origin. Compared to data-driven methods using ECG, ECGi methods are more general purpose, and the analysis that we performed using ECGi based methods demonstrated that – for specific tasks such as localizing the origin of activation – data-driven methods trained for the specific task may be better than the general-purpose ECGi based approach. Future work could involve combining the data-driven methods and ECGi methods for achieving benefits of both sides.

D. Deep Network Architecture for Electrocardiographic Data

In this study, we relied on CNN architecture (Section IV-B) as feature extraction building blocks. The presented architecture is comprised of five 1D convolution blocks. Although the intent of this study was not to search for the best architecture for feature extraction, we note recent studies which have demonstrated the use of other specialized architecture like very deep networks [16] or recurrent neural networks in our earlier work [19] to process electrocardiographic data. In [16], a 34-layer convolution neural network was designed to map a sequence of electrocardiograph samples to a sequence of rhythm classes and was trained end-to-end with complete supervision. In [19], a sequential factorized autoencoder made up of Gated Recurrent Units (GRU) was proposed to separate anatomical representation with task-relevant factors via weak supervision in the form of patient labels. Unlike these works, we considered unsupervised learning of disentangled features from the ECG data. Further, the nonparametric capacity of the IBP-VAE allowed us to capture the unbounded nature of underlying generative factors. The combination of sophisticated architecture presented in such works with the learning setup of our work could be an interesting future avenue.

VI. Conclusion

We presented a novel study of disentangling anatomical generative factors from ECG data and demonstrated that disentangling can benefit the downstream task confounded by such anatomical variations. For this, we simulated large-scale 12-lead ECG data sets with a controlled set of generative factors involving the geometry of the heart and torso and demonstrated the ability to disentangle factors of such geometrical factors. On both simulated and real-world clinical ECG data sets, we then demonstrated the benefit of such disentanglement representation learning on the downstream task of localizing the origin of ventricular activation.