Nature-inspired optimization algorithms and their significance in multi-thresholding image segmentation: an inclusive review

Abstract

Multilevel Thresholding (MLT) is considered as a significant and imperative research field in image segmentation that can efficiently resolve difficulties aroused while analyzing the segmented regions of multifaceted images with complicated nonlinear conditions. MLT being a simple exponential combinatorial optimization problem is commonly phrased by means of a sophisticated objective function requirement that can only be addressed by nondeterministic approaches. Consequently, researchers are engaging Nature-Inspired Optimization Algorithms (NIOA) as an alternate methodology that can be widely employed for resolving problems related to MLT. This paper delivers an acquainted review related to novel NIOA shaped lately in last three years (2019–2021) highlighting and exploring the major challenges encountered during the development of image multi-thresholding models based on NIOA.

Introduction

Numerous practical applications entail the optimization of specific goals such as energy conservation, environmental protection and performance, efficiency, and long-term viability (Yang 2020). The optimization problems which can be framed in several circumstances are very complex, with multimodal objective landscapes and a collection of complicated, nonlinear constraints (Yang 2020). Solving such difficulties is challenging. Using basic brute force tactics remains unrealistic and undesirable, despite the rising capability of modern computers. As a result, efficient algorithms are critical in such applications wherever feasible. Unfortunately, efficient techniques may not present again for majority of application optimization problems. MLT-based image segmentation is an example of such problem in which a proficient search of the solutions inside a complex search area is required to discover the best solution (Dhal et al. 2020a). MLT is useful for generating two or more homogenous classes by segmenting composite images. The main procedure in the field of MLT is to determine the best threshold levels. Nevertheless, the MLT techniques have a major drawback in terms of the computation time that basically tends to increase as the number of thresholds grows, making it computationally demanding. Such flaws of MLT can be resolved by the Nature-Inspired Optimization Algorithms (NIOA) and it has become an imperative possibility. This inspiring nature has triggered the inquisitiveness in many academic scholars thereby focusing on the development of NIOA by conceptualizing natural events in computational terms. NIOA and their improved variants have proved its efficacy in engineering optimization problem and also resolving several MLT problems. Therefore, this study concentrates to accomplish an up-to-date review on recent NIOA and their MLT applications during past three years i.e., 2019–2021.

The remaining sections of the paper are systematized as follows: The review and discussion on recent NIOA since 2019 is presented in Sect. 2. The application of NIOA over MLT problem has been reported in Sect. 3. Section 4 highlights the experimental results of some newly developed NIOA in the year 2021. Lastly, Sect. 5 discusses on the conclusion and the future research directions.

Survey on recent nature-inspired optimization algorithms

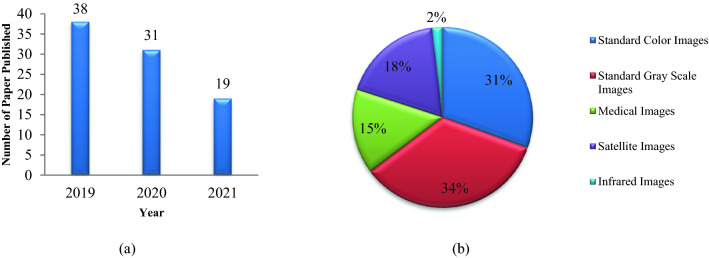
Since millions of years, flora and fauna have showcased mechanisms to protect and secure their survivability when sources are scant (Li et al. 2020a). It's realistic to opt these tactics for the prevalence and effectiveness while developing optimization algorithms. NIOA algorithms have offered a multitude of meta-heuristic algorithms for solving anticipated issues for the last few decades. According to the No Free Lunch (NFL) theorem, there exist no single NIOA that has the capability of solving all optimization problems (Dhal et al. 2019a, 2020a; Wolpert and Macready 1997). As a consequence, scholars are constantly proposing new NIOA, preserving the sector and propelling substantial progress year after year. In the work of Dhal et al. 2020a, the list of NIOA and their application in MLT domain has been reported up to the year 2018. Houssein et. al. (Houssein et al. 2021a) published a book chapter in 2021 in the same topic but their research does not contain the recent full list of NIOA. The complete list of the developed NIOA in the period of 2019–2021 is reported in Table 1. In recent times, the combinatorial optimization field has perceived an overflow with respect to "new" NIOA, the majority of which are based on some natural or artificial metaphor. Therefore, one only question that arises in the mind of the researchers when working in this field i.e., “which NIOA needs to be selected and focused on for the problem?”. Therefore, the Table 1 also highlights the citation of the NIOA because citation can be a good metric for selecting NIOA from this huge set. It can be observed that in the year 2019, 2020 and 2021, around 22, 25, and 16 different NIOA respectively have been developed and proposed world-wide. However, such speedy progress and introduction of new NIOA makes the research tough in this field. Sorensen (Sörensen 2015) also wrote in his paper that this massive numbers of algorithm drags the field of NIOA a step backward rather than forward. His research also gained enormous popularity thereby achieving 726 citations according to Google scholar (dated 26.10.2021). As a consequence, the most critical question that arises in the mind of many today is “Does the scientific community need new NIOA’s or the existing NIOA’s are enough?”. There are already enough "novel" NIOA, according to the author of Sörensen (2015) and Fister et al. (2016), and there is no need to introduce additional NIOA. The time has arrived for standardization, to permit the research society to emphasis on more promising research avenues in the NIOA literature and to identify the true mechanics underlying in these "new" NIOA. The year wise number of published papers over NIOA based MLT has been presented in Fig. 1a.

Table 1.

List of recently introduced NIOA

Sl	Name of the algorithm	Application area	Author’s name	Year	Citation
1	African Vulture’s Optimization Algorithm	Mathematical and Engineering Optimization problems (Abdollahzadeh et al. 2021a)	Abdollahzadeh et. al. (2021a)	2021	6
2	Remora Optimization Algorithm	Mathematical and Engineering Optimization problems (Jia et al. 2021)	Jia et. al. (2021)	2021	4
3	Chameleon Swarm Algorithm	Mathematical and Engineering Optimization problems Braik (2021) , Image Classification Umamageswari et al. (2021) Sentimental analysis and sarcasm detection (Sridharan 2021), Economic Load Dispatch (ELD) problems (Said 2021)	Braik (2021)	2021	8
4	Artificial Gorilla Troops Optimizer	Mathematical and Engineering Optimization problems (Abdollahzadeh et. al. 2021b), Solar Photo Voltaic Systems (Ginidi et al. 2021a, Image Segmentation (sayed et al. 2021)	Abdollahzadeh et. al. (2021b)	2021	5
5	Flow Direction Algorithm	Mathematical and Engineering Optimization problems (Karami et al. 2021),	Karami et. al. (2021)	2021	5
6	Aquila Optimizer	Mathematical and Engineering Optimization problems (Abualigah et. al. 2021a), Oil Production Forecasting (AlRassas et al. 2021), Industrial Optimization Problem (Wang et al. 2021a )Abd Elaziz, Image Classification (Abd Elaziz et al. 2021b)	Abualigah et. al. (2021a)	2021	66
7	QANA: Quantum-based Avian Navigation Optimizer	Mathematical and Engineering optimization problems (Zamani et al. 2021)	Zamani et. al. (2021)	2021	1
8	Atomic Orbital Search	Mathematical and Engineering Optimization problems (Azizi 2021), Feature selection (Elaziz et al. 2021)	Azizi (2021)	2021	10
9	Arithmetic Optimization Algorithm	Mathematical and Engineering Optimization problems (Abualigah et. al. 2021b ;Agushaka and Ezugwu 2021, Functionally Graded Material (FGM) plate structures (Khatir et al. 2021, MLT based Image Segmentation (Abualigah et al. 2021d), Feature Selection (Ibrahim et al. 2021; Ewees et al. 2021) Robot Path Planning (Wang et al. 2021b, Fog Computing (IoT) (Abd Elaziz et al. 2021c), PID controller (Izci et al. 2021)	Abualigah et. al. (2021b)	2021	160
10	Dingo Optimizer	Mathematical and Engineering Optimization problems (Bairwa et al. 2021)	Bairwa et. al. (2021)	2021	0
11	Red Colobuses Monkey	Mathematical and Engineering Optimization design problems (Al-Kubaisy et al. 2021)	Al-Kubaisy et al. (2021)	2021	0
12	Archimedes Optimization Algorithm	Mathematical and Engineering Optimization problems (Hashim et. al. 2021), Wind Speed Forecasting (Zhang et al. 2021a), Industrial Optimization (Yıldız et al. 2021), Wind Energy Generation System (Li et al. 2021), PEM Fuel Cell Parameter Identification (Houssein et al. 2021c; Sun et al. 2021a; Yao and Hayati 2021), Power Systems (Aribowo et al. 2021a), Feature Selection, Classification (Desuky et al. 2021; Chen and Rezaei 2021; Annrose et al. 2021; Neggaz and Fizazi 2021)	Hashim et. al. (2021)	2021	58
13	Rat Swarm Optimizer	Mathematical and Engineering Optimization problems (Dhiman et.al. 2021), Image Classification (Vasantharaj et al. 2021), Deep Neural Network (Ghadge and Prakash 2021)	Dhiman et.al. (2021)	2021	49
14	Hunger Games Search Optimizer	Mathematical and Engineering Optimization problems (Nguyen et al. 2021), (Onay and Aydemı̇r 2022), (Chakraborty et al. 2022), Detecting Attacks (IoT Network) (Toğaçar 2021), Feature Selection (Devi et al. 2022)Abd Elaziz, Image Segmentation (Abd Elaziz] et al. 2021d), PEM Fuel Cell Parameter Identification (Fahim et al. 2021)	Nguyen et al. (2021)	2021	3
15	Horse Herd Optimization Algorithm	Mathematical and Engineering Optimization problems (MiarNaeimi et al. 2021) , Scheduling of Nanogrids (Basu and Basu 2021), Feature Selection (Awadallah et al. 2021)	MiarNaeimi et al. (2021)	2021	10
16	Preaching-inspired Optimization Algorithm	Mathematical and Engineering Optimization problems (Wei et. al. 2021), MLT based image Segmentation (Wei et. al. 2021), Wu et al.(2021a)	Wei et. al. (2021)	2021	2
17	Battle Royale Optimization Algorithm	Mathematical and Engineering Optimization problems (Farshi 2021), Inverse Kinematics Problem (Farshi 2021)Agahian,, Artificial Neural Network (Agahian and Akan 2021)	Farshi (2021)	2021	14
18	Child Drawing Development Optimization	Mathematical and Engineering Optimization problems (Abdulhameed and Rashid 2021)	Abdulhameed and Rashid (2021)	2021	0
19	Cat and Mouse Based Optimizer	Mathematical and Engineering Optimization problems (Dehghani et al. 2021)	Dehghani et. al. (2021)	2021	0
20	Tuna Swarm Optimization	Mathematical and Engineering Optimization problems (Xie et al. 2021a)	Xie et. al. (2021a)	2021	0
21	Past Present Future: a new Human-based Algorithm	Mathematical and Engineering Optimization problems (Naik and Satapathy 2021)	Naik and Satapathy (2021)	2021	0
22	Aptenodytes Forsteri Optimization Algorithm	Mathematical and Engineering Optimization problems (Yang et al. 2021a)	Yang et. al. (2021a)	2021	0
23	Bonobo Optimizer	Mathematical and Engineering Optimization problems (Das and Pratihar 2021)	Das et. al. (2021)	2021	1
24	Reptile Search Algorithm	Mathematical and Engineering Optimization problems (Abualigah et. al. 2021c), Neuro-Fuzzy Inference System (Shinawi et al. 2021)	Abualigah et. al. (2021c)	2021	0
25	Chimp Optimization Algorithm	Mathematical and Engineering Optimization problems (Khishe and Mosavi 2020a; Kaur et al. 2021; Dhiman 2021) Digital Filters (Kaur et al. 2021), Neural Network (Khishe and Mosavi 2020a), Hu et al. 2021), MLT based Image Segmentation (Houssein et al. 2021d), Feature Selection (Wu et al. 2021b, Piri et al. 2021), Image Classification (Annalakshmi and Murugan 2021), Electrical Distribution Network (Fathy et al. 2021), Power System Stabilizer (Aribowo et al. 2021b), Solar Photovoltaic Systems (Nagadurga et al. 2021), Solar Dish Sterling Power plant (Zayed et al. 2021a), Tunnel FET architecture (Bhattacharya et al. 2021	Khishe and Mosavi (2020a)	2020	87
26	Slime Mould Algorithm	Mathematical and Engineering Optimization problems (Li et al. 2020b), Yin et al. 2022), Artificial Neural Network (Zubaidi et al. 2020), Solar Photovoltaic Systems (Kumar et al. 2020) (Mostafa et al. 2020 Yousri et al. 2021;El-Fergany 2021a), Power System Stabilizer (Ekinci et al. 2020), Servo Systems (Precup et al. 2021), MLT based Image Segmentation (Liu et al. 2021a; Naik et al. 2020; Lin et al. 2021; Zhao et al. 2021b), Image Classification (Wazery et al. 2021), Feature Selection (Abdel-Basset et al. 2021b), Numerical Optimization (Sun et al. 2021b), Urban Water Resources (Yu et al. 2021), PEM Fuel Cell Parameter Identification (Gupta et al. 2021)	Li et al. (2020b)	2020	363
27	Gradient-based Optimizer	Mathematical and Engineering Optimization problems (Ahmadianfar et al. 2021; Photovoltaic Systems (Ahmadianfar et al. 2021; Zhou et al. 2021; Edee 2021), Feature Selection (Jiang et al. 2021b)	Ahmadianfar et al. (2020)	2020	85
28	Marine Predators Algorithm	Mathematical and Engineering Optimization problems (Faramarz et al. (2020a), Image Classification (Sahlol et al. 2020a), Photovoltaic Systems (Yousri et al. 2020a), Fog Computing (IoT) (Abdel-Basset et al. 2020b) Ebeed, Wind-Solar Generation System (Ebeed et al. 2020)	Faramarz et al. (2020a)	2020	228
29	Mayfly Optimization Algorithm	Mathematical and Engineering Optimization problems (Zervoudakis and Tsafarakis 2020), PEM Fuel Cell Parameter Identification (Shaheen et al. 2021), Deep Learning (Rajakumar et al. 2021)	Zervoudakis and Tsafarakis (2020)	2020	63
30	Manta Ray Foraging Optimization	Mathematical and Engineering Optimization problems (Zhao et al. 2020a), Solar Cell based Systems (Fathy et al. 2020), Photovoltaic Systems (Houssein et al. 2021e), ECG Classification (Houssein et al. 2021f), MLT based Image Segmentation (Houssein et al. 2021g, Jena et al. 2021), Feature Selection Ghosh et al. 2021), Karuppusamy 2020), PEM Fuel Cell Parameter Identification (Xu et al. 2020), Waste Water Treatment plant (Elmaadawy et al. 2021), Thermo Electric Generation Systems (Aly and Rezk 2021), Deep Neural Network (Nguyen et al. 2021), Power Flow Problem (Kahraman et al. 2021), Photovoltaic / Diesel Generator / Pumped Water Reservoir Power System (Liu et al. 2021b), Electricity Theft Detection (Ayub et al. 2020), Inverted Pendulum System bin Abdul Razak et al. 2020), Distribution Network (Abdel-Mawgoud et al. 2021	Zhao et al. (2020a)	2020	135
31	Billiards-inspired Optimization Algorithm	Mathematical and Engineering Optimization problems (Kaveh et al. 2020a), Grid-Tied Wind Power Plants (Soliman et al. 2021), Construction Management (Rastegar Moghaddam et al. 2021, Ground-Water Systems (Gerey et al. 2021)	Kaveh et al. (2020a)	2020	21
32	Equilibrium Optimizer	Mathematical and Engineering Optimization problems (Faramarzi et al. 2020b) (Gupta et al. 2020), MLT based Image Segmentation (Abdel-Basset et al. 2021a, Wunnava et al. 2020), Feature Selection (Gao et al. 2020, Too and Mirjalili 2021), Photovoltaic Systems (Abdel-Basset et al. 2020c), Fuel Cell Dynamic Model (Seleem et al. 2021; Menesy et al. 2020), Machine Learning (Kardani et al. 2021), Solar Dish Collector (Zayed et al. 2021b), Thermoelectric Power Generation Systems (Mansoor et al. 2021), Automatic Voltage Regulator System ((Micev et al. 2021)	Faramarzi et al. (2020b)	2020	327
33	Coronavirus Optimization Algorithm	Deep Learning and Electricity Load Time Series Forecasting (Martínez-Álvarez et al. (2020), Combinatorial Problems (El Majdoubi et al. 2021), PID Controller (Shamseldin 2021), Container Retrieval Problem (Silva Firmino and Times 2022), Image Classification (Nassif et al. 2021)	Martínez-Álvarez et al. (2020)	2020	48
34	Sparrow Search Algorithm	Mathematical and Engineering Optimization problems (Xue and Shen (2020), Photovoltaic Systems (Yuan et al. 2021), Proton Exchange Membrane Fuel Cell (PEMFC) Stacks (Zhu and Yousefi 2021), Robotic Path Planning (Zhang et al. 2021b), UAV 3D Route Planning (Liu et al. 2021c), Deep learning (Liu et al. 2021c), Linear Antenna Array (Liang et al. 2021), Time-Series Production Forecasting (Li et al. 2022), Pulmonary Nodule Detection (Zhang et al. 2021c)	Xue and Shen (2020)	2020	103
35	Sandpiper Optimization Algorithm	Mathematical and Engineering Optimization problems (Kaur et. al. (2020), Software Engineering (Amandeep et al. 2020), Deep learning (Rajalakshmi and Annapurani Panaiyappan 2021), (Metan et al. 2021).	Kaur et. al. (2020)	2020	10
36	Black Widow Optimization Algorithm	Mathematical and Engineering Optimization problems (Hayyolalam and Kazem 2020)), MLT based Image Segmentation (Houssein et al. 2021h; ) (Al-Rahlawee and Rahebi 2021), Feature Selection (Hu et al. 2022), Internet of Things (IoT) (Ravikumar and Kavitha 2021), Wireless Sensor Networks(WSN) (Sheriba and Rajesh 2021), ), Human Object Detection (Mukilan and Semunigus 2021), ), Suspended Sediment Load Prediction (Panahi et al. 2021), Location-Inventory Routing Problem (Rahbari et al. 2021), PID Controller (Munagala and Jatoth 2021)	Hayyolalam and Kazem (2020)	2020	126
37	Forensic-Based Investigation Optimization	Resource-Constrained Scheduling Problem (Chou and Nguyen 2020), Structural Design Problems Chou and Nguyen 2020), Mathematical and Engineering Optimization problems (Chou and Nguyen 2020, ; Kuyu and Vatansever 2021), Parameter optimization of support vector machine (Cao et al. 2021)	Chou and Nguyen (2020)	2020	17
38	Bald Eagle Search	Mathematical and Engineering Optimization problems (Alsattar et. al. 2020), Photovoltaic Systems ((Ramadan et al. 2021, Nicaire et al. 2021), Parameter optimization of support vector machine (Angayarkanni et al. 2021), Resource Management in Cloud Computing (Singh et al. 2019), Parameter optimization of Neural Network (Xie et al. 2021b), Internet of Things (IoT) (Kapileswar and Phani Kumar 2022)	Alsattar et. al. (2020)	2020	47
39	Life Choice-Based Optimization	Mathematical and Engineering Optimization problems (Khatri et al. 2020), Visual Sentiment Analysis Afzal 2021)	Khatri et al. (2020)	2020	11
40	Social Ski-Driver Optimization	Mathematical and Engineering Optimization problems (Tharwat and Gabel 2020), Feature Selection (Chatterjee et al. 2020, Tharwat et al. 2020; Gunasekhar and Vijayalakshmi 2020), Recurrent Fuzzy Neural Network (Sreenivas et al. 2020), Autonomous Vehicle (Elsisi 2020)	Tharwat and Gabel (2020)	2020	37
41	Gaining Sharing Knowledge-based Algorithm	Mathematical and Engineering Optimization problems (Mohamed et al. 2020, ; Mohamed et al. 2021), Feature Selection (Agrawal et al. 2021b, ; Agrawal et al. 2021c), MLT based Image Segmentation (Ortega-Sánchez et al. 2021), Knapsack Problem (Agrawal et al. 2021b), Photovoltaic Systems (Sallam et al. 2021),	Mohamed et al. (2020)	2020	65
42	Artificial Ecosystem-based Optimization	Mathematical and Engineering Optimization problems (Zhao et. al. 2020b; Barshandeh et al. 2020), Identification of Hydro-geological Parameters (Zhao et. al. 2020b), feature selection (Sahlol et al. 2020b), Fuel Cell Dynamic Model (Rizk-Allah and El-Fergany 2021a), Photovoltaic Systems (Yousri et al. 2020b), PID Controller (Ćalasan et al. 2020)), Power Dispatch Problem (Mouassa et al. 2021)	Zhao et. al. (2020b)	2020	71
43	Giza Pyramids Construction based Optimizer	Mathematical and Engineering Optimization problems (Harifi et al. 2020a)), Image Clustering (Harifi et al. 2020a)	Harifi et al. (2020a)	2020	15
44	Heap-based Optimizer	Mathematical and Engineering Optimization problems (Askari et. al. (2020a), Industrial Solar Generation Systems (Rizk-Allah and El-Fergany 2021b), Fuel Cell Parameter Identification (Abdel-Basset et al. 2021c), Reactive Power Dispatch (Elsayed et al. 2021), DG allocation (Shaheen et al. 2022), Heat and Power Economic Dispatch Problem (Ginidi et al. 2021b)	Askari et. al. (2020a)	2020	51
45	Color Harmony Algorithm	Mathematical and Engineering Optimization problems (Zaeimi and Ghoddosian (2020), Interior Design (Shen et al. 2000) , 1996)	Zaeimi and Ghoddosian (2020)	2020	10
46	Stochastic Paint Optimizer	Mathematical and Engineering Optimization (Kaveh et al. 2020b)	Kaveh et. al. (2020b)	2020	8
47	Political Optimizer	Mathematical and Engineering Optimization problems (Askari et.al. (2020b), Feature Selection (Manita and Korbaa 2020), Photovoltaic Systems (Premkumar et al. 2020), Antenna Arrays(Durmus and Kurban 2021), Fuel Cell Parameter Identification (Diab et al. 2020), Energy-Management System for Microgrids (Suresh et al. 2021), Industrial Optimization problems (Yıldız et al. 2021))	Askari et.al. (2020b)	2020	59
48	Water Strider Algorithm	Mathematical and Engineering Optimization problems (Kaveh and Eslamlou 2020, ; (Kaveh et al. 2020c), Structural Health Monitoring (Kaveh and Eslamlou 2020), Damage Detection (Ali et al. 2021)	Kaveh and Eslamlou (2020)	2020	42
49	Newton Metaheuristic Algorithm	Mathematical and Engineering Optimization problems (Gholizadeh et al. 2020), Optimal placement and sizing of PV source (Montoya et al. 2021), Sizing optimization of Truss Structures (Danesh and Jalilkhani 2020)	Gholizadeh et al. (2020)	2020	22
50	Harris Hawks Optimization	Mathematical and Engineering Optimization problems Heidari et al. 2019), Photovoltaic Systems (Chen et al. 2020), Design and Manufacturing Problem (Yıldız et al. 2019), Artificial Neural Network (Moayedi et al. 2021), Feature Selection (Turabieh et al. 2021, Hussain et al. 2021), MLT based Image Segmentation (Rodríguez-Esparza et al. 2020)	Heidari et al. (2019)	2019	1019
51	Sailfish Optimizer	Mathematical and Engineering Optimization problems (Shadravan et al. 2019), Feature Selection (Ghosh et al. 2020), Wireless Sensor Networks (WSN) (Dao et al. 2020), Optimal STATCOM Allocation (Samal and Roshan 2020), Fibre Optic Communication (Venu et al. 2021)	Shadravan et al. (2019)	2019	129
52	Pathfinder Algorithm	Mathematical and Engineering Optimization problems (Yapici and Cetinkaya 2019), Fuel Cell Parameter Identification (Gouda et al. 2021), Optimal Reactive Power Dispatch problems ((Yapici 2021)	Yapici and Cetinkaya (2019)	2019	95
53	Seagull Optimization Algorithm	Mathematical and Engineering Optimization problems (Dhiman and Kumar 2019), PEM Fuel Cell Parameter Identification (Cao et al. 2019), Feature Selection (Jia et al. 2019f) (Ewees et al. 2022), Job Scheduling in Cloud (Garg and Dhiman 2021), Chemical Descriptors Classification (Houssein et al. 2021i)	Dhiman and Kumar (2019)	2019	208
54	Booster Algorithm	Mathematical and Engineering Optimization problems (Pakzad-Moghaddam et al. 2019)	Pakzad-Moghaddam et al. (2019)	2019	11
55	Henry Gas Solubility Optimization	Mathematical and Engineering Optimization problems (Hashim et al. 2019), Feature Selection (Neggaz et al. 2020), Task Scheduling in Cloud Computing (Abd Elaziz and Attiya 2021), Prediction of Soil Shear Strength (Ding et al. 2021)	Hashim et al. (2019)	2019	203
56	Sea Lion Optimization	Mathematical and Engineering Optimization problems (Masadeh et al. 2019), Underwater Acoustic Sensor Network (Kumar Gola et al. 2021), Cloud Computing (Masadeh et al. 2019), Deep Learning (Kumaraswamy and Poonacha 2021), Wireless Sensor Networks (WSN) (George and Mary 2021)	Masadeh et al. (2019)	2019	52
57	Naked Mole-Rat Algorithm	Mathematical and Engineering Optimization problems (Salgotra and Singh 2019, ; Salgotra et al. 2021), Wireless Sensor Networks (WSN) (Singh et al. 2021), Feature Selection (Guha et al. 2020), Antenna array (Singh et al. 2022), , Electromagnetic Design Problems (Taherdangkoo 2021)	Salgotra and Singh (2019)	2019	49
58	Nuclear Reaction Optimization	Mathematical and Engineering Optimization problems (Wei et. al. 2019)	Wei et. al. (2019)	2019	14
59	Atom Search Optimization	Mathematical and Engineering Optimization problems (Zhao et. al. 2019), Feature Selection (Too and Abdullah 2020), Antenna array (Almagboul et al. 2019), PID Controller (Zhao et al. 2021d), Fuel Cell Parameter Identification (Agwa et al. 2019)	Zhao et. al. (2019)	2019	148
60	Search and Rescue Optimization	Mathematical and Engineering Optimization problems (Shabani et. al. 2019), Feature Selection and classification (Houssein et al. 2022)	Shabani et. al. (2019)	2019	30
61	Wildebeest Herd Optimization	Mathematical and Engineering Optimization problems (Amali and Dinakaran 2019), Predicting optimal hydropower generation (Ren et al. 2021), Deep Learning (Zhou and Arandian 2021)	Amali and Dinakaran (2019)	2019	6
62	Butterfly Optimization Algorithm	Mathematical and Engineering Optimization problems (Arora and Singh 2019), Automobile Suspension Design (Yıldız et al. 2020), Feature Selection (Long et al. 2021), Data Classification (Jalali et al. 2019), Breast Cancer Prediction (Thawkar et al. 2021)	Arora and Singh ( 2019)	2019	367
63	Blue Monkey Optimization	Mathematical and Engineering Optimization problemsMahmood and Al-Khateeb (2019), Encrypting Digital Watermark (Abdulhammed 2021)	Mahmood and Al-Khateeb (2019)	2019	10
64	Emperor Penguins Colony Optimizer	Mathematical and Engineering Optimization problems (Harifi et. al. 2019), Neuro-Fuzzy Systems (Harifi et al. 2020b), Inventory Control Systems (Harifi et al. 2021)	Harifi et. al. (2019)	2019	50
65	Future Search Algorithm	Mathematical and Engineering optimization problems (Elsisi 2019)	Elsisi (2019)	2019	15

Number of NIOA in 2021 is 24, 2020 is 25, and 2019 is 16

Citation as per Google Scholar (Dated: 06.10.2021)

Fig. 1.

a Year wise published papers over NIOA based MLT; b General Flowchart of the NIOA

On the other hand, no matter how rapid and massive is the evolution of Nature Inspired algorithm, NIOA is the scorching research area that has not just attracted several researchers but proved to be the most rapid growing field in research. Therefore, the introduction and designing of an integrated framework in terms of algorithm structure is advantageous for implementation. Over the last few years, a large body of literature has offered priceless insight into how to comprehend the applied tactics and what the NIOA's general characteristics are (Dhal et al. 2019a, 2020a, b, 2021a). Based on the same, the common procedure of the NIOA is presented using flowchart depicted in Fig. 1b.

Most of NIOA follows the common flow comprising of four major steps as described in Fig. 1b. In Step 1, the population and its related initial parameters, representing possible solutions to the given optimization problem is initialized. Typically, random methods are applied to generate the initial parameter of the population ensuring that it conceals the solution space as much as possible. Based on the specific requirements of the experts and their past experience, the size of population (should be perhaps large) is selected. After initialization, in subsequent Step 2, the calculation in terms of the fitness value of an individual solution of population is performed and the concrete iteration loop starts, where every loop signifies a generation (Number of iterations). The fitness function which is most commonly considered as a unique pointer to echo the performance of each solution is premeditated by the help of the target function either comprising of the maximum value or minimum value. Commonly, each population has its own local optimal solution, and on the other hand, global optimum is owned by its complete population. The fitness values of the population are further computed in each of the iteration. Given the termination condition, if the global best solution satisfies the same, the output is generated (as shown in Step 4) else, Step 3 is instigated, that generally anticipates to accomplish the significant operations that is basically carried out for the purpose of information exchange amongst entire population to evolve excellent individuals. Further, updating in terms of population is carried thereby initiating the workflow to supplementary navigate towards Step 2 to accomplish the subsequent iteration. The generation counter is further amplified and till the stopping criteria is satisfied, the iteration undergoes. Stopping condition is a parameter that specifies when an algorithm should halt. For various NIOA, determining the stopping condition is critical. Number of Iterations, commonly known as NIs and number of Function Evaluations frequently known as FEs are two of the most prevalent types of stopping criteria. According to recent surveys, researchers prefer FEs to NIs (Dhal et al. 2020b).

Major challenges and problems with NIOA

Though there are immense number of researches and breakthroughs in regard to NIOA, it still has quite a few noteworthy challenges which can be pointed out by the following set of questions, especially from theoretical perspectives (Yang 2020):

1. Question on Mathematical Framework: How can a uniform mathematical framework be created so as to learn much about their convergence, convergence rate, consistency, and reliability? In reality, the core progressions of how such algorithms function, why it functions and under what circumstances are yet unknown and still mysterious.

2. Question on setting of NIOA’s parameters optimally: How to set the parameters of the NIOA to achieve efficient outcome for a set of problems? How can these parameters be meticulously changed or controlled to improve an algorithm's performance?

3. Question on importance of Benchmarking and NFL Theorem: The usage of benchmark functions to examine the performance of the new NIOA in contrast to other existing algorithms is of utmost importance. On the other hand, the NFL theorem asserts that if algorithm A outperforms algorithm B in achieving the best optimal values of certain objective functions, then B will outperform A on other functions. However, from experience the interpretation can be made that some algorithms are superior to others. So, how to reconcile these seeming inconsistency? Therefore, the questions are: What are different varieties of benchmarking that turns out to beneficial? Free lunches do exist or not? If so, what could be the available circumstances?

4. Question on Performance Measures: The present literature primarily focuses on accuracy, computing effort, stability, and success rates as the performance indicators. In general, Friedman test and the Wilcoxon’s rank sum test which are the widely accepted non-parametric tests can be used to compare and analyze efficiency among NIOA (Dhal et al. 2020b). However, it is unclear whether the aforementioned performance indicators are genuinely fair in comparison. Therefore, the questions are: What performance metrics can be considered in order to compare all the existing algorithms fairly? Is there any kind of possibilities to formalize a sole framework that allows entirely available algorithms to be related impartially and objectively?

5. Questions on Algorithm Scalability: The most crucial indicator of an algorithm's efficacy from the standpoint of application is how well it can tackle a wide range of issues. Therefore, the question is: How can algorithms that work effectively for small-scale problems is scaled up to efficiently handle truly large-scale, real-world challenges?

Apart from the above-mentioned issues, other ongoing difficulties with NIOA includes finding the best combination of exploitation and exploration, dealing successfully with nonlinear restraints, and applying these algorithms (NIOA) to machine learning techniques especially deep learning.

Recent trends in multi-level thresholding using nature-inspired optimization algorithms

It is reported in literature that when two or more segmentation approaches work together, they can yield better results than if they worked alone (Dhal et al. 2020a; Khan 2013). Multi-thresholding is computationally expensive combinatorial task that entail large and complex search spaces. The evaluation of all feasible outcomes leads to a time-consuming search process. As a result, researchers incorporated NIOA, a powerful search tool, in this domain to make it less complicated and fast. This section gives a brief mathematical formulation of MLT problem; general algorithm of the NIOA based MLT, literature survey on MLT since 2019, and the objectives functions which play crucial role for proper image segmentation.

Introduction to multi-level thresholding

The central concept behind multi-level thresholding is to identify threshold values which allow the segmented images to fulfill the required criteria. This would be accomplished by optimizing specific objective function/s, with the threshold values as input parameters (Dhal et al. 2020a).

Assume that the image f comprising of L gray levels needs to be segmented into p partitions $\left(C_1,,,C_2,,,\cdots ,,,C_i,,,\cdots ,C_p\right)$ using set of (p − 1) threshold values $TH=\left(t_1,,,t_2,,,\cdots ,,,t_i,,,.,.,.,,,t_{p-1}\right)$, where $t_1<t_2<,\cdots .,{<t}_{p-1}$. For example, L = 256 for an 8-bit image and the grey levels are between 0 and 255 (Dhal et al. 2020a). Hence, a pixel containing certain gray level $g$ belongs to class $C_i$ if $t_{i-1}<g<t_i$ for $i=1,2,\cdots ,p$.The technique of determining the set of optimal thresholds ${\mathit{TH}}^{\mathit{opt}}$ that optimizes the objective function $F\left(T,H\right)$ is referred to as single objective thresholding. The mathematical expression is as follows:

$${\mathit{TH}}^{\mathit{opt}}=\underset{0\le \mathit{TH}\le L-1}{\mathrm{argmax}/\min }\left\{F,\left(T,H\right)\right\}.$$ 1

For multi objective MLT, $F\left(T,H\right)=\left(F_1,\left(T,H\right),,,F_2,\left(T,H\right),,,\cdots ,,,F_j,\left(T,H\right),,,\cdots ,,,F_n,\left(T,H\right)\right)$, where $n>1$.

Objective functions

In the theme or context of Multi-Level Thresholding-based image segmentation, objective functions are crucial. Few widely employed objective functions that have been presented in the existing literature. Objective functions in Table 2 categorized into some classes such as Variance based like Otsu, 1-Dimensional histogram-based entropies like Kapur’s entropy, 2-Dimensional histogram based objective functions, 3-dimensional objective functions, hybrid objective functions like Fuzzy-Tsalli’s entropy. Finding novel objective functions or the optimum objective functions for various image kinds is likewise a difficult task. Recently, some entropy based objective functions have been devised for MLT based image segmentation like t-entropy, and Masi entropy. According to the research, the segmentation efficacy of objective functions is strongly influenced by the issue domain, i.e., image type. Figure 2 depicts the number of papers Surveyed using different types of objective functions in the last three years recorded in Table 3.

Table 2.

Different types of objective functions

SL	Type	Objective function
1	1-Dimensional objective functions	Otsu (Ray et al. 2021), Kapur’s entropy (Ray et al. 2021), Tsallis entropy (Ray et al. 2021), Cross entropy (Ray et al. 2021), Rényi entropy (Oliva et al. 2020), Fuzzy entropy (Dhal et al. 2019b), Type–II Fuzzy Entropy (Mahajan et al. 2021), Exponential Cross Entropy (Zhang et al. 2011), Kaniadakis Entropy (Lei and Fan 2021), Masi Entropy (Bhandari and Rahul 2019), t-Entropy (Chakraborty et al. 2021), Shannon entropy (Rajinikanth et al. 2021; Gong et al. 2020)
2	Hybrid and modified 1-dimensional objective functions	Fuzzy-Tsallis entropy (Sarkar et al. 2013), Fuzzy Masi Entropy (He et al. 2021), Tsallis–Havrda–Charv´at entropy (Borjigin and Sahoo 2019)
3	2-Dimensional objective funtions	2-Dimensional Kapur’s Entropy (Lei and Fan 2021), 2-dimensional Kullback–Leibler (K–L) (Zhao et al. 2016), 2-dimensional Otsu method (Bhandari and Kumar 2019), 2-dimensional Tsallis entropy (Sarkar and Das 2013), 2-dimensional Renyi entropy (Borjigin and Sahoo 2019), 2-dimensional Cross entropy (Akay 2013), Diagonal Class Entropy (DCE) (Xing and Jia 2019), 2-dimensional Masi entropy (Lei and Fan 2021; Naik et al. 2021), 2-dimensional Fuzzy entropy (Wu et al. 2004), Non-local 2-dimensional histogram-based entropy (Vig et al. 2019), 2-dimensionalKaniadakis entropy (Lei and Fan 2021)
4	3-Dimensional objective funtions	3-Dimensional Otsu (Bhandari and Kumar 2019), 3-Dimensional Tsallis (Jena et al. 2021)
5	Other objective funtions	Gaussian Mixture Model based objective function (Cuevas et al. 2020), Wavelet entropy (Öztürk et al. 2020)
6	Energy curve based objective functions	Energy-Otsu (Bhandari and Kumar 2019), Energy-Masi (Bhandari and Rahul 2019), Energy-Cross (Kandhway and Bhandari 2019b), and Energy-Tsallis (Liang et al. 2019)

Fig. 2.

Number of papers surveyed using different types of objective functions

Table 3.

Literature reports on NIOA based multi-level thresholding

SL	Proposed method	Objective function	Paper details	Image type	Comparison	Quality parameters considered	Observations
1	Random Spare Strategy & Chaotic Intensification Strategy based on ACOR (RCACO)	2D Kapur’s entropy	Zhao et al. (2021a)	Standard Color Images	Proposed method is compared with BA, ACOR, CS via Lévy flights, WOA, PSO, BLPSO, CGPSO, IWOA and IGWO	PSNR, SSIM and FSIM	Proposed RCACO attained quicker convergence speed along with accuracy to step out of Local Optima (LO). The obtained result proved that image segmentation quality is highly improved using the same
2	Diffusion Association Slime Mould Algorithm (DASMA)	Renyi’s entropy	Zhao et al. (2021b)	Computed Tomography (CT) Images: Medical Images	Proposed method is compared with IGWO, IWOA, DE SSA, SMA, CS via Lévy flights and CGPSO	PSNR, SSIM and FSIM	Proposed DASMA at different threshold levels outperforms other algorithm thereby enhancing the convergence capabilities and segmentation performance
3	CrissCross Ant Colony Optimization (CCACO)	2D Kapur’s entropy	Zhao et al. (2021c)	Standard Color Images	Proposed method is compared with DE, WOA, GWO, PSO, SCA, ACOR, HHO, m_SCA, IGWO, CGPSO, OBLGWO, ALCPSO, BMWOA, ACWOA, SCADE and AMFO	PSNR, SSIM and FSIM	Proposed CCACO converge faster and accurately than ACOR thereby possess strong ability to avoid falling into LO. CCACO is considered very effective in terms of optimizing various benchmark functions. However, on the other hand computational complexity inexorably upsurges further, mounting the CPU computational time
4	An MLS (Multi-Learning System) with Bat Algorithm for pre-processing, Shannon Entropy for multi-thresholding, Gaussian Filter for Image Enhancement, GLCM for Feature Extraction and SVM with Linear Kernel as Classifier	Shannon Entropy	Rajinikanth et al. (2021)	Retinal Images: Medical Images	The proposed MLS system uses SVM classifier that is compared with other classifiers: NB, DT, KNN and RF	Accuracy, FNR, FPR, Precision, NPV Sensitivity, F1-Score and Specificity	Experimental outcome of this research confirms that, SVM classifier offers superior accuracy (> 93% compared to other classifiers considered in this study
5	Infrared Pedestrian Segmentation Algorithm	2D Renyi’s, 2D Kaniadakis entropy	Lei and Fan (2021)	Infrared Images	Proposed method is compared with 2D-Otsu, FCM, 2D-Masi, FLICM and 2D Kapur Entropy	ME, PSNR, Jaccard, RAE and F-measure	The proposed algorithm when applied to on the images with noise and intricate background produces better results when compared to1D Kaniadak is and other five state-of-the-arts image segmentation methods
6	Moth-Flame Optimization (MFO) Algorithm	Kapur’s entropy	Ji and He (2021)	Standard Gray Images	Proposed method is compared with BA, PSO, FPA, MSA and WWO	Fitness value, Execution time, PSNR and SSIM	The proposed MFO is better in terms of convergence speed, stability, accuracy and segmentation effect.MFO could be further used to settle complicated high-threshold or color image by using different other objective functions
7	Gradient Based Method (GM) tailored for discrete objection function	Otsu’s thresholding and Kapur entropy	Shang et al. (2021)	Standard Gray Images	Proposed method is compared with FA, PSO, ABC, BA and GWO	PSNR, FSIM, IRU and CPU Time	The proposed GM is straightforward and simple to search for optimal threshold. Also, GM may be employed to search for optimal solution in more objective functions
8	Type-2 Neutrosophic-Entropy (T2NSEIF)	Kapur Entropy	Singh (2021)	MRI: Medical Images	Proposed method is compared with FCM, MFCM, FKMCA, KIFECM and NEATSA	JSC, CC, UM, Space and CPU time	The proposed T2NSEIF is employed to perform MRI’s segmentation using multiple thresholds with respect to locations of max T2NSE values. Further, other fields of Image Processing could be explored using the proposed method
9	Neighborhood Fitness Distance Ratio Teaching Learning based Optimization (NFDR-TLBO)	Kapur Entropy	Jiang et al. (2021a)	Standard Gray and Color Images	Proposed method is compared with TLBO, FDRPSO, FDR-TLBO, BBPSO, jDE and SaDE	PSNR, SSIM and FSIM	The proposed NFDR-TLBO algorithm shows exceptional result in most of the cases by suggestively improving TLBO. Though, more research and experiments need to be carried out to determine suitable objective functions to finally regulate optimal threshold values
10	Modified Whale Optimization Algorithm (MWOA)	Otsu’s thresholding and Kapur entropy	Anitha et al. (2021)	Standard Color Images	Proposed method is compared with GA, PSO, ABC and CS	PSNR, SSIM, FSIM and CPU time	The proposed MWOA offers improved performance as compare to other algorithms consuming a reduced amount of computational time
11	Volleyball Premier League using Whale Optimization Algorithm (VPLWOA)	Otsu’s thresholding	Abd Elaziz et al. (2021a)	Standard Gray Images	Proposed method is compared with SSO, FFA, WOA, VPL and SCA	PSNR, SSIM, FSIM and CPU time	The sports inspiration based on basic VPL is applied for the very first time in the field of multilevel thresholding. Experimental results confirm that the proposed algorithm outdoes other existing meta-heuristic algorithms
12	Manta Ray Foraging Optimization based on the Opposition-Based Learning (MRFO-OBL)	Otsu’s thresholding	Houssein et al. (2021b)	Computed Tomography (CT) Images: Medical Images	Proposed method is compared with SCA, MFO, EO, WOA, SSO and MRFO	PSNR and SSIM	The proposed MRFO-OBL basically finds the finest threshold values to further maximize Otsu’s function. However, in future hybridization mechanism can be tried and implemented by amalgamating proposed method with other optimization techniques
13	Bat Algorithm (BA)	Otsu thresholding and Kapur’s entropy	Yang et al. (2021b)	Gray scale images	Not Compared	PSNR and SSIM	The experiment results show that Otsu based method is more suitable for multi-level threshold image segmentation
14	A new entropy measure, called the t-entropy	t-entropy	Chakraborty et al. (2021)	Gray Scale Images	Proposed method is compared with k-means, W-k-means, MW-k-means, EW-k-means (Shannon)	NMI and ARI	The result shows that the proposed measure satisfies the major axiomatic properties of entropy. The application of t-entropy in the context of Power k-means clustering and sparse signal recovery is also some possible avenues for future research
15	Eagle Strategy—Whale Optimization Algorithm (ES-WOA)	Kapur’s, Fuzzy, Tsallis’, Otsu’s thresholding and Cross entropy	Ray et al. (2021)	Color Hematology Images: Medical Images	Proposed method is compared with ES-DE, ES-FA, ES-PSO and WOA	PSNR, FSIM and QILV	The proposed ES-WOA (Tsallis) acquires the best threshold values generating quicker execution times for all the images considered to be tested. However, other types of medical images namely histology, MRI, CT, Mammogram could be used with the proposed method
16	Multilevel Thresholding Based on Fuzzy-Masi Entropy	Fuzzy-Masi entropy	He et al. (2021)	Standard Color Images	Proposed method is compared with Masi and Tsalli’s entropy	PSNR, FSIM and SSIM	The results illustrate that fuzzy Masi entropy displays advanced quality and performance than other objective functions considered under the banner
17	Fuzzy Entropy Type II (FE-TII) combined with Marine Predators Algorithm (MPA) (FE-TII-MPA)	Type-II Fuzzy Entropy	Mahajan et al. (2021)	Standard Gray Scale Images	Proposed method is compared with PFA, PPA, DE, PSO and HPFPPA-D	PSNR, SSIM and MSE	Results achieved by FE-TII-MPA are comparatively better than other algorithms taken into consideration for the purpose of comparison
18	Leader Harris Hawks Optimization (LHHO)	Masi entropy	Naik et al. (2021)	Standard Gray Scale Images	Proposed method is compared with HHO, CS, PSO, FA, WDO, STOA and DE	PSNR, FSIM and SSIM	The proposed LHHO rapidly attains the optimum threshold values in regard to the iteration count
19	Attacking Manta Ray Foraging Optimization (AMRFO)	Maximum 3D Tsallis entropy	Jena et al. (2021)	MRI Images: Medical Images	Proposed method is compared with MRFO, EO, HHO, SFO, GWO, PSO and DE	PSNR, FSIM and SSIM	The proposed AMRFO produces better output in terms of quality as the 3D creation of histogram holds extra information of edge
20	Improved Particle Swarm Optimization (PSO)	Maximum Shannon Entropy	Gong et al. (2020)	Infrared Images	Proposed method is compared with standard PSO	SSIM and running time indicators	The experimental outcome projects that the improved PSO based total entropy image segmentation is difficult to descent towards local optimum, has greater efficiency and is reliable
21	Firefly Algorithm (FA) with levy flight and local search method	Kapur and Tsallis entropy	Sharma et al. (2020)	Standard Gray Scale Images	Kapur’s entropy and Tsallis entropy methods using improved FA algorithm are compared	PSNR and SSIM	Tsallis entropy is robust method then other method with a great standard deviation value. The proposed method may be in future used efficiently for other variants of noisy image
22	The proposed improved Teaching–Learning-based Optimization Algorithm (DI-TLBO)	Otsu’s thresholding and Kapur’s entropy	Wu et al. (2020)	Standard Gray Scale Images and X-Ray Images	Proposed method is compared with variants of DI-TLBO, TLBO, LETLBO, ITLBO, BSA and GWO	Mean fitness, standard deviation, CPU time, and MSSIM	The proposed DI-TLBO accomplishes healthier output when compared with other algorithms in terms of solution precision, and stability making the method promising in the respective field
23	The proposed Improved Lion Swarm Optimization (ILSO) algorithm; For global search and revise the updating function of LSO algorithm to improve the global and local search performance, Artificial Bee Colony optimization (ABC) is employed	Maximum Interclass Variance (Otsu’s thresholding)	Li and Jiang (2020)	Standard Gray Scale Images	Proposed method is compared with PSO, ABC and LSO	PSNR	The proposed ILSO algorithm has better performance of global and local in terms of searching (Both global and local) than the original LSO. Compared with PSO, ABC and LSO algorithm, ILSO has better convergence speed and optimization accuracy. Although the calculation speed is improved compared with the original LSO algorithm, there is still a certain gap with PSO and ABC algorithm
24	Locust Search (LS) with JNew as objective function in Gaussian mixture model, JNew + LS	Gaussian Mixture Model	Cuevas et al. (2020)	Standard Gray Scale Images	Proposed method is compared with J + ABC, J + AIS and J + DE	Convergence, Accuracy and Computational Cost	The proposed JNew + LS method removes the flaws encountered in preceding numerous evolutionary approaches
25	The proposed Improved Moth-Flame Algorithm by hybridizing Lévy flight and logarithmic function	Minimum Cross Entropy (MCE)	Nguyen et al. (2020)	Standard Gray and Color Images	Proposed method is compared with MFO, GWO, PSO, CS, DE, PPSO, variants of MFO such as EMFO and CMFO	MSE, PSNR, FSIM and ERC	The proposed algorithm adjust the flame-update positioning mode based on hybridizing the Lévy flight, adding inertia weight, and polynomial iteration feature to increase efficiency and produces better performance than the different competing algorithms
26	The proposed Optimized window based combined entropy segmentation using Genetic Algorithm	Tsallis and Renyi’s entropy	Sahoo et al. (2020)	Gray Scale Images	Proposed method is compared with segmentation using Otsu’s, Tsallis and Renyi’s Entropy	ME, Precision and Recall	The proposed method works well on different images and gives comparatively promising results The model can be further extended to adaptive window based combined entropy segmentation where number and size of the windows selected on the joint histogram can be made adaptive
27	An Improved Emperor Penguin Optimization (IEPO)	Kapur’s entropy	Xing (2020)	Standard Color Images and Satellite Images	Proposed method is compared with EPO, WOA and MVO	PSNR, FSIM and CPU Time	The proposed IEPO reveals the authoritative and controlling skill of Kapur entropy-based algorithm. In addition, IEPO may be extended in future to solve discrete and multi-objective optimization problems
28	Modified Thermal Exchange Optimization (Tsallis-LTEO)	Tsallis entropy	Xing and Jia (2020a)	Standard Color Images and Satellite Images	Proposed method is compared with TEO, CSA, FPA, BA and PSO	PSNR and FSIM	The proposed Tsallis-LTEO consumes less iteration but greater accuracy in terms of segmentation
29	Teaching Tactics for Image Segmentation based on TLBO	Minimum Cross Entropy (MCE) and Otsu’s thresholding	Kalyani et al. (2020)	Berkeley Standard Color Images	Proposed method is compared with CS at 4, 5, 6, and 7 threshold levels	Mean fitness values	Experimental results authenticate that TLBO based MLT outperforms CS and reveals optimal output of TLBO is more successful in precise image segmentation and aids in various real time applications. Otsu based TLBO is better compared to MCE
30	Hybrid Rice Optimization (HRO)	Otsu’s thresholding and Renyi’s entropy	Liu et al. (2020a)	Standard Gray Scale Images	Proposed method is compared with GA, PSO, DE, ALO, ABC, WOA and SSA	PSNR, FSIM and Average Fitness values	HRO-Renyi achieves better performance in comparison to that of HRO-Otsu. Further, HRO algorithm. May be combined with another local search mechanism and existing chaotic strategy
31	Chaotic Lightning Attachment Procedure Optimization (CLAPO)	2D Maximum entropy	Liu et al. (2020b)	Standard Gray Scale Images	Proposed method is compared with ALO, GOA, SCA, WOA, LAPO, FWA and GA	CPU Time, Maximum fitness value, Average fitness value, Excellent Rate and Iterations consumed	The proposed CLAPO claims better outcome when compared to the other algorithms in terms of efficiency, performance and segmentation effect. However, compared to GA, SCA proposed algorithm is slower in terms of running speed that needs further attention and improvisation
32	Improved Thermal Exchange Optimization based GLCM (GLCM-ITEO)	Diagonal Class Entropy (DCE) and Otsu thresholding	Xing and Jia (2019)	Color Natural Images, Satellite Images and Berkeley Images	Proposed method is compared with GLCM-PSO, GLCM-BA, GLCM-FPA, GLCM-ITEO, GLCM-CSA, Otsu-CSA, Otsu-BA, Otsu-FPA, Otsu-ITEO and Otsu-PSO	PRI, VoI, GCE, CPU Time and BDE	The proposed GLCM-ITEO algorithm is better in terms of segmentation ability and CPU time. Further, GLCM-ITEO algorithm outperforms Otsu algorithm in terms of segmentation effect
33	Improved Cuckoo Search	Otsu’s thresholding	Jayaseeli and Malathi (2020)	Satellite Images	Proposed method is compared with Gaussian Smoothing method, Symmetry duality, GA based method and Lambda method	Overall Accuracy, Kappa coefficient, Commission Error and Omission Error	The resultant factors show high accuracy when compared with other existing methodologies for efficient road region extraction. The proposed method can be extended with other local search techniques of heuristic methods for improving the accuracy of road region extraction
34	Improved Bloch Quantum Artificial Bee Colony Algorithm (IBQABC)	Kapur’s entropy	Huo et al. (2020)	Standard Gray Scale Images	Proposed method is compared with GA, PSO and ABC	PSNR and FSIM	The proposed IBQABC is comparatively better and superior in terms of its overall performance, segmentation effect and strong generalization ability, when compared to aforementioned algorithms
35	Modified Moth-Flame Optimization Algorithm (MMFO)	Minimum Cross Entropy	Khairuzzaman and Chaudhury (2020)	Standard Gray Scale Images	Proposed method is compared with PSO, MFO, BFO and WOA	MSSIM	The proposed MMFO is far better than the traditional MFO when considered for higher number of thresholds thereby drastically reducing the computation cost. In future, MMFO can be used along other entropy mechanism and also hybridized with other algorithms to solve the same
36	Minimum Cross Entropy- Self Adaptive Differential Evolution (MCE-SADE)	Minimum Cross-Entropy	Aranguren et al. (2021)	Magnetic Resonance Brain images (MRBI): Medical Images	Proposed method is compared with SADE, GWO and ICA	PSNR, FSIM and SSIM	The proposed MCE-SADE is better in terms of consistency and its quality when compared to GWO and ICA
37	Fuzzy-Entropy and Image Fusion Based method	Fuzzy-Entropy	Singh et al. (2020)	Magnetic Resonance Brain Images (MRBI): Medical Images	Proposed method is compared with multilevel, adaptive threshold method, K-means clustering algorithm and fuzzy c-means algorithm	PSNR and JSC	The proposed method outdoes the existing method. However, method is checked using only MRIs of brain tumors and in future it can be applied to other types of MRIs
38	Hybrid Slime Mould Algorithm with Whale Optimization Algorithm (HSMA_WOA)	Kapur’s entropy	Abdel-Basset et al. (2020a)	X-Ray Images	Proposed method is compared with LShade, WOA, FFA, HHA, SSA, and SMA	PSNR, SSIM, Fitness values, CPU time and UQI	The proposed HSMA_WOA outperforms SMA for all the metrics used
39	Study on recent Nature-Inspired Algorithms	Tsallis entropy	Wachs-Lopes et al. (2020)	Medical Images	Proposed method is compared with FFA, CSL, GOA, KHA, GWO, EHO and WOA	PSNR, J Index, and DC	Experimental findings projects that all algorithms taken in account in the study performs likewise when quality of segmentations is the factor taken into consideration. Nevertheless, KHA generates worst results. The GWO and WOA show fastest performance with respect to time taken
40	Hybrid meta-heuristics algorithms	Rényi entropy	Oliva et al. (2020)	Color Natural Images and Berkeley Images	PSO, SCA and 2DNLMeKGSA	PSNR, SSIM and FSIM	The solution of higher quality in some of the considered images is generated by 2DNLMSCA. On the other hand,2DNLMPSO exhibits better results for other images taken into account if focused on objective and subjective analysis of the method
41	Survey based on meta-heuristics optimization algorithms	Different objective functions ranging from Rényi entropy to Otsu’s to Kapur to Tsallis to Minimum cross-entropy to Between Class Variance, MCE, GLCM etc	Pare et al. (2020)	General Purpose and Satellite Images	PSO, QPSO, GA, DE, DE, SA, Tabu search, HBMO, BFO, MBFO, ABFO, FA, HSO, IQGA, FODPSO, MKTOA, EMO, Fuzzy c-means, QACO, CS-McCulloch, CS-Levy flight, CS-Mantegna, Darwinian PSO, CS-ELR, FPA, SSO, BA, PLBA, and BSA	MSE, PSNR, SSIM, FSIM and CPU time	The survey paper concludes based on the analysis of different algorithms that no algorithm can be considered good for all types of images neither all algorithms can be employed for specific category of image
42	Improved Equilibrium Optimization Algorithm (EOA)	Kapur Entropy	Abdel-Basset et al. (2021a)	Standard Gray Scale Images	Proposed method is compared with WOA, BA, SCA, SSA, HHA, CSA and PSO	PSNR, MAE, SSIM, SNR and Average of the fitness function	The proposed EOA seems to lag behind other algorithms in terms of standard deviation values and CPU time however it performs superiorly when parameters such as PSNR, fitness values, SSIM, MAE and SNR
43	Non-revisiting Quantum behaved Particle Swarm Optimization (NrQPSO)	Kapur’s entropy	Yang and Wu (2020)	Standard Gray Scale Images	Proposed method is compared with CQPSO, MABC, GWO and MFO	PSNR, Accuracy, Stability, CPU Time and Computation Efficiency	The proposed NrQPSO can outperform the other state-of-the-art algorithms in regard to various performance parameters such as efficiency, effectiveness and robustness making NrQPSO suitable for real-time massive image processing
44	Hyper-Heuristic Best (HHB) and Hyper-heuristic Union Best (HHUB)	Otsu’s and Kapur’s entropy	Abd Elaziz et al. (2020)	Standard Gray Scale Images	Proposed method is compared with SCA, ABC, SSO, FASSO, FAABC and ABCSCA	SSIM, PSNR, RMSE, CPU Time and Fitness values	The proposed method obtains greater performance making it best suitable for applications related to Feature selection, multi-objective method, Global optimization, and Cloud Computing
45	Survey on Artificial Bee Colony (ABC) based classification, clustering, enhancement and segmentation	Fuzzy C-partition entropy, Otsu thresholding, Kapur’s, maximum entropy, wavelet entropy	Öztürk et al. (2020)	Medical Images, Satellite Images, Standard Gray Scale Images	Classification: ABC with PSO and GA. Further, ABC-SVM with PSO-SVM and GA-SVM Clustering: ABC with PSO, GA and K-Means. FCM, PSO-FCM, ABC-FCM, MABC-FCM and MoABC-FCM. Segmentation: I-ABC, ABC, GA, AFS, PSO, DE and ABC	Xie-beni index, Partition coefficient, Classification entropy, separateness, compactness, Davies–Bould in Index, and XB Index	The analysis performed while surveying highlights that for classification, segmentation, clustering, and enhancement of medical images, ABC algorithm gives fruitful and promising result
46	Method using multi-level thresholding algorithm and Statistical Region Merging (SRM) technique with the help of the Alternating Direction Method of Multipliers (ADMM) and MEC	Minimum Cross Entropy	Li et al. (2019)	Standard Color Images	Proposed method is compared with PSO, BF, DE and CS	PSNR. FSIM and SSIM	The proposed ADMM shows some better properties such as faster calculation speed (the request time was under 0.1 s) and better stability
47	Crow Search Algorithm (CSA)	Kapur’s entropy	Upadhyay and Chhabra (2020)	Standard Gray Scale Images	Proposed method is compared with PSO, DE, GWO, MFO andCS	PSNR, FSIM and SSIM	The proposed CSA showcase high robustness, accuracy, efficiency, suitability and search capability when compared with other mentioned algorithms. Further, proposed method could be suitable to be applied over multispectral satellite images and moreover to focus on multi-objective optimization problems
48	Whale Optimization Algorithm (WOA)	Kapur’s entropy	Yan et al. (2020)	Gray Scale Images	Proposed method is compared with BA, FPA, MFO, MSA, PSO andWWO	The fitness value, PSNR, SSIM and execution time	The proposed WOA has the ability to explore and further navigate between the global and local search with the sole intention to obtain the optimum solution to the given problem. Further, the same is projected using the experimental results showing its better performance in terms of convergence speed and quality of segmentation
49	Bat Algorithm (BA1)	Kapur’s entropy	Dey et al. (2021)	Standard Color and Gray Scale Images	Proposed method is compared with BA2, BA3, BA4 and BA5	PSNR, NCC, AD, SC and NAE	Though the average IQPs attained using all BA methods are identical. However, the Levy-based BA presents better results when compared to other algorithms in terms of its convergence speed
50	Kapur's entropy-based thresholding method	Kapur’s entropy	Aalan Babu et al. (2020)	Satellite Images	Proposed method is compared with Otsu, Tsallis entropyand Fuzzy entropy	Precision, Recall, F-measure, Specificity, Overall Accuracy, SSIM and MAD	The proposed method yields better segmentation with an overall accuracy of 98.43% and SSIM rate of 0.9712
51	Stochastic Fractal Search (SFS)	Fuzzy Entropy	Dhal et al. (2019b)	Satellite Images	Proposed method is compared with PSO, CS, HSO and ABC	PSNR, FSIM) and QILV	The proposed SFS produces utmost satisfactory results injudicious computational time
52	Modified Salp Swarm Algorithm (MSSA)	Otsu’s thresholding, Kapur's and Renyi entropy	Wang et al. (2020)	Standard Color Images	Proposed method is compared with SSA, WOA and FPA using different entropy such as Kapur's, Otsu and Renyi entropy	Best Fitness values, PSNR, FSIM, PRI, VoI, GCE and BDE	The proposed MSSA is superior to. Kapur's entropy segmentation algorithm yielding FSIM and PSNR value superior as compared to other algorithms
53	RenyiElectromagnetism Mechanism Optimization (R-EMO)	Renyi’s, Tsallis and Kapur’s entropy	Bhandari et al. (2019)	Various Satellite and Standard Color Images	Proposed method is compared with BA, BSA, FA, PSO and WDO using Renyi, Tsallis and Kapur’s entropy	ME, MSE, PSNR, FSIM, SSIM and Entropy	The proposed EMO-Renyi’s outperforms other algorithm whenapplied with each of the objective function. The proposed scheme in future may be extended for medical image segmentation due to its rapid segmentation capability
54	Improved Particle Swarm Optimization (IPSO) algorithm aided with fuzzy-entropy, IPSO-Fuzzy. Output of IPSO-fuzzy is used to train SVM classifier	Fuzzy entropy	Chakraborty et al. (2019a)	Various Satellite and Standard Color Images	Proposed method is compared with CS, DE, FF, GA and PSO	PSNR, FSIM, Overall Accuracy, Kappa Index, Mean Accuracy and IoU	The proposed IPSO doesn’t prematurely converge and in future may be applied on some larger dataset like ImageNet, COCO with respect to object recognition
55	Improved Elephant Herding Optimization (IEHO)	Kapur’s entropy and between-class variance (Otsu’s thresholding)	Chakraborty et al. (2019b)	Standard Gray Scale Images	Proposed method is compared with CS, ABC, BA, PSO, EHO and DP	PSNR, FSIM and SSIM	The proposed IEHO performs better than that of the conventional algorithms both in terms of quality and convergence rate
56	Whale Optimization Algorithm-Differential Evolution(WOA-DE)	Kapur’s entropy	Lang and Jia (2019)	MRI: Medical Images, Satellite Images, standard gray scale Images	Proposed method is compared with WOA, SSA, SCA, ALO, HSO, BA, PSO, BDE and IDSA. Otsu WOA-DE is compared with Kapur WOA-DE	Average Fitness Values, PSNR, FSIM and SSIM	The proposed WOA-DE avoids the loss due to population diversity and dropping into local optimum. Kapur_WOA-DE is better than Otsu_WOA-DE as per the experimental outcome analysis
57	Spherical Search Optimizer and Sine Cosine Algorithm (SSOSCA)	Fuzzy Entropy	NajiAlwerfali et al. (2020)	Standard Gray scale Images	Proposed method is compared with CS, GWO, WOA, SSA, GOA and SSO. Optimizer (SSO)	Fitness value, PSNR and SSIM	The proposed SSO-SCA in terms of fitness value, PSNR and SSIM is better than other algorithms take into consideration for comparison purpose. In future, for time series forecasting, cloud computing, feature selection etc., proposed method may be effective
58	Differential Evolution and Whale Optimization (DEWO)	Non-local 2-dimensional histogram-based Entropy	Vig et al. (2019)	Standard color Images	Proposed method is compared with DE, ABC, CS and WOA. Different entropy functions such as Tsallis, Renyi and Kapur was compared	Mean fitness and number of function evaluation	The proposed DEWO offer a healthier stability amongst exploration and exploitation. The experimental result showcases that which so ever entropy function selected, proposed algorithm is able to attain maximized value of fitness function
59	Improved Particle Swarm Optimization (PSO)	Otsu’s thresholding	Khairuzzaman and Chaudhury (2019)	Brain MRI: Medical Images	Proposed method is compared with standard PSO and BFO	PSNR and MSSIM	The proposed method suggestively provides improved quality in terms of image segmentation which when applied to T2-weitghted brain MR images
60	Fractional Order Darwinian Particle Swarm Optimization (FODPSO)	Otsu’s thresholding	Astuti and Mardhia (2019)	Hyper spectral Images: Standard Color Images	Proposed method is compared with PSO and DPSO	Average CPU time, fitness value, PSNR, MSE and SSIM	The proposed FODPSO in the context of fitness value and processing time of CPU is better compared to the other algorithms considered
61	Teaching–Learning Optimization based Minimum Cross Entropy Thresholding (TLBO-MCET)	Minimum Cross entropy	Gill et al. (2019)	Standard Gray Scale Images	Proposed method is compared with FF- MCET), HBMO-MCET) and (QPSO-MCET)	Uniformity, Fitness values and PSNR	The proposed TLBO-MCET is considered to be an efficient method to determine optimal threshold values. TLBO-MCE has great potential in the field of image segmentation
62	Energy 3D Otsu Human Learning Optimization (HLO) (E-3D-HLO)	3D Otsu’s, Energy-Otsu thresholding	Bhandari and Kumar (2019)	Standard Color Images	Proposed method is compared to SCA, CFA, HLO, E-SCA and E-HLO. Also, E-3D-HLO is then compared to 1D, 2D and 3D-SCA, CFA and HLO	ME, MSE, PSNR, FSIM, SSIM and Entropy	Otsu in three-dimensional space possesses the ability to incorporate spatial context information making it better when compared with 1D and 2D Otsu methods. The segmentation accuracy upsurges significantly without distressing the original color image details making the proposed method better than the other algorithms used for the purpose of comparison
63	Improved Opposition based Symbiotic Organisms Search (IOSOS)	Otsu’s thresholding, Kapur’s and Tsallis entropy	Chakraborty et al. (2019c)	Standard Color Images	Proposed method is compared to OSOS, CS, BA, ABC and PSO	PSNR, FSIM and SSIM	The proposed IOSOS employing various entropy functions such as Otsu, Tsallis and Kapur performs significantly when compared with the different algorithms used for the purpose of comparison
64	Hybrid Adaptive-Cooperative Learning strategy with Fruit Fly Optimization Algorithm (FOA) (HACLFOA)	Otsu’s thresholding	Ding et al. (2019)	Standard Gray and Color Images	Proposed method is compared to FOA, LGMS-FOA, IFFO, CMFOA and SFOA. Further, HACLFOA is compared with PSO, FOA, QPSO and IDPSO	Fitness values and Computation time	The proposed HACLFOA has strongest global convergence ability among the compared algorithms thereby have a great potential in the image processing field
65	Thresholding Heuristic (TH) embedded into WOA, GWO and PSO (WOA-TH, GWO-TH, and PSO-TH)	Otsu’s thresholding	Bohat and Arya (2019)	Standard Gray Scale Images	Proposed method is compared with their respective base algorithm WOA, GWO and PSO	Mean Fitness values, MSSIM and Mean Execution Time	The proposed WOA-TH, GWO-TH and PSO-TH algorithms are better with improved computational time when compared with their respective base algorithm
66	Adaptive Differential Evolution with Levy Distribution (ALDE)	Otsu’s thresholding	Tarkhaneh and Shen (2019)	MRI: Medical Images	Proposed method is compared with SDE, BDE and hjDE	PSNR and SSIM	The proposed ALDE when equated with the benchmark algorithm performs better and has the capability to attain optimal threshold at a judicious computational cost
67	Sigmoid based optimal threshold selection technique with Differential Evolution (DE) and Tsallis Fuzzy	Tsallis-Fuzzy Entropy	Raj et al. (2019)	Standard Color Images	Proposed method is compared with PLBA, BFO, MBFO and BA	PSNR, SSIM, SNR and CPU time	The proposed method is more stable and converges to optimal thresholds much faster. Standard deviation values further suggest that the proposed method is highly robust when compared with other algorithms
68	Energy-Masi using Moth Swarm Algorithm (MASI-ENG-MSA)	Energy-Masi entropy	Bhandari and Rahul (2019)	Standard Color Images	Proposed method is compared with MASI-DA, MASI-SCA, MASI-WOA, MASI-GOA, MASI-MSA, MASI-ENG-DA, MASI-ENG-SCA, MASI-ENG-WOA and MASI-ENG-GOA	ME, Entropy, MSE, PSNR, SSIM and FSIM	The proposed MASI-ENG-MSA in regard to the parameters such as threshold quality and computational cost outperforms other algorithms
69	Particle Swarm Optimization. Using Gray Level &Local-Average histogram (GLLA) and Tsallis-Havrda-Charv´at entropy	Tsallis-Havrda-Charv´at entropy	Borjigin and Sahoo (2019)	Standard Color Images	The average of PRI, GCE, VOI and BDE of proposed model is compared with result from 2D K-L divergence model, 1D Tsallis-based model and 2D Renyi-based model	VOI, GCE, BDE and PRI	The experiments have been extensively conducted and highlight the effectiveness and reasonability of the proposed method
70	Masi-Water Cycle Algorithm (M-WCA)	Tsallis and Masi entropy	Kandhway and Bhandari (2019a)	Standard Color Images	Proposed method is compared with BA, PSO, WDO, MBO, GOA, and WCA. Further, Masi-BAT, Masi-PSO, Masi-WDO, Masi-MBO, Masi-GOA, and Masi-WCA, Tsallis-BAT, Tsallis-PSO, Tsallis-WDO, Tsallis-MBO, Tsallis-GOA, and Tsallis-WCA comparison is also highlighted	ME, MSE, PSNR, FSIM, SSIM, computational time and Entropy	The proposed Masi-WCA is capable of acquiring superior quality and convergence rate. The foremost constraint of M-WCA method is that it consumes long processing time for segmentation compared to Masi-MBO. However, when different optimization methods are coupled with Masi entropy always performs better than the Tsallis entropy-based optimization techniques
71	Multi-Verse Optimizer (MVO)	Energy-Minimum Cross Entropy (MCE)	Kandhway and Bhandari (2019b)	Standard Color Images	Proposed method is compared to BA, MFO, AGPSO, TSA and MVO	ME, MSE, PSNR, SSIM, FSIM and GMSD	The proposed MVO-Energy-MCE when compared to other mentioned algorithm performs much better in terms of segmented performance and thresholding making it efficient, robust and accurate algorithm
72	Optimized Thresholding Method Using Ant Colony Algorithm	Otsu’s thresholding	Khorram and Yazdi (2019)	Magnetic Resonance (MR) Brain Images: Medical Images	Proposed method is compared with PSO, ABC, K-means, and EM	Accuracy, Sensitivity, Specificity, FDR, PPV, FOR and NPV	The experimental outcomes prove the promising result of the proposed method when compared to other algorithms. In future, the proposed approach may be further prolonged over 3D MR brain images
73	Salp Swarm Algorithm using Levy Flight (LSSA) to GLCM (GLCM-LSSA)	Diagonal Class Entropy (DCE)	Xing and Jia (2020b)	Standard Color Images and Satellite Images	Proposed method is compared to WOA, SSA, FPA, PSO and BA. Further, GLCM-LSSA is compared GLCM-PSO, GLCM-BA, GLCM-FPA, Kapur-LSSA, Kapur-WOA, Kapur-FPA, Kapur-PSO and Kapur-BA	PSNR, FSIM, PRI, BDE, GCE, VoI and Computation Time	The proposed GLCM-LSSA algorithm has the capability to handle complex segmentation procedures as it possesses better segmentation effect
74	Self-Adaptive Moth-Flame Optimization Thresholding Heuristic (SAMFO-TH)	Otsu’s thresholding and Kapur’s entropy	Jia et al. (2019a)	Standard Color Images	Proposed method is compared with MVO, WOA, FPA, SCA, ACO and MFO	Computational time, MVTR, MSE, PSNR, SSIM, FSIM, PRI, VoI and TVD	The proposed SAMFO-TH is superior in terms of stability, convergence rate, accuracy and efficiency. Kapur-SAMFOTH outdoes Otsu’s-SAMFOTH; SAMFOTH outperforms MFO which is clearly highlighted in the experimental result
75	Multi-Strategy Emperor Penguin Optimizer (MSEPO)	Masi Entropy	Jia et al. (2019b)	Color Satellite Images	Proposed method is compared with FPA, CSA, TLBO, MABC, IDSA, LMVO, and EPO	PSNR, SSIM, FSIM and Computational time	The proposed MSEPO is capable of effectively identifying the core target areas and process its edges better. The binary and multi-objective versions of MSEPO algorithm may be developed in future to explore the capabilities of MSPO in a broader way
76	Cuckoo Search (CS)	Tsallis entropy	Widyantara et al. (2019)	Coastal video Images	–	PSNR, SSIM and FSIM	The amalgamation of CS algorithms along with Tsallis functions furnished better outcomes than that of conventional segmentation methods
77	Modified Grasshopper Optimization Algorithm (MGOA)	Energy-Tsallis entropy	Liang et al. (2019)	Standard Color Images	Proposed method is compared with GOA, WOA, FPA, PSO and BA	PSNR and SSIM	The proposed MGOA using energy based Tsallis entropy when certain performance parameters (accuracy, convergence speed, searching precision) are considered generates superior performance. Similarly, WOA and BA achieves acceptable outcome however, PSO generates substandard performance
78	Multi-objective Multi-verse Optimization (MOMVO)	Otsu’s thresholding and Kapur’s entropy	Abd Elaziz et al. (2019a)	Standard Gray Scale Images	Proposed method is compared with MOPSO, MOEAD and MOEADR	HV, SP and U	The proposed MOMVO is substantially better compared to the other algorithms in terms of hyper volume and spacing
79	Knee Evolutionary Algorithm (KnEA)	Kapur, Otsu, cross entropy, Tsalli’s entropy, Renyi entropy, fuzzy entropy	Abd Elaziz and Lu (2019)	Standard Gray Scale Images	Proposed method is compared with NSGA-III, RVEA and IMMOEA and LMEA	PSNR, SSIM and Computational Time	The proposed KnEA method produced a high-quality segmented image at different levels of threshold. In addition, the CPU time(s) achieved by the KnEA is lower than the CPU time(s) of others, except the RVEA, and IMMOEA methods
80	Swarm Selection (SS)	Otsu’s thresholding	Abd Elaziz et al. (2019b)	Standard Gray Scale Images	Proposed method is compared with ABCSCA, ABC, FAABC, FASSO and SCA	PSNR, FSIM, SSIM and Computational Time	The proposed SS method outperforms the other algorithms at most of the threshold levels along each image, based on different performance measures
81	Hybrid Bird Mating Optimization and Differential Evolutionary (BMO-DE)	Otsu’s thresholding, and Kapur’s entropy	Ahmadi et al. (2019)	Standard Gray Scale Images	Proposed method is compared with BF, MBF, PSO, GA and PSO-DE	Fitness function value, average CPU running time and SNR	The proposed BMO-DE with respect to parameters such as solution quality and stability is better than the subsequent algorithms employed for the sole purpose of comparison. In future, objective function may be integrated to the spatial constraints to improve the accuracy
82	Tournament based Lévy Multi-Verse Optimization (TLMVO)	Masi entropy	Jia et al. (2019c)	Standard Color Images	Proposed method is compared with MVO, LMVO, ALO, DA, FPA, PSO and CS	Fitness function value, average CPU running time, PSNR, SSIM and FSIM	The proposed TLMVO proved its significance in high-dimensional optimization problems, thereby generating good objective function value, image quality, convergence performance and robustness
83	GOA with self-adaptive Differential Evolution (GOA–jDE)	Minimum Cross Entropy (MCE)	Jia et al. (2019d)	Color and Gray Scale Satellite Images	Proposed method is compared with GOA, DE, MGOA, hjDE, BA, BDE and PSO	Average Fitness Function value, PSNR, FSIM, SSIM and computation time	The proposed GOA–jDE showcases through its experimental result, its capabilities to be adopted and implemented in several areas by outperforming other approaches. In future, apart from satellite images, medical images too may be explored using the proposed method
84	Dynamic Harris Hawks Optimization with a Mutation Mechanism (DHHOM)	Kapur’s, Tsallis entropy and Otsu thresholding	Jia et al. (2019e)	Color Satellite Images	Proposed method is compared with HHO, TLBO, WOA-TH, IDSA and BDE DHHO/M is then compared Tsallis-MGOA, Tsallis-MABC, Otsu-MFPA and Otsu-GWO	Average Fitness Function value, PSNR, SSIM and FSIM	The proposed DHHO/M based thresholding technique shows remarkable performance
85	Fractional Order Darwinian Particle Swarm Optimization (FODPSO)	Otsu’s and Kapur’s method	Ahilan et al. (2019)	Medical Images	Proposed method is compared with DPSO and PSO	Fitness Function value, PSNR and MSE	The proposed FODPSO generate superior results. The fractional coefficient in FODPSO algorithm makes it effective optimization with fast convergence rate
86	Bat Algorithm (BA)	Rényi’s entropy and Otsu’s thresholding	Pare et al. (2019)	Standard Color Images and Satellite Images	Proposed method is compared with Otsu-PSO and Renyi-PSO	PSNR, MSE and Computation Time	The proposed method is more competent and resourceful for image segmentation as compared to the different algorithm taken into account in this paper
87	Dragonfly Algorithm with Opposition-Based Learning (OBLDA)	Otsu’s thresholding and Kapur’s entropy	Bao et al. (2019)	Standard Color Images and Satellite Images	Proposed method is compared with DA, PSO, CSA, BA, HSO, ALO and SSA	Average Fitness Function value, PSNR, FSIM, SSIM and computation time	The proposed OBLDA is advantageous over the compared algorithm for segmentation because of its accuracy and notable stability
88	Improved Grey Wolf Optimization (IGWO)	Kapur’s entropy	Yao et al. (2019)	Standard Gray Scale Images	Proposed method is compared with PSO	PSNR	The proposed IGWO possesses great global convergence along with the computational robustness, thereby avoiding the fall into local optimum

From Fig. 2, it can be seen that Kapur’s entropy and Otsu maintain their popularity as objective function till date where some other new objective function have been developed. Now, a brief mathematical implementation of Kapur’s entropy has been given below for the help of the reader relate better to the Optimization being performed.

Kapur method (Ray et al. 2021) considers the combination of a probability distribution function of a given histogram with the concept of entropy. The principal idea behind this method, aims to find the best threshold combination that maximizes the entropy. Considering a binary class segmentation problem, the objective function for Kapur’s entropy is defined by:

$$f\left(\mathit{th}\right)=max\left(H_1(th)+H_2(th)\right),$$ 2

where the entropies of each class H₁ and H₂ are computed as follows:

$$H_1(th)=\sum _{i=1}^{\mathit{th}}\frac{P{h}_i}{w_1\left(\mathit{th}\right)}ln\left(\frac{P{h}_i}{w_1\left(\mathit{th}\right)}\right),H_2(th)=\sum _{i=th+1}^L\frac{P{h}_i}{w_2\left(\mathit{th}\right)}ln\left(\frac{P{h}_i}{w_2\left(\mathit{th}\right)}\right),$$ 3

where i represents the intensity of a given pixel such that $\left(0\le i\le L-\right)$; NP represents the total number of pixels; h indicates the image histogram; h_i indicates the quantity of pixels having i intensity; and Ph_i is the probability distribution of the i-th level which is defined as:

$$P{h}_i=\frac{h_i}{\mathit{NP}},\sum _{i=1}^{\mathit{NP}}P{h}_i=1,$$ 4

and the cumulative distribution function of each class is defined as:

$$w_1(th)=\sum _{i=1}^{\mathit{th}}P{h}_i,w_2(th)=\sum _{i=th+1}^{L}P{h}_i.$$ 5

For multi-level image segmentation, Kapur method can be extended to incorporate multi thresholding capabilities. In such case, the image I is divided into K classes. Under such circumstances, Eq. (2) is redefined as:

$$f(\mathbf{th})=max\left(\sum _{i=1}^K{H}_i\left(\mathbf{th}\right)\right),$$ 6

where $\mathbf{th}=[t{h}_1,t{h}_2,...,t{h}_{\mathit{nt}}]$, represents the vector of threshold values and the entropy values, corresponding to each threshold value for a multi-level segmentation problem is calculates as:

$$\begin{array}{c}{H}_1(t{h}_1)=\sum _{i=1}^{t{h}_1}\frac{P{h}_i}{w_1(t{h}_1)}ln\left(\frac{P{h}_i}{w_1(t{h}_1)}\right)\\ H_2(t{h}_2)=\sum _{i=t{h}_1+1}^{t{h}_2}\frac{P{h}_i}{w_2(t{h}_2)}ln\left(\frac{P{h}_i}{w_2(t{h}_2)}\right)\\ \begin{array}{cccc}& & ...& \end{array}\begin{array}{ccc}& ...& \end{array}\begin{array}{ccc}& ...& \end{array}\\ H_K(t{h}_{\mathit{nt}})=\sum _{i=t{h}_{\mathit{nt}}+1}^L\frac{P{h}_i}{w_K\left(t{h}_{\mathit{nt}}\right)}ln\left(\frac{P{h}_i}{w_K\left(t{h}_{\mathit{nt}}\right)}\right).\\ \end{array}$$ 7

The cumulative distribution function of each class is defined as:

$$w_1(t{h}_1)=\sum _{i=1}^{t{h}_1}P{h}_i,w_2(t{h}_2)=\sum _{i=t{h}_1+1}^{t{h}_2}P{h}_i,w_K(t{h}_{\mathit{nt}})=\sum _{i=t{h}_{\mathit{nt}}+1}^{L}P{h}_i.$$ 8

Recent literature on MLT using NIOA

This section encompasses an informed literature assessment on the usage of NIOA to solve the MLT problem. The study takes into account works that were released between 2019 and 2021.The general approach of MLT using NIOA is summarized as Algorithm 1 comprising of various steps. In the initial step i.e., Step 1, the objective function is considered. In MLT, the ideal thresholds is attained by optimizing a certain objective function or maximizing various entropy such as Kapur’s entropy, between-class variance etc. Further, the initial parameters of the population that essentially represents the solution to the given optimization problem are haphazardly initialized and created in the solution space. The fitness function, which is considered as one of the sole pointers to highlight the performance of each solution is calculated in Step 3. The recent literature of NIOA based MLT has been presented in Table 3. Different methods and parameter’s abbreviation used in the papers surveyed in Table 3 with its full form is tabularized respectively in Tables 4 and 5. Total 88 papers have been discussed in Table 3 where 19, 31, and 38 papers are collected from the years 2021, 2020 and 2019 respectively and presented in Fig. 3a. Whereas, Fig. 3b indicates the percentage of papers which are surveyed in Table 3 utilized different types of images.The mentioned papers have been collected from the following sources:

• (i)Google Scholar—http://scholar.google.com
• (ii)IEEE Xplore—http://ieeexplore.ieee.org
• (iii)ScienceDirect—http://www.sciencedirect.com
• (iv)SpringerLink—http://www.springerlink.com
• (v)DBLP—http://dblp.uni-trier.de
• (vi)ACM Digital Library—http://dl.acm.org

Algorithm 1.

General approach of multi-level thresholding using NIOA

Table 4.

Different method’s abbreviation used in the paper surveyed in Table 3 and its full form

SL	Method’s name (abbreviation)	Full form
1	RCACO	Random spare strategy and Chaotic intensification strategy based on ACOR
2	ACOR	Ant Colony Optimizer for Continuous Domain
3	PSO	Particle Swarm Optimization
4	WOA	Whale Optimization Algorithm
5	CS	Cuckoo Search
6	CSL	Cuckoo Search via Lévy Flights
7	BA	Bat Algorithm
8	BLPSO	Biogeography-based Learning Particle Swarm Optimization
9	CGPSO	Cluster Guide Particle Swarm Optimization
10	IWOA	Improved Whale Optimization Algorithm
11	IGWO	Enhanced Gray Wolf Optimization
12	SSA	Salp Swarm Algorithm
13	CGPSO	Cluster Guide Particle Swarm Optimization
14	SMA	Slime Mould Algorithm
15	CCACO	Criss Cross Ant Colony Optimization
16	HCS	Horizontal Crossover Search
17	VCS	Vertical Crossover Search
18	CSO	Crisscross Optimizer
19	DE	Differential Evolution
20	WOA	Whale Optimizer Algorithm
21	GWO	Gray Wolf Optimization
22	SCA	Sine Cosine Algorithm
23	HHO	Harris Hawks Optimization
24	OBLGWO	Oppositional Based Grey Wolf Optimization Algorithm
25	ALCPSO	Particle Swam Optimization with an Aging Leader and Challengers
26	m_SCA	Modified Sine Cosine Algorithm
27	BMWOA	Enhanced Associative Learning-based Exploratory Whale Optimization Algorithm
28	ACWOA	A-C parametric Whale Optimization Algorithm
29	SCADE	Hybridizing Sine Cosine Algorithm with Differential Evolution
30	MFO	Moth Flame Optimization
31	AMFO	Advanced variants of Moth Flame Optimization
32	FPA	Flower Pollination Algorithm
33	ABC	Artificial Bee Colony
34	MABC	Modified Artificial Bee Colony
35	IABC	Improved Artificial Bee Colony
36	FA	Firefly Algorithm
37	TLBO	Teaching–Learning-Based Optimization
38	FDRPSO	Fitness-Distance-Ratio-Based Particle Swarm Optimization
39	FDR-TLBO	Fitness-Distance-Ratio-Based Particle Swarm Optimization
40	BBPSO	Bare Bones Particle Swarm Optimization
41	jDE	j Differential Evolution
42	SADE	Self-Adaptive Differential Evolution
43	NFDR-TLBO	Neighborhood Fitness Distance Ratio-Teaching Learning Based Optimization
44	GA	Genetic Algorithm
45	MWOA	Modified Whale Optimization Algorithm
46	VPL	Volleyball Premier League
47	VPLWOA	Volleyball Premier League using Whale Optimization Algorithm
48	SSO	Social Spider Optimization
49	SOA	Seeker Optimization Algorithm
50	FFA	Firefly Algorithm
51	EO	Equilibrium Optimization
52	SSO	Slap Swarm Optimization
53	MRFO	Manta Ray Foraging Optimization
54	MRFO-OBL	Manta Ray Foraging Optimization based on the Opposition-Based Learning
55	ES-WOA	Eagle Strategy-Whale Optimization Algorithm
56	ES-DA	Eagle Strategy-Differential Evolution
57	ES-FA	Eagle Strategy-Firefly Algorithm
58	ES-PSO	Eagle Strategy-Particle Swarm Optimization
59	MPA	Marine Predators Algorithm
60	FE-TII-MPA	Fuzzy Entropy Type II-Marine Predators Algorithm
61	PFA	Paddy Field Algorithm
62	PPA	Plant Propagation Algorithm
63	HPFPPA-D	Hybrid Paddy Field Plant Propagation Algorithm with the Disruption Operator
64	LHHO	Leader Harris Hawks Optimization
65	HHO	Harris Hawks Optimization
66	WDO	Wind Driven Optimization
67	STOA	Sooty Tern Optimization Algorithm
68	AMRFO	Attacking Manta Ray Foraging Optimization
69	SFO	Sail Fish Optimizer
70	HBMO	Honey Bee Mating Optimization
71	ITLBO	Improved Teaching–Learning-based Optimization
72	BSA	Backtracking Search Optimization Algorithm
73	ILSO	Improved Lion Swarm Optimization
74	LSO	Lion Swarm Optimization
75	J + ABC	J + Artificial Bee Colony
76	J + AIS	J + Artificial Immune System
77	J + DE	J + Differential Evolution
78	PPSO	Parallel Particle Swarm Optimization
79	EMFO	Enhanced Moth-Flame Algorithm
80	CMFO	Chaos-enhanced Moth-Flame Algorithm
81	EPO	Emperor Penguin Optimization
82	MVO	Multi Verse Optimization
83	IEPO	Improved Emperor Penguin Optimization
84	Tsallis—LTEO	Tsallis—Modified Thermal Exchange Optimization
85	TEO	Thermal Exchange Optimization
86	CSA	Crow Search Algorithm
87	GA	Genetic Algorithm
88	ALO	Ant-Lion Optimization
89	LAPO	Lightning Attachment Procedure Optimization
90	CLAPO	Chaotic Lightning Attachment Procedure Optimization
91	GOA	Grasshopper Optimization Algorithm
92	FWA	Fire Works Algorithm
93	GLCM-PSO	Gray Level Co occurrence Matrix- Particle Swarm Optimization
94	GLCM-BA	Gray Level Co occurrence Matrix-Bat Algorithm
95	GLCM-FPA	Gray Level Co occurrence Matrix-Flower Pollination Algorithm
96	GLCM-ITEO	Gray Level Co occurrence Matrix-Improved Thermal Exchange Optimization
97	GLCM-CSA	Gray Level Co occurrence Matrix-Crow Search Algorithm
98	Otsu-CSA	Otsu-Crow Search Algorithm
99	Otsu-BA	Otsu-Bat Algorithm
100	Otsu-FPA	Otsu-Flower Pollination Algorithm
101	Otsu-PSO	Otsu-Particle Swarm Optimization
102	Otsu-ITEO	Otsu-Improved Thermal Exchange Optimization
103	MMFO	Modified Moth-Flame Optimization Algorithm
104	IBQABC	Improved Bloch Quantum Artificial Bee Colony Algorithm
105	BFO	Bacterial Foraging Optimization
106	ABFO	Adaptive Bacterial Foraging Optimization
107	MBFO	Modified Bacterial Foraging Optimization
108	MCE-SADE	Minimum Cross-Entropy-Self-Adaptive Differential Evolution
109	ICA	Competitive Imperialist Algorithm
110	KHA	Krill Herd Algorithm
111	EHO	Elephant Herding Optimization
112	PLBA	Patch Levy-based Bees Algorithm
113	EMO	Electromagnetism-like algorithm
114	MKTOA	Molecular Kinetic Theory Optimization Algorithm
115	HBMO	Honey Bee Mating Optimization
116	IQGA	Improved Quantum-inspired Genetic Algorithm
117	FODPSO	Fractional-order Darwinian Particle Swarm Optimization
118	QACO	Quantum-inspired Ant Colony Optimization
119	QDE	Quantum-inspired Differential Evolution
120	QPSO	Quantum-inspired Particle Swarm Optimization
121	QGA	Quantum-inspired Genetic Algorithm
122	BSA	Backtracking Search Algorithm
123	BA	Bee Algorithm
124	QBA	Quantum-inspired Bee Algorithm
125	HSO	Harmony Search Optimization
126	NrQPSO	Non-revisiting Quantum-behaved Particle Swarm Optimization
127	CQPSO	Chaotic Quantum-Behaved Particle Swarm Optimization
128	MABC	Modified Artificial Bee Colony
129	HHB	Hyper-Heuristic Best
130	HHUB	Hyper-heuristic Union Best
131	FASSO	Hybrid Firefly Algorithm and Social-Spider Optimization
132	FAABC	Hybrid Firefly Algorithm and Artificial Bee Colony
133	ABCSCA	Hybrid Artificial Bee Colony and Sine Cosine Algorithm
134	ABC-SVM	Artificial Bee Colony-Support Vector Machine
135	PSO-SVM	Particle Swarm Optimization-Support Vector Machine
136	GA-SVM	Genetic Algorithm -Support Vector Machine
137	PSO-FCM	Particle Swarm Optimization-Fuzzy C-Means
138	ABC-FCM	Artificial Bee Colony-Fuzzy C-Means
139	MABC-FCM	Modified Artificial Bee Colony-Fuzzy C-Means
140	MoABC-FCM	Multi-Objective Modified Artificial Bee Colony-Fuzzy C-Means
141	SFS	Stochastic Fractal Search
142	MSSA	Modified Salp Swarm Algorithm
143	WDO	Wind Driven Optimization (WDO)
144	IEHO	Improved Elephant Herding Optimization
145	BDE	Beta Differential Evolution
146	IDSA	Improved Differential Search Algorithm
147	SSO	Spherical Search Optimizer
148	SSOSCA	Spherical Search Optimizer and Sine Cosine Algorithm
149	FODPSO	Fractional Order Darwinian Particle Swarm Optimization
150	FF-MCET	Firefly-based Minimum Cross Entropy Thresholding
151	TLBO-MCET	Teaching–Learning based Optimization based Minimum Cross Entropy Thresholding
152	HBMO-MCET	Honey Bee Mating Optimization based Minimum Cross Entropy Thresholding
153	QPSO-MCET	Quantum Particle Swarm Optimization-based Minimum Cross Entropy Thresholding
154	OSOS	Opposition based Symbiotic Organisms Search
155	IOSOS	Improved Opposition based Symbiotic Organisms Search
156	CFA	Cuttle Fish Algorithm
157	HLO	Human Learning Optimization
158	E-SCA	Energy-Sine Cosine Algorithm
159	E-CFA	Energy-Cuttle Fish Algorithm
160	E-HLO	Energy-Human Learning Optimization
161	FOA	Fruit Fly Optimization Algorithm
162	HACLFOA	Hybrid Adaptive-Cooperative Learning strategy with Fruit Fly Optimization Algorithm
163	CMFOA	Cloud Model based Fruit Fly Optimization Algorithm
164	SFOA	Step Fruit Fly Optimization Algorithm
165	IDPSO	Particle Swarm Optimization based on Intermediate Disturbance Strategy
166	WOA-TH	Whale Optimization Algorithm-Thresholding Heuristic
167	GWO-TH	Gray Wolf Optimization-Thresholding Heuristic
168	PSO-TH	Particle Swarm Optimization-Thresholding Heuristic
169	ALDE	Adaptive Differential Evolution with Levy Distribution
170	SDE	Synergetic Differential Evolution
171	hjDE	Hybrid Differential Evolution
172	MSA	Moth Swarm Algorithm
173	MASI-ENG-MSA	Energy-Masi Moth Swarm Algorithm
174	MASI-DA	Masi Entropy based Differential Algorithm
175	MASI-SCA	Masi Entropy based Sine–Cosine Algorithm
176	MASI-WOA	Masi Entropy based Whale Optimization Algorithm
177	MASI-GOA	Masi Entropy based Grasshopper Optimization Algorithm
178	MASI-ENG-DA	Energy Masi Entropy based Differential Algorithm
179	MASI-ENG-SCA	Energy Masi Entropy based Sine–Cosine Algorithm
180	MASI-ENG-WOA	Energy Masi Entropy based Whale Optimization Algorithm
181	MASI-ENG-GOA	Energy Masi Entropy based Grasshopper Optimization Algorithm
182	WCA	Water Cycle Algorithm
183	MBO	Monarch Butterfly Optimization
184	Masi-BA	Masi Entropy based Bat Algorithm
185	Masi-PSO	Masi Entropy based Particle Swarm Optimization
186	Masi-WDO	Masi Entropy based Wind Driven Optimization
187	Masi-MBO	Masi Entropy based Monarch Butterfly Optimization
188	Masi-GOA	Masi Entropy based Grasshopper Optimization Algorithm
189	Masi-WCA	Masi Entropy based Water Cycle Algorithm
190	Tsallis-BA	Tsallis Entropy based Bat Algorithm
191	Tsallis-PSO	Tsallis Entropy based Particle Swarm Optimization
192	Tsallis-WDO	Tsallis Entropy based Wind Driven Optimization
193	Tsallis-MBO	Tsallis Entropy based Monarch Butterfly Optimization
194	Tsallis-GOA	Tsallis Entropy based Grasshopper Optimization Algorithm
195	Tsallis-WCA	Tsallis Entropy based Water Cycle Algorithm
196	AGPSO	Autonomous Particles Groups for Particle Swarm Optimization
197	GLCM-LSSA	Gray Level Co occurrence Matrix-Salp Swarm Algorithm using Levy Flight
198	Kapur-LSSA	Kapur Entropy based Salp Swarm Algorithm using Levy Flight
199	Kapur-WOA	Kapur Entropy based Whale Optimization Algorithm
200	Kapur-FPA	Kapur Entropy based Flower Pollination Algorithm
201	Kapur-SOA	Kapur Entropy based Seeker Optimization Algorithm
202	Kapur-BA	Kapur Entropy based Bat Algorithm
203	SAMFO-TH	Self-Adaptive Moth-Flame Optimization Thresholding Heuristic
204	MSEPO	Multi-Strategy Emperor Penguin Optimizer
205	IDSA	Improved Particle Swarm Optimization Search Algorithm
206	LMVO	Multi-Verse Optimization based on Levy Flight
207	EPO	Emperor Penguin Optimizer
208	MGOA	Modified Grasshopper Optimization Algorithm
209	MOPSO	Multi-Objective Particle Swarm Optimization
210	MOEAD	Multi-Objective Evolutionary Algorithm based on Decomposition
211	MOEADR	Multi-Objective Differential Evolution with Ranking-based Mutation Operator
212	KnEA	Knee Evolutionary Algorithm
213	NSGA-III	Non-dominated Sorting Genetic Algorithm for multi-objective optimization
214	RVEA	Vector Guided Evolutionary Algorithm
215	IMMOEA	Inverse Modeling Many-Objective Evolutionary Algorithm
216	LMEA	Large-scale Many-Objective Evolutionary Algorithm
217	MOEA	Many-Objective Evolutionary Algorithm
218	BMO-DE	Bird Mating Optimization and Differential Evolutionary
219	MBF	Modified Bacterial Foraging
220	PSO-DE	Hybrid Particle Swarm Optimization- Differential Evolution
221	TLMVO	Tournament-Based Lévy Multiverse Optimization Algorithm
222	LMVO	Lévy Multiverse Optimization Algorithm
223	DHHO/M	Dynamic Harris Hawks Optimization with a Mutation Mechanism
224	Tsallis-MGOA	Tsallis Entropy based Modified Grasshopper Optimization Algorithm
225	Tsallis-MABC	Tsallis Entropy based Modified Artificial Bee Colony
226	Otsu-MFPA	Otsu Entropy based Modified Flower Pollination Algorithm
227	Otsu-GWO	Otsu Entropy based Grey Wolf Optimization
228	DPSO	Darwinian Particle Swarm Optimization
229	FODPSO	Fractional Order Darwinian Particle Swarm Optimization
230	DA	Dragonfly Algorithm
231	OBLDA	Opposition-Based Learning- Dragonfly Algorithm
232	GLCM	Gray Level Co occurrence Matrix
233	SVM	Support Vector Machine
234	NB	Naïve–Bayes
235	DT	Decision-Tree
236	KNN	K-Nearest Neighbors
237	RF	Random-Forest
238	FCM	Fuzzy C-Means
239	FLICM	Fuzzy Local Information C-Means
240	T2NSEIF	Type-2 Neutrosophic-Entropy for granular feature representation
241	MFCM	Modified Fuzzy C-Means
242	FKMCA	Fuzzy-K-Means Clustering Algorithm
243	KIFECM	Kernel Intuitionistic Fuzzy Entropy C-Means
244	NEATSA	Neutrosophic Entropy-Based Adaptive Thresholding Algorithm
245	FE-TII	Fuzzy Entropy Type II
246	OBL	Opposition-Based Learning
247	TSA	Tree Seed Algorithm
248	EM	Expectation Maximization
249	GLLA	Gray Level & Local-Average histogram
250	DCM	Dynamic Cauchy Mutation
251	DP	Dynamic Programming
252	SRM	Statistical Region Merging
253	ADMM	Alternating Direction Method of Multipliers
254	MEC	Minimum Cross Entropy
255	AIRS	Aerial Imagery for Roof Segmentation
256	VHR	Very High Resolution
257	MCE	Minimum Cross Entropy
258	COCO	Common Objects in Context

Table 5.

Different qualitative parameters used in the paper surveyed in Table 3 and its full form

SL	Parameter’s (abbreviation)	Full form
1	PSNR	Peak Signal to Noise Ratio
2	SSIM	Structural Similarity Index Metric
3	FSIM	Feature Similarity Index Metric
4	FNR	False Negative Rate
5	FPR	False Positive Rate
6	NPV	Negative Predictive Value
7	ME	Misclassification Error
8	J-Index	Jaccard-Index
9	RAE	Relative Foreground Area Error
10	F	F-measure
11	IRU	Intra-class Region Uniform
12	JSC	Jaccard Similarity Coefficient
13	CC	Correlation Coefficient
14	UM	Uniformity Measure
15	NMI	Normalized Mutual Information
16	ARI	Adjusted Rand Index
17	QILV	Quality Index based on Local Variance
18	MSE	Mean Squared Error
18	ERC	Edge Retention Coefficient
20	PRI	Probability Rand Index
21	VoI	Variation of Information
22	GCE	Global Consistency Error
23	BDE	Boundary Displacement Error
24	MSSIM	Mean Structural SIMilarity
25	JSC	Jaccard Similarity Coefficient
26	UQI	Universal Quality Index
27	DC	Dice Coefficient
28	SNR	Signal-to-noise ratio (SNR)
29	MAE	Maximum Absolute Error
30	RMSE	Root Mean Squared Error
31	NCC	Normalized Cross Correlation
32	AD	Average Difference
33	SC	Structural Content
34	NAE	Normalized Absolute Error
35	MAD	Mean Absolute Distance
36	QILV	Quality Index based on Local Variance
37	ME	Mean Error
38	IoU	Intersection over Union
39	GMSD	Gradient Magnitude Similarity Deviation
40	FDR	False Discovery Rate
41	PPV	Positive Predictive Value
42	FOR	False Omission Rate
43	NPV	Negative Predictive Value
44	MVTR	Mean Value to Reach
45	TVD	Threshold Value Distortion
46	HV	HyperVolume Measure
47	SP	Spacing Measure
48	U	Uniformity Measure

Fig. 3.

Graphical analysis: a Year wise published papers; b number of papers surveyed using different types of images

Major challenges of NIOA based multi-level thresholding

Based on the literature, it can be practically believed that NIOA has an enormous impact over MLT problem despite of some issues pertaining to few NIOA, particularly from theoretical perspectives as summarized in Sect. 2.1 that has clearly emphasized on some realistic challenges. In addition, the challenges specifically in regard to NIOA based MLT for image segmentation. Is thereby summarized as follows:

1. Selection of NIOA for MLT: It can be noticed that a massive set of NIOA has been introduced and exist in literature. Though, theoretically and practically, each NIOA’s performance extensively depends on the problem under consideration i.e. the image type for MLT. Nonetheless, it is not at all feasible to apply each NIOA over a set of images and assess its performance. Subsequently, for a researcher, appropriate selection of NIOA for a set of images turns out to be reasonably challenging. Current tradition also illustrates the application of newly developed NIOA over MLT and highlights a rigorous comparative study with other well-established NIOA in the problem domain.

2. Selection of Objective Function: Proper selection of objective function for a NIOA based MLT model for a specific set of images is also very demanding. Numerous objective functions are developed in the literature which makes the selection more crucial for a type of images like medical or satellite. For example, Paulo claimed that Tsallis’ entropy outperformed Cross and Shannon entropies by considering the segmentation of gray level images (Rodrigues et al. 2017). Ray et. al. (2021) claimed that Tsallis entropy is better than Otsu, Cross, Fuzzy entropy, Kapur’s entropy for proper thresholding of color pathology images. Whereas, Suresh et. al. claimed that Cross entropy is superior to Tsallis’ entropy to segment satellite images (Suresh and Lal 2017). Therefore, it can be said that the efficiency of the objective functions crucially depend on the NIOA and Image type.

3. Selection of Quality Parameters: As such there is no single criterion for completing accurate segmentation for different variants of images. Furthermore, there is no one metric for evaluating the segmentation quality of an image segmentation technique across various image types (Dhal et al. 2020a). Several quality parameters have been listed in Table 4 and some of their selection will judge which NIOA based MLT model is best for the set of image type under consideration.

4. Selection of Random walk for NIOA in the MLT domain: Randomization is a crucial part of any intelligence system, including current NIOA. Randomization allows an NIOA to leave any local optimum and search globally. Several random walks (Dhal et al. 2020b) demonstrated their effectiveness with various NIOA in various domains. Essentially, no analytical conclusions exist that proclaims which random walk is preferable for which algorithm. The application of any specific random walk, on the other hand, is entirely dependent on the problem and the NIOA in concern. As a result, choosing the right random walk during the development or improvement of NIOA is critical.

In addition to the above challenges, improvement of NIOA, their optimal parameters setting, their performance comparison in MLT based image segmentation domain are few other major challenging tasks that can be looked upon in future.

Experimental results

This section presents the experimental results which have been computed with the help of six NIOA and Masi entropy over satellite images. The six NIOA are Aquila Optimizer (AQO) (Abualigah et al. 2021a), Arithmetic Optimization Algorithm (AOA) (Abualigah et al. 2021b), Archimedes Optimization Algorithm (AROA) (Hashim et al. 2021), Rat Swarm Optimization Algorithm (RSA) (Dhiman et al. 2021), Particle Swarm Optimization (PSO) (Dhal et al. 2019c), and Firefly Algorithm (FA) (Dhal et al. 2020d). It can be noticed that four NIOA i.e., AQO, AOA, AROA, and RSA are developed in 2021 and they are very popular NIOA according to citation in Table 1. PSO and FA are well-established NIOA and selected to compare to these new NIOA for proving their effectiveness. Now, Masi entropy has been opted because it is state-of-the-art entropy and attracted many researchers in MLT domain over different kind of images. We maximize the Masi entropy for image segmentation. So, it is a maximization problem. For the reasonable comparison amongst NIOA methodologies, each execution of the tested objective functions considers the Number of Function Evaluations, NFE = 1000 × d, as stopping criterion of the optimization process. This criterion has been designated to encourage compatibility with previously published works in the literature. The experiments are evaluated considering the number of threshold values (TH) set to 5, 7, and 9which correspond to the d-dimensional search space in an optimization problem formulation. Furthermore, FE is also a crucial performance index used to measure the efficiency of NIOA. In comparison to computational complexity, FE permits some technical aspects such as the computer system where the experiments run and is implemented, that has direct impact on the running CPU time thereby concentrating only on the capacity of the algorithm to search within the solution space. For measuring the optimization ability of the NIOA, mean fitness $\left(\overline{f}\right)$ and standard deviation $\left(\sigma \right)$ have been calculated. On the other hand, the segmentation efficiency of the NIOA based models have been measured by computing Peak Signal-to-Noise Ratio (PSNR), Quality Index based on Local Variance (QILV), and Feature Similarity Index (FSIM). These parameters are very well-known in image segmentation domain. Table 4 highlights the list of utilized segmentation quality parameters (Dhal et al. 2020c, 2021b, 2021c; Das et al. 2021).

With the intention to verify the efficiency of different NIOA, experiment is conducted using 20 color satellite images. Further, MatlabR2018b and Windows-10 OS, × 64-based PC, Intel core i5 CPU with 8 GB RAM are the hardware and software requirements incorporated during the experiment. The proposed algorithms are tried and explored on images extracted from the site of Indian Space Research Organization (ISRO) (Dhal et al. 2019b) [https://bhuvan-app1.nrsc.gov.in/imagegallery/bhuvan.html#]. Figure 4 represents the original images of different satellite images. The parameter setting of the NIOA is given in Table 6.

Fig. 4.

Original satellite images

Table 6.

Parameter setting of the NIOA

Algorithm	Parameters
Aquila Optimizer (AQO)	For AQO, α = 0.1; δ = 0.1, population size $\left(\mathrm{n}\right)=30$
Arithmetic Optimization Algorithm (AOA)	For AOA, $\alpha =5\mu =0.5$, and population size $\left(\mathrm{n}\right)=30$
Archimedes Optimization Algorithm (AROA)	For AROA, initialize C1, C2, C3 and C4 with 2, 6, 2 and 0.5 respectively and population size $\left(\mathrm{n}\right)\mathrm{to}30$
Rat Swarm Optimization Algorithm (RSA)	For RSA, Control parameter (R)$\in$ (Yang 2020; Wolpert and Macready 1997), Constant Parameter C ∈ [0, 2], population size $\left(\mathrm{n}\right)\mathrm{is}\mathrm{set}\mathrm{to}30$
Particle Swarm Optimization (PSO)	For PSO, acceleration coefficients (${\mathrm{c}}_1$, ${\mathrm{c}}_2\mathrm{initialized}\mathrm{to}2$) that intends to control the outcome of local and global best solution over the current solution. For the experiment, Population size $\left(\mathrm{n}\right)\mathrm{is}\mathrm{initialized}\mathrm{to}30$
Firefly Algorithm (FA)	For FA, different parameters are initialized with certain values as depicted: Attractiveness ${\mathrm{\beta }}_0=1$, Light absorption coefficient $\mathrm{\gamma }=1$, Lévy flight parameters $\alpha =0.1$, $\mathrm{\beta }=1.5$, population size $\left(\mathrm{n}\right)=30$

Figure 5 represents the segmented images of Fig. 4 by the tested NIOA. Table 7 signifies different parameters such as average numerical values of PSNR, QILV, FSIM, standard deviation $\left({\sigma }_f\right)$, Computational time, and fitness function $\left(\overline{f}\right)$ employed over satellite images to implement NIOAs with Masi entropy as an objective function. Average fitness and standard deviation clearly show that AROA provides the best results over thresholds 5, 7, and 9. PSO gives worst results among all the tested NIOAs. From Table 7, we can further conclude that if numbers of thresholds increase, value of PSNR, QILV, and FSIM also increase for the objective function. The fitness values of AROA are equated with other NIOAs using a nonparametric significance proof (Wilcoxon’s rank test) (García et al. 2009). Such proof permits evaluating differences in the outcome among two related methods. Wilcoxon's rank test at the 5% significance level is used to determine if the results attained with the best performing algorithm vary statistically significantly from the final results of the other competitors. A p-value of less than 0.05 (5% significance level) sturdily supports the condemnation of the null hypothesis, thereby signifying that the best algorithm's results vary statistically noteworthy from those of the other peer algorithms and that the discrepancy is not due to chance. Table 8 reports the p-values produced by Wilcoxon’s test for a pair-wise comparison of the fitness function between two groups formed as AROA vs. AOA, AROA vs. AQO, AROA vs. RSA, AROA vs. FA, and AROA vs. PSO for 5, 7, and 9 number of thresholds. All of the p-values in Table 8 are less than 0.05 (5% significance level), and h = 1 is clear proof against the null hypothesis, showing that the AROA fitness values for the performance are statistically higher, and this is not a fluke.

Fig. 5.

Segmented results of NIOA using Masi entropy over 5, 7, and 9 thresholds

Table 7.

Numerical comparison of NIOA for Masi entropy as objective function

Number of thresholds (nt)	NIOA	$\overline{f}$	${\sigma }_f$	Time (s)	PSNR	QILV	FSIM
5	AROA	35.2724	7.12E−10	4.356363	21.57856	0.8827	0.9181
	AOA	35.2717	8.84E−10	4.440363	21.18856	0.8686	0.8922
	AQO	35.2715	9.51E−09	5.662363	21.17856	0.8497	0.8917
	RSA	35.2695	8.85E−10	6.436363	21.13665	0.8456	0.8905
	FA	35.2689	3.48E−09	6.445363	21.12856	0.8464	0.8906
	PSO	35.1555	9.67E−10	6.641363	20.45856	0.8382	0.8873
7	AROA	41.4019	2.26E−10	5.725363	23.14856	0.9206	0.9314
	AOA	41.3983	5.92E−09	5.602363	23.09856	0.9135	0.9191
	AQO	41.3961	7.64E−10	6.817363	23.07856	0.9115	0.9085
	RSA	41.3953	4.90E−10	7.045363	22.20856	0.9101	0.9024
	FA	41.3896	7.17E−10	7.078363	23.02856	0.9134	0.903
	PSO	41.1121	9.18E−10	7.241363	22.10856	0.9048	0.8926
9	AROA	46.7711	3.25E−10	5.915363	26.13856	0.9562	0.9645
	AOA	46.7456	3.45E−10	5.825363	25.98561	0.9449	0.9541
	AQO	46.7136	2.52E−10	7.185363	25.95856	0.9384	0.9489
	RSA	46.7045	1.00E−09	7.405363	24.28856	0.9251	0.9197
	FA	46.6937	4.60E−09	7.393363	24.65856	0.9248	0.9244
	PSO	46.5771	4.51E−10	7.557363	24.07856	0.9129	0.9132

Best results are highlighted in bold

Table 8.

Comparison among NIOA depending on Wilcoxon p-values

Pair of NIOA	Masi entropy
	nt = 5		nt = 7		nt = 9
	p	h	p	h	p	h
AROA vs. AOA	< 0.05	1	< 0.05	1	< 0.05	1
AROA vs. AQO	< 0.05	1	< 0.05	1	< 0.05	1
AROA vs. RSA	< 0.05	1	< 0.05	1	< 0.05	1
AROA vs. FA	< 0.05	1	< 0.05	1	< 0.05	1
AROA vs. PSO	< 0.05	1	< 0.05	1	< 0.05	1

Conclusion and future directions

This study has three major contribution as a survey paper which are (i) List of recent NIOA which felicitate the researchers for selecting and employing these new NIOA over different engineering optimization field, (ii) A survey table of NIOA based MLT for image segmentation which will give idea about the application of different NIOA with different objective functions over different kind of images, (iii) lastly a comparative study among some newly proposed NIOA have been performed with recently developed Masi entropy for satellite image multi-level thresholding. The experimental results are very encouraging due to the application of different NIOA over Masi entropy-based image segmentation.

Therefore, it can be easy to infer that NIOA based MLT is a fresh and exciting research topic with innovative methodologies. Applying diverse NIOA with various objective functions over several types of images is considered a complicated task. The main challenging future direction is the testing of this huge set of NIOA in MLT domain. Selection of proper objective function is also a difficult task because it is reported in literature that proper segmentation of specific kind of images is significantly depends on objective function. Exploration of multi-objective MLT can also be a great future work. Recently histogram clustering has been emerged as good alternative of histogram thresholding (Dhal et al. 2021c; Das et al. 2021). Therefore, application of NIOA for histogram based image clustering can also be a good future direction. Another application of NIOA will be for fuzzy rule classifier (Zhou and Angelov 2007; Angelov and Zhou 2008) or data analytics (Angelov et al. 2017).

Funding

There is no funding related with this research.

Declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest. The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.