Abstract
Reinforcement learning (RL) models have advanced our understanding of how animals learn and make decisions, and how the brain supports some aspects of learning. However, the neural computations that are explained by RL algorithms fall short of explaining many sophisticated aspects of human decision making, including the generalization of learned information, one-shot learning, and the synthesis of task information in complex environments.. Instead, these aspects of instrumental behavior are assumed to be supported by the brain’s executive functions (EF). We review recent findings that highlight the importance of EF in learning. Specifically, we advance the theory that EF sets the stage for canonical RL computations in the brain, providing inputs that broaden their flexibility and applicability. Our theory has important implications for how to interpret RL computations in the brain and behavior.
Introduction
Our ability to learn rewarding actions lies at the core of goal-directed decision-making. Reward-driven choice processes have been extensively modeled using reinforcement learning (RL) algorithms [Sutton and Barto, 2018]. This formalized account of learning and decision making has contributed significantly to expanding the frontiers of artificial intelligence research [Botvinick et. al, 2019], our understanding of clinical pathologies [Wyckmans et. al, 2019, Radulescu & Niv, 2019], and research on developmental changes in learning [Segers et. al, 2018; Master et. al, 2019].
A key reason for the success of the RL framework is its ability to capture learning not only at the behavioral level, but also at the neural level. The neural foundations of reward-dependent learning [Schultz et. al, 1997], and its various successors [Dabney et. al, 2020], have established a well defined brain network that performs RL computations. In particular, cortico-striatal loops enable state-dependent value-based choice selection [Frank, 2011]. Furthermore, dopaminergic signaling of reward-prediction errors (RPEs) in the midbrain and striatum induces plasticity consistent with RL algorithms, incrementally increasing/decreasing the value of actions that yield better/worse than expected outcomes.
Despite its tremendous success, there are well known limitations of canonical RL algorithms [Vong et al., 2019]. Historically, many insights provided by RL research have been demonstrated in relatively simplistic learning tasks, casting doubt on how useful classic RL models are in explaining how humans learn and make choices in everyday life. To solve this problem, recent research often augments RL algorithms with learning and memory mechanisms from different cognitive systems.
Executive functions (EF) have been identified as psychological faculties that could interact with RL computations. For instance, working memory (WM), as a short-term cache which allows us to retain and manipulate task-relevant information over brief periods [Miller et al., 2018; Lundqvist et al., 2018; Nassar et al., 2018], occupies a central position in our ability to organize goal-directed behavior. Another core EF, attention, also contributes to behavioral efficiency through selective processing of subsets of environmental features relevant for learning [Radulescu, Niv & Ballard, 2019; Norman & Shallice, 1986; Allport, 1989]. Research on WM and attention points to the prefrontal cortex (PFC) as the primary site of these processes [Badre, 2020; Badre & Desrochers, 2019], suggesting that this network shapes information processing in the RL system during learning.
Several straightforward experimental manipulations have revealed that an isolated RL system fails to effectively capture human instrumental learning behavior. For example, while online maintenance of representations in WM is capacity-limited [Baddeley, 2012], standard RL models have no explicit capacity constraints. This property of RL suggests that if individuals rely on RL alone, learning should not be affected by the number of rewarding stimulus-response associations they are required to learn in a given task. However, humans learn much less efficiently when the number of associations to be learned in parallel exceeds WM capacity [Collins, 2018; Master et. al, 2019; Collins & Frank, 2017]. This suggests that RL operates with EFs like working memory for learning. Other work has similarly shown that EF-dependent planning contributes to choice alongside core RL computations implemented in the brain [Daw et. al 2011; Russek et. al, 2017].
However, there is also evidence that EF’s contributions to learning are not limited to providing a separate learning substrate: Rather, EF may also directly contribute to RL computations in the brain. Models of PFC-striatal loops [Hazy et al., 2007, Zhao et al. 2017], which posit that brain regions associated with EF and RL interact directly, has motivated behavioral experiments and computational modeling approaches aimed at identifying EF-RL interactions [Collins, 2018; Collins & Frank, 2018; Radulescu & Niv, 2018; Segers et. al, 2018]. The advent of these modeling tools has shown that an interaction of multiple neurocognitive domains (e.g., RL, WM, attention) may provide a more robust account of goal-directed behavior, one that still maintains the centrality of canonical RL computations in instrumental learning [Hernaus et. al, 2018; Quaedflieg et. al, 2019].
In this paper, we review recent work that provides converging evidence for direct, functionally coherent contributions of EF to RL computations. More specifically, we review how EF (WM and attention in particular) might set the stage for RL computations in the brain by defining the relevant state space, action space, and reward function (Figure 1). The ideas reviewed here can help inform future computational modeling efforts and experimental designs in the study of goal-directed behavior. Furthermore, it may shift our interpretations of past and future findings focused on isolated RL computations towards a broader framework that considers EF contributions.
Figure 1.
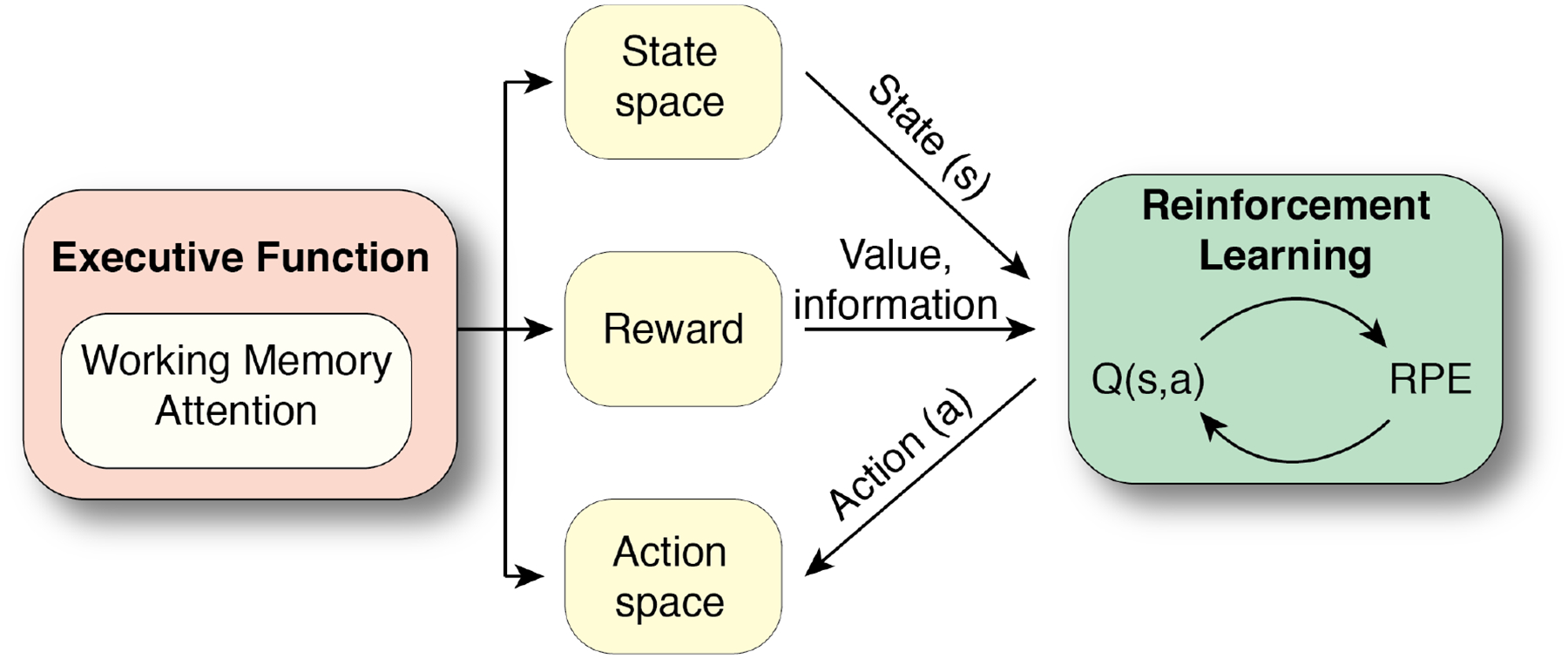
Schematic of EF contributions (WM, attention) to RL computations. EF can optimize RL computations in the domain of 3 relevant RL-components: state space, reward functions, and action space. Q(s,a) reflects the estimated value of a state and action. RPE is the reward prediction error used to update Q(s,a).
The ingredients of RL computations
Past work suggests that a specific brain network (primarily cortico-striatal loops) supports RL computations, like temporal difference learning [O’Doherty et al., 2003; Seymour et al., 2004] and actor-critic learning [Joel et al., 2002; Khamassi et al., 2005]. These learning algorithms update estimates of values via reward prediction errors (RPEs). In machine learning, such algorithms are defined not only by how they estimate value, but also by (at least) three fundamental components: 1) the state space (reflecting the possible states or contexts an agent may be in), 2) the action space (reflecting the possible choices to be made), and 3) the reward function (defining valuable outcomes). The specification of these variables can dramatically impact the behavior of a decision-making agent. How these three variables are input to the brain’s RL network is poorly understood - we explore here a role for EF in contributing this information.
State space
The RL framework defines a state space over which learning occurs. A state can be a location in the environment, a sensory feature of the environment (e.g. the presence of a stimulus such as a light), or a more abstract internally represented context (such as a point in time). At each state, a decision-making agent enacts a choice in pursuit of rewards [Sutton and Barto, 2018]. The specification of the state space crucially impacts the behavior of artificial RL agents. For example, in a large state space, RL performance is limited by what is known as the curse of dimensionality [Sutton & Barto 2018; Vong et al., 2019]: Learning a vast number of state-action values quickly becomes computationally intractable. Defining a smaller state space limited to only task-relevant states is one path toward overcoming this difficulty.
Simplifying the state space is a function sometimes attributed to attentional filters, which can specify important features of the environment [Radulescu & Niv, 2019]. In this framework, attention tags the task features that RL computes over [Zhang et. al, 2018; Niv, 2019; Radulescu, Niv & Ballard, 2019; Daniel, Radulescu & Niv, 2019]. This is accomplished by attention differentially weighing environmental features, assigning a higher weight to task-relevant ones [Niv, 2019] (Figure 2). For instance, if an agent is attempting to earn reward from various stimuli that differ along several dimensions (e.g. color, shape), with only one dimension predicting reward, an optimized learning agent would 1) identify that dimension, and 2) use it as the relevant state space for RL. That way, an agent can eschew computing values over a larger state space of all possible features [Leong, Radulescu et al., 2017*, Farashahi et al., 2017].
Figure 2.
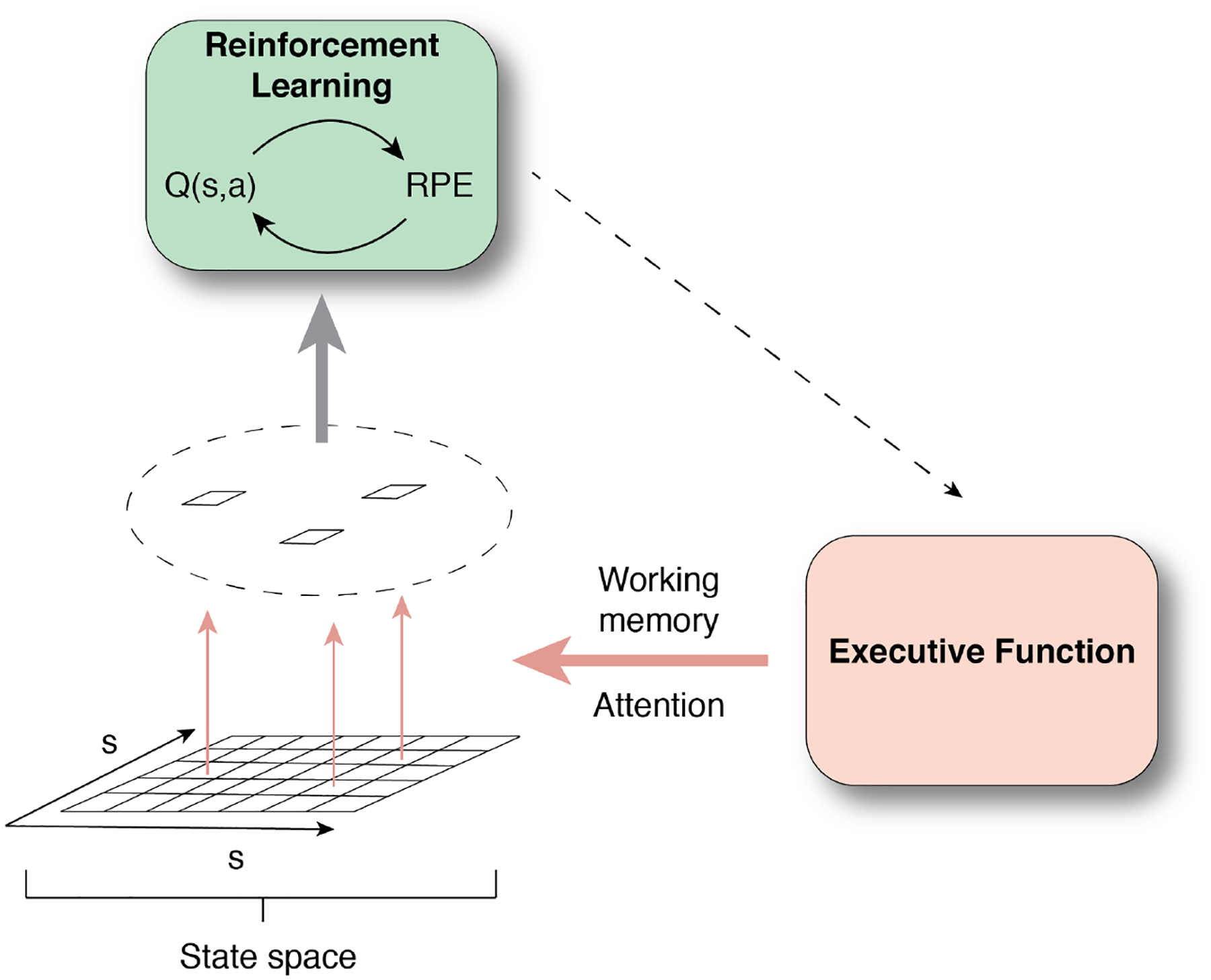
EF specifies the relevant state space, allowing the RL system to efficiently operate over a subset of task-relevant states. See Figure 1 for notations.
Computationally this can be achieved by implementing Bayesian inference to discover relevant task features that RL operates over [Radulescu, Niv & Ballard, 2019]. In addition to attention affording the reduction of the task complexity, attentional mechanisms serve another purpose. Many tasks share overlapping/competing state spaces, leading to potential interference in correct action selection (e.g. the Stroop Task). Thus, defining a low-dimensional representation which can be applied to multiple tasks in service of goal pursuit makes learning both more flexible and robust [Lieder et al., 2018].
The relevant state space is not always signaled by explicit sensory cues. Thus, an agent often has to make an inference about their current state [Gershman et al., 2013]. Recent work in animals suggests that RL computations in the striatum are likely performed over these latent belief states [Babayan et al., 2018; Samejima & Doya, 2007]. For example, by showing markedly different dopamine dynamics if an expected reward is sure to arrive (e.g., 100% chance) versus almost sure to arrive (e.g., 90% chance) [Starkweather et al., 2017]. In this example, an inference about the latent state, which indicates whether a reward will arrive or not, dramatically alters RL computations. It is hypothesized that RL computations over these belief states, may be mediated by input from frontal cortices involved in the discovery and representation of state spaces, further supporting a link between EF and RL [Wilson et al., 2014].
Action space
Above we reviewed a role of EF, such as working memory and attention, in attending to and carving out the appropriate state space for RL. A complementary idea is that EF also play a role in specifying (or simplifying) the action space for the RL system (Figure 3). The action space in the RL formalism is defined as the set of choices an agent can make. The choice can take the form of a basic motor action (e.g. a key press), a complex movement (e.g. walking to the door), or an abstract choice not defined by specific motor actions (e.g. choosing soup vs. salad). Defining the relevant action space may be as essential for learning as defining the relevant state space.
Figure 3.
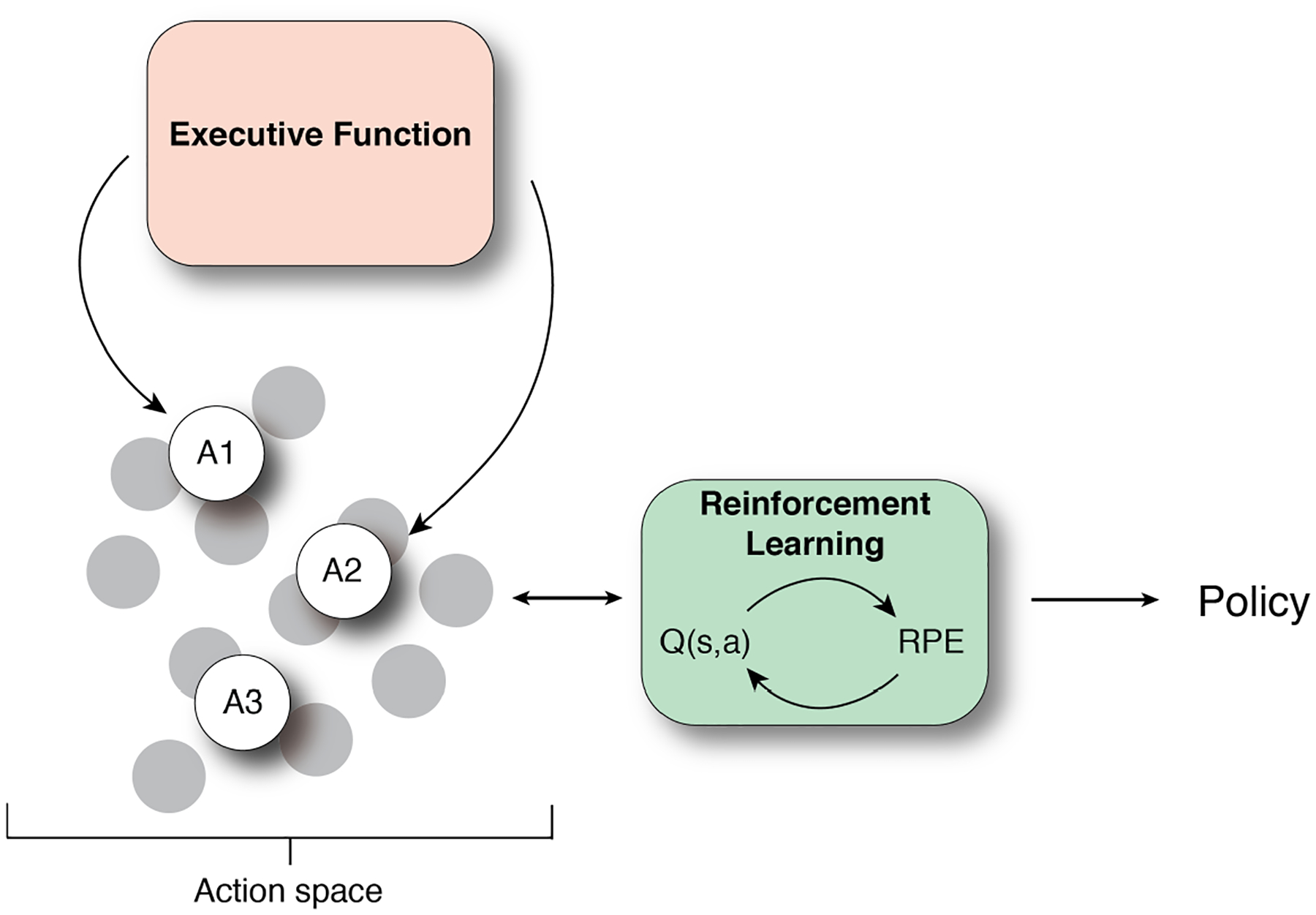
Contribution of executive functions in action selection.
Recent studies indicate that the action space is a separable dimension for RL. First, behavioral evidence suggests that reward outcomes can simultaneously be assigned to task-relevant choices as well as to task-irrelevant motor actions (i.e., reinforcing a right-finger button press regardless of the stimulus that was present) [Shahar et al., 2019]. Moreover, this process appears to be negatively related to the use of goal-directed planning strategies, suggesting that EF enables RL to focus in on the task-relevant action space. Similarly, recent modeling work suggests that a stateless form of action values can exert an influence on both choices and reaction times [McDougle & Collins, 2020], particularly when cognitive load is high. One hypothetical consequence of learning over the action dimension is that when executive functions are disrupted or taxed – and thus can not properly conjoin states and actions – action values may be learned in a vacuum. Speculatively, this bias could be linked to maladaptive forms of habitual behavior, such as addiction [Everitt & Robbins, 2016].
Because actions link predicted choice values with observed outcomes, one natural question beyond the selection of actions is how the RL system differentiates choice errors (e.g., which is the best object?) from choice execution errors (e.g., did I grasp the desired object?). In RL tasks that require reaching movements, behavioral data and fMRI responses in the striatum suggest that perceived action errors influence RPEs: That is, if the credit for a negative outcome is assigned to the motor system, the RL system appears to eschew updating the value of the choice that was made [McDougle et al., 2016; McDougle et al., 2019]. These results suggest that simple cognitive inferences about the cause of errors (e.g., choice errors versus action errors) affect RL computations.
In more complex situations with a large action space, EF can aid the learning process by attempting to reduce the size of this space. That is, the brain can create “task-sets”, or selective groupings of state-action associations and use contextual cues to retrieve the appropriate task set. To illustrate, if one learns the motor commands for copying text on both a PC and a Mac, to avoid interference it is beneficial to associate the specific motor sequences (ctrl-c versus command-c) with their respective contexts (typing on a PC keyboard versus a Mac keyboard). Indeed, humans appear to cluster subsets of actions with associated sensory contexts during instrumental learning [Collins & Frank, 2013; Franklin & Frank, 2018], and they do so in a manner which suggests that high-level inferences about task structure shape low-level reinforcement learning computations over actions.
Moreover, selecting a task-set can itself be seen as a choice made in a high-level context. Learning to make this abstract choice can also occur via RL, such that RL computations happen over two different state-action spaces in parallel -- an abstract context and task-set space, and a more concrete stimulus-action space [Eckstein & Collins, 2020; Ballard et al., 2018]. There is recent computational, behavioral, and neural evidence that hierarchies of RL computations happen in parallel over more and more abstract types of states and choices, facilitating complex learning abilities [Badre & Frank, 2012; Frank & Badre, 2012; Eckstein & Collins, 2020]. Such learning may be supported by hierarchies of representations in prefrontal context [Koechlin & Summerfield, 2007; Badre & D’Esposito 2009]. This again highlights a role for EF in setting the stage for RL computations to support complex learning.
Rewards & expectations
Goal-directed behavior is dependent on making correct predictions about the outcome of our choices. RPEs, which serve as a teaching signal, occupy a central position in the RL framework, linking midbrain dopaminergic activity with RL computations [Schultz, et. al, 1997]. Most RL research since has focused on simple forms of learning from outcomes that are primary or secondary rewards, such as food, money, or points. However, the path to an RPE is not always straightforward: For instance, recent work departs from the role of dopaminergic signaling in standard RPEs based on scalar rewards, extending the domain of RL to learning from indirect experiences (e,.g., secondary conditioning) and more abstract learning of associations based on sensory features [Langdon et. al, 2018, Sharpe et. al, 2020]. These findings suggest that the currency of RL computations goes beyond primary and secondary rewards. There is early evidence that EF could be implicated in setting this currency.
One such example relates to the value of information. Humans are motivated to reduce uncertainty about their environment [White et. al, 2019]. Thus, acquisition of novel information should in itself function as reinforcement. Most information-seeking mechanisms, however, are not accounted for in the traditional RL framework. By contrast, recent work has shown that uncertainty reduction and information gain are indeed reflected in neural RL computations [Mikhael et. al, 2019]. Evidence from fMRI studies suggests that corticostriatal circuits incorporate the utility of information in reward computations, such that information is conceptualized as a reward that reinforces choices [Charpentier et. al, 2018], even when it is not valenced [White et. al, 2019]. The prefrontal cortex also appears to track information and uncertainty [Starkweather et al., 2018], which can be held in working memory to influence decision making [Honig et. al 2020] (Figure 4).
Figure 4.
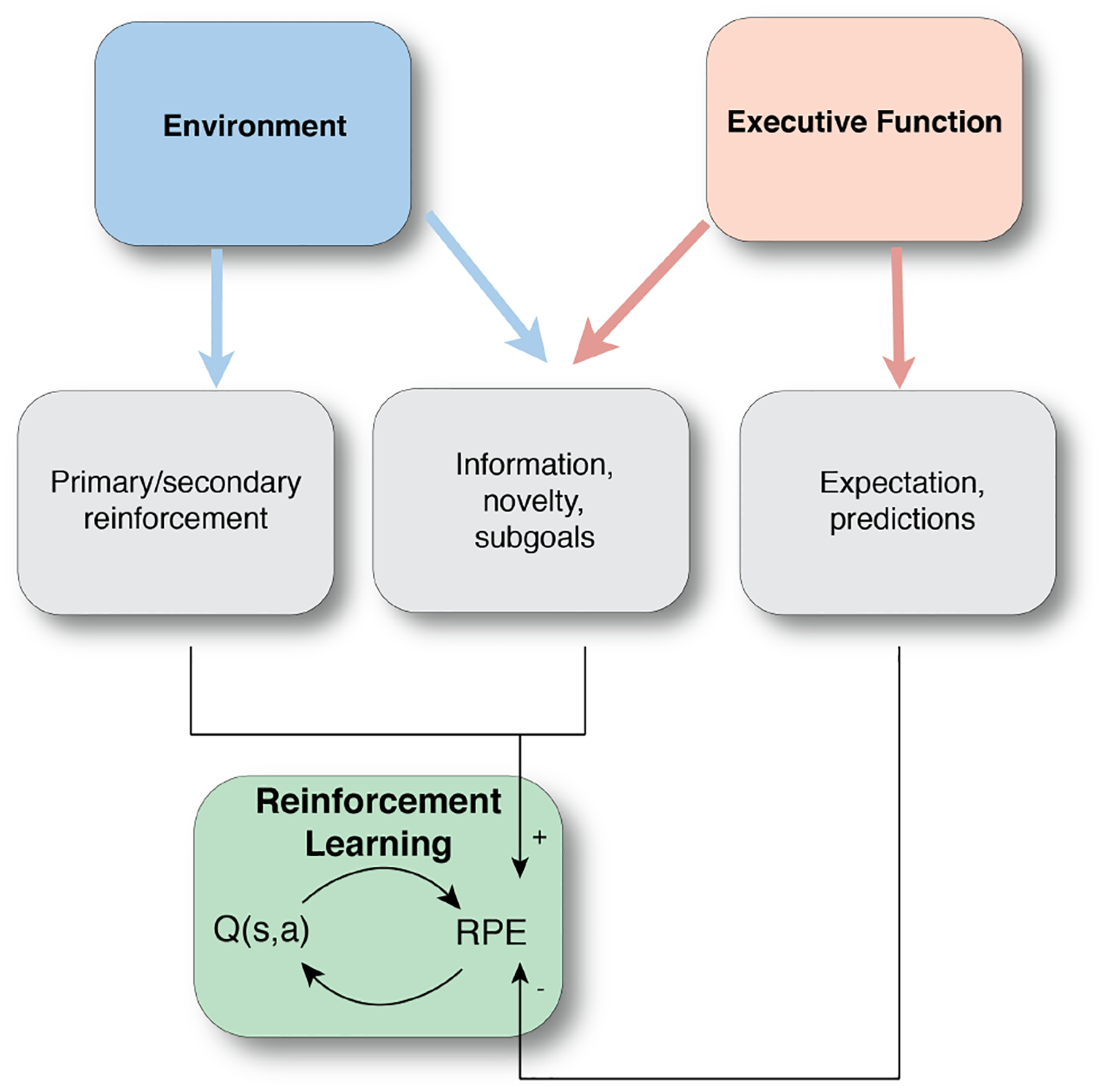
Traditional model of putative neural mechanisms involved in reward learning suggests that the RPEs are primarily driven by the primary and/or secondary reinforcement. More recent work posits that RPEs are also influenced by the factors other than the scalar rewards, including information, novelty and subgoal, as well as expectations/predictions.
The theoretical framework of hierarchical RL also dissociates the role of exploiting information about the environment from the role of primary/secondary rewards, while emphasizing that both act as a teaching signal [Botvinick et al., 2009]. In particular, when learning a multi-step policy that ultimately leads to a rewarding goal, agents identify and use subgoals en route to terminal rewards. These subgoals generate pseudo-rewards in hierarchical RL models, and appear to drive activity in the canonical reward-processing regions in the brain, even though these rewards are 1) not inherently rewarding, and 2) are clearly distinguished from terminal rewards [Mas-Herrero et. al, 2019; Diuk et al., 2013]. The processing of pseudo-rewards is additionally assumed to be driven by the prefrontal cortex, suggesting a link to EF [Ribas-Fernandes et al., 2019].
Beyond expanding the space of rewarding outcomes, there is also evidence that EF may affect RPEs in an alternative way: namely, by inputting reward expectations that have not yet been learned by the RL network. For example, work by Collins and colleagues (2017) has shown that the magnitude of RPEs in the striatum is affected by cognitive load such that learning a small number of stimulus-response associations leads to attenuated striatal RPEs. This result is explained by “top-down” input of predictions from working memory: Information held in working memory in simple learning environments creates expectations of reward that are learned faster than in the RL system, and thus weaken RL RPEs (Collins & Frank 2018, Collins 2018). Similar results are observed in planning tasks, where an EF-dependent planned expectation of reward modulates the classic representation of RPEs in the striatum (Daw et al 2011). Taken together, these results demonstrate a key role for EF in defining the reward function for the RL system, and in contributing to the value estimation process.
Conclusions & discussion
We have reviewed and summarized computational, behavioral and neural evidence which collectively suggest that (1) executive function shapes reinforcement learning computations in the brain, and (2) neural and cognitive models of this interaction provide useful accounts of goal-directed behavior. We discussed the EF-RL interaction vis-a-vis the specification of the state space, action space, and reward function that RL operates over.
This new framework has important implications for applying both neural and cognitive computational models to study individual differences in learning. Although it is tempting to study individual differences with simple RL models, it is essential that we carefully consider the role of alternative neurocognitive systems in learning. Evidence of individual learning differences captured by an RL model might not reflect differences in the brain’s RL process, but rather in upstream EF that shapes RL. Indeed, recent work on development [Segers et. al, 2018; Daniel et al, 2019], schizophrenia [Collins et. al, 2014], and addiction [Renteria et. al, 2018; Wyckmans et. al, 2019] has shown that individual variability in learning might be driven by both EF and RL, and/or the interaction of the two. Thus, building improved models of the interplay between different neurocognitive systems should help us better understand individual differences across the lifespan and in clinical disorders. This expansion of the RL theoretical framework can deepen our understanding of how learning is supported in the brain, and inform future interventions and treatments.
Highlights:
Learning is supported by the brain’s reinforcement learning (RL) network
Executive functions (EF) support other forms of learning, but also interact with and shape RL
EF help define the state and action spaces for the brain’s RL computations
EF signal non-rewarding reinforcing outcomes included in reward prediction error
Neural and cognitive models unifying RL and EF may improve our understanding of goal-directed behavior
References
- 1.Allport A (1989). Visual attention. In Posner MI (Ed.), Foundations of cognitive science (p. 631–682). The MIT Press. [Google Scholar]
- 2.Babayan BM, Uchida N & Gershman SJ Belief state representation in the dopamine system. Nat Communications 9, 1891 (2018). 10.1038/s41467-018-04397-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Baddeley A (2012). Working memory: theories, models, and controversies. Annual Review of Psychology, 63, 1–29. 10.1146/annurev-psych-120710-100422 [DOI] [PubMed] [Google Scholar]
- 4.Badre D (2020). Brain networks for cognitive control: Four unresolved questions. In Kalivas PW and Paulus MP (Eds.), Intrusive Thinking across Neuropsychiatric Disorders: From Molecules to Free Will. Strüngmann Forum Reports, vol. 30, Lupp JR, series editor. Cambridge, MA: MIT Press, in press. [Google Scholar]
- 5.Badre D, & Desrochers TM (2019). Chapter 9—Hierarchical cognitive control and the frontal lobes. In D’Esposito M & Grafman JH (Eds.), Handbook of Clinical Neurology (Vol. 163, pp. 165–177). Elsevier. 10.1016/B978-0-12-804281-6.00009-4 [DOI] [PubMed] [Google Scholar]
- 6.Badre D & Frank MJ (2012). Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 2: Evidence from fMRI. Cerebral Cortex, 22, 527–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Badre D, & D’Esposito M (2009). Is the rostro-caudal axis of the frontal lobe hierarchical? Nature Reviews Neuroscience, 10, 659–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ballard I, Miller EM, Piantadosi ST, Goodman ND, & McClure SM (2018). Beyond Reward Prediction Errors: Human Striatum Updates Rule Values During Learning. Cerebral Cortex, 28(11), 3965–3975. 10.1093/cercor/bhx259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Botvinick M, Ritter S, Wang JX, Kurth-Nelson Z, Blundell C, & Hassabis D (2019). Reinforcement Learning, Fast and Slow. Trends in Cognitive Sciences, 23(5), 408–422. 10.1016/j.tics.2019.02.006 [DOI] [PubMed] [Google Scholar]
- 10.Botvinick MM, Niv Y, & Barto AG (2009). Hierarchically organized behavior and its neural foundations: A reinforcement learning perspective. Cognition, 113(3), 262–280. 10.1016/j.cognition.2008.08.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Charpentier CJ, Bromberg-Martin ES, & Sharot T (2018). Valuation of knowledge and ignorance in mesolimbic reward circuitry. PNAS Proceedings of the National Academy of Sciences of the United States of America, 115(31), E7255–E7264. 10.1073/pnas.1800547115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Collins AGE, Ciullo B, Frank MJ, & Badre D (2017). Working Memory Load Strengthens Reward Prediction Errors. Journal of Neuroscience, 37(16), 4332–4342. 10.1523/JNEUROSCI.2700-16.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Collins AGE & Frank MJ (2018). Within- and across-trial dynamics of human EEG reveal cooperative interplay between reinforcement learning and working memory. Proceedings of the National Academy of Sciences, 115, 2502–2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Collins AGE (2018). The Tortoise and the Hare: Interactions between Reinforcement Learning and Working Memory. Journal of Cognitive Neuroscience, 30(10), 1422–1432. 10.1162/jocn_a_01238 [DOI] [PubMed] [Google Scholar]
- 15.Collins AGE, Brown JK, Gold JM, Waltz JA, & Frank MJ (2014). Working Memory Contributions to Reinforcement Learning Impairments in Schizophrenia. Journal of Neuroscience, 34(41), 13747–13756. 10.1523/JNEUROSCI.0989-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Collins AGE, Brown J, Gold J, Waltz J & Frank MJ (2014). Working memory contributions to reinforcement learning in schizophrenia. Journal of Neuroscience, 34, 13747–13756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collins AGE & Frank MJ (2013). Cognitive control over learning: Creating, clustering and generalizing task-set structure. Psychological Review, 120, 190–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dabney W, Kurth-Nelson Z, Uchida N, Starkweather CK, Hassabis D, Munos R, & Botvinick M (2020). A distributional code for value in dopamine-based reinforcement learning. Nature, 577(7792), 671–675. 10.1038/s41586-019-1924-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Daniel R, Radulescu A, & Niv Y (2020). Intact Reinforcement Learning But Impaired Attentional Control During Multidimensional Probabilistic Learning in Older Adults. Journal of Neuroscience, 40(5), 1084–1096. 10.1523/JNEUROSCI.0254-19.20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Daw ND, Gershman SJ, Seymour B, Dayan P, & Dolan RJ (2011). Model-based influences on humans’ choices and striatal prediction errors. Neuron, 69(6), 1204–1215. 10.1016/j.neuron.2011.02.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Diuk C, Tsai K, Wallis J, Botvinick M, & Niv Y (2013). Hierarchical Learning Induces Two Simultaneous, But Separable, Prediction Errors in Human Basal Ganglia. The Journal of Neuroscience, 33(13), 5797–5805. 10.1523/JNEUROSCI.5445-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Eckstein MK, & Collins AG (in press). Computational evidence for hierarchically-structured reinforcement learning in humans. Proceedings of the National Academy of Sciences. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Everitt BJ, & Robbins TW (2016). Drug Addiction: Updating Actions to Habits to Compulsions Ten Years On. Annual Review of Psychology, 67, 23–50. 10.1146/annurev-psych-122414-033457 [DOI] [PubMed] [Google Scholar]
- 24.Farashahi S, Rowe K, Aslami Z, Lee D, & Soltani A (2017). Feature-based learning improves adaptability without compromising precision. Nature Communications, 8(1), 1768. 10.1038/s41467-017-01874-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Frank MJ (2011). Computational models of motivated action selection in corticostriatal circuits. Current Opinion in Neurobiology, 21(3), 381–386. 10.1016/j.conb.2011.02.013 [DOI] [PubMed] [Google Scholar]
- 26.Franklin NT & Frank MJ (2018). Compositional clustering in task structure learning. PLOS Computational Biology, 14(4): e1006116,. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Frank MJ & Badre D (2012). Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 1: Computational analysis. Cerebral Cortex, 22, 509–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gershman SJ, Jones CE, Norman KA, Monfils MH, Niv Y (2013). Gradual extinction prevents the return of fear: implications for the discovery of state. Frontiers in Behavioral Neuroscience. 7: 164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hazy TE, Frank MJ, & O’Reilly RC (2007). Towards an executive without a homunculus: Computational models of the prefrontal cortex/basal ganglia system. Philosophical Transactions of the Royal Society B: Biological Sciences, 362(1485), 1601–1613. 10.1098/rstb.2007.2055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hernaus D, Xu Z, Brown EC, Ruiz R, Frank MJ, Gold JM, & Waltz JA (2018). Motivational deficits in schizophrenia relate to abnormalities in cortical learning rate signals. Cognitive, Affective, & Behavioral Neuroscience, 18(6), 1338–1351. 10.3758/s13415-018-0643-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Honig M, Ma WJ, & Fougnie D (2020). Humans incorporate trial-to-trial working memory uncertainty into rewarded decisions. Proceedings of the National Academy of Sciences, 117(15), 8391–8397. 10.1073/pnas.1918143117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Joel D, Niv Y, & Ruppin E (2002). Actor–critic models of the basal ganglia: New anatomical and computational perspectives. Neural Networks, 15(4), 535–547. 10.1016/S0893-6080(02)00047-3 [DOI] [PubMed] [Google Scholar]
- 33.Khamassi M, Lachèze L, Girard B, Berthoz A, & Guillot A (2005). Actor–Critic Models of Reinforcement Learning in the Basal Ganglia: From Natural to Artificial Rats. Adaptive Behavior, 13(2), 131–148. 10.1177/105971230501300205 [DOI] [Google Scholar]
- 34.Koechlin E, & Summerfield C (2007). An information theoretical approach to prefrontal executive function. Trends in Cognitive Sciences, 11(6), 229–235. 10.1016/j.tics.2007.04.005 [DOI] [PubMed] [Google Scholar]
- 35.Langdon AJ, Sharpe MJ, Schoenbaum G, & Niv Y (2018). Model-based predictions for dopamine. Current Opinion in Neurobiology, 49, 1–7. 10.1016/j.conb.2017.10.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lieder F, Shenhav A, Musslick S, & Griffiths TL (2018). Rational metareasoning and the plasticity of cognitive control. PLOS Computational Biology, 14(4), e1006043. 10.1371/journal.pcbi.1006043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lundqvist M, Herman P, & Miller EK (2018). Working Memory: Delay Activity, Yes! Persistent Activity? Maybe Not. The Journal of Neuroscience, 38(32), 7013–7019. 10.1523/JNEUROSCI.2485-17.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mas-Herrero E, Sescousse G, Cools R, & Marco-Pallarés J (2019). The contribution of striatal pseudo-reward prediction errors to value-based decision-making. NeuroImage. 10.1016/j.neuroimage.2019.02.052 [DOI] [PubMed] [Google Scholar]
- 39.Master SL, Eckstein MK, Gotlieb N, Dahl R, Wilbrecht L, & Collins AGE (2020). Disentangling the systems contributing to changes in learning during adolescence. Developmental Cognitive Neuroscience, 41, 100732. 10.1016/j.dcn.2019.100732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McDougle SD, Boggess MJ, Crossley MJ, Parvin D, Ivry RB, & Taylor JA (2016). Credit assignment in movement-dependent reinforcement learning. Proceedings of the National Academy of Sciences, 113(24), 6797–6802. 10.1073/pnas.152366911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McDougle SD, Butcher PA, Parvin DE, Mushtaq F, Niv Y, Ivry RB, & Taylor JA (2019). Neural Signatures of Prediction Errors in a Decision-Making Task Are Modulated by Action Execution Failures. Current Biology, 29(10), 1606–1613.e5. 10.1016/j.cub.2019.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McDougle S, & Collins A (2019). Modeling the influence of working memory, reinforcement, and action uncertainty on reaction time and choice during instrumental learning [Preprint]. PsyArXiv. 10.31234/osf.io/gcwxn [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mikhael JG, Kim HR, Uchida N, & Gershman SJ (2019). Ramping and State Uncertainty in the Dopamine Signal [Preprint]. Neuroscience. 10.1101/805366 [DOI] [Google Scholar]
- 44.Miller EK, Lundqvist M, & Bastos AM (2018). Working Memory 2.0. Neuron, 100(2), 463–475. 10.1016/j.neuron.2018.09.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nassar MR, Helmers JC, & Frank MJ (2018). Chunking as a rational strategy for lossy data compression in visual working memory. Psychological Review, 125(4), 486–511. 10.1037/rev0000101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Niv Y (2019). Learning task-state representations. Nature Neuroscience, 22(10), 1544–1553. 10.1038/s41593-019-0470-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Norman DA, Shallice T (1986) Attention to Action. In: Davidson RJ, Schwartz GE, Shapiro D (eds) Consciousness and Self-Regulation. Springer, Boston, MA [Google Scholar]
- 48.O’Doherty JP, Dayan P, Friston K, Critchley H, & Dolan RJ (2003). Temporal Difference Models and Reward-Related Learning in the Human Brain. Neuron, 38(2), 329–337. 10.1016/S0896-6273(03)00169-7 [DOI] [PubMed] [Google Scholar]
- 49.O’Reilly RC, & Frank MJ (2006). Making Working Memory Work: A Computational Model of Learning in the Prefrontal Cortex and Basal Ganglia. Neural Computation, 18(2), 283–328. 10.1162/089976606775093909 [DOI] [PubMed] [Google Scholar]
- 50.Quaedflieg CWEM, Stoffregen H, Sebalo I, & Smeets T (2019). Stress-induced impairment in goal-directed instrumental behaviour is moderated by baseline working memory. Neurobiology of Learning and Memory, 158, 42–49. 10.1016/j.nlm.2019.01.010 [DOI] [PubMed] [Google Scholar]
- 51.Radulescu A, Niv Y, & Ballard I (2019). Holistic Reinforcement Learning: The Role of Structure and Attention. Trends in Cognitive Sciences, 23(4), 278–292. 10.1016/j.tics.2019.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Radulescu A, & Niv Y (2019). State representation in mental illness. Current Opinion in Neurobiology, 55, 160–166. 10.1016/j.conb.2019.03.011 [DOI] [PubMed] [Google Scholar]
- 53.Renteria R, Baltz ET, & Gremel CM (2018). Chronic alcohol exposure disrupts top-down control over basal ganglia action selection to produce habits. Nature Communications, 9(1), 1–11. 10.1038/s41467-017-02615-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ribas-Fernandes JJF, Shahnazian D, Holroyd CB, & Botvinick MM (2019). Subgoal-and goal-related reward prediction errors in medial prefrontal cortex. Journal of Cognitive Neuroscience, 31(1), 8–23. 10.1162/jocn_a_01341 [DOI] [PubMed] [Google Scholar]
- 55.Russek EM, Momennejad I, Botvinick MM, Gershman SJ, & Daw ND (2017). Predictive representations can link model-based reinforcement learning to model-free mechanisms. PLOS Computational Biology, 13(9), e1005768. 10.1371/journal.pcbi.1005768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Samejima K, & Doya K (2007). Multiple representations of belief states and action values in corticobasal ganglia loops. Annals of the New York Academy of Sciences, 1104, 213–228. 10.1196/annals.1390.024 [DOI] [PubMed] [Google Scholar]
- 57.Schultz W, Dayan P, & Montague PR (1997). A Neural Substrate of Prediction and Reward. Science, 275(5306), 1593–1599. 10.1126/science.275.5306.1593 [DOI] [PubMed] [Google Scholar]
- 58.Schuck NW, Wilson R, & Niv Y (2018). Chapter 12—A State Representation for Reinforcement Learning and Decision-Making in the Orbitofrontal Cortex. In Morris R, Bornstein A, & Shenhav A (Eds.), Goal-Directed Decision Making (pp. 259–278). Academic Press. 10.1016/B978-0-12-812098-9.00012-7 [DOI] [Google Scholar]
- 59.Segers E, Beckers T, Geurts H, Claes L, Danckaerts M, & van der Oord S (2018). Working Memory and Reinforcement Schedule Jointly Determine Reinforcement Learning in Children: Potential Implications for Behavioral Parent Training. Frontiers in Psychology, 9. 10.3389/fpsyg.2018.00394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Seymour B, O’Doherty JP, Dayan P, Koltzenburg M, Jones AK, Dolan RJ, Friston KJ, & Frackowiak RS (2004). Temporal difference models describe higher-order learning in humans. Nature, 429(6992), 664–667. 10.1038/nature02581 [DOI] [PubMed] [Google Scholar]
- 61.Shahar N, Moran R, Hauser TU, Kievit RA, McNamee D, Moutoussis M, Consortium N, & Dolan RJ (2019). Credit assignment to state-independent task representations and its relationship with model-based decision making. Proceedings of the National Academy of Sciences, 116(32), 15871–15876. 10.1073/pnas.1821647116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sharpe MJ, Batchelor HM, Mueller LE, Yun Chang C, Maes EJP, Niv Y, & Schoenbaum G (2020). Dopamine transients do not act as model-free prediction errors during associative learning. Nature Communications, 11(1), 1–10. 10.1038/s41467-019-13953-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Starkweather CK, Babayan BM, Uchida N, & Gershman SJ (2017). Dopamine reward prediction errors reflect hidden-state inference across time. Nature neuroscience, 20(4), 581–589. 10.1038/nn.4520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sutton RS, & Barto AG (1998). Reinforcement learning: An introduction. MIT Press. [Google Scholar]
- 65.Sutton RS, & Barto AG (2018). Reinforcement learning: An introduction. MIT Press. [Google Scholar]
- 66.Viejo G, Girard B, Procyk E, & Khamassi M (2018). Adaptive coordination of working-memory and reinforcement learning in non-human primates performing a trial-and-error problem solving task. Behavioural Brain Research, 355, 76–89. 10.1016/j.bbr.2017.09.030 [DOI] [PubMed] [Google Scholar]
- 67.Vong WK, Hendrickson AT, Navarro DJ, & Perfors A (2019). Do Additional Features Help or Hurt Category Learning? The Curse of Dimensionality in Human Learners. Cognitive Science, 43(3), e12724. 10.1111/cogs.12724 [DOI] [PubMed] [Google Scholar]
- 68.White JK, Bromberg-Martin ES, Heilbronner SR, Zhang K, Pai J, Haber SN, & Monosov IE (2019). A neural network for information seeking. Nature Communications, 10(1), 1–19. 10.1038/s41467-019-13135-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wilson RC, Takahashi YK, Schoenbaum G, & Niv Y (2014). Orbitofrontal cortex as a cognitive map of task space. Neuron, 81(2), 267–279. 10.1016/j.neuron.2013.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wyckmans F, Otto AR, Sebold M, Daw N, Bechara A, Saeremans M, Kornreich C, Chatard A, Jaafari N, & Noël X (2019). Reduced model-based decision-making in gambling disorder. Scientific Reports, 9(1), 1–10. 10.1038/s41598-019-56161-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zhang Z, Cheng Z, Lin Z, Nie C, & Yang T (2018). A neural network model for the orbitofrontal cortex and task space acquisition during reinforcement learning. PLOS Computational Biology, 14(1), e1005925. 10.1371/journal.pcbi.1005925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zhao F, Zeng Y, Wang G, Bai J, & Xu B (2018). A Brain-Inspired Decision Making Model Based on Top-Down Biasing of Prefrontal Cortex to Basal Ganglia and Its Application in Autonomous UAV Explorations. Cognitive Computation, 10(2), 296–306. 10.1007/s12559-017-9511-3 [DOI] [Google Scholar]


