Abstract
Small noncoding RNAs such as piRNAs are guides for Argonaute proteins, enabling sequence-specific, post-transcriptional regulation of gene expression. The piRNAs of Caenorhabditis elegans have been observed to bind targets with high mismatch tolerance and appear to lack specific transposon targets, unlike piRNAs in Drosophila melanogaster and other organisms. These observations support a model in which C. elegans piRNAs provide a broad, indiscriminate net of silencing, competing with siRNAs associated with the CSR-1 Argonaute that specifically protect self-genes from silencing. However, the breadth of piRNA targeting has not been subject to in-depth quantitative analysis, nor has it been explained how piRNAs are distributed across sequence space to achieve complete coverage. Through a bioinformatic analysis of piRNA sequences, incorporating an original data-based metric of piRNA-target distance, we demonstrate that C. elegans piRNAs are functionally random, in that their coverage of sequence space is comparable to that of random sequences. By possessing a sufficient number of distinct, essentially random piRNAs, C. elegans is able to target arbitrary nonself sequences with high probability. We extend this approach to a selection of other nematodes, finding results which elucidate the mechanism by which nonself mRNAs are silenced, and have implications for piRNA evolution and biogenesis.
INTRODUCTION
Piwi-interacting RNAs, or piRNAs, are small RNAs often implicated in silencing of transgenes and deleterious transposons. The characteristics of piRNA targeting behavior differ among organisms (for a review, see Parhad and Theurkauf (1)). In D. melanogaster, piRNA sequences serve as a library of transposon subsequences, which enables silencing through sequence-specific target identification (2,3). In the nematode C.elegans, however, most piRNAs appear to lack complementarity to transposons—or indeed, any other clear target in the genome. Instead, researchers propose that the spectrum of C. elegans piRNAs can target virtually any reasonably sized mRNA sequence (4,5). Evidently, such broad silencing must be coupled with a licensing system to maintain a proper transcription profile. What can a quantitative understanding of piRNA targeting reveal about the functionality and evolution of this system, combining broad silencing with specific licensing? How do piRNAs achieve such broad sequence coverage, and is their capacity to target nonself sequences at all dependent on the piRNA sequences themselves?
The piRNAs of C. elegans are 21 nucleotides in length and serve as guide RNAs for the PRG-1 Argonaute, which triggers the RNA interference pathway to initiate epigenetic silencing of its targets (6,7). In prg-1 knockouts, sterility occurs in a temperature-dependent manner (8) or across the course of multiple generations (9), illustrating the importance of the piRNA system in maintaining proper gene expression. The expression of self-genes must be protected from piRNA-mediated silencing via a licensing system, which is not yet fully understood. One promising candidate for a licensing Argonaute is CSR-1, which binds siRNAs complementary to most germline-expressed genes, and when recruited to a transcript, protects it from piRNA-mediated silencing (10,11). A schematic of the putative C. elegans self/nonself discrimination system is presented in Figure 1. The licensing system maintains a memory of self-genes, allowing the piRNA-mediated silencing system to broadly target nonself sequences. This broad targeting is largely due to the mismatch-tolerant pairing rules between piRNAs and their targets. Studies of piRNA-mRNA crosslinking, and of the targets of synthetic piRNAs, have identified a ‘seed region’ at nucleotides 2–8 which is particularly important for targeting, along with a potential supplementary region at nts 14–19 (4,5) (Figure 1). Outside of these regions, piRNAs tolerate significant amounts of noncanonical base pairing—particularly GU wobbles, which appear less heavily penalized than other mismatches (5).
Figure 1.
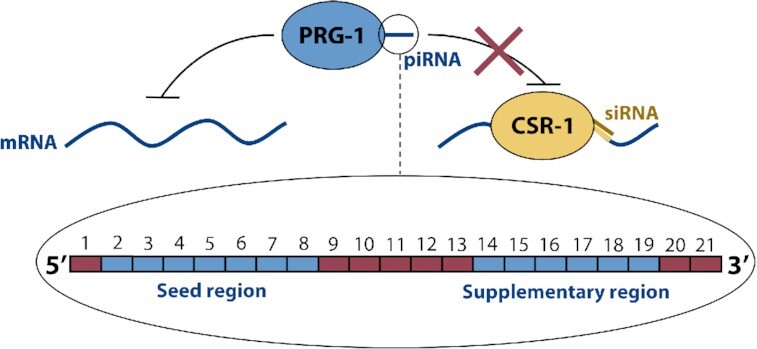
Schematic of the putative C. elegans self–nonself discrimination system, as mediated by small RNAs. PRG-1 Argonautes are guided by piRNAs to matching target sequences on self and nonself mRNA transcripts. As shown in the enlarged view, each piRNA is 21 nucleotides long, with a seed region at nt 2–8 and a supplementary region at nt 14–19 where canonical base pairing is particularly important for target recognition. When a PRG-1:piRNA binds to a valid target, RNA interference and downstream silencing are initiated. CSR-1 Argonautes are guided by siRNAs to matching sequences on self-transcripts. Binding by CSR-1:siRNA licenses a transcript, protecting it from silencing by PRG-1.
The theory that C. elegans piRNAs engage in broad, non-specific targeting is relatively well-supported by data. A cross-linking, ligation and sequencing of hybrids (CLASH) study revealed that piRNAs interact with a wide variety of germline mRNAs, with single piRNAs having numerous targets and single transcripts possessing multiple potential piRNA binding sites (4). A bioinformatic analysis which used a formalization of piRNA pairing rules to identify possible targeting sites found that about half of germline-expressed genes had a piRNA targeting site and calculated similar proportions for germline-silenced genes and control sequences (5). However, the mechanism through which piRNAs achieve their coverage of sequence space is still unclear: their sequences could minimize redundancy (maximizing their coverage with the minimum number of distinct sequences), or simply be effectively random, but exist in large enough numbers that at least one piRNA will have a suitable site on any target mRNA. Furthermore, it is unclear to what extent piRNA sequences match transposon sequences or avoid sequences of self-genes; despite the lack of clear matches, it is possible that piRNA sequences are more likely to target transposons than self-transcripts when considering the permissive piRNA targeting rules. Bagijn et al. (7), for instance, found that putative piRNA target loci are depleted of protein-coding genes but not transposons. Answering these questions is vital to developing a more complete understanding of the C. elegans genome defense system. In particular, the likelihood of a given nonself sequence being targeted by a piRNA can be used to investigate the timescale and accuracy of self/nonself discrimination.
To address these questions, we conducted a bioinformatic analysis of C. elegans piRNAs, by developing a distance metric based on the log-odds likelihood of observing a sequence of matches, mismatches and GU wobbles in a piRNA-target pair. We found that piRNA sequences are not self-avoiding (i.e. optimized to avoid redundancy in sequences), and are instead essentially random—but present in a large enough number to cover all of sequence space with a high probability. Furthermore, C. elegans piRNAs are functionally equivalent to random sequences with respect to transposon and self-transcript sequences, with only minor differences from random controls in terms of their targeting behavior. Indeed, after accounting for some basic statistical properties of real piRNAs (e.g. dinucleotide probabilities), real and random piRNAs achieve almost identical sequence coverage. We propose that C. elegans piRNAs evolved to be essentially random, employing a strategy that enables targeting of a wide variety of nonself sequences. Furthermore, we apply our methods to a selection of related nematodes, finding that they also display random targeting by piRNAs.
MATERIALS AND METHODS
Determining the closest-match probability distribution
As an initial method to detect and compare piRNA targeting of transposons in C. elegans and D. melanogaster, we used the proportion of mismatches between two transcripts to quantify sequence similarity. We wrote a script to check every piRNA against every same-length subsequence on each transposon, and to record the proportion of mismatches (i.e. noncanonical base pairs) at the site with fewest mismatches for each pair. This procedure was performed both for real piRNAs and random controls, in C. elegans and D. melanogaster. The random control piRNAs were generated to be the same lengths (21 nt for C. elegans, 15–30 nt for D. melanogaster) and number (17 849 and 13 904, respectively) as the original sets of piRNAs, but with randomized sequences. These sequences were generated such that the probability of a given nucleotide was equal to the probability of the nucleotide appearing in a real piRNA from the organism. (C. elegans: 31% A, 36% U, 16% C, 17% G. D. melanogaster: 20% A, 24% U, 21% C, 35% G. For C. elegans, we omitted the first nucleotide, usually U, when calculating these probabilities). This sampling procedure allowed us to estimate the probability density function describing the proportion of mismatches 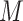 on the closest-matching site between a piRNA and transposon: i.e., the function
on the closest-matching site between a piRNA and transposon: i.e., the function 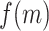 such that the probability ℙ
such that the probability ℙ 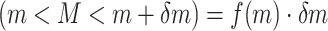 for small
for small 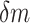 . By comparing the probability distributions for real and random piRNAs, particularly the weight of the left tail of the distribution (corresponding to the probability of ‘good matches’), we determined whether real piRNAs displayed more specific targeting of transposons than random controls.
. By comparing the probability distributions for real and random piRNAs, particularly the weight of the left tail of the distribution (corresponding to the probability of ‘good matches’), we determined whether real piRNAs displayed more specific targeting of transposons than random controls.
This same procedure was then conducted using a functional piRNA-target distance metric, rather than mismatch proportion, to quantify sequence similarity (detailed in the next section). In this case, the probability density function describes the piRNA-target distance between a piRNA and its closest-matching site on a target, where the ‘closest-matching’ site is the site with the smallest piRNA-target distance. This basic procedure was utilized throughout the study on various sets of piRNAs and target transposons or self-transcripts, and the resulting probability density function for each case is referred to as the ‘closest-match probability distribution’.
piRNA-target and piRNA-piRNA distance
We developed a functional piRNA-target distance metric, taking into account the importance of the position of each base for piRNA targeting. A smaller distance indicates a closer match, in the sense that the piRNA is more likely to successfully interact with the putative target. This metric is based on a log-likelihood estimate of observing a match, mismatch or GU wobble at each base in experimentally confirmed piRNA-target pairs, meaning that bases which are more or less likely to match in known piRNA-target pairs are weighted accordingly when calculating the distance. Past research has suggested that GU wobbles are more favorable for piRNA targeting than other mismatches, so we constructed the metric such that a GU wobble could have a smaller impact on the distance than an arbitrary mismatch (5). We defined the piRNA-target distance as
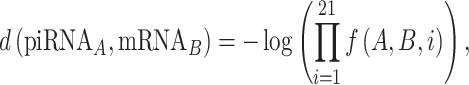 |
where
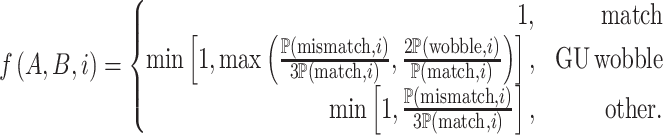 |
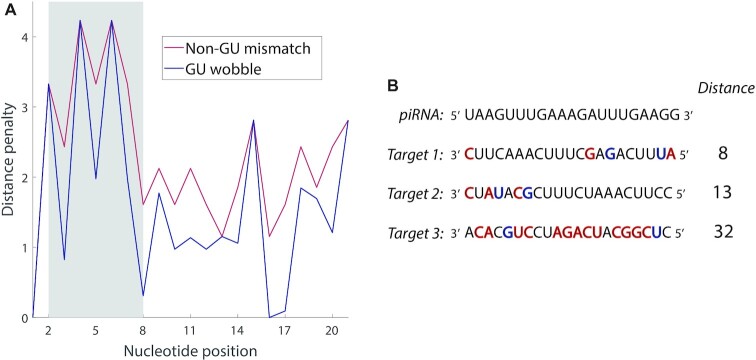
The probabilities ℙ are obtained from experimental data, and represent the probability of a canonical base pairing match, a GU wobble, or any non-canonical mismatch at each of the 21 sites for actual piRNA-target pairs. In our case, these probabilities were drawn from the 17 experimentally observed piRNA-target pairs used in Zhang et al., with an additional pseudocount of 1/16 for each of the 16 possible nucleotide pairs at each site (5). Defined this way, the piRNA-target distance has several key properties: (i) a mismatch or GU wobble at a given base will always increase the piRNA-target distance by a set penalty, (ii) the penalty for a mismatch will be at least as large as the penalty for a GU wobble at the same base and (iii) the penalties associated with a given base are commensurate with the frequency of matches at that base in experimentally verified piRNA-target pairs. These penalties, as well as piRNA-target distances for example sequences, are shown in Figure 2.
Figure 2.
Overview of the functional piRNA distance metric. (A) The penalty associated with a non-GU mismatch or GU wobble on each nucleotide of potential piRNA-target pairs. The gray shaded region shows the seed region of the piRNA, which has higher penalties than elsewhere. (B) Example piRNA-target distances for a piRNA and three potential targets, with mismatches shown in red and GU wobbles shown in blue. Target 1 is a ‘typical’ actual target for the piRNA. Target 2 possesses the same number of mismatches as Target 1, but they have been relocated to the seed region. Target 3 has roughly the number of mismatches and wobbles that a random 21-nt sequence would possess.
In addition to the piRNA-target distance, we used a piRNA-piRNA distance metric to measure the redundancy of piRNAs, where a smaller distance between piRNAs means that their targeting is more redundant. This metric is based on the ability of each piRNA to target the other’s perfect complement and is defined as
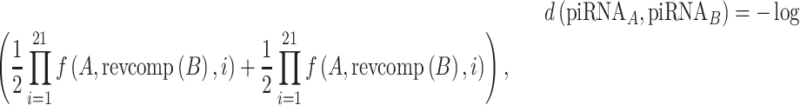 |
where 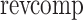 denotes the reverse complement of a sequence. Using this metric, we calculated the probability distribution of C. elegans piRNA-piRNA distances using every pair of piRNAs. This analysis also allowed us to cluster piRNAs into groups of piRNAs with redundant coverage, using hierarchical clustering with single linkage. In this clustering procedure, every pair of piRNAs with a piRNA-piRNA distance of <10 was merged into the same cluster, until every cluster was composed of piRNAs at least 10 distance units away from any piRNA not in that cluster.
denotes the reverse complement of a sequence. Using this metric, we calculated the probability distribution of C. elegans piRNA-piRNA distances using every pair of piRNAs. This analysis also allowed us to cluster piRNAs into groups of piRNAs with redundant coverage, using hierarchical clustering with single linkage. In this clustering procedure, every pair of piRNAs with a piRNA-piRNA distance of <10 was merged into the same cluster, until every cluster was composed of piRNAs at least 10 distance units away from any piRNA not in that cluster.
Validation of piRNA-target distance
The piRNA-target and piRNA-piRNA distances are dependent on the experimental data used to estimate the probabilities of a match, mismatch, or GU wobble at each base. In order to verify that the 17 experimentally confirmed pairs we used were sufficient to construct a self-consistent distance metric, we constructed leave-one-out test sets, eliminating one of the confirmed pairs from consideration when calculating the probabilities and then measuring its piRNA-target distance using the metric based on the 16 remaining pairs. We repeated this procedure for each of the 17 pairs, and compared these distances to those obtained from using all 17 piRNA-target pairs (the full training set). If the distance metric is self-consistent, eliminating one piRNA from consideration should only result in a small deviation in the distance, as we confirmed (Supplementary Figure S1A).
As an additional test of the dependency of the piRNA-target distance metric on the input sequences, we defined an alternative pool of putative piRNA-target pairs from piRTarBase, a database of bioinformatically predicted piRNA targeting sites on active genes in the C. elegans genome (12). We restricted our attention to the piRNA-target pairs predicted using piRTarBase’s relaxed targeting rules, that were also identified as physically associating in CLASH experiments, and where the target in question at least doubled in mRNA expression when the piRNA system was disabled in prg-1 knockouts. This yielded 354 putative piRNA-target pairs. 17 of these pairs were randomly selected, and treated as experimental input to calculate the probabilities used in the piRNA-target distance metric, essentially defining an alternative piRNA-target distance. Then, the piRNA-target distance of the 337 remaining putative pairs was measured using both this alternative distance and the actual piRNA-target distance, which utilized the piRNA-target pairs from Zhang et al. (5). This procedure was repeated for several choices of 17 alternative pairs, and the difference between the actual and alternative distances (i.e. the extent to which the piRNA-target distance is dependent on the precise choice of input sequences) was measured (Supplementary Figure S1B).
Random piRNAs with realistic statistical structure
In addition to generating random piRNAs with fixed nucleotide probabilities, we determined the effect of using more statistically realistic random controls, with mono-, di- or trinucleotide probabilities along the piRNA equal to those observed in nature. To keep the mononucleotide probability consistent with real piRNAs, we calculated the probability of each nucleotide appearing in each position, and generated random piRNAs with those nucleotide probabilities. To keep the dinucleotide probability consistent, we generated the first base in accordance with mononucleotide probabilities, and then determined the next nucleotide based on the conditional nucleotide frequencies of real piRNAs with the same previous nucleotide, continuing until we had selected the last nucleotide. For example, if the fourth random nucleotide was a U, then the probability that the fifth nucleotide was C would be the probability that the fifth nucleotide of a real piRNA is C, given that its fourth nucleotide is U. Keeping the trinucleotide probability consistent was done in much the same way, but by maintaining a ‘memory’ of two nucleotides back: i.e. if the fourth and fifth nucleotides were UC, the sixth nucleotide probabilities were based on those of real piRNAs with UC in the 4–5 nt position. Conducting this procedure resulted in a set of ‘piRNAs’ statistically similar to yet entirely distinct from real piRNAs.
The global closest-match probability distribution
The closest-match probability distribution describes the distance of the match between a single piRNA and its closest-matching site on a potential target. However, the ability of the piRNA system to target nonself transcripts is determined by how capable an entire set of piRNAs is of targeting a transposon or self-transcript. To address this question, we determined the ‘global’ closest-match probability distribution, describing the smallest piRNA-target distance among all C. elegans piRNAs and a target. To do this, we conducted the same procedure that we used to find the closest-match probability distribution, but only recorded the best match among all piRNAs (either real piRNAs, or random piRNAs with realistic statistical structure).
We sought to compare these results to a fully random control, in which the bases of ‘piRNAs’ and target ‘genes’ are independent and have an equal probability of being any nucleotide. In this fully random case, the ability of a set of piRNAs to match a target is dependent only on the length 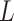 of the target and the number
of the target and the number 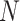 of distinct piRNAs: for larger values of these quantities, there are more opportunities for a good match to arise by chance. In particular, if
of distinct piRNAs: for larger values of these quantities, there are more opportunities for a good match to arise by chance. In particular, if 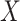 is a random variable equal to the piRNA-target distance between two random 21-nt sequences, we expect the global closest-match distance to be the minimum among
is a random variable equal to the piRNA-target distance between two random 21-nt sequences, we expect the global closest-match distance to be the minimum among 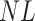 independent draws of
independent draws of 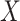 . We first determined the cumulative distribution function (CDF) of
. We first determined the cumulative distribution function (CDF) of 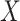 , i.e.
, i.e. 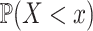 , via a sampling procedure described in the Appendix. Then, we calculated the CDF of this ‘random global closest-match distance’ using the equation
, via a sampling procedure described in the Appendix. Then, we calculated the CDF of this ‘random global closest-match distance’ using the equation
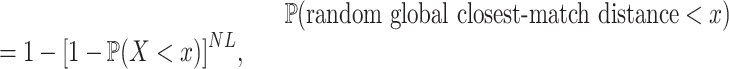 |
which allowed us to determine how the random global closest-match distance depends on target length and piRNA number. From this CDF, we calculated the mean random global closest-match distance, and determined its probability density function by numerical differentiation followed by smoothing with a spline curve.
Computational resources
C. elegans piRNA sequences, CLASH data, abundance data and putative piRNA-target pairs used in validation of the piRNA-target distance, were downloaded from piRTarBase at cosbi6.ee.ncku.edu.tw/piRTarBase/download/ (12). The original sources were Shen et al. for the CLASH data (4), McMurchy et al. for the expression data (13), and the mean of the results from Tang et al. and Gu et al. for the abundance data (14,15) Full-length transcript sequences for C. elegans, C. brenneri, C. briggsae and P. pacificus were obtained from WormBase ParaSite at parasite.wormbase.org (16,17). C. elegans transposon sequences were obtained from Laricchia et al., Supplementary Table S16 (18). Only the insertion sequences originally sourced from WormBase (the first 627 transposons in the table), and not the consensus sequences from RepBase, were used. D. melanogaster piRNA sequences associated with the Piwi Argonaute were obtained from Brennecke et al., with GEO accession number GSM154620 (2). Transposon sequences for D. melanogaster were taken from the Natural Transposable Element Project (version 9.4.1) of the Berkeley Drosophila Genome Project, at fruitfly.org/p_disrupt/TE.html (19). piRNA sequences for C. brenneri, C. briggsae and P. pacificus were obtained from Beltran et al., Supplementary Data S1 (20). Consensus transposon sequences from these organisms were obtained from RepBase; the specific sequences used are listed in Supplementary Table 1 (21).
RESULTS
piRNA-transposon match comparison between C. elegans and D. melanogaster
C. elegans is thought to employ a strategy of transposon silencing which utilizes mismatch-tolerant piRNA binding to achieve broad targeting (4,5). By contrast, D. melanogaster relies on complementary piRNAs specifically matching target transposon sequences (2,3). Before beginning an in-depth analysis of C. elegans piRNAs, we sought to quantitatively verify this key difference as a proof of concept, utilizing D. melanogaster as a positive control to contrast the relative lack of specific targeting in C. elegans. To use a metric consistent across organisms, we identified the closest-matching site of each piRNA along each transposon insertion sequence in the genome for both organisms and counted the proportion of mismatches, constructing the ‘closest-match probability distribution’ of mismatch proportions. We conducted the same analysis for real piRNAs and random controls, quantifying how biased piRNA sequences are toward targets on transposons in each organism (Figure 3).
Figure 3.
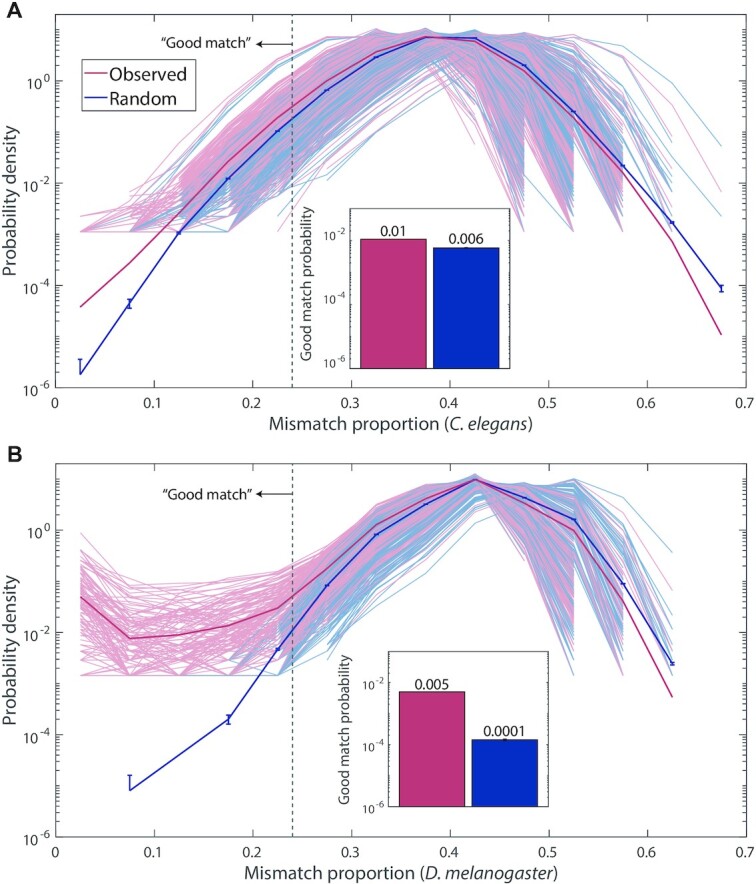
Bioinformatic comparison between C. elegans and D. melanogaster of piRNA-transposon sequence similarity. (A) C. elegans closest-match distribution of mismatch proportion between every pair of piRNAs (n = 17 849) and transposons (n = 627); results shown for real piRNAs and random control sequences. Each pale curve indicates the distribution of closest-match mismatch proportions for piRNAs with a single transposon; solid curve is the distribution of closest-match mismatch proportions across all pairs (for mismatch proportions that do not occur in the sample, no data are shown). Inset: proportion of piRNA-transposon pairs where the closest-matching site has fewer than 24% mismatches (left of the dashed vertical gray line in the main panel), for real piRNAs and random control sequences. Error bars indicate counting error (square root of the number of counts). (B) Same as (A), but for D. melanogaster piRNAs (n = 13 904) and transposons (n = 179).
As shown in Figure 3, the difference in the closest-match probability distribution between real and control piRNAs is much starker for D. melanogaster than C. elegans, particularly in the left tail (well-matching end) of the distribution of mismatches. Experimentally identified C. elegans piRNA-target matches have a mean mismatch proportion of 24%, so we use this cutoff to define a ‘good match’ (5). (Note that this cutoff is simply a way to measure the weight of the left tail of the distributions, and should not be taken as an actual prediction of targeting for either organism: piRNA binding rules are likely different for C. elegans and D. melanogaster, and cannot be simply described by mismatch proportion). While real C. elegans piRNAs are roughly twice as likely as random controls to be ‘good matches’ to a given transposon sequence, D. melanogaster piRNAs are about 50 times more likely than random controls to be good matches (Figure 3, inset). For the right tail (poorly matching end) of the distribution, real and random piRNAs yield a fairly similar shape in both organisms. There, the probability drops because the closest-matching site of a piRNA on a reasonably sized transposon is almost certain to have several matching base pairs, a statistical property independent of specific targeting. In addition to illustrating the different transposon silencing strategies employed by each organism, this result hints that the coverage of transposons achieved by C. elegans piRNAs might be comparable to coverage by random piRNAs. However, mismatch proportion is too simplistic a way to analyze piRNA-target matches, since it does not take into account piRNA binding rules. A fair comparison to random controls demands a more refined analysis of C. elegans piRNA coverage.
piRNA-target distance metric
How can sequence similarity be best measured in the context of piRNA binding? Previous studies have made an effort to systematize C. elegans piRNA targeting rules in order to locate piRNA binding sites. For example, the piRNA targeting site identification tool pirScan and the database piRTarBase utilize a targeting score which assigns differing penalties to mismatches or GU wobbles within or outside the seed region of the piRNA (22,23). While such a metric is useful for identifying targeting sites, the resulting score is highly dependent on the penalty values chosen and is difficult to interpret as a continuous parameter.
Instead, we developed a piRNA-target distance metric (see Materials and Methods) based on the log-odds probabilities of a match, mismatch, or GU wobble at each nucleotide position, obtained from the piRNA-target pairs experimentally confirmed by Zhang et al. (5). This metric is essentially the logarithm of a likelihood estimate of observing a given sequence of matches, mismatches or wobbles in a piRNA-target pair. When used to compare a piRNA and a target, a smaller distance indicates a closer match, in a manner that reflects the importance of each nucleotide position to piRNA binding. Perfectly-matching sequences will have a piRNA-target distance of zero, and deviations from canonical base-pairing will increase the distance by a set penalty, dependent on the location and type (GU wobble or other) of the mismatch. These base-specific penalties, as well as piRNA-target distances for example sequences, are shown in Figure 2. The higher penalties in the seed region, as well as the fact that there is no penalty for mismatches in the first nucleotide, are consistent with prior studies of C. elegans piRNA-target pairing, validating that our distance metric is comparable to prior methods of determining a piRNA-target binding score (4,5). The experimentally confirmed piRNA-target pairs used to construct the metric have a mean distance of 5.8 and a standard deviation of 2.2, so Target 1 in Figure 2B, which has a distance of 8 units from the example piRNA, is around the upper end of what we would expect for a match. Target 2 has the same number of mismatches and wobbles as Target 1, but they are concentrated in the seed region, leading to a much higher distance of 13. Finally, Target 3 is a random sequence, and has a distance of 32 from the example piRNA: this demonstrates that two random sequences are unlikely to constitute a good match.
In order to verify that the distance metric is self-consistent and not overly dependent on the experimentally verified piRNA-target pairs used to define it, we determined how much the distance changed when we altered the set of experimental sequences (see Materials and Methods). First, we performed leave-one-out cross-validation, calculating the piRNA-target distances for each of those experimentally verified pairs while omitting that pair from the set used to define the distance (Supplementary Figure S1A). We observed only small differences in the distance (0–3 units) when using these leave-one-out test sets instead of the full training set. Then, we identified 354 putative piRNA-target pairs from the piRTarBase database, which, while not experimentally confirmed, were supported by both CLASH data (indicating physical interaction between a piRNA and its target) and differential expression data in prg-1 knockouts, indicating a reasonable likelihood of silencing by piRNAs (12). We used random samples of 17 putative pairs from this set to construct alternative piRNA-target distance metrics, and compared them to the actual distance metric (i.e., the one used elsewhere in the study) by evaluating the distance between the remaining 337 pairs (Supplementary Figure S1B). The alternative piRNA distances generally differed from the actual distance by only ∼2 units, and showed nearly no systematic difference on average—even though they were constructed with an entirely different set of input pairs. So, we conclude that our distance metric generally describes C. elegans piRNA-target binding, independent of the precise choice of training sequences.
piRNA-transposon and piRNA-transcript targeting
The C. elegans piRNA system must silence transposons and unknown transgenes, while allowing self-genes to be expressed. If the expression of self-genes is protected by a separate licensing system, then the piRNA system could be largely agnostic to the identity of its targets. To what extent are piRNAs truly random with respect to the sequences they target?
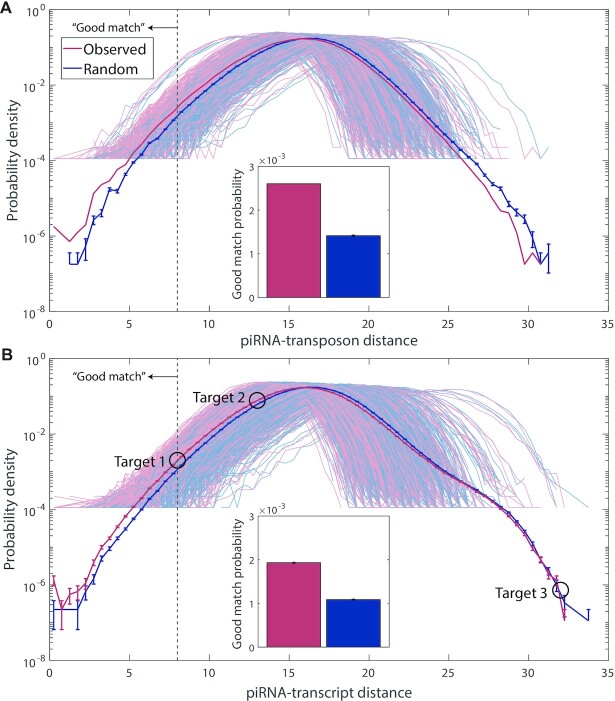
To answer this question, we determined the closest-match probability distribution of piRNA-target distances using all pairs of C. elegans piRNAs and transposons, as well as all pairs of piRNAs and a random sample of 1000 self-transcripts (Figure 4).
Figure 4.
Bioinformatic analysis of C. elegans piRNA-transposon and piRNA-transcript pairing using the functional piRNA-target distance metric. (A) Closest-match distribution of the piRNA-target distance for every pair of C. elegans piRNAs (n = 17 849) and transposons (n = 627); results shown for real piRNAs and random control sequences. Each pale curve indicates the distribution of closest-match distances for piRNAs with a single transposon; solid curve is the distribution of closest-match distances over all pairs. Note that the distribution for all pairs has a higher sample size and is thereby able to resolve lower probabilities than the distribution for pairs with a single transposon, so the solid curve extends lower than those for individual transposons (for piRNA-target distances that do not occur in the sample, no data are shown). Inset: proportion of piRNA-transposon pairs where the closest-matching site has a piRNA-target distance of <8 (left of the dashed vertical gray line in the main panel), for real piRNAs and random control sequences. Error bars indicate counting error. (B) Same as (A), but for a random sample of all C. elegans transcripts (n = 1000) rather than transposons. Circles show points corresponding to the three hypothetical piRNA-target pairs in Figure 2B.
The closest-match probability distributions appear very similar between real piRNAs and random controls, for both transposons and self-transcripts. Most closest-matches have a piRNA-target distance near or slightly larger than that of Target 2 from Figure 2B: significantly better than random (Target 3) but still not as good as an actual target (Target 1). We are particularly interested in the weight of the left (well-matching) tail of the distribution, to see whether real piRNAs are more likely than random controls to target transposons or self-transcripts (Figure 3, inset). We choose to define ‘good matches’ as those with a piRNA-target distance of <8, the mean distance of experimentally verified pairs plus one standard deviation. There are small but noticeable differences in the proportion of ‘good matches’ between the groups: transposons are more likely to be targeted than self-transcripts, and real piRNAs are more likely than random controls to target both transposons and self-transcripts. However, none of these differences approach the amount of specific targeting observed in D. melanogaster (Figure 3), and are certainly insufficient to explain how transposons and self-transcripts are differentially silenced. Instead of representing specific targeting, we hypothesize that the difference between real and random piRNAs is due to the statistical structure of piRNA sequences, i.e., the fact that certain pairs or triplets of nucleotides may be more likely than others at different points along the piRNA. Indeed, when performing the same analysis using random piRNAs which have the same position-specific dinucleotide and trinucleotide frequencies of real piRNAs (see Materials and Methods), the difference between real and random piRNAs almost vanishes (Supplementary Figure S2).
Another possible way piRNAs could deviate from random is based on their expression: perhaps more abundant piRNAs show more specific targeting, which would be undetectable looking at their sequences alone. To test this possibility, we split our piRNAs into five groups of increasing abundance, such that each group contains the same number of total reads per million (Supplementary Figure S3A). Then, we undertook the same procedure to find the closest-match probability distribution for each group (Supplementary Figure S3B,C). We found no trend relating abundance to transposon or self-transcript targeting; if anything, the highest-abundance group shows less targeting than the lower-abundance groups. As a final check, we plotted piRNA abundance against the piRNA-target distance of the piRNA’s best match on any transposon or self-transcript, and found no correlation (Supplementary Figure 3D). As such, we find that consideration of piRNA abundances does not change our conclusion that C. elegans piRNAs are functionally close to being random.
Global targeting of arbitrary sequences
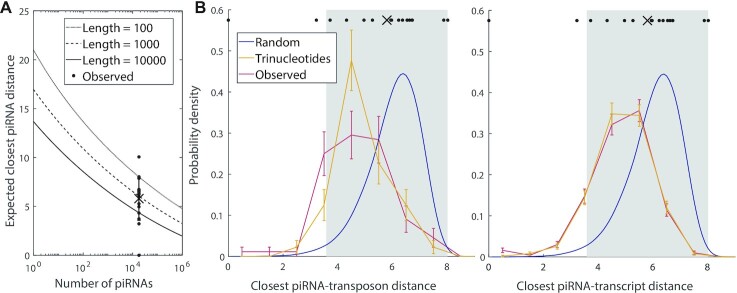
To fulfil their function, C. elegans piRNAs must be capable of targeting arbitrary nonself sequences. If these piRNAs are essentially random, then can real piRNAs and random sequences target nonself sequences with similar levels of reliability? To address this question, we investigated the probability distribution of ‘global’ closest-matches, i.e. the best match between a target of some length and any piRNA. Under the fully random framework, the coverage of piRNAs depends on the number of distinct piRNA sequences: with enough random sequences, at least one is likely to be able to target a subsequence on any given transcript. There are about 17 000 piRNAs in piRTarBase, which is a reasonable estimate; while there may be piRNAs not in this dataset, all piRNAs are not expressed simultaneously in an organism (12). We determined whether this number is consistent with the observed coverage of piRNAs by calculating the mean piRNA-target distance for the closest match between a set of random ‘piRNAs’ and a random ‘gene’, as a function of the number of piRNAs and the length of the ‘gene’ (see Materials and Methods). The average closest distance observed for the true number of C. elegans piRNAs is similar to the distances of the experimentally confirmed piRNA-target pairs, suggesting that the number of piRNAs is tuned to allow sufficient coverage by what are effectively random piRNA sequences (Figure 5A).
Figure 5.
Comparison of actual global targeting by all piRNAs to the random global closest-match distribution of piRNA-target distances (see Materials and Methods). (A) Predicted mean distance for the closest match between a ‘target’ (random sequence of length L = 100, 1000 or 10 000), and any of the ‘piRNAs’ (random 21 nt sequences) as a function of the number of distinct ‘piRNAs’. The data points plotted above the true number of C. elegans piRNAs (17 849) show the distances for the 17 actual piRNA-target pairs studied by Zhang et al. (5), with the cross and error bar indicating the mean and standard deviation. (B) Probability distribution of global closest-match distribution for actual transposons (left) and self-transcripts (right), of similar lengths, with real and random piRNAs. Red curves represent data for real piRNAs (n = 17 849) targeting 800–1200 nt C. elegans genes, either transposons (n = 90, left) or a random sample of self-transcripts (n = 500, right). Yellow curves represent targeting of the same transposons and transcripts by randomly generated piRNAs with the same position-specific trinucleotide probabilities as real piRNAs. Blue curves show the smoothed probability density of closest distances for 17 849 fully random ‘piRNAs’ with a fully random ‘gene’ of 1000 nt. Error bars indicate counting error. The data points plotted above the probability distributions show the distances for the 17 actual piRNA-target pairs presented in (A), while the cross and gray shaded region show the mean and standard deviation, respectively.
We next compared the global closest-match probability distributions for real and random piRNAs. We restricted our attention to transposons and self-transcripts of approximately 1000 nucleotides, and found the global closest-match probability distribution for real piRNAs, random piRNAs with real trinucleotide probabilities, and the fully random model with random piRNAs and genes (Figure 5B). On average, the closest-matching piRNA to a real transposon or transcript is a better match than the purely random model would predict (distances 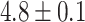 for self-transcripts,
for self-transcripts, 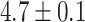 for transposons, and
for transposons, and 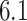 for random sequences, with error indicating standard error of the mean). However, this difference mostly vanishes when the random sequences are chosen with the same trinucleotide probabilities (distances
for random sequences, with error indicating standard error of the mean). However, this difference mostly vanishes when the random sequences are chosen with the same trinucleotide probabilities (distances 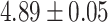 for self-transcripts and
for self-transcripts and 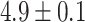 for transposons). This result indicates that the difference between real and random piRNAs is attributable to the statistical structure of piRNAs, rather than any specific targeting. Even when considering fully random piRNAs, their average global closest-match distance from an arbitrary target is well within the range of typical distances observed for real piRNA-target matches —in fact, almost all of the density of both the experimental and random distributions is concentrated within this range. Thus, we conclude that the binding rules (implicit in the piRNA-target distance) are tolerant enough that an equivalent number of random ‘piRNAs’ would be able to target a gene with the same accuracy observed in experimental piRNA-target pairs.
for transposons). This result indicates that the difference between real and random piRNAs is attributable to the statistical structure of piRNAs, rather than any specific targeting. Even when considering fully random piRNAs, their average global closest-match distance from an arbitrary target is well within the range of typical distances observed for real piRNA-target matches —in fact, almost all of the density of both the experimental and random distributions is concentrated within this range. Thus, we conclude that the binding rules (implicit in the piRNA-target distance) are tolerant enough that an equivalent number of random ‘piRNAs’ would be able to target a gene with the same accuracy observed in experimental piRNA-target pairs.
piRNA-piRNA distance analysis
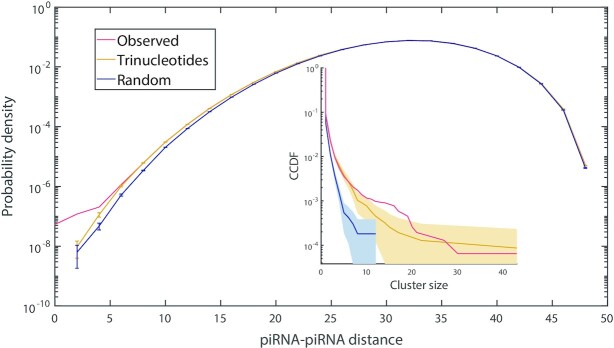
While C. elegans piRNAs appear nearly random with regards to the sequences they target, we also sought to determine how random they are with respect to each other. If piRNA sequences are self-avoiding, their coverage would be maximized with the minimum number of piRNAs. We therefore adapted the piRNA-target distance used earlier to measure piRNA-piRNA distance, where a smaller distance indicates more redundant coverage (see Materials and Methods). We calculated the distance between all pairs of C. elegans piRNAs, comparing the resulting probability distribution to that of random controls (Figure 6). The distributions appear similar, although the real piRNAs have a slightly larger left tail than the random controls, meaning that they have a higher frequency of pairs of piRNAs which possess similar coverage of targets. We investigated this difference further by performing hierarchical clustering on both the real piRNAs and the random controls, grouping them into clusters with similar coverage (Figure 6, inset; see Materials and Methods). Large clusters are significantly more likely to occur in real piRNAs than among fully random controls, but when random piRNAs are generated with the same trinucleotide probabilities as real piRNAs, the distribution of cluster sizes becomes more similar. Nevertheless, there are still slightly more clusters of size 15–20 in real piRNAs than these random controls. Despite the relatively large size of these clusters, their total expression across all member piRNAs is still smaller than the expression of the most highly-abundant lone piRNAs. We checked the closest-match probability distributions of consensus sequences for the five largest piRNA clusters, determining their ability to target transposons and self-transcripts, but found no significant difference from other piRNAs.
Figure 6.
Sequence similarity among C. elegans piRNAs. Probability distribution of piRNA-piRNA distances; results shown for all 17 849 real piRNAs (red), fully random control sequences (blue) and random piRNAs with the same position-specific trinucleotide probabilities as real piRNAs (yellow). Error bars indicate counting error. Inset: Complementary CDF (CCDF) of cluster sizes for real piRNAs and for both sets of random control sequences, as grouped via hierarchical clustering with single linkage (see Materials and Methods for details). The shaded region indicates a 95% confidence interval for the CCDF of the random sequences.
Since real piRNA sequences are no more distant from each other than random sequences, they do not appear to be self-avoiding or ‘optimally’ distributed. In fact, based on our clustering analysis, piRNAs are slightly more likely to have redundant coverage than random sequences, which may be a result of closely related piRNA sequences being generated via duplication and modification of existing sequences. Altogether, C. elegans piRNA targeting does not appear functionally different from what would be achieved by the same number of random sequences.
Extension to other nematodes
The approach we have used can be extended to other organisms in a straightforward manner, to investigate whether their piRNA targeting mechanism is random or specific. It is important to note that our piRNA distance metric relies on having the sequences of experimentally confirmed piRNA-target pairs, and is not necessarily generalizable across organisms. However, it is presumably still reasonably accurate for those closely related nematodes in the subclass Rhabditia which possess PRG-1 (20)—indeed, the piRTarBase database identifies putative piRNA targeting sites in both C. elegans and C. briggsae using the same piRNA targeting rules (12). Past research has identified two modes of piRNA organization within Rhabditia: organisms such as C. elegans, C. briggsae and C. brenneri have piRNAs located in clusters in the genome, while Pristonchus pacificus possesses piRNAs which are dispersed within introns (20). Do these organisms also employ functionally random piRNA targeting?
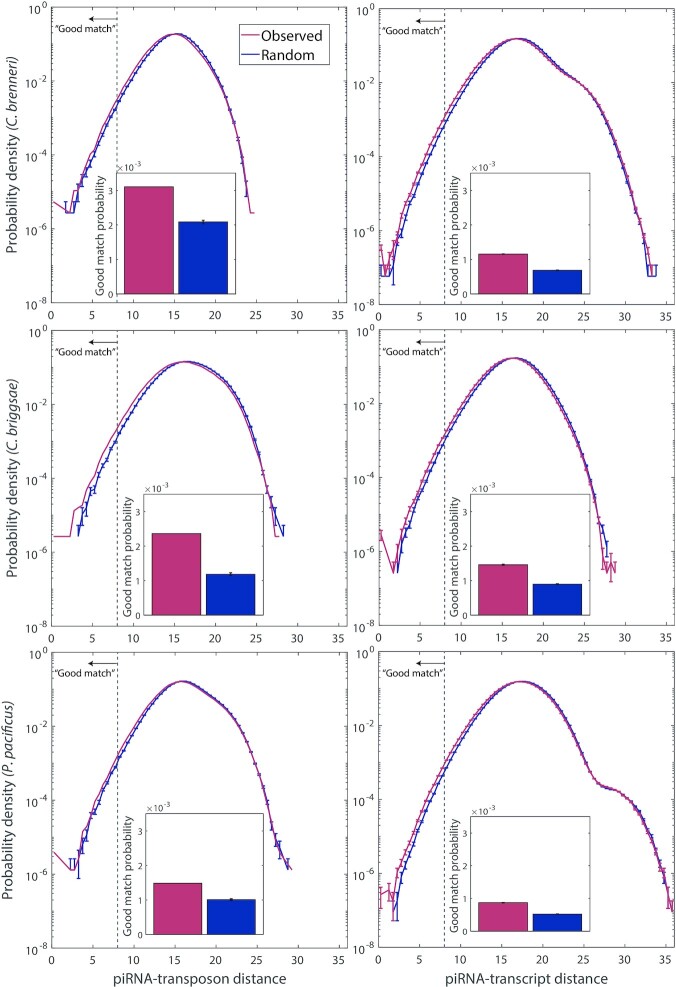
We generated the closest-match probability distribution of piRNA-target distance for C. briggsae, C. brenneri and P. pacificus transposons and transcripts. Since not all complete transposon insertion sequences in these organisms are annotated, we used a set of consensus transposon sequences available on RepBase (21). As shown in Figure 7, we found no more evidence of targeting in these organisms than in C. elegans. This result suggests that the role of piRNAs as functionally random sequences meant to target any nonself sequence is conserved within other species in Rhabditia, and demonstrates the applicability of the analysis to other organisms. (We note that several of the closest-match probability distributions possess a ‘shoulder’ where the probability density extends further into large piRNA-target distances, poor matches, than one would expect for a smooth curve. This is due to the presence of transcripts with a small number of independent binding sites, either due to high repetition or short length, which thereby lack good binding sites for piRNAs).
Figure 7.
Comparison between real and random piRNA-transposon and piRNA-transcript pairing for various nematode species. Left: closest-match probability distribution of piRNA-target distance for each pair of piRNAs and available consensus transposon sequences for each organism, for real piRNAs and random controls. Right: closest-match probability distribution of for each pair of piRNAs and a random sample of 1000 transcripts from each organism, for real piRNAs and random controls. Top row: data for C. brenneri (n = 49 341 piRNAs, 15 transposons). Middle row: data for C. briggsae (n = 11 053 piRNAs, 68 transposons). Bottom row: data for P. pacificus (n = 32 099 piRNAs, 48 transposons). Insets: proportion of piRNA-target pairs where the closest-matching site has a piRNA-target distance of <8 (left of the dashed line in the main panels). Error bars indicate counting error.
DISCUSSION
Using an original metric of piRNA-target distance, we compared piRNA targeting in C. elegans to that of random sequences. We found that piRNAs target both transposons and self-transcripts only slightly better than we would expect from fully random sequences, and virtually all of this difference can be attributed to the frequencies of dinucleotides and trinucleotides in piRNAs rather than to specific targeting; furthermore, piRNA expression levels appear uncorrelated with their targeting behavior. Random sequences are sufficient to target arbitrary sequences with the same accuracy observed in experimental piRNA-target pairs. In addition, we find that piRNA sequences are not self-avoiding or ‘optimally’ distributed, and instead are slightly more redundant than random sequences. The fact that piRNAs do not optimally cover sequence space is not particularly surprising, even though doing so would minimize the number of sequences necessary for adequate targeting, as minimizing redundancy over a large set of piRNAs is likely evolutionarily inaccessible. By contrast, simply expressing a larger number of random sequences can achieve the same coverage, similarly to how the wide range of antigen receptors on T and B cells in the immune system is achieved by random recombination and mutation. We conclude that C. elegans piRNAs achieve broad targeting by having a sufficient number of quasi-random sequences, which bind to targets with enough mismatch tolerance to cover all of sequence space. Furthermore, we extend our results to a selection of closely related nematodes which display different methods of piRNA organization, and yet find similar results for each of them: piRNAs target sequences virtually randomly.
Most of our analysis focused on comparing true C. elegans piRNAs and their targets to random sequences. The latter were generated by either assigning a constant frequency to each nucleotide (fully random), or by maintaining the position-specific mono-, di-, or trinucleotide frequencies observed in real piRNAs. In this way, we were able to show that the modest difference between random and real piRNAs can be simply ascribed to the statistical properties of the real sequences. For example, if a codon is more likely than others to appear in a sequence, a piRNA whose seed region targets this codon would raise the proportion of good matches relative to random controls without necessarily targeting a specific transposon. Such statistically enhanced targeting contrasts sharply with the precise targeting we noted in D. melanogaster, which utilizes piRNAs complementary to specific transposon sequences.
We analyzed targeting using an original piRNA distance metric (detailed in Materials and Methods). This metric is a log-odds score, corresponding to the logarithm of the likelihood estimate of observing a given sequence of matches, GU wobbles, and mismatches between a piRNA and its target. Based on experimental observations, the distance metric explicitly incorporates the assumption that canonical nucleotide matches at each position should pair at least as well as GU wobbles, and that GU wobbles in turn should be at least as favored as mismatches (5). The distance metric automatically incorporates the seed and supplementary regions via the position-specific data used to build the likelihood estimate. Thus the metric provides a continuous, data-based scale that takes into account the position-specific nuances of piRNA targeting, a generalizable alternative to methods that rely on defining ad hoc penalties or restrictions on nucleotides in various regions. There are a variety of ways to define similar metrics, but the precise details of the distance used are unlikely to have affected our conclusions, as confirmed by our cross-validation testing.
Biologically, what is required for C. elegans piRNAs to achieve such broad coverage? We analyzed the number of distinct piRNA sequences as a key factor in determining coverage, suggesting that it has been evolutionarily tuned. One possible mechanism to change the number of sequences is duplication and modification of piRNAs, which may explain our identification of clusters of similar piRNA sequences. While our analysis took the piRNA binding rules as given, piRNA binding specificity is also biologically determined, likely by the PRG-1 Argonaute protein that combines with piRNAs to seek out target sequences. Studies of human Argonaute-2 (hAgo2) indicate that hAgo2 undergoes conformational changes as certain nucleotides of its guide miRNA bind, increasing its binding stability by exposing more guide RNA (24). Mutations in the PRG-1 Argonaute, then, could affect the number of matching nucleotides needed for stable binding to an mRNA and thereby the specificity of target identification. Since the number of piRNA sequences and the binding specificity are sufficient to determine coverage if the sequences themselves are arbitrary, investigating their coupling across similar systems in different species could shed light on how these systems function.
Because the C. elegans piRNA system is capable of targeting virtually all sequences, the organism must maintain a memory of self-sequences and protect them from silencing. This licensing system is not yet fully understood, but the mechanism of piRNA binding provides some clues: since a single transcript may have numerous, unpredictably spaced piRNA binding sites, physically blocking piRNA binding across the entire transcript would be difficult and likely unfeasible. An attractive alternative involves phase separation: licensed transcripts could be sequestered from the silencing machinery in physical space. Dodson and Kennedy posit that piRNA targeting occurs in perinuclear compartments of germ cells known as P granules, while amplification of the silencing response takes place in the nearby Mutator foci (25). P granules have been shown to store newly transcribed mRNAs before releasing them into the cytoplasm for translation (26). Furthermore, the P granule has been found to contain both PRG-1 (8), which binds piRNAs, and the putative licensing Argonaute CSR-1 (27), which binds siRNAs complementary to most germline-expressed genes (10,11). These observations suggest a possible mechanism of licensing where newly transcribed mRNAs are allowed to bind to both PRG-1 and CSR-1 in the P granule, and whichever dominates determines whether transcripts are sequestered to the Mutator foci for downstream silencing or released from the P granule for translation (28). However, the precise mechanism of CSR-1 in licensing has not been confirmed, and other proposals for licensing systems exist: e.g. Zhang et al. argue that 10-base periodic An/Tn sequence clusters act as licensing signals (5). Regardless of the details of the licensing mechanism, the ubiquity and random locations of piRNA targeting sites on transcripts means that physical separation is likely to play a key role in distinguishing silenced transcripts from those destined for translation.
Why might C. elegans have evolved a silencing system so broad that it necessitates a parallel licensing system? Across a variety of organisms, the evolution and counter-evolution of transposons and the piRNA system constitutes an ‘arms race’ which drives rapid evolution and divergence between species (1). Indeed, C. elegans and its close relatives are the only nematodes to possess piRNAs; other nematodes employ different strategies of transposon silencing (29). One advantage of the C. elegans piRNA system over a ‘transposon library’ system such as that of D. melanogaster is that it allows for rapid silencing of novel sequences, independent of sequence mutations in transposons or piRNAs. This idea is consistent with research suggesting that activation of transposons in C. elegans is associated with failures of the piRNA system, but not mutations in individual piRNA sequences (30). A rapid response may be especially important because C. elegans has a fixed number of cells, potentially making a takeover of the transcription machinery by a virus or transposon more costly to the organism. Another possible benefit is that a broad silencing system might enable C. elegans to dynamically control transcription, by changing the profile of what is being licensed (for example, by transcribing different guide siRNAs for CSR-1). In support of this hypothesis, germ cells in C. elegans which lack key P granule components undergo spurious differentiation pathways into other cell types, indicating a failure in transcriptional regulation (31). An understanding of the purpose of broad targeting by piRNAs in C. elegans could elucidate the role of piRNAs in other species. For example, mice possess two classes of piRNAs: pre-pachytene piRNAs with high complementarity to transposons, and pachytene piRNAs that possess much fewer clear matches to transposons in the genome yet still have regulatory roles (1,32). These pachytene piRNAs are responsible for broad purging of mRNAs during spermiogenesis (33), suggesting that multiple organisms employ the strategy of using a variety of arbitrary sequences to target a swath of mRNAs.
There are a variety of experiments that could further elucidate how C. elegans determines whether to silence or license transcripts, and measure the reliability and efficiency of this process. First of all, the piRNA-target distance implemented in this study could be further verified and refined by determining how effectively it predicts the probability of silencing. This can be done through a GFP reporter assay such as that used by Zhang et al., where a GFP transgene modified to lack piRNA targeting sites is introduced to the organism, along with a synthetic piRNA which partially matches a subsequence of the transgene (5). Changing the sequence of the synthetic piRNA relative to the modified GFP would allow silencing probability to be determined as a function of piRNA-target distance. Another key line of investigation is how C. elegans is able to rapidly classify transcripts as self or nonself: transcripts destined for expression only spend about 15 min in the P granule before being released to the cytoplasm, suggesting that Argonaute binding and target identification must happen in this timeframe (26). A promising line of research to address this question would be to analyze the mRNA scanning properties of the Argonautes involved in this system, PRG-1 and CSR-1, to estimate their search speed—which would also determine whether different Argonautes have been evolutionarily tuned for different levels of mismatch tolerance. The FRET assay used by Chandradoss et al. to estimate the dwell time of the hAgo2-miRNA complex on a target subsequence with a given number of matches would be a useful tool to address this question (34). These experiments and others would help lead us toward a deeper quantitative understanding of how C. elegans utilizes small RNAs to efficiently differentiate self and nonself transcripts.
DATA AVAILABILITY
The resources used in this study are freely accessible online, detailed in the Computational Resources section of Materials and Methods.
Supplementary Material
ACKNOWLEDGEMENTS
We thank our colleagues at Princeton University for lending their expertise while we developed this study: Coleen Murphy and Rachel Kaletsky for their guidance on C. elegans and piRNAs, Joshua Riback for our discussion about phase separation, and Cameron Myhrvold for our discussion on experimental imaging methods. We also thank Wei-Sheng Wu at National Cheng Kung University for providing assistance with the pirScan tool he helped develop when we were performing initial investigations into this system.
APPENDIX.
Cumulative distribution function of piRNA-target distance between random sequences
To characterize the random global closest-match probability distribution, we sought to determine the CDF of the piRNA-target distance 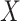 between two random 21-nt sequences, with equal and independent probabilities for each nucleotide. A simple approach would be to sample a large number of draws of
between two random 21-nt sequences, with equal and independent probabilities for each nucleotide. A simple approach would be to sample a large number of draws of 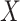 to empirically determine the CDF. However, because we are primarily interested in the minimum among many draws of
to empirically determine the CDF. However, because we are primarily interested in the minimum among many draws of 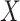 , it is crucial that the rare, small values of
, it is crucial that the rare, small values of 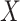 corresponding to well-matching sequences be adequately sampled. In order to do this, we took samples of
corresponding to well-matching sequences be adequately sampled. In order to do this, we took samples of 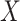 with a fixed number of matches, and took advantage of the known binomial probability of a random pair of sequences having a given number of matches. Specifically, we generated pairs of sequences where
with a fixed number of matches, and took advantage of the known binomial probability of a random pair of sequences having a given number of matches. Specifically, we generated pairs of sequences where 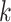 bases in each pair were randomly chosen to match, with
bases in each pair were randomly chosen to match, with 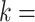 0…20, while the other bases were allowed to be GU wobbles or mismatches based on the corresponding probabilities expected for random sequences. For each value of
0…20, while the other bases were allowed to be GU wobbles or mismatches based on the corresponding probabilities expected for random sequences. For each value of 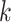 , we generated
, we generated 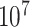 such randomized sequences. Then, we calculated the empirical CDF of distances for each set of
such randomized sequences. Then, we calculated the empirical CDF of distances for each set of 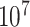 sequences, which closely approximates the true CDF of the piRNA-target distance for random sequences when the number of matches is fixed. We then added these 20 CDFs, together with the
sequences, which closely approximates the true CDF of the piRNA-target distance for random sequences when the number of matches is fixed. We then added these 20 CDFs, together with the 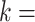 21 perfect-match (zero-distance) case, each weighted by the binomial probability of two 21-nt sequences having
21 perfect-match (zero-distance) case, each weighted by the binomial probability of two 21-nt sequences having 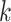 matches. This calculation produced the non-conditional CDF of the piRNA-target distance between two random 21-nt sequences:
matches. This calculation produced the non-conditional CDF of the piRNA-target distance between two random 21-nt sequences:
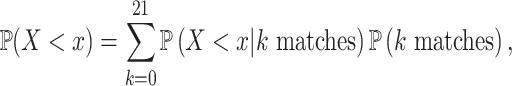 |
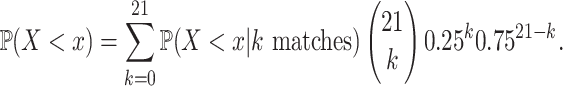 |
Contributor Information
John McEnany, Biophysics Program, Stanford University, Stanford, CA 94305, USA; Department of Physics, Princeton University, Princeton, NJ 08544, USA.
Yigal Meir, Department of Physics, Ben-Gurion University, Be’er Sheva, 84105, Israel; Department of Physics, Princeton University, Princeton, NJ 08544, USA.
Ned S Wingreen, Department of Molecular Biology, Princeton University, Princeton, NJ 08544, USA.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Science Foundation [PHY-1734030]. Funding for open access charge: Ned Wingreen.
Conflict of interest statement. None declared.
REFERENCES
- 1. Parhad S.S., Theurkauf W.E.. Rapid evolution and conserved function of the piRNA pathway. Open Biol. 2019; 9:180181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Brennecke J, Aravin A.A., Stark A., Dus M., Kellis M., Sachidanandam R., Hannon G.J.. Discrete small RNA-generating loci as master regulators of transposon activity in Drosophila. Cell. 2007; 128:1089–1103. [DOI] [PubMed] [Google Scholar]
- 3. Luo S., Zhang H., Duan Y., Yao X., Clark A.G., Lu J.. The evolutionary arms race between transposable elements and piRNAs in Drosophila melanogaster. BMC Evol. Biol. 2020; 20:14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Shen E., Chen H., Ozturk A.R., Tu S., Shirayama M., Tang W., Ding Y., Dai S., Weng Z., Mello C.C.. Identification of piRNA binding sites reveals the Argonaute regulatory landscape of the C. elegans germline. Cell. 2018; 172:937–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Zhang D., Tu S., Stubna M., Wu W., Huang W., Lee H.. The piRNA targeting rules and the resistance to piRNA silencing in endogenous genes. Science. 2018; 359:587–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Reed K.J., Svendsen J.M., Brown K.C., Montgomery B.E., Marks T.N., Vijayasarathy T., Parker D.M., Nishimura E.O., Updike D.L., Montgomery T.A.. Widespread roles for piRNAs and WAGO-class siRNAs in shaping the germline transcriptome of Caenorhabditis elegans. Nucleic Acids Res. 2020; 48:1811–1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bagijn M.P., Goldstein L.D., Sapetschnig A., Weick E., Bouasker S., Lehrbach N.J., Simard M.J., Miska E.A.. Function, targets and evolution of Caenorhabditis elegans piRNAs. Science. 2012; 337:574–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Batista P.J., Ruby G., Claycomb J.M., Chiang R., Fahlgren N., Kasschau K.D., Chaves D.A., Gu W., Vasale J.J., Duan S.et al.. PRG-1 and 21U-RNAs interact to form the piRNA complex required for fertility in C. elegans. Mol. Cell. 2008; 31:67–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Barberán-Soler S., Fontrodona L., Ribó A., Lamm A.T., Iannone C., Cerón J., Lehner B., Valcárcel J.. Co-option of the piRNA pathway for germline-specific alternative splicing of C. elegans TOR. Cell Rep. 2014; 8:1609–1616. [DOI] [PubMed] [Google Scholar]
- 10. Wedeles C.J., Wu M.Z., Claycomb J.M.. Protection of germline gene expression by the C. elegans Argonaute CSR-1. Dev. Cell. 2013; 27:664–671. [DOI] [PubMed] [Google Scholar]
- 11. Seth M., Shirayama M., Gu W., Ishidate T., Conte D. Jr, Mello C.C.. The C. elegans CSR-1 Argonaute pathway counteracts epigenetic silencing to promote germline gene expression. Dev. Cell. 2013; 27:656–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Wu W., Brown J.S., Chen T., Chu Y., Huang W., Lee H.. piRTarBase: a database of piRNA targeting sites and their roles in gene regulation. Nucleic Acids Res. 2019; 47:181–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. McMurchy A.N., Stempor P., Gaarenstroom T., Wysolmerski B., Dong Y., Aussianikava D., Appert A., Huang N., Kolasinska-Zwierz P., Sapetschnig A.et al.. A team of heterochromatin factors collaborates with small RNA pathways to combat repetitive elements and germline stress. eLife. 2017; 6:e21666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Tang W., Tu S., Lee H., Weng Z., Mello C.C.. The RNase PARN-1 trims piRNA 3’ ends to promote transcriptome surveillance in C. elegans. Cell. 2016; 164:974–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Gu W., Lee H., Chaves D., Youngman E.M., Pazour G.J., Conte Jr. D., Mello C.C.. CapSeq and CIP-TAP identify Pol II start sites and reveal capped small RNAs as C. elegans piRNA precursors. Cell. 2012; 151:1488–1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Howe K.L., Bolt B.J., Shafie M., Kersey P., Berriman M.. WormBase ParaSite – a comprehensive resource for helminth genomics. Mol. Biochem. Parasitol. 2015; 215:2–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Howe K.L., Bolt B.J., Cain S., Chan J., Chen W.J., Davis P., Done J., Down T., Gao S., Grove C.et al.. WormBase 2016: expanding to enable helminth genomic research. Nucleic Acids Res. 2016; 44:774–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Laricchia K.M., Zdraljevic S., Cook D.E., Andersen E.C.. Natural variation in the distribution and abundance of transposable elements across the Caenorhabditis elegans species. Mol. Biol. Evol. 2017; 34:2187–2202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Kaminker J.S., Bergman C.M., Kronmiller B., Carlson J., Svirskas R., Patel S., Frise E., Wheeler D.A., Lewis S.E., Rubin G.M., Ashburner M., Celniker S.E.. The transposable elements of the Drosophila melanogaster euchromatin: a genomics perspective. Genome Biol. 2002; 3:research0084.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Beltran T., Barroso C., Birkle T.Y., Stevens L., Schwartz H.T., Sternberg P.W., Fradin H., Gunsalus K., Piano F., Sharma G.et al.. Comparative epigenomics reveals that RNA Polymerase II pausing and chromatin domain organization control nematode piRNA biogenesis. Dev. Cell. 2019; 48:793–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Bao W., Kojima K.K., Kohany O.. Repbase Update, a database of repetitive elements in eukaryotic genomes. Mob. DNA. 2015; 6:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Wu W., Huang W., Brown J.S., Zhang D., Song X., Chen H., Tu S., Weng Z., Lee H.. pirScan: a webserver to predict piRNA targeting sites and to avoid transgene silencing in C. elegans. Nucleic Acids Res. 2018; 46:W43–W48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Wu W., Brown J.S., Chen T., Chu Y., Huang W., Tu S., Lee H.. piRTarBase: a database of piRNA targeting sites and their roles in gene regulation. Nucleic Acids Res. 2019; 47:D181–D187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Klein M., Chandradoss S.D., Depken M., Joo C.. Why Argonaute is needed to make microRNA target search fast and reliable. Semin. Cell Devol. Biol. 2017; 65:20–28. [DOI] [PubMed] [Google Scholar]
- 25. Dodson A.E., Kennedy S.. Phase separation in germ cells and development. Dev. Cell. 2020; 55:4–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Sheth U., Pitt J., Dennis S., Priess J.R.. Perinuclear P granules are the principal sites of mRNA export in adult C. elegans germ cells. Development. 2010; 137:1305–1314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Claycomb J.M., Batista P.J., Pang K.M., Gu W., Vasale J.J., van Wolfswinkel J.C., Chaves D.A., Shirayama M., Mitani S., Ketting R.F.et al.. The Argonaute CSR-1 and its 22G-RNA co-factors target germline genes and are required for holocentric chromosome segregation. Cell. 2009; 139:123–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Youngman M., Claycomb J.M.. From early lessons to new frontiers: the worm as a treasure trove of small RNA biology. Front. Genet. 2014; 5:416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Sarkies P., Selkirk M.E., Jones J.T., Blok V., Boothby T., Goldstein B., Hanelt B., Ardila-Garcia A., Fast N.M., Schiffer P.M.et al.. Ancient and novel small RNA pathways compensate for the loss of piRNAs in multiple independent nematode lineages. PLoS Biol. 2015; 13:e1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Bergthorsson U., Sheeba C.J., Konrad A., Belicard T., Beltran T., Katju V., Sarkies P.. Long-term experimental evolution reveals purifying selection on piRNA-mediated control of transposable element expression. BMC Biol. 2020; 18:162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Seydoux G. The P granules of C. elegans: a genetic model for the study of RNA-protein condensates. J. Mol. Biol. 2018; 430:4702–4710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Yamamoto Y., Watanabe T., Hoki Y., Shirane K., Li Y., Ichiiyanagi K., Kuramochi-Miyagawa S., Toyoda A., Fujiyama A., Oginuma M.et al.. Targeted gene silencing in mouse germ cells by insertion of a homologous DNA into a piRNA generating locus. Genome Res. 2013; 23:292–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Gou L., Dai P., Yang J., Xue Y., Hu Y., Zhou Y., Kang J., Wang X., Li H., Hua M.et al.. Pachytene piRNAs instruct massive mRNA elimination during late spermiogenesis. Cell Res. 2014; 24:680–700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Chandradoss S.D., Schirle N.T., Szczepaniak M., MacRae I.J., Joo C.. A dynamic search process underlies microRNA targeting. Cell. 2015; 162:96–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The resources used in this study are freely accessible online, detailed in the Computational Resources section of Materials and Methods.