Achieving depth-independent lateral resolution in AR-PAM using the synthetic-aperture focusing technique

Abstract

Acoustic-resolution photoacoustic microscopy (AR-PAM) is a promising imaging modality that renders images with ultrasound resolution and extends the imaging depth beyond the optical ballistic regime. To achieve a high lateral resolution, a large numerical aperture (NA) of a focused transducer is usually applied for AR-PAM. However, AR-PAM fails to hold its performance in the out-of-focus region. The lateral resolution and signal-to-noise ratio (SNR) degrade substantially, thereby leading to a significantly deteriorated image quality outside the focal area. Based on the concept of the synthetic-aperture focusing technique (SAFT), various strategies have been developed to address this challenge. These include 1D-SAFT, 2D-SAFT, adaptive-SAFT, spatial impulse response (SIR)-based schemes, and delay-multiply-and-sum (DMAS) strategies. These techniques have shown progress in achieving depth-independent lateral resolution, while several challenges remain. This review aims to introduce these developments in SAFT-based approaches, highlight their fundamental mechanisms, underline the advantages and limitations of each approach, and discuss the outlook of the remaining challenges for future advances.

1. Introduction

The photoacoustic (PA) technique [1], [2] is a hybrid imaging method that incorporates optical contrast and ultrasound wave detection. In PA imaging, light absorptive samples such as biological tissues are irradiated by a short-pulse laser beam, during which the absorbed photons are partially converted to heat, thereby inducing thermo-elastic expansion [3], [4]. This leads to a pressure rise that propagates in the form of wideband frequency ultrasonic waves that can be detected by an ultrasound transducer [5], [6], [7], [8]. Given that ultrasonic scattering is two to three orders of magnitude less than optical scattering, the transformation from photon to acoustic energy in the PA technique breaks the optical diffusion limit and significantly extends the imaging depth to ranges that are inaccessible by conventional optical imaging [9], [10], [11], [12]. Meanwhile, PA imaging preserves the rich optical absorption contrast, which is derived from photon absorption, as opposed to conventional ultrasound imaging techniques, where the imaging contrast is a result of mechanical properties. These features, i.e., a large penetration depth and rich optical contrast [13], [14], [15], [16], [17], [18], make PA imaging a revolutionary modality suitable for wide applications in biomedical research [19], [20], [21], [22], [23], [24], [25].

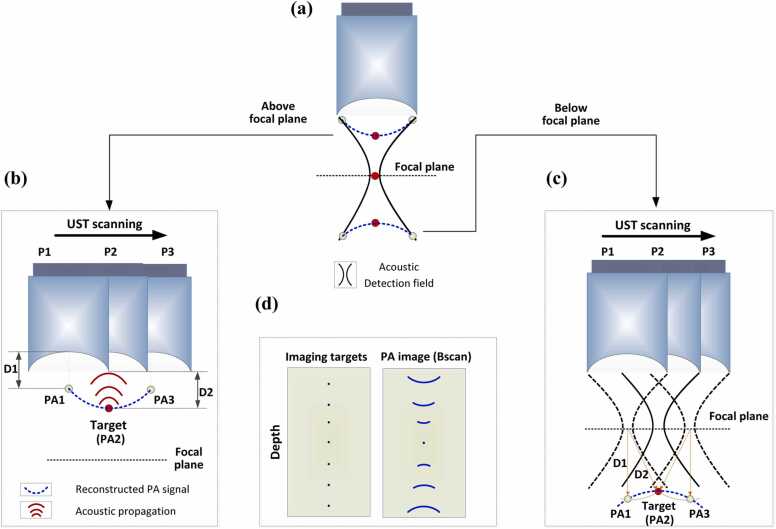
Photoacoustic microscopy (PAM) is one major implementation of PA imaging [26], [27]. There are two sub-categories of PAM: optical-resolution PAM (OR-PAM) and acoustic-resolution PAM (AR-PAM). OR-PAM achieves optical lateral resolution (micron or even submicron scale) at superficial depths using tight optical focusing [28], [29], [30], [31], [32]. AR-PAM renders images with acoustic lateral resolution (tens to hundreds of microns) at a much greater penetration depth using wide-beam optical illumination but tight acoustic focusing [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45]. This paper focuses on the second category (AR-PAM). In AR-PAM, the lateral resolution is determined by the acoustic numerical aperture, NA, and the PA center frequency, $f_0$ [2], as $R_{\mathit{lateral}}=0.71c/\left(\mathit{NA}{f}_0\right)$, where c denotes the speed of sound. To achieve high spatial resolution, a spherically focused transducer with a high center frequency, $f_0,$ and a large numerical aperture, $\mathit{NA}$, is usually employed for signal detection. Unfortunately, the lateral resolution and imaging depth are in a trade-off relationship. High spatial resolution limits the acoustic focal zone, thereby leading to a significantly deteriorated image quality (i.e., lateral resolution and signal-to-noise ratio (SNR)) in the out-of-focus regions [26], [46]. Specifically, the PA signals of targets outside the focal zone are distorted and curved away from the focus, as depicted in Fig. 1. The distorted signals generally exhibit a concave shape above the focus and a convex shape below (Fig. 1a); the mechanisms for these phenomena are described below.

Fig. 1.

Graphical illustration of signal blurring in the out-of-focus regions in AR-PAM. (a) Distorted shapes of the PA signals (blue dashed lines) above and below the focal plane. Black solid lines: acoustic detection field. Red circle: the imaging target. (b) Concave shape of the signal blurring when the target is located above the focal plane. (c) Convex shape of the signal blurring when the target is located below the focal plane. PAi: detected PA signal when the UST is at position Pi; i = 1, 2, 3. (d) Comparison between imaging targets and their corresponding signals in a B-scan image. The targets are arranged at different depths from the focus.

The two scenarios described above are illustrated in Fig. 1b and c, where the imaging target is represented by the red dot, and the ultrasound transducer (UST) scans horizontally from position 1 (P1) to position 3 (P3). In the case of concavely distorted PA signals (Fig. 1b), the PA waves generated by the target are depicted by the red solid lines. In PAM, the detected A-lines are combined next to each other to form a 2D image (B-scan). When the UST locates at P1, the acoustic waves (red solid lines) of the target are first detected by the right edge of the UST. PAM assumes that the target locates right below the UST. Thus, based on the time of flight, the signal of the target is projected as PA1. The distance between PA1 and the center of the UST detection surface (D1) equals the distance between the target and the right edge of the UST (D2). When the UST moves to P2, the acoustic wave arrives at the center of UST detection region first because (1) the transducer applied in AR-PAM is generally spherically focused, and (2) the target locates above the focus (the center point of a sphere). Based on the time of flight, the PA image of the target superposes the position of the target, i.e., PA2 reflects the actual position of the target. When the UST moves to P3, the acoustic waves are first detected by the left edge of the UST. Again, according to the time of flight, the signal of the target is projected as PA3. Connecting all of the PA signal projected positions during the UST scanning, a concave imaging shape of the target is achieved (dashed blue line in Fig. 1b). On the other hand, Fig. 1c demonstrates the case in which the target (red dot) locates below the focal plane. The hyperbola curves (dashed and solid black lines) indicate the acoustic detection regions of the UST at different depths. In contrast to the case where the target locates above the focus, the acoustic signals below the UST focus need to propagate through the middle region of the hyperbola for the PA signal to be detected by the UST, as imaging targets located outside the detection area generally cannot be imaged. When the UST locates at P1, the PA waves generated by the target first propagate through the middle of the hyperbola and then arrive at the detection surface of the UST. This takes more time than when the UST locates at P2, in which PA waves directly propagate through the detection region without a detour. For the former case (the UST at P1), the imaged signal of the target is projected as PA1, and the distance between PA1 and the focal point (D1) equals the distance between the target and the focal point (D2). For the latter case (the UST at P2), the imaged signal of the target superposes the position of the target, i.e., PA2 reflects the actual position of the target. When the UST moves to P3, similar to when it is located at P1, the pressure rise generated by the target (red circle) needs to travel through the middle region of the hyperbola and then arrive at the detection surface of the UST. Again, according to the time of flight, the imaged signal of the target is projected as PA3. By connecting all of the detected signals along the scanning direction of the UST, a convex shape of the distorted signals is formed (dashed blue line in Fig. 1c).

Consequently, AR-PAM exhibits inherent artifacts with distorted shapes (concave or convex) as a function of the imaging depth (Fig. 1d). Efforts have been made in the past to address this challenge, including model-based approaches [47], [48], [49], [50], time reversal strategies [51], [52], [53], [54], [55], and the synthetic aperture focusing technique (SAFT) [56], [57], [58], [59], [60], [61]. Compared with other schemes, SAFT is a far more commonly used approach to solve the blurring problem in the out-of-focus region. As a conventional post-processing method for image reconstruction, SAFT has been widely used in radar and ultrasound imaging [62], [63], [64], [65]. By employing the virtual detector concept [57], SAFT-based solutions can be extended to the focused transducer applications in AR-PAM. The SAFT-based approach along with coherent factor (CF) weighting has raised a lot of interest since their initial applications to AR-PAM by Liao et al. [56] and Li et al. [57]. By properly delaying and summing the signals received at adjacent scan lines (i.e., A-lines), SAFT improves the spatial resolution and SNR in the out-of-focus region. However, the effectiveness of SAFT is sensitive to the synthesis direction. Synthesizing in one dimension leads to anisotropy in the lateral resolution and SNR. To overcome this limitation, Deng et al. [66] developed a 2D-SAFT approach in which the synthesis of correlated signals was processed in both the x-z and y-z planes. Although a homogenous lateral resolution could be achieved, the resolution and SNR enhancement of the 2D-SAFT were worse than the best performance of 1D-SAFT when imaging vasculatures [66], owing to the mismatch between the spherical wavefront concept of the 2D algorithm and the cylindrical wavefronts of the targets [66], [67]. To address this challenge, an adaptive SAFT solution [68] that synthesizes signals perpendicular to an arbitrary direction of the targets has been proposed. Another approach, the frequency-domain SAFT [69], has also shown the potential to tackle such problems. Furthermore, to remove invalid signals involved in SAFT, the spatial impulse response (SIR) [70] of the transducer has been introduced to weigh the contributions of the SAFT at different depths.

Another research interest in SAFT-based strategies lies in the development of beamformers. Generally, the delay-and-sum (DAS)-based algorithm is employed for the synthesis owing to its simple implementation. However, DAS is a blind beamformer that treats all of the input A-lines equally, thereby resulting in a high level of noises and artifacts. To compensate for this limitation, DAS is usually applied in conjunction with CF weighting. Recent studies have shown that other approaches, such as the delay-multiply-and-sum algorithm (DMAS) [71] and double-state (DS) DMAS [72], can be applied for this purpose. With a correlation operation of the PA signals at each scanline, DMAS-based SAFT has shown an improved ability to reduce incoherent components such as noises and artifacts.

In brief, the above SAFT-based approaches have made progress in expanding the depth of focus and decreasing the dependence of lateral resolution and SNR on the imaging depth. However, these strategies have limitations and challenges. In this review, we introduce recent advances and outline their fundamental algorithms. The merits and limitations of different strategies are compared and analyzed. Furthermore, this review discusses the prospects and challenges of future advances in SAFT-based strategies for AR-PAM.

2. Basic principle of VD-based SAFT strategies

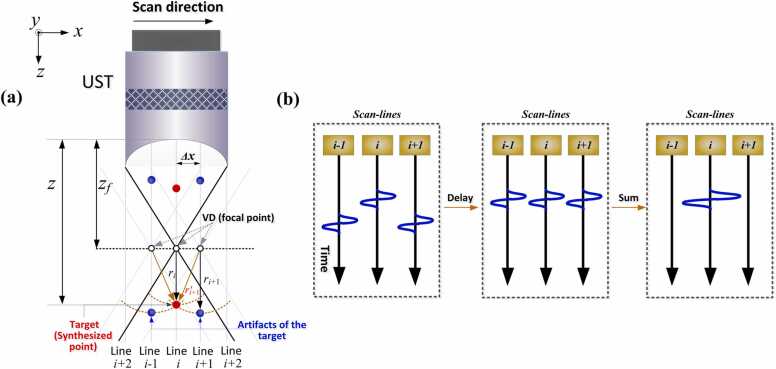
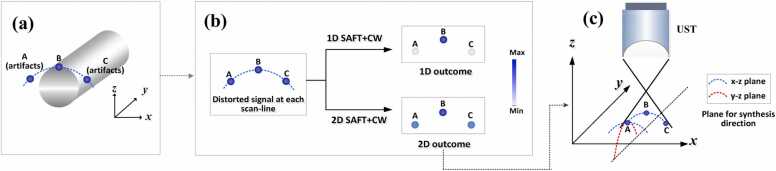
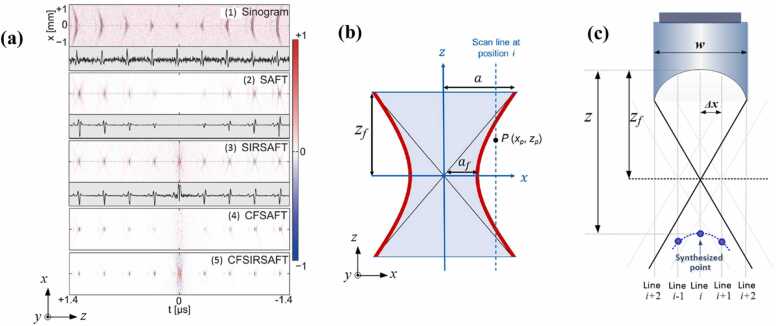
The schematic illustration of SAFT using the virtual detector (VD) concept is depicted in Fig. 2a, where the focus of the UST is usually considered as the VD. The red dots represent the imaging targets, and the blue dots are the artifacts of the targets, the connection of which forms the convex/concave shape of the distorted signals, as detailed illustrated by Fig. 1 in the Introduction. To restore the authentic target shape, the PA signals detected at adjacent scanning points are synthesized by considering their acoustic propagation delays, $∆t_j$ [56], [57]:

$${\mathit{RF}}_{\mathit{SAFT}}\left(i,t\right)=\sum _{j=-N}^N\mathit{RF}\left(i+j,t-∆t_j\right)$$ (1)

Fig. 2.

Principle of the VD-based SAFT strategy. (a) Geometric illustration of SAFT. Red dots: targets (synthesized imaging points). Blue dots: artifacts of the target, generated due to the signal blurring in AR-PAM. $\mathrm{z}$: depth of the synthesized imaging point. $z_f$: depth of the focal point (VD). $r_i$: distance between the synthesized point (target location) and the focal point. $r_{i+1}$: distance between the detected signal of the target (artifact) and the focal point when the UST moves to position i + 1. $r_{i+1}^{\prime }$: distance between the synthesized point and focal point when the UST moves to position i + 1. $∆x$: scanning step of the UST between A-lines. (b) Synthesis of new A-lines: Left: original detected A-lines; Middle: delayed versions of A-lines; Right: newly generated A-lines after summation.

On the left side of Eq. (1), ${\mathit{RF}}_{\mathit{SAFT}}$(i, t) denotes the signal after SAFT processing, where i and t are the two coordinates (the scanning direction and the depth direction (propagation time $t=z/c$), respectively) of a two-dimensional space (B-scan). On the right side of Eq. (1), a delay and sum (DAS) process is performed for the raw data (RF, i.e., A-line). More specifically, an appropriate time delay, $∆t_j$, is applied to the detected scanlines in the vicinity of the ith line, such that the correlated signals are adjusted to be in-phase, as illustrated in Fig. 2b. After this procedure, the adjacent A-lines can be correctly synthesized (Fig. 2b, right). In Eq. (1), $j$ defines the adjacent scanlines involved in the summation, the total number (N) of which is determined by the opening angle of the UST—a large NA of the focused transducer leads to a larger number of summed scanlines (as described in Section 3.4). The time delay, $∆t_j$, is quantified based on the difference in the detection time. For scanline (i + 1) shown in Fig. 2a, the time delay ($∆t_{i+1}$) relative to scanline (i) is calculated as $\left(r_{i+1}{-r}_i\right)/c$, where $r_i$ is the distance between the synthesized point (target location) and the focal point, $r_{i+1}$ is the distance between the detected signal of the target (artifact) and the focal point when the UST moves to position i + 1, and c is the speed of sound. The quantity $\left(r_{i+1}{-r}_i\right)/c$ represents the difference in the detection time between lines i and i + 1. Note that $r_{i+1}$ generally cannot be known a priori. Fortunately, $r_{i+1}$ is equal to $r_{i+1}^{\prime }$, as shown in Fig. 2a. The latter ($r_{i+1}^{\prime }$) is the distance between the VD of scanline (i + 1) and the synthesized point, which can be expressed as $\sqrt{{r_i}^2+{∆x}^2}$, where $∆x$ is the moving step of the UST during scanning between adjacent A-lines. Therefore, for an arbitrary scanline $i+j$, the time delay ($∆t_j$) applied to the received signal is given by:

$$∆t_j=\mathit{sign}(z-z_f)\frac{r_{i+j}^{\prime }-r_i}{c}=\mathit{sign}(z-z_f)\frac{\sqrt{{r_i}^2+{\left(j∆x\right)}^2}-r_i}{c}$$ (2)

where sign is the signum function; $∆t_j$ > 0 if the target locates below the focus, $∆t_j$ < 0 if the target locates below the focus, and $∆t_j$ = 0 if the target locates at the focus; z and$z_f$ signify the depth of the synthesized point and focal point, respectively. With the implementation of (1), (2), a set of new A-lines are synthetically generated by combining the delayed versions of the detected A-lines (Fig. 2b). This reconstruction solution is also referred to as VD-based SAFT because the A-lines can be considered to be detected at the VD location [56], [57].

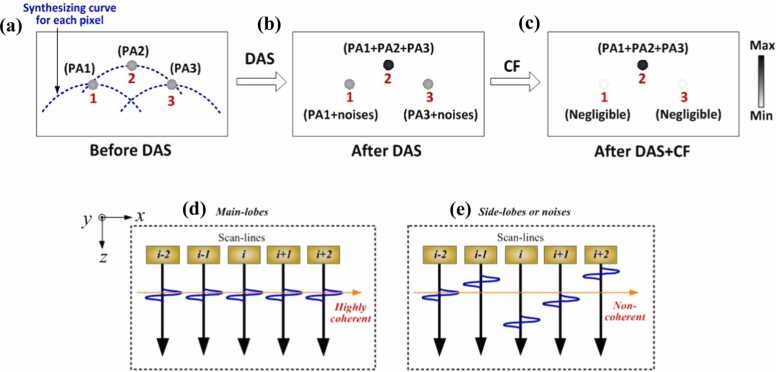
Note that SAFT is performed in a pixel-by-pixel manner, as illustrated in Fig. 3a. Thus, not only the main lobes (such as point 2) are processed with DAS, but also the artifacts (such as points 1 and 3). For the real target location (such as point 2), DAS synthesizes the signals of the target and neighboring points (i.e., the summation of PA1, PA2, and PA3). For artifacts (such as points 1 or 3), DAS synthesizes the artifact itself and adjacent noises (i.e., PA1+ noises, PA3+ noises). Generally, the image noises generated in PAM are randomly positive or negative. Therefore, the sum of noises becomes negligible when sufficient pixels are involved in the reconstruction, and the PA signals for artifacts (such as points 1 and 3) after SAFT are close to their original value (PA1 or PA3). In other words, the image after processing by DAS-based SAFT (Eq. (1)) still preserves the signals of artifacts (PA1 and PA3), as illustrated in Fig. 3b, although the main lobe signal (point 2) is greater than that of adjacent artifacts (points 1 and 3). The high level of noises and artifacts in DAS-based SAFT restricts its application. To compensate for this limitation, CF weighting is generally applied to the output of DAS to suppress the artifacts and noises [56], [57], [58], [59].

$$\mathit{CF}\left(i,t\right)=\frac{{\left|\sum _{j=-N}^N\mathit{RF}\left(i+j,t-∆t_j\right)\right|}^2}{N{{\sum }_{j=-N}^N\left|\mathit{RF}\left(i+j,t-∆t_i\right)\right|}^2}$$ (3)

Fig. 3.

Illustration of the limitation of the DAS beamformer in minimizing artifacts and noises, as well as the effectiveness of CF in compensating for this limitation. (a) Detected PA signals before DAS. The blue dashed lines indicate the adjacent signals involved in the summing process. Points 1, 2, and 3 are the representative pixels with PA signals labeled as PA1, PA2, and PA3, respectively. (b) Beamformed PA signals after DAS. For the main lobes (such as point 2), the PA signal after SAFT becomes the sum of PA1, PA2, and PA3. For the artifacts (such as points 1 or 3), the PA signal after SAFT becomes the sum of the original signal and the adjacent noises (i.e., PA1+ noises, PA3+ noises). (c) Beamformed PA signals after DAS+CF. The side lobes are effectively suppressed. (d) Case of the main lobes (such as point 2), in which the delayed signals are highly in-phase (coherent). (e) Case of the side lobes and background noises (such as points 1 or 3), in which the delayed signals are generally out-of-phase (incoherent).

The denominator of CF is the sum of the squares of the delayed versions of the A-lines (Fig. 2b, middle) used in SAFT, and the numerator is the square of the sum of the aforementioned A-lines. The CF value, which can be derived from Eq. (3), ranges from 0 to 1. To provide a straightforward understanding, Fig. 3(d and e) demonstrates the CF concept from a signal coherence perspective. It can be inferred from Fig. 3d and e and Eq. (3) that CF can be considered as the ratio of the coherent energy to the total energy of the delayed signals [73], [74]. To be more specific, CF reaches maximal (close to 1) when the delayed version of the signals is perfectly coherent (Fig. 3d) along the synthesis direction. In contrast, CF is minimized when the delayed signals are incoherent (Fig. 3e). The former case (CF close to 1) corresponds to the main lobes, where the adjacent delayed A-lines are highly coherent. The latter case (CF close to 0) corresponds to the side lobes and noises where the adjacent delayed A-lines are generally incoherent. By applying CF to the output of the SAFT, the CF-weighted SAFT is given by the following [56], [57], [58], [59], [66], [67]:

$${\mathit{RF}}_{\mathit{SAFT}-\mathit{CF}}\left(i,t\right)={\mathit{CF}\left(i,t\right)\times \mathit{RF}}_{\mathit{SAFT}}\left(i,t\right)$$ (4)

CF weighting is applied to the SAFT on a pixel-by-pixel basis, after which the side lobes and noises in the SAFT are suppressed, whereas the main lobe signals of the SAFT are reserved, as illustrated in Fig. 3c. This further increases the beam quality [66], [67], [68], [70]. It should be noted that this section discusses the CF-weighed SAFT based on the DAS beamformer, which is a commonly used strategy in SAFT. In addition to the DAS beamformer, the DMAS-based beamforming technique [71], [72], which has recently been employed in AR-PAM, is discussed in Section 3.5.

3. SAFT-based strategies in AR-PAM

3.1. 1D-SAFT

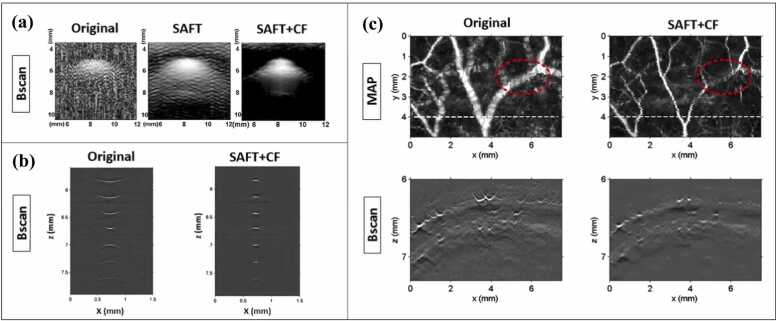
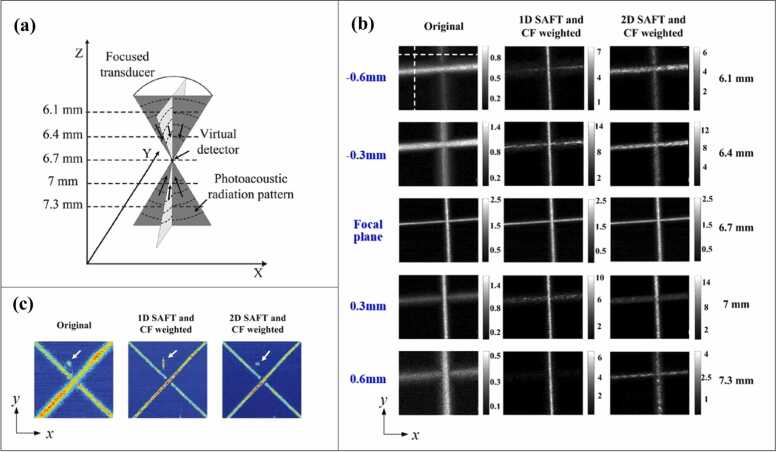
1D-SAFT indicates that SAFT is applied in one direction—normally along the B-scan direction of the UST, such that the distorted signals generated in the B-scan images are synthesized. 1D-SAFT is a commonly used strategy because of its straightforward nature. The first demonstration of this implementation was presented in Ref. [56], where the effectiveness of SAFT in conjunction with CF was validated using phantom experiments (Fig. 4a). Compared with the original image (Fig. 4a, left), in which the image quality is poor, the SAFT image (Fig. 4a, middle) exhibits enhanced resolution and SNR but still with large side lobes and high background noises, the reason of which has been elaborated in Section 2 (Fig. 3a, b). With the application of CF weighting, these artifacts and noises are significantly suppressed (Fig. 4a, right). The above results (Fig. 4a) are similar to the results of carbon fiber imaging [57] (Fig. 4b), in which the lateral resolution of the original image decreases rapidly when the carbon fibers are further from the focus (Fig. 4b, left). Consequently, the post-processing (SAFT+CF) expands the focal region and reduces the dependence of image quality on the focal depth (Fig. 4b, right). It is noteworthy that the distorted shapes of the signals above and below the focus (concave and convex, respectively) obtained from the experiments are consistent with our theoretical analysis (Fig. 1).

Fig. 4.

(a) PA images (B-scan) of a cylindrical object (vinyl alcohol): Original image (left), SAFT image (middle), SAFT+CF image (right). Figures reproduced with permission from [56] © The Optical Society. (b) PA images (B-scan) of carbon fibers located at different depths from the focus. Original image (left) and SAFT+CF image (right). Figures reproduced with publisher’s permission [57]. (c) In vivo PA images of vasculature in rat’s scalp. The major vessels are located out of focus. Original image (left) and SAFT+CF image (right). The first row shows MAP images and the second row exhibits the B-scan images corresponding to the white dashed line in MAP images. Figures reproduced with permission from [57] © The Optical Society.

The in vivo application of CF-weighted SAFT in AR-PAM was demonstrated for the first time in Ref. [57], where the vasculature of a rat’s scalp was placed out of focus. As expected, compared with the original image, the lateral resolution of the PA images (Fig. 4c, MAP and B-scan) improved considerably after SAFT+CF was performed. However, it should be noted that 1D-SAFT causes the anisotropy in the lateral resolution (between x and y directions) because only the vessels perpendicular to the synthetic direction (usually the scanning direction) can be well reconstructed. The inhomogeneous image quality will be showcased by Fig. 5b (middle, 1D-SAFT), in which the SNR and resolution of vessels along the x-axis are much worse than those of the vessels located along the y-axis. To summarize, the dependence on target orientation poses limitations for the use of 1D-SAFT in vivo, given that biological targets generally exhibit various directions that are not in a controllable manner.

Fig. 5.

(a) Concept of VD-based 2D-SAFT. (b) PA images (MAP) of two carbon fibers reconstructed using different strategies at various imaging depths: Original image (left column), 1D-SAFT image (middle column), 2D-SAFT image (right column). (c) PA images of another phantom (two carbon fibers) located 700 µm below the focal plane: Original image (left), 1D-SAFT image (middle), 2D-SAFT image (right). The white arrow indicates a dust particle of carbon fiber. Figures reproduced from [66] with the permission of AIP Publishing .

3.2. 2D-SAFT

To diminish the anisotropy in the lateral resolution caused by 1D-SAFT, Deng et al. [66] developed a 2D-based SAFT scheme (Fig. 5a) in which the image construction was performed in both the x-z and y-z planes for each pixel in the raw data.

$${\mathit{RF}}_{\mathit{SAFT}}\left(i,j,t\right)=\sum _{u=-N}^N\mathit{RF}\left(i+u,j,t-∆t_u\right)+\sum _{v=-N}^N\mathit{RF}\left(i,j+v,t-∆t_v\right)$$ (5)

where i, j, and t are the coordinates in three-dimensional space; i is the coordinate in the direction between adjacent A-lines, j is the coordinate in the direction between adjacent B-scans, and t is the coordinate in the depth direction (propagation time $t=z/c$). $∆t_u$ and $∆t_v$ are the time delays of the adjacent scanlines in the x-z and y-z planes, respectively. Eq. (5) is analogous to Eq. (1) (1D-SAFT) only with extra dimension included. Similarly, by considering another dimension, the CF weighting is given as

$$\mathit{CF}\left(i,j,t\right)=\frac{{\left|\sum _{u=-N}^N\mathit{RF}\left(i+u,j,t-∆t_u\right)+\sum _{v=-N}^N\mathit{RF}\left(i,j+v,t-∆t_v\right)\right|}^2}{2N\left({{\sum }_{j=-N}^N\left|\mathit{RF}\left(i+j,t-∆t_i\right)\right|}^2+{{\sum }_{j=-N}^N\left|\mathit{RF}\left(i+j,t-∆t_i\right)\right|}^2\right)}$$ (6)

The CF value also ranges from 0 to 1. With the combination of CF, the output of the 2D-SAFT is expressed as ${\mathit{RF}}_{\mathit{SAFT}-\mathit{CF}}\left(i,j,t\right)=\mathit{CF}\left(i,j,\mathit{t}\right)\times {\mathit{RF}}_{\mathit{SAFT}}\left(i,j,t\right)$. Note that all of the following 2D-SAFT image results refer to the outcomes of ${\mathit{RF}}_{\mathit{SAFT}-\mathit{CF}}\left(i,j,t\right)$. To validate the performance of the 2D-SAFT strategy, PA imaging of two carbon fibers was conducted at various imaging depths (Fig. 5b). In the original image (Fig. 5b, left column), the signal blurs considerably when the carbon fibers are out of focus. The 1D-SAFT images (Fig. 5b, middle column) show enhanced image quality along the y-axis direction outside the focal region, but no obvious improvement is observed along the x-axis because SAFT is conducted in the x-z plane. Note that the fibers along the x-axis outside the focal region seem to be diminished in the 1D-SAFT. This is because the improvement in the SNR along the y-axis is much greater than that along the x-axis. With 2D-SAFT adopted, the images become more homogenous compared with the 1D-SAFT (Fig. 5b, right column). The isotropic resolution is particularly essential when imaging point-like targets. For example, as shown in Fig. 5c, the dust of the carbon fiber (indicated by the white arrow), which can be approximated as a spherical target, displays a distorted shape (Fig. 5c, middle) in the 1D-SAFT image owing to the anisotropic lateral resolution of 1D-SAFT. As opposed, 2D-SAFT overcomes this limitation and retains the original shape of the target (Fig. 5c, right). However, 2D-SAFT has its limitation—the lateral resolution in 2D-SAFT is worse than the best performance of 1D-SAFT when the synthesis is performed perpendicular to the carbon located outside the focal region, as shown in Fig. 5b. This owes to the mismatch between the spherical wavefront concept of the 2D algorithm and the cylindrical wavefront of the carbon fiber, as described below.

To elaborate on the origin of this mechanism, Fig. 6 demonstrates the difference that 1D- and 2D-SAFT made on the lateral resolution of a cylindrical target placed perpendicular to the x-z plane. In Fig. 6a, Point B indicates the authentic signal of the cylindrical target’s edge, and A and C are the artifacts of B, generated as a result of the inherent signal blurring in AR-PAM. For the 1D-SAFT, SAFT was performed in the x-z plane on a pixel-by-pixel basis, and the artifacts of A and C were significantly suppressed after the application of SAFT+CF (see Figs. 3c, e and 6b, first row). For 2D-SAFT, SAFT+CW was performed in both the x-z and y-z planes for each pixel. Although the reconstruction results of the side lobes (such as A and C) were low in the x-z plane owing to the incoherence of the delayed signals (see Fig. 3c and e), the signals of the side lobes (A and C) increase after the signal summing in the y-z plane. This is due to the existence of a number of correlated signals of side lobes in the y-z plane generated by tubular-structured targets with a cylindrical wavefront. To be more specific, the distorted signals, indicated by the blue dashed line (including A and C) in Fig. 6a, exhibits an extension in the y-axis direction because the tubular target is placed along the y-axis. Therefore, the synthesis of artifacts (such as point A) in the y-z plane, as shown in Fig. 6c, leads to a constructive summation because the adjacent signals are highly in-phase. As a result, 2D-SAFT manifests points A and C with much higher values than those in 1D-SAFT, as depicted in Fig. 6b. This results in a wider full width at half maximum of the point spread function (PSF) for the target at point B in 2D-SAFT than in the 1D solution. The above description explains why 2D-SAFT shows a lower lateral image resolution along the B-scan direction than 1D-SAFT (Fig. 5b).

Fig. 6.

(a) A tubular object, such as a carbon fiber or blood vessel. Point B indicates the authentic signal of the cylindrical target’s edge; A and C are the artifacts of B, generated because of the signal blurring in AR-PAM. (b) Illustration of the relative magnitudes of PA signals between three points (A, B and C) after 1D- and 2D-SAFT are applied, respectively. (c) Synthesis of the correlated signals in both the x-z and y-z planes for the 2D-SAFT scheme.

Essentially, the occurrence of low lateral resolution in 2D-SAFT originates from the inconsistent wavefront between the 2D-SAFT concept (spherical wavefront) and the tubular object (cylindrical wavefront). As opposed, 1D-SAFT algorithm implies a spherical wavefronts concept and matches with tubular object. To summarize, the proposed 2D-based strategy helps minimize the anisotropic resolution feature exhibited in the 1D solution, but demonstrates a lower resolution for cylindrical targets such as vascular architecture, as summarized in Table 1. Interestingly, when the tubular targets are arranged along the diagonal directions (Fig. 5c), the resolution enhancement for carbon fibers is approximately equivalent between 1D- and 2D-SAFT because the SAFT is not optimal for either case. For the former, the synthesis direction is not perpendicular to the target direction. For the latter, as discussed previously, the cylindrical wavefront of the targets does not match the spherical wavefront in the 2D-based solution.

Table 1.

The comparison between different (representative) SAFT schemes.

		Algorithm description	Dimensions of improved lateral resolution	Achievable resolution (a)	Wave-shape concept	Processing speed	Suppress SNR at focus (b)
1D-SAFT+CF [56], [57]		Signals synthesized in one dimension (x-z or y-z)	1 (Anisotropic lateral resolution)	High (Comparable with resolution at focus)	Cylindrical wave	Fast	Yes (if without SIR)
2D-SAFT+CF [66]		Signals synthesized in two dimensions (x-z and y-z)	2 (Isotropic lateral resolution)	Medium (Less than resolution at focus)	Spherical wave		Yes (if without SIR)
A-SAFT +CF [68]	Tubular targets	Signals synthesized perpendicularly to each target’s orientation	2 (Isotropic lateral resolution)	High (Comparable with resolution at focus)	Cylindrical wave	Medium	Yes (if without SIR)
	Point-like (or circular) target		1(c) (Anisotropic lateral resolution)	High (Comparable with resolution at focus)			Yes (if without SIR)
SIR-based SAFT [70]		Transducer’s SIR used to weight contributions	Depends on its combination with 1D-, 2D-, or Adaptive-SAFT				No (Homogenous SNR achieved)
DMAS-SAFT [71]		Delay-multiply-and-sum used for beamforming	Depends on its implementation (in 1D-, 2D-, or Adaptive-SAFT manner)			Slow	Yes (if without SIR)

^(a)The best performance that could be achieved with each SAFT scheme. For 1D- and A-SAFT, the best resolution after reconstruction in the out-of-focus region is theoretically comparable with the original resolution at focus, thus achieving the depth-independent lateral resolution. 2D-SAFT shows a poorer performance compared to the 1D solution. ^(b) The SNR at the focal region is suppressed relative to the outside focal region if the SIR weight is not considered during the SAFT reconstruction. The weighing of SIR helps achieve a homogeneous SNR both far from and at the focus of the ultrasonic detector. ^(c) For point-like (or circular) targets, A-SAFT may lead to anisotropic lateral resolution, given that only one dimension synthesis is performed for a whole target’s shape when the target’s aspect ratio ≈ 1, as opposed to circular structured targets like vasculatures, where the synthesizing direction changes for each pixel based on the orientation of each branch of their network.

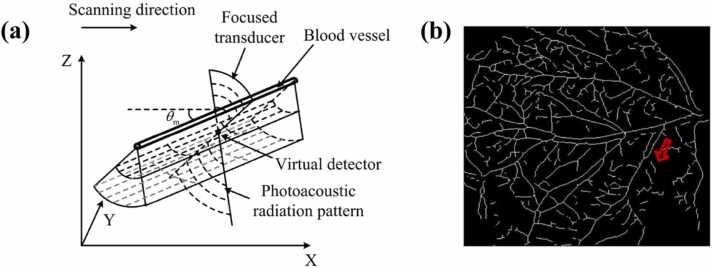
3.3. Adaptive-SAFT

In the complex in vivo environment, vascular architecture with different branches generally exhibits various directions. In such cases, 1D-SAFT leads to anisotropy in the lateral resolution. The 2D-based strategy helps minimize the resolution anisotropy, but provides a poorer performance in terms of resolution enhancement compared to the 1D solution. To address these challenges, the adaptive-SAFT (A-SAFT) [68] was developed, which allows SAFT to be automatically applied to each branch of the vascular network based on its orientation (Fig. 7a). Based on MAP images of the vasculature, a binary skeleton image (such as Fig. 7b) can be extracted, and the direction of each pixel is determined based on the linear fitting of the point and its consecutive surrounding points. According to the pre-determined directions, SAFT is performed in a plane perpendicular to the vessel branch (Fig. 7a),

$${\mathit{RF}}_{\mathit{SAFT}}\left(i,j,t\right)=\sum _{k=-N}^N\mathit{RF}\left(i+u,j+v,t-∆t_{\mathit{uv}}\right)$$ (7)

where $u=\left[\left|k\times \mathit{sin}{\theta }_m\right|\right]+1$, and $v=\left[\left|k\times \mathit{cos}{\theta }_m\right|\right]+1$; ${\theta }_m$ denotes the angle between the x-z plane and the direction of the vessel branch. The notation [□] signifies the nearest integer in the direction of negative infinity. Eq. (7) is analogous to Eq. (1) (1D-SAFT)—the synthesis is only performed in one dimension, as opposed to 2D-SAFT (Eq. (5)) where the signal summing is conducted in two dimensions (two summation notations) for each pixel. The difference between 1D- and A-SAFT is that the former is conducted in the x-z plane; thus, only two coordinates (i, t) are required to localize the pixel for synthesis, as shown in Eq. (1). In contrast, A-SAFT is performed in a plane perpendicular to the direction of the cylindrical targets; therefore, three coordinates (i, j, t) are needed to index each pixel.

Fig. 7.

(a) Illustration of the principle of adaptive-SAFT. (b) 2D skeleton image of a vascular network extracted from a MAP image. Figures reproduced with permission from [68] © The Optical Society.

To estimate the efficiency of this strategy, in vivo PA imaging of a vascular network was performed using different SAFT strategies for comparison, including 1D-, 2D-, and A-SAFT schemes. These solutions were performed in conjunction with CF weighting. Compared to the original image (Fig. 8a), the above three SAFT solutions exhibited noticeable enhancements of the lateral resolution and SNR (Fig. 8b–d). For a detailed analysis of the image quality improvements, three typical vessel orientations were particularly examined, with the outcomes interpreted as follows. For the direction along the x-axis, such as the vessel marked with the green rectangle, the above three strategies exhibit different efficacies in improving the lateral resolution. The decreasing order of their performances is evaluated as follows: Adaptive > 2D > 1D. Note that the 1D solution exhibits the worst performance because the SAFT was not conducted in that direction. For the direction along the y-axis, such as the vessel marked with the blue rectangle, Adaptive ≈ 1D > 2D. The A-SAFT and 1D-SAFT schemes show equivalent efficacies because the SAFT is implemented approximately in the same plane for both solutions. For the diagonal direction, such as the vessel marked with the red rectangle, Adaptive > 2D ≈ 1D. The 2D and 1D schemes are inferior to A-SAFT because neither is suitable for this situation (owing to the tubular-structured targets and diagonal direction, respectively), as demonstrated in Section 3.2. In summary, compared to 1D- and 2D-SAFT, A-SAFT enables images of blood vessels with better lateral resolution and retains the isotropic lateral resolution and SNR, overcoming the limitations of both 1D- and 2D-SAFT, as has been summarized in Table 1. Thus, A-SAFT is well suited for processing microvasculature imaging in AR-PAM. However, it should be mentioned that A-SAFT is developed based on cylindrical wavefront targets, and thus it may lead to image distortion when reconstructing spherical wavefront objects, given that only one-dimensional synthesis is applied for each pixel in A-SAFT. Note that in a complex in vivo environment, spherical wavefronts may coexist with cylindrical wavefronts, such as tumors, which are usually accompanied by vascular architectures. Therefore, more efforts should be made in the future to explore new methods to account for the diversity of target wavefronts, such that SAFT can be robustly applied to complex in vivo environments.

Fig. 8.

In vivo images of the vasculature of mice dorsal dermis. (a) Original PA image. (b) 1D-SAFT+CF image. (c) 2D-SAFT+CF image. (d) A-SAFT+CF image. Figures reproduced with permission from [68] © The Optical Society.

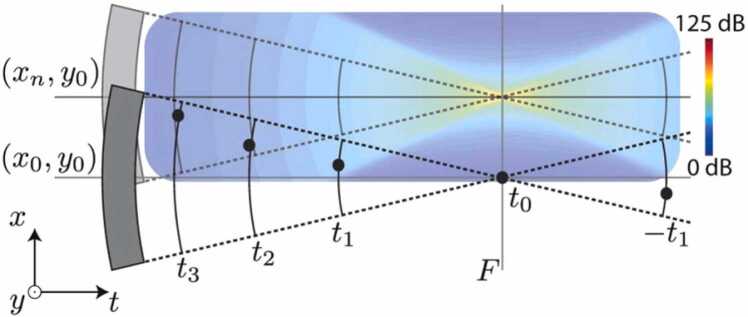
3.4. SIR-based SAFT

Another consideration of the SAFT algorithm lies in the weighting of the signal contribution at different depths. In SAFT, PA signals at each point are summed with those at neighboring points, but the number of adjacent scanlines (N) involved in the summation changes considerably with the depth. More specifically, N is minimized when the synthesized point locates at the focus. In contrast, N is large when the synthesized point is far from the focus of the UST, given that the angular extent of the UST leads to a large set of contributions to the summation, as depicted in Fig. 9. If signal summing is performed for a fixed region (i.e., N is independent of the depth in SAFT), a large number of invalid signals outside the detection zone are included in the summation, particularly in the region near the focal point. This decreases the SNR in the near-focus region. To avoid this phenomenon, the spatial impulse response (SIR) of a transducer was introduced to weight the spatial contributions in the SAFT algorithm [70]. The SIR defines the size of the sensitivity distribution of the focused ultrasound sensor in the horizontal direction at different depths, as depicted by the focal-cone geometric profiles in Fig. 9. To implement such spatial weighting in SAFT, a binary weighting mask ($W$) is applied to multiply the output of the conventional SAFT:

$${\mathit{RF}}_{\mathit{SAFT}}\left(i,t\right)=\sum _{j=-N}^N\mathit{RF}\left(i+j,t-∆t_j\right)W\left(i+j,t-∆t_j\right)$$ (8)

where the notation $W\left(i+j,\mathit{t}-∆t_j\right)$ indicates a binary contribution map of SIR, which equals 1 when the pixel ($i+j,\mathit{t}-∆t_j$) is within the focal cone (Fig. 9) and equals 0 elsewhere. Similarly, after considering the SIR weighting, the CF is modified as follows:

$$\mathit{CF}\left(i,t\right)=\frac{{\left|\sum _{j=-N}^N\mathit{RF}\left(i+j,t-∆t_j\right)W\left(i+j,t-∆t_j\right)\right|}^2}{N{{\sum }_{j=-N}^N\left|\mathit{RF}\left(i+j,t-∆t_i\right)W\left(i+j,t-∆t_j\right)\right|}^2}$$ (9)

Fig. 9.

Schematic illustration of the spatial impulse responses of a focused transducer. The focal-cone profile indicates the geometric focusing of the detector. Figure reproduced with permission from [70]. © The Optical Society.

(8), (9) indicate that SAFT and CF are performed for pixels located only within the SIR region, such that the final output signal (${\mathit{RF}}_{\mathit{SAFT}+\mathit{CF}}$) should be correctly rectified in the summing of adjacent A-lines. Note that the above solution portrays the SIR-based SAFT in one dimension for simplicity. For multi-dimensional SAFT accounting for SIR weighting, the algorithm can be easily extrapolated from (5), (6). More details can be found in Refs. [69], [70]. To demonstrate the efficacy of SIR weighing, Fig. 10a shows the simulated B-scan results of SAFT with and without considering the weighting function. For the case in which the SIR weighting is not accounted for, as displayed in Fig. 10a (2) and (4), the signal near the focus is lower than that outside the focus. As mentioned previously, this is because when spatial weighting is not considered (N is independent of the depth in SAFT), the number of invalid signals included in the region near the focus is greater than that outside the focal region. The invalid signals, which mostly come from background noises, are generally out-of-phase, thereby leading to a destructive summation in the calculation of the CF. According to Eq. (3) and Fig. 3e, this brings about a lower value of CF at the focus than outside the focal region, consequently giving rise to the mismatch in the SNR and resolution between locations outside and inside the focal region. As opposed, SIR-SAFT, as shown in Fig. 10a (3) and (5), can seamlessly rectify the signals at different depths, and provide a homogenous image in terms of lateral resolution and SNR at different depths.

Fig. 10.

(a) B-scan images (simulated data set) of nine targets (spheres) located at different depths from the focus. These include the sinogram (raw data), SAFT image, SIR+SAFT image, CF+SAFT image, and CF+SIR+SAFT image. Figure reproduced with permission from [70] © The Optical Society. (b) Hyperbolic function used as the binary weighting mask of SIR (red line) [75]. $a$ and $a_f$ are the half widths of the minimized and maximized acoustic spreading functions, respectively; $z_f$ represents the depth of the focal point (VD). Figure reproduced with publisher’s permission [75]. Copyright (2018) The JapanSociety of Applied Physics. (c) Linear function used as the binary weighting mask of SIR (black line). w is the width of the UST; $∆x$ indicates the scanning step of the UST between adjacent A-lines; $\mathrm{z}$ is the depth of the synthesized imaging point.

In Ref. [70], the zone applied for SAFT was determined by simulating the detector SIR using a software package (Field II). For simplification, other approaches have been proposed [72], [75] to delineate the SIR region (Fig. 10b and c). As shown in Fig. 10b, the contour of the angular sensitivity distribution is depicted using a hyperbolic function [75]:

$$x^2=a_f^2+\frac{z^2\left(a^2-a_f^2\right)}{z_f^2}$$ (10)

where $a$ and $a_f$ denote the half widths of the minimized and maximized acoustic spreading functions, respectively; $\mathrm{z}$ and $z_f$ are the depth of the synthesized imaging point and the depth of the focal point, respectively. Eq. (10) provides a criterion to determine whether an arbitrary point ($x_p$, $z_p$) should be involved in the SAFT, i.e., $x_p\le \sqrt{a_f^2+z_p^2\left({a^2-a}_f^2\right)/d_f^2}$. In addition, a further-simplified solution [72] uses a linear function (Fig. 10c) to account for N (the number of scanlines used for the summation) as a function of depth:

$$N=\frac{\left|z-z_f\right|}{z_f}\frac{w}{∆x}$$ (11)

where w is the transducer width, and $∆x$ represents the scanning step of the UST between adjacent A-lines. Eq. (11) indicates that pixels that should be involved in the signal summation are encompassed by the crossed area of the two solid black lines in Fig. 10c. The above approaches provide straightforward methods to account for SIR weighing, based on which the involvement of neighboring A-lines is tailored to reflect the SAFT results. However, more phantom and in vivo validations should be performed to examine these schemes with both computational efficiency and image quality taken into consideration. These efforts can help achieve homogeneous signals in terms of SNR and resolution both far from and at the focus of the ultrasonic detector, such that SAFT solutions can ultimately be employed in full three dimensions.

3.5. DMAS-based SAFT

For the synthesis of new A-lines, a beamforming algorithm is required. Generally, DAS is commonly used in SAFT because of its straightforward nature. However, as described in Section 3.1, DAS is a blind beamformer; it linearly combines the delayed A-lines for either the main lobes or side lobes [76], [77], [78], [79], [80], [81]. This linear treatment results in a high noise level and wide beam. To compensate for this blindness, various beamforming solutions and weighting mechanisms have been developed [82], [83], [84], [85], [86], [87], [88], [89], [90], [91], [92], [93], [94], [95], [96], [97]. One approach is the DMAS, which was first used for radar imaging applications [98], and then applied for PA tomography imaging [99], [100], [101], [102], [103], [104], [105], [106]. Recently, DMAS was introduced in the AR-PAM system [71], [72] to address the resolution degradation outside the focus. In contrast to the DAS algorithm, the delayed PA signals from the neighboring scanlines in the DMAS are combinatorially coupled and multiplied before summation. Therefore, the output of the DMAS is expressed as follows:

$${\mathit{RF}}_{\mathit{SAFT}}\left(i,t\right)=\sum _{i=1}^{N-1}\sum _{j=i+1}^N{s}_i\left(t\right)s_j\left(t\right)$$ (12)

where $s_i\left(t\right)$ indicates the delayed RF signals for an arbitrary scanline, which is a simplified version of $\mathit{RF}\left(i+j,\mathit{t}-∆t_j\right)$ in Eq. (1). The coupling operation in Eq. (12) can be interpreted as the extraction of spatial coherence information, which means that at each synthesized imaging point, the spatial cross-correlation is computed and emphasized along all of the scanlines. The nonlinear nature of DMAS enables the signals at the main lobes and side lobes to be weighted nonlinearly—signals at the main lobes are highly emphasized by Eq. (12) owing to their strong coherence, while signals at the side lobes are minimized because the artifacts and noises are generally out-of-phase. Consequently, a larger gap in PA amplitude between the main lobes and side lobes (or artifacts) is generated in the DMAS compared with the DAS; thus, better image contrast and resolution can be achieved. Note that Eq. (12) introduces dimensional mismatch because the PA signals are dimensionally squared. To compensate for this inconsistence, extra processing steps—a signed geometric mean to the coupled scanline signals—are added to the DMAS algorithm:

$${\hat{s}}_{ij}(t)=\frac{sign[s_i(t)s_j(t)]\sqrt{\left|s_i(t)s_j(t)\right|}}{\mathrm{Sign}\mathrm{preservation}\mathrm{Geometric}\mathrm{mean}}$$ (13)

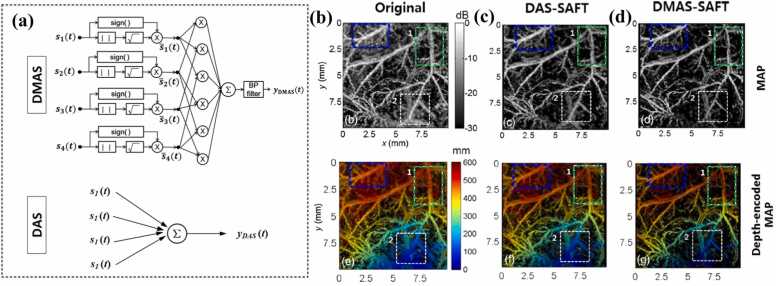
With the application of these additional procedures (Eq. (13)), the dimensionality of ${\hat{s}}_{\mathit{ij}}\left(t\right)$ can be made the same as that of $s_i\left(t\right)$ without losing its sign. Then, the output of the generated A-lines for DMAS is given as ${\mathit{RF}}_{\mathit{SAFT}}\left(i,t\right)=\sum _{i=1}^{N-1}\sum _{j=i+1}^N{\hat{s}}_{\mathit{ij}}\left(t\right)$. A schematic of the DMAS algorithm is presented in Fig. 11a. Note that direct current (DC) and harmonic components generally occur in the spectrum of ${\mathit{RF}}_{\mathit{SAFT}}\left(i,t\right)$, thus a bandpass (BP) filter needs to be applied to the output of the DMAS to attenuate the DC component and maintain the harmonic signals. Detailed information on the BP filter can be found in Ref. [71]. The proposed DMAS-based solution was validated experimentally through in vivo imaging of the vascular architecture (Fig. 11b–d). Compared with the original image (Fig. 11b) and DAS-based SAFT (DAS-SAFT) image (Fig. 11c), the image reconstructed using DMAS-based SAFT (DAMS-SAFT) showed better image quality in terms of the resolution and SNR (Fig. 11d), owing to the emphasis of the spatially coherent information. These outcomes verify the effectiveness of DMAS-SAFT for enhancing the coherent components along the scanlines by employing a spatial cross-correlation operation. Note that the algorithms (DMAS-SAFT and DAS-SAFT) shown in Fig. 11c and d are only carried out in one direction, thereby resulting in anisotropy in the lateral resolution. As shown in Fig. 11b–d, the vessel branch inclined to the x-axis (indicated by the blue dashed rectangle) exhibits a noticeably lower lateral resolution compared with the vessel branch along the y-axis (indicated by the green dashed rectangle).

Fig. 11.

(a) Schematic illustration of the DMAS algorithm (first row) in comparison with the DAS algorithm (second row). (b–d) PA images of a mouse abdomen reconstructed using different solutions: (b) original method; (c) DAS-SAFT image; (d) DMAS-SAFT image. The first row shows MAP images; the second row shows depth-encoded MAP images. Figures reproduced with publisher’s permission [71]. Copyright (2016) Society of Photo‑Optical Instrumentation Engineers (SPIE).

Although DMAS-SAFT provides higher SNR and lateral resolution than DAS-SAFT, it suffers a greater computational burden [71], [72] (Table 1). For example, to process one pixel with N scanlines, the DAS-SAFT requires only N summations (Fig. 11a, second row). In contrast, DMAS-SAFT requires $\left[\left(N^2-N\right)/2\right]$ multiplications and $\left[\left(N^2-N-2\right)/2\right]$ summations (Fig. 11a, first row). With the application of graphics processing unit (GPU) hardware [107], [108], the required processing time can be reduced. However, DMAS-SAFT still poses a high burden when applied in a multi-dimensional manner (Section 3.2) to address the anisotropy of the lateral resolution, or implemented in an A-SAFT fashion (Section 3.3) to tackle the wavefront mismatch. Therefore, computationally efficient implementations are required to reduce the computational cost and complexity and facilitate the robust application of DMAS-based SAFT.

3.6. Other SAFT-related and focal-depth expanding approaches

Other SAFT-related strategies, including the double stage (DS)-DMAS [72], the weighted-SAFT (W-SAFT) [60], SAFT-based 3D-deconvolution [67], and the frequency domain SAFT [58], [61], [69], have also been proposed to tackle the low image quality out-of-focus. The DS-DMAS [102], [109] is an extended version of the DMAS algorithm which weighs the calculations by using two stages of DMAS. More specifically, DS-DMAS firstly computes the column sum of the auto-covariance matrix and then employs the DMAS processing in the second stage, further emphasizing on the spatial coherence of received channel data [72]. Though DS-DMAS outperforms DMAS in terms of the resolution improvement and the artifact attenuation [72], [102], [109], DS-DMAS requires a higher computational cost owning to the double-stage procedure [72], [102]. More efforts should be made in future to boost the computational efficiency of the DS-DMAS solution.

W-SAFT [60] is an image formation approach specifically designed for the multiscale PAM—a transition from OR-PAM to AR-PAM. During the transition, the results obtained from a typical scanning PAM are not only influenced by the spatially-varying sensitivity field, but also the inhomogeneous light distribution of the imaged volume, as opposed to a pure AR-PAM system where the illumination was assumed homogenous. To tackle this challenge, W-SAFT was proposed to (1) restrict the voxel’s projection based on the light distribution as well as the FOV of the transducer, and (2) compensate for a moving and heterogeneous illumination distribution. Consequently, W-SAFT helps overcome the resolution degradation out-of-focus in the AR regime without influencing the lateral resolution in the OR regime [60].

The SAFT scheme has been incorporated with 3D-deconvolution for improving the spatial resolution in three dimensions [67]. In earlier studies, 3D-deconvolution algorithms [110] using depth-dependent PSFs were applied to improve both the lateral and axial resolution of AR-PAM, but the performance of the resolution enhancement was conducted only in the focal zone [110]. This restriction stem from the fact that the measured PSFs used for deconvolution at the focal zone differ from those outside the focus. Fortunately, SAFT approaches provide depth-independent PSFs. The combination of the SAFT algorithm helps 3D deconvolution achieve enhanced lateral and axial resolutions both in and outside the focal region [67].

Frequency-domain solutions using the Fourier reconstruction algorithm based on the SAFT concept have been proposed in previous studies [58], [61], [111], in which the ‘delay and sum’ algorithm was conducted in the frequency domain by compensating the phase shift (i.e., time-flight) between the transducer and the virtual detector. Though SAFT in the frequency-domain is principally mathematically equivalent to the time-domain, it has its own merits and limitations. Owing to the fast Fourier transform applied in this strategy, the frequency-domain SAFT shows potentials to reduce the computational cost and burden [58], [61], [111]. However, the frequency-domain SAFT has been reported to generate more reconstruction artifacts than time-domain solutions [112], [113]. Recently, a few studies [58], [61] has been proposed to deal with this specific issue.

To extend the focal region, low NA transducers could be employed but they would compromise the lateral resolution, owing to the tradeoff correlation between the focal depth and the spatial resolution. An alternative to SAFT solutions is to use the deep learning method [114], [115] for the improvement of the image resolution out-of-focus. Deep learning approaches use the results of high-resolution images at the focal region as the ground truth to enhance the out-of-focus results based on the neural network training. Compared with SAFT, deep learning approaches have both merits and disadvantages. The advantages stem from its independence of resolution improvement on the orientation of the sample [115], in contrast with 1D-SAFT in which only targets with orientations perpendicular to the synthetic direction can be well reconstructed. However, in the learning process, a large dataset (acquired images and their corresponding ground truth) is needed for both training, validation and testing [114], [115], as opposed to SAFT strategies where only the measured raw data is required.

4. Conclusions and outlook

AR-PAM is an important imaging modality that renders images with ultrasound resolution and extends the imaging depth beyond the optical ballistic regime. To achieve a high lateral resolution, a large NA of a focused transducer is usually applied for AR-PAM. However, AR-PAM fails to maintain its performance outside the focal region. Based on the concept of the synthetic aperture focusing technique (SAFT), a number of approaches have emerged to address this challenge, including 1D-SAFT, 2D-SAFT, A-SAFT, SIR-based solutions, and DMAS-based strategies. These schemes have shown progress in achieving depth-independent lateral resolution but have various limitations and challenges. This review systematically examines these SAFT-based mechanisms, highlights their essential principles, and underlines the merits and disadvantages of each approach. The origins of various SAFT-based solutions for dealing with focusing-related distortions are geometrically illustrated with detailed mathematical reasoning (2, 3). These analyses can help improve the understanding of the essence of different SAFT-based algorithms for AR-PAM.

The advantages and limitations of each SAFT-based approach originate from their corresponding reconstruction algorithms. 1D-SAFT is considered as a time-efficient approach but causes anisotropy in the lateral resolution. Multi-dimensional SAFT can achieve isotropic lateral resolution but shows inferior performance to the 1D scheme for reconstructing tubular targets such as vascular architecture, owing to the wavefront mismatch mechanism elaborated in Section 3. To date, the most promising algorithm for reconstructing microvasculature is A-SAFT, yet this method is only suitable for tubular-structured targets (cylindrical wavefronts). Given that cylindrical wavefronts may coexist with spherical wavefronts in in vivo environments, such as tumors that are usually accompanied by angiogenesis, effort should be made in the future to incorporate various structured imaging objects in the development of reconstruction algorithms. In addition, further studies are also required to boost the advancements in beamformers. Nonlinear beamforming strategies (e.g., DMAS and DS-DMAS) outperform linear strategies (e.g., DAS) in reducing artifacts and side lobes, but require advanced computational hardware and large image acquisition times owing to the computational complexity arising from the cross-correlation operation. The computational burdens become even greater if nonlinear approaches are used in a multi-dimensional manner to address the wavefront mismatch. Computationally efficient implementations are needed to allow nonlinear SAFT to be applied in a robust and time-efficient manner.

In addition to the aforementioned considerations, future improvements can be made to explore the advantages of both the adaptive feature (Section 3.3) and SIR weighting (Section 3.4). Combining these two approaches may enable SAFT solutions to be employed in a full three-dimensional manner, given that both isotropic resolution in the lateral plane (A-SAFT) and homogeneous resolution and SNR in the axial direction (both far from and at the UST focus (SIR-SAFT)) can be achieved simultaneously. To further improve the imaging quality, SAFT-based schemes can be implemented by incorporating existing approaches of resolution enhancement, such as structured illumination [116], [117], model-based approaches [47], [48], [49], [50], and frequency band filtering [118], [119]. While some of the combined merits have been explored in previous studies [59], [67], [75], further model validations and comprehensive mathematical analyses are required to reinforce these methods. More phantom and in vivo validations should be performed to examine these schemes with both computational efficiency and image quality taken into consideration. This will facilitate a robust performance of the SAFT-based reconstruction methodology and ultimately promote the in vivo applications of AR-APM.

Declaration of Competing Interest

The authors declare that there are no conflicts of interest.

Biographies

Rongkang Gao is an Associate Professor at SIAT, CAS. She received her Ph.D. degree from the University of New South Wales, Australia, 2018. She joined SIAT in November, 2018. Dr. Gao’s research focuses on nonlinear photoacoustic techniques and algorithm in photoacoustic imaging.

Qiang Xue is a guest student at SIAT, CAS. He received his bachelor degree from Northwest A&F University, 2020. His research interests focus on photoacoustic molecular imaging and the nano-drug delivery system.

Yaguang Ren is an Assistant Professor at SIAT, CAS. In 2018, she got the Ph.D. degree in bioengineering at the Hong Kong University of Science and Technology, Hong Kong, China. Her research interest includes the development of photoacoustic imaging, fluorescent microscope imaging and image processing.

Hai Zhang is a Chief Doctor at Ultrasound Image Department of Shenzhen People’s Hospital and a professor at the First Affiliated Hospital of Southern University of Science and Technology. He received his Master’s degree from Tongji Medical University, 1992. His research interests include the development of multifunctional photoacoustic nanoprobes and their applications in biomedical fields.

Liang Song is a Professor at SIAT, CAS and founding directors of The Research Lab for Biomedical Optics, and the Shenzhen Key Lab for Molecular Imaging. Prior to joining SIAT, he studied at Washington University, St. Louis and received his Ph.D. in Biomedical Engineering. His research focuses on multiple novel photoacoustic imaging technologies.

Chengbo Liu is a Professor at SIAT, CAS. He received both his Ph.D. and Bachelor degree from Xi'an Jiaotong University, each in 2012 in Biophysics and 2007 in Biomedical Engineering. During his Ph.D. training, he spent two years doing tissue spectroscopy research at Duke University as a visiting scholar. Now he is working on multi-scale photoacoustic imaging and its translational research.